引言
在工程结构分析中,计算结构动力响应具有重要意义.由于在实际工程问题中结构参数存在不确定性,结构动力响应与结构参数相关,所以需要考虑这些不确定性对结构系统的动力响应的影响. 传统研究不确定参数结构动力响应的方法大都基于概率统计模型.然而,不确定参数的概率统计信息并不总是足够的.在这种情况下,考虑将不确定参数用区间数进行描述,如果区间的上下界已知,那么就可以计算出结构动力响应范围.
在处理区间参数结构动力响应问题时,现有的区间分析方法局大多局限于一阶区间分析方法.基于直接动力学迭代与一阶泰勒展开,Qiu等[1, 2]提出了一种非概率分析方法来求解区间参数结构动力学响应范围.Chen等[3]和Qiu等[4]分别基于一阶矩阵摄动法与一阶参数摄动法提出了计算区间参数结构动力响应范围的方法.Ni等[5]基于模态叠加法与一阶摄动法研究了承受区间不确定载荷的结构动力响应问题.基于一阶泰勒展开法与区间数学,吴杰 等[6]将动力学响应区间优化问题转化为一个确定性优化问题.此问题优化的目标为动力响应的上界最小.Chen等[7]将基于一阶参数摄动的区间分析方法推广到结构振动鲁棒控制问题.邱志平等[8]将基于一阶泰勒展开的区间分析方法推广到复合材料层合梁自由振动问题.
虽然采用一阶区间分析方法可以对区间参数结构动力响应进行分析,但是当参数的不确定量稍大时,采用一阶区间分析方法对结构动力响应范围进行估计可能会失效. 所以需要考虑二阶区间分析方法.Qiu等[9]基于二阶泰勒展开与区间运算,对具有区间参数非线性结构动力响应范围问题进行了讨论.然而由于此方法涉及到区间运算,得到的结果可能对动力响应范围过分高估,使得这一方法失去实际的工程意义.
为了克服这个缺点,本文首先基于二阶摄动展开法得到采用结构参数描述的结构动力响应广义函数.然后通过求解此动力响应函数 的最大值与最小值,将结构动力响应范围的问题转化为箱型约束下的二次规划问题.接着采用基于对偶理论的DC算法(difference of convex functionsalgorithm)求解在箱型约束下二次规划问题的全局最优解[10].DC算法只涉及到内积计算,采用DC算法可以有效在多项式时间内求解在箱型约束下二次规划问题的全局最优解.这样可以在不引入过多计算量的情况下,避免了对动力响应范围的过分估计.最后通过数值算例,将本方法和其他区间分析方法进行比较,验证了本方法的精确性与有效性.
1 问题描述
n自由度结构系统的振动控制方程可以表示为
|
${ K x}(t)+{ C}\dot{ x}(t)+{ M}\ddot{ x}(t)={ F}(t)$
|
(1)
|
其中,,
K,M,C分别为结构的总体刚度矩阵、总体质量矩阵和总体阻尼矩阵;
x(
t),$\dot{ x} (t)$,$ \ddot {x} (t)$分别为结构结点位移向量、速度向量和加速度向量;${F}(t)$为时变的载荷向量. 通常结构刚度阵
k,质量阵
M,阻尼阵
C,载荷向量
F为结构参数向量 ${b} = (b_1 ,b_2 ,\cdots,b_p )$的函数,其中$p$为参数的个数. 显然结构动力响应
x(
t)也是参数向量$b$的函数.
K;M;F;C;x (
t)可以用
K (
b);
M (
b);
C (
b);
F (
b);
x (
t;b)来描述.如果结构参数
bk,k=1;2;…;
p是确定的,则系统的动力响应也是确定的.而在实际工程结构中,由于结构参数的不确定,可能会导致系统的动力响应存在不确定性.基于区间分析的思想,可以假设结构不确定参数${b_k} \in b_k^{\text{I}} = [\underline {{b_k}} ,\overline {{b_k}} ]$为区间参数(有界不确定参数). $b_k^{\rm I}$为区间数,$\underline{b_k },\overline {b_k } $分别是$b_k^{\rm I}$的下界和上界. 基于区间理论,$b_k $可以写为以下形式
|
$b_k=b^{\rm c}_k+\delta_k$
|
(2)
|
其中,$b_k^{\rm c} = 0.5(\underline{b_k } + \overline {b_k } )$为$b_k $的中值,${\delta _k} \in \delta _k^I = [ - \Delta {b_k},\Delta {b_k}]$为$b_k $的不确定性部分,$\Delta b_k = 0.5(\overline {b_k } - \underline{b_k}),k = 1,2,\cdots,p$. 那么基于一阶泰勒展开,${ K}({ b}),{ M}({ b}),{ C}({ b}),{ F}({ b}),{ x} (t,{ b})$可以近似表示为
|
$\left. \begin{gathered}
K(b) = {K_0} + \Delta K = {K_0} + \sum\limits_{k = 1}^p {{K_k}{\delta _k}} \hfill \\
C(b) = {C_0} + \Delta C = {C_0} + \sum\limits_{k = 1}^p {{C_k}{\delta _k}} \hfill \\
M(b) = {M_0} + \Delta M = {M_0} + \sum\limits_{k = 1}^p {{M_k}{\delta _k}} \hfill \\
F(t,b) = {F_0}(t) + \Delta (t) = {F_0}(t) + \sum\limits_{k = 1}^p {{F_k}(t){\delta _k}} \hfill \\
\end{gathered} \right\}$
|
(3)
|
其中,${ K }_0 = { K }({ b }^{\rm c})$是${ K }$的确定部分,$\Delta { K }$是${ K}$的不确定部分,$ { K }_k = \dfrac{\partial { K }({ b }^{\rm c})}{\partial b_k }$为与$b_k$相关联的矩阵. 以上其他项具有与${ K }_0 $和$\Delta { K }$相类似的定义.当考虑不确定性时,振动系统的控制方程可以重新写为
|
$\begin{gathered}
({K_0} + \Delta K)x(t) + ({C_0} + \Delta C)\dot x(t) + \hfill \\
({M_0} + \Delta M)\ddot x(t) = {F_0}(t) + \Delta F(t) \hfill \\
\end{gathered}$
|
(4)
|
由于不确定参数向量${ b } = [b_1 ,b_2 ,\cdots,b_p]$限定在区间${B^{\text{I}}} = [b_1^{\text{I}},b_2^I, \cdots ,b_p^{\text{I}}]$内,同时动力响应${ x }(t)$是与$b_k ,k = 1,2,\cdots,p$相关的函数,所以${ x}(t)$也在一定的区间内进行变化. 即$ { x }(t) \in { x }^{\rm I} (t) = [\underline{ x} (t),\bar{ x} (t)]$,其中
|
$\left. \begin{gathered}
\bar x(t) = {G_{\max }}\left\{ {x(t):Kx(t) + C\dot x(t) + M\ddot x(t) = F(t)} \right\} \hfill \\
\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} (t) = {G_{\min }}\left\{ {x(t):Kx(t) + C\dot x(t) + M\ddot x(t) = F(t)} \right\} \hfill \\
\end{gathered} \right\}$
|
(5)
|
通常很难求解区间参数结构动力响应范围${ x}^{\rm I}(t)$,需要采用其他近似方法来估计动力响应的范围.
2 基于二阶摄动展开法求解区间参数结构
2.1 采用摄动法求解区间参数结构响应
基于摄动理论,可以假设控制方程(4)的解可以表示为以下形式
|
$x(t) = {x_0}(t) + {x_1}(t) + {x_2}(t) + {x_3}(t) + \cdots $
|
(6)
|
这里${ x}_0 (t)$为动力响应${ x}(t)$的名义值,满足以下条件
|
${K_0}{x_0}(t) + {C_0}{\dot x_0}(t) + {M_0}{\ddot x_0}(t) = {F_0}(t)$
|
(7)
|
${x_1}(t)$表示当动力系统参数存在不确定量 $\delta_k$,$k = 1,2,\cdots,p$时的动力响应的一阶小量; ${x}_2 (t)$表示动力响应的二阶小量;式(6)中其他项以此类推. 设$\Delta { x}_0 (t) = { x}(t) - { x}_0(t)$. 将${ x}(t) = { x}_0 (t) + \Delta { x}_0 (t)$ 代人方程(4)中,可以得到
|
$\begin{gathered}
({K_0} + \Delta K)\Delta {x_0}(t) + ({C_0} + \Delta C)\Delta {{\dot x}_0}(t) + \hfill \\
({M_0} + \Delta M)\Delta {{\ddot x}_0}(t) = {F_1}(t) \hfill \\
\end{gathered} $
|
(8)
|
其中
|
$\begin{gathered}
{F_1}(t) = \Delta F(t) - (\Delta K{x_0}(t) + \Delta C{{\dot x}_0}(t) + \Delta M{{\ddot x}_0}(t)) = \hfill \\
\sum\limits_{k = 0}^p {{\delta _k}({F_k}(t) - {K_k}{x_0}(t) - {C_k}{{\dot x}_0}(t) - {M_k}{{\ddot x}_0}(t))} \hfill \\
\end{gathered} $
|
(9)
|
忽略高阶小量,一阶动力响应小量的控制方程为
|
${K_0}{x_1}(t) + {C_0}{\dot x_1}(t) + {M_0}{\ddot x_1}(t) = {F_1}(t)$
|
(10)
|
基于线性叠加理论,${x_1}(t)$可以表示为线性组合形式
|
${x_1}(t) = {\text{ }}\sum\limits_{k = 1}^p {{\delta _k}{x_{1k}}(t)} $
|
(11)
|
其中,${x_{1k}}\left( t \right)$满足
|
$\begin{gathered}
{K_0}{x_{1k}}(t) + {C_0}{{\dot x}_{1k}}(t) + {M_0}{{\ddot x}_{1k}}(t) = \hfill \\
{F_k}(t) - ({K_k}{x_0}(t) + {C_k}{{\dot x}_0}(t) + \hfill \\
{M_k}{{\ddot x}_0}(t)),k = 1,2,\cdots ,p \hfill \\
\end{gathered} $
|
(12)
|
采用同样的方法,${\text{x(t)}}$可以分解为如下形式
|
$x(t) = {x_0}(t) + {x_1}(t) + \Delta {x_1}(t)$
|
(13)
|
式中,$\Delta { x}_1 (t)$是${ x}(t)$与${ x}_0 (t) + { x}_1 (t)$之间的差异.然后将方程(13)代入到方程(4)中,可以得到动力响应的二阶小量的控制方程
|
${K_0}{x_2}(t) + {C_0}{\dot x_2}(t) + {M_0}{\ddot x_2}(t) = {F_2}(t)$
|
(14)
|
其中
|
$\begin{gathered}
{F_2}(t) = - (\Delta K{x_1}(t) + \Delta C{{\dot x}_1}(t) + \Delta M{{\ddot x}_1}(t)) = \hfill \\
- \sum\limits_{k = 1}^p {{\delta _k}({K_k}{x_1}(t) + {C_k}{{\dot x}_1}(t) + {M_k}{{\ddot x}_1}(t))} = \hfill \\
- \sum\limits_{k = 1}^p {\sum\limits_{l = 1}^p {{\delta _k}{\delta _l}({K_k}{x_{1l}}(t) + {C_k}{{\dot x}_{1l}}(t) + {M_k}{{\ddot x}_{1l}}(t))} } \hfill \\
\end{gathered} $
|
(15)
|
同理${x_2}(t)$可以表示为如下的线性组合形式
|
${x_2}(t) = {\text{ }}\sum\limits_{k = 1}^p {\sum\limits_{l = 1}^p {{\delta _k}{\delta _l}{x_{2kl}}(t){\text{ }}} } $
|
(16)
|
${x_{2kl}}(t)$满足
|
$\begin{gathered}
{K_0}{x_{2kl}}(t) + {C_0}{{\dot x}_{2kl}}(t) + {M_0}{{\ddot x}_{2kl}}(t) = \hfill \\
- ({K_k}{x_{1l}}(t) + {C_k}{{\dot x}_{1l}}(t) + {M_k}{{\ddot x}_{1l}}(t)),\hfill \\
k,l = 1,2,\cdots ,p \hfill \\
\end{gathered} $
|
(17)
|
余下的动力响应小量可以采用同样的方法求得. 对于实际的工程问题,二阶摄动即可提供足够的计算精度. 在考虑结构参数在名义值处存在不确定量时,基于二阶摄动展开法的结构动力响应广义表达式为
|
$x(t) = {x_0}(t) + {\text{ }}\sum\limits_{k = 1}^p {{\delta _k}{x_{1k}}(t)} + \sum\limits_{l = 1}^p {{\delta _k}{\delta _l}{x_{2kl}}(t)} $
|
(18)
|
当采用摄动法对于带有不确定参数的结构进行动力分析时,久期项问题,即在摄动计算中引入了不应存在的数值共振,是引人关注的问题之一. 文献 [11] 研究表明当结构阻尼比与结构固有频率较大时,久期项效应对一阶(二阶)摄动响应影响较小.本文所采用的二阶摄动展开方法适用于以上情况.当结构阻尼比较小,就会有久期项现象发生,此时可以用阻带滤波的方式来抑制久期项影响[12],可以推导出与方程(18)形式相同的结构动力响应区间广义表达式.
2.2 基于优化分析得到动力响应的界限
在进行不确定分析时,往往最关心的是结构响应的界限. 本文基于优化思想,将区间参数不确定结构动力响应(18)的界限(全局最大最小值)问题转化下列低维优化问题进行求解
|
$\left. \begin{gathered}
\bar x(t) = {x_0}(t) + {G_{\max }}(\sum\limits_{k = 1}^p {{\delta _k}{x_{1k}}(t)} + \sum\limits_{k = 1}^p {\sum\limits_{l = 1}^p {{\delta _k}{\delta _l}{x_{2kl}}(t)} } ) \hfill \\
\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} (t) = {x_0}(t) + {G_{\min }}(\sum\limits_{k = 1}^p {{\delta _k}{x_{1k}}(t)} + \sum\limits_{k = 1}^p {\sum\limits_{l = 1}^p {{\delta _k}{\delta _l}{x_{2kl}}(t)} } ) \hfill \\
\end{gathered} \right\}$
|
(19)
|
其中不确定参数$\delta _k $限定在区间$ - \Delta b_k \leqslant \delta_k \leqslant \Delta b_k$,$k = 1,2,\cdots,p$内. 在第$i$个自由度上的分量的上下界为
|
$\begin{gathered}
{{\bar x}_i}(t) = {x_{i,0}}(t) + {G_{\max }}(\sum\limits_{k = 1}^p {{\delta _k}{x_{i,1k}}(t)} + \sum\limits_{k = 1}^p {\sum\limits_{l = 1}^p {{\delta _k}{\delta _l}{x_{i,2kl}}(t)} } \hfill \\
{\text{s}}.{\text{t}}.\; - \Delta {b_j} \leqslant {\delta _j} \leqslant \Delta {b_j},j = 1,2,\cdots ,p \hfill \\
{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_i}(t) = {x_{i,0}}(t) + {G_{\min }}((\sum\limits_{k = 1}^p {{\delta _k}{x_{i,1k}}(t)} + \sum\limits_{k = 1}^p {\sum\limits_{l = 1}^p {{\delta _k}{\delta _l}{x_{i,2kl}}(t)} } ) \hfill \\
{\text{s}}.{\text{t}}.\; - \Delta {b_j} \leqslant {\delta _j} \leqslant \Delta {b_j},j = 1,2,\cdots ,p \hfill \\
\end{gathered} $
|
(20)
|
优化问题(20)可以转化为以下箱型约束下二次型全局最优问题
|
$\begin{gathered}
{G_{\min }}({G_{\max }}){x_{i,0}}(t) + f(Y) = {x_{i,0}}(t) + \frac{1}{2}{Y^{\text{T}}}AY + {d^{\text{T}}}Y \hfill \\
{\text{s}}.{\text{t}}. - \Delta {b_j} \leqslant {y_j} \leqslant \Delta {b_j} \hfill \\
\end{gathered} $
|
(21)
|
其中,向量${ d } = [x_{i,11} (t),x_{i,12} (t),\cdots,x_{i,1p} (t)]$,实对称矩阵${ A}$中元素$a_{kl}= x_{i,2kl} (t) + x_{i,2lk} (t)$,$k,l = 1,2,\cdots,p$.
由于问题的复杂性,带有箱型约束的二次规划问题的全局最优解很难被有效求解.虽然可以采用如粒子群方法
[13]、移动渐进法
[14]等对初始条件设定不是很敏感的鲁棒优化算法求解二次规划问题(21).但是这些方法不能保证求解到的最优值为全局最优解,只能大概率得到全局最优解.
DC算法是Pham Dinh Tao[15]于1988年提出的基于局部最优性条件和DC对偶理论的算法.由于该方法只涉及到内积计算,计算速度相对很快,得到了广泛的关注与应用.采用DC算法可以有效在多项式时间内求解在箱型约束下二次规划问题的全局最优解[10].基于DC算法求解箱型约束下的二次规划问题的方法,主要有3个组成部分:(1)基于DC算法求解包含箱型可行域的外接超球约束下二次规划问题的全局最优值作为原问题全局最优值的下界[16](以求解全局最小值为例);(2)基于DC算法求解箱型约束下的二次规划问题的全局最优值的上界;(3)配合恰当的分支定界方法不断分割可行域得到全局最优解.那么结构动力响应的上界与下界分别为
|
$\left. \begin{gathered}
{{\bar x}_i}(t) = {x_{i,0}}(t) + {G_{\max }}(f(Y)),\;\;i = 1,2,\cdots ,n \hfill \\
3mm{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_i}(t) = {x_{i,0}}(t) + {G_{\min }}(f(Y)),\;\;i = 1,2,\cdots ,n \hfill \\
\end{gathered} \right\}$
|
(22)
|
式中,$G_{\max}(f({ Y}))$,$G_{\min}(f({ Y}))$为基于DC算法求解二次规划问题(21)的全局最大值与最小值.
3 本文方法与其他区间分析方法的对比
在这一章中,对基于区间运算的一阶和二阶区间分析方法进行介绍,并将它们与本文所提供方法进行对比. 基于区间扩张原理与方程(18),可得区间参数结构动力响应范围的一阶区间估计[1]
|
${x^{\text{I}}}(t) = {x_0}(t) + _{k = 1}^p\delta _k^{\text{I}}{x_{1k}}(t)$
|
(23)
|
和区间参数结构动力响应范围的二阶区间估计
[9]
|
${x^{\text{I}}}(t) = {x_0}(t) + \sum\limits_{k = 1}^p {\delta _k^{\text{I}}{x_{1k}}(t) + \sum\limits_{k = 1}^p {\sum\limits_{l = 1}^p {\delta _k^{\text{I}}\delta _l^{\text{I}}{x_{2kl}}(t)} } } $
|
(24)
|
对于任意区间数$a^{\rm I} = [\underline{a},\bar {a}]$和$b^{\rm I} = [\underline{b},\bar {b}] \in I(R)$,区间运算的法则为
|
$\left. \begin{gathered}
{a^I} + {b^I} = [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} ,\bar a + \bar b] \hfill \\
{a^I} - {b^I} = [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} - \bar b,\bar a - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b}] \hfill \\
{a^I} \times {b^I} = [\min \{ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} \bar b,\bar a\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} ,\bar a\bar b\} ,\max \{ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} \bar b,\bar a\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b} ,\bar a\bar b\}] \hfill \\
{a^I}/{b^I} = [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} ,\bar a] \times [1/\bar b,1/\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b}],0 \notin {b^I} \hfill \\
\end{gathered} \right\}$
|
(25)
|
那么基于区间运算与方程(23),可以得到区间参数结构一阶参数摄动响应的上界与下界
|
$\begin{gathered}
{{\bar x}_i}(t) = {x_{i,0}}(t) + \sum\limits_{k = 1}^p {\Delta {b_k}\left| {{x_{i,1k}}(t)} \right|} ,\;\;I = 1,2,\cdots ,n \hfill \\
{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_i}(t) = {x_{i,0}}(t) - \sum\limits_{k = 1}^p {\Delta {b_k}\left| {{x_{i,1k}}(t)} \right|} ,\;\;i = 1,2,\cdots ,n \hfill \\
\end{gathered} $
|
(26)
|
其中 $\Delta b_k = 0.5(\overline {b_k } - \underline{b_k })$,$k = 1,2,\cdots,p$.
基于区间运算与方程(24),可以得到区间参数结构二阶参数摄动响应的上界与下界
|
$\begin{gathered}
{{\bar x}_i}(t) = {x_{i,0}}(t) + _{k = 1}^p\Delta {b_k}\left| {{x_{i,1k}}(t)} \right| + \hfill \\
\sum\limits_{k = 1}^p {\sum\limits_{l = 1}^p {\Delta {b_k}\Delta {b_l}\left| {{x_{i,2kl}}(t)} \right|} } ,\;\;i = 1,2,\cdots ,n \hfill \\
{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }_i}(t) = {x_{i,0}}(t) - _{k = 1}^p\Delta {b_k}\left| {{x_{i,1k}}(t)} \right| - \hfill \\
\sum\limits_{k = 1}^p {\sum\limits_{l = 1}^p {\Delta {b_k}\Delta {b_l}\left| {{x_{i,2kl}}(t)} \right|} } ,\;\;i = 1,2,\cdots ,n \hfill \\
\end{gathered}$
|
(27)
|
当区间参数的不确定量较小时,基于区间运算的一阶区间分析方法可以有效地对区间参数结构动力响应范围进行估计.但是当 参数的不确定量稍大时,采用一阶区间分析方法对结构动力响应范围进行估计可能会失效.同时由于基于区间运算的二阶区间分析方法涉及到区间运算,得到的结果可能对动力响应范围过分高估,使得采用此方法得到结果失去实际的工程意义.因为本文方法考虑到了在动力响应函数(18)中的各项的参数的耦合关系,所以采用基于优化分析的二阶摄动展开法得到的结果更接近于真实的动力响应范围.
4 算例
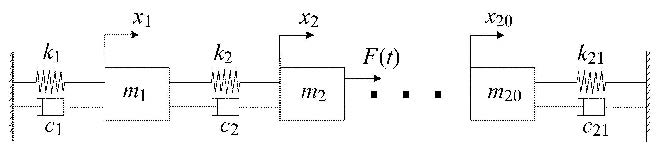
算例1 考虑如图1所示的有阻尼20自由度弹簧质量块系统. 设$m_1$,$m_2$,$\cdots$,$m_{20} = m$,$k_1$,$k_2$,$\cdots$,$k_{21} = k$,其中$m$和$k$为不确定区间参数,$m \in m^I =[0.97,1.03]$ kg,$k \in k^I = [97,103]$ N/m. 系统阻尼为瑞利阻尼,与刚度阵和质量阵相关的阻尼系数均为0.01. 在质量块2处施加$F(t) = 2\sin (\pi + t) - 10\left| {x_2 } \right|x_2 + 20x_2^3 $的非线性载荷. 各个质量块的初始位移为$x_1 (0),x_2 (0)\cdots,x_{20} (0) = 0.05$.
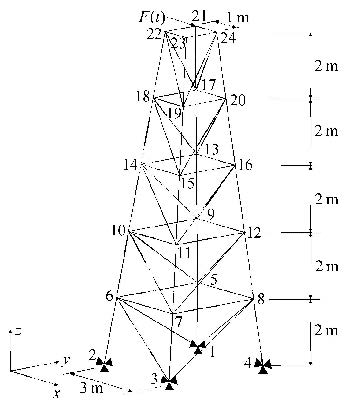
算例2 如图5所示60杆空间桁架,各个杆的截面积均为0.001 m$^{2}$,材料阻尼比为0.05,杆的密度和弹性模量为不确定区间参数,分别属于区间 $[0.95\rho ,1.05\rho]$和$[0.9E,1.1E]$,其中,$E = 2.5\times 10^{10}$ Pa,$\rho =2 300$ kg/m$^{3}$. 在结点21处施加沿$X$轴方向的激励$F(t) = 1 000a_1\left| {\sin (10\pi t)}\right| + 600a_2\left| {\sin (9\pi t)} \right|$,其中$a_1 \in [0.98,1.02],a_2 \in[0.98,1.02]$为不确定区间参数.
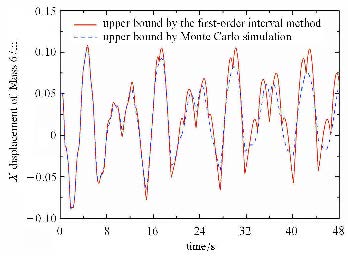
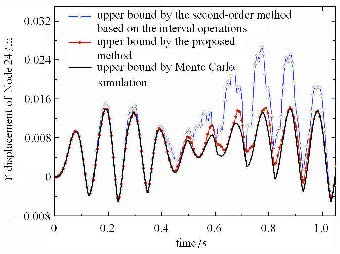
如图2和图6所示对于算例1和算例2,采用一阶区间分析方法与蒙特卡洛方法得到上界差异较大.采用一阶区间分析方法得到上界 不能包络采用蒙特卡洛方法得到的上界.由于采用蒙特卡洛方法得到的界限是实际动力响应范围的低估近似. 也就是说当参数的不确定量稍大时,采用一阶区间分析方法对结构动力响应范围进行估计可能会失效.
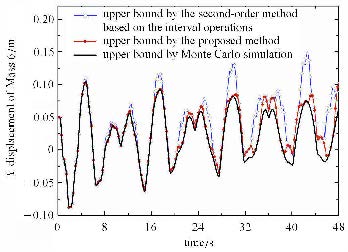
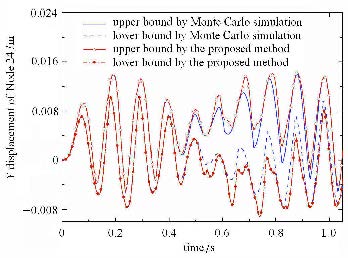
如图3和图7所示,采用基于区间运算的二阶区间分析方法与本文所提出的基于优化分析的二阶区间分析方法得到区间参数结构动力响应上界都可以包络采用蒙特卡洛方法得到动力响应上界.但采用基于区间运算的二阶区间分析方法得到的结构动力响应上界被过分高估. 而如图3,图4,图7,图8所示,本文方法可以有效对区间参数结构动力响应范围进行估计.
5 结论
当区间参数的不确定量较小时,采用忽略动力响应二阶摄动小量的一阶区间分析方法对区间参数结构动力响应范围进行估计,可以得到较高精度的结果. 但当区间参数的不确定量稍大时,动力响应二阶摄动小量对动力响应的贡献不可忽略.此时采用一阶区间分析方法得到结构动力响应范围的精度可能会较差,所以需要考虑二阶区间分析方法.本文基于二阶摄动展开法与DC算法,提出一种估计区间参数结构动力响应范围的方法:将求解区间参数结构动力响应范围问题转化为求解序列低阶箱型约束下的二次规划问题.采用这种方法可以在不引入过多计算量的情况下,避免区间运算带来的对结构动力响应的过高估计,得到更接近于实际的不确定结构的响应范围.通过数值算例,将本方法和基于区间运算的区间分析方法、蒙特卡洛方法进行相比,可以验证本方法的有效性与精确性.
参考文献
| [1] |
Lyon RH, Maidanik G. Power flow between linearly coupled oscillators. J Acoust Soc Am, 1962, 34(5): 632-639
|
| [2] |
游进, 孟光, 李鸿光. 声振系统中高频能量流分析法研究进展. 振动与冲击, 2012, 31(11): 62-69 (You Jin, Meng Guang, Li Hongguang. Review of mid-to-high frequency energy flow analysis method for vibro-acoustic systems. J Vib Shock, 2012, 31(11): 62-69 (in Chinese))
|
| [3] |
Lyon RH, Maidanik G. Statistical methods in vibration analysis. AIAA J, 1964, 2(6): 1015-1024
|
| [4] |
Lafont T, Totaro N, LeBot A. Review of statistical energy analysis hypotheses in vibroacoustics. Proc R Soc A, 2013, 470(2162)
|
| [5] |
Nefske DJ, Sung SH. Power flow finite element analysis of dynamic systems: basic theory and application to beams. J Vib Acoust, 111(1): 94-100
|
| [6] |
Wohlever JC, Bernhard RJ. Mechanical energy flow models of rods and beams. J Sound Vib, 1992, 153(1): 1-19
|
| [7] |
Cho PE, Bernard RJ. Energy flow analysis of coupled beams. J Sound Vib, 1998, 211(4): 593-605
|
| [8] |
张猛, 陈花玲, 祝丹晖 等. 高频弯曲振动梁的随机参数能量有限元分析. 西安交通大学学报, 2013, 47(11) (Zhang Meng, Chen Hualing, Zhu Danhui, et al, Stochastic parameter energy finite element analysis of high-fequency flexural vibration beam. Journal of Xi'an Jiaotong University, 2013, 47(11) (in Chinese))
|
| [9] |
韩敬永. 基于统计能量及混合法的航天器有效载荷声振环境预示.[硕士论文]. 哈尔滨:哈尔滨工业大学, 2012 (Hang Jingyong. Research on vibro-acoutic environment prediction of space craft pay load based on statistical energy and hybrid method.[Master Thesis]. Harbin: Harbin Institute of Technology, 2012 (in Chinese))
|
| [10] |
Renno JM, Mace BR. Calculation of reflection and transmission coefficients of joints using a hybrid finite element/wave and finite element approach. J Vib Sound, 2013, 332(9):2149-2164.
|
| [11] |
姚煜中, 周俊, 饶柱石等. 充液管道能量传递途径及减振分析. 噪声与振动控制, 2011, 31(5): 13-16 (Yao Yuzhong, Zhou Jun, Rao Zhushi, et al. Analysis and assessment of vibration energy transmission of fluid-filled pipelines. Noise and Vibration Control, 2011, 31(5): 11-16 (in Chinese))
|
| [12] |
Goyder, HGD, White RG. Vibrational power flow from machines into built-up structures, part I: introduction and approximate analyses of beam and plate-like foundations. J Sound Vib, 1980, 68(1): 59-75
|
| [13] |
Miller, DW, von Flotow AH. A travelling wave approach to power flow in structural networks. J Sound Vib, 1989, 128(1): 145-162
|
| [14] |
Lase Y, Ichchou MN. Energy flow analysis of bars and beams: theoretical formulations. J Sound Vib, 1996, 192(1): 281-305
|
| [15] |
Mead DJ. Free wave propagation in periodically supported, infinite beams. J Sound Vib, 1970, 11(2): 181-197
|
| [16] |
Mead DJ. Wave propagation in continuous periodic structures: research contributions from Southampton, 1964-1995. J Sound Vib, 1996, 190(3): 495-524
|
| [17] |
von Flotow AH. Disturbance propagation in structural networks. J Sound Vib, 1986, 106(3):433-450
|
| [18] |
von Flotow AH. Traveling wave control for large space craft structures. Journal of Guidance, Control, and Dynamics, 1986, 9(4): 462-468
|
| [19] |
von Flotow AH.The acoustic limit of control of structural dynamics. In: Atluri SN, Amos AK, eds. Large Space Structures: Dynamics and Control. Berlin Heidelberg: Springer, 1988. 213-237.
|
| [20] |
程伟, 褚德超, 王大均. 梁传播的固有特性. 力学学报, 1997, 29(2): 175-181 (Cheng Wei, Zhu Dechao, Wang Dajun. Natural characteristics of wave propagation in beam. Acta Mechanica Sinica, 1997, 29(2): 175-181 (in Chinese))
|
| [21] |
朱桂东, 郑钢铁, 邵成勋. 框架结构模态分析的行波方法. 宇航学报, 1999, 20(3): 1-6 (Zhu Guidong, Zheng Gangtie, Shao Chengxun. Modal analysis for frame structures via traveling wave approach. Journal of Astronautics, 1999, 20(3): 1-6 (in Chinese))
|
| [22] |
田艳. 航天器空间桁架结构的振动特性研究.[硕士论文]. 哈尔滨: 哈尔滨工业大学, 2012 (Tian Yan. Study on vibration characteristic for space truss structure of space craft.[Master Thesis]. Harbin: Harbin Institute of Technology, 2012 (in Chinese))
|
| [23] |
周国良, 叶欣, 李小军 等. 结构动力分析中多点激励问题的研究综述. 世界地震工程, 2009, 25(4): 25-32 (Zhou Guoliang, Ye Xin, Li Xiaojun, et al. Renew on dynamic analyses of structures under multi-support excitation. World Earthquake Engineering, 2009, 25(4): 25-32 (in Chinese))
|
| [24] |
Pavić G. Vibration damping, energy and energy flow in rods and beams: governing formulae and semi-infinite systems. J Sound Vib, 2006, 291(3-5): 932-962
|
| [25] |
李思简. 大学工程力学手册. 上海: 上海交通大学出版社, 2000. 337-337 (Li Sijian. Handbook of University Engineering Mechanics. Shanghai: SJTU Press, 2000. 337-337 (in Chinese))
|
SECOND-ORDER PARAMETER PERTURBATION METHOD FOR DYNAMIC STRUCTURES WITH INTERVAL PARAMETERS
Li Qi

, Qiu Zhiping, Zhang Xudong
School of Aeronautic Science and Technology, Beijing University of Aeronautics and Astronaut ics, Beijing 100191, China
Fund: The project was supported by the 111 Project (B07009),the National Natural Science Foundation of China (11372025,11002013),the Defense Industrial Technology Development Program (A0820132001,JCKY2013601B) and Aeronautical Science Foundation of China (2012ZA51010).
Abstract: When considering the problem of the dynamic responses of structures with interval parameters, previous interval analysis methods are mostly restricted to its first-order. But if the uncertainties of the parameters are fairly large, the response region obtained using the first-order interval analysis method would fail to contain the real region of the dynamic response of uncertain structures. Therefore, the second-order analysis method should be considered. However, the second-order analysis method relating to operations of interval may result in an exorbitantly overestimated dynamic response region, which makes the result useless for practical engineering problems. To circumvent this drawback, firstly the general function of the dynamic response of structures in terms of structural parameters is obtained based on the second-order parameter perturbation method. Then via solving the maximum and minimum of the function, the problem of determining the bounds of the dynamic response of uncertain structures is changed into a series of low dimensional box constrained quadratic problems, and these box constrained quadratic programming problems can be solved using the DC algorithm (difference of convex functions algorithm) effectively. The proposed method can avoid the exorbitant overestimate of the dynamic response region of uncertain structures, while does not introduce much more computational expense. A numerical example is used to illustrate the accuracy and the efficiency of the proposed method when comparing with other methods.
Key words:
interval parameters second-order parameter perturbation method dynamical response of uncertain structures quadratic problems DC algorithm


 2015, Vol. 47
2015, Vol. 47