2. 湖南科技大学, 工程力学系, 湘潭 411201
纤维增强聚合物复合材料的强度和韧性,极大地依赖于纤维/基体界面的粘结.单纤维拔出实验是理解和量化纤维/基体粘结行为最常 用的方法之一[1, 2].在拔出实验中,单纤维受拉伸载荷,从周围基体中拔出,纤维拔出的宏观过程,由细观尺度的界面粘结行为所决定[3].
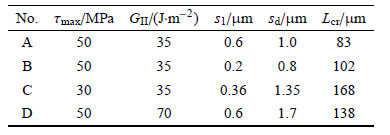
科克斯(Cox)模型[4]是分析纤维复合材料界面剪切应力分布最流行的解析方法.科克斯模型的实质是,假设界面剪切应力与界面切向位移(纤维和基体之间的相对位移)成线性关系,界面以此关系在基体和纤维之间传递载荷.使用科克斯模型分析单纤维拔出过程时[5, 6],纤维端处的界面剪切应力不断增加,达到界面的剪切强度时,界面出现脱粘而失效,如图1(a)所示.

|
图 1 界面的科克斯 模型(a)和弹性-软化内聚力模型(b) Fig.1 (a) the Cox model and (b) elastic-softening cohesive zone model for the interface |
文献[7]在钨丝/铜基体的纤维拔出实验中发现:脱粘时,施加在纤维上的载荷与纤维的埋入长度成直线关系 $F_{\rm d}=2\pi rL\tau $ (其中${{F}_{d}}$是脱粘载荷,$\tau$是界面剪切应力,$r$是纤维半径,$L$是纤维埋入长度),也称为K-$\!$-T公式.这是一种可以假设沿界面有均匀剪切应力分布的情况,由此认为,脱粘时整个界面处于屈服的状态.用此式所求出的界面剪切应力,作为平均界面剪切强度[8, 9],用来衡量纤维/聚合物界面的粘结程度.
从单相材料的实验观察中已知,例如聚合物和陶瓷,在拉伸和剪切状态,材料有两种主要失效模式,即屈服(有时包含硬化)和脆性断裂. 屈服是连续和稳定的过程,脆性断裂则是瞬间的、伴随载荷急剧下降的过程.若纤维/基体间的界面也可能表现出以上两种行为,则科克斯模型所模拟的界面属于脆性断裂,K-$\!$-T公式所假设的界面属于屈服失效.
文献[10, 11]所提出的内聚力模型(cohesive zonemodel),以作用在界面上的应力(正应力或剪切应力)和位移不连续(纤维和基体间的张开位移或切向滑移位移)之间的关系,表达界面的粘结行为.如,在弹性-软化内聚力模型中,如图1(b),随单调增加的界面位移,界面应力首先线性增加,直到界面裂纹萌生时的$\tau_{\max}$,这一过程与科克斯模型的本质是相同的;随后是软化部分,在该部分界面损伤累积,粘结程度逐渐减弱,直到界面裂纹生成位移$s_{\rm d}$时,界面脱粘.弹性-软化内聚力模型在描述纤维/聚合物的界面行为中被广泛采用[12, 13, 14, 15].
使用以上任何界面模型,结合实验确定出的表征界面粘结程度的量,通常足以区分界面粘结的强弱.然而,界面本身的失效机 理仍旧没有被完全理解,脆性断裂、屈服或软化,是完全不同的界面失效过程.微观的界面粘结与宏观的界面行为之间存在一定的关系.已有广泛的关于单纤维拔出载荷-位移关系的研究,即:界面的宏观行为.其中大量的工作集中在基于科克斯模型、K-$\!$-T模型和弹性-软化内聚力模型[16, 17, 18]上.而将科克斯模型与K-$\!$-T假设相结合,形成的弹性-塑性屈服内聚力模型[19, 20],其所对应的纤维拔出界面宏观行为的分析还少见报道.因此,本文使用弹性-塑性屈服内聚力模型,用解析法模拟纤维从聚合物中的拔出过程,分析不同长度的纤维表现出的界面宏观响应的特征,以及界面粘结参数对界面宏观行为的影响.
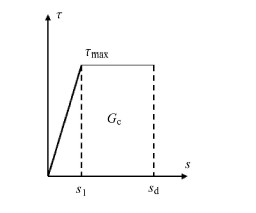
1 计算模型 1.1 内聚力模型本文采用弹性-塑性屈服内聚力模型,如图2所 示. 在单纤维拔出实验中,界面的受力主要以剪切方式为主,因 此,界面的剪切应力$\tau$,和界面两侧的切向相对位移$s$之间的关系可由下式表达
|
图 2 界面的弹性-塑性模型 Fig.2 The elastic-plastic model for the interface |
| $\tau =\left\{ \begin{align} & ks,\ \ \ \ \ 0\le s\le {{s}_{1}} \\ & {{\tau }_{\max }},\ \ \ {{s}_{1}}<s\le {{s}_{d}} \\ & {{\tau }_{f}},\ \ \ \ \ s>{{s}_{d}} \\ \end{align} \right.$ | (1) |
其中,$k = \dfrac{\tau _{\max } }{s_1 }$是图2中上升线段的斜率;$\tau _{\max }$是界面裂纹萌生所对应的应力,称为界面的剪切强度;$s_1 $和$s_{\rm d}$分别是界面裂纹萌生位移和界面裂纹生成位移; $\tau_{f}$是脱粘后界面的摩擦剪切应力. 图2中曲线所包围的面积代表了II型断裂模式下的界面断裂韧性,该值为$G_{\rm II}=\tau_{\max} \Big(s_{\rm d} - \dfrac{1}{2}s_1 \Big)$.
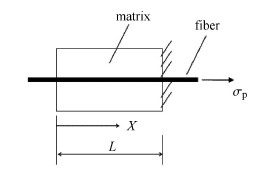
1.2 控制方程纤维拔出实验中,半径为$r_{\rm f}$ 的圆柱形单根纤维置于有效半径为$r_{\rm m}$的圆柱形基体中心,纤维的埋入长度为$L$,基体顶部受约束,沿纤维方向$x$,$\sigma_{\rm p}$施加在纤维自由端,几何模型如图3所示. 令$u_{\rm f} (x)$表示纤维的轴向位移,由于基体受到约束,则界面的位移$s$为
|
图 3 单纤维拔出几何模型 Fig.3 Schematic diagram of single fiber pull-out |
| $s(x) = u_{\rm f} (x) $ | (2) |
沿$x$方向,界面剪切应力$\tau $与纤维的轴向应力$\sigma _{\rm f} $之间的平衡关系为
| $\frac{d{{\sigma }_{f}}\left( x \right)}{dx}=\frac{2}{{{r}_{f}}}\tau \left( x \right) $ | (3) |
假设纤维为线弹性变形,则
| ${{\sigma }_{\text{f}}}(x)={{E}_{\text{f}}}\frac{d{{u}_{\text{f}}}(x)}{dx}$ | (4) |
其中$E_{\rm f} $为纤维的弹性模量.
对方程(2)中的界面位移进行微分,并结合 式(3)和式(4),得到关于界面剪切应力和界面位移的二阶微分方程
| $\frac{{{d}^{2}}s}{d{{x}^{2}}}-\frac{2\tau }{{{E}_{\text{f}}}{{r}_{\text{f}}}}=0$ | (5) |
细观上,界面上的任意一点,随着位移的增加会处于不同的状态:$s \leqslant s_1 $时,为弹性状态(E);$s_1 < s\leqslant s_{\rm d} $时,为塑性屈服状态(P);$s > s_{\rm d} $时,为 脱粘状态(D).宏观上,在纤维的拔出过程,整个界面会经历不同的阶段:弹性阶段(E)、弹性+屈服阶段(E+P)、弹性+屈服+脱粘阶段(E+P+D)、屈服阶段(P)、屈服+脱粘阶段(P+D)、脱粘阶段(D).
1.3 拔出过程各阶段的解将式(1)所表达的界面内聚力关系,代入控制方程(5)中,根据边界条件,和/或不同界面状态之间的连续性条件,可得到相应阶段的解.
(1) E 阶段
当施加在纤维自由端的载荷较小时,界面上的所有点都处于弹性的状态. 此时沿纤维的各点的位移、应力分别为
| $\left. \begin{array}{*{35}{l}} \begin{align} & {{s}^{\text{e}}}(x)=\frac{{{\sigma }_{\text{p}}}}{{{E}_{\text{f}}}\lambda }\frac{\cosh (\lambda x)}{\sinh (\lambda L)} \\ & \sigma _{\text{f}}^{\text{e}}(x)={{E}_{\text{f}}}\lambda {{s}^{e}}(x)\frac{\sinh \left( \lambda x \right)}{\cosh (\lambda x)} \\ \end{align} \\ \end{array} \right\} $ | (6) |
其中,$\lambda ^2 = \dfrac{2k}{E_{\rm f} r_{\rm f}}$;上标e表示变量所适用的范围为界面的弹性状态.
(2) E+P 阶段
随着载荷的增加,纤维自由端的位移达到界面裂纹萌生位移$s_1$后,部分界面开始进入屈服的状态. 界面的弹性、屈服区域的解分别为
| $\left. \begin{matrix} {{s}^{\text{e}}}(x)=\frac{{{s}_{1}}\cosh \left( \lambda x \right)}{\cosh \left[ \lambda (L-a) \right]} \\ \sigma _{\text{f}}^{\text{e}}(x)=\frac{{{E}_{\text{f}}}\lambda {{s}_{1}}\sinh \left( \lambda x \right)}{\cosh \left[ \lambda \left( L-a \right) \right]} \\ \end{matrix} \right\} $ | (7a) |
| $\left. \begin{align} & {{s}^{\text{p}}}(x)=\frac{1}{2}M{{x}^{2}}+\{\lambda {{s}_{1}}\tanh \left[ \lambda \left( L-a \right) \right]- \\ & M\left( L-a \right)\}x+\{{{s}_{1}}+\frac{1}{2}M{{\left( L-a \right)}^{2}}- \\ & \left( L-a \right)\lambda {{s}_{1}}\tanh \left[ \lambda \left( L-a \right) \right]\} \\ & \sigma _{\text{f}}^{\text{p}}(x)={{E}_{\text{f}}}Mx+{{E}_{\text{f}}}\{\lambda {{s}_{1}}\tanh \left[ \lambda \left( L-a \right) \right]- \\ & M\left( L-a \right)\} \\ \end{align} \right\}$ | (7b) |
其中,$M = \dfrac{2\tau _{\max } }{E_{\rm f} r_{\rm f} }$,$a$表示界面屈服的长度,上标p表示屈服区域的解.
(3) E+P+D 阶段
当纤维自由端的位移大于界面裂纹生成位移$s_{\rm d} $时,部分界面出现脱粘,脱粘后的界面受到摩擦阻力$\tau _{\rm f} $的作用. 此时界面的弹性、屈服、脱粘3部分的解为
| $\left. \begin{align} & {{s}^{\text{e}}}(x)=\frac{{{s}_{1}}\cosh (\lambda x)}{\cosh [\lambda (L-{{a}_{\text{d}}}-d)]} \\ & \sigma _{\text{f}}^{\text{e}}(x)=\frac{{{E}_{\text{f}}}\lambda {{s}_{1}}\sinh (\lambda x)}{\cosh [\lambda \left( L-{{a}_{\text{d}}}-d \right)]} \\ \end{align} \right\}$ | (8a) |
| $\left. \begin{align} & {{s}^{\text{p}}}(x)=\frac{1}{2}M{{x}^{2}}+\{\lambda {{s}_{1}}\tanh [\lambda (L-{{a}_{\text{d}}}-d)]- \\ & M(L-{{a}_{d}}-d)\}x+ \\ & \{{{s}_{1}}-(L-{{a}_{d}}-d)\lambda {{s}_{1}}\tanh [\lambda \left( L-{{a}_{\text{d}}}-d \right)]+ \\ & \frac{1}{2}M{{(L-{{a}_{\text{d}}}-d)}^{2}}\} \\ & \sigma _{\text{f}}^{\text{p}}(x)={{E}_{\text{f}}}\{Mx+\lambda {{s}_{1}}\tanh \left[ \lambda (L-{{a}_{\text{d}}}-d) \right]- \\ & M(L-{{a}_{\text{d}}}-d)\} \\ \end{align} \right\}$ | (8b) |
| $\left. \begin{align} & {{s}^{\text{d}}}(x)=\frac{1}{2}N{{x}^{2}}+\left[ (M-N)(L-d)+C \right]x+ \\ & [{{s}_{\text{d}}}-(M-\frac{1}{2}N){{(L-d)}^{2}}-C(L-d)] \\ & \sigma _{\text{f}}^{\text{d}}(x)={{E}_{f}}\left[ Nx+(M-N)(L-d)+C \right] \\ \end{align} \right\}$ | (8c) |
其中,$C = \lambda s_1 \tanh [\lambda (L - a_{\rm d} - d)] - M(L - a_{\rm d} - d)$;$N =\dfrac{2\tau _{\rm f} }{E_{\rm f} r_{\rm f} }$;$a_{\rm d}$是此阶段的屈服长度;$d$表示脱粘界面的长度;上标d表示适用于脱粘区域的解.
(4) P 阶段
和 E+P+D 阶段不同的是,当纤维的埋入长度不足时,在拔出过程,界面不会出现 E+P+D 的阶段,而是直接从 E+P 阶段,随着弹性区域的消失而进入 P 阶段,此时的解为
| $\left. \begin{array}{*{35}{l}} \begin{align} & {{s}^{\text{p}}}(x)=\frac{1}{2}M{{x}^{2}}+D \\ & \sigma _{\text{f}}^{\text{p}}(x)={{E}_{\text{f}}}Mx \\ \end{align} \\ \end{array} \right\} $ | (9) |
其中,$s_1 \leqslant D \leqslant \Big(s_{\rm d} - \dfrac{1}{2}ML^2\Big)$.
在纤维埋入端位移达到界面裂纹萌生位移时,即:$s^{\rm p} (0) = D = s_1$,同时,纤维自由端位移达到界面裂纹生成位移,即$s^{\rm p} (L) = s_{\rm d} $,此时纤维的埋入长度定义为临界长度,用$L_{\rm cr} $表示,则有如下关系:$s_{\rm d} =\dfrac{1}{2}ML_{\rm cr}^2 + s_1 $,于是
| $L_{\rm cr} = \left[{\dfrac{2\left( {s_{\rm d} - s_1 } \right)}{M}}\right]^{\tfrac{1}{2}} $ | (10) |
因此,只有纤维长度$L \leqslant L_{\rm cr} $时,拔出过程才会出现 P 阶段.
(5) P+D 阶段
纤维埋入端位移达到界面裂纹萌生位移后,界面上的弹性区域消失,界面成为屈服+脱粘的阶段,两区域的解分别为
| $\left. \begin{align} & {{s}^{\text{p}}}(x)=\frac{1}{2}M{{x}^{2}}+[{{s}_{\text{d}}}-\frac{1}{2}M{{(L-{d}')}^{2}}] \\ & \sigma _{\text{f}}^{\text{p}}(x)={{E}_{\text{f}}}Mx \\ \end{align} \right\}$ | (11a) |
| $\left. \begin{align} & {{s}^{\text{d}}}(x)=\frac{1}{2}N{{x}^{2}}+[(M-N)(L-{d}')]x+ \\ & [{{s}_{\text{d}}}-(M-\frac{1}{2}N){{(L-{d}')}^{2}}] \\ & \sigma _{\text{f}}^{\text{d}}(x)={{E}_{\text{f}}}[Nx+(M-N)(L-{d}')] \\ \end{align} \right\}$ | (11b) |
$d'$表示此阶段的界面脱粘长度. 对纤维长度$L \leqslant L_{\rm cr} $的情况,$0 \leqslant d'\leqslant L$;对纤维长度$L > L_{\rm cr} $的情况,$L - L_{\rm cr} \leqslant d' \leqslant L$.
(6) D 阶段
界面的屈服区域完全消失后,沿纤维的全部界面均脱粘,纤维在拔出时只受界面摩擦阻力的作用,此时的解为
| $\left. \begin{array}{*{35}{l}} \begin{align} & {{s}^{\text{d}}}(x)=\frac{1}{2}N{{x}^{2}}+{{s}_{\text{d}}} \\ & \sigma _{\text{f}}^{\text{d}}(x)={{E}_{\text{f}}}Nx \\ \end{align} \\ \end{array} \right\} $ | (12) |
根据1.3节拔出过程界面各阶段的解,可得到纤维自由端的载荷与位移的关系,以及脱粘时的载荷与纤维埋入长度的关系. 为了得到理论的预测,取纤维的半径和弹性模量分别为3.75 $μ $m和230 GPa;假设界面参数为:$\tau_{\max}=50$ MPa,$s_{1}=0.6 μ$m,$s_{\rm d}=1.0 μ $m,则$G_{\rm n}=35$ J/m$^{2}$. 根据式(10),计算出临界纤维长度为:$L_{\rm cr}=83 μ $m.
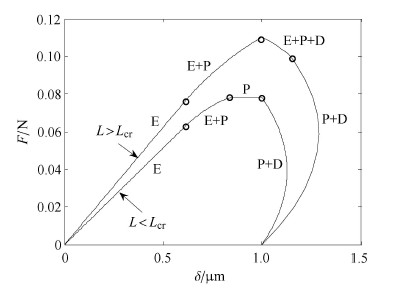
2.1 长、短纤维拔出时的界面宏观行为两种纤维长度$L<L_{\rm cr}$和$L>L_{\rm cr}$的拔出载荷$F$-$\!$-$\!$位移 $\delta $ 曲线见图4. 由图4可见,两种长度的载荷-位移曲线在形状上有明显的区别. 当纤维埋入长度$L > L_{\rm cr}$时,纤维从基体中拔出,依次经历 E,E+P,E+P+D,P+D 和 D 的阶段;对纤维埋入长度$L < L_{\rm cr}$,则按 E,E+P,P,P+D 和 D 的顺序,纤维从基体中拔出. 对$L > L_{\rm cr}$的情况,界面脱粘前(即 E+P+D阶段前)的曲线斜率,以及载荷-位移曲线的峰值载荷,均大于$L < L_{\rm cr}$曲线中的值.在没有摩擦力影响下,各曲线的峰值载荷均等于脱粘载荷. 界面出现脱粘后,即 P+D 和 E+P+D阶段,两种情况的拔出载荷,都呈下降的趋势.
|
图 4 两种纤维埋入长度的载荷-位移曲线 Fig.4 Force versus displacement for two fiber embedded length |
图5为理论的脱粘载荷 $F_{\rm d} $与纤维埋入长度 $L $的关系. $F_{\rm d}$-$L$曲线由两部分组成,当纤维埋入长度 $L< L_{\rm cr}$时,脱粘载荷随纤维埋入长度线性增加(图5中oa段),在这一范围内,脱粘出现的瞬间,所对应的界面状态为界面的全部屈服;当纤维埋入长度$L> L_{\rm cr}$后,脱粘载荷随纤维埋入长度缓慢增加,增加幅度较小且很快近似为常数(曲线中ab段),这表明,当纤维埋入长度超过临界长度后,长度的增加对脱粘载荷的影响很小,可用临界长度所对应的脱粘载荷近似表示.

|
图 5 脱粘载荷-纤维埋入长度曲线 Fig.5 Debonding force versus fiber embedded length |
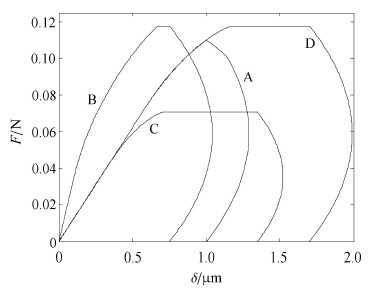
界面粘结参数会改变临界纤维长度,及纤维拔出载荷-位移曲线的形状.本节选择了4组界面粘结参数,列于表1,其中,A 组 作为参照组; B 组的界面剪切强度,$\tau_{\max}$,和断裂韧性,$G_{\rm II}$,均与 A 组相同; C 组的 $\tau _{\max}$降低,$G_{\rm II}$保持不变; D组的 $\tau_{\max}$保持不变,$G_{\rm II}$增加. 对相同的纤维埋入长度$L =100μ$m,4组参数所对应的拔出载荷-位移曲线在图6中分别表示为 A,B,C 和 D.
| 表 1 界面的参数 Table 1 Interfacial parameters |
|
图 6 界面参数对载荷-位移曲线的影响 Fig.6 The influences of interfacial parameters on the force-displacementcurve |
图6中,A和B 两曲线比较: A 曲线为$L > L_{\rm cr}$的情况,B 曲线为$L < L_{\rm cr}$的情况;由于 A 组的界面裂纹萌生位移,$s_{1}$,和界面裂纹生成位移,$s_{\rm d}$,均大于 B 组的值,较小的$s_{1}$使$k$值增大,提高了 B 上脱粘出现前的曲线斜率,使界面脱粘载荷增加. A 和D 两曲线比较: $\tau_{\max}$相同、$k$值不变时,A和D 曲线在脱粘出现前的斜率不变;通过增加$s_{\rm d}$使$G_{\rm II}$增加一倍,则 D 曲线为$L < L_{\rm cr}$的情况,界面脱粘载荷有所提高. 另外,通过同时增加$s_{1}$和$s_{\rm d}$,使界面的$G_{\rm II}$从B组到D组增加一倍时,由于$k$值的减小,使脱粘载荷降低,而$G_{\rm II}$值的增加,使脱粘载荷增加,二者的影响抵消,B和D 两组界面的脱粘载荷相同. A和C 两曲线比较:$G_{\rm II}$相同,$\tau_{\max}$降低,并保持$k$值不变时,$s_{1}$值的降低、$s_{\rm d}$值的增大,使 C 曲线为$L < L_{\rm cr}$的情况,且曲线有明显降低的峰值载荷或脱粘载荷.
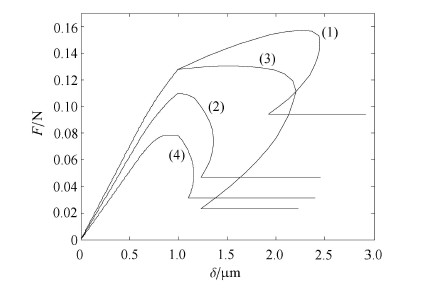
载荷-位移曲线上的脱粘载荷与峰值载荷之间的关系,是由纤维的埋入长度和脱粘后界面的摩擦应力大小所决定.此处 选择了不同纤维埋入长度与界面摩擦应力相组合的4种情况,分别是:(1) $L =200 μ $m,$\tau_{\rm f}=20$ MPa;(2) $L =100 μ $m,$\tau_{\rm f} =20$ MPa;(3) $L =200 μ $m,$\tau_{\rm f}=10$ MPa;(4) $L =65 μ $m,$\tau_{\rm f} =20$ MPa.4种情况下的载荷-位移曲线分别用(1),(2),(3),(4)表示,见图7.由图7可知,当界面摩擦应力相同时(曲线(1)、(2)和(4)),纤维的埋入长度越长,曲线的峰值载荷越大,并在某一长度后,出现峰值载荷大于脱粘载荷;当纤维埋长相同时(曲线(1)和(3)),界面摩擦应力增大,不影响界面的脱粘载荷,但会在某一摩擦应力值后,导致峰值载荷大于脱粘载荷.因此,界面脱粘后,使峰值载荷大于脱粘载荷,不仅需要界面有较高的摩擦应力,还需要纤维有较长的埋入长度.
|
图 7 $L$和 $\tau_{\rm f}$对载荷-位移曲线的影响 Fig.7 The influences of $L$ and $\tau_{\rm f}$ on the force-displacement curve |
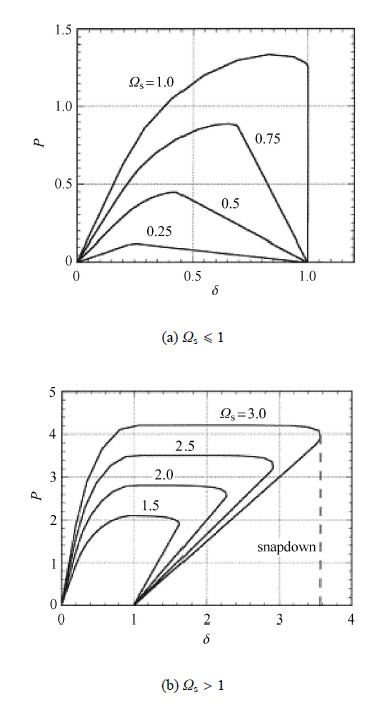
文献[16]使用解析法,假设界面为双线性弹性-软化内聚力行为,分析了纤维拔出的宏观响应.该分析没有考虑脱粘后界 面摩擦的影响,见图8,因此将其结果与图4进行比较. 图8中$\varOmega_{\rm s} \leqslant1$对应的是短纤维的拔出,$\varOmega _{\rm s} >1$对应长纤维.
|
图 8 纤维拔出载荷-位移曲线, (a)短纤维,(b)长纤维[16] Fig.8 Force versus displacement of fiber pull-out for (a) short fiber andfor (b) long fiber[16] |
文献[16]的分析指出,对$\varOmega _{\rm s} \leqslant 1$,纤维拔出时界面的弹性+软化+脱粘、软化+脱粘过程不会发生,整个界面直接从弹性+软化进入到全部软化状态;在全部 软化过程,载荷随界面末端位移增加而线性增加(图8(a)). 而对弹性-塑性屈服模型,对$L < L_{\rm cr}$短纤维的情况,界面依 次经历弹性、弹性+塑性、全部塑性、塑性+脱粘过程. 在全部塑性过程,载荷随末端位移增加而保持不变,在曲线上表现为水平的一段.
使用弹性-软化模型,对$\varOmega _{\rm s}>1$,界面依次经历弹性、弹性+软化、弹性+软化+脱粘、软化+脱粘过程. 在弹性+软化+脱粘过程,载荷随位移的增加而保持不变,在力-位移曲线上为水平的一段;在随后的软化+脱粘过程,位移回缩,直至界面裂纹生成位移值,同时载荷随之线性下降到零(图8(b)). 而使用弹性-塑性屈服模型,对$L > L_{\rm cr}$情况,界面依次经历弹性、弹性+塑性、弹性+塑性+脱粘、塑性+脱粘过程.由于不考虑界面脱粘后的摩擦作用,载荷在弹性+塑性阶段达到峰值;在塑性+脱粘过程末,位移回缩到界面裂纹生成位移值,载荷下降到零,与弹性-软化模型结果相同.
2.5 理论与实验的比较一般为确定界面参数,需要将理论的与实验的单纤维拔出载荷-位移曲线比较获得[21, 22]. 本文将模拟的界面宏观响应与碳纤维/环氧树脂的典型实验结果[19]进行了比较. 界面参数由如下步骤确定:由实验拔出曲线上脱粘后的形状,判断界面没有明显摩擦,因此忽略摩擦对结果的影响;实验曲线有平台阶段,则属于短纤维拔出;较短的平台段表明界面参数$s_{1}$和$s_{\rm d}$接近;实验载荷-位移曲线上脱粘点对应的位移即为参数$s_{\rm d}$;根据 式(6)中应力和位移的关系知,界面参数$k$影响弹性阶段的斜率,通过不断取值 $\tau_{\max}$,$s_{1}$并试算,确定与实验曲线相匹配的$k$值(计算$k$值的参数$\tau_{\max}$和$s_{1}$不是唯一的);根据 式(10)计算临界长度,用$L\leqslant L_{\rm cr}$的条件,缩小$\tau_{\max}$和$s_{1}$的取值范围.
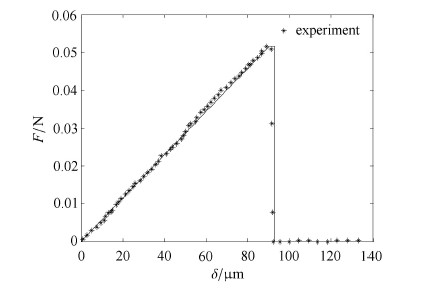
得到的一组界面参数: $\tau_{\max}=82$ MPa,$\tau_{\rm f} =0$,$s_{1} =90 μ $m,$s_{\rm d} =93 μ$m,合理地表达了实验结果,如图9所示. 图9中界面全部屈服阶段(平台段)较短,一是由于整个界面长度(纤维埋入长度)仅40 $μ $m,较短,二是从界面参数来看,($s_{\rm d}-s_{1})/s_{1}=3{\%}$,界面屈服程度低,说明界面有以脆性断裂方式失效的倾向.
|
图 9 理论与实验的载荷-位移曲线的比较 Fig.9 Comparisons between theoretical and experimental results offorce-displacement curve |
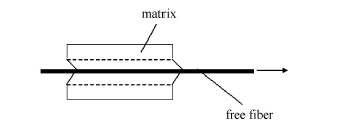
虽然理论的曲线与实验的数据非常吻合,但界面断裂韧性$G_{\rm II}= 3 936$ J/m$^{2}$,而文献中常见的碳纤维/环氧界面的断 裂韧性多数在1 500 J/m$^{2}$以内[8, 18],相比较,此处界面断裂韧性值偏高,原因可能如下:一方面,实验中纤维埋入长度$L =40 μ$m,峰值载荷(即脱粘载荷)所对应的位移大约为90 $μ$m,此值远大于纤维的埋入长度.用较大的位移值确定出的$s_{\rm d}$偏大,这是造成理论界面断裂韧性值偏高的主要原因;另一方面,实验的位移值,可能是以下因素共同构成的:(1)埋入纤维相对于其附近基体的位移,即理论计算出的位移;(2)未被基体包裹的自由纤维(见图10),在轴向拉伸作用下所产生的位移;(3)由加载刀片所控制的纤维和其附近的基体共同组成的整体(图10中虚线所示),相对于外围基体的位移,这种位移在有限元模拟微脱粘实验[19]中明显存在.由于未从实验中得到自由纤维长度,以及加载刀片之间的距离,因此,理论中没有考虑第(2)和(3)两点因素的影响.
|
图 10 纤维拔出变形示意图 Fig.10 Schematic diagram of the deformation in fiber pull-out process |
(1)将经典科克斯和K-$\!$-T界面模型相结合,假设界面为弹性-塑性屈服内聚力行为,用解析法分析单纤维的拔出过程,确定临界长度,定量区分出长、短纤维及其在拔出过程的特征及区别. 当纤维的埋入长度大于、小于临界长度时,纤维的拔出过程、拔出载荷-位移曲线的形状均不同.
(2)纤维埋入长度小于临界长度时,界面的脱粘载荷与纤维的埋长成正比;纤维埋入长度超过临界长度后,界面的脱粘载荷近似为常数,可用临界长度所对应的脱粘载荷近似表示.
(3)增加界面的剪切强度和断裂韧性、减小界面裂纹萌生位移,均能提高界面的脱粘载荷.
(4)在无界面摩擦应力影响下,拔出载荷-位移曲线的峰值载荷等于界面的脱粘载荷;界面摩擦应力存在时,纤维埋入长度越长、界面摩擦应力越大,越易使峰值载荷大于脱粘载荷.
(5)与双线性弹性-软化内聚力模型结果比较,在无界面摩擦应力影响下,弹性-软化内聚力模型在长纤维拔出的载荷-位移曲线上出现平台阶段;而弹性-塑性屈服模型在短纤维的载荷-位移曲线上有平台段.
| [1] | 杜善义, 王晓宏, 张博明 等. 单丝复合体系界面力学行为的表征. 哈尔滨工业大学学报, 2010, 42(7): 1095-1099 (Du Shanyi, Wang Xiaohong, Zhang Boming, et al. Research progress in characterization of interface mechanical behavior of single fiber reinforced composites. Journal of Harbin Institute of Technology, 2010, 42(7): 1095-1099 (in Chinese)) |
| [2] | Koyanagi J, Nakatani H, Ogihara S. Comparison of glass-epoxy interface strengths examined by cruciform specimen and single-fiber pull-out tests under combined stress state. Composites: Part A, 2012, 43: 1819-1827 |
| [3] | Sockalingam S, Nilakantan G. Fiber-matrix interface characterization through the microbond test. International Journal of Aeronautical and Space Science, 2012, 13(3): 282-295 |
| [4] | Cox HL. The elasticity and strength of paper and other fibrous materials. British Journal of Applied Physics, 1952, 3: 72-79 |
| [5] | Lawrence P. Some theoretical considerations of fibre pull-out from an elastic matrix. Journal of Materials Science, 1972, 7: 1-6 |
| [6] | Piggott MR. Failure processes in the fibre-polymer interphase. Composites Science and Technology, 1991, 42: 57-76 |
| [7] | Kelly A, Tyson WR. Tensile properties of fibre-reinforced metals: copper/tungsten and copper/molybdenum. Journal of Mechanics and Physics Solids, 1965, 13: 329-350 |
| [8] | 王伟霞,顾轶卓,李敏 等.单丝断裂双树脂法研究碳纤维/环氧树脂界面粘结性能.复合材料学报,2013,30(4):1-6 (Wang Weixia,Gu Yizhuo,Li Min,et al.Characterization of interfacial bonding property of carbon fiber/epoxy resin using single fiber fragmentation test with dual matrix composites.Acta Materiae Compositae Sinica,2013,30(4):1-6 (in Chinese)) |
| [9] | Yang L, Thomason J. Development and application of micromechanical techniques for characterizing interfacial shear strength in fibre-thermoplastic composites. Polymer Testing, 2012, 31: 895-903 |
| [10] | Barenblatt GI.The mathematical theory of equilibrium cracks in brittle fracture.Advances in Applied Mechanics,1962,7:55-129 |
| [11] | Dugdale DS.Yielding of steel sheets containing slits.Journal of the Mechanics and Physics of Solids,1960,8:100-104 |
| [12] | 赵朋飞, 尚福林, 闫亚宾 等. 纳米悬臂梁Si/Cu界面破坏的弹塑性内聚力模拟. 固体力学学报, 2011, 32(1): 11-19 (Zhao Pengfei, Shang Fulin, Yan Yabin, et al. Elasto-plastic cohesive zone modeling of delamination of Si/Cu interface in a nano-cantilever. Chinese Journal of Solid Mechanics, 2011, 32(1): 11-19 (in Chinese)) |
| [13] | Kushch VI, Shmegera SV, Brondsted P, et al. Numerical simulation of progressive debonding in fiber reinforced composite under transverse loading. International Journal of Engineering Science, 2011, 49: 17-29 |
| [14] | Yang L, Yan Y, Ma J, et al. Effects of inter-fiber spacing and thermal residual stress on transverse failure of fiber-reinforced polymer-matrix composites. Computational Materials Science, 2013, 68: 255-262 |
| [15] | Sapora A, Paggi M. A coupled cohesive zone model for transient analysis of thermoelastic interface debonding. Computer Mechanics, 2014, 53: 845-857 |
| [16] | Schreyer HL, Peffer A. Fiber pullout based on a one-dimensional model of decohesion. Mechanics of Materials, 2000, 32: 821-836 |
| [17] | Subramani S,Moutushi D,John WG Jr, et al. Finite element analysis of the microdroplet test method using cohesive zone model of the fiber/matrix interface.Composites:Part A,2014,56:239-247 |
| [18] | Jia YY,Yan WY,Liu HY.Carbon fibre pullout under the influence of residual thermal stresses in polymer matrix composites.Computational Materials Science, 2012, 62: 79-86 |
| [19] | Nishikawa M, Okabe T, Hemmi K, et al. Micromechanical modeling of the microbond test to quantify the interfacial properties of fiber-reinforced composites. International Journal of Solids and Structures, 2008, 45: 4098-4113 |
| [20] | Nishikawa M, Okabe T, Takeda N. Determination of interface properties from experiments on the fragmentation process in single-fiber composites. Materials Science and Engineering A, 2008, 480: 549-557 |
| [21] | Zhandarov S, Mäder E. Determination of interfacial parameters in fiber-polymer systems from pull-out test data using a bilinear bond law. Composite Interfaces, 2004, 11: 361-391 |
| [22] | Banholzer B, Brameshuber W, Jung W. Analytical simulation of pull-out tests-the direct problem. Cement & Concrete Composites, 2005, 27: 93-101 |
2. Department of Engineering mechanics, Hunan University of Science and Technology, Xiangtan 411201, China
 2015, Vol. 47
2015, Vol. 47