含能单晶HMX (Octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine,环四亚甲基四硝胺,奥克托今)和 RDX(1,3,5-Trinitroperhydro-1,3,5-triazine,环三亚甲基三硝胺,黑索金)是常用塑料粘结炸药(PBX)的主体成分,因此研究含能单晶的力学性能参数和微观破坏机理对含能材料的合成、制备以及起爆性能和安全性能有重要的作用[1, 2, 3, 4].含能材料发生点火起爆的局部区域成为"热点"[5, 6].在复合含能材料中,晶粒间的摩擦以及孔洞的压缩坍塌能够使能量集中形成热点.而在含能单晶内部,产生热点的机制主要有两种:(1)位错塞积到一定程度发生坍塌释放大量的能量;(2)含能单晶内部空间位阻模型由于缺少滑移系引起分子缠结以及化学分解[7].正是由于含能单晶位错滑移机制以及位阻机制,导致含能单晶的力学响应具有很强的各向异性,不同取向下,含能单晶的塑性流动不同,因此导致含能单晶的点火起爆具有很强的各向异性[8, 9].通过实验手段获取与以上细观机制相关的参数,能够为细观计算参数的选取提供一定的依据,同时对实验后样品的分析还可以为研究含能材料的点火起爆机理提供支撑.
常温常压下能够稳定存在的相为$\beta $-HMX以及$\alpha $-RDX.由于含能单晶的尺寸很小、脆性大,因此很难直接对其进行常规拉伸压缩试验方法获得力学参数. 早在20世纪70年代,Hagen和Chaudhri[10]根据显微硬度实验测出RDX的维氏硬度,然后通过维氏硬度和弹性模量的关系估计出RDX的弹性模量为18.4 GPa,之后Palmer和Field[11]也估计出$\beta $-HMX的弹性模量为31 GPa.Zaug[12]运用脉冲激光散射试验方法(ISLS)首次获得HMX单晶的弹性模量.随后Stevens等[13]和Haycraft等[14]采用布里渊散射的方法也得到了$\beta $-HMX和RDX的弹性模量参数.由于实验的复杂性,Sewell等[15],Menikoff等[16],Conroy等[17]运用基于量子化学的力场进行不同分子动力 学计算,分别得到HMX和RDX的弹性模量参数.然而以上不同方法得到的结果常常差异较大,且主要得到弹性力学参数,难以了解含能单晶非弹性力学参数及微观损伤机制.
Rae等[18]通过 HMX 单晶颗粒的准静态压缩实验,粗略地得到了HMX单晶的应力应变曲线,发现HMX单晶不仅表现出准脆性,还出现孪晶现象.Ramos等[19]对含能单晶RDX的破坏机理作出一系列的研究,不同晶面力学响应的不同,表明RDX明显的各向异性,同时推测塑性变形机制较为复杂,并不是单一滑移系作用结果.
微纳米压痕技术常用来测定尺寸较小样品的力学性能参数,而且可以加载到塑性直至断裂破坏阶段.本文利用微纳米压痕加载方法,对载荷位移曲线利用常用的Oliver-$\!$-Pharr方法[20, 21, 22]可以得到材料基本的力学性能参数,如弹性模量与硬度. 利用原子力显微镜在样品表面扫描,得到样品微纳米级的表面特征.本文将采用纳米压痕技术以及原子力显微镜研究含能单晶$\beta $-HMX和$\alpha$-RDX的力学性能参数以及细微观破坏机理.
1 微纳米压痕实验 1.1 试验方法微纳米压痕试验在MTS公司生产的Nano-$\!$-IndenterXP压痕试验机上进行,选取的样品为经过重结晶之后的$\beta $-HMX和$\alpha$-RDX单晶,如图1所示. 含能单晶的尺寸约为2 mm$\times $2 mm$\times$1 mm. 同时,HMX单晶与RDX单晶在丙酮溶液中的最大生长面分别为(010)面和(210)面.

|
图 1 试验所用的含能单晶 Fig.1 Energetic crystals used in the experiments |
加载所使用的压头为玻式压头(Berkovich).分别在样品表面做5个压痕点,压点之间的距离大于压入深度的30倍,以保证每个压点得 到独立的测试结果.为了探测压深对材料硬度和模量的影响,设定纳米压入最大载荷分别为100 mN,200 mN,300 mN,400 mN,500 mN.各压痕之间的距离大于50 μm,以消除压痕之间的干扰.
加载时选取恒定的加卸载速率,卸载至最大载荷的10%,当达到载荷峰值时,需保持载荷不变一段时间后再卸载,以消除温漂的影响.
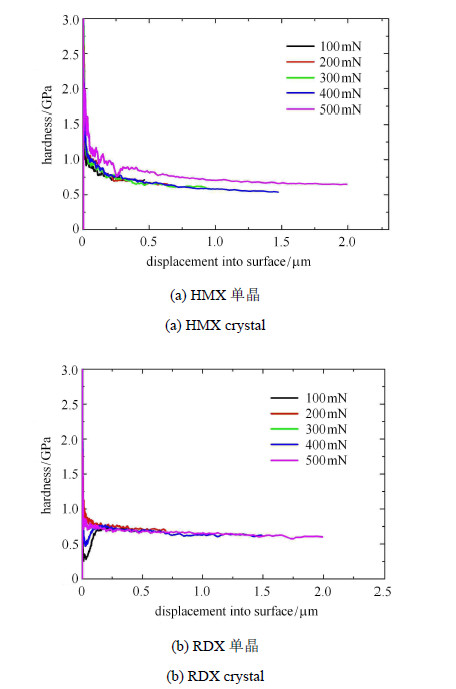
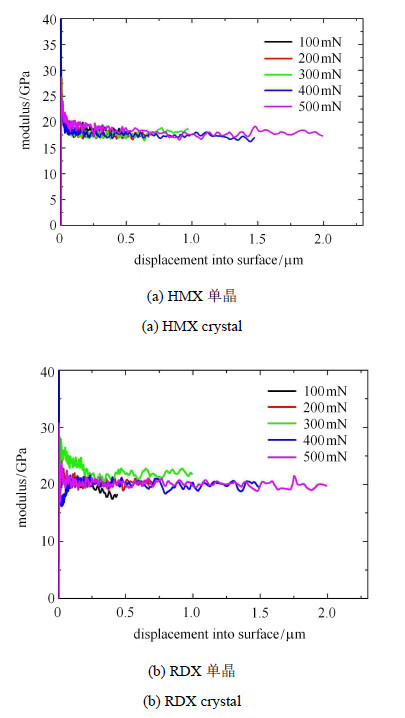
2 实验结果讨论与分析 2.1 模量与硬度的分析由试验得出$\beta $-HMX单晶(010)晶面和$\alpha $-RDX单晶(210)晶面硬度和弹性模量随压深变化,典型曲线如图2和图3.从图2和图3可以看出,硬度和模量值在压入深度较浅时 出现大幅度震荡,随后基本趋于平稳状态. 产生这种现象的原因有2个:第一,压针的影响.由于磨损等客观条件导致压针存在较大的曲率半径成为非理想的压针,导致测量时参数发生波动;第二,材料的表面效应.含能单晶的表层由于直接与空气接触,表层的原子与内部不同,导致压入初始阶段会产生震荡.
|
图 2 HMX单晶和RDX单晶的硬度随压深变化的曲线 Fig.2 Displacement hardness curves of HMX and RDX under different load |
|
图 3 HMX单晶和RDX单晶模量随压深变化的曲线 Fig.3 Displacement modulus curves of HMX under different load |
图4为将HMX(010)晶面和RDX(210)晶面的模量和硬度进行整理得到的散点图,可以看到,HMX(010)晶面和RDX(210)晶面的硬度值随压深的增大而变小,这一现象称为硬度值的尺寸效应[23, 24, 25].产生硬度的尺寸效应的原因有很多,包括压痕的凸起或凹陷、施加载荷的误差、裂纹、压头的几何形状误差、材料表面的粗糙度等.也有人认为是压痕加载过程中,产生了压痕的弹性恢复加工硬化、弹塑性变形的交叉作用、压头与试件之间的摩擦阻力及弹性阻力、与位错有关的应变梯度、压痕的边界作用等因素造成的. 而模量并没有出现尺寸效应. 比较看来,RDX的弹性模量和硬度值都比HMX的弹性模量和硬度值高.

|
图 4 HMX和RDX单晶模量和硬度与载荷的散点图 Fig.4 Load modulus and load hardness scatter plot of HMX and RDX |
对表1和表2得出的试验数据取平均值,得到HMX单晶(010)晶面的弹性模量为17.48 GPa,硬度为0.682 GPa.RDX单晶(210)晶面的 弹性模量为20.58 GPa,硬度为0.698 GPa.
| 表 1 弹塑性损伤模型材料参数[28] Table 1 Parameters of damaged plasticity model |
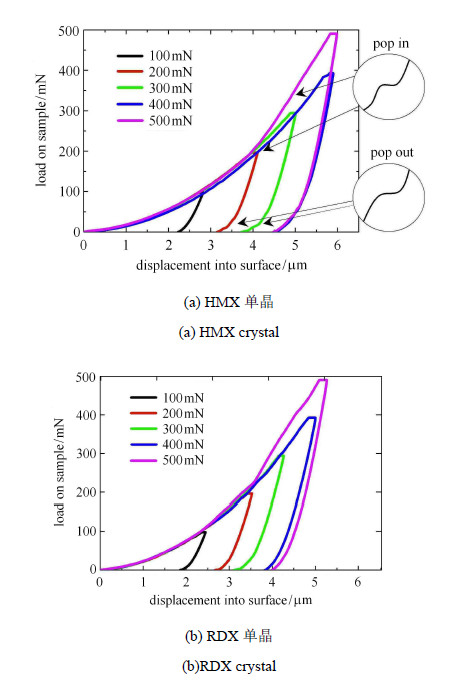
图5为HMX和RDX在不同载荷下的载荷-位移曲线,由上图可知,HMX和RDX加卸载曲线并不光滑,存在很多断点,也称为pop-in(加载突进)和pop-out (卸载突退)[19].这些不连续现象由HMX单晶和RDX单晶的内部缺陷如微裂纹、微孔洞等缺陷所导致的.从力学行为和变形机制角度解释,就是含能单晶与压针接触的晶面先发生弹性变形,在到达屈服强度后,发生塑性变形,目前认为,含能单晶塑性变形的主要形式是晶面间的位错滑移,从而使得压针接触部分的材料发生脆裂,位移突然增加,于是出现加载曲线上的不连续现象(pop-in),称为加载突进.之后脆裂部分下面的晶面继续发生弹性变形,当载荷继续增加达到屈服强度后,该部分晶体再发生脆裂.因此,在加载过程中加载方向的晶面自外向内不断重复这个过程,导致加载曲线上存在很多加载突进现象.在卸载的过程中,由于晶体内部在加载过程中导致的和晶体本身具有的损伤缺陷(微裂纹或微孔洞)等导致卸载曲线上出现的小平台(pop-out),称为卸载突退.
|
图 5 HMX和RDX在不同载荷下的载荷-位移曲线 Fig.5 Displacement load curves of HMX and RDX under different load |
单晶和HMX单晶均属于硬脆类材料,其塑性持续的时间很短,表现为"微塑性",同时其载荷位移曲线的加载阶段的曲率很快增大.当晶体晶面所承受的压缩载荷达到一定的数值,晶体开始发生断裂,此时,应力随着裂纹尖端开始向里扩展.通过比较图5(a)和图5(b),在相同载荷条件下,RDX单晶卸载后的残余深度比HMX单晶小,根据纳米硬度的定义,这表明RDX抵抗变形的能力较强,硬度更大[22].
2.3 原子力显微镜压痕分析图6为HMX(010)晶面压痕的三维原子力显微镜(AFM)图像,可以看出当载荷较小时,100 mN时,并未达到HMX单晶的断裂极限,即HMX单晶只表现为弹塑性变形,即仅在HMX单晶表面留下压痕.当最大载荷为200 mN时,由于在压头棱角周围产生应力集中,当该应力超过HMX单晶的断裂极限时,产生径向裂纹. 因此随着载荷的进一步增大,达到400$\sim$500 mN时,裂纹达到一定长度后不再继续长大,而是在压痕周围即应力高度集 中区域产生新的侧向裂纹.观察到这些侧向裂纹的扩展方向一致,该方向为最易解理破坏方向.

|
图 6 HMX原子力显微镜图像分析 Fig.6 AFM observation of HMX under different load |
图7为RDX单晶(210)晶面压痕的三维AFM图像,可以看出当载荷较小时,100 mN时,除了发生弹塑性变形外,在压痕棱角部位发生了断裂破坏,产生了径向的裂纹,这与HMX单晶得到的压痕图像不尽相同.

|
图 7 RDX原子力显微镜图像分析 Fig.7 AFM observation of RDX under different load |
比较图6和图7可得出结论:RDX单晶与HMX单晶相比,更容易发生断裂破坏,产生更多的裂纹,表明RDX的脆性更大.RDX单晶断裂破坏的 程度更大,由图7看出RDX压痕的右上角有断裂破坏,可以解释为解理方向和径向裂纹共同作用的结果.
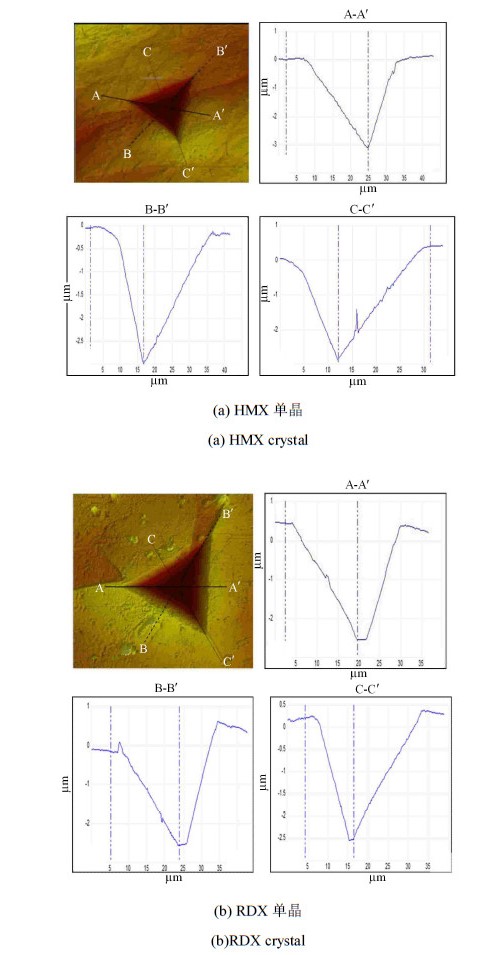
同时,可以得到HMX单晶和RDX单晶压痕的二维压深剖面图. HMX单晶和RDX单晶在所受载荷为200 mN时的二维压深剖面图如图8.
|
图 8 200 mN时HMX和RDX单晶压痕的二维压深剖面图 Fig.8 Depth profiles of HMX and RDX under 200 mN |
由图8可以看出在压痕周围有明显的凸起现象,尖端处凸起很小,边线的中间部位凸起最大.这是由于尖端在加载过程中产生了裂 纹而释放了应变能. 这些凸起,可能是压针退出过程中将脆裂碎片带出堆积而成(pileup).
3 微纳米压痕实验数值模拟 3.1 弹塑性损伤本构由于含能单晶HMX和RDX的脆性特征,本文选择有限元软件ABAQUS中常用来描述准脆性材料的弹塑性损伤本构模型[26](damaged plasticity model)进行纳米压痕的数值分析.该模型通过考虑各向同性的损伤以及拉伸压缩下各向同性的塑性表征含能单晶的非弹性响应.
弹塑性损伤本构方程可以表示为
| ${\pmb\sigma} = (1 - d){\pmb E}_0^{\rm el} :({\pmb\varepsilon }-{\pmb \varepsilon}^{\rm pl}) ={\pmb E}^{\rm el}:({\pmb\varepsilon} -{\pmb \varepsilon}^{\rm pl}) $ | (1) |
式中,$ d$是损伤度因子,$E_0^{\rm el} $为初始弹性刚度,$E^{\rm el}$为退化弹性刚度,$\varepsilon^{\rm pl}$为塑性应变.
有效应力定义为
| $\bar{\pmb \sigma } = {\pmb E}_0^{\rm el} :({\pmb \varepsilon }- {\pmb \varepsilon}^{\rm pl}) $ | (2) |
损伤度因子$d$用来表征含能单晶在拉伸情况下产生裂纹和压缩状态下破碎失效. 其演化规律与有效应力$\bar {\sigma }$以及等效塑性应变$\tilde {\varepsilon }^{\rm pl}$有关
| $d = d(\bar {\pmb \sigma },\tilde {\varepsilon }^{\rm pl}) $ | (3) |
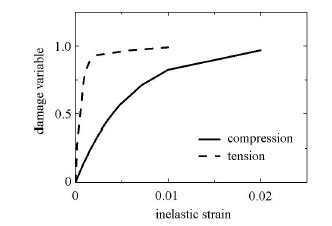
图9为数值计算中所用拉伸和压缩状态下损伤度与非弹性应变关系曲线[27].
|
图 9 不同状态下损伤度与非弹性应变关系曲线 Fig.9 Damage variable inelastic strain curves under different conditions |
模型采取的是非关联流动法则
| $\dot{\pmb \varepsilon }^{\rm pl} = \dot {\lambda }\dfrac{\partial G(\bar{\pmb \sigma })}{\partial \bar {\pmb\sigma }} $ | (4) |
式中,$\dot {\lambda }$为非负塑性比例系数,$\bar{\pmb \sigma }$为有效应力.
塑性势$G$取为Drucker-$\!$-Prager双曲函数的形式
| $G = \sqrt {( \varepsilon \sigma _{t0} \tan \varPsi )^2 + \bar {q}^2} - \bar {p}\tan \varPsi $ | (5) |
式中,$\bar {p}$是静水压力,$\bar {q}$是Mises等效应力,$\varPsi$是$p$-$q$面内高围压时的膨胀角,$\sigma _{t0} $是单轴抗拉强度,$\varepsilon$是势函数偏心率,它描述势函数向其渐近线逼近的速度. 流动势函数的连续光滑性保证了流动方向的唯一性.
具体选取的材料本构模型参数如表1所示,其中$\sigma_{b0}/\sigma_{c0}$为初始等双轴压缩屈服应力与初始单轴压缩屈服应力的比值;$K_{\rm c}$为拉伸子午线与压缩子午线应力第二不变量的比值;$\mu $为黏性系数.
为了和压痕实验结果进行对比,取RDX的弹性模量为$E=20.58$ GPa,泊松比$\nu =0.25$.取HMX单晶的弹性模量为$E=17.48$ GPa,泊松比$\nu =0.25$.
3.2 三维计算模型的建立纳米压痕试验使用金刚石玻氏压针,其泊松比为0.07,杨氏模量为1 141 GPa,比HMX单晶和RDX单晶的弹性模量大得多,所以在数值模拟中可以将压针设置约束为刚体.
计算模型中三棱锥压针边长为6 μm,其边长和高度满足$l / h =7.531 5$,HMX单晶材料尺寸为13 μm$\times $13 μm$\times $1 μm.划分网格用于计算时模型共计50 200个单元、54 929个节点,单元类型为C3D8R (8节点六面体线性减缩积分单元),最小网格尺寸为100 nm,最小时间步长为10 μs.在模拟中,并不考虑摩擦因素的影响,因此采用硬接触并定义摩擦系数为0.
有限元建模压针参考点初始时刻6个自由度全为0,加载阶段和卸载阶段通过控制参考点竖直方向的加载位移来实现分析步.
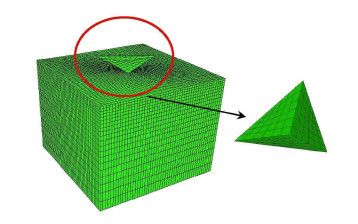
|
图 10 数值仿真构建的模型 Fig.10 Finite element model of nanoindentation experiment |
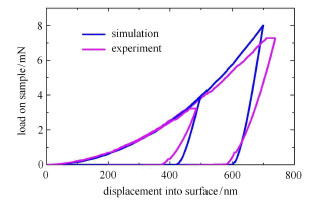
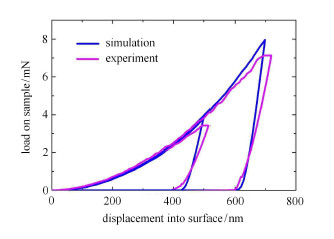
图11和图12为HMX单晶和RDX单晶在不同压深时数值模拟与实验的载荷-位移曲线对比的情况,从图中可以看出数值模拟的结果与试验结果在宏观上基本吻合,在加载阶段,试验曲线与模拟曲线吻合程度很高.而在卸载阶段,数值仿真的结果并不能很好地与试验曲线吻合,这是因为卸载阶段为带有损伤的弹性卸载,受到材料本构参数选取的影响.同时,试验曲线在最大载荷保载阶段出现平台段,这可能与仪器的位移漂移有一定关系,并且无法在数值模拟中体现,因此出现与试验曲线并不相符的尖点.
|
图 11 HMX单晶不同压深数值模拟与实验的载荷-位移曲线 Fig.11 Load displacement curves of HMX under experiments and simulations |
|
图 12 RDX单晶不同压深数值模拟与实验的载荷-位移曲线对比 Fig.12 Load displacement curves of RDX under experiments and simulations |
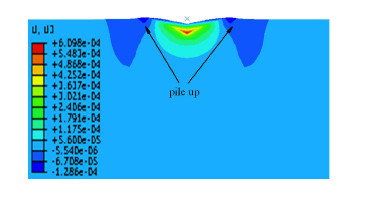
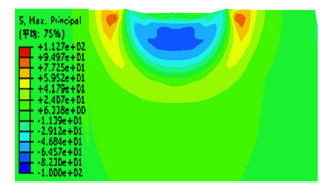
图13为HMX单晶数值模拟卸载时压痕附近的位移云图,可以看到在压痕附近的区域,有堆积现象,根据图14,卸载时压痕附近的主应力云图,在压痕附近的拉应力较大,造成压痕附近出现堆积现象,这与AFM图像得出的变形结果相同.
|
图 13 卸载后压痕处的位移云图 Fig.13 Displacement contour after unloading |
|
图 14 卸载时主应力云图 Fig.14 Principle stress contour when unloading |
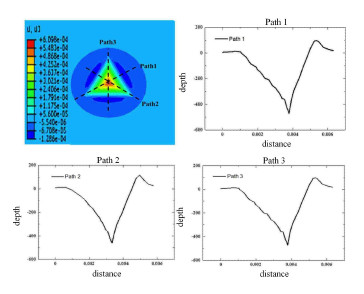
图15 为不同路径的压深剖面图,从图中可以看出,在压痕附近有明显的凸起(pile-up).
|
图 15 HMX不同路径的压深剖面图 Fig.15 Depth profiles of HMX |
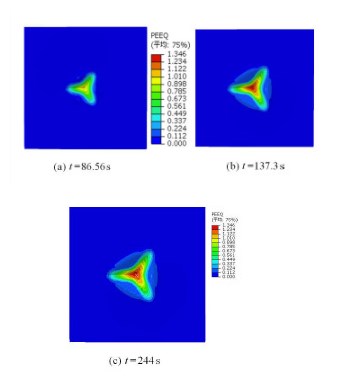
图16为不同时刻的塑性应变云图,图16(a)$\sim$图16(c)分别加载过程中、加载峰值以及卸载后的塑性应变云图. 在加 载的过程中,塑性应变集中在压痕区域.加载到最大值时,塑性应变扩展到侧向.比较图16(b)和图16(c),说明卸载阶段产生的塑性变形很小,大部分的塑性变形是在加载阶段产生的.
|
图 16 不同时刻的塑性应变云图 Fig.16 Plastic strain contour at different time |
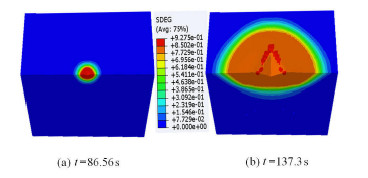
图17为不同时刻的损伤因子的变化云图,从图中可以看出,随着加载的进行,损伤逐渐从压头周围扩展到压头侧向区域,并且损伤度随着加载的增加而增大. 当加载达到最大值时,损伤度达到最大值0.927 5.
|
图 17 不同时刻的损伤度云图 Fig.17 Damage at different time |
从微纳米压痕实验和数值模拟两个方面研究了$\beta $-HMX单晶及$\alpha$-RDX单晶的力学性能,采用微纳米压痕方法,由加卸载的载荷-位移曲线测定其力学性能参数,利用AFM观测压痕的微观破坏特征,比较分析了$\beta $-HMX和$\alpha $-RDX的微观破坏机理.采用ABAQUS有限元软件进行纳米压痕的数值模拟,通过与实验结果的对比确定其本构参数. 得出的主要结论有:
(1) 利用微纳米压痕测试技术测定$\beta $-HMX单晶(010)晶面和$\alpha$-RDX单晶(210)晶面的弹性模量和硬度,得到HMX单晶的平均模量为$E=17.48$ GPa、平均硬度为$H=0.682$ GPa,RDX单晶的平均模量为$E=20.58$ GPa、平均硬度为$H=0.698$ GPa.比较得知RDX单晶的硬度和模量都大于HMX单晶.
(2) 分析材料弹性模量、硬度的压深相关性,通过分析HMX单晶和RDX单晶的载荷-位移曲线,得到HMX单晶和RDX单晶的弹性模量值随压入深度的增加而趋于稳定值,硬度值随压入深度的增加而减小,硬度表现出尺寸效应.
(3)原子力显微镜的观测结果中,很重要的就是可以确定产生径向或侧向裂纹的临界压深和临界最大载荷,通过纳米压痕和原子力显微镜的表征,可以了解到含能单晶的弹塑性变形和裂纹破坏之间的关联性.
(4) 运用ABAQUS有限元软件做纳米压痕数值模拟,通过与实验结果的对比,即载荷位移曲线和模拟得到微观力学响应,可以基本确定含能单晶的损伤本构参数.
以上运用微纳米压痕方法研究HMX单晶和RDX单晶的力学性能,得到了相应的力学参数,并分析了微观破坏机制,可为研究含能材料点火和起爆性能的理论研究提供支撑.
| [1] | Hooks DE, Ramos KJ, Martinez AR. Elastic-plastic shock wave profiles in oriented single crystals of cyclotrimethylene trinitramine (RDX) at 2.25GPa. Journal of Applied Physics, 2006, 100(2): 024908 |
| [2] | Hooks DE, Ramos KJ. Initiation mechanisms in single crystal explosives: dislocations, elastic limits and initiation thresholds. In: Proc. of Thirteenth International Detonation Symposium, 2006: 351-07 |
| [3] | Walley SM, Field JE, Greenaway MW. Crystal sensitivities of energetic materials. Materials Science and Technology, 2006, 22(4): 402-413 |
| [4] | Armstrong RW. Dislocation mechanisms for shock-induced hot spots. Le Journal de Physique IV, 1995, 5(C4): C4-89-C4-102 |
| [5] | Armstrong RW. Dislocation - assisted initiation of energetic materials. Central European Journal of Energetic Materials, 2005, 2 (3): 55-69 |
| [6] | Walley SM, Field JE, Greenaway MW. Crystal sensitivities of energetic materials. Materials Science and Technology, 2006, 22(4): 402-413 |
| [7] | Dick JJ, Ritchie JP. Molecular mechanics modeling of shear and the crystal orientation dependence of the elastic precursor shock strength in pentaerythritol tetranitrate. Journal of Applied Physics, 1994, 76(5): 2726-2737 |
| [8] | Dick JJ, Hooks DE, Menikoff R, et al. Elastic-plastic wave profiles in cyclotetramethylene tetranitramine crystals. Journal of Applied Physics, 2004, 96(1): 374-379 |
| [9] | Dick JJ, Mulford RN, Spencer WJ, et al. Shock response of pentaerythritol tetranitrate single crystals. Journal of Applied Physics, 1991, 70(7): 3572-3587 |
| [10] | Hagan JT, Chaudhri MM. Fracture surface energies of high explosives PETN and RDX. Journal of Materials Science, 1977, 12(5): 1055-1058 |
| [11] | Palmer SJP, Field JE. The Deformation and Fracture of β-HMX. A. Mathematical and Physical Sciences, 1982, 383(1785): 399-407 |
| [12] | Zaug JM. Elastic constants of b-HMX and tantalum, equations of state of supercritical fluids and fluid mixtures and thermal transport determinations. In: Proceedings of the 11th International Detonation Symposium, Snowmass, CO, 1998 |
| [13] | Stevens LL, Eckhardt CJ. The elastic constants and related properties of β-HMX determined by Brillouin scattering. The Journal of Chemical Physics, 2005, 122: 174701 |
| [14] | Haycraft JJ, Stevens LL, Eckhardt CJ. The elastic constants and related properties of the energetic material cyclotrimethylene trinitramine (RDX) determined by Brillouin scattering. The Journal of Chemical Physics, 2006, 124: 024712 |
| [15] | Sewell TD. A molecular dynamics simulation study of elastic properties of HMX. The Journal of Chemical Physics, 2003, 119: 7417 |
| [16] | Menikoff R, Dick JJ, Hooks DE. Analysis of wave profiles for single-crystal cyclotetramethylene tetranitramine. Journal of Applied Physics, 2004, 97(2): 023529 |
| [17] | Conroy MW, Oleynik II, Zybin SV, et al. First-principles anisotropic constitutive relationships in β -cyclotetramethylene tetranitramine (β -HMX). Journal of Applied Physics, 2008, 104(5): 053506 |
| [18] | Rae PJ, Hooks DE, Liu C. The stress versus strain response of single β -hmx crystals in quasi-static compression. In: Proceedings of the Thirteenth International Detonation Symposium, Office of Naval Research, 2006 |
| [19] | Ramos KJ, Hooks DE, Bahr DF. Direct observation of plasticity and quantitative hardness measurements in single crystal cyclotrimethylene trinitramine by nanoindentation. Philosophical Magazine, 2009, 89(27): 2381-2402 |
| [20] | Oliver WC, Pethica JB. U.S. Patent [R] No.4848141 |
| [21] | Pharr GM, Oliver WC, Brotzen FR. On the generality of relationship among contact stiffness, Contact area, and elastic modulus during indentation. Mater Res, 1992, 7: 613-617 |
| [22] | 张泰华,杨业敏.纳米硬度技术的发展和应用.力学进展, 2002, 32(3): 349-363 (Zhang Taihua, Yang Yemin. Development and application of nano hardness techniques. Advances in Mechanics, 2002,32(3):349-363 (in Chinese)) |
| [23] | Gong J, Wu J, Guan Z. Examination of the indentation size effect in low-load Vickers hardness testing of ceramics. Journal of the European Ceramic Society, 1999, 19(15): 2625-2631 |
| [24] | Atkinson M. Further analysis of the size effect in indentation hardness tests of some metals. Journal of Materials Research, 1995, 10(11): 2908-2915 |
| [25] | 易大可, 王自强. 能量非局部模型和新的应变梯度理论. 力学学报, 2009, 41(1): 60-66 (Yi Dake,Wang Ziqiang. Energy non-local model and new strain gradient theory. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(1): 60-66 (in Chinese)) |
| [26] | Abaqus Users Manual, Version 6.8, Simulia Inc, 2012. |
| [27] | Yu T, Teng JG, Wong YL, et al. Finite element modeling of confined concrete-II: Plastic-damage model. Engineering Structures, 2010, 32(3): 680-691 |
| [28] | Jankowiak T, Lodygowski T. Identification of parameters of concrete damage plasticity constitutive model. Foundations of Civil and Environmental Engineering, 2005, 6: 53-69 |
 2015, Vol. 47
2015, Vol. 47
