2. 大连理工大学航空航天学院, 大连 116024;
3. 国防科学技术大学理学院, 长沙 410073;
4. 中国人民解放军95972 部队2站, 兰州 735018
化学非平衡流动由于反应特征时间尺度比流动特征时间尺度小若干量级,致使描述化学非平衡流动的控制方程存在严重的刚性问题.如果采用显式方法求解,则受计算格式稳定性限制,时间步长将主要由化学反应特征时间决定,对于很多实际问题而言所需的计算时间是无法承受的,一般问题所要求的时间精度也根本不需要用如此小的时间步长来计算.为了解决化学非平衡带来的刚性问题,目前主要采用三类方法进行求解:全隐算法,点隐算法以及时间分裂法.
全隐算法[1, 2]将控制方程中的流动项(对流项,黏性项)和化学反应源项都进行隐式处理,因此时间步长不受稳定性限制.但是需要存储雅克比矩阵和进行矩阵求逆运算,当采用详细的化学反应机理模型时,反应组元和反应方程式可以达到成百上千个,因此使用全隐算法将带来巨大的存储量,矩阵求逆需要巨大的计算量;另外一方面,即便存储量和计算量的困难可以克服,由于物理问题的限制,采用全隐算法也不能采用较大的时间步长.
点隐算法只对刚性的化学反应源项进行隐式处理,而对非刚性的流动项进行显式处理.因为化学反应源项的雅克比矩阵只与化学反应机理的组元数有关,而与空间维数无关,因此称这种方法为"点隐"方法[3].点隐算法得到了广泛的应用.杨顺华等[4]利用巨型计算机对煤油超燃冲压发动机进行了大规模并行计算,计算控制方程为带详细化学反应模型的雷诺平均纳维-斯托克斯(Navier-$\!$-Stokes)方程,化学反应源项采用点隐法处理.点隐算法仍然需要存储化学反应源项的雅克比矩阵和进行矩阵求逆运算,如果采用详细化学反应机理仍然需要很大的存储量和计算量;一般而言点隐算法至多只具有一阶时间精度,这对于模拟非定常现象是不够的.Zhong[5]提出了附加半隐的龙格-库塔(Runge-$\!$-Kutta)法处理源项的刚性问题,可以达到二阶以上时间精度.基于详细基元反应和二维Euler反应流方程,对流项采用五阶加权基本无振荡(weighted essentially non-oscillatory,WENO)差分格式离散,采用二阶附加半隐的龙格-库塔法处理化学反应源项引起的刚性,王昌建和徐胜利[6]对直管内胞格爆轰进行了数值模拟,Mevel等[7]模拟了激光诱导的包含稀释剂的H$_{2}$/O$_{2}$混合气体的爆轰波.
目前得到大量应用的化学非平衡流动计算方法是时间分裂算法,或者又称为算子分裂法、分数步法[8].整个物理过程被分解为刚性的化学反应部分和非刚性的流动部分,对各个部分独立求解,然后将刚性和非刚性部分的解组合起来.由于刚性和非刚性部分独立出来了,因此可以采用各自适合的方法进行求解,具有很强的灵活性和可操作性.时间分裂方法只有在采用Strang分裂格式时才具有时间二阶精度[8].Ferrer等[9]对根据时间分裂法建立的多组分反应可压缩纳维-斯托克斯方程求解器进行了详细的验证,该求解器对流项采用7阶WENO有限差分格式,黏性项采用8阶中心差分格式. 潘振华等[10],Liu和Liu[11],Taylor等[12],Uemura等[13]以及Tsuboi等[14]采用时间分裂方法求解带详细基元化学反应的欧拉(Euler)方程或纳维-斯托克斯方程,对二维爆轰进行了数值模拟.以上列举的方法可以称为常规的化学非平衡流解耦算法,在求解流动部分时不能直接采用已有的在量热完全气体假设下发展的流动求解算法,还需要重新推导雅克比矩阵、特征向量等特征量.对于一般的格式,推导特征往往是很困难的,甚至不能得到显式的表达式.
刘君[15, 16]以时间分裂法为基础,构造了一种新型的化学非平衡流动解耦算法.这种解耦算法将反应气体内能中与温度无关的那部分能量,即有效零点能或化学焓分离出来并添加到化学反应源项中.进行时间分裂后,物理问题被分解成流动和化学反应两个部分,具有明确的物理意义.流动部分控制方程中内能是去掉了有效零点能之后的内能,同时引入等效比热比,构造了在形式上与量热完全气体完全相同的能量与压力之间的关系式,并用等效比热比计算等效声速,经过这些处理后,流动部分控制方程的求解与量热完全气体的求解方法完全相同,所以在原则上可以采用现有的所有在量热完全气体基础上发展的计算格式,因此算法的实施十分方便.利用这一新型解耦算法,刘君对冲压加速器非平衡流动进行了数值模拟[17];在国内率先对钝头体激波诱导振荡燃烧现象进行了成功的数值模拟,得到了振荡燃烧结构[18];对化学动力学模型对H$_{2}$/Air超声速燃烧模拟的影响进行了研究[19].利用这一新型解耦算法,刘世杰等[20, 21]对钝头体激波诱导振荡燃烧进行了模拟;刘瑜等对3种化学反应动力学计算方法:梯形公式、VODE以及$\alpha$-QSS拟稳态逼近方法进行了比较,对钝头体激波诱导燃烧现象进行了详细的数值研究[15],并将解耦算法推广到非结构有限体积方法中[22, 23];
化学非平衡流动一般具有十分复杂的流场结构,为了精细的捕捉到流场结构需要采用高阶流场计算格式和网格自适应.WENO格式是一种广泛采用的高阶数值格式,目前已成为数值求解双曲守恒律问题最流行的方法之一.Harten等[24]提出了本质无振荡的3阶ENO格式.Liu和Osher提出了加权本质无振荡格式WENO,提出计算$r$个可选模板上的数值通量,并根据模板上解的光滑性构造子模板的权系数,然后将这些子模板上的数值通量加权组合形成最终的通量,他们的方法利用$r$个可选模板上的$r$阶ENO格式,构造了$r+1$阶精度的格 式[25].Jiang和Shu[26]在Liu和Osher的基础上,提出了一种新的光滑指示器,以此构造了对应的子模板上的非线性权系数,利用3个可选模板,构造了5阶WENO格式. Balsara和Shu [27]将WENO格式推广到$(2r-1)$阶精度,$r \geqslant 3$.
Henrick等[28]对经典的5阶WENO格式进行了严格的分析,得到了5阶WENO格式在临界点处具有5阶精度的充分条件,并证明经典的5阶WENO格式在一阶临界点处的收敛精度只有3阶;构造了WENO格式子模板权系数的映射函数,经典的5阶WENO格式的权系数经过映射后更接近于理想权系数,并满足5阶收敛的充分条件,根据这种方法,WENO格式在一阶临界点不会降阶,能够比经典的5阶WENO格式更好地捕捉流场间断,这种改进后的格式被称为WENO5M. Borges等[29]在Henrick 等[28]提出的5阶WENO格式保持5阶收敛的充分条件的基础上,构造了一种高阶光滑指示器,对经典的5阶WENO格式的权系数进行了修正,这种方法称为WENO-Z;证明了WENO-Z格式当$p =1$时,在一阶临界点的收敛阶为4;而当$p=2$时,收敛阶是5,并且论证了WENO-Z格式增加了含有间断子模板的权系数,这是WENO-Z格式能比经典的5阶WENO格式更好地捕捉间断的原因,同时也通过计算说明WENO5M也具有相同的性质. Castro等[30]将WENO-Z格式推广到了所有的奇数阶精度.
本文在一种求解量热完全气体流动的高阶有限差分方法WENO5M的基础上,采用刘君提出的化学非平衡解耦算法框架,将之改造成可以用于求解高速化学非平衡流动,并通过典型的算例对算法的精度进行验证.
1 计算方法 1.1 控制方程为了说明的问题的清晰,本文将只给出一维欧拉反应流的控制方程.推广到包含多维,黏性的非平衡流动将是直接的,不存在任何本质上的困难.包含$n_{s}$个热完全气体组元的混合气体和热化学反应源项的一维无黏化学非平衡流动控制方程为
| $\dfrac{\partial {\pmb Q}}{\partial t} + \dfrac{\partial {\pmb F }({\pmb Q})}{\partial x} = {\pmb S} $ | (1) |
式中,守恒变量${\pmb Q}$,对流通量${\pmb F}$和化学反应源项${\pmb S}$的表达式如下
| $\begin{align} & Q={{\left( \rho \ \ \rho u\ \ \rho {{e}_{t}}\ \ {{\rho }_{1}}\ \cdots \ {{\rho }_{{{n}_{s}}-1}} \right)}^{\text{T}}} \\ & {{F}^{\prime }}={{\left( \rho u\ \ \rho {{u}^{2}}+p\ \ (\rho {{e}_{t}}+p)u\ \ {{\rho }_{1}}u\ \ \cdots \ \ {{\rho }_{{{n}_{s}}-1}}u \right)}^{\text{T}}} \\ & {{S}^{\prime }}={{\left( \ \ 0\ \ 0\ \ {{\omega }_{1}}\ \ \cdots \ {{\omega }_{{{n}_{s}}-1}} \right)}^{\text{T}}} \\ \end{align}$ |
其中,总的混合气体密度$\rho =\sum\limits_{i=1}^{{{n}_{s}}}{{{\rho }_{i}}}$,$p$和$u$分别表示混合气体的压力和速度. 为了封闭控制方程,需要提供混合气体状态方程,即$p=\sum\limits_{i=1}^{{{n}_{s}}}{{{\rho }_{i}}{{R}_{i}}T}$.
比内能满足的关系式为$\rho {{e}_{t}}=\text{ }\sum\limits_{i=1}^{{{n}_{s}}}{{{\rho }_{i}}{{e}_{i}}}+\frac{1}{2}\rho {{u}^{2}}$. 此处$e_i$表示第$i$个组元气体的比内能.本文考虑的是热完全气体,比热是温度的函数,采用NASA的7参数多项式拟合体系计算比热,内能等物理量. $\omega_i$为第$i$个组元气体的化学反应源项,由下式计算得到
| $\omega _i = \sum\limits_{j = 1}^{n_r } (\nu"_{ij} - \nu'_{ ij} )\left( k_{fj} \prod\limits_{s = 1}^{n_s }[X_s]^{\nu'_{ sj}}- k_{bj} \prod\limits_{s = 1}^{n_s } [X_s]^{\nu"_{sj}} \right) [M]^{\nu _{jM} }$ | (2) |
其中,$n_{r}$为反应机理的基元反应数目,$\nu"_{ij} $和$\nu'_{ij}$分别表示生成物和反应物的化学反应计量系数,$\nu _{jM} $为第$j$个基元反应的三体系数,$[X_s]$为组元$s$的摩尔浓度,$M_{i}$为组元的摩尔质量.$k_{fj}$和$k_{bj}$分别为第$j$个基元反应的正、逆反应速率,本文中通过阿累尼乌斯(Arrhenius)公式计算正反应速率,逆反应速率通过平衡常数和正反应速率得到.
1.2 刘君的化学非平衡流解耦算法刘君[16]提出的化学非平衡流解耦算法与其他解耦算法的区别的关键在于对反应流控制方程进行了变换.变换的第1步是将组元气体的生成能从总内能中提取出来,将总内能中剩余的那部分能量记为$e'_t$,本文中称为等效内能.总内能可以表示为
| $e_t = e'_t + \sum\limits_{i = 1}^{n_s } {C_i \left( {\Delta h_{f,298}^0 } \right)_i } $ | (3) |
其中$\Delta h_{f,298}^0 $表示$t =298.15$ K时,热完全气体的生成能. 将 式(3)代入到式(1)中的能量方程,整理后得到关于等效内能的方程,即
| $\dfrac{\partial }{\partial t}(\rho e'_t ) + \dfrac{\partial }{\partial x}\left[{(\rho e'_t + p)u} \right]= - \sum\limits_{i = 1}^{n_s } {\omega _i \left( {\Delta h_{f,298}^0 } \right)_i } $ | (4) |
式(4)的右端项表现为化学反应源项,其物理意义是明显的,只有发生化学反应时,这部分能量才能释放出来,这部分能量是和化学反应密切相关的,因此将这部分能量放到化学反应源项中去是合理的.上式中左端项中不再出现与化学反应能量直接相关的项.
变换的第2步是引入等效比热比. 对于量热完全气体,其比热比可以定义为
| $\gamma = \dfrac{h}{e} $ | (5) |
其中,$h$和$e$分别为量热完全气体的焓和内能.热完全气体的混合气体,在去掉了生成热后得到的等效内能和等效焓,仿照量热完全气体比热比的表达式,定义了一个热完全气体混合气体的等效比热比,即
| $\gamma' = \dfrac{h'}{e'} $ | (6) |
式中$h'$和$e'$分别表示去掉生成热之后的混合气体的等效比焓和等效比内能,其各自表达式为
| $h' = \sum\limits_{i = 1}^{n_s } {C_i \left( {aT + \dfrac{bT^2}{2} + \dfrac{cT^3}{3} + \dfrac{dT^4}{4}+ \dfrac{eT^5}{5}} \right)} R_i $ | (7) |
| $e' = h' - RT $ | (8) |
上式中温度$T$前的系数$a$,$b$,$c$,$d$,$e$为NASA七参数体系中的拟合系数,$C_{i}$为组元$i$的质量分数. 由式(6)$\sim$式(8)可以得到等效内能,等效焓和压力之间的关系,即
| $e' = \dfrac{p / \rho }{(\gamma' - 1)} $ | (9) |
| $h' = \dfrac{\gamma'}{\gamma' - 1}\dfrac{p}{\rho } $ | (10) |
同时等效总内能可以表示为
| $\rho e'_t = \dfrac{p}{\gamma' - 1} + \dfrac{1}{2}\rho u^2 $ | (11) |
可见,式(9) $\sim$ (11)与量热完全气体的形式完全一致. 将 式(11)代入 式(3),得到总内能的一种表达形式为
| $e_t = \dfrac{p}{(\gamma' - 1)\rho } + \dfrac{u^2}{2} + \sum\limits_{i = 1}^{n_s } {C_i \left( {\Delta h_{f,298}^0 }\right)_i } $ | (12) |
注意到采用简化化学反应模型的多方完全气体的总内能的表达式为[36]
| $e_t = \dfrac{p}{(\gamma - 1)\rho } + \dfrac{u^2}{2} + \sum\limits_{i = 1}^{\rm nreact} {\beta _i Q_i } $ | (13) |
其中$\beta _i $和$Q_i $分别表示第$i$个化学反应的反应进程变量和热释放. 比较 式(12)和式(13),可知这两者具有形式上的一致性. 这同时也为等效比热比的引入提供了一种解释. 变换后的求解变量为$ {\pmb Q}'= \left( \rho \ \ {\rho u} \ \ {\rho e'_t } \ \ {\rho _1 } \ \ \cdots \ \ {\rho _{n_s - 1} } \right)^{\rm T}$,将其代入 式(1),得到变换后的反应流控制方程组,即
| $\dfrac{\partial {\pmb Q}'}{\partial t} + \dfrac{\partial {\pmb F}'({\pmb Q}')}{\partial x} = {\pmb S}' $ | (14) |
| $\begin{align} & Q={{\left( \rho \ \ \rho u\ \ \rho {{{{e}'}}_{t}}\ \ {{\rho }_{1}}\ \cdots {{\rho }_{{{n}_{s}}-1}} \right)}^{\text{T}}} \\ & {{F}^{\prime }}={{\left( \rho u\ \ \rho {{u}^{2}}+p\ \ (\rho {{{{e}'}}_{t}}+p)u\ {{\rho }_{1}}u\ \ \cdots \ \ {{\rho }_{{{n}_{s}}-1}}u \right)}^{\text{T}}} \\ & {{S}^{\prime }}={{\left( 0\ \ 0\ \ -\sum\limits_{i=1}^{{{n}_{s}}-1}{{{\omega }_{i}}{{\left( \Delta h_{f,298}^{0} \right)}_{i}}}\ \ {{\omega }_{1}}\ \ \cdots \ \ {{\omega }_{{{n}_{s}}-1}} \right)}^{\text{T}}} \\ \end{align} $ |
本文通过求解变换后的控制方程(14)来模拟化学非平衡流动.式(14)具有很强的刚性,这里的刚性主要体现在流动的时间尺度和最小的化学反应的时间尺度一般会相差数个量级,化学反应的最大和最小反应时间尺度也相差数个量级.因此直接对方程进行求解,难度很大,一般采用解耦算法.解耦算法又称为算子分裂方法或分数步方法,在计算物理中应用广泛.本文采用应用最广的Strang算子分裂方法,对方程(14)进行解耦计算.
算子分裂方法的关键在于将不同的物理过程分开求解,显然在化学非平衡流动中,存在着两个不同的物理过程,即流动过程和化学反应过程.这两个过程在控制方程(14)中各自由物理意义明确的项来描述,因而可将控制方程(14)分裂为流动和化学反应两部分,即
流动部分
| $\dfrac{\partial {\pmb Q}'}{\partial t} + \dfrac{\partial {\pmb F} ({\pmb Q}')} {\partial x} =0 $ | (15) |
化学反应部分
| $\dfrac{\partial {\pmb Q}'}{\partial t} = {\pmb S}' $ | (16) |
采用算子分裂法进行求解时,按照确定的顺序分别对式(16)和(17)进行求解,记流动部分和化学反应部分的数值求解算子分别${\rm L}_{f}$为${\rm L}_{c}$,Strang算子分裂可以表示为
| $Q'^{n + 1} = {\rm L}_c (\Delta t / 2) {\rm L}_f (\Delta t) {\rm L}_c (\Delta t / 2)Q'^n $ | (17) |
上式在理论上具有二阶时间精度.
(1) 化学反应部分计算方法
描述化学反应部分的控制方程是刚性常微分方程组,通过分析可以发现该方程组实际上是和描述等容爆炸的方程相同,对其求解采用VODE和$\alpha $-QSS拟稳态逼近求解器,具体算法见文献[31].
(2) 流动部分计算方法
流动部分的求解采用有限差分离散,采用5阶修正的WENO格式WENO5M,可以避免原始的WENO格式在临界点降阶的缺陷.WENO5M的具体算法见文献 [28],本文采用特征分解和Lax-$\!$-Friedrichs格式计算对流通量.由于刘君的化学非平衡流动解耦算法引入了等效比热比,因此将量热完全气体的流场求解算法推广到用于化学非平衡流的求解是直接的,用可变的等效比热比代替常值比热比即可,具体推广的实施过程细节参见文献[31]. 流动部分求解的时间推进采用具有TVD性质的3阶龙格-库塔格式.
(3) 新型解耦算法的特点
根据以上分析,新型解耦算法具有以下特点:
① 通过引入等效内能和等效比热比,对描述化学非平衡流的控制方程进行了变换;
②对变换后的化学非平衡流控制方程进行算子分裂,得到的流动控制方程组和化学反应动力学方程组分别描述的是多组分冻结流动和等容爆炸过程,算子分裂的物理意义清晰;
③ 由于引入了等效内能和等效比热比,以及关系式 (9)$\sim$(11),在形式上描述流动部分的控制方程和描述量热完全气体流动的控制方程是一致的,因此可以直接在求解量热完全气体流动的算法上进行很小的改造,就能得到计算冻结流动控制方程的算法;
④ 可以直接采用现有的计算等容爆炸化学反应的程序来计算描述化学反应部分的控制方程,不需做任何修改;
⑤ 流动部分和化学反应部分的求解是相互独立的,因此程序具有很好的模块化特点;
⑥算法实施简单,在已有的量热完全气体流动计算程序和等容爆炸计算程序的基础上,可以很快的将这两种程序结合并改造成化学非平衡流计算程序.
2 算法验证 2.1 Osher-$\!$-Shu问题这一算例模拟了激波与光滑密度波动相互作用的问题. 无量纲初始条件是
| $ \rho = 1 + 0.2\sin (5x) ,\ u = 0 ,\ p = 1 ,\ x \geqslant - 4 $ |
| $ \rho = 3.857 143 ,\ u = 2.629 369 ,\ p = 31 / 3 ,\ x \leqslant - 4 $ |
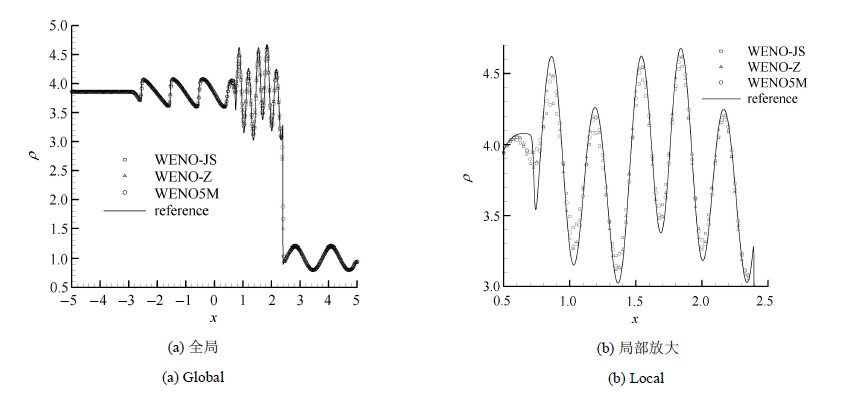
计算域为$[-5, 5]$,该问题没有分析解,但是网格收敛解可以得到,本例中用网格点数4 000,采用WENO格式的计算解作为参考解.计算网格点数为400,网格均匀分布;使用5阶WENO格式计算,时间推进采用3阶总变差减小(total variation diminishing,TVD) 龙格-库塔格式,CFL数取0.6.采用3种WENO格式,即经典的WENO格式(WENO-JS [26]),WENO5M [28]和WENO-Z [29]格式进行了计算.图1给出了$t=1.8$时刻的密度分布,其中图1(a)是整体的密度分布,图1(b)是大幅度密度振荡区的局部显示.WENO5M和WENO-Z格式在波峰和波谷处的精度明显要高于WENO-JS,这是由于这两种格式对WENO-JS进行了修正,在波峰和波谷处的临界点保持了高阶精度.
|
图 1 由不同格式计算的密度在$t=1.8$时刻的分布 Fig.1 Calculated density distributions computed by different schemes as $t=1.8$} |
为了验证化学反应计算程序,模拟了按照H$_{2}$/O$_{2}$/Ar=2/1/7摩尔比例混合的气体的等容爆炸过程.为了比较本文所计算的结果,采用激波和爆轰波工具箱SD-Toolbox[32]的计算结果作为参考.化学反应机理采用SD-Toolbox提供了的一种机理,h2air{\_}highT [32].
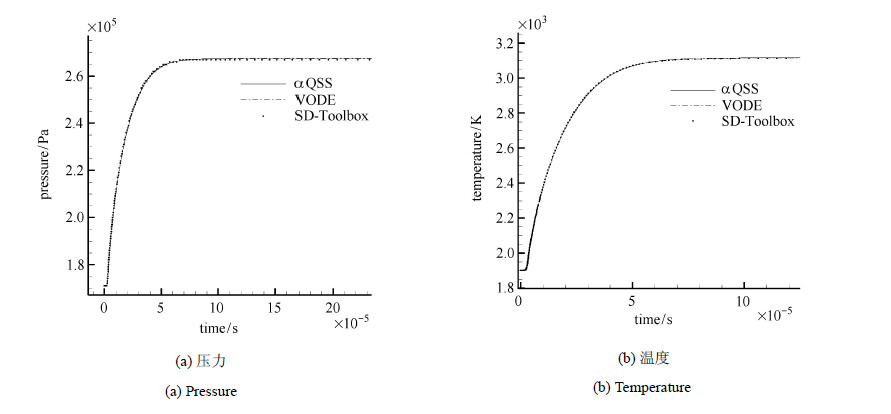
该混合气体的初始状态:$p_{0} = 6.67$ kPa,$T_0 = 300 $ K.以在该状态下发生查普曼-儒盖(Chapmann-$\!$-Jouguet)爆轰时的激波后状态作为等容爆炸的初始状态.经计算可得,激波后状态为:$p =173.24 $ kPa,$T=1 900.95$ K. 以此状态作为初始条件,分别采用VODE和 $\alpha$-QSS积分描述等容爆炸的常微分方程组(17),并与激波爆轰波工具箱SD-Toolbox的计算结果进行了比较.图2给出了等容爆炸的压力和温度历程,本文所用的两种刚性常微分方程组求解器的计算结果基本上是吻合的,并与SD-Toolbox的计算结果符合很好.
|
图 2 等容爆炸的压力和温度时间历程 Fig.2 The time evolution of pressure and temperature of constant volume explosion |
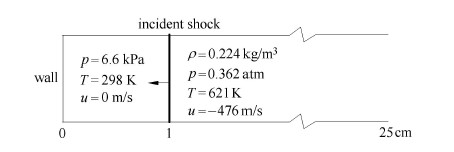
该算例取自Oran等[33]的工作,对马赫数为2.165的入射激波,经固壁反射后形成的反射波诱导的爆轰波进行了模拟.初始反应系统的气体由摩尔比例为2:1:7的H$_{2}$/O$_{2}$/Ar组成,压力和温度分别为66 087 Pa和298 K.计算域和初始条件由图3给出.计算的管道长25 cm,入射激波初始时刻位于距左端1 cm处,左端为反射固壁,右端为以入射激波速度运动的未反应气体.因为有实验数据作为数值模拟结果的比较,该算例成为考核反应流数值模拟方法的一个经典算例,除Oran[33]外,Im等[34],Wu等[35]和Ng [36]都对该算例进行了模拟.
|
图 3 反射激波诱导爆轰波计算域和初始条件示意图 Fig.3 The schematic of computation domain and initial condition for case of detonation induced byreflecting |
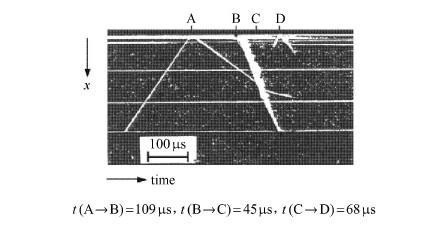
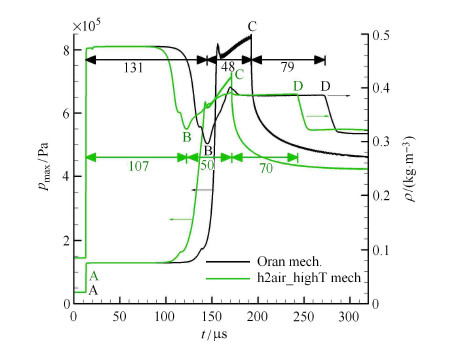
采用两种化学反应机理对该问题进行模拟,分别是Oran机理[34]和h2air{\_}highT机理[32].网格采用均匀网格,网格间距为0.1 mm. CFL数为0.9. 化学反应部分采用$\alpha $-QSS进行计算.激波管实验中,时间分辨纹影图片[33] ( 图4 )给出了入射激波被壁面反射形成反射激波,燃烧波形成并赶上反射激波与激 波融合的时间顺序.纹影图片中的4个事件分别为:A,入射激波在壁面处发生反射;B,反应波开始形成;C,反应波赶上反射激波,与激波发生融合;D,燃烧波与反射激波融合时形成的稀疏波向左端传播到达固壁.为了与实验进行比较,计算过程中记录了每一时刻全系统的最大压力和反射壁面处的密度值,图5给出了由两种化学反应机理模拟得到的结果.采用Oran机理计算的各个事件之间的间隔分别为:$t ({\rm A} \to {\rm B})=131 $s,$t ( {\rm B} \to {\rm C})=48 $s,$t ({\rm C} \to {\rm D})=79 $s;而采用h2air{\_}highT机理计算得到的各个事件之间的间隔分别为$t ({\rm A} \to {\rm B} )=107 $s,$t ({\rm B} \to {\rm C})=50 $s,$t ({\rm C} \to {\rm D})=70 $s.可以发现由h2air{\_}highT机理计算的各个事件的时序与实验符合更好,尤其是在${\rm A} \to {\rm B}$段. 由于 ${\rm A} \to {\rm B}$段主要是反应的诱导阶段,因此这两种化学反应机理的差异很有可能是反应描述的诱导时间上的差异.为此对一系列初始温度下的反应诱导时间进行了模拟,诱导时间定义为混合气体thermicity(归一化的化学反应放热速率)出现最大值的时刻.两种机理的诱导时间对比如图6所示,根据反射激波后的温度(约1 034 K)计算的这两种机理的反应诱导时间的差值约为19 $$s,与这两种机理在诱导阶段的时间差异(24 $$s)符合较好. 这说明由这两种机理模拟该实验,${\rm A} \to {\rm B}$段的时间差异主要是由反应诱导时间决定的.
|
图 4 激波管实验时间分辨纹影图[33] Fig.4 Time-resolved schlieren photograph of shock reflection-reation wave formation process |
|
图 5 最大压力和壁面密度时变曲线 (Oran机理和h2air\_highT机理的比较) Fig.5 Time evolution of maximum pressure in chamber and density at reflecting wall |

|
图 6 Oran机理和h2air\_highT机理的诱导时间比较 Fig.6 The induction time comparison between Oran and h2air_highT mechanism |
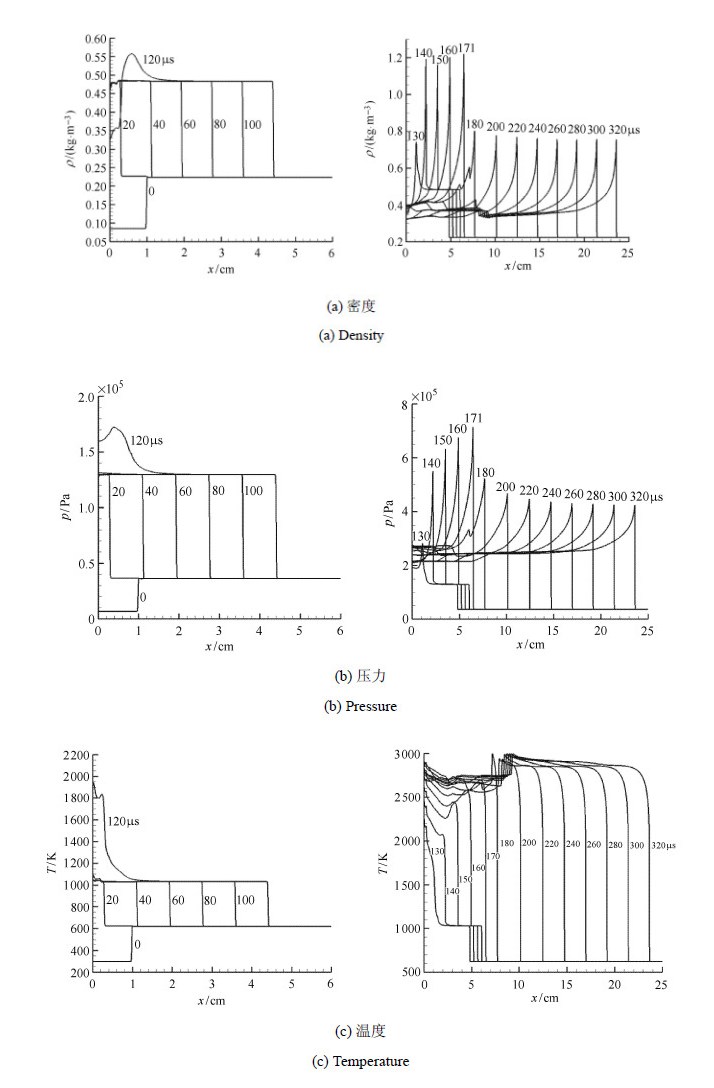
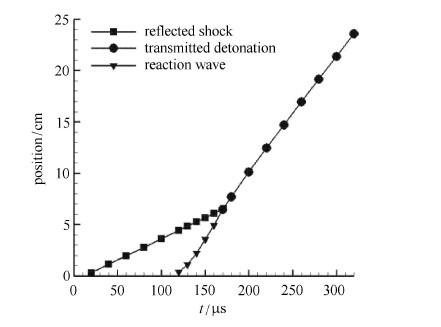
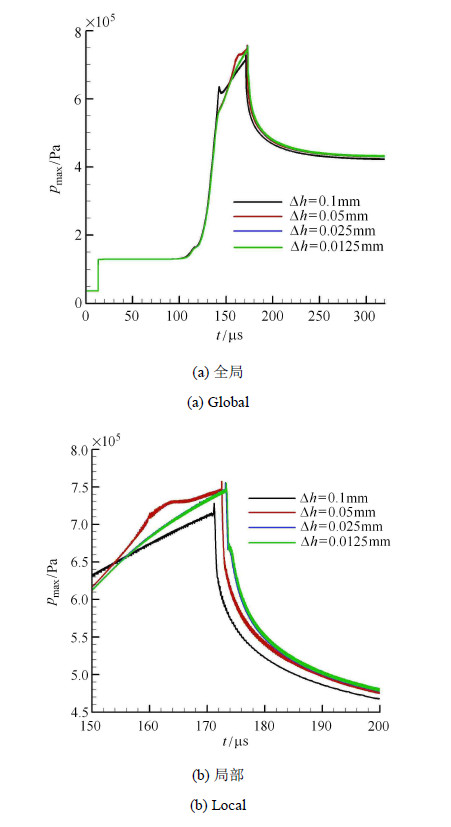
图7给出了由h2air{\_}highT机理(Oran机理的结果与之相似)计算的不同时刻的流场密度、压力和温度的空间分布,从这些曲线中可以清晰的识别爆轰点燃和发展的各个阶段.图8给出了记录的反射激波,燃烧波以及燃烧波与反射激波融合后形成的爆轰波阵面位置的时间变化曲线.根据爆轰波阵面的位置随时间的变化关系,经拟合计算可以得到爆轰波阵面的运动速度.表1给出了本文计算得到的爆轰波速与Wu等[35]的计算结果和SD-Toolbox计算的查普曼-儒盖爆轰波速的对比,可见本文的计算结果与理论和文献给出的结果符合较好.为了验证计算的网格收敛性,另外采用三套逐渐细化的网格进行了计算,网格间距$\Delta h$分别为0.05 mm,0.025 mm,0.012 5 mm.由h2air{\_}highT机理计算的爆轰波速如表2所示,可见不同网格计算的爆轰波速是一致的.图9给出了不同网格计算的全场最大压力的时变曲线,其中(a)是整体,(b)显示的是局部曲线. 图9表明$\Delta h$分别为0.025 mm和0.012 5 mm时的压力曲线几乎是重合的.
|
图 7 不同时刻密度,压力和温度的空间分布 (h2air_highT机理) Fig.7 Calculated density and pressure andtemperature distributions in chamber at various times (h2air_highT mechanism) |
|
图 8 反射激波,反应波和爆轰波阵面位置随时间的变化关系(h2air_highT机理) Fig.8 Calculated position of the reflected shock front, reaction wave, transmitted detonation as afunction of time for ignition behind a reflected shock (h2air_highT mechanism) |
| 表 1 爆轰波速比较 ($\Delta h =0.1$ mm) Table 1 The comparisons of detonation wave speed calculated bydifferent method (the grid spacing is 0.1 mm) |
|
图 9 不同网格计算的最大压力时变曲线 (h2air_highT机理) Fig.9 Comparison of time evolution of maximum pressurein chamber with different grid spacing (h2air_highT mechanism) |
| 表 2 同网格计算的爆轰波速 (h2air_highT机理) Table 2 The calculated detonation speed via different grid spacing (h2air_highT mechanism |
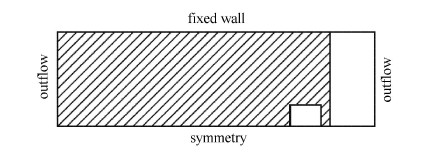
本节对H$_{2}$/O$_{2}$/Ar二维爆轰进行数值模拟,以检验本文算法模拟多维化学反应流的能力.当惰性气体Ar占混合气体的浓度较大时,产生的爆轰会形成很规则的爆轰胞格结构,因此很多学者通过计算H$_{2}$/O$_{2}$/Ar爆轰来考核他们的程序.本节计算的爆轰气体的初始条件与Oran等[37]采用的相同:初始化学配比为2:1:7,初始温度和压力分别为6 670 Pa和298 K,爆轰在高度为0.06 m的管道中传播.爆轰的计算需要能够分辨最小的空间尺度,需要能够捕捉到反应诱导距离和能量释放距离等,按照本问题的初始条件,爆轰的诱导距离约为1 mm,为了较好的模拟爆轰,诱导区至少需要分布约10个网格.如果采用固定的计算域进行计算,则需要计算域在爆轰运动方向上具有较长的距离,这将使得计算的网格量很大.本文采用Deiterding[38]的方法,在运动的计算域上进行计算,这样可以大大缩减计算域的长度.在运动计算域上计算爆轰传播,实际上是在以爆轰速度$D_{cj}$运动的坐标系上进行计算.本文所采用的计算域的长度为10 cm. 首先计算定常一维爆轰波结构,然后将一维爆轰结构作为二维爆轰计算的初场.爆轰阵面位于8.6 cm处.数值计算产生的扰动不足以在较短的时间内得到不稳定的爆轰结构,按照Deiterding[38]采用的方法,在爆轰阵面后设置一未反应气囊,该气囊的长度和高度分别为10 mm和14 mm,并沿轴线对称分布,气囊中心距爆轰阵面的距离为8 mm.未反应气囊内气体的温度和压力为来流未反应气体的7倍. 基于对称性,只取了管道的一半进行计算.计算域示意如图10所示. 本文所采用的计算网格为700$\times $200的均匀网格. 计算采用的化学反应模型为Oran机理.流动部分计算采用的WENO5M格式,时间推进采用3阶TVD Runge-$\!$-Kutta方法;化学反应部分采用 $\alpha$-QSS进行计算.
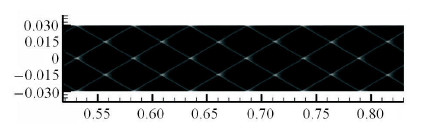
实验上研究爆轰结构的一个重要方法是观察爆轰传播过程中三波点留下的胞格结构.为了得到数值上的胞格结构,按照王昌建等的方法[6]记录了流场中每一网格点的最大压力.由于本文采用的是运动坐标系,而需要记录的是所有爆轰波经过之处的胞格结构,所以记录时需要做一定的变换,具体方法见Deiterding的论文[38]. 图11给出的是本文计算得到的数值爆轰结构.本文计算的胞格结构十分规则,计算的胞格尺寸与其他文献的结果比较如表3所示.
|
图 11 计算的胞格结构(长度单位:m) Fig.11 The calculated detonation cell structure (length unit: m) |
| 表 3 胞格尺寸与文献比较 Table 3 The comparisons of cell length and width |
为了显示爆轰发展的过程,图12显示了不同时刻流场的数值纹影,从图中可以清晰的识别入射激波,马赫杆,横向激波和滑移线等流场结构. 本文显示的数值纹影按照文献[39]中的方法得到. 在40 $$s之后,流场形成了明显的三波点结构.在110 $ $s之前,流场具有两个三波点;而在110 $ $s之后,流场出现了4个三波点. 即爆轰模数由2变成了4.随后爆轰的三波点数目保持稳定. 为了探求爆轰波模数是如何发生变化的,图13给出了$t=110\sim 114 $s间隔内OH的质量分数和温度云图. 可以看出,在这一时间段内马赫杆曲率变大,马赫杆后存在低温区以及燃烧阵面与马赫杆解耦. 这与Oran数值模拟得到的结果是一致的.从111 $$s开始,在三波点附近OH的质量分数最大,意味着此处发生了反应;随着时间的推移,三波点附近的反应区逐渐增大.实际上可以认为在三波点处发生了爆炸,爆炸波在传播过程中与马赫杆发生作用,最终形成了新的三波点,如图12中120 $ $s时的纹影所示. 从纹影图亦可以看出,在新的三波点的形成过程中滑移线是不稳定的.本文认为新的三波点的形成是由于在旧的三波点处发生了爆炸所致.但是三波点处为什么发生爆炸,以及何时发生爆炸仍然有待进一步的研究.

|
图 12 二维爆轰数值纹影图 Fig.12 The numerical schelieren of 2D detonation |

|
图 13 新的三波点形成过程中,OH的质量分数和温度的云图 Fig.13 The contours of mass fraction of OH and temperature in the process of the developelemt of the new triple point |
本文在一种简单但物理意义明确的化学非平衡流解耦算法的框架下,将近些年来发展的在临界点处不降阶的5阶WENO格式用于高速化学非平衡流动的数值模拟.通过对一维反射激波诱导爆轰波和二维H$_{2}$/O$_{2}$/Ar爆轰波这两个经典算例的模拟,计算结果与实验值和其他文献的计算结果符合很好,表明本文所采用的这种化学非平衡流解耦算法在应用高阶的流场计算格式时仍然具有较好的性质.应用这种解耦算法,仅需对现有的基于量热完全气体的可压缩流动计算程序做很小的修改,即能改造成化学反应流动计算程序,这样可以大大减少程序的编制时间,利于应用已有的基于量热完全气体假设的算法来模拟化学非平衡流动,因此这种解耦算法值得进行推广.
| [1] | Choi J-Y, Jeung I-S, Yoon Y. Computational fluid dynamics algorithns for unsteady shock-induced combustion, part 1: validation. AIAA Journal, 2000, 38(7): 1175-1185. |
| [2] | Kirk BS, Stognery RH, Olivery TA, et al. Recent advancements in fully implicit numerical methods for hypersonic reacting flows. AIAA 2013-2559, 2013 |
| [3] | Bussing TRA, Murman EM. A finite volume method for the calculation of compressible chemically reaction flows. AIAA-85-0331, 1985 |
| [4] | 杨顺华, 乐嘉陵, 赵慧勇等. 煤油超然冲压发动机三维大规模并行数值模拟. 计算物理, 2009, 26(4): 534-540 (Yang Shunhua, Le Jialing, Zhao Huiyong, et al. Three-dimensional massively parallel numerical simulation of kerosene-fueled scramjet. Chinese Journal of Computational Physics, 2009, 26(4): 534-540 (in Chinese)) |
| [5] | Zhong X. Additive semi-implicit Runge-Kutta methods for computing high-speed nonequilibrium reactive flows. Journal of Computational Physics, 1996, 128(1): 19-31 |
| [6] | 王昌建, 徐胜利. 直管内胞格爆轰的基元反应数值研究. 爆炸与冲击, 2005, 25(5): 405-416 ( Wang Changjian, Xu Shengli. Numerical study on cellular detonation in a straight tube based on detailed chem ical reaction model. Explosionand Shock Waves, 2005, 25(5): 405-416 (in Chinese)) |
| [7] | Mevel R, Davidenko D, Austin JM, et al. Application of a laser induced fluorescence model to the numerical simulation of detonation waves in hydrogene-oxygene-diluent mixtures. International Journal of Hydrogen Energy, 2014, 39(11): 6044-6060 |
| [8] | Leveque RJ. Finite Volume Methods for Hypersonic Problems. Cambridge, UK: Cambridge University Press, 2004 |
| [9] | Ferrer PJM, Buttay R, Lehnasch G, et al. A detailed verification procedure for compressible reactive multicomponent Navier-Stokes solvers. Computers & Fluids, 2014, 89: 88-110 |
| [10] | 潘振华, 范春宝, 张旭东等. 连续旋转爆轰三维流场的数值模拟. 兵工学报, 2012, 33(5): 594-599 (Pan Zhenhua, Fan Chunbao, Zhang Xudong, et al. Numerical simulation of three-dimensional flow field of continuous rotating detonation. Acta Armamentarii, 2012, 33(5): 594-599 (in Chinese)) |
| [11] | Liu Y, Liu X. Detonation propagation characteristic of H2-O2-N2 mixture in tube and effect of various initial conditions on it. International Journal of Hydrogen Energy, 2013, 38(30): 13471-13483 |
| [12] | Taylor BD, Kessler DA, Gamezo VN, et al. Numerical simulations of hydrogen detonations with detailed chemical kinetics. Proceedings of the Combustion Institute, 2013, 34(2): 2009-2016 |
| [13] | Uemura Y, Hayashi AK, Asahara M, et al. Transverse wave generation mechanism in rotating detonation. Proceedings of the Combustion Institute, 2013, 34(2): 1981-1989 |
| [14] | Tsuboi N, Morii Y, Hayashi AK. Two-dimensional numerical simulation on galloping detonation in a narrow channel. Proceedings of the Combustion Institute, 2013, 34(2): 1999-2007 |
| [15] | 刘君, 刘瑜, 周松柏. 基于新型解耦算法的激波诱导燃烧过程数值模拟. 力学学报, 2010, 42(3): 572-577 (Liu Jun, Liu Yu, Zhou Songbai. Simulation of shock induced combustion based on a novel uncoupled method. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(3): 572-578 (in Chinese)) |
| [16] | 刘君, 张涵信, 高树椿. 一种新型的计算化学非平衡流动的解耦方法. 国防科技大学学报, 2000, 22(5): 19-23 (Liu Jun, Zhang Hanxin, Gao Shuchun. A new uncoupled method for numerical simulation of nonequilibrium flow. Journal of National University of Defense Technology, 2000, 22(5): 19-22 (in Chinese)) |
| [17] | 刘君. 冲压加速器非平衡流动数值模拟. 弹道学报, 2002, 14(4): 31-35 (Liu Jun. Numerical study on the non-equilibrium flow of ram accelerator in the combustive mixture gas. Journal of Ballistics, 2002, 14(4): 31-35 (in Chinese)) |
| [18] | 刘君. 非平衡流计算方法及其模拟激波诱导振荡燃烧. 空气动力学学报, 2003, 21(1): 53-58 (Liu Jun. A new nonequilibrium numerical method and simulation of oscillating shock-induced combustion. Acta Aeronautica et Astronautica Sinica, 2003, 21(1): 53-57 (in Chinese)) |
| [19] | 刘君. 化学动力学模型对H2/Air超燃模拟的影响. 推进技术, 2003, 24(1): 67-70 (Liu Jun. Numerical study on chemical mechanism in supersonic H2/Air mixture gas flow. Journal of Propulsion Technology, 2003, 24(1): 67-70 (in Chinese)) |
| [20] | 刘世杰. 连续旋转爆震波结构、转播模态及自持机理研究. 长沙: 国防科学技术大学, 2011 (Liu Shijie. Investigations on the Structure, Rotating Mode and Lasting Mechanism of Continuous Rotating Detonation Wave. Changsha: National University of Defense Technology, 2012 (in Chinese)) |
| [21] | 刘世杰, 孙明波, 林志勇等. 钝头体激波诱导振荡燃烧现象的数值模拟. 力学学报, 2010, 42(4): 597-605 (Liu Shijie, Sun Mingbo, Lin Zhiyong, et al. Numerical research on blunt body shock-induced oscillating combustion. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(4): 597-605 (in Chinese)) |
| [22] | Liu J, Liu Y, Liu R. New uncoupling finite volume method for simulation of non-equilibrium flow and its application to supersonic combustion instability. Transaction of Nanjing University of Aeronautics & Astronautics, 2013, 30(5) |
| [23] | 刘瑜, 刘君, 白晓征. 基于新型非结构有限体积解耦算法的激波诱导燃烧数值模拟. 国防科技大学学报, 2011, 33(6): 139-143 (Liu Yu, Liu Jun, Bai Xiaozheng. Numerical simulation of shock-induced combustion with a new uncoupled algorithm in unstructured finite volume method. Journal of National University of Defense Technology, 2011, 33(6): 139-144 (in Chinese)) |
| [24] | Harten A, Engquist B, Osher S. Uniformly high order essentially non-oscillatory schemes, III. Journal of Computational Physics, 1987, 71(2): 231-303 |
| [25] | Liu XD, Osher S, Chan T. Weighted essentially non-oscillatory schemes. Journal of Computational Physics, 1994, 115(1): 200-212 |
| [26] | Jiang GS, Shu CW. Efficient implementation of weighted ENO Schemes. Journal of Computational Physics, 1996, 126(1): 202-228 |
| [27] | Balsara DS, Shu CW. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy. Journal of Computational Physics, 2000, 160(2): 405-452 |
| [28] | Henrick AK, Aslam TD, Powers JM. Mapped weighted essentially non-oscillatory schemes: achieving optimal order near critical points. Journal of Computational Physics, 2005, 207(2): 542-567 |
| [29] | Borges R, Carmona M, Costa B, et al. An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws. Journal of Computational Physics, 2008, 227(6): 3191-3211 |
| [30] | Castro M, Costa B, Don WS. High order weighted essentially non-oscillatory WENO-Z schemes for hyperbolic conservation laws. Journal of Computational Physics, 2011, 230(5): 1766-1792 |
| [31] | 刘瑜. 化学非平衡流动的计算方法研究及其在激波诱导燃烧现象模拟中的应用. [硕士论文]. 长沙: 国防科学技术大学, 2008 (Liu Yu. Numerical study of chemical nonequilibrium flow and its' application in shock-induced combustion. [Master thesis]. National Univerity of Defense Technology, 2008 (in Chinese)) |
| [32] | Shepherd JE. SD-Toolbox http://www2.galcit.caltech.edu/EDL/public/ cantera/html/SD_Toolbox/. 2013. |
| [33] | Oran ES, Boris JP. Numerical methods in reacting flows. AIAA-87-0057, 1987 |
| [34] | Im K-S, Yu S-T J, Kim C-K. Application of the CESE mehod to detontion with realistic finite-rate chemistry. AIAA-2002-1020, 2002 |
| [35] | Wu Y, Ma F, Yang V. Space-time method for detonation problems with finite-rate chemical kinetics. International Journal of Computational Fluid Dynamics, 2004, 18(3): 277-287 |
| [36] | Ng HD. The effect of chemical reaction kinetics on the structure of gaseous detonations. [PhD Thesis]. McGill University, 2005 |
| [37] | Oran ES, Weber JM, Stefaniw EI, et al. A numerical study of a two-dimensional H2-O2-Ar detonation using a detailed chemical reaction model. Combustion and Flame, 1998, 113(1-2): 147-163 |
| [38] | Deiterding R. Parallel adaptive simulation of multi-dimensional detonation structures. [PhD Thesis]. Branderburg University of Technology Cottbus, 2003 |
| [39] | Arienti M, Shepherd JE. A numerical study of detonation diffraction. Journal of Fluid Mechanics, 2005, 529: 117-146 |
2. School of Aeronautics and Astronautics, Dalian University of Technology, Dalian 116024, China;
3. College of Science, National University of Defense Technology, Changsha 410073, China;
4. Station No.2 of Group 95792, Lanzhou 735018, China
 2015, Vol. 47
2015, Vol. 47