薄液膜在固体壁面上的流动行为展现出丰富的动力学特征,其破断机理及稳定性一直是研究学者关注的热点问题[1, 2].尤其当薄液膜中含有表面活性剂时,活性剂浓度梯度驱使液膜由表面张力低的区域流向表面张力高的区域,即形成Marangoni效应[3, 4, 5],这一性质在汽车涂膜、数字储存设备制造及医疗领域有着广泛应用[6, 7, 8].近年来,微机电系统技术使微纳尺度下的液膜流动成为研究热点,与宏观尺度相比,微观尺度下的惯性力很小,黏性力突出.另外,粗糙度、壁面微结构等基底性质也是影响微尺度流体动力学特征的重要因素.一方面,微电子元件制造过程中元件表面的不平整性会导致镀膜厚度发生变化,进而影响产品质量;另一方面,基底表面的不平整性则有利于增强基底表面的流动和传热传质性能.
对于非平整壁面上的液膜流动,Kalliadasis等[9]模拟了流经矩形凹槽时的液膜表面形态,表明在进入凹槽或离开凸起前液膜表面会形成隆起结构,而最小液膜高度位于基底凹处,且隆起高度和最小液膜高度与基底凹槽深度和陡峭程度密切相关.Yuan等[10]基于亲水性柱状列壁面结构上的润湿现象,发现当流体接近柱体时,粗糙壁面多余面积会提供额外驱动力加速液滴的铺展.Pozrikidis等[11]研究了活性剂对波状结构基底上液膜流动的影响,结果表明,活性剂加剧了液膜表面变形程度.
当铺展液膜厚度处于微纳米量级时,其演化特性不仅受活性剂和基底性质的作用,还需考虑由分子间作用力引起的分离压对液膜流动的影响,Saprykin等[12]针对受底部加热的波状结构壁面上液膜流动行为,加入分离压影响,研究表明,分离压能有效阻止基底波峰处液膜破断现象. Stubenrauch等[13]测量了含活性剂薄膜的分离压,指出分离压作用的强弱与活性剂本身的种类、解离度和浓度密切相关.Warner等[14]建立了与活性剂浓度有关的分离压模型,对超薄液膜去润湿现象的研究表明,分子间引力是致使液膜不稳定,并导致破断或去润湿现象发生的主要诱因.叶学民等[15]在研究分离压对含活性剂液膜去润湿影响时还考虑了静电斥力的作用.结果表明,忽略静电斥力时分离压会导致液膜失稳,形成静态的去润湿结构,分离压对稳定性的影响与活性剂类型紧密相关.
但上述研究仅限于表面活性物质、基底表面性质和分离压中两者对液膜流动的影响. 对于含活性剂液滴在波状基底上铺展,仅见文献[16]. 但并未考虑铺展过程中当液膜很薄时铺展液膜与基底间存在的分离压效应.而同时考虑表面活性物质、基底表面特征和分离压作用下含活性剂液滴的铺展过程,目前尚未有报道.本文根据润滑理论[17, 18, 19, 20],通过建立分离压作用下波纹状基底上含不溶性活性剂液滴铺展过程的演化模型,借助数值计算研究表面活性物质、基底表面特征及分离压耦合作用下的液滴铺展历程,进而分析分离压的独特影响.
1 理论模型及演化方程组 1.1 液滴铺展物理模型当液滴在固体表面铺展时,需满足无滑移边界条件.为避免在固/气/液三相接触线处的应力奇异性问题,Zhao[21]认为接 触线前存在一层很薄的前驱膜,呈类固体性质.为得到同一效果,本文首先用溶液将基底填平,然后预置一层厚度为$H_{b}^{\ast}$的液膜,由此可视为液滴在预置液膜上的铺展过程,满足无滑移边界条件. 如图1所示,$s^{\ast }(x^{\ast})$为基底函数,$D^{\ast}$为基底高度,初始时刻将一滴含不溶性活性剂的液滴放置在此液膜上,则液滴在活性剂浓度、基底和分离压的共同作用下铺展.假设活性剂液滴为不可压缩牛顿流体,动力黏度$\mu^{\ast }$和密度$\rho^{\ast }$均为常数,基底为无滑移、无渗透壁面,忽略气体黏性影响. 液滴最大高度$H^{\ast }$与流动方向尺度$L^{\ast }$相比非常小,即满足$ \varepsilon = H^{\ast }/L^{\ast } \ll 1$,符合润滑理论[17 -20].(上标"$^{\ast }$" 代表有量纲量)
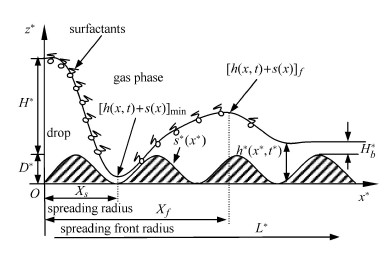
|
图 1 波状基底上含不溶性活性剂液滴的铺展示意图 Fig. 1 Schematic diagram of the spreading of liquid droplet with insoluble surfactants on corrugated topography |
控制方程组包括连续性方程、运动方程和浓度扩散方程,边界条件为壁面上的无滑移无穿透条件及界面的法向和切向力平 衡方程[3]. 对比文献[3],本研究运动方程中增加了分离压项$\varPi $. 通过对控制方程组及边界条件的无量纲化,依据润滑理论保留数量级为$\geqslant O( \varepsilon)$的项(推导过程与文献[3]类似),可得
无量纲连续性方程、运动方程和浓度扩散方程为
| $u_x + w_z = 0 $ | (1) |
| $u_{zz} = \left( {p + { \varPi}} \right)_x $ | (2) |
| $\left( {p + { \varPi} } \right)_z = 0 $ | (3) |
| $\varGamma _t + \left( {u_s \varGamma } \right)_x = \dfrac{1}{Pe}\varGamma _{xx}$ | (4) |
式中,气液界面处的Peclet数$Pe = {U^\ast L^\ast } / {D_s^\ast }$,下角标($x$,$z$,$t)$为对($x$,$z$,$t)$的导数,下角标$s$为界面处的相关量,$D_{s}^{\ast }$为界面处浓度 扩散系数. $U^\ast = S^\ast H^\ast /\mu ^\ast L^\ast $为Marangoni速度,表示Marangoni应力与黏性力的平衡.
表面张力关系式为
| $\sigma = 1 - M\varGamma $ | (5) |
式中,Marangoni数$M = \alpha _\varGamma \varGamma _m^\ast / S^\ast $,$\alpha_{\varGamma }$为表面张力梯度,$\varGamma_{m}^{\ast }$为活性剂最大浓度,$S^{\ast }=\sigma^{\ast }_{c}-\sigma^{\ast}_{m}$为膨胀压,$\sigma _c^\ast $和$\sigma _m^\ast $分别为未加入和加入活性剂时的液膜表面张力.
无量纲边界条件为
| $z = s ,\quad u = w = 0 $ | (6) |
| $z = h + s ,\quad u_z = \sigma _x $ | (7) |
| $z = h + s ,\quad p = - C\left( {h_{xx} + s_{xx} } \right) $ | (8) |
| $z = h + s ,\quad h_t + u_s \left( {h_x + s_x } \right) = w_s $ | (9) |
式中,毛细数$C = { \varepsilon^2\sigma _m^\ast } / {S^\ast }$.
分离压采用与Warner等[14]所提模型类似的形式
| ${ \varPi} = - \dfrac{A}{h^3} + \dfrac{Bh_\infty }{h^4} $ | (10) |
式中,$ - \dfrac{A}{h^3}$为范德华引力,$\dfrac{Bh_\infty}{h^4}$为Born斥力,$A$和$B$分别表示引力和斥力的强度系数;$h_{\infty }$为液膜平衡高度,其无量纲化参见文献[14].加入活性剂除改变界面张力分布形成的Marangoni效应外,对分离压 也存在一定影响.为此,Warner等[14]和叶学民等[15]在研究液膜在平整基底上的流动问题时,建立了引力强度系数$A$与活性剂浓度呈线性关系的分离压模型.而本文所建模型不同之处在于引力和斥力强度系数$A$和$B$均为与活性剂浓度有关的线性函数(对应Bhakta和Ruchkenstein[19]的部分实验结果),并将本模型应用于含活性剂液滴在波状基底上的铺展问题.
结合式(1)$\sim $式(10),通过积分可得液膜高度$h$和活性剂浓度$\varGamma $ 的演化方程组
| $ h_t = \left[{ - \dfrac{C}{3}h^3\left( {h_{xxx} + s_{xxx} } \right) + \dfrac{M}{2}h^2\varGamma_x - } \right. \\ \qquad \left.{\dfrac{h^3}{3}\left( { - \dfrac{A}{h^3} + \dfrac{Bh_\infty}{h^4}} \right)_x } \right]_x $ | (11) |
| $ \varGamma_t = \dfrac{\varGamma_{xx} }{Pe} - \left[{\dfrac{C}{2}h^2\varGamma\left({h_{xxx} + s_{xxx} } \right) - Mh \varGamma \varGamma_x + } \right. \\ \qquad \left.{\dfrac{1}{2}h^2\varGamma\left( { - \dfrac{A}{h^3} + \dfrac{Bh_\infty }{h^4}} \right)_x } \right]_x $ | (12) |
式中$M$和$C$项分别代表Marangoni效应和毛细力对$h$和$\varGamma $演化的贡献,通过求解该方程组可获得液滴铺展特征.
2 数值模拟和结果分析 2.1 数值模拟初始条件及边界条件采用PDECOL程序[22, 23]求解演化方程式(11)和式(12). 根据演化尺度选取$0 < x < 15$一维区域进行计算,模拟中将其划分为2 000个均匀网格,与网格数为3 000对比,计算精度仅降低0.06{\%},满足计算精度要求,且模拟时间大为减少.Afsar-siddiqui等[24]以AOT系列阴离子型表面活性剂为对象,实验研究了活性剂浓度对含活性剂液膜演化过程的影响.本文参照该实验数据,并结合相关资料[23, 25]得到文中所用无量纲参数的数量级范围如表1所示.下文计算中所用无量纲参数,如无特殊说明取值如下:$C =0.1$,$M =100$,$Pe =100$.
| 表 1 无量纲参数定义及数量级范围 Table 1 Representation and order of magnitude estimates of the relevant dimensionless groups |
壁面函数为
| $s\left( x \right) = D / 2\left[{\sin \left( {kx} \right) + 1} \right] $ | (13) |
式中,基底高度$D =0.2$,波数$k =2$.
初始液膜高度和活性剂浓度分布为
| $\begin{array}{l} h\left( {x,0} \right) = \left( {1 + {H_b} - {x^2}} \right)F\left( {1 - x} \right) + \\ \qquad {H_b}F\left( {x - 1} \right) + D - s\left( x \right) \end{array}$ | (14) |
| $ \varGamma\left( {x,0} \right) = \varGamma_0 F\left( {1 - x} \right) $ | (15) |
式中,$F(x)=0.5[1+ {\rm tanh} (100x)]$为海氏阶跃函数.其中,预置液膜高度$H_{b}=0.1$;初始活性剂浓度$\varGamma_{0}=1$.
液滴铺展过程中保证活性剂摩尔总量守恒,这也是确保数值模拟结果准确性的另一重要方面. 即
| $\int_{ - \infty }^{ + \infty } {\varGamma} {\rm{d}} x = 1 $ | (16) |
数值模拟时,为保证数值计算结果的正确性,对式(16)在整个计算区域进行计算,可得每一时刻的活性剂总量,如 图2所示.该图表明,$\varPi =0$时的活性剂总量保持不变,$\varPi \ne0$时活性剂总量在0.995以上,与式(16)相比误差均小于0.5{\%},由此可认为活性剂在整个计算区域质量守恒.
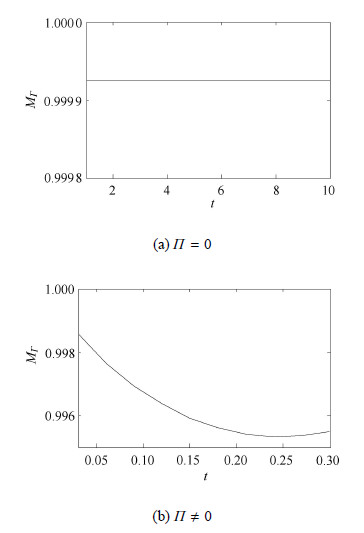
|
图 2 活性剂总量 Fig. 2 The total amount of surfactant |
图3为$\varPi=0$时波状基底上液膜高度和活性剂浓度的演化历程. 该图表明,随演化过程进行,液滴中心厚度不 断降低.铺展后期($7 < t < 10$),最小液膜高度附近的液膜开始紧贴壁面,诱发去润湿特征的形成[16],而铺展前沿处衍生出不规则子波随时间$t$数量不断增加(图3(b)),Pozrikidis等[11]在研究活性剂液膜在波状结构基底上流动时,指出活性剂放大了液膜表面的变形程度,本文亦得出相同结论.图3(c)表明,活性剂浓度随铺展范围增大不断降低,而在铺展前沿附近活性剂浓度剖面不再光滑,受基底作用呈现轻微的波动特征,这与平整基底上的浓度演化历程有所不同.
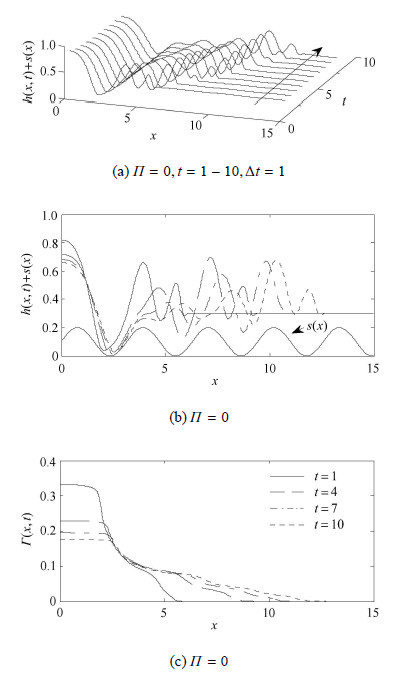
|
图 3 $\varPi$ = 0 时液膜高度和活性剂浓度的演化历程 (M = 100, C = 0:1, Pe = 100) Fig. 3 Evolutions of the film height and surfactant concentration at $\varPi$ = 0 (M = 100, C = 0:1, Pe = 100) |
$\varPi \ne 0$时的演化历程如图4所示. 此时,液膜高度演化时间缩减为$t =0.3$,受分离压影响,铺展前沿后的预置液膜呈现出与基底形状相似的波状结构[12],形成与$\varPi =0$时截然不同的演化特征. 基底第一波谷处的$[h(x,t)+s(x)]_{\min}$随时间逐渐下降,但由于受到分离压中Born斥力阻碍作用,下降速率逐渐减缓,最终在分离压、活性剂及波状基底耦合作用下,基本保持不变. 但与$\varPi =0$时相比,其高度明显增大,去润湿现象消失.这与Saprykin等[12]得出的分离压有助于抑制受热波状基底波峰处液膜破断现象的结论吻合. $\varPi \ne0$时铺展前沿处衍生出的子波结构明显减少. 相对于$\varPi =0$情形,分离压影响下铺展过程更加稳定.叶学民等[26]在分析分离压作用下液滴铺展时亦得出相同结论.
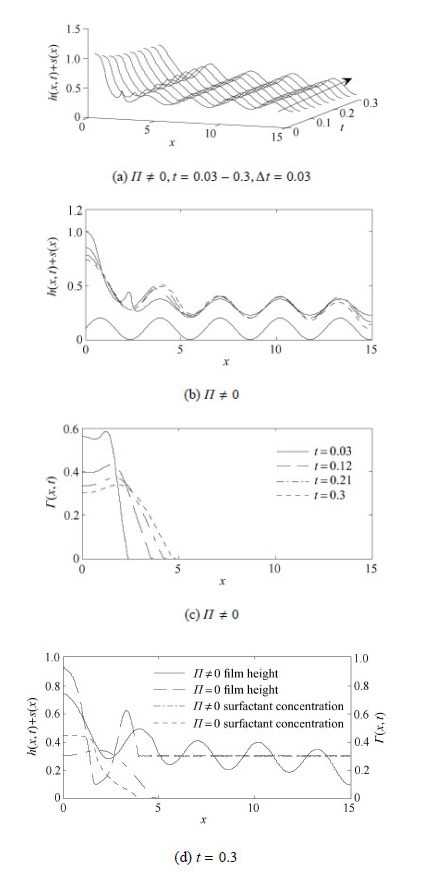
|
图 4 $\varPi \ne 0$时液膜高度和活性剂浓度的演化历程 ($\alpha_{1}= - 1$, $\alpha_{2} =1$, $M =100$, $C =0.1$, $ Pe =100$) Fig. 4 Evolutions of the film height and surfactant concentration at $\varPi \ne 0$ ($\alpha_{1}=-1$, $\alpha _{2}=1$, $M =100$, $C =0.1$, $Pe =100$) |
另外,铺展前沿$X_{f}$在向前推移的同时,受基底及分离压影响,其液膜高度呈现先增后降的趋势,并在基底波峰处达到最大值. 图4(c)和4(d)表明,$\varPi \ne0$时活性剂的分布范围变宽,液滴中心处活性剂浓度不断减小进而形成凹陷状. 而铺展前沿处的活性剂浓度梯度较$\varPi =0$时明显增大如(图4(d)),表明Marangoni效应增强,液滴铺展速率加快.
2.4 初始液滴位置对演化影响初始条件的选取对液滴的铺展具有重要影响,因此有必要讨论液滴初始位置改变对铺展特性的影响. 图5给出了初始液滴位于波峰处时液滴的演化过程.可知,初始液滴位于波峰处时,各时刻的最小液膜高度分别位于不同波谷处,且液膜高度相对较大,并没有形成明显的去润湿现象.对比图3(b)和图3(c)可知,同一时刻液滴中心高度下降速率加快,活性剂扩散范围增大,说明$\varPi=0$时初始液滴位于波峰处时会加速铺展. $\varPi \ne 0$时液膜高度与浓度演化近似与图4(b)和图4(c)一致,表明分离压减弱了基 底对液滴演化过程的影响.
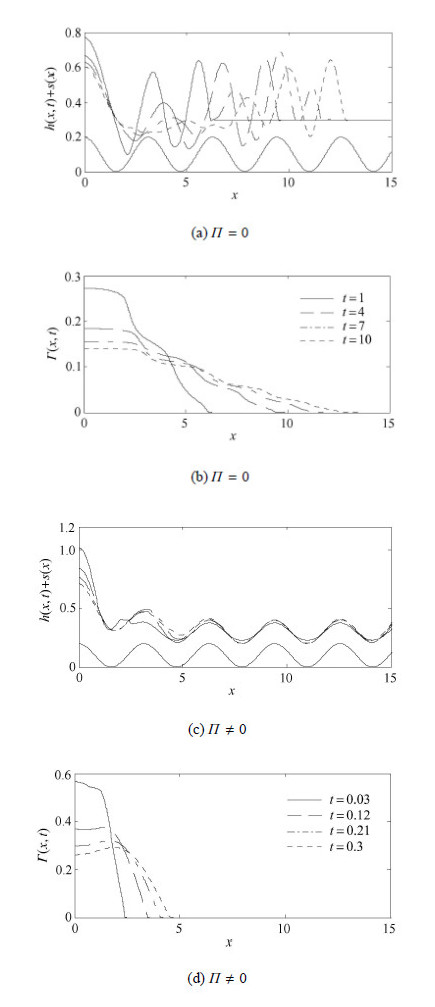
|
图 5 初始液滴位于波峰处对液滴演化影响 ($M =100$, $C =0.1$, $Pe =100$) Fig. 5 Effect of initial droplet at the crest on evolutions ($M =100$, $C =0.1$, $Pe =100$) |
图6为$t =0.3$时液滴完全铺展情形下毛细力、Marangoni力和分离压对液膜高度垂直方向的影响情况. 可知,在铺展前沿处($x=4.7$)Marangoni力急剧上升,为平衡其对液膜高度的影响,毛细力和分离压骤然下降,其合力大致和Marangoni力相等,液滴铺展达到平衡.在$0 < x < 4.7$内分离压与Marangoni力大致呈对称分布,说明分离压有利于抑制Marangoni力,从而缓解液膜的变形,使铺展前沿处子波结构明显减小,铺展前沿高度$[h(x,t)+s(x)]_{f}$降低,最小液膜高度$[h(x,t)+s(x)]_{\min}$上升.

|
图 6 Marangoni力、毛细力和分离压对液膜高度演化的影响 ($M =100$, $C =0.1$, $Pe =100$) Fig. 6 Effect of Marangoni stress, capillary force and disjoiningpressure on the film height evolution ($M =100$, $C =0.1$, $Pe =100$) |
4mm上述分析表明,分离压是影响液滴铺展过程的重要因素,因此有必要研究不同阶段的分离压对液膜高度演化造成的影响.如图7所示,$t =0.000 3$时刻液滴刚开始铺展,在活性剂浓度梯度驱使下铺展前沿处[3] ($x=1.1$)液膜高度开始增大,但幅度较小,铺展前沿后预置液膜仍然保持水平状态(如图7(b)).而分离压对液膜高度的变化较敏感,$t=0.000 3$时刻铺展前沿附近分离压出现波动,强度较大;而在铺展前沿后基底波峰处液膜较薄,Born斥力较大,分离压为正值,而波谷处液膜较厚,范德华力作用明显,分离压为负值(如图7(a)).随时间持续,分离压强度减小,铺展前沿向前推移,铺展前沿高度增大.铺展前沿后受Born斥力影响基底波峰处液膜出现隆起,而波谷处液膜在范德华力作用下出现凹陷.液膜高度变化又会对分离压造成影响,使基底波峰处分离压减小,波谷处分离压增大.最终在两者协同作用下,铺展前沿后的分离压逐渐趋向于0,而液膜高度则呈现基底形状的波状结构,液滴铺展达到平衡状态.
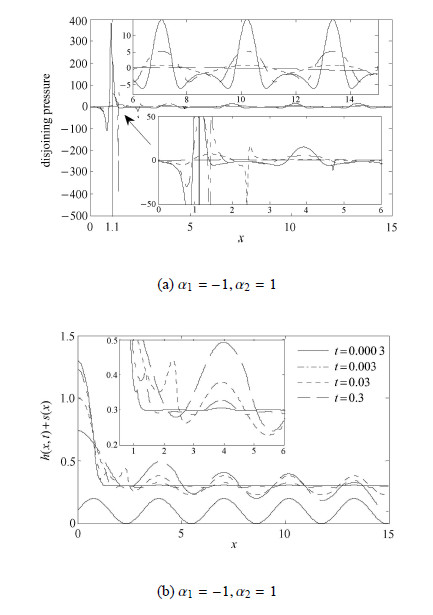
|
图 7 分离压演化过程及对液膜高度的影响 ($M =100$, $C =0.1$, $Pe =100$) Fig. 7 The disjoining pressure evolution and its effect on filmheight ($M =100$, $C =0.1$, $Pe =100$) |
如前所述,与Warner等[14]不同,本文所用分离压模型考虑了活性剂浓度对范德华力和Born斥力的影响. 定义 $A =1+\alpha_{1} \varGamma $,$B =1+ \alpha_{2} \varGamma $,其中$\alpha_{1}$,$\alpha_{2}$表征与活性剂浓度关联系数,并考虑了浓度对强度系数的两种不同影响,即$A$和$B$随浓度增加而线性减小($\alpha_{1}$,$\alpha_{2}= - 1 \sim 0)$和随浓度增加而线性增大($\alpha_{1}$,$\alpha_{2} =0 \sim 1$),可更合理评价活性剂特性对液滴演化历程的影响[13, 14, 15].
图8(a)表明,引力强度系数$\alpha_{1}$增大使液滴中心高度增加,铺展范围缩小,这是因增大$\alpha_{1}$提高了Hamaker系数$A$,从而增强了范德华力,抑制了液滴铺展,这与文献[26]所得结论吻合. 与此同时引发最小液膜高度持续下降.为便于比较,图8(b)给出了$0.003 < t < 0.3$铺展前沿高度$[h(x,t)+s(x)]_{f}$和最小液膜高度$[h(x,t)+s(x)]_{\min}$的演化特征. 该图表明,$\varPi =0$时$[h(x,t)+s(x)]_{f}$随时间$t$呈增长趋势,且增长速率逐渐减小,这是因为铺展刚开始时活性剂浓度分布不均匀,进而引起Marangoni梯度较大,从而驱动液滴快速向外扩展;而随铺展过程进行,活性剂浓度分布逐渐趋于均匀,Marangoni效应引起的驱动力较小,致使液滴铺展减缓.$\varPi \ne 0$时,基底波谷处受到范德华引力作用(图7)$[h(x,t)+s(x)]_{f}$较小,而波峰处受到Born斥力作用$[h(x,t)+s(x)]_{f}$较大,使$[h(x,t)+s(x)]_{f}$随时间$t$则呈现波状变化(如图8(b)).在 $0.003 < t < 0.03$和$0.05 < t < 0.2$,$[h(x,t)+s(x)]_{f}$随时间$t$持续增长,且随$\alpha_{1}$增大高度减小;而$0.03 < t < 0.05$和$0.2 < t < 0.3$范围内$[h(x,t)+s(x)]_{f}$随时间$t$不断降低,在$0.03 < t < 0.05$其高度随$\alpha_{1}$基本保持一致;而在铺展后期$(0.2 < t < 0.3)$,受到基底波谷处范德华引力作用,$[h(x,t)+s(x)]_{f}$呈下降趋势,$\alpha_{1}$增大液滴铺展速率减慢,引力作用更不明显,致使$0.2 < t < 0.3$范围内$[h(x,t)+s(x)]_{f}$随$\alpha_{1}$提高而增大. 对比两种情况发现,$\varPi \ne 0$时$0.003 < t < 0.03$内$[h(x,t)+s(x)]_{f}$ 大于$\varPi=0$时的值,这是因为$\varPi \ne 0$时液滴刚开始铺展,铺展前沿正处于基底第一波峰附近,受Born斥力及活性剂浓度影响,$[h(x,t)+s(x)]_{f}$较大,而$\varPi =0$时只受到活性剂浓度影响,且处于液滴铺展初期,$[h(x,t)+s(x)]_{f}$较小. $t =0.03$之后,分离压的阻碍作用逐渐显现(图6),造成前者的$[h(x,t)+s(x)]_{f}$均小 于后者的高度. 图8(b)表明,$\varPi=0$时$[h(x,t)+s(x)]_{\min}$始终随时间$t$持续下降,且下降速率逐渐减小;而$\varPi \ne 0$时,总体上液膜高度随时间$t$呈下降趋势,铺展后期最小液膜高度不再变化达到恒定值,且在$0.003 < t < 0.3$范围内随$\alpha_{1}$增大最小液膜高度下降,与图4(b)和图8(a)一致.
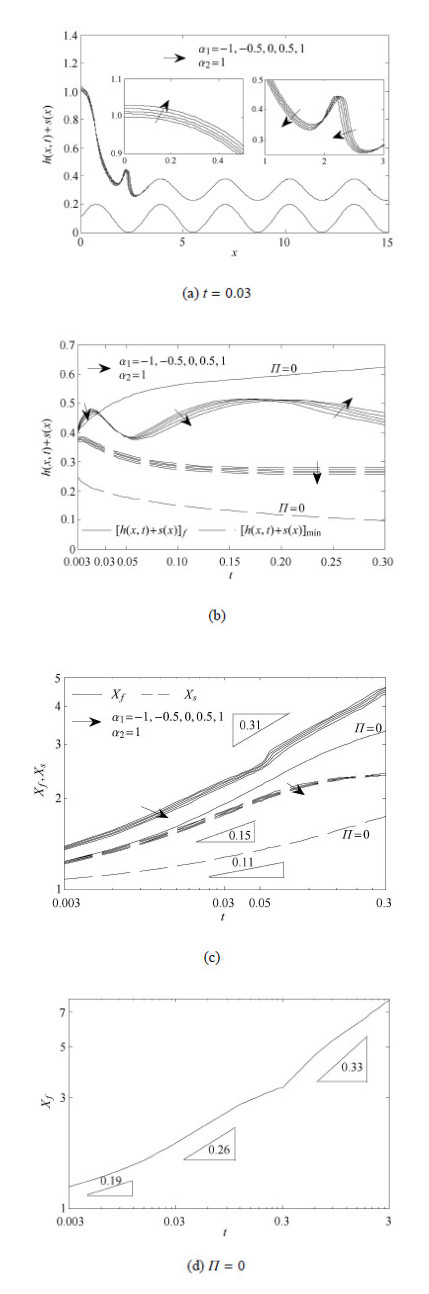
|
图 8 关联系数$\alpha_{1}$的影响 ($M =100$, $C =0.1$, $Pe =100$) Fig. 8 Effect of Correlation coefficient $\alpha_{1}$ ($M =100$, $C =0.1$, $Pe =100$) |
图8(c)和图8(d)为液滴铺展前沿半径$X_{f }$(对应活性剂浓度为0时的液膜铺展范围)和铺展半径$X_{s}$(对应液膜高度最小时的液滴铺展范围)随时间$t$的变化情况. 文中采用$X_{f}$,$X_{s}$$\sim$$t^{n}$在总体上表征液滴在基底上铺展的快慢程度. 其中$\varPi=0$时$X_{f}$在$0.003 < t < 0.03$内以$t^{0.19}$速率增长,$0.03 < t < 0.3$内增大至$t^{0.26}$(如图8(d)). 而对于$\varPi\ne 0$时,$X_{f}$在$0.003 < t < 0.3$内则始终以$t^{0.31}$稳定增长,高于$\varPi =0$时的变化率. 图8(d)给出了$\varPi =0$时,$0.003 < t < 3$内铺展前沿$X_{f}$的变化.可知$X_{f}$增长率随时间$t$持续增加,在演化后期$t>0.3$时其增长率为$t^{0.33}$,与赵亚溥等[10]在研究柱状表面的液滴动态润湿特性时所得的结论完全吻合.而$\varPi \ne 0$时铺展半径$X_{s}$在$0.003 < t < 0.3$内符合关系$t^{0.15}$高于$\varPi=0$时的$t^{0.11}$(如图8(c)),说明分离压具有加快铺展速率的作用,与图4(d)所得结果一致.
2.6 关联系数$\alpha_{2}$ 的影响}图9为与Born斥力有关的强度系数$\alpha_{2}$对演化过程的影响. 图9(a)表明,减小$\alpha_{2}$将抑制液滴铺展,尤其当$\alpha_{2}= -1$时,演化时间极度缩减,出现"冻结"现象,并在铺展前沿处出现明显的震荡特征,造成液滴的铺展不稳定,文献[26]亦得出相同结论.由图9(b)可知,增大$\alpha_{2}$铺展前沿高度$[h(x,t)+s(x)]_{f}$的变化趋势有所不同,当$\alpha_{2}$较大时,Born斥力作用明显,铺展前期$(0.003 < t < 0.05)$,铺展前沿作用范围较小[16],$[h(x,t)+s(x)]_{f}$形成高而陡的波峰,而到了后期$(0.1 < t < 0.25)$铺展前沿被拉长,作用范围增大[16],形成的波峰较为平缓;对于较小的$\alpha_{2}$,Born斥力作用较弱,前期$[h(x,t)+s(x)]_{f}$波峰低而平缓,后期由于液滴铺展范围减小,受基底第二波峰处Born斥力影响较弱,则$[h(x,t)+s(x)]_{f}$并未形成明显波峰,而呈现随时间$t$缓慢增长的特征. 对比$\varPi =0$,仅在$\alpha_{1} =1$,$\alpha_{2} =1$,$0.003 < t < 0.026$范围内铺展前沿高度大于$\varPi =0$时,其余范围均小于$\varPi =0$时.而最小液膜高度随时间$t$的推移,两种情形都呈降低趋势,但$\varPi=0$时,最小液膜高度更小甚至紧贴壁面,极易发生破断(如图3(b)). 图9(c)表明,$\alpha_{1} =1$,$\alpha_{2} =1 \to0$时$X_{f}$始终大于$\varPi =0$时. 而随$\alpha_{2}$减小,Born斥力减弱,液滴铺展速率变慢,致使$\alpha_{2}= -0.2$时,在$0.003 < t < 0.15$内$X_{f}$小于$\varPi =0$时,$t =0.15$后大于$\varPi =0$时,而$\alpha_{2}= - 0.5$时$X_{f}$始终小于$\varPi =0$时的铺展前沿高度. 另外,$\alpha_{1} =1$,$\alpha_{2} =1$时$X_{f}$近似以 $t^{0.31}$速率增长,随$\alpha_{2}$减小$X_{f}$增长速率略有减小. 而$X_{s}$增长速率与图8(c)无异,快于$\varPi =0$时的增长速率. 图9表明,相对于范德华引力,液滴的演化过程对Born斥力的影响更为敏感,这与文 献[14, 15, 26]所得结论一致.
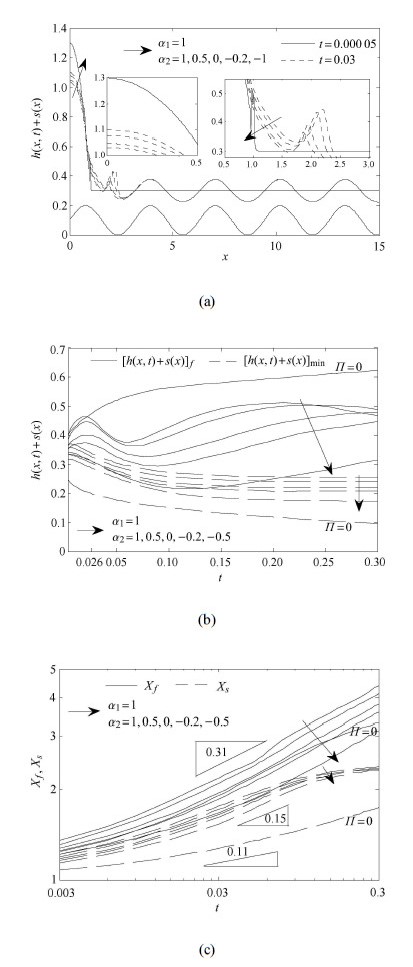
|
图 9 关联系数$\alpha_{2}$的影响 ($M =100$, $C =0.1$, $Pe =100)$ Fig. 9 Effect of correlation coefficient $\alpha _{2}$ ($M =100$, $C =0.1$, $Pe =100)$ |
上述研究表明,$\alpha_{1}= -1$,$\alpha_{2}=1$时液滴的演化特征比较明显,故选取其为特征参数讨论基底参数的影响. 图10为基底高度$D$对液滴铺展和分离压的影响.在较小的基底高度$D$下,液膜形成的波峰低而平缓;随$D$增高,基底不平整度突出,铺展前沿处形成的子波高度也相应增大,这是因增高$D$使得铺展前沿处分离压强度减小,Marangoni力克服分离压逐渐占支配地位(如图10(b)).而$[h(x,t)+s(x)]_{\min}$则增加较少,尤其是$D =0.4$,其高度基本与$D =0.3$持平.基底高度对活性剂浓度的影响主要体现在液滴中心处,如图10(a)所示,$D =0.1$时,液滴中心处浓度明显低于铺展前沿侧的浓度,随$D$增加其中心浓度升高,浓度分布趋于平台状;而铺展前沿处的浓度梯度减小,表明液滴不平整度增大会减弱Marangoni效应,使液滴铺展变得缓慢.

|
图 10 $t =0.3$时,基底高度$D$对演化历程和Marangoni项及分离压项的影响 ($M =100$, $C =0.1$, $Pe =100$) Fig. 10 Effect of height $D$ on spreadingevolution, Marangoni item and disjoining pressure at$t =0.3$ ($M =100$, $C =0.1$, $Pe =100$) |
基底波数$k$也是影响液滴铺展的重要参数,如图11所示,$k=1$时液滴铺展比较平滑,铺展前沿处形成的波峰微小,铺展前沿 后的液膜几乎处于平面状. 随$k$增加,尤其当$k=4$时,使得当地的基底表面曲率增大,此时对应的液滴中心增厚,铺展前沿高度也明显增大,而最小液膜高度急剧下降,加剧基底对液膜高度的扰动程度,并引起分离压变化,而分离压又作用于演化历程,致使铺展前沿后液膜高度和分离压产生相似的变化(如图11(a)和11(c)).图11(b)表明,铺展前沿处活性剂浓度梯度随波数增加有小幅度减少,说明$k$增加液滴铺展速度减慢.

|
图 11 $t =0.003$时,基底波数$k$对演化历程和分离压项的影响 ($M =100$, $C =0.1$, $Pe=100$) Fig. 11 Effect of wave-number $k $ on spreading evolution and disjoining pressure at $t =0.003$ ($M =100$,$C =0.1$, $Pe =100$) |
为进一步研究波状基底上分离压对液滴铺展的影响,图12给出了第1 $\sim $第5基底波峰和波谷处液膜高度的演化特征(由数字1 $\sim $5表示). 该图表明,第1 $\sim$5波峰波谷处的液膜高度演化特征(图中以斜率$\gamma $ 表示)明显不同,但总体上可分为快速和缓慢两个阶段,但两阶段的转变时间又有所不同. 其中,波峰处的液膜高度总体呈单驼峰状变化,第1和第2的转变时间为$t =0.015$和$t=0.175$,第3 $\sim $5波峰处的变 化近似,其转变时间均为$t=0.05$;而波谷处,除第1波谷呈驼峰型变化外,其余均为类似的逐渐减小特征,但其波谷处液膜高度的转变时间均为$t=0.03$.

|
图 12 波峰波谷处液膜高度$h(x,t)+s(x)$演化过程 ($M =100$, $C =0.1$, $Pe =100$) Fig. 12 The evolution of film height at the peak andTrough ($M =100$, $C =0.1$, $Pe =100$) |
对于基底第1波峰处的液膜高度,在$t =0.003 \sim 0.015$内,由于液滴刚开始铺展活性剂浓度梯度较大,液膜高度以$\gamma =4.5$快速增长,随铺展前沿推进,液膜高度开始降低,在$t =0.015 \sim 0.3$范围内以$\gamma = - 0.35$缓慢下降. 对于基底第2波峰,出现波峰的时间推迟到演化后期$t =0.175$;在$t =0.003 \sim 0.05$时,因波峰处液膜较薄,受到Born斥力影响,液膜高度增长率较大$\gamma =2.9$;在$t =0.05 \sim 0.175$,变化率减为$\gamma =0.69$,这是因随时间推进铺展前沿开始与此处波峰叠加造成液膜高度持续上升的缘故;而后期$t =0.175 \sim 0.3$则以$\gamma =-0.17$缓慢下降. 对于基底第3 $\sim$第5波峰处液膜高度的变化在$t =0.003 \sim 0.05$与第2波峰处完全相同,不同之处表现$t=0.05$后,其液膜高度或基本保持不变(对应第3和第4波峰),或以小速率$\gamma =-0.22$持续下降(对应第5波峰).
对于基底第1波谷处的液膜高度,在$t =0.003 \sim 0.018$受范德华力作用,液膜高度以$\gamma = - 2.6$下降;随铺展前沿推进到此处,在$t =0.018 \sim 0.03$Marangoni力逐渐占支配作用,液膜高度以$\gamma =8.5$急剧上升;而铺展前沿继续推进,Marangoni力影响逐渐减弱,液膜高度开始降低,在$t =0.03 \sim 0.1$降低速率$\gamma = - 3.8$;最终在分离压、毛细力和Marangoni力的共同作用下,在$t =0.1 \sim 0.3$液膜高度不再变化. 对于基底第2 $\sim$第5波谷在$0.003 < t < 0.03$下降速率基本相同$\gamma = - 2.6$;而在$0.03 < t < 0.3$第2波谷以$\gamma =0.27$缓慢上升;第3波谷基本保持不变;而第5波谷近似以$\gamma =- 0.36$下降,快于第4波谷处的$\gamma =-0.16$.
3 结 论(1)分离压作用下液滴在波状基底上铺展时,受Marangoni力和分离压共同作用,铺展前沿高度在基底波峰处达到最大值,铺展前沿后的预置液膜呈现出与基底形状相似的波状结构;与$\varPi =0$相比,其铺展速率更快,铺展前沿处衍生出的不规则子波数量明显减少,液滴铺展更加稳定.
(2)分离压对液滴铺展稳定性的影响与活性剂关联强度密切相关,减小引力强度系数$\alpha_{1}$可促进液滴铺展,而减小斥力强度系数$\alpha_{2}$则起到抑制作用,尤其是$\alpha_{2}= - 1$时,液滴几乎不能铺展,处于"冻结"状态,分离压放大了液滴的演化扰动能量,使液膜高度在铺展前沿处出现震荡特征.
(3) $\varPi =0$时铺展前沿高度随时间$t$持续增加,而$\varPi \ne 0$时则呈现明显的波状变化;提高引力强度系数$\alpha_{1}$,铺展前沿$X_{f}$减小但增长率不变,提高斥力强度系数$\alpha_{2}$使铺展前沿$X_{f}$增加,增长率也略有提高;增大基底高度$D$或波数$k$则加剧基底对液滴铺展的扰动,使铺展速率减慢;另外,分离压是造成铺展前沿后液膜呈现类似基底形状的主要原因.
| [1] | 叶学民, 李春曦, 阎维平. 切应力协同下受热过冷层流液膜的破断特性. 力学学报, 2011, 43(3): 461-467 (Ye Xuemin, Li Chunxi, Yan Weiping. Breakdown of locally heated and subcooled laminar films with interfacial shear. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 461-467 (in Chinese)) |
| [2] | 叶学民, 李春曦, 王松岭. 界面剪切力作用下波状液膜流的水动力稳定性. 力学学报, 2009, 41(3): 307-312 (Ye Xuemin, Li Chunxi, Wang Songling. Hydrodynamic stability of a liquid wavy film with interfacial shear. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(3): 307-312 (in Chinese)) |
| [3] | 李春曦. 含活性剂液滴的铺展过程研究. [博士论文]. 保定: 华北电力大学, 2011 (Li Chunxi. Spreading of a surfactant-laden drop on thin liquid film. [PhD Thesis]. Baoding: North China Electric Power University, 2011 (in Chinese)) |
| [4] | Edmonstone BD, Craster RV, Matar OK. Surfactant-induced fingering phenomena beyond the critical micelle concentration. Journal of Fluid Mechanics, 2006, 564: 105-138. |
| [5] | 王松岭, 李春曦, 叶学民. 温度和活性剂浓度梯度协同驱动的液滴铺展特性. 化工学报, 2011, 62(9): 2512-2519 (Wang Songling, Li Chunxi, Ye Xuemin. Drop spreading characteristics driven by gradients of temperature and surfactant concentration. Journal of Chemical Industry and Engineering, 2011, 62: 2512-2519 (in Chinese)) |
| [6] | Mavromoustaki A, Matar OK, Craster RV. Dynamics of a climbing surfactant-laden film - I Base-state flow. Journal of Colloid and Interface Science, 2012, 371(1): 107-120. |
| [7] | Craster RV, Matar OK. Dynamics and stability of thin liquid films. Review of Modern Physics, 2009, 81(3): 1131-1189. |
| [8] | Zhang YL, Craster RV, Matar OK. Surfactant driven flows overlying a hydrophobic epithelium: film rupture in the presence of slip. Journal of Colloid and Interface Science , 2003, 264(1): 160-175. |
| [9] | Kalliadasis S, Bielarz C, Homsy GM. Steady free-surface thin film flows over topography. Physics of Fluids, 2000, 12(8): 1889-1898. |
| [10] | Yuan QZ, Zhao YP. Multiscale dynamic wetting of a droplet on a lyophilic pillar-arrayed surface. Journal of Fluid Mechanics, 2013, 716: 171-188. |
| [11] | Pozrikidis C. Effect of surfactants on film flow down a periodic wall. Journal of Fluid Mechanics, 2003, 496: 105-127. |
| [12] | Saprykin S, Trevelyan PMJ, Koopmans RJ, et al. Free-surface thin-film flows over uniformly heated topography. Physical Review E, 2007, 75(2): 026306. |
| [13] | Stubenrauch C, Schlarmann J, Strey R. A disjoining pressure study of n-dodecyl-b-D-maltoside foam films. Physical Chemistry Chemical Physics, 2002, 4: 4504-4513. |
| [14] | Warner MRE, Craster RV, Matar OK. Dwetting of ultrathin surfactant-covered films. Physics of Fluids, 2002, 14 (11): 4040-4054. |
| [15] | 叶学民, 沈雷, 李春曦. 分离压对含活性剂液膜流去湿过程的影响. 西安交通大学学报, 2013, 47(3): 96-101 (Ye Xuemin, Shen Lei, Li Chunxi. Effect of disjoining pressure on dewetting of thin film flows containing surfactant. Journal of Xi'an Jiaotong University, 2013, 47(3): 96-101(in Chinese)) |
| [16] | 李春曦, 裴建军, 叶学民. 波纹状基底上含不溶性活性剂液滴的铺展过程. 化工学报, 2013, 64(9): 3308-3316 (Li Chunxi, Pei Jianjun, Ye Xuemin. Spreading of liquid droplet containing insoluble surfactant over corrugated surface. Journal of Chemical Industry and Engineering, 2013, 64(9): 3308-3316 (in Chinese)) |
| [17] | 赵亚溥, 表面与界面物理力学. 北京: 科学出版社, 2012 (Zhao Yapu. Physical Mechanics of Surface and Interface. Beijing: Science Press, 2012 (in Chinese)) |
| [18] | 叶学民, 姜凯, 沈雷等. 含活性剂超薄液膜演化过程的稳定性研究. 力学学报, 2013, 45(5): 681-689 (Ye Xuemin, Jiang Kai, Shen Lei, et al. Stability of ultrathin liquid film evolution with surfactant. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(5): 681-689 (in Chinese)) |
| [19] | Bhakta A, Ruchkenstein E. Decay of standing foams: Drainage, coalescence and collapse. Advances in Colloid and Interface Science, 1997, 70(18): 1-124 |
| [20] | 李春曦, 陈朋强, 叶学民. 二维微柱阵列壁面对活性剂液滴铺展的影响. 力学学报, 2014, 46(5): 665-672 (Li Chunxi, Chen Pengqiang, Ye Xuemin. Effect of two-dimensional micropillar arrayed topography on spreading of insoluble surfactant-laden droplet. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(5): 665-672 (in Chinese)) |
| [21] | Zhao YP. Moving contact line problem: Advances and perspectives. theoretical & Applied Mechanics Letters, 2014, 4(3): 1-034002 |
| [22] | Akyurtlu A, Akyurtlu JF, Denison KS, et al. Application of the general purpose collocation software, pdecol, to the graetz problem. Computers and Chemical Engineering, 1986 10(3): 169-187 |
| [23] | Warner MRE, Craster RV, Matar OK. Fingering phenomena created by a soluble surfactant deposition on a thin liquid film. Physics of Fluids, 2004, 16(8): 2933-2951. |
| [24] | Afsar-Siddiqui AB, Luckham PF, Matar OK. Unstable spreading of aqueous anionic surfactant solutions on liquid films. 2. Highly soluble surfactant. Langmuir, 2003, 19: 703-708 |
| [25] | Edmonstone BD, Matar OK. Simultaneous thermal and surfactant-induced Marangoni effects in thin liquid films. Journal of Colloid and Interface Science, 2004, 274: 183-199. |
| [26] | 叶学民, 姜凯, 李春曦. 分离压结合压作用下的活性剂液滴演化特征. 化工学报, 2013, 64(10): 3581-3589 (Ye Xuemin, Jiang Kai, Li Chunxi. Droplet spreading with soluble surfactant under disjoining pressure/conjoining pressure. Journal of Chemical Industry and Engineering, 2013, 64(10): 3581-3589 (in Chinese)) |
 2015, Vol. 47
2015, Vol. 47
