在当前化石能源日渐枯竭,环境日益恶化的情况下,太阳能、余热等低品位能源的开发利用成为热点[1].有机工质朗肯循环可以 有效实现低品位能源的吸收,并以较高效率输出有用功率为人所利用.有机工质朗肯循环的蒸发器与冷凝器端都涉及到气液两相流的相变传热.由于低品位热源与换热工质温差较小,所以可以保证低的换热熵增,维持系统整体的高效率.但是,也正因为传热温差较小,传热动力不足,往往需要极大以致难以承担的换热面积.这些就对两相流传热强化提出了较高的要求.
已有的两相流强化传热研究多是以增加管内流体的湍流扰动为目的,抑制边界层的发展与增厚从而实现强化传热.如Graham等[2]提出在管内壁加工微细沟槽,Cavallini等[3]提出了微翅片管,Miyara和Otsubo [4]提出了人字纹管,Suriyan和Somchai [5]则提出了上行内螺纹管.这些方法虽然可在一定程度上强化管内传热,但往往加大了流动阻力要付出高泵功的代价,并且达成的效果对于低品位能源实现极小温度梯度传热还是不够的. 因此,新的强化传热机理以及基于这一机理的强化手段迫切需要被开发.
在两相流传热方面,"协同流动与传热"这一强化机理逐渐被认识到,并得到了重视.间歇流型是气液两相流的常见流型,包括 泡状流、弹状流、塞状流.间歇流型在圆管内呈现的分布往往是气相趋于中心而液相趋于周围,对于冷凝传热,附在管壁上的厚液膜阻碍了气相进一步冷凝受热,所以减薄液膜厚度对于冷凝传热具有重要意义. 对于减薄液膜厚度这一机理,很多学者做出了研究与证实.Han等[6]指出液膜厚度是影响传热的重要参数,Lips和Meyer[7]实验研究了R134a在倾斜圆管内的对流传热影响因素.
基于流动与传热协同机理,我们研究组陈宏霞、徐进良等[8, 9]提出了一种含有内插丝网,可进行相分离流型调控 的强化传热管.其原理在于,利用微尺度结构对气液界面的毛细力学特性,有选择的通过气相与液相,从而实现将两相流型分布调整为强化传热所需要的状态.该原理完全有别于传统的增加流体湍流扰动的强化传热机理,有望在较小地增加流动阻力的条件下实现较大程度的传热强化.对于这一内插丝网流型调控管(简称丝网管),本组陈宏霞等[8, 9]开展了广泛工况的实验研究,证明了其具有较好的流型调控与强化传热效果. 本组陈奇成、孙东亮等[10]开展了低速层流条件下的详细数值模拟.}然而,实验测点总归是有限的,不可能描述到流动的具体细节,并且实验研究在深入探究机理层面还是比较受限的;而多尺度两相流数值模拟需要耗费巨大的计算机资源与时间,目前还主要停留在层流模拟.因此,本文从理论分析入手,结合实验得出的数据,建立描述丝网管流型调控机理的数学模型,以期对丝网管的强化原理有更进一步的认识,并尝试找到一种较为简捷的模拟方法,对丝网管机理做出描述与评价.
1 问题及物理模型在换热管中插入同轴的圆筒形丝网管,使换热管内流动区域分为环隙与核心区,如图1所示,丝网管一端有网底而另一端是开口的.当气液两相来流进入调控区后,网底通过毛细力抽吸作用,将液相吸入核心区,而气相因表面张力不能进入核心区,只能被挤入环隙.如此就加大了气相与管壁的接触面积,将"气在中心,液在周围"的间歇流型调控为"液在中心,气在周围",减薄了气相与管壁间的液膜厚度,使冷凝传热得到强化. 丝网与丝网管实物图如图2所示.

|
图 1 内分液调控管示意图 Fig. 1 The proposed heat transfer tube |

|
图 2 流型调控管的丝网示意图 Fig. 2 The stainless steel mesh to fabricate the mesh cylinder |
当丝网网孔足够小时,丝网可以完全阻碍气相进入核心区. 这是因为当气泡从大空间进入小空间 时,气相的表面能要增加[11],下面据此推导满足怎样的压差条件气泡才能穿过网孔.假设一个直径与管道内径相等的气泡试图穿过丝网方形网孔(图3). 由状态1到状态2,气泡表面能的增量是
| ${\rm{d}} E = 4\sigma w {\rm{d}} s_2 - \sigma \pi D {\rm{d}} s_1 $ | (1) |
式中,$E$是表面能,$\sigma $是表面张力系数,$w$是方孔宽度,$D$是管道内径,${\rm{d}} s_1$是从状态1到状态2光管中气泡的移动距离,${\rm{d}} s_2 $是穿过网孔的移动距离.
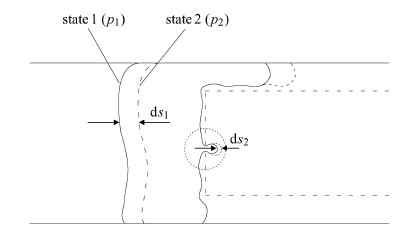
|
图 3 大气泡试图穿过丝网孔示意图 Fig. 3 Large bubble surface energy required to prevent the bubble from entering the mesh cylinder |
由质量守恒可得
| $w^2 {\rm{d}} s_2 = \frac{\pi D^2}{4} {\rm{d}} s_1 $ | (2) |
因此,将气泡由状态1变为状态2压力差将要做出功是
| ${\rm{d}} K = p_1 \frac{\pi D^2}{4} {\rm{d}} s_1 - p_2 w^2 {\rm{d}} s_2 $ | (3) |
式中,$K$是功,$p_1 $与$p_2 $分别是气泡在 位置1与 位置2的压强.考虑临界条件即压力差做出的功刚好实现气泡由状态1到2,则有${\rm{d}} K = {\rm{d}} E$,联立质量守恒方程(2)有
| $ p_1 - p_2 = 4 \sigma \Big (\frac{1}{w} - \frac{1}{D} \Big)$ | (4) |
上式即为气泡突破丝网孔判据. 考虑到$D \gg w$,可忽略$1 / D$项的影响.对于20${^\circ}$C空气$\!$-$\!$-$\!$水两相流体,$\sigma = 0.072 75$ N/m,$w = 150 \mu$m,则有$p_1 - p_2= 1.94$ kPa.据本组陈宏霞等实验结果[8, 9]显示,对于绝大多数工况,环隙与核心区不会形成如此大的压差,故而可以做出假设核心区内只是单相液体.
将三维的流动过程简化为一维物理模型,主要考察流体沿丝网管轴向的流动规律,如图4所示. 一维物理模型是后续采用集总方法建立数学模型的基础.

|
图 4 丝网管一维物理模型示意图 Fig. 4 Sketch map of the physics picture |
根据一维物理模型,建立描述内插丝网管内流动的数学模型.环隙与核心区相当于并联的两个流道,丝网网孔的存在使得两流 道连通. 限于一维,采用截面平均值作为各量的集总参数.本文所涉及的两相流流型是泡状流、弹状流与塞状流,均是非定常间歇流型,但其流动参数在一周期内对时间的平均值可视为定值.做出假设:(1)气泡不能突破网孔,核心区只有单相液体流动;(2)时均定常假设,即模型主要针对各流动参数的时均值.
2.1 质量方程(1)质量守恒
虽然环隙与核心区之间存在质量迁移,但对于任一流道截面,两者的质量流量之和保持不变,有
| $m_a + m_c = {\rm const } $ | (5) |
式中,$m_a $为环隙流体的质量流量,$m_c $为核心区流体质量流量.
(2)质量迁移
由于环隙与核心区存在压差,沿程不断有液相流体通过丝网渗入核心区,由于丝网属于多孔介质,这一过程可由多孔介质的达西公式[12]描述
| $G_p = \rho \frac{\kappa }{\mu } \frac{{\rm{d}}elta p}{{\rm{d}}elta } $ | (6) |
式中,$G_p $为丝网中渗透流体的质量流速;$\rho = \rho _f $,液相密度;$\mu =\mu _f $为液相黏度;$\kappa $为渗透率,为丝网参数,通过实验测定;${\rm{d}}elta p =p_a - p_c $,环隙压力与核心区压力之差;${\rm{d}}elta $为丝网厚度.
(3)有效面积
忽略丝网厚度则可认为丝网内、外侧面积相等.陈奇成等[10]数值模拟指出,在气泡包裹着丝网的区域,没有液相通过丝网渗透. 定义润湿比$r_w$,表征有效渗透面积对丝网总面积占比.
以弹状流为例,图5表征了某一特定工况下的气弹与液桥. 对于弹状流,整体流动区域即是由气弹加液桥这样的单元组成,因此有
| $r_w = \frac{L_l }{L_l + L_s } = 1 - \frac{L_s }{L_l + L_s } $ | (7) |
式中,$L_s $是气弹长度,$L_l $是液桥长度.
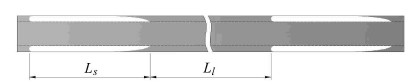
|
图 5 润湿比定义的示意图 Fig. 5 Sketch map of wet ratio |
忽略气弹与管壁间的薄液膜,右式第二项即等于空泡份额(截面含气率)$\varepsilon$. 空泡份额可根据流动参数由半理论半经验公式计算得出,故而给出以空泡份额形式表达的润湿比
| $r_w = 1 - \varepsilon $ | (8) |
式(8)虽是基于弹状流推导得出,但将式(8)应用于泡状流、塞状流也取得了较精确的结果,随后的模型验证可以看到.
所以,有效渗透面积$A_{\rm eff} $可表述为
| $A_{\rm eff} = \pi d l P r_w $ | (9) |
式中,$P$是丝网的孔隙率,是丝网固有的结构参数.
由以上分析,给出环隙与核心区迁移质量流量$m_p $函数关系
| $m_p = G_p A_{\rm eff} $ | (10) |
(1)压降
核心区只有液相,采用单相流压降方程[13]描述
| $\left( {\frac{{\rm{d}} p}{{\rm{d}} z}} \right)_{sp} = - \frac{2 f G^2}{\rho d} - \rho g $ | (11) |
式中,$f$是摩擦系数;$G$是质量流速;$\rho $是流体密度;$d$是特征长度,此处即是丝网管内径.
环隙区为气液两相流,采用Lockhart 和Martinelli提出的气液两相分相模型[14],两相流压降方程如(12)所描述
| $\begin{array}{l} {\left( {\frac{{{\rm{d}}p}}{{{\rm{d}}z}}} \right)_{tp}} = \varphi _l^2{\left( {\frac{{{\rm{d}}p}}{{{\rm{d}}z}}} \right)_l} - \frac{{\rm{d}}}{{{\rm{d}}z}}\left( {\frac{{{G^2}{x^2}}}{{{\rho _g}\varepsilon }} + \frac{{{G^2}{{(1 - x)}^2}}}{{{\rho _l}(1 - \varepsilon )}}} \right) - \\ \qquad g\left[ {\varepsilon {\rho _g} + \left( {1 - \varepsilon } \right){\rho _l}} \right] \end{array} $ | (12) |
式中,$\varphi _l $即是双相因子,由式(13)计算;$x$是气相干度;$\varepsilon $是空泡份额.
| $\varphi _l ^2 = \left( {1 + \frac{C}{X} + \frac{1}{X^2}} \right) $ | (13) |
式中,$X$是马蒂内利数,由式(14)所定义
| $X^2 = \frac{( {\rm{d}} p / {\rm{d}} z)_l }{( {\rm{d}} p / {\rm{d}} z)_g } = \frac{f_l }{f_g } \frac{\rho_g }{\rho _l } \Big (\frac{1 - x}{x} \Big)^2 $ | (14) |
$C$是奇泽姆数,取值5$\sim$20[14].
(2)摩擦系数$f$
布拉修斯型方程是计算管内流动摩擦系数的经典公式. 对于层流区、过渡区、湍流光滑管区、湍流粗糙管区等不同的流动条件,有形式统一但具体参数不同的布拉修斯方程计算其摩擦系数.本文所涉及的流速范围,全部位于层流区、过渡区与湍流光滑管区.所以对于层流区,无论核心区的$f$还是环隙液相与气相各自的$f$[15],有公式
| $f = 16 / Re $ | (15) |
式中,$Re < 2 320$.
对于湍流光滑管区[15]有
| $f = 0.079 / Re^{0.25} $ | (16) |
式中,$4\times 10^3 < Re < 1\times 10^5$.
对于过渡区$2 320 < Re < 4 000$,其可能为层流也可能为湍流,无法确切给出公式[15],$f$真实值介于式(15)与式(16)计算值之间.鉴于式(16)式更宽泛的雷诺数范围,文献[14]中采用式(16)计算这一范围的摩擦系数,本文采用同样的方式.
环隙区的尺度是毫米级,且入口有气液两相分离,相当于有局部扰流的小槽道. 对于小槽道入口处有局部扰流的情况,刘东等[16]给出局部阻力与沿程阻力对厘米级长度槽道压降影响相当,折合摩擦系数应修正.对于本文情况,由于管道长度为米级,局部厘米级的影响可以忽略,并且后续求解过程对入口采用了专门的两相局部公式,故而摩擦系数不必修正.
(3)空泡份额$\varepsilon $
空泡份额$\varepsilon $是两相流动中的重要参数,前人提出了许多模型与计算方法. 20世纪40年代末,Armand通过竖直管与水平管空气$\!$-$\!$-$\!$水混合物实验[17]得出,当$\beta \leqslant0.91$时,空泡份额与容积 含气率$\beta $的简单的关系式
| $\varepsilon = 0.833 \beta $ | (17) |
苏联1961年与1978年锅炉水动力计算标准[18]的空泡份额计算式与Armand的方法是同样的形式,$\varepsilon = C \beta$,通过垂直上升管实验数据得出的插值曲线图,查表求得比例系数$C$.
这种简单的形式使用范围较广,但往往针对特定流型精度不高. 对于泡状、弹状、塞状间歇流型,Zuber与Findlay提出了漂移流动模型[19]
| $\varepsilon = \frac{J_g }{C_0 J + u_{gj} } $ | (18) |
式中,$J_g $是气相折合容积流速,$J$是总折合容积流速,$u_{gj}$是漂移速度,$C_0 $是由实验得出的经验系数.
针对不同的流速范围、工况条件,学者们给出了许多$u_{gj} $,$C_0 $的经验计算公式. Zuber与Findlay自己给出的是
| $C_0 = 1.2 ,\ \ u_{gj} = 1.53 \left[{\frac{g\sigma \left( {\rho _l - \rho _g }\right)}{\rho _l ^2}} \right]^{1 / 4} $ | (19) |
上式有相对广泛的适用范围,但是精度不足. Ishii [20]给出了对于成熟的垂直湍流弹状流动有
| $C_0 = 1.2 ,\ \ u_{gj} = 0.35 \left[{\frac{gD\left( {\rho _l - \rho _g }\right)}{\rho _l }} \right]^{1 / 2} $ | (20) |
模型计算在选用空泡份额计算式时,比较了各种计算方法的精度,发现在较高流速时,液相雷诺数$Re_l > 3 000$时,Ishii给出的方法精度最好,这也因本研究的工况条件与Ishii的公式适用范围最为吻合. 但$Re_l \leqslant 3 000$时,Ishii方法有一定误差,反而形式简单的Armand公式精度较好. 所以,$Re_l > 3 000$时,模型计算选用漂移模型Ishii公式计算空泡份额,$Re_l \leqslant 3 000$,选用Armand公式.
3 模型求解与算法 3.1 预估$\!$-$\!$-$\!$修正量$S_{\rm ep} $与收敛判据环隙与核心区相当于两条并联支管,进口流量在两区分配以使两区最终出口压力相等. 定义分流比
| $ S_{\rm ep} = \frac{Q_a }{Q_c + Q_a } $ | (21) |
式中,$Q_a $是环隙进口混合物容积流量,m$^3$/s;$Q_c $是核心区进口混合物容积流量,m$^3$/s.
将分流比$S_{\rm ep} $作为预估$\!$-$\!$-$\!$修正量,将环隙与核心区的出口压力作为收敛判据,即
| $p_{a,{\rm out}} = p_{c,{\rm out}} $ | (22) |
模型求解中,首先预估$S_{ep} $,计算后若收敛判据不满足则修正分流比继续迭代计算,直至使收敛条件满足.
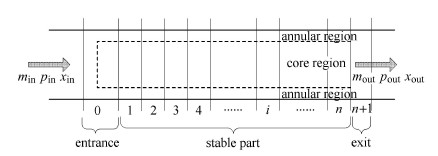
3.2 边界条件图6给出了待求解流动区域的网格划分. 流动区域被分为了3个部分,入口段、稳定段、出口段.在稳定段中流动充分发展,是最 主要的部分,为第2节中微分方程模型所描述,将其连续均匀划分为$n$个控制元体,编号$1\sim n$.入口段与出口段采用两相流局部公式[14]处理,限于篇幅不再列出,为整体连贯,将入口段编为第0个控制元体,出口段编为第$n+1$个控制元体,但其尺度与稳定段的每个元体尺度是不相同的.
|
图 6 流动区域网格划分图 Fig. 6 Control volumes of flow region |
经两相流局部公式,根据已知的入口$m_{\rm in} $,$p_{\rm in} $,$x_{\rm in} $,预估的分流比$S_{\rm ep}$,即可得出环隙第一个网格的$m_{a,1} $,$p_{a,1} $,$x_{a,1} $与核心区第一个网格的$m_{c,1} $,$p_{c,1} $,$x_{c,1} $. 整理成边界条件的形式
| $\left. \begin{array}{l} p_a = p_{a,1} ,m_a = m_{a,1} ,x_a = x_{a,1} , z = 0 \\ p_c = p_{c,1} ,m_c = m_{c,1} ,x_c = p_{c,1} , z = 0 \end{array}\!\! \right\} $ | (23) |
模型为一阶常微分方程组,据一组定解条件即可求解,式(23)给出的是一组第一类边界条件.
3.3 求解流程模型求解的已知条件是两相流的流动参数、流体物性参数、丝网管尺寸结构参数;模型求解的任务是流体的流动参数,包括流量、压力和干度在管内沿程分布.描述流体在丝网管内流动模型为微分方程,求解的基本思想是将连续的流动区域离散化,化微分方程为代数方程,从而实现计算机迭代求解.
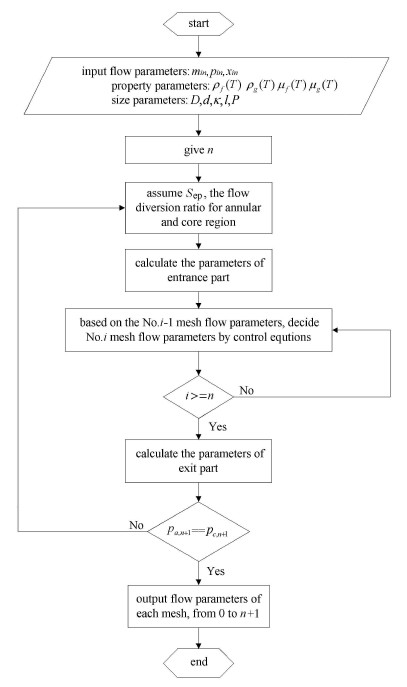
整体的求解流程图如图7所示. 首先输入计算的已知参数,确定离散网格数. 假定分流比$S_{\rm ep} $,据两相流局部公式计算入口段,其出口参数即为稳定段的入口参数.离散求解描述稳定段的微分方程组,据其出口参数与两相流局部公式计算出口段.判定出口段环隙与核心区压力是否相等,即$p_{a,n + 1} = p_{c,n + 1} $,迭代收敛判据.不收敛的情况下需要调整$S_{\rm ep} $值,然后重新计算,直至程序收敛.
|
图 7 模型求解流程图 Fig. 7 Flow chart of solving process |
陈宏霞等[8]开展了内分液调控管竖直向上流动实验,采用工质为空气$\!$-$\!$-$\!$水.陈奇成等[10]针对实验中的某一典型工况做 了计算流体力学数值模拟.本文同样采用文献[8]中主要实验工况进行计算,从而便于与实验、数值模拟结果比对. 实验主要参数:有机玻璃管内径$D=15.7$ mm,丝网管直径$d = 10.4$ mm,丝网管长度$L = 730$ mm,丝网管厚度${\rm{d}}elta = 0.07$ mm,孔隙率$P =0.464 9$,渗透率$\kappa = 7\times 10^{-6}$ mm$^2$. 采用相同实验参数,进行模型求解计算.
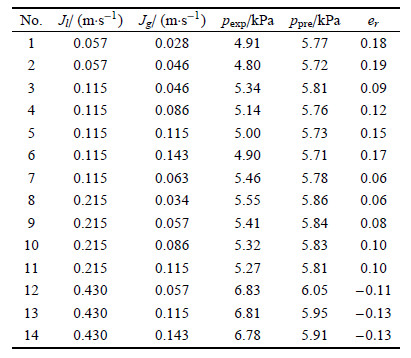
表1给出了14组工况,覆盖较广的流速范围. 通过丝网管压降值是重要的流动参数. 对比压降的实验值与计算值,并计算相对误差.
| 表 1 工况表 Table 1 Work conditions |
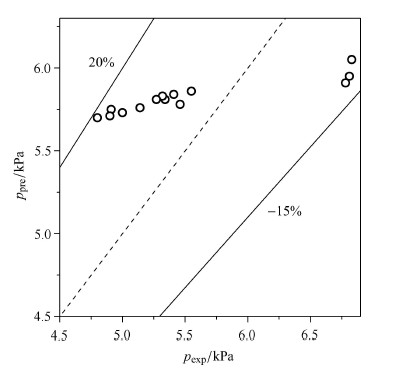
图8形象给出了实验值与计算值的对比. 可以看出,模型计算值与实验值的正误差在20%以内,负误差在15%以内.可以说,模型具有较好的准确性.
|
图 8 压降实验值与模型预测值对比 Fig. 8 Comparison between experimental and predicted pressure drop |
根据流动参数的沿程变化趋势可以将工况分为两类.以工况2与工况12作为两类工况的代表(将类如工况2的称为第1类工况,将类如工 况12的称为第2类工况).图9给出了这两类工况流动参数沿程变化的对比.由于压强沿程呈现线性变化,故而采用中间打断方式制图,重点看入口部分的压强差与出口部分的压强收敛.
|
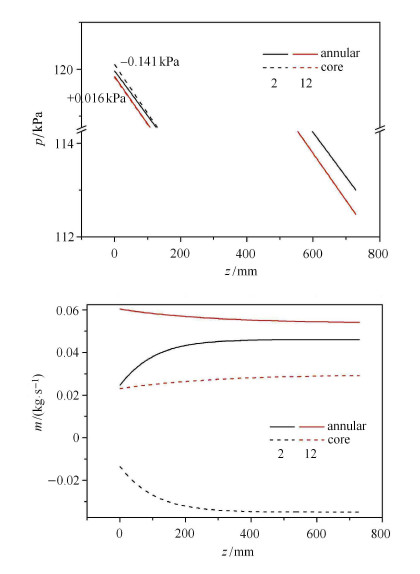
图 9 两类工况流动参数沿程对比图 Fig. 9 Contrast of the second and the twelfth work condition |
如图9所示,工况2入口处核心区压强大于环隙,${\rm{d}}eltap=p_a-p_c=-0.141$ kPa,而工况12在入口处核心区压强小于环隙,${\rm{d}}elta p=p_a-p_c=-0.016$ kPa.由于压强是质量迁移的驱动力,所以表现在质量流量上,工况2环隙的质量流量沿程上升,而工况12环隙的质量流量沿程下降.另外,工况2核心区的质量流量为负值,代表核心区时均流速竖直向下,环隙与核心区出现逆流;而对于工况12,环隙与核心区同为竖直向上流.这里的质量流量指的是气液混合物的流量,利用另一流动参数干度$x$,可分别求出液相与气相各自的质量流量,当然是对于核心区$x = 0$.分析两类工况产生的原因,并找出流动状态随气速、液速的转变规律,做出同一气速下不同液速流量沿程变化与同一液速下不同气速流量的沿程变化,如图10 $\sim$图12所示.
|
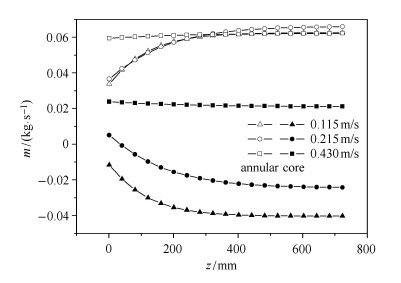
图 10 气速0.115m/s,不同液速,工况5, 11, 13 Fig. 10 Gas velocity 0.115m/s, contrast of mass flow of different liquid velocity, cases 5, 11, 13 |

|
图 11 液速0.115m/s,不同气速,工况3, 4, 5, 6 Fig. 11 Liquid velocity 0.115m/s, contrast of mass flow of different gas velocity, cases 3, 4, 5, 6 |
|
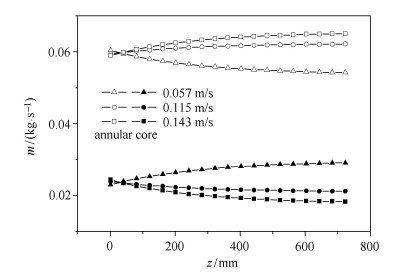
图 12 液速0.430m/s,不同气速,工况12, 13, 14 Fig. 12 Liquid velocity 0.430m/s, contrast of mass flow of different gas velocity, cases 12, 13, 14 |
图10给出了相同气速条件下,不同液速的工况环隙与核心区质量流量沿程变化. 图11与图12给出了相同液速条件下,不同气速的工况环隙与核心 区质量流量沿程变化. 综合3图可知,对于特定的工况,环隙流量曲 线与核心区流量曲线是对称的.液速决定了流动状态的大致轮廓,液速越高,曲线的对称线位置越靠上,这是因为即使$J_l $与$J_g $数值相当,由于$\rho_g \ll \rho _l$,干度仍旧较低,液速对质量流量起主导作用;气速决定了曲线的细节弯折趋势,气速越高,曲线弯折曲率越大,这代表沿程环隙与核心区质量交换越剧烈.另外,第2类工况出现频次远低于第1类工况,在较高液速且气速不是很高的情况下才能出现第2类工况.
对上述现象作出分析.流速较低时(主要指液速),重力压降起到主导因素,核心区全部为液体重力压降远高于环隙,虽然环隙的摩擦压降大于核心区,但此时即使核心区速度滞止为零也不足以使环隙较大的摩擦压降弥补核心区较大的重力压降,故而核心区出现竖直向下流,且流体的渗透方向为从核心区渗向环隙;当流速较高时(主要指液速),摩擦压降起到主导作用,环隙摩擦压降大于核心区,然而在入口处网底对核心区的局部损失要大于环隙,故而沿程的整个过程,核心区较小的沿程压降一直在弥补入口造成的损失,直至出口两者平衡. 环隙与核心区都是竖直向上流,且流体由环隙渗向核心区.另外值得注意的是此时气速不能太高,否则会拉大环隙与核心区的重力压降差,使核心区再度出现竖直向下流.
4.3 流动状态定量分析上文给出了液速$J_l $,气速$J_g $影响流动状态的定性关系,在此基础上试图找到一种$J_l $,$J_g $与流动状态的定量关系.
由分流比$S_{\rm ep}$定义式(21)可知,其表征了入口处分流入环隙与核心区的流量状况,在一定程度上可作为描述流动状态的指标.
$S_{\rm ep} >1$代表核心区一定出现竖直向下流(第1类工况),为保证管道截面的净流量为竖直向上,环隙的竖直向上容积流量必然应大于管道截面净流量.$0 < S_{\rm ep} < 1$,则可能为第1类工况也可能为第2类工况.虽然入口处有竖直向上流穿过网底,但随后因渗流速度逐渐滞止为零进而转变为竖直向下流.这揭示了核心区出现速度滞止点的现象,与文献[10]数值模拟速度滞止点现象相符.
为给出第1类工况与第2类工况的$S_{\rm ep} $临界取值,采用程序试取参数,发现$S_{\rm ep} =0.77$的试取工况流量曲线接近平线,例如工况$J_l = 0.410$ m/s,$J_g = 0.064$ m/s,此时环隙与核心区互不渗透应为临界工况. 所以有$0 < S_{\rm ep} \leqslant 0.77$出现第2类工况,$S_{\rm ep} > 0.77$出现第1类工况.
任一流动工况都对应一$S_{\rm ep} $值,而确定的$J_l $,$J_g $唯一确定流动工况,所以有二元函数
| $S_{\rm ep} = f(J_l ,J_g ) $ | (24) |
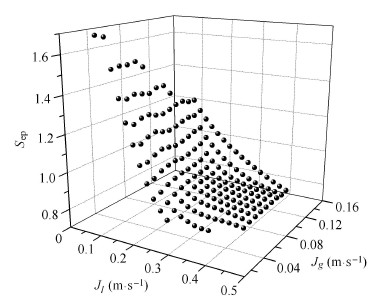
从计算所得数据采用数值分析的方法找到上式的确切关系.由于获得的数据点相对于函数拟合偏少,假设二元函数连续,则小范围插值数 据应是合理的.采用三角立方插值使数据点加密,如图13所示.
|
图 13 采用三角立方插值加密数据点 Fig. 13 Data interpolation by cubic method |
根据加密数据点,采用最小二乘B样条拟合获得二元函数的确切表达. 最小二乘B样条拟合原理是采用最小二乘法找到以控制点做出的样条曲线对数据点拟合的均方根误差最小. B样条曲线参数方程[21]
| $p(t) = {\rm{d}}sum_{i = 0}^n d_i N_{i,k} (t) $ | (25) |
式中,$d_i $是控制点,$N_{i,k} (t)$是最小二乘基函数.
以最小二乘法求得
| $d = (N^\tau WN)^{ - 1}N^\tau WP $ | (26) |
| ${\rm{d}}sum_{j = 1}^m \left[{p_j - {\rm{d}}sum_{i = 0}^n d_i N_{i,k} (t_j) } \right]^2 = \min $ | (27) |
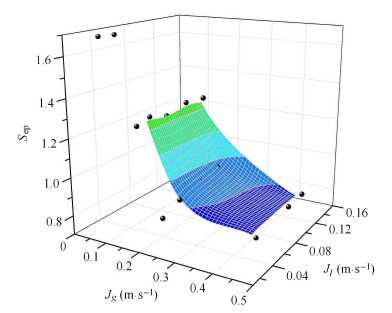
|
图 14 拟合曲面与原始数据点 Fig. 14 Fitting surface and raw data |
如此就给出了对于确定$J_l $,$J_g $定量计算流动状态的关系式,便于分析$\frac{\partial S_{\rm ep} }{\partial J_l }$ 与$\frac{\partial S_{\rm ep} }{\partial J_g }$. 同时可以找到由第1类工况向第2类工况转变的定量规律.
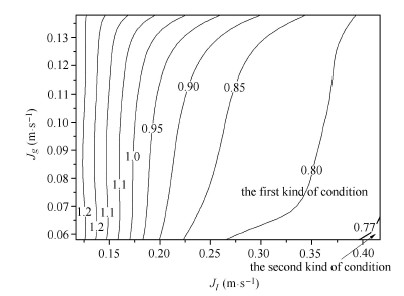
图15给出了曲面的等值线图,图示0.77等值线即是第1类工况与第2类工况的临界线,其上的工况点,如(0.410,0.064)即是临 界工况. 据上图对4.2中的结论给出定量的表达:当$J_l < 0.395$ m/s时($Re_l < 6 937$),一定出现第1类工况;当$J_l> 0.395$ m/s且$J_g < 0.065$ m/s时($Re_l > 6 937$,$Re_g < 67$),可能会出现第2类工况,此时较低的气速会促使第2类工况的出现.
|
图 15 Sep 等值线图 Fig. 15 Contour map of Sep |
(1) 模型计算结果与实验误差在20%以内,吻合较好,可以说模型较好地解读了丝网管内的流动机理.
(2) 液速决定流动状态的大致轮廓,气速决定流动状态的细节.液速越高,沿程流量曲线位置越高,代表整体流量越大;而气速越高,沿程流量曲线越弯折,代表经丝网的渗透作用越剧烈.
(3) 当$Re_l < 6 937$时,核心区与环隙流体流动方向相反;$Re_l > 6 937$且$Re_g < 67$时,可能出现核心区与环隙流体流动方向相同现象,此时较低的气速会促使现象的出现.
冷态实验、数值模拟、建模计算证明了内分液流型调控管具有良好的相分离特性与流动特性,这预示了其在热态强化传热方面将会发挥较好作用.但是计算发现,所期望的由环隙向核心区渗透的第2类工况的出现条件是相对苛刻的,这要求液速较高而气速相对较低.对于实际工程,通过确定管路的流动工况往往是单一的,根据单一工况设计丝网管,力图出现第2类工况,可实现最好的强化传热.
| [1] | 陈子乾, 何小荣, 王铁柱 等. 太阳能海水淡化系统经济性分析与研究. 工程热物理学报, 2012, 1: 002 (Chen Ziqian, He Xiaorong, Wang Tiezhu, et al. Economical Analysis of a solar Desalination System. Journal of Engineering Thermophysics, 2012, 1: 002 (in Chinese)) |
| [2] | Graham D, Chato JC, Newell TA. Heat transfer and pressure drop during condensation of refrigerant 134a in an axially grooved tube. International Journal of Heat and Mass Transfer, 1998, 42(11): 1935-1944 |
| [3] | Cavallini A, Del Col D, Doretti L, et al. Heat transfer and pressure drop during condensation of refrigerants inside horizontal enhanced tubes. International Journal of Refrigeration, 2000, 23(1): 4-25. |
| [4] | Miyara A, Otsubo Y. Condensation heat transfer of herringbone micro fin tubes. International Journal of Thermal Sciences, 2002, 41(7): 639-645. |
| [5] | Laohalertdecha S, Wongwises S. Condensation heat transfer and flow characteristics of R-134a flowing through corrugated tubes. International Journal of Heat and Mass Transfer, 2011, 54(11): 2673-2682 |
| [6] | Han Y, Shikazono N, Kasagi N. The effect of liquid film evaporation on flow boiling heat transfer in a micro tube. International Journal of Heat and Mass Transfer, 2012, 55(4): 547-555. |
| [7] | Lips S, Meyer JP. Experimental study of convective condensation in an inclined smooth tube. Part I: Inclination effect on flow pattern and heat transfer coefficient. International Journal of Heat and Mass Transfer, 2012, 55(1): 395-404 |
| [8] | Chen Hongxia, Xu Jinliang, Xie Jian, et al. Mudulated flow patterns for vertical upflows by the phase separation concept. Experimental Thermal and Fluid Science, 2014, 52: 297-307. |
| [9] | Chen Hongxia, Xu Jinliang, Li Zijin, et al. Stratified two-phase flow pattern modulation in a horizontal tube by the mesh pore cylinder surface. Applied Energy, 2013, 112: 1283-1290. |
| [10] | Chen Q, Xu J, Sun D, et al. Numerical simulation of the modulated flow pattern for vertical upflows by the phase separation concept. International Journal of Multiphase Flow, 2013, 56: 105-118. |
| [11] | Tsai JH, Lin L. Active microfluidic mixer and gas bubble filter driven by thermal bubble micropump. Sensors and Actuators A: Physical, 2002, 97-98: 665-671 |
| [12] | Lawson KW, Lloyd DR. Membrane distillation. Journal of Membrane Science, 1997, 124(1): 1-25. |
| [13] | Handbook of Single-phase Convective Heat Transfer. New York: Wiley, 1987 |
| [14] | Collier JG, Thome JR. Convective Boiling and Condensation. Oxford: University Press, 1994 |
| [15] | Munson BR, Young DF, Okiishi TH. Fundamentals of Fluid Mechanics. New York, 1990 |
| [16] | 刘东,刘明侯,王亚青等. 带扰流小槽道内单相流动阻力特性实验. 力学学报, 2010, 42(6): 1006-1012 (Liu Dong, Liu Minghou, Wang Yaqing, et al. Experimental study on the frictional pressure drop of water flow in mini-channels with circular cylinder disturbed flow. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(6): 1006-1012 (in Chinese)) |
| [17] | Armand AA. The Resistance During the Movement of a Two-Phase System in Horizontal Pipes. Atomic Energy Research Establishment, 1959 |
| [18] | 林宗虎, 王树众, 王栋. 气液两相流和沸腾传热. 西安: 西安交通大学出版社, 2003(Lin Zonghu, Wang Shuzhong, Wang Dong. Gas-liquid two-phase flow and boiling heat transfer. Xi'an: Xi'an Jiaotong University Press, 2003 (in Chinese)) |
| [19] | Zuber N, Findlay JA. Average volumetric concentration in two-phase flow systems. Journal of Heat Transfer, 1965, 87(4): 453-468. |
| [20] | Ishii M. One-dimensional drift-flux model and constitutive equations for relative motion between phases in various two-phase flow regimes. Argonne National Lab., Ill.(USA), 1977 |
| [21] | 李岳生, 齐东旭. 样条函数方法. 北京: 科学出版社, 1979 (Li Yuesheng, Qi Dongxu. Spline Function Method. Beijing: Science Press, 1979 (in Chinese)) |
 2015, Vol. 47
2015, Vol. 47