多体系统动力学模型被认为是复杂机械系统分析、设计、优化、控制、仿真的重要工具[1, 2, 3, 4, 5, 6].在理想的多体系统动力 学分析中一般不考虑关节效应对系统性能的影响[7].然而,实际多体系统中的关节效应不仅降低了多体系统的寿命和可靠性[8],而且影响了系统的精度和稳定性[9];严重的甚至导致多体系统的崩溃与失效[10, 11].
所谓关节效应主要是指运动副即关节处的间隙、摩擦、接触变形与磨损[1, 2, 12, 13].关节是构成多体系统的重要组成部分,而关节效应则是实际多体系统中不可避免的动态表现形式[14, 15],其中各因素之间的相互关系见图1.
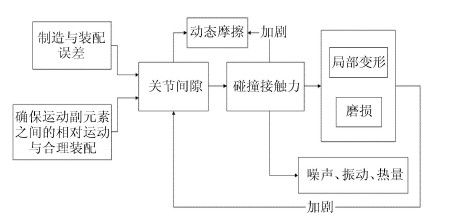
|
图 1 关节效应流程图 Fig. 1 Flow chart of the joint effective |
由于关节元素在制造和装配过程中产生的误差导致了运动副中的间隙[16],同时间隙也是确保关节元素相对运动与合理装配的必要条件[17]. 关节中间隙的存在不仅改变了运动副构件之间的自由度和受力状态[18, 19],并且当关节元素处于分离状态时产生的碰撞与冲击力加剧了关节元素之间的动态摩擦[20, 21, 22],造成了关节元素的局部变形和磨损[23, 24],产生了噪声、振动和热量[1, 2, 25].由于磨损和局部变形与多体系统动力学之间的交互作用使关节间隙进一步加大,而间隙越大接触碰撞力越大将导致更加严重的磨损[26],由此多体系统的动力学性能进入了一种恶性循环直到其失效[27]. 所以关节效应各因素之间密不可分且相互耦合,即其中任何一个因素发生变化就会影响其他因素,并且最终对整个多体系统的动力学性能产生影响甚至导致系统失效. 在此,称该现象为多体系统动力学中的" 蝴蝶效应",即将关节效应作为一个有机整体来研究.
本文较为全面地概括和总结了关节效应中的间隙、摩擦特性[28, 29]与接触特性[30]的研究方法,并着重分析了多体系统动力学中关节磨损现象的研究进展.由于高速重载的高精度多体系统是机械系统的发展趋势[31],因此,分析与预测关节效应对多体系统动力学性能的影响显得尤为重要[32].
在多体系统动力学中关节间隙的类型可分为3类:(1)理想多体系统下的零间隙[33];(2)实际多体系统中的固定装配间隙[1, 2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 13, 14, 15];(3)实际多体系统中考虑关节磨损的非规则磨损间隙[26, 27, 34, 35].近年来许多文献都集中于对多体系统中理想关节与装配间隙的研究,而较少注重关节磨损引起关节间隙的非规则变化[36, 37, 38],忽视了磨损对关节间隙尺寸的影响,限制了多体系统中关节效应的进一步研究.
1 多体系统中关节接触碰撞现象的描述物体之间的接触碰撞类型有2类:(1)基于Newton碰撞定律的正碰撞;(2)偏心斜碰撞;其中偏心斜碰撞更符合一般的碰撞问题,即斜碰撞在考虑关节间隙的多体系统动力学中是主要研究对象[30].而关节中间隙的存在导致关节元素之间发生接触碰撞现象,接触体之间的运动状态模型主要有3类[39, 40, 41, 42]:(1)将间隙运动副元素之间的运动分为"接触$\!$-$\!$-$\!$分离"二状态;(2)将间隙运动副元素的运动约束转化成力约束,视间隙运动副元素的运动状态为"接触$\!$-$\!$-$\!$分离$\!$-$\!$-$\!$碰撞"的三状态[43, 44](文献[45]提出了包含"过渡"状态的四状态模型);(3)将关节间隙量视为"无质量杆"[46, 47, 48]的连续接触模型来描述该运动状态;上述3种间隙运动副的状态模型均各有优缺点,具体选用哪种模型对间隙运动副元素的运动状态进行描述将由具体研究对象决定[49].
1.1 关节间隙的运动学模型在描述多体系统关节的接触碰撞现象时,必须要经历含间隙关节的运动学建模,当接触体处于分离状态时,其关节间隙元素如图2所示. 其中$P_{i}$和$P_{j}$为接触体的潜在接触点.目前潜在接触点主要识别方法:首先计算系统运动过程中所有接触点出现的位置,再建立潜在接触点之间的缝隙函数,如果缝隙函数等于0则认为对应的潜在接触点发生接触,否则,不发生接触[34].
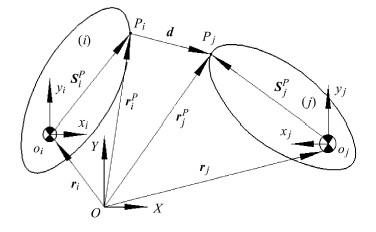
|
图 2 分离状态的接触体 Fig. 2 Two bodies in the state of separation |
间隙运动学建模的3个目的:
(1)计算含间隙关节元素之间潜在接触点的位置(该潜在接触点是含间隙多体系统动态分析的参考点).
| ${\pmb r}_k^P = {\pmb r}_k + {\pmb A}_k {\pmb s}_k^P ,\ \ \ \ k = i,j $ | (1) |
其中,${\pmb A}_k $为局部坐标系到固定坐标系的转换矩阵. ${\pmb r}_i^P $,${\pmb r}_j^P$为潜在接触点在固定坐标系$XOY$中的位置;${\pmb r}_i $,${\pmb r}_j$为接触体质心在固定坐标系$XOY$中的位置,${\pmb s}_i^P $,${\pmb s}_j^P$为潜在接触点在局部坐标系$x_i o_i y_i $,$x_j o_j y_j $中的位置.
(2)计算其潜在接触点的实际几何距离.
| ${\pmb d} = {\pmb r}_j^P - {\pmb r}_i^P $ | (2) |
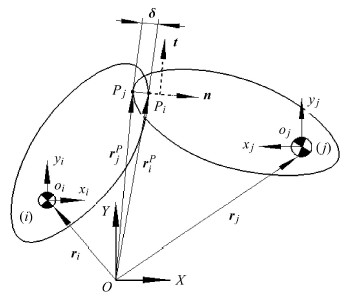
其中,间隙关节元素之间的潜在接触点是建模的关键,当接触体处于接触状态时如图3. 其中,${\pmb n}$为接触面的法向矢量,${\pmb t}$为接触面的切向矢量,$\delta $为接触变形量.
|
图 3 接触状态 Fig. 3 Two bodies in the state of contact |
而接触体的潜在接触点必须满足以下几何约束条件:(1)潜在接触点的距离对应接触体的最小距离,其中接触面的法向矢量为
| ${\pmb n} = \dfrac{\pmb d}{d} $ | (3) |
其中$d = \sqrt {d_x^{2} + d_y^{2} } $.(2)拥有最小距离的潜在接触点矢量必须与接触碰撞表面的法向矢量共线,(3)来自2个接触体的潜在接触点,其各自接触碰撞表面的法向矢量必须共线[30].
| ${\pmb n}_j \times {\pmb n}_i =0 $ | (4) |
| ${\pmb d}\times {\pmb n}_i = 0 $ | (5) |
其中,${\pmb n}_i $,${\pmb n}_j $分别为各接触体的法向向量.
当接触体处于接触状态时,通过式(4)与式(5)可求出其潜在接触点,即可导出接触体之间的接触变形量为
| $\delta = \sqrt {{\pmb d}^{\rm T}{\pmb d}} $ | (6) |
| $v_n = {\pmb n}^{\rm T}\left( { \dot{\pmb r}_j^P - \dot{\pmb r}_i^P } \right) $ | (7) |
| $v_t = {\pmb t}^{\rm T}\left( {\dot{\pmb r}_j^P - \dot{\pmb r}_i^P } \right) $ | (8) |
在对关节间隙模型正确描述以后将面临着对关节元素之间运动状态的判定,找到接触体之间运动状态的切换时间非常重要,否则会导致多体系统动力学模型的数值仿真出现严重的偏差. 常用的方法有2种[52, 53, 54]:(i)直接利用接触变形量来判定关节元素之间接触与分离;当接触变形量小于0时,表明接触体处于分离状态;当接触变形量等于0时,表明接触体开始接触;当接触变形量大于0时,表明接触体处于接触碰撞状态[55, 56]. (ii)利用接触元素之间的相对法向速度来判定接触元素的接近和分离,利用相对切向速度来判定接触元素的相对滑动和黏滞;当接触体的相对法向速度为正值时,表明接触体元素正在接近处于压缩阶段,在终止时刻其接触变形量达到最大值. 此时,压缩过程中储存的一部分能量用来分开正处于接触状态的接触体,另一部分变形能量将以热量、振动和噪声等形式耗散[57],其主要原因来自于接触体材料的内部阻尼[58]. 当接触点的相对法向速度为负值时,表明接触体元素正在分离处于恢复阶段[59].
1.2 间隙关节中切向接触力模型描述在斜碰撞过程中,碰撞体在接触点同时具有相对法向速度和切向速度;前者导致法向挤压变形,后者借助摩擦引起切向畸变[60, 61]. 在众多静态与动态摩擦模型中[62],描述切向接触力使用最为广泛的摩擦模型为"Coulomb"摩擦模型[55, 56, 63],除此之外,很少有其他摩擦模型出现在多体系统动力学的切向接触力模型中. 其原因有3点:(1)多体系统动力学自身的强耦合性和非线性,不再适合嵌入参数识别困难的动态摩擦模型;(2)"Coulomb"摩擦模型是所有静态摩擦模型中结构最简单,且适用范围最广泛的摩擦模型;(3)"Coulomb"摩擦模型认为摩擦力与法向接触力成正比且与接触面积无关,因此避免了对真实接触面积的求解,大大简化了建模过程,且该模型基本能描述斜碰撞过程中的摩擦现象. 然而,原始的"Coulomb"摩擦模型在多体系统动力学的仿真计算中容易发生切向速度方向突变,从而影响了数值积分的稳定性.
为了避免数值计算中的摩擦力突变,常见的对"Coulomb"摩擦模型修正的形式一般有2种:(1)Ambrósio[64]提出的拥有固定摩擦系数的修正"Coulomb"摩擦模型,该模型中引入了动态修正系数有效地防止了切向速度在0附近时摩擦力方向的改变,使得数值积分运算变得稳定[56].(2)为了能够描述接触体在相对低速情况下出现的黏滞与滑移现象;文献[55]把摩擦系数修正为接触体相对切向滑动速度的函数,在一定程度上体现了接触体在相对低速情况下的黏滞与滑移现象.
然而修正"Coulomb"摩擦模型的应用涉及到对接触面之间黏滞与滑移相互转换过程的离散,该离散给数值计算引入了新的难题,即如何确定黏滞与滑移的切换标准以及计算效率低. 目前,通过静摩擦临界速度$v_s $和最大动摩擦临界速度$v_d$作为黏滞和滑移相互转换的标准,但是如何确定$v_s $和$v_d $目前还没有具体的实现方法.单纯依靠经验确定的参数值将导致该模型的仿真精度存在疑问[57],即该模型对低速下的黏滞与滑移摩擦现象的捕捉不够精确.为此,大多学者都致力于研究一种连续的摩擦模型,通过引入一个"规则因子"来光滑不连续的摩擦力,并利用低速情况下的"爬行现象"代替接触体之间的黏滞现象.虽然,含有"规则因子"的摩擦模型表面上完全能代替修正后的"Coulomb"摩擦模型,然而其近似方法不但改变了接触体之间真实摩擦的物理现象,而且在相对切向速度较低且又要求很小的时间迭代步长时将会忽视间隙关节元素中的碰撞现象[65].
为了克服以上缺点,LuGre摩擦模型[66]利用有效的摩擦系数对黏滞和滑移摩擦现象进行了建模,该有效摩擦系数是接触体相对切向速度与其内部状态变量(接触表面鬃毛的平均变形量)的函数.LuGre摩擦模型不仅能准确地捕捉Stribeck效应(在低速情况下摩擦力随着速度的增加而减小),还包含了"Coulomb"摩擦、黏性摩擦、预滑动、可变静摩擦和摩擦滞后等摩擦模型的属性,较其他摩擦模型更能体现真实的摩擦现象.
以上摩擦模型虽然在建模方法与侧重点上各不相同,但是摩擦力正比于法向接触力这一特点保持不变.含动态修正因子的"Coulomb"摩擦模型的结构与参数识别相比含非线性摩擦系数的"Coulomb"摩擦模型和LuGre摩擦模型更加简单,且便于嵌入多体系统动力学模型中,但是该模型忽视了低速下接触体之间的黏滞与滑移现象.含非线性摩擦系数的"Coulomb"摩擦模型在一定程度上缓解了该缺点,但是其精度存在疑问.而LuGre摩擦模型具有准确捕捉摩擦中黏滞与滑移现象的能力,避免接触体在碰撞过程中能量的增长.该模型的参数识别是LuGre摩擦模型应用的关键. 研究者可以根据具体研究对象的侧重点选择合适的摩擦模型.另外,摩擦模型除了与法向接触力和滑移速度有关以外,接触体在摩擦过程产生的摩擦热引起接触材料属性和表面清洁度的变化对摩擦模型的影响也是一个值得深入研究的问题[61, 67].
1.3 接触力模型的研究进展固体接触分为2种:协调接触(conforming contact)和非协调接触(non-conforming contact).其中协调接触:如果两个固体的表面在无变形时精确地或者相当接近的"贴合"在一起,那么称这种接触是协调的(例如平的滑动轴承以及轴颈轴承).非协调接触:具有不相似外形的物体称为非协调,当无变形地的接触时,它们将首先在一个点或沿一条线相碰,分别称为点接触 和线接触,即非协调接触(例如滚珠轴承和圆柱轴承).而接触力模型是研究考虑关节效应对多体系统动力学影响的必经途径,因为关节效应中的摩擦模型与磨损模型都直接或间接的与接触力模型相关[26, 27, 68].而建立接触力模型首先必须要解决的3个难点:(1)如何选择合适的接触力模型来描述一个包含接触体几何特征、材料属性和运动学特性的接触碰撞事件[69];(2)如何识别接触力模型中接触参数,如:刚度系数、阻尼系数、恢复系数、初始碰撞速度与幂指数系数等[70];(3)最重要的是如何量化接触碰撞过程中的能量损失[71].只有解决了上述3个问题才能有效的研究多体系统中关节效应对其动力学特性的影响.
接触碰撞动力学的分析方法有2种:(1)基于接触体几何约束的非光滑离散分析方法[72, 73];(2)基于接触体表面变形量的连续分析方法[67, 74]. 非光滑是由于刚体接触过程中其运动状态的切换不光滑导致的,其中碰撞产生的速度跳跃就是典型的非光滑系统[75]. 与非光滑模式相反,连续分析方法允许接触体在接触区域变形,且接触力模型是接触变形量的函数表现出该方法的连续性. 文献[30]总结并分析了2种分析方法的优缺点,非光滑离散分析方法虽然简化了接触过程且计算效率高,但该方法为了避免接触体在接触碰撞过程中的相互变形侵入而利用了单边约束理论[76],导致了在考虑关节摩擦效应时存在多解或者无解[77],另一方面离散分析方法中的线性补偿策略可能会违反考虑摩擦时接触过程中的能量守恒定律[78]. 而连续分析方法则不会出现上述缺点,且该分析方法不仅描述了接触碰撞过程中的能量损失,而且能有效地集成到多体系统的动力学中,最重要的是目前关于连续分析方法的仿真软件提高了该方法的计算效率[79].
在确定以连续分析方法来研究多体系统中关节间隙元素之间的接触碰撞问题之后,需要根据相关的接触理论建立对应的接触力模型.多体系统动力学的接触碰撞问题研究中常见的4种接触理论[80]:(1)著名的Hertz接触理论[81],该接触理论常适用于运动副含有大间隙小载荷的低速无摩擦理想弹性固体的非协调接触问题.(2)Steuermann接触理论[82, 83],该接触理论主要适用于协调接触问题,但是,该理论非常依赖对表示接触体表面形状的$N$次多项式,尤其当指数$N$选择不合适时就会出现较大误差;且没有适合描述所有间隙元素表面形状类型的$N$次多项式,所以该接触理论一般很少使用.以上2种接触理论都认为每一个接触体就是一个弹性半空间[83]来研究接触问题;还有2个不符合弹性半空间假设的接触理论:(3)采用分层接触的Winkler弹性基础理论[24]与弹性半空间接触形成鲜明的对比.该理论忽略了接触体之间的剪切作用力,将接触界面模拟为一系列的弹簧,且相邻弹簧之间保持相互独立,利用接触变形量与弹簧刚度系数计算接触体表面的接触应力,然后结合近似接触面积计算其接触力,该方法虽然简单高效但其接触力模型精度较低.(4)Persson接触理论[80, 81, 82, 83, 84],该理论假设忽略接触体的径向位移与切向位移的耦合关系,并且其径向位移和接触体之间的最大法向变形量之间的关系必须满足刚体接触的几何刚性条件.当上述假设成立时就能利用接触体几何刚性约束方程建立的Persson理论对含间隙的圆柱副接触问题提供一个完全封闭式的解,且该理论只适在运动副拥有小间隙的场合使用[80].
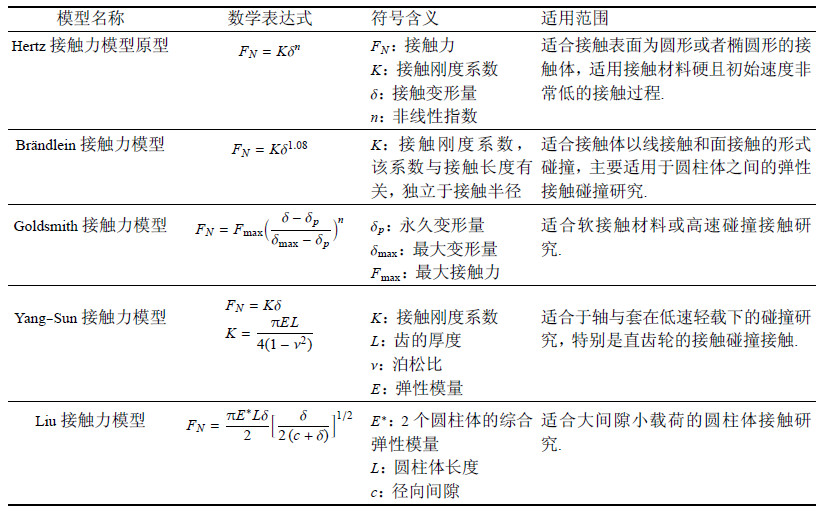
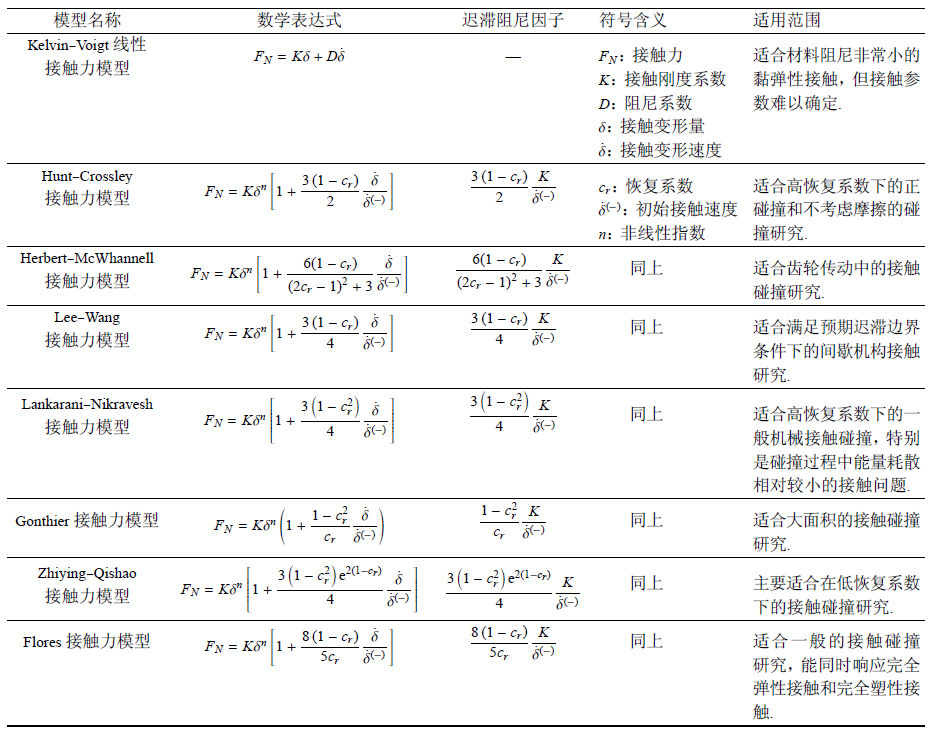
以上基于各种接触假设条件得出的4种接触理论各有优缺点且拥有各自的适用范围,其中Hertz接触理论[81, 85, 86]是适用范围最广泛研究历史最悠久的接触力模型.文献[30]对 数十年来Hertz接触模型的研究现状进行了系统的分析总结. 其中讨论了5种[58, 87]不考虑能量损失的接触力模型(见表1)与8种引入阻尼系数之后的接触力模型(见表2),着重讨论了接触力模型中阻尼系数的发展过程,通过接触力与接触变形量的函数关系讨论了迟滞环与接触能量损失之间的关系;证明了不考虑接触能量损失的接触力模型不符合实际情况.
| 表 1 纯弹性接触力模型 Table 1 Pure elastic contact force model |
| 表 2 能量损耗接触力模型 Table 2 Dissipative contact force models |
虽然5种纯弹性接触力模型数学表达各异,且应用范围不一致,但本质上均是在弹性范围内,单纯地研究接触变形量与材料属性之间的关系,没有考虑接触碰撞过程中接触体动能与弹性势能和耗散能之间的转换关系,导致该类接触力模型精度较低,但由于该类接触力模型结构简单,通俗易懂有利于工程应用.
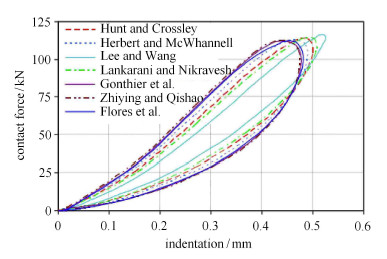
考虑接触能量损失的8种接触力模型虽然数学表达式各异,但其整体形式一致,均是由接触体的刚度系数、接触变形量、接触速度和材料阻尼系数组成的函数.其主要不同点在于迟滞阻尼因子,该因子决定了接触力模型在接触过程中能量耗散的方式见图4[30].观察表2可知,考虑能量耗散的接触力模型进展本质上是迟滞阻尼因子的进展,其目的是为了不断提高迟滞阻尼因子对接触过程中能量耗散的描述精度;而阻尼因子是接触刚度、初始接触速度和恢复系数的函数,当接触刚度与初始接触速度一定时,只有恢复系数在[0,1]之间变化,即考虑能量耗散的接触力模型的适用范围受到恢复系数的限制.一般由接触碰撞前后速度的固定比值来定义恢复系数或者由恢复阶段与压缩阶段的冲量之比定义恢复系数[88](实际上恢复系数与接触体表面的几何形状、初始碰撞速度、局部材料属性、接触的持续性、温度和摩擦等密切相关[89]),比值小于0.5的称为低恢复系数,比值大于0.5的称为高恢复系数. 8种考虑能量损失的接触力模型中除了线性模型的 Kelvin-$\!$-Voigt接触力模型以外,Hunt-$\!$-Crossley接触力模型、Herbert-$\!$-McWhannell接触力模型、Lee-$\!$-Wang接触力模型与Lankarani-$\!$-Nikravesh接触力模型均适合在拥有高恢复系数的接触碰撞问题中使用.而Zhiying-$\!$-Qishao接触力模型[90]、Gonthier接触力模型[91]与Flores接触力模型[14]在拥有高恢复系数的接触碰撞问题中具有相近的接触特性,且对低恢复系数也有良好的动态响应,尤其是Zhiying-$\!$-Qishao接触力模型.
|
图 4 接触力与变形量的关系 Fig. 4 Force–indentation relation |
值得注意的是:上述8种考虑能量耗散的接触力模型的适用范围不仅受到恢复系数大小的限制(Kelvin-$\!$-Voigt线性接触力模型不含恢复系数不予讨论),还受到其接触类型的限制. 然而,表2中不是所有的接触力模型均受到以上2点接触特性的限制,其中Hunt-$\!$-Crossley接触力模型、Lankarani-$\!$-Nikravesh接触力模型与Zhiying-$\!$-Qishao接触力模型只受到恢复系数的限制;Herbert-$\!$-McWhannell接触力模型、Lee-$\!$-Wang接触力模型与Gonthier接触力模型受到接触形式的限制;而Flores接触力模型适用于一般的机械碰撞,无明显的限制条件.
在考虑接触能量损失的接触力模型中恢复系数、阻尼系数、刚度系数、初始碰撞速度与幂指数系数的识别非常重要,其中初始碰撞速度一般根据研究的具体多体系统人为的给定,但规定接触初始碰撞速度要低于碰撞弹性波在接触体中的传播速度[92]. 同时一般令幂指数系数等于3/2,说明接触体表面的接触应力呈抛物线分布[91]. 而对于刚度系数文献[30]则忽略了其在接触力模型中的演化过程,接触刚度系数仅仅与接触体半径和材料属性有关,显然不符合实际的接触情况,因为刚度系数与接触体的材料属性,几何属性,间隙尺寸以及接触体的变形有关,即刚度系数在接触碰撞过程中是不断变化而不是一个常量[68]. 在实际的接触过程中,由于关节磨损导致关节间隙尺寸进一步扩大,且接触体表面形貌的改变不仅影响了其接触刚度和应力分布而且影响了整个磨损过程[70],即接触刚度系数与关节间隙尺寸大小有关,而间隙尺寸随磨损不断变化,所以在建立考虑关节磨损的接触力模型中应视其接触刚度为变量.
2 多体系统中关节磨损现象的研究进展磨损是相互接触的物体在相对运动中表层材料不断损伤的过程,它是伴随摩擦而产生的必然结果[93].磨损不但与接触体的几 何特征、材料的物理和化学属性有关,还与接触体的接触温度、接触表面的动态载荷有关.特别是在多体系统动力学中考虑接触体物理和化学属性以及接触热效应[94]时,其含间隙关节的磨损现象将十分复杂[27].根据接触体之间磨损机理的不同其磨损类型一般分为4大类:(1)磨粒磨损[95],(2)黏着磨损,(3)疲劳磨损,(4)腐蚀磨损.在不考虑润滑的情况下,当多体系统中关节元素接触表面洁净且产生相对滑动时,由于黏着效应形成的粘结点被剪切断裂,发生材料由一个表面向另一个表面转移的现象,即黏着磨损.目前关于黏着磨损问题的研究大多集中于实验,实验方法不仅成本高而且对于复杂的动态磨损实验方法只能得到材料磨损率与各影响因素之间的简单函数关系,不能满足实际工程问题对间隙运动副磨损预测的迫切需求[96].基于磨损模型(源于实验)的数值计算方法为多体系统中磨损预测提供了另一路径.
2.1 比较Reye's hypothesis和Archard磨损模型研究多体系统中关节磨损的数值方法主要有2种:(1)基于磨损模型的有限元分析法[97];(2)结合磨损模型与多体系统动力学模型对间隙运动副的磨损深度进行预测[27, 93]. 有限元分析法虽然能精确的处理拥有复杂几何外形的接触磨损问题(利用有限元分析接触体之间的接触应力,再基于Archard磨损模型预测磨损深度)[98],然而从计算效率的观点来看,有限元分析法需要大量的计算资源,特别是在分析复杂多体系统间隙关节的磨损现象时,可能由于计算模型过于庞大而不可行;而结合磨损模型与多体系统动力学模型对间隙运动副的磨损深度进行预测,则直接利用关节元素之间的接触力除以其近似接触面积计算接触应力,再基于Archard 磨损模型预测其磨损深度,但由于利用近似接触面积代替真实接触面积(接触体表面形貌较复杂其真实接触面积难以获得)计算接触应力降低了该方法的精度,所以该方法较之有限元分析其计算过程简单但计算精度较低.
磨损类型不同其相对应的磨损模型也不同,且大多数磨损模型中所包含的参数与常量只有在特定的应用环境中才有效[99]. 任何运动副元素之间都会发生黏着(只是黏着的程度不同),而黏着现象是导致黏着磨损的主要原因,所以多体系统中关节元素之间的磨损类型主要是黏着磨损;而在摩擦学中研究黏着磨损且具有相对普遍适用性的磨损模型有2类.
2.1.1 Archard磨损模型[100]Archard磨损模型是一种线性磨损模型,该磨损模型与间隙关节元素之间的法向接触力和滑移距离成正比,而与运动副软材料的硬度成反比[101, 102]
| $\dfrac{V}{s} = \dfrac{kF_n }{H} $ | (9) |
其中,$V$和$s$分别为磨损体积和相对滑移距离; $F_n$为法向接触力,$k$为无量纲磨损系数,由组成运动副的材料和磨损条件求得; $H$为较软材料的布氏硬度.
式(9)中的法向接触力一般根据间隙运动副之间的接触力模型计算得出[26, 27],即多体系统中关节磨损的预测是集关节间隙、接触力模型和Archard磨损模型为一体的整体研究,并不是单纯的依靠理想多体系统中关节的正压力来研究关节磨损.当然这里并不是完全否定了利用理想多体系统关节的正压力充当接触力的计算方法,该方法的应用应分为以下2种情况:(1)在多体系统的运行初期,在视装配间隙量等于0的情况下,利用关节正压力代替接触力基于Archard磨损模型来预测关节磨损量,该方法在多体系统分析的一定精度要求内可以接受.(2)在机构系统运行一段时间后当关节间隙量变大,关节间隙引起的碰撞力是理想机构关节正压力的几倍甚至十几倍[1, 2],此时应采用关节间隙碰撞力来计算磨损. Archard磨损模型对以上2种情况均适合.
由于磨损深度比磨损体积更利于工程应用,所以对式(9)两边除以接触面积得到Archard磨损模型的另一种表达式
| $\dfrac{h}{s} = k_d p $ | (10) |
其中,$k_d = \dfrac{k}{H}$为线性磨损系数,$h$为磨损深度,$p$为法向接触应力.
2.1.2 Reye's hypothesis模型[103, 104]Reye's hypothesis模型也称为能量耗散假设,该模型认为在干摩擦的情况下,磨损体积与摩擦力所做的功成正比,与相对滑动接触体之间的剪切应力成反比.
| $\dfrac{V}{s} = \dfrac{F_T }{\tau } $ | (11) |
其中,$V$和$s$为磨损体积和相对滑移距离,$F_T $为切向摩擦力;$\tau$为相对滑动体的剪切应力. Reye's hypothesis模型可改写为
| $\frac{{{\rm{d}}h}}{{{\rm{d}}s}} = \frac{{\mu p}}{\tau }$ | (12) |
其中,$\mu $为摩擦系数,$p$为接触应力.
式(10)与式(12)在结构上非常相似,其区别在于Archard磨损模型是利用法向接触力解释磨损,而Reye'shypothesis模型是利用切向摩擦力解释磨损(虽然摩擦和磨损基本上总是一起出现,但定性的看,它们是不同的现象[12]),即Archard磨损模型为无摩擦的磨损描述,Reye'shypothesis模型为摩擦与磨损一起出现的描述. 但是这2种磨损模型在多体系统关节磨损预测的应用中是一致的,因为2种磨损模型中其法向接触力和摩擦力可以相互转化.
2.2 Archard 磨损模型的演变过程Archard磨损模型本质上是一个宏观磨损模型. 因为该模型没有直接考虑接触体的表面微凸体变形和材料撕裂等微观效应[105],而是利用一个宏观的磨损系数来等效这些微观效应. 且该模型对接触体的运动速度和负载有严格的要求:(1)接触体之间的滑移速度不宜过高,避免摩擦热引起接触材料物理属性的变化[106];(2)接触体之间的动态负载不宜过大,避免大负载引起接触体之间发生咬死和黏滞[27].
Holm在1946年基于实验研究得出的Archard磨损模型经过 几十年的研究发展主要演变出2种适合不同研究环境的磨损模型.
(1)式(10)为Archard磨损模型最常用的形式[26, 27, 36],含间隙关节元素的接触碰撞点在机构运行过程中不断变化,并且频繁的接触区域通常发生在某些特殊的接触位置,该现象导致了间隙关节元素非规则的接触磨损,而不是所谓的均匀磨损[26, 27];另外动态的接触碰撞力使间隙接触元素的接触碰撞点的滑移距离也时刻变化,因此一般采用微分的形式来研究含间隙多体系统的动态磨损特性.
| $\dfrac{\rm{d} h}{\rm{d} s} = k_d p $ | (13) |
相比滑移距离其接触碰撞点的速度更容易求解,利用$\rm{d} s =v \rm{d} t$对式(13)进行了修改得到
| $\rm{d} h = k_d p\rm{d} s = k_d pv\rm{d} t $ | (14) |
式(14)两边对接触时间积分就能得到接触区域的磨损深度.
(2)以考虑真实接触面积的角度将线性Archard磨损模型改进为非线性磨损模型[107 -180].非线性Archard磨损模型认为真实接触面积与表面微凸体的微观进化伴随着接触表面形状与接触区域的 宏观进化.在准稳态磨损中真实接触面积$A_{\rm r}$与理论接触面积$A_{\rm c}$的比值为
| $\alpha = \dfrac{A_{\rm r} }{A_{\rm c} } $ | (15) |
非线性Archard磨损模型的具体形式为
| $W = \dfrac{k_{\rm w} }{H}Fs = \beta Fs $ | (16) |
式(16)两边均除以真实接触面积$A_{\rm r} $得到磨损深度$h_{\rm c} $的求解公式
| $h_{\rm c} = \beta p_{\rm n} s $ | (17) |
其中,磨损体积$W=h_{\rm c} A_{\rm r} $,$k_{\rm w}$为无量纲磨损系数,$H$为接触体硬度(一般视接触体为同一种材料),$p_{\rm n}$接触应力,$s$为相对滑移距离,$\beta = \dfrac{k_{\rm w}}{H}$为相对硬度系数,$F$为固定法向载荷,以时间$t$为变量对$F = p_{\rm n} A_{\rm r}$两边微分得
| $\dot F = \dot p_{\rm n} A_{\rm r} + p_{\rm n} \dot A_{\rm r} = { 0} $ | (18) |
式(17)两边对时间$t$求导就能得出磨损深度的增长率
| $\dot h_{\rm c} = \beta \dot p_{\rm n} s + \beta p_{\rm n} v_{\rm r} $ | (19) |
将式(18)代入式(19)得磨损深度的变化函数
| $\dot h_{\rm c} = \beta \Big ( 1 - \dfrac{ \ln \dot A_{\rm r} }{ \ln \dot s } \Big) p_{\rm n} v_{\rm r} =\tilde\beta p_{\rm n} v_{\rm r} $ | (20) |
其中,$v_{\rm r}$为相对滑动速度,非线性磨损系数为滑动距离的函数$\tilde\beta = \tilde \beta (s)$.
相对于只是为了对稳态磨损进行研究且拥有常数磨损系数的Archard磨损模型,式(20)给出的模型虽然能研究准稳态和稳态磨损且拥有非线性磨损系数,但是从非线性磨损模型的推导过程可知,该模型只适合拥有固定接触载荷的磨损中[109, 110],因为在该模型中认为法向接触力不再是接触变形量的函数而是一个常数(见式(18)),所以该非线性磨损模型不适合在考虑运动副非规则间隙的多体系统动力学中应用.
2.3 Archard 磨损模型中主要磨损参数分析从上述Archard磨损模型的不同表现形式可以得出该模型所涉及的主要磨损参数有磨损系数、材料硬度、滑移距离、实际接触面积和接触体表面的接触应力分布[111]. 其中磨损系数与材料硬度一般通过实验给出[112],剩下的磨损参数是含间隙关节元素磨损预测的主要研究对象.
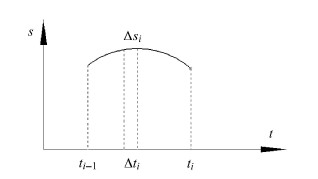
2.3.1 滑移距离$s$的研究方法由于间隙运动副元素之间接触点位置和滑移距离均随着多体系统的运动而不断变化,且在每一个接触瞬间认为接触条件是保持不变的,所以为了达到稳定的磨损过程必须要把连续的接触过程离散 化[26, 96],如图5所示.
|
图 5 滑移距离离散化示意图 Fig. 5 Discretization slip distance |
图中曲线$s$表示间隙运动副元素之间一段相对连续接触滑动的曲线,足够小的时间$\Delta _i $内的滑移距离为$\Delta s_i $,因此瞬态滑移距离的表达式为
| $\Delta s_i = \left( {R + \delta } \right)\left( {\alpha _{t_i } - \alpha_{t_{i - 1} } } \right) $ | (21) |
其中,$R$为接触体曲率半径; $\delta $为接触体变形量; $\alpha _{t_i } $与$\alpha_{t_{i - 1} } $为对应时刻下间隙运动副所连接的2个构件的角位移差,即$\alpha _t= \phi _i - \phi _j $,$\phi _i $与$\phi _j $分别为构件$i$和$j$的角位移.
2.3.2 接触面积$A_{\rm r} $的研究方法在多体系统动力学的磨损研究中一般难以对间隙元素之间的真实接触面积进行计算[26],有2点原因:(1)间隙元素接触体之间的接触点、滑移距离和接触变形均随着多体系统的运行不断发生变化,导致接触体之间的真实接触面积不易确定;(2)接触体的真实接触表面几何属性过于复杂. 以上2点原因给接触体之间的真实接触面积的定量计算带来了困难.
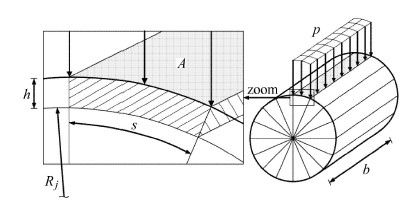
目前对真实接触面积的计算主要采用有限元分析法[36, 113],另外通过Winkler表面模型在不改变接触区域的尺寸和形状的情况下把离散化的接触表面近似为矩形或圆形[95, 27],如图6所示.
|
图 6 接触面积放大示意图 Fig. 6 Diagram of exaggerated contact areas |
图6中$h$为磨损深度,$A$为近似接触面积,$s$为滑移距离,$b$为销轴的长度,$p$为接触应力,$R_J$为轴套的 接触半径. 则近似接触面积
| $A = sb $ | (22) |
|
图 7 Winkler 弹性基础平面模型 Fig. 7 Winkler planar model |
然而需要指出式(22)只适合转动副与圆柱副的真实接触面积$A_{\rm r}$的近似计算,而对于含间隙球面副的近似接触面积的计算将需要另行设计.
2.3.3 接触应力$p$的研究方法磨损模型中接触应力分布的循环计算是多体系统动力学中磨损仿真的主要难点,也是校核关节强度与预测系统疲劳寿命的前提条件. 接触应力分布是接触面积和滑移距离的函数.目前研究接触体表面接触应力分布的主要方法有:(1)有限元分析法[36, 80, 114, 115];(2)边界元法[116];(3)实验方法[85];(4)根据接触应力强度与接触尺寸参数的关系[107],结合修正的Hertz接触理论与接触面积分析其接触应力分布[27]. (5) Winkler弹性基础理论[24, 85, 117, 118]. 其中有限元法虽精确但不经济,边界元法需要对每一步的滑移增量进行优化来提高计算效率以及保持接触表面的光滑[116],即该方法不够简单直接[119];实验方法其研究对象单一且成本高,而利用接触力模型结合接触面积计算其接触应力是最常用的方法,但该模型涉及对真实接触面积的近似计算导致精度较低.
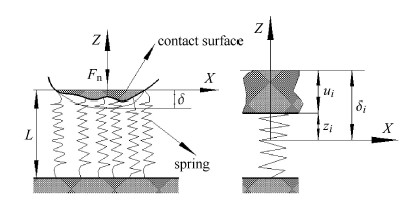
Winkler弹性基础理论以接触体之间的弹性变形为基础,忽略了接触体之间的剪切作用力,将接触界面模拟为一系列的弹簧,且相邻弹簧之间保持相互独立[85],如图7所示.Winkler弹 性基础理论的本质就是利用接触体之间接触点的弹性位移来计算接触面上接触点的接触应力.该模型建立了每一根弹簧的接触应力与其接触变形的函数关系式[80, 86].
| $p = \dfrac{E_{\rm w} }{L}u_z $ | (23) |
该模型中每一根弹簧的刚度系数为
| $K_{\rm N} = \dfrac{E_{\rm w} }{L} $ | (24) |
其中,$p$为接触应力; $E_{\rm w} $为弹性层的弹性模量; $L$为弹性层的厚度; $u_z$为弹性层的法向位移,在磨损的循环迭代中,每一次迭代的法向位移$u_i = \delta_i - z_i $,式中$\delta _i $为侵入深度,$z_i $为弹性层的弹性变形量.
研究间隙运动副接触应力的Winkler弹性基础理论来源于纯弯曲梁理论提出的Winkler地基模型[120, 121] (将地基看成许多互不联系的弹簧,并假定土体表面任一点的压力强度与该点的沉降成正比)
| $P = ks $ | (25) |
其中,$P$为土体表面某点单位面积上的压力,$k$为基床系数,$s$为相应于某点的竖向位移.
将Winkler地基模型应用到机构系统中间隙运动副的接触应力计算,由于基于式(23)与式(24)可利用弹簧的刚度系数和法向位移直接计算接触应力(弹簧的刚度系数为常数),而不必利用有限元法或通过接触力模型和近似接触面积计算其接触应力,所以该方法拥有较高的计算效率[24],但同时也存在下列问题:(1)弹簧刚度系数如何计算,虽然式(24)将弹簧刚度系数的计算转化为对接触体表面弹性层厚度的确定,但关键在于含间隙运动副接触表面的弹性层厚度本身就没有明确的定义,且没有具体的确定准则[24, 85].(2)凭经验确定的侵入深度$\delta_i $初值降低了整个机构系统的关节磨损预测的计算精度[85].(3)由于Winkler弹性基础理论忽略了接触体之间的剪切作用力,所以该理论成立的前提就是不考虑机构系统中间隙关节元素之间的摩擦效应.(4)Winkler弹性基础理论能够在一定精度范围内对间隙运动副元素之间的磨损预测达到与有限元分析方法同样的效果[115],但是在多体系统跑合阶段的磨损预测与接触应力的计算结果具有偏差[122].主要是因为跑合阶段的局部应变效应比稳定磨损阶段的磨损要强烈[85].另外由于该模型忽略了接触体之间的剪切作用力,所以该模型不能通过某个接触点的接触应力来说明它如何影响其他接触点的变形问题[119].
综上所述,以上5种接触应力的求解方法各具优缺点,如何选择合适的接触应力求解方法,应该结合计算效率与模型精度2方面综合考虑.
3 具体关节间隙的运动学模型多体系统动力学中关节效应模型包括:间隙运动副的运动学模型、接触力模型、摩擦力模型和磨损模型.以上分析的所有关节效应模型均是多体系统研究关节效应对系统动力学性能影响所应用的模型,且从分析结果可以得出:除了间隙运动副的运动学模型(关节不同其运动方式不同)和Archard磨损模型(关节不同导致接触面积的计算模型不一致,而其他磨损参数与关节类型无直接关系)与关节类型有关以外,其他关节效应模型均与关节的具体类型(转动副,移动副、圆柱副与球面副)无直接关系.原因有3点:(1)利用接触体之间的接触刚度与接触材料内部阻尼,以及接触变形量和相对接触速度建立线性或非线性的接触力模型,该过程中接触刚度与阻尼系数的计算与关节的类型无直接关系[30],而与关节间隙尺寸、磨损以及接触体材料属性有关[21].也就是说,基于Hertz接触理论的接触力模型对于多体系统中任何类型的关节都适用[26, 56, 84, 191].(2)既然接触力模型与关节的类型无直接关系,那么基于法向接触力与摩擦系数建立的摩擦力模型也同样与关节的具体类型无直接关系[55, 57, 64, 65].(3)研究接触体之间黏着磨损的Archard磨损模型,其主要磨损参数有磨损系数、材料硬度、滑移距离、接触面积和接触应力;其中磨损系数与材料硬度由实验提供,滑移距离模型与关节所连接2构件之间的相对转角有关(与关节类型无关),接触应力由接触体之间的法向接触力和接触面积确定,其中间隙关节元素之间的接触面积与关节类型密切相关,因为不同关节其接触运动方式不同.因此,对含间隙转动副、移动副、圆柱副与球面副的运动学模型进行简单介绍.建立含间隙运动副的运动学模型目的是为了计算多体系统动力学模型中的广义力,为装配多体系统的动力学模型奠定基础.所有含间隙运动副的运动学模型均是为了求出接触体之间的潜在接触点,并导出接触体之间的接触变形量为判定接触体是否接触做准备,以及建立接触体之间的相对法向与切向速度模型为计算广义力做准备.由于文章篇幅有限,且鉴于转动副相比其他运动副更常见且应用广泛,因此,本文将对含间隙转动副的运动学模型进行详细介绍,而其他含间隙运动副的运动学模型只做简单介绍.
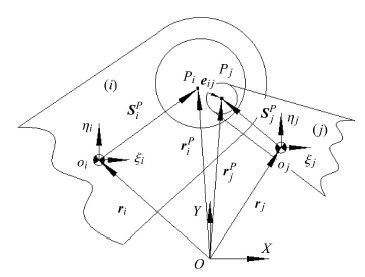
3.1 转动副的间隙运动学模型理想转动副由轴套和轴颈2部分组成,它们之间只发生相对转动.而在转动副中引入间隙后该运动副原来的运动约束被2个沿径向移动 自由度代替. 假设转动副的装配间隙$c=R_{i}-R_{j}$(其中$R_{i}$与$R_{j}$分别为轴套和轴颈的回转半径).图8中接触体$i$和接触体$j$分别代表转动副的轴套和轴颈,其中$O_{i}$和$O_{j}$分别表示接触体$i$与$j$的质心,局部坐标系$\xi_i\eta _i o_i $与$\xi _j \eta _j o_j $分别与接触体$i$与$j$的质心固结,点$P_i $与$P_j$分别为轴套和轴颈的回转中心.
|
图 8 含间隙的转动副 Fig. 8 Revolute joint with clearance |
根据图8 可以得出含间隙转动副的偏心距
| ${\pmb e}_{ij} = {\pmb r}_j^P - {\pmb r}_i^P $ | (26) |
其中,${\pmb r}_j^P $与${\pmb r}_i^P $分别为接触体回转中心在固定坐标系$XOY$中的位置向量
| ${\pmb r}_k^P = {\pmb r}_k +{\pmb A}_k {\pmb s}_k^P ,\ \ \ k = i,j $ | (27) |
其中,${\pmb r}_k $为接触体$i$与$j$的质心在固定坐标系$XOY$中的位置向量,${\pmb A}_k$为局部坐标相对于固定坐标$XOY$之间的转换矩阵,${\pmb s}_k^P $为接触体回转中心$P_i $与$P_j $在局部坐标系$\xi_i \eta _i o_i $与$\xi _j \eta _j o_j $中的位置矢量.
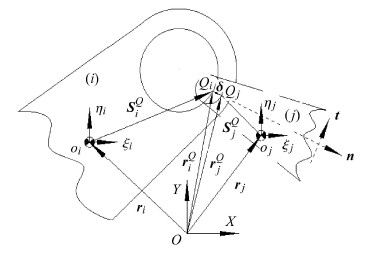
图9描述了轴套与轴颈之间的接触状态,其接触面的法向矢量为
| ${\pmb n} = \dfrac{{\pmb e}_{ij} }{e_{ij} } $ | (28) |
其中$e_{ij} = \sqrt {{\pmb e}_{ij}^{\rm T} {\pmb e}_{ij} } $.
|
图 9 含间隙转动副的接触运动 Fig. 9 Revolute joint clearance with contact |
其接触变形量为
| $\delta = e_{ij}- c $ | (29) |
含间隙转动副元素在接触后其各自接触点$Q_i $与$Q_j$在固定坐标$XOY$中的位置矢量为
| ${\pmb r}_k^Q = {\pmb r}_k + {\pmb A}_k {\pmb s}_k^Q + R_k {\pmb n} ,\ \ \ \ k = i,j $ | (30) |
其中,${\pmb s}_k^Q $为接触点$Q_i $与$Q_j $在局部坐标系$\xi _i \eta _i o_i $与$\xi _j \eta _j o_j $中的位置向量,${\pmb r}_k^Q $为接触点$Q_i $与$Q_j $在固定坐标系$XOY$中的位置向量.
由此可得含间隙转动副元素之间的相对接触速度
| $\left.\!\!\begin{array}{l} v_N = \left( {\dot {\pmb r}_j^Q - \dot {\pmb r}_i^Q } \right)^{\rm T}{\pmb n} \\ v_T = \left( {\dot{\pmb r}_j^Q - \dot {\pmb r}_i^Q } \right)^{\rm T} {\pmb t} \end{array}\!\! \right\} $ | (31) |
其中$\dot{\pmb r}_j^Q $与$\dot {\pmb r}_i^Q $为各自接触体的接触速度.
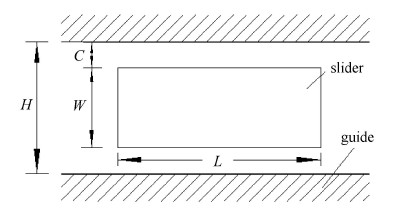
3.2 移动副的间隙运动学模型理想移动副包含滑块和导轨两部分,它们之间没有相对转动和垂直移动.而含间隙的移动副则消除了理想移动副的2个运动约束,从而引入了1个垂直于轴线的移动自由度和1个绕垂直于移动平面的转动自由度,定义含间隙平面移动副的间隙量$c$为滑块和导轨表面之间的距离,滑块的长为$L$,宽为$W$,导轨的2个表面之间的距离为$H$,如图10.
|
图 10 含间隙平面移动副 Fig. 10 Planar translational joint with clearance |
该运动副的间隙量为
| $c = \dfrac{H - W}{2} $ | (32) |
由于含间隙的移动副导致滑块能在导轨内自由运动,其具体的运动形式见图11.
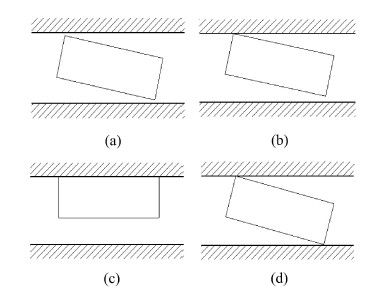
|
图 11 含间隙移动副的运动形式 Fig. 11 Motion form of translational joint with clearance |
其中图11(a)描述了滑块在导轨内自由运动,此时该关节中没有产生接触力.图11(b)滑块的一个顶点与导轨表面相接触. 图1(c)1滑块 两相邻顶点与导轨表面相接触.图11(d)滑块两对角线顶点与导轨表面相接触. 其具体运动学模型详见文献[91, 123, 124].
3.3 圆柱副的间隙运动学模型理想圆柱副中轴与轴套的轴线相互平行,实际圆柱副中由于间隙的存在导致轴与轴套的轴线不再平行,且在垂直于圆柱副轴线的方向其间隙圆柱副元素发生相对转动和移动.然而真实圆柱副中的间隙量相比圆柱副的长度和自身回转半径要小得多,所以认为轴套与轴的几何中心$P$保持重合如图12.真实圆柱副的间隙为轴与轴套的半径差$c=R_{\rm b}-R_{\rm j}$,其中$R_{\rm b}$与Rj分别为轴套与轴的回转半径. 含间隙圆柱副的运动学模型详见文献[60, 80, 84, 87, 125, 126].
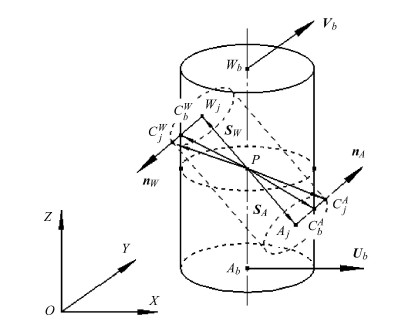
|
图 12 含间隙圆柱副的接触运动 Fig. 12 Cylindrical joint clearance with contact |
理想球面副认为连接2构件的球体和球套的几何中心重合,拥有3个转动的自由度,但是实际球面副由于间隙的存在导致球关节分成2部分,即球体能在球套内自由运动;使理想的3自由度球面副变为无约束的6自由度含间隙球面副,原来的3个运动约束被3个接触力约束所代替,含间隙球面副由代表球套的接触体$i$和代表球体的接触体$j$组成,球体与球套各自的半径为$R_{j}$与$R_{i}$,即径向间隙为$c=R_{i}-R_{j}$. 含间隙球面副的运动学模型详见文献[50, 56].
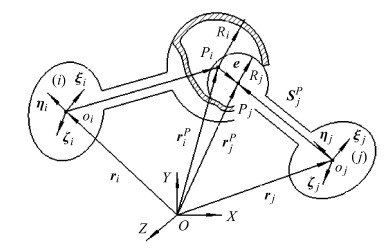
|
图 13 含间隙的球面副 Fig. 13 Spherical joint with clearance |
以上分别讨论了含间隙平面运动副(转动副和移动副)和含间隙空间运动副(圆柱副和球面副)的间隙运动学建模过程,其中1自由度转动副的轴向长度较小导致含间隙转动副元素之间只有1个潜在接触点;1自由度移动副的轴向长度较大导致含间隙移动副元素之间拥有4种不同的接触方式,每一种接触方式的运动学模型均需要独立分析;2自由度圆柱副与1自由度移动副类似,其轴向长度较大导致含间隙圆柱副元素之间出现2个潜在接触点,每一个潜在接触点之间的接触速度和接触变形量均需要独立分析;3自由度球面副相比1自由度转动副仅增加了维数但建模过程相似.虽然各运动副的运动方式各异,但是建立含间隙关节运动学模型的主要目的一致:(1)计算含间隙关节元素之间潜在接触点的位置或偏心距,(2)计算其潜在接触点的实际几何距离与接触变形量,(3)获得间隙关节元素之间的相对法向与切向速度.为含间隙多体系统动力学中的接触力模型、摩擦力模型和磨损模型的建立做铺垫.
4 考虑关节效应的多体系统动力学建模方法研究关节效应的目的是为了能够把关节中的间隙、摩擦、磨损以及接触变形与多体系统的动力学模型有机的集成在一起,分析关节效应对多体系统性能的影响,预测系统的工作寿命,提高系统的运动精度,减少系统的维护成本.其中建立考虑关节效应的多体系统动力学模型是关键,见图14.
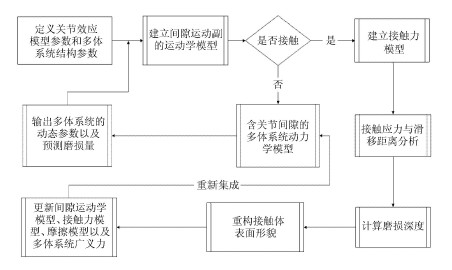
|
图 14 考虑关节效应的多体系统动力学建模流程图 Fig. 14 Molding flow chart of multi-body system dynamics considering joint effect |
图14给出了考虑关节效应的多体系统动力学模型的建模方法流程图. 其步骤如下:
(1)给出接触力模型、摩擦模型、磨损模型的物理属性系数,以及定义多体系统的结构参数和间隙参数;
(2)建立初始装配间隙的运动学模型,其中包括找出接触体的潜在接触点,计算接触点的距离以及建立接触体之间的相对接触速度模型;
(3)根据间隙的运动学模型判定其接触体之间是否接触,如果不接触,就建立含间隙关节的多体系统动力学模型(该模型中不含广义接触力);
(4)当接触体之间连续接触时,利用接触力模型建立法向接触力模型,基于摩擦模型建立切向摩擦力模型,并将接触力向间隙关节所连接的活动构件质心转化并获得多体系统的广义接触力;
(5)利用接触力模型与接触面积计算接触体表面的应力分布;
(6)利用接触应力分布和相对滑移距离或相对接触速度的结论基于Archard磨损模型计算间隙运动副元素之间的磨损深度;
(7)由于间隙运动副元素之间的磨损导致接触体表面形貌发生变化,根据磨损深度重构其接触体表面的几何属性;
(8)接触体几何特征的变化引起了间隙运动学模型、接触力模型、摩擦力模型中接触变量的更新,最终导致多体系统中广义接触力的更新;
(9)利用更新后的广义接触力与磨损前的多体系统动力学模型重新集成磨损后的多体系统动力学模型;
(10)利用磨损后的多体系统动力学模型不仅能预测磨损深度,而且能得到理想动态输出参数与实际动态输出参数的偏差. 在得到磨损后的动态输出参数后再重新建立磨损后的间隙运动学模型,然后继续步骤(3)以后的研究内容直到循环计算次数达到其预定的迭代数量. 关于磨损的具体仿真迭代过程见文献[26, 27, 36, 127].
一般来说,多体系统可分为3类:第1类不考虑关节效应的理想多体系统;第2类考虑关节间隙(间隙尺寸为常数)的多体系统;第3类考虑非规则磨损间隙(间隙尺寸随着磨损过程不断增加)的多体系统. 3类不同的多体系统导致其动力学建模过程各异.其中理想多体系统直接利用多体系统动力学方程建立其模型,不需要考虑关节元素之间的接触碰撞和磨损;考虑关节间隙为常数的多体系统在动力学建模过程中由于关节间隙尺寸不变,其动力学建模不涉及Archard磨损模型和磨损深度对接触半径的更新,以致于该动力学建模过程在进行到步骤(4)时即可完成动力学模型的装配;第3类多体系统与实际多体系统最接近,其建模过程涉及了接触模型,摩擦力模型与Archard磨损模型,其中基于磨损模型预测间隙关节元素之间的磨损深度并更新接触体的接触半径是该系统动力学建模过程的关键,该过程更加精确的描述了考虑关节间隙多体系统在运行过程中关节效应对系统动态性能的影响.
4.1 考虑关节磨损的平面五杆机构动力学建模以考虑关节磨损的平面五杆机构为例,对上述建模过程进行了详细的说明. 如图15所示的含间隙平面五杆机构中转动副$B$处存在径向间隙(初始的装配间隙$r= R_{\rm B} - R_{\rm J} $,其中$R_{\rm B} $和 $R_{\rm J} $分别为轴套与轴的原始半径),轴与轴套中心距离为中心距$e$(在$OXY$坐标系下的分量为$e_x $和 $e_y $),其中心连线与$X$轴的夹角为间隙方位角$\theta $. 各杆杆长与质量分别为$l_1 ,l_2 ,l_3 ,l_4 ,l_5 ,m_1 ,m_2 ,m_3 ,m_4$,各杆的质心与位置角分别为$S_1 ,S_2 ,S_3 ,S_4 ,\varphi _1 ,\varphi _2,\varphi _3 ,\varphi _4 $;$ J_i$为各杆件绕通过质心且与回转轴平行的轴的转动惯量$\left( {i = 1,2,3,4}\right)$. $x_{Si} $和$y_{Si} $为各构件质心$S_i $在坐标系$OXY$中的横纵坐标.
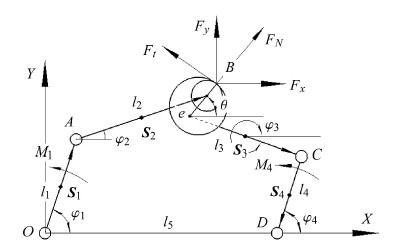
|
图 15 含间隙平面五杆机构 Fig. 15 Planar five-bar linkage with clearance |
为了便于描述五杆机构的运动学状态,取该机构的位形坐标为
| ${\pmb q} = \left[{x_{S{1}} ,y_{S{1}} ,\varphi _{1} ,x_{S{2}},y_{S{2}} ,\varphi _{2} ,x_{S{3}} ,y_{S{3}} ,\varphi_{3} ,x_{S{4}} ,y_{S{4}} ,\varphi _{4} }\right]^{\rm T} $ | (33) |
根据该机构的位形坐标写出其考虑$B$关节间隙的位置方程
| ${\pmb\varPhi} \left( { {\pmb q},t} \right) =0 $ | (34) |
式(34)对时间$t$求一阶导数和二阶导数导出该机构的速度与加速度方程
| ${\pmb\varPhi}_q \dot{\pmb q} ={\pmb \upsilon} $ | (35) |
| ${\pmb \varPhi}_q \ddot{\pmb q} ={\pmb \gamma}$ | (36) |
其中,${\pmb\varPhi}_q $为该机构的Jcobian矩阵,${\pmb\upsilon} $,${\pmb\gamma }$为含速度,位移和时间的函数.
增广法通过引入拉格朗日乘子${\pmb\lambda} $释放该系统的约束导出其运动微分方程
| $ {\pmb M}\ddot {\pmb q} + {\pmb\varPhi}_q {\pmb\lambda }={\pmb Q} $ | (37) |
其中,${\pmb M}$为质量矩阵;$\ddot {\pmb q} $为加速度矢量;${\pmb\lambda}$为拉格朗日乘子矢量,该矢量对应该机构的关节约束反力;${\pmb Q}$为广义外力,其中包括系统的摩擦力、碰撞力、重力与外载荷.
通过组装多体系统的运动微分方程和约束方程得到该机构的动力学方程
| $ \left[\!\! \begin{array}{cc}{\pmb M} & {\pmb\varPhi}_q^{\rm T} \\ {\pmb\varPhi}_q & 0 \end{array}\!\! \right]\left[\!\! \begin{array}{ c} \ddot{\pmb q} \\{\pmb \lambda}\end{array}\!\! \right] = \left[\!\! \begin{array}{c}{\pmb Q} \\{\pmb \gamma }\end{array} \!\! \right] $ | (38) |
(1)含间隙关节运动学建模的具体过程详见第1.1节,按照上述求解过程导出含间隙关节元素之间的相对法向接触速度$v_n$、相对切向接触速度$v_t $、偏心距$e$、接触变形量$\delta$以及间隙方位角$\theta$,为判定含间隙关节元素之间是否接触以及接触力建模做准备.
(2)在已知含间隙关节元素之间的接触变形量与相对接触速度后,根据表2中的接触力模型计算接触体之间法向接触力,最后基于摩擦力模型计算接触体之间的切向摩擦力.
(3)含间隙关节由于碰撞产生的接触力工作方向为接触表面的法向方向,另外,含间隙关节所连接的2个活动构件的局部坐标系与活动构件质心固接,所以含间隙关节元素的接触力必须向其活动构件的质心上转化,而不是作用在接触点上. 因此,把作用在接触点的接触力向活动构件质心转化的同时将会产生一个额外力矩施加在活动构件的质心上,具体过程详见文献[15].
4.1.3 含间隙关节的磨损深度预测间隙关节磨损深度的具体预测过程分以下3个主要步骤:
(1)首先,在求出装配间隙下接触力和接触变形量后,可以通过式(22)得出近似接触面积,再结合通过接触力模型得到的接触力和近似接触面积导出其接触体的表面接触应力,其次,通过式(21)得出接触体之间的相对滑移距离.最后,把接触应力和相对滑移距离代入式(10)计算含间隙关节的磨损深度$h_i $.
磨损后接触体半径的更新一般分2种情况:(i)假设接触体材料相同,轴套与轴各磨损一半[27, 118];(ii)由于材料相同的金属或者互溶性大的材料组成的运动副其磨损较严重,实际中运动副为了抗黏着磨损往往选择不同的接触体材料[128],此时只考虑轴套的磨损. 一般来说,脆性材料的抗黏着磨损的能力比塑性材料高,且脆性材料的破坏由正应力引起,而塑性材料的破坏由剪应力决定. 另外,金属和非金属组成的运动副其抗黏着磨损的能力高于异种金属组成的运动副;且从材料的组织结构看,多相金属比单相金属的抗黏着磨损能力高[129].
笼统的认为轴套与轴各磨损一半或者只考虑轴套磨损而忽视轴磨损[12, 128],均不是十分准确的假设. 关节总磨损量在间隙运动副元素中的定量分配不仅与接触材料属性密切相关,而且与接触温度和金相成分等有关,具体该如何分配关节总磨损量有待进一步深入研究.
(2)将以上更新结果代入间隙关节的运动学模型式(29)、式(30)与式(31)更新间隙关节元素之间的接触变形量$\delta $以及相对接触速度$v_n $和$v_t$,然后重复第4.1.2节的第(2)与第(3)步得到关节磨损后的系统广义力${\pmb Q}$. 最后根据式(38)重新集成考虑关节磨损后的平面五杆机构的动力学模型,通过求解该方程导出磨损后的系统的加速度,在对其积分运算后就能得到关节磨损对系统输出轨迹的影响,即求出平面五杆机构在关节磨损前后运动轨迹的偏差量,为该机构的结构设计与实际应用提供理论依据.
(3)利用步骤(2)中平面五杆机构第1次磨损循环得出的系统速度与位置作为下一次系统磨损循环的初始条件,另外利用步骤(2)中磨损后更新的含间隙关节运动学参数重新建立间隙运动学模型,然后继续步骤(1)与步骤(2)的研究内容直到循环计算次数达到其预定的迭代数量. 最终计算出在预定循环次数下含间隙关节的磨损深度以及磨损后系统动力学性能的整体退化结果.
5 结论与发展趋势(1)关节效应中的间隙效应导致了间隙运动副元素之间的接触碰撞,从而加剧了接触体之间的动摩擦以及引起了接触变形和磨损. 通过对近十几年多体系统动力学中关节效应研究方法的分析与总结了间隙运动学模型、摩擦模型、接触力模型和磨损模型的研究方法,其中着重分析了多体系统动力学中关节磨损模型的研究进展,详细的介绍了Archard磨损模型中的滑移距离、接触面积以及接触应力分布等磨损参数的计算方法.
(2)通过对多体系统动力学中关节效应模型的分析得出其摩擦力模型、接触力模型和磨损模型(接触面积与关节类型有关)几乎与多体系统中的关节类型没有直接的联系,但间隙运动副的运动学模型与关节类型直接相关,于是对含间隙的转动副、移动副、圆柱副和球面副的运动学模型分别进行了分析,得出间隙运动副的运动学建模的目的都是一致的,即为含间隙多体系统动力学中的接触力模型、摩擦力模型和磨损模型的建立做铺垫.
(3)通过现有的研究证明多体系统中的关节磨损是一种非规则行为[26, 27, 107, 114, 115, 127]. 而现有的Archard磨损模型只建立了磨损深度与接触应力和滑移距离的函数关系,其中固定磨损系数已不能完全反映其非规则磨损行为[130, 131]. 未来的磨损模型不仅要考虑接触体的几何特征、物理属性,而且还应注重接触体的化学属性以及摩擦热[88, 89]对磨损特性的影响.
(4)鉴于多体系统动力学自身的非线性和关节效应模型的复杂性,目前对于考虑单间隙的多体系统干接触问题研究较多,但实际的多体系统不但各运动副都含有间隙[125, 132]且关节润滑[125, 133, 134]和构件柔性[56, 105, 135]均不能被忽视. 随着计算机的发展与多体系统动力学模型的合理简化,综合多间隙与构件柔性的湿接触将是多体系统动力学研究的趋势.
(5)目前多体系统动力学中关节效应的研究对象主要是平面多体系统,特别是关节磨损引起的多体系统性能退化的研究还处于初级阶段[26, 27, 127]. 而作为承载能力强且运动精度高的并联机构[20, 136, 137, 138, 139, 140, 141],以及具有较大工作空间且承载能力稳定的航天机构[96],关节的非规则磨损对其空间机构性能的影响将更加明显,且随着将来并联机构在生产生活中的广泛应用以及航天事业的飞速发展,关节磨损的研究由平面多体系统转换到空间多体系统的研究势在必行.
(6)多体系统中关节效应的研究使系统的动力学性能更加贴近实际情况,对于一般的机械系统寿命预测、可靠性以及动力学研究均适用. 例如:目前在航空领域中广泛应用的可展开空间结构[96, 142],其非线性动力学性能在考虑关节效应的环境下研究将更利于该结构的设计与校正,同时也有利用提高该系统的可靠性.
| [1] | Onesmus M, John K, Bernard I. Numerical study of parametric effects on the dynamic response of planar multi-body systems with differently located frictionless revolute clearance joints. Mechanism and Machine Theory, 2012, 53: 30-49. |
| [2] | Xu LX, Yang YH, Li YG, et al. Modeling and analysis of planar multibody systems containing deep groove ball bearing with clearance. Mechanism and Machine Theory, 2012, 56: 69-88. |
| [3] | de Jálon JG, Bayo E. Kinematic and Dynamic Simulations of Multibody Systems. New York: Springer-Verlag, 1994 |
| [4] | Erkaya S, Uzmay Ī. Effects of balancing and link flexibility on dynamics of a planar mechanism having joint clearance. Scientia Iranica B, 2012, 19(3): 483-490. |
| [5] | Shabana AA. Dynamics of Multibody Systems. Cambridge University Press, England: Cambridge, 2005 |
| [6] | Erkaya S, Uzmay I. Determining link parameters using genetic algorithm in mechanisms with joint clearance. Mechanisms and Machine Theory, 2009, 44: 222-234. |
| [7] | Yoo WS, Kim KN, Kim HW, et al. Developments of multibody system dynamics: Computer simulations and experiments. Multibody System Dynamics, 2007, 18(1): 35-58. |
| [8] | Wang JG, Zhang JF, Du XP. Hybrid dimension reduction for mechanism reliability analysis with random joint clearances. Mechanism and Machine Theory, 2011, 46: 1396-1410. |
| [9] | Huang XZ, Zhang YM. Robust tolerance design for function generation mechanisms with joint clearances. Mechanism and Machine Theory, 2010, 45: 1286-1297. |
| [10] | Dubowsky S, Deck JF, Costello H. The dynamic modeling of flexible spatial machine system with clearance connections. Transactions of the ASME, 1987, 109: 87-94 |
| [11] | Erkaya S, Uzmay I. Optimization of transmission angle for slider-crank mechanism with joint clearances. Structural Multidiscipine Optimization, 2009, 37: 493-508. |
| [12] | Popov VL. Contact Mechanics and Friction: Physical Principles and Applications. New York: Springer, 2010 |
| [13] | Tsai MJ, Lai TH. Accuracy analysis of a multi-loop linkage with joint clearances. Mechanism and Machine Theory, 2008, 43: 1141-1157. |
| [14] | Flores P, Machado M, Silva MT, et al. On the continuous contact force models for soft materials in multibody dynamics. Multibody System Dynamics, 2011, 25: 357-375. |
| [15] | Flores P, Ambrosio J. Revolute joints with clearance in multibody systems. Computers and Structures, 2004, 82: 1359-1369. |
| [16] | Erkaya S, Uzmay I. Experimental investigation of joint clearance effects on the dynamics of a slider-crank mechanism. Multibody System Dynamics, 2010, 24: 81-102. |
| [17] | Pham HT, Wang DA. A constant-force bistable mechanism for force regulation and overload protection. Mechanism and Machine Theory, 2011, 46: 899-909. |
| [18] | González-Péréz I, Iserte JL, Fuentes A. Implementation of Hertz theory and validation of a finite element model for stress analysis of gear drives with localized bearing contact. Mechanism and Machine Theory, 2011, 46: 765-783. |
| [19] | Dopico D, Luaces A, Gonzalez M, et al. Dealing with multiple contacts in a human-in-the-loop application. Multibody System Dynamics, 2011, 25: 167-183. |
| [20] | Shiau TN, Tsai YJ, Tsai MS. Nonlinear dynamic analysis of a parallel mechanism with consideration of joint effects. Mechanism and Machine Theory, 2008, 43: 491-505. |
| [21] | Gummer A, Sauer B. Influence of contact geometry on local friction energy and stiffness of revolute joints. Journal of Tribology, 2012, 134(2): 021402-1-021402-9. |
| [22] | Houssem A, Bodo H. Computational efficient inverse dynamics of 6-DOF fully parallel manipulators by using the Lagrangian formalism. Mechanism and Machine Theory, 2009, 44: 192-207. |
| [23] | Kim NH, Won D, Burris D, et al. Finite element analysis and experiments of metal/metal wear in oscillatory contacts. Wear, 2005, 258: 1787-1793. |
| [24] | Saad M, Kim NH, Mauntler NA, et al. Comparison between elastic foundation and contact force models in wear analysis of planar multibody system. ASME, Journal of Tribology, 2010, 132: 1-11 |
| [25] | Dong X, Jin S, Jin Y, et al. Kinetic uncertainty analysis of the reheat-stop-valve mechanism with multiple factors. Mechanism and Machine Theory, 2010, 45: 1745-1765. |
| [26] | Mukras S, Kim NH, Mauntler NA, et al. Analysis of planar multibody systems with revolute joint wear. Wear, 2010, 268: 643-652. |
| [27] | Flores P. Modeling and simulation of wear in revolute clearance joints in multibody systems. Mechanism and Machine Theory, 2009, 44: 1211-1222. |
| [28] | Muvengei O, Kihiu J, Ikua B. Dynamic analysis of planar multi-body systems with LuGre friction at differently located revolute clearance joints. Multibody System Dynamics, 2012, 28(4): 369-393. |
| [29] | Schmitz TL, Action JE, Ziegert JC, et al. The difficulty of measuring low friction: Uncertainty analysis for friction coefficient measurement. Journal of Tribology, 2005, 127: 673-678. |
| [30] | Margarida M, Pedro M, Paulo F, et al. Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory. Mechanism and Machine Theory, 2012, 53: 99-121. |
| [31] | Zhong W, Hu JJ, Shen P, et al. Experimental investigation between rolling contact fatigue and wear of high-speed and heavy-haul railway and selection of rail material. Wear, 2011, 271: 2485-2493. |
| [32] | Nayak N, Laksminarayanan PA, Badu MKG, et al. Predictions of cam follower wear in diesel engines. Wear, 2006, 260: 181-192. |
| [33] | Shang WW, Cong S, Zhang YX. Nonlinear friction compensation of a 2-DOF planar parallel manipulator. Mechatronics, 2008, 18: 340-346. |
| [34] | 齐朝晖, 罗晓明, 黄志浩. 含非理想空间棱柱铰的多体系统接触分析.力学学报, 2011, 43(3): 570-578 (Qi Zhaohui, Luo Xiao-ming, Huang Zhihao. Frictional contact analysis of spatial prismatic joints in multibody systems. Acta Mechanica Sinica, 2011, 43(3): 570-578 (in Chinese)) |
| [35] | Niclas S. A method for structural dynamic contact problems with friction and wear. International Journal for Numerical Methods in Engineering, 2003, 58(15): 2371-2385. |
| [36] | Mukras S, Kim NH, Sawyer WG, et al. Numerical integration schemes and parallel computation for wear prediction using finite element method. Wear, 2009, 266: 822-831. |
| [37] | Mukras S, Mauntler NA, Kim NH, et al. Modeling a slider-crank mechanism with joint wear. SAE Internationa, 2009-01-0403: 1-11 |
| [38] | Su Y, Chen W, Tong Y, et al. Wear prediction of clearance joint by integrating multi-body kinematics with finite-element method. In: Proc. IMechE Part J: J Engineering Tribology, 2010, 224: 1-9. |
| [39] | 刘迎春, 余跃庆. 考虑运动副间隙的连杆及机器人机构研究进展. 机械科学与技术, 2004, 23(4): 454-460 (Liu Yingchun, Yu Yueqing. A survey of mechanism and robot with clearances. Mechanical Science and Technology, 2004, 23(4): 454-460 (in Chinese)) |
| [40] | 董富祥,洪嘉振.多体系统动力学碰撞问题研究综述.力学进展, 2009, 39(3): 352-359 (Dong Fuxiang, Hong Jiazhen. Review of impact problem for dynamics of multibody system. Advances in Mechanics, 2009, 39(3): 352-359 (in Chinese)) |
| [41] | 曹登庆, 初世明, 李郑发 等. 空间可展机构非光滑力学模型和动力学研究.力学学报, 2013, 45(1): 3-15 (Cao Dengqing, Chu Shiming, Li Zhengfa, et al. Study on the non-smooth mechanical models and dynamics for space development mechanisms. Acta Mechanica Sinica, 2013, 45(1): 3-15 (in Chinese)) |
| [42] | Megahed SM, Haroun AF. Analysis of the dynamic behavioral performance of mechanical systems with multibody clearance joints. ASME, J Comput Nonlinear Dyn , 2012, 7: 011002. |
| [43] | Gonthier Y, McPhee J, Lange C, et al. A regularized contact model with asymmetric damping and dwell-time dependent friction. Multibody System Dynamics, 2004, 11: 209-233. |
| [44] | Liu CS, Zhang K, Yang L. Normal force displacement relationship of spherical joints with clearances. ASME Jounral Comput Nonlinear Dynam, 2006, 1(2): 160-168. |
| [45] | Soong K, Thompson BS. A theoretical and experimental investigation of the dynamic response of a slider-crank mechanism with radial clearance in the gudgeon-pin joint. Journal of Mechanical Design, 1990, 112(2): 183-189. |
| [46] | Parenti-Castelli V, Venanzi S. Clearance influence analysis on mechanisms. Mechanism and Machine Theory, 2005, 40: 1316-1329. |
| [47] | Erkaya S, Uzmay I. Investigation on effect of joint clearance on dynamics of four-bar mechanism. Nonlinear Dynamics, 2009, 58: 179-198. |
| [48] | Bu WH, Liu ZY, Tan JR, et al. Detachment avoidance of joint elements of a robotic manipulator with clearances based on trajectory planning. Mechanism and Machine Theory, 2010, 45: 925-940. |
| [49] | 阎绍泽,陈鹿民,季林红等.含间隙铰的机械多体系统动力学模型.振动工程学报, 2003, 16(3): 290-294 (Yan Shaoze, Chen Lumin, Ji Linhong, et al. Dynamic modeling of multibody system with clearance joints. Journal of Vibration Engineering , 2003, 16(3): 290-294 (in Chinese)) |
| [50] | Machado M, Flores P, Claro JCP, et al. Development of a planar multi-body model of the human knee joint. Nonlinear Dynamics, 2010, 60: 459-478. |
| [51] | Gilardi G, Sharf I. Literature survey of contact dynamics modeling. Mechanism and Machine Theory, 2002, 37: 1213-1239. |
| [52] | Flores P, Ambro'sio J, Claro JCP, et al. Dynamics of multibody systems with spherical clearance joints. Computer Nonlinear Dynamics, 2006, 1: 240-247. |
| [53] | Flores P, Ambrósio J. On the contact detection for contact-impact analysis in multibody systems. Multibody System Dynamics, 2010, 24: 255-280. |
| [54] | Hippmann G. An algorithm for compliant contact between complexly shaped bodies. Multibody System Dynamics, 2004, 12: 345-362. |
| [55] | Bai ZF, Zhao Y. Dynamic behaviour analysis of planar mechanical systems with clearance in revolute joints using a new hybrid contact force model. International Journal of Mechanical Sciences, 2012, 54: 190-205. |
| [56] | Tian Q, Zhang YQ, Chen LP, et al. Dynamics of spatial flexible multibody systems with clearance and lubricated spherical joints. Computers and Structures, 2009, 87: 913-929. |
| [57] | Bauchau OA, Ju C. Modeling friction phenomena in flexible multibody dynamics. Computer Methods in Applied Mechanics and Engineering, 2006, 195(50): 6909-6924 |
| [58] | Goldsmith W. Impact-The Theory and Physical Behaviour of Colliding Solids. England, London, Edward Arnold Ltd, 1960 |
| [59] | Lopes DS, Silva MT, Ambrósio JA, et al. A mathematical framework for rigid contact detection between quadric and superquadric surfaces. Multibody System Dynamics , 2010, 24: 103-122. |
| [60] | Xuan BT, Nur H, Hideki Y. Modeling of dynamic friction behaviors of hydraulic cylinders. Mechatronics , 2012, 22: 65-75. |
| [61] | Flores P. Dynamic analysis of mechanical systems with imperfect kinematic joints. [PhD Thesis]. Portugal: Universidade Do Minho, 2004 |
| [62] | 刘丽兰, 刘宏昭, 吴子英,等.机械系统中摩擦模型的研究进展.力学进展, 2008, 38(2): 201-213 (Liu Lilan, Liu Hongzhao, Wu Ziying, et al. An overview of friction models in mechanical systems. Advances in Mechanics, 2008, 38(2): 201-213 (in Chinese)) |
| [63] | Schmitz TL, Action JE, Ziegert JC, et al. The difficulty of measuring low friction: Uncertainty analysis for friction coefficient measurement. Journal of Tribology , 2005, 127: 673-678. |
| [64] | Ambrósio JAC. Impact of rigid and flexible multibody systems:deformation description and contact models. Virtual Nonlinear Multibody Systems, Nato Advanced Study Institute, Prague, 2002, 2: 15-33 |
| [65] | Bauchau QA, Rodriguez J. Modeling of joints with clearance in flexible multibody systems. International Journal of Solids and Structures, 2002, 39: 41-63. |
| [66] | 丁千, 翟红梅. 机械系统摩擦动力学研究进展.力学进展, 2013, 43(1): 112-131 (Ding Qian, Zhai Hongmei. The advance in researches of friction dynamics in mechanics system. Advances in Mechanics , 2013, 43(1): 112-131 (in Chinese)) |
| [67] | Paulo F. A parametric study on the dynamic response of planar multibody systems with multiple clearance joints. Nonlinear Dynamics , 2010, 61(4): 633-653. |
| [68] | Machado M, Flores P, Ambrósio J, et al. Influence of the contact model on the dynamic response of the human knee joint. In: Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2011, 225(4): 344-358. |
| [69] | González-Péréz I, Iserte JL, Fuentes A. Implementation of Hertz theory and validation of a finite element model for stress analysis of gear drives with localized bearing contact. Mechanism and Machine Theory, 2011, 46: 765-783. |
| [70] | Alexander G, Bernd S. Influence of contact geometry on local friction energyand stiffness of revolute joints. Journal of Tribology, 2012, 134(2): 021402-1-021402-9. |
| [71] | Dietl P, Wensing J, van Nijen GC. Rolling bearing damping for dynamic analysis of multi-body systems-experimental and theoretical results. Journal of Multi-body Dynamics, 2000, 214: 33-43 |
| [72] | Wriggers P. Computational Contact Mechanics. 2nd edn. Berlin: Springer-Verlag, 2006 |
| [73] | Gilardi G, Sharf I. Literature survey of contact dynamics modelling. Mechanism and Machine Theory, 2002, 37: 1213-1239. |
| [74] | Zhao Y, Bai ZF. Dynamics analysis of space robot manipulator with joint clearance. Acta Astronautica, 2011, 68: 1147-1155. |
| [75] | Glocker C. Formulation of spatial contact situations in rigid multibody systems. Computer Methods in Applied Mechanics and Engineering, 1999, 177: 199-214. |
| [76] | 王琪,庄方方,郭易圆 等.非光滑多体系统动力学数值算法的研究进展 .力学进展, 2013, 43(1): 101-111 (Wang Qi, Zhuang Fangfang, Guo Yiyuan, et al. Advances in the research on numerical methods for non-smooth dynamics of multibody systems. Advances in Mechanics , 2013, 43(1): 101-111 (in Chinese)) |
| [77] | Wang YT, Kumar V. Simulation of mechanical systems with multiple frictional contacts. Journal of Mechanical Design, 1994, 116: 571-580. |
| [78] | 富立, 岳凤桐. 多体系统摩擦接触问题的 DAE-LCP 方法. 力学学报, 2011, 43(2): 400-407 (Fu Li, Yue Fengtong. DAE-LCP mixed method for multibody system dynamics with frictional contacts. Acta Mechanica Sinica, 2011, 43(2): 400-407 (in Chinese)) |
| [79] | Tasora A, Anitescu M. A convex complementarity approach for simulating large granular flows. Journal of Nonlinear and Computational Dynamics, 2010, 5, 031004, 10. |
| [80] | Liu CS, Zhang K, Yang R. The FEM analysis and approximate model for cylindrical joints with clearances. Mechanism and Machine Theory, 2007, 42: 183-97. |
| [81] | Hertz H. Über die Berührung fester elastischer Körper. Journal reine und Angewandte Mathematik, 1881, 92: 156-171 |
| [82] | Hussain N. Exact solution of certain dual series for indentation and inclusion problems. Int J Eng Sci,1969, 7: 1149-1161. |
| [83] | Johnson KL. Contact Mechanics. London: Cambridge University Press, 1992 |
| [84] | Ciavarella M, Decuzzi P. The state of stress induced by the plane frictionless cylindrical contact 1: The case of elastic similarity. International Journal of Solids and Structures, 2001, 38: 4507-4523. |
| [85] | Priit P, Sören A. Wear simulation with the Winkler surface model. Wear , 1997, 207: 79-85. |
| [86] | Tanel T. Simulation of wear in a rolling-sliding contact by a semi-Winkler model and the Archard's wear law. Wear, 2004, 256: 817-831. |
| [87] | Liu C, Zhang K, Yang L. The compliance contact model of cylindrical joints with clearances. Acta Mechanica Sinica, 2005, 21: 451-458. |
| [88] | Seifried R, Schiehlen W, Eberhard P. The role of the coefficient of restitution on impact problems in multi-body dynamics. Journal of Multi-body Dynamics, 2010, 224: 279-306 |
| [89] | Jackson RL, Green I, Marghitu DB. Predicting the coefficient of restitution of impacting elastic-perfectly plastic spheres. Nonlinear Dynamics, 2010, 60: 217-229. |
| [90] | 秦志英,陆启韶.基于恢复系数的碰撞过程模型分析.动力学与控制学报, 2006, 4: 294-298 (Qing Zhiying, Lu Qishao. Analysis of impact process based on restitution coefficient. Journal of Dynamics and Control, 2006, 4: 294-298 (in Chinese)) |
| [91] | Flores P, Ambrosio J, Claro JCP, et al. Translational joints with clearance in rigid multibody systems. ASME, 2008, 3(1): 01100 71-10 |
| [92] | Schiehlen W, Seifried R. Three approaches for elastodynamic contact in multibody systems. Multibody System Dynamics , 2004, 12(1): 1-16. |
| [93] | Bhushan B. Principles and Applications of Tribology. Wiley-Interscience, 2013 |
| [94] | Mróz Z, Páczelt I. Analysis of thermo-elastic wear problems. Therm. Stresses, 2011, 34: 569-606. |
| [95] | 樊瑜瑾, 杨晓京, 李浙昆 等. 磨粒磨损中微观接触过程的有限元分析. 机械工程学报, 2005, 41(4): 35-37 (Fan Yujin, Yang Xiaojing, Li Zhekun, et al. Micro contact process analysis in abrasive wear by finite element method. Chinese Journal of Mechanical Engineering , 2005, 41(4): 35-37 (in Chinese)) |
| [96] | Li TJ, Guo J, Cao YY. Dynamic characteristics analysis of deployable space structures considering joint clearance. Acta Astronautica , 2011, 68: 974-983. |
| [97] | Hegadekatte V, Huber N, Kraft O. Finite element based simulation of dry sliding wear. Modelling and Simulation in Materials Science and Engineering, 2005, 13(1): 57. |
| [98] | Wojnarowski J, Onishchenko V. Tooth wear effects on spur gear dynamics. Mechanism and Machine Theory, 2003, 38(2): 161-178. |
| [99] | Põdra P, Andersson S. Finite element analysis wear simulation of a conical spinning contact considering surface topology. Wear, 1999, 224: 13-21. |
| [100] | Holm R, Electric Contacts. Almqvist & Wiksells Boktryckeri, Sweeden: Uppsala, 1946 |
| [101] | Johansson A, Andersson C. Out-of-round railway wheels a study of wheel polygonalization through simulation of three-dimensional wheel-rail interaction and wear. Vehicle System Dynamics, 2005, 43(8): 539-559. |
| [102] | Archard JF. Contact and rubbing of flat surfaces. Journal of Applied Physics, 1953, 24: 981-988. |
| [103] | Cosmi F, Hoglievina M, Fancellu G, et al. A finite element method comparison of wear in two metal-on-metal total hip prostheses. In: Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine, 2006, 220(8): 871-879. |
| [104] | Tasora A, Prati E, Silvestri M. Experimental investigation of clearance effects in a revolute joint. In: Proceedings of the 2004 AIMETA International Tribology Conference, Rome, Italy, September 2004: 14-17 |
| [105] | Dupac M, Beale DG. Dynamic analysis of a flexible linkage mechanism with cracks and clearance. Mechanism and Machine Theory, 2010, 45: 1909-1923. |
| [106] | Erdemir A. Review of engineered tribological interfaces for improved boundary lubrication. Tribology International , 2005, 38(3): 249-256. |
| [107] | Páczelt I, Kucharski S, Mróz Z. The experimental and numerical analysis of quasi-steady wear processes for a sliding spherical indenter. Wear, 2012, 274-275: 127-148 |
| [108] | Paczelt I, Mroz Z. On the analysis of steady-state sliding wear processes. Tribology International, 2009, 42: 275-283. |
| [109] | Yang LJ. A test methodology for the determination of wear coefficient. Wear , 2005, 259: 1453-1461. |
| [110] | Yang LJ. The effect of nominal specimen contact area on the wear coefficient of A6061 aluminium matrix composite reinforced with alumina particles. Wear, 2007, 263: 939-948. |
| [111] | Pereira MP, Yan WY, Rolfe BF. Sliding distance, contact pressure and wear in sheet metal stamping. Wear, 2010, 268: 1275-1284. |
| [112] | Schmitz TL, Action JE, Burris DL, et al. Wear-rate uncertainty analysis. ASME, Journal of Tribology, 2004, 126 (4): 802-808. |
| [113] | Podra P, Andersson S. Finite element analysis wear simulation of a conicalspinning contact considering surface topography. Wear, 1999, 224: 13-21. |
| [114] | McColl IR, Ding J, Leen SB. Finite element simulation and experimental validation of fretting wear. Wear, 2004, 256: 1114-1127. |
| [115] | Pereira MP, Yan W, Rolfe BF. Contact pressure evolution and its relation to wear in sheet metal forming. Wear, 2008, 265: 1687-1699. |
| [116] | Sfantos GK, Aliabadi MH. Wear simulation using an incremental sliding boundary element method. Wear, 2006, 260: 1119-1128. |
| [117] | Christer S, Sören A. Simulation of friction and wear in the contact between the valve bridge and rocker arm pad in a cam mechanism.Wear, 2006, 261: 58-67. |
| [118] | Fregly BJ, Bei Y, Sylvester ME. Experimental evaluation of an elastic foundation model to predict contact pressures in knee replacements. Journal of Biomechanics, 2003, 36(11): 1659-1668. |
| [119] | Söderberg A, Björklund S. Validation of a simplified numerical model. Tribol Int, 2008, 41: 926-933. |
| [120] | Chen WQ, Lü CF, Bian ZG. A mixed method for bending and free vibration of beams resting on a Pasternak elastic foundation. Applied Mathematical Modelling, 2004, 28(10): 877-890. |
| [121] | Civalek Ö. Nonlinear analysis of thin rectangular plates on Winkler-Pasternak elastic foundations by DSC-HDQ methods. Applied Mathematical Modelling, 2007, 31(3): 606-624. |
| [122] | Hattori T, Watanabe T. Fretting fatigue strength estimation considering the fretting wear process. Tribology International, 2006, 39(10): 1100-1105. |
| [123] | Zhuang F, Wang Q. Modeling and simulation of the nonsmooth planar rigid multibody systems with frictional translational joints. Multibody System Dynamics, 2013: 1-21 |
| [124] | Flores P, Leine R, Glocker C. Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach. Multibody System Dynamics, 2010, 23(2): 165-190. |
| [125] | Tian Q, Liu C, Machado M, et al. A new model for dry and lubricated cylindrical joints with clearance in spatial flexible multibody system. Nonlinear Dynamics, 2011, 64: 25-47. |
| [126] | Liu C, Tian Q, Hu HY. Dynamics and control of a spatial rigid-flexible multibody system with multiple cylindrical clearance joints. Mechanism and Machine Theory, 2012, 52: 106-129. |
| [127] | Bai ZF, Zhao Y, Chen J. Dynamics analysis of planar mechanical system considering revolute clearance joint wear. Tribology International, 2013, 64: 85-95. |
| [128] | Cora Ö N, Namiki K, Koç M. Wear performance assessment of alternative stamping die materials utilizing a novel test system. Wear, 2009, 267(5): 1123-1129 |
| [129] | Heintze SD, Zellweger G, Cavalleri A, et al. Influence of the antagonist material on the wear of different composites using two different wear simulation methods. Dental Materials, 2006, 22(2): 166-175. |
| [130] | Fabio AD, Rubens S. Some results on the random wear coefficient of the archard model.Journal of Applied Mechanics, 2012, 79: 051008-1-051008-7. |
| [131] | Flores P. A parametric study on the dynamic response of planar multibody systems with multiple clearance joints. Nonlinear Dynamics, 2010, 61: 633-653. |
| [132] | Megahed SM, Haroun AF. Analysis of the dynamic behavioral performance of mechanical systems with multi-cleaerance joints. Journal of Computational and Nonlinear Dynamics, 2012, 7(1): 011002-0110011. |
| [133] | Flores P, Ambrosio J, Claro JCP, et al. A study on dynamics of mechanical systems including joints with clearance and lubrication.Mechanism and Machine Theory, 2006, 41: 247-261. |
| [134] | Daniel GB, Cavalca KL. Analysis of the dynamics of a slider-crank mechanism with hydrodynamic lubrication in the connecting rod- slider joint clearance. Mechanism and Machine Theory , 2011, 46: 1434-1452. |
| [135] | Zhao B, Zhang ZN, Dai XD. Modeling and prediction of wear at revolute clearance joints in flexible multibody systems. Journal of Mechanical Engineering Science, 2013 |
| [136] | Chebbi AH, Affi Z, Romdhane L. Prediction of the pose errors produced by joints clearance for a 3-UPU parallel robot. Mechanism and Machine Theory, 2009, 44: 1768-1783. |
| [137] | Frisoli A, Solazzi M, Pellegrinetti D, et al. A new screw theory method for the estimation of position accuracy in spatial parallel manipulators with revolute joint clearances. Mechanism and Machine Theory , 2011, 46: 1929-1949. |
| [138] | Chaker A, Mlika A, Laribi MA, et al. Clearance and manufacturing errors' effects on the accuracy of the 3-RCC Spherical Parallel Manipulator. European Journal of Mechanics A/Solids, 2013, 37: 86-95. |
| [139] | Huang T, Chetwynd DG, Mei JP, et al. Tolerance design of a 2-DOF overconstrained translational parallel robot. IEEE Transactions on Robotics , 2006, 22(1): 167-172. |
| [140] | 王庚祥,刘宏昭, 邓培生.考虑球面副间隙的并联机构动力学模型.振动与冲击, 2014, 33(10): 43-49 (Wang Gengxiang, Liu Hongzhao. Dynamics modeling of parallel mechanism with spherical joint clearance. Journal of Vibration and Shock, 2014, 33(10): 43-49 (in Chinese)) |
| [141] | 王庚祥,刘宏昭.考虑球面副间隙的 4-SPS/CU 并联机构动力学分析. 机械工程学报(网络出版)(Wang Gengxiang, Liu Hongzhao. Dynamics analysis of 4-SPS/CU parallel mechanism with spherical joint clearance. Chinese Journal of Mechanical Engineering, (http://ewww.cnki.net/kcms/detail/11.2187.TH.20140528.1022.081.html) |
| [142] | 胡海岩, 田强, 张伟 等.大型网架式可展开空间结构的非线性动力学与控制. 力学进展, 2013, 43(4): 390-414 (Hu Haiyan, Tian Qiang, Zhang Wei, et al. Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes. Advances in Mechanics, 2013, 43(4): 390-414 (in Chinese)) |
 2015, Vol. 47
2015, Vol. 47