2. 北京航天飞行控制中心, 北京 100094
甚长基线干涉测量(very long baseline interferometry,VLBI)技术能够获取深空探测器高精度的角位置信息,广泛应用 于航天器导航定位[1, 2, 3, 4]. 基于差分思想的VLBI技术最早由JPL于20世纪70年代提出,其采取对航天器以及角距接近的参考射电源进行短时交替观测的工作 模式,由于参考射电源的位置精确已知,因此通过对参考射电源的处理能够获取射电源观测时的干涉测量系统误差,进而内插出 观测航天器时的系统误差,实现对航天器时延观测量的修正[5, 6, 7]. 通常该技术测量元素为双差分单向测距,称之为$\vartriangle $DOR (delta differential one way ranging)[8, 9, 10].
采用短时交替的工作模式需要测站天线间隙性偏离航天器而指向射电源,造成目标航天器测控信息中断[11, 12],这对 于担负实时测控任务的跟踪天线(如中国深空网测站)无疑增大了测控风险,因此需要解决测控需求与干涉测轨需求之间的矛盾. 本文结合中国深空网测控工作模式,通过对各种测量误差的分解及建模,论述了测控模式下的深空探测器差分干涉测量技术. 对嫦娥3号(CE$'$3号) 100 km $\times$ 15 km环月轨道期间的实测数据分析表明,在不影响测控信息实时通信的同时,实现了高精度的干涉测量轨道测定.
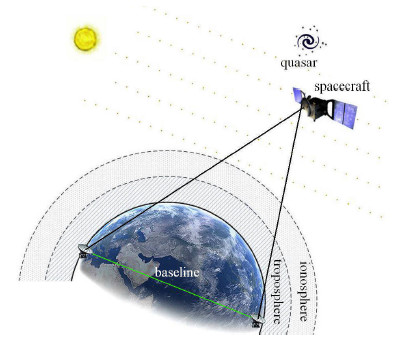
1 差分干涉测量原理简介[13, 14, 15]差分干涉测量技术通过引入对参考射电源的观测来实现系统误差校正[16, 17],图1显示了$\vartriangle $DOR测量技 术的基本原理.
|
图 1 $\vartriangle $DOR测量基本原理图 Fig. 1 Theory of $\vartriangle $DOR tracking |
理论上干涉测量时延观测量仅取决于目标与基线间的几何构型,但实际测量过程中会引入信号传播介质时延、测站钟差以及设 备链路时延等误差.
| $ \tau _{SC} = \tau _{g\_SC} + \Delta \tau _{SC} =\\ \qquad \tau _{g\_SC} + \tau _{{\rm clock}\_SC} + \tau_{{\rm atm}\_SC} + \tau _{{\rm path}\_SC} $ | (1) |
式中,$\tau _{SC} $为相关处理得到的时延观测量,$\tau _{g\_SC} $表示几何构型时延值,$\Delta \tau _{SC} $ 表示观测误差之和,$\tau _{{\rm clock}\_SC} $表示测站钟差,$\tau _{{\rm atm}\_SC} $表示传播介质引入的时延误差,$\tau _{{\rm path}\_SC} $表示通道时延.
射电源时延观测量为
| $ \tau _{\rm egrs} = \tau _{g\_{\rm egrs}} + \Delta \tau _{\rm egrs} =\\ \qquad \tau _{g\_{\rm egrs}} + \tau _{\rm clock\_egrs} + \tau_{\rm atm\_egrs} + \tau _{\rm path\_egrs} $ | (2) |
式中变量下标的物理意义与式(1)一致.
几何时延$\tau _{g\_{\rm egrs}} $精确已知,则射电源时延观测量误差为
| $ \Delta \tau _{\rm egrs} = \tau _{\rm egrs} - \tau _{g\_{\rm egrs} } $ | (3) |
利用相邻射电源观测时的误差修正量插值出航天器观测时的修正量,用于修正航天器观测量误差.
2 测控模式差分干涉测量技术建模对于中国深空网测控系统,为最大限度的确保航天器稳定在轨运行,在航天器可视弧段内,深空测站需要全时段跟踪指向航天器,以保证遥测信号的实时接收以及应急遥控指令的实时发送. 此时,短时交替的差分干涉测量模式已不再适用,需要研究适合深空测控模式的差分干涉测量技术.
差分处理的目的是修正公式(1)中的各类系统误差,因此通过各类误差源的建模分析可以为差分处理提供理论依据.
2.1 站间时间同步测量测站记录原始数据的时间同步精度直接影响时延观测量的精度,目前中国深空网测站采用GPS共视法实现站间时间同步. 通过长时间观测测站本地时钟与GPS标准时钟的差异(简称为钟差),构造钟差随时间的线性变化模型[18, 19]
| $ \tau _{{\rm clock}\_SC} = k_1 (t - t_0 ) + k_0 $ | (4) |
式中,$k_1 $,$k_0 $分别为钟差模型的一次项、常数项,$t_0 $为参考起始时刻点.
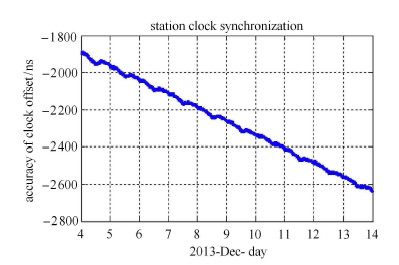
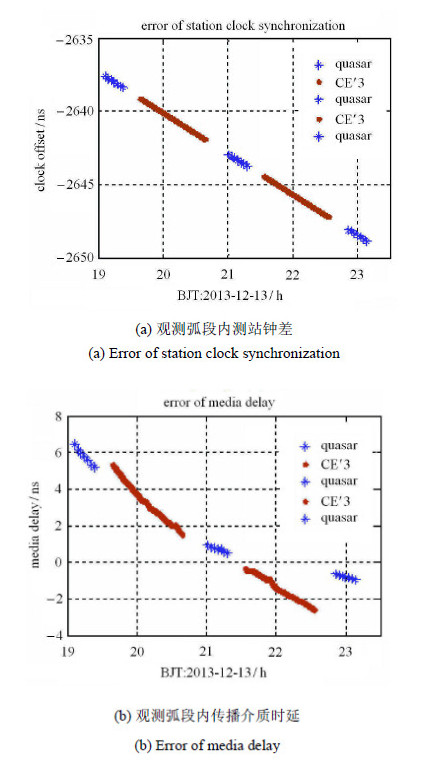
图2显示了CE$'$3号落月前,深空网测站的钟差测量值,通过事后建模分析,其钟速约在7$\times$10$^{-13}$ s/s量级;钟差精度在纳秒量级.
|
图 2 站间时间同步精度分析 Fig. 2 Analysis of station clock synchronization |
时延观测量误差对上述各项误差源的敏感度方程可表示为
| $ \Delta_{\Delta { \tau}_{SC}} = ( 1 \ \ 1 \ \ 1) \left( \!\!\begin{array}{c} {\Delta \tau _{{\rm clock}\_SC} } \\ {\Delta \tau _{{\rm med}\_SC} } \\ {\Delta \tau _{{\rm path}\_SC} } \end{array} \!\! \right) $ | (5) |
代入式(4),钟差模型精度对时延观测量的精度影响可表示为
| $ \Delta_{\Delta \tau _{SC}} = \Delta k_1 (t - t_0 ) + \Delta k_0 $ | (6) |
钟差模型的常数项以及线性项误差共同影响观测量精度,以月球卫星3 ns测量精度要求为例,单纯依靠GPS共视技术进行误差修正 无法满足高精度测量需求,需要进一步结合下文论述的射电源稀疏标校技术.
2.2 传播介质时延误差修正观测目标发出的射频无线电波必须穿过电离层、对流层才能够被地面测站天线接收,引起无线电信号的传播路径不可避免发生折射、弯曲. 要提高航天器定位、测量精度,必须分析温度、湿度、气压等各种传播介质参数对无线电测量的影响[20, 21, 22],并对所测得的观测量进行修正,补偿由于空间环境引起的各种测量误差.
传播介质时延主要包括对流层延迟以及电离层延迟,对X波段测控体制信号,对流层延迟起主要作用. 对流层延迟映射函数 有多种,以Hopfield函数为例
| $ \Delta S = \dfrac{K_d }{\sin (E^2 + 6.25)^{1 / 2}} + \dfrac{K_w }{\sin (E^2 + 2.25)^{1 / 2}} $ | (7) |
式中,$K_d $和$K_w $与环境温度、气压、水汽压、高程等参数有关;$E$即为卫星的高度角.
对于短时交替模式的差分干涉测量技术,一方面在短时间内(如5 min),测站的环境参数变化缓慢,接近恒定;另一方面短时 间内航天器高度角变化小,同时射电源与目标航天器角距较小(如几度以内). 此时航天器观测与射电源观测的传播介质延时误差量值接近,通常采用以时间为变量的线性插值进行消除.
而对于深空网测控模式,通常对标校射电源的观测与航天器观测间隔数个小时,同时对航天器的观测弧段内,测站视角变化 接近几十度的量级,此时短时交替模式的传播介质时延修正技术已不适用. 目前深空站布置微波水汽辐射计、GNSS双频接收机、气象仪等大气参数测量设备,用于实时测量目标视线向的传播介质时延 误差,测量设备精度指标在亚纳秒量级.
2.3 设备链路时延误差修正设备链路时延误差是指从天线相位中心至数据采集端的传输时延,在VLBI技术领域,论述较多的是相位校正技术(phase calibration,PCAL)[23]. 其利用窄脉冲形成器生成初相为零的相位校正信号注入到接收机的前端,信号被采集记录后通过提取相位校准信号的相位,就可以计算接收设备的链路时延,用于修正相关计算得到的时延观测量. 应用中通常无法保证PCAL产生器与天线相位中心重合,难以通过PCAL技术校正设备链路的绝对时延;但通过提取PCAL信号的相位,能够精确反映设备链路的时延相对变化,结合射电源标校,最终实现设备链路时延误差的消除.
相位校正信号的数学模型如下
| $ x_{\rm pcal} (t) = A\exp ( {\rm i}2\pi f_{\rm pcal} (t - \tau _{\rm path} )) $ | (8) |
式中,$f_{\rm pcal} $为相位校正信号的频率,$A$为相位校正信号的幅度.
通过构建参考信号$x_{\rm ref} (t)$与接收信号进行相关处理,提取相位校正信号的相位$\varPhi $,该相位值直接反映设备链路的时延.
| $ \begin{array}{l} \Phi = {\rm{angle}}(\int {{x_{{\rm{pcal}}}}(t) \cdot {\rm{conj}}\left\{ {{x_{{\rm{ref}}}}(t)} \right\}{\rm{d}}t} ) = \\ \qquad - 2\pi {f_{{\rm{pcal}}}}{\tau _{{\rm{path}}}} \end{array} $ | (9) |
依据以上分析,时间同步误差模型的常数项以及线性项误差可以通过射电源标校修正,而模型误差的非线性项影响可忽略;设备链路时延通过射电源标校修正,同时利用相位校正信号实时监测链路时延变化,理论上交替观测的时间间隔不再受限. 在射电源选取过程中,优先选择流量密度更大、结构更致密的参考源;此处重点分析射电源标校模式的选择.
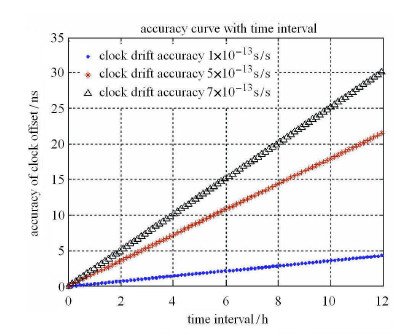
依据上文分析,目前深空网钟差模型的钟速项重构精度在1$\times$10$^{-13}$ s/s量级,若采用"射电源"---"航天器"观 测模式(QS观测模式),需要利用钟速项重构射电源观测时的钟差修正量,显然修正量精度直接受钟速精度的影响.图3显示了误差修正量精度与观测时间间隔的关系.
|
图 3 误差修正精度与观测时间间隔的关系图 Fig. 3 Accuracy curve with time interval |
图3可见,现有的钟差模型重构技术无法适用于QS观测模式,还需要结合第2个射电源标校,即射电源---航天器---射电源观测模式(QSQ观测模式),采用QSQ观测模式的缺点是高精度测量结果需要在第2个射电源观测时才能够获取,影响测量实时性.
在CE$'$3号转移轨道,可利用目标的进站前以及出站后弧段进行射电源标校;而在环月段当卫星绕行至月球背面一侧,此时航天器 对深空网测站不可见,这为进行射电源观测提供了有利时机(可称之为"月影"$\vartriangle $DOR). 以CE$'$3号100 km$\times$15 km环月轨道为例,轨道运行周期约114 min,考虑测站有效地平高度角,在一个轨道周期内,有 效共视时间约60 min,设计间隔约60 min的射电源---航天器---射电源(QSQ)交替观测,在不影响常规测控的同时,可以对CE$'$3号进 行差分干涉测量. 此外,采用"月影"$\vartriangle $DOR交替观测间隔时间约为60 min,在此量级的间隔时间内,深空站站内设备链路时延特性较稳定,相对于ns量级的测量 精度而言可认为设备链路时延恒定.
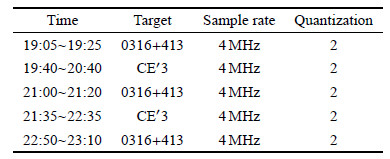
3 精度分析与验证CE$'$3号于2013年12月2日发射,12月6日进入100 km$\times$100 km环月轨道,12月10日降轨至100 km$\times$15 km轨道. CE$'$3号在轨运行期间,中国深空网佳木斯深空站、喀什深空站负责CE$'$3号的测控任务. 实验观测选择2013年12月13日北京时间19:00$\sim $23:10,在该时段内CVN (China VLBI Net)网同期进行了CE$'$3号传统短时交替模式的差分干涉测量. 下表列出了本次实验深空网的具体观测信息及采集参数.
| 表 1 系统参数 Table 1 System parameters |
应用上文分析的站间时间同步误差模型以及深空站实测的环境参数信息,图4显示了该观测弧段内的时间同步误差以及传播介质时延误差,其中"*"号表示射电源观测量,而"."号表示航天器观测量.
|
图 4 观测弧段内钟差与传播介质时延分析 Fig. 4 Error of clock synchronization and media delay |
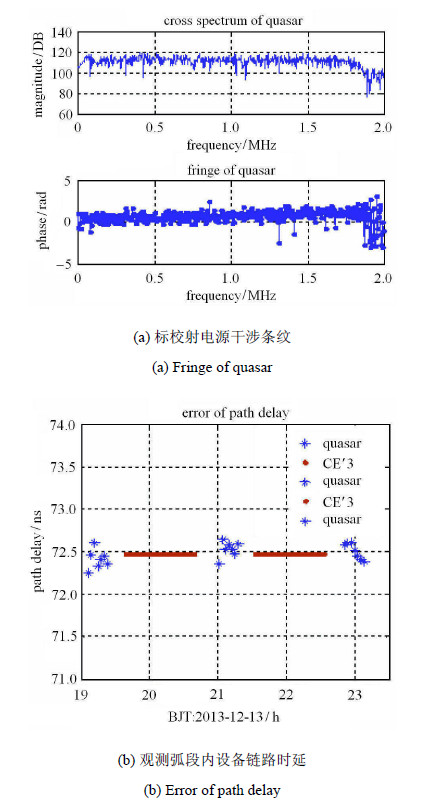
对参考射电源信号进行相关处理[24, 25, 26]得到干涉相位条纹如图5所示,其中积分时间约为168 s,从射 电源计算观测量中扣除几何时延、钟差以及传播介质时延后,得到干涉测量系统的设备链路时延.
|
图 5 观测弧段内射电源干涉条纹与链路时延分析 Fig. 5 Fringe of quasar and path delay |
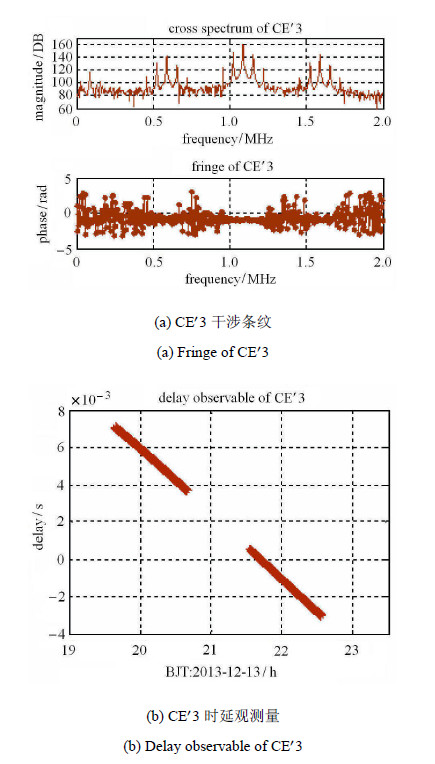
CE$'$3号干涉测量信号体制为相干转发模式,主载波上调制有遥测信息,两组DOR侧音信号与主载波相干. 图6显示了航天器主 载波通道的互相关谱以及相关计算时延观测量.
|
图 6 观测弧段内CE$'$3干涉条纹与观测量 Fig. 6 Fringe of CE$'$3 and delay observable |
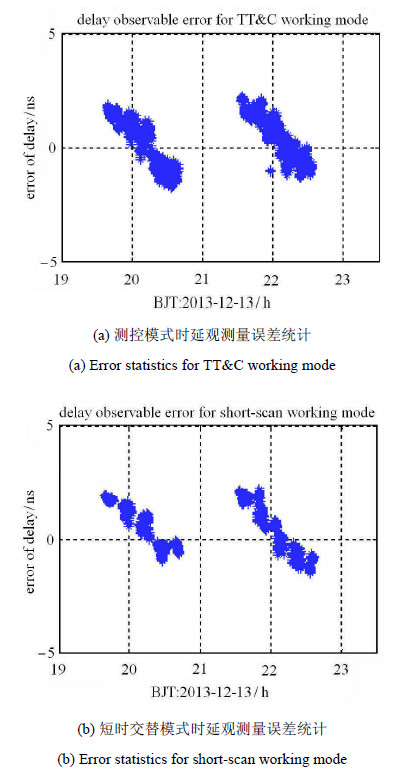
在航天器时延观测量基础上,扣除钟差(图4(a))、传播介质误差(图4(b))、设备链路时延误差(图5(b))后,得到几何时延,并与事 后精密轨道比对结果如图7(a)所示;同弧段内采用短时(8$\sim$10 min)交替观测模式的CVN网(以北京---乌鲁木齐基线为例,原因是该基线构型与深空网喀什---佳木斯基线构型方向接近)差分干涉测量结果如图7(b)所示.
|
图 7 观测量误差统计 Fig. 7 Error statistics of delay observable |
统计结果表明,测控模式下深空网干涉测量系统的测量值均方根误差为1.062 ns,在4 350 km基线情况下,测角精度为 97 nard(对380 000 km距离,位置精度37 m). 同弧段内CVN网时延测量精度在1 ns量级,二者系统精度一致.
4 结 论为支撑探月三期、火星探测等深空测控任务,中国初步建成了佳木斯、喀什深空网测控系统,后续还将在南美布设第3个深空测 站,用于探测器导航测轨. 为充分利用有限的深空网测控资源,研究测控模式下的航天器差分干涉测量技术具有重要意义. 本文以CE$'$3号任务为契机,对测控模式差分干涉测量技术进行了研究验证,取得了1 ns量级的测量结果.
后续还将紧密结合深空网系统特性开展进一步研究工作,如开展高精度载波相位授时(GNSSCPTT)的数据处理方法研究,基于高精 度GNSS轨道与钟差产品进行高精度网解与精密单点定位(PPP)数据处理,实现亚纳秒量级的时间同步精度. 从而将现有QSQ观测模式改进为QS观测,增强深空干涉测量系统的实时测轨导航能力,为我国深空测控干涉测量系统在探测器导 航测轨中的应用提供理论与实验依据.
| [1] | Plank L, Böhm J, Schuh H. Precise station positions from VLBI observations to satellites: a simulation study. Journal of Geodesy, 2014, 88 (7): 659-673 |
| [2] | 李海涛, 周欢, 郝万宏 等. 深空导航无线电干涉测量技术的发展历程和展望. 飞行器测控学报, 2013, 32(6): 470-478 (Li Haitao, Zhou Huan, Hao Wanhong, et al. Development of radio interferometry and its prospect in deep space navigation. Journal of Spacecraft TT&C Technology, 2013, 32(6): 470-478(in Chinese)) |
| [3] | Roberto M, Trevor M, Ricard A. Delta-DOR a new technique for ESA's deep space navigation. ESA Bulletin, 2006, (128): 69-74 |
| [4] | Tornatore V, Haas R, Casey S, et al. Earth on the edge: Science for a sustainable planet. Springer Berlin Heidelberg, 2014, (139): 247-252 |
| [5] | 吴伟仁, 王广利, 节德刚 等. 基于Δ DOR信号的高精度VLBI技术. 中国科学:信息科学, 2013, 36(2): 185-196 (Wu Weiren, Wang Guangli, Jie Degang, et al. High-accuracy VLBI technique using Δ DOR signals. Science China: Information, 2013, 36(2): 185-196 (in Chinese)) |
| [6] | Curkendall DW, Border JS. Delta-DOR: The one-nanoradian navigation measurement system of the deep space network——history, architecture, and componentry. Interplanetary Network Progress Report, JPL, Pasadena, California, 2013, 12-33 |
| [7] | Border JS. Innovations in delta differential one-way range: from viking to mars science laboratory. The 21st International Symposium on Space Flight Dynamics, Toulouse, France, Sep 28- Oct 2, 2009 |
| [8] | Bagri DS, Majid WA. Estimating accurate relative spacecraft angular position from deep space network very long baseline interferometry phases using X-band telemetry or differential one-way ranging tones. The Interplanetary Network Progress Report, JPL, Pasadena, California, 2007, 2-12 |
| [9] | Lanyi G, Bagri DS, Border JS. Angular position determination of spacecraft by radio interferometry. Proceedings of the IEEE, 2007,95(11): 2193-2201 |
| [10] | 朱新颖,李春来,张洪波. 深空探测VLBI技术综述及我国的现状和发展. 宇航学报,2010,31(8): 1893-1899 (Zhu Xinying, Li Chunlai, Zhang Hongbo. A survey of VLBI technique for deep space exploration and trend in China current situation and development. Journal of Astronautics, 2010, 31(8): 1893-1899 (in Chinese)) |
| [11] | 于志坚. 深空测控通信系统. 北京:国防工业出版社,2009(Yu Zhijian. Deep Space TT&C System. Beijing: National Defence Industry Press, 2009 (in Chinese)) |
| [12] | Bagri DS, Majid WA. Accurate spacecraft angular position from DSN VLBI phases using X-band telemetry or DOR tones. IEEE Aerospace Conference, Montana, USA, Mar 7-14, 2009 |
| [13] | James N, Abello R, Lanucara M, et al. Implementation of an ESA delta-DOR capability. Acta Astronautica, 2009, (64): 1041-1049 |
| [14] | 唐歌实. 深空测控无线电测量技术. 北京: 国防工业出版社, 2012(Tang Geshi. Radiometric Measurement Technique for Deep Space Navigation. 2012(in Chinese)) |
| [15] | 韩松涛, 陈略, 任天鹏 等. 中国深空网首次 Δ DOR 联合测轨试验分析. 飞行器测控学报, 2014, 33(3): 258-261 (Han Songtao, Chen Lue, Ren Tianpeng, et al. Analysis of the first multi-agency joint Δ DOR tracking of China's deep space network. Journal of Spacecraft TT&C Technology, 2014, 33(3): 258-261 (in Chinese)) |
| [16] | Ichikawa T. Application of high-precision two-way ranging to the spacecraft navigation. Sice Annual Conference, Proceedings of IEEE, 2010: 817-821 |
| [17] | 丁溯泉, 李海涛. 相对差分单向测距 (Δ DOR) 技术在探月工程中的应用研究. 空间科学学报, 2011, 31(6): 789-793.(Ding Suquan, Li Haitao. Research of Δ DOR technique in lunar exploration project. Chinese Journal of Space Science, 2011, 31(6): 783-793 (in Chinese)) |
| [18] | Yang X, Hu Y, Li Z, et al. An algorithm for a near real-time data processing of GPS common-view observations. Chinese Astronomy and Astrophysics, 2003, 27(4): 470-480 |
| [19] | 贾赞杰, 朱昱, 史线龙等. 基于GPS 的时钟同步模型选择与实验分析. 测绘科学, 2011, 26(3): 152-154 (Jia Zanjie, Zhu Yu, Shi Xianlong, et al. Test and choice of clock synchronization model based on GPS. Science of Surveying and Mapping, 26(3): 152-154(in Chinese)) |
| [20] | Muhleman DO, Anderson JD. Solar wind electron densities from Viking dual-frequency radio measurements. APJ, 1981, (247): 1093-1101 |
| [21] | Bird MK, Patzold M, Edenhofer P, et al. Coronal radio sounding with Ulysses: solar wid electron density near 0.1AU during the 1995 conjunction. Astrophys, 1996, (316): 441-448 |
| [22] | Sun W, Akasofu SI. Calibration of the kinematic method of studying solar wind disturbances between 22 November and 6 December 1977. Planet Space Science, 1985, (33): 933-943 |
| [23] | 姜坤, 王元钦, 侯孝民 等. 相位校准信号高效提取方法及误差分析. 信号处理, 2014, 30(2): 197-204 (Jiang Kun, Wang Yuanqing, Hou Xiaomin, et al. Extraction of phase calibration signal and accuracy analysis. Signal Processing, 2014, 30(2): 197-204(in Chinese)) |
| [24] | Deller AT, Tingay SJ, Bailes M. DiFX: a software correlator for very long baseline interferometry using multiprocessor computing environments. Publications of the Astronomical Society of the Pacific, 2007, 119: 318-336 |
| [25] | 韩松涛, 唐歌实, 刘成军 等. VLBI并行处理方式比较分析. 遥测遥控, 2013, 34(1): 29-33 (Han Songtao, Tang Geshi, Liu Chengjun, et al. Analysis on parallel processing of VLBI. Journal of Telemetry Tracking and Command, 2013, 34(1): 29-33(in Chinese)) |
| [26] | Böhm J, Nilsson T. The New Vienna VLBI Software VieVS, Geodesy for Planet Earth, 2012, (136): 1007-1011 |
2. Beijing Aerospace Control Center, Beijing 100094, China
 2015, Vol. 47
2015, Vol. 47