2. 上海卫星工程研究所, 上海 200240;
3. 上海市深空探测技术重点实验室, 上海 200240
火星探测是人类深空探测活动的重点之一. 火星探测器经过8至10个月的地火转移飞行后,到达火星时的双曲线剩余速度约为3km/s (具体数值随发射窗口不同而有所变化). 受火星引力影响,探测器飞行至近火点时速度将达到5.4km/s (火心惯性系下). 对于远火点8万千米的火星大椭圆轨道,其近火点速度约为4.5km/s,因此必须在近火点实施捕获制动,以确保探测器形成环火轨道. 一旦制动失败,探测器将坠入火星大气层或直接飞越火星.
火星探测制动捕获段器上操作多、天地通信时延大(器地距离约2×108km,双向时延超过1300s),且机会唯一,是 火星探测飞行全过程中最关键的任务阶段. 1990年后发射的深空探测器共失败7次,其中与制动捕获直接相关的就有4次.
火星制动捕获段的动力学环境相比其他飞行阶段更为复杂. 在地火转移段,探测器以太阳为中心引力天体运动,太阳系其他天体 距离探测器较远,摄动作用不明显,可以采用二体动力学加摄动模型进行描述. 在地火转移段末期,探测器从以太阳为中心的椭圆轨道过渡到以火星为中心的双曲线轨道,期间探测器受到的太阳引力与火星系统 引力量级相当,二体模型已无法完全准确描述,必须对火星引力影响范围边界处的动力学进行精细建模,避免圆锥曲线拼接过程 中出现动力学突变,造成设计轨道与实际轨道间的偏差. 当探测器距离火星表面小于约1.0×105km后,火星引力场的非球型摄动作用也将无法忽略,使动力学模型更为复 杂[1];当远火点高度超出火星引力范围后,探测器受到的太阳引力将超过火星引力,处于逃逸与捕获的边缘,研究临界轨 道稳定性及误差扰动敏感性十分重要.
除了动力学模型外,制动捕获发动机点火过程的姿态控制也将对捕获结果产生直接影响. 如何在燃料、能源、时间等约束条件下进 行姿态控制,确保探测器形成稳定环绕轨道,是制动捕获段需要讨论的又一项重点内容[2, 3].
中国以火星探测为代表的深空探测工程刚刚起步,深入研究火星系统(含火卫一、火卫二)捕获过程动力学问题非常重要. 从火星引 力边界附近的动力学模型出发,分析了初始导航误差、发动机推力误差、点火时间误差源等对捕获轨道产生的影响,指出了影响捕获 精度的主要因素,为火星探测器的可靠捕获提供参考. 捕获段其他关键问题,如非球型引力摄动、临界环绕轨道稳定性、制动捕获姿态优化控制等[4]将在未来工作中进一步深入研究.
1 火星引力捕获动力学 1.1 工程定义制动捕获段并不仅指制动发动机的点火阶段,而是以进入火星环绕轨道为目标的一系列器上动作和地面操 作所组成的飞行阶段[5].
具体探测任务的制动捕获段将根据其任务需求与特点进行界定. 如``火星快车(MEX)''的制动捕获段定义为从``猎兔犬2''着陆器 分离开始至探测器进入环火轨道结束[6];``火星勘测轨道器 (MRO)''则将制动捕获点火的27min定义为制动捕获段,之前的准备阶段划为火星接近段[7, 8];``火星全球观测者 (MGS)''定义为从执行制动捕获序列的首个动作开始至探测器形成科学任务轨道结束[9, 10].
根据火星环绕探测任务的特点与工程实际,本文中制动捕获段的定义为从探测器进入火星作用球开始(距离火星约 50×104km,见下节),至探测器形成环火轨道结束.
为对火星探测器制动捕获段动力学进行建模,需找出作用在探测器上主要引力的空间边界,即需要引入引力球、作用球和希尔球的概念.
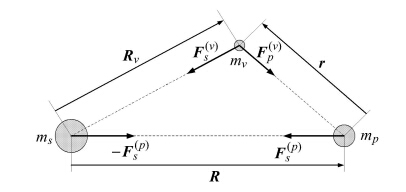
1.2 引力球、作用球与希尔球理论上,天体的引力场可以到达空间无限远处,但在一定空间范围内,某个天体产生的引力场将占据主导地位. 火星探测器在 接近火星直至被火星捕获的过程中,受到太阳、火星、火卫以及其他太阳系大天体等的引力作用,属于多体动力学问题,但其中太阳和 火星起到了主导作用[11]. 考虑到探测器质量相对与火星与太阳可忽略不计,因此火星制动捕获动力学模型可简化为限制性三体模型,如\linebreak 图 1所示.
|
图 1 限制性三体引力关系示意图 Fig. 1 Restricted three-body problem diagram |
图 1中mv为探测器质量,ms为太阳质量,mp为火星质量. ${\pmb R}$为火星相对太阳的位置矢量,${\pmb R}_{v}$为探 测器相对太阳的位置矢量,${\pmb r}$为探测器相对火星的位置矢量. ${\pmb F}_{s}^{(v)}$为太阳作用在航天器上的引力,${\pmb F}_{p}^{(v)}$为火星作用在探测器上的引力,${\pmb F}_{s}^{(p)}$为太阳作用在火星上的引力. 由于是限制性问题,探测器作用在太阳和火星上的引力忽略不计.
一般地,以引力大小相等为判据得到的作用范围称为引力球;以摄动力相等为判据得到的作用范围称为作用球(也称为影响球)[12]. 下面对引力球、作用球和希尔球半径的计算公式进行推导.
1.2.1 引力球计算公式推导火星引力球半径是太阳与火星作用在探测器上的引力大小相等处的距离. 根据牛顿万有引力定律,探测器受到太阳与火星的引力可表示为
| ${\pmb F}_s^{(v)} = - \dfrac{Gm_v m_s }{{ R}_v^3}{\pmb R}_v $ | (1) |
| ${\pmb F}_p^{(v)} = - \dfrac{Gm_v m_p }{r^3}{\pmb r} $ | (2) |
| $\dfrac{Gm_v m_s }{R^2_v}=\dfrac{Gm_vm_p}{r^2} $ | (3) |
| $r_1 \approx \left( {\dfrac{m_p }{m_s }} \right)^{\tfrac 12}R $ | (4) |
位于作用球边界处的探测器,其受到的火星摄动力与太阳中心引力的比值,与受到的太阳摄动力与火星中心引力的比值相等[12].
根据牛顿第二运动定律,在日心惯性系下的探测器动力学方程为
| $m_v \ddot{\pmb R}_v = {\pmb F}_s^{(v)} + {\pmb F}_p^{(v)} = - \dfrac{Gm_v m_s }{R_v ^3}{\pmb R}_v - \dfrac{Gm_v m_p }{r^3}{\pmb r} $ | (5) |
| $ \ddot{\pmb R}_v = - \dfrac{Gm_s }{R_v ^3}{\pmb R}_v - \dfrac{Gm_p }{r^3}{\pmb r} $ | (6) |
| $ \dfrac{ | {\pmb P}_p | }{ | {\pmb A}_s | } = \dfrac{m_p }{m_s }\left( {\dfrac{R_v }{r}} \right)^2 \approx \dfrac{m_p }{m_s }\left( {\dfrac{R}{r}} \right)^2 $ | (7) |
同理,在火星惯性系下的探测器动力学方程为
| $ \ddot{\pmb r} = \ddot{\pmb R}_v - \ddot{\pmb R} = - \dfrac{Gm_p }{r^3}{\pmb r} - \left( {\dfrac{Gm_s }{R_v ^3}{\pmb R}_v -\dfrac{Gm_s }{R^3}{\pmb R}} \right) $ | (8) |
等式右边第1项为火星中心引力项${\pmb a}_{p}$,第2项为太阳引起的摄动项${\pmb p}_{s}$. 由于$| {\pmb p}_{s} |$无法 直接得到,可采用以下两种近似方法.
设探测器位于日火连线上,则${\pmb R}_v / R_v = {\pmb R} / R$,有
| $ | {\pmb p}_s | = \left| { - Gm_s \left( {\dfrac{1}{R_v ^2} - \dfrac{1}{R^3}} \right)\dfrac{{\pmb R}}{R} } \right| = Gm_s \left( {\dfrac{1}{R_v^2} - \dfrac{1}{R^2}} \right) $ | (9) |
| $\frac{{|{p_s}|}}{{|{a_p}|}} = \frac{{{m_s}}}{{{m_p}}}\left( {\frac{1}{{R_v^2}} - \frac{1}{{{R^2}}}} \right){r^2}{\rm{ }}$ | (10) |
将$R_{v}=R-r$代入上式,得
| $ \dfrac{ | {\pmb p}_s | }{ | {\pmb a}_p | } = \dfrac{m_s }{m_p }\dfrac{(2R - r)r^3}{(R - r)^2R^2} $ | (11) |
| $ \rho = 2^{ - \tfrac 15}\left( {\dfrac{m_p }{m_s }} \right)^{\tfrac 25}R $ | (12) |
根据定义,希尔球半径等于三体系统中$L_{1}$或$L_{2}$点距离次天体的距离[13],其值可表示为幂级数形\linebreak 式[14]
| $ \rho _{\rm Hill} = \left( {\dfrac{m_p }{3m_s }} \right)^{\tfrac{1}{3}}\left[{1 - \sum\limits_{n = 1}^\infty {\left( {\dfrac{1}{3}} \right)^n\left( {\dfrac{m_p }{3m_s }} \right)^{\tfrac{n}{3}}} } \right]R $ | (13) |
将式(13)中的$n \geqslant 1$的高阶项忽略后,可得希尔球半径的计算公式
| $\rho _{\rm Hill} \approx \left( {\dfrac{m_p }{3m_s }} \right)^{\tfrac{1}{3}}R $ | (14) |
根据引力球的定义,位于日火连线上且距离火星1.293×105km处所受到的太阳引力与火星引力大小相等、方向相反. 该位置也称为引力中和点. 严格来说,太阳与火星引力大小相等的点组成的曲面是一个经过引力中和点,且平均半径略大于引力球半径的近似球面. 一般的,在引力球半径内的探测器轨道可近似为探测器-火星的二体问题[15].
但在限制性三体问题中,主天体引力和摄动天体摄动力同时作用于探测器. 对于在火星作用球内的探测器,应以火星为主天体,太阳 为摄动天体来进行动力学建模. 反之则应以太阳为主天体、火星为摄动天体.
希尔球一般用于描述次天体卫星所能维持的最大半径. 超出该距离后,即会逐渐脱离次天体的影响而最终围绕主天体(太阳)运行. 引力球、作用球与希尔球比较见表 1.
| 表 1 火星引力球、作用球和希尔球比较 Table 1 Comparison of the Mars gravity sphere,influence sphere and Hill sphere |
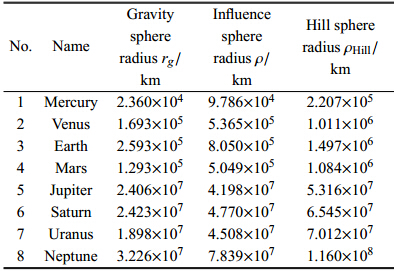
表 2列出了太阳系行星引力球、作用球和希尔球半径的计算结果,可以看出引力球半径,小于作用球半径,作用球半径更小于 希尔球半径.
| 表 2 太阳系行星的引力球、作用球和希尔球半径 Table 2 Gravity sphere,influence sphere and Hill sphere of solar system planets |
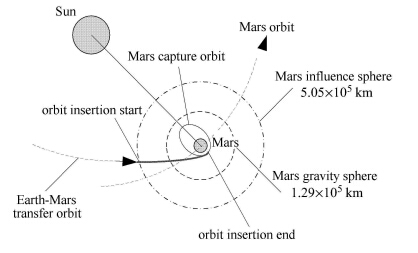
根据制动捕获段定义及1.2节的讨论,制动捕获段应以火星为主天体、太阳等为摄动天体建立动力学模型. 火星 制动捕获过程如图 2所示.
|
图 2 火星制动捕获过程示意图 Fig. 2 Mars orbit insertion process |
设${\pmb r} = (x,y,z)^{\rm T}$为探测器在火星惯性系下的位置矢量,${\pmb v} = (v_x ,v_y ,v_z )^{\rm T}$为速度矢量. 则轨道动力学方程的一般形式为
| $ \ddot{\pmb r} = - \dfrac{\mu }{r^3}{\pmb r} + {\pmb a }_N + {\pmb a }_{NS} + {\pmb a }_R + {\pmb a }_A + {\pmb a }_M $ | (15) |
在进入火星作用球后,火星中心引力、太阳摄动力与制动发动机推力是影响探测器运动状态的主要因素. 为简化计算,可对 式(15)进行工程化处理
| $ \ddot{\pmb r} = - \dfrac{\mu }{r^3}{\pmb r} + {\pmb a }_N + {\pmb a }_M $ | (16) |
| $ {\pmb a}_M = {\pmb F} / m $ | (17) |
| $ \dot {m} = \dfrac{F}{I_{sp} g_0 } $ | (18) |
捕获后的轨道参数由探测器初始状态、制动点火时间、发动机推力和比冲、火星引力场等决定. 影响捕获轨道精度的误差源可分 为系统误差与随机误差. 其中系统误差主要为动力学模型误差;随机误差则可进一步分为初值误差和执行误差. 误差源分解如图 3所示.

|
图 3 制动捕获误差源分解框图 Fig. 3 Mars orbit insertion error constitution diagram |
下面就导航定位误差、导航定速误差、发动机推力大小误差、推力方向误差、制动点火开、关机时刻误差等对捕获轨道高度的影响进行仿真分析.
2.2 仿真条件捕获误差源对各类误差对捕获轨道的影响情况进行计算机仿真,仿真条件如表 3~表 5所示.
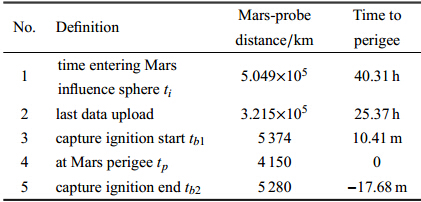
| 表 3 捕获前后轨道参数(标称值) Table 3 Orbit parameters after orbit capture (nominal) |
| 表 4 制动捕获关键时间变量(标称轨道) Table 4 Timetable for orbit capture (nominal) |
| 表 5 探测器制动捕获前初始状态 Table 5 Initial state of the probe before orbit capture |
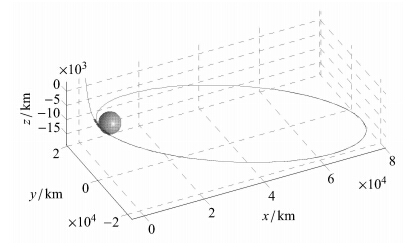
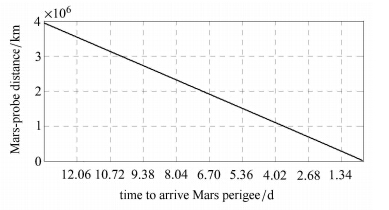
根据仿真条件,标称捕获轨道仿真结果如图 4所示. 探测器在到达近火点前12d内的器火距离变化如图 5所示.
|
图 4 标称捕获轨道 Fig. 4 Nominal capture orbit |
|
图 5 到达近火点前12d内的器火距离变化 Fig. 5 Mars-probe distance since 12 days before orbit capture |
从图 5中可以看出,当探测器到达火星作用球边缘时(5.049×105km),距离抵达近火点还有约1.5d的时间.
下面将在上述标称轨道的基础上,加入各项误差后进行蒙特卡洛仿真. 蒙特卡洛仿真次数为1000次,初始历元为最后一次数据上注的时刻.
2.3 仿真结果与分析 2.3.1 导航定位初始误差拉偏设导航定位三轴误差相互独立,服从0均值、方差为50km的高斯分布. 对捕获后轨道的近火点与远火点高度进行 蒙特卡洛仿真,其概率分布如图 6所示.

|
图 6 导航定位初始误差影响 Fig. 6 Navigation position initial error effects |
由导航定位误差造成的捕获轨道远火点高度方差为2903km,近火点高度方差为50km.
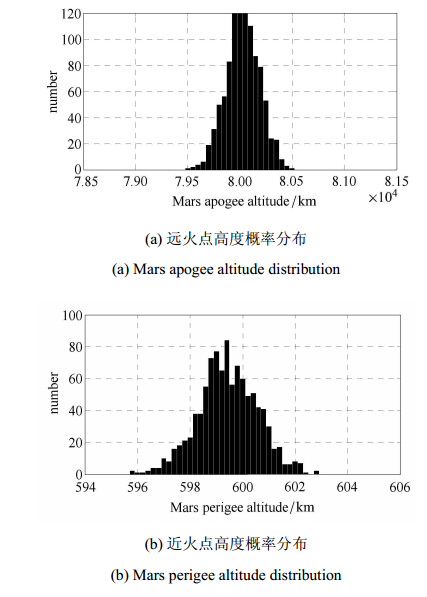
2.3.2 导航定速初始误差拉偏设导航定速三轴误差相互独立,服从0均值、方差为0.2m/s的高斯分布. 对捕获后轨道的近火点与远火点高度进行蒙特 卡洛仿真,结果如图 7所示.
|
图 7 导航定速初始误差影响 Fig. 7 Navigation velocity initial error effects |
由导航定速误差造成的捕获轨道远火点高度方差为1121km,近火点高度方差为18km.
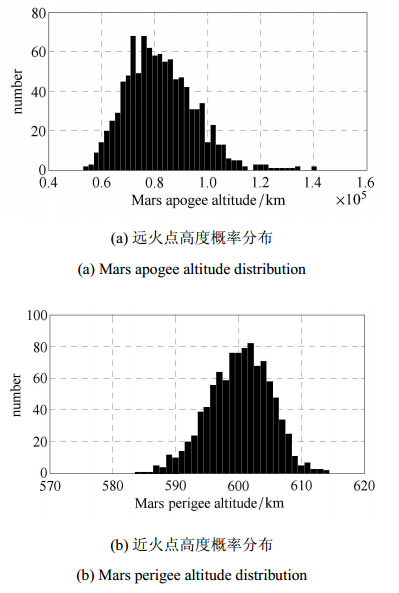
2.3.3 发动机推力误差拉偏发动机点火的执行误差包括推力大小误差与推力方向误差两部分. 其中推力大小误差可认为服从0均值,方差为标称推力大 小1%的高斯分布. 捕获后轨道的近火点与远火点高度概率分布如图 8所示.
|
图 8 制动发动机推力大小误差影响 Fig. 8 Capture engine thrust magnitude error effects |
由发动机1%推力大小误差造成的捕获轨道远火点高度方差达到了13236km,近火点高度方差为5km.
推力方向误差由制动捕获段的探测器姿态指向精度决定,可认为三轴误差相互独立,服从0均值、方差为 0.3$^\circ$的高斯分布. 捕获后轨道的近火点与远火点高度概率分布如图 9所示.

|
图 9 制动发动机推力方向误差影响 Fig. 9 Capture engine thrust direction error effects |
由发动机推力方向误差造成的捕获轨道远火点高度方差为5km,近火点高度方差为0.2km. 可见由推力方向误差造成 的近火点、远火点高度误差较小.
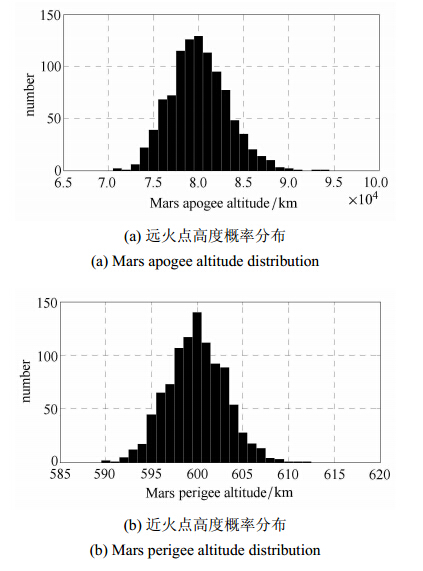
2.3.4 制动点火时间误差拉偏制动点火起始时刻由器上时钟决定,制动点火结束时刻由器上时钟和惯导组合联合决定. 仿真算例中制动点火起始时 刻与结束时刻为相互独立的随机变量. 起始时刻误差变量服从0均值、方差为1s的高斯分布;结束时刻误差变量服从0均值、方差为5s的高斯分布. 捕获后轨道的近火点与远火点高度概率分布如图 10所示.
|
图 10 制动点火时间误差影响 Fig. 10 Capture engine ignition time error effects |
由制动点火时间误差造成的捕获轨道远火点高度方差为3200km,近火点高度方差为3km.
2.3.5 综合影响分析在上述误差源的综合作用下进行仿真,可得各类误差对制动捕获轨道远火点高度与近火点高度的影响情况,如表 6所示.
若火星大气高度为200km,当捕获后轨道近火点高度hp偏差小于400km时,可认为在探测器未进入大气层,在工程上仍是安全的. 由引力球定义可知,当捕获轨道远火点高度ha大于引力球半径(1.3×105km)时,环绕轨道将难以稳定. 因此,在ha标称值为8.0×105km的条件下,当ha偏差小于5×104km时,可认为环绕轨道是稳定的.
将400km作为hp的超差门限,将5×104km作为ha的超差门限,可以得到各误差源影响下的超差概率,见表 6.
| 表 6 各类误差对捕获轨道高度影响分析 Table 6 Analysis of the capture orbit accuracy caused by different error sources |
通过对制动捕获段的动力学建模与误差仿真可知,制动发动机推力大小对捕获轨道高度,特别是远火点高度的影响最为明显,在本 文讨论的所有误差源中占据主导. 1%的发动机推力误差即能导致超过1×104km的远火点高度误差. 但对于远火点8×104km的标称捕获轨道,在本文采用的各误差源综合影响下,远火点ha的超差概率仍几乎为零. 因此在误差源可控的前提下,可进一步降低捕获轨道的近火点高度(或增加远火点高度)以减少制动捕获对速度增量的需求,达到减小重 力损失、提高推进剂利用效率的目的. 本文的研究结果具有一定的工程应用价值,未来将进一步提高误差源模型的准确性,并在考虑火星非球形引力与太阳光压摄动的条件下, 对误差源与捕获轨道根数之间的映射关系开展进一步研究.
| [1] | 刘林, 汤靖师. 火星轨道器运动的轨道变化特征. 宇航学报, 2008, 29(2): 461-466 (Liu Lin, Tang Jingshi. Orbit variation characteristics of the Mars' orbiters. Journal of Astronautics, 2008, 29(2): 461-466 (in Chinese)) |
| [2] | 刘林, 赵玉晖, 张巍等. 环火卫星运动的坐标系附加摄动及相应坐标系的选择. 天文学报, 2010, 51(4): 412-421 (Liu Lin, Zhao Yuhui, Zhang Wei, et al. The coordinate additional perturbations to Mars orbiters and the choice of corresponding coordinate system. Acta Astronomica Sinica, 2010, 51(4): 412-421 (in Chinese)) |
| [3] | 陈杨, 赵国强, 宝音贺西等. 精确动力学模型下的火星探测轨道设计. 中国空间科学技术, 2012, 1: 8-15 (Chen Yang, Zhao Guoqiang, Baoyin Hexi, et al. Orbit design for Mars exploration by the accurate dynamic model. Chinese Space Science and Technology, 2012, 1: 8-15 (in Chinese)) |
| [4] | 李俊峰, 宝音贺西. 深空探测中的动力学与控制. 力学与实践, 2007, 29(4): 1-8 (Li Junfeng, Baoyin Hexi. Dynamics and control in deep space exploration. Mechanics in Engineering, 2007, 29(4): 1-8 (in Chinese)) |
| [5] | Fischer J, Denis M. Mars orbit insertion —— a new challenge for Europe success with ESA's Mars Express. European Space Operations Centre. IEEEAC, 2004, 1370 |
| [6] | Liever P, Habchi S, Burnell S, et al. Computational fluid dynamics prediction of the Beagle 2 aerodynamic database. Journal of Spacecraft and Rocket, 2003, 40(5): 632-638 |
| [7] | Jai B, Wenker D, Hammer B, et al. An overview of Mars reconnaissance orbiter mission and operations challenges. AIAA SPACE Conference & Exposition, Long Beach, California. 2007, AIAA 2007-6090 |
| [8] | Liechty D. Aeroheating analysis for the Mars reconnaissance orbiter with comparison to flight data. Journal of Spacecraft and Rocket, 2007, 44(6): 1226-1231 |
| [9] | Lyons D, Beerer J, Esposito P, et al. Mars global surveyor: aerobraking mission overview. Journal of Spacecraft and Rocket, 1999, 36(3): 307-313 |
| [10] | Jet Propulsion Laboratory. Orbit insertion phase. http://www.msss. com/mars/global_surveyor/mgs_msn_plan/section5/section5.html, 2010 |
| [11] | 尚海滨, 崔平远, 栾恩杰. 地球-火星的燃料最省小推力转移轨道的设计与优化. 宇航学报, 2006, 27(6): 1168-1173 (Shang Haibin, Cui Pingyuan, Luan Enjie. Design and optimization of Earth-Mars optimal fuel low thrust trajectory. Journal of Astronautics, 2006, 27(6): 1168-1173 (in Chinese)) |
| [12] | 杨嘉摨. 航天器轨道动力学与控制(上). 北京: 中国宇航出版社, 2004 (Yang Jiaxi. Spacecraft Orbital Dynamics and Control (Vol.1). Beijing: China Aerospace Press, 2004 (in Chinese)) |
| [13] | Chebotarev G. On the dynamical limits of the solar system. Soviet Astronomy, 1965, 8(5): 787-796 |
| [14] | 刘林, 侯锡云. 深空探测器轨道力学. 北京: 电子工业出版社, 2012 (Liu Lin, Hou Xiyun. Deep Space Probe Orbital Mechanics. Beijing: Electronic Industry Press, 2012 (in Chinese)) |
| [15] | 郝岩. 深空测控网. 北京: 国防工业出版社, 2004 (Hao Yan. Deep Space Telemetry Network. Beijing: National Defense Industry Press, 2004 (in Chinese)) |
| [16] | 徐福祥. 卫星工程概论. 北京: 中国宇航出版社, 2004 (Xu Fuxiang. Introduction of Satellite Engineering. Beijing: China Aerospace Press, 2004 (in Chinese)" |
2. Shanghai Institute of Satellite Engineering, Shanghai 200240, China;
3. Shanghai Key Laboratory of Deep Space Exploration Technology, Shanghai 200240, China
 2015, Vol. 47
2015, Vol. 47