目前,火星探测是国际深空探测发展的主要趋势,也是我国深空探测领域的重要研究方向. 火星探测技术风险高,特别是在火星 进入飞行阶段[1],探测器面临复杂的火星大气环境,气动特性不确定性大,确保探测器稳定飞行并且精确、安全着陆的 设计难度大. 解决该问题的一种高效可行的途径是采用气动测量技术,测量进入飞行中探测器的气动特性数据以及火星大气环境,如大气密度 等,积累实际飞行气动数据,为后续任务的可靠实施奠定技术基础.
火星进入飞行气动测量方法包括基于惯性测量组件(inertia measurement unit,IMU)数据测量、基于地面气动数据递推测量和基于嵌入式大气数据传感系统(flush air data system, FADS)数据测量3类[2] 其中,前两者是火星探测器进入飞行气动测 量的基本方法,在海盗号、火星漫步者和凤凰号中得到了工程应用[3, 4, 5] 基于IMU数据测量方法利用进入飞行中IMU测量获取的角速度和加速度数据,以进入时刻的弹道信息为积分初值,递推获得进入弹道 的攻角和侧滑角,并且结合火星大气模型获取进入动压. 基于地面气动数据递推测量方法在基于IMU数据测量方法进一步发展,利用攻角和侧滑角对应的气动力系数比与加速度计测量的气动 力系数比之间的差异,迭代修正攻角和侧滑角. 上述两种方法均需基于较强的先验信息,必须给定火星大气模型或地面气动数据才可以实现气动测量,同时,测量精度依赖于大气模 型和地面气动数据的精度,难以度量测量数据的准确性. 为解决这一问题,在好奇号火星实验室飞行试验中,引入了FADS数据测量方法. 通过布置在探测器头部的若干微小孔洞,引入气流而敏感飞行中压强变化,建立不同位置传感器敏感到的压强矢量与攻角、侧滑角和 动压的函数关系,通过辨识算法实现气动测量,首次实现了攻角、侧滑角和动压的独立测量[2],不依赖于IMU测量数据、火星大 气模型或地面气动数据. 在飞行动压大于850Pa情况下,攻角和侧滑角精度达0.2]\^\circ]\,动压测量精度达2%. 尽管基于FADS数据测量方法具有独立测量的技术优势,但是由于飞行动压较低时,传感器压强延迟明显,并且传感器测量精度与被测 量量值接近,因此,低动压区的攻角和侧滑角的测量精度低.
上述3类气动测量方法均未考虑使用进入飞行中的外测弹道信息,即附加额外冗余信息,以提升气动测量精度. 鉴于此,本文提出 一种新的火星探测器进入飞行气动测量方法,在具备FADS数据测量方法独立测量优势的同时,将实现全弹道下攻角和侧滑 角的高精度测量. 一方面,融合火星进入时刻的位置、速度与姿态信息及进入飞行中位置信息,基于输出误差法进行弹道重建,解算进入时刻位置、 速度、姿态误差和IMU的测量误差,进而,利用修正的初始条件及IMU测量数据,积分递推进入弹道的位置、速度和姿态,并利用几何 关系确定攻角和侧滑角. 另一方面,基于FADS数据测量方法获得动压,同时,FADS数据测量获取的攻角和侧滑角作为弹道重建的备份测量输出,相较于现有气 动测量方法,明显提升测量冗余性能. 需要指出,本文方法所需的外测弹道信息可以通过火星进入UHF导航获得. Morabito指出UHF无线电信号在进入飞行中大部分时间内可穿透探测器周围等离子鞘[6],好奇号火星实验室进入过程中与多个 火星轨道器间实现了全程UHF通信[7],基于该发现,利用火星轨道器或火星表面信标实施与探测器的UHF通信,可以进行导航解算 而提供较高精度的外测弹道[8, 9, 10]
以下首先针对火星探测器进入飞行任务,提出火星探测器气动测量系统的组成以及总体测量方法,而后逐一阐述攻角、侧滑角 和动压的测量方法. 最后,仿真分析本文所提方法的测量精度,明确方法的可行性和有效性.
1 气动测量系统模型 1.1 进入飞行任务火星探测器在进入火星大气前,完成配平姿态调整,经历滑行飞行后,在约125 km高度进入火星大气,启动升力控制模式,利用RCS (reaction control system,RCS)发动机调整升力方向,控制纵向和横向航程,实现可控进入. 当接近火星表面时,探测器先后打开降落伞和反推发动机,平稳着陆并完成载荷释放. 火星探测器与火星轨道器间通过UHF链路实现弹道测量.
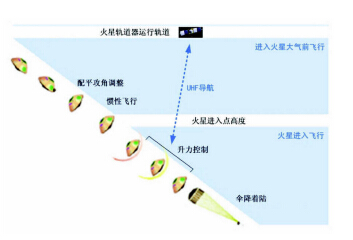
火星探测器进入飞行任务剖面如图 1所示.
|
图 1 火星探测器进入飞行任务示意图 Fig. 1 Entry flight profile of Mars exploration vehicle |
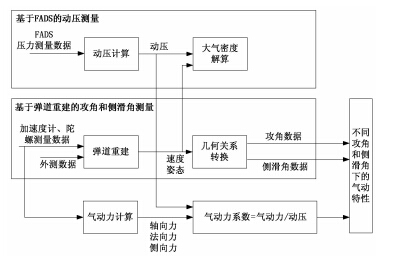
火星探测器进入气动测量目标是获取其在真实火星大气环境下进入气动特性参数,包括进入飞行中的攻角、侧滑角和动压. 与火星进 入气动测量目标相对应,气动测量系统需要实现攻角和侧滑角测量、动压测量三项功能. 气动测量系统将通过弹道重建获取攻角和侧滑角,通过FADS测量获取动压,气动测量总体方案如图 2所示.
|
图 2 气动测量系统测量方案示意图 Fig. 2 Measurement scheme of aerodynamic characteristics |
根据配置在进入探测器大底上的传感器输出数据,经FADS辨识算法确定进入动压;进一步,根据器载IMU的加速度计输出和陀螺输 出,以及进入飞行中外测弹道位置数据,进行弹道重建,确定进入中的位置、速度等弹道参数,并按几何关系解算攻角和侧滑角数据. 在完成弹道重建和FADS测量后,结合动压和速度可以直接解算大气密度;结合动压和加速度计输出的气动力可以直接解算气动力系 数,进而,构建不同攻角和侧滑角下的气动特性.
与上述气动测量总体方案相匹配,气动测量系统组成如下:
(1)压强传感器:组成FADS测量系统,测量火星进入过程中的动压.
(2)加速度计:测量进入过程中的气动过载,结合探测器质量,用于获取气动力;
(3)陀螺,测量进入探测器的姿态角速率,用于弹道重建,获取攻角和侧滑角数据.
(4)外测系统:提供探测器的弹道外测位置数据,作为弹道重建的数据基准. 该项数据可通过环火轨道卫星的UHF设备实现.
FADS测量系统包括多个压强传感器,与各传感器对应的引压孔位置对于气动测量影响显著. 当前,火星探测器大底引压孔布局多 采用十字叉线布局,本文沿用该布局形式,如图 3所示. 在探测器纵向高压区配置3个传感器P1-P3,用于敏感进入动压,同时辅助攻角和侧滑角测量;在探测器中心与高压区连线上, 配置3个传感器P4-P6,用于敏感攻角和侧滑角,同时辅助动压测量;在探测器中心与大底低压区连线上,布置2个传感器P7-P8, 辅助进一步提高攻角和侧滑角测量精度;在探测器两侧各布置2个传感器P9-P12,用于敏感进入侧滑角,同时辅助动压测量. 需要指出,FADS系统同样可以测量进入飞行中攻角和侧滑角,本文将其作为弹道重建获取攻角和侧滑角数据的冗余备份输出,这 样处理可以大幅提高气动测量的可靠性.

|
图 3 引压孔布局示意图 Fig. 3 Location of pressure measurement points |
弹道重建是指重建探测器进入全程的位置、速度和姿态信息,其基本思路是利用外测的弹道位置数据,估计火星进入初 始条件、加速度计和陀螺的零位误差,根据估计结果,修正进入初始条件和IMU(加速度计和陀螺)的内测数据,递推获取全弹 道位置、速度和姿态.
考虑到火星进入过程中探测器为刚体模型,因此,从系统辨识角度而言,其系统建模误差可忽略,该情况下适宜采用输出误差 法开展弹道重建工作. 首先,建立进入动力学与运动学模型以及各项测量误差的误差模型,基于估计的进入初始条件和误差模型进行弹道外推,以外 测弹道位置为基准,利用融合最大似然轨迹辨识准则和Newton-Raphson算法的输出误差法,进行进入初始条件和误差模型的 估计、修正,上述过程反复迭代,直至精度满足要求[11] 弹道重建具体算法如下.
首先,确定探测器的进入动力学模型、观测模型和IMU测量误差模型.
探测器进入动力学模型为
| $\dot{\pmb x}_e = f\left({\pmb x}_e ,{\pmb a}_e , {\pmb\omega} _e ,t \right) $ | (1) |
进入外测系统观测模型为
| ${\pmb Y}_e = {\pmb Y}_m + {\pmb \delta} _d $ | (2) |
探测器IMU测量误差模型为
| $ {\pmb a } _e = {\pmb a } _m + {\pmb a } _d $ | (3) |
| ${\pmb \omega }_e = {\pmb \omega }_m + {\pmb \omega}_d $ | (4) |
而后,确定进入过程中的待估计变量 ${\pmb \varTheta } $为
| ${\pmb \varTheta} = \left({\pmb Y}_e \left( 0 \right), {\pmb V}_e \left( 0 \right), {\pmb \phi }_e \left( 0 \right), {\pmb a}_d ,{\pmb \omega }_d \right) $ | (5) |
| ${\pmb\varTheta} _i = {\pmb\varTheta} _{i - 1} + \Delta {\pmb\varTheta} _i $ | (6) |
| $\Delta {\pmb\varTheta} _i = - \left( {\dfrac{\partial ^2J}{\partial \varTheta _p \varTheta _q }} \right)_{\varTheta _p ,\varTheta _q \in {\pmb\varTheta} }^{ - 1} \left( {\dfrac{\partial J}{\partial \varTheta _p }} \right)_{\varTheta _p \in {\pmb\varTheta} } $ | (7) |
极大似然准则函数J定义为
| $J\left( {\pmb\varTheta} \right) = {\pmb v } {\pmb W }^{ - 1}{\pmb v }^{\rm T} ,\ {\pmb v } = {\pmb Y } _e - {\pmb Y } _m $ | (8) |
最后,根据待估计变量的估计结果,可以获得探测器进入过程中IMU(加速度计和陀螺)的零位误差,在真实测量值中减去测量误差,可获取全程估计测量结果,结合位置、速度以及姿态初值的估计结果,通过探测器进入动力学模型积分递推,重建进入弹道并获得进入速度在探测器体坐标系内的投影$V_x ,V_y ,V_z $,则攻角和侧滑角解算公式为
| $\left. \alpha = \arctan \left( {{ - V_y } /{V_x }} \right) \\ \beta = \arcsin \left( {{V_z } / {\left( {V_x^2 + V_y^2 + V_z^2 } \right)^{1 / 2}}} \right) \right\} $ | (9) |
FADS测量指通过探测器大底上布置的引压孔,将进入探测器激波后壁面冲压经测压管引至探测器内的传感器敏感压强,进而通过最小二乘最优估计算法确定自由流动压.
以$f_i \left( {\pmb X} \right)$表示第$i$个测压点压强与气动状态矢量的函数,第$i$个引压孔测量压强值可表示为
| $P_i = f_i \left( {\pmb X} \right) + \varepsilon _i = q_c \cos ^2\theta _i + p_\infty + \varepsilon _i $ | (10) |
| $\cos \left( {{\theta _i}} \right) = \cos \left( \alpha \right)\cos \left( \beta \right)\cos \left( {{\lambda _i}} \right) +\\ \qquad \sin \left( \beta \right)\sin \left( {{\varphi _i}} \right)\sin \left( {{\lambda _i}} \right) + \\ \qquad \sin \left( \alpha \right)\cos \left( \beta \right)\cos \left( {{\varphi _i}} \right)\sin \left( {{\lambda _i}} \right)n$ | (11) |
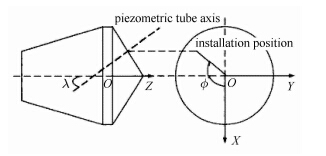
|
图 4 引压孔位置关系示意图[12] Fig. 4 Location relationship of pressure measurement points |
t时刻,n个传感器的测量输出形成下述矢量,
| $\left. \begin{array}{l} P = {\left( {{P_1}\;{P_2}\; \cdots \;{P_n}} \right)^{\rm{T}}}\\ f = {\left( {{f_1}\left( X \right){f_2}\left( X \right)\; \cdots {f_n}\left( X \right)} \right)^{\rm{T}}}\\ \varepsilon = {\left( {{\varepsilon _1}{\rm{ }}{\varepsilon _2}\; \cdots \;{\varepsilon _n}} \right)^{\rm{T}}} \end{array} \right\}$ | (12) |
测量矢量${\pmb P}$和状态方程矢量${\pmb X}$的关系可由如下方程给出
| ${\pmb P} = {\pmb f}\left( {\pmb X} \right) + {\pmb \varepsilon } $ | (13) |
上式近似为
| ${\pmb P} = {\pmb f}\left( {{\pmb X}_0 } \right) + \left( {\dfrac{\partial {\pmb f}}{\partial {\pmb X}}} \right)_{{ X} = { X}_0 } \cdot \Delta {\pmb X} + {\pmb \varepsilon } $ | (14) |
定义$n\times $4维的敏感度矩阵${\pmb H}$
| ${\pmb H} = \left( {\dfrac{\partial {\pmb f}}{\partial {X}}} \right)_{{X} = {X}_0 }$ | (15) |
| ${\pmb y} = {\pmb P} - {\pmb f}\left( {{\pmb X}_0 } \right)$ | (16) |
| ${\pmb y} ={\pmb H} \cdot \Delta {\pmb X} + {\pmb \varepsilon } $ | (17) |
则$\Delta {\pmb X}$的最优线性最小无偏估计为
| $\Delta {\pmb X} = \left( {{\pmb H}^{\rm T}{\pmb S}^{ - 1}{\pmb H}} \right)^{ - 1}{\pmb H}^{\rm T}{\pmb S}^{ - 1} {\pmb y} $ | (18) |
| ${\pmb S}_E = \left(\!\!\begin{array}{ccccc} {\sigma _1^2 } & 0 & \cdots & \cdots & 0 \\ 0 & {\sigma _2^2 } & 0 & \cdots & \vdots \\ \vdots & 0 & \ddots & 0 & \vdots \\ \vdots & \vdots & 0 & {\sigma _{n - 1}^2 } & 0 \\ 0 & 0 & \cdots & 0 & {\sigma _n^2 } \end{array}\!\! \right) $ | (19) |
获得正激波后壁面冲压后,由压力比R(自由来流静压与正激波后的总压比值)反算马赫数Ma
| $\begin{array}{l} R = \frac{{{p_\infty }}}{{{q_c} + {p_\infty }}} = {\left[ {\frac{2}{{\left( {\gamma + 1} \right)M{a^2}}}} \right]^{{\textstyle{\gamma \over {\gamma - 1}}}}} \cdot \\ \qquad {\left[ {\frac{{2\gamma M{a^2} - \left( {\gamma - 1} \right)}}{{\left( {\gamma + 1} \right)}}} \right]^{{\textstyle{1 \over {\gamma - 1}}}}},\\ \gamma = 1.335,\;Ma > 1 \end{array}$ | (20) |
则动压$q_\infty $为
| $q_\infty = \dfrac{\gamma }{2}\left( {q_c + p_\infty } \right) R Ma^2 $ | (21) |
在获得动压数据后,可以结合加速度计测量的气动力获取气动力系数,也可以结合弹道重建获得的进入速度获得大气密度参数,计算方式分别如下.
轴向力系数$C_A $,法向力系数 $C_N $和侧向力系数$ $C_Z $ 为
| $C_A = \dfrac{ma_x}{q_\infty S} ,\ C_N = \dfrac{ma_y}{q_\infty S} ,\ C_Z = \dfrac{ma_z}{q_\infty S} $ | (22) |
| ${\pmb a}_e - {\pmb a}_d = \left( {a_x ,a_y ,a_z } \right) $ | (23) |
进入过程中沿弹道的大气密度为
| $\rho = {2q_\infty }/ (V_x^2+V_y^2+V_z^2) $ | (24) |
本节针对前述各节提出的气动测量方法进行仿真计算,分析其具体精度水平,特别是攻角和侧滑角的测量精度. 火星 探测进入飞行任务的总体参数如表 1,气动测量仿真参数如表 2.
| 表 1 火星探测进入飞行任务总体参数 Table 1 Parameters of entry flight mission |
| 表 2 气动测量系统方案仿真参数 Table 2 Simulation parameters of aerodynamics measurement system |
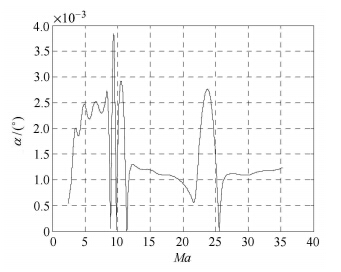
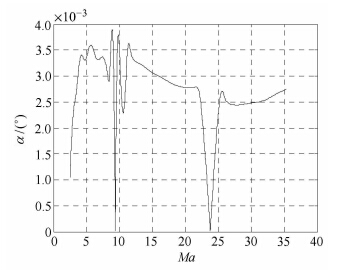
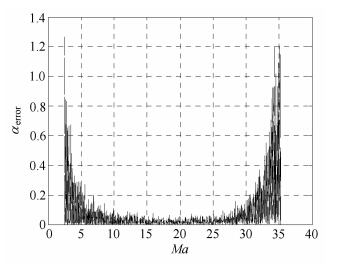
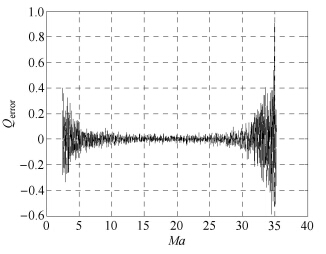
通过仿真计算,获得了进入探测器进入全程的攻角和侧滑角测量结果、动压测量结果和气动力系数测量结果,如图 5 ~图 9所示. 由仿真分析结果可知,基于弹道重建的攻角和侧滑角测量精度优于4×10-3度,相较于FADS测量的攻角和侧滑角,精 度提升2个量级. 同时,基于FADS测量的动压精度优于1%. 随着外测位置精度水平的降低,攻角和侧滑角精度呈线性下降,但在外测位置精度为10 km时 (UHF导航的外测精度 可达约5 km左右[8]),测量精度仍优于4×10-2度,与FADS测量的攻角和侧滑角相比,精度提升1个量级,如图 10所示.
|
图 5 基于弹道重建的攻角测量精度 Fig. 5 Angle of attack error based on trajectory reconstruction |
|
图 6 基于弹道重建的侧滑角测量精度 Fig. 6 Angle of sideslip error based on trajectory reconstruction |
|
图 7 基于FADS测量的攻角测量精度 Fig. 7 Angle of attack error based on FADS |

|
图 8 基于FADS测量的侧滑角测量精度 Fig. 8 Angle of sideslip error based on FADS |
|
图 9 动压精度水平 Fig. 9 Dynamic pressure error |

|
图 10 不同外测精度下的攻角和侧滑角测量精度 Fig. 10 Angle of attack and angle of sideslip error on different trajectory measurement error |
本节气动测量方法的仿真分析结果,验证了测量方案的有效性和可行性.
5 结 论本文针对火星探测器进入飞行任务,提出了一种基于弹道重建和嵌入式大气数据传感系统的气动测量方法. 通过融合火星进入外 测弹道位置信息,利用输出误差法,实现攻角以及侧滑角的高精度测量,同时,基于嵌入式大气数据传感系统完成动压的高精度测量. 仿真分析表明,本文气动测量方案精度高,进入动压测量精度优于1%,攻角和侧滑角测量精度相较于当前的火星探测器进入气动 测量而言,至少提升1个量级. 本文研究将为火星探测等深空探测任务进入飞行气动测量提供技术参考.
| [1] | Gazarik MJ, Wright MJ. Overview of the MEDLI project. IEEE 2008 Aerospace Conference, 2008 |
| [2] | Christopher DK, Prasad K, Mark S, et al. Mars entry atmospheric data system trajectory reconstruction algorithms and flight results. AIAA 2013-0028, 2003 |
| [3] | Euler EA, Adams GL, Hopper FW. Design and reconstruction of the viking lander descent trajectories. Journal of Guidance and Control, 1978, 1(5): 372-378 |
| [4] | Spencer DA, Blanchard RC, Braun RD, et al. Mars pathfinder entry, descent and landing reconstruction. Journal of Spacecraft and Rockets, 1999, 36(3): 357-366 |
| [5] | Blanchard RC, Desai PN. Mars phoenix entry, descent, and landing trajectory and atmosphere reconstruction. Journal of Spacecraft and Rockets, 2011, 48(5): 809-821 |
| [6] | Morabito DD. The spacecmn communications blackout problem encountered during passage or entry of planetary atmospheres. Pasadena, Califomia: Jet Propulsion Laboratory, August, 2002 |
| [7] | Edwards CD, Bell DJ, Gladden RE, et al. Relay support for the Mars science laboratory mission. Pasadena, Califomia: Jet Propulsion Laboratory, March, 2013 |
| [8] | Jean FL, Jean L. Innovative navigation schemes for state and parameter estimation during Mars entry. Journal of Guidance, Control & Dynamics, 2007, 30(1): 169-184 |
| [9] | Glenn L, Andreas EM, Daniel B. Real-time navigation for Mars missions using the Mars network. Journal of Spacecraft and Rockets, 2008, 45(3): 519-533 |
| [10] | 崔平远, 于正湜, 朱圣英. 火星进入段自主导航技术研究现状与展望. 宇航学报, 2013, 34(4): 443-456 (Cui Pingyuan, Yu Zhengshi, Zhu Shengying. Research progress and prospect of autonomous navigation techniques for Mars entry phase. Journal of Astronautics, 2013, 34(4): 443-456 (in Chinese)) |
| [11] | 汪清, 和争春, 方方等. 返回舱弹道重建与黑障区弹道再现研究. 宇航学报, 2004, 25(6): 595-615 (Wang Qing, He Zhengchun, Fang Fang, et al. Trajectory reconstruction and black-out-area trajectory makeup for reentry capsules of spacecraft. Journal of Astronautics, 2004, 25(6): 595-615 (in Chinese)) |
| [12] | 王文强. 火星探测中进入弹道与大气模型重建. 航天返回与遥感, 2013, 34(2): 8-15, (Wang Wenqiang. Atmospheric entry trajectory and atmosphere model reconstruction in Mars exploration. Spacecraft Recovery and Remote Sensing, 2013, 34(2): 8-15 (in Chinese) |
 2015, Vol. 47
2015, Vol. 47
