引言
由于中西部地区地形复杂, 山谷、大河、深沟众多,连续梁、连续刚构是跨越山区的优选桥型. 而中国西部地区又属于地震频发地区,对于山区地形, 地震动的传播有着显著的空间效应. 当山高、谷深时,连续刚构是优选方案. 此时, 一方面结构跨度大; 另一方面, 连续刚构框架结构,使得结构对地震动传播空间效应敏感. 因此, 较为准确地预测跨峡谷桥梁的地震响应,应考虑地震动的空间效应.
跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响.
1 基本理论
考虑平面波入射情形时, 跨峡谷桥梁地震反应的问题(如图1 所示),其本质为波动散射问题.
图1
图1
三维峡谷-桥梁分析模型示意图
Fig.1
Schematic diagram of 3D canyon-bridge analysis model
分析模型包含桥梁及其附近的峡谷地形, 在边界处设置人工边界模拟远区介质的影响.假定沿边界面外法向, 介质按边界面形状向无穷远均匀延伸,远区介质的这种假定对本文所关心的桥梁地震反应影响较小.对于该大型复杂的波动散射问题,其求解的关键在于波动输入及人工边界的实施、土-结相互作用分析的高效计算方法.土-结相互作用分析可采用高效的分区方法[31 -32 ] ,但与平坦场地的情形不同, 峡谷场地边界面不规则, 其输入较为复杂.下面就跨峡谷桥梁的地震反应分析理论和方法进行介绍,包括土体内部区域和桥梁的计算方法, 自由场的计算和人工边界条件的实施.
1.1 土体内部节点的运动
土体采用集中质量显式有限元法来模拟. 经有限元离散得到如下运动方程
(1) $m_i\ddot{ u}_i+\sum_e c^e_{ij}\dot{ u}_j+\sum_e k^e_{ij} u_j= P_i$
式中, $ m_{i} $表示集中于节点$i$的质量, $\ddot{{ u}}_{i}$表示节点$i$的加速度; 假设包含节点$i$的单元共有$e$个, 则$ k_{ij}^{e}$和$ c_{ij}^{e}$表示含节点$i$的单元中节点$i$, $j$间的刚度和阻尼阵; $\dot{{ u}}_{j} $和$ u_{j}$表示单元中节点$j$的速度和位移; $ P_{i}$表示集中在节点$i$的外力.
(2) $\ddot{ u}^p=\frac{ u^{p+1}-2 u^p+ u^{p-1}}{\Delta t^2},\ \ \dot{ u}^p=\frac{ u^{p}- u^{p-1}}{\Delta t^2}$
将式(2)代入式(1), 可得节点$i$在$(p+1)$时刻的位移
(3) $u_{i}^{p+1} =2 u_{i}^{p} - u_{i}^{p-1} -\frac{\Delta t^{2}}{ m_{i}}(\sum\limits_e { k_{ij}^{e} u_{j}^{p} - P_{i}} )- \\ \frac{\Delta t}{ m_{i}}\sum\limits_e c_{ij}^{e} ( u_{j}^{p}- u_{j}^{p-1} )$
式中, $ u_{i}^{p+1}$, $ u_{i}^{p}$和$ u_{i}^{p-1}$为节点$i$在$(p+1)$, $p$和$(p-1)$时刻的位移, $ u_{j}^{p} $和$ u_{j}^{p-1}$为节点$i$相邻单元中节点$j$在$p$和$(p-1)$时刻的位移, $\Delta t$为离散时间步长.
1.2 人工边界条件及自由场计算
在计算跨峡谷大桥的地震响应时, 只有大桥邻近的地基介质对大桥的影响比较明显,因此截取一部分有限范围的土体进行模拟, 故而引入了虚拟边界, 即人工边界.本文采用廖振鹏等[33 ] 提出的透射边界, $(p+1)$时刻的位移为
(4) $u_{so}^{p+1}=\sum_{n=1}^N(-1)^{n+1}C_n^N u_{sn}^{p+1-n}$
式中, $N$为透射阶数, $ u_{so}^{p+1} $表示边界节点$(p+1)$时刻散射场的位移, $ u_{sn}^{p+1-n}$指的是沿过$o$点的边界法线向内第$n$个结点$(p+1-n)$时刻散射场的位移. 散射场位移$u_{sn}^{p+1-n}$可以由总场位移$ u_t$减去自由场位移$ u_f $求得, 即
(5) $u_{sn}^{p+1-n}= u_{tn}^{p+1-n}- u_{fn}^{p+1-n}$
其中$ u_{tn}^{p+1-n}$可以由上节所述的集中质量显示有限元方法求得.
通过透射公式求得边界节点的散射场位移$ u_{so}^{p+1}$后, 便能通过以下公式求得边界点的总场位移
(6) $u_{to}^{p+1}= u_{fo}^{p+1}+ u_{so}^{p+1}$
对于自由场的求解. 三维场地地震动的输入由4个侧面和底面的自由场实现. 对于规则场地, 自由场分析模型一般为成层半空间, 采用传递矩阵的方法[34 ] 或一维化数值方法[35 ] . 对于峡谷这样地形变化和介质不均匀场地, 可采用如下方法求解各边界区的自由场.
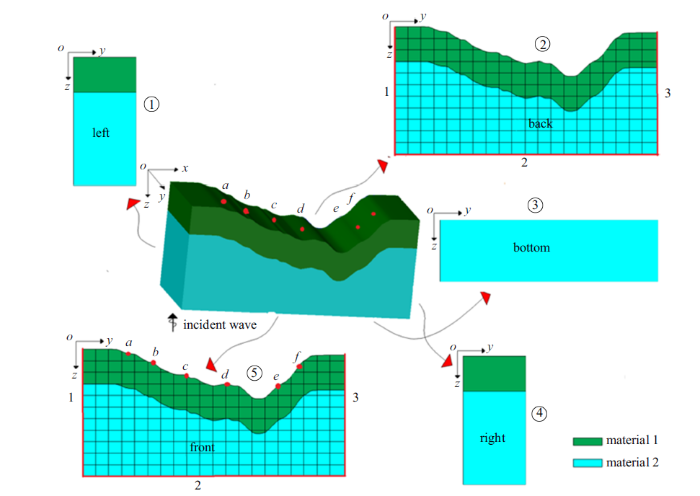
如图2 所示峡谷地形分析模型, 左、右侧面①和④的自由场分析模型为成层半空间, 可采用传递矩阵或一维有限元方法计算; 前、后侧面⑤和②的自由场分析模型为二维不规则半无限场地, 可采用二维有限元结合人工边界求解, 其边界1,2和3的自由场可采用前述的①和④界面中的自由场; 底边界③的自由场, 可采用①或④界面中的自由场.
图2
图2
峡谷场地输入场
Fig.2
Canyon site input field
1.3 桥梁上部结构的运动
(7) $M\ddot{ u}+ C\dot{ u}+ K { u}= F$
采用Newmark时步积分算法, 可用如下方程求得桥梁$(p+1)$时刻的反应
(8) $( K+a M+b C) u^{p+1}= F^{p+1}+ M(a u^p+c\dot{ u}^p+d\ddot{ u}^p)+ \\ C(b u^p+e\dot{ u}^p+f\Delta t\dot{ u}^p)$
(9) $\left.\begin{array}{l} a=\dfrac{1}{\beta \Delta t^{2}},\ \ b=\dfrac{\gamma}{\beta \Delta t},\ \ c=\dfrac{1}{\beta \Delta t} \\ d=\dfrac{1}{2\beta}-1,\ \ e=\dfrac{\gamma}{\beta}-1,\ \ f=\dfrac{\gamma}{2\beta}-1 \\ \end{array} \right\}$
1.4 承台的运动
假设承台为刚性, 其运动可由6个分量描述, 即3个平动分量和3个转动分量.桩基础和桥梁结构作用在承台上的合力使承台产生刚体运动,第$j$个承台的运动方程为
(10) ${ M}_{fj} \ddot{{u}}_{fj} ={ F}_{Sj} +{ F}_{Dj}$
式中, ${ M}_{fj}$为第$j$个承台的集中质量阵,对角线元素分别依次为3个平动自由度的质量$M_{fjx}$, $M_{fjy}$和$M_{fjz} $与3个转动自由度的转动惯量; $\ddot{{ u}}_{fj}$为第$j$个承台的加速度矢量, ${ F}_{Sj} $和${ F}_{Dj}$分别为土体和桥梁上部结构作用于第$j$个承台上的力矢量. 运用中心差分方法,承台$(p+1)$时刻的位移为
(11) $u_{fj}^{p+1} =2 u_{fj}^{p} - u_{fj}^{p-1} +\Delta t^{2} M_{fj}^{-1} \left( { F_{Sj}^{p} + F_{Dj}^{p}} \right)$
式中, $ u_{fj}^{p-1} $, $ u_{fj}^{p}$, $ u_{fj}^{p+1}$和分别是第$j$个承台$(p-1)$、$p$和$(p+1)$时刻的位移矢量,$F_{Sj}^{p} $和$F_{Dj}^{P} $分别是土体和桥梁上部结构$p$时刻作用于第$j$个承台上的力, $\Delta t$是时间步距.
由于承台为刚性, 与第$j$个承台相接触的土节点或结构节点的位移矢量$ u_{tj} $, 可通过基础位移表示为
(12) $u_{tj} = A u_{fj}$
式中, $ A$是$6N\times 6$的转换矩阵
$A=\left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {\bf1} & {\bf0} & {\bf0} & {\bf0} & z & - y \\ {\bf0} & {\bf1} & {\bf0} & - z & {\bf0} & x \\ {\bf0} & {\bf0} & {\bf1} & y & - x & {\bf0} \\ {\bf0} & {\bf0} & {\bf0} & {\bf1} & {\bf0} & {\bf0} \\ {\bf0} & {\bf0} & {\bf0} & {\bf0} & {\bf1} & {\bf0} \\ {\bf0} & {\bf0} & {\bf0} & {\bf0} & {\bf0} & {\bf1} \\ \end{array} \right]$
(13) $\left. \begin{array}{l} {{ x}=\left( {x_{1} ,x_{2} ,\cdots ,x_{n}} \right)^T} \\ {{ y}=\left( {y_{1} ,y_{2} ,\cdots ,y_{n}} \right)^T} \\ {{ z}=\left( {z_{1} ,z_{2} ,\cdots ,z_{n}} \right)^T} \\ {{\bf 1}=\left( {1,1,\cdots ,1} \right)^T} \\ {{\bf 0}=\left( {0,0,\cdots ,0} \right)^T} \\ \end{array} \right\}$
式中, $x_{i}$, $y_{i}$, $z_{i}$为桥梁静止时与承台接触的第$i$个节点相对于承台质心的直角坐标.
1.5 分析流程
由于桥梁上部结构使用无条件稳定的Newmark隐式积分算法, 因此时间步距的选取满足精度要求即可, 可比土体分析的时间步距大,即桥梁和土体可以使用不同的时间步距(具体可参考文献[32 ]). 设已知$p$时刻以及$p$时刻以前各个时刻的土体、承台和桥梁的响应,求解$(p+1)$时刻系统的响应, 其基本流程如下:
(1) 先根据1.2节所述模型, 计算边界区的自由场时程;
(2) 根据递推公式(3)计算土体(桩)内部节点$p+1$时刻的位移响应;
(3) 根据式(4) $\sim\!$式(6), 得到人工边界节点$p+1$时刻的位移响应;
(4) 根据式(11), 计算各承台在$p+1$时刻的位移, 进而由式(12)求得土体、桩和桥梁与承台相联接点$p+1$时刻的位移;
(5) 以桥墩底部节点$p+1$时刻的位移作为桥梁的约束, 由式(8)可以得到桥梁的位移响应(可以使用商业软件, 本文采用ANSYS软件), 并得到$p+1$时刻桥墩底部对承台施加的力;
(6) 重复步骤(2) $\sim$ (5), 即可以得到土(桩)-承台-桥梁体系各个时刻的响应.
2 算例分析
2.1 波动输入方法验证
选取如图2 所示的模型对边界输入方法进行验证. 该模型沿$Y$方向不变,考虑SV垂直入射, 因此本质上为二维问题. 建立三维有限元模型,按前述边界输入方法进行分析, 将其结果与二维有限元的结果进行对比,验证三维峡谷场地波动输入和边界实施的正确性.三维土体模型尺寸为1100 m$\times$80 m$\times$300 m, 采用2 m$\times$2 m$\times$2 m的六面体八节点实体单元对土体进行离散, 其单元总数为3 300 000,节点总数为3 411 241.二维土体模型尺寸为1100 m$\times$300 m, 用2 m$\times$2 m的矩形单元进行离散, 单元总数为82 500, 节点总数为83 201.二维模型和三维模型采用相同的土体材料, 土层材料参数见表1 .
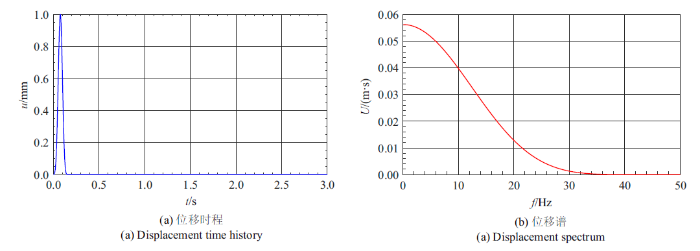
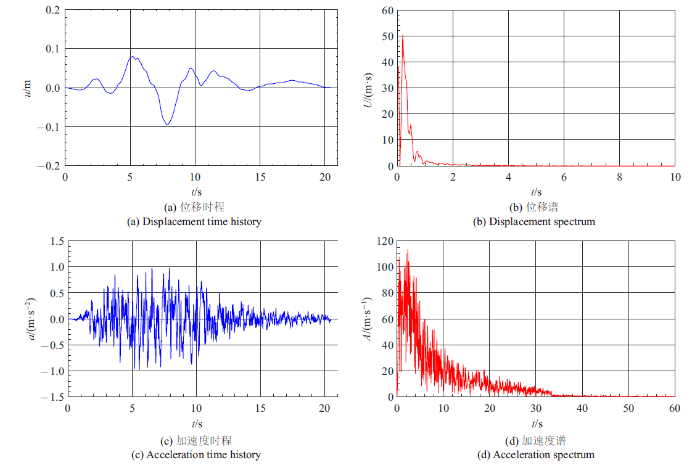
采用脉冲宽度为0.15 s, 持续时间为3.0 s, 时间步距$\Delta t=1.0\times 10^{-3}$的SV波于土体底部垂直入射, 其位移时程和频谱见图3 .
图3
图3
脉冲波输入
Fig.3
Pulse wave input
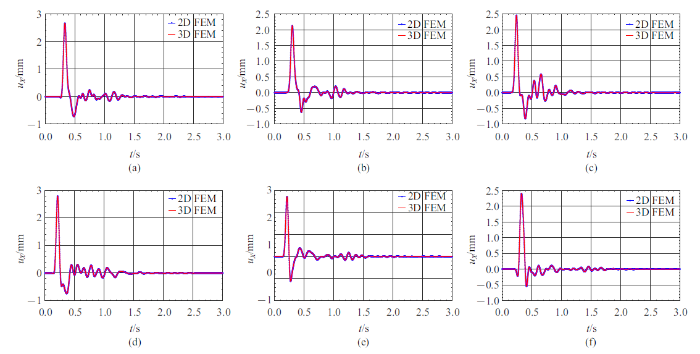
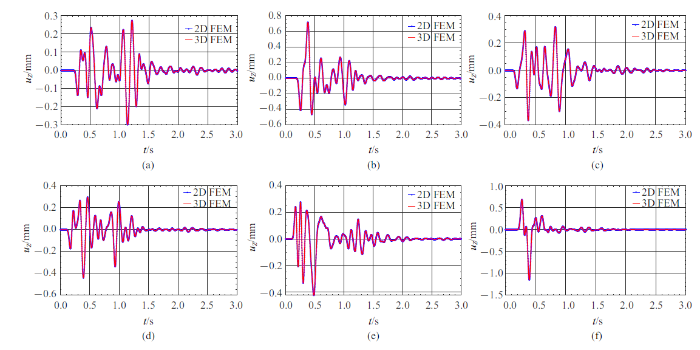
三维土体和二维土体分别选取$x$和$z$坐标相同6个监测点(见图3 ). 其二维和三维的位移时程对比见图4 和图5 .
图4
图4
$a$点至$f$点$x$方向脉冲响应
Fig.4
$X$-direction impulse response from point $a$ to point $f$
图5
图5
$a$点至$f$点$z$方向脉冲响应
Fig.5
$Z$-direction impulse response from point $a$ to point $f$
从$a$点至$f$点的位移时程图可以看出,三维有限元和二维有限元模型在$x$方向和$z$方向的位移完全重合,即在不考虑场地的地形沿$y$方向变化时, 在峡谷模型底部垂直输入SV波,二维有限元计算结果和三维有限元计算结果相同,验证了峡谷场地波动散射问题分析的边界输入方法和人工边界实施的正确性.
2.2 跨峡谷桥梁地震反应分析
为了分析峡谷地形效应和土-结相互作用效应, 考虑如下不同分析模型:
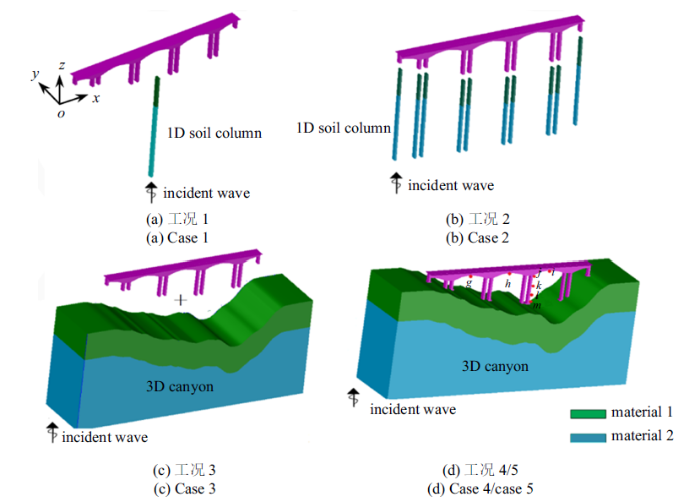
(1)不考虑场地地形效应以及场地与桥梁之间的土-结动力相互作用效应. 直接将地震安全性评价或规范给定的桥址处的地震动一致输入到各桥墩底部, 在算例中为工况1 (case 1). (2) 近似考虑地形效应, 但不考虑土-结相互作用效应.将各桥墩底部的土层当做水平成层场地(图6 (b)中的各一维土柱模型), 分别计算各桥墩底部处场地地表地震动, 并将其输入到各桥墩底部进行桥梁地震反应分析, 在算例中为工况2 (case 2). (3) 考虑场地的地形效应, 但不考虑土-结动力相互作用效应.先计算三维峡谷场地的地震响应(图6 (c)中三维峡谷模型), 再将各桥墩位置处地震动作为输入分析桥梁的地震响应, 在算例中为工况3 (case 3). (4) 同时考虑峡谷地形效应和土-结相互作用效应, 考虑桩基(材料参数见表1 ), 分析峡谷场地-桥梁体系的地震反应(采用本文前述分析理论), 在算例中为工况4 (case 4). (5) 不考虑桩基, 其余与工况4相同, 在算例中为工况5 (case 5). Case 1 $\sim$ case 3中, 在地震动输入方向, 墩底的位移即为输入的地震动位移, 其余自由度约束; case 4和case 5中, 地震波从底部入射, 通过自由场从边界面输入(见1.2节), 墩底、承台、桩、土体在接触面上满足位移和力的连续条件. Case 1 $\sim$ case 3之间的比较, 可以考察地形效应的影响; case 3和case 4 (case 5)之间的比较, 可以考察土-结相互作用的影响.
图6
图6
各工况分析模型示意图
Fig.6
Schematic diagram of analysis model for each working condition
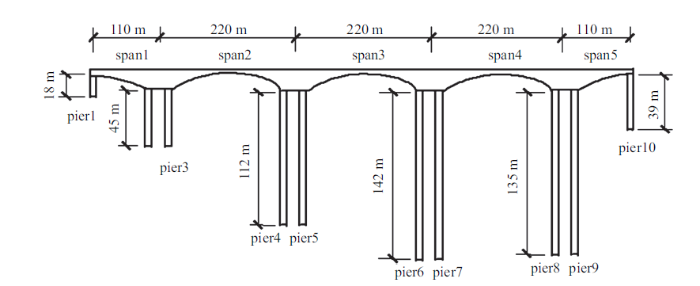
对于case 4和case 5模型, 由于采用土-结相互作用分区计算方法,土体和结构可以独立建模. 本文以马水河大桥为研究对象,根据实际地质资料建立场地模型. 建立三维场地模型需要考虑多方面因素,包括场地模型尺寸的取值、材料属性和单元网格尺寸的确定等.本文根据大桥模型和实际地质来估计场地的尺寸, 大桥总跨径为880 m,承台最大尺寸为24 m$\times$18 m$\times$4 m, 桥墩最高为142 m,图8 为马水河大桥纵向的示意图. 由于大桥的峡谷两岸地形变化不明显,则距离边墩承台一定距离后, 土体对大桥的地震响应可以忽略不计,则选取土体的尺寸为1100 m$\times$80 m$\times$300 m.根据表1 中的材料参数和图10 中的输入地震波频率, 土体单元的尺寸取为2 m$\times$2 m$\times$2 m, 满足波动模拟的精度要求, 即${\Delta x}/{\lambda _{\min}}\leqslant {1}/{10}$.
马水河大桥采用的是五跨一联预应力砼变截面箱形连续刚构方案, 跨径布置为: 110 m + 3$\times$220 m +110 m = 880 m. 桥梁的上部采用预应力混凝土刚构箱梁, 箱梁支点梁高12.00 m, 跨中梁高3.50 m, 箱梁跨中底板厚58.70 cm, 支点底板厚125.00 cm, 箱梁顶板厚60.00 cm, 腹板厚度按直线变化, 其中跨中厚度为50.00 cm, 支点厚度为90.00 cm. 边跨桥墩为单薄壁桥墩, 墩身采用变截面矩形空心墩, 墩高分别为18 m, 45 m, 112 m, 142 m, 135 m和39 m, 中跨桥墩为双薄壁墩. 该桥的箱梁和桥墩分别采用C50和C40的混凝土. 本文采用商业通用软件ANSYS对桥梁建模, 选用梁单元BEAM188对其进行有限元划分, BEAM188单元适合分析细长和中等细长的桥梁结构, 该单元总共有两个节点,且每个节点都有6个自由度. 桥梁上部结构模型(含箱梁和桥墩)共划分862个节点, 877个单元, 如图7 所示, 承台和桩在土体模型中考虑.
图7
图7
马水河大桥有限元模型
Fig.7
Finite element model of Mashuihe Bridge
图8
图8
纵桥向模型
Fig.8
Longitudinal bridge model
选用Block Lanczos法进行大桥的模态提取,表2 为马水河大桥的模态分析结果.
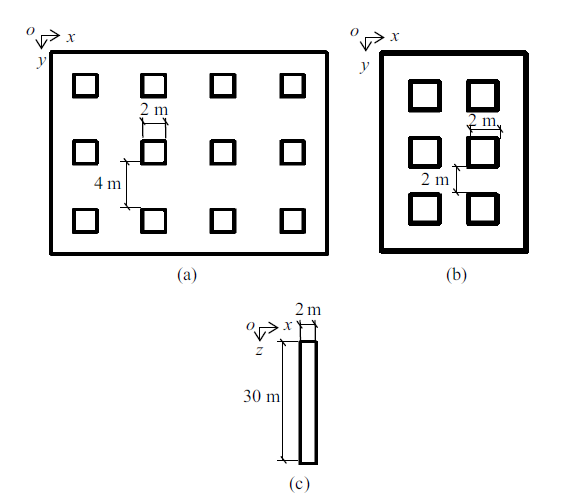
图8 为马水河大桥的纵桥向模型图. 图9 为桩的示意图, 其中图9 (a)为墩2 $\sim$ 墩9桩位置的示意图, 图9 (b)为墩1和墩10桩位置的示意图, 桩长皆为30 m, 具体参考图9 (c).
图9
图9
桩示意图
Fig.9
Pile diagram
采用根据反应谱生成的人工波(见图10 ), 时长为20.48 s, 计算时间步距$\Delta t=5.0\times 10^{-3}$, 按SV波于土体底部垂直入射(质点振动方向沿纵桥向)计算.
图10
图10
输入地震波
Fig.10
Seismic wave input
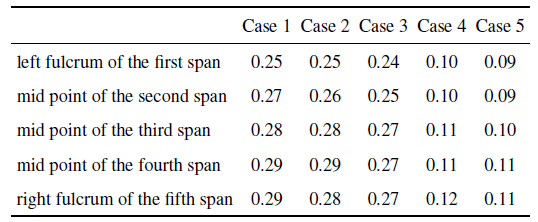
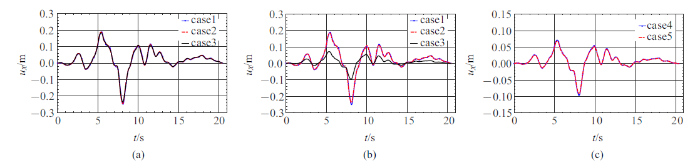
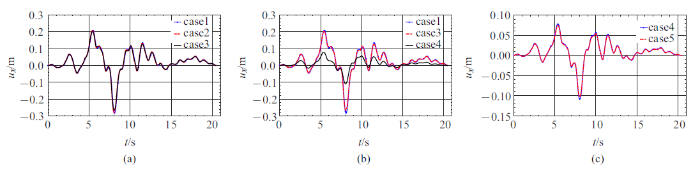
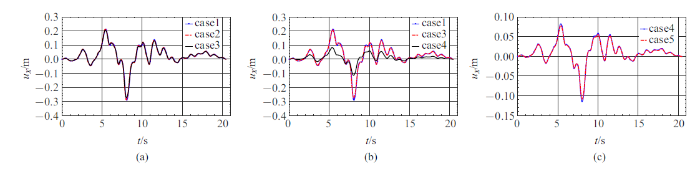
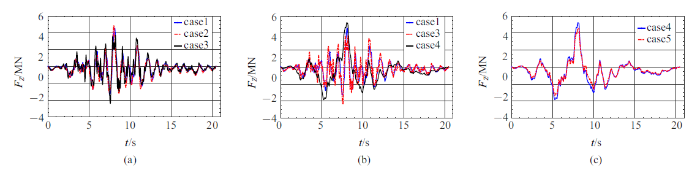
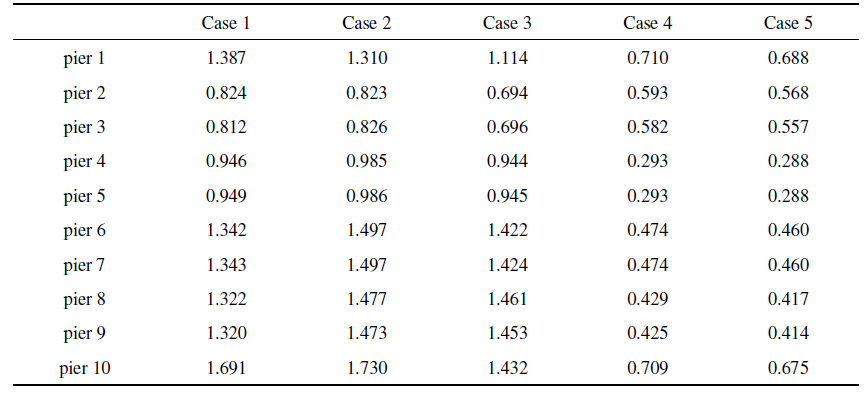
由于地形模型在横桥向变化不明显,且只考虑了质点振动方向沿纵桥向的地震波输入(SV波),因此桥梁在横桥向的反应很小, 主要为纵桥向($x$方向)和竖向($z$方向)反应,这里仅给出纵桥向的位移. 图11 $\sim\!$图13 分别跨1左支点、跨3和跨4中点处各工况情形的$x$方向位移时程. 从图中可以看出, case 1, case 2, case 3 三种工况位移差别不大, case 1略大于case 2, case 2略大于case 3, 表明该算例中地形效应对位移反应影响不大, 主要因为位移受低频控制(见图10 ), 主要周期成分大于2 s, 对应的最小波长为1800 m (按表1 中土层最小剪切波速900 m/s计算), 超过峡谷地形的尺度(约880 m), 因此该峡谷地形对该位移波影响较小. case 1, case 3, case 4 三种工况对比可看出, case 4的结果要明显小于case 1和case 3的结果, 土-结相互作用效应明显. case 4和case 5的结果比较接近, 可能是由于桩基和土层材料参数较为接近.表3 位桥梁部分位置处各工况下的最大位移.
图11
图11
第1跨左支点$x$方向位移
Fig.11
Displacement in $x$ direction of the left fulcrum of the first span
图12
图12
第3跨中点$x$方向位移
Fig.12
Displacement in $x$ direction at the midpoint of the third span
图13
图13
第4跨中点$x$方向位移
Fig.13
Displacement in $x$ direction at the midpoint of the fourth span
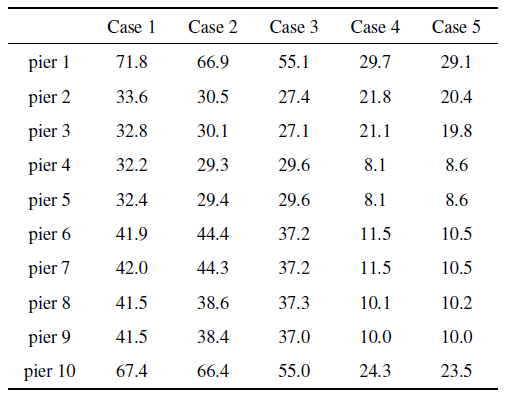
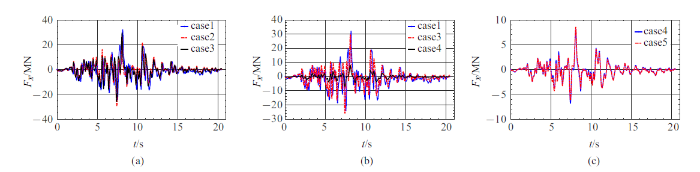
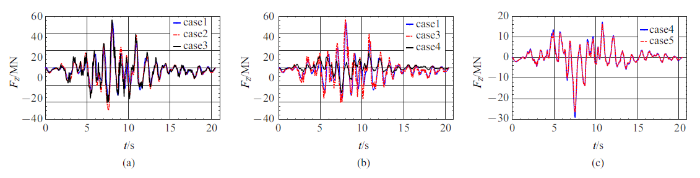
表4 为5种工况下各桥墩底部最大剪力, 图14 $\sim\!$图16 为1, 4, 6墩底部剪力时程. 对比case 1, case 2, case 3的结果,地形效应对底部剪力有明显影响, 总体而言, 地形效应减小了墩底剪力.剪力受惯性力影响, 与加速度有关, 受高频成分控制, 与受低频控制的位移相比,该算例中峡谷对加速度影响较大, 所以地形效应对剪力的影响比对位移的影响要大.对比case 1, case 3和case 4, 土-结相互作用效应较大, 远大于地形效应.
图14
图14
墩1底部剪力
Fig.14
Shear force at the bottom of pier 1
图15
图15
墩4底部剪力
Fig.15
Shear force at the bottom of pier 4
图16
图16
墩6底部剪力
Fig.16
Shear force at the bottom of pier 6
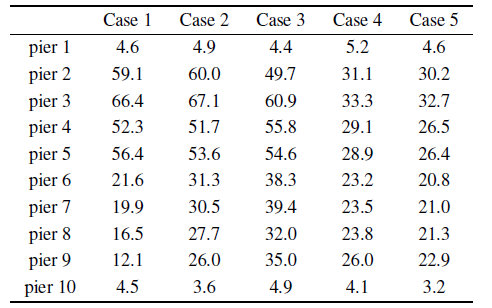
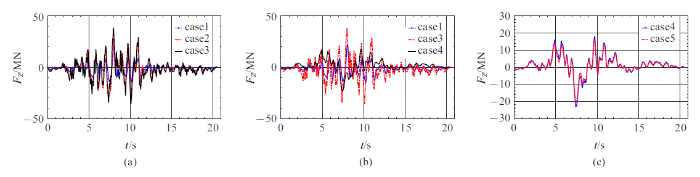
表5 为各桥墩的最大轴力, 图17 $\sim\!$图19 为1, 4, 6墩的轴力时程. 对比case 1, case 2, case 3结果, 地形效应对桥墩轴力有明显影响, 地形效应增大了部分桥墩轴力. 对比case 1, case 3和case 4,土-结相互作用对轴力有较大影响, 其效应要大于地形效应.
图17
图17
墩1轴力
Fig.17
Axial force of pier 1
图18
图18
墩4轴力
Fig.18
Axial force of pier 4
图19
图19
墩6轴力
Fig.19
Axial force of pier 6
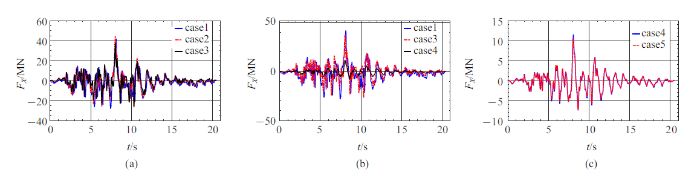
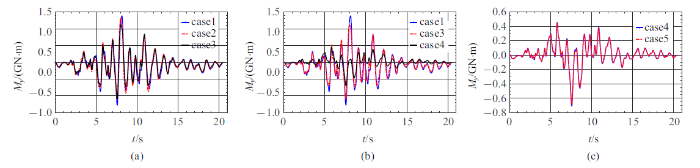
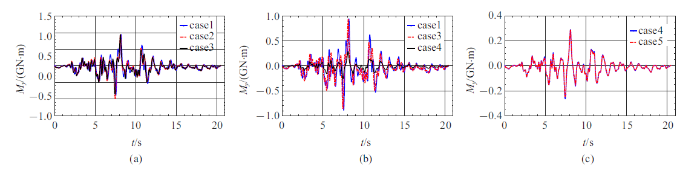
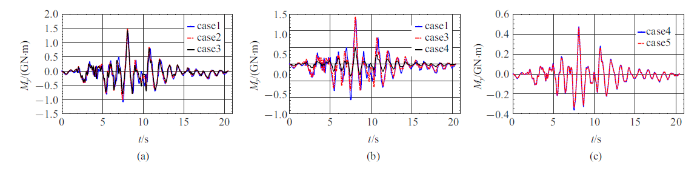
表6 为各桥墩底部最大弯矩, 图20 $\sim\!$图22 为1, 4, 6墩底的弯矩时程. 同样, 地形效应对桥墩底部弯矩有明显影响, 地形效应增大了部分桥墩底部弯矩. 土-结相互作用较大地减小了墩底弯矩, 其效应要大于地形效应.
图20
图20
墩1底部弯矩
Fig.20
Bending moment at the bottom of pier 1
图21
图21
墩4底部弯矩
Fig.21
Bending moment at the bottom of pier 4
图22
图22
墩6底部弯矩
Fig.22
Bending moment at the bottom of pier 6
3 结语
本文提出了一种可综合考虑行波效应、地形效应和土-结相互作用效应的跨峡谷桥梁地震反应分析方法. 以马水河大桥为对象, 设计了5种工况, 分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. 就本算例结果而言, 主要结论如下:
(1)地形效应对桥墩底部剪力、弯矩和轴力影响较明显, 引起部分墩底剪力、弯矩和轴力的增大; 对位移的影响要比剪力、弯矩等的影响要小.
(2)土-结相互作用对桥梁地震反应的影响较大, 可较大地减小其反应.
本文仅考虑了SV波垂直入射情形, 若在自由场计算中考虑非垂直入射, 可计入行波效应, 将在后续工作中进行分析.
参考文献
View Option
[1]
Gazetas G Kallou PV Psarropoulos PN . Topography and soil effects in the M S 5.9 Parnitha (Athens) earthquake: The case of Adàmes
Natural Hazards 2002 , 27 (1 ): 133 -169
DOI
URL
[本文引用: 1]
[2]
2周国良 , 李小军 , 侯春林 等 . SV波入射下河谷地形地震动分布特征分析
岩土力学 , 2012 , 33 (4 ): 1162 -1166
[本文引用: 1]
(Zhou Guoliang Li Xiaojun Hou Chun1in , et al . Characteristic analysis of ground motions of canyon topography under incident SV seismic waves
Rock and Soil Mechanics 2012 , 33 (4 ): 1161 -1166 (in Chinese))
[本文引用: 1]
[3]
Jia HY Zhang DY Zheng SX , et al . Local site effects on a high-pier railway bridge under tridirectional spatial excitations: Nonstationary stochastic analysis
Soil Dynamics and Earthquake Engineering 2013 , 52 : 55 -69
DOI
URL
[本文引用: 1]
[4]
王蕾 , 赵成刚 , 屈铁军 . SV 波入射下地形条件对大跨钢构桥地震响应的影响
地震学报 , 2008 , 30 (3 ): 307 -314
(Wang Lei Zhao Chenggang Qu Tiejun . Seismic response of long-span rigid-framed bridge to incident SV wave with topographic effect being considered
Acta Seismologica Sinica 2008 , 30 (3 ): 307 -314 (in Chinese))
[5]
梅泽洪 , 李小军 , 王玉石 等 . 考虑场地效应的非一致激励下桥梁地震响应特点分析
震灾防御技术 , 2017 , 12 (3 ): 646 -654
[本文引用: 1]
(Mei Zehong Li Xiaojun Wang Yushi , et al . Analysis of seismic response characteristics of bridges under non-uniform excitation considering site effects
Technology for Earthquake Disaster Prevention 2017 , 12 (3 ): 646 -654 (in Chinese))
[本文引用: 1]
[6]
张会远 . 纵桥向行波作用下大跨度连续刚构桥的地震反应分析
中外公路 , 2014 , 34 (6 ): 92 -96
[本文引用: 1]
(Zhang Huiyuan . Seismic response analysis of long-span continuous rigid frame bridge under longitudinal traveling wave
Journal of China & Foreign Highway 2014 , 34 (6 ): 92 -96 (in Chinese))
[本文引用: 1]
[7]
陈兴冲 , 吴海燕 , 张永亮 . 行波效应对铁路大跨长联连续刚构桥地震反应的影响
世界地震工程 , 2010 (1 ): 191 -196
(Chen Xingchong Wu Haiyan Zhang Yongliang . The effect of traveling waves on seismic response of railway long-span and long-cunjunction continuous rigid-frame bridges under multi-support excitations
World Earthquake Engineering 2010 (1 ): 191 -196 (in Chinese))
[8]
刘正楠 , 陈兴冲 , 张永亮 等 . 考虑行波效应的无砟轨道铁路桥梁纵桥向地震响应
振动与冲击 , 2020 , 39 (4 ): 142 -149
[本文引用: 1]
(Liu Zhengnan Chen Xingchong Zhang Yongliang , et al . Longitudinal seismic response of ballastless railway bridges considering traveling wave effect
Journal of Vibration and Shock 2020 , 39 (4 ): 142 -149 (in Chinese))
[本文引用: 1]
[9]
Mylonakis G Gazetas G . Seismic soil-structure interaction: Beneficial or detrimental
Journal of Earthquake Engineering 2000 , 4 (3 ): 277 -301
[本文引用: 1]
[10]
Wu JN . Seismic effectiveness of tuned mass dampers considering soil-structure interaction
Earthquake Engineering and Structure Dynamic 1999 , 28 (11 ): 1219 -1233
DOI
URL
[11]
杨美良 , 李振华 , 钟扬 . 桩土效应对矮墩刚构连续组合梁桥的受力影响分析
中外公路 , 2012 , 32 (05 ): 112 -115
(Yang Meiliang Li Zhenhua Zhong Yang . Analysis of pile-soil effect on the stress of low pier rigid frame continuous composite beam bridge
Journal of China & Foreign Highway 2012 , 32 (5 ): 112 -115 (in Chinese))
[12]
Zani G Martinelli P Galli A , et al . Seismic assessment of a 14th-century stone arch bridge: Role of soil-structure interaction
Journal of Bridge Engineering
[13]
Vahid S Ali G Ali M . Analytical model for time history analysis of single pier bridges considering soil-pile structure interaction effects
Applied Mathematical Modelling 2021 (93 ): 257 -275
[14]
Farshad H Mahdi Y . The probabilistic seismic assessment of aged concrete arch bridges: The role of soil-structure interaction
Structures 2020 , 28 : 894 -904
DOI
URL
[15]
Emad NT Todd T Farhad A . Effects of near-field ground motions and soil-structure interaction on dynamic response of a cable-stayed bridge
Soil Dynamics and Earthquake Engineering 2020 , 133 : 106115
DOI
URL
[16]
Fiorentino G Cengiz C Luca FD , et al . Integral abutment bridges: Investigation of seismic soil-structure interaction effects by shaking table testing
Earthquake Engineering Structural Dynamics 2021 , 50 (6 ): 1517 -1538
DOI
URL
[本文引用: 1]
[17]
范立础 , 王君杰 , 陈玮 . 非一致地震激励下大跨度斜拉桥的响应特征
计算力学学报 , 2001 , 18 (3 ): 358 -363
[本文引用: 1]
(Fan Lichu Wang Junjie Chen Wei . Response characteristics of long-span cable-stayed bridges under non-uniform seismic excitation
Chinese Journal of Computational Mechanics 2001 , 18 (3 ): 358 -363 (in Chinese))
[本文引用: 1]
[18]
闫晓宇 , 李忠献 , 韩强 等 . 多点激励下大跨度连续刚构桥地震响应振动台阵试验研究
土木工程学报 , 2013 , 46 (7 ): 81 -89
(Yan Xiaoyu Li Zhongxian Han Qiang , et al . Shaking tables test study on seismic responses of a long-span rigid-framed bridge under multi-support excitations
China Civil Engineering Journal 2013 , 46 (7 ): 81 -89 (in Chinese))
[19]
Karmakara D Ray-Chaudhuri S Shinozuka M . Seismic response evaluation of retrofitted Vincent Thomas bridge under spatially variable ground motions
Soil Dynamics and Earthquake Engineering 2012 , 42 : 119 -127
DOI
URL
[20]
Soyluk K . Comparison of random vibration methods for multi-support seismic excitation analysis of long-span bridges
Engineering Structures 2004 , 26 (11 ): 1573 -1583
DOI
URL
[21]
Shiravand MR Parvanehro P . Spatial variation of seismic ground motion effects on nonlinear responses of cable stayed bridges considering different soil types
Soil Dynamics and Earthquake Engineering 2019 , (119 ): 104 -117
[22]
Zhong J Jeon JS Reny WX . Risk assessment for a long-span cable-stayed bridge subjected to multiple support excitations
Engineering Structures 2018 (176 ): 220 -230
[23]
Li C Li HN Hao H , et al . Seismic fragility analyses of sea-crossing cable-stayed bridges subjected to multi-support ground motions on offshore sites
Engineering Structures 2018 , (165 ): 441 -456
[24]
Nurdan MA Selcuk B Ebru H . Response of the Fatih Sultan Mehmet Suspension Bridge under spatially varying multi-point earthquake excitations
Soil Dynamics and Earthquake Engineering 2016 , 84 : 44 -54
DOI
URL
[本文引用: 1]
[25]
Anastasios GS Kyriazis DP Andreas JK . Inelastic dynamic analysis of RC bridges accounting for spatial variability of ground motion, site effects and soil-structure interaction phenomena. Part 1: Methodology and analytical tools
Earthquake Engng Struct. Dyn 2003 , 32 : 607 -627
DOI
URL
[本文引用: 1]
[26]
Anastasios GS Andreas JK Kyriazis DP . Inelastic dynamic analysis of RC bridges accounting for spatial variability of ground motion, site effects and soil-structure interaction phenomena. Part 2: Parametric study
Earthquake Engng Struct. Dyn 2003 , 32 : 629 -652
DOI
URL
[27]
Xie W Sun LM Lou ML . Shaking table test verification of traveling wave resonance in seismic response of pile-soil-cable-stayed bridge under non-uniform sine wave excitation
Soil Dynamics and Earthquake Engineering 2020 , 134 : 106151
DOI
URL
[本文引用: 1]
[28]
周国良 李小军 , 李铁萍 等 . SV波入射下峡谷地形对多支撑大跨桥梁地震反应影响分析
岩土力学 , 2012 , 33 (5 ): 1572 -1578
[本文引用: 1]
(Zhou Guoliang Li Xiaojun Li Tieping , et al . Canyon topography effects on seismic responses of multi-support bridge under incident SV seismic waves
Rock and Soil Mechanics 2012 , 33 (5 ): 1572 -1578 (in Chinese))
[本文引用: 1]
[29]
王笃国 , 赵成刚 . 地震波斜入射下考虑场地非线性、地形效应和土结动力相互作用的大跨连续刚构桥地震响应分析
工程力学 , 2017 , 34 (4 ): 32 -41
[本文引用: 1]
(Wang Duguo Zhao Chenggang . Seismic analysis of long-span continuous rigid frame bridge considering site nonlinearity, topographical effects and soil-structure dynamic interaction under oblique incidence
Engineering Mechanics 2017 , 34 (4): 32-41) (in Chinese))
[本文引用: 1]
[30]
谷音 , 江梦霞 , 卓卫东 等 . 考虑地震波斜入射下河谷地形的大跨桥梁动力反应研究
福州大学学报(自然科学版) , 2013 , 41 (4 ): 517 -522
[本文引用: 1]
(Gu Yin Jiang Mengxia Zhuo Weidong , et al . Seismic response analysis of long - span bridges subjected to spatially non - uniform seismic ground motions
Journal of Fuzhou University (Natural Science Edition )2013 , 41 (4 ): 517 -522 (in Chinese))
[本文引用: 1]
[31]
陈少林 , 赵宇昕 . 一种三维饱和土-基础-结构动力相互作用分析方法
力学学报 , 2016 , 48 (6 ): 1362 -1371
DOI
[本文引用: 2]
地震波入射时土与结构动力相互作用分析是地震工程领域的重要问题.由于问题的复杂性,以往的研究大多考虑地基土为干土情形.而实际工程中,土体中经常充满孔隙水,土层往往是含水层或部分含水层.孔隙水对土层的地震反应影响较大,进而影响支撑于其上的基础和上部结构的响应.因此,有必要考虑饱和土-基础-结构动力相互作用问题.基于此,土体采用Biot模型,利用集中质量显式有限元方法并结合多次透射人工边界进行模拟;结构经有限元离散后,采用Newmark隐式时步积分方法进行分析,可通过ANSYS等有限元软件实现;基础假定为刚性,采用显式时步积分进行求解;土体和结构(及基础)可分别采用不同的时间步距;通过FORTRAN程序实现了三维饱和土-基础-结构系统在地震作用下的整体分析.从饱和多孔介质动力微分方程出发可知,干土是饱和土的特殊情形,通过将流体体积模量及孔隙率置为零,可将饱和土退化到干土,从而将干土统一到饱和土的计算框架中,通过土-结构相互作用算例对此进行了验证,进一步实现了干土与饱和土混合情形时的土-结构动力相互作用分析,使得问题的模拟更贴近实际工程(如考虑地下水位情形).通过算例对比了饱和土地基、干土地基、干土覆盖饱和土地基(考虑地下水位)情形时,土-结构相互作用对基础和结构响应的影响,结果表明地下水位对基础和结构响应的影响较大.
(Chen Shaolin Zhao Yuxin . A method for three-dimensional saturated soil-foundation-structure dynamic interaction analysis
Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (6 ): 1362 -1371 (in Chinese))
[本文引用: 2]
[32]
陈少林 , 王俊泉 , 刘启方 等 . 基于显-隐式格式的三维时域土-结相互作用分析的异步并行算法
中国科学(技术科学) , 2017 , 12 : 1321 -1330
[本文引用: 3]
(Chen Shaolin Wang Junquan Liu Qifang , et al . Asynchronous parallel algorithm for three-dimensional soil-structure interaction analysis based on explicit-implicit integration scheme
Scientia Sinica (Technologica )2017 , 12 : 1321 -1330 (in Chinese))
[本文引用: 3]
[33]
廖振鹏 . 工程波动理论导引 . 北京 : 科学出版社 , 1996
[本文引用: 1]
(Liao Zhenpeng . Introduction to Engineering Wave Theory . Beijing : Science Press , 1996 (in Chinese))
[本文引用: 1]
[34]
陈少林 , 宗娟 . 平面波任意角度入射时波动散射问题输入的一种实现方法
固体力学学报 , 2018 , 39 : 80 -89
[本文引用: 1]
(Chen Shaolin Zong Juan . A realization method of wave scattering problem input when plane wave is incident at any angle
Chinese Journal of Solid Mechanics 2018 , 39 : 80 -89 (in Chinese))
[本文引用: 1]
[35]
刘晶波 , 王艳 . 成层半空间出平面自由波场的一维化时域算法
力学学报 , 2006 , 38 (2 ): 219 -225
DOI
[本文引用: 1]
提出了一种计算出平面SH波斜入射时弹性水平成层半空间中自由波场时域计算的一维化有限元方法. 在进行有限元网格划分时,竖向单元取满足有限元模拟精度的任意尺寸,水平向网格尺寸由时间离散步长和水平视波速确定,并自动进行虚拟网格划分. 基底设置人工边界,并将波动输入转化为等效荷载施加在边界节点上. 然后将集中质量有限元法和中心差分法相结合建立节点运动方程,并将水平方向相邻节点的运动用该节点相邻时刻的运动表示,从而将求解节点运动的二维方程组转化为一维方程组. 求解此方程组,即得到自由场中竖向一列节点的运动. 最后根据行波传播的特点,可方便地确定全部自由波场. 理论分析和数值算例表明,该方法具有较高的精度和良好的稳定性.
(Liu Jingbo Wang Yan . A one-dimensional time-domain algorithm for generating a plane free wave field in a layered half-space
Chinese Journal of Theoretical and Applied Mechanics 2006 , 38 (2 ): 219 -225 (in Chinese))
[本文引用: 1]
Topography and soil effects in the M S 5.9 Parnitha (Athens) earthquake: The case of Adàmes
1
2002
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
SV波入射下河谷地形地震动分布特征分析
1
2012
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
SV波入射下河谷地形地震动分布特征分析
1
2012
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
Local site effects on a high-pier railway bridge under tridirectional spatial excitations: Nonstationary stochastic analysis
1
2013
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
SV 波入射下地形条件对大跨钢构桥地震响应的影响
0
2008
SV 波入射下地形条件对大跨钢构桥地震响应的影响
0
2008
考虑场地效应的非一致激励下桥梁地震响应特点分析
1
2017
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
考虑场地效应的非一致激励下桥梁地震响应特点分析
1
2017
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
纵桥向行波作用下大跨度连续刚构桥的地震反应分析
1
2014
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
纵桥向行波作用下大跨度连续刚构桥的地震反应分析
1
2014
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
行波效应对铁路大跨长联连续刚构桥地震反应的影响
0
2010
行波效应对铁路大跨长联连续刚构桥地震反应的影响
0
2010
考虑行波效应的无砟轨道铁路桥梁纵桥向地震响应
1
2020
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
考虑行波效应的无砟轨道铁路桥梁纵桥向地震响应
1
2020
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
Seismic soil-structure interaction: Beneficial or detrimental
1
2000
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
Seismic effectiveness of tuned mass dampers considering soil-structure interaction
0
1999
桩土效应对矮墩刚构连续组合梁桥的受力影响分析
0
2012
桩土效应对矮墩刚构连续组合梁桥的受力影响分析
0
2012
Seismic assessment of a 14th-century stone arch bridge: Role of soil-structure interaction
0
Analytical model for time history analysis of single pier bridges considering soil-pile structure interaction effects
0
2021
The probabilistic seismic assessment of aged concrete arch bridges: The role of soil-structure interaction
0
2020
Effects of near-field ground motions and soil-structure interaction on dynamic response of a cable-stayed bridge
0
2020
Integral abutment bridges: Investigation of seismic soil-structure interaction effects by shaking table testing
1
2021
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
非一致地震激励下大跨度斜拉桥的响应特征
1
2001
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
非一致地震激励下大跨度斜拉桥的响应特征
1
2001
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
多点激励下大跨度连续刚构桥地震响应振动台阵试验研究
0
2013
多点激励下大跨度连续刚构桥地震响应振动台阵试验研究
0
2013
Seismic response evaluation of retrofitted Vincent Thomas bridge under spatially variable ground motions
0
2012
Comparison of random vibration methods for multi-support seismic excitation analysis of long-span bridges
0
2004
Spatial variation of seismic ground motion effects on nonlinear responses of cable stayed bridges considering different soil types
0
2019
Risk assessment for a long-span cable-stayed bridge subjected to multiple support excitations
0
2018
Seismic fragility analyses of sea-crossing cable-stayed bridges subjected to multi-support ground motions on offshore sites
0
2018
Response of the Fatih Sultan Mehmet Suspension Bridge under spatially varying multi-point earthquake excitations
1
2016
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
Inelastic dynamic analysis of RC bridges accounting for spatial variability of ground motion, site effects and soil-structure interaction phenomena. Part 1: Methodology and analytical tools
1
2003
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
Inelastic dynamic analysis of RC bridges accounting for spatial variability of ground motion, site effects and soil-structure interaction phenomena. Part 2: Parametric study
0
2003
Shaking table test verification of traveling wave resonance in seismic response of pile-soil-cable-stayed bridge under non-uniform sine wave excitation
1
2020
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
SV波入射下峡谷地形对多支撑大跨桥梁地震反应影响分析
1
2012
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
SV波入射下峡谷地形对多支撑大跨桥梁地震反应影响分析
1
2012
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
地震波斜入射下考虑场地非线性、地形效应和土结动力相互作用的大跨连续刚构桥地震响应分析
1
2017
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
地震波斜入射下考虑场地非线性、地形效应和土结动力相互作用的大跨连续刚构桥地震响应分析
1
2017
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
考虑地震波斜入射下河谷地形的大跨桥梁动力反应研究
1
2013
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
考虑地震波斜入射下河谷地形的大跨桥梁动力反应研究
1
2013
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
一种三维饱和土-基础-结构动力相互作用分析方法
2
2016
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
... 分析模型包含桥梁及其附近的峡谷地形, 在边界处设置人工边界模拟远区介质的影响.假定沿边界面外法向, 介质按边界面形状向无穷远均匀延伸,远区介质的这种假定对本文所关心的桥梁地震反应影响较小.对于该大型复杂的波动散射问题,其求解的关键在于波动输入及人工边界的实施、土-结相互作用分析的高效计算方法.土-结相互作用分析可采用高效的分区方法[31 -32 ] ,但与平坦场地的情形不同, 峡谷场地边界面不规则, 其输入较为复杂.下面就跨峡谷桥梁的地震反应分析理论和方法进行介绍,包括土体内部区域和桥梁的计算方法, 自由场的计算和人工边界条件的实施. ...
一种三维饱和土-基础-结构动力相互作用分析方法
2
2016
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
... 分析模型包含桥梁及其附近的峡谷地形, 在边界处设置人工边界模拟远区介质的影响.假定沿边界面外法向, 介质按边界面形状向无穷远均匀延伸,远区介质的这种假定对本文所关心的桥梁地震反应影响较小.对于该大型复杂的波动散射问题,其求解的关键在于波动输入及人工边界的实施、土-结相互作用分析的高效计算方法.土-结相互作用分析可采用高效的分区方法[31 -32 ] ,但与平坦场地的情形不同, 峡谷场地边界面不规则, 其输入较为复杂.下面就跨峡谷桥梁的地震反应分析理论和方法进行介绍,包括土体内部区域和桥梁的计算方法, 自由场的计算和人工边界条件的实施. ...
基于显-隐式格式的三维时域土-结相互作用分析的异步并行算法
3
2017
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
... 分析模型包含桥梁及其附近的峡谷地形, 在边界处设置人工边界模拟远区介质的影响.假定沿边界面外法向, 介质按边界面形状向无穷远均匀延伸,远区介质的这种假定对本文所关心的桥梁地震反应影响较小.对于该大型复杂的波动散射问题,其求解的关键在于波动输入及人工边界的实施、土-结相互作用分析的高效计算方法.土-结相互作用分析可采用高效的分区方法[31 -32 ] ,但与平坦场地的情形不同, 峡谷场地边界面不规则, 其输入较为复杂.下面就跨峡谷桥梁的地震反应分析理论和方法进行介绍,包括土体内部区域和桥梁的计算方法, 自由场的计算和人工边界条件的实施. ...
... 由于桥梁上部结构使用无条件稳定的Newmark隐式积分算法, 因此时间步距的选取满足精度要求即可, 可比土体分析的时间步距大,即桥梁和土体可以使用不同的时间步距(具体可参考文献[32 ]). 设已知$p$时刻以及$p$时刻以前各个时刻的土体、承台和桥梁的响应,求解$(p+1)$时刻系统的响应, 其基本流程如下: ...
基于显-隐式格式的三维时域土-结相互作用分析的异步并行算法
3
2017
... 跨峡谷桥梁的地震响应取决于各桥墩底部的有效地震动输入,而地形和场地效应、行波效应以及土-结相互作用效应将导致有效地震动输入的空间差异性:(1)地形和场地效应. 地形和场地条件会影响地震动场[1 -2 ] ,进而改变桥梁结构的有效地震动输入, 影响桥梁地震响应[3 -5 ] .先对地形和场地进行地震反应分析, 然后将桥墩位置的地震动作为输入,进行桥梁地震反应分析, 一般不考虑土-结相互作用. (2)行波效应.由于桥梁跨度较大, 非垂直入射的地震波将引起各桥墩底部地震动的相位差,导致桥梁各墩的非一致激励[6 -8 ] , 一般假定纵桥向的地震波视速度,根据桥梁各跨尺寸考虑输入地震动的相位(到时)差,不考虑地震动的幅值差异和土-结相互作用.(3)土-结构相互作用效应.地基与上部结构之间存在相互作用, 当地基的刚度相对于上部结构的刚度越小,土-结相互作用的影响越明显.运动相互作用和惯性相互作用会改变结构的有效地震动输入,影响桥梁结构的地震响应[9 -16 ] .地形和场地效应、行波效应也可通过考虑地震动的空间相干性, 生成空间地震动场,从而通过非一致激励分析桥墩地震响应[17 -24 ] . 由于问题的复杂性,同时考虑地形和场地效应、行波效应以及土-结相互作用效应较为困难,一些研究考虑其中两种效应[25 -27 ] ;少数研究者同时考虑了3种效应,但局限于二维情形[28 -29 ] , 或在自由场输入时未考虑地形影响[30 ] .本文将跨峡谷桥梁三维地震响应分析问题看做波动散射问题,结合人工边界条件实现峡谷场地的波动输入,并基于土-结相互作用分区分析方法[31 -32 ] ,实现了可综合考虑地形效应、行波效应及土-结相互作用效应的跨峡谷桥梁三维地震响应分析,以马水河特连续刚构桥为例,分析了地形效应和土-结相互作用效应对桥梁地震反应的影响. ...
... 分析模型包含桥梁及其附近的峡谷地形, 在边界处设置人工边界模拟远区介质的影响.假定沿边界面外法向, 介质按边界面形状向无穷远均匀延伸,远区介质的这种假定对本文所关心的桥梁地震反应影响较小.对于该大型复杂的波动散射问题,其求解的关键在于波动输入及人工边界的实施、土-结相互作用分析的高效计算方法.土-结相互作用分析可采用高效的分区方法[31 -32 ] ,但与平坦场地的情形不同, 峡谷场地边界面不规则, 其输入较为复杂.下面就跨峡谷桥梁的地震反应分析理论和方法进行介绍,包括土体内部区域和桥梁的计算方法, 自由场的计算和人工边界条件的实施. ...
... 由于桥梁上部结构使用无条件稳定的Newmark隐式积分算法, 因此时间步距的选取满足精度要求即可, 可比土体分析的时间步距大,即桥梁和土体可以使用不同的时间步距(具体可参考文献[32 ]). 设已知$p$时刻以及$p$时刻以前各个时刻的土体、承台和桥梁的响应,求解$(p+1)$时刻系统的响应, 其基本流程如下: ...
1
1996
... 在计算跨峡谷大桥的地震响应时, 只有大桥邻近的地基介质对大桥的影响比较明显,因此截取一部分有限范围的土体进行模拟, 故而引入了虚拟边界, 即人工边界.本文采用廖振鹏等[33 ] 提出的透射边界, $(p+1)$时刻的位移为 ...
1
1996
... 在计算跨峡谷大桥的地震响应时, 只有大桥邻近的地基介质对大桥的影响比较明显,因此截取一部分有限范围的土体进行模拟, 故而引入了虚拟边界, 即人工边界.本文采用廖振鹏等[33 ] 提出的透射边界, $(p+1)$时刻的位移为 ...
平面波任意角度入射时波动散射问题输入的一种实现方法
1
2018
... 对于自由场的求解. 三维场地地震动的输入由4个侧面和底面的自由场实现. 对于规则场地, 自由场分析模型一般为成层半空间, 采用传递矩阵的方法[34 ] 或一维化数值方法[35 ] . 对于峡谷这样地形变化和介质不均匀场地, 可采用如下方法求解各边界区的自由场. ...
平面波任意角度入射时波动散射问题输入的一种实现方法
1
2018
... 对于自由场的求解. 三维场地地震动的输入由4个侧面和底面的自由场实现. 对于规则场地, 自由场分析模型一般为成层半空间, 采用传递矩阵的方法[34 ] 或一维化数值方法[35 ] . 对于峡谷这样地形变化和介质不均匀场地, 可采用如下方法求解各边界区的自由场. ...
成层半空间出平面自由波场的一维化时域算法
1
2006
... 对于自由场的求解. 三维场地地震动的输入由4个侧面和底面的自由场实现. 对于规则场地, 自由场分析模型一般为成层半空间, 采用传递矩阵的方法[34 ] 或一维化数值方法[35 ] . 对于峡谷这样地形变化和介质不均匀场地, 可采用如下方法求解各边界区的自由场. ...
成层半空间出平面自由波场的一维化时域算法
1
2006
... 对于自由场的求解. 三维场地地震动的输入由4个侧面和底面的自由场实现. 对于规则场地, 自由场分析模型一般为成层半空间, 采用传递矩阵的方法[34 ] 或一维化数值方法[35 ] . 对于峡谷这样地形变化和介质不均匀场地, 可采用如下方法求解各边界区的自由场. ...