引言
在当今迅速发展的工业时代, 输流管道已成为众多工程装备的重要组成元部件.海洋工程中的海洋立管、核电装备中的管束结构等都是输流管道应用的典型实例.在管内流体的激励下, 管道因流体-固体耦合作用可产生自激振动和有害噪声.当其他外界激励频率与输流管道固有频率相近时还可能引起共振, 从而诱发受迫振动与自激振动的协同作用. 事实上, 输流管的流固耦合过程也表现出一种较强的非线性流固耦合特征, 正因为如此, 输流管结构的动力学问题研究已成为流固耦合力学领域的重要研究内容之一[1 -7 ] .
悬臂输流管道是典型的非保守系统, 在流速较大时会丧失稳定性并发生动态的非线性颤振现象, 这显著不同于两端支承输流管道只可能出现的静态屈曲失稳现象.悬臂输流管道失稳后的大幅颤振行为可加速管道构件的疲劳破坏, 严重时甚至可造成不可估量的安全事故.
在学术界, 输流管道出现失稳时的流速值被称为临界流速. 近年来, 人们通过对临界流速的调节已成为输流管动力学控制研究的一个重要内容; 此外, 还有学者采用各种控制方法来降低管道振动幅值, 从而达到降低管道破裂或疲劳损伤等风险[8 -15 ] .
输流管振动控制方法主要包括主动和被动两种.主动控制方法通常借助外界能量的输入来实现对输流管系统的实时控制, 从理论上来看具有较好的控制效果[16 -18 ] . 例如, Abbasnejad等[19 ] 研究了含有轴向分布压电层的微流体管道的稳定性, 同时还探讨了支撑边界对稳定性的影响, 其研究结果表明: 通过对压电层施加电压差, 可显著抑制流体对管道振动频率的影响, 从而扩大了稳定性区域.Ge等[20 ] 通过对管道施加一个与时间相关的位移函数, 采用自适应边界控制技术对欧拉-伯努利梁进行振动抑制, 验证了该控制方法的有效性.Szmidt等[21 ] 利用在悬臂管道上安装电磁装置的方式, 使得运动中的电板在切割磁感线过程中产生阻力, 以此来提高悬臂输流管的动态稳定性, 也得到了较好的控制效果.
相比于主动控制, 被动控制方式因其结构简单、不需要外界能量输入, 且具有一定的鲁棒性等特点, 在工程实践中得到广泛应用.输流管被动控制的方法有很多, 比如动力减振器法[22 -23 ] 、阻尼器法[24 -25 ] 、非线性能量汇法[26 -27 ] 等.Zhou等[28 ] 通过在悬臂管道上安装非线性能量汇对管道振动进行控制, 分析了不同能量汇参数对提高悬臂管道临界流速的影响. Gourdon等[29 ] 通过实验方法验证了不同类型激励下非线性能量汇的减振效果, 其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果. Li等[30 ] 提出了一种冲击式调谐质量阻尼器(PTMD), 通过质量块与黏弹性材料的碰撞方式来耗散振动能量, 发现这种新型阻尼器可有效的控制振动.
近年来, 有学者提出了将惯容器应用到结构的振动控制问题之中, 获得了较好的被动控制效果[31 -36 ] .惯容器相比于传统的质量块而言体积更小. 对于相同质量的惯容器和普通质量块, 惯容器能提供更大的惯性效应, 它产生的惯性力与其两自由端的加速度之差成正比关系, 这使得惯容器方式已在多个工程实践中得到了应用. Shi等[37 ] 研究了在拉索一端安装接地惯性阻尼器, 探讨了惯性系数和阻尼系数对拉索振动响应的影响规律, 并由此提出一种优化后的最佳惯性阻尼器设计方法.陈杰等[38 ] 借助含有惯容器和负刚度的动力减振器对结构进行振动控制, 发现相比于传统的动力减振器, 这种新型减振器在抑制梁的横向振动时更加有效.综合已有研究报道来看, 现有研究工作已将惯容器用于单自由度和多自由度结构的振动控制之中, 但这类减振器对非保守的悬臂输流管系统是否有控制效果, 目前还未可知.
本文针对悬臂输流管系统, 试图通过安装带有接地惯容器的减振器, 探究惯容器对悬臂管临界流速和动力学响应的影响. 该惯容器既可产生惯性力, 还引入了线性刚度、非线性刚度和阻尼等因素. 首先, 通过Hamilton原理, 给出了带有接地惯容器非保守输流管系统的控制方程; 然后, 借助数值方法进行求解, 验证此控制方法的有效性; 最后, 通过典型算例分析, 得到不同参数取值下惯容器对悬臂输流管道的控制效果.
1 理论模型
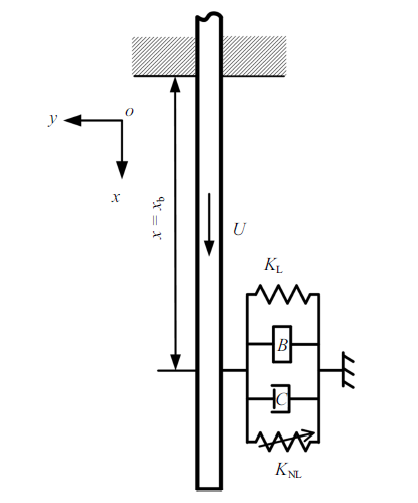
本文设计的减振器结构由线性弹簧、阻尼器、惯容器和非线性弹簧并联组成, 安装在悬臂管道$x=x_b$处, 减振器的另一端连接在地面, 如图1 所示.记悬臂管道沿$y$轴的横向位移用$y(s, t)$表示, 它是管轴线曲线坐标$s$和时间$t$的函数.为方便研究, 忽略管道的转动惯量和剪切变形; 假设管内流速恒定不变;管道中心线不可伸长; 管道可发生较大横向变形, 但应变较小.
图1
图1
带有惯容减振装置的悬臂输流管示意图
Fig.1
Schematic diagram of a cantilever pipe with an inerter-based absorber
基于以上假设, 引入广义的Hamilton原理[4 ]
(1) $ \Delta \int_{t_{1} }^{t_{2} } {(T_tot -V_tot )} dt+\int_{t_{1}}^{t_{2} } {\Delta W} dt = \\ \int_{t_{1} }^{t_{2} } {\left[ {MU\left( {{\partial { r}_L/\partial t} +U{ \tau }_L } \right)\cdot \Delta { r}_L }\right]} dt$
其中$T_tot$和$V_tot$分别表示悬臂管道系统的总动能与总势能, $\Delta W$表示非保守力所做的虚功;式(1)中等式右边项代表流体从管道自由端流出时所做的虚功, $ r_L$和 $\tau_L$分别表示管道末端的位置矢量和切线矢量.式(1)中系统的动能、势能与非有势力做功项的详细表达式可见附录, 由该式可推导得出带有惯容减振器的悬臂管运动微分方程为
(2) $\begin{align} (m+M)\ddot{{y}}+2MU\dot{{y}}'\left( {1+{y'}^{2}} \right)+E^{\ast }I\dot{y}"" + \\ (m+M)g{y}'(1+\dfrac{1}{2}{y'}^{2})+{y}"\bigg[ MU^{2}\left( {1+{y'}^{2}} \right)- \\ (m+M)g(L-s)\bigg(1+\dfrac{3}{2}{y'}^{2}\bigg) \bigg] + \\ {y}'\int_0^s (m+M) \left( {\dot{y}}^{\prime2}+{y}'{\ddot{{y}}}' \right)ds + \\ EI\bigg[ y""\left( {1+{y'}^{2}} \right)+4{y}'{y}"{y}"'+{y"}^{3} \bigg] - \\ {y}"\bigg[ \int_s^L {\int_0^s {(m+M)} } \left( {{\dot{{y}}}^{\prime2}+{y}'{\ddot{{y}}}'} \right)dsds + \\ \int_s^L {\left( {2MU{y}'{\dot{{y}}}'+MU^{2}{y}'{y}"} \right)} ds \bigg] + \\ \left( {B\ddot{{y}}+C\dot{{y}}+K_L y+K_NL y^{3}} \right)\Delta \left( {s-s_b } \right)=0 \end{align}$
其中, $L$为悬臂管道长度, $m$为单位长度的管道质量, $M$为单位长度的流体质量, $U$为管道内流体的速度, $EI$为管道的抗弯刚度, $E^{\ast }$为Kelvin-Voigt阻尼系数, $g$为重力加速度, $K_L$和$K_NL$分别为线性和非线性弹簧刚度系数, $B$和$C$分别为惯容系数和阻尼系数, $(\prime)$和$(\cdot)$分别表示对曲线坐标$s$和时间$t$的一阶偏导, $\Delta (s)$为Dirac delta函数.
为方便分析, 得到更有普遍性的结论, 引入下列无量纲参数
(3) $\left.\begin{array}{l} \xi =\dfrac{s}{L}, \ \ \eta =\dfrac{y}{L}, \ \ \tau =\sqrt {\dfrac{EI}{m+M}}\dfrac{t}{L^{2}}\\ u=\sqrt{\dfrac{M}{EI}} UL, \ \ \alpha =\sqrt{\dfrac{I}{E(M+m)}}\dfrac{E^{\ast }}{L^{2}} \\ \beta =\dfrac{M}{m+M}, \ \ b_f =\dfrac{B}{(m+M)L}, \ \ \gamma =\dfrac{m+M}{EI}L^{3}g \\ c_f =\dfrac{CL}{\sqrt {EI(M+m)} }, \ \ k_l =\dfrac{K_L L^{3}}{EI}, \ \ k_n =\dfrac{K_NL L^{5}}{EI} \\ \end{array} \right\}$
将式(3)代入运动微分方程(2)中得到无量纲化后的控制方程为
(4) $\begin{align} \alpha \dot{\eta} ""+\eta ""+\ddot{{\eta }}++\gamma {\eta}'\bigg(1+\dfrac{1}{2}{\eta }^{\prime2}\bigg) + \\ {\eta }"\bigg[ u^{2}\left( {1+{\eta }^{\prime2}} \right)-\gamma (1-\xi )\bigg(1+\dfrac{3}{2}{\eta }^{\prime2}\bigg)\bigg] + \\ \eta ""{\eta }^{\prime2}+4{\eta }'{\eta }"{\eta }"'+{\eta }^{\prime\prime3} + \\ 2u\sqrt \beta {\dot{{\eta }}}'\left( {1+{\eta }^{\prime2}} \right)+{\eta }'\int_0^\xi {\left( {{\dot{{\eta }}}^{\prime2}+{\eta }'{\ddot{{\eta }}}'} \right)} d\xi - \\ {\eta }"\Bigg[ \int_\xi^1 \int_0^\xi \left( {{\dot{{\eta }}}^{\prime2}+{\eta }'{\ddot{{\eta }}}'} \right) d\xi d\xi + \\ \int_\xi^1 {\left( {2u\sqrt \beta {\eta }'{\dot{{\eta }}}'+u^{2}{\eta }'{\eta }"} \right)} d\xi \Bigg] + \\ \left( {b_f \ddot{{\eta }}+c_f \dot{{\eta }}+k_l \eta +k_n \eta ^{3}} \right)\Delta \left( {\xi -\xi_b } \right)=0 \end{align}$
2 Galerkin法离散化
借助Galerkin方法对方程(4)进行离散化, 取悬臂梁的前$N$阶模态函数进行截断近似, 此时管道横向位移可写为
(5) $\eta (\xi , \tau )=\sum\limits_{r=1}^N {\varphi_{r} } (\xi )q_{r} (\tau)={ \varphi q}$
其中, $\varphi_r(\xi)$是悬臂梁无量纲化的模态函数, $q_r(\tau)$是相应离散系统的广义坐标, $\varphi=[\varphi_1, \varphi_2, \cdots , \varphi_N]$和$ q = [q_1, q_2, \cdots , q_N]^T$分别为特征函数和广义坐标向量.将式(5)代入无量纲方程(4)中, 利用模态函数的正交性, 在整个等式同时左乘$ \varphi^T$并在区间[0 , 1 ] 上积分后可得
(6) $\begin{align} \left( {{ M}_L +{ M}_NL } \right)\ddot{{ q}}+\left( {{ C}_L +{ C}_NL } \right)\dot{{ q}}+\left( {{ K}_L +{ K}_NL } \right){ q} + \\ { \varphi }^{T}\left( {\xi_d } \right)\Big\{ b_f { \varphi }\left( {\xi_d } \right){\ddot{{ q}}}+c_f { \varphi }\left( {\xi_d } \right){\dot{{ q}}}+k_l { \varphi }\left( {\xi _d } \right){ q} + \\ k_n \left[ {{ \varphi }\left( {\xi_d } \right){ q}} \right]^{3} \Big\} =0 \end{align}$
其中, $ M_L$和$ M_NL$为质量矩阵, $ C_L$和$ C_NL$为阻尼矩阵, $ K_L$和$ K_NL$为刚度矩阵, 下标L和NL分别表示线性和非线性项;质量、阻尼和刚度矩阵的维数均为$N\times N$; $\dot{ q}=(\dot{q}_1, \dot{q}_2, \cdots , \dot{q}_N, )^T$和$\ddot{ q}=(\ddot{q}_1, \ddot{q}_2, \cdots , \ddot{q}_N, )^T$分别为管道离散系统所对应的广义坐标速度和广义坐标加速度, 均为$N\times 1$的向量.
(7) $\eta (0, \tau )={\eta }'(0, \tau )={\eta }"(1, \tau )={\eta }"'(1, \tau )=0$
(8) $q(0)=\{0.001, 0, 0, 0\}^T, \dot{{ q}}(0)=\{0, 0, 0, 0\}^T$
借助四阶龙格库塔方法对非线性常微分方程组(6)进行数值求解, 可以得到输流管系统的非线性动力学响应.
3 算法验证
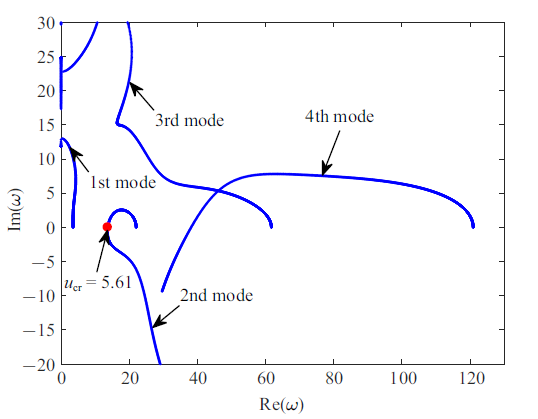
为验证本文算法的有效性, 本节首先给出了无减振器作用的悬臂管道前四阶无量纲复频率随流速变化的Argand图, 如图2 所示. 为确定该悬臂管道系统的临界流速, 可将方程(6)线性化后得到如下形式的线性齐次方程组
(9) ${ M\ddot{{ q}}}+{ C\dot{{ q}}}+{ K q}=0$
图2
图2
无减振装置的悬臂输流管的Argand图
Fig.2
Argand diagram of the cantilevered pipe without vibration absorber
(10) ${ M}={ M}_L +b_f { \varphi }^T\left( {\xi_d }\right){ \varphi }\left( {\xi_d } \right)$
(11) ${ C}={ C}_L +c_f { \varphi }^T\left( {\xi_d } \right){ \varphi }\left( {\xi_d } \right)$
(12) ${ K}={ K}_L +k_l { \varphi }^T\left( {\xi_d } \right){ \varphi }\left( {\xi_d } \right)$
为了与Paidoussis[1 ] 的经典结果进行对比, 取参数$\alpha =0$, $\beta =0.2$和$\gamma =0$. 记方程(6)的特征值$\lambda =i\omega $, 则实部Re($\omega$ )表示无量纲化的振动频率, Im($\omega$ )表征了系统的阻尼.从图2 可知, 随着管内流体速度的不断增大, 第二阶模态阻尼从正值变为负值, 这表明系统可以从流体中吸收能量, 同时将能量传送给管道, 此时系统会发生颤振失稳, 管道因此而出现周期振动现象. 从图2 还可看出, 悬臂管第二阶模态发生颤振失稳的临界流速约为$u_cr=5.61$. 随着流速的不断增大, 悬臂管的特征值演化曲线与文献[1 ]的经典结果是一致的, 从而验证了本文方法所获得解答是可靠的.
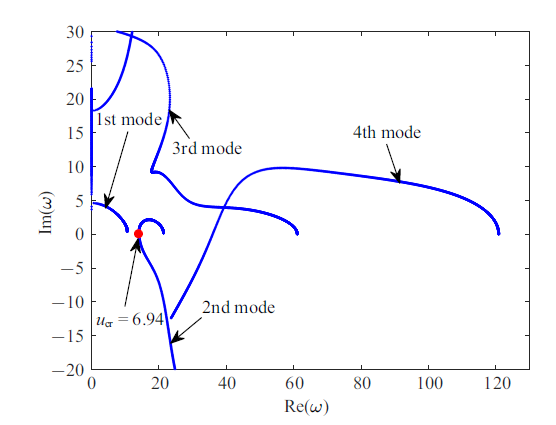
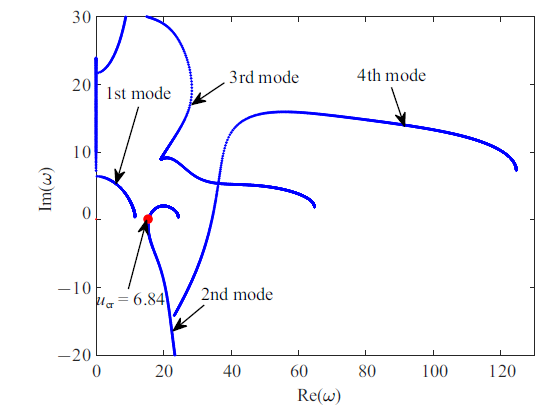
若将惯容减振器安装在悬臂管道$\xi_b=0.9$位置, 且减振器各参数分别取值为$b_f=0.2$, $c_f=0.5$, $k_l=60$和$k_n=8 000$, 管道的3个关键参数仍取为$\alpha=0$, $\beta =0.2$和$\gamma =0$, 可得到如图3 所示的Argand图. 从该图可以看到, 引入减振器后的悬臂管道的临界流速从5.61增大到6.94, 且仍然是第二阶模态率先发生失稳, 这显示本文所提出的减振装置能提高管道系统的稳定性. 接下来, 本文将进一步探讨减振器各参数对系统稳定性及非线性动力学行为的影响.
图3
图3
含减振装置的悬臂输流管的Argand图
Fig.3
Argand diagram of the cantilevered pipe with vibration absorber
4 稳定性分析
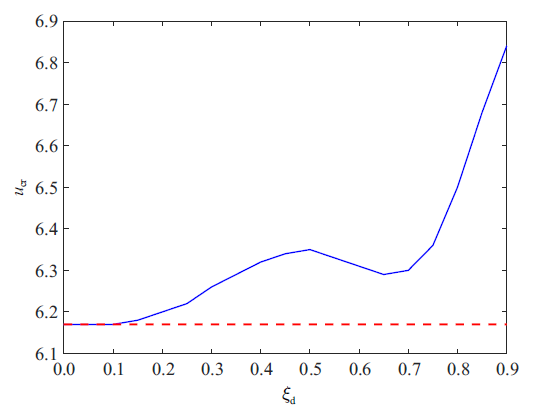
本节主要对带有减振器的悬臂管稳定性进行分析, 考查不同减振器参数下管道的临界流速的变化. 从式(10) $\sim\!$式(12)可以看出, 减振器的线性弹簧刚度、阻尼系数、惯容系数和安装位置都可能对悬臂管的稳定性产生影响. 首先, 研究不同安装位置对临界流速的影响, 取计算参数为$\alpha =0.001$, $\beta =0.142$, $\gamma =18.9$, $b_f=0.2$, $c_f=0.5$和$k_l=60$, 得到减振器安装在不同位置时临界流速的变化曲线, 如图4 所示. 从该图可以看出, 当$\xi_b=0$时相当于没有减振器作用, 此时临界流速$u_cr=6.17$. 随着安装位置坐标$\xi_b$的增大, 临界流速除端部外也都相对有所增大. 在安装位置坐标$\xi_b$小于0.5时, 临界流速不断增大; 当$\xi_ b$在0.5 $\sim$ 0.65之间临界流速有所减小, 但相比无减振器时还是有所增大; 随着安装距离的不断增大, 系统的临界流速出现明显增大, 且大约在$\xi_b=0.9$处取得最大值, 此时$u_cr=6.84$, 其对应的Argand如图5 所示. 由此可见, 在安装减振器时适当接近端部位置安装能显著提高管道系统的临界流速, 这同时也说明不同的安装位置对系统临界流速有较大影响.
图4
图4
临界流速随减振器安装位置变化曲线
Fig.4
Variation curve of the critical flow velocity with vibration absorber installation position
图5
图5
安装位置在$\xi_b=0.9$时系统的Argand图
Fig.5
Argand diagram for the pipe system when the installation position is $\xi_b=0.9$
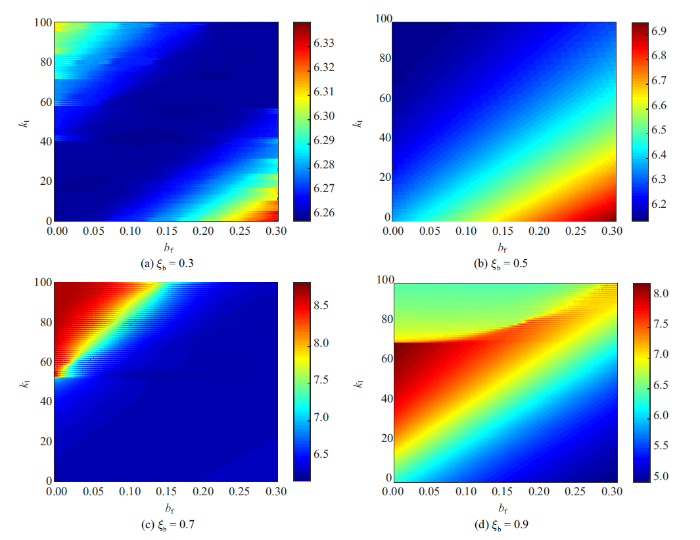
改变减振器的惯性系数和线性弹簧刚度, 得到系统的临界流速变化云图如图6 所示, 显示了临界流速的逐渐演化过程. 从图6 (a)中可以看出, 在安装位置$\xi_b=0.3$处, 当线性弹簧刚度较小时, 系统的临界流速随着惯容系数的增大而增大; 但当弹簧刚度较大时, 随着惯容系数的增大, 系统临界流速有所减小. 可见不同的线性弹簧刚度会使得惯容系数对管道系统临界流速有不同的影响效果. 当减振器安装位置在$\xi_b=0.5$时, 从图6 (b)可以看出系统的临界流速随着惯容系数的增大而增大, 但是增大弹簧刚度反而会对系统的稳定性产生消极效果, 即降低临界流速. 图6 (c)中的结果显示, 当$\xi_b=0.7$时, 随着惯容系数的增大, 系统的临界流速有所减小; 与此同时, 线性弹簧刚度越大, 则系统的临界流速越大, 故其对系统的稳定性有正面作用, 在弹簧刚度在55 $\sim$ 100区间时效果更明显. 当安装位置$\xi_b=0.9$时, 从图6 (d)可以看出随着弹簧刚度的增大, 管道系统的临界流速先有所增大, 但当弹簧刚度继续增大后临界流速有所减小, 同时临界流速随着惯性系数的增大而减小.
图6
图6
管道无量纲临界流速随惯容系数和线性弹簧系数变化云图
Fig.6
Contour maps of the dimensionless critical flow velocity for the pipe changing with the inertia coefficient and linear spring coefficient
5 收敛性分析
在进行非线性动力学分析之前, 有必要对Galerkin法的模态截断问题进行收敛性分析, 从而确定合适的模态截断数$N$.
选取管道参数$\alpha =0.001$, $\beta =0.142$和$\gamma =18.9$, 将减振器安装在管道$\xi_b=0.5$位置处, 减振器各元件参数分别取为$b_f=0.3$, $c_f=0.5$, $k_l=60$及$k_n=8000$.
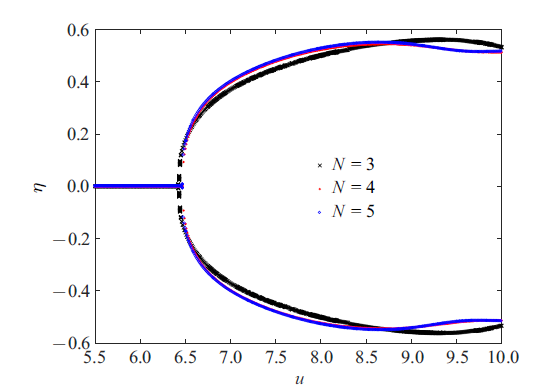
Galerkin法的模态截断数$N$分别取为3, 4和5, 得到3种取值下管道自由端响应位移幅值的分岔图, 如图7 所示. 该分岔图的取点规则为: 对某一给定的流速, 当管道运动达到稳态后开始取点; 每当管道自由端运动速度为0时, 记录该时刻管道端点处的位移数据, 以此来得到管道端点位移幅值随流速变化的分岔图. 从图7 可以看出: 当$N=3$时, 管道响应的分岔图与$N=4$或5时的相差较大; 当$N$取为4和5时, 管道响应的分岔图差异很小, 因此可认为当$N$取4时就已达到收敛. 为减小计算量, 在接下来的分析中, 选取$N=4$进行计算.
图7
图7
不同$N$时管道端部位移幅值随流速变化的分岔图
Fig.7
Bifurcation diagram for the displacement amplitude of the pipe end with various flow velocities, for different $N$
6 非线性分析
本节研究不同流速下带有减振器的悬臂输流管道的非线性动力学行为. 首先, 讨论当减振器安装位置在$\xi_b=0.5$和$\xi _b=0.9$时惯容系数$b_f$对管道动态响应的影响. 分别选取$b_f=0.1$, 0.2和0.3, 同时固定减振器其余各参数为$c_f=0.5$, $k_l=60$及$k_n=8000$, 且管道的3个主要参数取值为$\alpha =0.001$, $\beta =0.142$, $\gamma =18.9$. 这些参数取值都是无量纲的, 这可使得后续的计算结果更具有普遍意义.
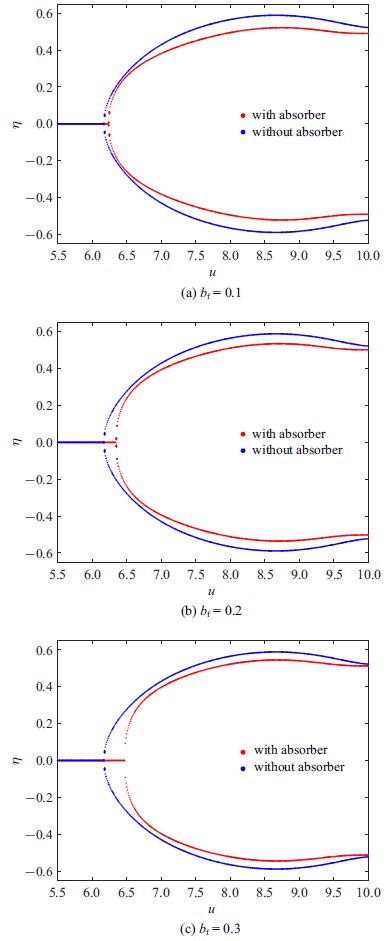
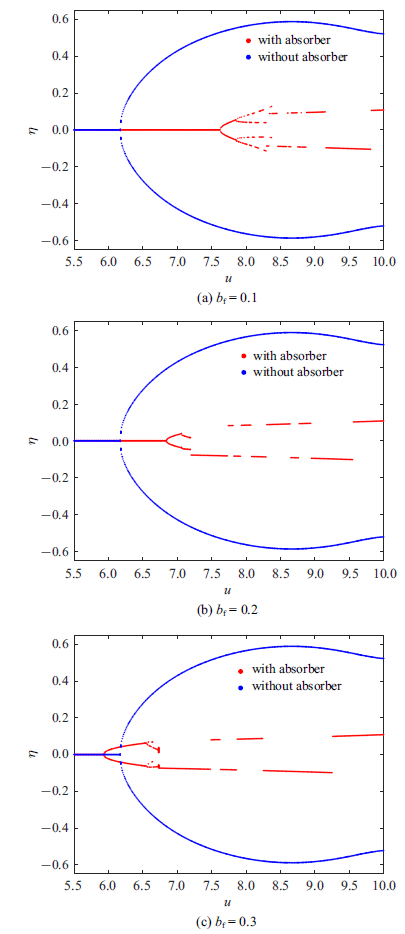
图8 和图9 分别给出了安装位置$\xi_b=0.5$和$\xi_b=0.9$时不同流速下管道端部($\xi =1$)的位移响应幅值, 展示了管道系统在无减振器和有减振器时管道端部位移幅值随流速变化的分岔图. 从图8 (a)中可以看出, 当惯容系数$b_f=0.1$时, 管道的临界流速略有增高, 管道振动的振幅有所减小. 随着惯容系数的增大, 如图8 (b)和图8 (c)所示, 管道系统的临界流速也会增高, 同时管道振幅相较无减振器时也有所减小, 这说明减振器对提高系统的稳定性有一定作用.
图8
图8
$\xi_b=0.5$时不同惯容系数下管道端部位移幅值随流速变化的分岔图
Fig.8
Bifurcation diagrams for the displacement amplitude of the pipe end with various flow velocities under different coefficients of inertia when $\xi_b=0.5$
图9
图9
$\xi_b=0.9$时不同惯容系数下管道端部位移幅值随流速变化的分岔图
Fig.9
Bifurcation diagrams for the displacement amplitude of the pipe end with various flow velocities under different coefficients of inertia when $\xi_b=0.9$
图9 为安装位置在$\xi_b=0.9$时的分岔图, 当惯容系数$b_f=0.1$时, 管道系统的临界流速有明显增大, 当管道失稳振动后, 管道振幅也被控制在小范围内振动, 可以看出此时减振器的振动抑制效果比较显著. 但是随着惯容系数的不断增大, 如图9 (b)和图9 (c)所示, 管道的临界流速却有所减小. 对于安装位置在$\xi_b=0.5$和$\xi _b=0.9$时惯容系数对系统稳定性的不同影响, 这说明惯容系数的增大对管道临界流速有积极作用, 但却无法在所有位置产生正面的控制效果.
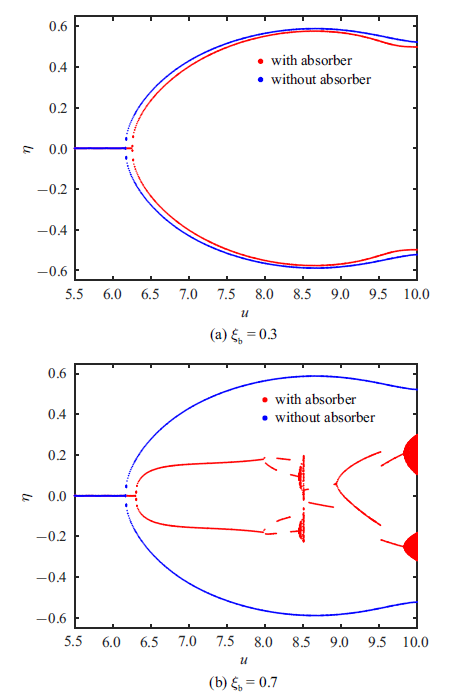
接下来, 研究安装位置对管道非线性动力学行为的影响. 为此, 安装位置$\xi _b$分别取为0.3, 0.5, 0.7和0.9, 通过非线性计算得到不同流速下管道端部处的振动位移. 数值计算时, 取各系统参数值为$b_f=0.2$, $c_f=0.5$, $k_l=60$和$k_n=8000$. 从图10 (a)可以看出, 当$\xi_b=0.3$时, 减振器对管道振动响应幅值的影响较小, 此时临界流速略有提高. 关于这一点, 从图4 中给出的临界流速变化曲线也可得到进一步的理解: 当减振器安装位置距固定端较近时, 减振器对系统的稳定性几乎没有影响. 当$\xi_b$增大到0.5时, 从图8 (b)可以看到, 含减振器悬臂管道出现Hopf分岔的临界流速变大, 同时减振器使管道系统的振幅也有所减小. 随着安装位置增大至$\xi _b=0.7$时, 从图10 (b)可以看出, 临界流速相比无减振器控制时有所增大, 当管道失稳后, 减振器的安装对管道振动控制效果显著, 明显减小了管道振动幅值. 值得注意的是, 当流速在[8.51, 8.9]范围变化时, 管道可发生黏附现象, 即管道只出现静态变形. 当流速继续增大时, 管道振动行为可能比较复杂, 分岔图中表现处较强的非线性特征, 管道还出现了复杂的混沌运动现象. 当$\xi _b=0.9$时, 如图9 (b)所示, 可以看出临界流速显著增大, 同时管道发生黏附现象的流速范围变大, 整个流速区间内减振器对管道振动的抑制作用都较为显著.
图10
图10
减振器在不同位置时管道端部位移随流速变化的分岔图
Fig.10
Bifurcation diagrams for the displacement amplitude of the pipe end with various flow velocities when the absorber is placed at different positions
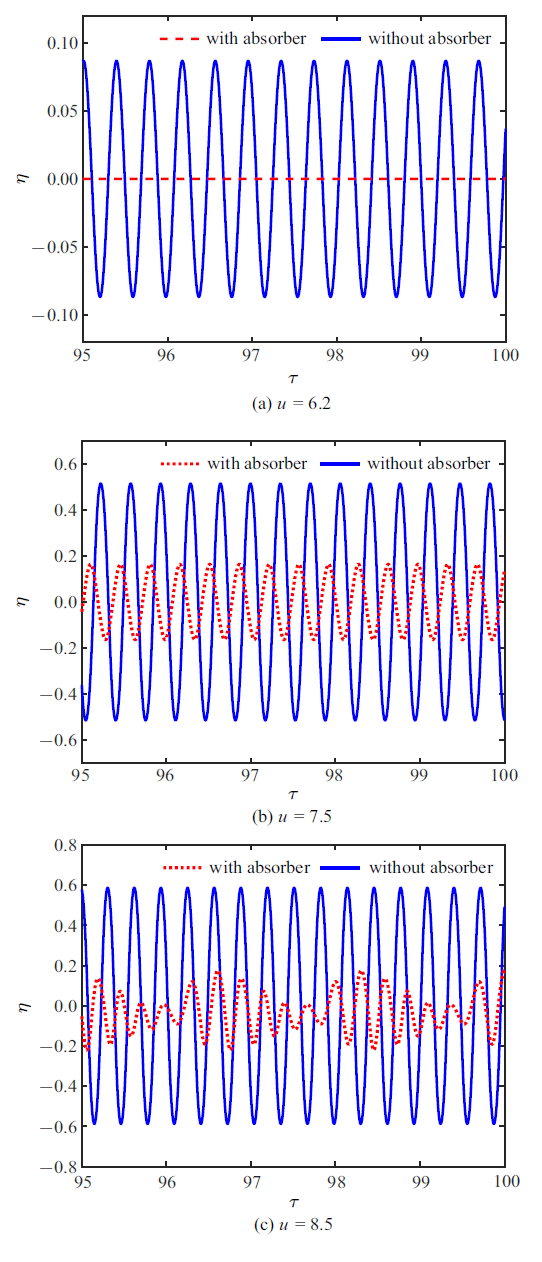
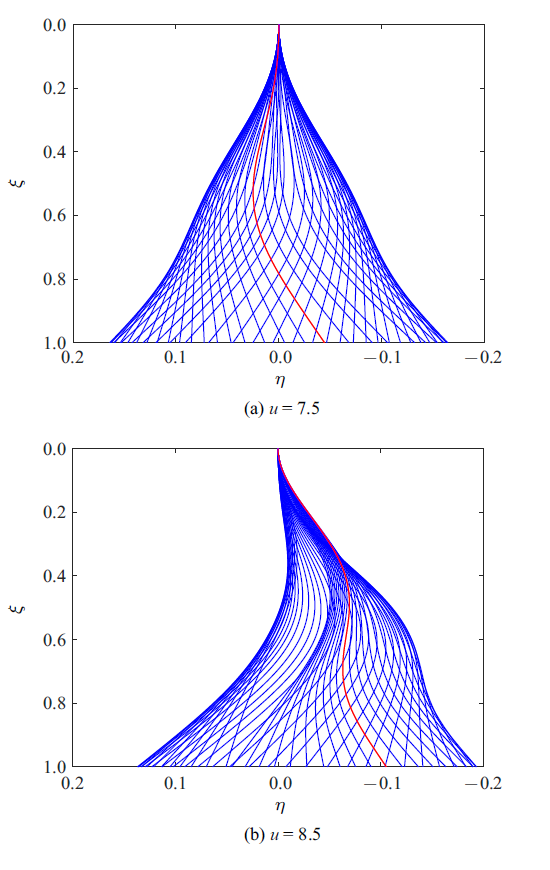
为了进一步理解$\xi_b=0.7$时减振器对管道动态响应的影响规律, 图11 给出了3种流速下管道中点位移随时间变化的历程曲线. 由该图可以看出, 当流速$u=6.2$时, 没有安装减振器的管发产生了周期振动, 而有减振器的管道却没有发生振动, 这说明此时减振器提高了管道系统的稳定性. 如图11 (b)所示, 当流速$u=7.5$时, 带有减振器和无减振器的管道在内部流体的激励下都发生了周期振动, 但有减振器的管道振动响应振幅相对较小, 这说明减振器对管道的振动幅值有抑制作用. 图12 (a)显示了$u=7.5$时带有减振器管道在不同时刻的振动形态, 其中虚线代表该流速下某一时刻的管道振动形状, 可以看到管道形态主要以第一阶模态和第二阶模态形状的成分为主. 当管道流速增大到8.5时, 从图11 (c)可以看到, 减振器能将管道振幅控制到较小幅值, 而且从图12 (b)还可看到管道的振动形态有更高阶模态参与振动的迹象.
图11
图11
$\xi_b=0.7$时端部位移随时间变化曲线
Fig.11
Displacements of the pipe end versus time when $\xi_b=0.7$
图12
图12
$\xi_b=0.7$时管道振动的实时形态图
Fig.12
Oscillation shapes of the pipe for $\xi_b=0.7$
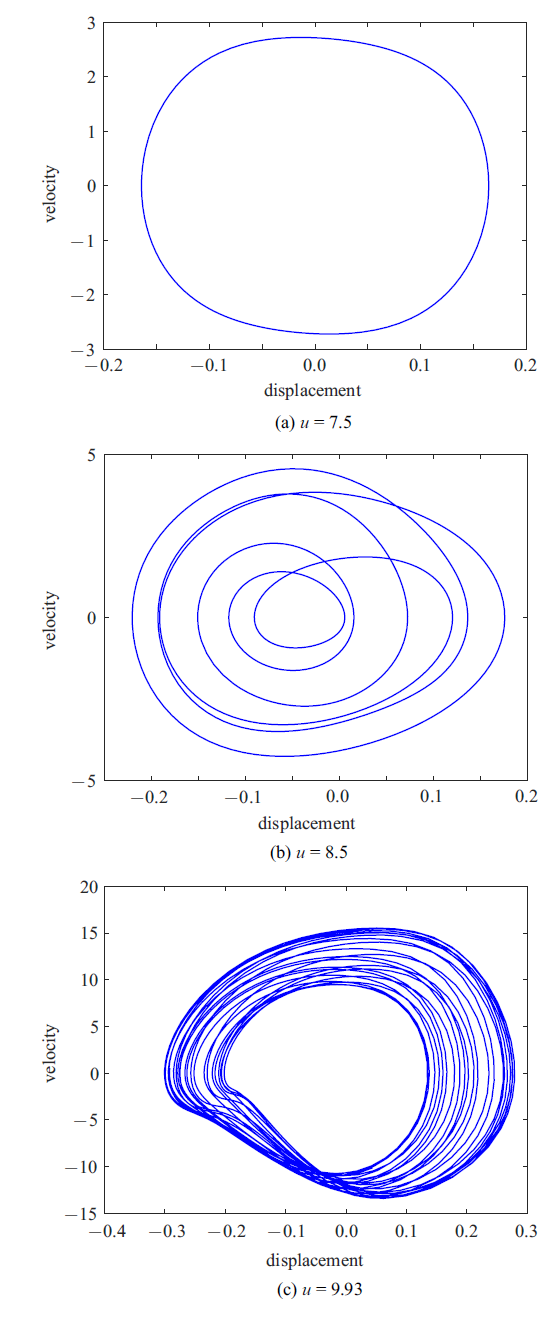
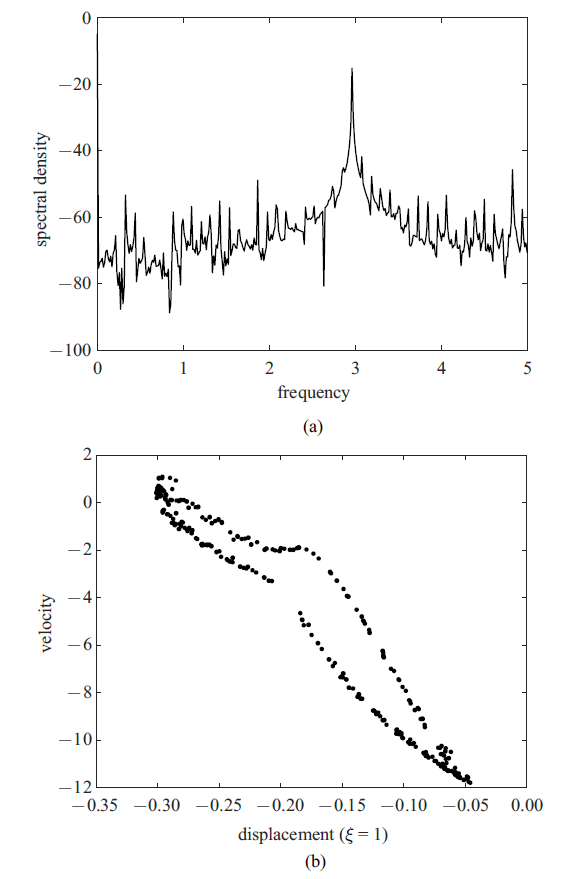
在图10 的分岔图中, 曾注意到当安装位置$\xi_b$从0.3增大至0.7的过程中, 管道还可能诱发出混沌运动行为. 图13 描述的是当减振器安装位置在$\xi _b=0.7$时管道内流速分别为7.5, 8.5和9.93时管道端部处的振动相图曲线, 该图中的横坐标和纵坐标分别表示管道中点处的振动位移和速度. 由图13 可知, 当管内流速$u=7.5$时, 管道表现为简单的周期运动. 随着流速的不断增大至8.5时, 管道呈现倍周期运动. 当流速继续增大至9.93时, 管道自由端振动的相轨迹如图13 (c)所示. 为更清晰地判断其运动状态, 图14 给出了此时管道响应位移的功率谱图和庞加莱映射图, 可发现此时管道振动呈混沌状态, 这种混沌响应行为是由于系统的各种非线性因素产生的.
图13
图13
$\xi_b=0.7$时不同流速下管道端部的相轨迹图
Fig.13
Phase portraits of the pipe end under different flow velocities when $\xi_b=0.7$
图14
图14
在$\xi _b=0.7$下流速为9.93时管道响应的(a)功率谱图和(b)庞加莱映射图
Fig.14
Responses of the pipe end when the flow velocity is 9.93 with $\xi _b=0.7$: (a) Power spectra diagram and (b) Poincare map
7 结论
本文基于哈密顿原理引入了含有接地惯容减振器的悬臂输流管的振动控制模型, 得到了非保守悬臂管道系统的非线性运动控制方程.通过Galerkin方法对控制方程进行离散化处理, 并借助数值求解方法对含减振器悬臂管道系统的稳定性和非线性动力学行为进行了分析, 探讨了不同参数下减振器在悬臂输流管振动控制中的应用效果. 特别地, 利用线性分析, 探究了惯容系数、线性弹簧刚度和减振器安装位置对管道发生颤振失稳时临界流速的影响.利用非线性分析, 还探讨了减振器对管道非线性动态行为的影响规律, 揭示了含有接地惯容减振器悬臂管的周期和混沌运动等动力学行为.
对于未安装减振器的悬臂管道, 当管内流速超过某一临界流值时, 系统会因颤振而失去稳定性. 当安装减振器后, 通过调节减振器位置等参数取值, 管道的颤振失稳临界流速可以得到明显的增大. 通过线性分析发现, 惯性系数和线性刚度对管道稳定性的影响与减振器安装位置不同而有不同的作用效果.还应指出的是, 通过非线性分析发现:减振器对管道振幅的抑制效果与流速取值和减振器安装位置密切相关.在不同的流速区间, 减振器不仅会使得系统的稳定性得到较大提高, 还会在较大流速时会改变管道的动态响应特征, 例如产生倍周期和混沌运动等.总体而言, 减振器在接近管道端部位置时能使得管道系统产生较大的临界流速, 在中高流速区间取值时对管道振幅有较好的抑制作用.
附录
为了应用广义Hamilton原理, 本附录给出含接地惯容器悬臂管道系统的动能、势能及非有势力做功项的具体表达式.
取悬臂管道上任意一点进行研究. 管道变形时该点的位置矢量和切向矢量可分别用$ r$和 $\tau $表示[1 ]
${ \tau }=\dfrac{\partial { r}}{\partial s}=\dfrac{\partial x}{\partial s}{ i}+\dfrac{\partial y}{\partial s}{ j}$
$T_tot =T_p +T_f=\dfrac{1}{2}m\int_0^L {{ v}_p^{2} }ds+\dfrac{1}{2}M\int_0^L {{ v}_f^{2} } ds$
其中, $ v_p$和$ v_f$分别表示管道和流体的运动速度, 可写为如下形式[1 ]
${ v}_p =\dfrac{\partial { r}}{\partial t}=\dot{{x}}{ i}+\dot{{y}}{ j}$
${ v}_f ={ v}_p +U{ \tau }=\left( {\dot{{x}}+U{x}'} \right){ i}+\left( {\dot{{y}}+U{y}'} \right){ j}$
系统总势能包括管道的应变能、管内流体的重力势能和减振器的弹簧势能, 可写成
$V_tot =V_p +V_g +V_k= \\ \dfrac{1}{2}EI\int_0^L {\kappa^{2}} ds-(m+M)g\int_0^L x ds+ \\ \dfrac{1}{2}K_L y(s_d , t)^{2}+\dfrac{1}{4}K_NL y(s_d , t)^{4}$
$\kappa =\dfrac{\partial ^{2}z/\partial s^{2}}{\sqrt {1-(\partial z/\partial s)^{2}} }$
为管道轴线的曲率, $y(s_d, t)$表示管道在减振器安装位置处的横向位移.
系统非有势力做功包括阻尼器和惯容器所做功, 可写成
$W=W_C +W_B=-\int_0^{y(s_d , t)} {C\dot{{y}}} (s_d , t)dy(s_d , t)- \\ \int_0^{y(s_d , t)} {B\ddot{{y}}} (s_d , t)dy(s_d , t)$
参考文献
View Option
[1]
Paidoussis MP . Fluid-structure interactions: Slender Structures and Axial Flow(Vol.1). 2 ed. San Diego: Elsevier Academic Press , 2014
[本文引用: 7]
[2]
Wadham-Gagnon M Paidoussis MP Semler C . Dynamics of cantilevered pipes conveying fluid. Part 1: Nonlinear equations of three-dimensional motion
Journal of Fluids Structures 2007 , 23 (4 ): 545 -567
DOI
URL
[3]
王乙坤 , 王琳 . 分布式运动约束下悬臂输液管的参数共振研究
力学学报 , 2019 , 51 (2 ): 558 -568
DOI
输液管道结构在航空、航天、机械、海洋、水利和核电等工程领域都有广泛应用,其稳定性、振动与安全评估备受关注.针对具有分布式运动约束悬臂输液管的非线性动力学模型,分别采用立方非线性弹簧和修正三线性弹簧来模拟运动约束的作用力,研究了管道在脉动内流激励下的参数共振行为.首先,从输液管系统的非线性控制方程出发,利用Galerkin方法进行离散化;然后,由Floquet理论得出线性系统在失稳前两个不同平均流速下脉动幅值和脉动频率变化时的共振参数区域;最后,考虑系统的几何非线性项和分布式非线性运动约束力的影响,求解了管道的非线性动力学响应,讨论了非线性项及运动约束力对管道参数共振行为的影响.研究结果表明,系统非线性共振响应的参数区域与线性系统的共振参数区域是一致的,分布式运动约束力对发生参数共振时管道的位移响应有显著影响;立方非线性弹簧和修正三线性弹簧模型所预测的分岔路径存有较大差异,但都可诱发管道在一定的参数激励下出现混沌运动.
(Wang Yikun Wang Lin . Parametricresonance of a cantilevered pipe conveying fluid subjected to distributed motion constraints
Chinese Journal of Theoretical and Applied Mechanics 2019 , 51 (2 ): 558 -568 (in Chinese))
[4]
Semler C Li GX Paidoussis MP . The non-linear equations of motion of pipes conveying fluid
Journal of Sound Vibration 1994 , 169 (5 ): 577 -599
DOI
URL
[本文引用: 1]
[5]
易浩然 , 周坤 , 代胡亮 等 . 含集中质量悬臂输流管的稳定性与模态演化特性研究
力学学报 , 2020 , 52 (6 ): 1800 -1810
DOI
本文主要研究通过调控集中质量对悬臂输流管稳定性和振动模态特性的影响规律,为输流管动力学性能的可控性提供理论指导和实验依据. 首先基于扩展的哈密顿原理,建立了含集中质量悬臂输流管的非线性动力学理论模型. 基于线性动力学特性分析,研究发现集中质量沿管道轴向位置变化对输流管发生颤振失稳的临界流速有重要影响.并通过伽辽金前四阶模态截断处理线性矩阵方程式,定性地分析了集中质量位置与质量比的变化对于输流管稳定性影响的变化.实验结果表明, 输流管的颤振失稳模态随集中质量位置的变化发生了转迁. 此外,基于动力学理论分析, 发现集中质量比值对失稳临界流速也有重要的影响,且主要取决于集中质量的安装位置. 基于非线性特性,进一步分析了集中质量对输流管振动幅值的影响. 实验和理论研究发现,集中质量位置从固定端向自由端变化时, 输流管振幅表现出先增大后减小趋势,且振动模态也从二阶转迁到三阶.本研究有望为输流管振动驱动应用提供理论支撑与指导意义.
(Yi Haoran Zhou Kun Dai Huliang , et al . Stability and mode evolution characteristics of a cantilevered fluid-conveying pipe attached with the lumped mass
Chinese Journal of Theoretical and Applied Mechanics 2020 , 52 (6 ): 1800 -1810 (in Chinese))
[6]
Peng G Xiong Y Gao Y , et al . Non-linear dynamics of a simply supported fluid-conveying pipe subjected to motion-limiting constraints: Two-dimensional analysis
Journal of Sound and Vibration 2018 , 435 : 192 -204
DOI
URL
[7]
金基铎 , 邹光胜 , 张宇飞 . 悬臂输流管道的运动分岔现象和混沌运动
力学学报 , 2002 , 34 (6 ): 863 -873
[本文引用: 1]
(Jin Jiduo Zhou Guangsheng Zhang Yufei , et al . Bifurcations and chaotic motions of a cantilevered pipe conveying fluid
Chinese Journal of Theoretical and Applied Mechanics 2002 , 34 (6 ): 863 -873 (in Chinese))
[本文引用: 1]
[8]
Dai HL Wang L . Dynamics and stability of magnetically actuated pipes conveying fluid
International Journal of Structural Stability and Dynamics 2016 , 16 (6 ): 1550026
DOI
URL
[本文引用: 1]
[9]
He W Meng T Huang D , et al . Adaptive boundary iterative learning control for an Euler-Bernoulli beam system with input constraint
IEEE Trans Neural Netw Learn Syst 2018 , 29 (5 ): 1539 -1549
DOI
URL
[10]
张登博 , 唐有绮 , 陈立群 . 非齐次边界条件下轴向运动梁的非线性振动
力学学报 , 2019 , 51 (1 ): 218 -227
DOI
轴向运动系统的横向非线性振动一直是国内外研究的热点课题之一.目前相关研究大都是针对齐次边界条件的.但是在工程实际中,非齐次边界条件更为常见,而针对非齐次边界条件的研究相对较少.为深入研究非齐次边界条件对轴向运动系统横向非线性振动的影响,本文以轴向变速运动黏弹性Euler梁为例,引入由黏弹性引起的非齐次边界条件,同时还引入由轴向加速度引起的径向变化张力,建立梁横向振动的积分-偏微分型运动方程,并导出了相应的非齐次边界条件.采用直接多尺度法分析了梁的次谐波参数共振.由可解性条件得到了梁的稳态响应,并根据Routh-Hurvitz判据确定了系统稳态响应的稳定性.通过数值例子讨论了黏弹性系数,轴向运动速度,轴向速度脉动幅值和非线性系数对幅频响应的影响,并详细对比分析了非齐次边界条件和齐次边界条件对幅频响应的影响.结果表明:随着黏弹性系数的增大,非齐次边界条件下的零解失稳区域和稳态响应幅值比齐次边界条件下的失稳区域和幅值大,非齐次边界条件对高阶次谐波参数共振的影响更加显著.最后,引入微分求积法来验证直接多尺度法的近似解结果.
(Zhang Dengbo Tang Youqi Chen Liqun . Nonlinear vibrations of axially moving beams with nonhomogeneous boundary conditions
Chinese Journal of Theoretical and Applied Mechanics 2019 , 51 (1 ): 218 -227 (in Chinese))
[11]
He W Nie S Meng T , et al . Modeling and vibration control for a moving beam with application in a drilling riser
IEEE Transactions on Control Systems Technology 2017 , 25 (3 ): 1036 -1043
DOI
URL
[12]
Liu ZY Wang L Dai HL , et al . Nonplanar vortex-induced vibrations of cantilevered pipes conveying fluid subjected to loose constraints
Ocean Engineering 2019 , 178 (APR.15 ): 1 -19
DOI
URL
[13]
顾伟 , 张博 , 丁虎 等 . 2:1内共振条件下变转速预变形叶片的非线性动力学响应
力学学报 , 2020 , 52 (4 ): 1131 -1142
DOI
在工程实际中,涡轮机叶片的转速在很多应用场景下不是一个定常值,比如发动机在启动、变速、停机等工况下,转子输入与输出功率失衡,伴随产生扭振,产生速度脉冲. 另外,由于服役环境、安装误差等因素会引起叶片在所难免的预变形. 本文主要研究预变形叶片,在变转速条件下的非线性动力学行为. 考虑叶片转速由一定常转速和一简谐变化的微小扰动叠加而成. 应用拉格朗日原理得到变转速叶片的动力学控制方程,并采用假设模态法将偏微分方程转为常微分方程,通过引入无量纲,使方程更具有一般性. 运用多尺度方法求解了该参激振动系统,得到了在 2:1 内共振情形下的平均方程,进而获得系统的稳态响应. 详细研究温度梯度、阻尼以及转速扰动幅值等系统参数对叶片动力学响应的影响规律,同时考察了立方项在 2:1 内共振下对方程的影响. 对原动力方程进行正向、反向扫频积分来观察其跳跃现象,并对解析解进行验证. 结果发现参数的变化对叶片均有不同程度影响,在 2:1 内共振下立方项对系统响应的影响很小,解析解与数值解吻合很好.
(Gu Wei Zhang Bo Ding Hu , et al . Nonlinear dynamic response of pre-deformed blade with variable rotational speed under 2:1 internal resonance
Chinese Journal of Theoretical and Applied Mechanics 2020 , 52 (4 ): 1131 -1142 (in Chinese))
[14]
Sazesh S Shams S . Vibration analysis of cantilever pipe conveying fluid under distributed random excitation
Journal of Fluids and Structures 2019 , 87 : 84 -101
DOI
In this study, vibration analysis of a cantilever pipe conveying fluid under distributed random excitation was performed using stochastic approach. The equation of motion was first discretized by means of the Galerkin method. Next, the classic flutter analysis of the pipe conveying fluid was performed in absence of random excitation. Then, the random load was taken into account as a white noise excitation. Spectral density of response and response variance were calculated versus the velocity of internal flow in the pipe. The velocity of the maximum of the response variance in case of white noise excitation was regarded as flutter speed. The effects of viscoelastic dissipation, mass ratio and damping ratio of surrounding environment were investigated for the pipe under random excitation and results showed a good agreement with other studies. The spectral density of response was used to obtain the flutter frequency. Random time history and probability density function were exploited to study the pipe's random behavior near the flutter speed. This novel approach for pipe conveying fluid was also used to investigate all possible flutter speeds. The results provided a better understanding of dynamical behavior of pipes conveying fluid under random excitation. (C) 2019 Elsevier Ltd.
[15]
张文勇 , 牛牧青 , 陈立群 . 含串联非线性能量汇的整星系统吸振效果研究
振动与冲击 , 2020 , 39 (21 ): 151 -155
[本文引用: 1]
(Zhang Wenyong Niu Muqing Chen Liqun . Vibration absorption effect of whole satellite system with series nonlinear energy sink
Journal of the Vibration and Shock 2020 , 39 (21 ): 151 -155 (in Chinese))
[本文引用: 1]
[16]
Yang Y Xu D Liu Q . Milling vibration attenuation by eddy current damping
The International Journal of Advanced Manufacturing Technology 2015 , 81 (1-4 ): 445 -454
DOI
URL
[本文引用: 1]
[17]
王在华 , 胡海岩 . 具有采样反馈的力控制系统稳定性
力学学报 , 2016 , 48 (6 ): 1372 -1381
DOI
基于计算机的数字采样控制对离散信号进行运算并向作动器提供控制输入,是当前的主流控制技术.数字采样控制系统是这样一类控制系统,其控制对象由微分方程(组)描述,而控制律由离散采样信号给出.以采样PD(proportional-derivative)反馈作用下的单自由度力控制系统为例,基于离散系统的稳定性分析方法,研究采样控制律对控制系统稳定性的影响.为了突出采样反馈的作用,将系统取为无刚度、无阻尼的最简单形式.不同于已有研究假设位移采样信号与速度采样信号相互同步,本文研究当位移采样信号与速度采样信号不同步时受控系统的稳定性,发现位移采样信号与速度采样信号的采样周期不同组合对受控系统在增益平面上的稳定性区域有重要影响.结果表明,对所关心的三种数字采样反馈控制律,当位移采样信号滞后于速度采样信号一个采样周期时,受控系统具有最大的稳定性区域且对相同的增益值可以有最好的稳定效果.论文对这种现象进行分析,给出了一种力学解释.
(Wang Zaihua Hu Haiyan . Stability of a force control system with sampled-data feedback
Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (6 ): 1372 -1381 (in Chinese))
[18]
Ji N Liu Z Liu J , et al . Vibration control for a nonlinear three-dimensional Euler-Bernoulli beam under input magnitude and rate constraints
Nonlinear Dynamics 2018 , 91 (4 ): 2551 -2570
DOI
URL
[本文引用: 1]
[19]
Abbasnejad B Shabani R Rezazadeh G . Stability analysis of a piezoelectrically actuated micro-pipe conveying fluid
Microfluidics and Nanofluidics 2015 , 19 (3 ): 577 -584
DOI
URL
[本文引用: 1]
[20]
Ge SS Zhang S He W . Vibration control of an Euler-Bernoulli beam under unknown spatiotemporally varying disturbance
International Journal of Control 2011 , 84 (5 ): 947 -960
DOI
URL
[本文引用: 1]
[21]
Szmidt T Pisarski D Konowrocki R . Semi-active stabilisation of a pipe conveying fluid using eddy-current dampers: State-feedback control design, experimental validation
Meccanica 2019 , 54 (6 ): 761 -777
DOI
URL
[本文引用: 1]
[22]
彭海波 , 申永军 , 杨绍普 . 一种含负刚度元件的新型动力吸振器的参数优化
力学学报 , 2015 , 47 (2 ): 320 -327
DOI
[本文引用: 1]
提出了一种含有负刚度弹簧元件的新型动力吸振器模型,对该模型的最优参数进行了详细研究. 通过拉氏变换得到了系统的解析解,发现该系统存在着两个固定点,利用固定点理论得到了动力吸振器的最优阻尼比和最优频率比. 进一步研究发现接地刚度取负值时能够得到更好的减振效果,根据负刚度的特性得到了在保证系统稳定情况下的最优负刚度比. 通过数值解与解析解的对比证明了解析解的正确性. 通过与两种已有的典型动力吸振器模型在简谐激励和随机激励情况下的对比,说明了负刚度模型在主系统减振方面具有很大的优势,减振效果远优于两种已有动力吸振器模型,从而为设计新型动力吸振器模型提出了理论上的依据.
(Peng Haibo Shen Yongjun Yang Shaopu . Parameters optimization of a new type of dynamic vibration absorber with negative stiffness
Chinese Journal of Theoretical and Applied Mechanics 2015 , 47 (2 ): 320 -327 (in Chinese))
[本文引用: 1]
[23]
Wong WO Tang SL Cheung YL , et al . Design of a dynamic vibration absorber for vibration isolation of beams under point or distributed loading
Journal of Sound and Vibration 2007 , 301 (3-5 ): 898 -908
DOI
URL
[本文引用: 1]
[24]
Rechenberger S Mair D . Vibration control of piping systems and structures using tuned mass dampers//Proceedings of the ASME Pressure Vessels and Piping Conference, Waikoloa, Hawaii, USA , 2017
[本文引用: 1]
[25]
宾滔 , 王修勇 , 方豪杰 等 . 调谐双质阻尼器减振性能分析
噪声与振动控制 , 2020 , 40 (4 ): 223 -226
[本文引用: 1]
(Bin Tao Wang Xiuyong Fang Haojie , et al . Noise and Vibration Control 2020 , 40 (4 ): 223 -226 (in Chinese))
[本文引用: 1]
[26]
Yang TZ Yang XD Li Y , et al . Passive and adaptive vibration suppression of pipes conveying fluid with variable velocity
Journal of Vibration and Control 2013 , 20 (9 ): 1293 -1300
DOI
URL
[本文引用: 1]
[27]
Duan N Fang B Teng Y . Passive vibration control of pipes conveying fluid with parallel nonlinear energy sinks//International Congress on Computation Algorithms in Engineering, Bangkok, Thailand , 2016
[本文引用: 1]
[28]
Zhou K Xiong FR Jiang NB , et al . Nonlinear vibration control of a cantilevered fluid-conveying pipe using the idea of nonlinear energy sink
Nonlinear Dynamics 2018 , 95 (2 ): 1435 -1456
DOI
URL
[本文引用: 1]
[29]
Gourdon E Alexander NA Taylor CA , et al . Nonlinear energy pumping under transient forcing with strongly nonlinear coupling: Theoretical and experimental results
Journal of Sound and Vibration 2007 , 300 (3-5 ): 522 -551
DOI
URL
[本文引用: 1]
[30]
Li H Zhang P Song G , et al . Robustness study of the pounding tuned mass damper for vibration control of subsea jumpers
Smart Materials and Structures 2015 , 24 (9 ): 095001
DOI
URL
[本文引用: 1]
[31]
叶昆 , 舒率 . 基于性能需求的基础隔震结构附加调谐惯容阻尼器的优化设计研究
动力学与控制学报 , 2020 , 18 (5 ): 40 -45
[本文引用: 1]
(Ye Kun Shu Shuai . Optimal design of base-isolated structure with supplemental tuned inerter damper based on performance requirement
Journal of Dynamics and Control 2020 , 18 (5 ): 40 -45 (in Chinese))
[本文引用: 1]
[32]
Shi X Zhu S . A comparative study of vibration isolation performance using negative stiffness and inerter dampers
Journal of the Franklin Institute 2019 , 356 (14 ): 7922 -7946
DOI
URL
[33]
Xu K Bi K Han Q , et al . Using tuned mass damper inerter to mitigate vortex-induced vibration of long-span bridges: Analytical study
Engineering Structures 2019 , 182 (MAR.1 ): 101 -111
DOI
URL
[34]
Zhang Z Lu ZQ Ding H , et al . An inertial nonlinear energy sink
Journal of Sound and Vibration 2019 , 450 : 199 -213
DOI
The demand for large mass limits the engineering application of traditional nonlinear energy sinks. In this paper, a novel type of nonlinear energy sink is proposed to overcome this drawback. The mass in the traditional nonlinear energy sink is replaced by an inerter. A substantial reduction in the mass of nonlinear energy sinks has been achieved. At the same time, the effect of vibration suppression is improved. Introducing the inertance without the mass, the equation of motion for the inertial nonlinear energy sink is established. By applying the harmonic balance method, the nonlinear forced vibration response of the system is predicted. The analytical results are supported by numerical simulations. By comparing with the traditional nonlinear energy sink, the benefits of using inertial nonlinear energy sink are explored. For examples, the additional mass required to achieve the same vibration suppression effect is smaller. The same additional mass enables better vibration suppression. Moreover, the optimum mass ratio is searched by the maximum amplitude trajectory. Furthermore, amplitude-frequency responses are generated for different parameters. The numerical results demonstrate that the inertial design could enhance the vibration suppression performance. In general, this work shows that the inertial design can significantly reduce the additional mass. Therefore, this study promotes the practical application of the NES. (C) 2019 Elsevier Ltd.
[35]
Sun L Hong D Chen L . Cables interconnected with tuned inerter damper for vibration mitigation
Engineering Structures 2017 , 151 (Nov.15 ): 57 -67
DOI
URL
[36]
Wang Y Li HX Cheng C , et al . A nonlinear stiffness and nonlinear inertial vibration isolator
Journal of Vibration and Control 2020 , doi: 10.1177/1077546320940924
[本文引用: 1]
[37]
Shi X Zhu S . Dynamic characteristics of stay cables with inerter dampers
Journal of Sound and Vibration 2018 , 423 : 287 -305
DOI
URL
[本文引用: 1]
[38]
陈杰 , 孙维光 , 吴杨俊 等 . 基于惯容负刚度动力吸振器的梁响应最小化
振动与冲击 , 2020 , 39 (8 ): 15 -22
[本文引用: 1]
(Chen Jie Sun Weiguang Wu Yangjun , et al . Minimization of beam response using inerter- based dynamic vibration absorber with negative stiffness
Journal of the Vibration and Shock 2020 , 39 (8 ): 15 -22 (in Chinese))
[本文引用: 1]
7
2014
... 在当今迅速发展的工业时代, 输流管道已成为众多工程装备的重要组成元部件.海洋工程中的海洋立管、核电装备中的管束结构等都是输流管道应用的典型实例.在管内流体的激励下, 管道因流体-固体耦合作用可产生自激振动和有害噪声.当其他外界激励频率与输流管道固有频率相近时还可能引起共振, 从而诱发受迫振动与自激振动的协同作用. 事实上, 输流管的流固耦合过程也表现出一种较强的非线性流固耦合特征, 正因为如此, 输流管结构的动力学问题研究已成为流固耦合力学领域的重要研究内容之一[1 -7 ] . ...
... 其中, $\varphi_r(\xi)$是悬臂梁无量纲化的模态函数, $q_r(\tau)$是相应离散系统的广义坐标, $\varphi=[\varphi_1, \varphi_2, \cdots , \varphi_N]$和$ q = [q_1, q_2, \cdots , q_N]^T$分别为特征函数和广义坐标向量.将式(5)代入无量纲方程(4)中, 利用模态函数的正交性, 在整个等式同时左乘$ \varphi^T$并在区间[0 , 1 ] 上积分后可得 ...
... 为了与Paidoussis[1 ] 的经典结果进行对比, 取参数$\alpha =0$, $\beta =0.2$和$\gamma =0$. 记方程(6)的特征值$\lambda =i\omega $, 则实部Re($\omega$ )表示无量纲化的振动频率, Im($\omega$ )表征了系统的阻尼.从图2 可知, 随着管内流体速度的不断增大, 第二阶模态阻尼从正值变为负值, 这表明系统可以从流体中吸收能量, 同时将能量传送给管道, 此时系统会发生颤振失稳, 管道因此而出现周期振动现象. 从图2 还可看出, 悬臂管第二阶模态发生颤振失稳的临界流速约为$u_cr=5.61$. 随着流速的不断增大, 悬臂管的特征值演化曲线与文献[1 ]的经典结果是一致的, 从而验证了本文方法所获得解答是可靠的. ...
... 还可看出, 悬臂管第二阶模态发生颤振失稳的临界流速约为$u_cr=5.61$. 随着流速的不断增大, 悬臂管的特征值演化曲线与文献[1 ]的经典结果是一致的, 从而验证了本文方法所获得解答是可靠的. ...
... 取悬臂管道上任意一点进行研究. 管道变形时该点的位置矢量和切向矢量可分别用$ r$和 $\tau $表示[1 ] ...
... 由此可得悬臂管道系统的总动能为[1 ] ...
... 其中, $ v_p$和$ v_f$分别表示管道和流体的运动速度, 可写为如下形式[1 ] ...
Dynamics of cantilevered pipes conveying fluid. Part 1: Nonlinear equations of three-dimensional motion
0
2007
分布式运动约束下悬臂输液管的参数共振研究
0
2019
分布式运动约束下悬臂输液管的参数共振研究
0
2019
The non-linear equations of motion of pipes conveying fluid
1
1994
... 基于以上假设, 引入广义的Hamilton原理[4 ] ...
含集中质量悬臂输流管的稳定性与模态演化特性研究
0
2020
含集中质量悬臂输流管的稳定性与模态演化特性研究
0
2020
Non-linear dynamics of a simply supported fluid-conveying pipe subjected to motion-limiting constraints: Two-dimensional analysis
0
2018
悬臂输流管道的运动分岔现象和混沌运动
1
2002
... 在当今迅速发展的工业时代, 输流管道已成为众多工程装备的重要组成元部件.海洋工程中的海洋立管、核电装备中的管束结构等都是输流管道应用的典型实例.在管内流体的激励下, 管道因流体-固体耦合作用可产生自激振动和有害噪声.当其他外界激励频率与输流管道固有频率相近时还可能引起共振, 从而诱发受迫振动与自激振动的协同作用. 事实上, 输流管的流固耦合过程也表现出一种较强的非线性流固耦合特征, 正因为如此, 输流管结构的动力学问题研究已成为流固耦合力学领域的重要研究内容之一[1 -7 ] . ...
悬臂输流管道的运动分岔现象和混沌运动
1
2002
... 在当今迅速发展的工业时代, 输流管道已成为众多工程装备的重要组成元部件.海洋工程中的海洋立管、核电装备中的管束结构等都是输流管道应用的典型实例.在管内流体的激励下, 管道因流体-固体耦合作用可产生自激振动和有害噪声.当其他外界激励频率与输流管道固有频率相近时还可能引起共振, 从而诱发受迫振动与自激振动的协同作用. 事实上, 输流管的流固耦合过程也表现出一种较强的非线性流固耦合特征, 正因为如此, 输流管结构的动力学问题研究已成为流固耦合力学领域的重要研究内容之一[1 -7 ] . ...
Dynamics and stability of magnetically actuated pipes conveying fluid
1
2016
... 在学术界, 输流管道出现失稳时的流速值被称为临界流速. 近年来, 人们通过对临界流速的调节已成为输流管动力学控制研究的一个重要内容; 此外, 还有学者采用各种控制方法来降低管道振动幅值, 从而达到降低管道破裂或疲劳损伤等风险[8 -15 ] . ...
Adaptive boundary iterative learning control for an Euler-Bernoulli beam system with input constraint
0
2018
非齐次边界条件下轴向运动梁的非线性振动
0
2019
非齐次边界条件下轴向运动梁的非线性振动
0
2019
Modeling and vibration control for a moving beam with application in a drilling riser
0
2017
Nonplanar vortex-induced vibrations of cantilevered pipes conveying fluid subjected to loose constraints
0
2019
2:1内共振条件下变转速预变形叶片的非线性动力学响应
0
2020
2:1内共振条件下变转速预变形叶片的非线性动力学响应
0
2020
Vibration analysis of cantilever pipe conveying fluid under distributed random excitation
0
2019
含串联非线性能量汇的整星系统吸振效果研究
1
2020
... 在学术界, 输流管道出现失稳时的流速值被称为临界流速. 近年来, 人们通过对临界流速的调节已成为输流管动力学控制研究的一个重要内容; 此外, 还有学者采用各种控制方法来降低管道振动幅值, 从而达到降低管道破裂或疲劳损伤等风险[8 -15 ] . ...
含串联非线性能量汇的整星系统吸振效果研究
1
2020
... 在学术界, 输流管道出现失稳时的流速值被称为临界流速. 近年来, 人们通过对临界流速的调节已成为输流管动力学控制研究的一个重要内容; 此外, 还有学者采用各种控制方法来降低管道振动幅值, 从而达到降低管道破裂或疲劳损伤等风险[8 -15 ] . ...
Milling vibration attenuation by eddy current damping
1
2015
... 输流管振动控制方法主要包括主动和被动两种.主动控制方法通常借助外界能量的输入来实现对输流管系统的实时控制, 从理论上来看具有较好的控制效果[16 -18 ] . 例如, Abbasnejad等[19 ] 研究了含有轴向分布压电层的微流体管道的稳定性, 同时还探讨了支撑边界对稳定性的影响, 其研究结果表明: 通过对压电层施加电压差, 可显著抑制流体对管道振动频率的影响, 从而扩大了稳定性区域.Ge等[20 ] 通过对管道施加一个与时间相关的位移函数, 采用自适应边界控制技术对欧拉-伯努利梁进行振动抑制, 验证了该控制方法的有效性.Szmidt等[21 ] 利用在悬臂管道上安装电磁装置的方式, 使得运动中的电板在切割磁感线过程中产生阻力, 以此来提高悬臂输流管的动态稳定性, 也得到了较好的控制效果. ...
Vibration control for a nonlinear three-dimensional Euler-Bernoulli beam under input magnitude and rate constraints
1
2018
... 输流管振动控制方法主要包括主动和被动两种.主动控制方法通常借助外界能量的输入来实现对输流管系统的实时控制, 从理论上来看具有较好的控制效果[16 -18 ] . 例如, Abbasnejad等[19 ] 研究了含有轴向分布压电层的微流体管道的稳定性, 同时还探讨了支撑边界对稳定性的影响, 其研究结果表明: 通过对压电层施加电压差, 可显著抑制流体对管道振动频率的影响, 从而扩大了稳定性区域.Ge等[20 ] 通过对管道施加一个与时间相关的位移函数, 采用自适应边界控制技术对欧拉-伯努利梁进行振动抑制, 验证了该控制方法的有效性.Szmidt等[21 ] 利用在悬臂管道上安装电磁装置的方式, 使得运动中的电板在切割磁感线过程中产生阻力, 以此来提高悬臂输流管的动态稳定性, 也得到了较好的控制效果. ...
Stability analysis of a piezoelectrically actuated micro-pipe conveying fluid
1
2015
... 输流管振动控制方法主要包括主动和被动两种.主动控制方法通常借助外界能量的输入来实现对输流管系统的实时控制, 从理论上来看具有较好的控制效果[16 -18 ] . 例如, Abbasnejad等[19 ] 研究了含有轴向分布压电层的微流体管道的稳定性, 同时还探讨了支撑边界对稳定性的影响, 其研究结果表明: 通过对压电层施加电压差, 可显著抑制流体对管道振动频率的影响, 从而扩大了稳定性区域.Ge等[20 ] 通过对管道施加一个与时间相关的位移函数, 采用自适应边界控制技术对欧拉-伯努利梁进行振动抑制, 验证了该控制方法的有效性.Szmidt等[21 ] 利用在悬臂管道上安装电磁装置的方式, 使得运动中的电板在切割磁感线过程中产生阻力, 以此来提高悬臂输流管的动态稳定性, 也得到了较好的控制效果. ...
Vibration control of an Euler-Bernoulli beam under unknown spatiotemporally varying disturbance
1
2011
... 输流管振动控制方法主要包括主动和被动两种.主动控制方法通常借助外界能量的输入来实现对输流管系统的实时控制, 从理论上来看具有较好的控制效果[16 -18 ] . 例如, Abbasnejad等[19 ] 研究了含有轴向分布压电层的微流体管道的稳定性, 同时还探讨了支撑边界对稳定性的影响, 其研究结果表明: 通过对压电层施加电压差, 可显著抑制流体对管道振动频率的影响, 从而扩大了稳定性区域.Ge等[20 ] 通过对管道施加一个与时间相关的位移函数, 采用自适应边界控制技术对欧拉-伯努利梁进行振动抑制, 验证了该控制方法的有效性.Szmidt等[21 ] 利用在悬臂管道上安装电磁装置的方式, 使得运动中的电板在切割磁感线过程中产生阻力, 以此来提高悬臂输流管的动态稳定性, 也得到了较好的控制效果. ...
Semi-active stabilisation of a pipe conveying fluid using eddy-current dampers: State-feedback control design, experimental validation
1
2019
... 输流管振动控制方法主要包括主动和被动两种.主动控制方法通常借助外界能量的输入来实现对输流管系统的实时控制, 从理论上来看具有较好的控制效果[16 -18 ] . 例如, Abbasnejad等[19 ] 研究了含有轴向分布压电层的微流体管道的稳定性, 同时还探讨了支撑边界对稳定性的影响, 其研究结果表明: 通过对压电层施加电压差, 可显著抑制流体对管道振动频率的影响, 从而扩大了稳定性区域.Ge等[20 ] 通过对管道施加一个与时间相关的位移函数, 采用自适应边界控制技术对欧拉-伯努利梁进行振动抑制, 验证了该控制方法的有效性.Szmidt等[21 ] 利用在悬臂管道上安装电磁装置的方式, 使得运动中的电板在切割磁感线过程中产生阻力, 以此来提高悬臂输流管的动态稳定性, 也得到了较好的控制效果. ...
一种含负刚度元件的新型动力吸振器的参数优化
1
2015
... 相比于主动控制, 被动控制方式因其结构简单、不需要外界能量输入, 且具有一定的鲁棒性等特点, 在工程实践中得到广泛应用.输流管被动控制的方法有很多, 比如动力减振器法[22 -23 ] 、阻尼器法[24 -25 ] 、非线性能量汇法[26 -27 ] 等.Zhou等[28 ] 通过在悬臂管道上安装非线性能量汇对管道振动进行控制, 分析了不同能量汇参数对提高悬臂管道临界流速的影响. Gourdon等[29 ] 通过实验方法验证了不同类型激励下非线性能量汇的减振效果, 其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果. Li等[30 ] 提出了一种冲击式调谐质量阻尼器(PTMD), 通过质量块与黏弹性材料的碰撞方式来耗散振动能量, 发现这种新型阻尼器可有效的控制振动. ...
一种含负刚度元件的新型动力吸振器的参数优化
1
2015
... 相比于主动控制, 被动控制方式因其结构简单、不需要外界能量输入, 且具有一定的鲁棒性等特点, 在工程实践中得到广泛应用.输流管被动控制的方法有很多, 比如动力减振器法[22 -23 ] 、阻尼器法[24 -25 ] 、非线性能量汇法[26 -27 ] 等.Zhou等[28 ] 通过在悬臂管道上安装非线性能量汇对管道振动进行控制, 分析了不同能量汇参数对提高悬臂管道临界流速的影响. Gourdon等[29 ] 通过实验方法验证了不同类型激励下非线性能量汇的减振效果, 其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果. Li等[30 ] 提出了一种冲击式调谐质量阻尼器(PTMD), 通过质量块与黏弹性材料的碰撞方式来耗散振动能量, 发现这种新型阻尼器可有效的控制振动. ...
Design of a dynamic vibration absorber for vibration isolation of beams under point or distributed loading
1
2007
... 相比于主动控制, 被动控制方式因其结构简单、不需要外界能量输入, 且具有一定的鲁棒性等特点, 在工程实践中得到广泛应用.输流管被动控制的方法有很多, 比如动力减振器法[22 -23 ] 、阻尼器法[24 -25 ] 、非线性能量汇法[26 -27 ] 等.Zhou等[28 ] 通过在悬臂管道上安装非线性能量汇对管道振动进行控制, 分析了不同能量汇参数对提高悬臂管道临界流速的影响. Gourdon等[29 ] 通过实验方法验证了不同类型激励下非线性能量汇的减振效果, 其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果. Li等[30 ] 提出了一种冲击式调谐质量阻尼器(PTMD), 通过质量块与黏弹性材料的碰撞方式来耗散振动能量, 发现这种新型阻尼器可有效的控制振动. ...
1
2017
... 相比于主动控制, 被动控制方式因其结构简单、不需要外界能量输入, 且具有一定的鲁棒性等特点, 在工程实践中得到广泛应用.输流管被动控制的方法有很多, 比如动力减振器法[22 -23 ] 、阻尼器法[24 -25 ] 、非线性能量汇法[26 -27 ] 等.Zhou等[28 ] 通过在悬臂管道上安装非线性能量汇对管道振动进行控制, 分析了不同能量汇参数对提高悬臂管道临界流速的影响. Gourdon等[29 ] 通过实验方法验证了不同类型激励下非线性能量汇的减振效果, 其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果. Li等[30 ] 提出了一种冲击式调谐质量阻尼器(PTMD), 通过质量块与黏弹性材料的碰撞方式来耗散振动能量, 发现这种新型阻尼器可有效的控制振动. ...
调谐双质阻尼器减振性能分析
1
2020
... 相比于主动控制, 被动控制方式因其结构简单、不需要外界能量输入, 且具有一定的鲁棒性等特点, 在工程实践中得到广泛应用.输流管被动控制的方法有很多, 比如动力减振器法[22 -23 ] 、阻尼器法[24 -25 ] 、非线性能量汇法[26 -27 ] 等.Zhou等[28 ] 通过在悬臂管道上安装非线性能量汇对管道振动进行控制, 分析了不同能量汇参数对提高悬臂管道临界流速的影响. Gourdon等[29 ] 通过实验方法验证了不同类型激励下非线性能量汇的减振效果, 其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果. Li等[30 ] 提出了一种冲击式调谐质量阻尼器(PTMD), 通过质量块与黏弹性材料的碰撞方式来耗散振动能量, 发现这种新型阻尼器可有效的控制振动. ...
调谐双质阻尼器减振性能分析
1
2020
... 相比于主动控制, 被动控制方式因其结构简单、不需要外界能量输入, 且具有一定的鲁棒性等特点, 在工程实践中得到广泛应用.输流管被动控制的方法有很多, 比如动力减振器法[22 -23 ] 、阻尼器法[24 -25 ] 、非线性能量汇法[26 -27 ] 等.Zhou等[28 ] 通过在悬臂管道上安装非线性能量汇对管道振动进行控制, 分析了不同能量汇参数对提高悬臂管道临界流速的影响. Gourdon等[29 ] 通过实验方法验证了不同类型激励下非线性能量汇的减振效果, 其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果. Li等[30 ] 提出了一种冲击式调谐质量阻尼器(PTMD), 通过质量块与黏弹性材料的碰撞方式来耗散振动能量, 发现这种新型阻尼器可有效的控制振动. ...
Passive and adaptive vibration suppression of pipes conveying fluid with variable velocity
1
2013
... 相比于主动控制, 被动控制方式因其结构简单、不需要外界能量输入, 且具有一定的鲁棒性等特点, 在工程实践中得到广泛应用.输流管被动控制的方法有很多, 比如动力减振器法[22 -23 ] 、阻尼器法[24 -25 ] 、非线性能量汇法[26 -27 ] 等.Zhou等[28 ] 通过在悬臂管道上安装非线性能量汇对管道振动进行控制, 分析了不同能量汇参数对提高悬臂管道临界流速的影响. Gourdon等[29 ] 通过实验方法验证了不同类型激励下非线性能量汇的减振效果, 其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果. Li等[30 ] 提出了一种冲击式调谐质量阻尼器(PTMD), 通过质量块与黏弹性材料的碰撞方式来耗散振动能量, 发现这种新型阻尼器可有效的控制振动. ...
1
2016
... 相比于主动控制, 被动控制方式因其结构简单、不需要外界能量输入, 且具有一定的鲁棒性等特点, 在工程实践中得到广泛应用.输流管被动控制的方法有很多, 比如动力减振器法[22 -23 ] 、阻尼器法[24 -25 ] 、非线性能量汇法[26 -27 ] 等.Zhou等[28 ] 通过在悬臂管道上安装非线性能量汇对管道振动进行控制, 分析了不同能量汇参数对提高悬臂管道临界流速的影响. Gourdon等[29 ] 通过实验方法验证了不同类型激励下非线性能量汇的减振效果, 其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果. Li等[30 ] 提出了一种冲击式调谐质量阻尼器(PTMD), 通过质量块与黏弹性材料的碰撞方式来耗散振动能量, 发现这种新型阻尼器可有效的控制振动. ...
Nonlinear vibration control of a cantilevered fluid-conveying pipe using the idea of nonlinear energy sink
1
2018
... 相比于主动控制, 被动控制方式因其结构简单、不需要外界能量输入, 且具有一定的鲁棒性等特点, 在工程实践中得到广泛应用.输流管被动控制的方法有很多, 比如动力减振器法[22 -23 ] 、阻尼器法[24 -25 ] 、非线性能量汇法[26 -27 ] 等.Zhou等[28 ] 通过在悬臂管道上安装非线性能量汇对管道振动进行控制, 分析了不同能量汇参数对提高悬臂管道临界流速的影响. Gourdon等[29 ] 通过实验方法验证了不同类型激励下非线性能量汇的减振效果, 其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果. Li等[30 ] 提出了一种冲击式调谐质量阻尼器(PTMD), 通过质量块与黏弹性材料的碰撞方式来耗散振动能量, 发现这种新型阻尼器可有效的控制振动. ...
Nonlinear energy pumping under transient forcing with strongly nonlinear coupling: Theoretical and experimental results
1
2007
... 相比于主动控制, 被动控制方式因其结构简单、不需要外界能量输入, 且具有一定的鲁棒性等特点, 在工程实践中得到广泛应用.输流管被动控制的方法有很多, 比如动力减振器法[22 -23 ] 、阻尼器法[24 -25 ] 、非线性能量汇法[26 -27 ] 等.Zhou等[28 ] 通过在悬臂管道上安装非线性能量汇对管道振动进行控制, 分析了不同能量汇参数对提高悬臂管道临界流速的影响. Gourdon等[29 ] 通过实验方法验证了不同类型激励下非线性能量汇的减振效果, 其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果. Li等[30 ] 提出了一种冲击式调谐质量阻尼器(PTMD), 通过质量块与黏弹性材料的碰撞方式来耗散振动能量, 发现这种新型阻尼器可有效的控制振动. ...
Robustness study of the pounding tuned mass damper for vibration control of subsea jumpers
1
2015
... 相比于主动控制, 被动控制方式因其结构简单、不需要外界能量输入, 且具有一定的鲁棒性等特点, 在工程实践中得到广泛应用.输流管被动控制的方法有很多, 比如动力减振器法[22 -23 ] 、阻尼器法[24 -25 ] 、非线性能量汇法[26 -27 ] 等.Zhou等[28 ] 通过在悬臂管道上安装非线性能量汇对管道振动进行控制, 分析了不同能量汇参数对提高悬臂管道临界流速的影响. Gourdon等[29 ] 通过实验方法验证了不同类型激励下非线性能量汇的减振效果, 其实验结果表明在适当的外力幅值范围内有较好的振动抑制效果. Li等[30 ] 提出了一种冲击式调谐质量阻尼器(PTMD), 通过质量块与黏弹性材料的碰撞方式来耗散振动能量, 发现这种新型阻尼器可有效的控制振动. ...
基于性能需求的基础隔震结构附加调谐惯容阻尼器的优化设计研究
1
2020
... 近年来, 有学者提出了将惯容器应用到结构的振动控制问题之中, 获得了较好的被动控制效果[31 -36 ] .惯容器相比于传统的质量块而言体积更小. 对于相同质量的惯容器和普通质量块, 惯容器能提供更大的惯性效应, 它产生的惯性力与其两自由端的加速度之差成正比关系, 这使得惯容器方式已在多个工程实践中得到了应用. Shi等[37 ] 研究了在拉索一端安装接地惯性阻尼器, 探讨了惯性系数和阻尼系数对拉索振动响应的影响规律, 并由此提出一种优化后的最佳惯性阻尼器设计方法.陈杰等[38 ] 借助含有惯容器和负刚度的动力减振器对结构进行振动控制, 发现相比于传统的动力减振器, 这种新型减振器在抑制梁的横向振动时更加有效.综合已有研究报道来看, 现有研究工作已将惯容器用于单自由度和多自由度结构的振动控制之中, 但这类减振器对非保守的悬臂输流管系统是否有控制效果, 目前还未可知. ...
基于性能需求的基础隔震结构附加调谐惯容阻尼器的优化设计研究
1
2020
... 近年来, 有学者提出了将惯容器应用到结构的振动控制问题之中, 获得了较好的被动控制效果[31 -36 ] .惯容器相比于传统的质量块而言体积更小. 对于相同质量的惯容器和普通质量块, 惯容器能提供更大的惯性效应, 它产生的惯性力与其两自由端的加速度之差成正比关系, 这使得惯容器方式已在多个工程实践中得到了应用. Shi等[37 ] 研究了在拉索一端安装接地惯性阻尼器, 探讨了惯性系数和阻尼系数对拉索振动响应的影响规律, 并由此提出一种优化后的最佳惯性阻尼器设计方法.陈杰等[38 ] 借助含有惯容器和负刚度的动力减振器对结构进行振动控制, 发现相比于传统的动力减振器, 这种新型减振器在抑制梁的横向振动时更加有效.综合已有研究报道来看, 现有研究工作已将惯容器用于单自由度和多自由度结构的振动控制之中, 但这类减振器对非保守的悬臂输流管系统是否有控制效果, 目前还未可知. ...
A comparative study of vibration isolation performance using negative stiffness and inerter dampers
0
2019
Using tuned mass damper inerter to mitigate vortex-induced vibration of long-span bridges: Analytical study
0
2019
An inertial nonlinear energy sink
0
2019
Cables interconnected with tuned inerter damper for vibration mitigation
0
2017
A nonlinear stiffness and nonlinear inertial vibration isolator
1
2020
... 近年来, 有学者提出了将惯容器应用到结构的振动控制问题之中, 获得了较好的被动控制效果[31 -36 ] .惯容器相比于传统的质量块而言体积更小. 对于相同质量的惯容器和普通质量块, 惯容器能提供更大的惯性效应, 它产生的惯性力与其两自由端的加速度之差成正比关系, 这使得惯容器方式已在多个工程实践中得到了应用. Shi等[37 ] 研究了在拉索一端安装接地惯性阻尼器, 探讨了惯性系数和阻尼系数对拉索振动响应的影响规律, 并由此提出一种优化后的最佳惯性阻尼器设计方法.陈杰等[38 ] 借助含有惯容器和负刚度的动力减振器对结构进行振动控制, 发现相比于传统的动力减振器, 这种新型减振器在抑制梁的横向振动时更加有效.综合已有研究报道来看, 现有研究工作已将惯容器用于单自由度和多自由度结构的振动控制之中, 但这类减振器对非保守的悬臂输流管系统是否有控制效果, 目前还未可知. ...
Dynamic characteristics of stay cables with inerter dampers
1
2018
... 近年来, 有学者提出了将惯容器应用到结构的振动控制问题之中, 获得了较好的被动控制效果[31 -36 ] .惯容器相比于传统的质量块而言体积更小. 对于相同质量的惯容器和普通质量块, 惯容器能提供更大的惯性效应, 它产生的惯性力与其两自由端的加速度之差成正比关系, 这使得惯容器方式已在多个工程实践中得到了应用. Shi等[37 ] 研究了在拉索一端安装接地惯性阻尼器, 探讨了惯性系数和阻尼系数对拉索振动响应的影响规律, 并由此提出一种优化后的最佳惯性阻尼器设计方法.陈杰等[38 ] 借助含有惯容器和负刚度的动力减振器对结构进行振动控制, 发现相比于传统的动力减振器, 这种新型减振器在抑制梁的横向振动时更加有效.综合已有研究报道来看, 现有研究工作已将惯容器用于单自由度和多自由度结构的振动控制之中, 但这类减振器对非保守的悬臂输流管系统是否有控制效果, 目前还未可知. ...
基于惯容负刚度动力吸振器的梁响应最小化
1
2020
... 近年来, 有学者提出了将惯容器应用到结构的振动控制问题之中, 获得了较好的被动控制效果[31 -36 ] .惯容器相比于传统的质量块而言体积更小. 对于相同质量的惯容器和普通质量块, 惯容器能提供更大的惯性效应, 它产生的惯性力与其两自由端的加速度之差成正比关系, 这使得惯容器方式已在多个工程实践中得到了应用. Shi等[37 ] 研究了在拉索一端安装接地惯性阻尼器, 探讨了惯性系数和阻尼系数对拉索振动响应的影响规律, 并由此提出一种优化后的最佳惯性阻尼器设计方法.陈杰等[38 ] 借助含有惯容器和负刚度的动力减振器对结构进行振动控制, 发现相比于传统的动力减振器, 这种新型减振器在抑制梁的横向振动时更加有效.综合已有研究报道来看, 现有研究工作已将惯容器用于单自由度和多自由度结构的振动控制之中, 但这类减振器对非保守的悬臂输流管系统是否有控制效果, 目前还未可知. ...
基于惯容负刚度动力吸振器的梁响应最小化
1
2020
... 近年来, 有学者提出了将惯容器应用到结构的振动控制问题之中, 获得了较好的被动控制效果[31 -36 ] .惯容器相比于传统的质量块而言体积更小. 对于相同质量的惯容器和普通质量块, 惯容器能提供更大的惯性效应, 它产生的惯性力与其两自由端的加速度之差成正比关系, 这使得惯容器方式已在多个工程实践中得到了应用. Shi等[37 ] 研究了在拉索一端安装接地惯性阻尼器, 探讨了惯性系数和阻尼系数对拉索振动响应的影响规律, 并由此提出一种优化后的最佳惯性阻尼器设计方法.陈杰等[38 ] 借助含有惯容器和负刚度的动力减振器对结构进行振动控制, 发现相比于传统的动力减振器, 这种新型减振器在抑制梁的横向振动时更加有效.综合已有研究报道来看, 现有研究工作已将惯容器用于单自由度和多自由度结构的振动控制之中, 但这类减振器对非保守的悬臂输流管系统是否有控制效果, 目前还未可知. ...