引言
呼吸是一种重要的生理活动, 是包括人类在内的所有哺乳动物维持生命的必要条件之一. 研究发现, 哺乳动物新生儿神经系统中的呼吸节律可能是由pre-Bötzinger复合体(简称为pre-BötC)中的条件起搏神经元的同步活动引起的[1 -2 ] . 此后, 生理实验研究证实了pre-BötC是呼吸节律产生的主要部位[3 ] , 是离体实验中呼吸节律产生的关键[4 ] . 实验结果表明$g_{ NaP}$和$g_{ Leak}$代表亚阈电导的函数集, 赋予pre-BötC节律性特征[5 ] . 光子成像测量树突状Ca$^{2+}$瞬态的实验表明, 呼吸节律发生可能取决于网络活动中激活的树突簇产生的电导[6 ] . 此外, 药物刺激也可对pre-BötC的呼吸节律产生影响[7 -12 ] , 这表明pre-BötC可能与人类某些神经系统疾病有关, 在呼吸节律的神经控制中占有重要地位.
神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性.
电磁场对神经元放电活动的影响也成为近年来的研究热点. Zhan和Liu[27 ] 研究了具有电磁辐射或高斯白噪声的Morris-Lecar模型, 发现电磁感应可以将簇或峰放电转换为静息态. Duan等[28 ] 研究发现, 磁通量使pre-BötC神经元在电流值较低的情况下振荡, 改变外激励条件, 可以观察到常规簇和混合簇类型. Guo和Lü[29 ] 研究了磁流和外部刺激电流这两个因素对单个pre-BötC神经元混合簇放电模式的影响. Ma等[30 ] 利用磁通和电荷分别描述磁场和电磁感应、电场的变化, 考虑电磁场的影响建立新的神经元模型, 在这种新的神经元模型上进行了非线性分析, 并应用外部电磁辐射来检测神经元活动中的模式转换. 随后, 他们又设计了一种简单的神经电路, 通过结合两个物理电子元件来估计磁场对神经元活动的影响[31 ] . 虽然磁流对神经元放电节律转迁的动力学行为已有一定的研究[32 -35 ] , 但是其对混合簇的影响的研究还不够深入, 还有很多值得进一步研究的内容.
本文通过对模型的分析和计算, 研究外部刺激电流和磁通量对混合簇放电模式的影响, 包括: (1) 借助无量纲化分析, 将模型中变量的时间尺度进行划分, 无量纲化结果表明模型包含快、慢和超慢3个时间尺度; (2) 通过无量纲化后的模型研究外部刺激电流$I$和磁流反馈系数$k_{1}$对混合簇放电模式的影响, 并通过分岔分析来研究混合簇产生的动力学机制. 结果发现, 减小$I$和$k_{1}$的值会使混合簇中胞体簇的个数减少, 同时使簇的放电类型发生改变. 全系统轨线在鞍结分岔曲线和同宿轨分岔曲线之间来回跃迁, 导致混合簇的产生. 研究结果可为深入了解电流和磁流对神经元的影响提供参考.
1 模型描述
Butera等[36 ] 建立了最小pre-BötC神经元模型, 该模型由钠电流($I_{ Na}$)和钾电流($I_{ K}$)产生动作电位并通过持续钠电流($I_{ NaP}$)的缓慢失活来终止放电过程. Toporikova和Butera把这一模型发展为具有胞体$\!-\!$树突双室的神经元模型(TB模型)[37 ] , 该模型使用Butera描述的pre-BötC神经元模型作为胞体室, 而树突室仅包含钙激活的非特异性阳离子电流($I_{ CAN}$). Park和Rubin[38 ] 发现当TB模型简化为单室时会定性地产生相似的动力学特征.
根据电磁感应的物理定律, 带电离子在膜上的持续交换会引起离子浓度的复杂变化. 神经元的膜电位波动被认为是电磁感应效应[39 ] . 因此需要建立随时间变化的电磁场来调节神经元的膜电位, 而跨膜磁通量可以满足这一要求. 磁通量$\varphi$作为附加变量来描述电磁感应和电场的影响、检测电磁场的变化, 且用来模拟磁通量的忆阻器能够与神经元膜电位的物理单位保持一致. Wu等[30 ] 通过设计一个带有外刺激电流和忆阻器的HR模型的神经元电路图证明了带有外部刺激的电流和磁通量的模型的有效性[40 ] .
本工作在Park和Rubin[38 ] 提出的pre-BötC单室细胞模型中引入了电流和磁通控制忆阻器. 模型描述如下
(1a) $\frac{{ d}V}{{ d}t}=[ -I_{{ K}}-I_{{ Na}}-I_{{ NaP}}-I_{{ CAN}}-I_{{ L}}-I_{{ tonic\_e}}+ I-k_{{ 1}}V\rho \left( \varphi \right) ]/C$
(1b) $\frac{{ d}n}{{ d}t}=\left[ n_{\infty }\left( V \right)-n \right]/\tau_{ n}\left( V\right)$
(1c) $\frac{{ d}h}{{ d}t}=\left[ h_{\infty}\left( V \right)-h \right]/\tau_{ h}\left( V \right)$
(1d) $\frac{d\varphi }{{ d}t}=V-k_{{ 2}}\varphi$
(1e) $\frac{{ d}[Ca]}{{ d}t}=f_{ m}\left(J_{{{ ER}}_{{ IN}}}-J_{{{ ER}}_{{ OUT}}} \right)$
(1f) $\frac{{ d}l}{{ d}t}=AK_{{ d}}\left( 1-l \right)-A[Ca]l$
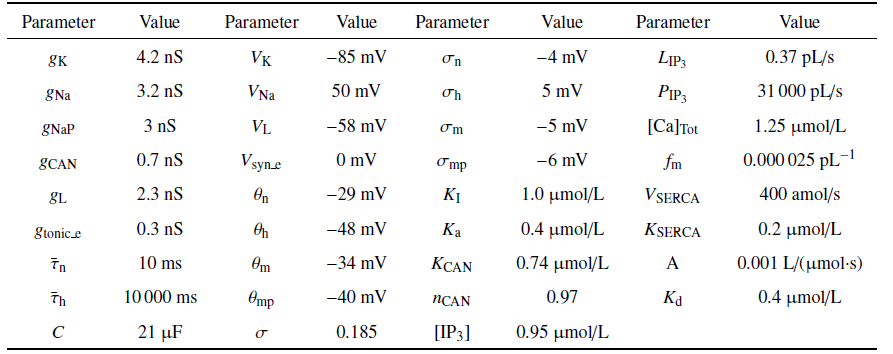
式中, $V$是膜电位, $C$是膜电容, $n$和$h$是电压门控钾和钠通道的门控变量. $I_{{ K}}$, $I_{{ Na}}$, $I_{{ NaP}}$, $I_{{ CAN}}$, $I_{{ L}}$和$I_{{ tonic\_e}}$分别代表钾电流、钠电流、 持续钠电流、 钙激活的非特异性阳离子电流、 漏电流和兴奋性刺激产生的电流. $I$是外部刺激的直流电. [Ca]是指细胞内钙浓度, $l$表示未被灭活的IP$_{3}$通道, 该通道会影响由$J_{{{ ER}}_{{ IN}}}$和$J_{{{ ER}}_{{ OUT}}}$表示的胞浆和内质网之间钙的通量.
磁通量$\varphi$可以描述电磁感应和磁场的影响, 而$\rho \left( \varphi\right)$是磁通控制忆阻器的记忆电导, 用来描述磁通量$\varphi$与膜电位$V$之间的关系, 其表达式为$\rho \left( \varphi \right)=\alpha +3\beta\varphi^{2}$, 式中$\alpha $, $\beta $是给定的参数值. $k_{1}V\rho \left(\varphi \right)$用于描述电磁感应引起的感应电流. $k_{1}$和$k_{2}$描述膜电位与磁通量之间的相互作用. 定义$I_{ app}=I-k_{1}V\rho \left( \varphi \right)$. 各离子电流表示为
$I_{{ K}}=g_{{ K}}n^{4}\left( V-V_{{ K}} \right)$
$I_{{ Na}}=g_{{ Na}}m_{\infty}^{3}\left( V \right)\left( 1-n \right)\left( V-V_{{ Na}} \right)$
$I_{{ NaP}}=g_{{ NaP}}{mp}_{\infty}\left( V \right)h\left( V-V_{{ Na}} \right)$
$I_{{ CAN}}=g_{{ CAN}}f\left( [Ca] \right)\left( V-V_{{ Na}} \right)$
$I_{{ L}}=g_{{ L}}\left( V-V_{{ L}} \right), \ \ I_{{ tonic\_ e}}=g_{{ tonic\_e}}\left( V-V_{{ syn\_ e}} \right)$
平衡函数$n_{\infty}\left( V \right)$, $h_{\infty}\left( V \right)$, $m_{\infty}\left( V \right)$, ${mp}_{\infty}\left( V \right)$具有如下形式
$x_{\infty}\left( V \right)={1/{\left[ 1+\exp\left( V-{\theta_{x}/\sigma_{x}} \right) \right], \ \ x\in \left\{ n, h, m, mp \right\}}}$
$\tau_{x}\left( V \right)={\bar{\tau }_{x}/{\cosh\left[{\left( V-\theta_{x} \right)/{2\sigma_{x}}} \right], x\in\left\{ n, h \right\}}}$
$f\left( [Ca] \right)={1/\left[ 1+\left({K_{{ CAN}}/[Ca]} \right)^{n_{{ CAN}}} \right]}$
$J_{{{ ER}}_{{ IN}}}={ L_{{{ IP}}_{{ 3}}}+P_{{{ IP}}_{{ 3}}} \left[ \frac{[ {{ IP}}_{{ 3}} ][ { Ca} ]l}{( [ {{ IP}}_{{ 3}} ]+K_{{ I}} )( [ { Ca} ]+K_{{ a}} )} \right]^{3} } \cdot ( [ { Ca} ]_{{ ER}}-[ { Ca} ] )$
$J_{{{ ER}}_{{ OUT}}}=V_{{ SERCA}}\frac{\left[ { Ca} \right]^{2}}{K_{{ SERCA}}^{{ 2}}+\left[ { Ca} \right]^{2}}$
$\left[ { Ca} \right]_{{ ER}}=\frac{\left[ { Ca} \right]_{{ Tot}}{ -}\left[ { Ca} \right]}{\sigma }$
本文设置${ [IP_3]}=0.95$ $\mu$mol/L, 使[Ca]处于活跃状态, 即呈现周期波动. 参数取值详见表1 .
2 主要结果
采用快慢分解的方法来研究系统放电模式的动力学. 为了清楚地识别不同变量的时间尺度, 对整个系统(1a) $\sim$ (1f)进行了无量纲化处理[25 ] .
2.1 无量纲化分析
重新对变量进行缩放来揭示各变量的时间尺度. 为此, 定义电压、钙、磁通量和时间的无量纲变量$v, c, \bar{\varphi }, \tau $以及其对应的标度, 分别为$Q_{v}$, $Q_{c}$, $Q_{\bar{\varphi }}$和$Q_{\tau}$
$V=Q_{ v} \cdot v, \ \ [Ca]=Q_{ c} \cdot c, \ \ \varphi =Q_{\bar{\varphi }} \cdot \bar{\varphi}, \ \ t=Q_{\tau } \cdot \tau$
注意到$n$, $h$和$l$在方程中已经是无量纲的.
由于膜电位$V\in [-70,-5]$, 在这个范围下定义$T_{x}={ max}\left( {1/{\tau_{x}\left( V \right)}} \right)$, $x\in\left\{ n, h \right\}$和$t_{x}\left( V \right)=T_{x}\tau_{x}\left( V \right)$. 而$[Ca]\in [0, 1]$, 在这个范围下定义
$G\left( [Ca] \right)=\frac{\left[ {{ IP}}_{{ 3}}\right]\left[ { Ca} \right]}{\left( \left[ {{ IP}}_{{ 3}} \right]+{ K}_{{ I}} \right)\left( \left[ { Ca}\right]+{ K}_{{ a}} \right)}$
$g_{{ SERCA}}\left([Ca] \right)=V_{{ SERCA}}\frac{[Ca]}{K_{{ SERCA}}^{{ 2}}+\left[ { Ca}\right]^{2}}$
$P_{ max}={ max}\left\{ L_{{{ IP}}_{{ 3}}}, P_{{{ IP}}_{{ 3}}} \cdot G_{{ c}}, G_{{ S}} \right\}$
$G_{{ c}}={ max}\left( G^{3}\left( [Ca] \right) \right)$
$G_{{ S}}={ max}\left( g_{{ SERCA}}\left( [Ca] \right) \right)$
$g_{ max}={ max}\left\{g_{{ K}}, g_{{ Na}}, g_{{ NaP}}, g_{{ CAN}}, g_{{ L}}, g_{{ tonic\_e}}, I, k_{1} \right\}.$
把这些变量代入方程(1a) $\sim$ (1f), 得到以下系统
(2a) $\begin{align} \frac{C}{Q_{ t} \cdot g_{ max}}\frac{{ d}v}{{ d}\tau }=-\bar{g}_{ K}n^{4}\left( v-\bar{V}_{{ K}} \right) - \\ \bar{g}_{{ Na}}m_{\infty}^{3}\left( v \right)\left( 1-n \right)\left( v-\bar{V}_{{ Na}} \right)- \\ \bar{g}_{{ NaP}} {mp}_{\infty}\left( v \right)h\left( v-\bar{V}_{{ Na}} \right) - \\ \bar{g}_{{ CAN}}f\left( c \right)\left( v-\bar{V}_{{ Na}} \right)-\bar{g}_{{ L}}\left( v-\bar{V}_{{ L}} \right)- \\ \bar{g}_{ tonic\_e}\left( v-\bar{V}_{{ syn\_e}} \right)+\bar{I}-\bar{k}_{{ 1}}v\rho ( \varphi ) \end{align}$
(2b) $\frac{1}{Q_{ t} \cdot T_{ n}}\frac{{ d}n}{{ d}\tau }={\left[ n_{\infty}\left( v \right)-n \right]/{t_{ n}\left( v \right)}}$
(2c) $\frac{1}{Q_{ t} \cdot T_{ h}}\frac{{ d}h}{{ d}\tau }={\left[ h_{\infty}\left( v \right)-h \right]/{t_{ h}\left( v \right)}}$
(2d) $\frac{1}{Q_{ t}}\frac{{ d}\bar{\varphi }}{{ d}\tau }=v-\bar{k}_{2}\bar{\varphi}$
(2e) $\frac{\sigma }{Q_{ t} \cdot P_{ max} \cdot f_{{ m}}}\frac{{ d}c}{{ d}\tau }=\left[ \bar{L}_{{{ IP}}_{{ 3}}}+\bar{P}_{{{ IP}}_{{ 3}}}G^{3}\left( c \right)l^{3} \right] \cdot \\ \left( \left[ \bar{Ca} \right]_{{ Tot}}-c-\sigma \cdot c \right) -\bar{g}_{{ SERCA}}\left( c \right) \cdot c \cdot \sigma$
(2f) $\frac{1}{Q_{ t} \cdot Q_{ c} \cdot A}\frac{{ d}l}{{ d}\tau }=\bar{K}_{ d}\left( 1-l \right)-cl$
$\bar{g}_{{ x}}={g_{{ x}}/g_{ max}}, { x}\in\left\{ { K, Na, NaP, CAN, L, tonic\_ e} \right\}$
$\bar{V}_{{ x}}={V_{{ x}}/Q_{{ v}}}, \ \ { x}\in\left\{ { K, Na, L, syn\_ e} \right\}$
$\bar{I}={I/\left( Q_{{ v}} \cdot g_{ max}\right)}, \ \ \bar{k}_{1}={k_{1}/g_{ max}}$
$\bar{k}_{2}=k_{2}, \ \ \bar{\varphi }={\varphi /Q_{\bar{\varphi }}}, \ \ \bar{L}_{{{ IP}}_{{ 3}}}={L_{{{ IP}}_{{ 3}}}/P_{ max}}$
$\bar{P}_{{{ IP}}_{{ 3}}}\left( c \right)={P_{{{ IP}}_{{ 3}}}/P_{ max}}$
$\bar{g}_{{ SERCA}}\left( c \right)={{g_{{ SERCA}}\left( [Ca]\right)}/P_{ max}}, \ \ \bar{K}_{{ d}}={K_{{ d}}/Q_{{ c}}}$
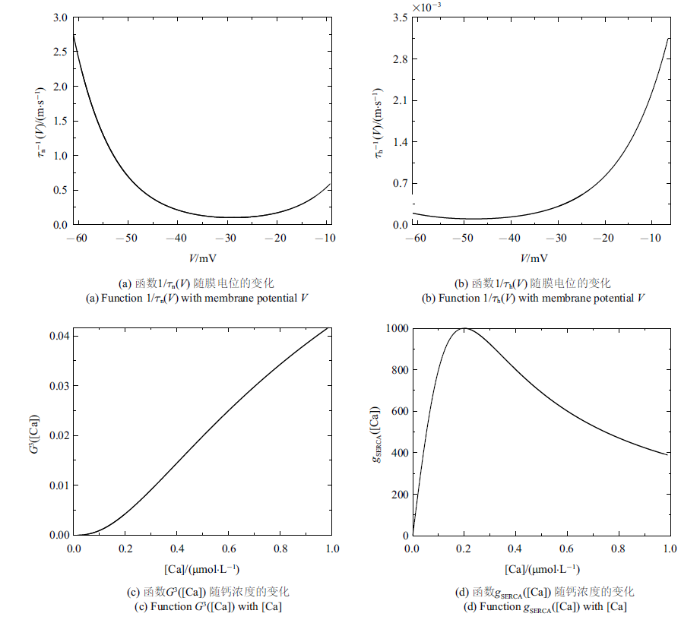
结合$V$, $\varphi $和[Ca]的范围, 取$Q_{ v}=Q_{\bar{\varphi }}=100$ mV, $Q_{ c}=1$ $\mu$m. $m_{\infty}\left( V \right)$, ${mp}_{\infty}\left( V \right)$, $n_{\infty}\left( V\right)$, $h_{\infty}\left( V \right)$, $f\left( [Ca]\right)\cdot$ $G\left( [Ca] \right)$, $\bar{g}_{{ SERCA}}\left([Ca] \right)$, $n$, $h$和$l$的值均在$\left[ 0, 1 \right]$范围内. 结合表1 中的参数值和文中变量的取值, $g_{ max}=\left| I_{ max}\right|=35$ $\mu$A. 由${1/{\tau_{ n}\left( V \right)}}$和${1/{\tau _{ h}\left( V \right)}}$与$V$的关系可得: $T_{ n}\approx 2.5$ ms$^{-1}$和$T_{ h}\approx 0.003 5$ ms$^{-1}$ (如图1 (a)和图1 (b)). 同理, 由$G_{{ c}}$和$G_{{ S}}$与[Ca]的关系可得$G_{{ c}}\approx 0.042$和$G_{{ S}}\approx 1000$ pL/ms (如图1 (c)和图1 (d)), 故有$P_{ max}\approx1302$ pL/ms. 将这些值代入(2a) $\sim$ (2f), 可使方程(2a) $\sim$ (2f)右侧的所有项均以1为(绝对值)界. 选择快时间尺度即$Q_{ t}=1 { ms}$作为参考时间, 方程左边导数的系数能够揭示变量的相对变化速率
图1
图1
无量纲化过程中的函数图像
Fig.1
Function graph in the nondimensionalization process
$C/(Q_{ t}\cdot g_{ max})=0.6\ \ { ms} \sim O(1)\ { ms}$
$1/(Q_{ t}\cdot T_{ n})\approx 0.4\ \ { ms}\sim O(1)\ { ms}$
$1/(Q_{ t}\cdot T_{ h})\approx 285.71\ \ { ms} \sim {O}(100)\ { ms}$
$1/Q_{ t}=1\ \ { ms} \sim {O}(1)\ { ms}$
$\sigma/(Q_{ t} \cdot P_{ max} \cdot f_{ m})\approx 5.68\ \ { ms}\sim O(10)\ { ms}$
$1/(Q_{ t}\cdot Q_{ c} \cdot A)=1000 \ \ { ms}\sim O(1000)\ { ms}$
(3a) $R_{ v}\triangleq \frac{C}{Q_{ t} \cdot g_{\max}}={O}\left( 1 \right)$
(3b) $R_{ n}\triangleq\frac{1}{Q_{ t} \cdot T_{ n}}= {O}\left( 1 \right)$
(3c) $R_{ h}\triangleq\frac{1}{Q_{ t} \cdot T_{ h}}= {O}\left( 100 \right)$
(3d) ${R}_{\bar{\varphi }}\triangleq\frac{1}{Q_{ t}}= {O}\left( 1 \right)$
(3e) $R_{ c}\triangleq\frac{\sigma }{Q_{ t} \cdot P_{ max} \cdot f_{{ m}}}= {O}\left( 10 \right)$
(3f) $R_{ l}\triangleq\frac{1}{Q_{ t} \cdot Q_{ c \cdot A}}= {O}\left( 1000 \right)$
则无量纲系统(2a) $\sim$ (2f)即为系统(4a) $\sim$ (4f)
(4a) $\begin{align} R_{ v}\frac{{ d}v}{{ d}\tau }=-\bar{g}_{{ K}}n^{4}\left( v-\bar{V}_{ K} \right)- \\ \bar{g}_{{ Na}}m_{\infty}^{3}\left( v \right)\left( 1-n \right)\left( v-\bar{V}_{{ Na}} \right)- \\ \bar{g}_{{ NaP}}{mp}_{\infty}\left( v \right)h(v-\bar{V}_{ Na} )-\bar{g}_{{ CAN}}f\left( c \right)\left( v-\bar{V}_{{ Na}} \right)- \\ \bar{g}_{{ L}}\left( v-\bar{V}_{L} \right)-\bar{g}_{{ tonic\_ e}}\left( v-\bar{V}_{{ syn\_ e}} \right)+ \\ \bar{I}-\bar{k}_{{ 1}}v\rho \left( \varphi \right)=f_{1}\left( v, n, h, c, I, \varphi \right) \end{align}$
(4b) $R_{ n}\frac{{ d}n}{{ d}\tau }={\left( n_{\infty}\left( v \right)-n \right)/{t_{ n}\left( v \right)=}}{{f_{2}\left( v, n \right)}/{t_{ n}\left( V \right)}}$
(4c) $R_{ h}\frac{{ d}h}{{ d}\tau }={\left( h_{\infty}\left( v \right)-h \right)/{t_{ h}\left( v \right)=}}{{f_{3}\left( v, h \right)}/{t_{ h}\left( V \right)}}$
(4d) $R_{\bar{\varphi }}\frac{{ d}\bar{\varphi }}{{ d}\tau }=v-\bar{k}_{2}\bar{\varphi }=f_{4}\left( v, \varphi \right)$
(4e) $R_{ c}\frac{{ d}c}{{ d}\tau }=\left( \bar{L}_{{{ IP}}_{{ 3}}}+\bar{P}_{{{ IP}}_{{ 3}}}G^{3}\left( c \right)l^{3} \right) \cdot \left( \left[ \bar{Ca} \right]_{{ Tot}}-c-\bar{\sigma } \cdot c \right)- \\ \bar{g}_{{ SERCA}}\left( c \right) \cdot c \cdot \bar{\sigma }=g_{1}\left( c, l \right)$
(4f) $R_{ l}\frac{{ d}l}{{ d}\tau }=\bar{K}_{{ d}}\left( 1-l \right)-cl=g_{2}\left( c, l \right)$
式中$R_{ v}$, $R_{ n}$, $R_{ h}$, $R_{\bar{\varphi }}$, $R_{ c}$和$R_{ l}$是方程(3a) $\sim$ (3f)中给出的无量纲参数.
$R_{ v}={O}\left( 1 \right), \ \ R_{ n}={O}\left( 1 \right), \ \ R_{ h}={O}\left( 100 \right)$
$R_{\bar{\varphi }}={O}\left( 1 \right), \ \ R_{ c}={O}\left( 10 \right), \ \ R_{ l}={O}\left( 1000 \right)$
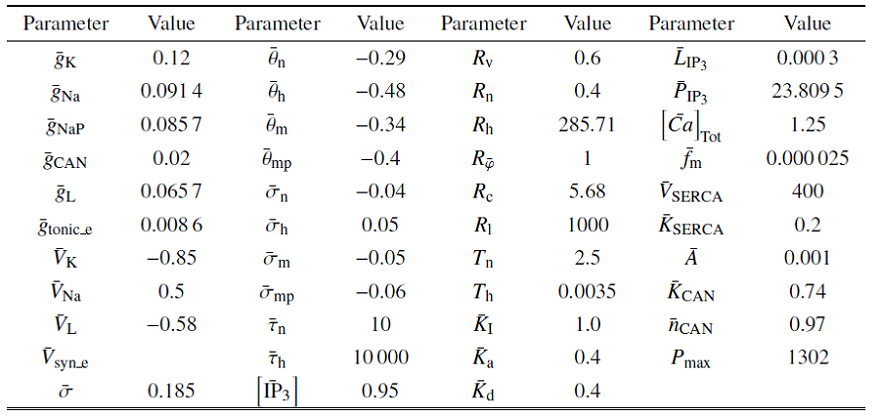
由此可得 $v$, $n$, $\bar{\varphi}$在一个快速的时间尺度上演化, $h$和$c$在一个较慢的时间尺度上演化, 而$l$在一个超慢的时间尺度上演化, 即模型具有3个不同的时间尺度. 因此, 上述模型可以被视作包含快、慢和超慢变量的动力学模型. 方程(1a), (1b)和(1d)构成快子系统, (1c)和(1e)为慢子系统, 方程(1f)是超慢子系统. 无量纲变换后的参数取值详见表2 .
$\bar{x}={x/Q_{ v}}, \ x\in \{ \theta_{ n}, \ {\theta }_{ h}, \ {\theta }_{ m}, \ {\theta }_{ mp}, {\sigma }_{ n}, \ {\sigma }_{ h}, \ { \sigma }_{ m}, \ {\sigma }_{ mp} \}, $
$\bar{y}=y, y\in \{ \sigma , \ \left[ {{ IP}}_{3} \right], \ {f}_{ m}, \ A, \ {K}_{ I}, \ {K}_{ a}, {K}_{ CAN}, \ {n}_{ CAN}, \ {V}_{ SERCA}, \ {K}_{ SERCA} \}$
实验表明Ca$^{2+}$振荡起源于pre-BötC神经元的树突[41 ] , 因此仅在树突室中包含Ca$^{2+}$动力学, 其中Ca$^{2+}$的动力学受细胞内Ca$^{2+}$浓度[Ca]和IP$_{3}$通道门控变量$l$控制. 方程(1a) $\sim$ (1f)称为全系统. 当使用单室模型时, 模型中没有树突部分, 不过本文沿用Park和Rubin[38 ] 的命名方式, 称子系统(1a) $\sim$ (1d)为胞体子系统, 子系统(1e) $\sim$ (1f)为树突子系统. $l$的变化间接影响胞体子系统 (1a) $\sim$ (1d), 因为$l$会影响[Ca], [Ca]会影响$V$, 且这种影响是单向的, 但$l$不直接出现在膜电位$V$的方程中, 即树突子系统独立于胞体子系统, 而胞体子系统却受到树突子系统的影响. 下面主要对无量纲化之后的系统(4a) $\sim$ (4f)进行研究.
2.2 无外界刺激($\bar{I}_{ \mathbf{app}}\mathbf{=0}$)时的放电模式和分岔分析
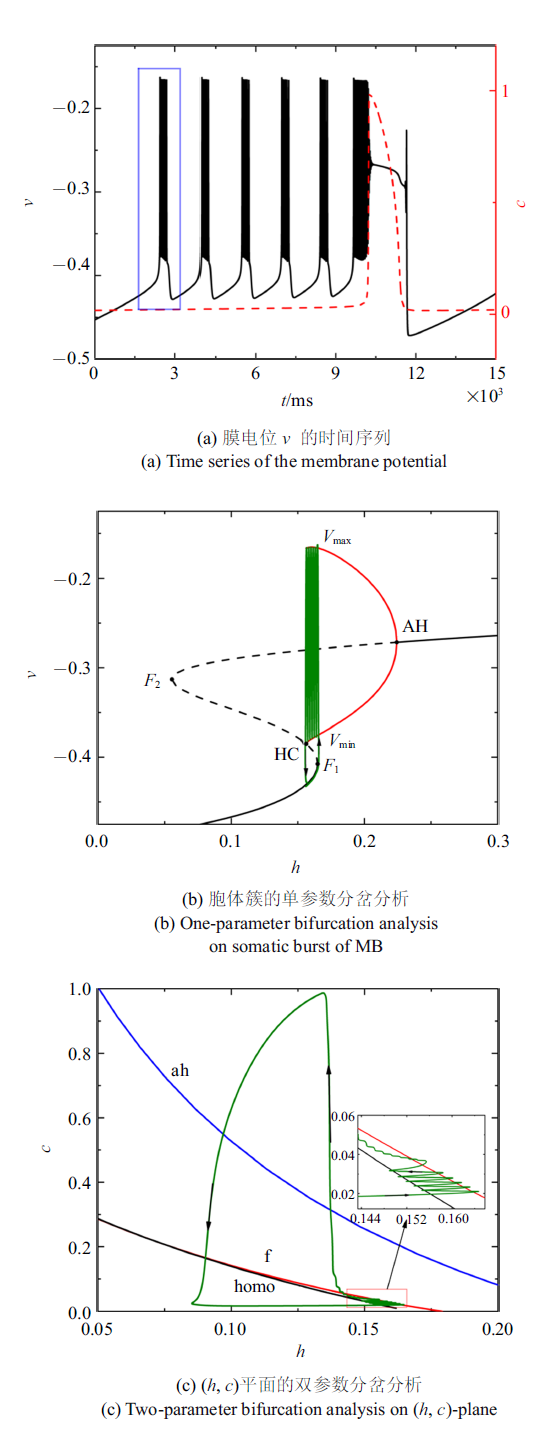
当外部电磁刺激$\bar{I}_{{ app}}=0$时, 系统(4a) $\sim$ (4f)的放电模式如图2 (a)所示. 黑色实线是膜电位$v$随时间$t$的变化过程, 红色和蓝色虚线分别是细胞内钙浓度$c$和门控变量$h$随时间$t$的变化过程. 一个周期内的混合簇通过细胞内Ca$^{2+}$浓度是否产生波动来区分胞体簇和树突簇. 随着时间的延长, 胞体部分的钙浓度几乎保持不变, 而在树突部分钙浓度会出现周期性波动. ($\star)$表示初始时刻. 第一个胞体簇放电由静息态转迁为放电态($\bullet$)和由放电态跃迁回静息态($\blacksquare$)时分岔发生的关键点如图2 (a)所示.
图2
图2
$\bar{I}_{{ app}}=0$时的混合簇放电模式和分岔分析
Fig.2
Firing patterns and bifurcation analysis when $\bar{I}_{{ app}}=0$
无量纲化的结果表明, $c$和$h$都属于慢变量. 但是在胞体部分$c$几乎不变, 从而在胞体部分$h$的相对演化速率比$c$快. 所以, 在分析胞体簇时, 可将慢变量$h$作为胞体子系统的分岔参数, 而将$c$看作常数, 研究快子系统的动力学. 树突部分$c$的突然增大, 导致在$c$和$h$两个慢变量中, $c$的相对演化速率比$h$快, 故分析树突簇时要将慢变量$c$作为树突子系统的分岔参数而把$h$看做常数, 即细胞内钙浓度是否产生波动不仅可以区分胞体部分和树突部分, 而且可以决定每一部分的分岔参数.
由于混合簇中胞体部分的簇的类型都相同, 所以只对第一个胞体簇进行分岔分析. 以$h$为慢变量, 取第一个胞体簇所对应的$c$的平均值为$0.020 7$, 对应快子系统的分岔如图2 (b)所示. 平衡点形成S形曲线, 曲线的下分支(黑色实线)和中支(黑色虚线)分别由稳定结点和不稳定鞍点组成. 曲线的上分支由稳定和不稳定的焦点组成, 不稳定焦点经由Andronov-Hopf (AH)分岔变为稳定焦点, 并在AH分岔处产生稳定的极限环(红色实线). 稳定极限环通过同宿轨分岔(HC)消失. 点$F_{1}$和$F_{2}$表示平衡点的鞍结分岔. 全系统的轨线(绿色曲线)也叠加在分岔图上. 当慢变量$h$增大时, S形曲线下支的静息态经由平衡点的鞍结分岔$F_{1}$跃迁至上支的稳定极限环, 并由于稳定极限环的吸引反复振荡, 振荡态经由同宿轨分岔(HC)跃迁至下支的静息态, 从而完成了一个周期振荡. 根据Izhikevich簇放电分类的标准[42 ] , 此时的簇放电模式为"fold/homoclinic"型簇放电.
快子系统在($h$, $c)$平面上的双参数分岔如图2 (c)所示, 其中f, ah, homo分别代表鞍结分岔曲线(红色), AH分岔曲线(蓝色)和同宿轨分岔曲线(黑色). 在本文选取的参数范围内, 双参数平面中没有出现余维2分岔. 全系统的轨线(绿色)也叠加在($h$, $c$)平面上. 插图是局部放大, 分岔发生的关键点与图2 (a)对应, ($\star$)仍表示初始时刻. 结果表明, ($h$, $c$) 平面的全系统轨线为逆时针方向, 随着慢变量$c$的逐渐增大, 轨线在鞍结分岔曲线$f $和同宿轨分岔曲线homo之间来回穿梭, 意味着混合簇中胞体簇的产生与这两类分岔相关. 全系统轨线在鞍结分岔曲线和同宿轨分岔曲线之间跃迁5次, 对应于混合簇中的5个胞体簇. 之后, $c$的突然增大, 使得混合簇的胞体部分结束, 转换到树突部分.
2.3 电流对混合簇放电模式的影响和动力学分析
设置参数$\bar{k}_{1}=0.002 86$, $\bar{k}_{2}=3$, $\bar{\alpha }=1$, $\bar{\beta }=0.000 06$. 本节研究电流对混合簇的影响. 无量纲化之后电流$\bar{I}$所对应无量纲化之前$I$的值见表3 .
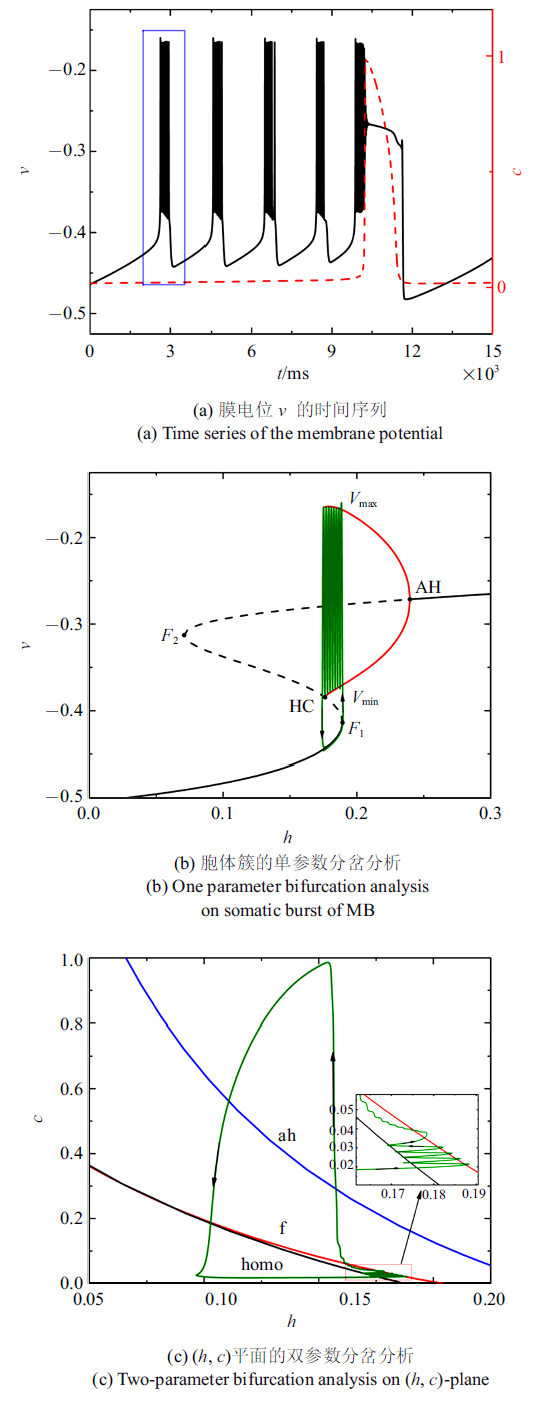
当电流$\bar{I}=-0.000 57$时, 全系统(4a) $\sim$ (4f)呈现混合簇放电状态, 如图3 (a)所示. $c$取第一个胞体簇所对应的平均值$c=0.020 7$. 图3 (b)和图3 (c)分别是对应第一个胞体簇的快子系统的单、双参数分岔图. 与$\bar{I}_{{ app}}=0$类似, 胞体簇的簇放电模式为"fold/homoclinic"型簇放电. 在$c$突然增大之前, 全系统轨线在鞍结分岔和同宿轨分岔曲线之间跃迁5次, 对应混合簇的5个胞体簇.
图3
图3
$\bar{I}=-0.000 57$时的混合簇放电模式和分岔分析
Fig.3
Firing patterns and bifurcation analysis when $\bar{I}=-0.000 57$
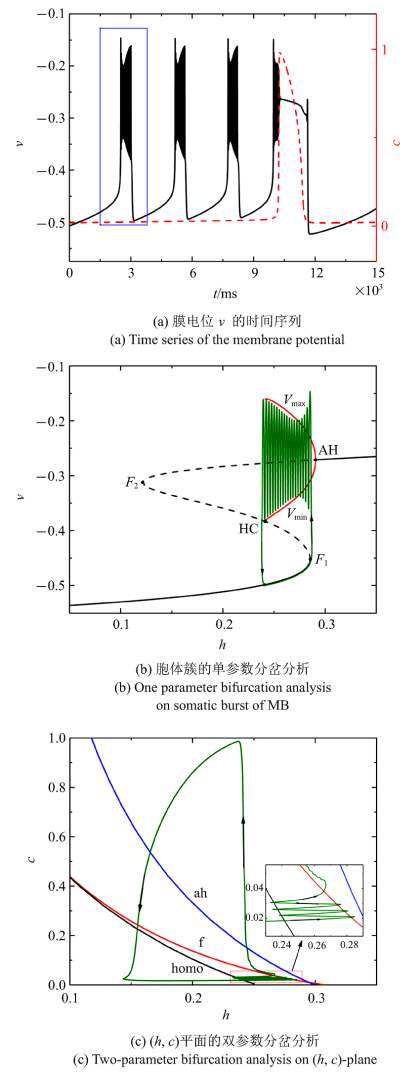
随着电流的减小, 混合簇中胞体簇的个数也在减少. 图4 (a) $\sim\!$图4 (c)分别是电流值$\bar{I}=-0.001 43$时的全系统簇放电模式以及单、双参数分岔分析($c$取平均值0.020 5). 胞体簇的个数减少为4个, 与之对应, ($h$, $c$) 平面双参数分岔分析中全系统轨线在鞍结分岔曲线与同宿轨分岔曲线之间跃迁4次. 此时, 胞体簇的放电类型仍为"fold/homoclinic"型簇放电.
图4
图4
$\bar{I}=-0.001 43$时的混合簇放电模式和分岔分析
Fig.4
Firing patterns and bifurcation analysis when $\bar{I}=-0.001 43$
当$\bar{I}$减小为$-0.004 29$时, 混合簇中胞体簇的个数减少为3个, 如图5 (a)所示. $c$取平均值0.020 2, 对胞体簇进行单参数分岔分析. 簇放电类型仍是"fold/homoclinic"型簇放电, 如图5 (b)所示. ($h$, $c$)平面双参数分岔分析中全系统轨线在鞍结分岔曲线与同宿轨分岔曲线之间来回跃迁3次, 与混合簇中的3个胞体簇相对应, 如图5 (c)所示.
图5
图5
$\bar{I}=-0.004 29$时的混合簇放电模式和分岔分析
Fig.5
Firing patterns and bifurcation analysis when $\bar{I}=-0.004 29$
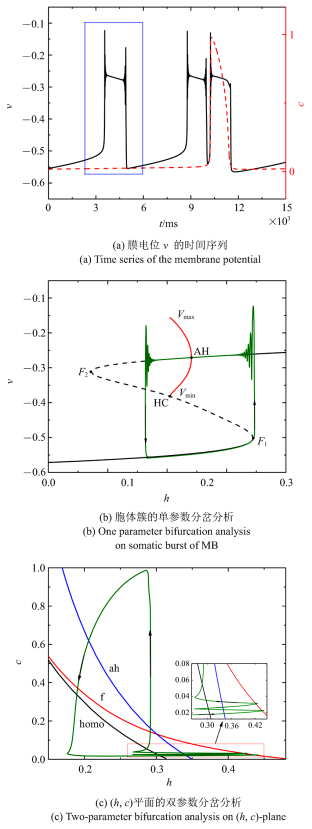
当$\bar{I}$减小为$-0.007 14$时, 混合簇中胞体簇的个数会继续减少为两个, 如图6 (a)所示. 单参数分岔分析($c =0.021 3$)如图6 (b)所示. 与前面情况不同, 全系统轨线从下静息态通过鞍结分岔($F_{1}$)转变为放电状态. 由于稳定焦点的吸引, 振荡的幅度迅速减小, 直到轨线穿过AH分岔. 然后, 由于不稳定焦点的排斥和稳定极限环的吸引作用, 轨线的振幅又开始逐渐增大, 最终从放电状态过渡到较低的静息状态, 完成周期振荡. 因此, 此时的放电状态转变为经由"fold/homoclinic"滞后环的"Hopf/Hopf"型簇放电. 双参数分岔分析如图6 (c)所示, 在$c$突然增加之前, 全系统轨线在鞍结分岔曲线与同宿轨分岔曲线之间跃迁两次.
图6
图6
$\bar{I}=-0.007 14$时的混合簇放电模式和分岔分析
Fig.6
Firing patterns and bifurcation analysis when $\bar{I}=-0.007 14$
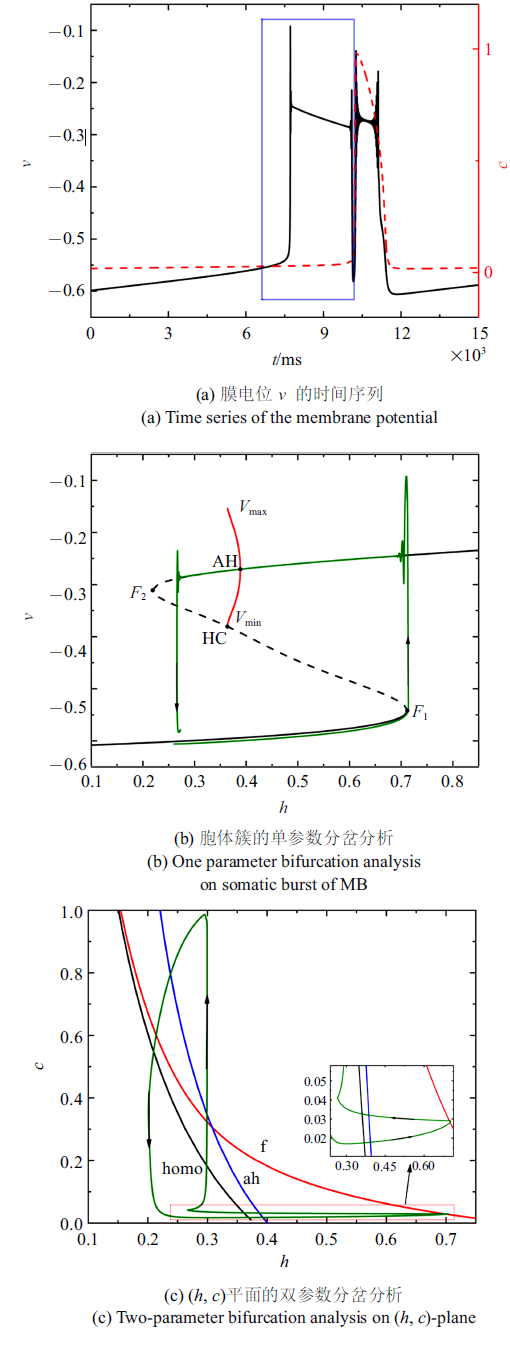
当$\bar{I}$减小至$-0.01$时, 混合簇中胞体簇的个数减少为一个, 如图7 (a)所示. 胞体簇的单参数分岔分析($c= 0.028 5$)如图7 (b)所示. 与$\bar{I}=-0.007 14$时的情况相同, 簇放电类型为经由"fold/homoclinic"滞后环的"Hopf/Hopf"型簇放电. 全系统轨线在鞍结分岔曲线与同宿轨分岔曲线之间跃迁一次, 如图7 (c)所示.
图7
图7
$\bar{I}=-0.01$时的混合簇放电模式和分岔分析
Fig.7
Firing patterns and bifurcation analysis when $\bar{I}=-0.01$
本节给出了簇放电行为如何随$\bar{I}$的变化而变化. 利用快慢分解和分岔分析对不同电流值下的混合簇中的胞体簇进行分类, 并揭示了混合簇的产生机制. 随着电流值$\bar{I}$的减小, 混合簇中胞体簇的个数逐渐减少, 同时簇的放电类型发生改变. 树突簇在不同电流值下的放电模式也有所不同. 双参数分岔分析中, 随着$c$的逐渐增大, 全系统轨线在鞍结分岔曲线和同宿轨分岔曲线之间跃迁, 意味着混合簇中胞体簇的产生与这两类分岔相关. 全系统轨线在鞍结分岔曲线和同宿轨分岔曲线之间跃迁的次数, 与混合簇中胞体簇的个数相对应.
2.4 磁流对混合簇的影响
固定$\bar{I}=0$, 设置参数$\bar{k}_{2}=3$, $\bar{\alpha }=1$, $\bar{\beta}=0.000 06$研究磁流反馈系数$\bar{k}_{1}$对混合簇的影响. 参数$\bar{k}_{1}$所对应$k_{1}$的值参见表4 .
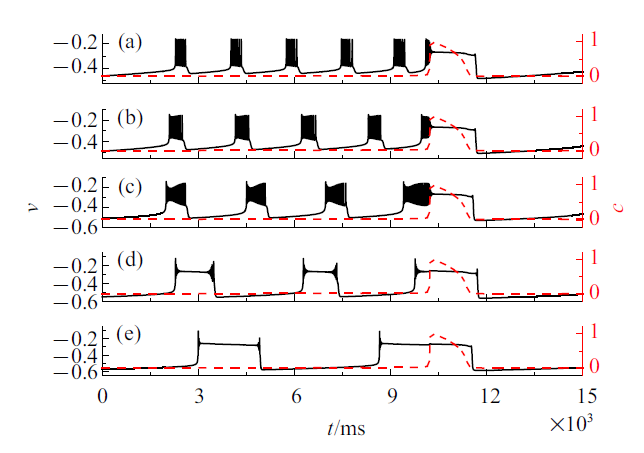
系统(4a) $\sim$ (4f)在不同$\bar{k}_{1}$值下的混合簇放电模式如图8 所示. 黑色实线是膜电位$v$随时间$t$的变化过程, 红色虚线是细胞内钙浓度$c$随时间$t$的变化过程. 与电流的影响类似, 随着$\bar{k}_{1}$的减小, 混合簇中胞体簇的个数逐渐减少, 同时簇放电类型改变. 树突簇在不同电流值下的放电模式也有所不同.
图8
图8
不同$\bar{k}_{1}$值时的混合簇放电模式 ($\bar{I}=0$)
Fig.8
Firing patterns of mixed bursting with different $\bar{k}_{1}(\bar{I}=0)$
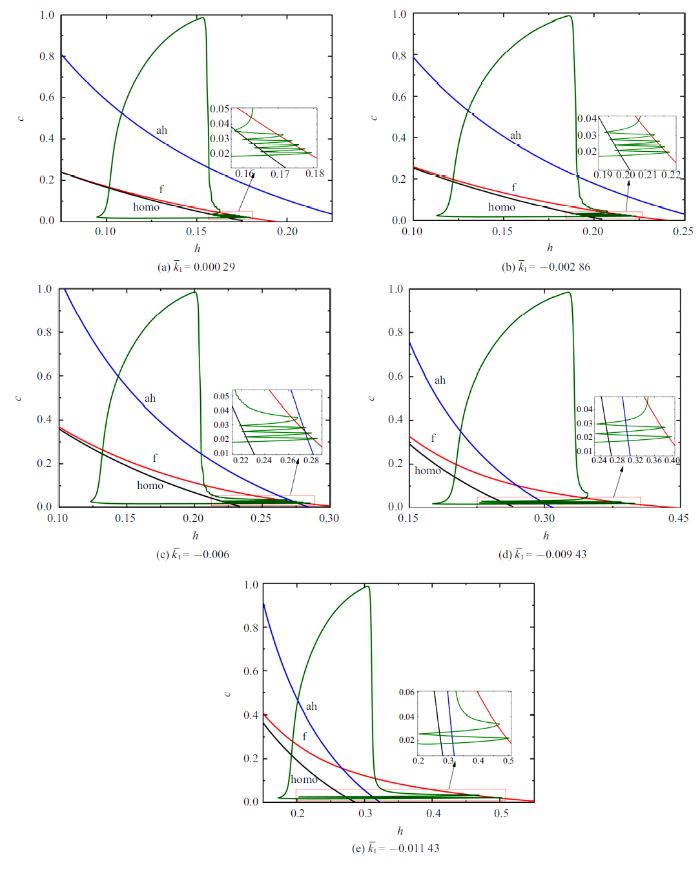
不同$\bar{k}_{1}$值所对应的双参数分岔分析如图9 所示. 随着$\bar{k}_{1}$的减小, 混合簇中胞体簇的个数由5个减少至1个, 全系统轨线在鞍结分岔曲线和同宿轨分岔曲线之间跃迁次数与混合簇中胞体簇的个数相同.
图9
图9
不同$\bar{k}_{1}$值时的双参数分岔分析 ($\bar{I}=0$)
Fig.9
Two-parameter bifurcation analysis with different $\bar{k}_1$ values ($\bar{I}=0$)
3 结论和展望
神经系统十分复杂, 包括不同的空间层次、不同的功能状态(生理、病理和药理状态)和不同的动力学行为. 参数激励下的多时间尺度非线性系统可以产生非常复杂的簇放电行为. 探讨簇放电模式各种可能的诱发机制一直是簇放电研究的重要问题之一. 虽然pre-BötC神经元中混合簇放电行为已有一定的研究, 但电流和磁流影响混合簇放电的研究不多. 模型所描述的规律应该独立于量纲的影响, 与已有的直接分析神经元动力学行为方法不同, 本文排除量纲的影响, 对模型进行无量纲化处理, 利用无量纲量来分析神经元混合簇放电、转迁行为, 保持了与原始数据变化趋势整体的一致性和关联系数一致性, 为揭示神经元复杂动力学行为提供了新的分析方法, 进一步丰富了神经元非线性动力学行为的内容.
本研究用忆阻器模拟磁通量, 在Butera神经元模型中引入电流和磁通量, 应用多时间尺度及分岔分析的方法, 分析电流和磁流对神经元混合簇放电模式的影响. 通过无量纲化的方法对时间尺度进行划分, 并用尺度变换后的无量纲动力系统进行分析. 通过将混合簇分为胞体部分和树突部分[38 ] , 区分了混合簇放电模式并对胞体簇进行了动力学分析. 研究表明: 电流和磁流都可以显著影响pre-BötC细胞的混合簇放电节律. 减小电流$\bar{I}$和磁流反馈系数$\bar{k}_{{ 1}}$的值会使混合簇中胞体簇的个数减少, 同时使簇放电类型由"fold/homoclinic"型簇放电转迁为经由"fold/homoclinic"滞后环的"Hopf/Hopf"型簇放电. 利用双参数分岔分析, 我们揭示了混合簇模式的产生机制. 如果全系统轨线可以在鞍结分岔曲线和同宿轨分岔曲线之间跃迁, 整个系统出现混合簇. 上述研究结果可以加深我们对神经元放电动力学的理解, 为电流和磁流对神经元放电模式的影响提供参考.
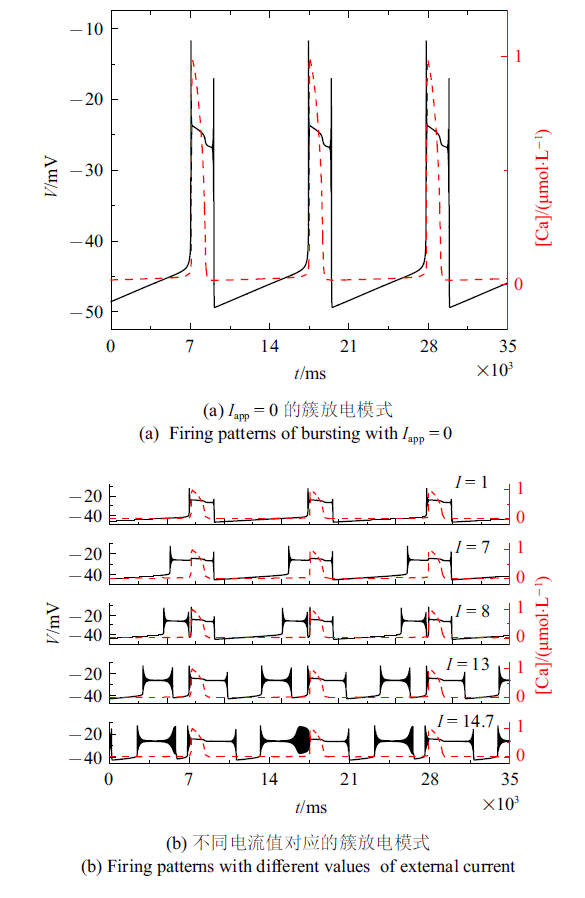
类似实验中, 药物刺激可以使一个周期内只有一种类型的簇转化为周期内含有两种或多种类型的混合簇[43 ] , 发现外部电流刺激也可以达到同样的效果.设置$k_{1}=0.1$, $k_{2}=3$ s$^{-1}$, $\alpha =1$ mol/(L$\cdot$$\Omega$), $\beta =0.000 06$ mol/(L$\cdot$$\Omega$$\cdot$${ V}^{2}$$\cdot$s$^{2}$)增大电流可使同一周期内含有两种或多种类型的簇, 如图10 (b)所示. 图10 (a)是相同离子浓度时$I_{{ app}}=0$的情况. 对这一现象的动力学分析, 更多讨论将在未来进一步研究. 除此之外, 也可以在模型中考虑噪声、时滞等因素, 模拟更复杂环境下的神经元模型, 对不同环境状态下的神经元模型进行动力学行为研究.
图10
图10
不同电流值所对应的混合簇放电模式 ($g_{ NaP}=1.7$ nS, $g_{ Na}=4.2$ nS, $g_{ K}=1.4$ nS, [IP$_{3}$] = 0.97 $\mu$mol/L)
Fig.10
The mixed bursting corresponding to different current values ($g_{ NaP}=1.7$ nS, $g_{ Na}=4.2$ nS, $g_{ K}=1.4$ nS, [IP$_{3}$] =0.97 $\mu$mol/L)
参考文献
View Option
[1]
Smith JC Ellenberger HH Ballanyi K , et al . Pre-Bötzinger complex: A brainstem region that may generate respiratory rhythm in mammals
Science 1991 , 254 (5032 ): 726 -729
DOI
URL
[本文引用: 1]
[2]
Rekling JC Feldman JL . Pre-Bötzinger complex and pacemaker neurons: Hypothesized site and kernel for respiratory rhythm generation
Annual Review of Physiology 1998 , 60 : 385 -405
DOI
URL
[本文引用: 1]
[3]
Solomon IC . Ionotropic excitatory amino acid receptors in pre-Bötzinger complex play a modulatory role in hypoxia-induced gasping in vivo
Journal of Applied Physiology 2004 , 96 (5 ): 1643 -1650
PMID
[本文引用: 1]
Activation of ionotropic excitatory amino acid (EAA) receptors in pre-Bötzinger complex (pre-BötC) not only influences the eupneic pattern of phrenic motor output but also modifies hypoxia-induced gasping in vivo by increasing gasp frequency. Although ionotropic EAA receptor activation in this region appears to be required for the generation of eupneic breathing, it remains to be determined whether similar activation is necessary for the production and/or expression of hypoxia-induced gasping. Therefore, we examined the effects of severe brain hypoxia before and after blockade of ionotropic EAA receptors in the pre-BötC in eight chloralose-anesthetized, deafferented, mechanically ventilated cats. In each experiment, before blockade of ionotropic EAA receptors in the pre-BötC, severe brain hypoxia (6% O2 in a balance of N2 for 3-6 min) produced gasping. Although bilateral microinjection of the broad-spectrum ionotropic EAA receptor antagonist kynurenic acid (20-100 mM; 40 nl) into the pre-BötC eliminated basal phrenic nerve discharge, severe brain hypoxia still produced gasping. Under these conditions, however, the onset latency to gasping was increased (P < 0.05), the number of gasps was reduced for the same duration of hypoxic gas exposure (P < 0.05), the duration of gasps was prolonged (P < 0.05), and the duration between gasps was increased (P < 0.05). These findings demonstrate that hypoxia-induced gasping in vivo does not require activation of ionotropic EAA receptors in the pre-BötC, but ionotropic EAA receptor activation in this region may modify the expression of the hypoxia-induced response. The present findings also provide additional support for the pre-BötC as the primary locus of respiratory rhythm generation.
[4]
Solomon IC Edelman NH Neubauer JA . Patterns of phrenic motor output evoked by chemical stimulation of neurons located in the pre-Bötzinger complex in vivo
Journal of Neurophysiology 1999 , 81 (3 ): 1150 -1161
DOI
URL
[本文引用: 1]
[5]
Koizumi H Smith JC . Persistent Na$+$ and K$+$-dominated leak currents contribute to respiratory rhythm generation in the pre-Bötzinger complex in vitro
Journal of Neuroscience 2008 , 28 (7 ): 1773 -1785
DOI
URL
[本文引用: 1]
[6]
Del Negro CA Hayes JA Rekling JC . Dendritic calcium activity precedes inspiratory bursts in pre-Bötzinger complex neurons
Journal of Neuroscience 2011 , 31 (3 ): 1017 -1022
DOI
URL
[本文引用: 1]
[7]
Ramirez JM Schwarzacher SW Pierrefiche O , et al . Selective lesioning of the cat pre-Bötzinger complex in vivo eliminates breathing but not gasping
Journal of Physiology 1998 , 507 (3 ): 895 -907
DOI
URL
[本文引用: 1]
[8]
VanDam RJ Shields EJ Kelty JD . Rhythm generation by the pre-Bötzinger complex in medullary slice and island preparations: Effects of adenosine A$_{1}$ receptor activation
BMC Neuroscience 2008 , 9 (1 ): 95 -111
DOI
URL
[9]
Krause KL Neumueller SE Marshall BD , et al . $\mu $-Opioid receptor agonist injections into the presumed pre-Bötzinger complex and the surrounding region of awake goats do not alter eupneic breathing
Journal of Applied Physiology 2009 , 107 (5 ): 1591 -1599
DOI
URL
[10]
Iovino L Mutolo D Cinelli E , et al . Breathing stimulation mediated by 5-HT$_{1A}$ and 5-HT$_{3}$ receptors within the pre-Bötzinger complex of the adult rabbit
Brain Research 2019 , 1704 : 26 -39
DOI
URL
[11]
Kruszynski S Stanaitis K Brandes J , et al . Doxapram stimulates respiratory activity through distinct activation of neurons in the nucleus hypoglossus and the pre-Bötzinger complex
Journal of Neurophysiology 2019 , 121 (4 ): 1102 -1110
DOI
PMID
Doxapram is a respiratory stimulant used for decades as a treatment option in apnea of prematurity refractory to methylxanthine treatment. Its mode of action, however, is still poorly understood. We investigated direct effects of doxapram on the pre-Bötzinger complex (PreBötC) and on a downstream motor output system, the hypoglossal nucleus (XII), in the transverse brainstem slice preparation. While doxapram has only a modest stimulatory effect on frequency of activity generated within the PreBötC, a much more robust increase in the amplitude of population activity in the subsequent motor output generated in the XII was observed. In whole cell patch-clamp recordings of PreBötC and XII neurons, we confirmed significantly increased firing of evoked action potentials in XII neurons in the presence of doxapram, while PreBötC neurons showed no significant alteration in firing properties. Interestingly, the amplitude of activity in the motor output was not increased in the presence of doxapram compared with control conditions during hypoxia. We conclude that part of the stimulatory effects of doxapram is caused by direct input on brainstem centers with differential effects on the rhythm generating kernel (PreBötC) and the downstream motor output (XII). NEW & NOTEWORTHY The clinically used respiratory stimulant doxapram has distinct effects on the rhythm generating kernel (pre-Bötzinger complex) and motor output centers (nucleus hypoglossus). These effects are obliterated during hypoxia and are mediated by distinct changes in the intrinsic properties of neurons of the nucleus hypoglossus and synaptic transmission received by pre-Bötzinger complex neurons.
[12]
Cinelli E Bongianni F Pantaleo T , et al . Activation of $\mu $-opioid receptors differentially affects the pre-Bötzinger complex and neighbouring regions of the respiratory network in the adult rabbit
Respiratory Physiology & Neurobiology 2020 , 280 : 103482
DOI
URL
[本文引用: 1]
[13]
王如彬 , 张志康 , 余婧 . 关于注意和记忆的神经动力学机制
力学学报 , 2006 , 38 (6 ): 816 -824
DOI
[本文引用: 1]
利用随机的相变动力学理论研究了一个具有不同相位的神经振子群模型,并考察神经振子群对刺激信息的处理及神经编码的动态演化. 通过对动力学模型的数值分析,在二维相空间上描述了神经元集群内不同振子簇发放动作电位时,数密度随时间演化的图像. 数值分析的结果表明该模型能够用来描述注意和记忆的神经动力学机制,并且证明了只有高维的神经动力学模型才能更深刻地描述神经元集群的动力学特性,而以往的编码模型丢失了大量有用的神经信息.
(Wang Rubin Zhang Zhikang Yu Jing . Mechanism of neurodynamics on attention and memory
Chinese Journal of Theoretical and Applied Mechanics 2006 , 38 (6 ): 816 -824 (in Chinese))
[本文引用: 1]
[14]
董玮 , 王如彬 , 张志康 . 大脑皮层信号作用下人体步态节律运动的探讨
应用数学和力学 , 2011 , 32 (2 ): 247 -252
[本文引用: 1]
(Dong Wei Wang Rubin Zhang Zhikang . Exploring human rhythmic gait movement in the role of cerebral cortex signal
Applied Mathematics and Mechanics 2011 , 32 (2 ): 247 -252 (in Chinese))
[本文引用: 1]
[15]
古华光 . 神经系统信息处理和异常功能的复杂动力学
力学学报 , 2017 , 49 (2 ): 410 -420
DOI
[本文引用: 2]
神经系统通过电活动实现信息处理及生物功能,电活动的节律和时空行为是功能的动力学表征.神经电生理实验结合理论模型,借助于分岔揭示了外界激励、参数和噪声调控下的周期、混沌和随机等多样性的节律模式及其节律的复杂转迁规律,揭示了感觉神经对信息(如血压压力信号和痛觉信息)的节律编码机制,揭示了突触噪声扩大脑神经元的信息传递能力并对能力强弱进行了分类,结果可用于提高信息检测能力和指导镇痛;借助于单神经元节律的动力学——如分岔和簇放电节律的快慢动力学——解释了网络功能异常的时空行为,如药物调控脑皮层的螺旋波/癫痫和慢抑制耦合调控的运动网络的同步转迁/运动模式异常,结果给出了调控系统功能的途径;通过大数据分析获得自闭症患者的脑功能网络的时空行为特征——症状相关脑区的同步活动降低,给出了用于诊断的潜在指标.通过新实验发现、新建理论模型、新分析方法和新观点阐释,揭示了神经系统的复杂动力学,认识和解释了神经系统的信息处理机制和异常生物功能/疾病,具有重要科学意义和潜在应用价值.
(Gu Huaguang . Complex dynamics of the nervous system for information processing and abnormal functions
Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (2 ): 410 -420 (in Chinese))
[本文引用: 2]
[16]
蓝昱群 , 关利南 , 古华光 . 负反馈诱发神经电振荡的反常现象的复杂动力学
力学学报 , 2019 , 51 (4 ): 1122 -1133
DOI
传统观念认为,负反馈容易使系统达到稳定平衡点而正反馈容易引起振荡.本研究基于神经元理论模型,提出了负反馈可以诱发稳定平衡点、也就是静息、变为振荡、也就是放电的新观点.在Hopf分岔点附近,作用在静息上的一次足够大的负向脉冲电流的抑制性刺激,能够引起一个动作电位及随后的衰减振荡的后电位;而能够在后电位上诱发出动作电位的负脉冲电流强度阈值也是衰减振荡的.在模型中,引入具有时滞($\tau$)的负反馈来模拟抑制性自突触,一个动作电位诱发的负反馈自突触电流会作用到比动作电位延迟$\tau$的后电位上.随时滞增加,能够诱发出放电的负反馈增益强度阈值呈现出具有衰减振荡特点的类似多重相干共振的特性,衰减振荡的周期与电流阈值曲线的周期以及分岔点附近的放电周期相关.另外,负反馈还能诱发出放电与静息共存的复杂行为.本研究的结果不仅揭示了负反馈的新的反常调控作用,还有助于理解在现实神经系统中存在的慢抑制性自突触的潜在功能.
(Lan Yuqun Guan Linan Gu Huaguang . The complex dynamics of abnormal phenomenon of neural electronic oscillations induced by negative feedback
Chinese Journal of Theoretical and Applied Mechanics 2019 , 51 (4 ): 1122 -1133 (in Chinese))
[17]
杨永霞 , 李玉叶 , 古华光 . Pre-Bötzinger复合体的从簇到峰放电的同步转迁及分岔机制
物理学报 , 2020 , 69 (4 ): 040501
[本文引用: 2]
(Yang Yongxia Li Yuye Gu Huaguang . Synchronization transition from bursting to spiking and bifurcation mechanism of the pre-Bötzinger complex
Acta Physica Sinica 2020 , 69 (4 ): 040501 (in Chinese))
[本文引用: 2]
[18]
魏梦可 , 韩修静 , 张晓芳 等 . 正负双向脉冲式爆炸及其诱导的簇发振荡
力学学报 , 2019 , 51 (3 ): 904 -911
DOI
[本文引用: 1]
簇发振荡普遍存在.探索通向簇发振荡的可能路径是簇发研究的热点问题之一."脉冲式爆炸(pulsed-shaped explosion,PSE)"是一种最近被报道的可以诱发簇发振荡的新机制,其特征为平衡点和极限环表现出了与参数变化相关的脉冲式急剧量变.PSE会导致系统轨线急剧跃迁,从而诱发典型的簇发振荡.然而,目前报道的PSE中仅含有"单向的尖峰",未发现"双向的尖峰",且由其诱发的簇发振荡仅含单向的振荡簇.本文以多频激励Rayleigh系统为例,旨在揭示PSE的不同表现形式以及与此相关的簇发动力学.利用频率转换快慢分析法得到了Rayleigh系统的快子系统和慢变量.针对快子系统的分析表明,PSE表现出了较为复杂的动力学特性,其特征是PSE包含了正负双向两个不同的尖峰,此即所谓的正负双向PSE.其急剧量变行为,导致了系统轨线在单个振荡周期内出现正向和负向的多次跃迁,由此得到了由正负双向PSE所诱发的簇发振荡.根据吸引子类型分别揭示了点--点型和环--环型两类簇发振荡模式的产生机制.本文的研究给出了PSE的不同表现形式,丰富了多时间尺度下的簇发振荡的诱发机制.
(Wei Mengke Han Xiujing Zhang Xiaofang , et al . Positive and negative pluse-shaped explosion as well as bursting oscillations induced by it
Chinese Journal of Theoretical and Applied Mechanics 2019 , 51 (3 ): 904 -911 (in Chinese))
[本文引用: 1]
[19]
马新东 , 姜文安 , 张晓芳 等 . 一类三维非线性系统的复杂簇发振荡行为及其机理
力学学报 , 2020 , 52 (6 ): 1789 -1799
DOI
[本文引用: 1]
由多时间尺度耦合效应引起的簇发振荡行为是非线性动力学研究的重要课题之一.本文针对一类参数激励下的三维非线性电机系统(该系统可以描述两种自激同极发电机系统的动力学行为,两种系统在数学上等效),研究了当参数激励频率远小于系统自然频率时的各种复杂簇发振荡行为及其产生机理.通过快慢分析方法, 将参数激励作为慢变参数,得到了非自治系统对应的广义自治系统及快子系统和慢变量,并给出了快子系统的稳定性和分岔条件以及系统关于典型参数的单参数分岔图.借助转换相图与分岔图的叠加, 分析了对称式delayed subHopf/fold cycle簇发振荡的产生机理及其动力学转迁, 即delayed subHopf/fold cycle簇发振荡、焦点/焦点型对称式叉形分岔滞后簇发振荡和焦点/焦点型叉形分岔滞后簇发振荡.研究结果表明, 系统会出现两种不同的分岔滞后形式, 一种是亚临界Hopf分岔滞后,另一种是叉形分岔滞后,而且控制参数显著影响平衡点的稳定性和分岔滞后区间的宽度.同时初始点的选取则会影响系统动力学行为的对称性.本文的研究进一步加深了对由分岔滞后引起的簇发振荡的认识和理解.
(Ma Xindong Jiang Wenan Zhang Xiaofang , et al . Complicated bursting behaviors as well as the mechanism of a three dimensional nonlinear system
Chinese Journal of Theoretical and Applied Mechanics 2020 , 52 (6 ): 1789 -1799 (in Chinese))
[本文引用: 1]
[20]
Duan LX Liang WJ Ji WC , et al . Bifurcation patterns of bursting within pre-Bötzinger complex and their control
International Journal of Bifurcation and Chaos 2020 , 30 (13 ): 2050192
DOI
URL
[本文引用: 1]
[21]
程璇 , 刘深泉 . 房室化神经元Chay模型的放电节律研究
应用数学进展 , 2020 , 9 (2 ): 204 -219
[本文引用: 1]
(Cheng Xuan Liu Shenquan . Firing rhythm of compartmentalized neuron Chay model
Advances in Applied Mathematics 2020 , 9 (2 ): 204 -219 (in Chinese))
[本文引用: 1]
[22]
Dunmyre JR Negro CAD Rubin JE . Interactions of persistent sodium and calcium-activated nonspecific cationic currents yield dynamically distinct bursting regimes in a model of respiratory neurons
Journal of Computational Neuroscience 2011 , 31 (2 ): 305 -328
DOI
PMID
[本文引用: 1]
The preBötzinger complex (preBötC) is a heterogeneous neuronal network within the mammalian brainstem that has been experimentally found to generate robust, synchronous bursts that drive the inspiratory phase of the respiratory rhythm. The persistent sodium (NaP) current is observed in every preBötC neuron, and significant modeling effort has characterized its contribution to square-wave bursting in the preBötC. Recent experimental work demonstrated that neurons within the preBötC are endowed with a calcium-activated nonspecific cationic (CAN) current that is activated by a signaling cascade initiated by glutamate. In a preBötC model, the CAN current was shown to promote robust bursts that experience depolarization block (DB bursts). We consider a self-coupled model neuron, which we represent as a single compartment based on our experimental finding of electrotonic compactness, under variation of g (NaP), the conductance of the NaP current, and g (CAN), the conductance of the CAN current. Varying these two conductances yields a spectrum of activity patterns, including quiescence, tonic activity, square-wave bursting, DB bursting, and a novel mixture of square-wave and DB bursts, which match well with activity that we observe in experimental preparations. We elucidate the mechanisms underlying these dynamics, as well as the transitions between these regimes and the occurrence of bistability, by applying the mathematical tools of bifurcation analysis and slow-fast decomposition. Based on the prevalence of NaP and CAN currents, we expect that the generalizable framework for modeling their interactions that we present may be relevant to the rhythmicity of other brain areas beyond the preBötC as well.
[23]
Desroches M Kaper TJ Krupa M . Mixed-mode bursting oscillations: Dynamics created by a slow passage through spike-adding canard explosion in a square-wave burster
Chaos 2013 , 23 (4 ): 37 -119
[本文引用: 1]
[24]
Bacak BJ Kim T Smith JC , et al . Mixed-mode oscillations and population bursting in the pre-Bötzinger complex
eLife 2016 , 5 : e13403
DOI
URL
[本文引用: 1]
[25]
Wang YY Rubin JE . Multiple timescale mixed bursting dynamics in a respiratory neuron model
Journal of Computational Neuroscience 2016 , 41 (3 ): 1 -24
DOI
URL
[本文引用: 2]
[26]
Lü ZS Chen LN Duan LX . Bifurcation analysis of mixed bursting in the pre-Bötzinger complex
Applied Mathematical Modelling 2019 , 67 : 234 -251
DOI
URL
[本文引用: 1]
[27]
Zhan FB Liu SQ . Response of electrical activity in an improved neuron model under electromagnetic radiation and noise
Frontiers in Computational Neuroscience 2017 , 11 : 107
DOI
URL
[本文引用: 1]
[28]
Duan LX Cao QY Wang ZJ , et al . Dynamics of neurons in the pre-Bötzinger complex under magnetic flow effect
Nonlinear Dynamics 2018 , 94 : 1961 -1971
DOI
URL
[本文引用: 1]
[29]
29Guo DD Lü ZS . Effect of magnetic flow and external forcing current on mixed bursting in the pre-Bötzinger complex
Chinese Physics B 2019 , 28 (11 ): 110501
DOI
URL
[本文引用: 1]
[30]
30Wu FQ Ma J Zhang G . A new neuron model under electromagnetic field
Applied Mathematics and Computation 2019 , 347 (15 ): 590 -599
DOI
URL
[本文引用: 2]
[31]
Zhang Y Xu Y Yao Z , et al . A feasible neuron for estimating the magnetic field effect
Nonlinear Dynamics 2020 , 102 : 1849 -1867
DOI
URL
[本文引用: 1]
[32]
李佳佳 , 吴莹 , 独盟盟 等 . 电磁辐射诱发神经元放电节律转迁的动力学行为研究
物理学报 , 2016 , 48 (5 ): 1019 -1032
[本文引用: 1]
(Li Jiajia Wu Ying Du Mengmeng , et al . Dynamic behavior in firing rhythm transitions of neurons under electromagnetic radiation
Acta PhysicaSinica 2016 , 48 (5 ): 1019 -1032 (in Chinese))
[本文引用: 1]
[33]
Wang HT Chen Y . Spatiotemporal activities of neural network exposed to external electric fields
Nonlinear Dynamics 2016 , 85 (2 ): 881 -891
DOI
URL
[34]
Xu Y Ying HP Jia Y , et al . Autaptic regulation of electrical activities in neuron under electromagnetic induction
Scientific Reports 2017 , 7 : 43452
DOI
PMID
Realistic neurons may hold complex anatomical structure, for example, autapse connection to some internuncial neurons, which this specific synapse can connect to its body via a close loop. Continuous exchanges of charged ions across the membrane can induce complex distribution fluctuation of intracellular and extracellular charged ions of cell, and a time-varying electromagnetic field is set to modulate the membrane potential of neuron. In this paper, an autapse-modulated neuron model is presented and the effect of electromagnetic induction is considered by using magnetic flux. Bifurcation analysis and sampled time series for membrane potentials are calculated to investigate the mode transition in electrical activities and the biological function of autapse connection is discussed. Furthermore, the Gaussian white noise and electromagnetic radiation are considered on the improved neuron model, it is found appropriate setting and selection for feedback gain and time delay in autapse can suppress the bursting in neuronal behaviors. It indicates the formation of autapse can enhance the self-adaption of neuron so that appropriate response to external forcing can be selected, this biological function is helpful for encoding and signal propagation of neurons. It can be useful for investigation about collective behaviors in neuronal networks exposed to electromagnetic radiation.
[35]
Ge MY Jia Y Xu Y , et al . Mode transition in electrical activities of neuron driven by high and low frequency stimulus in the presence of electromagnetic induction and radiation
Nonlinear Dynamics 2018 , 91 : 515 -523
DOI
URL
[本文引用: 1]
[36]
Butera RJ Rinzel J Smith JC . Models of respiratory rhythm generation in the pre-Bötzinger complex. I. Bursting pacemaker neurons
Journal of Neurophysiology 1999 , 81 : 382 -397
[本文引用: 1]
[37]
Toporikova N Butera RJ . Two types of independent bursting mechanisms in inspiratory neurons: An integrative model
Journal of Computational Neuroscience 2011 , 30 (3 ): 515 -528
DOI
PMID
[本文引用: 1]
The network of coupled neurons in the pre-Bötzinger complex (pBC) of the medulla generates a bursting rhythm, which underlies the inspiratory phase of respiration. In some of these neurons, bursting persists even when synaptic coupling in the network is blocked and respiratory rhythmic discharge stops. Bursting in inspiratory neurons has been extensively studied, and two classes of bursting neurons have been identified, with bursting mechanism depends on either persistent sodium current or changes in intracellular Ca(2+), respectively. Motivated by experimental evidence from these intrinsically bursting neurons, we present a two-compartment mathematical model of an isolated pBC neuron with two independent bursting mechanisms. Bursting in the somatic compartment is modeled via inactivation of a persistent sodium current, whereas bursting in the dendritic compartment relies on Ca(2+) oscillations, which are determined by the neuromodulatory tone. The model explains a number of conflicting experimental results and is able to generate a robust bursting rhythm, over a large range of parameters, with a frequency adjusted by neuromodulators.
[38]
Park C Rubin JE . Cooperation of intrinsic bursting and calcium oscillations underlying activity patterns of model pre-Bötzinger complex neurons
Journal of Computational Neuroscience 2013 , 34 : 345 -366
DOI
URL
[本文引用: 4]
[39]
Ge MY Jia Y Xu Y , et al . Mode transition in electrical activities of neuron driven by high and low frequency stimulus in the presence of electromagnetic induction and radiation
Nonlinear Dynamics 2018 , 91 : 515 -523
DOI
URL
[本文引用: 1]
[40]
Lü M Wang CN Ren GD , et al . Model of electrical activity in a neuron under magnetic flow effect
Nonlinear Dynamics 2016 , 85 : 1479 -1490
DOI
URL
[本文引用: 1]
[41]
Mironov SL . Metabotropic glutamate receptors activate dendritic calcium waves and TRPM channels which drive rhythmic respiratory patterns in mice
The Journal of Physiology 2008 , 586 : 2277 -2291
DOI
PMID
[本文引用: 1]
Respiration in vertebrates is generated by a compact network which is located in the lower brainstem but cellular mechanisms which underlie persistent oscillatory activity of the respiratory network are yet unknown. Using two-photon imaging and patch-clamp recordings in functional brainstem preparations of mice containing pre-Bötzinger complex (preBötC), we examined the actions of metabotropic glutamate receptors (mGluR1/5) on the respiratory patterns. The agonist DHPG potentiated and antagonist LY367385 depressed respiration-related activities. In the inspiratory neurons, we observed rhythmic activation of non-selective channels which had a conductance of 24 pS. Their activity was enhanced with membrane depolarization and after elevation of calcium from the cytoplasmic side of the membrane. They were activated by a non-hydrolysable PIP(2) analogue and blocked by flufenamate, ATP4- and Gd3+. All these properties correspond well to those of TRPM4 channels. Calcium imaging of functional slices revealed rhythmic transients in small clusters of neurons present in a network. Calcium transients in the soma were preceded by the waves in dendrites which were dependent on mGluR activation. Initiation and propagation of waves required calcium influx and calcium release from internal stores. Calcium waves activated TPRM4-like channels in the soma and promoted generation of inspiratory bursts. Simulations of activity of neurons communicated via dendritic calcium waves showed emerging activity within neuronal clusters and its synchronization between the clusters. The experimental and theoretical data provide a subcellular basis for a recently proposed group-pacemaker hypothesis and describe a novel mechanism of rhythm generation in neuronal networks.
[42]
Izhikevich EM . Neural excitability, spiking and bursting
International Journal of Bifurcation and Chaos 2000 , 10 (6 ): 1171 -1266
DOI
URL
[本文引用: 1]
[43]
Lieske SP Thoby-Brisson M Telgkamp P , et al . Reconfiguration of the neural network controlling multiple breathing patterns: Eupnea, sighs and gasps
Nature Neuroscience 2000 , 3 (6 ): 600 -607
DOI
URL
[本文引用: 1]
Pre-B?tzinger complex: A brainstem region that may generate respiratory rhythm in mammals
1
1991
... 呼吸是一种重要的生理活动, 是包括人类在内的所有哺乳动物维持生命的必要条件之一. 研究发现, 哺乳动物新生儿神经系统中的呼吸节律可能是由pre-Bötzinger复合体(简称为pre-BötC)中的条件起搏神经元的同步活动引起的[1 -2 ] . 此后, 生理实验研究证实了pre-BötC是呼吸节律产生的主要部位[3 ] , 是离体实验中呼吸节律产生的关键[4 ] . 实验结果表明$g_{ NaP}$和$g_{ Leak}$代表亚阈电导的函数集, 赋予pre-BötC节律性特征[5 ] . 光子成像测量树突状Ca$^{2+}$瞬态的实验表明, 呼吸节律发生可能取决于网络活动中激活的树突簇产生的电导[6 ] . 此外, 药物刺激也可对pre-BötC的呼吸节律产生影响[7 -12 ] , 这表明pre-BötC可能与人类某些神经系统疾病有关, 在呼吸节律的神经控制中占有重要地位. ...
Pre-B?tzinger complex and pacemaker neurons: Hypothesized site and kernel for respiratory rhythm generation
1
1998
... 呼吸是一种重要的生理活动, 是包括人类在内的所有哺乳动物维持生命的必要条件之一. 研究发现, 哺乳动物新生儿神经系统中的呼吸节律可能是由pre-Bötzinger复合体(简称为pre-BötC)中的条件起搏神经元的同步活动引起的[1 -2 ] . 此后, 生理实验研究证实了pre-BötC是呼吸节律产生的主要部位[3 ] , 是离体实验中呼吸节律产生的关键[4 ] . 实验结果表明$g_{ NaP}$和$g_{ Leak}$代表亚阈电导的函数集, 赋予pre-BötC节律性特征[5 ] . 光子成像测量树突状Ca$^{2+}$瞬态的实验表明, 呼吸节律发生可能取决于网络活动中激活的树突簇产生的电导[6 ] . 此外, 药物刺激也可对pre-BötC的呼吸节律产生影响[7 -12 ] , 这表明pre-BötC可能与人类某些神经系统疾病有关, 在呼吸节律的神经控制中占有重要地位. ...
Ionotropic excitatory amino acid receptors in pre-B?tzinger complex play a modulatory role in hypoxia-induced gasping in vivo
1
2004
... 呼吸是一种重要的生理活动, 是包括人类在内的所有哺乳动物维持生命的必要条件之一. 研究发现, 哺乳动物新生儿神经系统中的呼吸节律可能是由pre-Bötzinger复合体(简称为pre-BötC)中的条件起搏神经元的同步活动引起的[1 -2 ] . 此后, 生理实验研究证实了pre-BötC是呼吸节律产生的主要部位[3 ] , 是离体实验中呼吸节律产生的关键[4 ] . 实验结果表明$g_{ NaP}$和$g_{ Leak}$代表亚阈电导的函数集, 赋予pre-BötC节律性特征[5 ] . 光子成像测量树突状Ca$^{2+}$瞬态的实验表明, 呼吸节律发生可能取决于网络活动中激活的树突簇产生的电导[6 ] . 此外, 药物刺激也可对pre-BötC的呼吸节律产生影响[7 -12 ] , 这表明pre-BötC可能与人类某些神经系统疾病有关, 在呼吸节律的神经控制中占有重要地位. ...
Patterns of phrenic motor output evoked by chemical stimulation of neurons located in the pre-B?tzinger complex in vivo
1
1999
... 呼吸是一种重要的生理活动, 是包括人类在内的所有哺乳动物维持生命的必要条件之一. 研究发现, 哺乳动物新生儿神经系统中的呼吸节律可能是由pre-Bötzinger复合体(简称为pre-BötC)中的条件起搏神经元的同步活动引起的[1 -2 ] . 此后, 生理实验研究证实了pre-BötC是呼吸节律产生的主要部位[3 ] , 是离体实验中呼吸节律产生的关键[4 ] . 实验结果表明$g_{ NaP}$和$g_{ Leak}$代表亚阈电导的函数集, 赋予pre-BötC节律性特征[5 ] . 光子成像测量树突状Ca$^{2+}$瞬态的实验表明, 呼吸节律发生可能取决于网络活动中激活的树突簇产生的电导[6 ] . 此外, 药物刺激也可对pre-BötC的呼吸节律产生影响[7 -12 ] , 这表明pre-BötC可能与人类某些神经系统疾病有关, 在呼吸节律的神经控制中占有重要地位. ...
Persistent Na$+$ and K$+$-dominated leak currents contribute to respiratory rhythm generation in the pre-B?tzinger complex in vitro
1
2008
... 呼吸是一种重要的生理活动, 是包括人类在内的所有哺乳动物维持生命的必要条件之一. 研究发现, 哺乳动物新生儿神经系统中的呼吸节律可能是由pre-Bötzinger复合体(简称为pre-BötC)中的条件起搏神经元的同步活动引起的[1 -2 ] . 此后, 生理实验研究证实了pre-BötC是呼吸节律产生的主要部位[3 ] , 是离体实验中呼吸节律产生的关键[4 ] . 实验结果表明$g_{ NaP}$和$g_{ Leak}$代表亚阈电导的函数集, 赋予pre-BötC节律性特征[5 ] . 光子成像测量树突状Ca$^{2+}$瞬态的实验表明, 呼吸节律发生可能取决于网络活动中激活的树突簇产生的电导[6 ] . 此外, 药物刺激也可对pre-BötC的呼吸节律产生影响[7 -12 ] , 这表明pre-BötC可能与人类某些神经系统疾病有关, 在呼吸节律的神经控制中占有重要地位. ...
Dendritic calcium activity precedes inspiratory bursts in pre-B?tzinger complex neurons
1
2011
... 呼吸是一种重要的生理活动, 是包括人类在内的所有哺乳动物维持生命的必要条件之一. 研究发现, 哺乳动物新生儿神经系统中的呼吸节律可能是由pre-Bötzinger复合体(简称为pre-BötC)中的条件起搏神经元的同步活动引起的[1 -2 ] . 此后, 生理实验研究证实了pre-BötC是呼吸节律产生的主要部位[3 ] , 是离体实验中呼吸节律产生的关键[4 ] . 实验结果表明$g_{ NaP}$和$g_{ Leak}$代表亚阈电导的函数集, 赋予pre-BötC节律性特征[5 ] . 光子成像测量树突状Ca$^{2+}$瞬态的实验表明, 呼吸节律发生可能取决于网络活动中激活的树突簇产生的电导[6 ] . 此外, 药物刺激也可对pre-BötC的呼吸节律产生影响[7 -12 ] , 这表明pre-BötC可能与人类某些神经系统疾病有关, 在呼吸节律的神经控制中占有重要地位. ...
Selective lesioning of the cat pre-B?tzinger complex in vivo eliminates breathing but not gasping
1
1998
... 呼吸是一种重要的生理活动, 是包括人类在内的所有哺乳动物维持生命的必要条件之一. 研究发现, 哺乳动物新生儿神经系统中的呼吸节律可能是由pre-Bötzinger复合体(简称为pre-BötC)中的条件起搏神经元的同步活动引起的[1 -2 ] . 此后, 生理实验研究证实了pre-BötC是呼吸节律产生的主要部位[3 ] , 是离体实验中呼吸节律产生的关键[4 ] . 实验结果表明$g_{ NaP}$和$g_{ Leak}$代表亚阈电导的函数集, 赋予pre-BötC节律性特征[5 ] . 光子成像测量树突状Ca$^{2+}$瞬态的实验表明, 呼吸节律发生可能取决于网络活动中激活的树突簇产生的电导[6 ] . 此外, 药物刺激也可对pre-BötC的呼吸节律产生影响[7 -12 ] , 这表明pre-BötC可能与人类某些神经系统疾病有关, 在呼吸节律的神经控制中占有重要地位. ...
Rhythm generation by the pre-B?tzinger complex in medullary slice and island preparations: Effects of adenosine A$_{1}$ receptor activation
0
2008
$\mu $-Opioid receptor agonist injections into the presumed pre-B?tzinger complex and the surrounding region of awake goats do not alter eupneic breathing
0
2009
Breathing stimulation mediated by 5-HT$_{1A}$ and 5-HT$_{3}$ receptors within the pre-B?tzinger complex of the adult rabbit
0
2019
Doxapram stimulates respiratory activity through distinct activation of neurons in the nucleus hypoglossus and the pre-B?tzinger complex
0
2019
Activation of $\mu $-opioid receptors differentially affects the pre-B?tzinger complex and neighbouring regions of the respiratory network in the adult rabbit
1
2020
... 呼吸是一种重要的生理活动, 是包括人类在内的所有哺乳动物维持生命的必要条件之一. 研究发现, 哺乳动物新生儿神经系统中的呼吸节律可能是由pre-Bötzinger复合体(简称为pre-BötC)中的条件起搏神经元的同步活动引起的[1 -2 ] . 此后, 生理实验研究证实了pre-BötC是呼吸节律产生的主要部位[3 ] , 是离体实验中呼吸节律产生的关键[4 ] . 实验结果表明$g_{ NaP}$和$g_{ Leak}$代表亚阈电导的函数集, 赋予pre-BötC节律性特征[5 ] . 光子成像测量树突状Ca$^{2+}$瞬态的实验表明, 呼吸节律发生可能取决于网络活动中激活的树突簇产生的电导[6 ] . 此外, 药物刺激也可对pre-BötC的呼吸节律产生影响[7 -12 ] , 这表明pre-BötC可能与人类某些神经系统疾病有关, 在呼吸节律的神经控制中占有重要地位. ...
关于注意和记忆的神经动力学机制
1
2006
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
关于注意和记忆的神经动力学机制
1
2006
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
大脑皮层信号作用下人体步态节律运动的探讨
1
2011
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
大脑皮层信号作用下人体步态节律运动的探讨
1
2011
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
神经系统信息处理和异常功能的复杂动力学
2
2017
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
... [15 -17 ]. 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
神经系统信息处理和异常功能的复杂动力学
2
2017
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
... [15 -17 ]. 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
负反馈诱发神经电振荡的反常现象的复杂动力学
0
2019
负反馈诱发神经电振荡的反常现象的复杂动力学
0
2019
Pre-B?tzinger复合体的从簇到峰放电的同步转迁及分岔机制
2
2020
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
... -17 ]. 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
Pre-B?tzinger复合体的从簇到峰放电的同步转迁及分岔机制
2
2020
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
... -17 ]. 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
正负双向脉冲式爆炸及其诱导的簇发振荡
1
2019
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
正负双向脉冲式爆炸及其诱导的簇发振荡
1
2019
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
一类三维非线性系统的复杂簇发振荡行为及其机理
1
2020
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
一类三维非线性系统的复杂簇发振荡行为及其机理
1
2020
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
Bifurcation patterns of bursting within pre-B?tzinger complex and their control
1
2020
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
房室化神经元Chay模型的放电节律研究
1
2020
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
房室化神经元Chay模型的放电节律研究
1
2020
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
Interactions of persistent sodium and calcium-activated nonspecific cationic currents yield dynamically distinct bursting regimes in a model of respiratory neurons
1
2011
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
Mixed-mode bursting oscillations: Dynamics created by a slow passage through spike-adding canard explosion in a square-wave burster
1
2013
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
Mixed-mode oscillations and population bursting in the pre-B?tzinger complex
1
2016
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
Multiple timescale mixed bursting dynamics in a respiratory neuron model
2
2016
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
... 采用快慢分解的方法来研究系统放电模式的动力学. 为了清楚地识别不同变量的时间尺度, 对整个系统(1a) $\sim$ (1f)进行了无量纲化处理[25 ] . ...
Bifurcation analysis of mixed bursting in the pre-B?tzinger complex
1
2019
... 神经系统中簇放电行为的产生和转迁的动力学机制已有大量研究. 王如彬等[13 -14 ] 研究了关于注意和记忆的神经动力学机制以及大脑皮层信号对人体步态节律运动的调节作用. 古华光等[15 -17 ] 研究了神经系统中丰富的动力学行为[15 -17 ] . 魏梦可等[18 ] 和马新东等[19 ] 对各种复杂簇发振荡行为及其产生机理进行了研究. Duan等[20 ] 研究了pre-BötC在washout滤波器控制下的簇放电模式及转迁机理. 程璇和刘深泉[21 ] 对房室化神经元Chay模型进行了非线性动力学分析和神经计算. 持续钠电导($g_{ NaP}$)和钙激活的非特异性阳离子电导($g_{ CAN}$)对pre-BötC的节律有重要影响, 电导的变化会引起一系列放电节律的产生, 如峰放电、方波簇、 DB簇以及由方波簇和DB簇组成的混合簇(mixed bursting, MB)[22 ] . 混合簇是一种特殊的胞体$\!-\!$树突状簇, 其特征是在每个周期内包含两种或更多种不同类型的簇. Desroches等[23 ] 介绍了一种在快、慢时间尺度微分方程组中产生混合簇振荡的新机制. Bacak等[24 ] 研究了pre-BötC中的混合簇振荡模式. Wang等[25 ] 从多时间尺度和分岔分析的角度, 研究了混合簇产生的动力学机理. Lü等[26 ] 探讨了pre-BötC吸气神经元单室模型中的MB解并利用快慢分解和分岔分析方法研究了混合簇的动力学机制, 这些工作说明了混合簇在理论及实验研究中的重要性. ...
Response of electrical activity in an improved neuron model under electromagnetic radiation and noise
1
2017
... 电磁场对神经元放电活动的影响也成为近年来的研究热点. Zhan和Liu[27 ] 研究了具有电磁辐射或高斯白噪声的Morris-Lecar模型, 发现电磁感应可以将簇或峰放电转换为静息态. Duan等[28 ] 研究发现, 磁通量使pre-BötC神经元在电流值较低的情况下振荡, 改变外激励条件, 可以观察到常规簇和混合簇类型. Guo和Lü[29 ] 研究了磁流和外部刺激电流这两个因素对单个pre-BötC神经元混合簇放电模式的影响. Ma等[30 ] 利用磁通和电荷分别描述磁场和电磁感应、电场的变化, 考虑电磁场的影响建立新的神经元模型, 在这种新的神经元模型上进行了非线性分析, 并应用外部电磁辐射来检测神经元活动中的模式转换. 随后, 他们又设计了一种简单的神经电路, 通过结合两个物理电子元件来估计磁场对神经元活动的影响[31 ] . 虽然磁流对神经元放电节律转迁的动力学行为已有一定的研究[32 -35 ] , 但是其对混合簇的影响的研究还不够深入, 还有很多值得进一步研究的内容. ...
Dynamics of neurons in the pre-B?tzinger complex under magnetic flow effect
1
2018
... 电磁场对神经元放电活动的影响也成为近年来的研究热点. Zhan和Liu[27 ] 研究了具有电磁辐射或高斯白噪声的Morris-Lecar模型, 发现电磁感应可以将簇或峰放电转换为静息态. Duan等[28 ] 研究发现, 磁通量使pre-BötC神经元在电流值较低的情况下振荡, 改变外激励条件, 可以观察到常规簇和混合簇类型. Guo和Lü[29 ] 研究了磁流和外部刺激电流这两个因素对单个pre-BötC神经元混合簇放电模式的影响. Ma等[30 ] 利用磁通和电荷分别描述磁场和电磁感应、电场的变化, 考虑电磁场的影响建立新的神经元模型, 在这种新的神经元模型上进行了非线性分析, 并应用外部电磁辐射来检测神经元活动中的模式转换. 随后, 他们又设计了一种简单的神经电路, 通过结合两个物理电子元件来估计磁场对神经元活动的影响[31 ] . 虽然磁流对神经元放电节律转迁的动力学行为已有一定的研究[32 -35 ] , 但是其对混合簇的影响的研究还不够深入, 还有很多值得进一步研究的内容. ...
Effect of magnetic flow and external forcing current on mixed bursting in the pre-B?tzinger complex
1
2019
... 电磁场对神经元放电活动的影响也成为近年来的研究热点. Zhan和Liu[27 ] 研究了具有电磁辐射或高斯白噪声的Morris-Lecar模型, 发现电磁感应可以将簇或峰放电转换为静息态. Duan等[28 ] 研究发现, 磁通量使pre-BötC神经元在电流值较低的情况下振荡, 改变外激励条件, 可以观察到常规簇和混合簇类型. Guo和Lü[29 ] 研究了磁流和外部刺激电流这两个因素对单个pre-BötC神经元混合簇放电模式的影响. Ma等[30 ] 利用磁通和电荷分别描述磁场和电磁感应、电场的变化, 考虑电磁场的影响建立新的神经元模型, 在这种新的神经元模型上进行了非线性分析, 并应用外部电磁辐射来检测神经元活动中的模式转换. 随后, 他们又设计了一种简单的神经电路, 通过结合两个物理电子元件来估计磁场对神经元活动的影响[31 ] . 虽然磁流对神经元放电节律转迁的动力学行为已有一定的研究[32 -35 ] , 但是其对混合簇的影响的研究还不够深入, 还有很多值得进一步研究的内容. ...
A new neuron model under electromagnetic field
2
2019
... 电磁场对神经元放电活动的影响也成为近年来的研究热点. Zhan和Liu[27 ] 研究了具有电磁辐射或高斯白噪声的Morris-Lecar模型, 发现电磁感应可以将簇或峰放电转换为静息态. Duan等[28 ] 研究发现, 磁通量使pre-BötC神经元在电流值较低的情况下振荡, 改变外激励条件, 可以观察到常规簇和混合簇类型. Guo和Lü[29 ] 研究了磁流和外部刺激电流这两个因素对单个pre-BötC神经元混合簇放电模式的影响. Ma等[30 ] 利用磁通和电荷分别描述磁场和电磁感应、电场的变化, 考虑电磁场的影响建立新的神经元模型, 在这种新的神经元模型上进行了非线性分析, 并应用外部电磁辐射来检测神经元活动中的模式转换. 随后, 他们又设计了一种简单的神经电路, 通过结合两个物理电子元件来估计磁场对神经元活动的影响[31 ] . 虽然磁流对神经元放电节律转迁的动力学行为已有一定的研究[32 -35 ] , 但是其对混合簇的影响的研究还不够深入, 还有很多值得进一步研究的内容. ...
... 根据电磁感应的物理定律, 带电离子在膜上的持续交换会引起离子浓度的复杂变化. 神经元的膜电位波动被认为是电磁感应效应[39 ] . 因此需要建立随时间变化的电磁场来调节神经元的膜电位, 而跨膜磁通量可以满足这一要求. 磁通量$\varphi$作为附加变量来描述电磁感应和电场的影响、检测电磁场的变化, 且用来模拟磁通量的忆阻器能够与神经元膜电位的物理单位保持一致. Wu等[30 ] 通过设计一个带有外刺激电流和忆阻器的HR模型的神经元电路图证明了带有外部刺激的电流和磁通量的模型的有效性[40 ] . ...
A feasible neuron for estimating the magnetic field effect
1
2020
... 电磁场对神经元放电活动的影响也成为近年来的研究热点. Zhan和Liu[27 ] 研究了具有电磁辐射或高斯白噪声的Morris-Lecar模型, 发现电磁感应可以将簇或峰放电转换为静息态. Duan等[28 ] 研究发现, 磁通量使pre-BötC神经元在电流值较低的情况下振荡, 改变外激励条件, 可以观察到常规簇和混合簇类型. Guo和Lü[29 ] 研究了磁流和外部刺激电流这两个因素对单个pre-BötC神经元混合簇放电模式的影响. Ma等[30 ] 利用磁通和电荷分别描述磁场和电磁感应、电场的变化, 考虑电磁场的影响建立新的神经元模型, 在这种新的神经元模型上进行了非线性分析, 并应用外部电磁辐射来检测神经元活动中的模式转换. 随后, 他们又设计了一种简单的神经电路, 通过结合两个物理电子元件来估计磁场对神经元活动的影响[31 ] . 虽然磁流对神经元放电节律转迁的动力学行为已有一定的研究[32 -35 ] , 但是其对混合簇的影响的研究还不够深入, 还有很多值得进一步研究的内容. ...
电磁辐射诱发神经元放电节律转迁的动力学行为研究
1
2016
... 电磁场对神经元放电活动的影响也成为近年来的研究热点. Zhan和Liu[27 ] 研究了具有电磁辐射或高斯白噪声的Morris-Lecar模型, 发现电磁感应可以将簇或峰放电转换为静息态. Duan等[28 ] 研究发现, 磁通量使pre-BötC神经元在电流值较低的情况下振荡, 改变外激励条件, 可以观察到常规簇和混合簇类型. Guo和Lü[29 ] 研究了磁流和外部刺激电流这两个因素对单个pre-BötC神经元混合簇放电模式的影响. Ma等[30 ] 利用磁通和电荷分别描述磁场和电磁感应、电场的变化, 考虑电磁场的影响建立新的神经元模型, 在这种新的神经元模型上进行了非线性分析, 并应用外部电磁辐射来检测神经元活动中的模式转换. 随后, 他们又设计了一种简单的神经电路, 通过结合两个物理电子元件来估计磁场对神经元活动的影响[31 ] . 虽然磁流对神经元放电节律转迁的动力学行为已有一定的研究[32 -35 ] , 但是其对混合簇的影响的研究还不够深入, 还有很多值得进一步研究的内容. ...
电磁辐射诱发神经元放电节律转迁的动力学行为研究
1
2016
... 电磁场对神经元放电活动的影响也成为近年来的研究热点. Zhan和Liu[27 ] 研究了具有电磁辐射或高斯白噪声的Morris-Lecar模型, 发现电磁感应可以将簇或峰放电转换为静息态. Duan等[28 ] 研究发现, 磁通量使pre-BötC神经元在电流值较低的情况下振荡, 改变外激励条件, 可以观察到常规簇和混合簇类型. Guo和Lü[29 ] 研究了磁流和外部刺激电流这两个因素对单个pre-BötC神经元混合簇放电模式的影响. Ma等[30 ] 利用磁通和电荷分别描述磁场和电磁感应、电场的变化, 考虑电磁场的影响建立新的神经元模型, 在这种新的神经元模型上进行了非线性分析, 并应用外部电磁辐射来检测神经元活动中的模式转换. 随后, 他们又设计了一种简单的神经电路, 通过结合两个物理电子元件来估计磁场对神经元活动的影响[31 ] . 虽然磁流对神经元放电节律转迁的动力学行为已有一定的研究[32 -35 ] , 但是其对混合簇的影响的研究还不够深入, 还有很多值得进一步研究的内容. ...
Spatiotemporal activities of neural network exposed to external electric fields
0
2016
Autaptic regulation of electrical activities in neuron under electromagnetic induction
0
2017
Mode transition in electrical activities of neuron driven by high and low frequency stimulus in the presence of electromagnetic induction and radiation
1
2018
... 电磁场对神经元放电活动的影响也成为近年来的研究热点. Zhan和Liu[27 ] 研究了具有电磁辐射或高斯白噪声的Morris-Lecar模型, 发现电磁感应可以将簇或峰放电转换为静息态. Duan等[28 ] 研究发现, 磁通量使pre-BötC神经元在电流值较低的情况下振荡, 改变外激励条件, 可以观察到常规簇和混合簇类型. Guo和Lü[29 ] 研究了磁流和外部刺激电流这两个因素对单个pre-BötC神经元混合簇放电模式的影响. Ma等[30 ] 利用磁通和电荷分别描述磁场和电磁感应、电场的变化, 考虑电磁场的影响建立新的神经元模型, 在这种新的神经元模型上进行了非线性分析, 并应用外部电磁辐射来检测神经元活动中的模式转换. 随后, 他们又设计了一种简单的神经电路, 通过结合两个物理电子元件来估计磁场对神经元活动的影响[31 ] . 虽然磁流对神经元放电节律转迁的动力学行为已有一定的研究[32 -35 ] , 但是其对混合簇的影响的研究还不够深入, 还有很多值得进一步研究的内容. ...
Models of respiratory rhythm generation in the pre-B?tzinger complex. I. Bursting pacemaker neurons
1
1999
... Butera等[36 ] 建立了最小pre-BötC神经元模型, 该模型由钠电流($I_{ Na}$)和钾电流($I_{ K}$)产生动作电位并通过持续钠电流($I_{ NaP}$)的缓慢失活来终止放电过程. Toporikova和Butera把这一模型发展为具有胞体$\!-\!$树突双室的神经元模型(TB模型)[37 ] , 该模型使用Butera描述的pre-BötC神经元模型作为胞体室, 而树突室仅包含钙激活的非特异性阳离子电流($I_{ CAN}$). Park和Rubin[38 ] 发现当TB模型简化为单室时会定性地产生相似的动力学特征. ...
Two types of independent bursting mechanisms in inspiratory neurons: An integrative model
1
2011
... Butera等[36 ] 建立了最小pre-BötC神经元模型, 该模型由钠电流($I_{ Na}$)和钾电流($I_{ K}$)产生动作电位并通过持续钠电流($I_{ NaP}$)的缓慢失活来终止放电过程. Toporikova和Butera把这一模型发展为具有胞体$\!-\!$树突双室的神经元模型(TB模型)[37 ] , 该模型使用Butera描述的pre-BötC神经元模型作为胞体室, 而树突室仅包含钙激活的非特异性阳离子电流($I_{ CAN}$). Park和Rubin[38 ] 发现当TB模型简化为单室时会定性地产生相似的动力学特征. ...
Cooperation of intrinsic bursting and calcium oscillations underlying activity patterns of model pre-B?tzinger complex neurons
4
2013
... Butera等[36 ] 建立了最小pre-BötC神经元模型, 该模型由钠电流($I_{ Na}$)和钾电流($I_{ K}$)产生动作电位并通过持续钠电流($I_{ NaP}$)的缓慢失活来终止放电过程. Toporikova和Butera把这一模型发展为具有胞体$\!-\!$树突双室的神经元模型(TB模型)[37 ] , 该模型使用Butera描述的pre-BötC神经元模型作为胞体室, 而树突室仅包含钙激活的非特异性阳离子电流($I_{ CAN}$). Park和Rubin[38 ] 发现当TB模型简化为单室时会定性地产生相似的动力学特征. ...
... 本工作在Park和Rubin[38 ] 提出的pre-BötC单室细胞模型中引入了电流和磁通控制忆阻器. 模型描述如下 ...
... 实验表明Ca$^{2+}$振荡起源于pre-BötC神经元的树突[41 ] , 因此仅在树突室中包含Ca$^{2+}$动力学, 其中Ca$^{2+}$的动力学受细胞内Ca$^{2+}$浓度[Ca]和IP$_{3}$通道门控变量$l$控制. 方程(1a) $\sim$ (1f)称为全系统. 当使用单室模型时, 模型中没有树突部分, 不过本文沿用Park和Rubin[38 ] 的命名方式, 称子系统(1a) $\sim$ (1d)为胞体子系统, 子系统(1e) $\sim$ (1f)为树突子系统. $l$的变化间接影响胞体子系统 (1a) $\sim$ (1d), 因为$l$会影响[Ca], [Ca]会影响$V$, 且这种影响是单向的, 但$l$不直接出现在膜电位$V$的方程中, 即树突子系统独立于胞体子系统, 而胞体子系统却受到树突子系统的影响. 下面主要对无量纲化之后的系统(4a) $\sim$ (4f)进行研究. ...
... 本研究用忆阻器模拟磁通量, 在Butera神经元模型中引入电流和磁通量, 应用多时间尺度及分岔分析的方法, 分析电流和磁流对神经元混合簇放电模式的影响. 通过无量纲化的方法对时间尺度进行划分, 并用尺度变换后的无量纲动力系统进行分析. 通过将混合簇分为胞体部分和树突部分[38 ] , 区分了混合簇放电模式并对胞体簇进行了动力学分析. 研究表明: 电流和磁流都可以显著影响pre-BötC细胞的混合簇放电节律. 减小电流$\bar{I}$和磁流反馈系数$\bar{k}_{{ 1}}$的值会使混合簇中胞体簇的个数减少, 同时使簇放电类型由"fold/homoclinic"型簇放电转迁为经由"fold/homoclinic"滞后环的"Hopf/Hopf"型簇放电. 利用双参数分岔分析, 我们揭示了混合簇模式的产生机制. 如果全系统轨线可以在鞍结分岔曲线和同宿轨分岔曲线之间跃迁, 整个系统出现混合簇. 上述研究结果可以加深我们对神经元放电动力学的理解, 为电流和磁流对神经元放电模式的影响提供参考. ...
Mode transition in electrical activities of neuron driven by high and low frequency stimulus in the presence of electromagnetic induction and radiation
1
2018
... 根据电磁感应的物理定律, 带电离子在膜上的持续交换会引起离子浓度的复杂变化. 神经元的膜电位波动被认为是电磁感应效应[39 ] . 因此需要建立随时间变化的电磁场来调节神经元的膜电位, 而跨膜磁通量可以满足这一要求. 磁通量$\varphi$作为附加变量来描述电磁感应和电场的影响、检测电磁场的变化, 且用来模拟磁通量的忆阻器能够与神经元膜电位的物理单位保持一致. Wu等[30 ] 通过设计一个带有外刺激电流和忆阻器的HR模型的神经元电路图证明了带有外部刺激的电流和磁通量的模型的有效性[40 ] . ...
Model of electrical activity in a neuron under magnetic flow effect
1
2016
... 根据电磁感应的物理定律, 带电离子在膜上的持续交换会引起离子浓度的复杂变化. 神经元的膜电位波动被认为是电磁感应效应[39 ] . 因此需要建立随时间变化的电磁场来调节神经元的膜电位, 而跨膜磁通量可以满足这一要求. 磁通量$\varphi$作为附加变量来描述电磁感应和电场的影响、检测电磁场的变化, 且用来模拟磁通量的忆阻器能够与神经元膜电位的物理单位保持一致. Wu等[30 ] 通过设计一个带有外刺激电流和忆阻器的HR模型的神经元电路图证明了带有外部刺激的电流和磁通量的模型的有效性[40 ] . ...
Metabotropic glutamate receptors activate dendritic calcium waves and TRPM channels which drive rhythmic respiratory patterns in mice
1
2008
... 实验表明Ca$^{2+}$振荡起源于pre-BötC神经元的树突[41 ] , 因此仅在树突室中包含Ca$^{2+}$动力学, 其中Ca$^{2+}$的动力学受细胞内Ca$^{2+}$浓度[Ca]和IP$_{3}$通道门控变量$l$控制. 方程(1a) $\sim$ (1f)称为全系统. 当使用单室模型时, 模型中没有树突部分, 不过本文沿用Park和Rubin[38 ] 的命名方式, 称子系统(1a) $\sim$ (1d)为胞体子系统, 子系统(1e) $\sim$ (1f)为树突子系统. $l$的变化间接影响胞体子系统 (1a) $\sim$ (1d), 因为$l$会影响[Ca], [Ca]会影响$V$, 且这种影响是单向的, 但$l$不直接出现在膜电位$V$的方程中, 即树突子系统独立于胞体子系统, 而胞体子系统却受到树突子系统的影响. 下面主要对无量纲化之后的系统(4a) $\sim$ (4f)进行研究. ...
Neural excitability, spiking and bursting
1
2000
... 由于混合簇中胞体部分的簇的类型都相同, 所以只对第一个胞体簇进行分岔分析. 以$h$为慢变量, 取第一个胞体簇所对应的$c$的平均值为$0.020 7$, 对应快子系统的分岔如图2 (b)所示. 平衡点形成S形曲线, 曲线的下分支(黑色实线)和中支(黑色虚线)分别由稳定结点和不稳定鞍点组成. 曲线的上分支由稳定和不稳定的焦点组成, 不稳定焦点经由Andronov-Hopf (AH)分岔变为稳定焦点, 并在AH分岔处产生稳定的极限环(红色实线). 稳定极限环通过同宿轨分岔(HC)消失. 点$F_{1}$和$F_{2}$表示平衡点的鞍结分岔. 全系统的轨线(绿色曲线)也叠加在分岔图上. 当慢变量$h$增大时, S形曲线下支的静息态经由平衡点的鞍结分岔$F_{1}$跃迁至上支的稳定极限环, 并由于稳定极限环的吸引反复振荡, 振荡态经由同宿轨分岔(HC)跃迁至下支的静息态, 从而完成了一个周期振荡. 根据Izhikevich簇放电分类的标准[42 ] , 此时的簇放电模式为"fold/homoclinic"型簇放电. ...
Reconfiguration of the neural network controlling multiple breathing patterns: Eupnea, sighs and gasps
1
2000
... 类似实验中, 药物刺激可以使一个周期内只有一种类型的簇转化为周期内含有两种或多种类型的混合簇[43 ] , 发现外部电流刺激也可以达到同样的效果.设置$k_{1}=0.1$, $k_{2}=3$ s$^{-1}$, $\alpha =1$ mol/(L$\cdot$$\Omega$), $\beta =0.000 06$ mol/(L$\cdot$$\Omega$$\cdot$${ V}^{2}$$\cdot$s$^{2}$)增大电流可使同一周期内含有两种或多种类型的簇, 如图10 (b)所示. 图10 (a)是相同离子浓度时$I_{{ app}}=0$的情况. 对这一现象的动力学分析, 更多讨论将在未来进一步研究. 除此之外, 也可以在模型中考虑噪声、时滞等因素, 模拟更复杂环境下的神经元模型, 对不同环境状态下的神经元模型进行动力学行为研究. ...