引言
工程上大多数机械振动是有害的, 会加剧结构损伤、缩短设备使用寿命、降低舒适度和其他缺点. 为了抑制有害的振动, Frahm[1]第一次提出了一种在单自由度主系统上耦合上无阻尼式吸振器, 该型吸振器只有在外激励频率等于主系统频率附近其减振效果才明显, 也导致其有效减振频带宽度比较窄. 为了进一步减振和拓宽频带宽度, 文献[2,3]发展了无阻尼吸振器, 研究的有阻尼吸振器克服了Frahm吸振器的缺点, 有效减低幅值的同时拓宽有效减振频带宽度, 并发现主系统的频响曲线始终通过两固定点, 即频率和幅值不受吸振器阻尼值的影响. Brock[4]在文献[2]基础之上给出了阻尼值优化公式. Liu[5]改进了文献[4]优化方法, 设计了悬空阻尼器和接地阻尼器等两种阻尼吸振器, 给出了详细的推导过程并数值验证了优化方法. Asami和Nishihara[6-7]不考虑主系统结构阻尼, 在保证两个共振峰幅值相等并且最小的前提下, 利用固定点理论原理, 对阻尼吸振器优化系统结构参数并给出解析表达式. 然而, 调谐质量阻尼器(tuned mass damper, TMD)在比较窄的频带范围内有效并且依赖于固定的结构参数, 当外激励频率在变化时, 不能很好地减振.
彭海波等[8]研究了一种含有负刚度弹簧元件的新型动力吸振器模型, 利用固定点理论, 得到动力吸振器的最优阻尼比和最优频率比, 其减振效果远优于传统的调谐质量阻尼器吸振器模型. 邢昭阳等[9]对一种含有放大机构的负刚度动力吸振器模型进行参数优化, 其优化结果表明能够大幅降低共振振幅、拓宽减振频带并且降低系统的谐振频率. Benacchio等[10]把磁铁产生的磁力搭建一个变刚度的磁吸振器(magnetic vibration absorber, MVA), 通过调节MVA的几何参数, 可以在含有线性负刚度元件下实现MVA的非线性动力吸振器、非线性能量阱和双稳态的转换. 刘刚等[11]设计了一种新型连续可调的变质量-负刚度动力吸振器, 具有较好的低频有效性和较宽有效频带宽度. 李强等[12]提出一种由柔性螺旋弹簧(spiral flexure spring, SFS)及磁性负刚度弹(magnetic negative stiffness spring, MNSS)组成的新型可调动力吸振器, 很好地抑制了航天设备上的低频和超低频振动. 胡方圆等[13]提出了一种基于回复力曲面的时域非参数辨识方法, 研究了4种典型负刚度振子, 实验结果表明表面识别结果与实测回复力面吻合较好, 解决了负刚度非线性系统回复力的辨识困难问题.
同样, 半主动吸振器(semi-active vibration absorbers, SAVs)也经常用在变外激励频率的振动减振. 郎君等[14]将两个半主动开关控制策略应用到Voigt型动力吸振器中, 经过优化设计给出了最优控制策略. 张婉洁等[15]研究了3种基于相对速度反馈的控制策略, 通过转换控制开关在低频共振区域、高频共振区域和瞬态响应振幅方面具有很好的抑制振幅的效果. 李锁斌等[16]研究的超结构夹层板很好地满足低宽频振动带隙减振. 某些智能材料也被用在半主动吸振器上, 如介电弹性体功能材料[17] (dielectric elastomers, DE)、压电材料[18] (piezoelectric material, PM)、磁流变液[19] (magnetorheological elastomers, MRE)和形状记忆合金[20] (shape memory alloys, SMA). 然而, SAVs也仅仅是在外激励缓慢变化的一段频带有效.
传统的TMD和SAVs有作用的减振频带较窄, 对变频和宽频带的减振降幅效果差. 国内外学者发展了很多应用于动力吸振器上的控制方法, 如经典PID/PD[21]、 PPF[22]、 鲁棒控制[23]、 神经网络控制[24]、 模糊控制[25]和滑膜控制[26]等. 文献[27,28]提出在线性动力吸振器系统耦合时滞位移和加速度反馈控制, 能根据外激励频率实时调节时滞反馈的状态量并提出一种针对时滞系统稳定的方法(cluster treatment of characteristic roots, CTCR). Zhao和Xu[29-30]进行了非线性系统的时滞减振的研究, 研究发现时滞反馈控制在非线性系统具有更宽的有效减振频带. 文献[31,32]利用时滞反馈在线性系统和非线性系统进行反共振峰优化, 通过调节增益系数和时滞量, 把反共振频率点的幅值降低到零. Sun等[33]在非线性系统研究了非线性吸振器的等峰和去非线性问题, 通过等峰优化方法对非线性吸振器的非线性系数进行优化后, 实现了非线性系统的等峰特性, 同时也消除了不利非线性振动现象, 最后的实验结果很好地验证了理论结果. Meng等[34]在时滞非线性系统设计等峰优化准则, 利用时滞非线性吸振器对非线性系统进行减振, 即使外激励幅值较大时非线性吸振器减振效果也非常明显.
综上所述, 鉴于负刚度吸振器和时滞反馈控制作动器在减低幅值和拓宽有效减振频带方面具有很好的效果, 本文在负刚度吸振器系统耦合时滞反馈控制作动器, 进行等峰优化后收到了更好的控制效果. 为了评价等峰优化的效果, 定义了有效减振频带宽度和共振峰幅值与反共振峰幅值差等指标, 并在幅频响应曲线图中标示出指标值. 为了定量分析减幅情况, 定义了减幅百分比, 直观表示出各个频带内的减幅情况.
1 负刚度时滞反馈控制振动系统
1.1 力学模型
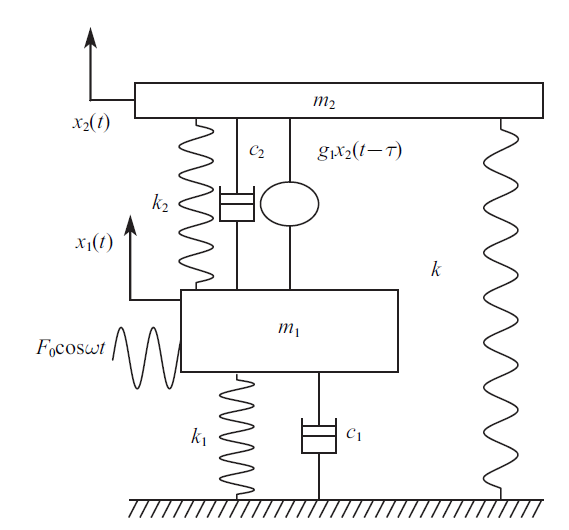
为了进一步完善振动系统, 本文在彭海波等[8]学者研究的负刚度系统等峰优化模型中考虑了主系统的结构阻尼; 同时为了进一步控制和优化等峰的幅值和拓宽负刚度系统的减振频带, 又在该振动系统中加入位移时滞反馈控制;本文研究的负刚度时滞反馈控制吸振器系统的力学模型化简为图1.其中$k$是变负刚度的刚度系数; $m_{1}$, $m_{2}$, $c_{1}$, $c_{2}$, $k_{1}$和$k_{2} $分别是主系统和吸振器的质量、阻尼和刚度系数; $g_{1}$和$\tau$分别是时滞反馈增益系数和时滞量; $x_{1} $和$x_{2}$分别是主系统和吸振器的位移; $F_{0} $是外激励力的幅值, $\omega$是外激励频率.
图1
图1
时滞耦合负刚度吸振器系统的力学模型
Fig.1
Mechanical model of delay-coupled negative stiffness system
由牛顿第二定律得到系统的运动微分方程
为了优化参数的方便和使方程更具有通用性, 对方程式(1)进行无量纲处理, 为此引入如下相关参数及无量纲量
为书写方便仍记为$x_{1} =\bar{{x}}_{1} $, $x_{2} =\bar{{x}}_{2}$, $t=\bar{{t}}$, $\tau =\bar{{\tau }}$, 有量纲的运动微分方程(1)转化为无量纲运动微分方程(3)
其中$\left( \cdot \right)^{\prime }={d\left( \cdot \right)}/{dt}$, $\left( \cdot \right)^{\prime \prime }={d^{2}\left( \cdot \right)}/{dt^{2}}$. 设方程组(3)的解为
将解(4)代入方程组(3)解得
其中$\varDelta \left( \varOmega \right)$为
引入变量$A_{1} $和$A_{2} $, 分别代表主系统和吸振器的振幅, 如下式
1.2 被动负刚度吸振系统
其中$A_{1} ( s p, \varOmega )$是主系统频率响应, $\varOmega_{1} $和$\varOmega_{2} $分别是第一阶共振频率和第二阶共振频率. 通过式(8)的优化过程, 文献[8]得到最优的一组结构参数, 如下式
Asami和Nishihara[6]通过固定点理论和$H_{\infty }$优化理论得到满足幅值相等的结构参数如下
图2
图2
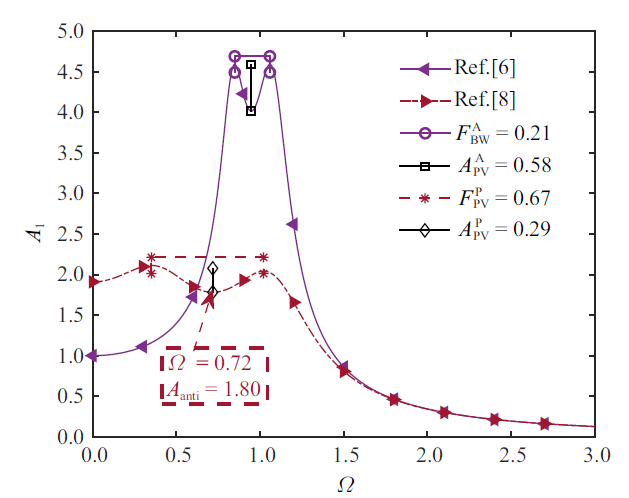
最优结构参数下的幅频响应曲线
Fig.2
Amplitude-frequency response curves for optimal structural parameters
其中$A_{res1} $, $A_{res2} $和$A_{anti}$分别是第一、第二共振峰和反共振峰的振幅; $\varOmega_{res1}$, $\varOmega_{res2} $和$\varOmega_{anti}$分别是第一、第二共振频率和反共振频率; $A_PV$是两个共振峰幅值的中间值与反共振峰幅值的差值; 定义$F_{BW}$是在满足一定$A_{PV} $值时的有效减振频带宽度.
虽然被动式接地负刚度吸振器具有很好的降幅效果, 但为了进一步降低幅值, 同时兼顾有效减振频带宽度和适当的共振峰幅值与反共振峰幅值差, 本文考虑在负刚度吸振器系统加入主动时滞反馈控制.
1.3 时滞耦合振动系统
为了解决进一步降低幅值、增大有效减振频带宽度和适当的共振峰幅值与反共振峰幅值差等问题, 考虑在含有负刚度的吸振器中耦合入时滞反馈控制, 此时系统的运动微分方程即为方程组(3), 该方程组考虑了以下两种条件:
(1) 考虑到主系统存在结构阻尼且不可以忽略, 此时主系统的阻尼系数为$\xi_{1} \ne 0$.
(2) 考虑到控制器硬件设备的限制, 时滞反馈控制增益系数$g$和时滞量$\tau $的取值范围做适当的限定, $g$和$\tau $的实际取值区间为: $r_{0} =\left\{(g, \tau)|0\leqslant g\leqslant 2, 0\leqslant \tau \leqslant 2\right\}$.
依据等峰优化条件式(8), 对含有时滞反馈控制的负刚度吸振器系统进行初步的等峰优化设计, 其优化条件如下
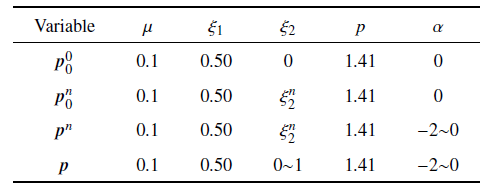
其中$ p=\left\{ {\mu , \xi_{1} , \xi_{2} , p, \alpha }\right\}$反映的是系统结构参数. 为了减小优化分析过程计算量, 考虑实际结构模型, 并对结构参数进行取值的限定, 假设质量比$\mu ={{m_{2} }/{m_{1} }}=0.1$和$\xi_{1} =0.501 7$固定不变, $ p$的其他结构参数初始值$ p_{0} $由式(9)确定.
2 时滞反馈控制的等峰优化设计
2.1 系统稳定性分析
时滞反馈控制会引起系统不稳定, 需要对反馈增益参数$g$和时滞量$\tau$进行稳定性分析, 判定方程组(3)稳定性的特征方程如下
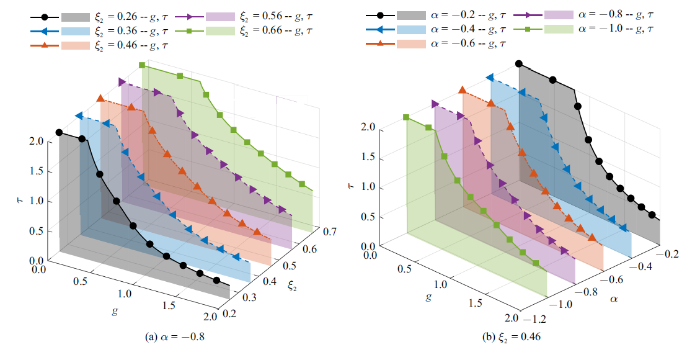
根据罗斯-霍尔维茨准则, 时滞耦合系统稳定的条件是特征方程(13)的特征根均为负实部, 其稳定区间的边界是特征方程(13)的特征根均为纯虚根, 即$\lambda =j\varOmega_c $, $\varOmega_c \in R^{+}$, 令$0\leqslant \varOmega_c \tau \leqslant 2\pi $, $\varOmega_c $是根的虚部. 本文考虑用CTCR[28]方法对系统进行稳定性分析, 进而得到如图3所示的$g$和$\tau $的稳定区间$r_{1} =\{(g, \tau )|Re[ C E( p, g, \tau)]<0\}\cap r_{0} $, 阴影部分代表稳定区间. 其中, 图3(a)以负刚度系数$\alpha =-0.8$为例, 给出了不同吸振器阻尼系数下$g$和$\tau $的稳定区间;图3(b)以吸振器阻尼系数$\xi_{2} =0.46$为例, 给出了不同负刚度系数下$g$和$\tau$的稳定区间, 此时结构参数$ p=\left\{ {\mu , \xi_{1} , \xi_{2} , p, \alpha } \right\}$.
图3
图3
不同结构参数下$g$和$\tau $的稳定区间
Fig.3
Stable intervals of $g$ and $\tau$ for different structural parameters
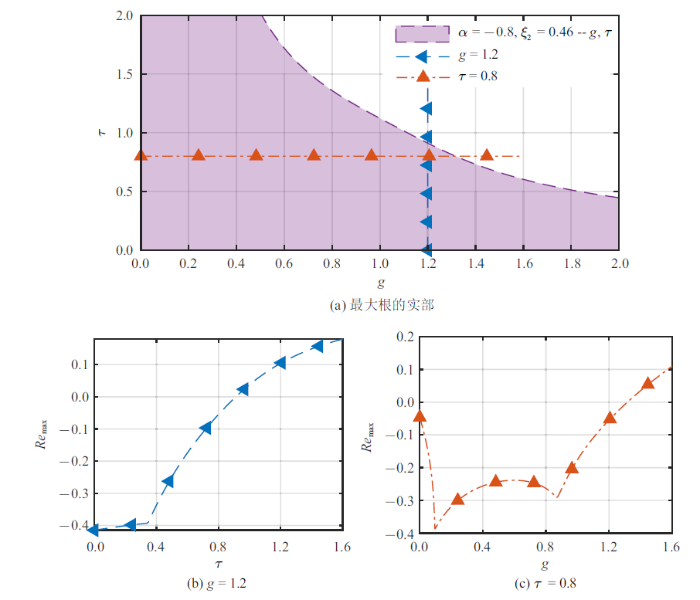
为了验证CTCR法求得的稳定区间, 以系统参数$\alpha =-0.8$, $\xi_{2}=0.46$为例, 给出$g$和$\tau $的稳定区域图如图4(a)所示. 从图4(a)中可以看出当$g=1.2$, $\tau =0.8$时, 时滞反馈控制系统是稳定的; 将上述时滞控制参数值分别代入特征方程(13), 用"quasi-polynomial mapping based root-finder"[36]法得到特征根, 取所有特征根中的实部最大值$Re_{\max } $, 分别得到图4(b)的$\tau-Re_{\max}$曲线和图4(c)的$g-Re_{\max}$曲线. 观察上述图可知, 图4(a)中的阴影区域是稳定的, 同时图4(b)和图4(c)中的临界值等于图4(a)的临界曲线上的值, 验证了CTCR方法求得的稳定区间是正确的.
图4
2.2 等峰优化准则
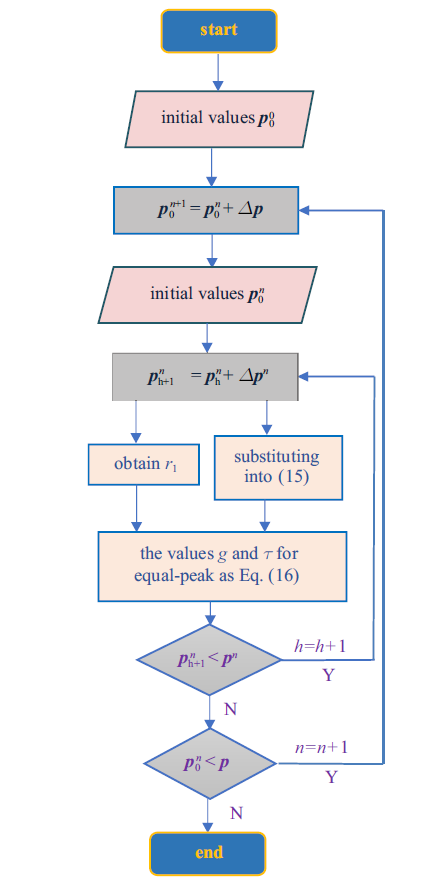
鉴于以上原因, 本文通过耦合入位移时滞反馈主动控制来对减振系统的等峰优化进行改善, 等峰优化同时能够实现控制和降低等峰振幅的目的. 但是, 运动微分方程中含有位移时滞反馈项, 对于这样的无限维振动系统, 无法通过固定点理论获得如式(9)所示的优化参数解析表达式. 本文采用半解析-半数值方法对该振动系统进行等峰优化设计, 数值计算的步长影响求解最优结构参数的精度, 设计一种等峰优化准则, 过程如下.
本文研究的是二自由度线性系统的等峰优化问题, 可以通过求解主系统振幅的极大值来进行等峰优化. 首先, 通过极值原理得到主系统极大值条件如下
其中${dA_{1}}/{d\varOmega }$, ${d^{2}A_{1} }/{d\varOmega^{2}}$是由式(7)求导得到. 进而得到共振点的频率值$\varOmega_res1 $和$\varOmega_res2 $, 代入式(7)求得共振频率点的幅值$A_res1 $和$A_res2$. 其次, 从满足降低共振峰幅值的角度, 本文将共振峰幅值控制在1.8以下, 同时使得两个共振峰的峰值相等, 考虑利用位移时滞反馈控制来调控共振点的幅值及共振频率的位置, 需要设计共振点振幅相等准则, 即设计如下等峰值小于给定值同时小于给定适当$A_PV $值的等峰准则
设定$r_{2} $为满足共振峰幅值相等且共振峰小于给定值和小于给定适当值$A_PV=0.5$的稳定$g$和$\tau $的区间, 如下式所示
计算$r_{2} $的详细过程如流程图5所示. 其中对系统结构参数$ p_{0}$和$ p$之间划分为$N$等份, 即$\Delta p=\left( { p- p_{0} } \right)/N$, 接着对结构参数$ p_{0}^{n} $和$ p^{n}$之间划分为$H$等份, 即$\Delta p^{n}=\left( { p^{n}- p_{0}^{n} } \right)/H$, $N$和$H$的取值越大, $\Delta p$和$\Delta p^{n}$越小精度越高, 本文中取$N=40$, $H=100$. $\Delta p$中的参数变化只针对$\xi_{2}^{n} $, $\Delta p^{n}$中的参数变化只针对$\alpha $, 其他参数如表1所示.
图5
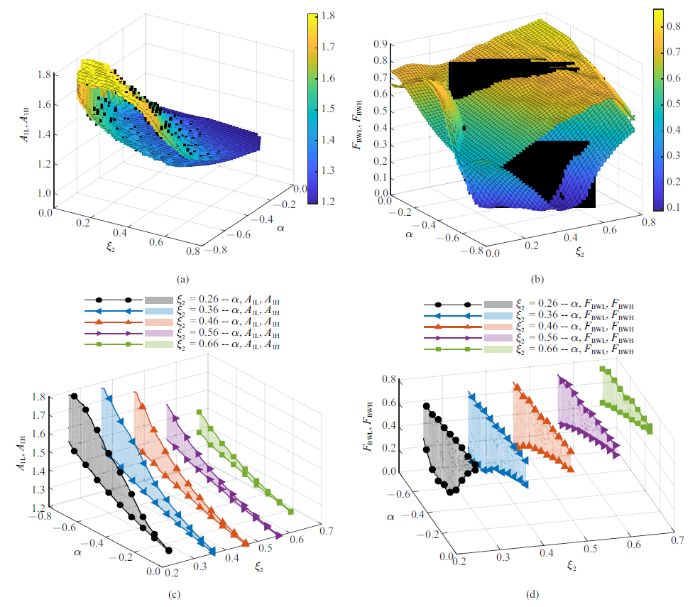
应用流程图5, 在不同结构参数$\alpha $和$\xi_{2}$下得到如图6(a)所示的增益系数$g$和时滞$\tau $所能调节共振峰的最大值$A_1H$曲面和最小值$A_1L $曲面, 其$\xi_{2} $截面如图6(c)的阴影区域所示; 同时得到增益系数$g$和时滞$\tau$所能调节的频带宽度最大值$F_BWH $曲面和最小值$F_BWL $曲面如图6(b)所示, 其$\xi_{2} $截面如图6(d)的阴影区域. 从图6(a)和图6(c)中知, 对于固定的负刚度值$\alpha $, 吸振器阻尼系数$\xi_{2} $取值越小, 位移时滞反馈控制所能优化降低共振峰的幅值越大, 减幅效果越不明显, 但都控制在1.8内; 对于固定的吸振器阻尼系数, 负刚度值$\alpha $的绝对值越小, 增益系数$g$和时滞$\tau $优化降低共振峰的幅值越小, 减幅效果越明显, 但最低幅值并没有低于1.2; 综上所述, 吸振器阻尼系数$\xi_{2}$对共振峰的影响较小, 负刚度值$\alpha $对共振峰的影响较大. 从图6(b)和图6(d)中知, 对于固定的负刚度值$\alpha $, 随着吸振器阻尼系数取值增大, $F_BWL $先减小后增大, $F_BWH $则一直增大, 即增益系数$g$和时滞$\tau $所能调节的有效频带宽度值$F_BW $呈增大趋势; 对于固定的吸振器阻尼系数, 随着负刚度值$\alpha $的绝对值越小, $F_BWL $-$\alpha $先减小后增大呈凹型抛物线状, 然后随着$\xi_{2} $增大$F_BWL $-$\alpha $的曲线呈凸型抛物线状, 而$F_BWH $-$\alpha$一直在增大. 这种$F_BWL $由凹变凸的变化趋势和$F_BWH$增大有助于增宽有效减振频带$F_BW $宽度.
图6
图6
(a) $A_{1}$, $\xi_{2}$, $\alpha $响应曲面; (b) $F_BW$, $\xi_{2}$, $\alpha $ 响应曲面; (c)不同$\xi_{2}$参数下$A_{1}-\alpha $ 响应截面图;(d) 不同$\xi_{2}$参数下$F_BW-\alpha $ 响应截面图
Fig.6
(a) Response curved surfaces of $A_{1}$, $\xi_{2}$ and $\alpha $; (b) response curved surfaces of $F_BW$, $\xi_{2}$ and $\alpha $; (c) response curves $A_{1}-\alpha$ on the section of different $\xi_{2}$; (d) response curves $F_BW-\alpha$ on the section of different $\xi_{2}$
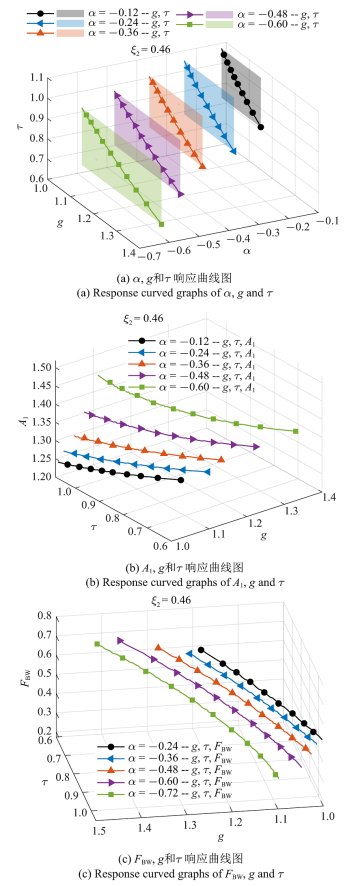
以吸振器阻尼系数$\xi_{2} =0.46$为例, 下面分析负刚度值$\alpha$分别对$g$-$\tau$稳定曲线、共振峰幅值$A_1$和有效减振频带宽度$F_BW $的影响, 经过流程图5得到图7.为了便于从$\alpha$轴观察, 在图7(a)中画出不同负刚度值$\alpha$的截面, 随着负刚度值$\alpha$的绝对值增大, 满足所提等峰优化方法的$g$和$\tau$曲线范围越大. 图7(b)是不同负刚度值$\alpha$下的$g$, $\tau$和$A_1$的曲线, 从图中知, 负刚度值$\alpha$的绝对值越小, 使系统稳定的$g$和$\tau$所能降低共振峰$A_1$的幅值越小. 图7(c)是不同负刚度值$\alpha$下的$g$, $\tau$和$F_BW$的曲线, 从图中知, 负刚度值$\alpha$的绝对值越大, 使系统稳定的$g$和$\tau$所能拓宽有效减振频带宽度$F_BW $的范围越大.
图7
图7
在$\xi_{2}=0.46$时, 不同参数$\alpha $ 时等峰优化的各参数关系图
Fig.7
Parameter relationship graphs of equal-peak optimization under $\xi_{2}=$ 0.46 for different $\alpha $
2.3 频域验证
图8
图8
稳定$g$-$\tau $曲线上3个标记圆点的幅频响应曲线: $\alpha =-0.24$; $\xi_{2}= 0.46$
Fig.8
Amplitude-frequency response curves for three dots on the stability curve of $g$-$\tau $: $\alpha=-0.24$; $\xi_{2}=0.46$
3 模型对比分析
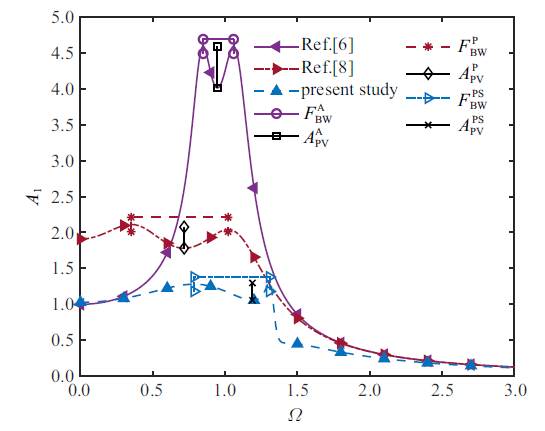
把3种模型的结构参数分别代入式(7)得到3种吸振器的幅频响应曲线如图9所示, 其中实线是文献[6]模型的幅频响应曲线, 点划线是文献[8]模型的幅频响应曲线, 虚线是本文研究模型的幅频响应曲线. 从图9中可以看出, 与文献[6]的吸振器模型相比, 外激励频率$\varOmega $在$\left( {0.5\sim 1.3} \right)$区间内, 本文的位移时滞负刚度吸振器的减幅效果明显, 同时也极大的降低了共振频率点的幅值并且具有较宽的有效减振频带; 与文献[8]的吸振器模型相比, 当外激励频率$\varOmega $在$\left( {0\sim 1.3}\right)$区间, 本文的模型具有较好的减幅效果, 同时也把共振峰的幅值控制在1.3附近, 并且有效减振频带宽度与文献[8]的相差不到0.1.
图9
图9
不同吸振器模型下的幅频响应曲线
Fig.9
Amplitude-frequency response curves for different vibration absorber models
为了定量上对比分析本文吸振器模型与其他两种吸振器模型的减幅效果, 定义减幅百分比, 定义如下
图10
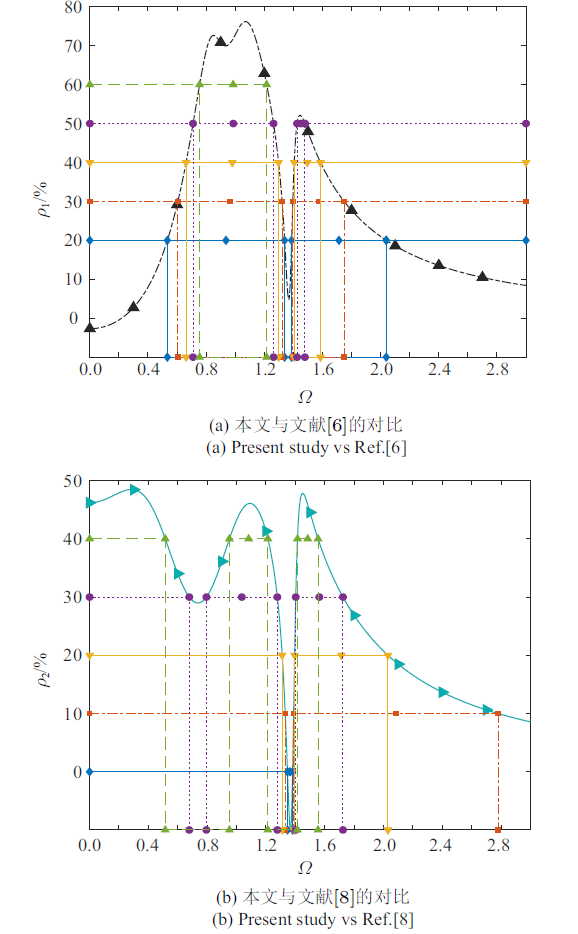
图10是本文模型分别与Asami模型[6]和Peng模型[8]的主系统减振幅值百分比. 从图10(a)和图10(b)中可以看出, 均存在3个最大减振幅值百分比, 在$\varOmega \in \left( {0.5\sim 1.3} \right)$内的两个减幅百分比最大值对应文献[6]模型和文献[8]模型的两个共振频率;第三个最大的减幅百分比是由于本文模型的幅频响应曲线在第二共振峰后急剧下降引起的. 与文献[8]模型相比, 外激励$\varOmega $在$\left( {0\sim 1.3} \right)$内都能控制在20%以上, 特别在文献[8]的共振频率处能达到以上45%; 与文献[6]模型相比, 外激励$\varOmega $在$\left( {0.53\sim 1.3} \right)$内都能控制在20%以上, 特别在文献[6]的共振频率处能达到70%以上.
图11
4 结论
本文对时滞负刚度吸振器在共振频率点的幅值进行等峰优化设计, 优化过程兼顾了控制和降低共振峰幅值以及拓宽有效减振频带宽度, 得到以下主要几点结论.
(1) 对稳定区间的影响: 负刚度值$\alpha $的绝对值越小和吸振器阻尼系数$\xi_{2} $越大, 增益系数$g$和时滞$\tau $的稳定曲线所围成的阴影区域面积越大.
(2) 对共振峰的影响: 负刚度值$\alpha $的绝对值越小和吸振器阻尼系数$\xi_{2}$越大, 在增益系数$g$和时滞$\tau $的有效调节范围内降低共振峰幅值的效果越好, 共振峰最低能控制在1.3附近.
(3) 对有效减振频带宽度的影响: 随着负刚度值$\alpha $的绝对值减少和吸振器阻尼系数$\xi_{2} $增大, 增益系数$g$和时滞$\tau $所能调节的有效减振频带宽度最大值$F_BWH $一直在增大, 所能调节的频带宽度最小值$F_BWL $曲线先减少后增大, 其变化趋势由凹型抛物线变为凸型抛物线.
参考文献
The theory of dynamic vibration absorber
A note on the damped vibration absorber
The damped dynamic vibration absorbers: Revisited and new result
Closed-form exact solution to $H_{\infty }$ optimization of dynamic vibration absorbers (application to different transfer functions and damping systems)
Closed-form solutions to the exact optimizations of dynamic vibration absorbers (minimizations of the maximum amplitude magnification factors)
一种含负刚度元件的新型动力吸振器的参数优化
提出了一种含有负刚度弹簧元件的新型动力吸振器模型,对该模型的最优参数进行了详细研究. 通过拉氏变换得到了系统的解析解,发现该系统存在着两个固定点,利用固定点理论得到了动力吸振器的最优阻尼比和最优频率比. 进一步研究发现接地刚度取负值时能够得到更好的减振效果,根据负刚度的特性得到了在保证系统稳定情况下的最优负刚度比. 通过数值解与解析解的对比证明了解析解的正确性. 通过与两种已有的典型动力吸振器模型在简谐激励和随机激励情况下的对比,说明了负刚度模型在主系统减振方面具有很大的优势,减振效果远优于两种已有动力吸振器模型,从而为设计新型动力吸振器模型提出了理论上的依据.
Parameters optimization of a new type of dynamic vibration absorber with negative stiffness
一种含放大机构的负刚度动力吸振器的参数优化
在大多数情况下机械振动是有害的,它不仅产生噪声还会降低设备的工作精度和使用寿命.采用正刚度特性的吸振、隔振系统往往难以达到满意效果,这种情况在低频振动控制系统中尤其明显.放大机构与负刚度元件在振动控制领域均表现出良好性能,但是较少有对同时含有放大机构与负刚度装置的动力吸振系统的研究.以Voigt型动力吸振器为基础提出了一种将放大机构应用于含负刚度弹簧元件的动力吸振器模型,对该模型的最优参数进行了研究.首先建立了系统的运动微分方程并得到了其解析解,发现该系统存在两个固定点,利用固定点理论得到了动力吸振器的最优频率比.根据负刚度的特性,在保证系统稳定的前提下得到了最优负刚度比,并推导了系统的近似最优阻尼比.通过数值仿真验证了解析解的正确性.与多种动力吸振器在简谐激励与随机激励下进行了对比,说明了本文模型相比于已有的动力吸振器,能够大幅降低共振振幅、拓宽减振频带并且降低系统的谐振频率,为设计新型动力吸振器模型提供了理论依据.
Parameters optimization of a dynamic vibration absorber with amplifying mechanism and negative stiffness
Design of a magnetic vibration absorber with tunable stiffnesses
变质量-负刚度动力吸振器试验研究
Experimental study on variable ma- ss negative stiffness dynamic vibration absorbers
新型可调动力吸振器设计及参数优化
Design and parameter optimization of a new tunable dynamic vibration absorber
负刚度非线性系统的回复力曲面参数辨识方法
Restoring force surface-based parameter identification method for negative stiffness nonlinear system
一种半主动动力吸振器参数优化及性能比较
Parametric optimization and performance comparison for 2 semi-active voigt DVAs
一类阻尼控制半主动隔振系统的解析研究
研究了一类基于相对速度反馈的含立方刚度的单自由度非线性半主动隔振系统.通过平均法得到了系统分别在基于加速度-相对速度反馈的加速度驱动阻尼控制策略、速度-相对速度反馈的天棚阻尼控制策略和位移-相对速度反馈的地棚阻尼控制策略下主共振响应的近似解析解,并利用数值解验证了近似解析解的准确性.通过 Lyapunov 理论对不同控制策略下系统的稳定性进行了分析,讨论了系统参数对控制效果的影响.分析结果表明,对 3 种基于相对速度反馈的控制策略进行解析研究时,切换条件中的控制参数具有相同的表达式;在抑制共振响应振幅方面,基于速度-相对速度反馈的天棚阻尼控制策略在低频时的减振效果最好,而基于加速度-相对速度反馈的加速度驱动阻尼控制策略在高频时的减振效果最优;在抑制瞬态响应振幅方面,基于速度-相对速度反馈的天棚阻尼控制策略的减振效果最好.此类解析研究方法可应用到其他半主动开关控制策略中,为半主动隔振系统的控制策略研究提供了有效的方法和手段.
Dynamical analysis on a kind of semi-active vibration isolation systems with damping control
超结构夹芯板及其低宽频振动带隙机理
Sandwich type metamaterial plate and its mechanism of low-frequency broad vibration band gap
Stacked dielectric elastomer actuator (SDEA): Casting process, modeling and active vibration isolation
An adaptive piezoelectric vibration absorber enhanced by a negative capacitance applied to a shell structure
Development of an MRE adaptive tuned vibration absorber with self-sensing capability
Adaptive tuned vibration absorber based on magnetorheological elastomer-shape memory alloy composite
Stability analysis of active vibration control of building structures using PD/PID control
Slewing and vibration control of a single-link flexible manipulator by positive position feedback (PPF)
A robust active control system for shimmy damping in the presence of free play and uncertainties
Based on interval type-2 fuzzy-neural network direct adaptive sliding mode control for SISO nonlinear systems
A robust adaptive tuned vibration absorber using semi-passive shunt electronics
Sliding mode control of wind-induced vibrations using fuzzy sliding surface and gain adaptation
A novel active vibration absorption technique: delayed resonator
A stability study on first-order neutral systems with three rationally independent time delays
Vibration suppression of a saturation control system using delayed feedback control
Effects of delayed feedback control on nonlinear vibration absorber system
Time-delayed feedback control design and its application for vibration absorption
Parameter design for a vibration absorber with time-delayed feedback control
Design and experiment of nonlinear absorber for equal-peak and de-nonlinearity
The generalization of equal-peak method for delay-coupled nonlinear system
振子质量非均布的有限结构梁减振频带优化
Optimization of damping frequency band in finite structure beam with uneven mass distribution of oscillator
Delay Systems: From Theory to Numerics and Applications