柔性梁的动力学广泛存在于力学系统当中, 其研究发展不断与固体力学、流体力学、非线性动力学、生物力学等其他学科进行交叉^[1-4]. 几何精确梁模型作为容许大范围运动、大变形的柔性梁的理想模型, 自提出后在分析、数值、应用等方向吸引了大量关注^[5-11]. 在柔性机器人的运动控制^[12-13]、 DNA动力学的研究^[14]中有广泛的应用.

在几何精确梁的数值算法方面, 传统数值格式直接离散动力学方程, 可以实现连续系统的计算仿真, 但是很难保持系统内在的对称性、守恒性等物理特性, 如能量、动量等. Marsden等^[15]提出的变分积分子是一种从Lagrange函数出发, 通过离散变分原理直接得到保结构数值格式的方法. Demoures等^[16]提出的几何精确梁的李群积分子和李代数积分子可以自然保持能量动量, 但没有充分利用系统对称性, 对于几何精确梁等对称性很强的系统离散格式复杂程度很高. 在此基础上, Ball等^[17]对有限维系统提出了Hamel变分积分子, 主要适用于带对称性的约束力学系统, 特别是带对称性的非完整约束力学系统. Shi等^[18-20] 进一步应用无穷维几何中的活动标架法结合变分原理, 得到约束无穷维力学系统和经典场论中刻画运动的标准型—Hamel 形式, 进而得到能用于经典场论动力学计算的保结构格式—Hamel场变分积分子. Hamel 场变分积分子可以无需额外的Lagrange乘子来求解无穷维约束力学系统, 特别是非完整力学系统. 其是一种分布式算法, 每一次计算只需利用待计算点周围的信息, 具有计算效率高的特点. 王亮等^[7]将Hamel场变分积分子应用于几何精确梁, 并通过数值算法验证了Hamel场变分积分子能长时间保结构的特征.

保结构性质对非线性力学系统的长时间定性行为的了解和定量分析是非常必要的. 这里结构包括 辛结构、酉结构、体积结构、接触结构、泊松结构 等几何结构, 也包括能量、动量、系统特征值等首次积分结构^[21]. 在天体力学^[22-23]、 量子力学^[24]、电磁学^[25]等学科中许多模型数值算法的构造中, 尽可能多地保持原系统的内在对称性、守恒性等物理特征的算法往往表现出很强的数值预测能力和跟踪能力^[21]. 例如, 电磁学中受到广泛应用的Yee格式已被证明保持多辛结构和动量映射^[26]. 在保结构算法的理论研究上, 钟万勰等^[27]建立了一套Hamilton动力系统的辛几何方法, 张素英等^[28]在此基础上,对Poisson流形上的广义Hamilton系统的数值算法进行了研究, 提出了广义Hamilton 系统显式的保持真解典则性的数值方法. 刘世兴等^[29]研究了特定的非完整系统的辛算法, 并将其与Runge-Kutta法进行对比, 说明了辛算法具有高的精确度. 满淑敏等^[30]提出了一类求解非完整系统的保结构算法, 并证明了其对称性, 说明了其收敛性和长时间保结构的特性.

对Hamel变分积分子的现有研究结果在数值上充分表现出了其对非线性系统, 包括有限维系统、无穷维系统、完整系统与非完整系统, 长时间动力学行为的良好预测^{[7, 17, 20]}. 本文以几何精确梁为例, 利用离散Noether定理, 研究了Hamel场变分积分子的保动量性质, 以期为进一步研究其保结构性质提供参考依据.

考虑一个在空间中运动的质量均匀的弹性梁. 设$\{ E_1, E_2, E_3\}$为物质标架的一组基, 初始时刻梁沿$ E_2$轴水平自然放置(无弹性形变), 一端位于原点(见图1). 设梁长为$l$, 密度为$\rho $, 截面面积为$A$ 的正方形.

在几何精确梁的模型中, 梁的截面做刚体运动, 其位形可由

$ { g} = \begin{pmatrix} {\varLambda}&{\varphi} \\{\bf0} & {\bf1} \end{pmatrix} \in SE(3) $

描述, 其中$ \varphi :{\bf R}\times[0,l]\rightarrow {\bf R}^3$ 为中线位置函数, $ \varLambda:{\bf R}\times [0,l] \rightarrow SO(3)$ 为截面旋转矩阵. 引入对流速度

和对流应变

其中顶标$\cdot$和上标$'$分别表示对时间变量$t$和空间变量$s$求导, $ e _2$为$ E_2$ 方向的单位向量. 此处利用了李代数$\mathfrak{se}(3)$与${\bf R}^6$的等同. 对流速度$\zeta$包含了截面运动的角速度$\omega$和平移速度$\pi$的信息, 对流应变包含了弹性拉伸、弯曲和剪切信息. 从而, 几何精确梁的Lagrange密度可写作

$L(\zeta, \gamma) = \frac12 [\langle {\mathcal{K}}\zeta, \zeta \rangle - \langle {\mathcal{P}\gamma}, \gamma\rangle]$

其中$\langle \cdot, \cdot \rangle$为$\mathfrak{se}^\ast (3)$与$\mathfrak{se}(3)$配对, $\mathcal{K}$, $\mathcal{P}$分别为常对角阵.

从而作用泛函为

$\mathcal{L} = \int_a^b \int^l_0 \frac12 [\langle {\mathcal{K} \zeta}, \zeta \rangle - \langle {\mathcal{P}\gamma}, \gamma \rangle] dsdt$

令$\eta = { g}^{-1} \Delta { g} $为独立变分, 易知$\eta$与$\zeta$, $\gamma$满足如下变分公式^[20]

其中$[\cdot , \cdot]$为$\mathfrak{se}(3)$上的李括号.

根据变分公式和Hamilton原理, 计算得到自由几何精确梁的动力学方程

$\frac{\partial }{\partial t} {\mathcal{K} \zeta} - \frac{\partial }{\partial s} {\mathcal{P} \gamma}- [\zeta, {\mathcal{K} \zeta}]^\ast + [ \gamma + e_2, {\mathcal{P}\gamma}]^\ast = {\bf0}$

和自由边界条件

$\gamma(t,0) = \gamma(t,l) = 0, \forall t\in (a,b)$

其中$[\cdot,\cdot]^\ast $为$\mathfrak{se}(3)$李括号$[\cdot , \cdot]$的对偶括号. 同时, 由式(1)和式(2) 可知, $ \zeta$和$ \gamma$满足相容性条件

相容性条件描述了对流速度和对流应变生成的分布的可积性. 在场论框架下, 位形$ g$ 是以时空为底流形, 纤维为的主丛$SE(3)$的截面, 相容性条件在几何上可解释为主丛的局部平坦性条件. 对一般纤维丛情况下的相容性条件的讨论参见文献[19]. 对于给定初始条件和边界条件的几何精确梁, 其运动由动力学方程(3)和相容性条件(5) 共同确定, 将式(3)和式(5)构成的方程组称为几何精确梁的Hamel场方程组^[18-19].

通过离散Hamilton原理得到Hamel场变分积分子. 设离散梁的空间节点数为$K$, 空间步长为$\Delta h$, 时间步数为$N$, 时间步长为$\Delta t$. 梁的位形由序列$\{ g^n_j\} $, $n = 0,1,2,\cdots ,N-1,\ j = 1,2,\cdots ,K$ 描述, $ g^n_j$表示在$n$时刻第$j$ 个截面的位形. 分别定义离散对流速度$\zeta^{n+1/2}_j$和离散对流应变$\gamma^n_{j+1/2}$如下

由于指数映射$\exp:\mathfrak{se}(3) \to SE(3)$是局部微分同胚, 在$\exp:\mathfrak{se}(3) \to SE(3)$与${ g}^{n+1}_j$相距较近, 即$({ g}^n_j)^{-1}{ g}^{n+1}_j$在$\exp$的值域中时, 上式唯一确定了离散对流速度, 离散对流应变的情形类似. 从而, 离散Lagrange密度为

相应的作用和为

$A^d = \Delta t\Delta h\sum_{n=0}^{N-1} \sum_{j=0}^{K}\frac12 \Big[\Big\langle {\mathcal K\zeta}^{n+1/2}_{j}, \zeta^{n+1/2}_{j} \Big\rangle - \\ \Big\langle {\mathcal P\gamma}^n_{j+1/2}, \gamma^n_{j+1/2} \Big\rangle\Big]$

注: 上式中第一项的求和范围应为$n=0,1,2,\cdots ,N-1,\ j = 1,2,\cdots ,K$, 第二项的求和范围应为$n=1,2,\cdots ,N-1,\ j = 0,1,2,\cdots ,K$. 为了后续计算表达式的简洁, 本文将上式求和范围统一写为$n=0,1,2,\cdots ,N-1,\ j = 0,1,2,\cdots ,K$, 将指标溢出的变量统一记为$0$.

定义离散变分$\eta^n_j = ({ g}^n_j)^{-1}\Delta { g}^n_j$. 利用离散变分原理可以得到结论^[20]:

离散变分原理$\Delta A^d = 0$成立当且仅当$\Big\{\zeta^{n+1/2}_j\Big\}$, $\Big\{\gamma^n_{j+1/2}\Big\}$ 满足离散Hamel场方程

离散边界条件

及离散相容性条件

本节首先证明自由的(不受外力、外力矩)的几何精确梁系统具有动量守恒性质, 随后通过离散Noether定理^[31]证明Hamel场变分积分子可以保持精确离散动量.

根据经典力学理论, 一个不受外力(矩)的完整力学系统总动量保持不变, 故自由运动的几何精确梁系统具有动量守恒性质. 动量守恒往往是在空间坐标下进行验证的, 由于Hamel场变分积分子是在活动标架下给出的, 为建立其离散动量守恒, 用活动标架表述的梁的动量.

根据Noether定理, 令 $\phi :[a,b]\times[0,l]\times (-\epsilon_0, \epsilon_0) \to {\bf R},\ \epsilon_0 >0$为任意一个以时空和变分变量为自变量的$C^1$光滑的函数, 并且满足$\phi (a,s,\epsilon) = \phi (b,s,\epsilon) = \phi (t,0,\epsilon)=\phi (t,l,\epsilon)=\phi (t,s,0) = 0, \ \forall t\in [a,b], \ \forall s\in [0,l]$.取定李代数中任意一个元素$\xi \in \mathfrak{se}(3)$, 构造变分曲线

$\widetilde { g}(t,s,\epsilon) = \exp(\phi (t,s,\epsilon)\xi) { g}(t,s)$

其中${ g}(t,s)$为Hamel场方程的任意一个精确解. 下文中均用 $ \widetilde{}$ 表示变量依赖于变分参数$\epsilon$. 于是$\widetilde { g}$的偏导数和无穷小变分$\Delta { g}$ 可分别写作

$\dot{\widetilde { g}} = \exp(\phi \xi) \dot { g} + \exp(\phi \xi) \dot{\phi } \xi { g} $

$\widetilde { g} '= \exp(\phi \xi) { g}'+ \exp(\phi \xi) \phi ' \xi { g} $

$\Delta { g} = \frac{\partial }{\partial \epsilon}\Big|_{\epsilon=0}\widetilde { g}(t,s,\epsilon) = \phi \xi { g}$

从而, 变分曲线对应的对流速度、对流应变和体坐标系下的变分分别为

${\widetilde \zeta} = \widetilde { g }^{-1} \dot{\widetilde { g}} = \zeta + \dot \phi \mbox{Ad}_{{ g}^{-1}}\xi $

${\widetilde \gamma} = \widetilde { g }^{-1} {\widetilde { g }'} = \gamma + \phi '\mbox{Ad}_{{ g}^{-1}}\xi$

$\eta = \Delta \phi \mbox{Ad}_{{ g }^{-1}}\xi.$

将变分曲线代入作用泛函并对其变分, 得到

$\begin{align} 0 = \Delta \mathcal{L} =\Delta \int_a^b \int^l_0 \frac12 \Big[\Big\langle {\mathcal K \widetilde \zeta}, {\widetilde \zeta} \Big\rangle - \Big\langle{ \mathcal P \widetilde \gamma}, {\widetilde \gamma}\Big\rangle\Big] dsdt = \\ \int_a^b \int^l_0 \Big[\Big\langle {\mathcal K \zeta}, \Delta { \widetilde \zeta} \Big\rangle - \Big\langle {\mathcal P\gamma}, \Delta {\widetilde \gamma}\Big\rangle\Big]dsdt = \\ \int_a^b \int^l_0 \Big[\Big\langle {\mathcal K \zeta},\Delta \zeta + \Delta {\dot\phi }\mbox{Ad}_{{ g}^{-1}}\xi \Big\rangle - \\ \Big\langle {\mathcal P\gamma}, \Delta \gamma + \Delta \phi '\mbox{Ad}_{{ g}^{-1}}\xi\Big\rangle\Big] dsdt \end{align}$

将式(3)代入, 得到

$\begin{align} 0 = \int_a^b \int^l_0 \Big[\Big\langle {\mathcal K \zeta}, \Delta {\dot\phi }\mbox{Ad}_{{ g}^{-1}}\xi \Big\rangle-\Big\langle {\mathcal P\gamma}, \Delta \phi '\mbox{Ad}_{{ g}^{-1}}\xi\Big\rangle\Big]dsdt \\ = \int_a^b \int^l_0 \bigg\langle -\frac{\partial }{\partial t} \Big(\mbox{Ad}^\ast _{{ g}^{-1}} {\mathcal K\zeta}\Big) + \\ \frac{\partial }{\partial s}\Big(\mbox{Ad}^\ast _{{ g}^{-1}} {\mathcal P\gamma}\Big) ,\xi \bigg\rangle \Delta \phi dsdt \end{align}$

其中$\text{Ad}^\ast $表示$\text{Ad}$算子的伴随算子. 由于$\Delta \phi $和$\xi$ 的任意性可知

此式为场论框架下的动量律. 进一步, 对式(11)在$[0,l]$上积分, 利用空间边界条件(4) 可以得到

即系统总动量守恒. 将此表达式改写到空间坐标系中, 即可得到角动量守恒和平动动量守恒的经典表达式. 下面, 在上述连续情形动量守恒证明的基础上, 利用离散Noether定理进一步证明Hamel变分积分子也可以自然保持系统离散动量. 定义变分序列

其中$\phi _j ^n(\epsilon)$为依赖于时空节点的变分参数的$C^1$光滑函数, 且满足

$\phi _j^0(\epsilon) = \phi _j^{N-1}(\epsilon) = \phi _1^n(\epsilon)= \phi _K^n(\epsilon)=\phi _j^n(0) = 0$

$\xi \in \mathfrak{se}(3)$为李代数中任一给定元素. 定义$\Big\{ {\widetilde g}^n_j \Big\}$的离散对流速度$\Big\{\widetilde {\zeta}^{n+1/2}_j\Big\}$和离散对流应变$\Big\{\widetilde{ \gamma}^{n}_{j+1/2}\Big\}$ 为

体坐标下的变分为

$\eta^n_j = { ({{ g}^n_j})^{-1}\Delta { g}^n_j} = \Delta \phi _j^n(\epsilon)\text{Ad}_{({{ g}^n_j})^{-1}}\xi$

根据式(13)和式(14)和BCH公式^[32]可知

$\begin{align} \widetilde { g}^{n+1}_j =\exp(\phi _j^{n+1}\xi ){ g}^{n+1}_j = \\ \exp(\phi _j^{n+1} \xi ){ g}^n_j \exp(\Delta t \zeta^{n+1/2}_j ) = \\ \exp[(\phi _j^{n+1} - \phi _j^n ) \xi ]\widetilde { g}^n_j \exp(\Delta t \zeta^{n+1/2}_j ) = \\ \widetilde { g}^n_j \exp[(\phi _j^{n+1} - \phi _j^n ) \text{Ad}_{({\widetilde { g}^n_j} )^{-1}}\xi ]\exp(\Delta t \zeta^{n+1/2}_j ) = \\ \widetilde { g}^n_j \exp\Big[\Delta t \zeta^{n+1/2}_j+(\phi _j^{n+1} - \phi _j^n ) I(\Delta t \zeta^{n+1/2}_j )\cdot \\ \text{Ad}_{({\widetilde { g}^n_j} )^{-1}}\xi +o(\epsilon )\Big] \end{align}$

其中算子$I: \mathfrak{se}(3)\to \mathfrak{se}(3)^\ast $为

$\mathcal{T}(X) = \sum_{k\geqslant 0}\frac{(-1)^k}{k+1}[\exp(\Delta t \text{ad} X)-I]^k, \ X\in \mathfrak{se}(3)$

同理可得

$\widetilde { g}^n_{j+1} = \widetilde { g}^n_j \exp[\Delta h \gamma^n_{j+1/2}+(\phi _{j+1}^n - \phi _j^n) I(\Delta h \gamma^n_{j+1/2})\cdot \\ \text{Ad}_{({\widetilde { g}^n_j})^{-1}}\xi +o(\epsilon)]$

故可知当$\Delta t$$\epsilon $充分小时, ${\widetilde \zeta}^{n+1/2}_j$ 与$\zeta^{n+1/2}_j$, 及${\widetilde \gamma}^{n}_{j+1/2}$ 与$\gamma^{n}_{j+1/2}$ 存在如下关系

根据离散Noether定理, 将变分序列代入离散Lagrange 密度并对其作用和变分, 得到

$\begin{align} 0=\Delta {A}^d = \\ \Delta t\Delta h \Delta \sum_{n=0}^{N-1} \sum_{j=0}^{K} \frac12 \bigg[\bigg\langle {\mathcal K \widetilde \zeta}^{n+1/2}_j, {\widetilde \zeta}^{n+1/2}_j \bigg\rangle - \\ \bigg\langle {\mathcal P \widetilde \gamma}^n_{j+1/2}, {\widetilde \gamma}^n_{j+1/2}\bigg\rangle \bigg] = \\ \Delta t\Delta h \sum_{n=0}^{N-1} \sum_{j=0}^{K}\bigg[\bigg \langle {\mathcal K \zeta}^{n+1/2}_j, \Delta {\widetilde \zeta}^{n+1/2}_j \bigg\rangle - \\ \bigg\langle {\mathcal P \gamma}^n_{j+1/2}, \Delta {\widetilde \gamma}^n_{j+1/2} \bigg\rangle \bigg] = \\ \Delta t\Delta h \sum_{n=0}^{N-1} \sum_{j=0}^{K}\bigg[\bigg\langle {\mathcal K \zeta}^{n+1/2}_j, \Delta \zeta^{n+1/2}_j + \\ \frac{\Delta \phi _j^{n+1} - \Delta \phi _j^n}{\Delta t} \left (I\left (\Delta t \zeta^{n+1/2 }_j \right )\text{Ad}_{({ g^n_j})^{-1}}\xi \right )\bigg\rangle - \\ \bigg\langle {\mathcal P \gamma}^n_{j+1/2}, \Delta \gamma^n_{j+1/2} +\frac{\Delta \phi ^n_{j+1} - \Delta \phi ^n_j}{\Delta h}\cdot \\ I(\Delta h \gamma^n_{j+1/2})\text{Ad}_{({{ g}^n_j})^{-1}}\xi \bigg\rangle \bigg] \end{align}$

其中最后一个等式利用了变分的定义, 可知小量$o(\epsilon)$的变分为零. 将离散Hamel方程代入上式可得

$\begin{align} 0=\Delta t\Delta h \sum_{n=0}^{N-1} \sum_{j=0}^{K} \bigg\langle {\mathcal K \zeta}^{n+1/2}_j, \frac{\Delta \phi _j^{n+1} - \Delta \phi _j^n}{\Delta t}\cdot \\ \left (I\left (\Delta t \zeta^{n+1/2 }_j \right )\text{Ad}_{({{ g}^n_j})^{-1}}\xi \right)\bigg\rangle - \\ \left \langle {\mathcal P \gamma}^n_{j+1/2},\frac{\Delta \phi ^n_{j+1} - \Delta \phi ^n_j}{\Delta h}I(\Delta h \gamma^n_{j+1/2})\text{Ad}_{({{ g}^n_j})^{-1}}\xi \right \rangle = \\ \Delta t \Delta h \sum_{n=0}^{N-1} \sum_{j=0}^{K} \frac{\Delta \phi _j^{n+1} - \Delta \phi _j^n}{\Delta t}\cdot \\ \left \langle \text{Ad}^\ast _{({ { g}^n_j})^{-1}} I^\ast \left (\Delta t \zeta^{n+1/2 }_j \right ){ \mathcal K \zeta}^{n+1/2}_j, \xi \right \rangle - \\ \frac{\Delta \phi _{j+1}^n - \Delta \phi _j^n}{\Delta h} \left \langle \text{Ad}^\ast _{({ { g}^n_j})^{-1}} I^\ast \left (\Delta h \gamma^n_{j+1/2} \right ) {\mathcal P \gamma}^n_{j+1/2}, \xi \right \rangle= \\ \Delta t \Delta h\sum_{n=1}^{N} \sum_{j=1}^{K} \Delta \phi ^n_j \bigg\langle \text{Ad}^\ast _{({ { g}^{n-1}_j})^{-1}} I^\ast \left (\Delta t \zeta^{n-1/2 }_j \right ) {\mathcal K \zeta}^{n-1/2}_j - \\ \text{Ad}^\ast _{({ { g}^n_j})^{-1}} I^\ast \left(\Delta t \zeta^{n+1/2 }_j \right ) {\mathcal K \zeta}^{n+1/2}_j , \xi \bigg \rangle - \\ \Delta \phi ^n_j \bigg\langle \text{Ad}^\ast _{({ { g}^n_{j-1}})^{-1}} I^\ast \left (\Delta h \gamma^n_{j-1/2} \right ) {\mathcal P \gamma}^n_{j-1/2} - \\ \text{Ad}^\ast _{({ { g}^n_j})^{-1}} I^\ast \left (\Delta h \gamma^n_{j+1/2} \right ) {\mathcal P \gamma}^n_{j+1/2} , \xi \bigg \rangle \end{align}$

对任意给定的$\xi$, 由于$\Delta \phi _j^n$的任意性可知

$\begin{align} \frac{1}{\Delta t}\bigg[\text{Ad}^\ast _{({ { g}^{n-1}_j})^{-1}} I^\ast \left (\Delta t \zeta^{n-1/2 }_j \right ) {\mathcal K \zeta}^{n-1/2}_j - \\ \text{Ad}^\ast _{({ { g}^n_j})^{-1}} I^\ast \left (\Delta t \zeta^{n+1/2 }_j \right ) {\mathcal K \zeta}^{n+1/2}_j\bigg] - \\ \frac{1}{\Delta s}\bigg[\text{Ad}^\ast _{({ { g}^n_{j-1}})^{-1}} I^\ast \left (\Delta h \gamma^n_{j-1/2} \right ) {\mathcal P \gamma}^n_{j-1/2} + \\ \text{Ad}^\ast _{({ { g}^n_j})^{-1}} I^\ast \left (\Delta h \gamma^n_{j+1/2} \right ){ \mathcal P \gamma}^n_{j+1/2}\bigg]= 0 \end{align}$

上式为式(11)的离散对应形式.

上式对$j$在$1,2,\cdots ,K$上求和并用离散边界条件(9)可得

$\sum_{j=1}^{K} \text{Ad}^\ast _{({ { g}^n_j})^{-1}} I^\ast \left (\Delta t \zeta^{n+1/2 }_j \right ){\mathcal K \zeta}^{n+1/2}_j = \text{constant vector}$

其中$I^\ast $为$I$的伴随算子.

综上, 可以得到如下定理定理3.1.

几何精确梁的Hamel场变分积分子(8)和(10)在边界条件(9)下满足如下定义的离散动量守恒

$J_d:= \Delta h \sum_{j=1}^{K} \text{Ad}^\ast _{({ { g}^n_j})^{-1}} I^\ast \left (\Delta t \zeta^{n+1/2 }_j \right ){\mathcal K \zeta}^{n+1/2}_j$

即随着离散系统的演化轨迹$\Big( g^{n-1}_j$, $\zeta^{n-1/2}_j\Big)$ $\to$ $\Big( g^n_j,$ $\zeta^{n+1/2}_j\Big)$ 是守恒的.

$J_d$表达式中级数的存在技术上是李代数$\mathfrak{se}(3)$非交换性在BCH公式中的反映, 而根本上由于在Hamel框架下, 离散对流速度$\zeta^{n+1/2}_j$处于位形${ g}^n_j$与${ g}^{n+1}_j$之间, 故位形和离散对流速度值无法完全匹配, 需离散动量表达式中出现级数来弥补. 这种不匹配对于Hamel场变分积分子的构造是必要的, 可以使所得变分积分子具有更高精度^[20]. 值得注意的是, 上式中的离散动量可以展开为

$J_d = \Delta h \sum_{j=1}^{K} \text{Ad}^\ast _{({ { g}^n_j})^{-1}} {\mathcal K \zeta}^{n+1/2}_j +O(\Delta t)$

这里的首项可作为连续动量(11)的直接离散, 从而Hamel变分积分子在$O(\Delta t)$ 误差范围内可以保持此离散动量的首项^[7].

下面通过两个例子分别从分析和数值角度验证上述结论.

例一 考虑一个沿$ E_3$方向以$ v_0$初速度做匀速直线运动的几何精确梁, 不妨设梁长$l = 1$ , 梁的质量和转动惯量均为1, 那么系统总动量非零分量为$J_lin3= v_0$.

在Hamel框架下, 梁的位形可写作

$g = \begin{pmatrix} 1& 0 & 0 &0 \\ 0 & 1 & 0 & y \\0 & 0 & 1 & z \\0 &0 &0 & 1 \end{pmatrix}$

其中$y$, $z$分别为截面中线在$ E_2$, $ E_3$ 方向的坐标. 从而对流速度有表达式

$\zeta = \begin{pmatrix} 0& 0 & 0 &0 \\ 0 & 0 & 0 & 0 \\0 & 0 & 0 & \dot z \\0 &0 &0 & 0 \end{pmatrix} \in \mathfrak{se}(3)$

在$\mathfrak{se}(3)$与${\bf R}^6$的等同下, $\zeta = (0,0,0,0,0,\dot z)^T$. 令$ a = (0,0,0,0,0,1)^T$, 由式(12)可得系统在$ E_3$方向上的动量为

$ \langle\int_0^1 \mbox{Ad}^\ast _{{ g}^{-1}}{\mathcal K \zeta} ds , a \rangle = \langle \zeta , \mbox{Ad}_{{ g}^{-1}} a \rangle = \dot z = v_0$

考虑系统的离散动量, 由于在此场景下非平凡的对称群为沿$E_3$轴做平移运动的加法群, 指数映射$\exp$退化为线性映射, 于是可得

$\zeta^{n+1/2}_j = \frac{{ g}^{n+1}_j- g^n_j}{\Delta t}= \begin{pmatrix} 0& 0 & 0 &0 \\ 0 & 0 & 0 & 0 \\0 & 0 & 0 & \dfrac{z^{n+1}_j-z^n_j}{\Delta t} \\0 &0 &0 & 0 \end{pmatrix}$

$E_3$方向上离散动量表达式为

$\langle J_d, a \rangle = \Bigg\langle \Delta h \sum_{j=1}^{K} \text{Ad}^\ast _{({ { g}^n_j})^{-1}} {\mathcal K \zeta}^{n+1/2}_j +O(\Delta t) , a \Bigg\rangle = \\ \Big\langle \zeta^{n+1/2}_j, \text{Ad}_{({ { g}^n_j})^{-1}} a \Big\rangle +O(\Delta t) = \frac{z^{n+1}_j-z^n_j}{\Delta t}+O(\Delta t)$

这与空间坐标系下的经典动量表达一致.

例二 考虑初始位形如图1所示的不受外力的几何精确梁. 其参数^[33] 如下: 梁长 $l = 1$, 横截面是边长为$0.1$ 的正方形, 密度$\rho = 1000$, 杨氏模量 $E= 10^7$, 泊松比 $\nu = 0.35$.

取时间步长$\Delta t = 10^{-4}$ s, 空间节点数 $K = 10$, 给定梁的初始对流速度为

$\omega_1 = 0.1,\ \omega_2 = 1,\ \omega_3 = 0.2, \ \pi_3 = 0$

$\pi_1 =\left\{ \begin{array}{ll} 2, &\ \ \ \mbox{fifth and sixth sections}\\ 0, &\ \ \ \mbox{other sections} \end{array} \right.$

$\pi_2 =\left\{ \begin{array}{ll} 3,& \ \ \ \mbox{second and third sections}\\ 0,& \ \ \ \mbox{other sections} \end{array} \right.$

初始对流应变为

$\varOmega = \varPi = 0$

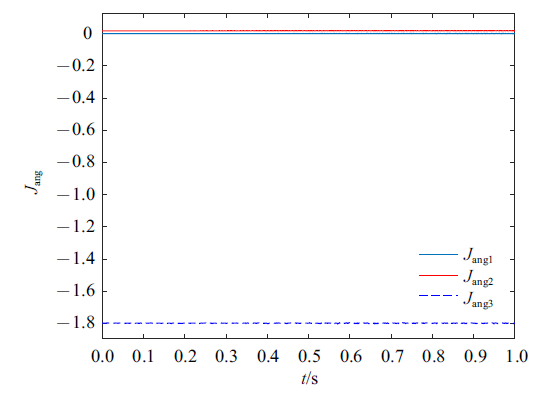
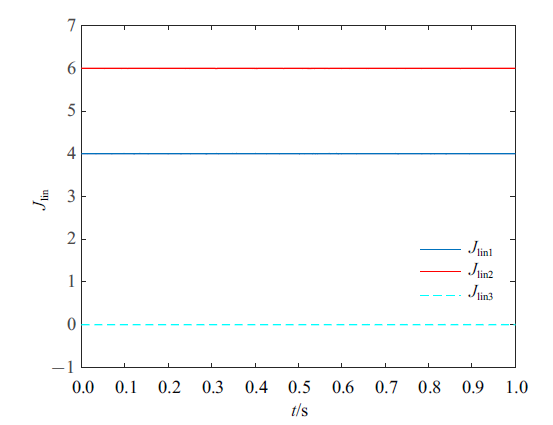
通过Hamel场变分积分子(8) $\sim$ (10)迭代计算10 000步, 得到几何精确梁的角动量和线动量如图2和图3所示, 说明了Hamel场变分积分子可以长时间以$O(\Delta t)$精度保持系统角动量和线动量.

对于不受外力、外力矩的力学系统, 动量守恒是一个基本的守恒律. 对几何精确梁模型, 传统方法往往将其看作大量刚体的串联或位形空间为无穷维流形的无穷维力学系统来研究其动量, 而本文在协变场论观点下, 从时空角度用活动标架法研究Hamel场变分积分子的保动量性质, 进一步说明了Hamel场变分积分子保结构的性质, 同时也间接说明其具有长时间数值稳定性. 本文所给的证明方法也同样适用于一般经典场论场景下的Hamel 场变分积分子. 下一步将探究Hamel形式及变分积分子的保能量、保辛结构等保结构性质, 并将其应用到壳、膜等更复杂力学系统的建模与仿真中.