引言
20世纪中期, 美国建筑师Fuller[1 ] 从艺术家Snelson[2 ] 的雕塑作品中获得灵感, 将"tension"和"integrity"融合为一个新的单词, 提出了"tensegrity" (张拉整体)的概念. 早期的张拉整体结构大多是从艺术角度设计的作品, 未考虑其工程应用价值, 直到20世纪80年代, 在Pellegrino[3 -4 ] 和Connelly等[5 ] 的推动下, 张拉整体结构才被越来越多的工程师所熟知.
张拉整体结构具有整体均匀承载、轻质、高收纳比等优异结构特性, 因此逐渐得到航天、生物力学、机器人等领域研究人员的广泛关注. 在航天工程领域, Tibert和Pellegrino[6 ] 提出了一种可展开张拉整体棱柱结构, 通过对其几何和内力分析及其实验验证, 证明了该结构具备较好的展开可靠度和较高的收纳比; SunSpiral等[7 ] 提出了张拉整体行星探测器的概念, 模拟和分析了张拉整体结构展开、降落和表面移动过程的动力学行为, 验证了其用于Titan行星探测任务的可行性; Caluwaerts等[8 ] 对用于行星探测的球形张拉整体机器人进行动力学仿真, 研究不同控制方法下系统动力学响应, 提出了生物启发的张拉整体结构控制策略; Iscen等[9 ] 通过分析不同层级和频率的测量信号, 获得了保持其以适当速度自主滚动的分布式驱动信号. 在生物力学领域, Ingber[10 -11 ] 利用张拉整体结构模拟细胞及其骨架整体结构的力学行为, 解释细胞结构的形变、运动和对机械信号的感知与传导机理, 进一步理解生物体的分级组织机理. 在机器人领域, Rovira和Tur[12 ] 推导了由刚性杆和弹性绳组成的棱柱张拉整体机器人动力学普遍方程, 并通过仿真研究了在指定运动下分布变长度绳的多状态离散控制方法; 陈竑希[13 ] 对四杆张拉整体机器人进行驱动方案设计和动力学仿真分析, 并通过实验验证了理论结果的正确性; Tietz等[14 ] 首次采用CPG (central pattern generators)控制实现多节机器人爬行运动的波形调控, 使其可在各种复杂地形上运动.
虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性.
以往对张拉整体结构或系统力学建模中, 一般假设绳索只发生纯拉伸变形, 且杆只发生纯压缩变形或假设为不变形的刚体. 在上述假设下, 当张拉整体系统发生大变形时, 部件会发生大转动而引起几何非线性问题, 使结构线性分析失效. Kebiche等[28 ] 基于非线性有限元思想, 利用虚功原理的增量分析, 在完全拉格朗日框架下推导了杆的非线性刚度矩阵, 实现了张拉整体系统的几何非线性分析; 在此基础上, Kahla和Kebiche[29 ] 引入了材料非线性本构, 将上述方法拓展到张拉整体系统的非线性弹塑性分析; 此外, Zhang等[30 ] 针对大位移小应变系统的高效分析, 采用共旋坐标法实现了张拉整体系统的几何和材料非线性分析. 进一步, 对于由细长杆或软材料杆组成的柔软张拉整体系统, 在系统变形或运动中杆还可能发生弯曲变形, 需研究杆后屈曲局部变形对系统整体承载性能与动力学行为的影响. Rimoli[31 ] 提出了张拉整体结构柔性杆的一种等效建模方法, 将杆的连续模型等效为集中参数模型, 采用较少的自由度捕捉了杆的屈曲、后屈曲行为及动力学特性, 可用于柔性张拉整体着陆器[31 ] 、复杂张拉整体点阵材料[32 ] 的动力学和非线性响应高效分析; 然而, 由于文献[31 ]中计算两端简支杆弯曲振动固有频率的解析表达式有误(即原文式(26)中固有频率应与阶数平方成正比, 而不是与阶数成正比), 致使在合适取值下计算的离散模型前两阶固有频率相对误差均为4.5%, 而事实上第二阶固有频率相对误差应为15%, 即弯曲固有振动的计算精度不高.
针对张拉整体结构中柔性细长杆动力学等效建模和高效计算, 本文提出了考虑拉压和弯曲变形的五节点离散杆模型, 从能量角度推导了连续模型与离散模型的动力学等效过程, 改进了Rimoli降阶模型[31 ] , 使得连续模型和离散模型的杆弯曲振动前两阶固有频率相对误差均降低至1%以内, 提高了动力学计算精度. 进一步, 以六杆球形张拉整体结构为研究对象, 建立和求解多柔体系统动力学方程, 开展压缩、模态和冲击的静/动态仿真与实验测试, 对比验证本文动力学建模和计算方法的有效性.
1 屈曲细长杆的动力学等效
1.1 连续模型与离散模型
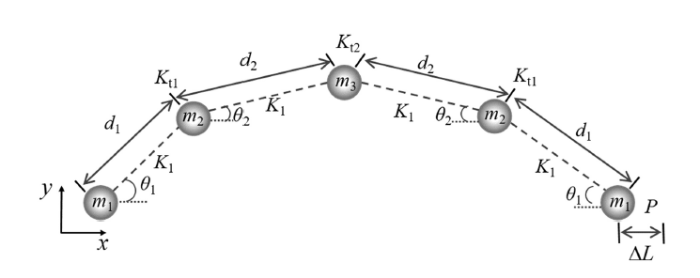
本节给出了细长杆连续模型的降阶离散模型, 该离散模型采用五节点弹/扭簧集中质量模型来等效连续杆的动力学特性, 如图1 所示. 其中, 均质连续杆的长度为$L$, 截面面积为$A$, 截面惯性矩为$I$, 材料密度为$\rho $, 杨氏模量为$E$. 离散模型5个节点的位置和轴向刚度假设为均匀分布, 轴向弹簧自由长度均为$L/4$且刚度均为$K_{1} $; 而其分布集中质量大小和分布弯曲刚度假设为非均匀, 考虑受压杆件变形对称性, 设集中质量和弯曲刚度在质心两侧对称分布, 分布集中质量大小表示为$m_{1} $, $m_{2} $和$m_{3} $, 分布弯曲刚度大小表示为$K_{t1} $和$K_{t2} $. 1.2 $\sim$ 1.4节将从能量角度给出上述集中参数动力学等效过程.
图1
图1
细长杆连续模型和离散模型示意图
Fig.1
Schematic diagram of the continuous and discrete model of a slender bar
1.2 刚度大小等效
根据材料力学中杆的拉压变形理论, 容易得到等效轴向刚度为
(1) $K_{1} =\dfrac{4EA}{L}$
随着轴向压力增大, 杆会发生屈曲, 为了描述杆弯曲变形受力状态, 引入弯曲刚度$K_{t1} $和$K_{t2} $. 如图2 所示, 离散模型在轴向载荷$P$的作用下呈现压缩和弯曲耦合变形状态, 且关于中心点对称, 此时系统的总势能表达为
(2) $\begin{align} \varPi =2\times \dfrac{1}{2}K_{1} (d_{1} -L_{1} )^{2}+2\times \dfrac{1}{2}K_{1} (d_{2} -L_{1} )^{2}+ \\ 2\times \dfrac{1}{2}K_{t1} (\theta_{1} -\theta_{2} )^{2}+\dfrac{1}{2}K_{t2} (2\theta_{2} )^{2}-P\Delta L = \\ K_{1} (d_{1} -L_{1} )^{2}+K_{1} (d_{2} -L_{1} )^{2}+K_{t1} (\theta_{1} -\theta_{2} )^{2}+ \\ 2K_{t2} \theta_{2}^{2}-PL+2Pd_{1} \cos \theta_{1} +2Pd_{2} \cos \theta_{2} \end{align}$
图2
图2
离散模型的屈曲构型示意图
Fig.2
Schematics of buckling configuration for the discretization scheme
其中$d_{1} $, $d_{2} $, $\theta_{1} $和$\theta_{2} $等为局部变量, 如图2 所示, $L_{1} =0.25L$, $\Delta L$是载荷$P$引起的位移, 可表示为
(3) $\Delta L=L-2d_{1} \cos \theta_{1} -2d_{2} \cos \theta_{2}$
以$d_{1} $, $d_{2} $, $\theta_{1} $和$\theta_{2} $为广义坐标, 由最小势能原理可得以下平衡方程
(4) $\left. {\begin{array}{l} \dfrac{\partial \varPi }{\partial d_{1} }=2K_{1} (d_{1} -L_{1} )+2P\cos \theta_{1} =0 \\ \dfrac{\partial \varPi }{\partial d_{2} }=2K_{1} (d_{2} -L_{1} )+2P\cos \theta_{2} =0 \\ \dfrac{\partial \varPi }{\partial \theta_{1} }=2K_{t1} (\theta_{1} -\theta_{2} )-2Pd_{1} \sin \theta_{1} =0 \\ \dfrac{\partial \varPi }{\partial \theta_{2} }=2K_{t1} (\theta _{2} -\theta_{1} )+4K_{t2} \theta_{2} -2Pd_{1} \sin \theta_{2} =0 \\ \end{array}} \right\}$
为了捕捉屈曲临界载荷, 考虑对上述后屈曲段非线性平衡方程进行转角趋于零的线性化. 当转角$\theta_{1}$和$\theta_{2} $趋于零时有
(5) $\left. \begin{array}{l} \cos \theta_{1} \approx 1, \ \sin \theta_{1} \approx \theta_{1}\\ \cos \theta_{2} \approx 1, \ \sin \theta_{2} \approx \theta_{2}\\ \end{array} \right\}$
(6) $\left. {\begin{array}{l} \dfrac{\partial \varPi }{\partial d_{1} }=2K_{1} (d_{1} -L_{1} )+2P=0 \\ \dfrac{\partial \varPi }{\partial d_{2} }=2K_{1} (d_{2} -L_{1} )+2P=0 \\ \dfrac{\partial \varPi }{\partial \theta_{1} }=2K_{t1} (\theta_{1} -\theta_{2} )-2Pd_{1} \theta_{1} =0 \\ \dfrac{\partial \varPi }{\partial \theta_{2} }=2K_{t1} (\theta _{2} -\theta_{1} )+4K_{t2} \theta_{2} -2Pd_{2} \theta _{2} =0 \\ \end{array}} \right\}$
(7) $d_{1} =d_{2} =L_{1} -\dfrac{P}{K_{1} }=\dfrac{L}{4}-\dfrac{P}{K_{1} }$
(8) $\left[ {{\begin{array}{*{20}c} {K_{t1} -Pd_{1} } & {-K_{t1} } \\ {-K_{t1} } & {K_{t1} +2K_{t2} -Pd_{2} } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\theta_{1} } \\ {\theta_{2} } \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} }} \right]$
显然, 式(8)的一组平凡解为$\theta_{1} =\theta_{2} =0$, 该零解与式(7)描述了杆屈曲前纯压缩状态; 由式(8)的非零解条件可得到屈曲临界载荷$P_cr $应满足的关系式, 即
(9) $\left|\begin{array}{cc} {K_{t1} -P_cr d_{1} } & {-K_{t1} }\\ {-K_{t1} } & {K_{t1} +2K_{t2} -P_cr d_{2} } \\ \end{array}\right| = \\ 2K_{t1} K_{t2} -P_cr (d_{1} +d_{2} )K_{t1} -2P_cr d_{1} K_{t2} + d_{1} d_{2} P_cr^{2}=0$
设弯曲刚度分布参数为$n$, 使得$K_{t2} =nK_{t1} $, 将该式和式(7)代入式(9)得
(10) $2nK_{t1}^{2} -2(1+n)(\dfrac{L}{4}-\dfrac{P_cr }{K_{1} } )P_cr K_{t1} + \\ (\dfrac{L}{4}-\dfrac{P_cr }{K_{1} } )^{2}P_cr^{2} =0$
(11) $P_cr =\dfrac{\pi^{2}EI}{L^{2}}$
将式(11)代入式(10), 求解关于$K_{t1} $的一元二次方程, 得其二根为
(12) $K_{t1}^{1, 2} =K_{t2}^{1, 2} /n= \dfrac{(1+n\pm \sqrt {1+n^{2}} )\pi^{2}EI}{8nL}(1-\dfrac{\pi^{2}I}{AL^{2}} )$
其中, 刚度分布参数$n$将通过1.4节弯曲振动固有特性等效确定, $\pm$分别对应$K_{t1} $的较大根和较小根. 对于同一根杆的等效离散模型, 当$K_{t1} $取较大根时, 后文确定的刚度分布参数$n<1$, 即$K_{t2}<K_{t1} $, 则中心点承受的弯矩小于其两侧点承受的弯矩; 反之, $n>1$, 则中心点承受的弯矩大于其两侧点承受的弯矩. 由于后者方式等效的弯曲振动固有频率误差较大, 本文仅选取前者方式等效, 即上式取正号. 此外, 当模拟细长杆时, $\pi^{2}I/(AL^{2})\ll 1$, 可忽略上式中的该项.
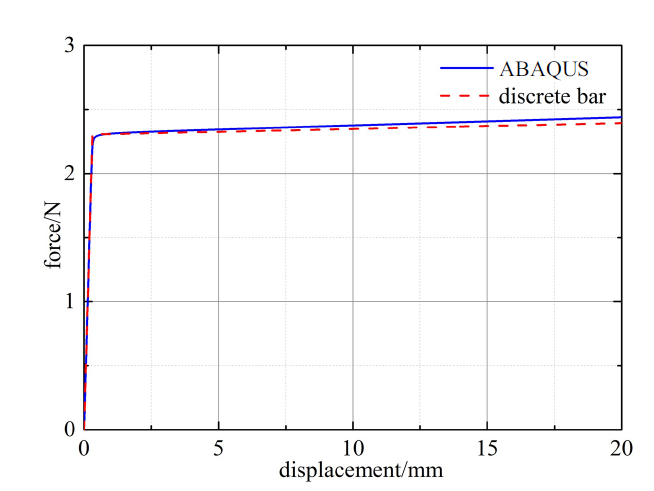
进一步, 为了验证该离散模型是否可较准确地预测细长杆的后屈曲变形, 将其计算结果与商用软件ABAQUS的有限元计算结果进行对比. 设截面半径为5 mm、长度为0.2 m和杨氏模量为19 MPa的杆, 两端为简支约束, 一端位置固定, 另一端可沿两端点连线方向滑动并在该端施加纵向压力, 分别采用离散模型和有限元软件计算其受压屈曲全过程. 图3 所示为压力与纵向位移对比图, 可见两者结果吻合较好.
图3
图3
受压杆有限元模型与离散模型载荷-位移对比图
Fig.3
Load-displacement comparison for the continuous and discrete bar under compression
1.3 质量大小等效
通过对比连续杆和离散杆的动能可求出节点的质量. 假设连续杆上存在线速度场$u$和$v$
(13) $u(x)=c_{1} x+c_{2}, \ \ v(x)=c_{3} x+c_{4}$
其中, $u$代表惯性坐标系下沿杆轴向的速度分量, $v$代表惯性坐标系下沿杆横向的速度分量, $x\in [-L/2, \ L/2]$表示参考构型下沿杆轴向的局部坐标, $c_{1} $, $c_{2} $, $c_{3} $和$c_{4} $表示任意常数. 该线速度场虽不能描述平面柔性杆的全部运动, 但可表示部分主要发生的运动, 即刚体平移、刚体转动及轴向均匀变形. 在该线速度场描述下, 连续杆的动能可表达为
(14) $T_{con} =\dfrac{1}{2}\int_{-L/2}^{L/2} {\rho A[u(x)^{2}+v(x)^{2}]}dx = \\ \dfrac{1}{24}\rho AL^{3}(c_{1}^{2} +c_{3}^{2} )+\dfrac{1}{2}\rho AL(c_{2}^{2} +c_{4}^{2} )$
另一方面, 通过线速度场$u$和$v$, 离散模型的动能可表达为
(15) $T_{dis} =(\dfrac{m_{1} L^{2}}{4}+\dfrac{m_{2} L^{2}}{16} )(c_{1}^{2} +c_{3}^{2} )+ (m_{1} +m_{2} +\dfrac{1}{2}m_{3} )(c_{2}^{2} +c_{4}^{2} )$
由于$c_{1} $, $c_{2} $, $c_{3} $和$c_{4} $表示任意常数, 为了使连续杆和离散模型的动能相等, $(c_{1}^{2} +c_{3}^{2} )$和$(c_{2}^{2} +c_{4}^{2} )$前面的系数须保持一致, 因此由式(14)和式(15)可得
(16) $\left. \begin{array}{l} \dfrac{1}{4}m_{1} L^{2}+\dfrac{1}{16}m_{2} L^{2}=\dfrac{1}{24}\rho AL^{3} \\ m_{1} +m_{2} +\dfrac{1}{2}m_{3} =\dfrac{1}{2}\rho AL \\ \end{array} \right\}$
式(16)只有两个方程, 无法直接求得$m_{1} $, $m_{2} $和$m_{3} $的解, 故设质量分布参数为$c$, 使得$m_{3} =cm_{2} $, 则由式(16)解得
(17) $\left. \begin{array}{l} m_{1} =\dfrac{1+2c}{18+12c}\rho AL \\ m_{2} =\dfrac{4}{9+6c}\rho AL \\ m_{3} =\dfrac{4c}{9+6c}\rho AL \\ \end{array} \right\}$
至此, 已全部求出离散模型的轴向刚度、弯曲刚度和节点质量. 但是其中的弯曲刚度和节点质量并不是完全不变的, 通过调节参数$n$和$c$可对弯曲刚度和节点质量进行分配. 1.4节将对$n$和$c$的取值进行讨论, 使离散模型可以更准确地描述连续杆的动力学行为.
1.4 弯曲刚度和集中质量分布特性的确定
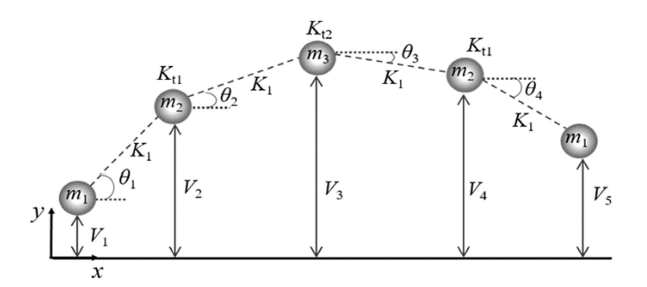
当计算离散模型在无应力状态时的固有频率时, 轴向振动模态和弯曲振动模态可以独立研究. 杆横向运动构型描述如图4 所示, $V_{1}$, $V_{2} $, $V_{3} $, $V_{4} $和$V_{5}$表示各质点横向位移(即与水平参考线的距离), $\theta_{1} $, $\theta_{2} $, $\theta_{3} $和$\theta_{4} $表示各离散直线段的转角(即与水平参考线的夹角), 则弯曲应变能可表达为
(18) $W=\dfrac{1}{2}K_{t1} (\theta_{2} -\theta_{1} )^{2}+\dfrac{1}{2}K_{t2} (\theta_{3} -\theta_{2} )^{2} + \dfrac{1}{2}K_{t1} (\theta_{4} -\theta _{3} )^{2}$
图4
图4
模态分析的构型示意图
Fig.4
Schematics of configuration for modal analysis
当杆横向运动在水平参考线附近进行线性化时, 各转角趋于零, 有
(19) $\left. {\begin{array}{l} \theta_{1} \approx \sin \theta_{1} =\dfrac{4(V_{2} -V_{1} )}{L} \\ \theta_{2} \approx \sin \theta_{2} =\dfrac{4(V_{3} -V_{2} )}{L} \\ \theta_{3} \approx \sin \theta_{3} =\dfrac{4(V_{4} -V_{3} )}{L} \\ \theta_{4} \approx \sin \theta_{4} =\dfrac{4(V_{5} -V_{4} )}{L} \\ \end{array}} \right\}$
(20) $W=8K_{t1} (\dfrac{V_{3} -2V_{2} +V_{1} }{L} )^{2}+8K_{t2} (\dfrac{V_{4} -2V_{3} +V_{2} }{L} )^{2}+ \\ 8K_{t1} (\dfrac{V_{5} -2V_{4} +V_{3} }{L} )^{2}$
上述弯曲应变能对横向位移求两次偏导, 可得离散系统的对称刚度矩阵表达为
(21) $K=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {K_{11} } & {K_{12} } & {K_{13} } & {K_{14} } & {K_{15} } \\ & {K_{22} } & {K_{23} } & {K_{24} } & {K_{25} } \\ & & {K_{33} } & {K_{34} } & {K_{35} } \\ & {sym} & & {K_{44} } & {K_{45} }\\ & {K_{55} } \\ \end{array} }} \right]$
其中$K_{ij} =\partial ^{2}W/(\partial V_{i} \partial V_{j} )$且$i$, $j=1$, 2, 3, 4, 5.文末附录给出了当考虑细长杆时上述刚度矩阵各分量的表达式.
根据式(17)所求的质点质量, 可得出离散系统的质量矩阵为
(22) $M=\rho AL\left[ {{\begin{array}{ccccc} {\dfrac{1+2c}{18+12c}} & 0 & 0 & 0 & 0 \\ 0 & {\dfrac{4}{9+6c}} & 0 & 0 & 0 \\ 0 & 0 & {\dfrac{4c}{9+6c}} & 0 & 0 \\ 0 & 0 & 0 & {\dfrac{4}{9+6c}} & 0 \\ 0 & 0 & 0 & 0 & {\dfrac{1+2c}{18+12c}} \\ \end{array} }} \right]$
计算固有频率时, 边界条件可通过消去对应自由度的方式施加. 假设杆两端为简直边界条件, 则分别消去以上刚度矩阵和质量矩阵的首行首列和尾行尾列, 利用剩余部分$\tilde{ K}$和$\tilde{ M}$求解广义特征值方程, 即
(23) $\det(\tilde{ K}-\omega^{2}\tilde{ M})=0$
解关于$\omega^{2}$的一元三次方程, 得离散模型前三阶固有频率平方为
(24) $\left. {\begin{array}{l} \omega_{1, dis}^{2} =\dfrac{K_{22} m_{3} +K_{24} m_{3} +K_{33} m_{2}-\sqrt \varDelta }{2m_{2} m_{3} } \\ \omega_{2, dis}^{2} =\dfrac{K_{22} -K_{24} }{m_{2} } \\ \omega_{3, dis}^{2} =\dfrac{K_{22} m_{3} +K_{24} m_{3} +K_{33} m_{2}+\sqrt \varDelta }{2m_{2} m_{3} } \\ \end{array}} \right\}$
(25) $\varDelta =(K_{22} +K_{24} )^{2}m_{3}^{2}-2(K_{22} K_{33} -4K_{23}^{2}+ K_{24} K_{33} )m_{2} m_{3} +K_{33}^{2}m_{2}$
(26) $\left. {\begin{array}{l} \omega_{1, con}^{2} =\dfrac{\pi^{4}EI}{\rho AL^{4}} \\ \omega_{2, con}^{2} =\dfrac{16\pi^{4}EI}{\rho AL^{4}} \omega_{3, con}^{2} =\dfrac{81\pi^{4}EI}{\rho AL^{4}} \\ \end{array}} \right\}$
通过计算离散模型与连续模型的固有频率相对误差来确定参数$n$和$c$的取值, 定义如下频率相对误差
(27) $\varepsilon_{i} (n, c)=\dfrac{\omega_{i, dis} (n, c)-\omega _{i, con} }{\omega_{i, con} }, \ \ i=1, 2, 3$
本文构造的离散模型, 考虑对连续模型前两阶固有特性进行捕捉, 因此定义前两阶固有频率均方根误差如下
(28) $Re(n, c)=\sqrt {\varepsilon_{1}^{2} (n, c)+\varepsilon_{2}^{2} (n, c)}$
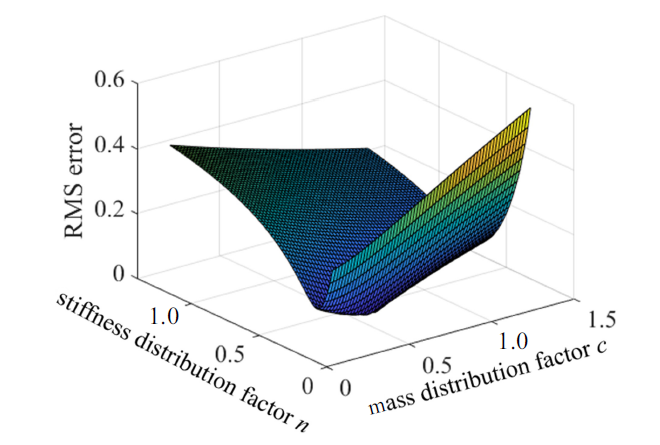
由此将$Re(n, c)$表示为分布参数$n$和$c$的函数, 其函数图像如图5 所示.
图5
图5
离散模型随$n$和$c$变化的前两阶固有频率均方根误差
Fig.5
RMS (root-mean-square) error in the first two natural frequencies of the discrete bar as the function of $n$ and $c$
由图5 函数图像可得当$n=0.39$且$c=0.60$时, 前两阶固有频率的均方根误差达到最小值. 将求得的$n$和$c$代入式(27)可得到前三阶固有频率误差. 如式(29)所示, 前两阶固有频率误差较小, 但第三阶固有频率误差较大, 原因是考虑到张拉整体结构柔软特性和实际工况受载情况, 式(28)在求解调节参数$n$和$c$时仅考虑了对系统动力学行为产生主要影响的前两阶固有模态, 而截断了影响较小的更高阶模态.
(29) $\left. {\begin{array}{l} \varepsilon_{1} =0.000 8 \\ \varepsilon_{2} =0.004 0 \\ \varepsilon_{3} =0.278 3 \\ \end{array}} \right\}$
至此, 细长杆的降阶离散模型分布刚度和分布质量动力学等效全部完成, 考虑了杆的轴向拉压刚度等效、受压屈曲弯曲刚度等效、线性速度场下动能等效以及杆的弯曲振动固有特性近似等效, 可描述细长杆大范围运动、轴向拉压变形和横向弯曲变形耦合动力学特性. 下一步, 将该降阶模型运用到张拉整体结构的动力学建模, 建立并数值求解系统动力学方程.
2 张拉整体系统瞬态动力学方程
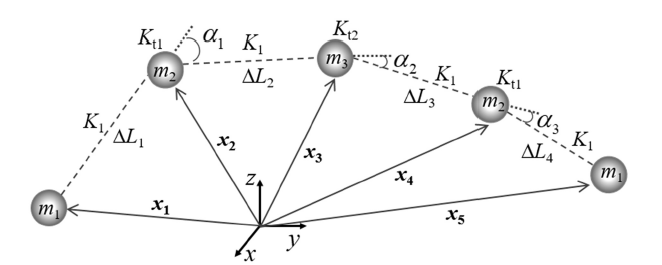
(30) $U^{bar}=\dfrac{1}{2}K_{1} \sum\limits_{i=1}^4 {\Delta L_{i}^{2} } +\dfrac{1}{2}K_{t1} (\alpha_{1}^{2} +\alpha_{3}^{2} )+\dfrac{1}{2}K_{t2} \alpha_{2}^{2}$
图6
图6
离散杆变形构型示意图
Fig.6
Schematic representation of the deformed configuration for the discrete bar
其中, $\Delta L_{i} $ ($i=1, 2, 3, 4$)表示各弹簧的长度变化量, $\alpha_{j} $ ($j=1, 2, 3$)表示各扭簧的转角.
如图6 所示, ${ x}_{k}$ ($k=1, 2, 3, 4, 5$)表示离散模型各节点在全局坐标系下的位置向量, 为了用${ x}_{k} $表示式(30)中的局部变量, 定义如下各式
(31) ${ t}_{i} ={ x}_{i+1} -{ x}_{i}, \ \ { u}_{i} =\dfrac{{ t}_{i} }{\left| {{ t}_{i} } \right|}, \ \ i=1, 2, 3, 4$
(32) $\Delta L_{i} =\left| {{ t}_{i} } \right|-\dfrac{L}{4}, \ \ i=1, 2, 3, 4$
(33) $\cos (\alpha_{j} )={ u}_{j} \cdot { u}_{j+1} , \ \ j=1, 2, 3$
离散杆的应变能式(30)对广义坐标求偏导可得由杆内力导致的第$k$个节点广义内力列阵表达为
(34) ${ f}_{k}^{ bar} =\dfrac{\partial U^{bar}}{\partial { x}_{k} }, \ \ k=1, 2, 3, 4, 5$
同时, 对于张拉整体结构, 杆的两个端点还受到绳索张力作用, 设一根杆端点$a$与另一根杆端点$b$通过绳索相连, 则由绳内力导致的端点$a$广义内力列阵(端点$b$同理)表达为
(35) ${ f}_{a}^{ string} =\left\{ {\begin{array}{l@{\quad }l} k\Delta l\dfrac{{ x}_{a} -{ x}_{b} }{\left| {{ x}_{a} -{ x}_{b} } \right|}, & \Delta l>0 \\ 0, & \Delta l\leqslant 0 \\ \end{array}} \right.$
其中, $k$为绳索的抗拉刚度, $\Delta l=\left| {{ x}_{a} -{ x}_{b} } \right|-l_{0} $为绳索的长度变化量, $l_{0} $为绳索的自然长度.
由于张拉整体结构中一般采用轻质绳索, 故可忽略绳索惯性力影响. 将所有杆各个节点全局位置向量、等效质量、上述广义内力及受到的其他广义外力进行组装, 得到系统广义坐标列阵${ q}$、质量矩阵${ M}$、广义内力列阵${ F}_{int}$及广义外力列阵${ F}_{ext} $. 考虑系统可能受到约束, 引入约束方程和拉格朗日乘子, 可得系统在时刻$t$的瞬态动力学方程为
(36) $\left. {\begin{array}{l} { M\ddot{{ q}}}+{ F}_{int} +{ \varPhi }_{, { q}}^T { \lambda }-{ F}_{ext} ={\bf 0} \\ { \varPhi }({ q}, t)={\bf 0} \\ \end{array}} \right\}$
其中, $\ddot{ q}=d^{2}{ q}/dt^{2}$表示广义加速度列阵, ${ \varPhi }$为广义约束列阵, ${ \varPhi }_{, { q}} =\partial { \varPhi }/\partial { q}$为约束的雅可比矩阵, ${ \lambda }$为拉格朗日乘子列阵. 最后, 采用广义$\alpha $时间离散算法将式(36)微分-代数方程组转化为非线性代数方程组, 并采用牛顿迭代法求解非线性代数方程组, 进而得到系统广义坐标列阵在不同时刻的数值解.
进一步, 为了提高动力学计算效率, 可将图6 所示杆的内部自由度${ x}_{2}$, ${ x}_{3} $和${ x}_{4} $缩聚至端部自由度${ x}_{1} $和${ x}_{5} $, 即利用静力缩聚法将内部自由度刚度等效至端部自由度的广义刚度矩阵[33 -34 ] , 并将杆的总质量均布在端部节点上, 从而大大降低迭代过程中系统动力学方程(36)的维数. 当杆承受的压力超过其屈曲临界载荷时, 需计算杆的后屈曲构型, 此时以计算得到端部位置坐标作为输入, 利用后屈曲内力平衡关系式(4), 迭代求解杆内部节点的位置.
3 数值算例与实验验证
3.1 球形张拉整体结构构型与参数
图7 为球形张拉整体结构构型图, 由6根杆和24根绳索组成. 实验中, 制作了两种不同的六杆球形张拉整体结构, 一种由弹性模量较大的木杆和弹性模量较小的松紧绳构成, 另一种由弹性模量较小的橡胶杆和弹性模量较大的尼龙绳构成. 两种结构的几何参数相同, 每根杆长度均为0.2 m, 横截面均为圆形且直径均为1 cm; 木杆张拉整体结构材料参数分别为: 杨氏模量10 GPa, 密度675 kg/m$^3$, 松紧绳拉伸刚度150 N/m, 预拉伸4.5 N. 橡胶杆张拉整体结构材料参数分别为: 杨氏模量19 MPa, 密度1354 kg/m$^3$, 尼龙绳拉伸刚度30 kN/m, 无预拉伸.
图7
图7
张拉整体结构构型图(红色粗线: 杆, 绿色细线: 绳)
Fig.7
Configuration diagram of tensegrity structure (thick red lines: bars, thin green lines: cables)
3.2 准静态压缩
采用万能试验机(Instron E44.104), 对上述两种张拉整体结构进行准静态压缩实验. 将张拉整体结构的底端固定在试验机平台上, 对上端节点进行缓慢压缩, 测得压力和压缩位移的关系, 并通过数值模型模拟了这一过程. 图8 所示为橡胶杆张拉整体结构在不同压缩位移下仿真和实验构型图, 随着压缩位移的增大, 橡胶杆由纯压缩变形转变为屈曲变形.
图8
图8
仿真(左)和实验(右)中橡胶杆张拉整体结构不同压缩位移下变形图
Fig.8
Deformed configurations of the rubber tensegrity under difference compressions in the simulation (left) and experiment (right)
图9 所示为压力与压缩位移曲线的实验与仿真对比, 其中实验数据表现为3次实验测量的平均值与标准差. 仿真结果与实验结果基本吻合, 且实验数据的标准差较小, 说明实验具有较好的可重复性. 图9 (a)中, 木杆张拉整体结构力-位移曲线呈现近似线性, 由于松紧绳模量远小于木杆模量, 所以压缩时木杆几乎不发生变形, 系统的弹性势能主要储存在松紧绳内, 且杆不发生屈曲. 图9 (b)中, 橡胶杆张拉整体结构力-位移曲线呈现明显非线性, 由于尼龙绳模量远大于橡胶杆模量, 所以压缩时尼龙绳几乎不伸长, 系统的弹性势能主要存储在橡胶杆内; 当压缩位移达到8 mm左右时, 曲线出现了拐点, 此时橡胶杆开始屈曲, 在后屈曲段张拉整体结构虽然刚度有所下降, 但仍具有较高的承载能力.
图9
图9
压力与压缩位移的实验与仿真对比图: (a) 木杆张拉整体结构; (b) 橡胶杆张拉整体结构
Fig.9
Comparison for the compressive forces versus displacements of experiments and simulations: (a) Wooden tensegrity; (b) rubber tensegrity
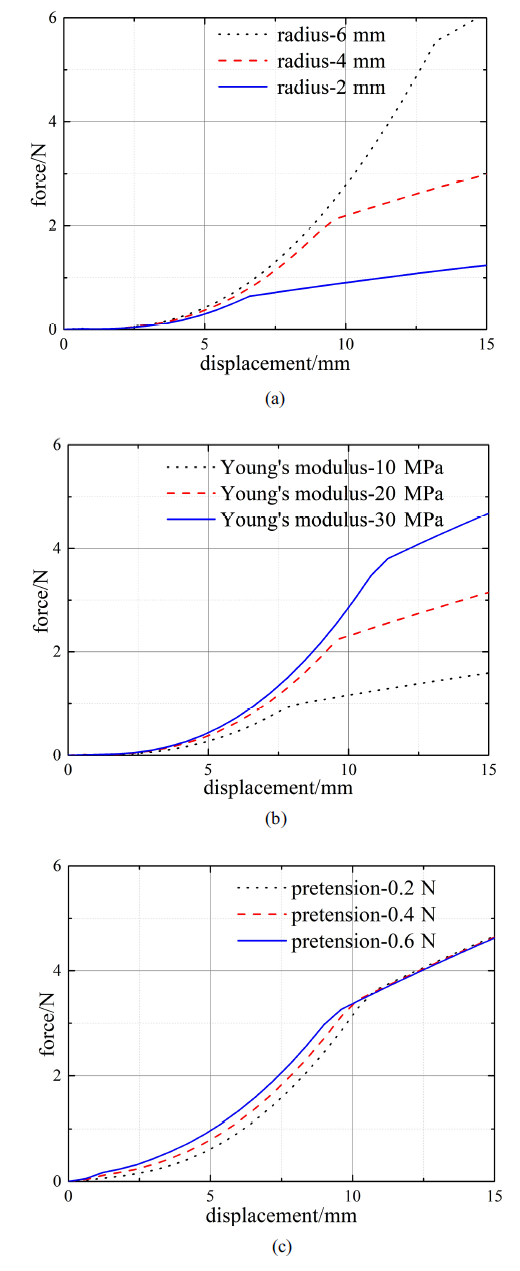
为进一步理解张拉整体结构静态承载能力变化规律, 开展不同参数下准静态压缩数值实验. 改变杆件的截面半径、模量和绳索的预张力, 得到如图10 所示不同的力-位移曲线. 从图10 可以看出, 杆件屈曲之前, 结构的整体刚度随位移的增大而增大, 而杆件屈曲之后, 结构的整体刚度趋于不变. 如图10 (a)和图10 (b)所示, 杆件的半径和模量改变时, 在杆件屈曲前对结构的整体刚度影响较小, 在杆件屈曲后对结构的整体刚度影响较大. 如图10 (c)所示, 当绳索预张力改变时, 在杆件屈曲前对结构的整体刚度影响较大, 在杆件屈曲后对结构的整体刚度基本没有影响.
图10
图10
压力与压缩位移曲线在不同结构参数下的对比: (a) 杆截面半径变化; (b) 杆模量变化; (c) 绳索预张力变化
Fig.10
Comparison for the compressive forces versus displacements under different structural parameters: (a) Cross-section radii of bars; (b) moduli of bars; (c) pretensions of strings
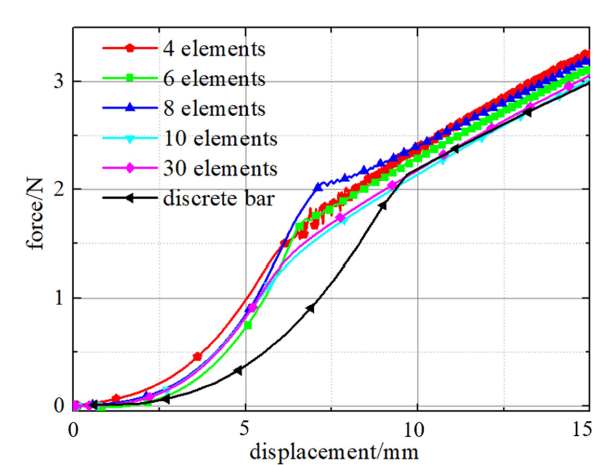
为验证本文离散模型的高效性, 采用ABAQUS商用有限元分析软件建立张拉整体结构模型, 与本文等效模型的仿真时间进行对比. 计算机配置为4核(Intel(R) Xeon(R) CPU E3-1226 v3 @3.30GHz)、8GB内存, 采用单线程运行, 时间步长为$1.0\times10^{-5}$ s. 图11 为ABAQUS单元收敛性测试, 杆单元类型为B31, 由图可知每根杆取10个单元与取30个单元的力-位移曲线基本重合, 说明此时计算收敛, 故ABAQUS模型中每根杆取10个单元. 与图3 压缩单根杆不同, 用ABAQUS压缩张拉整体结构时每根杆需引入较大初始缺陷才能保证算法收敛, 故在杆屈曲前与本文离散模型存在一定误差, 但在屈曲后与本文离散模型基本一致. 整个计算过程本文离散模型所需时间为120 s, ABAQUS所需时间为426 s, 在相同计算精度下计算效率提高了3倍以上, 说明本文提出的等效方法具有较高的计算效率. 此外, 本算例也说明, 采用有限单元分析张拉整体结构后屈曲过程时, 需引入较大的初始几何缺陷, 由缺陷敏感性造成仿真结果可能存在较大偏差, 而本文等效模型则不需引入过大的初始几何缺陷.
图11
图11
ABAQUS有限元分析收敛性测试和与本文离散杆模型的计算结果对比
Fig.11
Convergence test of finite element analysis by ABAQUS and comparison with the computation result by the proposed discrete bar
3.3 模态分析
本节对张拉整体结构的模态进行了实验和仿真分析. 将底部3个节点固定在振动试验台上, 对结构进行扫频测试, 用高速相机对其振动进行拍摄. 当频率为15 Hz时, 张拉整体结构发生较大幅度的上下晃动, 此时上端节点的振幅达到最大, 由此确定张拉整体结构的基频约为15 Hz, 由数值仿真求得的基频为15.37 Hz, 两者基本一致. 实验和仿真对应的第一阶振型如图12 所示, 可以看到上部3根杆有明显向上扩张的趋势.
图12
图12
木杆张拉整体结构第一阶固有振型的实验(左)和仿真(右)图
Fig.12
The first natural mode of vibration of the wooden tensegrity in the experiment (left) and simulation (right)
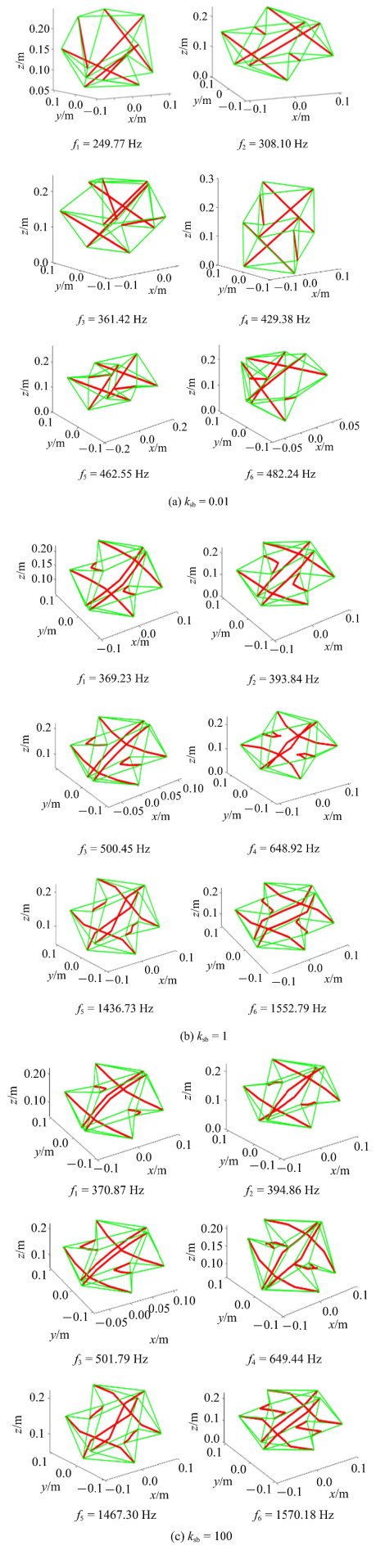
进一步, 研究绳索与杆件不同刚度比对张拉整体结构固有振动特性的影响规律. 改变绳索抗拉刚度, 使其与杆件等效抗压刚度的比值$k_sb$分别取0.01, 1和100, 通过数值计算画出前六阶固有振型图如图13 所示. 当两者比值为0.01时, 绳索的刚度较小, 其固有振型更容易被激发, 如图13 (a)所示; 当两者比值为1时, 弹簧和杆件的固有频率被同时激发, 如图13 (b); 当两者比值为100时, 杆件的固有频率被优先激发, 如图13 (c). 因此, 张拉整体结构的动态力学特性具有可设计性.
图13
图13
不同绳索和杆刚度比$k_sb$下前六阶固有振型图
Fig.13
The first six natural modes of vibration under different stiffness ratios of strings and bars $k_sb$
3.4 碰撞动力学分析
研究两种张拉整体结构自由下落后与平面碰撞的动力学行为, 进行仿真和实验的对比分析. 实验中, 张拉整体结构底端节点与固定在实验平台上的压电传感器发生碰撞, 通过压电传感器可测得碰撞力, 采用高速相机对结构运动过程进行拍摄, 对图像数据进行处理可得结构顶端节点的位移. 图14 所示为橡胶杆张拉整体结构在不同碰撞时刻的仿真和实验构型图, 碰撞过程中橡胶杆会发生屈曲以缓冲能量.
图14
图14
橡胶杆张拉整体结构碰撞仿真(左)和实验(右)的动态构型图
Fig.14
Dynamic configurations of the rubber tensegrity in the simulation (left) and experiment (right) of impact
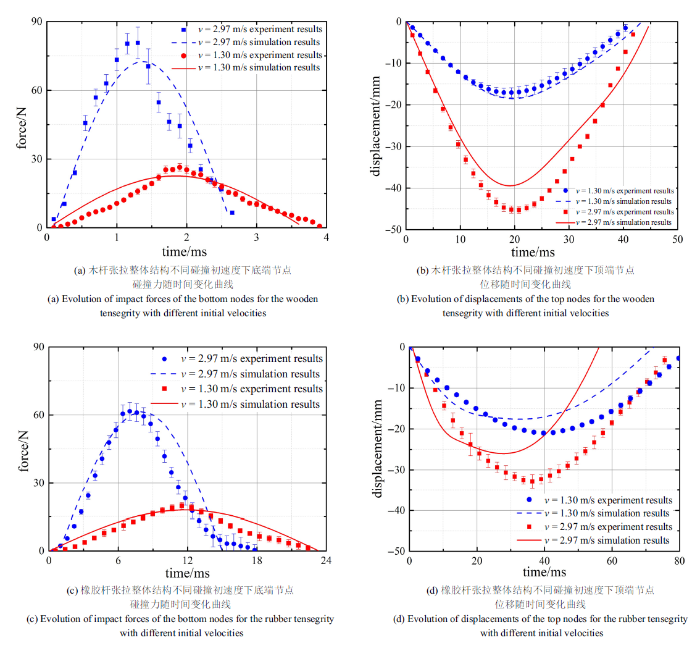
图15 为两种张拉整体结构底端节点碰撞力和顶端节点位移随时间变化曲线在不同碰撞初速度下仿真与实验对比图. 从图15 中可看出, 仿真和实验的曲线基本一致, 碰撞力和位移都呈现先增大后减小的趋势. 当碰撞力减小为零时, 结构底端节点开始与地面分离反弹, 而由于弹性波在结构中的传播效应, 结构顶端节点反弹时刻远滞后于底端节点反弹时刻. 此外, 通过图15 (a)、图15 (b)和图15 (c)、图15 (d)对比可知, 橡胶杆张拉整体结构较木杆张拉整体结构具有更长的动力学响应时间, 可见其柔性更高. 由图15 (c)和图15 (d)可知, 虽然在碰撞过程中橡胶杆会发生屈曲, 但结构的整体刚度没有发生太大变化, 结构仍然具有较高的抗冲击性. 图15 (d)显示, 橡胶杆张拉整体结构在$v=2.97$ m/s时, 仿真结果与实验结果误差较为明显, 考虑到橡胶为超弹性材料, 其弹性模量随应变增大会先增大, 后减小, 最后再增大. 当碰撞速度较小时, 橡胶杆取小应变阶段弹性模量, 此时弹性模量较大, 与实验结果吻合较好. 随碰撞速度增大, 橡胶杆的应变也随之增大, 弹性模量变小, 但在计算时橡胶杆仍取小应变阶段较大的弹性模量, 因此与实验值相比, 其顶端节点位移变化幅度较小.
图15
图15
张拉整体结构碰撞实验与仿真结果对比
Fig.15
Comparison for the experimental and simulation results of impact for tensegrity structures
4 结论
本文提出了张拉整体结构的动力学等效建模与计算方法, 通过理论推导、建模仿真及实验验证, 得到以下结论:
(1)提出了用五节点弹/扭簧集中质量的离散模型来等效连续杆力学特性, 通过静力学和动能等效推导了离散模型等效刚度和等效质量表达式. 通过弯曲振动固有特性等效确定了弯曲刚度分布参数$n$和质量分布参数$c$, 使离散模型前两阶固有频率相对误差降到1%以内, 提高了系统动力学响应预测的准确性.
(2)通过对准静态压缩实验和仿真进行对比, 验证了本文模型预测张拉整体结构静力学行为的准确性. 对橡胶杆张拉整体结构承载能力进行了分析, 杆件半径和模量的变化, 对杆件屈曲前结构整体刚度影响较小, 对杆件后屈曲段结构整体刚度影响较大, 而预张力变化对结构整体刚度影响则相反.
(3)对张拉整体结构的模态进行了实验和仿真分析, 验证了本文模型预测张拉整体结构固有振动特性的准确性. 分析了绳索与杆轴向刚度比变化对张拉整体结构前六阶模态的影响, 发现当绳索刚度低于杆件刚度时, 绳索的局部固有振型被优先激发, 反之, 则杆件的局部固有振型被优先激发, 即张拉整体结构的固有动力学特性具有可设计性.
(4)对张拉整体结构与刚性平面的碰撞过程进行了实验和仿真分析, 验证了本文模型预测张拉整体结构瞬态动力学行为的准确性. 证明了当杆件屈曲时, 六杆球形张拉整体结构仍具有较高抗冲击刚度. 因此当柔性张拉整体结构用作行星着陆器时可扩大其承载的设计域.
本文提出的动力学等效建模和计算方法, 将有望为以张拉整体结构为元胞的行星探测器、大型可展开结构及点阵材料等复杂柔性系统的动力学高效分析与控制提供理论和仿真基础.
附录
对于细长杆($\pi^{2}I/(AL^{2})\ll 1$)的离散模型, 式(21)表示的其横向振动刚度矩阵各分量表达式为
(A1) $K_{11} =K_{1\mbox{3}} =K_{35} =K_{55} =\dfrac{16K{ }_{t1}}{L^{2}}=\dfrac{2\beta_{n} \pi^{2}EI}{nL^{3}}$
(A2) $K_{12} =K_{45} =-2K_{11}$
(A3) $K_{14} =K_{1\mbox{5}} =K_{25} =0$
(A4) $K_{22} =K_{44} =\dfrac{16(4K_{t1} +K_{t2} )}{L^{2}}=\dfrac{2(4+n)\beta_{n} \pi^{2}EI}{nL^{3}}$
(A5) $K_{23} =K_{34} =-\dfrac{32(K_{t1} +K_{t2} )}{L^{2}}=-\dfrac{4(1+n)\beta_{n} \pi^{2}EI}{nL^{3}}$
(A6) $K_{24} =\dfrac{16K_{t2} }{L^{2}}=\dfrac{2\beta _{n} \pi^{2}EI}{L^{3}}$
(A7) $K_{33} =\dfrac{32(K_{t1} +2K_{t2} )}{L^{2}}=\dfrac{4(1+2n)\beta_{n} \pi^{2}EI}{nL^{3}}$
其中$\beta_{n} =1+n+\sqrt {1+n^{2}} $.
参考文献
View Option
[1]
Fuller RB . Synergetics: Explorations in the Geometry of Thinking
Sebaftopol: Estate of R. Buckminster Fuller , 1982
[本文引用: 1]
[2]
Snelson KD . Continuous tension, discontinuous compression structures: Google Patents , 1965
[本文引用: 1]
[3]
Pellegrino S . Analysis of prestressed mechanisms
International Journal of Solids & Structures 1990 , 26 (12 ): 1329 -1350
[本文引用: 1]
[4]
Pellegrino S . A class of tensegrity domes
International Journal of Space Structures 1992 , 7 (2 ): 127 -142
DOI
URL
[本文引用: 1]
[5]
Connelly R Whiteley W . The stability of tensegrity frameworks
International Journal of Space Structures 1992 , 7 (2 ): 153 -163
DOI
URL
[本文引用: 1]
[6]
Tibert AG Pellegrino S . Deployable tensegrity reflectors for small satellites
Journal of Spacecraft and Rockets 2002 , 39 (5 ): 701 -709
DOI
URL
[本文引用: 1]
[7]
SunSpiral V Gorospe G Bruce J , et al . Tensegrity based probes for planetary exploration: Entry, descent and landing (EDL) and surface mobility analysis//Proc. 10th Int
Planetary Probe Workshop, San Jose, CA , 2013 : 17 -21
[本文引用: 1]
[8]
Caluwaerts K Despraz J Işçen A , et al . Design and control of compliant tensegrity robots through simulation and hardware validation
Journal of the Royal Society Interface 2014 , 11 (98 ): 20140520
[本文引用: 1]
[9]
Iscen A Caluwaerts K Bruce J , et al . Learning tensegrity locomotion using open-loop control signals and coevolutionary algorithms
Artificial Life 2015 , 21 (2 ): 119 -140
DOI
URL
[本文引用: 1]
[10]
Ingber DE . Tensegrity: The architectural basis of cellular mechanotransduction
Annual Review of Physiology 1997 , 59 : 575 -599
DOI
URL
[本文引用: 1]
[11]
Ingber DE. Tensegrity I . Cell structure and hierarchical systems biology
Journal of Cell Science 2003 , 116 : 1157 -1173
DOI
URL
[本文引用: 1]
[12]
Rovira AG Tur JMM . Control and simulation of a tensegrity-based mobile robot
Robotics and Autonomous Systems 2008 , 57 (5 ): 526 -535
DOI
URL
[本文引用: 1]
[13]
陈竑希 . 四杆张拉整体机器人动力学分析. [硕士论文]
哈尔滨: 哈尔滨工程大学 , 2018
[本文引用: 1]
(Chen Hongxi . Kinetics analysis for four-bar tensegrity robot. [Master Thesis]
Harbin: Harbin Engineering University , 2018 (in Chinese))
[本文引用: 1]
[14]
Tietz BR Carnahan RW Bachmann RJ , et al . Tetraspine: Robust terrain handling on a tensegrity robot using central pattern generators//International Conference on Advanced Intelligent Mechatronics , 2013 : 261 -267
[本文引用: 1]
[15]
Barnes MR . Form finding and analysis of tension structures by dynamic relaxation
International Journal of Space Structures 1999 , 14 (2 ): 89 -104
DOI
URL
[本文引用: 1]
[16]
Vassart N Motro R . Multiparametered formfinding method: Application to tensegrity systems
International Journal of Space Structures 1999 , 14 (2 ): 147 -154
DOI
URL
[本文引用: 1]
[17]
Koohestani K . Form-finding of tensegrity structures via genetic algorithm
International Journal of Solids and Structures 2012 , 49 (5 ): 739 -747
DOI
URL
[本文引用: 1]
[18]
Chen Y Feng J Wu Y , et al . Novel form-finding of tensegrity structures using ant colony systems
Journal of Mechanisms and Robotics 2011 , 4 (3 ): 031001
DOI
URL
[本文引用: 1]
[19]
Lee S Lee J . A novel method for topology design of tensegrity structures
Composite Structures 2016 , 152 : 11 -19
DOI
URL
[本文引用: 1]
[20]
Wang Y Xu X Luo Y . Topology design of general tensegrity with rigid bodies
International Journal of Solids and Structures 2020 , 202 : 278 -298
DOI
URL
[本文引用: 1]
[21]
Liu K Paulino G H . Tensegrity topology optimization by force maximization on arbitrary ground structures
Structural and Multidisciplinary Optimization 2019 , 59 (6 ): 2041 -2062
DOI
[本文引用: 1]
This paper presents an optimization approach for design of tensegrity structures based on graph theory. The formulation obtains tensegrities from ground structures, through force maximization using mixed integer linear programming. The method seeks a topology of the tensegrity that is within a given geometry, which provides insight into the tensegrity design from a geometric point of view. Although not explicitly enforced, the tensegrities obtained using this approach tend to be both stable and symmetric. Borrowing ideas from computer graphics, we allow restriction zones (i.e., passive regions in which no geometric entity should intersect) to be specified in the underlying ground structure. Such feature allows the design of tensegrities for actual engineering applications, such as robotics, in which the volume of the payload needs to be protected. To demonstrate the effectiveness of our proposed design method, we show that it is effective at extracting both well-known tensegrities and new tensegrities from the ground structure network, some of which are prototyped with the aid of additive manufacturing.
[22]
Goyal R Skelton RE . Tensegrity system dynamics with rigid bars and massive strings
Multibody System Dynamics 2019 , 46 (3 ): 203 -228
DOI
URL
[本文引用: 1]
[23]
Goyal R Skelton RE Peraza Hernandez EA . Efficient design of lightweight reinforced tensegrities under local and global failure constraints
Journal of Applied Mechanics 2020 , 87 : 111005
DOI
URL
[本文引用: 1]
[24]
朱世新 , 张立元 , 李松雪 等 . 数字状张拉整体结构的构型设计与力学性能模拟
力学学报 , 2018 , 50 (4 ): 798 -809
DOI
[本文引用: 1]
针对大型张拉整体结构的设计问题,选取四棱柱状张拉整体结构和截角正八面体状张拉整体结构作为基本胞元,采用节点连接节点的方式建立球柱组合式数字状张拉整体结构,并使用基于结构刚度矩阵的大变形非线性数值求解方法对其进行力学性能分析.在两类胞元满足各自的自平衡条件和稳定性条件的前提下,组合得到的数字状张拉整体结构亦处于自平衡稳定状态,搭建了实物模型进行验证.以数字8状张拉整体结构为例,模拟研究了结构承受自重等分布载荷和单轴拉压等端部载荷时的静力学响应,以及结构无阻尼振动时的固有频率和模态等动力学性能.结果表明,结构在自重作用下的变形行为受初始预应力、压杆密度和拉索刚度的影响较大,对其进行合理配置方可确保结构具有足够刚度抵抗自重;结构在单轴拉压作用下呈现非线性的载荷-位移曲线,拉伸刚度随变形量的增大而增大,压缩刚度随变形量的增大而减小;结构的固有频率随初始预应力的增大而增大,而模态振型基本不变.研究结果丰富了大型张拉整体结构的外形种类,有望推动此类结构在土木建筑、结构材料等领域的应用.
(Zhu Shixin Zhang Liyuan Li Songxue , et al . Number-shaped tensegrity structures: Configuration design and mechanical properties analysis
Chinese Journal of Theoretical and Applied Mechanics 2018 , 50 (4 ): 798 -809 (in Chinese))
[本文引用: 1]
[25]
沈黎元 , 李国强 , 罗永峰 . 预应力索结构位移控制
同济大学学报(自然科学版) , 2006 , 34 (3 ): 291 -295
[本文引用: 1]
(Shen Liyuan Li Guoqiang Luo Yongfeng . Displacement control of prestressed cable structures
Journal of Tongji University (Natural Science) 2006 , 34 (3 ): 291 -295 (in Chinese))
[本文引用: 1]
[26]
(Shea K Fest E Smith IFC . Developing intelligent tensegrity structures with stochastic search
Advanced Engineering Informatics 2002 , 16 : 21 -40
[本文引用: 1]
[27]
Begey J Vedrines M Andreff N , et al . Selection of actuation mode for tensegrity mechanisms: The case study of the actuated Snelson cross
Mechanism and Machine Theory 2020 , 152 : 103881
DOI
URL
[本文引用: 1]
[28]
Kebiche K Kaziaoual MN Motro R . Geometrical non-linear analysis of tensegrity systems
Engineering Structures 1999 , 21 : 864 -876
DOI
URL
[本文引用: 1]
[29]
Kahla NB Kebiche K . Nonlinear elastoplastic analysis of tensegrity systems
Engineering Structures 2000 , 23 : 1552 -1566
[本文引用: 1]
[30]
Zhang L Lu MK Zhang HW , et al . Geometrically nonlinear elasto-plastic analysis of clustered tensegrity based on the co-rotational approach
International Journal of Mechanical Sciences 2015 , 93 : 154 -165
DOI
URL
[本文引用: 1]
[31]
Rimoli JJ . A reduced-order model for the dynamic and post-buckling behavior of tensegrity structures
Mechanics of Materials 2018 , 116 : 146 -157
DOI
URL
[本文引用: 4]
[32]
Rimoli JJ Pal RK . Mechanical response of 3-dimensional tensegrity lattices
Composites Part B 2017 , 115 : 30 -42
DOI
URL
[本文引用: 1]
[33]
Li P Liu C Tian Q , et al . Dynamics of a deployable mesh reflector of satellite antenna: Parallel computation and deployment simulation
Journal of Computational and Nonlinear Dynamics 2016 , 11 (6 ): 061005
DOI
URL
[本文引用: 1]
[34]
Wilson EL . The static condensation algorithm
International Journal for Numerical Methods in Engineering 2010 , 8 (1 ): 198 -203
DOI
URL
[本文引用: 1]
Synergetics: Explorations in the Geometry of Thinking
1
1982
... 20世纪中期, 美国建筑师Fuller[1 ] 从艺术家Snelson[2 ] 的雕塑作品中获得灵感, 将"tension"和"integrity"融合为一个新的单词, 提出了"tensegrity" (张拉整体)的概念. 早期的张拉整体结构大多是从艺术角度设计的作品, 未考虑其工程应用价值, 直到20世纪80年代, 在Pellegrino[3 -4 ] 和Connelly等[5 ] 的推动下, 张拉整体结构才被越来越多的工程师所熟知. ...
1
1965
... 20世纪中期, 美国建筑师Fuller[1 ] 从艺术家Snelson[2 ] 的雕塑作品中获得灵感, 将"tension"和"integrity"融合为一个新的单词, 提出了"tensegrity" (张拉整体)的概念. 早期的张拉整体结构大多是从艺术角度设计的作品, 未考虑其工程应用价值, 直到20世纪80年代, 在Pellegrino[3 -4 ] 和Connelly等[5 ] 的推动下, 张拉整体结构才被越来越多的工程师所熟知. ...
Analysis of prestressed mechanisms
1
1990
... 20世纪中期, 美国建筑师Fuller[1 ] 从艺术家Snelson[2 ] 的雕塑作品中获得灵感, 将"tension"和"integrity"融合为一个新的单词, 提出了"tensegrity" (张拉整体)的概念. 早期的张拉整体结构大多是从艺术角度设计的作品, 未考虑其工程应用价值, 直到20世纪80年代, 在Pellegrino[3 -4 ] 和Connelly等[5 ] 的推动下, 张拉整体结构才被越来越多的工程师所熟知. ...
A class of tensegrity domes
1
1992
... 20世纪中期, 美国建筑师Fuller[1 ] 从艺术家Snelson[2 ] 的雕塑作品中获得灵感, 将"tension"和"integrity"融合为一个新的单词, 提出了"tensegrity" (张拉整体)的概念. 早期的张拉整体结构大多是从艺术角度设计的作品, 未考虑其工程应用价值, 直到20世纪80年代, 在Pellegrino[3 -4 ] 和Connelly等[5 ] 的推动下, 张拉整体结构才被越来越多的工程师所熟知. ...
The stability of tensegrity frameworks
1
1992
... 20世纪中期, 美国建筑师Fuller[1 ] 从艺术家Snelson[2 ] 的雕塑作品中获得灵感, 将"tension"和"integrity"融合为一个新的单词, 提出了"tensegrity" (张拉整体)的概念. 早期的张拉整体结构大多是从艺术角度设计的作品, 未考虑其工程应用价值, 直到20世纪80年代, 在Pellegrino[3 -4 ] 和Connelly等[5 ] 的推动下, 张拉整体结构才被越来越多的工程师所熟知. ...
Deployable tensegrity reflectors for small satellites
1
2002
... 张拉整体结构具有整体均匀承载、轻质、高收纳比等优异结构特性, 因此逐渐得到航天、生物力学、机器人等领域研究人员的广泛关注. 在航天工程领域, Tibert和Pellegrino[6 ] 提出了一种可展开张拉整体棱柱结构, 通过对其几何和内力分析及其实验验证, 证明了该结构具备较好的展开可靠度和较高的收纳比; SunSpiral等[7 ] 提出了张拉整体行星探测器的概念, 模拟和分析了张拉整体结构展开、降落和表面移动过程的动力学行为, 验证了其用于Titan行星探测任务的可行性; Caluwaerts等[8 ] 对用于行星探测的球形张拉整体机器人进行动力学仿真, 研究不同控制方法下系统动力学响应, 提出了生物启发的张拉整体结构控制策略; Iscen等[9 ] 通过分析不同层级和频率的测量信号, 获得了保持其以适当速度自主滚动的分布式驱动信号. 在生物力学领域, Ingber[10 -11 ] 利用张拉整体结构模拟细胞及其骨架整体结构的力学行为, 解释细胞结构的形变、运动和对机械信号的感知与传导机理, 进一步理解生物体的分级组织机理. 在机器人领域, Rovira和Tur[12 ] 推导了由刚性杆和弹性绳组成的棱柱张拉整体机器人动力学普遍方程, 并通过仿真研究了在指定运动下分布变长度绳的多状态离散控制方法; 陈竑希[13 ] 对四杆张拉整体机器人进行驱动方案设计和动力学仿真分析, 并通过实验验证了理论结果的正确性; Tietz等[14 ] 首次采用CPG (central pattern generators)控制实现多节机器人爬行运动的波形调控, 使其可在各种复杂地形上运动. ...
Tensegrity based probes for planetary exploration: Entry, descent and landing (EDL) and surface mobility analysis//Proc. 10th Int
1
2013
... 张拉整体结构具有整体均匀承载、轻质、高收纳比等优异结构特性, 因此逐渐得到航天、生物力学、机器人等领域研究人员的广泛关注. 在航天工程领域, Tibert和Pellegrino[6 ] 提出了一种可展开张拉整体棱柱结构, 通过对其几何和内力分析及其实验验证, 证明了该结构具备较好的展开可靠度和较高的收纳比; SunSpiral等[7 ] 提出了张拉整体行星探测器的概念, 模拟和分析了张拉整体结构展开、降落和表面移动过程的动力学行为, 验证了其用于Titan行星探测任务的可行性; Caluwaerts等[8 ] 对用于行星探测的球形张拉整体机器人进行动力学仿真, 研究不同控制方法下系统动力学响应, 提出了生物启发的张拉整体结构控制策略; Iscen等[9 ] 通过分析不同层级和频率的测量信号, 获得了保持其以适当速度自主滚动的分布式驱动信号. 在生物力学领域, Ingber[10 -11 ] 利用张拉整体结构模拟细胞及其骨架整体结构的力学行为, 解释细胞结构的形变、运动和对机械信号的感知与传导机理, 进一步理解生物体的分级组织机理. 在机器人领域, Rovira和Tur[12 ] 推导了由刚性杆和弹性绳组成的棱柱张拉整体机器人动力学普遍方程, 并通过仿真研究了在指定运动下分布变长度绳的多状态离散控制方法; 陈竑希[13 ] 对四杆张拉整体机器人进行驱动方案设计和动力学仿真分析, 并通过实验验证了理论结果的正确性; Tietz等[14 ] 首次采用CPG (central pattern generators)控制实现多节机器人爬行运动的波形调控, 使其可在各种复杂地形上运动. ...
Design and control of compliant tensegrity robots through simulation and hardware validation
1
2014
... 张拉整体结构具有整体均匀承载、轻质、高收纳比等优异结构特性, 因此逐渐得到航天、生物力学、机器人等领域研究人员的广泛关注. 在航天工程领域, Tibert和Pellegrino[6 ] 提出了一种可展开张拉整体棱柱结构, 通过对其几何和内力分析及其实验验证, 证明了该结构具备较好的展开可靠度和较高的收纳比; SunSpiral等[7 ] 提出了张拉整体行星探测器的概念, 模拟和分析了张拉整体结构展开、降落和表面移动过程的动力学行为, 验证了其用于Titan行星探测任务的可行性; Caluwaerts等[8 ] 对用于行星探测的球形张拉整体机器人进行动力学仿真, 研究不同控制方法下系统动力学响应, 提出了生物启发的张拉整体结构控制策略; Iscen等[9 ] 通过分析不同层级和频率的测量信号, 获得了保持其以适当速度自主滚动的分布式驱动信号. 在生物力学领域, Ingber[10 -11 ] 利用张拉整体结构模拟细胞及其骨架整体结构的力学行为, 解释细胞结构的形变、运动和对机械信号的感知与传导机理, 进一步理解生物体的分级组织机理. 在机器人领域, Rovira和Tur[12 ] 推导了由刚性杆和弹性绳组成的棱柱张拉整体机器人动力学普遍方程, 并通过仿真研究了在指定运动下分布变长度绳的多状态离散控制方法; 陈竑希[13 ] 对四杆张拉整体机器人进行驱动方案设计和动力学仿真分析, 并通过实验验证了理论结果的正确性; Tietz等[14 ] 首次采用CPG (central pattern generators)控制实现多节机器人爬行运动的波形调控, 使其可在各种复杂地形上运动. ...
Learning tensegrity locomotion using open-loop control signals and coevolutionary algorithms
1
2015
... 张拉整体结构具有整体均匀承载、轻质、高收纳比等优异结构特性, 因此逐渐得到航天、生物力学、机器人等领域研究人员的广泛关注. 在航天工程领域, Tibert和Pellegrino[6 ] 提出了一种可展开张拉整体棱柱结构, 通过对其几何和内力分析及其实验验证, 证明了该结构具备较好的展开可靠度和较高的收纳比; SunSpiral等[7 ] 提出了张拉整体行星探测器的概念, 模拟和分析了张拉整体结构展开、降落和表面移动过程的动力学行为, 验证了其用于Titan行星探测任务的可行性; Caluwaerts等[8 ] 对用于行星探测的球形张拉整体机器人进行动力学仿真, 研究不同控制方法下系统动力学响应, 提出了生物启发的张拉整体结构控制策略; Iscen等[9 ] 通过分析不同层级和频率的测量信号, 获得了保持其以适当速度自主滚动的分布式驱动信号. 在生物力学领域, Ingber[10 -11 ] 利用张拉整体结构模拟细胞及其骨架整体结构的力学行为, 解释细胞结构的形变、运动和对机械信号的感知与传导机理, 进一步理解生物体的分级组织机理. 在机器人领域, Rovira和Tur[12 ] 推导了由刚性杆和弹性绳组成的棱柱张拉整体机器人动力学普遍方程, 并通过仿真研究了在指定运动下分布变长度绳的多状态离散控制方法; 陈竑希[13 ] 对四杆张拉整体机器人进行驱动方案设计和动力学仿真分析, 并通过实验验证了理论结果的正确性; Tietz等[14 ] 首次采用CPG (central pattern generators)控制实现多节机器人爬行运动的波形调控, 使其可在各种复杂地形上运动. ...
Tensegrity: The architectural basis of cellular mechanotransduction
1
1997
... 张拉整体结构具有整体均匀承载、轻质、高收纳比等优异结构特性, 因此逐渐得到航天、生物力学、机器人等领域研究人员的广泛关注. 在航天工程领域, Tibert和Pellegrino[6 ] 提出了一种可展开张拉整体棱柱结构, 通过对其几何和内力分析及其实验验证, 证明了该结构具备较好的展开可靠度和较高的收纳比; SunSpiral等[7 ] 提出了张拉整体行星探测器的概念, 模拟和分析了张拉整体结构展开、降落和表面移动过程的动力学行为, 验证了其用于Titan行星探测任务的可行性; Caluwaerts等[8 ] 对用于行星探测的球形张拉整体机器人进行动力学仿真, 研究不同控制方法下系统动力学响应, 提出了生物启发的张拉整体结构控制策略; Iscen等[9 ] 通过分析不同层级和频率的测量信号, 获得了保持其以适当速度自主滚动的分布式驱动信号. 在生物力学领域, Ingber[10 -11 ] 利用张拉整体结构模拟细胞及其骨架整体结构的力学行为, 解释细胞结构的形变、运动和对机械信号的感知与传导机理, 进一步理解生物体的分级组织机理. 在机器人领域, Rovira和Tur[12 ] 推导了由刚性杆和弹性绳组成的棱柱张拉整体机器人动力学普遍方程, 并通过仿真研究了在指定运动下分布变长度绳的多状态离散控制方法; 陈竑希[13 ] 对四杆张拉整体机器人进行驱动方案设计和动力学仿真分析, 并通过实验验证了理论结果的正确性; Tietz等[14 ] 首次采用CPG (central pattern generators)控制实现多节机器人爬行运动的波形调控, 使其可在各种复杂地形上运动. ...
Cell structure and hierarchical systems biology
1
2003
... 张拉整体结构具有整体均匀承载、轻质、高收纳比等优异结构特性, 因此逐渐得到航天、生物力学、机器人等领域研究人员的广泛关注. 在航天工程领域, Tibert和Pellegrino[6 ] 提出了一种可展开张拉整体棱柱结构, 通过对其几何和内力分析及其实验验证, 证明了该结构具备较好的展开可靠度和较高的收纳比; SunSpiral等[7 ] 提出了张拉整体行星探测器的概念, 模拟和分析了张拉整体结构展开、降落和表面移动过程的动力学行为, 验证了其用于Titan行星探测任务的可行性; Caluwaerts等[8 ] 对用于行星探测的球形张拉整体机器人进行动力学仿真, 研究不同控制方法下系统动力学响应, 提出了生物启发的张拉整体结构控制策略; Iscen等[9 ] 通过分析不同层级和频率的测量信号, 获得了保持其以适当速度自主滚动的分布式驱动信号. 在生物力学领域, Ingber[10 -11 ] 利用张拉整体结构模拟细胞及其骨架整体结构的力学行为, 解释细胞结构的形变、运动和对机械信号的感知与传导机理, 进一步理解生物体的分级组织机理. 在机器人领域, Rovira和Tur[12 ] 推导了由刚性杆和弹性绳组成的棱柱张拉整体机器人动力学普遍方程, 并通过仿真研究了在指定运动下分布变长度绳的多状态离散控制方法; 陈竑希[13 ] 对四杆张拉整体机器人进行驱动方案设计和动力学仿真分析, 并通过实验验证了理论结果的正确性; Tietz等[14 ] 首次采用CPG (central pattern generators)控制实现多节机器人爬行运动的波形调控, 使其可在各种复杂地形上运动. ...
Control and simulation of a tensegrity-based mobile robot
1
2008
... 张拉整体结构具有整体均匀承载、轻质、高收纳比等优异结构特性, 因此逐渐得到航天、生物力学、机器人等领域研究人员的广泛关注. 在航天工程领域, Tibert和Pellegrino[6 ] 提出了一种可展开张拉整体棱柱结构, 通过对其几何和内力分析及其实验验证, 证明了该结构具备较好的展开可靠度和较高的收纳比; SunSpiral等[7 ] 提出了张拉整体行星探测器的概念, 模拟和分析了张拉整体结构展开、降落和表面移动过程的动力学行为, 验证了其用于Titan行星探测任务的可行性; Caluwaerts等[8 ] 对用于行星探测的球形张拉整体机器人进行动力学仿真, 研究不同控制方法下系统动力学响应, 提出了生物启发的张拉整体结构控制策略; Iscen等[9 ] 通过分析不同层级和频率的测量信号, 获得了保持其以适当速度自主滚动的分布式驱动信号. 在生物力学领域, Ingber[10 -11 ] 利用张拉整体结构模拟细胞及其骨架整体结构的力学行为, 解释细胞结构的形变、运动和对机械信号的感知与传导机理, 进一步理解生物体的分级组织机理. 在机器人领域, Rovira和Tur[12 ] 推导了由刚性杆和弹性绳组成的棱柱张拉整体机器人动力学普遍方程, 并通过仿真研究了在指定运动下分布变长度绳的多状态离散控制方法; 陈竑希[13 ] 对四杆张拉整体机器人进行驱动方案设计和动力学仿真分析, 并通过实验验证了理论结果的正确性; Tietz等[14 ] 首次采用CPG (central pattern generators)控制实现多节机器人爬行运动的波形调控, 使其可在各种复杂地形上运动. ...
四杆张拉整体机器人动力学分析. [硕士论文]
1
2018
... 张拉整体结构具有整体均匀承载、轻质、高收纳比等优异结构特性, 因此逐渐得到航天、生物力学、机器人等领域研究人员的广泛关注. 在航天工程领域, Tibert和Pellegrino[6 ] 提出了一种可展开张拉整体棱柱结构, 通过对其几何和内力分析及其实验验证, 证明了该结构具备较好的展开可靠度和较高的收纳比; SunSpiral等[7 ] 提出了张拉整体行星探测器的概念, 模拟和分析了张拉整体结构展开、降落和表面移动过程的动力学行为, 验证了其用于Titan行星探测任务的可行性; Caluwaerts等[8 ] 对用于行星探测的球形张拉整体机器人进行动力学仿真, 研究不同控制方法下系统动力学响应, 提出了生物启发的张拉整体结构控制策略; Iscen等[9 ] 通过分析不同层级和频率的测量信号, 获得了保持其以适当速度自主滚动的分布式驱动信号. 在生物力学领域, Ingber[10 -11 ] 利用张拉整体结构模拟细胞及其骨架整体结构的力学行为, 解释细胞结构的形变、运动和对机械信号的感知与传导机理, 进一步理解生物体的分级组织机理. 在机器人领域, Rovira和Tur[12 ] 推导了由刚性杆和弹性绳组成的棱柱张拉整体机器人动力学普遍方程, 并通过仿真研究了在指定运动下分布变长度绳的多状态离散控制方法; 陈竑希[13 ] 对四杆张拉整体机器人进行驱动方案设计和动力学仿真分析, 并通过实验验证了理论结果的正确性; Tietz等[14 ] 首次采用CPG (central pattern generators)控制实现多节机器人爬行运动的波形调控, 使其可在各种复杂地形上运动. ...
四杆张拉整体机器人动力学分析. [硕士论文]
1
2018
... 张拉整体结构具有整体均匀承载、轻质、高收纳比等优异结构特性, 因此逐渐得到航天、生物力学、机器人等领域研究人员的广泛关注. 在航天工程领域, Tibert和Pellegrino[6 ] 提出了一种可展开张拉整体棱柱结构, 通过对其几何和内力分析及其实验验证, 证明了该结构具备较好的展开可靠度和较高的收纳比; SunSpiral等[7 ] 提出了张拉整体行星探测器的概念, 模拟和分析了张拉整体结构展开、降落和表面移动过程的动力学行为, 验证了其用于Titan行星探测任务的可行性; Caluwaerts等[8 ] 对用于行星探测的球形张拉整体机器人进行动力学仿真, 研究不同控制方法下系统动力学响应, 提出了生物启发的张拉整体结构控制策略; Iscen等[9 ] 通过分析不同层级和频率的测量信号, 获得了保持其以适当速度自主滚动的分布式驱动信号. 在生物力学领域, Ingber[10 -11 ] 利用张拉整体结构模拟细胞及其骨架整体结构的力学行为, 解释细胞结构的形变、运动和对机械信号的感知与传导机理, 进一步理解生物体的分级组织机理. 在机器人领域, Rovira和Tur[12 ] 推导了由刚性杆和弹性绳组成的棱柱张拉整体机器人动力学普遍方程, 并通过仿真研究了在指定运动下分布变长度绳的多状态离散控制方法; 陈竑希[13 ] 对四杆张拉整体机器人进行驱动方案设计和动力学仿真分析, 并通过实验验证了理论结果的正确性; Tietz等[14 ] 首次采用CPG (central pattern generators)控制实现多节机器人爬行运动的波形调控, 使其可在各种复杂地形上运动. ...
1
2013
... 张拉整体结构具有整体均匀承载、轻质、高收纳比等优异结构特性, 因此逐渐得到航天、生物力学、机器人等领域研究人员的广泛关注. 在航天工程领域, Tibert和Pellegrino[6 ] 提出了一种可展开张拉整体棱柱结构, 通过对其几何和内力分析及其实验验证, 证明了该结构具备较好的展开可靠度和较高的收纳比; SunSpiral等[7 ] 提出了张拉整体行星探测器的概念, 模拟和分析了张拉整体结构展开、降落和表面移动过程的动力学行为, 验证了其用于Titan行星探测任务的可行性; Caluwaerts等[8 ] 对用于行星探测的球形张拉整体机器人进行动力学仿真, 研究不同控制方法下系统动力学响应, 提出了生物启发的张拉整体结构控制策略; Iscen等[9 ] 通过分析不同层级和频率的测量信号, 获得了保持其以适当速度自主滚动的分布式驱动信号. 在生物力学领域, Ingber[10 -11 ] 利用张拉整体结构模拟细胞及其骨架整体结构的力学行为, 解释细胞结构的形变、运动和对机械信号的感知与传导机理, 进一步理解生物体的分级组织机理. 在机器人领域, Rovira和Tur[12 ] 推导了由刚性杆和弹性绳组成的棱柱张拉整体机器人动力学普遍方程, 并通过仿真研究了在指定运动下分布变长度绳的多状态离散控制方法; 陈竑希[13 ] 对四杆张拉整体机器人进行驱动方案设计和动力学仿真分析, 并通过实验验证了理论结果的正确性; Tietz等[14 ] 首次采用CPG (central pattern generators)控制实现多节机器人爬行运动的波形调控, 使其可在各种复杂地形上运动. ...
Form finding and analysis of tension structures by dynamic relaxation
1
1999
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
Multiparametered formfinding method: Application to tensegrity systems
1
1999
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
Form-finding of tensegrity structures via genetic algorithm
1
2012
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
Novel form-finding of tensegrity structures using ant colony systems
1
2011
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
A novel method for topology design of tensegrity structures
1
2016
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
Topology design of general tensegrity with rigid bodies
1
2020
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
Tensegrity topology optimization by force maximization on arbitrary ground structures
1
2019
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
Tensegrity system dynamics with rigid bars and massive strings
1
2019
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
Efficient design of lightweight reinforced tensegrities under local and global failure constraints
1
2020
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
数字状张拉整体结构的构型设计与力学性能模拟
1
2018
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
数字状张拉整体结构的构型设计与力学性能模拟
1
2018
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
预应力索结构位移控制
1
2006
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
预应力索结构位移控制
1
2006
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
Developing intelligent tensegrity structures with stochastic search
1
2002
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
Selection of actuation mode for tensegrity mechanisms: The case study of the actuated Snelson cross
1
2020
... 虽然张拉整体结构涉及的领域不同, 但研究的问题大多围绕找形与拓扑、结构分析和形态控制这3方面展开. 找形即在给定张拉整体结构拓扑(即节点连接方式)情况下求解其自平衡节点位置坐标, Barnes[15 ] 基于动力松弛法提出了张拉整体结构找形的数值计算流程, 构造了较稳定和较快收敛的人工运动阻尼过程, 该方法的优势是可实现大扰动找形和考虑了几何非线性、材料非线性等. 找形的另一类方法是力密度法, 而力密度法原本仅适用于纯张力结构的找形, 当用于同时包含张力和压力部件的结构找形时, 其平衡方程可能发生奇异, 对此Vassart和Motro[16 ] 给出了详细的理论分析, 并提出了"冗余"节点的概念, 基于多输入参数实现张拉整体结构找形; Koohestani[17 ] 和Chen等[18 ] 分别采用基于仿生学的遗传算法和蚁群算法, 将张拉整体结构找形转化为优化问题求解, 提升了基于力密度找形方法的适用性. 相比找形研究, 张拉整体结构的拓扑研究相对较少, Lee等[19 ] 以张拉整体结构节点坐标为输入, 在节点全部连接中给出满足杆不连续条件的杆编号集合, 利用极小张拉整体构型理论消去非必要绳连接, 并利用力密度法和遗传算法给出找力结果; Wang等[20 ] 提出了含刚体张拉整体结构拓扑设计的普适方法, 利用MILP (混合整数规划优化)算法求解了拓扑设计的优化问题; Liu和Paulino[21 ] 基于基结构法和MILP算法实现张拉整体结构的拓扑优化, 通过最大化自平衡力之和进行构型提取, 得到了稳定和对称的张拉整体结构. 在结构分析方面, Goyal和Skelton[22 ] 考虑张拉整体结构绳的质量而忽略杆的弹性, 建立了以刚性杆和分段弹簧集中质量的绳模型组成多体动力学模型, 通过动力学仿真研究典型张拉整体结构动力学行为; Goyal等[23 ] 提出了考虑局部和全局失效的轻质张拉整体结构设计方法, 在几何设计的基础上进一步考虑了结构的轻量化和承载能力; 朱世新等[24 ] 建立了组合式数字状张拉整体结构, 对其大变形非线性力学行为进行数值模拟以实现力学性能分析, 并通过实验测试研究了数字8状结构的静力学和动力学特性. 在结构的形态控制方面, 沈黎元等[25 ] 基于索杆体系矩阵分析理论, 给出了预应力索结构位移控制的线性求解方法, 可望用于精密结构的形状控制; Shea等[26 ] 结合动力松弛法和模拟退火搜索算法提出了自适应张拉整体结构的全局形态控制框架; Begey等[27 ] 评估了驱动类型和位置对Snelson cross张拉整体机构的影响, 给出不同驱动模式的性能图, 以拓展张拉整体机器人的设计可能性. ...
Geometrical non-linear analysis of tensegrity systems
1
1999
... 以往对张拉整体结构或系统力学建模中, 一般假设绳索只发生纯拉伸变形, 且杆只发生纯压缩变形或假设为不变形的刚体. 在上述假设下, 当张拉整体系统发生大变形时, 部件会发生大转动而引起几何非线性问题, 使结构线性分析失效. Kebiche等[28 ] 基于非线性有限元思想, 利用虚功原理的增量分析, 在完全拉格朗日框架下推导了杆的非线性刚度矩阵, 实现了张拉整体系统的几何非线性分析; 在此基础上, Kahla和Kebiche[29 ] 引入了材料非线性本构, 将上述方法拓展到张拉整体系统的非线性弹塑性分析; 此外, Zhang等[30 ] 针对大位移小应变系统的高效分析, 采用共旋坐标法实现了张拉整体系统的几何和材料非线性分析. 进一步, 对于由细长杆或软材料杆组成的柔软张拉整体系统, 在系统变形或运动中杆还可能发生弯曲变形, 需研究杆后屈曲局部变形对系统整体承载性能与动力学行为的影响. Rimoli[31 ] 提出了张拉整体结构柔性杆的一种等效建模方法, 将杆的连续模型等效为集中参数模型, 采用较少的自由度捕捉了杆的屈曲、后屈曲行为及动力学特性, 可用于柔性张拉整体着陆器[31 ] 、复杂张拉整体点阵材料[32 ] 的动力学和非线性响应高效分析; 然而, 由于文献[31 ]中计算两端简支杆弯曲振动固有频率的解析表达式有误(即原文式(26)中固有频率应与阶数平方成正比, 而不是与阶数成正比), 致使在合适取值下计算的离散模型前两阶固有频率相对误差均为4.5%, 而事实上第二阶固有频率相对误差应为15%, 即弯曲固有振动的计算精度不高. ...
Nonlinear elastoplastic analysis of tensegrity systems
1
2000
... 以往对张拉整体结构或系统力学建模中, 一般假设绳索只发生纯拉伸变形, 且杆只发生纯压缩变形或假设为不变形的刚体. 在上述假设下, 当张拉整体系统发生大变形时, 部件会发生大转动而引起几何非线性问题, 使结构线性分析失效. Kebiche等[28 ] 基于非线性有限元思想, 利用虚功原理的增量分析, 在完全拉格朗日框架下推导了杆的非线性刚度矩阵, 实现了张拉整体系统的几何非线性分析; 在此基础上, Kahla和Kebiche[29 ] 引入了材料非线性本构, 将上述方法拓展到张拉整体系统的非线性弹塑性分析; 此外, Zhang等[30 ] 针对大位移小应变系统的高效分析, 采用共旋坐标法实现了张拉整体系统的几何和材料非线性分析. 进一步, 对于由细长杆或软材料杆组成的柔软张拉整体系统, 在系统变形或运动中杆还可能发生弯曲变形, 需研究杆后屈曲局部变形对系统整体承载性能与动力学行为的影响. Rimoli[31 ] 提出了张拉整体结构柔性杆的一种等效建模方法, 将杆的连续模型等效为集中参数模型, 采用较少的自由度捕捉了杆的屈曲、后屈曲行为及动力学特性, 可用于柔性张拉整体着陆器[31 ] 、复杂张拉整体点阵材料[32 ] 的动力学和非线性响应高效分析; 然而, 由于文献[31 ]中计算两端简支杆弯曲振动固有频率的解析表达式有误(即原文式(26)中固有频率应与阶数平方成正比, 而不是与阶数成正比), 致使在合适取值下计算的离散模型前两阶固有频率相对误差均为4.5%, 而事实上第二阶固有频率相对误差应为15%, 即弯曲固有振动的计算精度不高. ...
Geometrically nonlinear elasto-plastic analysis of clustered tensegrity based on the co-rotational approach
1
2015
... 以往对张拉整体结构或系统力学建模中, 一般假设绳索只发生纯拉伸变形, 且杆只发生纯压缩变形或假设为不变形的刚体. 在上述假设下, 当张拉整体系统发生大变形时, 部件会发生大转动而引起几何非线性问题, 使结构线性分析失效. Kebiche等[28 ] 基于非线性有限元思想, 利用虚功原理的增量分析, 在完全拉格朗日框架下推导了杆的非线性刚度矩阵, 实现了张拉整体系统的几何非线性分析; 在此基础上, Kahla和Kebiche[29 ] 引入了材料非线性本构, 将上述方法拓展到张拉整体系统的非线性弹塑性分析; 此外, Zhang等[30 ] 针对大位移小应变系统的高效分析, 采用共旋坐标法实现了张拉整体系统的几何和材料非线性分析. 进一步, 对于由细长杆或软材料杆组成的柔软张拉整体系统, 在系统变形或运动中杆还可能发生弯曲变形, 需研究杆后屈曲局部变形对系统整体承载性能与动力学行为的影响. Rimoli[31 ] 提出了张拉整体结构柔性杆的一种等效建模方法, 将杆的连续模型等效为集中参数模型, 采用较少的自由度捕捉了杆的屈曲、后屈曲行为及动力学特性, 可用于柔性张拉整体着陆器[31 ] 、复杂张拉整体点阵材料[32 ] 的动力学和非线性响应高效分析; 然而, 由于文献[31 ]中计算两端简支杆弯曲振动固有频率的解析表达式有误(即原文式(26)中固有频率应与阶数平方成正比, 而不是与阶数成正比), 致使在合适取值下计算的离散模型前两阶固有频率相对误差均为4.5%, 而事实上第二阶固有频率相对误差应为15%, 即弯曲固有振动的计算精度不高. ...
A reduced-order model for the dynamic and post-buckling behavior of tensegrity structures
4
2018
... 以往对张拉整体结构或系统力学建模中, 一般假设绳索只发生纯拉伸变形, 且杆只发生纯压缩变形或假设为不变形的刚体. 在上述假设下, 当张拉整体系统发生大变形时, 部件会发生大转动而引起几何非线性问题, 使结构线性分析失效. Kebiche等[28 ] 基于非线性有限元思想, 利用虚功原理的增量分析, 在完全拉格朗日框架下推导了杆的非线性刚度矩阵, 实现了张拉整体系统的几何非线性分析; 在此基础上, Kahla和Kebiche[29 ] 引入了材料非线性本构, 将上述方法拓展到张拉整体系统的非线性弹塑性分析; 此外, Zhang等[30 ] 针对大位移小应变系统的高效分析, 采用共旋坐标法实现了张拉整体系统的几何和材料非线性分析. 进一步, 对于由细长杆或软材料杆组成的柔软张拉整体系统, 在系统变形或运动中杆还可能发生弯曲变形, 需研究杆后屈曲局部变形对系统整体承载性能与动力学行为的影响. Rimoli[31 ] 提出了张拉整体结构柔性杆的一种等效建模方法, 将杆的连续模型等效为集中参数模型, 采用较少的自由度捕捉了杆的屈曲、后屈曲行为及动力学特性, 可用于柔性张拉整体着陆器[31 ] 、复杂张拉整体点阵材料[32 ] 的动力学和非线性响应高效分析; 然而, 由于文献[31 ]中计算两端简支杆弯曲振动固有频率的解析表达式有误(即原文式(26)中固有频率应与阶数平方成正比, 而不是与阶数成正比), 致使在合适取值下计算的离散模型前两阶固有频率相对误差均为4.5%, 而事实上第二阶固有频率相对误差应为15%, 即弯曲固有振动的计算精度不高. ...
... [31 ]、复杂张拉整体点阵材料[32 ] 的动力学和非线性响应高效分析; 然而, 由于文献[31 ]中计算两端简支杆弯曲振动固有频率的解析表达式有误(即原文式(26)中固有频率应与阶数平方成正比, 而不是与阶数成正比), 致使在合适取值下计算的离散模型前两阶固有频率相对误差均为4.5%, 而事实上第二阶固有频率相对误差应为15%, 即弯曲固有振动的计算精度不高. ...
... 的动力学和非线性响应高效分析; 然而, 由于文献[31 ]中计算两端简支杆弯曲振动固有频率的解析表达式有误(即原文式(26)中固有频率应与阶数平方成正比, 而不是与阶数成正比), 致使在合适取值下计算的离散模型前两阶固有频率相对误差均为4.5%, 而事实上第二阶固有频率相对误差应为15%, 即弯曲固有振动的计算精度不高. ...
... 针对张拉整体结构中柔性细长杆动力学等效建模和高效计算, 本文提出了考虑拉压和弯曲变形的五节点离散杆模型, 从能量角度推导了连续模型与离散模型的动力学等效过程, 改进了Rimoli降阶模型[31 ] , 使得连续模型和离散模型的杆弯曲振动前两阶固有频率相对误差均降低至1%以内, 提高了动力学计算精度. 进一步, 以六杆球形张拉整体结构为研究对象, 建立和求解多柔体系统动力学方程, 开展压缩、模态和冲击的静/动态仿真与实验测试, 对比验证本文动力学建模和计算方法的有效性. ...
Mechanical response of 3-dimensional tensegrity lattices
1
2017
... 以往对张拉整体结构或系统力学建模中, 一般假设绳索只发生纯拉伸变形, 且杆只发生纯压缩变形或假设为不变形的刚体. 在上述假设下, 当张拉整体系统发生大变形时, 部件会发生大转动而引起几何非线性问题, 使结构线性分析失效. Kebiche等[28 ] 基于非线性有限元思想, 利用虚功原理的增量分析, 在完全拉格朗日框架下推导了杆的非线性刚度矩阵, 实现了张拉整体系统的几何非线性分析; 在此基础上, Kahla和Kebiche[29 ] 引入了材料非线性本构, 将上述方法拓展到张拉整体系统的非线性弹塑性分析; 此外, Zhang等[30 ] 针对大位移小应变系统的高效分析, 采用共旋坐标法实现了张拉整体系统的几何和材料非线性分析. 进一步, 对于由细长杆或软材料杆组成的柔软张拉整体系统, 在系统变形或运动中杆还可能发生弯曲变形, 需研究杆后屈曲局部变形对系统整体承载性能与动力学行为的影响. Rimoli[31 ] 提出了张拉整体结构柔性杆的一种等效建模方法, 将杆的连续模型等效为集中参数模型, 采用较少的自由度捕捉了杆的屈曲、后屈曲行为及动力学特性, 可用于柔性张拉整体着陆器[31 ] 、复杂张拉整体点阵材料[32 ] 的动力学和非线性响应高效分析; 然而, 由于文献[31 ]中计算两端简支杆弯曲振动固有频率的解析表达式有误(即原文式(26)中固有频率应与阶数平方成正比, 而不是与阶数成正比), 致使在合适取值下计算的离散模型前两阶固有频率相对误差均为4.5%, 而事实上第二阶固有频率相对误差应为15%, 即弯曲固有振动的计算精度不高. ...
Dynamics of a deployable mesh reflector of satellite antenna: Parallel computation and deployment simulation
1
2016
... 进一步, 为了提高动力学计算效率, 可将图6 所示杆的内部自由度${ x}_{2}$, ${ x}_{3} $和${ x}_{4} $缩聚至端部自由度${ x}_{1} $和${ x}_{5} $, 即利用静力缩聚法将内部自由度刚度等效至端部自由度的广义刚度矩阵[33 -34 ] , 并将杆的总质量均布在端部节点上, 从而大大降低迭代过程中系统动力学方程(36)的维数. 当杆承受的压力超过其屈曲临界载荷时, 需计算杆的后屈曲构型, 此时以计算得到端部位置坐标作为输入, 利用后屈曲内力平衡关系式(4), 迭代求解杆内部节点的位置. ...
The static condensation algorithm
1
2010
... 进一步, 为了提高动力学计算效率, 可将图6 所示杆的内部自由度${ x}_{2}$, ${ x}_{3} $和${ x}_{4} $缩聚至端部自由度${ x}_{1} $和${ x}_{5} $, 即利用静力缩聚法将内部自由度刚度等效至端部自由度的广义刚度矩阵[33 -34 ] , 并将杆的总质量均布在端部节点上, 从而大大降低迭代过程中系统动力学方程(36)的维数. 当杆承受的压力超过其屈曲临界载荷时, 需计算杆的后屈曲构型, 此时以计算得到端部位置坐标作为输入, 利用后屈曲内力平衡关系式(4), 迭代求解杆内部节点的位置. ...