引言
周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果.
在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法.
能量法具有将求解微分方程边值问题转化为泛函极值问题的优点,这有利于复杂结构系统耦合问题的求解,因而传统能量法(如Rayleigh-Ritz法[34 -35 ] )被广泛应用于分析一些复杂组合结构的自由振动问题[36 -37 ] ,近年来也被引入周期结构带隙计算中[38 -39 ] .但在利用传统能量法计算周期结构带隙时, 存在如下问题:(1)能量法需要基于Bloch定理构造满足周期性边界的位移场形函数[40 -41 ] ,从数学角度而言, 形函数的周期性重构难度较大,而且不同形函数的构造方式不一定相同; (2)重构以后的位移场形函数包含波数,这会导致涉及形函数的结构的质量和刚度矩阵中含有波数, 在计算带隙时,结构的质量和刚度矩阵需随着波数的变化进行反复计算,随着结构质量和刚度矩阵维度的增大, 或者扫描波数点数的增多,计算成本也会随之增大. 因此, 对于能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作.
鉴于此, 本文对传统能量法进行了改进,提出了一种利用人工弹簧[42 -44 ] 来模拟周期边界条件的方法,将形函数与周期边界条件分离, 无需构造满足周期边界的形函数,这样可解决传统能量法中构造满足周期边界条件的形函数的困难问题; 同时,利用人工弹簧模拟周期边界条件, 将周期边界约束转化为人工弹簧的弹性势能,这样只有包含波数的周期边界弹性势能矩阵需参与随波数扫描的循环计算,其他矩阵只需计算一次, 因而能提高传统能量法计算带隙的效率. 此外,人工弹簧模型使用灵活、便捷,可进一步拓展到更为复杂的周期性组合结构的带隙分析中.
1 人工弹簧模拟周期边界的基本原理
1.1 问题陈述
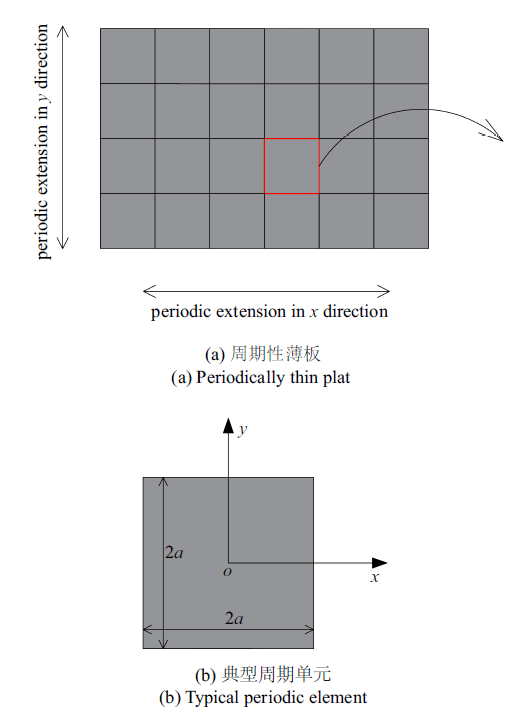
以图1 所示周期性薄板为例, 对引言中提到的传统能量法计算周期结构带隙时存在的问题进行具体阐述.
图1
图1
周期性薄板自由振动分析模型
Fig.1
Vibration analysis model of a periodically thin plate with free boundary
对于图1 所示的周期薄板结构, 取出一个周期单元进行分析.根据Kirchhoff-Love薄板理论,平面内位移$u$和$v$可以通过一阶泰勒级数围绕中面层展开, 表示为平面外位移$w$,位移向量可以表示为
(1) $ [ u \ \ v \ \ w]^T=\left[-z\frac{\partial w}{\partial x} \ \ -z\frac{\partial w}{\partial y} \ \ w\left( {x,y,t} \right) \right]^T$
将式(1)中的横向位移$w$表示为基函数$\xi_{i} \left( {x,y}\right)$和一个未知的权重系数$d_{i} \left( t \right)$的组合, 即
(2) $\left. \begin{array}{l} w\left( {x,y,t} \right)= \sum_i {d_{i} \left( t \right)\xi_{i} \left( {x,y} \right)} =\\\qquad d^T\xi =\xi^T d, \ \ \xi =\varphi \otimes \psi\\ \left.\begin{array}{l} \varphi =\left[ {\varphi_{1} \left( x \right),\varphi_{2} \left( x \right),\cdots ,\varphi_{i} \left( x \right),\cdots ,\varphi_{m} \left( x \right)} \right]^T \\ \psi =\left[ {\psi_{1} \left( y \right),\psi_{2} \left( y \right),\cdots ,\psi_{i} \left( y \right),\cdots ,\psi_{n} \left( y \right)} \right]^T \\ \end{array} \right. \\ \end{array} \right\}$
根据Bloch定理, 周期单元在$x$, $y$方向上的位移、转角、弯矩和剪力需要满足Bloch周期性边界条件, 即
(3) $ w ( {-a,y} )=w( {a,y} )e^{-ik_{x} 2a}, {w( {x,-a} )=w( {x,a} )e^{-ik_{y} 2a}}$
(4) $ \left.\begin{array}{l} {\dfrac{\partial w\left( {-a,y} \right)}{\partial x}=\dfrac{\partial w\left({a,y} \right)}{\partial x}e^{-ik_{x} 2a}} \\ {\dfrac{\partial w\left({x,-a} \right)}{\partial y}=\dfrac{\partial w\left( {x,a} \right)}{\partial y}e^{-ik_{y} 2a}} \\ \end{array} \right\}$
(5) $\left.\begin{array}{l} {\dfrac{\partial ^{2}w\left( {-a,y} \right)}{\partial x^{2}}=\dfrac{\partial ^{2}w\left( {a,y} \right)}{\partial x^{2}}e^{-ik_{x} 2a}}\\ {\dfrac{\partial ^{2}w\left( {x,-a} \right)}{\partial y^{2}}=\dfrac{\partial ^{2}w\left( {x,a} \right)}{\partial y^{2}}e^{-ik_{y} 2a}} \\ \end{array} \right\}$
(6) $\left.\begin{array}{l} {\dfrac{\partial ^{3}w\left( {-a,y} \right)}{\partial x^{3}}=-\dfrac{\partial ^{3}w\left( {a,y} \right)}{\partial x^{3}}e^{-ik_{x} 2a}} \\ {\dfrac{\partial ^{3}w\left( {x,-a} \right)}{\partial y^{3}}=-\dfrac{\partial ^{3}w\left( {x,a} \right)}{\partial y^{3}}e^{-ik_{y} 2a}} \\ \end{array} \right\}$
式中, $k_{x}$, $k_{y}$表示沿着$x$, $y$方向的波数.方程(3) $\sim$ (6)要求式(2)中的形函数$\xi_{i} \left( {x,y}\right)$满足Bloch-Floquet周期性条件. 从数学角度而言,形函数的重构过程具有相当大的难度, 且不同的形函数构造方式不一定相同,这给利用传统能量法求解周期结构振动带隙问题带来了困难.
重构以后的形函数表示为$\xi_{i}^{\ast } \left( {k_{x} ,k_{y} ,x,y} \right)$, 对于图1 (b)所示的周期单元, 其动能和应变能可以表示为
(7) $\begin{align} E_{k}^{\ast } =\frac{1}{2}\int_{-a}^a {\int_{-a}^a {\rho h\dot{{w}}^{2}dxdy} } = \\ \frac{1}{2}\dot{{ d}}^{H}\Bigg[ \int_{-a}^a \int_{-a}^a \rho h \xi^{{\ast }}\left( {k_{x} ,k_{y} ,x,y} \right)\xi^{\ast H}\cdot \\ \left( {k_{x} ,k_{y} ,x,y} \right)dxdy \Bigg]\dot{{ d}}= \frac{1}{2}\dot{{ d}}^{H} M^{{\ast }}\left( {k_{x} ,k_{y} } \right)\dot{{ d}} \end{align}$
(8) $\begin{align} U_{p}^{\ast } =\frac{1}{2}\int_{-a}^a \int_{-a}^a D\Bigg[ \left( {\frac{\partial ^{2}w}{\partial x^{2}}} \right)^{2}+\left( {\frac{\partial ^{2}w}{\partial y^{2}}} \right)^{2}+ \\ \nu \Bigg( \frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial ^{2}w}{\partial y^{2}} +\frac{\partial ^{2}w}{\partial y^{2}}\frac{\partial ^{2}w}{\partial x^{2}} \Bigg)+ \\ 2\left( {1-\nu } \right)\left( {\frac{\partial ^{2}w}{\partial x\partial y}} \right)^{2} \Bigg]dxdy = \\ \frac{1}{2} d^{H}\{\int_{-a}^a \int_{-a}^a D[\frac{\partial ^{2}\xi^{{\ast }}\left( {k_{x} ,k_{y} ,x,y} \right)}{\partial x^{2}}\cdot \\ \frac{\partial ^{2} \xi^{\ast H}\left( {k_{x} ,k_{y} ,x,y} \right)}{\partial x^{2}}+\frac{\partial ^{2} \xi^{{\ast }}\left( {k_{x} ,k_{y} ,x,y} \right)}{\partial y^{2}}\cdot \\ \frac{\partial ^{2} \xi^{\ast H}\left( {k_{x} ,k_{y} ,x,y} \right)}{\partial y^{2}} +\nu ( \frac{\partial ^{2} \xi^{{\ast }}\left( {k_{x} ,k_{y} ,x,y} \right)}{\partial x^{2}}\cdot \\ \frac{\partial ^{2} \xi^{\ast H}\left( {k_{x} ,k_{y} ,x,y} \right)}{\partial y^{2}}+\frac{\partial ^{2} \xi^{{\ast }}\left( {k_{x} ,k_{y} ,x,y} \right)\xi }{\partial y^{2}}\cdot \\ \frac{\partial ^{2} \xi^{\ast H}\left( {k_{x} ,k_{y} ,x,y} \right)}{\partial x^{2}} ) +2\left( {1-\nu } \right)\frac{\partial ^{2} \xi^{{\ast }}\left( {k_{x} ,k_{y} ,x,y} \right)}{\partial x\partial y}\cdot \\ \frac{\partial ^{2} \xi ^{\ast H}\left( {k_{x} ,k_{y} ,x,y} \right)}{\partial y\partial x} ]dxdy \} d =\frac{1}{2} d^{H} K^{{\ast }}\left( k_{x} ,k_{y} \right) d \end{align}$
其中, $\rho $, $h$, $\nu $分别表示板的材料密度、板的厚度以及板材料泊松比;$D={{E^\ast h^{3}}\Big/{\left[ {12\left( {1-\nu^{2}} \right)}\right]}}$表示板的抗弯刚度. 由式(7)、式(8)可以得到周期单元的整体拉格朗日量
(9) $L=E_{k}^{\ast } -U_{p}^{\ast } =\frac{1}{2}\dot{{ d}}^{H} M^{{\ast }}\left( {k_{x} ,k_{y} } \right)\dot{{ d}}-\frac{1}{2} d^{H} K^{{\ast }}\left( {k_{x} ,k_{y} } \right) d$
进一步地, 定义未知的与时间相关向量$ d\left( t \right)=\overset{\frown }{\mathop{D}} e^{i\omega t}$, 结合Eular-Lagrange方程
$\frac{\partial }{\partial t}\left( {\frac{\partial L}{\partial \dot{{d}}}} \right)-\frac{\partial L}{\partial d}=0$
(10) $\left[ {K^{{\ast }}\left( {k_{x} ,k_{y} } \right)-\omega ^{2}M^{{\ast }}\left( {k_{x} ,k_{y} } \right)} \right] \overset{\frown }{\mathop{D}} ={\bf 0}$
式(10)是一个标准的特征值方程问题, 在第一布里渊区$ k_{x} \times k_{y} =[-\pi /a,\ \ \pi/a]\times [-\pi/a,\ \ \pi/a]$扫描波数, 即能得到周期薄板结构弯曲振动的频散曲线.值得注意的是, 由于重构以后的形函数$\xi_{i}^{\ast } \left( {k_{x} ,k_{y},x,y} \right)$必然包含波数, 这就导致利用位移形函数表征的结构动能表达式(7)和应变能表达式(8)中也含有波数,进而使得薄板结构运动方程(10)中的质量矩阵$M^{{\ast }}\left( {k_{x},k_{y} } \right)$、刚度矩阵$K^{{\ast }}\left( {k_{x} ,k_{y} }\right)$同样包含波数. 因此, 在扫描波数进行带隙计算时,结构的质量和刚度矩阵需要随着波数的变化进行循环计算,计算时间会随着结构的质量和刚度矩阵维度以及扫描波数点数的增大而呈倍数增大,计算成本也会急剧增大. 因此, 如上所述, 对于传统能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作.
1.2 人工弹簧模拟周期性边界条件
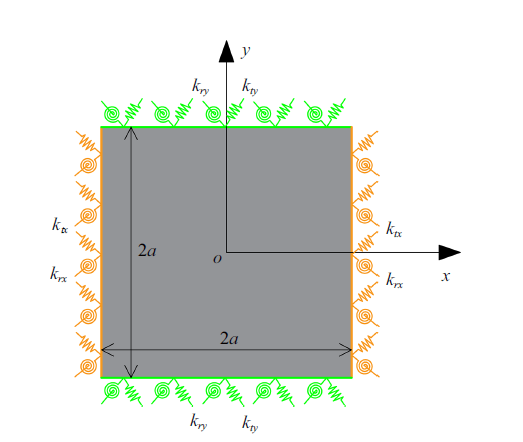
尝试将特殊的周期性边界条件与位移形函数完全分离,即无需对形函数进行重新构造, 用人工弹簧的形式来模拟周期性边界条件. 如图2 所示,在周期单元的4条边界处定义线弹簧和转角弹簧两类弹簧,它的物理意义是在$x$和$y$两个方向通过人工弹簧将上一周期单元的尾端与下一周期单元的首端相连.文献[3 ]证明了, 只需要位移和转角满足周期性条件, 解即收敛于真实解.
图2
图2
人工弹簧定义周期性边界的分析示意图
Fig.2
Analysis schematic diagram of periodic boundary defined by artificial spring
(11) $U_{p}^{(p_{x} )} =\frac{1}{2}\int_{-a}^a \Bigg\{k_{tx} \left[ {w\left( {-a,y} \right)-w\left( {a,y} \right)e^{-ik_{x} 2a}} \right]^{2} + \\ k_{rx} \left[ \frac{\partial w\left( {-a,y} \right)}{\partial x}-\frac{\partial w\left( {a,y} \right)}{\partial x}e^{-ik2a} \right]^{2} \Bigg\}dy$
式中$w( -a,y)-w( a,y)e^{-ik_{x} 2a}$,${\partial w(-a,y)}/({\partial x})-[{\partial w(a,y)}/$ $({\partial x})]$ $e^{- ik2a}$分别表示第一个周期首端与第二个周期首端的位移、 转角差值. 同时,由式(3)、 式(4)可知位移和转角的差值趋于0, 即
(12) $\left. \begin{array}{l} \lim \left[ {w\left( {-a,y} \right)-w\left( {a,y} \right)e^{-ik_{x} 2a}}\right]=\\\qquad \lim \left( {-\dfrac{F}{k_{tx} }} \right)=0 \\ \lim \left[ {\dfrac{\partial w\left( {-a,y} \right)}{\partial x}-\dfrac{\partial w\left( {a,y} \right)}{\partial x}e^{-ik2a}} \right]=\\\qquad \lim\left( {-\dfrac{M}{k_{tx} }} \right)=0 \\ \end{array} \right\}$
结构的剪力和弯矩都是一个有限值, 因此式(12)若要成立, 则需要满足$\lim k_{tx} =\infty$, $\lim k_{tx} =\infty$, 同理考虑$y$方向的周期性边界, 式(11)改写为
(13) $\begin{align} U_{p}^{(p_{xy} )} =\frac{1}{2}\Bigg\{\int_{-a}^a \Bigg\{ k_{tx} \left[ {w\left( {-a,y} \right)-w\left( {a,y} \right)e^{-ik_{x} 2a}} \right]^{2} + \\ k_{rx} \left[ {\frac{\partial w\left( {-a,y} \right)}{\partial x}-\frac{\partial w\left( {a,y} \right)}{\partial x}e^{-ik2a}} \right]^{2}dy \Bigg\} + \\ \int_{-a}^a \Bigg\{ k_{ty} \left[ {w\left( {x,-a} \right)-w\left( {x,a} \right)e^{-ik_{y} 2a}} \right]^{2} + \\ k_{ry} \left[ {\frac{\partial w\left( {x,-a} \right)}{\partial y}-\frac{\partial w\left( {x,a} \right)}{\partial y}e^{-ik_{y} 2a}} \right]^{2}dx \Bigg\}\Bigg\} = \\ \frac{1}{2} d^{H}\Bigg\{\int_{-a}^a \Bigg\{k_{tx} \left[ {\xi \left( {-a,y} \right)-\xi \left( {a,y} \right)e^{-ik_{x} 2a}} \right]^{2}+ \\ k_{rx} \left[ {\frac{\partial \xi \left( {-a,y} \right)}{\partial x}-\frac{\partial \xi \left( {a,y} \right)}{\partial x}e^{-ik_{x} 2a}} \right]^{2}dy\Bigg\} + \\ \int_{-a}^a \Bigg\{ k_{ty} \left[ {\xi \left( {x,-a} \right)-\xi \left( {x,a} \right)e^{-ik_{y} 2a}} \right]^{2} + \\ k_{ry} \left[ {\frac{\partial \xi \left( {x,-a} \right)}{\partial y}-\frac{\partial \xi \left( {x,a} \right)}{\partial y}e^{-ik_{y} 2a}} \right]^{2}dx\Bigg\}\Bigg\} d = \\ \frac{1}{2} d^{H}K_periodic \left( {k_{x} ,k_{y} } \right) d \end{align} $
在式(13)中, 周期性边界条件表示为包含波数在内的弹性势能的形式,与位移形函数分离. 此时, 形函数$\xi_{i} \left( {x,y}\right)$无需进行构造以满足周期性边界, 周期单元的动能和应变能表示为
(14) $E_{k} =\frac{1}{2}\int_{-a}^a {\int_{-a}^a {\rho h\dot{{w}}^{2}dxdy} } = \\ \frac{1}{2}\dot{{ d}}^{H}\left[ {\int_{-a}^a {\int_{-a}^a {\rho h\xi \left( {x,y} \right)\xi ^{H}\left( {x,y} \right)dxdy} } } \right]\dot{{ d}}= \frac{1}{2}\dot{{ d}}^{H} M\dot{{ d}}$
(15) $\begin{align} U_{p} =\frac{1}{2}\int_{-a}^a \int_{-a}^a D\Bigg[ \left( {\frac{\partial ^{2}w}{\partial x^{2}}} \right)^{2}+\left( {\frac{\partial ^{2}w}{\partial y^{2}}} \right)^{2}+ \\ \nu \left( \frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial ^{2}w}{\partial y^{2}} +\frac{\partial ^{2}w}{\partial y^{2}}\frac{\partial ^{2}w}{\partial x^{2}} \right)+ \\ 2\left( {1-\nu } \right)\left( {\frac{\partial ^{2}w}{\partial x\partial y}} \right)^{2} \Bigg]dxdy = \\ \frac{1}{2} d^{H}\Bigg\{ \int_{-a}^a \int_{-a}^a D\Bigg[ \frac{\partial ^{2}\xi \left( {x,y} \right)}{\partial x^{2}}\frac{\partial ^{2}\xi^{^{H}}\left( {x,y} \right)}{\partial x^{2}}+ \\ \frac{\partial ^{2}\xi \left( {x,y} \right)}{\partial y^{2}}\frac{\partial ^{2}\xi ^{^{H}}\left( {x,y} \right)}{\partial y^{2}} +\nu \Bigg( \frac{\partial ^{2}\xi \left( {x,y} \right)}{\partial x^{2}}\frac{\partial ^{2}\xi^{^{H}}\left( {x,y} \right)}{\partial y^{2}}+ \\ \frac{\partial ^{2}\xi \left( {x,y} \right)\xi }{\partial y^{2}}\frac{\partial ^{2}\xi^{^{H}}\left( {x,y} \right)}{\partial x^{2}} \Bigg) +2\left( {1-\nu } \right)\frac{\partial ^{2}\xi \left( {x,y} \right)}{\partial x\partial y}\cdot \\ \frac{\partial ^{2}\xi^{^{H}}\left( {x,y} \right)}{\partial y\partial x}\Bigg]dxdy \Bigg\} d =\frac{1}{2} d^{H} K d \end{align}$
(16) $L=E_{k} -U_{p} -U_{p}^{(p_{xy} )} =\frac{1}{2}\dot{{ d}}^{H} M\dot{{ d}}- \\ \frac{1}{2} d^{H}\left[{ K+ K_periodic \left( {k_{x} ,k_{y} } \right)} \right] d$
结合前述定义的与时间相关未知向量$ d\left( t \right)=\overset{\frown }{\mathop{D}} e^{i\omega t}$以及Eular-Lagrange方程
$\frac{\partial }{\partial t}\left( {\frac{\partial L}{\partial \dot{{ d}}}} \right)-\frac{\partial L}{\partial d}={\bf0}$
(17) $\left\{ {\left[ { K+ K_periodic \left( {k_{x} ,k_{y} } \right)} \right]-\omega^{2} M} \right\} \overset{\frown }{\mathop{D}} ={\bf 0}$
通过比较方程(14)和(15)与方程(7)和(8)可以发现,利用人工弹簧模拟周期性边界, 将位移形函数与周期性边界条件分离,选取的形函数无需满足周期性边界,进而用形函数表征的结构动能和应变能表达式中没有包含波数,同时通过对比最后的特征值方程(17)和(10)可以看出,仅有周期边界势能刚度矩阵中包含波数, 质量与应变能刚度矩阵中都不包含波数,在扫描波数进行求解时, 除了周期边界弹性势能矩阵参与波数扫描循环计算,其他的矩阵仅需计算一次, 这将大幅度提高计算效率, 进而降低计算成本.后续的算例验证中, 将进一步证明本文方法的准确性和效率性.
2 算例验证: 周期开口板弯曲振动带隙计算
开口板广泛应用于土木、船舶等结构中. 开孔板的振动在能量传递中起着重要作用,但也与辐射噪声对周围环境的影响有直接关系. 因此, 本节以周期开口板为例,验证人工弹簧模拟周期性边界的准确性, 同时说明该方法与传统能量法相比,在计算效率上的优势性.
2.1 位移形函数的选取及特征值方程求解
由于开口板出现了局部厚度突变,若选用改进傅里叶级数、切比雪夫级数等(适用于描述连续性较好的结构)作为位移形函数可能需要多项级数来进行拟合以达到精度要求,进而降低计算效率. 因此,本文选取具有局域化特性的高斯小波函数[45 -46 ] 为位移形函数,以确保能够准确捕捉到厚度变化区域的波动特征, 即对于式(2)定义
(18) $\left.\begin{array}{l} \varphi_{i} \left( x \right)=2^{p/2}\exp \left[ {-\dfrac{\left( {2^{p}x-k} \right)^{2}}{2}} \right]\\ \psi_{i} \left( y \right)=2^{q/2}\exp \left[ {-\dfrac{\left( {2^{q}x-r} \right)^{2}}{2}} \right] \end{array} \right\}$
式中, $p,q$和$k, r$分别表示伸缩因子和平移因子. 伸缩因子$p,q$控制着解的精度,采用越大的尺度因子使得形函数具有更高的分辨率,进而能更精确地模拟更高频的波场, 但同时要求更多的计算资源.平移因子$k,r$由伸缩因子$p,q$决定, 其数量控制着式(18)中$i$的取值范围,也就是形函数的个数和矩阵的维度. 伸缩因子与平移因子的取值满足
(19) $\left. \begin{array}{ll} p\geqslant \Delta _{x}, &\Delta _{x} = ceil\left( {\log_{2} \dfrac{8}{2a}} \right) \\ q\geqslant \Delta _{y}, &\Delta _{y} = ceil\left( {\log_{2} \dfrac{8}{2a}} \right) \\ \end{array} \right\}$
(20) $\left.\begin{array}{l} k=\left[ {{\begin{array}{ll} {-4+floor\left( {-2^{p}a} \right),} & ceil\left( {2^{p}a} \right)+4\\ \end{array} }} \right] \\ r=\left[ {{\begin{array}{*{20}c} {-4+floor\left( {-2^{q}a} \right),} & ceil\left( {2^{q}a} \right)+4\\ \end{array} }} \right] \\ \end{array} \right\}$
式中, ceil(*)表示最接近并大于*的整数, floor(*)表示最接近并小于*的整数.关于高斯小波函数的详细介绍可以参考文献[45 ,46 ]. 定义一个厚度函数$h\left({x,y} \right)$满足
(21) $h\left( {x,y} \right)=\left\{ \begin{array}{ll} h_{u}, & \sqrt {\left( {x_{0}^{2} +y_{0}^{2} } \right)} \geqslant r\\ 0, & \sqrt {\left( {x_{0}^{2} +y_{0}^{2} } \right)} \leqslant r \\ \end{array} \right.$
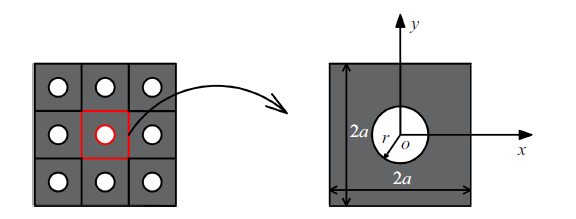
其中, $x_{0}$和$y_{0}$分别表示图3 所示开口板坐标系内任意一点的横坐标和纵坐标;$h_{u} $表示板的标准厚度; $r$表示圆形开口半径. 利用式(21)中的$h\left( {x,y}\right)$替换式(14)、式(15)中的$h$, 扫描波数求解特征值方程(17)即能得到周期开口板弯曲振动的频散曲线.
图3
图3
周期开口板分析模型
Fig.3
Analysis model of periodic plate with opening
2.2 准确性分析
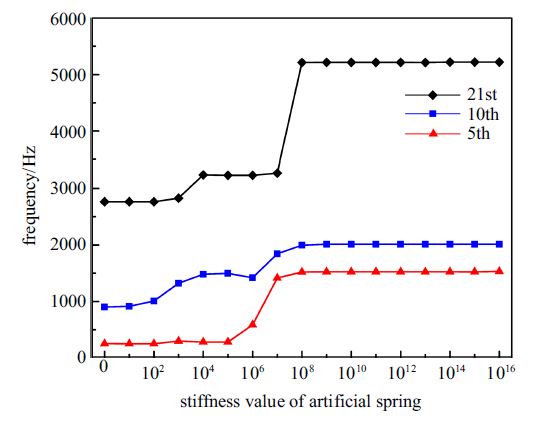
由前述分析可知, 当用人工弹簧模拟周期边界条件时, 人工弹簧刚度需要取为无穷,但在实际计算过程中需要用一个较大的值来代替,因此位移约束弹簧和转角约束弹簧刚度的取值在很大程度上影响了计算结果的准确性,需要对人工弹簧刚度取值进行收敛性分析, 找到解收敛时的弹簧刚度取值,从而能够准确替代人工弹簧刚度取无穷这一情况. 板的长度和宽度都为0.12 m,板的均质厚度取0.001 m, 圆形开口半径为0.036 m, 选取钢材料为板的材料,密度为7800 kg/m$^3$, 弹性模量为210 GPa, 泊松比为0.3.从频散曲线中随机选取3条曲线波数位于$k_{x} =k_{y} ={\pi /a}$处的频率为研究对象, 其结果如图4 所示.
图4
图4
人工弹簧刚度取值收敛性分析
Fig.4
Convergence analysis of stiffness of artificial spring
由图4 可以看出, 当弹簧刚度系数数值大于10$^{10}$时,得到的波模态频率值已经趋于稳定, 基本不再变化, 认为结果已收敛于周期性边界.表明当利用人工弹簧周期性边界条件时,实际计算中只要将刚度系数的数值取为$k_{tx} =k_{ty} =10^{10}$ N/m$^{2}$, $k_{rx} =k_{ry} =10^{10}$ N/rad时即可得到收敛的解.
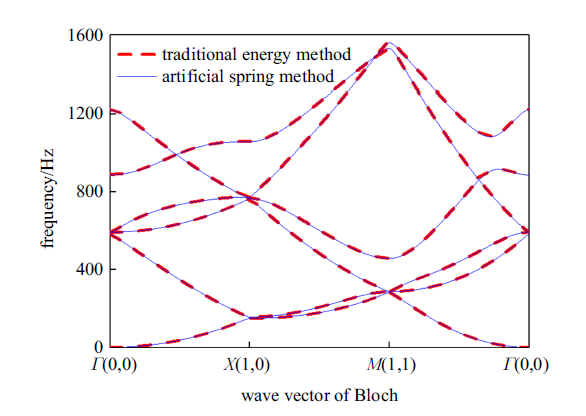
图5 给出了本文方法计算得到的周期开口板弯曲振动频散曲线, 为了对比,同时给出了利用文献[41 ]中重构位移形函数的方法计算得到的结果.其中两种方法采用的形函数均为高斯函数, 板的几何和材料参数一致,伸缩因子、平移因子取值以及扫描波数均保持一致.
图5
图5
周期开口板弯曲振动频散曲线
Fig.5
Dispersion curve of bending vibration of periodic plate with opening
由图5 可以看出, 两种方法计算得到的结果基本一致, 即0 $\sim$ 1500 Hz范围内,图3 所示的这种周期开口板结构没有产生完全带隙和方向带隙,进一步说明了利用人工弹簧模拟周期边界的准确性.
2.3 效率对比分析
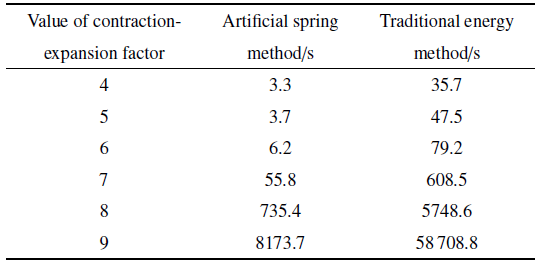
扫描波数决定了频散曲线上点的个数, 越大的扫描波数能够得到更为平滑的频散曲线.本节分析了不同扫描波数下, 两种方法计算频散曲线的时效性, 将对比结果列于表1 .分析中保持伸缩因子为6不变.
由表1 可以看出, 当扫描波数为30时, 本文方法求解仅需要4.5 s,而传统能量法需要27.5 s, 约为本文方法的6.1倍; 随着扫描波数的增大,时间倍数越来越大, 本文方法效率性体现得更加明显, 当扫描波数为300时,传统能量法需要268.2 s, 约为本文方法的21.8倍.这是因为传统能量法需要对位移场形函数进行重构以满足周期性边界条件,这就导致结构的动能和应变能矩阵中都含有波数, 每扫描一次波数,结构的动能和应变能矩阵都要计算一次, 随着扫描波数的增大,动能和应变能矩阵的计算次数也随之增大, 这极大地延长了求解时间.而本文提出的利用人工弹簧模拟周期性边界条件的方法,通过将周期性约束条件转变为弹性势能, 仅在有边界弹性势能矩阵中包含波数,结构的动能和应变能矩阵只需要计算一次,只有弹性势能矩阵参与扫描波数的循环计算, 这就使得求解时间大大缩短.
前文中提到, 伸缩因子控制着解的精度,采用越大的尺度因子使形函数具有更高的分辨率, 但同时要求更多的计算资源.平移因子由伸缩因子决定, 其数量控制着形函数的个数和矩阵的维度.本节分析了不同伸缩因子(矩阵维度)条件下, 两种方法计算频散曲线的时效性,将对比结果列于表2 .分析中保持扫描波数为100不变.
传统能量法需要对位移场形函数进行重构以满足周期性边界条件,这就导致结构的动能和应变能矩阵中都含有波数,结构的动能和应变能矩阵需要随着波数变化进行反复计算, 随着伸缩因子取值的增大,平移因子的取值范围也随之增大, 动能和应变能矩阵的维度也随之增大,这就导致每次循环计算动能和应变能矩阵的时间增大.
本文提出的利用人工弹簧定义周期性边界的方法, 仅在边界弹性势能矩阵中包含波数,结构的动能和应变能矩阵不需要参与波数循环, 只需要计算一次,仅有边界弹性势能矩阵参与随波数的循环计算.虽然伸缩因子的增大也导致了边界弹性势能矩阵维度的增大,但其计算量远小于增大结构的动能和应变能矩阵维度的计算量,这就使得随着伸缩因子的增大,本文提出的人工弹簧定义周期边界的方法求解时间增长量远小于传统能量法:由表2 可以看出, 当伸缩因子由4增大到5时, 本文方法求解时间由3.3 s延长到3.7 s,求解时间延长0.4 s; 而传统能量法求解时间由35.7 s延长到47.5 s, 求解时间延长11.8 s,约为本文方法的29.5倍. 同时, 在编程计算中, 随着矩阵维度的增大,不仅结构的动能和应变能计算时间增大, 最后特征值求解的时间也随之增大,因此在表3 中, 当伸缩因子由7增大到8时, 本文方法求解时间从55.8 s延长到735.4 s,延长了679.6 s. 但相比于传统能量法, 优势还是很明显, 对传统能量法,伸缩因子由7增大到8时, 求解时间从608.5 s延长到5748.6 s, 延长了5140.1 s. 因此,相较于传统能量法, 随着模型复杂程度的增加以及分析精度要求的提高,结构的质量刚度矩阵维度以及扫描波数点数随之增大,本文提出的用人工弹簧模拟周期性边界的方法在计算效率上的优势也会越来越明显.
3 周期组合结构振动带隙计算
在铁路工程、土木工程、机械工程等领域, 组合结构是一种常见的结构类型.这类结构通常也具有周期性, 研究这类组合结构的带隙特性,能够更全面地理解弹性波在结构中的传播特性, 从而更好地指导其减振降噪设计.在简化建模过程中, 由于组合结构的复杂性,可能是由梁-板耦合、多块板耦合甚至是板-圆柱壳耦合等,这就导致在利用位移形函数进行结构动能和势能的表征时,形成的质量和刚度矩阵维度很大. 针对这种大维度矩阵问题,若通过重构满足周期性边界的位移形函数的方法来进行带隙计算,将会面临相当大的计算成本. 因此, 本节以我国CRSTIII型无砟轨道结构为例,采用人工弹簧定义周期性边界的方法, 计算了周期性组合结构弯曲振动的带隙,并与有限元结果进行了比较.
3.1 模型简化
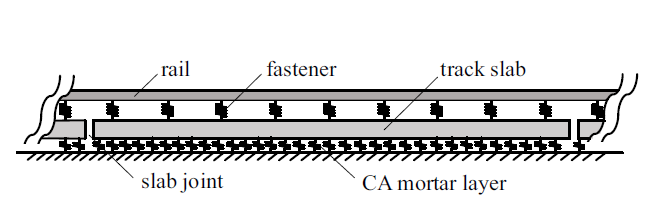
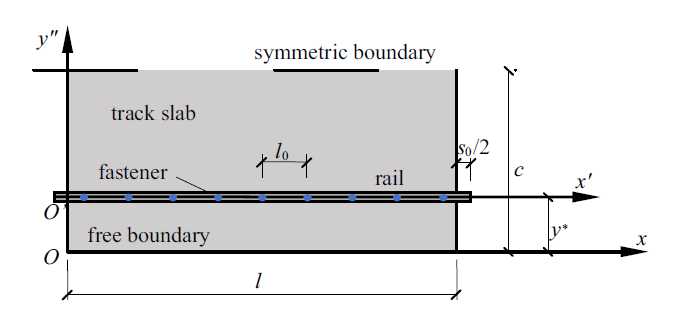
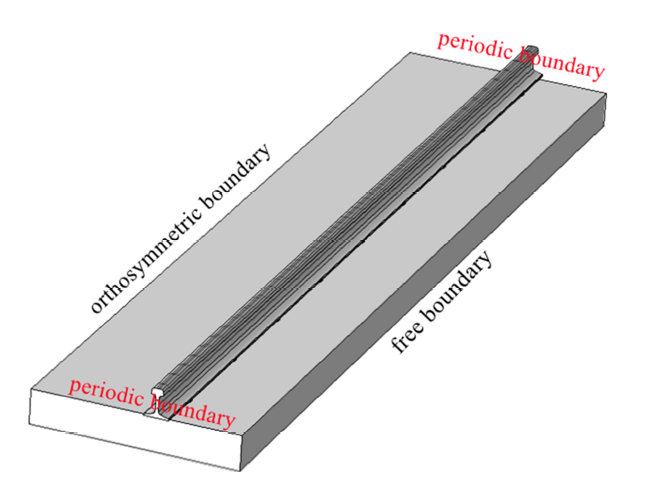
建立图6 所示的由钢轨、扣件、轨道板和CA砂浆层组成的无限周期结构.扣件与CA砂浆层简化为弹簧单元; 为同时考虑钢轨和轨道板的弯曲和剪切性质,钢轨简化为Timoshenko梁单元, 轨道板简化为Mindlin板单元, 钢轨选用60 kg/m钢轨.本文基于钢轨和轨道板的周期性与对称性(假设结构对称及载荷形式对称),可以取一个周期下结构的一半进行建模, 模型如图7 所示. $l$为单个轨道板的长度,相邻轨道板之间是不连续的, $s_{0} $为轨道板间缝隙的大小. $l+s_{0}$为钢轨周期, 其小周期为$l_{0} $, 且$l_{0} =({l+s_{0} })/{9}$.$c$为轨道板宽度的一半, $y^{{\ast }}$为钢轨距轨道板外侧边缘的宽度.图中分别针对钢轨和轨道板建立了两个笛卡尔坐标系${x}'{O}'{y}'$和$xOy$.
图6
图6
CRTSIII无砟轨道结构纵断面示意图
Fig.6
Schematic diagram of the longitudinal section of the CRTSIII track structure
图7
图7
CRTSIII型无砟轨道结构典型单元示意图
Fig.7
Schematic diagram of CRTSIII track structure of a cell
3.2 运动方程的建立
钢轨和轨道板的位移场可以分别写为与式(2)类似的形式, 即
(22) $\left. {\begin{array}{l} w_b \left( {{x}',t} \right)= \sum_i {a_{i} \left( t \right)\alpha _{i} \left( {{x}'} \right)} = a^T\alpha =\alpha^T a \\ \theta_b \left( {{x}',t} \right)= \sum_i {b_{i} \left( t \right)\alpha_{i} \left( {{x}'} \right)} = b^T\alpha =\alpha ^T b \\ \end{array}} \right\}$
(23) $\left. {\begin{array}{l} w_{p} \left( {x,y,t} \right)= \sum_i {c_{i} \left( t \right) \beta _{i} \left( {x,y} \right)} = c^T \beta = \beta^T c \\ \theta_{px} \left( {x,y,t} \right)= \sum_i {d_{i} \left( t \right) \beta_{i} \left( {x,y} \right)} = d^T \beta = \beta ^T d \\ \theta_{py} \left( {x,y,t} \right)= \sum_i {e_{i} \left( t \right) \beta_{i} \left( {x,y} \right)} = e^T \beta = \beta ^T e \\ \end{array}} \right\}$
其中, $w_b \left( {{x}',t} \right)$和$\theta_b \left( {{x}',t}\right)$分别表示钢轨的垂向位移和截面转角函数; $w_{p} \left( {x,y,t}\right)$, $\theta_{px} \left( {x,y,t} \right)$, $\theta_{py} \left({x,y,t}\right)$分别表示轨道板弯曲振动位移、沿$x$方向转角以及沿$y$方向转角函数.钢轨与轨道板位移场形函数都采用第2节提到的高斯函数.
分析中钢轨考虑为Timoshenko梁, 因此其动能包含了平动动能和转动动能, 应变能包含了弯曲应变能和剪切应变能, 即
(24) $\begin{align} E_{k}^rail=\frac{1}{2}\int_0^{l+s_{0} } {\rho _b A_b \dot{{w}}_b ^{2}d{x}'} +\frac{1}{2}\int_0^{l+s_{0} } {\rho _b I_b \dot{{\theta }}_b^{2}d{x}'} = \\ \frac{1}{2}\dot{{a}}^{H}\left[ {\int_0^{l+s_{0} } {\rho _b A_b \alpha \alpha^{H}d{x}'} } \right]\dot{{a}}+ \\ \frac{1}{2}\dot{{b}}^{H}\left[ {\int_0^{l+s_{0} } {\rho _b I_b \alpha \alpha ^{H}d{x}'} } \right]\dot{{b}} =\frac{1}{2}\dot{{\gamma }}_{1}^{H}M_rail \dot{{\gamma }}_{1} \end{align}$
(25) $\begin{align} U_{p}^rail=\frac{1}{2}\int_0^{l+s_{0} } {E_b I_b \left( {\frac{\partial \theta_b }{\partial {x}'}} \right)^{2}d{x}'} + \\ \frac{1}{2}\int_0^{l+s_{0} } {\kappa_b G_b A_b \left( {\frac{\partial w_b }{\partial {x}'}-\theta_b } \right)^{2}d{x}'} = \frac{1}{2}\gamma_{1}^{H}K_rail \gamma_{1} \end{align}$
式中, 时间权重函数$\dot{{\gamma }}_{1}^{H}=\left[{\dot{{a}}^{H}} \ \ {\dot{{b}}^{H}} \right]$, $\gamma_{1}^{H}=\left[ {a^{H}} \ \ {b^{H}} \right]$; $\rho _b$和$A_b $分别表示钢轨的密度和截面积; $E_b$和$I_b$分别表示钢轨的弹性模量和截面惯性矩; $\kappa_b$和$G_b$分别表示钢轨的剪切系数和抗剪强度.
分析中轨道板考虑为Mindlin板, 其动能$E_{k}^plate$和应变能$U_{p}^plate$可表示为
(26) $\begin{align} E_{k}^plate=\frac{1}{2}\int_0^l \int_0^c \rho _{p} h_{p} \dot{{w}}_{p}^{2}dxdy+ \\ \frac{1}{2}\int_0^l {\int_0^c {\frac{\rho _{p} h_{p}^{3} }{12}\left( {\dot{{\theta }}_{px}^{2} +\dot{{\theta }}_{py}^{2} } \right)dxdy} } = \\ \frac{1}{2}\dot{{c}}^{H}\left[ {\int_0^l {\int_0^c {\rho _{p} h_{p} \beta \beta^{H}dxdy} } } \right]\dot{{c}}+ \\ \frac{1}{2}\dot{{d}}^{H}\left[ {\int_0^l {\int_0^c {\frac{\rho _{p} h_{p}^{3} }{12} \beta \beta ^{H}dxdy} } } \right]\dot{{d}} + \\ \frac{1}{2}\dot{{e}}^{H}\left[ {\int_0^l {\int_0^c {\frac{\rho _{p} h_{p}^{3} }{12} \beta \beta^{H}dxdy} } } \right]\dot{{e}} = \\ \frac{1}{2}\dot{{\gamma }}_{2}^{H}M_plate \dot{{\gamma }}_{2} \end{align}$
(27) $\begin{align} U_{p}^plate=\frac{1}{2}\int_0^l \int_0^c D_{p} \Bigg[ \left( \frac{\partial \theta_{px} }{\partial x}+\frac{\partial \theta _{py} }{\partial y} \right)^{2}- 2\left( {1-\nu } \right)\cdot \\ \frac{\partial \theta_{px} }{\partial x}\frac{\partial \theta_{py} }{\partial y} +\frac{1}{2}\left( {1-\nu } \right)\left( {\frac{\partial \theta_{px} }{\partial y}+\frac{\partial \theta_{py} }{\partial x}} \right)^{2} \Bigg]dxdy + \\ \frac{1}{2}\int_0^l \int_0^c \kappa_{p} G_{p} A_{p} \Bigg[ \left( {\theta_{px} +\frac{\partial w_{p} }{\partial x}} \right)^{2}+ \\ \left( {\theta_{py} +\frac{\partial w_{p} }{\partial y}} \right)^{2} \Bigg]dxdy =\frac{1}{2}\gamma_{2}^{H}K_plate \gamma_{2} \end{align}$
其中, $\dot{{\gamma }}_{2}^{H}=\left[{\dot{{c}}^{H}} \ \ {\dot{{d}}^{H}}\ \ {\dot{{e}}^{H}}\right]$, $\gamma_{2}^{H}=\left[ {c^{H}} \ \ {d^{H}} \ \ {e^{H}} \right]$; $\rho _{p}$和$h_{p} $分别表示轨道板的密度和厚度; $E_{p}$, $\nu_{p}$, $\kappa_{p}$, $G_{p}$, $A_{p}$分别表示轨道板的弹性模量、泊松比、剪切系数、剪切刚度、截面积.
(28) $\begin{align} U_{p}^fastener=\frac{1}{2}\sum_{n=1}^9 k_f \Bigg\{ w_b \left[ {\frac{l_{0} }{2}+\left( {n-1} \right)l_{0} } \right]- \\ w_{p} \left[ \frac{l_{0} -s_{0} }{2}+\left( {n-1} \right)l_{0},\ y^{{\ast }}\right] \Bigg\}^{2} = \\ \frac{1}{2}\gamma^{H}K_fastener \gamma \end{align}$
其中, $\gamma^{H}=\left[{\gamma_{1}^{H}}\ \ {\gamma_{2}^{H}} \right]=\left[ { a^{H}} \ \ { b^{H}} \ \ { c^{H}} \ \ { d^{H}} \ \ { e^{H}} \right]$. 轨道板下部的CA砂浆层模拟为均布弹簧,可以通过对轨道板底面进行二重积分得到, 即
(29) $U_{p}^ca=\frac{1}{2}\int_0^l {\int_0^c {k_ca w_{p}^{2} dxdy} } =\frac{1}{2}\gamma_{2}^{H}K_ca \gamma_{2}$
图7 中$xOy$坐标系$y=c$处边界为正对称边界, 可认为板边界上转角为0, 位移自由,利用人工弹簧模拟正对称边界条件, 线弹簧和转角弹簧刚度分别表示为$k_{ts}$和$k_{rs} $, 刚度取值参考文献[43 ].在${x}'{O}'y$坐标系上${x}'=0$和${x}'=l+s_{0} $处为Floquet周期性边界,由于CRSTIII型轨道板结构是不连续的, 相邻轨道板之间存在板缝,因此轨道板没有Floquet周期性边界. 整体结构的边界势能可表示为
(30) $U_{p}^symmetric=\frac{1}{2}\int_0^l[ {k_{ts} } w_{p}^{2} \left( {x,c} \right)+k_{rs} \theta_{py}^{2} \left( {x,c} \right) ]dx= \\ \frac{1}{2}\gamma_{2}^{H}K_symmetric \gamma_{2}$
(31) $\begin{align} U_{p}^periodic=\frac{1}{2}\Big\{ k_{tx} \left[ {w_b \left( 0 \right)-w\left( {l+s_{0} } \right)e^{-ik\left( {l+s_{0} } \right)}} \right]^{2} + \\ k_{rx} \left[ {\theta_b \left( 0 \right)-\theta_b \left( {l+s_{0}} \right)e^{-ik\left( {l+s_{0} } \right)}} \right]^{2}\Big\} = \\ \frac{1}{2}\gamma_{1}^{H}K_periodic \left( k \right)\gamma_{1} \end{align}$
其中, $U_{p}^symmetric$和$U_{p}^periodic$分别表示正对称边界势能和周期性边界势能; $k$表示沿钢轨纵向传播的弹性波波数.
(32) $\begin{align} E_{k} =E_{k}^rail+E_{k}^plate=\frac{1}{2}\dot{{\gamma }}_{1} ^{H}M_rail \dot{{\gamma }}_{1} +\frac{1}{2}\dot{{\gamma }}_{2} ^{H}M_plate \dot{{\gamma }}_{2} = \\ \frac{1}{2}\dot{{\gamma }}^{H}\left[ {{\begin{array}{cc} {M_rail } & \\[-2mm] & {M_plate } \\ \end{array} }} \right]\dot{{\gamma }}=\frac{1}{2}\dot{{\gamma }}^{H}M\dot{{\gamma }} \end{align}$
(33) $\begin{align} U_{p} =U_{p}^rail+U_{p}^plate+U_{p}^fastener+ U_{p} ^{ca}+U_{p}^symmetric+U_{p}^periodic =\\ \frac{1}{2}\gamma^{H}\Bigg\{\Bigg[ \begin{array}{cc} K_rail +K_periodic( k) & \\[-2mm] & {K_plate +K_ca +K_symmetric } \\ \end{array} \Bigg]+ K_fastener \Bigg\}\gamma \end{align}$
(34) $\begin{align} L=E_{k} -U_{p} =\frac{1}{2}\dot{{\gamma }}^{H}M\dot{{\gamma }}- \\ \frac{1}{2}\gamma^{H}\Bigg\{\Bigg[ \begin{array}{cc} K_rail +K_periodic( k) & \\[-2mm] & {K_plate +K_ca +K_symmetric } \\ \end{array} \Bigg]+ \\ K_fastener \Bigg\}\gamma \end{align}$
结合前文中提到的欧拉-拉格朗日方程, 可以将式(34)转化为标准特征值方程问题, 即
(35) $\Bigg| \Bigg\{ \Bigg[\begin{array}{*{20}c} {K_rail +K_periodic \left( k \right)} & \\[-2mm] & {K_plate +K_ca +K_symmetric } \\ \end{array} \Bigg]+ \\ K_fastener \Bigg\}-\omega^{2}M \Bigg|=0$
在第一布里渊区扫描波矢$ k=[-\pi/(l+s_{0}),\ \ \pi/(l+s_{0})]$, 求解特征值方程(35)就能得到周期梁-板组合结构弯曲振动的频散曲线.
3.3 算例分析
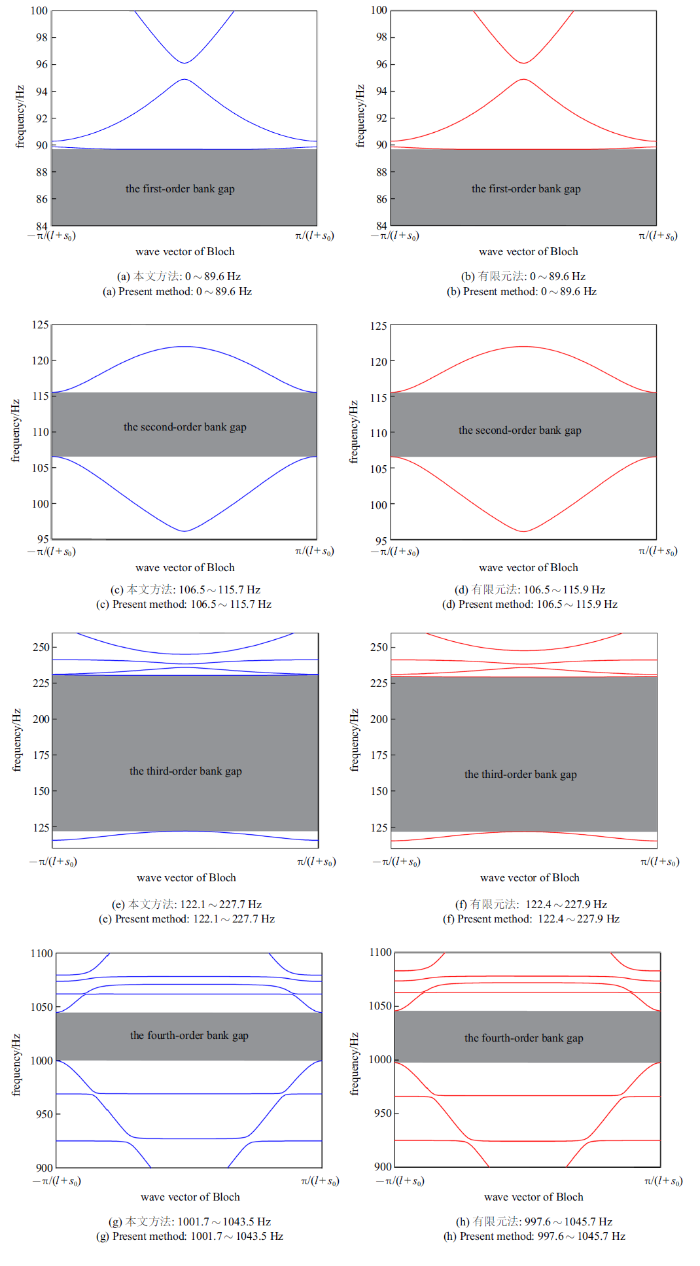
为了进一步验证本文方法的正确性,建立了单个周期CRSTIII型无砟轨道结构有限元模型, 如图8 所示.钢轨与轨道板均考虑为实体单元, 扣件与CA砂浆层分别简化为点弹簧和均布弹簧,其中, 钢轨与轨道板通过扣件弹簧连接, 轨道板与基础通过CA砂浆均布弹簧连接.轨道板的内边界添加正对称边界条件, 在钢轨两端添加Floquet周期性边界条件,其余边界为自由边界.钢轨、轨道板的几何和材料参数以及扣件刚度、CA砂浆均布刚度取值与上述半解析模型一致,钢轨密度 $\rho _b=7850$ kg/m$^{3}$, 截面积$A_b= 77.45$ cm$^{2}$, 截面惯性比 $I_b=3217$ cm$^{4}$, 弹性模量$E_b=210$ GPa, 泊松比$\nu_b=0.3$; 轨道比密度$\rho _{p}=2300$ kg/m$^{3}$, 半宽度$C=1.25$ m, 长度$l=5.6$ m, 厚度$h=0.21$ m, 弹性模量$E_{p}=25$ GPa, 泊松比$\nu_b=0.2$; 轨道板间缝系$S_{0}=0.07$ m, 轨道与FSB间距$y^{\ast }=0.492 2$ m, 垂直连接钢度$k_f=7.2\times10^7$ N/m, CA砂浆层的均匀支撑钢度$k_ca=1.723\times10^8$ N/m$^3$. 选用多物理场仿真软件Comsol Multiphysics中的固体力学模块进行求解,通过设置扫描波数求解得到了周期性无砟轨道结构的振动模态,从中挑选出垂向振动模态进行绘制即能得到垂向振动频散曲线.0 $\sim$ 1500 Hz范围内,CRSTIII型无砟轨道结构垂向振动产生了四阶带隙, 图9 给出了两种方法计算结果对比.
图8
图8
CRTSIII无砟轨道结构典型单元有限元模型
Fig.8
FEM model of typical cell of CRTSIII track structure
图9
图9
CRTSIII型无砟轨道结构垂向振动频散曲线
Fig.9
Vertical vibration dispersion curve of CRTSIII track structure
由图9 可以看出,利用人工弹簧定义周期性边界这种方法进行带隙计算与有限元计算结果吻合度很好,再次证明了该方法的准确性. 目前, 针对此类复杂的周期性组合结构带隙计算问题,主要是通过商业有限元软件来实现.其中仅有Comsol等少数有限元软件可通过直接设置Floquet周期性边界并扫描波矢来实现带隙计算.然而由于这类商业软件目前计算模块尚未完善, 以Comsol为例,对于图6 所示的无砟轨道结构(梁-板组合结构)需要采用实体单元建模, 计算量较大.利用人工弹簧模拟周期性边界,除周期边界处人工弹簧弹性势能矩阵需随波数变化而重复计算,其他矩阵均只需计算一次, 可以解决计算量大的问题.
4 结论
本文基于能量法的基本框架, 对传统能量法进行了改进,提出了利用人工弹簧模拟周期性边界条件的方法,实现了周期性边界条件与位移形函数的分离. 首先以周期开口板为例,验证了本文方法的准确性, 并与传统能量法比较了计算效率; 然后,针对周期性组合结构, 以我国CRTSIII型无砟轨道结构为例,分析了其垂向振动带隙特性, 并与有限元法进行了比较. 通过本文的研究,可得如下结论:
(1) 与传统能量法以及有限元法的对比结果表明了本文方法具有很好的准确性. 同时,相较于传统能量法, 利用人工弹簧模拟周期性边界条件,无需构造满足周期边界的位移形函数, 进一步实现了周期边界与位移形函数的分离,成功解决了传统能量法中构造满足周期性边界条件形函数的困难问题,提高了能量法的适用性.
(2) 与传统能量法相比, 利用人工弹簧模拟周期边界,除周期边界处弹性势能矩阵需随波数变化而重复计算, 其他矩阵均只需计算一次,这极大地提高了计算效率,实现了以较低的计算成本对复杂周期结构的带隙进行精确计算.随着模型复杂程度的增加以及分析精度要求的提高,结构质量、刚度矩阵的维度以及扫描波数点数也随之增多,本文方法在计算效率上的优势会更加明显.
参考文献
View Option
[1]
卢一铭 , 曹东兴 , 申永军 等 . 局域共振型声子晶体板缺陷态带隙及其俘能特性研究
力学学报 , 2021 , 53 (4 ): 1114 -1123
DOI
[本文引用: 1]
设计了一种由圆柱形散射体嵌入环氧树脂基体而组成的周期阵列局域共振型声子晶体板结构, 分析了其平直带区域以及缺陷态的能量集中特性, 并研究了其振动能量采集特性. 首先基于超元胞法结合有限元方法分析了5 $\times$ 5完美声子晶体结构和缺陷态声子晶体结构的能带曲线和能量传输特性; 考虑点缺陷局域共振声子晶体结构的能量集中特性, 利用压电材料代替超元胞中某点的散射体材料引入点缺陷, 分析其振动能量采集特性, 结果表明单个5 $\times$ 5点缺陷超胞结构共振频带较窄; 为提升俘能效率, 提出两种由3个具有不同缺陷态数量和构型的5 $\times$ 5超元胞结构并联而成的5 $\times$ 15声子晶体板结构, 机电耦合特性分析结果表明: 所提出的局域共振型声子晶体板结构克服了单个点缺陷超胞结构缺陷模过少、共振频带过窄的局限性, 拓宽了俘能器的工作频带, 提高了输出电压; 此外, 引入不同的缺陷态数量和构型, 可以进一步拓宽俘能带宽, 实现更好的俘能效果.
(Lu Yiming Cao Dongxing Shen Yongjun , et al . Study on the bandgaps of defect states and application of energy harvesting of local resonant phononic crystal plate
Chinese Journal of Theoretical and Applied Mechanics 2021 , 53 (4 ): 1114 -1123 (in Chinese))
[本文引用: 1]
[2]
Mei J Wu Y Liu Z Y . Effective medium of periodic fluid-solid composites
Europhysics Letters 2012 , 98 (5 ): 54001
DOI
URL
[本文引用: 1]
[3]
温激鸿 , 郁殿龙 , 王刚 等 . 周期结构细直梁弯曲振动中的振动带隙
机械工程学报 , 2005 , 41 (4 ): 1 -6
[本文引用: 2]
(Wen Jihong Yu Dianlong Wang Gang , et al . Elastic wave band gaps in flexural vibration of straight beams
Journal of Mechanical Engineering 2005 , 41 (4 ): 1 -6 (in Chinese))
[本文引用: 2]
[4]
Jr EJPM Nobrega ED Rodrigues SF , et al . Wave attenuation in elastic metamaterial thick plates: Analytical, numerical and experimental investigations
International Journal of Solids and Structures 2020 , 205 : 138 -152
[本文引用: 1]
[5]
Wen J Wang G Yu D , et al . Theoretical and experimental investigation of flexural wave propagation in straight beams with periodic structures: Application to a vibration isolation structure
Journal of Applied Physics 2005 , 97 : 114907
DOI
URL
[本文引用: 1]
[6]
陈阿丽 , 王新萌 , 汪越胜 . 圆弧形超表面对透射声波的可调控制与功能转换
力学学报 , 2021 , 53 (3 ): 789 -801
DOI
[本文引用: 1]
基于“螺丝-螺母”的工作原理, 设计了可调的透射型三通道螺旋单元,通过调节螺丝的旋拧深度来改变声通道的长度, 从而实现对透射声波相位的调节.利用有限元方法计算了单元的透射波相位差和透射系数随频率和旋拧深度的变化规律.在平面广义Snell定律基础上推导了适用于圆弧形曲面的广义Snell定律.设计了圆弧形超表面, 包括弧状和圆环状两种, 实现了对透射声波波前的可调控制.根据所要实现的声学功能和给定的工作频率,利用单元的透射波相位差随旋拧深度的变化规律和圆弧形表面的广义Snell定律,确定超表面上所需的相位分布梯度及每个单元的旋拧深度,并同时考虑透射系数随旋拧深度的变化规律来对单胞旋拧深度进行适当的调整,以保证超表面具有较高的透射率.利用圆弧形超表面实现了宽频范围内声波的定向折射、波束分离和声束聚焦等声学功能的转换;利用圆环形超表面则实现了三向分波、波场螺旋化及源位置虚拟移动等声学功能的转换.同时针对上述功能进行了全波场的有限元数值模拟和相应的声学实验,实验结果与有限元模拟结果吻合良好, 验证了所设计超表面对声波波前调控的有效性.研究结果将为不规则非平面可调声学器件的设计提供理论指导.
(Chen Ali Wang Xinmeng Wang Yuesheng . Tunable control and functional switch of transmitted acoustic waves by an arch-shaped metasurface
Chinese Journal of Theoretical and Applied Mechanics 2021 , 53 (3 ): 789 -801 (in Chinese))
[本文引用: 1]
[7]
Vinícius Fonseca Dal Poggetto Serpa AL . Elastic wave band gaps in a three-dimensional periodic metamaterial using the plane wave expansion method
International Journal of Mechanical Sciences 2020 , 184 : 105841
DOI
URL
[本文引用: 1]
[8]
陈圣兵 , 韩小云 , 郁殿龙 等 . 不同压电分流电路对声子晶体梁带隙的影响
物理学报 , 2010 , 59 (1 ): 387 -392
[本文引用: 1]
(Chen Shengbing Han Xiaoyun Yu Dianlong , et al . Influences of different types of piezoelectric shunting circuits on band gaps of phononic beam
Acta Physica Sinica 2010 , 59 (1 ): 387 -392 (in Chinese))
[本文引用: 1]
[9]
Qian DH Wu JH He FY . Electro-mechanical coupling band gaps of a piezoelectric phononic crystal Timoshenko nanobeam with surface effects
Ultrasonics 2021 , 109 : 106225
DOI
URL
[本文引用: 1]
[10]
Qian DH Shi ZY Ning CW , et al . Nonlinear bandgap properties in a nonlocal piezoelectric phononic crystal nanobeam
Physics Letters A 2019 , 383 : 3101 -3107
DOI
URL
[本文引用: 1]
[11]
许振龙 , 吴福根 , 黄亮国 . 局域共振型磁流变隔振支座低频完全禁带研究
压电与声光 , 2015 , 37 (2 ): 330 -333
[本文引用: 1]
(Xu Zhenlong Wu Fugen Huang Liangguo . Study on low-frequency complete band gaps of local resonant magnetorheological vibration isolators
Piezoelectrics and Acoustooptics 2015 , 37 (2 ): 330 -333 (in Chinese))
[本文引用: 1]
[12]
吴旭东 , 左曙光 , 倪天心 等 . 并联双振子声子晶体梁结构带隙特性研究
振动工程学报 , 2017 , 30 (1 ): 79 -85
[本文引用: 1]
(Wu Xudong Zuo Shuguang Ni Tianxin , et al . Study on the bandgap characteristics of a locally resonant phononic crystal beam with attached double oscillators in parallel
Journal of Vibration Engineering 2017 , 30 (1 ): 79 -85 (in Chinese))
[本文引用: 1]
[13]
Fomenko SI Golub MV Chen A , et al . Band-gap and pass-band classification for oblique waves propagating in a three-dimensional layered functionally graded piezoelectric phononic crystal
Journal of Sound and Vibration 2019 , 439 : 219 -240
DOI
Three-dimensional time-harmonic wave motion in a layered functionally graded (FG) piezoelectric periodic composite (phononic crystal) composed of a finite or an infinite number of unit-cells is considered. A longitudinal or transverse plane waves incident obliquely to the interfaces of a finite phononic crystal between two half-spaces is studied. The paper proposes a semi-analytical method to simulate and analyse the wave fields in a phononic crystal in the case of arbitrary angles of incidence. It is shown that the method is numerically stable for an arbitrary number of unit-cells in finite phononic crystals. Several kinds of pass-bands and band-gaps can be distinguished by employing the derived semi-analytical expressions: band-gaps, pass-bands, low transmission pass-bands, quasi-longitudinal and quasi-transverse band-gaps. Using the present approach a detailed parametric analysis of the influences of the type and incidence angle of an incident wave, and the material and geometrical parameters of the FG interlayers on wave propagation is conducted. (C) 2018 Elsevier Ltd.
[14]
Wang T Sheng MP , et al . Flexural wave suppression by an acoustic metamaterial plate
Applied Acoustics 2016 , 114 : 118 -124
DOI
URL
[15]
Wang T . Tunable band gaps in an inertant metamaterial plate with two-degree-of-freedom local resonance
Physics Letters A 2020 , 384 (21 ): 126420
DOI
URL
[本文引用: 1]
[16]
Huang ZG Chen ZY . Acoustic waves in two-dimensional phononic crystals with reticular geometric structures
Journal of Vibration and Acoustics 2013 , 133 (3 ): 031011
DOI
URL
[本文引用: 1]
[17]
朱晓辉 , 李隆球 , 张广玉 等 . 基于层状周期性结构的声波调控技术研究
机械工程学报 , 2017 , 53 (6 ): 10 -15
(Zhu Xiaohui Li Longqiu Zhang Guangyu , et al . Investigation of acoustic manipulation by layered periodic composites
Journal of Mechanical Engineering 2017 , 53 (6 ): 10 -15 (in Chinese))
[18]
Wu LY Chen LW . Acoustic band gaps of the woodpile sonic crystal with the simple cubic lattice
Journal of Physics D: Applied Physics 2011 , 44 (4 ): 045402
DOI
URL
[19]
李静茹 , 黎胜 . 周期新型超材料板多阶弯曲波带隙研究
振动与冲击 , 2018 , 37 (1 ): 163 -171
[本文引用: 1]
(Li Jingru Li Sheng . Multi-flexural wave band gaps of a new periodic metamaterial plate
Journal of Vibration and Shock 2018 , 37 (1 ): 163 -171 (in Chinese))
[本文引用: 1]
[20]
Hoang T Duhamel D Foret G . Wave finite element method for waveguides and periodic structures subjected to arbitrary loads
Finite Elements in Analysis and Design 2020 , 179 : 103437
DOI
URL
[本文引用: 1]
[21]
Jean-Mathieu M . A wave finite element approach for the analysis of periodic structures with cyclic symmetry in dynamic substructuring
Journal of Sound and Vibration 2018 , 431 : 1 -17
DOI
URL
[本文引用: 1]
[22]
Nobrega ED Gautier F Pelat A , et al . Vibration band gaps for elastic metamaterial rods using wave finite element method
Mechanical Systems and Signal Processing 2016 , 79 (15 ): 192 -202
DOI
URL
[本文引用: 1]
[23]
Zhou CW Lainé JP Ichchou MN , et al . Numerical and experimental investigation on broadband wave propagation features in perforated plates
Mechanical Systems and Signal Processing 2016 , 75 : 556 -575
DOI
URL
[本文引用: 1]
[24]
Hong J He X Zhang D , et al . Vibration isolation design for periodically stiffened shells by the wave finite element method
Journal of Sound and Vibration 2018 , 419 : 90 -102
DOI
URL
[本文引用: 1]
[25]
Li FM Zhang CX Liu C . Active tuning of vibration and wave propagation in elastic beams with periodically placed piezoelectric actuator/sensor pairs
Journal of Sound and Vibration 2017 , 393 : 14 -29
DOI
URL
[本文引用: 1]
[26]
Atari AK Stephen NG . On wave propagation in repetitive structures: Two forms of transfer matrix
Journal of Sound and Vibration 2019 , 439 : 99 -112
DOI
URL
[本文引用: 1]
[27]
吴健 , 白晓春 , 肖勇 等 . 一种多频局域共振型声子晶体板的低频带隙与减振特性
物理学报 , 2016 , 65 (6 ): 064602
[本文引用: 1]
(Wu Jian Bai Xiaochun Xiao Yong , et al . Low frequency band gaps and vibration reduction properties of a multi-frequency locally resonant phononic plate
Acta Physica Sinica 2016 , 65 (6 ): 064602 (in Chinese))
[本文引用: 1]
[28]
Miranda Jr. EJP Nobrega ED Ferreira AHR , et al . Flexural wave band gaps in a multi-resonator elastic metamaterial plate using Kirchhoff-Love theory
Mechanical Systems and Signal Processing 2019 , 116 (1 ): 480 -504
DOI
URL
[本文引用: 1]
[29]
Wang P Yi Q Zhao C , et al . Wave propagation in periodic track structures: Band-gap behaviours and formation mechanisms
Archive of Applied Mechanics 2017 , 87 (3 ): 503 -519
DOI
URL
[本文引用: 1]
[30]
Wang P Yi Q Zhao C , et al . Elastic wave propagation characteristics of periodic track structure in high-speed railway
Journal of Vibration and Control 2019 , 25 (3 ): 517 -528
DOI
URL
[本文引用: 1]
[31]
Jin G Zhang C Ye T , et al . Band gap property analysis of periodic plate structures under general boundary conditions using spectral-dynamic stiffness method
Applied Acoustics 2017 , 121 : 1 -13
DOI
URL
[本文引用: 1]
[32]
闫志忠 , 汪越胜 . 一维声子晶体弹性波带隙计算的小波方法
中国科学: 物理学力学天文学 , 2007 , 37 (4 ): 544 -551
[本文引用: 1]
(Yan Zhizhong Wang Yuesheng . Wavelet-based method for computing elastic band gaps of one-dimensional phononic crystals
Sci Sin-Phys Mech Astron 2007 , 37 (4 ): 544 -551 (in Chinese))
[本文引用: 1]
[33]
Carter BG McIver P . Water-wave propagation through an infinite array of floating structures
Journal of Engineering Mathematics 2013 , 81 (1 ): 9 -45
DOI
URL
[本文引用: 1]
[34]
Chen M Jin G Zhang Y , et al . Three-dimensional vibration analysis of beams with axial functionally graded materials and variable thickness
Composite Structures 2019 , 207 : 304 -322
DOI
URL
[本文引用: 1]
[35]
华洪良 , 廖振强 , 张相炎 . 轴向移动悬臂梁高效动力学建模及频率响应分析
力学学报 , 2017 , 49 (6 ): 1390 -1398
DOI
[本文引用: 1]
轴向移动梁动力学问题具有广泛的工程应用背景,如:机械手、机床主轴、武器身管等.计算轴向移动梁动力学响应是评估结构动力学性能以及最终指导结构设计的一个重要手段.采用Rayleigh-Ritz法、拉格朗日方程推导了轴向移动悬臂梁时变动力学方程.选取幂级数函数构造试函数对轴向移动系统动力问题进行求解.幂级数函数良好的积分与微分性能,使得推导容易以矩阵的形式快速进行,便于符号运算软件直接生成MATLAB程序.由于MATLAB基本数据单位为矩阵,符号软件生成的程序只需经过简单修改便可进行动力学计算.大大缩短了轴向移动梁从建模到动力学分析的时间,过程十分高效.通过四组算例,将本文方法计算得到的动力学响应与文献数据进行对比,对该方法准确性进行了验证,并给出了幂级数函数拟合阶数的选取原则.以此为基础,研究了轴向移动梁的频率响应特性.分为考虑重力与忽略重力两种情况,讨论了轴向振动幅度对其频率响应特性的影响.
(Hua Hongliang Liao Zhenqiang Zhang Xiangyan . An efficient dynamic modeling method of an axially moving cantilever beam and frequency response analysis
Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (6 ): 1390 -1398 (in Chinese))
[本文引用: 1]
[36]
Qu Y Wu S Chen Y , et al . Vibration analysis of ring-stiffened conical-cylindrical-spherical shells based on a modified variational approach
International Journal of Mechanical Sciences 2013 , 69 : 72 -84
DOI
URL
[本文引用: 1]
[37]
Qu Y Chen Y Long X , et al . A modified variational approach for vibration analysis of ring-stiffened conical-cylindrical shell combinations
European Journal of Mechanics, A/Solids 2013 , 37 : 200 -215
DOI
URL
[本文引用: 1]
[38]
Wang T Sheng MP Qin QH . Multi-flexural band gaps in an Euler-Bernoulli beam with lateral local resonators
Physics Letters A 2016 , 380 (4 ): 525 -529
DOI
URL
[本文引用: 1]
[39]
Wang T Qin QH Zhu X . Reaction force and power flow analysis of an acoustic metamaterial beam with multi-band gaps
Acoustics Australia 2020 , 48 (1 ): 59 -67
DOI
URL
[本文引用: 1]
[40]
Tang L Cheng L . Broadband locally resonant band gaps in periodic beam structures with embedded acoustic black holes
Journal of Applied Physics 2017 , 121 : 194901
DOI
URL
[本文引用: 1]
[41]
Deng J Guasch O Zheng L . A semi-analytical method for characterizing vibrations in circular beams with embedded acoustic black holes
Journal of Sound and Vibration 2020 , 476 : 115307
DOI
URL
[本文引用: 2]
[42]
Jin G Ye T Wang X , et al . A unified solution for the vibration analysis of FGM doubly-curved shells of revolution with arbitrary boundary conditions
Compos Part B-Eng 2016 , 89 : 230 -252
DOI
URL
[本文引用: 1]
[43]
Zhang C Jin G Ma X , et al . Vibration analysis of circular cylindrical double-shell structures under general coupling and end boundary conditions
Applied Acoustics 2016 , 110 : 176 -193
DOI
URL
[本文引用: 1]
[44]
Chen Y Ye T Jin G . Quasi-3D solutions for the vibration of solid and hollow slender structures with general boundary conditions
Computers & Structures 2018 , 211 : 14 -26
DOI
URL
[本文引用: 1]
[45]
Deng J Zheng L Guasch O , et al . Gaussian expansion for the vibration analysis of plates with multiple acoustic black holes indentations
Mechanical Systems and Signal Processing 2019 , 131 : 317 -334
DOI
[本文引用: 2]
The acoustic black hole (ABH) effect can be achieved embedding cuneate indentations with power-law profile in plates. That results in remarkable properties like the reduction of plate vibrations, the potential for energy harvesting thanks to the focalization of energy, or the design of new metamaterials to manipulate acoustics waves. The analysis of such phenomena demands simulating the modal shapes and response to external excitations of ABH plates. This is usually done by means of numerical approaches, like the finite element method (FEM). However, if one is interested in performing long parametric analyses and in capturing the ABH plate behavior at high frequencies, the computational cost associated to numerical methods may become too demanding. In this work, a semi-analytical approach is suggested to circumvent the situation. The Rayleigh-Ritz method is applied using two-dimensional Gaussian functions to expand the flexural motion of a plate with non-uniform thickness. Then, a matrix-replacing strategy is proposed to embed the multiple ABHs in the plate. That results in low dimensional matrix systems, which yet provide very accurate solutions. After presenting all theoretical developments, the semi-analytical method is first applied to analyze the performance of a single ABH when varying several of its parameters. Then, various configurations involving multiple ABHs are considered. Those range from long strips exhibiting frequency attenuation bands, to plates containing ABH indentations in many shapes and sizes. (C) 2019 Elsevier Ltd. All rights reserved.
[46]
Deng J Zheng L Zeng P , et al . Passive constrained viscoelastic layers to improve the efficiency of truncated acoustic black holes in beams
Mechanical Systems and Signal Processing 2018 , 118 : 461 -476
DOI
URL
[本文引用: 2]
局域共振型声子晶体板缺陷态带隙及其俘能特性研究
1
2021
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
局域共振型声子晶体板缺陷态带隙及其俘能特性研究
1
2021
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
Effective medium of periodic fluid-solid composites
1
2012
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
周期结构细直梁弯曲振动中的振动带隙
2
2005
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
... 尝试将特殊的周期性边界条件与位移形函数完全分离,即无需对形函数进行重新构造, 用人工弹簧的形式来模拟周期性边界条件. 如图2 所示,在周期单元的4条边界处定义线弹簧和转角弹簧两类弹簧,它的物理意义是在$x$和$y$两个方向通过人工弹簧将上一周期单元的尾端与下一周期单元的首端相连.文献[3 ]证明了, 只需要位移和转角满足周期性条件, 解即收敛于真实解. ...
周期结构细直梁弯曲振动中的振动带隙
2
2005
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
... 尝试将特殊的周期性边界条件与位移形函数完全分离,即无需对形函数进行重新构造, 用人工弹簧的形式来模拟周期性边界条件. 如图2 所示,在周期单元的4条边界处定义线弹簧和转角弹簧两类弹簧,它的物理意义是在$x$和$y$两个方向通过人工弹簧将上一周期单元的尾端与下一周期单元的首端相连.文献[3 ]证明了, 只需要位移和转角满足周期性条件, 解即收敛于真实解. ...
Wave attenuation in elastic metamaterial thick plates: Analytical, numerical and experimental investigations
1
2020
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
Theoretical and experimental investigation of flexural wave propagation in straight beams with periodic structures: Application to a vibration isolation structure
1
2005
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
圆弧形超表面对透射声波的可调控制与功能转换
1
2021
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
圆弧形超表面对透射声波的可调控制与功能转换
1
2021
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
Elastic wave band gaps in a three-dimensional periodic metamaterial using the plane wave expansion method
1
2020
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
不同压电分流电路对声子晶体梁带隙的影响
1
2010
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
不同压电分流电路对声子晶体梁带隙的影响
1
2010
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
Electro-mechanical coupling band gaps of a piezoelectric phononic crystal Timoshenko nanobeam with surface effects
1
2021
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
Nonlinear bandgap properties in a nonlocal piezoelectric phononic crystal nanobeam
1
2019
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
局域共振型磁流变隔振支座低频完全禁带研究
1
2015
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
局域共振型磁流变隔振支座低频完全禁带研究
1
2015
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
并联双振子声子晶体梁结构带隙特性研究
1
2017
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
并联双振子声子晶体梁结构带隙特性研究
1
2017
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
Band-gap and pass-band classification for oblique waves propagating in a three-dimensional layered functionally graded piezoelectric phononic crystal
0
2019
Flexural wave suppression by an acoustic metamaterial plate
0
2016
Tunable band gaps in an inertant metamaterial plate with two-degree-of-freedom local resonance
1
2020
... 周期结构因其具有良好的弹性波衰减特性[1 -2 ] (带隙特性),在结构振动与噪声控制领域体现出了巨大的潜力. 近年来,周期性结构中弹性波的波动特性研究发展迅速,从单一的周期性梁[3 ] 、板结构[4 -5 ] 拓展到复杂的三维结构[6 -7 ] .与此同时, 作为周期结构最为重要的特性,带隙频率的放大和调谐技术已成为当前研究的一个热点, 大量的学者立足于此,以梁板结构为基础,将智能材料(如压电材料[8 -9 ] 、磁流变材料[10 ] 、功能梯度材料[11 ] 等)和弹簧-振子系统[12 -15 ] 引入周期结构中,以实现带隙的主动调控和带宽的增大, 并取得了很好的效果. ...
Acoustic waves in two-dimensional phononic crystals with reticular geometric structures
1
2013
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
基于层状周期性结构的声波调控技术研究
0
2017
基于层状周期性结构的声波调控技术研究
0
2017
Acoustic band gaps of the woodpile sonic crystal with the simple cubic lattice
0
2011
周期新型超材料板多阶弯曲波带隙研究
1
2018
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
周期新型超材料板多阶弯曲波带隙研究
1
2018
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
Wave finite element method for waveguides and periodic structures subjected to arbitrary loads
1
2020
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
A wave finite element approach for the analysis of periodic structures with cyclic symmetry in dynamic substructuring
1
2018
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
Vibration band gaps for elastic metamaterial rods using wave finite element method
1
2016
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
Numerical and experimental investigation on broadband wave propagation features in perforated plates
1
2016
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
Vibration isolation design for periodically stiffened shells by the wave finite element method
1
2018
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
Active tuning of vibration and wave propagation in elastic beams with periodically placed piezoelectric actuator/sensor pairs
1
2017
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
On wave propagation in repetitive structures: Two forms of transfer matrix
1
2019
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
一种多频局域共振型声子晶体板的低频带隙与减振特性
1
2016
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
一种多频局域共振型声子晶体板的低频带隙与减振特性
1
2016
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
Flexural wave band gaps in a multi-resonator elastic metamaterial plate using Kirchhoff-Love theory
1
2019
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
Wave propagation in periodic track structures: Band-gap behaviours and formation mechanisms
1
2017
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
Elastic wave propagation characteristics of periodic track structure in high-speed railway
1
2019
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
Band gap property analysis of periodic plate structures under general boundary conditions using spectral-dynamic stiffness method
1
2017
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
一维声子晶体弹性波带隙计算的小波方法
1
2007
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
一维声子晶体弹性波带隙计算的小波方法
1
2007
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
Water-wave propagation through an infinite array of floating structures
1
2013
... 在过去的几十年里, 学者们提出了大量的周期结构带隙计算的数值和解析方法.有限元法[16 -19 ] 作为一种纯数值方法,其在计算复杂周期结构带隙方面表现出强大的能力. 但是,有限元方法的精度依赖于离散单元的网格尺寸, 高精度往往意味着很大的计算成本.且有限元法中构件耦合和端部边界条件的处理过程比较繁琐.后续也有部分学者针对复杂周期结构的带隙计算, 为提高传统有限元法的计算效率,提出了一些新的数值方法, 如波动有限元法[20 -21 ] ,并将其迅速推广到超材料杆[22 ] 、多孔板[23 ] 、周期性加筋壳[24 ] 等结构的带隙计算之中.但是无论从检验数值法的角度, 还是从揭示复杂系统振动机理的角度,解析或半解析方法不可或缺.目前带隙计算的常用解析方法主要有传递矩阵法[25 -26 ] 、平面波展开法[27 -28 ] 等.传递矩阵法对研究一维周期结构的带隙特性非常方便高效,例如带有周期弹簧支撑的轨道结构[29 -30 ] . 对于一维结构,传递矩阵法是一种通用的方法, 但用传递矩阵法难以处理多维以上的结构.平面波展开法是计算一维、二维和三维周期结构带隙的传统方法,但是由于该方法基于对微分方程组的直接求解, 因此,在处理一些具有复杂边界条件的周期性组合结构时存在一定的困难. 此外,也有学者提出了一些新的周期结构带隙计算方法,诸如谱动刚度法[31 ] 、小波法[32 ] 、渐进匹配展开法[33 ] 等,这些方法虽各有特点, 但处理一些复杂周期结构模型(如周期性组合结构)并不适用.因此, 有必要发展分析复杂周期结构振动带隙特性的解析或半解析方法. ...
Three-dimensional vibration analysis of beams with axial functionally graded materials and variable thickness
1
2019
... 能量法具有将求解微分方程边值问题转化为泛函极值问题的优点,这有利于复杂结构系统耦合问题的求解,因而传统能量法(如Rayleigh-Ritz法[34 -35 ] )被广泛应用于分析一些复杂组合结构的自由振动问题[36 -37 ] ,近年来也被引入周期结构带隙计算中[38 -39 ] .但在利用传统能量法计算周期结构带隙时, 存在如下问题:(1)能量法需要基于Bloch定理构造满足周期性边界的位移场形函数[40 -41 ] ,从数学角度而言, 形函数的周期性重构难度较大,而且不同形函数的构造方式不一定相同; (2)重构以后的位移场形函数包含波数,这会导致涉及形函数的结构的质量和刚度矩阵中含有波数, 在计算带隙时,结构的质量和刚度矩阵需随着波数的变化进行反复计算,随着结构质量和刚度矩阵维度的增大, 或者扫描波数点数的增多,计算成本也会随之增大. 因此, 对于能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作. ...
轴向移动悬臂梁高效动力学建模及频率响应分析
1
2017
... 能量法具有将求解微分方程边值问题转化为泛函极值问题的优点,这有利于复杂结构系统耦合问题的求解,因而传统能量法(如Rayleigh-Ritz法[34 -35 ] )被广泛应用于分析一些复杂组合结构的自由振动问题[36 -37 ] ,近年来也被引入周期结构带隙计算中[38 -39 ] .但在利用传统能量法计算周期结构带隙时, 存在如下问题:(1)能量法需要基于Bloch定理构造满足周期性边界的位移场形函数[40 -41 ] ,从数学角度而言, 形函数的周期性重构难度较大,而且不同形函数的构造方式不一定相同; (2)重构以后的位移场形函数包含波数,这会导致涉及形函数的结构的质量和刚度矩阵中含有波数, 在计算带隙时,结构的质量和刚度矩阵需随着波数的变化进行反复计算,随着结构质量和刚度矩阵维度的增大, 或者扫描波数点数的增多,计算成本也会随之增大. 因此, 对于能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作. ...
轴向移动悬臂梁高效动力学建模及频率响应分析
1
2017
... 能量法具有将求解微分方程边值问题转化为泛函极值问题的优点,这有利于复杂结构系统耦合问题的求解,因而传统能量法(如Rayleigh-Ritz法[34 -35 ] )被广泛应用于分析一些复杂组合结构的自由振动问题[36 -37 ] ,近年来也被引入周期结构带隙计算中[38 -39 ] .但在利用传统能量法计算周期结构带隙时, 存在如下问题:(1)能量法需要基于Bloch定理构造满足周期性边界的位移场形函数[40 -41 ] ,从数学角度而言, 形函数的周期性重构难度较大,而且不同形函数的构造方式不一定相同; (2)重构以后的位移场形函数包含波数,这会导致涉及形函数的结构的质量和刚度矩阵中含有波数, 在计算带隙时,结构的质量和刚度矩阵需随着波数的变化进行反复计算,随着结构质量和刚度矩阵维度的增大, 或者扫描波数点数的增多,计算成本也会随之增大. 因此, 对于能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作. ...
Vibration analysis of ring-stiffened conical-cylindrical-spherical shells based on a modified variational approach
1
2013
... 能量法具有将求解微分方程边值问题转化为泛函极值问题的优点,这有利于复杂结构系统耦合问题的求解,因而传统能量法(如Rayleigh-Ritz法[34 -35 ] )被广泛应用于分析一些复杂组合结构的自由振动问题[36 -37 ] ,近年来也被引入周期结构带隙计算中[38 -39 ] .但在利用传统能量法计算周期结构带隙时, 存在如下问题:(1)能量法需要基于Bloch定理构造满足周期性边界的位移场形函数[40 -41 ] ,从数学角度而言, 形函数的周期性重构难度较大,而且不同形函数的构造方式不一定相同; (2)重构以后的位移场形函数包含波数,这会导致涉及形函数的结构的质量和刚度矩阵中含有波数, 在计算带隙时,结构的质量和刚度矩阵需随着波数的变化进行反复计算,随着结构质量和刚度矩阵维度的增大, 或者扫描波数点数的增多,计算成本也会随之增大. 因此, 对于能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作. ...
A modified variational approach for vibration analysis of ring-stiffened conical-cylindrical shell combinations
1
2013
... 能量法具有将求解微分方程边值问题转化为泛函极值问题的优点,这有利于复杂结构系统耦合问题的求解,因而传统能量法(如Rayleigh-Ritz法[34 -35 ] )被广泛应用于分析一些复杂组合结构的自由振动问题[36 -37 ] ,近年来也被引入周期结构带隙计算中[38 -39 ] .但在利用传统能量法计算周期结构带隙时, 存在如下问题:(1)能量法需要基于Bloch定理构造满足周期性边界的位移场形函数[40 -41 ] ,从数学角度而言, 形函数的周期性重构难度较大,而且不同形函数的构造方式不一定相同; (2)重构以后的位移场形函数包含波数,这会导致涉及形函数的结构的质量和刚度矩阵中含有波数, 在计算带隙时,结构的质量和刚度矩阵需随着波数的变化进行反复计算,随着结构质量和刚度矩阵维度的增大, 或者扫描波数点数的增多,计算成本也会随之增大. 因此, 对于能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作. ...
Multi-flexural band gaps in an Euler-Bernoulli beam with lateral local resonators
1
2016
... 能量法具有将求解微分方程边值问题转化为泛函极值问题的优点,这有利于复杂结构系统耦合问题的求解,因而传统能量法(如Rayleigh-Ritz法[34 -35 ] )被广泛应用于分析一些复杂组合结构的自由振动问题[36 -37 ] ,近年来也被引入周期结构带隙计算中[38 -39 ] .但在利用传统能量法计算周期结构带隙时, 存在如下问题:(1)能量法需要基于Bloch定理构造满足周期性边界的位移场形函数[40 -41 ] ,从数学角度而言, 形函数的周期性重构难度较大,而且不同形函数的构造方式不一定相同; (2)重构以后的位移场形函数包含波数,这会导致涉及形函数的结构的质量和刚度矩阵中含有波数, 在计算带隙时,结构的质量和刚度矩阵需随着波数的变化进行反复计算,随着结构质量和刚度矩阵维度的增大, 或者扫描波数点数的增多,计算成本也会随之增大. 因此, 对于能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作. ...
Reaction force and power flow analysis of an acoustic metamaterial beam with multi-band gaps
1
2020
... 能量法具有将求解微分方程边值问题转化为泛函极值问题的优点,这有利于复杂结构系统耦合问题的求解,因而传统能量法(如Rayleigh-Ritz法[34 -35 ] )被广泛应用于分析一些复杂组合结构的自由振动问题[36 -37 ] ,近年来也被引入周期结构带隙计算中[38 -39 ] .但在利用传统能量法计算周期结构带隙时, 存在如下问题:(1)能量法需要基于Bloch定理构造满足周期性边界的位移场形函数[40 -41 ] ,从数学角度而言, 形函数的周期性重构难度较大,而且不同形函数的构造方式不一定相同; (2)重构以后的位移场形函数包含波数,这会导致涉及形函数的结构的质量和刚度矩阵中含有波数, 在计算带隙时,结构的质量和刚度矩阵需随着波数的变化进行反复计算,随着结构质量和刚度矩阵维度的增大, 或者扫描波数点数的增多,计算成本也会随之增大. 因此, 对于能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作. ...
Broadband locally resonant band gaps in periodic beam structures with embedded acoustic black holes
1
2017
... 能量法具有将求解微分方程边值问题转化为泛函极值问题的优点,这有利于复杂结构系统耦合问题的求解,因而传统能量法(如Rayleigh-Ritz法[34 -35 ] )被广泛应用于分析一些复杂组合结构的自由振动问题[36 -37 ] ,近年来也被引入周期结构带隙计算中[38 -39 ] .但在利用传统能量法计算周期结构带隙时, 存在如下问题:(1)能量法需要基于Bloch定理构造满足周期性边界的位移场形函数[40 -41 ] ,从数学角度而言, 形函数的周期性重构难度较大,而且不同形函数的构造方式不一定相同; (2)重构以后的位移场形函数包含波数,这会导致涉及形函数的结构的质量和刚度矩阵中含有波数, 在计算带隙时,结构的质量和刚度矩阵需随着波数的变化进行反复计算,随着结构质量和刚度矩阵维度的增大, 或者扫描波数点数的增多,计算成本也会随之增大. 因此, 对于能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作. ...
A semi-analytical method for characterizing vibrations in circular beams with embedded acoustic black holes
2
2020
... 能量法具有将求解微分方程边值问题转化为泛函极值问题的优点,这有利于复杂结构系统耦合问题的求解,因而传统能量法(如Rayleigh-Ritz法[34 -35 ] )被广泛应用于分析一些复杂组合结构的自由振动问题[36 -37 ] ,近年来也被引入周期结构带隙计算中[38 -39 ] .但在利用传统能量法计算周期结构带隙时, 存在如下问题:(1)能量法需要基于Bloch定理构造满足周期性边界的位移场形函数[40 -41 ] ,从数学角度而言, 形函数的周期性重构难度较大,而且不同形函数的构造方式不一定相同; (2)重构以后的位移场形函数包含波数,这会导致涉及形函数的结构的质量和刚度矩阵中含有波数, 在计算带隙时,结构的质量和刚度矩阵需随着波数的变化进行反复计算,随着结构质量和刚度矩阵维度的增大, 或者扫描波数点数的增多,计算成本也会随之增大. 因此, 对于能量法而言,以较低的计算成本对复杂周期结构的带隙进行精确计算是一项具有挑战性的工作. ...
... 图5 给出了本文方法计算得到的周期开口板弯曲振动频散曲线, 为了对比,同时给出了利用文献[41 ]中重构位移形函数的方法计算得到的结果.其中两种方法采用的形函数均为高斯函数, 板的几何和材料参数一致,伸缩因子、平移因子取值以及扫描波数均保持一致. ...
A unified solution for the vibration analysis of FGM doubly-curved shells of revolution with arbitrary boundary conditions
1
2016
... 鉴于此, 本文对传统能量法进行了改进,提出了一种利用人工弹簧[42 -44 ] 来模拟周期边界条件的方法,将形函数与周期边界条件分离, 无需构造满足周期边界的形函数,这样可解决传统能量法中构造满足周期边界条件的形函数的困难问题; 同时,利用人工弹簧模拟周期边界条件, 将周期边界约束转化为人工弹簧的弹性势能,这样只有包含波数的周期边界弹性势能矩阵需参与随波数扫描的循环计算,其他矩阵只需计算一次, 因而能提高传统能量法计算带隙的效率. 此外,人工弹簧模型使用灵活、便捷,可进一步拓展到更为复杂的周期性组合结构的带隙分析中. ...
Vibration analysis of circular cylindrical double-shell structures under general coupling and end boundary conditions
1
2016
... 图7 中$xOy$坐标系$y=c$处边界为正对称边界, 可认为板边界上转角为0, 位移自由,利用人工弹簧模拟正对称边界条件, 线弹簧和转角弹簧刚度分别表示为$k_{ts}$和$k_{rs} $, 刚度取值参考文献[43 ].在${x}'{O}'y$坐标系上${x}'=0$和${x}'=l+s_{0} $处为Floquet周期性边界,由于CRSTIII型轨道板结构是不连续的, 相邻轨道板之间存在板缝,因此轨道板没有Floquet周期性边界. 整体结构的边界势能可表示为 ...
Quasi-3D solutions for the vibration of solid and hollow slender structures with general boundary conditions
1
2018
... 鉴于此, 本文对传统能量法进行了改进,提出了一种利用人工弹簧[42 -44 ] 来模拟周期边界条件的方法,将形函数与周期边界条件分离, 无需构造满足周期边界的形函数,这样可解决传统能量法中构造满足周期边界条件的形函数的困难问题; 同时,利用人工弹簧模拟周期边界条件, 将周期边界约束转化为人工弹簧的弹性势能,这样只有包含波数的周期边界弹性势能矩阵需参与随波数扫描的循环计算,其他矩阵只需计算一次, 因而能提高传统能量法计算带隙的效率. 此外,人工弹簧模型使用灵活、便捷,可进一步拓展到更为复杂的周期性组合结构的带隙分析中. ...
Gaussian expansion for the vibration analysis of plates with multiple acoustic black holes indentations
2
2019
... 由于开口板出现了局部厚度突变,若选用改进傅里叶级数、切比雪夫级数等(适用于描述连续性较好的结构)作为位移形函数可能需要多项级数来进行拟合以达到精度要求,进而降低计算效率. 因此,本文选取具有局域化特性的高斯小波函数[45 -46 ] 为位移形函数,以确保能够准确捕捉到厚度变化区域的波动特征, 即对于式(2)定义 ...
... 式中, ceil(*)表示最接近并大于*的整数, floor(*)表示最接近并小于*的整数.关于高斯小波函数的详细介绍可以参考文献[45 ,46 ]. 定义一个厚度函数$h\left({x,y} \right)$满足 ...
Passive constrained viscoelastic layers to improve the efficiency of truncated acoustic black holes in beams
2
2018
... 由于开口板出现了局部厚度突变,若选用改进傅里叶级数、切比雪夫级数等(适用于描述连续性较好的结构)作为位移形函数可能需要多项级数来进行拟合以达到精度要求,进而降低计算效率. 因此,本文选取具有局域化特性的高斯小波函数[45 -46 ] 为位移形函数,以确保能够准确捕捉到厚度变化区域的波动特征, 即对于式(2)定义 ...
... 式中, ceil(*)表示最接近并大于*的整数, floor(*)表示最接近并小于*的整数.关于高斯小波函数的详细介绍可以参考文献[45 ,46 ]. 定义一个厚度函数$h\left({x,y} \right)$满足 ...