引言
脆性材料构成的细长杆(rod)在准静态载荷作用下发生变形, 一旦出现突然断裂, 会激发出一系列卸载应力波, 在卸载波的作用下, 脆性杆在特定时刻、特定位置可能发生二次断裂, 伴随不同大小的碎片产生.
脆性杆因为突发断裂而产生的二次断裂现象, 最早见于Miklowitz[1 ] 对玻璃杆进行拉伸实验观察到的二次断裂的报道; 随后, Phillips[2 ] , Kolsky[3 ] 和Kinra[4 ] 对因拉伸断裂而激发出的卸载拉伸应力波、以及因此产生的后续断裂等现象进行了研究. 接着, Bodner[5 ] , Kinra等[6 ] , Schindler等[7 ] 把关注重点从拉伸断裂转移到弯曲断裂, 对因弯曲断裂而激发出的卸载弯曲应力波、及其因此产生的后续断裂等现象进行了研究. 特别是Schindler和Kolsky[7 ] 对方形截面的聚酯纤维棒进行纯弯曲加载, 通过粘贴在试件表面的应变片测量到因弯曲断裂而激发出的卸载弯曲应力波, 观察到因此导致的二次断裂现象, 并基于欧拉伯努利梁理论(Euler-Bernoulli beamtheory, 简称"欧拉梁")给出了一个关于卸载弯曲应力波的解析解.
近年来, 脆性梁在弯曲加载下的多次断裂现象再次得到关注, Audoly等[8 ] 、Heisser等[9 ] 对意大利面条的雪崩式断裂进行了一系列的理论和实验研究. Audoly等[8 ] 使用欧拉梁理论, 给出了卸载弯曲波的自相似解, 通过这些解可以看出, 脆性梁的突然弯曲断裂, 会激发出一系列卸载弯曲波, 这些卸载波会导致梁中局部弯矩超越断裂时刻的整体弯矩(称之为"过冲"), 从而引发后续的二次断裂. Audoly等[8 ] 从理论上阐明了二次断裂的必然性, 但是, 受限于欧拉梁的局限性, 所分析的模型问题缺少特征时间, 因此无法进一步研究二次断裂相关特征参数, 特别是具体的发生时刻和位置. 作者前期工作[10 ] 指出, 脆性梁在纯弯曲作用下的第一次断裂并不是瞬时发生的, 因此断裂位置的弯矩变化不是突然卸载, 而是需要经历一个降时; 考虑卸载时间相关, 给出了基于欧拉梁的一个带有特征时间的卸载弯曲波的解析解, 并因此预测了依赖于特征时间的二次断裂的碎片尺寸.
以上分析的模型问题都基于简单的欧拉梁, 根据此理论, 弹性弯曲波的行波波速与其波长成反比[11 ] , 如果波长无限小, 则波速无限大. 换言之, 一个瞬时变化的弯曲脉冲将以无限大速度传播, 这显然不符合物理原理. 事实上, 欧拉梁只适用于行波波长远大于梁横向特征尺寸的情况, 如果这两个尺寸能够相比较, 梁的旋转惯性就不能被忽略, Rayleigh[12 ] 最早提出了关于旋转惯性的修正. Timoshenko[13 ] 进一步指出, 当行波波长能够与梁横向特征尺寸相比较时, 剪力导致的剪切变形对梁的整体横向位移有贡献, 因此关于切应力效应的修正与关于旋转惯性的修正同样重要;同时考虑切应力效应和旋转惯性, Timoshenko[13 ] 给出了形式复杂但更加合理的控制方程.
综上讨论, 在欧拉梁理论框架下, 一旦弹性梁突然断裂, 所激发的卸载弯曲波将瞬间影响整个梁, 相应的半无限长梁问题只能得到自相似解, 虽然说明了局部曲率高于断裂时刻曲率的"过冲"现象, 但无法进一步研究二次断裂相关特征参数. 而复杂梁理论, 包括考虑了旋转惯性的瑞利梁理论(Rayleigh beam theory, 简称为"瑞利梁")以及同时考虑旋转惯性和切应力效应的铁木辛柯梁理论(Timoshenkobeam theory, 简称为"铁木辛柯梁"), 其弯曲应力波波速为有限值, 因此本质上具有一个特征时间, 有可能给出发生二次断裂的时刻和位置的预测. 本文在复杂梁理论框架下研究脆性梁突然弯曲断裂所产生的卸载弯曲应力波传播问题, 采用拉普拉斯变换方法得到卸载弯曲波传播的响应解, 通过计算事例观察其传播特征, 并给出了二次断裂碎片尺寸的数值预测.
1 控制方程和初边值条件
1.1 铁木辛柯梁和控制方程
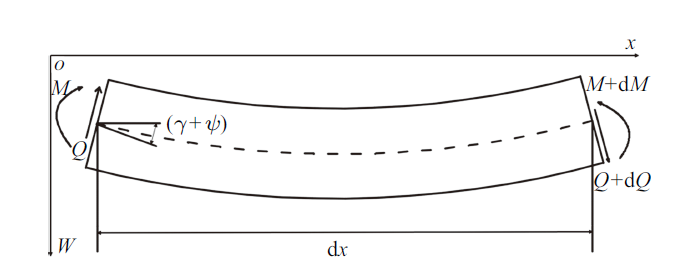
在铁木辛柯梁的分析模型中, 如图1 所示, 独立变量为梁轴向坐标$x$和时间$t$, 所有未知量均为$x$, $t$的函数; 同时考虑旋转惯性和切应力效应, 梁任意截面发生的横向位移(挠度) $w$被区分为两个分量, 即弯矩作用下的分量$w_{M}$和剪力导致的剪切应变作用下的分量$w_{Q}$. 共定义10个未知函数, 包括3个位移类函数: 总横向位移$w$、弯曲变形对应的横向位移$w_{M}$和剪切变形对应的横向位移$w_{Q}$;2个力函数: 弯矩$M$和剪力$Q$; 2个速度函数: 横向位移速度$v$和横截面转动角速度$\omega $; 以及3个应变类函数: 曲率$\kappa$、剪力导致的横截面转角$\gamma $和弯矩导致的转角$\psi $.
图1
图1
铁木辛柯梁微元示意图
Fig.1
Schematic of a micro element in a Timoshenko beam
经过一系列动力学、运动学和几何关系分析, 可以得到铁木辛柯梁的10个基本方程
(1a) $\frac{\partial Q}{\partial x}=\rho A\frac{\partial v}{\partial t}$
(1b) $Q-\frac{\partial M}{\partial x}=\rho I\frac{\partial \omega }{\partial t}$
(1c) $w=w_{M}+w_{Q}$
(1d) $\kappa =-\frac{\partial ^{2}w_{M}}{\partial x^{2}}$
(1e) $\omega =\frac{\partial ^{2}w_{M}}{\partial t\partial x}$
(1f) $v=\frac{\partial w}{\partial t}$
(1g) $\gamma =\frac{\partial w_{Q}}{\partial x}$
(1h) $\psi =\frac{\partial w_{M}}{\partial x}$
(1i) $M=EI\kappa$
(1j) $Q=GAk\gamma$
式(1a)和式(1b)为动力学方程, 式(1c) $\sim\!$式(1h)为运动学方程, 式(1i)和式(1j)为本构方程. 以上10个方程中涉及的材料或结构常数为: 体积密度$\rho $、横截面面积$A$、横截面对中性轴的惯性矩$I$、材料弹性模量$E$和剪切模量$G$.
由于铁木辛柯梁的横截面发生了翘曲变形, 其横截面上的剪切应变并非均匀分布, 因此剪力导致的横截面转角$\gamma $并非由平均剪切应变导致;在横截面上的总剪切力$Q$与剪切转角$\gamma $之间通过式(1j)联系, 其中$k$是与梁横截面形状和泊松比$\nu $有关的系数, 被称之为铁木辛柯剪切系数[14 ] . 许多科学家通过复杂的弹性力学分析尝试给出其精确数值, 如Timoshenko[15 , 20 ] , Mindlin等[16 ] , Cowper[17 ] , Stephen[18 ] , Hutchinson[19 ] 等. 根据Cowper[17 ] 的研究, 如果梁横截面是方形, $k={10\left( 1+\nu \right)}/({12+11\nu })$, 如果梁横截面是圆形, $k={6\left( 1+\nu \right)}/({7+6\nu })$, 因此对于大多数常见材料, $k$的取值范围为${5}/{6}\sim {10}/{9}$.
把式(1c)和式(1j)代入式(1a)和式(1b), 可以把控制方程组写成简单的、仅包含两个未知函数$w$和$\psi $的形式
(2) $GAk\left( \frac{\partial ^{2}w}{\partial x^{2}}-\frac{\partial \psi }{\partial x} \right)=\rho A\frac{\partial ^{2}w}{\partial t^{2}}$
(3) $GAk\left( \frac{\partial w}{\partial x}-\psi \right)+EI\frac{\partial ^{2}\psi }{\partial x^{2}}=\rho I\frac{\partial ^{2}\psi }{\partial t^{2}}$
归并式(2)和式(3), 并做适当的参数定义后, 可以得到仅涉及1个未知函数$w$的4阶控制方程
(4) $\frac{\partial ^{4}w}{\partial x^{4}}-\left( \frac{1}{C_{0}^{2}}+\frac{1}{C_{Q}^{2}} \right)\frac{\partial ^{4}w}{\partial x^{2}\partial t^{2}}+ \frac{1}{C_{0}^{2}C_{Q}^{2}}\frac{\partial ^{4}w}{\partial t^{4}}+\frac{1}{C_{0}^{2}R^{2}}\frac{\partial ^{2}w}{\partial t^{2}}=0$
式中, $C_{0}=\sqrt {E/\rho } $ 表示材料的纵向弹性波速度, $C_{Q}=\sqrt{Gk/\rho } $ 表示$\sqrt k $倍的横向弹性剪切波速度, 或可称之为等效剪切波速, $R=\sqrt {I/A} $ 表示横截面对中性轴的回转半径. 对于对半径为$r$的圆形截面梁来说, $R=r/2$, 而对于边长为$l$的正方形截面梁来说, $R=l/(2\sqrt 3 )$.
1.2 瑞利梁和欧拉梁的控制方程
在铁木辛柯梁的控制方程(4)中$-({1}/{C_{0}^{2}})$ $\cdot$ $[{\partial ^{4}w}/({\partial x^{2}\partial t^{2}})]$为旋转惯性的修正, $-({1}/{C_{Q}^{2}})[{\partial ^{4}w}/(\partial x^{2}\cdot \partial t^{2})]+({1}/{C_{0}^{2}C_{Q}^{2}})[{\partial ^{4}w}/({\partial t^{4}})]$为切应力效应的修正. 如果仅考虑旋转惯性修正而忽略切应力修正(相当于假设材料的剪切刚度非常大, 即$C_{Q}$趋于无限大), 则式(4)退化为瑞利梁的控制方程
(5) $\frac{\partial ^{4}w}{\partial x^{4}}-\frac{1}{C_{0}^{2}}\frac{\partial ^{4}w}{\partial x^{2}\partial t^{2}}+\frac{1}{C_{0}^{2}R^{2}}\frac{\partial ^{2}w}{\partial t^{2}}=0$
如果既不考虑切应力的修正, 也不考虑旋转惯性的修正, 则式(5)中第二项可以忽略, 式(5)进一步的退化为欧拉梁的控制方程
(6) $\frac{\partial ^{4}w}{\partial x^{4}}+\frac{1}{C_{0}^{2}R^{2}}\frac{\partial ^{2}w}{\partial t^{2}}=0$
1.3 不同梁理论的行波解和弥散关系
将简单行波解 $w\left(x, t \right)=w_{0}exp\left[i{{2\pi \left( x-Ct \right)}/\varLambda } \right]$ (其中$C$为波速, 取正数; $\varLambda $为波长)代入欧拉梁控制方程(6), 可得
(7) $C=C_{0}\left( {{2\pi R}/\varLambda } \right)$
即行波波速反比于波长, 因此欧拉梁中的弯曲波具有强烈的弥散效应, 且波长趋于0的短波传播速度无限大.
(8) $C=C_{0}\left( {1\Bigg/\sqrt {1+\frac{\varLambda ^{2}}{4\pi^{2}R^{2}}} }\right)$
因此, 与欧拉梁不同, 在瑞利梁模型中, 波长趋于0的短波的极限波速为纵向弹性波速$C_{0}$.
将行波解代入铁木辛柯梁控制方程(4), 可以得到一个较复杂的弥散关系
${K\left( \frac{C}{C_{0}} \right)}^{4}-\left( 1+K+\frac{\varLambda ^{2}}{4\pi^{2}R^{2}} \right)\left( \frac{C}{C_{0}} \right)^{2}+1=0$
式中$K=C_{0}^{2}/C_{Q}^{2}=E/(Gk)=2\left( 1+\nu \right)/k$.
对于任何给定波长$\varLambda $, 由上式可以解出绝对值不同的两个行波波速$C$, 分别为
(9) $C=\frac{C_{0}}{\sqrt {2K}}\Bigg\{\left[ K+1+\left( \frac{\varLambda }{2\pi R} \right)^{2} \right]\pm \bigg[\left( \frac{\varLambda }{2\pi R} \right)^{4}+ \\ 2\left( K+1 \right)\left( \frac{\varLambda }{2\pi R} \right)^{2}+\left( K-1 \right)^{2}\bigg]^{1/2} \Bigg\}^{1/2}$
这意味着有两个以不同绝对值的速度传播的行波与$\varLambda $对应. 特别是, 对于波长趋于0的短波, 行波波速$C=C_{0}$或$C={C_{0}/\sqrt K }=C_{Q}$, 从物理上分析, 任何瞬时变化的扰动在梁中将激发出两种波动现象, 分别以弹性杆波的速度$C_{0}$和等效剪切波速$C_{Q}$传播.
1.4 无量纲化替换
注意到在铁木辛柯梁理论框架中存在特征尺度和特征速度, 可以对基本方程进行无量纲化, 以便计算和分析过程更加简洁. 选取基本特征参数如下: 特征长度$R$、特征时间$R/C_{0}$、特征速度$C_{0}$、特征应力$E$、特征弯矩$ER^{3}$、特征剪力$ER^{2}$. 无量纲化的参数由原参数除以特征参数得到
$ \bar{w}=\dfrac{w}{R}, \ \ \bar{x}=\dfrac{x}{R}, \ \ \bar{t}=\dfrac{tC_{0}}{R}, \ \ \bar{A}=\dfrac{A}{R^{2}}$
$\bar{I}=\dfrac{I}{R^{4}}, \ \ \bar{M}=\dfrac{M}{ER^{3}}, \ \ \bar{Q}=\dfrac{Q}{ER^{2}} $
因此, 铁木辛柯梁的控制方程组(2)和(3)可以无量纲表示为仅包含$\bar{w}$和$\bar{\psi}$的形式
(10) $\frac{\partial ^{2}\bar{w}}{\partial \bar{t}^{2}}-\frac{1}{K}\left( \frac{\partial ^{2}\bar{w}}{\partial \bar{x}^{2}}-\frac{\partial \bar{\psi }}{\partial \bar{x}} \right)=0$
(11) $\frac{\partial ^{2}\bar{\psi }}{\partial \bar{x}^{2}}+\frac{1}{K}\left( \frac{\partial \bar{w}}{\partial \bar{x}}-\bar{\psi } \right)-\frac{\partial ^{2}\bar{\psi }}{\partial \bar{t}^{2}}=0$
由式(1i)和式(1j)可得到仅包含$\bar{w}$和$\bar{\psi }$的无量纲化的弯矩$\bar{M}$和切应力$\bar{Q}$
(12) $\bar{M}=-\bar{A}\frac{\partial \bar{\psi }}{\partial \bar{x}}$
(13) $\bar{Q}=\frac{\bar{A}}{K}\left( \frac{\partial \bar{w}}{\partial \bar{x}}-\bar{\psi } \right)$
同样可以对瑞利梁控制方程(5)和欧拉梁控制方程(6)进行无量纲化, 分别为
(14) $\frac{\partial ^{4}\bar{w}}{\partial \bar{x}^{4}}-\frac{\partial ^{4}\bar{w}}{\partial \bar{x}^{2}\partial \bar{t}^{2}}+\frac{\partial ^{2}\bar{w}}{\partial t^{2}}=0$
(15) $\frac{\partial ^{4}\bar{w}}{\partial \bar{x}^{4}}+\frac{\partial ^{2}\bar{w}}{\partial \bar{t}^{2}}=0$
1.5 受纯弯矩作用梁的突然卸载问题
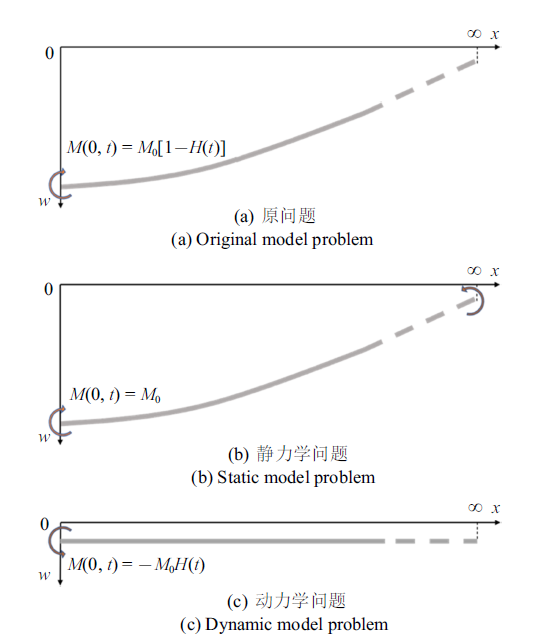
考虑模型问题(原问题)如图2 (a)所示: 一根半无限长的梁, 左端为自由端 $x=0$, 右端为无限远端 $x=\infty $; 在自由端施加了一个幅值为$M_{0}$的恒定弯矩, 在弯矩作用下, 梁发生了均匀弯曲; 在初始时刻 $t=0$, 自由端$x=0$处的弯矩$M_{0}$突然被释放、瞬时卸载到零, 因此激发出一系列的卸载弯曲应力波, 进而导致梁的变形、运动和受力状态的变化.
图2
图2
半无限长梁突然卸载模型问题图示
Fig.2
Schematic of the sudden release model problem of a half-infinite beam
由于整个系统的线性特征, 将上述原问题分解成两部分: (1)静力学问题(图2 (b)): 受恒定弯矩$M_{0}$作用下静止梁的受力和变形问题; (2)动力学问题(图2 (c)): 静止的半无限梁, 在$t=0$时刻, 其自由端$x=0$处突加一个值为$-M_{0}$的弯矩, 分析其变形和受力情况随时间的变化规律. 前者属于静力学问题, 其解很容易通过控制方程组写出: 作为积分初值, 假设$x=0$的变形量均为0, 可以得到静力学解弯矩$\bar{M}_{s}\left( \bar{x}\right)=\bar{M}_{0}$、剪力$\bar{Q}_{s}\left( \bar{x}\right)=0$、转角$\bar{\psi }_{s}\left( \bar{x}\right)=-({\bar{M}_{0}}/{\bar{A}})\bar{x}$、横向位移$\bar{w}_{s}\left(\bar{x} \right)=-({\bar{M}_{0}}/{\bar{A}})\bar{x}^{2}/2$.
动力学问题的解和时间相关, 需要给出初始条件. 对于一个静止梁边界突然承受弯矩作用的问题, 梁的初始条件全部为零, 即
(16) $\bar{w}\left( \bar{x}, 0 \right)=\bar{\psi }\left( \bar{x}, 0 \right)=\bar{M}\left( \bar{x}, 0 \right)=\bar{Q}\left( \bar{x}, 0 \right)=0$
在自由端承受突加弯矩, 自由端的剪力为零, 无量纲化后的边界条件为
(17a) $\bar{M}\left( 0, \bar{t} \right)={-\bar{M}}_{0}H\left( \bar{t} \right)$
(17b) $\bar{Q}\left( 0, \bar{t} \right)=0$
如果求得此问题(称之为突加弯矩问题)的动力学解, 即包括横向位移$\bar{w}\left(\bar{x}, \bar{t} \right)$、弯矩导致转角$\bar{\psi }\left( \bar{x}, \bar{t}\right)$、弯矩$\bar{M}\left( \bar{x}, \bar{t} \right)$和剪力$\bar{Q}\left(\bar{x}, \bar{t} \right)$的各个响应函数, 则原问题中对应的$\bar{w_{1}}$、$\bar{\psi_{1}}$、$\bar{M_{1}}$和$\bar{Q_{1}}$的表达式如下
(18a) $\bar{w}_{1}\left( \bar{x}, \bar{t} \right)=\bar{w}\left( \bar{x}, \bar{t} \right)-\frac{1}{2}\frac{\bar{M}_{0}}{\bar{A}}\bar{x}^{2}$
(18b) $\bar{\psi }_{1}\left( \bar{x}, \bar{t} \right)=\bar{\psi }\left(\bar{x}, \bar{t} \right)-\frac{\bar{M}_{0}}{\bar{A}}\bar{x}$
(18c) $\bar{M}_{1}\left( \bar{x}, \bar{t} \right)=\bar{M}\left( \bar{x}, \bar{t} \right)+\bar{M}_{0}H\left( \bar{t} \right)$
(18d) $\bar{Q}_{1}\left( \bar{x}, \bar{t} \right)=\bar{Q}\left( \bar{x}, \bar{t} \right)$
式中, $H(y)=\left\{\begin{array}{ll}1, & y\geqslant 0\\0, & y<0\\\end{array} \right. $为阶跃函数.
2 拉普拉斯正变换和频域的解析解
2.1 铁木辛柯梁
以下求解铁木辛柯梁的突加弯矩问题, 在考虑所有函数的零值初始条件式(16), 对无量纲化的铁木辛柯梁的控制方程组(7)和(8)进行拉普拉斯变换, 可以得到
(19) $s^{2}\hat{w}-\frac{1}{K}\left( \frac{\partial ^{2}\hat{w}}{\partial \bar{x}^{2}}-\frac{\partial \hat{\psi }}{\partial \bar{x}} \right)=0$
(20) $\frac{\partial ^{2}\hat{\psi }}{\partial \bar{x}^{2}}+\frac{1}{K}\left( \frac{\partial \hat{w}}{\partial \bar{x}}-\hat{\psi } \right)-s^{2}\hat{\psi }=0$
其中, 符号$\hat{\ }$表示时域中的原函数以参数$s$进行拉普拉斯变换, 所得到的同函数在复数频域的像函数: $\hat{f}\left( x, s \right)=\mathcal{L}\left[ f\left(x, t \right), t\to s \right]=\int_0^\infty {f\left( x, t\right)e^{-st}dt} $. 结合式(19)和式(20), 可得横向位移$\bar{w}$在频域的像函数$\hat{w}$的控制方程, 这是一个以复数$s$为参数的对变量$\bar{x}$的4阶常微分方程
(21) $\frac{d^{4}\hat{w}}{d\bar{x}^{4}}-\left( 1+K \right)s^{2}\frac{d^{2}\hat{w}}{d\bar{x}^{2}}+\left( 1+Ks^{2} \right)s^{2}\hat{w}=0$
假设解的形式为: $\hat{w}={C}exp(\lambda \bar{x})$, 代入式(21)可以得到如下的特征方程
$\lambda^{4}-\left( 1+K \right)s^{2}\lambda^{2}+\left( 1+Ks^{2}\right)s^{2}=0$
(22) $\left. \begin{array}{l} \lambda_{1}=-\lambda_{3}=B\sqrt s \sqrt {s+N\sqrt {s^{2}-a^{2}} } \\ \lambda_{2}=-\lambda_{4}=B\sqrt s \sqrt {s-N\sqrt {s^{2}-a^{2}} } \\ \end{array} \right\}$
式中, $B=\sqrt{({K+1})/{2}}$, $N=({K-1})/({K+1})$, $a={2}/({K-1})$. 因此, 铁木辛柯梁中的横向位移$\bar{w}$的像函数可以写为如下形式
$\hat{w}\left( \bar{x}, s \right)=C_{1}\exp \left( -\lambda_{1}\bar{x} \right)+C_{2}\exp \left( -\lambda_{2}\bar{x} \right)+ \\ C_{3}\exp \left( \lambda_{1}\bar{x} \right)+C_{4}\exp \left( \lambda_{2}\bar{x} \right)$
式中, $C_{1}$, $C_{2}$, $C_{3}$, $C_{4}$为待定系数. 梁为半无限长, 对于动力学问题而言在$\bar{x}=\infty $处的横向位移为有限值, 因此$C_{3}=C_{4}=0$, 上式可以简化写为
(23) $\hat{w}\left( \bar{x}, s \right)=C_{1}\exp {\left( -\lambda_{1}\bar{x} \right)+}C_{2}\exp \left( -\lambda_{2}\bar{x} \right)$
同样地, 结合式(19)和式(20)可得$\hat{\psi }$形式的控制方程的像函数, 其像函数解也可以写为如下形式
$\hat{\psi }\left( \bar{x}, s \right)=D_{1}\exp {\left( -\lambda_{1}\bar{x} \right)+}D_{2}\exp \left( -\lambda_{2}\bar{x} \right)$
式中, $D_{1}$, $D_{2}$为待定系数.
注意由于式(19)和式(20)的联立关系, 待定系数$D_{1}$, $D_{2}$和$C_{1}$, $C_{2}$并不独立, 可以根据式(20)得到其之间的关系
$\frac{D_{1}}{C_{1}}=\frac{Ks^{2}-\lambda_{1}^{2}}{\lambda_{1}}$
$\frac{D_{2}}{C_{2}}=\frac{Ks^{2}-\lambda_{2}^{2}}{\lambda_{2}}$
因此, 弯矩导致的转角$\bar{\psi }$的像函数解可以写为如下形式
(24) $\hat{\psi }\left( \bar{x}, s \right)=\frac{Ks^{2}-\lambda_{1}^{2}}{\lambda _{1}}C_{1}\exp \left( -\lambda_{1}\bar{x} \right)+ \frac{Ks^{2}-\lambda _{2}^{2}}{\lambda_{2}}C_{2}\exp \left( -\lambda_{2}\bar{x} \right)$
而把式(23)和式(24)代入式(12)和式(13)可得, 弯矩$\bar{M}$和剪力$\bar{Q}$在频域的像函数解
(25) $\hat{M}\left( \bar{x}, s \right)=\overline A \Big[ \left( Ks^{2}-\lambda _{1}^{2} \right)C_{1}\exp \left( -\lambda_{1}\bar{x} \right)+ \left( Ks^{2}-\lambda_{2}^{2} \right)C_{2}\exp \left( -\lambda_{2}\bar{x} \right) \Big]$
(26) $\hat{Q}\left( \bar{x}, s \right)=-\overline A s^{2}\bigg[ \frac{1}{\lambda _{1}}C_{1}\exp \left( -\lambda_{1}\bar{x} \right)+ \frac{1}{\lambda _{2}}C_{2}\exp \left( -\lambda_{2}\bar{x} \right) \bigg]$
为计算待定系数, 对边界条件(17a)和(17b)进行拉普拉斯变换, 可得频域上的边界条件为
(27a) $\hat{M}\left( 0, s \right)=-\frac{\bar{M}_{0}}{s}$
(27b) $\hat{Q}\left( 0, s \right)=0$
将式(27a)和式(27b)代入式(25)和式(26), 可解得待定系数$C_{1}$, $C_{2}$
$C_{1}=\dfrac{\bar{M}_{0}}{\overline A }\dfrac{\lambda_{1}}{s\left( \lambda _{1}-\lambda_{2} \right)\left( \lambda_{1}^{2}+\lambda_{1}\lambda _{2}+\lambda_{2}^{2}-Ks^{2} \right)}$
$C_{2}=-\dfrac{\bar{M}_{0}}{\overline A }\dfrac{\lambda_{2}}{s\left( \lambda _{1}-\lambda_{2} \right)\left( \lambda_{1}^{2}+\lambda_{1}\lambda _{2}+\lambda_{2}^{2}-Ks^{2} \right)}$
最后, 在频域得到铁木辛柯梁在边界承受突加弯矩时的响应, 列举如下:
(28) $ \begin{align} \hat{w}\left( \bar{x}, s \right)=-\frac{\bar{M}_{0}}{\overline A }\frac{\left[ {-\lambda }_{1}\exp{\left( -\lambda_{1}\bar{x} \right)+}\lambda_{2}\exp \left( -\lambda_{2}\bar{x} \right) \right]}{s\left( \lambda_{1}-\lambda_{2} \right)\left( \lambda _{1}^{2}+\lambda_{1}\lambda_{2}+\lambda_{2}^{2}-Ks^{2} \right)} \end{align} $
(2)弯矩导致转角$\bar{\psi }$的像函数
(29) $\begin{align} \hat{\psi }\left( \bar{x}, s \right)=-\frac{\bar{M}_{0}}{\overline A}\Big[ -\left( Ks^{2}-\lambda_{1}^{2} \right)\exp \left( -\lambda_{1}\bar{x} \right)+ \\ \left( Ks^{2}-\lambda_{2}^{2} \right)\exp \left( -\lambda_{2}\bar{x} \right)\Big]\Big/\Big[s\left( \lambda_{1}-\lambda_{2} \right)\cdot \left( \lambda_{1}^{2}+\lambda_{1}\lambda_{2}+\lambda _{2}^{2}-Ks^{2} \right)\Big]\end{align} $
(30) $\begin{align} \hat{M}\left( \bar{x}, s \right)={-\bar{M}}_{0}\Big[ -\lambda_{1}\left( Ks^{2}-\lambda_{1}^{2} \right)\exp \left( -\lambda_{1}\bar{x} \right)+ \\ \lambda_{2}\left( Ks^{2}-\lambda_{2}^{2} \right)\exp \left( -\lambda_{2}\bar{x} \right)\Big]\Big/\Big[s\left( \lambda_{1}-\lambda_{2} \right)\cdot \\ \left( \lambda_{1}^{2}+\lambda_{1}\lambda_{2}+\lambda _{2}^{2}-Ks^{2} \right)\Big] \end{align} $
(31) $\hat{Q}\left( \bar{x}, s \right)=-\bar{M}_{0}s\frac{ \exp \left( -\lambda_{1}\bar{x} \right)-\exp \left( -\lambda_{2}\bar{x} \right) }{\left( \lambda_{1}-\lambda_{2} \right)\left( \lambda _{1}^{2}+\lambda_{1}\lambda_{2}+\lambda_{2}^{2}-Ks^{2} \right)}$
2.2 瑞利梁
基于同样方法, 使用拉普拉斯变换方法求解瑞利梁的关于横向位移的无量纲化控制方程(14), 以及相应的弯矩和剪力, 在边界条件(27a)和(27b)下的解为
(32) $\hat{w}\left( \bar{x}, s \right)=-\frac{\bar{M}_{0}}{\overline A}\Big[ \left( \lambda_{6}^{2}-s^{2} \right)\exp\left( -\lambda _{5}\bar{x} \right)- \\ \left( \lambda_{5}^{2}-s^{2} \right)\exp \left( -\lambda_{6}\bar{x} \right)\Big]\Big/ \Big[{s\lambda_{5}\left( \lambda _{5}-\lambda_{6} \right)\left( \lambda_{5}\lambda_{6}+s^{2} \right)}\Big]$
(33) $\hat{M}\left( \bar{x}, s \right)=\bar{M}_{0}\Big[ \lambda _{5}^{2}\left( \lambda_{6}^{2}-s^{2} \right)\exp\left( -\lambda_{5}\bar{x} \right)- \\ \lambda_{6}^{2}\left( \lambda_{5}^{2}-s^{2} \right)\exp \left( -\lambda_{6}\bar{x} \right) \Big]\Big/ \Big[s\lambda_{5}\left( \lambda _{5}-\lambda_{6} \right)\left( \lambda_{5}\lambda_{6}+s^{2} \right)\Big]$
(34) $\hat{Q}\left( \bar{x}, s \right)=-\bar{M}_{0}\Big\{\left( \lambda _{5}^{2}-s^{2} \right)\left( \lambda_{6}^{2}-s^{2} \right)\Big[ \lambda _{5}\exp\left( -\lambda_{5}\bar{x} \right)- \\ \lambda_{6}\exp \left( -\lambda_{6}\bar{x} \right) \Big]\Big\}\Big/\Big[s\lambda_{5}\left( \lambda _{5}-\lambda_{6} \right)\left( \lambda_{5}\lambda_{6}-s^{2} \right)\Big]$
$\lambda_{5}=\sqrt{\dfrac{s}{2}}\sqrt{s-\sqrt{s^{2}-4}}$
$\lambda_{6}=\sqrt{\dfrac{s}{2}}\sqrt{s+\sqrt{s^{2}-4}}$
2.3 欧拉梁
进一步也可以求解欧拉梁的控制方程(15), 在边界条件(27a)和(27b)下的解分别如下
(35) $\hat{w}(\bar{x}, s)=-\frac{\bar{M}_{0}}{\overline A s^{2}}exp\left( -x\sqrt{\frac{s}{2}} \right)\cdot \left[cos\left( x\sqrt{\frac{s}{2}} \right)-sin\left( x\sqrt{\frac{s}{2}} \right) \right]$
(36) $\hat{M}\left( \bar{x}, s \right)=-\frac{\bar{M}_{0}}{s}exp\left( -x\sqrt{\frac{s}{2}} \right)\cdot \\ \left[ sin\left( x\sqrt{\frac{s}{2}} \right)+cos\left( x\sqrt{\frac{s}{2}} \right) \right]$
(37) $\hat{Q}\left( \bar{x}, s \right)=-\frac{\bar{M}_{0}\sqrt 2 }{\sqrt s }exp\left( -x\sqrt{\frac{s}{2}} \right)sin\left( x\sqrt{\frac{s}{2}} \right)$
3 拉普拉斯反变换和时域求解
为获得梁的动力学响应, 需要对上述得到的频域上的像函数解进行拉普拉斯反变换
$f\left( x, t \right)=\mathcal{L}^{-1}\left[ \hat{f}\left( x, s \right), s\to t \right]=\frac{1}{2\pi i}\int_{\sigma -i\infty }^{\sigma +i\infty } {\hat{f}\left( x, s \right)e^{st}ds}$
其中, 后一个等式为Bromwich积分, $\sigma$为像函数在复变数$s$的右侧解析区域的某个实数值, 再利用式(18a) $\sim\!$式(18d), 可以得到一个承受恒定弯矩作用的梁端部突然卸载后的响应解.
3.1 欧拉梁的解析解
对于欧拉梁的像函数(35) $\sim$ (37), 参照文献[7 -8 , 10 ]可以对原函数进行解析反变换, 代入式(18a) $\sim\!$式(18d), 最后得到时间域的解析解
(38) $\bar{w_1}\left(\bar{x}, \bar{t}\right)=\frac{\bar{M}_{0}}{\overline A}\Bigg[\bar{t}-\bar{x}\sqrt{\frac{2\bar{t}}{\pi }} \cos \left( \frac{\bar{x}^{2}}{4\bar{t}} \right)-2\bar{t}{C}\left( \frac{1}{\sqrt {2\pi } }\frac{\bar{x}}{\sqrt{\bar{t}} } \right)- \\ \bar{x}^{2}{S}\left( \frac{1}{\sqrt{{2\pi }} }\frac{\bar{x}}{\sqrt{\bar{t}} } \right)-\frac{1}{2}\bar{x}^{2} \Bigg]$
(39) $\bar{M_{1}}\left( \bar{x}, \bar{t} \right)=2\bar{M}_{0}{S}\left( \frac{1}{\sqrt {2\pi } }\frac{\bar{x}}{\sqrt{\bar{t}} } \right)$
(40) $\bar{Q_{1}}\left( \bar{x}, \bar{t} \right)=\bar{M}_{0}\sqrt{\frac{2}{\pi \bar{t}}}\sin\left( \frac{\bar{x}^{2}}{4\bar{t}} \right)$
式中, ${S}\left( y \right)=\int_0^y {sin\left({\pi z^{2}}/{2} \right)dz}$, ${C}\left( y\right)=\int_0^y {cos\left( {\pi z^{2}}/{2} \right)dz}$ 分别为菲涅尔正弦积分函数和菲涅尔余弦积分函数.
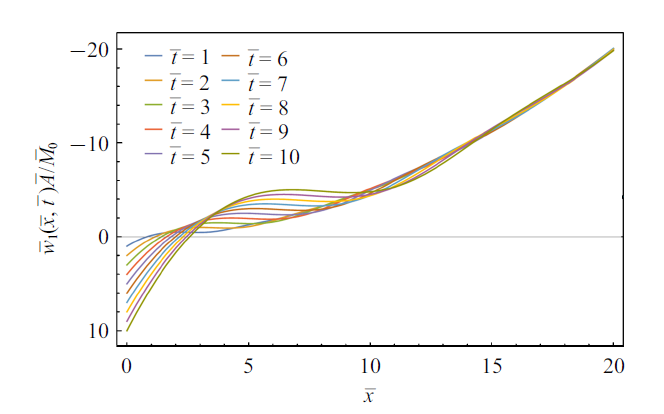
图3 根据解析解(38)绘出欧拉梁突然卸载后的变形情况. 在$\bar{t}=0$时刻, 梁的弯曲形状为$\bar{w}_{s}\left( \bar{x} \right)=-({\bar{M}_{0}}/{\bar{A}})\bar{x}^{2}/2$ (静力学解, 以向下为正); 在其他时刻, 梁的变形为静力学解叠加动力学变形响应. 为凸显梁的动力学变形, 图3 将静力学解缩小到1/10, 下同. 一旦边界突然卸载, 所激发的应力波导致梁的挠度发生明显变化, $\bar{x}=0$的自由端向下方回弹, $\bar{x}>0$的各个位置也发生相应的挠度变化.
图3
图3
欧拉梁中的横向位移(挠度)的变形特征
Fig.3
Deformation characteristics of lateral deflection in an Euler-Bernoulli beam
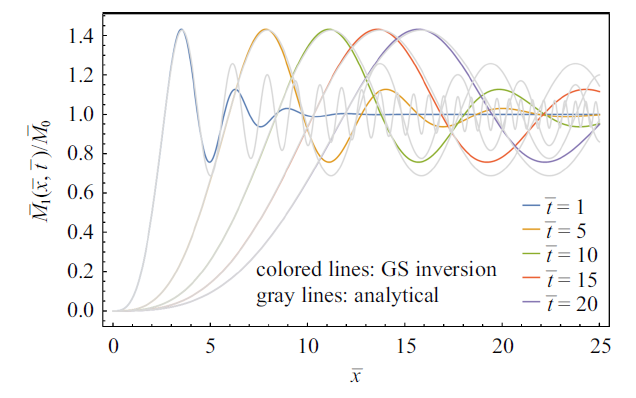
注意在式(38) $\sim\!$式(40)中, 独立变量$\left( x, t \right)$总以${x/\sqrt t }$的形式出现, 即未知函数是${x/\sqrt t}$的单变量函数, 该解反映了半无限长欧拉梁在突然卸载时, 其响应的自相似特征. 以解式(39)为例, 不同时刻弯矩$\bar{M}_{1}\left( \bar{x}, \bar{t}\right)$在梁中的分布曲线如图4 中灰线所示, 这些曲线都是相似的, 具有峰值$1.43\bar{M}_{0}$, 即应力波激发产生的弯矩峰值超过初始弯矩的43%, 反映了弯矩的"过冲"; 随着传播时间$\bar{t}$的延长, $\bar{M}_{1}$ - $\bar{x}$的分布曲线逐渐散开; 如果$\bar{t}\to 0$, 则$\bar{M}_{1}$第一个峰值(过冲)的位置无限接近于自由端.
图4
图4
欧拉梁的卸载应力波对应弯矩分布图: 解析解和GS数值反变换解
Fig.4
Bending moment profiles in a Euler-Bernoulli beam, comparation between the analytical solution and the GS numerical inversion solution
3.2 拉普拉斯数值反变换
复杂梁理论下的像函数式(28)$\sim\!$式(31), 式(32) $\sim\!$ 式(34)非常复杂, 很难直接通过拉普拉斯反变换得到原函数的解析解. 本文中使用一种数值反变换方法, 即Gaver-Stehfest法(简称为GS法), 进行计算求解.
首先检验GS法的准确性. 利用GS法来数值反变换式(36)的欧拉梁中的弯矩的像函数, 并与解析解式(39)进行比较, 数值反变换的解如图4 所示. 与解析解对比, 可以看出, GS数值反变换的结果基本接近解析解结果: 在不同时刻, GS法结果在第一个波峰及之前的数值结果与解析解基本一致, 但在后期表现出一定的分散性. 对于我们的问题, 关注重点是自由端初始弯矩的突然释放所激发出的卸载弯曲波, 特别是卸载波峰值发生的时刻和距离, 即图4 中第一个波峰所处阶段, 而在这一阶段, GS法的结果能够较好地反应出真实结果(解析解), 因此, 使用数值反拉普拉斯变换的GS算法求解我们的模型问题是可行的.
根据上面讨论, 使用GS算法对铁木辛柯梁中的弯矩式(30)、横向位移式(28)和剪力式(31)的像函数进行数值反拉普拉斯变换, 进一步代入式(18a) $\sim\!$式(18d), 可以得到预弯曲的铁木辛柯梁突然卸载所激发的卸载弯曲波的响应解.
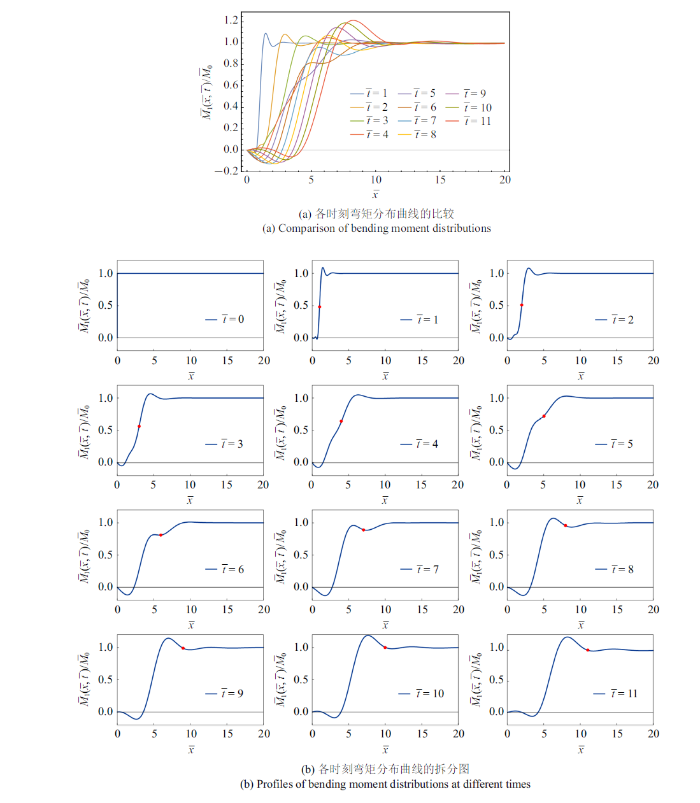
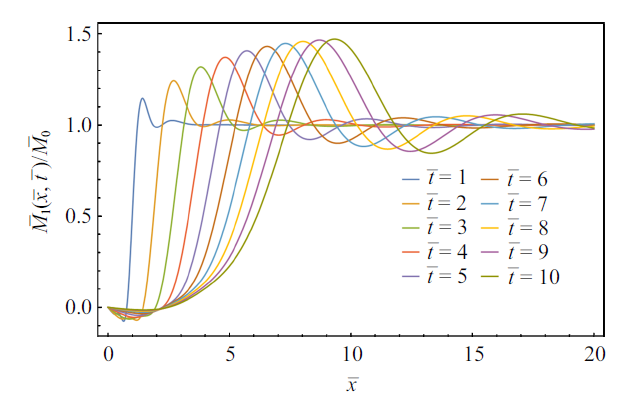
图5 展示了半无限长铁木辛柯梁在自由端初始弯矩突然释放、瞬时卸载为零值后, 在较早的时刻($\bar{t}=0\sim11$)梁中激发出的弯矩形式的卸载弯曲波的波形图, 其中图5 (a)在一张图中比较了各个时刻的弯矩分布曲线, 图5 (b)为各个时刻拆分的弯矩分布图. 首先可以看到铁木辛柯梁中卸载弯曲波传播的局部化效应: 在自由端$\bar{x}=0$处, 弯矩值始终是零值, 符合自由端初始弯矩突降为零的边界条件;而离自由端较远的位置并没有受到自由端卸载的影响, 其弯矩值仍保持初始弯矩值. 定性而言, 铁木辛柯梁中弯曲波的传播速度为有限值, 与欧拉梁不一样;图5 (b)中红点标志以$C_{0}$速度传播的瞬时脉冲在不同时刻到达的位置, 可见, 定量而言, 数值反变换得到的弯矩扰动的近似解的传播速度与$C_{0}$接近. 另一方面, 突然卸载激发出来的卸载波表现出了一定的震荡和杂乱、特别在早期时刻, 这是由于自由端的初始弯矩突降为零的奇异性所导致的.
图5
图5
卸载后较早时刻的铁木辛柯梁中的弯曲卸载波
Fig.5
Unloading bending moment waves in a Timoshenko beam at early moments
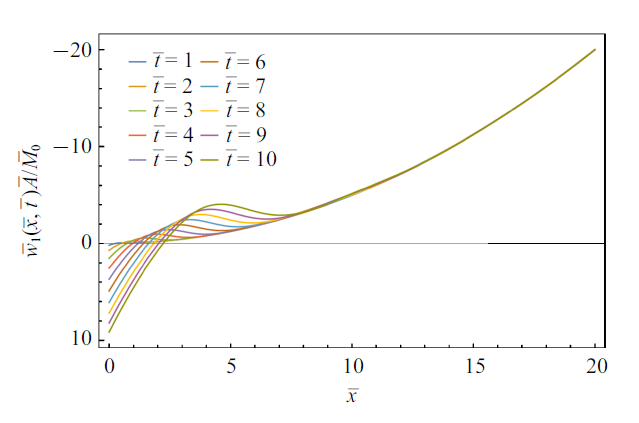
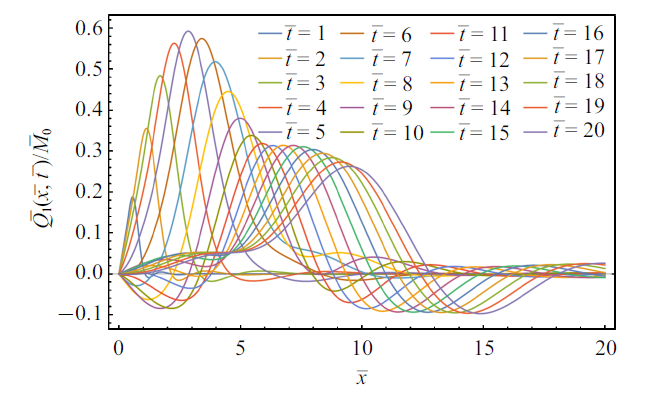
图6 和图7 分别展示了不同时刻铁木辛柯梁中的横向位移(挠度)的图形和剪力的波形图. 从图6 可以看出, 随着自由端初始弯矩的突然释放、瞬时卸载, 梁从自由端开始发生回弹, 并激发出一系列的弯曲扰动. 而从图7 可以看出, 梁自由端的剪力始终为零, 这符合只承受弯矩而不承受剪力的边界条件;自由端弯矩的突然释放、瞬时卸载在铁木辛柯梁中激发出一系列的切应力形式的应力波. 在梁中的不同位置, 切应力的值也并不相同, 也展现出一定的局部化效应, 切应力形式的应力波也以有限速度在梁中传播, 并不影响远离自由端的梁中部分, 其仍保持初始的零值. 梁中的剪力从自由端开始从零值逐渐增加, 达到峰值后回落, 后在零值附近震荡. 在不同时刻, 剪力峰值首先随着时间不断增大, 在到达最大切应力峰值后, 随着逐渐降低.
图6
图6
铁木辛柯梁中的横向位移(挠度)的变形特征
Fig.6
Deformation characteristics of lateral deflection in a Timoshenko beam
图7
图7
不同时刻铁木辛柯梁中的剪力分布
Fig.7
Shear force distribution in a Timoshenko beam at different moments
由于弯矩是导致梁发生二次断裂的关键力学量, 本工作关注激发出的应力波所对应的弯矩分布. 总体而言, 铁木辛柯梁中激发的弯矩峰值, 在各个时刻大小不同, 弯矩峰值随着时间逐渐增大, 表现出与欧拉梁明显的不同, 这是由于多考虑了旋转惯性和切应力的影响. 从图5 与图4 的对比中可以看到: 欧拉梁中的卸载弯曲波, 在任意时刻, 弯矩峰值都是相同的(图4 ), 这也是由于其自相似解的数学特性决定的, 换句话说, 在任意时刻, 欧拉梁中都总有一个位置, 会达到这个峰值; 而在铁木辛柯梁中可以看到, 不同时刻弯矩峰值的幅值是不相同的, 在早期, 弯矩峰值随着时间而延长.
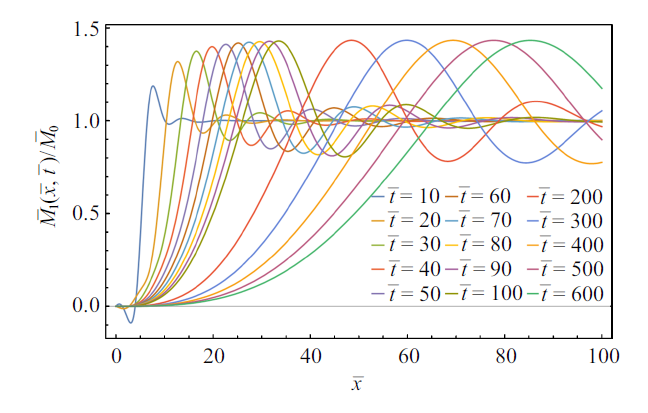
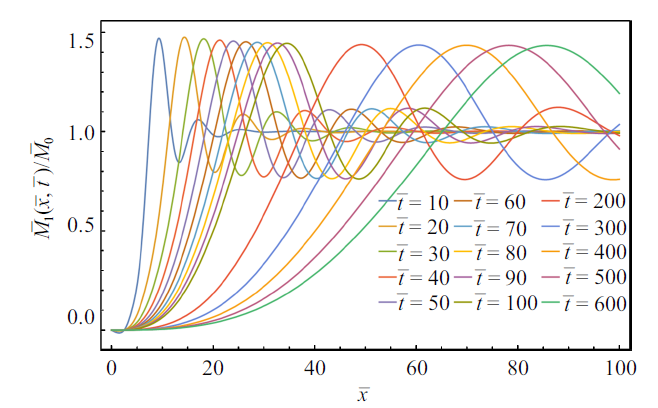
为了进一步探讨这个变化的弯矩峰值, 继续给出更大时刻中卸载弯曲波的波形图, 如图8 所示. 从图8 可以看出, 随着传播时间的延长, 弯矩峰值也逐渐增大, 最终趋于一个渐近最大值, 其值为1.43, 该数值恰好是2倍的菲涅尔正弦积分的最大值, 与欧拉梁中的弯矩峰值相同.
图8
图8
卸载后较晚时刻的铁木辛柯梁中的弯曲卸载波
Fig.8
Unloading bending moment waves in a Timoshenko beam at later moments
使用GS法来数值反变换瑞利梁中的弯矩式(33)、横向位移式(32)和剪力式(34)的像函数, 可以得到瑞利梁中相应的卸载弯曲波的响应解.
图9 和图10 所示分别为半无限长瑞利梁在自由端弯曲突然释放、瞬时卸载为零值后, 不同时刻梁中激发的弯矩形式的卸载弯曲波的波形图. 从图9 和图10 可以看出, 在不同时刻, 自由端处的弯矩始终是零值, 这符合模型问题的边界条件;而在离自由端较远的瑞利梁中, 弯矩值仍保持初始弯矩值, 这也体现了瑞利梁中卸载弯曲波传播的局部化效应, 这说明旋转惯性的引入改进了简单梁理论的不足, 将无限大的弯曲波波速降为有限值. 但是, 从图9 和图5 的对比可以看出, 在卸载弯曲波传播的早期, 瑞利梁中的波形图比较规整, 并没有明显的杂乱, 这说明图5 中铁木辛柯梁中早期的卸载弯曲波呈现出的一定的震荡与切应力效应有关. 结合图9 和图10 , 在不同时刻, 瑞利梁中的弯矩峰值的变化, 首先是随着时间不断增大的, 这与铁木辛柯梁中的情况相一致, 但是, 从图10 中可以看出, 与铁木辛柯梁所不同, 瑞利梁中的卸载弯曲波并不是单调增大的, 而是在增大到其弯矩峰值的最大值后缓慢下降的, 并有一个渐近最小值, 这体现了切应力对卸载弯曲波的影响.
图9
图9
卸载后较早时刻的瑞利梁中的弯曲卸载波
Fig.9
Unloading flexural stress waves in a Rayleigh beam at early moments
图10
图10
卸载后较晚时刻的瑞利梁中的弯曲卸载波
Fig.10
Unloading flexural stress waves in a Rayleigh beam at later moments
图11 和图12 所示分别为不同时刻瑞利梁中的横向位移(挠度)的图形和剪力的波形图. 从图11 可以看出, 随着自由端初始弯矩的瞬时卸载, 瑞利梁从自由端开始发生回弹, 并激发出一系列的弯曲扰动. 而从图12 可以看出, 瑞利梁中也激发出一系列的切应力形式的应力波, 其值从自由端开始从零值逐渐增大, 达到峰值后回落, 后在零值附近震荡, 展现出一定的局部化效应.
图11
图11
瑞利梁中的横向位移(挠度)的变形特征
Fig.11
Deformation characteristics of lateral deflection in a Rayleigh beam
图12
图12
不同时刻瑞利梁中的剪力分布
Fig.12
Shear force distribution in a Rayleigh beam at different moments
然而, 瑞利梁中的卸载弯曲波和铁木辛柯梁的卸载弯曲波还是存在一定的不同. 比如对于梁中横向位移来说, 同样的在$\bar{t}=10$时刻, 横向位移的谷值, 瑞利梁在$\bar{x}=5$左右, 而铁木辛柯梁中则在$\bar{x}=4$左右, 对于梁中的剪力来说, 瑞利梁在$\bar{t}=2$时就出现了切应力峰值的最大值, 而铁木辛柯梁则在$\bar{t}=5$时才达到切应力峰值的最大值, 这说明瑞利梁中弯曲波的传播速度大于铁木辛柯梁. 而对于梁中弯矩来说, 两种梁理论的区别更加明显, 瑞利梁中的弯矩峰值先增大后降低, 最终存在一个渐近最小值, 而铁木辛柯梁中的弯矩峰值是单调增大的, 最终存在一个渐近最大值. 同样的在$\bar{t}=9$时刻, 瑞利梁的弯矩峰值在$\bar{x}=9$处, 其值为1.46, 而铁木辛柯梁的弯矩峰值在$\bar{x}=7$处, 其值为1.15.这说明, 切应力的引入, 进一步降低了卸载弯曲波的波速, 铁木辛柯梁中的弯曲卸载波的波速小于瑞利梁中的波速, 切应力的影响还包括拉低了弯矩峰值的最大值.
4 弯矩峰值和梁的二次断裂
脆性梁的二次弯曲断裂是一个经典问题, Schindler等[7 ] 基于经典的欧拉梁, 证明突然断裂的纯弯曲梁中将激发出一个用菲涅尔正弦积分函数表示的弯曲波, 如式(39)所表征, 其弯矩峰值的"过冲"导致二次断裂. Audoly等[8 ] 重新求解了此问题, 并将其结论用于解释意大利面条掰断时总伴随的二次断裂现象. 对于欧拉梁来说, 波速无限大, 故而不存在特征时间, 因此在欧拉梁中的任意位置, 弯矩峰值都能够达到其最大值, 并且在任意位置的弯矩峰值的最大值相同, 根据式(39)可算出弯矩峰值最大值为2倍的菲涅尔正弦积分函数的最大值, 约为1.43.
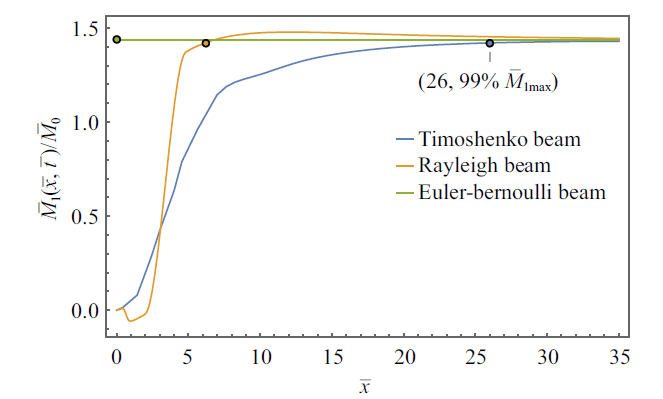
事实上, 在一个瞬态断裂的过程中, 梁的结构惯性效果不可避免. 如果考虑了梁的旋转惯性以及切应力效应, 则激发弯曲波的传播速度将为有限值, 从而带来一个"特征时间"概念. 比较图4 (欧拉梁)、图9 和图10 (瑞利梁)、图5 和图8 (铁木辛柯梁)的卸载弯曲波激励的不同时刻的弯矩分布曲线, 可以看出: 由于旋转惯性以及切应力效应的引入, 卸载导致的弯矩"过冲"现象并非瞬时发生在断裂点(即瞬态卸载的自由端)紧邻, 而是需要一定的时间、且距离断裂点有一定的距离.
为了定量分析二次断裂的位置, 给出了在欧拉梁、瑞利梁和铁木辛柯梁下模型问题中卸载弯曲波诱发的弯矩峰值("过冲")的发生位置, 即图4 、图9 和图10 、图5 和图8 中不同时刻弯矩分布曲线的包络线, 如图13 所示. 显然, 欧拉梁的峰值包络线是一条幅值恒为1.43的水平线. 对于瑞利梁来说, 旋转惯性的引入使得弯曲波波速降为有限值, 边界突然卸载后, 弯曲波的峰值发展达到其峰值最大值需要一段时间, 其峰值随着传播距离的增大先增大, 超过其峰值最大值之后再缓慢下降, 最终达到渐近的水平值. 而对于铁木辛柯梁, 切应力效应的引入进一步拉低了弯曲波的波速, 也抑制了早期弯矩峰值过冲的发展, 其结果就是: 随着传播距离的增大, 不同位置经历的弯矩峰值逐渐增大, 最后达到渐进的水平值. 无论时瑞利梁还是铁木辛柯梁, 弯矩峰值在不同位置的空间渐进峰值$\bar{M_{1}}_{max}$都是1.43, 和欧拉梁一样.
图13
图13
3种梁理论下卸载弯矩峰值包络线图
Fig.13
Envelope schematic of unloading peak values of bending moment in three beams
作者前期工作[10 ] 指出梁中的弯矩峰值包络线图可以用来预测二次断裂发生位置和时刻. 在一个半无限长弹性梁问题中, 令初始弯矩$M_{0}$等于准静态下的临界断裂弯矩$M_{c}$, 初始弯矩的突然卸载可以看成准静态下自由端的突然断裂, 即第一次断裂. 断裂所激发的卸载波在梁中导致弯矩过冲, 即图13 中三种梁理论预测的弯矩峰值都超越了1, 因此很可能会发生二次断裂.
二次断裂的位置与材料局部强度有关, 然而显然, 局部弯矩越大该点发生二次断裂的概率越大. 假设达到0.99渐近值$\bar{M_{1}}_{max}$的位置为二次断裂的特定位置, 那么图13 中最先达到这个幅度的点就是二次断裂点. 对于瑞利梁来说, $0.99\bar{M_{1}}_{max}$所对应的位置为$\bar{x}=6$, 即6倍横截面回转半径. 对于圆形截面梁来说, 该位置为离开断口1.5倍横截面直径(圆形截面回转半径$=$1/4圆直径), 这个估计远小于实验和模拟中所报导的二次断裂碎片尺寸[9 -10 ] .
事实上, 对于一个突然断裂、弯矩瞬间降为0的物理场景, 瑞利梁并不适用于卸载弯曲波分析, 因为切应力效应将导致卸载波结构更加复杂. 铁木辛柯梁同时考虑了旋转惯性和切应力效应的作用, 是一个更加合理的模型. 由于剪力的影响, 剪切波将进一步减缓弯矩的增长, 从而延迟特定位置处弯矩达到峰值的时间. 根据图13 的包络线的结果, 局部弯矩达到$0.99\bar{M_{1}}_{max}$所对应的位置为$\bar{x}=26$, 即约为7倍梁横截面直径, 与实验[9 -10 ] 所报道的二次断裂的碎片尺寸约为6到13倍梁横截面厚度的结果一致.
5 结论和讨论
本文研究了半无限长弹性梁在准静态弯曲加载条件下, 由于自由端的初始弯矩突然释放而在梁中激发出的一系列卸载弯曲应力波问题. 该问题的提出背景对应着脆性梁的突然断裂所导致的二次断裂现象. 传统的基于欧拉梁的模型问题缺乏特征时间, 因此不能给出二次断裂位置的预测.
本文提出了基于铁木辛柯梁和瑞利梁的模型问题, 采用拉普拉斯变换方法求解问题, 给出了卸载弯曲波的像函数解, 并采用数值反变换方法得到的原函数的时域响应解, 给出了突然卸载(即断裂)发生后, 欧拉梁、瑞利梁和铁木辛柯梁的回弹变形图像. 计算结果表明: 包含了旋转惯性和切应力效应的铁木辛柯梁的回弹变形具有明显的滞后现象, 代表了有限应力波传播速度的特性.
本文计算了梁中不同时刻的弯矩分布情况, 结果表明: 旋转惯性的引入使铁木辛柯梁和瑞利梁中的卸载弯曲波的传播具有强烈的局部化效应, 梁中的卸载弯曲波随着时间逐渐变化, 梁中各个位置经历的弯矩峰值大小不同;对于瑞利梁来说, 峰值弯矩先增大后降低, 在达到最大值后缓慢下降到一个渐近值, 对于铁木辛柯梁来说其峰值弯矩总体上随着时间单调增大到同一个渐近值, 这两个渐近值与欧拉梁的峰值弯矩相同, 均为2倍的菲涅尔正弦积分函数的最大值;切应力的引入进一步地降低了铁木辛柯梁中的卸载弯曲波的波速, 同时也使得铁木辛柯梁中的弯矩峰值的最大值小于瑞利梁中的最大值. 对于脆性细长梁的纯弯曲断裂, 铁木辛柯梁可以较好地预测二次断裂, 对应的碎片尺寸为7倍梁横截面厚度. 对本文工作的一些讨论如下:
(1)脆性梁的突然断裂导致卸载波、弯矩过冲以及二次断裂的现象久为人知, 对半无限长梁模型采用欧拉梁方法进行的分析简洁、具有解析解, 但缺乏关键的特征时间参数. 对于一个真实的物理过程, 二次断裂涉及的时间因素可能来自于以下方面: (a)梁的模型本身—需要采用复杂梁理论如铁木辛柯梁; (b)断裂过程—无论多脆的材料, 其断裂都需要一个过程, 因此卸载需要一定的时间;(c) 对于有限长度梁, 弯曲应力波将在另一端产生反射, 导致结构效应. 本文分析了第一个因素的结果, 更复杂的时间效应有待进一步分析.
(2)由于数学处理的复杂性, 本文采用数值反拉普拉斯变换变换方法计算梁的动力学响应, 虽然属于解析解, 但不可避免地带来数值误差. 本文计算结果所揭示的突然卸载的动力学响应过程定性看基本合理, 但对于更复杂的物理问题, 可能需要采用全数值模拟的方法进行分析.
参考文献
View Option
[1]
Miklowitz J . Elastic waves created during tensile fracture--The phenomenon of a second fracture
Journal Applied Mechanics 1953 , 3 : 122 -130
[本文引用: 1]
[2]
Phillips JW . Stress pulses produced during the fracture of brittle tensile specimens
International Journal of Solids and Structures 1970 , 6 : 1403 -1412
DOI
URL
[本文引用: 1]
[3]
Kolsky H . The stress pulses propagated as a result of the rapid growth of brittle fracture
Engineering Fracture Mechanics 1973 , 5 : 513 -522
DOI
URL
[本文引用: 1]
[4]
Kinra V . Stress pulses emitted during fracture in tension
International Journal of Solids and Structures 1976 , 12 , 803 -808
DOI
URL
[本文引用: 1]
[5]
Bodner SR . Stress waves due to fracture of glass in bending
Journal of the Mechanics and Physics of Solids 1973 , 21 : 1 -6
DOI
URL
[本文引用: 1]
[6]
Kinra V Kolsky H . The interaction between bending fractures and the emitted stress waves
Engineering Fracture Mechanics 1977 , 9 : 423432
[本文引用: 1]
[7]
Schindler HJ Kolsky H . Multiple fractures produced by the bending of brittle beams
Journal of the Mechanics and Physics of Solids 1983 , 31 : 427 -436
DOI
URL
[本文引用: 4]
[8]
Audoly B Neukirch S . Fragmentation of rods by cascading cracks: Why spaghetti does not break in half
Physical Review Letters 2005 , 95 : 095505
DOI
URL
[本文引用: 5]
[9]
Heisser RH Patil VP Stoop N , et al . Controlling fracture cascades through twisting and quenching
Proceedings of the National Academy of Sciences of the United States of America 2018 , 115 : 65 -70
[本文引用: 3]
[10]
Long L Zheng Y Zhou F , et al . Towards further understanding the secondary fracture during spaghetti bent break
Materials 2021 , 14 : 189
DOI
URL
[本文引用: 5]
[11]
王礼立 . 应力波基础 . 北京 : 国防工业出版社 , 2005
[本文引用: 1]
(Wang Lili . Foundation of Stress Wave . Beijing : National Defence Industry Press , 2005 (in Chinese))
[本文引用: 1]
[12]
Rayleigh L . The Theory of Sound
Dover: New York , 1945 : 1877 -1878
[本文引用: 1]
[13]
Timoshenko SP . On the correction factor for shear of the differential equation for transverse vibrations of bars of uniform cross-section
Philosophical Magazine 1921 : 744
[本文引用: 2]
[14]
Graff KF . Wave Motions in Solids
New York: Dover Publications, Inc , 1975 : 186
[本文引用: 1]
[15]
Timoshenko SP . Schwingungsprobleme der Technik
Julius Springer , 1932
[本文引用: 1]
[16]
Mindlin RD Deresiewicz H . Timoshenko's shear coefficient for flexural vibrations of beams
Technical Report No. 10, ONR Project NR064-388, 1953, Department of Civil Engineering, New York: Columbia University
[本文引用: 1]
[17]
Cowper GR . The shear coefficient in Timoshenko's beam theory
Journal Applied Mechanics 1966 , 33 (2 ): 335 -340
DOI
URL
[本文引用: 2]
[18]
Stephen NG . Timoshenko's shear coefficient from a beam subjected to gravity loading
Journal of Applied Mechanics 1980 , 47 (1 ): 121 -127
DOI
URL
[本文引用: 1]
[19]
Hutchinson JR . Transverse vibration of beams, exact versus approximate solutions
Journal of Applied Mechanics 1981 , 48 (12 ): 923 -928
DOI
URL
[本文引用: 1]
[20]
Timoshenko S James MG . Mechanics of Materials
Van Nostrand Reinhold Co. , 1972 : 207
[本文引用: 1]
Elastic waves created during tensile fracture--The phenomenon of a second fracture
1
1953
... 脆性杆因为突发断裂而产生的二次断裂现象, 最早见于Miklowitz[1 ] 对玻璃杆进行拉伸实验观察到的二次断裂的报道; 随后, Phillips[2 ] , Kolsky[3 ] 和Kinra[4 ] 对因拉伸断裂而激发出的卸载拉伸应力波、以及因此产生的后续断裂等现象进行了研究. 接着, Bodner[5 ] , Kinra等[6 ] , Schindler等[7 ] 把关注重点从拉伸断裂转移到弯曲断裂, 对因弯曲断裂而激发出的卸载弯曲应力波、及其因此产生的后续断裂等现象进行了研究. 特别是Schindler和Kolsky[7 ] 对方形截面的聚酯纤维棒进行纯弯曲加载, 通过粘贴在试件表面的应变片测量到因弯曲断裂而激发出的卸载弯曲应力波, 观察到因此导致的二次断裂现象, 并基于欧拉伯努利梁理论(Euler-Bernoulli beamtheory, 简称"欧拉梁")给出了一个关于卸载弯曲应力波的解析解. ...
Stress pulses produced during the fracture of brittle tensile specimens
1
1970
... 脆性杆因为突发断裂而产生的二次断裂现象, 最早见于Miklowitz[1 ] 对玻璃杆进行拉伸实验观察到的二次断裂的报道; 随后, Phillips[2 ] , Kolsky[3 ] 和Kinra[4 ] 对因拉伸断裂而激发出的卸载拉伸应力波、以及因此产生的后续断裂等现象进行了研究. 接着, Bodner[5 ] , Kinra等[6 ] , Schindler等[7 ] 把关注重点从拉伸断裂转移到弯曲断裂, 对因弯曲断裂而激发出的卸载弯曲应力波、及其因此产生的后续断裂等现象进行了研究. 特别是Schindler和Kolsky[7 ] 对方形截面的聚酯纤维棒进行纯弯曲加载, 通过粘贴在试件表面的应变片测量到因弯曲断裂而激发出的卸载弯曲应力波, 观察到因此导致的二次断裂现象, 并基于欧拉伯努利梁理论(Euler-Bernoulli beamtheory, 简称"欧拉梁")给出了一个关于卸载弯曲应力波的解析解. ...
The stress pulses propagated as a result of the rapid growth of brittle fracture
1
1973
... 脆性杆因为突发断裂而产生的二次断裂现象, 最早见于Miklowitz[1 ] 对玻璃杆进行拉伸实验观察到的二次断裂的报道; 随后, Phillips[2 ] , Kolsky[3 ] 和Kinra[4 ] 对因拉伸断裂而激发出的卸载拉伸应力波、以及因此产生的后续断裂等现象进行了研究. 接着, Bodner[5 ] , Kinra等[6 ] , Schindler等[7 ] 把关注重点从拉伸断裂转移到弯曲断裂, 对因弯曲断裂而激发出的卸载弯曲应力波、及其因此产生的后续断裂等现象进行了研究. 特别是Schindler和Kolsky[7 ] 对方形截面的聚酯纤维棒进行纯弯曲加载, 通过粘贴在试件表面的应变片测量到因弯曲断裂而激发出的卸载弯曲应力波, 观察到因此导致的二次断裂现象, 并基于欧拉伯努利梁理论(Euler-Bernoulli beamtheory, 简称"欧拉梁")给出了一个关于卸载弯曲应力波的解析解. ...
Stress pulses emitted during fracture in tension
1
1976
... 脆性杆因为突发断裂而产生的二次断裂现象, 最早见于Miklowitz[1 ] 对玻璃杆进行拉伸实验观察到的二次断裂的报道; 随后, Phillips[2 ] , Kolsky[3 ] 和Kinra[4 ] 对因拉伸断裂而激发出的卸载拉伸应力波、以及因此产生的后续断裂等现象进行了研究. 接着, Bodner[5 ] , Kinra等[6 ] , Schindler等[7 ] 把关注重点从拉伸断裂转移到弯曲断裂, 对因弯曲断裂而激发出的卸载弯曲应力波、及其因此产生的后续断裂等现象进行了研究. 特别是Schindler和Kolsky[7 ] 对方形截面的聚酯纤维棒进行纯弯曲加载, 通过粘贴在试件表面的应变片测量到因弯曲断裂而激发出的卸载弯曲应力波, 观察到因此导致的二次断裂现象, 并基于欧拉伯努利梁理论(Euler-Bernoulli beamtheory, 简称"欧拉梁")给出了一个关于卸载弯曲应力波的解析解. ...
Stress waves due to fracture of glass in bending
1
1973
... 脆性杆因为突发断裂而产生的二次断裂现象, 最早见于Miklowitz[1 ] 对玻璃杆进行拉伸实验观察到的二次断裂的报道; 随后, Phillips[2 ] , Kolsky[3 ] 和Kinra[4 ] 对因拉伸断裂而激发出的卸载拉伸应力波、以及因此产生的后续断裂等现象进行了研究. 接着, Bodner[5 ] , Kinra等[6 ] , Schindler等[7 ] 把关注重点从拉伸断裂转移到弯曲断裂, 对因弯曲断裂而激发出的卸载弯曲应力波、及其因此产生的后续断裂等现象进行了研究. 特别是Schindler和Kolsky[7 ] 对方形截面的聚酯纤维棒进行纯弯曲加载, 通过粘贴在试件表面的应变片测量到因弯曲断裂而激发出的卸载弯曲应力波, 观察到因此导致的二次断裂现象, 并基于欧拉伯努利梁理论(Euler-Bernoulli beamtheory, 简称"欧拉梁")给出了一个关于卸载弯曲应力波的解析解. ...
The interaction between bending fractures and the emitted stress waves
1
1977
... 脆性杆因为突发断裂而产生的二次断裂现象, 最早见于Miklowitz[1 ] 对玻璃杆进行拉伸实验观察到的二次断裂的报道; 随后, Phillips[2 ] , Kolsky[3 ] 和Kinra[4 ] 对因拉伸断裂而激发出的卸载拉伸应力波、以及因此产生的后续断裂等现象进行了研究. 接着, Bodner[5 ] , Kinra等[6 ] , Schindler等[7 ] 把关注重点从拉伸断裂转移到弯曲断裂, 对因弯曲断裂而激发出的卸载弯曲应力波、及其因此产生的后续断裂等现象进行了研究. 特别是Schindler和Kolsky[7 ] 对方形截面的聚酯纤维棒进行纯弯曲加载, 通过粘贴在试件表面的应变片测量到因弯曲断裂而激发出的卸载弯曲应力波, 观察到因此导致的二次断裂现象, 并基于欧拉伯努利梁理论(Euler-Bernoulli beamtheory, 简称"欧拉梁")给出了一个关于卸载弯曲应力波的解析解. ...
Multiple fractures produced by the bending of brittle beams
4
1983
... 脆性杆因为突发断裂而产生的二次断裂现象, 最早见于Miklowitz[1 ] 对玻璃杆进行拉伸实验观察到的二次断裂的报道; 随后, Phillips[2 ] , Kolsky[3 ] 和Kinra[4 ] 对因拉伸断裂而激发出的卸载拉伸应力波、以及因此产生的后续断裂等现象进行了研究. 接着, Bodner[5 ] , Kinra等[6 ] , Schindler等[7 ] 把关注重点从拉伸断裂转移到弯曲断裂, 对因弯曲断裂而激发出的卸载弯曲应力波、及其因此产生的后续断裂等现象进行了研究. 特别是Schindler和Kolsky[7 ] 对方形截面的聚酯纤维棒进行纯弯曲加载, 通过粘贴在试件表面的应变片测量到因弯曲断裂而激发出的卸载弯曲应力波, 观察到因此导致的二次断裂现象, 并基于欧拉伯努利梁理论(Euler-Bernoulli beamtheory, 简称"欧拉梁")给出了一个关于卸载弯曲应力波的解析解. ...
... [7 ]对方形截面的聚酯纤维棒进行纯弯曲加载, 通过粘贴在试件表面的应变片测量到因弯曲断裂而激发出的卸载弯曲应力波, 观察到因此导致的二次断裂现象, 并基于欧拉伯努利梁理论(Euler-Bernoulli beamtheory, 简称"欧拉梁")给出了一个关于卸载弯曲应力波的解析解. ...
... 对于欧拉梁的像函数(35) $\sim$ (37), 参照文献[7 -8 , 10 ]可以对原函数进行解析反变换, 代入式(18a) $\sim\!$式(18d), 最后得到时间域的解析解 ...
... 脆性梁的二次弯曲断裂是一个经典问题, Schindler等[7 ] 基于经典的欧拉梁, 证明突然断裂的纯弯曲梁中将激发出一个用菲涅尔正弦积分函数表示的弯曲波, 如式(39)所表征, 其弯矩峰值的"过冲"导致二次断裂. Audoly等[8 ] 重新求解了此问题, 并将其结论用于解释意大利面条掰断时总伴随的二次断裂现象. 对于欧拉梁来说, 波速无限大, 故而不存在特征时间, 因此在欧拉梁中的任意位置, 弯矩峰值都能够达到其最大值, 并且在任意位置的弯矩峰值的最大值相同, 根据式(39)可算出弯矩峰值最大值为2倍的菲涅尔正弦积分函数的最大值, 约为1.43. ...
Fragmentation of rods by cascading cracks: Why spaghetti does not break in half
5
2005
... 近年来, 脆性梁在弯曲加载下的多次断裂现象再次得到关注, Audoly等[8 ] 、Heisser等[9 ] 对意大利面条的雪崩式断裂进行了一系列的理论和实验研究. Audoly等[8 ] 使用欧拉梁理论, 给出了卸载弯曲波的自相似解, 通过这些解可以看出, 脆性梁的突然弯曲断裂, 会激发出一系列卸载弯曲波, 这些卸载波会导致梁中局部弯矩超越断裂时刻的整体弯矩(称之为"过冲"), 从而引发后续的二次断裂. Audoly等[8 ] 从理论上阐明了二次断裂的必然性, 但是, 受限于欧拉梁的局限性, 所分析的模型问题缺少特征时间, 因此无法进一步研究二次断裂相关特征参数, 特别是具体的发生时刻和位置. 作者前期工作[10 ] 指出, 脆性梁在纯弯曲作用下的第一次断裂并不是瞬时发生的, 因此断裂位置的弯矩变化不是突然卸载, 而是需要经历一个降时; 考虑卸载时间相关, 给出了基于欧拉梁的一个带有特征时间的卸载弯曲波的解析解, 并因此预测了依赖于特征时间的二次断裂的碎片尺寸. ...
... [8 ]使用欧拉梁理论, 给出了卸载弯曲波的自相似解, 通过这些解可以看出, 脆性梁的突然弯曲断裂, 会激发出一系列卸载弯曲波, 这些卸载波会导致梁中局部弯矩超越断裂时刻的整体弯矩(称之为"过冲"), 从而引发后续的二次断裂. Audoly等[8 ] 从理论上阐明了二次断裂的必然性, 但是, 受限于欧拉梁的局限性, 所分析的模型问题缺少特征时间, 因此无法进一步研究二次断裂相关特征参数, 特别是具体的发生时刻和位置. 作者前期工作[10 ] 指出, 脆性梁在纯弯曲作用下的第一次断裂并不是瞬时发生的, 因此断裂位置的弯矩变化不是突然卸载, 而是需要经历一个降时; 考虑卸载时间相关, 给出了基于欧拉梁的一个带有特征时间的卸载弯曲波的解析解, 并因此预测了依赖于特征时间的二次断裂的碎片尺寸. ...
... [8 ]从理论上阐明了二次断裂的必然性, 但是, 受限于欧拉梁的局限性, 所分析的模型问题缺少特征时间, 因此无法进一步研究二次断裂相关特征参数, 特别是具体的发生时刻和位置. 作者前期工作[10 ] 指出, 脆性梁在纯弯曲作用下的第一次断裂并不是瞬时发生的, 因此断裂位置的弯矩变化不是突然卸载, 而是需要经历一个降时; 考虑卸载时间相关, 给出了基于欧拉梁的一个带有特征时间的卸载弯曲波的解析解, 并因此预测了依赖于特征时间的二次断裂的碎片尺寸. ...
... 对于欧拉梁的像函数(35) $\sim$ (37), 参照文献[7 -8 , 10 ]可以对原函数进行解析反变换, 代入式(18a) $\sim\!$式(18d), 最后得到时间域的解析解 ...
... 脆性梁的二次弯曲断裂是一个经典问题, Schindler等[7 ] 基于经典的欧拉梁, 证明突然断裂的纯弯曲梁中将激发出一个用菲涅尔正弦积分函数表示的弯曲波, 如式(39)所表征, 其弯矩峰值的"过冲"导致二次断裂. Audoly等[8 ] 重新求解了此问题, 并将其结论用于解释意大利面条掰断时总伴随的二次断裂现象. 对于欧拉梁来说, 波速无限大, 故而不存在特征时间, 因此在欧拉梁中的任意位置, 弯矩峰值都能够达到其最大值, 并且在任意位置的弯矩峰值的最大值相同, 根据式(39)可算出弯矩峰值最大值为2倍的菲涅尔正弦积分函数的最大值, 约为1.43. ...
Controlling fracture cascades through twisting and quenching
3
2018
... 近年来, 脆性梁在弯曲加载下的多次断裂现象再次得到关注, Audoly等[8 ] 、Heisser等[9 ] 对意大利面条的雪崩式断裂进行了一系列的理论和实验研究. Audoly等[8 ] 使用欧拉梁理论, 给出了卸载弯曲波的自相似解, 通过这些解可以看出, 脆性梁的突然弯曲断裂, 会激发出一系列卸载弯曲波, 这些卸载波会导致梁中局部弯矩超越断裂时刻的整体弯矩(称之为"过冲"), 从而引发后续的二次断裂. Audoly等[8 ] 从理论上阐明了二次断裂的必然性, 但是, 受限于欧拉梁的局限性, 所分析的模型问题缺少特征时间, 因此无法进一步研究二次断裂相关特征参数, 特别是具体的发生时刻和位置. 作者前期工作[10 ] 指出, 脆性梁在纯弯曲作用下的第一次断裂并不是瞬时发生的, 因此断裂位置的弯矩变化不是突然卸载, 而是需要经历一个降时; 考虑卸载时间相关, 给出了基于欧拉梁的一个带有特征时间的卸载弯曲波的解析解, 并因此预测了依赖于特征时间的二次断裂的碎片尺寸. ...
... 二次断裂的位置与材料局部强度有关, 然而显然, 局部弯矩越大该点发生二次断裂的概率越大. 假设达到0.99渐近值$\bar{M_{1}}_{max}$的位置为二次断裂的特定位置, 那么图13 中最先达到这个幅度的点就是二次断裂点. 对于瑞利梁来说, $0.99\bar{M_{1}}_{max}$所对应的位置为$\bar{x}=6$, 即6倍横截面回转半径. 对于圆形截面梁来说, 该位置为离开断口1.5倍横截面直径(圆形截面回转半径$=$1/4圆直径), 这个估计远小于实验和模拟中所报导的二次断裂碎片尺寸[9 -10 ] . ...
... 事实上, 对于一个突然断裂、弯矩瞬间降为0的物理场景, 瑞利梁并不适用于卸载弯曲波分析, 因为切应力效应将导致卸载波结构更加复杂. 铁木辛柯梁同时考虑了旋转惯性和切应力效应的作用, 是一个更加合理的模型. 由于剪力的影响, 剪切波将进一步减缓弯矩的增长, 从而延迟特定位置处弯矩达到峰值的时间. 根据图13 的包络线的结果, 局部弯矩达到$0.99\bar{M_{1}}_{max}$所对应的位置为$\bar{x}=26$, 即约为7倍梁横截面直径, 与实验[9 -10 ] 所报道的二次断裂的碎片尺寸约为6到13倍梁横截面厚度的结果一致. ...
Towards further understanding the secondary fracture during spaghetti bent break
5
2021
... 近年来, 脆性梁在弯曲加载下的多次断裂现象再次得到关注, Audoly等[8 ] 、Heisser等[9 ] 对意大利面条的雪崩式断裂进行了一系列的理论和实验研究. Audoly等[8 ] 使用欧拉梁理论, 给出了卸载弯曲波的自相似解, 通过这些解可以看出, 脆性梁的突然弯曲断裂, 会激发出一系列卸载弯曲波, 这些卸载波会导致梁中局部弯矩超越断裂时刻的整体弯矩(称之为"过冲"), 从而引发后续的二次断裂. Audoly等[8 ] 从理论上阐明了二次断裂的必然性, 但是, 受限于欧拉梁的局限性, 所分析的模型问题缺少特征时间, 因此无法进一步研究二次断裂相关特征参数, 特别是具体的发生时刻和位置. 作者前期工作[10 ] 指出, 脆性梁在纯弯曲作用下的第一次断裂并不是瞬时发生的, 因此断裂位置的弯矩变化不是突然卸载, 而是需要经历一个降时; 考虑卸载时间相关, 给出了基于欧拉梁的一个带有特征时间的卸载弯曲波的解析解, 并因此预测了依赖于特征时间的二次断裂的碎片尺寸. ...
... 对于欧拉梁的像函数(35) $\sim$ (37), 参照文献[7 -8 , 10 ]可以对原函数进行解析反变换, 代入式(18a) $\sim\!$式(18d), 最后得到时间域的解析解 ...
... 作者前期工作[10 ] 指出梁中的弯矩峰值包络线图可以用来预测二次断裂发生位置和时刻. 在一个半无限长弹性梁问题中, 令初始弯矩$M_{0}$等于准静态下的临界断裂弯矩$M_{c}$, 初始弯矩的突然卸载可以看成准静态下自由端的突然断裂, 即第一次断裂. 断裂所激发的卸载波在梁中导致弯矩过冲, 即图13 中三种梁理论预测的弯矩峰值都超越了1, 因此很可能会发生二次断裂. ...
... 二次断裂的位置与材料局部强度有关, 然而显然, 局部弯矩越大该点发生二次断裂的概率越大. 假设达到0.99渐近值$\bar{M_{1}}_{max}$的位置为二次断裂的特定位置, 那么图13 中最先达到这个幅度的点就是二次断裂点. 对于瑞利梁来说, $0.99\bar{M_{1}}_{max}$所对应的位置为$\bar{x}=6$, 即6倍横截面回转半径. 对于圆形截面梁来说, 该位置为离开断口1.5倍横截面直径(圆形截面回转半径$=$1/4圆直径), 这个估计远小于实验和模拟中所报导的二次断裂碎片尺寸[9 -10 ] . ...
... 事实上, 对于一个突然断裂、弯矩瞬间降为0的物理场景, 瑞利梁并不适用于卸载弯曲波分析, 因为切应力效应将导致卸载波结构更加复杂. 铁木辛柯梁同时考虑了旋转惯性和切应力效应的作用, 是一个更加合理的模型. 由于剪力的影响, 剪切波将进一步减缓弯矩的增长, 从而延迟特定位置处弯矩达到峰值的时间. 根据图13 的包络线的结果, 局部弯矩达到$0.99\bar{M_{1}}_{max}$所对应的位置为$\bar{x}=26$, 即约为7倍梁横截面直径, 与实验[9 -10 ] 所报道的二次断裂的碎片尺寸约为6到13倍梁横截面厚度的结果一致. ...
1
2005
... 以上分析的模型问题都基于简单的欧拉梁, 根据此理论, 弹性弯曲波的行波波速与其波长成反比[11 ] , 如果波长无限小, 则波速无限大. 换言之, 一个瞬时变化的弯曲脉冲将以无限大速度传播, 这显然不符合物理原理. 事实上, 欧拉梁只适用于行波波长远大于梁横向特征尺寸的情况, 如果这两个尺寸能够相比较, 梁的旋转惯性就不能被忽略, Rayleigh[12 ] 最早提出了关于旋转惯性的修正. Timoshenko[13 ] 进一步指出, 当行波波长能够与梁横向特征尺寸相比较时, 剪力导致的剪切变形对梁的整体横向位移有贡献, 因此关于切应力效应的修正与关于旋转惯性的修正同样重要;同时考虑切应力效应和旋转惯性, Timoshenko[13 ] 给出了形式复杂但更加合理的控制方程. ...
1
2005
... 以上分析的模型问题都基于简单的欧拉梁, 根据此理论, 弹性弯曲波的行波波速与其波长成反比[11 ] , 如果波长无限小, 则波速无限大. 换言之, 一个瞬时变化的弯曲脉冲将以无限大速度传播, 这显然不符合物理原理. 事实上, 欧拉梁只适用于行波波长远大于梁横向特征尺寸的情况, 如果这两个尺寸能够相比较, 梁的旋转惯性就不能被忽略, Rayleigh[12 ] 最早提出了关于旋转惯性的修正. Timoshenko[13 ] 进一步指出, 当行波波长能够与梁横向特征尺寸相比较时, 剪力导致的剪切变形对梁的整体横向位移有贡献, 因此关于切应力效应的修正与关于旋转惯性的修正同样重要;同时考虑切应力效应和旋转惯性, Timoshenko[13 ] 给出了形式复杂但更加合理的控制方程. ...
The Theory of Sound
1
1945
... 以上分析的模型问题都基于简单的欧拉梁, 根据此理论, 弹性弯曲波的行波波速与其波长成反比[11 ] , 如果波长无限小, 则波速无限大. 换言之, 一个瞬时变化的弯曲脉冲将以无限大速度传播, 这显然不符合物理原理. 事实上, 欧拉梁只适用于行波波长远大于梁横向特征尺寸的情况, 如果这两个尺寸能够相比较, 梁的旋转惯性就不能被忽略, Rayleigh[12 ] 最早提出了关于旋转惯性的修正. Timoshenko[13 ] 进一步指出, 当行波波长能够与梁横向特征尺寸相比较时, 剪力导致的剪切变形对梁的整体横向位移有贡献, 因此关于切应力效应的修正与关于旋转惯性的修正同样重要;同时考虑切应力效应和旋转惯性, Timoshenko[13 ] 给出了形式复杂但更加合理的控制方程. ...
On the correction factor for shear of the differential equation for transverse vibrations of bars of uniform cross-section
2
1921
... 以上分析的模型问题都基于简单的欧拉梁, 根据此理论, 弹性弯曲波的行波波速与其波长成反比[11 ] , 如果波长无限小, 则波速无限大. 换言之, 一个瞬时变化的弯曲脉冲将以无限大速度传播, 这显然不符合物理原理. 事实上, 欧拉梁只适用于行波波长远大于梁横向特征尺寸的情况, 如果这两个尺寸能够相比较, 梁的旋转惯性就不能被忽略, Rayleigh[12 ] 最早提出了关于旋转惯性的修正. Timoshenko[13 ] 进一步指出, 当行波波长能够与梁横向特征尺寸相比较时, 剪力导致的剪切变形对梁的整体横向位移有贡献, 因此关于切应力效应的修正与关于旋转惯性的修正同样重要;同时考虑切应力效应和旋转惯性, Timoshenko[13 ] 给出了形式复杂但更加合理的控制方程. ...
... [13 ]给出了形式复杂但更加合理的控制方程. ...
Wave Motions in Solids
1
1975
... 由于铁木辛柯梁的横截面发生了翘曲变形, 其横截面上的剪切应变并非均匀分布, 因此剪力导致的横截面转角$\gamma $并非由平均剪切应变导致;在横截面上的总剪切力$Q$与剪切转角$\gamma $之间通过式(1j)联系, 其中$k$是与梁横截面形状和泊松比$\nu $有关的系数, 被称之为铁木辛柯剪切系数[14 ] . 许多科学家通过复杂的弹性力学分析尝试给出其精确数值, 如Timoshenko[15 , 20 ] , Mindlin等[16 ] , Cowper[17 ] , Stephen[18 ] , Hutchinson[19 ] 等. 根据Cowper[17 ] 的研究, 如果梁横截面是方形, $k={10\left( 1+\nu \right)}/({12+11\nu })$, 如果梁横截面是圆形, $k={6\left( 1+\nu \right)}/({7+6\nu })$, 因此对于大多数常见材料, $k$的取值范围为${5}/{6}\sim {10}/{9}$. ...
Schwingungsprobleme der Technik
1
1932
... 由于铁木辛柯梁的横截面发生了翘曲变形, 其横截面上的剪切应变并非均匀分布, 因此剪力导致的横截面转角$\gamma $并非由平均剪切应变导致;在横截面上的总剪切力$Q$与剪切转角$\gamma $之间通过式(1j)联系, 其中$k$是与梁横截面形状和泊松比$\nu $有关的系数, 被称之为铁木辛柯剪切系数[14 ] . 许多科学家通过复杂的弹性力学分析尝试给出其精确数值, 如Timoshenko[15 , 20 ] , Mindlin等[16 ] , Cowper[17 ] , Stephen[18 ] , Hutchinson[19 ] 等. 根据Cowper[17 ] 的研究, 如果梁横截面是方形, $k={10\left( 1+\nu \right)}/({12+11\nu })$, 如果梁横截面是圆形, $k={6\left( 1+\nu \right)}/({7+6\nu })$, 因此对于大多数常见材料, $k$的取值范围为${5}/{6}\sim {10}/{9}$. ...
Timoshenko's shear coefficient for flexural vibrations of beams
1
... 由于铁木辛柯梁的横截面发生了翘曲变形, 其横截面上的剪切应变并非均匀分布, 因此剪力导致的横截面转角$\gamma $并非由平均剪切应变导致;在横截面上的总剪切力$Q$与剪切转角$\gamma $之间通过式(1j)联系, 其中$k$是与梁横截面形状和泊松比$\nu $有关的系数, 被称之为铁木辛柯剪切系数[14 ] . 许多科学家通过复杂的弹性力学分析尝试给出其精确数值, 如Timoshenko[15 , 20 ] , Mindlin等[16 ] , Cowper[17 ] , Stephen[18 ] , Hutchinson[19 ] 等. 根据Cowper[17 ] 的研究, 如果梁横截面是方形, $k={10\left( 1+\nu \right)}/({12+11\nu })$, 如果梁横截面是圆形, $k={6\left( 1+\nu \right)}/({7+6\nu })$, 因此对于大多数常见材料, $k$的取值范围为${5}/{6}\sim {10}/{9}$. ...
The shear coefficient in Timoshenko's beam theory
2
1966
... 由于铁木辛柯梁的横截面发生了翘曲变形, 其横截面上的剪切应变并非均匀分布, 因此剪力导致的横截面转角$\gamma $并非由平均剪切应变导致;在横截面上的总剪切力$Q$与剪切转角$\gamma $之间通过式(1j)联系, 其中$k$是与梁横截面形状和泊松比$\nu $有关的系数, 被称之为铁木辛柯剪切系数[14 ] . 许多科学家通过复杂的弹性力学分析尝试给出其精确数值, 如Timoshenko[15 , 20 ] , Mindlin等[16 ] , Cowper[17 ] , Stephen[18 ] , Hutchinson[19 ] 等. 根据Cowper[17 ] 的研究, 如果梁横截面是方形, $k={10\left( 1+\nu \right)}/({12+11\nu })$, 如果梁横截面是圆形, $k={6\left( 1+\nu \right)}/({7+6\nu })$, 因此对于大多数常见材料, $k$的取值范围为${5}/{6}\sim {10}/{9}$. ...
... [17 ]的研究, 如果梁横截面是方形, $k={10\left( 1+\nu \right)}/({12+11\nu })$, 如果梁横截面是圆形, $k={6\left( 1+\nu \right)}/({7+6\nu })$, 因此对于大多数常见材料, $k$的取值范围为${5}/{6}\sim {10}/{9}$. ...
Timoshenko's shear coefficient from a beam subjected to gravity loading
1
1980
... 由于铁木辛柯梁的横截面发生了翘曲变形, 其横截面上的剪切应变并非均匀分布, 因此剪力导致的横截面转角$\gamma $并非由平均剪切应变导致;在横截面上的总剪切力$Q$与剪切转角$\gamma $之间通过式(1j)联系, 其中$k$是与梁横截面形状和泊松比$\nu $有关的系数, 被称之为铁木辛柯剪切系数[14 ] . 许多科学家通过复杂的弹性力学分析尝试给出其精确数值, 如Timoshenko[15 , 20 ] , Mindlin等[16 ] , Cowper[17 ] , Stephen[18 ] , Hutchinson[19 ] 等. 根据Cowper[17 ] 的研究, 如果梁横截面是方形, $k={10\left( 1+\nu \right)}/({12+11\nu })$, 如果梁横截面是圆形, $k={6\left( 1+\nu \right)}/({7+6\nu })$, 因此对于大多数常见材料, $k$的取值范围为${5}/{6}\sim {10}/{9}$. ...
Transverse vibration of beams, exact versus approximate solutions
1
1981
... 由于铁木辛柯梁的横截面发生了翘曲变形, 其横截面上的剪切应变并非均匀分布, 因此剪力导致的横截面转角$\gamma $并非由平均剪切应变导致;在横截面上的总剪切力$Q$与剪切转角$\gamma $之间通过式(1j)联系, 其中$k$是与梁横截面形状和泊松比$\nu $有关的系数, 被称之为铁木辛柯剪切系数[14 ] . 许多科学家通过复杂的弹性力学分析尝试给出其精确数值, 如Timoshenko[15 , 20 ] , Mindlin等[16 ] , Cowper[17 ] , Stephen[18 ] , Hutchinson[19 ] 等. 根据Cowper[17 ] 的研究, 如果梁横截面是方形, $k={10\left( 1+\nu \right)}/({12+11\nu })$, 如果梁横截面是圆形, $k={6\left( 1+\nu \right)}/({7+6\nu })$, 因此对于大多数常见材料, $k$的取值范围为${5}/{6}\sim {10}/{9}$. ...
Mechanics of Materials
1
1972
... 由于铁木辛柯梁的横截面发生了翘曲变形, 其横截面上的剪切应变并非均匀分布, 因此剪力导致的横截面转角$\gamma $并非由平均剪切应变导致;在横截面上的总剪切力$Q$与剪切转角$\gamma $之间通过式(1j)联系, 其中$k$是与梁横截面形状和泊松比$\nu $有关的系数, 被称之为铁木辛柯剪切系数[14 ] . 许多科学家通过复杂的弹性力学分析尝试给出其精确数值, 如Timoshenko[15 , 20 ] , Mindlin等[16 ] , Cowper[17 ] , Stephen[18 ] , Hutchinson[19 ] 等. 根据Cowper[17 ] 的研究, 如果梁横截面是方形, $k={10\left( 1+\nu \right)}/({12+11\nu })$, 如果梁横截面是圆形, $k={6\left( 1+\nu \right)}/({7+6\nu })$, 因此对于大多数常见材料, $k$的取值范围为${5}/{6}\sim {10}/{9}$. ...