引言
在自然界和工业领域, 流体中的颗粒碰撞普遍存在[1 ] . 如泥沙流中的砂粒碰撞与沉积[2 ] , 石油开采携砂压裂液中的颗粒碰撞与管壁冲蚀等. 这些颗粒群与流体运移的两相流动中, 流体输运的湍流效应和颗粒运动的碰撞相互影响[3 ] . 在颗粒体积分数低至$4.0\times 10^{-4}$情况下[4 ] , 颗粒间的碰撞效应也不应被忽略. 通常采用数值模拟手段来量化整个流场以及单个颗粒的动力学[5 ] .
固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键.
前人对颗粒碰撞搜索算法进行了大量研究, 如分割单元算法也称网格单元算法[13 -15 ] , 将计算域划分成均匀的立方体单元, 单元长度为颗粒直径的整数倍. 计算时间步结束时刻根据颗粒当前位置被分配到某个单元, 只有同一单元或相邻单元内颗粒可能发生碰撞. 一个颗粒最多占据8个单元, 当其成为目标颗粒时, 只对其占据的单元内其他颗粒进行碰撞检测. 该算法遗漏了那些时间步结束前, 离开或穿过立方体单元, 可能与目标颗粒发生碰撞的颗粒. Allen等[16 ] 提出的邻居列表算法, 规定了一个阈值距离来确定颗粒间相互作用的影响半径. 碰撞搜索只对列表内的颗粒对进行搜索, 如果两个颗粒之间的距离大于阈值距离, 其就不可能在下一个时间步中发生碰撞. 所以, 邻居列表需要几个时间步更新一次. 该算法构建的搜索列表内颗粒众多, 在高浓度颗粒存在的应用中, 每对颗粒进行一次判定计算代价过高. Vemuri等[17 ] 提出的八叉树算法, 建立一个能够容纳任意方向上最大颗粒的立方体, 将其作为划分域的基本单元. 在对小颗粒进行搜索碰撞时, 基本单元将会被多次划分八叉树, 每个颗粒根据其大小与单元的关系, 配置到对应单元中. 在计算域内有多种尺寸颗粒时, 需多次划分基本单元, 计算过程繁琐.
Baraff[14 ] 提出了边界盒算法, 使用轴向对齐的边界盒来确定颗粒之间的碰撞. 如果两个颗粒相撞, 其在$x$, $y$和$z$维度上的正交投影将会重叠. 3个列表包含对轴的投影坐标, 每个维度对应一个列表. 在下一个时间步骤, 需要再次对之前排序的列表进行排序. Li等[18 ] 提出的时间相干碰撞搜索算法 (SMB), 是将包围盒AABB投影在笛卡尔坐标轴上, 根据投影间距递增排序建立初步碰撞搜索列表, 通过对列表内所有间距搜索检查确定是否重叠, 建立碰撞列表. 该算法适用于大量移动AABB的系统, 并支持对象的动态插入和删除, 不受物体大小的限制.
上面几种方法对颗粒碰撞的判定, 都采用较小的时间步长进行推进计算, 根据计算时间步结束时颗粒位置, 判断颗粒是否与目标颗粒碰撞. 若时间步选取过大, 会遗漏计算时间步内的颗粒碰撞效应[19 ] , 无法对颗粒碰撞导致的颗粒位置、速度、加速度等变化进行描述影响计算精度. 而无限缩小颗粒计算时间步, 又会造成推进次数的增加, 影响计算效率.
此外, 由于颗粒碰撞搜索方式的改变, 颗粒与流体耦合方式也相应发生变化. 传统CFD-DEM耦合方法, 流体计算时间步长是颗粒计算时间步长的整数倍($\Delta t_f =n\cdot \Delta t_p)$[20 ] . 流体完成一个时间步$\Delta t_f $, 颗粒完成$n$个时间步$\Delta t_p $, 颗粒与流体才进行一次相间力的交换, 导致颗粒在流体内部受力及运动与实际误差较大.
针对CFD-DEM耦合计算时, 颗粒碰撞搜索时间步选取过小导致计算效率低、选取过大导致碰撞颗粒漏判的问题. 本工作通过对颗粒碰撞搜索算法的研究, 使颗粒计算时间步的选取尽可能大、且不受颗粒碰撞时间限制;依据颗粒与流体耦合条件, 自适应调整流体计算时间步长, 实时更新相间力. 以期为颗粒-流体耦合计算提供一种高计算精度、高计算效率的计算方法.
1 流体与颗粒群耦合的数值分析方法
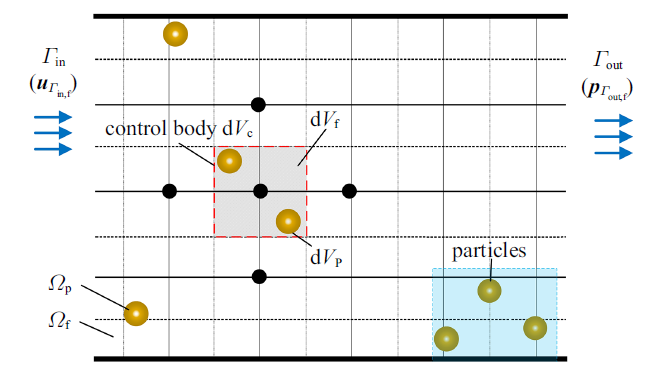
取管道内流体与颗粒群为研究对象, 建立圆管内流体与颗粒群耦合的两相流模型, 如图1 所示. 该模型共分2个域, 颗粒群域$\varOmega_p $和流体域$\varOmega_f $. 流体域入口采用速度边界$\varGamma _in $, 出口采用压力边界$\varGamma _out$, 速度和压力用${ u}_{\varGamma in, f} $和${ p}_{\varGamma out, f} $表示. 管道内壁面边界(流体域与管道域耦合界面) $\varGamma _int $假定为无滑移, 用${ u}_{\varGamma \rm I, f} ={\bf0}$表示. 在圆管内两相流体系中任取一控制体d$V_c $, 该控制体内流体和颗粒占据的体积分别为d$V_f$和d$V_p $.
图1
图1
流体与颗粒群耦合模型示意图
Fig.1
Schematic diagram of fluid and particle group coupling model
1.1 流体控制方程
(1) $\dfrac{\partial (\alpha_f \rho _f )}{\partial t}+\nabla \cdot \rho _f \alpha_f { u}_f =0$
(2) $\dfrac{\partial }{\partial t}\left( {\alpha_f \rho _f { u}_f } \right)+\nabla \cdot \left( {\alpha_f \rho _f { u}_f { u}_f } \right)= \\ -\alpha_f \nabla p_f +\alpha_f \nabla \cdot \overline {\overline {\tau}} + { S}_f +\alpha_f \rho _f { g}$
式中, $\rho _f $为流体密度, ${ u}_f $为流体速度矢量, $p_f$为流体压力, ${ g}$为重力加速度, $\alpha_f $为流体的体积分数; $\overline {\overline {\tau}} $为流体黏性应力张量, ${ S}_f$为流体与颗粒动量交换力源项.
两相流与单相流的主要区别在于, 流体相中流体体积分数$\alpha_f $和源项${ S}_f $的变化. 流体体积分数$\alpha_f$是流体单元中流体所占有的体积份额[22 ] , ${ S}_f $是颗粒与流体间动量交换力源项[23 ] , 如图2 所示.
(3) $\alpha_f =1-\alpha_p =1-\dfrac{1}{V_E}\sum_{i=1}^{n_p } {V_p^{\left( i \right)} }$
(4) ${ S}_f =\dfrac{1}{V_E }({ F}_E +{ M}_E)=\dfrac{1}{V_E }\left[ {\sum_{i=1}^{n_p } {({ F}_f^{(i)}+{ F}_f^{(i)} \times H)} } \right]$
图2
图2
两相流体计算单元示意图
Fig.2
Schematic diagram of two-phase fluid calculation unit
式中, $V_E $为流体单元体积, $\alpha_p $为流体单元内颗粒占有的体积分数, $V_p^{(i)} $为流体单元内第$i$个颗粒体积, ${ F}_f^{(i)}$为流体单元内第$i$个颗粒受到流体作用力, $n_p$为流体单元内颗粒个数; ${ F}_E $和${ M}_E $分别为流体单元内所有颗粒与流体作用力的合力和合力矩, $H$为颗粒到流体单元质心的距离.
1.2 颗粒受力分析及动力学方程
颗粒被裹挟在流体内部, 跟随流体运动, 不稳定的流态会对颗粒产生多种作用力, 其合力${ F}_f $可表示为
(5) ${ F}_f ={ F}_d +{ F}_p +{ F}_vm +{ F}_saff +{ F}_ml +{ F}_b$
式中, ${ F}_d $为颗粒在流体中受到的阻力(曳力), ${ F}_p$为压力梯度力, ${ F}_vm$为虚拟质量力[24 ] , ${ F}_saff $为Saffman剪切升力[25 ] , ${ F}_ml$为Magnus旋转升力[26 ] , ${ F}_b$为倍瑟特力[27 ] .
由于颗粒直径较小, 忽略Saffman剪切升力、 Magnus旋转升力、 压力梯度力、 虚拟质量力、 倍瑟特力对颗粒的影响[28 ] . 阻力(曳力)在流体作用于颗粒上的力中起主要作用[29 ] . 当颗粒的运动速度大于流体的流速时, 流体作用在颗粒上的力表现为阻力, 当流体的流速大于颗粒速度时, 作用在颗粒上的力表现为曳力. 计算公式为[30 ]
(6) ${ F}_d =\dfrac{1}{8}C_d \pi \rho _f D_p^{2} \left| {{ u}_f -{ u}_p } \right|({ u}_f -{ u}_p )$
(7) $C_d =\left\{ {\begin{array}{ll} \dfrac{24}{Re_p }(1+0.15Re_p^{0.687}), & Re_p <1000 \\ 0.44, & Re_p \geqslant 1000 \\ \end{array}} \right.$
(8) $Re_p =\dfrac{\alpha_f \rho _f D_p \left| {{ u}_{f} -{ u}_p } \right|}{\mu_f}$
式中, $C_d $为曳力系数, $Re_p $为颗粒雷诺数, $D_p $为颗粒直径, $\mu_f $为流体表观黏度.
取任一颗粒$i$为研究对象, 其运动由平移和旋转组成, 根据牛顿第二定律得[31 ]
(9) $m_{i} \dfrac{d{ u}_{i} }{dt}=({ F}_{cn, ij} +{ F}_{ct, ij} )+{ F}_{f, i} +{ F}_{g, i}$
(10) $I_{i} \dfrac{d{ \omega }_{i} }{dt}={ M}_c$
式中, $m_{i} $为颗粒$i$质量, ${ F}_{cn, ij} $和${ F}_{ct, ij}$分别为颗粒$i$与颗粒$j$的法向和切向碰撞力, ${ F}_{g, i} $为颗粒$i$重力, $I_{i} $为颗粒$i$的惯性矩, ${ \omega }_{i} $为颗粒$i$的角速度, ${ M}_c$为颗粒碰撞引起的力矩
(11) ${ M}_c =\dfrac{D_p^{i} }{2}{ F}_{ct, ij}$
假设颗粒在任意$t$时刻, 合力为${ F}_{(t)} $, 速度为${ u}_{\left( t\right)} $, 位置为$\left( {x_{\left( t \right)} , y_{\left( t \right)}, z_{\left( t \right)} } \right)$. 此时颗粒的加速度为${ a}_{(t)} ={ F}_{(t)} /m_{i} $. 当颗粒运动$\Delta t$后, 其瞬时速度为[32 ]
(12) ${ u}_{(t+\Delta t)} ={ u}_{(t)} +(1-\gamma ){ a}_{\left( t \right)} \Delta t+\gamma { a}_{(t+\Delta t)} \Delta t, \ 0\leqslant \gamma \leqslant 1$
(13) ${ s}_{(t+\Delta t)} ={ s}_{(t)} +{ u}_{(t)} \Delta t+(1-\gamma ){ a}_{(t)} \dfrac{\Delta t^{2}}{2}+\gamma { a}_{(t+\Delta t)} \dfrac{\Delta t^{2}}{2}$
式中, $\gamma $为插值系数, $\gamma =0.5$为中心差分.
在空间直角坐标系下, 颗粒在$t+\Delta t$时刻颗粒的位置为$\left( {x_{\left({t+\Delta t} \right)} , y_{\left( {t+\Delta t} \right)} , z_{\left( {t+\Delta t} \right)} } \right)$, 其计算公式为
(14) $\left. {\begin{array}{l} x_{\left( {t+\Delta t} \right)} =x_{\left( t \right)} +\Delta t\left( {u_{\left( {t+\Delta t} \right)}^{x} } \right) \\ y_{\left( {t+\Delta t} \right)} =y_{\left( t \right)} +\Delta t\left( {u_{\left( {t+\Delta t} \right)}^{y} } \right) \\ z_{\left( {t+\Delta t} \right)} =z_{\left( t \right)} +\Delta t\left( {u_{\left( {t+\Delta t} \right)}^{z} } \right) \\ \end{array}} \right\}$
1.3 颗粒碰撞模型
颗粒碰撞过程的假设: (1)颗粒是球形的刚体; (2)颗粒间只存在二体碰撞; (3)颗粒密度相同、直径可以不同, 颗粒群初始状态为均匀分布. 为了建立颗粒间碰撞的计算方法, 不妨取颗粒群中任两颗粒记为颗粒$i$和颗粒$j$, 设颗粒$i$直径为$D_p^{i}$、质量为$m_{i} $、颗粒$j$直径为$D_p^{j} $、质量为$m_{j} $, 两颗粒质量比为$q={m_{i}}/{m_{j}}$.
两颗粒发生碰撞满足动量定理, 如图3 所示[33 ] .
(15) $-m_{i} \left( {{ {u}'}_{i} -{ u}_{i} } \right)= m_{j} \left( {{ {u}'}_{j} -{ u}_{j} } \right)={ J}$
(16) $\left. \begin{array}{l} I_{i} \left( {{ {\omega }'}_{i} -{ \omega }_{i} } \right)=\dfrac{D_p^{i} }{2}\left( {{ k}\times { J}} \right)\\ -I_{j} \left( {{ {\omega }'}_{j} -{ \omega }_{j} } \right)=\dfrac{D_p^{j} }{2}\left( {{ k}\times { J}} \right) \end{array} \right\}$
图3
图3
颗粒碰撞示意图
Fig.3
Schematic diagram of particle collision
式中, ${ u}_{i} $和${ {u}'}_{i} $为颗粒$i$碰撞前、后平动速度; ${ \omega }_{i} $和${ {\omega }'}_{i} $为颗粒$i$碰撞前、后转动速度; ${ k}$为颗粒相对速度的法向单位向量; ${ J}$为颗粒碰撞时的冲量; $I_{i}$和$I_{j} $为颗粒$i$与颗粒$j$的转动惯量.
当两个颗粒碰撞后有滑移时, 碰撞后平动速度和转动速度为
(17) ${ {u}'}_{i} ={ u}_{i} -({ k}+\lambda { t})\left( {1+e} \right)\left( {{ k}\cdot { u}_{ij} } \right)\dfrac{1}{1+q}$
(18) ${ {u}'}_{j} ={ u}_{j} -({ k}+\lambda { t})\left( {1+e} \right)\left( {{ k}\cdot { u}_{ij} } \right)\dfrac{q}{1+q}$
(19) ${ {\omega }'}_{i} ={ \omega }_{i} +\dfrac{5}{D_p^{i} }\left( {1+e} \right)\left( {{ k}\times { \tau }} \right)\left( {{ k}\cdot { u}_{ij} } \right)\dfrac{1}{1+q}$
(20) ${ {\omega }'}_{j} ={ \omega }_{j} +\dfrac{5}{D_p^{j} }\left( {1+e} \right)\left( {{ k}\times { \tau }} \right)\left( {{ k}\cdot { u}_{ij} } \right)\dfrac{1}{1+q}$
颗粒在碰撞时停止滑移, 碰撞后平动速度和转动速度为
(21) ${ {u}'}_{i} ={ u}_{i} -\left[ {\left( {1+e} \right){{ k}\cdot { u}_{ij} } +\dfrac{2}{7}\left| {{ u}_{ij, \tau } } \right|{ \tau }} \right]\dfrac{1}{1+q}$
(22) ${ {u}'}_{j} ={ u}_{j} -\left[ {\left( {1+e} \right){{ k}\cdot { u}_{ij} } +\dfrac{2}{7}\left| {{ u}_{ij, \tau } } \right|{ \tau }} \right]\dfrac{q}{1+q}$
(23) ${ {\omega }'}_{i} ={ \omega }_{i} - {\dfrac{10}{7D_p^{i} }} \left| {{ u}_{ij, \tau } } \right|\left( {{ k}\times { \tau }} \right)\dfrac{1}{1+q}$
(24) ${ {\omega }'}_{j} ={ \omega }_{j} - {\dfrac{10}{7D_p^{j} }} \left| {{ u}_{ij, \tau } } \right|\left( {{ k}\times { \tau }} \right)\dfrac{q}{1+q}$
式中, $\lambda $为摩擦系数, $e$为颗粒碰撞恢复系数, ${ \tau}$为颗粒相对速度的切向单位向量, ${ u}_{ij} $为颗粒碰撞前相对速度, ${ u}_{ij, \tau } $为颗粒碰撞前相对速度的切向分量.
(25) ${J}_{\tau } >-\dfrac{2}{7}\dfrac{m_{i} m_{j} }{m_{i} +m_{j} }\left| {{ u}_{ij, \tau } } \right|$
式中, ${J}_{\tau } $为颗粒碰撞冲量的切向分量.
根据弹性力学碰撞理论[34 ] , 两颗粒碰撞时间$t_c$为
(26) $t_c =1.47 {\dfrac{5M}{4w}}\dfrac{1}{|{ u}_{ij}^{\ast } |} \left( {1+\dfrac{1}{e}} \right)$
式中, ${ u}_{ij}^{\ast } $为修正后颗粒相对速度, ${ u}_{ij}^{\ast }=(1-\chi ){ u}_{ij} +\chi { {u}'}_{ij} $, ${ {u}'}_{ij}$为碰撞后相对速度; $\chi $加权系数; $M$为颗粒$i$与颗粒$j$等效质量, $M=m_{i}m_{j} /(m_{i} +m_{j})$; $w$为碰撞力相关系数$w={4}/[{3\pi \left( {\alpha_{1} +\alpha_{2} } \right)}]\sqrt{{D_p^{i} D_p^{j} }/({D_p^{i}+D_p^{j} } )}$, $\alpha_{1} =\left( {1-\mu_{i}^{2} } \right)/(\pi E_{i}) $;$\alpha_{2} =\left( {1-\mu_{j}^{2} } \right)/(\pi E_{j})$; $\mu_{i}$和$\mu_{j} $分别为颗粒$i$与颗粒$j$的泊松比; $E_{i} $和$E_{j}$分别为颗粒$i$与颗粒$j$的弹性模量.
(27) ${ F}_{c, ij} =\dfrac{{ J}}{t_c }=\dfrac{e{{ k}\cdot { u}_{ij}^{\ast } }{ k}E_{i} E_{j} }{E_{i} \left( {1-\mu_{i}^{2} } \right)+E_{j} \left( {1-\mu_{j}^{2} } \right)}\sqrt {\dfrac{D_p^{i} D_p^{j} }{D_p^{i} +D_p^{j} }}$
由式(15)和式(16)可知, 两颗粒碰撞过程满足动量守恒, 但碰撞过程能量发生耗散, 不考虑颗粒旋转时的能量损失, 则颗粒碰撞耗散能量为[35 ]
(28) $\Delta E_{k} =-m_{i} \dfrac{1-e^{2}}{4}{ u}_{ji}^{2} \cdot { k}$
(29) $\Delta E_{q} =\dfrac{1}{2}m_{i} ({ {u}'}^{2}_{i} -{ u}_{i(t+\Delta t)}^{2} )$
由式(28)和式(29), 得到颗粒$i$能量耗散率为
(30) $\dfrac{\Delta E_{k} +\Delta E_{q} }{Q}=\dfrac{e^{2}{ u}_{ji}^{2} \cdot { k}+2{ {u}'}_{i}^{2} -2{ u}_{i(t+\Delta t)}^{2} }{2{ u}_{i}^{2} }$
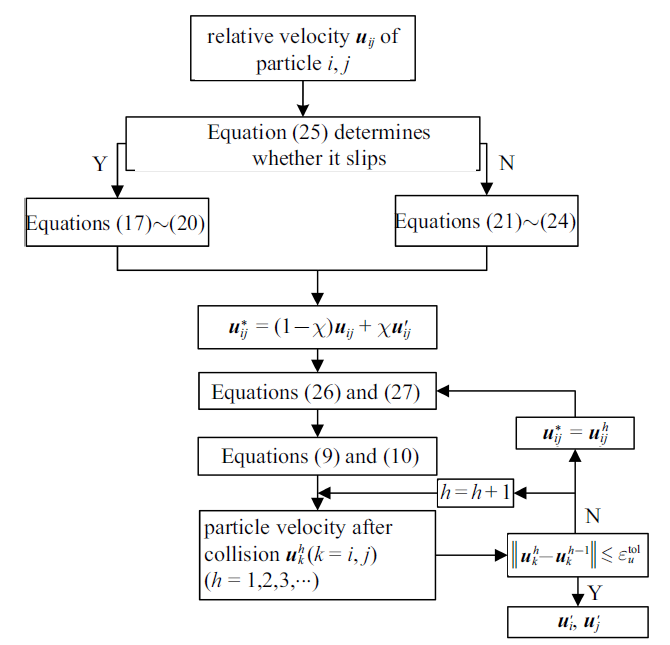
颗粒碰撞计算流程如图4 所示, 碰撞颗粒$i$与颗粒$j$相对速度${ u}_{ij}$通过式(25)判断颗粒是否发生滑移, 若发生滑移则通过式(17) $\sim\!$式(20)计算颗粒碰撞后速度, 若颗粒不发生滑移则通过式(21) $\sim\!$式(24)计算颗粒碰撞后速度. 采用插值算法, 将颗粒碰撞前相对速度${ u}_{ij} $与碰撞后相对速度${ {u}'}_{ij}$进行加权插值得到${ u}_{ij}^{\ast } $, 代入式(26)和式(27)得到颗粒碰撞时间$t_c $和碰撞力${ F}_{c, ij} $, 然后将其代入式(9)和式(10)得到颗粒碰撞后的速度, 并对碰撞后速度的设定和求得值进行比较判断, 若不满足$\left\| {{ u}_{k}^{h}-{ u}_{k}^{h-1} } \right\|\leqslant \varepsilon_{u}^tol $, 需修正碰撞后速度, 重复式(26)、式(27)和式(9)、式(10)计算; 否则, 求得颗粒碰撞后速度值. 其中, $h$为求解次数, $\varepsilon_{u}^tol $为速度收敛容差.
图4
图4
颗粒碰撞后速度计算流程
Fig.4
Calculation flowchart of velocity for Particle collision
1.4 耦合分析计算方法
颗粒位置变化直接导致流体体积分数和动量交换力源项的变化, 因此, 根据流体单元内流体体积分数和动量交换力源项的变化, 建立流体与颗粒群耦合的收敛条件
(31) $\left\| {\alpha_{f, N} -\alpha_{f, 0} } \right\|\leqslant \varepsilon_{f, \alpha }^tol$
(32) $\left\| {{ S}_{f, N} -{ S}_{f, 0} } \right\|\leqslant \varepsilon_{f, S}^tol$
式中, $\varepsilon_{f, \alpha }^tol $为流体体积分数收敛容差; $\varepsilon_{f, S}^tol $为动量交换力源项收敛容差.
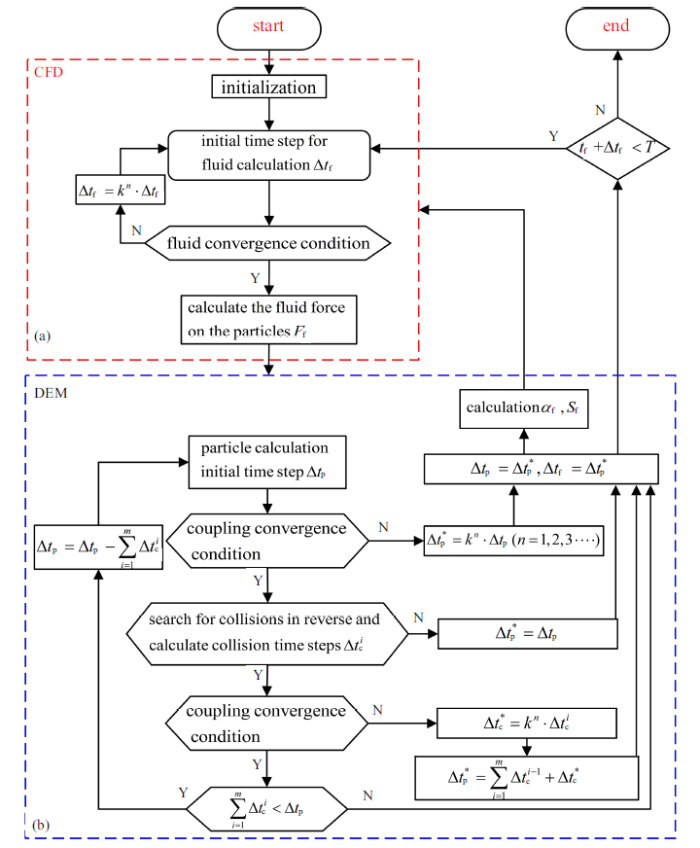
CFD-DEM耦合分析时, 其耦合计算流程如图5 所示, CFD计算采用SIMPLE算法求解流体域连续性方程和动量方程, 根据颗粒和流体的相对速度, 计算颗粒受到的流体作用力${ F}_f $, 传递给DEM求解器, 并启动DEM计算. DEM采用牛顿第二运动定律求解颗粒运动方程, 根据颗粒在$\Delta t_p $的运动轨迹, 搜索和判断颗粒碰撞, 若颗粒产生碰撞, 需修正颗粒计算时间步长. 根据颗粒在计算域内位置和受力的变化计算得到流体的体积分数$\alpha_f$和动量交换力源项${ S}_f $, 若不满足式(31)和式(32), 传递给CFD求解器, 自动更新流体计算时间步长, 并推进CFD计算.
图5
图5
CFD-DEM耦合计算流程图
Fig.5
Flow chart of CFD-DEM coupling calculation
CFD求解如图5 (a)所示, 对流体计算域进行初始化, 设置流体初始计算时间步长$\Delta t_f $, 判断流体是否满足收敛条件, 若满足, CFD求解结束. 若不满足, 缩短流体时间步$\Delta t_f =k^{n}\cdot \Delta t_f$ $(k\leqslant 1$为修正系数, $n=1, 2, 3, \cdots $为流体时间步缩短次数), 重新进行CFD计算, 直至满足流体收敛条件, CFD求解结束.
CFD求解结束后, 计算$\Delta t_f $时刻颗粒受到的流体力${ F}_f$传递给DEM, 并启动DEM求解.
DEM求解如图5 (b)所示, 设置颗粒计算初始时间步长$\Delta t_p =\Delta t_f $, 判断颗粒在$\Delta t_p$时刻计算结果是否满足式(31)、式(32)颗粒与流体耦合收敛条件, 若不满足, 缩短颗粒时间步$\Delta t_p^{\ast } =k^{n}\cdot \Delta t_p $, 重新进行DEM求解, 直至满足耦合收敛条件, DEM求解结束, 此时耦合分析的时间步为$\Delta t_p^{\ast } $. 若满足, 根据颗粒在$\Delta t_p $的运动轨迹, 搜索和判断颗粒是否产生碰撞, 若无碰撞, $\Delta t_p^{\ast } =\Delta t_p $, DEM求解结束. 若存在碰撞, 计算得到最先发生碰撞的时间$\Delta t_c^{i} \leqslant \Delta t_p $, 并根据$\Delta t_c^{1} $的颗粒位置, 判断是否满足耦合收敛条件. 若不满足, 缩短颗粒求解时间$\Delta t_c^{\ast } =k^{n}\cdot \Delta t_c^{i} $, 重新进行DEM求解, 直至满足耦合收敛条件, DEM求解结束, 此时耦合分析的时间步为$\Delta t_p^{\ast } =\sum_{i=1}^m {\Delta t_c^{i-1} } +\Delta t_c^{\ast } $(其中$i=$1时, 时间步内第1次搜索到碰撞, $\Delta t_p^{\ast } =\Delta t_c^{\ast } )$. 若满足, 需判断碰撞累计时长是否满足$\sum_{i=1}^m {\Delta t_c^{i} }<\Delta t_p $, 若不满足, DEM求解结束. 若满足, 则以剩余时间$\Delta t_p=\Delta t_p -\sum_{i=1}^m {\Delta t_c^{i} }$作为新的颗粒时间步长重新进行颗粒计算, 并搜索颗粒碰撞, 根据$\Delta t_c^{2}$的颗粒位置, 判断是否满足耦合收敛条件, 若不满足, 缩短颗粒求解时间$\Delta t_c^{\ast } =k^{n}\cdot \Delta t_c^{2} $, 重新进行DEM求解, 直至满足耦合收敛条件, DEM求解结束, 此时耦合分析的时间步为$\Delta t_p^{\ast } =\sum_{i=1}^m {\Delta t_c^{i-1} } +\Delta t_c^{\ast }$ (其中$i=$2时, 时间步内第2次搜索到碰撞, $\Delta t_p^{\ast } =\Delta t_c^{1} +\Delta t_c^{\ast } )$. 若满足耦合条件, 再次判断碰撞累计时长是否满足$\sum_{i=1}^m {\Delta t_c^{i} } <\Delta t_p (i=$2时, $\Delta t_c^{1} +\Delta t_c^{2} <\Delta t_p )$, 若不满足DEM求解结束. 若满足, 重新以剩余时间$\Delta t_p =\Delta t_p-\sum_{i=1}^m {\Delta t_c^{i} }$进行颗粒计算直至碰撞累计时长$\sum_{i=1}^m {\Delta t_c^{i} }<\Delta t_p $不成立, 或者不满足耦合收敛条件, 此时$\Delta t_p^{\ast }=\sum_{i=1}^m {\Delta t_c^{n-1} } +\Delta t_c^{\ast }$ (时间步内进行$n$次碰撞) DEM求解结束.
DEM求解结束后, 计算流体体积分数$\alpha_f $和动量交换力源项${ S}_f $, 并根据耦合分析时间步$\Delta t_p^{\ast } $, 对颗粒和流体计算时间步进行修正$\Delta t_p =\Delta t_p^{\ast } , \Delta t_f =\Delta t_p^{\ast } $, 判断流体计算时间$t_f +\Delta t_f<T$是否成立, 若成立, 将$\alpha_f $和${ S}_f $传递给CFD, 重新开始CFD求解; 若不成立, 则耦合计算结束.
其中, 颗粒碰撞的搜索采用的是逆向迭代算法, 增大计算时间步长不会影响颗粒碰撞搜索的计算精度. 颗粒不发生碰撞时, 计算时间步长的增大, 使颗粒运动位移增大, 导致流体计算单元内流体体积分数$\alpha_f $和动量交换力源项$ S_f$变化过快, 造成颗粒-流体耦合计算误差. 式(31)和式(32)限制误差的大小, 保证颗粒-流体耦合计算误差不随计算时间步长变化.
2 颗粒碰撞搜索的逆向迭代算法
流体内部的大量颗粒群随流体进行不规则运动, 颗粒与颗粒、颗粒与壁面存在碰撞, 快速、准确判断颗粒间发生碰撞, 是提高颗粒与流体耦合计算效率的有效方法.
2.1 目标颗粒的变网格构造
在数值模拟颗粒间碰撞时, 在一个时间步内颗粒只能与周边颗粒发生碰撞[36 ] , 将目标颗粒与周围可能发生碰撞的颗粒组成一个搜索空间网格进行碰撞搜索. 具体方法如下: 将目标颗粒在计算时间步的运动位移, 作为空间网格对角线, 建立搜索空间网格体, 如图6 (a)所示. 由于计算域内不同颗粒在$\Delta t$时间步内运动的位移不同, 所构建的空间网格也会出现不同尺寸, 即为变网格.
图6
图6
颗粒碰撞搜索示意图: (a)变网格建立示意图; (b)颗粒运动轨迹穿过空间搜索网格示意图; (c)颗粒间距筛选示意图
Fig.6
Search diagram of particle collision: (a) Schematic diagram of variable grid establishment; (b) schematic diagram of particle trajectories passing through the spatial search grid; (c) schematic diagram of particle spacing screening
2.2 目标颗粒碰撞列表建立
为了缩短颗粒碰撞搜索和判定时间, 对目标颗粒周围颗粒筛选, 保留与目标颗粒可能发生碰撞的颗粒, 建立碰撞搜索列表, 具体步骤如下.
(1)在计算时间步内, 筛选运动轨迹与空间网格体存在交集的颗粒, 如图6 (a)所示.
设目标颗粒在$t$时刻和$t+\Delta t$时刻的坐标为$(x_{0} , y_{0} , z_{0})$和$(x_{1} , y_{1} , z_{1} )$, 以此两点连线为对角线, 构建目标颗粒的碰撞搜索空间网格体.
对计算域内任一颗粒$j$, 从$t$到$t+\Delta t$时刻的运动轨迹与目标颗粒所建空间网格体若有交集, 则可能产生碰撞;否则无碰撞. 颗粒运动轨迹穿过空间网格体必定与空间网格体对角面$H$或$W$相交, 因此计算颗粒运动轨迹与对角面的交点, 并判断交点是否在空间网格体的范围内即可, 如图6 (b)所示.
不妨取颗粒$j$运动轨迹经过坐标$(x_{j} , y_{j} , z_{j} )$, 且方向向量为${ m}=(X_{j} , Y_{j} , Z_{j} )$, 在$H$平面经过点$(x_{0} , y_{0} , z_{0} )$, 法向量为${ n}=(n_{1} , n_{2} , n_{3} )$, 运动轨迹与$H$平面交点$o(x, y, z)$.
(33) $\left. {\begin{array}{l} x=x_{j} +\phi \cdot X_{j} \\ y=y_{j} +\phi \cdot Y_{j} \\ z=z_{j} +\phi \cdot Z_{j} \\ \end{array}} \right\}$
(34) $n_{1} \cdot (x-x_{0} )+n_{2} \cdot (y-y_{0} )+n_{3} \cdot (z-z_{0} )=0$
其中, 颗粒$j$运动轨迹与$H$平面的交点$o(x, y, z)$一定满足式(33)和式(34),
(35) $\phi =\dfrac{(x_{0} -x_{j} )\cdot n_{1} +(y_{0} -y_{j} )\cdot n_{2} +(z_{0} -z_{j} )\cdot n_{3}}{n_{1} \cdot X_{j} +n_{2} \cdot Y_{j} +n_{3} \cdot Z_{j}}$
将$\phi $代入式(33)得到交点$o(x, y, z)$坐标, 若交点坐标在空间网格体范围内, 则说明运动轨迹穿过空间网格体. 若交点坐标不在空间网格体范围内, 或式(35)分母为0 (运动轨迹与$H$平面平行), 则运动轨迹与$H$平面不相交. 需用相同方法判断运动轨迹与$W$平面是否相交, 若运动轨迹与$W$平面相交, 说明运动轨迹穿过空间网格体.
(2)依据颗粒与目标颗粒运动轨迹间距离小于或等于两颗粒半径之和的条件, 再次筛选可能碰撞颗粒, 如图6 (c)所示.
目标颗粒$i$运动轨迹方向向量为${ e}=(X_{i} , Y_{i} , Z_{i} )$, 颗粒$j$运动轨迹方向向量为${ b}=(X_{j} , Y_{j} , Z_{j} )$. 将${ e}\times { b}={ c}_{\bot } $得到向量${ e}, { b}$的公垂向量${ c}_{\bot } =(X, Y, Z)$.
(36) ${ e}\times { b}=\left| \begin{array}{*{20}c} i&j & k \\ {X_{i} }&{Y_{i} }& {Z_{i} } \\ {X_{j} }&{Y_{j} }&{Z_{j} } \\ \end{array} \right|=\langle i\left| \begin{array}{*{20}c} {Y_{i} }&{Z_{i} } \\ {Y_{j} }&{Z_{j} } \\ \end{array} \right|, \ \ -j\left| \begin{array}{*{20}c} {X_{i} }& {Z_{i} } \\ {X_{j} }& {Z_{j} } \\ \end{array} \right|, \\ k\left|\begin{array}{*{20}c} {X_{i} }& {Y_{i} } \\ {X_{j} }&{Y_{j} } \\ \end{array} \right| \rangle=(X, Y, Z)$
取目标颗粒$i$运动轨迹上任意一点$E$和颗粒$j$运动轨迹上任意一点$B$, 得到向量${ e b}$, 将向量${ e b}$在公垂向量${ c}_{\bot } $方向上做投影, 得到目标颗粒$i$与颗粒$j$运动轨迹间最短距离$d$如下
(37) $d=\dfrac{\left| {{ e b}\times { c}_{\bot } } \right|}{\left| {{ c}_{\bot } } \right|}$
在计算时间步内, 若两颗粒运动轨迹最近距离$d\leqslant (D_p^{i}+D_p^{j})/2$, 则目标颗粒$i$可能与颗粒$j$发生碰撞, 颗粒$j$保留. 若$d>(D_p^{i} +D_p^{j} )/2$, 则目标颗粒$i$不会与颗粒$j$发生碰撞.
经(1)(2)两步筛选后, 保留下来的颗粒形成目标颗粒碰撞搜索列表.
2.3 碰撞颗粒的逆向搜索算法
在提高颗粒碰撞计算效率时, 采用了较大的计算时间步$\Delta t_p $后, 为了解决颗粒碰撞漏判状况, 沿颗粒走过的运行轨迹采用逆向搜索方式, 搜索判断两颗粒是否存在碰撞. 若不存在, 说明该时间步内计算结果正确, 可进行下一个时间步计算, 若存在碰撞, 确定发生碰撞时间, 修正颗粒计算时间步.
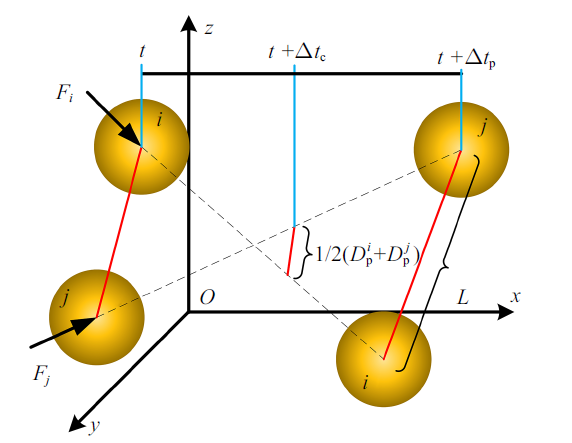
如图7 所示, 假设在计算时间步$\Delta t_p $内存在$t+\Delta t_c $时刻, 颗粒$i$与颗粒$j$产生碰撞. 根据颗粒运动轨迹计算方法, 得到颗粒$i$与颗粒$j$在时间增量为$\Delta t_c $时颗粒的位置坐标为
(38a) $\left. {\begin{array}{l} x_{i\left( {t+\Delta t_c } \right)} =x_{i\left( t \right)} +\Delta t_c \left[ {ku_{i\left( t \right)}^{x} +(1-k)u_{i\left( {t+\Delta t_c } \right)}^{x} } \right] \\ y_{i\left( {t+\Delta t_c } \right)} =y_{i\left( t \right)} +\Delta t_c \left[ {ku_{i\left( t \right)}^{y} +(1-k)u_{i\left( {t+\Delta t_c } \right)}^{y} } \right] \\ z_{i\left( {t+\Delta t_c } \right)} =z_{i\left( t \right)} +\Delta t_c \left[ {ku_{i\left( t \right)}^{z} +(1-k)u_{i\left( {t+\Delta t_c } \right)}^{z} } \right] \\ \end{array}} \right\}$
(38b) $\left. {\begin{array}{l} x_{j\left( {t+\Delta t_c } \right)} =x_{j\left( t \right)} +\Delta t_c \left[ {ku_{j\left( t \right)}^{x} +(1-k)u_{j\left( {t+\Delta t_c } \right)}^{x} } \right] \\ y_{j\left( {t+\Delta t_c } \right)} =y_{j\left( t \right)} +\Delta t_c \left[ {ku_{j\left( t \right)}^{y} +(1-k)u_{j\left( {t+\Delta t_c } \right)}^{y} } \right] \\ z_{j\left( {t+\Delta t_c } \right)} =z_{j\left( t \right)} +\Delta t_c \left[ {ku_{i\left( t \right)}^{z} +(1-k)u_{i\left( {t+\Delta t_c } \right)}^{z} } \right] \\ \end{array}} \right\}$
图7
图7
颗粒碰撞时间求解示意图
Fig.7
Schematic diagram of particle collision time solution
颗粒$i$与颗粒$j$在$\Delta t_c $处的距离和发生碰撞条件为
(39) $\Big[\left( {x_{i\left( {t+\Delta t_c } \right)} -x_{j\left( {t+\Delta t_c } \right)} } \right)^{2}+\left( {y_{i\left( {t+\Delta t_c } \right)} -y_{j\left( {t+\Delta t_c } \right)} } \right)^{2}+ \\ \left( {z_{i\left( {t+\Delta t_c } \right)} -z_{j\left( {t+\Delta t_c } \right)} } \right)^{2}\Big]^{1/2} =\dfrac{1}{2}\left( {D_p^{i} +D_p^{j} } \right)$
方程中颗粒$i$和颗粒$j$在$t$时刻的速度和坐标均为已知, 方程可化简成一元四次方程
(40) $\Delta t_c^{4}+A\Delta t_c^{3}+B\Delta t_c^{2}+C\Delta t_c +D=0\left( {0<\Delta t_c <\Delta t_p } \right)$
(41) $\left. \begin{array}{l} A=2\bigg[ \left( {x_{i\left( t \right)} -x_{j\left( t \right)} } \right)\left( {a_{i\left( t \right)}^{x} -a_{j\left( t \right)}^{x} } \right)+\left( {y_{i\left( t \right)} -y_{j\left( t \right)} } \right)\cdot\\[2.5mm]\qquad \left( {a_{i\left( t \right)}^{y} -a_{j\left( t \right)}^{y} } \right) +\left( {z_{i\left( t \right)} -z_{j\left( t \right)} } \right)\left( {a_{i\left( t \right)}^{z} -a_{j\left( t \right)}^{z} } \right) \bigg]\bigg/\\[2.5mm]\qquad \Big( {a_{i\left( t \right)}^{x} -a_{j\left( t \right)}^{x} } + {a_{i\left( t \right)}^{y} -a_{j\left( t \right)}^{y} } + {a_{i\left( t \right)}^{z} -a_{i\left( t \right)}^{z} }\Big) \\[2.5mm] B=\bigg[ \left( {u_{i\left( t \right)}^{x} -u_{j\left( t \right)}^{x} } \right)^{2}+\left( {u_{i\left( t \right)}^{y} -u_{j\left( t \right)}^{y} } \right)^{2}+\left( {u_{i\left( t \right)}^{z} -u_{j\left( t \right)}^{z} } \right)^{2}+\\[2.5mm]\qquad 2\left( {x_{i\left( t \right)} -x_{j\left( t \right)} } \right)\left( {a_{i\left( t \right)}^{x} -a_{j\left( t \right)}^{x} } \right)+2\left( {y_{i\left( t \right)} -y_{j\left( t \right)} } \right)\cdot\\[2.5mm]\qquad \left( {a_{i\left( t \right)}^{y} -a_{j\left( t \right)}^{y} } \right) +2\left( {z_{i\left( t \right)} -z_{j\left( t \right)} } \right)\left( {a_{i\left( t \right)}^{z} -a_{j\left( t \right)}^{z} } \right) \bigg]\bigg/\\[2.5mm]\qquad \Big( {a_{i\left( t \right)}^{x} -a_{j\left( t \right)}^{x} } + {a_{i\left( t \right)}^{y} -a_{j\left( t \right)}^{y} } + {a_{i\left( t \right)}^{z} -a_{i\left( t \right)}^{z} } \ \Big)\\[2.5mm] C=\bigg[ 2\left( {u_{i\left( t \right)}^{x} -u_{j\left( t \right)}^{x} } \right)\left( {x_{i\left( t \right)} -x_{j\left( t \right)} } \right)+2\left( {u_{i\left( t \right)}^{y} -u_{j\left( t \right)}^{y} } \right)\cdot\\[2.5mm]\qquad \left( {y_{i\left( t \right)} -y_{j\left( t \right)} } \right) +2\left( {u_{i\left( t \right)}^{z} -u_{j\left( t \right)}^{z} } \right)\left( {z_{i\left( t \right)} -z_{j\left( t \right)} } \right) \bigg]\bigg/\\[2.5mm]\qquad\Big( {a_{i\left( t \right)}^{x} -a_{j\left( t \right)}^{x} } + {a_{i\left( t \right)}^{y} -a_{j\left( t \right)}^{y} } + {a_{i\left( t \right)}^{z} -a_{i\left( t \right)}^{z} } \Big) \\[2.5mm] D=\bigg\{\bigg[ \left( {x_{i\left( t \right)} -x_{j\left( t \right)} } \right)^{2}+\left( {y_{i\left( t \right)} -y_{j\left( t \right)} } \right)^{2}+\left( {z_{i\left( t \right)} -z_{j\left( t \right)} } \right)^{2} \bigg]-\\[2.5mm]\qquad \dfrac{1}{4}\left( {D_p^{i} +D_p^{j} } \right)^{2}\bigg\}\bigg/\Big( {a_{i\left( t \right)}^{x} -a_{j\left( t \right)}^{x} } + {a_{i\left( t \right)}^{y} -a_{j\left( t \right)}^{y} }+\\[2.5mm]\qquad a_{i\left( t \right)}^{z} -a_{i\left( t \right)}^{z} \Big)\\ \end{array} \right\}$
对方程求解得到$\Delta t_{c1} , \Delta t_{c2} , \Delta t_{c3} , \Delta t_{c4}$ 四个解, 依据$\left( {0<\Delta t_{ci} \leqslant \Delta t_p } \right)$条件, 判断解的有效性. 若存在真解, 取最小值作为颗粒$i$与颗粒$j$碰撞时间步. 若无真解, 说明颗粒在计算时间步内不发生碰撞.
在一个计算时间步内, 假设目标颗粒$i$与碰撞列表内颗粒$m_{i} $发生碰撞, 其碰撞时间步为$\Delta t_c^{i} (i=1, 2, \cdots , m)$. 因只考虑颗粒二体碰撞, 最早与目标颗粒相遇的颗粒$k$才是发生碰撞的颗粒, 则碰撞时间步取为$\Delta t_c^{k} $.
2.4 颗粒群碰撞求解流程
对于由$n$个颗粒组成的颗粒群, 依据前述方法, 可选择$n-1$个目标颗粒, 完成$n-1$个变网格和碰撞搜索列表建立. 假设目标颗粒$i$对颗粒$j$进行搜索判断后建立碰撞搜索列表, 颗粒$j$作为目标颗粒进行列表建立时, 无需对颗粒$i$重新进行判断, 直接从总的碰撞列表内映射即可.
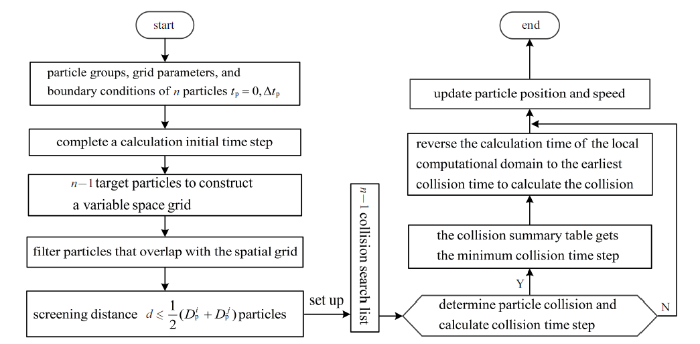
将每个列表内的最小碰撞时间步长, 放入总表内, 得到最小碰撞时间步, 局部求解域的计算时间步逆向到最先发生碰撞时刻, 执行碰撞. 碰撞计算完成后, 碰撞颗粒重新更新碰撞列表, 并计算最小碰撞时间步长, 其他未发生碰撞颗粒, 只需在原有碰撞时间步长基础上减去已经完成的碰撞时间步长, 更新碰撞时间步总表. 颗粒群碰撞求解流程如图8 所示.
图8
图8
颗粒群碰撞搜索求解流程
Fig.8
Particle swarm collision search solution process
3 CFD-DEM耦合分析及颗粒碰撞搜索算法验证
基于Fluent和DEM平台, 采用Delphi编程二次开发了流体与颗粒群耦合动力学分析程序.
3.1 两个颗粒碰撞算例
采用现有的DEM软件和本文提出的改进颗粒碰撞搜索算法MDEM分别对两个颗粒碰撞进行数值模拟. 预期验证本文方法的计算精度和计算效率.
如图9 所示, 取$A$, $B$两颗粒的半径$R=5$ mm, 弹性模量为210 GPa, 泊松比为0.27, $A$颗粒初始速度$u_{A}^{x} =2$ m/s, $u_{A}^{y} =-2$ m/s, $B$颗粒初始速度$u_{B}^{x} =u_{B}^{y} =2$ m/s, $A$, $B$颗粒初始圆心间距100 mm. 为了便于讨论, 记${u}_{A}^{'x}$. ${u}_{A}^{'y} $和${u}_{B}^{'x} $, ${u}_{B}^{'y}$分别为$A$, $B$颗粒碰撞后$x, y$方向速度, $F_{cn} $为$A$, $B$颗粒的碰撞力. 工况1: $A$, $B$颗粒匀速运动. 工况2: $A$, $B$颗粒变速运动, 沿$x$方向加速度为$-$10 m/s$^{2}$, 沿$y$方向加速为$-$10 m/s$^{2}$. 根据颗粒碰撞理论和解析解, 得到$A$, $B$颗粒的碰撞速度、碰撞位置和发生碰撞的时间、碰撞力如表1 所示.
图9
图9
颗粒位置示意图
Fig.9
Schematic diagram of particle position
DEM和MDEM取计算时间0.1 s, 计算时间步为10$^{-4}$ s, 10$^{-5}$ s, 10$^{-6}$ s, 10$^{-7}$ s对颗粒匀速、变速运动进行数值模拟, 得到碰撞力、碰撞速度、碰撞位置等结果一并列入表1 .模拟所用计算机为英特尔 Corei7-9700 @3.00 GHz 八核, 主显卡AMD Radeon RX 550 Series, 内存16 GB.
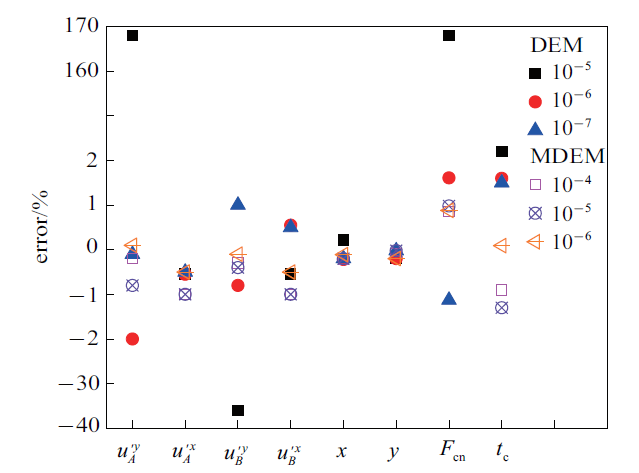
由图10 可知, 在匀速工况下, 采用DEM方法, 只有当计算时间步在10$^{-6}$ s及以下, 得到的计算结果与理论解误差才不大于2%, 其中速度最大误差为2%和1%, 碰撞位置最大误差均为0.2%, 碰撞力误差为1.61%和1.13%, 发生碰撞时刻误差为1.6%和1.5%, A$_2$和A$_3$计算耗时分别为24.73 s和54.04 s. 由此可见, DEM方法的计算精度受计算时间步影响较大, 计算效率随着时间步的减小而显著降低. 采用MDEM方法, 不同计算时间步得到的计算结果与理论结果误差均小于2%, 其中速度最大误差为1%, 1%, 0.5%, 碰撞位置最大误差均为0.22%, 0.2%, 0.2%, 碰撞力误差为0.85%, 0.98%, 0.88%, 发生碰撞时刻误差为0.9%, 1.3%, 0.09%, B$_1$, B$_2$, B$_3$计算耗时分别为20.01 s, 23.14 s, 37.06 s. 由此可见, 本文提出的MEDM方法, 计算精度不受计算时间步的影响, 且随着时间步的减小计算效率呈下降趋势, 其中B$_2$计算时间步长比A$_2$计算时间步长大一个量级, 计算耗时缩短4.59 s (6.4%). B$_1$计算时间步长比A$_2$计算时间步长大两个量级, 计算耗时缩短4.72 s (19.1%).
图10
图10
两颗粒匀速运动误差分析图
Fig.10
Error analysis diagram of two particles in uniform motion
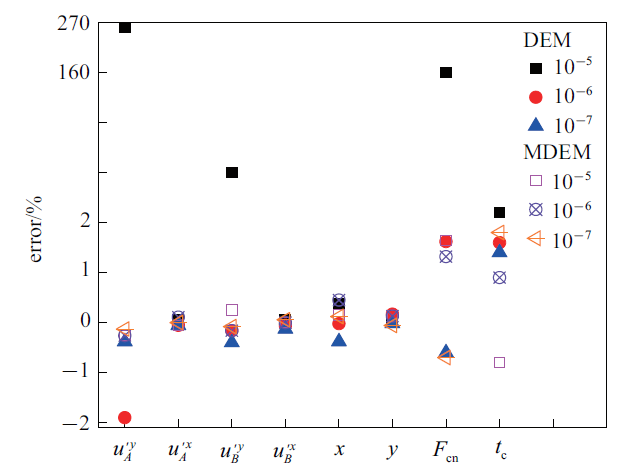
由图11 可知, 在变速工况下, 采用DEM方法, 只有当计算时间步在10$^{-6}$ s及以下, 得到的计算结果与理论解误差均小于2%, 其中速度最大误差为1.930%和0.400%, 碰撞位置最大误差均为0.17%和0.38%, 碰撞力误差为1.62%和1.13%, 发生碰撞时刻误差为1.6%和1.4%, C$_2$和C$_3$计算耗时27.73和58.21s. 采用MDEM方法, 不同计算时间步得到的计算结果与理论结果误差均小于2%, 其中速度最大误差为0.26%, 0.26%, 0.13%, 碰撞位置最大误差均为0.15%, 0.45%, 0.12%, 碰撞力误差为1.64%, 1.32%, 0.9%, 发生碰撞时刻误差为0.9%, 0.9%, 1.8%, D$_1$, D$_2$, D$_3$计算耗时22.2 s, 25.1 s, 38.11 s. D$_2$计算时间步长比C$_2$计算时间步长大一个量级, 计算耗时缩短2.63 s (9.48%), D$_1$计算时间步长比C$_2$计算时间步长大两个量级, 计算耗时缩短5.53 s (19.9%). 由此可见, 两种方法在模拟变速运动时的结论和规律同匀速运动.
图11
图11
两颗粒变速运动误差分析图
Fig.11
Error analysis diagram of variable speed movement of two particles
综上所述, 采用本文方法对颗粒匀速、变速运动进行数值模拟, 选取不同时间步均能得到近似的计算结果, 当计算时间步比DEM大两个量级时, 匀速运动的计算效率提高19.1%, 变速运动的计算效率提高19.9%, 使时间步选取过小、计算效率低的问题得到有效解决.
3.2 多个颗粒碰撞算例
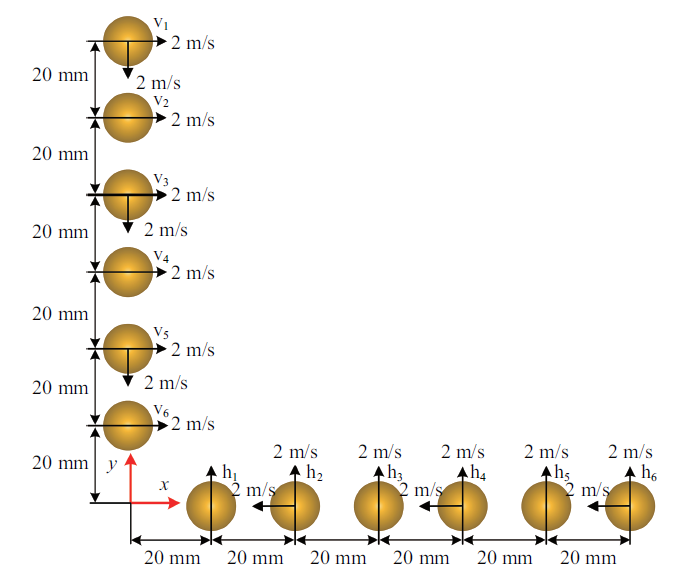
颗粒几何形状、材质属性同3.1算例. 颗粒初始位置如图12 所示, 水平设置6个颗粒, 颗粒间距20 mm, 编号h$_{1}$, h$_{2}$, h$_{3}$, h$_{4}$, h$_{5}$, h$_{6}$, 其中h$_{1}$, h$_{3}$, h$_{5}$颗粒水平速度均为0 m/s, 垂直向下速度均为2 m/s, h$_{2}$, h$_{4}$, h$_{6} $颗粒水平和垂直速度均为2 m/s. 竖直设置6个颗粒, 颗粒间距20 mm, 编号v$_{1}$, v$_{2}$, v$_{3}$, v$_{4}$, v$_{5}$, v$_{6} $, 其中v$_{1}$, v$_{3}$, v$_{5}$颗粒水平速度均为2 m/s, 垂直速度均为0 m/s, v$_{2}$, v$_{4}$, v$_{6}$颗粒水平和垂直速度均为2 m/s, 颗粒做匀速运动.
图12
图12
多颗粒碰撞初始位置示意图
Fig.12
Schematic diagram of initial position of multi-particle collision
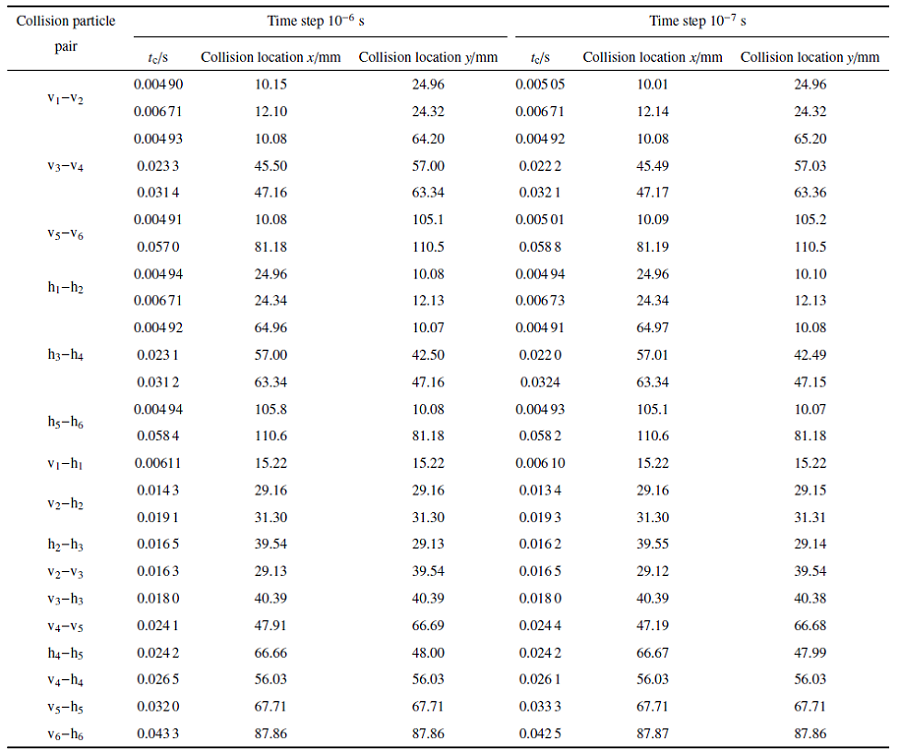
采用理论分析, 可得6对颗粒h$_{1}$-h$_{2}$, h$_{3}$-h$_{4}$, h$_{5}$-h$_{6}$, v$_{1}$-v$_{2}$, v$_{3}$-v$_{4}$, v$_{5}$-v$_{6}$首次发生碰撞时刻为0.005 0 s, 碰撞位置分别为(25, 10), (65, 10), (105, 10), (10, 25), (10, 65), (10, 105), 后继颗粒碰撞较复杂, 无法得到理论解. 在DEM和MDEM数值模拟中, 分别选取计算时间步为10$^{-5}$ s, 10$^{-6}$ s, 10$^{-7}$ s和10$^{-4}$ s, 10$^{-5}$ s, 10$^{-6}$ s, 计算时间取0.1 s.
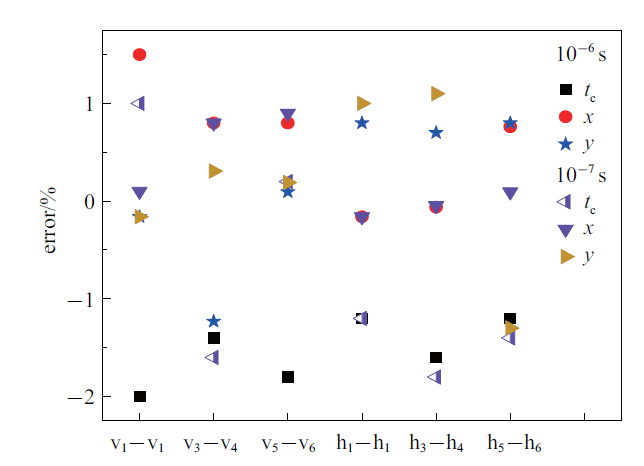
由DEM数值模拟结果可知, 计算时间步为10$^{-5}$ s得到23次颗粒对碰撞, 而计算时间步为10$^{-6}$ s和10$^{-7}$ s, 得到25次颗粒对碰撞, 部分结果见表2 .由图13 可知, 在10$^{-6}$ s和10$^{-7}$ s计算时间步得到的首次发生碰撞时刻、碰撞位置与理论解的误差均不大于2%. 计算耗时分别为60.31 s和90.12 s. 由此可见, 计算时间步取10$^{-5}$ s时, DEM方法漏判了2次颗粒碰撞, 随着计算时间步的减小, 多颗粒碰撞数值模拟的计算效率降低.
图13
图13
DEM颗粒碰撞时间、位置误差分析图
Fig.13
DEM particle collision time and position error analysis diagram
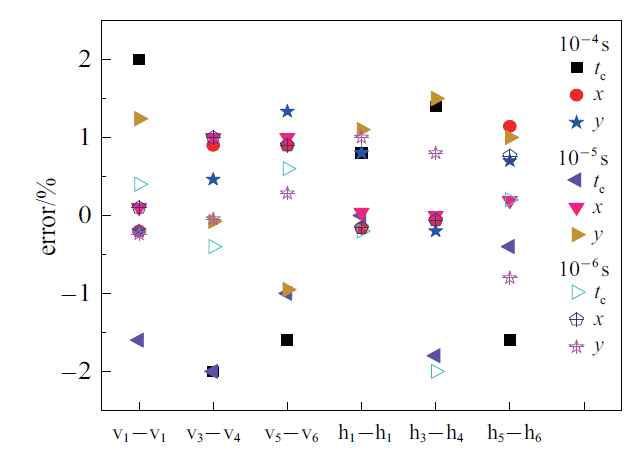
由MDEM数值模拟结果可知, 计算时间步取10$^{-4}$ s, 10$^{-5}$ s, 10$^{-6}$ s时, 均得到25次颗粒对碰撞, 部分结果如表2 和表3 所示. 由图14 可知, 不同计算时间步得到的首次发生碰撞时刻、碰撞位置与理论解的误差均不大于2%. 计算耗时分别为51.31 s, 56.22 s, 65.21 s. 由此可见, 在模拟多颗粒碰撞时, MEDM方法的计算精度不受计算时间步大小影响, 可采用较大的时间步来提高计算效率.
图14
图14
MDEM颗粒碰撞时间、位置误差分析图
Fig.14
MDEM particle collision time and position error analysis diagram
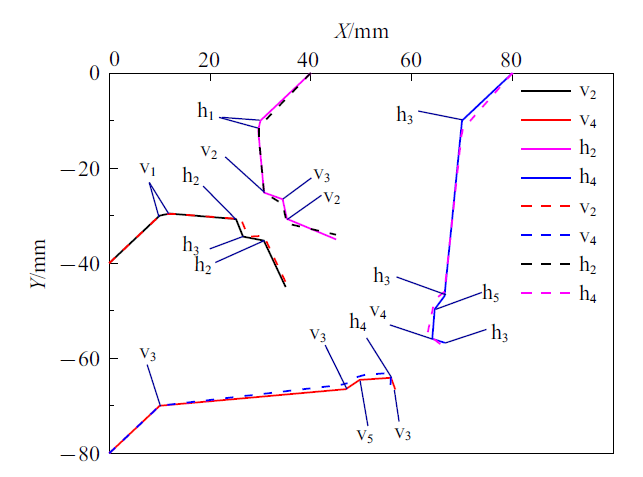
当DEM和MDEM计算时间步均取10$^{-6}$ s时, MDEM比DEM计算时间增加4.9 s, 这是由于每个计算时间步内的逆向搜索耗时所致. 当MDEM的计算时间步扩大一个量级(10$^{-5}$ s)时, 比DEM计算时间缩短4.09 s, 即计算耗时降低了6.8%; 当MDEM的时间步取10$^{-4}$ s时, 比DEM计算时间缩短了9 s, 即计算耗时降低了14.9%. 其中h$_{4}$, v$_{4}$, h$_{2}$, v$_{2}$均发生5次碰撞, 运动轨迹如图15 所示, 虚线为MDEM, 实线为DEM.
图15
图15
多颗粒运动轨迹与碰撞示图
Fig.15
Movement trajectories and collisions of more than one particle
综上所述, 采用本文方法选取10$^{-6}$ s, 10$^{-5}$ s, 10$^{-4}$ s时间步对多个颗粒碰撞进行数值模拟, 均能得到精确的计算结果, 计算时间步选取可比DEM方法大两个量级, 其计算耗时降低了14.9%.
3.3 CFD-DEM耦合分析算例
采用CFD-DEM和CFD-MDEM方法分别对3.2算例中的多个颗粒与流体耦合进行数值模拟. 计算流体域为300 mm$\times$300 mm$\times$300 mm的矩形域, 流体密度$\rho =1$ g/cm$^{3}$、黏度$\mu_f =0.1$ g/(cm$\cdot$s), 流体初始状态为静止. 计算域采用规则的矩形网格离散, 除上部边界设置为开边界外, 其余壁面采用无滑移边界条件. 颗粒几何参数、材质、初始位置及计算参数等与算例3.2完全相同, CFD-DEM流体计算时间步长设置为颗粒计算时间步长的10倍. CFD-MDEM颗粒计算初始时间步长与流体计算初始时间步相等, 颗粒与流体真实计算时间步在耦合计算过程中, 根据耦合收敛条件实时调整和修正, 时间步长设置如表4 所示.
CFD-DEM计算结果表明: 在A$_{1}$, A$_{2}$, A$_{3}$计算时间步得到颗粒碰撞次数分别为18次、22次、22次, 与算例3.2相比碰撞次数减少了3次, 原因在于流体的阻力使颗粒做减速运动, 计算耗时分别为18 min, 27 min, 42 min, 只有在颗粒计算时间步小于等于10$^{-6}$ s时, CFD-DEM耦合计算才能得到精确值.
CFD-MDEM计算结果表明: 在B$_{1}$, B$_{2}$, B$_{3}$计算时间步, 得到的颗粒碰撞次数均为22次, 计算耗时分别为22.5 min, 24 min, 31 min, 颗粒计算初始时间步的改变不影响CFD-MDEM耦合计算精度.
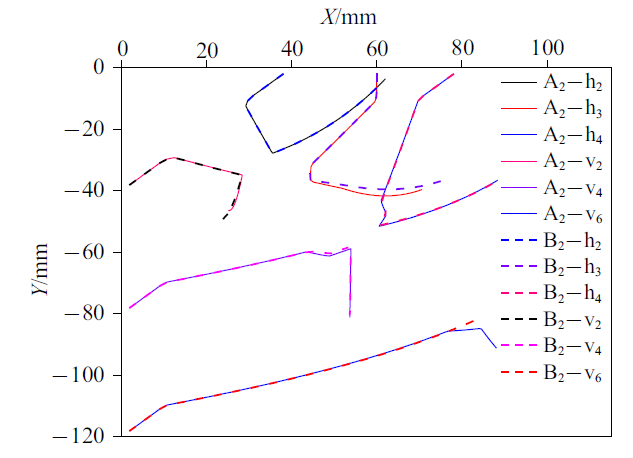
A$_{2}$流体计算时间步比B$_{3}$流体计算初始时间步大一个量级, A$_{2}$流体求解器启动10$^{4}$次, 颗粒求解器启动10$^{5}$次, B$_{3}$流体与颗粒求解器均启动100 383次. B$_{3}$比A$_{2}$多启动383次, 是由于MDEM算法根据耦合收敛条件, 修正计算初始时间步, 得到真实计算时间步比计算初始时间步小, B$_{3}$比A$_{2}$计算多耗时4 min. B$_{2}$流体计算初始时间步与A$_{2}$流体计算时间步相等, B$_{2}$颗粒计算初始时间步比A$_{2}$颗粒计算时间步大一个量级, B$_{2}$流体与颗粒求解器启均动11 479次, 与A$_{2}$流体求解次数相比求解器多启动1479次, 与B$_{3}$相比求解器多启动次数由383次增加到1479次, 是由于颗粒计算初始时间步的扩大, 颗粒求解不满足收敛条件次数增多造成. B$_{2}$比A$_{2}$计算少耗时3 min, 降低11.1%. B$_{1}$流体计算初始时间步比A$_{2}$流体计算时间步大一个量级, 颗粒计算初始时间步比A$_{2}$颗粒计算时间步大两个量级, B$_{1}$流体与颗粒求解器均启动3254次, 比A$_{2}$计算少耗时4.5 s, 降低16.7%. A$_{2}$和B$_{1}$颗粒h$_{2}$, h$_{3}$, h$_{4}$和v$_{2}$, v$_{4}$, v$_{6}$的运动轨迹基本一致, 如图16 所示.
图16
图16
颗粒运动轨迹
Fig.16
Multiple particle trajectories in fluid
综上所述, 采用CFD-MDEM方法对多个颗粒与流体进行耦合数值模拟, 流体与颗粒计算初始时间步取10$^{-4}$ s, 10$^{-5}$ s, 10$^{-6}$ s均能得到精确的计算结果, 计算耗时比CFD-DEM方法降低了16.7%.
4 结论
本文针对CFD-DEM耦合计算中, 颗粒时间步选取过小、计算效率低, 时间步选取过大、碰撞颗粒漏判的问题, 通过算法研究和算例验证, 取得如下结论和认识.
(1)提出了颗粒碰撞搜索的改进算法, 以目标颗粒运动位移构建可变空间搜索网格, 筛选可能碰撞颗粒建立搜索列表, 减少了颗粒碰撞的搜索时间;采用逆向搜索方式判断颗粒碰撞, 避免了时间步选取过大对颗粒碰撞漏判, 确保了颗粒碰撞的准确描述. 通过两个颗粒和多个颗粒的运动和碰撞算例表明, 本方法计算时间步选取的大小对颗粒碰撞计算精度影响不大;两个颗粒在匀速和变速工况下的数值模拟计算耗时比DEM方法降低了19.1%和19.9%, 多个颗粒的数值模拟计算耗时比DEM方法降低了14.9%.
(2)建立了颗粒与流体计算时间步自动调整的耦合算法, 颗粒与流体计算初始时间步选取可以相同, 根据颗粒推进时间实时调整流体计算时间, 实现流体计算时间步随颗粒计算时间自动调整, 提高了颗粒与流体耦合的计算效率. 多个颗粒与流体耦合算例的数值模拟表明, 该算法的计算精度受颗粒和流体的初始计算时间步长影响较小, 可通过较大的颗粒时间来提高计算效率, 该算法在求解算例的耗时比CFD-DEM方法降低了16.7%.
参考文献
View Option
[1]
Saini N Kleinstreuer C . A new collision model for ellipsoidal particles in shear flow
Journal of Computational Physics 2019 , 376 : 1028 -1050
DOI
[本文引用: 1]
All natural and a growing number of manufactured solid particles are non-spherical. Interesting fluid-particle dynamics applications include the transport of granular material, piling of seeds or grains, inhalation of toxic aerosols, use of nanofluids for enhanced cooling or improved lubrication, and optimal drug-targeting of tumors. A popular approach for computer simulations of such scenarios is the multi-sphere (MS) method, where any non-spherical particle is represented by an assemblage of spheres. However, the MS approach may lead to multiple sphere-to-sphere contact points during collision, and subsequently to erroneous particle transport and deposition. In cases where non-spherical particles can be approximated as ellipsoids with arbitrary aspect ratios, a new theory for particle transport, collision and wall interaction is presented which is more accurate computationally and more efficient than the MS method. In general, with the new ellipsoidal particle interaction (EPI) model, contact points and planes of ellipsoids, rather than spheres, are obtained based on a geometric potential algorithm. Then, interaction forces and torques of the colliding particles are determined via inscribed 'pseudo-spheres', employing the soft-particle approach. The off-center forces and moments are then transferred to the mass center of the ellipsoids to solve the appropriate translatory and angular equations of motion. Considering ellipses to illustrate the workings and predictive power of the new collision model, turbulent fluid-particle flow with the EPI model in a 2-D channel is simulated and compared with 3-D numerical benchmark results which relied on the MS method. The 2-D concentrations of micron particles with different aspect ratios matched closely with the 3-D cases. However, interesting differences occurred when comparing the particle-velocity profiles for which the 2-D EPI model generated somewhat larger particle velocities due to out-of-plane collisions, slightly higher particle-wall interactions, and two-way coupling effects. (C) Published by Elsevier Inc.
[2]
刘诚 , 沈永明 . 定床弯道内水沙两相运动的数值模拟
力学学报 , 2009 , 41 (3 ): 318 -328
DOI
[本文引用: 1]
在适体同位网格中采用非正交曲线坐标系下的三维k-ε-kp固液两相双流体湍流模型研究弯道内水流和悬浮泥沙运动,主要计算了试验室S型水槽内清水流动的三维流场、120°弯道内水沙两相流动中底沙与底流的运动轨迹以及S型水槽内水沙两相流动的两相流场和泥沙浓度场. 对于S型水槽内清水流动,数值结果与试验结果吻合良好. 120°弯道内水沙两相流动中固液两相的运动轨迹在弯道直线段基本重合,在弯道内泥沙轨迹逐步偏离水体轨迹,其偏离程度随泥沙粒径增大而增大. 从S型水槽内水沙两相流动计算结果中发现泥沙纵向流速在壁面附近比水流纵向速度大,在远离壁面区域比水流纵向速度小;弯道内泥沙横向流速比水流横向流速小;垂向流速在直线段和泥沙沉速相当,在弯道内受螺旋水流影响而变化;两相流速差别随泥沙粒径增大而变大;泥沙浓度呈现下浓上稀的分布,在弯道内横向断面上呈现凸岸大凹岸小的分布,泥沙浓度随泥沙粒径增大而减小.
(Liu Cheng Shen Yongming . Numerical simulation of two-phase movement of water and sand in a fixed bed curve
Chinese Journal of Theoretical and Applied Mechanics 2009 , 41 (3 ): 318 -328 (in Chinese))
[本文引用: 1]
[3]
Ge L Evans GM Moreno-Atanasio R . CFD-DEM investigation of the interaction between a particle swarm and a stationary bubble: Particle-bubble collision efficiency
Powder Technology 2020 , 366 : 641 -652
DOI
URL
[本文引用: 1]
[4]
Tanaka T Tsuji M . Numerical simulation of gas-solid two-phase flow in a vertical pipe: On the effect of inter-particle collision
ASME/FED Gas-Solid Flows 1991 , 121 : 123 -128
[本文引用: 1]
[5]
Acmae El Y Xu S Wang J . A New method for computing particle collisions in Navier-Stokes flows
Journal of Computational Physics 2019 , 99 : 108919
[本文引用: 1]
[6]
刘向军 , 石磊 , 徐旭常 . 稠密气固两相流欧拉-拉格朗日法的研究现状
计算力学学报 , 2007 , 24 (2 ): 166 -172
[本文引用: 1]
(Liu Xiangjun Shi Lei Xu Xuchang . Research status of the Euler-Lagrangian method for dense gas-solid two-phase flow
Chinese Journal Computational Mechanics 2007 , 24 (2 ): 166 -172 (in Chinese))
[本文引用: 1]
[7]
Chen X Wang J . A comparison of two-fluid model, dense discrete particle model and CFD-DEM method for modeling impinging gas-solid flows
Powder Technology 2014 , 254 : 94 -102
DOI
URL
[本文引用: 1]
[8]
GidaGidaspow D . Multiphase Flows and Fluidization. San Diego : Academic Press Inc , 1994
[本文引用: 1]
[9]
傅旭东 , 王光谦 . 低浓度固液两相流的颗粒相动理学模型
力学学报(英文版) , 2003 , 35 (6 ): 650 -659
[本文引用: 1]
(Fu Xudong Wang Guangqian . The particle phase kinetic model of low-concentration solid-liquid two-phase flow
Acta Mechanic Sinica 2003 , 35 (6 ): 650 -659 (in Chinese))
[本文引用: 1]
[10]
刘安源 , 刘石 . 流化床内颗粒碰撞传热的理论研究
中国电机工程学报 , 2003 , 23 (3 ): 161 -165
[本文引用: 1]
(Liu Anyuan Liu Shi . Theoretical study on collision and heat transfer of particles in a fluidized bed
Proceedings of the CSEE 2003 , 23 (3 ): 161 -165 (in Chinese))
[本文引用: 1]
[11]
刘向军 , 徐旭常 . 循环流化床内稠密气固两相流动的数值模拟
中国电机工程学报 , 2003 , 23 (5 ): 162 -166
[本文引用: 1]
(Liu Xiangjun Xu Xuchang . Numerical simulation of dense gas-solid two-phase flow in circulating fluidized bed
Proceedings of the CSEE 2003 , 23 (5 ): 162 -166 (in Chinese))
[本文引用: 1]
[12]
孙平 , 樊建人 , 夏振海 等 . 计及颗粒间碰撞的湍流气固两相流模型及验证
自然科学进展 , 1998 , 5 (8 ): 572 -580
[本文引用: 1]
(Sun Ping Fang Jianren Xia Zhenhai , et al . Model and verification of turbulent gas-solid two-phase flow considering collisions between particles
Progress in Natural Science 1998 , 5 (8 ): 572 -580 (in Chinese))
[本文引用: 1]
[13]
Hockney RW Eastwood JW . Computer simulation using particles
Institute of Physics 1988 , 76 : 249 -256
[本文引用: 1]
[14]
Baraff D . Interactive simulation of solid rigid bodies
IEEE Computer Graphics & Applications 1995 , 15 (3 ): 63 -75
[本文引用: 1]
[15]
Schaefer BC Quigley SF Chan AHC . Acceleration of the discrete element method (DEM) on a reconfigurable co-processor
Computers & Structures 2004 , 82 (21 ): 1707 -1718
DOI
URL
[本文引用: 1]
[16]
Allen M Tildesley D . Computer Simulation of Liquids. Oxford : Clarendon Press , 1987
[本文引用: 1]
[17]
Vemuri BC Chen L Waltin O , et al . Efficient and accurate collision detection for granular flow simulation
Graphical Models & Image Processing 1998 , 60 (6 ): 403 -422
[本文引用: 1]
[18]
Li CF Feng YT Owen DRJ . SMB: Collision detection based on temporal coherence
Computer Methods in Applied Mechanics & Engineering 2006 , 195 (22 ): 2252 -2269
[本文引用: 1]
[19]
Sigurgeirsson H Stuart A Wan W . Algorithms for particle-field simulations with collisions
Journal of Computational Physics 2001 , 172 : 766 -807
DOI
URL
[本文引用: 1]
[20]
Yao LM Xiao ZM Liu JB , et al . An optimized CFD-DEM method for fluid-particle coupling dynamics analysis
International Journal of Mechanical ences 2020 , 174 : 105503
[本文引用: 1]
[21]
Banaei M Jegers J van Sint Annaland J . Tracking of particles using TFM in gas-solid fluidized beds
Advanced Powder Technology 2018 , 29 (10 ): 2538 -2547
DOI
URL
[本文引用: 1]
[22]
Sharma K Mallick SS Mittal A . A study of energy loss due to particle to particle and wall collisions during fluidized dense-phase pneumatic transport
Powder Technology 2019 , 362 : 707 -716
DOI
URL
[本文引用: 1]
[23]
Ariane B Gregory S . Experimental methods in chemical engineering: Unresolved CFD-DEM
Canadian Journal of Chemical Engineering 2020 , 98 (2 ): 424 -440
DOI
URL
[本文引用: 1]
[24]
Auton TR Hunt JCR Prud'Homme M . The force exerted on a body in inviscid unsteady non-uniform rotational flow
J Fluids Mech 1988 , 197 : 241 -257
DOI
URL
[本文引用: 1]
[25]
Eskin D Ratulowski J Akbarzadeh K . Modeling of particle deposition in a vertical turbulent pipe flow at a reduced probability of particle sticking to the wall
Chemical Engineeringence 2011 , 66 (20 ): 4561 -4572
[本文引用: 1]
[26]
Liu RJ Xiao R Ye M , et al . Analysis of particle rotation in fluidized bed by use of discrete particle model
Advanced Powder Technology 2018 , 29 (7 ): 1655 -1663
DOI
URL
[本文引用: 1]
[27]
Thomas PJ . On the influence of the Basset history force on the motion of a particle through a fluid
Physics of Fluids A Fluid Dynamics 1992 , 4 (9 ): 2090 -2093
DOI
URL
[本文引用: 1]
[28]
Cheng J Dou Y Zhang N , et al . A new method for predicting erosion damage of suddenly contracted pipe impacted by particle cluster via CFD-DEM
Materials 2018 , 11 (10 ): 1858 -1869
DOI
URL
[本文引用: 1]
[29]
Zhang Y . Application and improvement of computational fluid dynamics (CFD) in solid particle erosion modeling. [PhD Thesis]
The University of Tulsa , 2006
[本文引用: 1]
[30]
Salmana AD Gorhamb DA Szabó M , et al . Spherical particle movement in dilute pneumatic conveying
Powder Technology 2005 , 153 : 43 -50
DOI
URL
[本文引用: 1]
[31]
凡凤仙 , 王志强 , 刘举 等 . 竖直振动管中颗粒毛细效应的离散元模拟
力学学报 , 2019 , 51 (2 ): 415 -424
DOI
[本文引用: 1]
将一根细管插入填充有颗粒的静止容器中并对管施加竖直振动,颗粒将在管内发生上升运动,并最终稳定在一定高度,这一现象与液体毛细效应类似,被称为颗粒毛细效应.为探究颗粒毛细效应过程中伴随的颗粒尺度动力学行为及机理,基于离散元方法建立颗粒运动模型,对颗粒毛细效应动力学过程和特性开展数值模拟研究.模拟再现了文献中实验得到的颗粒毛细效应全过程,给出了管内颗粒柱高度随时间的演变规律,结果表明,受到颗粒系统参数的影响,本模拟条件下颗粒毛细效应过程呈现单周期上升、倍周期上升和倍周期稳定三个阶段,在倍周期上升阶段颗粒柱上升速度逐渐减小,平缓过渡到稳定阶段.在此基础上,分析了管内颗粒速度场和填充率分布随时间的演变特性,揭示了颗粒毛细效应过程中由容器传输到管内的颗粒的占比分布.研究发现,管内不同高度位置颗粒的运动并不同步,随着管的振动,管内出现速度波,速度波的传播引起管内颗粒出现膨胀和压缩交替的情况,从而管内颗粒填充率随时间发生周期性波动;在上升阶段,越接近管壁由容器传输到管内的颗粒占比越大,在稳定阶段,管内上层颗粒的对流引起容器传输到管内的颗粒占比发生反转.
(Fan Fengxian Wang Zhiqiang Liu Ju , et al . Discrete element simulation of particle capillary effect in vertical vibrating tube
Chinese Journal of Theoretical and Applied Mechanics 2019 , 51 (2 ): 415 -424 (in Chinese))
[本文引用: 1]
[32]
李鸿晶 , 梅雨辰 , 任永亮 . 一种结构动力时程分析的积分求微方法
力学学报 , 2019 , 51 (5 ): 1507 -1516
DOI
[本文引用: 1]
传统采用微分求积(differential quadrature,DQ)法求解动力问题时都是以位移响应作为基本未知量,而将速度响应和加速度响应表示为位移响应的加权和的形式.如此做法需要处理线性方程组或者矩阵方程(Sylvester方程)才能求得动力响应,导出的算法一般为有条件稳定算法.本文利用动力响应的Duhamel积分解,逆用DQ原理,提出了一种计算卷积的高精度显式算法.该算法可以逐时段地求解出动力时程响应,当各时段内DQ节点分布完全一致时,仅须进行一次Vandermonde矩阵求逆计算即可应用于各个时段,一次性获得时段内多个时刻的位移响应值,因而具有计算效率高的优点.通过分析动力方程积分格式,证明本文动力算法传递矩阵的谱半径恒等于1,因而该算法具有无条件稳定特性,且计算过程中不会产生数值耗散. 本文算法的数值精度取决于分析时段内布置的DQ节点数量$N$,具有$N-1$阶代数精度.实际操作时可以取10个甚至更多的DQ节点数,从而获得比较高的数值精度.
(Li Hongjing Mei Yuchen Ren Yongliang . An integral differential method for structural dynamic time history analysis
Chinese Journal of Theoretical and Applied Mechanics 2019 , 51 (5 ): 1507 -1516 (in Chinese))
[本文引用: 1]
[33]
魏新容 , 段绍臻 , 孙金龙 等 . 基于碰撞模型的斜坡滚石颗粒速度预测
力学学报 , 2020 , 52 (3 ): 707 -715
DOI
[本文引用: 1]
滑坡滚石灾害是西部山区常见的地质灾害类型,具有突发性和随机性强的特点,是山区地质灾害预测和防治工作的重点和难点. 本文基于颗粒接触理论,考虑影响斜坡滚石碰撞过程中的随机因素,建立了用于预测斜坡滚石颗粒碰撞后速度的理论模型. 根据冲量及冲量矩定理建立滚石颗粒碰撞基本方程,得到斜坡滚石颗粒碰撞后反弹速度的解析解. 结果表明:斜坡滚石碰撞后反弹速度的解析解包含了坡角、坡体上被碰颗粒速度以及角度、入射速度和角度以及撞击角度等随机因素;当考虑入射滚石颗粒与坡体上被碰颗粒的撞击角度变化时,模型预测结果与试验结果吻合较好;本文进一步预测了滚石颗粒碰撞后颗粒反弹线速度和角度以及反弹旋转角速度的概率分布情况. 结果显示,反弹颗粒速度和角度以及反弹旋转角速度的概率分布均服从高斯分布;当坡体上被碰颗粒速度和坡角发生变化时,其对反弹颗粒速度和角度以及反弹旋转角速度概率分布定性上没有影响,但是对概率分布的中心参数有显著影响.
(Wei Xinrong Duan Shaozhen Sun Jinlong , et al . Particle velocity prediction of slope rolling rock based on impact model
Chinese Journal of Theoretical and Applied Mechanics 2020 , 52 (3 ): 707 -715 (in Chinese))
[本文引用: 1]
[34]
徐芝纶 . 弹性力学简明教程 . 北京 : 高等教育出版社 , 2002
[本文引用: 1]
(Xu Zhilun . Concise Course of Elasticity. Beijing : Higher Education Press , 2002 (in Chinese))
[本文引用: 1]
[35]
王帅 , 郝振华 , 徐鹏飞 等 . 粗糙颗粒动理学及稠密气固两相流动的数值模拟
力学学报 , 2012 , 44 (2 ): 278 -286
DOI
[本文引用: 1]
考虑颗粒碰撞过程中摩擦作用, 给出了粗糙颗粒碰撞动力学. 引入颗粒相拟总温来表征颗粒平动和转动脉动能量的特征. 基于气体分子运动论, 建立颗粒碰撞中平动和旋转共同作用的粗糙颗粒动理学, 给出了颗粒相压力和黏度等输运参数计算模型. 运用基于颗粒动理学的欧拉-欧拉气固两相流模型, 数值模拟了流化床内气体颗粒两相流动特性, 分析了颗粒旋转流动对颗粒碰撞能量交换和耗散的影响. 模拟得到的流化床内径向颗粒浓度和提升管内颗粒轴向速度与他人实验结果相吻合. 模拟结果表明随着颗粒浓度的增加, 颗粒相压力和能量耗散逐渐增加, 而颗粒拟总温先增加后下降. 随着颗粒粗糙度系数的增加, 床内平均颗粒相拟总温和能量耗散增加, 表明颗粒旋转产生的摩擦将导致颗粒旋转脉动能量的改变, 影响床内气体-颗粒两相宏观流动特性.
(Wang Shuai Hao Zhenhua Xu Pengfei , et al . Coarse particle kinetics and numerical simulation of dense gas-solid two-phase flow
Chinese Journal of Theoretical and Applied Mechanics 2012 , 44 (2 ): 278 -286 (in Chinese))
[本文引用: 1]
[36]
Alobaid F Baraki N Epple B . Investigation into improving the efficiency and accuracy of CFD/DEM simulations
Particuology 2014 , 16 (5 ): 41 -53
DOI
URL
[本文引用: 1]
A new collision model for ellipsoidal particles in shear flow
1
2019
... 在自然界和工业领域, 流体中的颗粒碰撞普遍存在[1 ] . 如泥沙流中的砂粒碰撞与沉积[2 ] , 石油开采携砂压裂液中的颗粒碰撞与管壁冲蚀等. 这些颗粒群与流体运移的两相流动中, 流体输运的湍流效应和颗粒运动的碰撞相互影响[3 ] . 在颗粒体积分数低至$4.0\times 10^{-4}$情况下[4 ] , 颗粒间的碰撞效应也不应被忽略. 通常采用数值模拟手段来量化整个流场以及单个颗粒的动力学[5 ] . ...
定床弯道内水沙两相运动的数值模拟
1
2009
... 在自然界和工业领域, 流体中的颗粒碰撞普遍存在[1 ] . 如泥沙流中的砂粒碰撞与沉积[2 ] , 石油开采携砂压裂液中的颗粒碰撞与管壁冲蚀等. 这些颗粒群与流体运移的两相流动中, 流体输运的湍流效应和颗粒运动的碰撞相互影响[3 ] . 在颗粒体积分数低至$4.0\times 10^{-4}$情况下[4 ] , 颗粒间的碰撞效应也不应被忽略. 通常采用数值模拟手段来量化整个流场以及单个颗粒的动力学[5 ] . ...
定床弯道内水沙两相运动的数值模拟
1
2009
... 在自然界和工业领域, 流体中的颗粒碰撞普遍存在[1 ] . 如泥沙流中的砂粒碰撞与沉积[2 ] , 石油开采携砂压裂液中的颗粒碰撞与管壁冲蚀等. 这些颗粒群与流体运移的两相流动中, 流体输运的湍流效应和颗粒运动的碰撞相互影响[3 ] . 在颗粒体积分数低至$4.0\times 10^{-4}$情况下[4 ] , 颗粒间的碰撞效应也不应被忽略. 通常采用数值模拟手段来量化整个流场以及单个颗粒的动力学[5 ] . ...
CFD-DEM investigation of the interaction between a particle swarm and a stationary bubble: Particle-bubble collision efficiency
1
2020
... 在自然界和工业领域, 流体中的颗粒碰撞普遍存在[1 ] . 如泥沙流中的砂粒碰撞与沉积[2 ] , 石油开采携砂压裂液中的颗粒碰撞与管壁冲蚀等. 这些颗粒群与流体运移的两相流动中, 流体输运的湍流效应和颗粒运动的碰撞相互影响[3 ] . 在颗粒体积分数低至$4.0\times 10^{-4}$情况下[4 ] , 颗粒间的碰撞效应也不应被忽略. 通常采用数值模拟手段来量化整个流场以及单个颗粒的动力学[5 ] . ...
Numerical simulation of gas-solid two-phase flow in a vertical pipe: On the effect of inter-particle collision
1
1991
... 在自然界和工业领域, 流体中的颗粒碰撞普遍存在[1 ] . 如泥沙流中的砂粒碰撞与沉积[2 ] , 石油开采携砂压裂液中的颗粒碰撞与管壁冲蚀等. 这些颗粒群与流体运移的两相流动中, 流体输运的湍流效应和颗粒运动的碰撞相互影响[3 ] . 在颗粒体积分数低至$4.0\times 10^{-4}$情况下[4 ] , 颗粒间的碰撞效应也不应被忽略. 通常采用数值模拟手段来量化整个流场以及单个颗粒的动力学[5 ] . ...
A New method for computing particle collisions in Navier-Stokes flows
1
2019
... 在自然界和工业领域, 流体中的颗粒碰撞普遍存在[1 ] . 如泥沙流中的砂粒碰撞与沉积[2 ] , 石油开采携砂压裂液中的颗粒碰撞与管壁冲蚀等. 这些颗粒群与流体运移的两相流动中, 流体输运的湍流效应和颗粒运动的碰撞相互影响[3 ] . 在颗粒体积分数低至$4.0\times 10^{-4}$情况下[4 ] , 颗粒间的碰撞效应也不应被忽略. 通常采用数值模拟手段来量化整个流场以及单个颗粒的动力学[5 ] . ...
稠密气固两相流欧拉-拉格朗日法的研究现状
1
2007
... 固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键. ...
稠密气固两相流欧拉-拉格朗日法的研究现状
1
2007
... 固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键. ...
A comparison of two-fluid model, dense discrete particle model and CFD-DEM method for modeling impinging gas-solid flows
1
2014
... 固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键. ...
1
1994
... 固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键. ...
低浓度固液两相流的颗粒相动理学模型
1
2003
... 固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键. ...
低浓度固液两相流的颗粒相动理学模型
1
2003
... 固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键. ...
流化床内颗粒碰撞传热的理论研究
1
2003
... 固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键. ...
流化床内颗粒碰撞传热的理论研究
1
2003
... 固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键. ...
循环流化床内稠密气固两相流动的数值模拟
1
2003
... 固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键. ...
循环流化床内稠密气固两相流动的数值模拟
1
2003
... 固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键. ...
计及颗粒间碰撞的湍流气固两相流模型及验证
1
1998
... 固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键. ...
计及颗粒间碰撞的湍流气固两相流模型及验证
1
1998
... 固液两相流动中, 颗粒间接触和碰撞十分剧烈、复杂[6 ] , 成为影响两相流动行为的关键因素[7 ] , 也是数值模拟研究的热点和难点. 固液两相流的数值模型主要有欧拉-欧拉双流体模型(TFM)[8 -9 ] 和欧拉-拉格朗日离散颗粒模型(CFD-DEM)[10 ] 两大类. 前者将颗粒与流体视为互相渗透的拟流体或拟连续介质, 在欧拉坐标系研究;双流体模型可以全面考虑颗粒相的输运特性, 适合进行大规模的工程问题计算, 但忽略了颗粒离散特性, 对颗粒流动行为的预测会与实际过程产生偏差[11 ] , 无法得到颗粒的运动轨迹[12 ] . 后者采用欧拉-拉格朗日坐标系研究两相流动, 即流体作为连续介质, 在欧拉坐标系研究, 颗粒作为离散相, 在拉格朗日坐标系基于牛顿运动定律求解颗粒动力学方程, 跟踪颗粒在流场中的复杂运动. 欧拉-拉格朗日模型对流体与颗粒耦合计算的模拟精确程度, 取决于能否准确地刻画颗粒间的碰撞, 而颗粒碰撞搜索算法成为解决这一难题的关键. ...
Computer simulation using particles
1
1988
... 前人对颗粒碰撞搜索算法进行了大量研究, 如分割单元算法也称网格单元算法[13 -15 ] , 将计算域划分成均匀的立方体单元, 单元长度为颗粒直径的整数倍. 计算时间步结束时刻根据颗粒当前位置被分配到某个单元, 只有同一单元或相邻单元内颗粒可能发生碰撞. 一个颗粒最多占据8个单元, 当其成为目标颗粒时, 只对其占据的单元内其他颗粒进行碰撞检测. 该算法遗漏了那些时间步结束前, 离开或穿过立方体单元, 可能与目标颗粒发生碰撞的颗粒. Allen等[16 ] 提出的邻居列表算法, 规定了一个阈值距离来确定颗粒间相互作用的影响半径. 碰撞搜索只对列表内的颗粒对进行搜索, 如果两个颗粒之间的距离大于阈值距离, 其就不可能在下一个时间步中发生碰撞. 所以, 邻居列表需要几个时间步更新一次. 该算法构建的搜索列表内颗粒众多, 在高浓度颗粒存在的应用中, 每对颗粒进行一次判定计算代价过高. Vemuri等[17 ] 提出的八叉树算法, 建立一个能够容纳任意方向上最大颗粒的立方体, 将其作为划分域的基本单元. 在对小颗粒进行搜索碰撞时, 基本单元将会被多次划分八叉树, 每个颗粒根据其大小与单元的关系, 配置到对应单元中. 在计算域内有多种尺寸颗粒时, 需多次划分基本单元, 计算过程繁琐. ...
Interactive simulation of solid rigid bodies
1
1995
... Baraff[14 ] 提出了边界盒算法, 使用轴向对齐的边界盒来确定颗粒之间的碰撞. 如果两个颗粒相撞, 其在$x$, $y$和$z$维度上的正交投影将会重叠. 3个列表包含对轴的投影坐标, 每个维度对应一个列表. 在下一个时间步骤, 需要再次对之前排序的列表进行排序. Li等[18 ] 提出的时间相干碰撞搜索算法 (SMB), 是将包围盒AABB投影在笛卡尔坐标轴上, 根据投影间距递增排序建立初步碰撞搜索列表, 通过对列表内所有间距搜索检查确定是否重叠, 建立碰撞列表. 该算法适用于大量移动AABB的系统, 并支持对象的动态插入和删除, 不受物体大小的限制. ...
Acceleration of the discrete element method (DEM) on a reconfigurable co-processor
1
2004
... 前人对颗粒碰撞搜索算法进行了大量研究, 如分割单元算法也称网格单元算法[13 -15 ] , 将计算域划分成均匀的立方体单元, 单元长度为颗粒直径的整数倍. 计算时间步结束时刻根据颗粒当前位置被分配到某个单元, 只有同一单元或相邻单元内颗粒可能发生碰撞. 一个颗粒最多占据8个单元, 当其成为目标颗粒时, 只对其占据的单元内其他颗粒进行碰撞检测. 该算法遗漏了那些时间步结束前, 离开或穿过立方体单元, 可能与目标颗粒发生碰撞的颗粒. Allen等[16 ] 提出的邻居列表算法, 规定了一个阈值距离来确定颗粒间相互作用的影响半径. 碰撞搜索只对列表内的颗粒对进行搜索, 如果两个颗粒之间的距离大于阈值距离, 其就不可能在下一个时间步中发生碰撞. 所以, 邻居列表需要几个时间步更新一次. 该算法构建的搜索列表内颗粒众多, 在高浓度颗粒存在的应用中, 每对颗粒进行一次判定计算代价过高. Vemuri等[17 ] 提出的八叉树算法, 建立一个能够容纳任意方向上最大颗粒的立方体, 将其作为划分域的基本单元. 在对小颗粒进行搜索碰撞时, 基本单元将会被多次划分八叉树, 每个颗粒根据其大小与单元的关系, 配置到对应单元中. 在计算域内有多种尺寸颗粒时, 需多次划分基本单元, 计算过程繁琐. ...
1
1987
... 前人对颗粒碰撞搜索算法进行了大量研究, 如分割单元算法也称网格单元算法[13 -15 ] , 将计算域划分成均匀的立方体单元, 单元长度为颗粒直径的整数倍. 计算时间步结束时刻根据颗粒当前位置被分配到某个单元, 只有同一单元或相邻单元内颗粒可能发生碰撞. 一个颗粒最多占据8个单元, 当其成为目标颗粒时, 只对其占据的单元内其他颗粒进行碰撞检测. 该算法遗漏了那些时间步结束前, 离开或穿过立方体单元, 可能与目标颗粒发生碰撞的颗粒. Allen等[16 ] 提出的邻居列表算法, 规定了一个阈值距离来确定颗粒间相互作用的影响半径. 碰撞搜索只对列表内的颗粒对进行搜索, 如果两个颗粒之间的距离大于阈值距离, 其就不可能在下一个时间步中发生碰撞. 所以, 邻居列表需要几个时间步更新一次. 该算法构建的搜索列表内颗粒众多, 在高浓度颗粒存在的应用中, 每对颗粒进行一次判定计算代价过高. Vemuri等[17 ] 提出的八叉树算法, 建立一个能够容纳任意方向上最大颗粒的立方体, 将其作为划分域的基本单元. 在对小颗粒进行搜索碰撞时, 基本单元将会被多次划分八叉树, 每个颗粒根据其大小与单元的关系, 配置到对应单元中. 在计算域内有多种尺寸颗粒时, 需多次划分基本单元, 计算过程繁琐. ...
Efficient and accurate collision detection for granular flow simulation
1
1998
... 前人对颗粒碰撞搜索算法进行了大量研究, 如分割单元算法也称网格单元算法[13 -15 ] , 将计算域划分成均匀的立方体单元, 单元长度为颗粒直径的整数倍. 计算时间步结束时刻根据颗粒当前位置被分配到某个单元, 只有同一单元或相邻单元内颗粒可能发生碰撞. 一个颗粒最多占据8个单元, 当其成为目标颗粒时, 只对其占据的单元内其他颗粒进行碰撞检测. 该算法遗漏了那些时间步结束前, 离开或穿过立方体单元, 可能与目标颗粒发生碰撞的颗粒. Allen等[16 ] 提出的邻居列表算法, 规定了一个阈值距离来确定颗粒间相互作用的影响半径. 碰撞搜索只对列表内的颗粒对进行搜索, 如果两个颗粒之间的距离大于阈值距离, 其就不可能在下一个时间步中发生碰撞. 所以, 邻居列表需要几个时间步更新一次. 该算法构建的搜索列表内颗粒众多, 在高浓度颗粒存在的应用中, 每对颗粒进行一次判定计算代价过高. Vemuri等[17 ] 提出的八叉树算法, 建立一个能够容纳任意方向上最大颗粒的立方体, 将其作为划分域的基本单元. 在对小颗粒进行搜索碰撞时, 基本单元将会被多次划分八叉树, 每个颗粒根据其大小与单元的关系, 配置到对应单元中. 在计算域内有多种尺寸颗粒时, 需多次划分基本单元, 计算过程繁琐. ...
SMB: Collision detection based on temporal coherence
1
2006
... Baraff[14 ] 提出了边界盒算法, 使用轴向对齐的边界盒来确定颗粒之间的碰撞. 如果两个颗粒相撞, 其在$x$, $y$和$z$维度上的正交投影将会重叠. 3个列表包含对轴的投影坐标, 每个维度对应一个列表. 在下一个时间步骤, 需要再次对之前排序的列表进行排序. Li等[18 ] 提出的时间相干碰撞搜索算法 (SMB), 是将包围盒AABB投影在笛卡尔坐标轴上, 根据投影间距递增排序建立初步碰撞搜索列表, 通过对列表内所有间距搜索检查确定是否重叠, 建立碰撞列表. 该算法适用于大量移动AABB的系统, 并支持对象的动态插入和删除, 不受物体大小的限制. ...
Algorithms for particle-field simulations with collisions
1
2001
... 上面几种方法对颗粒碰撞的判定, 都采用较小的时间步长进行推进计算, 根据计算时间步结束时颗粒位置, 判断颗粒是否与目标颗粒碰撞. 若时间步选取过大, 会遗漏计算时间步内的颗粒碰撞效应[19 ] , 无法对颗粒碰撞导致的颗粒位置、速度、加速度等变化进行描述影响计算精度. 而无限缩小颗粒计算时间步, 又会造成推进次数的增加, 影响计算效率. ...
An optimized CFD-DEM method for fluid-particle coupling dynamics analysis
1
2020
... 此外, 由于颗粒碰撞搜索方式的改变, 颗粒与流体耦合方式也相应发生变化. 传统CFD-DEM耦合方法, 流体计算时间步长是颗粒计算时间步长的整数倍($\Delta t_f =n\cdot \Delta t_p)$[20 ] . 流体完成一个时间步$\Delta t_f $, 颗粒完成$n$个时间步$\Delta t_p $, 颗粒与流体才进行一次相间力的交换, 导致颗粒在流体内部受力及运动与实际误差较大. ...
Tracking of particles using TFM in gas-solid fluidized beds
1
2018
A study of energy loss due to particle to particle and wall collisions during fluidized dense-phase pneumatic transport
1
2019
... 两相流与单相流的主要区别在于, 流体相中流体体积分数$\alpha_f $和源项${ S}_f $的变化. 流体体积分数$\alpha_f$是流体单元中流体所占有的体积份额[22 ] , ${ S}_f $是颗粒与流体间动量交换力源项[23 ] , 如图2 所示. ...
Experimental methods in chemical engineering: Unresolved CFD-DEM
1
2020
... 两相流与单相流的主要区别在于, 流体相中流体体积分数$\alpha_f $和源项${ S}_f $的变化. 流体体积分数$\alpha_f$是流体单元中流体所占有的体积份额[22 ] , ${ S}_f $是颗粒与流体间动量交换力源项[23 ] , 如图2 所示. ...
The force exerted on a body in inviscid unsteady non-uniform rotational flow
1
1988
... 式中, ${ F}_d $为颗粒在流体中受到的阻力(曳力), ${ F}_p$为压力梯度力, ${ F}_vm$为虚拟质量力[24 ] , ${ F}_saff $为Saffman剪切升力[25 ] , ${ F}_ml$为Magnus旋转升力[26 ] , ${ F}_b$为倍瑟特力[27 ] . ...
Modeling of particle deposition in a vertical turbulent pipe flow at a reduced probability of particle sticking to the wall
1
2011
... 式中, ${ F}_d $为颗粒在流体中受到的阻力(曳力), ${ F}_p$为压力梯度力, ${ F}_vm$为虚拟质量力[24 ] , ${ F}_saff $为Saffman剪切升力[25 ] , ${ F}_ml$为Magnus旋转升力[26 ] , ${ F}_b$为倍瑟特力[27 ] . ...
Analysis of particle rotation in fluidized bed by use of discrete particle model
1
2018
... 式中, ${ F}_d $为颗粒在流体中受到的阻力(曳力), ${ F}_p$为压力梯度力, ${ F}_vm$为虚拟质量力[24 ] , ${ F}_saff $为Saffman剪切升力[25 ] , ${ F}_ml$为Magnus旋转升力[26 ] , ${ F}_b$为倍瑟特力[27 ] . ...
On the influence of the Basset history force on the motion of a particle through a fluid
1
1992
... 式中, ${ F}_d $为颗粒在流体中受到的阻力(曳力), ${ F}_p$为压力梯度力, ${ F}_vm$为虚拟质量力[24 ] , ${ F}_saff $为Saffman剪切升力[25 ] , ${ F}_ml$为Magnus旋转升力[26 ] , ${ F}_b$为倍瑟特力[27 ] . ...
A new method for predicting erosion damage of suddenly contracted pipe impacted by particle cluster via CFD-DEM
1
2018
... 由于颗粒直径较小, 忽略Saffman剪切升力、 Magnus旋转升力、 压力梯度力、 虚拟质量力、 倍瑟特力对颗粒的影响[28 ] . 阻力(曳力)在流体作用于颗粒上的力中起主要作用[29 ] . 当颗粒的运动速度大于流体的流速时, 流体作用在颗粒上的力表现为阻力, 当流体的流速大于颗粒速度时, 作用在颗粒上的力表现为曳力. 计算公式为[30 ] ...
Application and improvement of computational fluid dynamics (CFD) in solid particle erosion modeling. [PhD Thesis]
1
2006
... 由于颗粒直径较小, 忽略Saffman剪切升力、 Magnus旋转升力、 压力梯度力、 虚拟质量力、 倍瑟特力对颗粒的影响[28 ] . 阻力(曳力)在流体作用于颗粒上的力中起主要作用[29 ] . 当颗粒的运动速度大于流体的流速时, 流体作用在颗粒上的力表现为阻力, 当流体的流速大于颗粒速度时, 作用在颗粒上的力表现为曳力. 计算公式为[30 ] ...
Spherical particle movement in dilute pneumatic conveying
1
2005
... 由于颗粒直径较小, 忽略Saffman剪切升力、 Magnus旋转升力、 压力梯度力、 虚拟质量力、 倍瑟特力对颗粒的影响[28 ] . 阻力(曳力)在流体作用于颗粒上的力中起主要作用[29 ] . 当颗粒的运动速度大于流体的流速时, 流体作用在颗粒上的力表现为阻力, 当流体的流速大于颗粒速度时, 作用在颗粒上的力表现为曳力. 计算公式为[30 ] ...
竖直振动管中颗粒毛细效应的离散元模拟
1
2019
... 取任一颗粒$i$为研究对象, 其运动由平移和旋转组成, 根据牛顿第二定律得[31 ] ...
竖直振动管中颗粒毛细效应的离散元模拟
1
2019
... 取任一颗粒$i$为研究对象, 其运动由平移和旋转组成, 根据牛顿第二定律得[31 ] ...
一种结构动力时程分析的积分求微方法
1
2019
... 假设颗粒在任意$t$时刻, 合力为${ F}_{(t)} $, 速度为${ u}_{\left( t\right)} $, 位置为$\left( {x_{\left( t \right)} , y_{\left( t \right)}, z_{\left( t \right)} } \right)$. 此时颗粒的加速度为${ a}_{(t)} ={ F}_{(t)} /m_{i} $. 当颗粒运动$\Delta t$后, 其瞬时速度为[32 ] ...
一种结构动力时程分析的积分求微方法
1
2019
... 假设颗粒在任意$t$时刻, 合力为${ F}_{(t)} $, 速度为${ u}_{\left( t\right)} $, 位置为$\left( {x_{\left( t \right)} , y_{\left( t \right)}, z_{\left( t \right)} } \right)$. 此时颗粒的加速度为${ a}_{(t)} ={ F}_{(t)} /m_{i} $. 当颗粒运动$\Delta t$后, 其瞬时速度为[32 ] ...
基于碰撞模型的斜坡滚石颗粒速度预测
1
2020
... 两颗粒发生碰撞满足动量定理, 如图3 所示[33 ] . ...
基于碰撞模型的斜坡滚石颗粒速度预测
1
2020
... 两颗粒发生碰撞满足动量定理, 如图3 所示[33 ] . ...
1
2002
... 根据弹性力学碰撞理论[34 ] , 两颗粒碰撞时间$t_c$为 ...
1
2002
... 根据弹性力学碰撞理论[34 ] , 两颗粒碰撞时间$t_c$为 ...
粗糙颗粒动理学及稠密气固两相流动的数值模拟
1
2012
... 由式(15)和式(16)可知, 两颗粒碰撞过程满足动量守恒, 但碰撞过程能量发生耗散, 不考虑颗粒旋转时的能量损失, 则颗粒碰撞耗散能量为[35 ] ...
粗糙颗粒动理学及稠密气固两相流动的数值模拟
1
2012
... 由式(15)和式(16)可知, 两颗粒碰撞过程满足动量守恒, 但碰撞过程能量发生耗散, 不考虑颗粒旋转时的能量损失, 则颗粒碰撞耗散能量为[35 ] ...
Investigation into improving the efficiency and accuracy of CFD/DEM simulations
1
2014
... 在数值模拟颗粒间碰撞时, 在一个时间步内颗粒只能与周边颗粒发生碰撞[36 ] , 将目标颗粒与周围可能发生碰撞的颗粒组成一个搜索空间网格进行碰撞搜索. 具体方法如下: 将目标颗粒在计算时间步的运动位移, 作为空间网格对角线, 建立搜索空间网格体, 如图6 (a)所示. 由于计算域内不同颗粒在$\Delta t$时间步内运动的位移不同, 所构建的空间网格也会出现不同尺寸, 即为变网格. ...