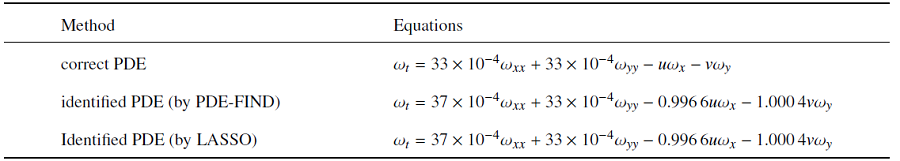引言
非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感.
近年来, 数据驱动方法在流场中的应用颇受研究者[4 , 22 -27 ] 的重视. 2019年, Chang和Zhang[23 ] 使用LASSO方法从数据出发, 识别出了单相地下水流动方程和污染物输运方程. 2020年, Raissi等[24 ] 使用深度学习, 对流场可视化的图片进行学习, 并反演了流场的压力和速度分布场, 可以帮助得到实验难以测量的数据. Zhang和Ma[25 ] 采用PDE-FIND方法, 对基于直接模拟蒙特卡罗(direct simulation Monte Carlo, DSMC)方法模拟产生的数据进行稀疏识别, 反演了流体的对流、扩散以及涡量输运方程, 从数据驱动角度清晰地展示了玻尔兹曼方程和 Navier-Stokes方程之间的相关性. Schmelzer等[26 ] 采用SINDy框架在数值模拟的数据中是识别出了代数雷诺应力模型. 张亦知等[27 ] 构建了基于数据驱动的湍流模型修正框架并在槽道流中进行了验证.
本文采用基于数据驱动的稀疏识别方法(PDE-FIND方法和LASSO方法)对圆柱绕流、顶盖驱动方腔流、RB对流和三维槽道湍流的控制方程进行稀疏识别, 研究了不同流场, 不同控制方程以及不同区域数据对于流场控制方程稀疏识别的影响.
1 流动控制方程的识别方法
非线性系统的控制方程大多是非线性偏微分方程(组), 例如Burgers方程(1), 科尔特弗-德弗里斯(korteweg-de Vries, kdV)方程(2)
(1) $\frac{\partial u}{\partial t}=-u\frac{\partial u}{\partial x}+\varepsilon \frac{\partial ^{2}u}{\partial x^{2}}$
(2) $\frac{\partial u}{\partial t}=-\alpha\frac{\partial u}{\partial x}-\beta u\frac{\partial u}{\partial x}-\gamma\frac{\partial ^3u}{\partial x^3}$
(3) $u_{t} =N\left( {u, u_{x} , u_{xx} , u_{xxx}, \cdots , x, t, \mu } \right)$
其中, $u$表示时空变量, $u_{t} $表示变量$u$的时间导数, 下标$x$的个数表示变量$u$的空间$n$阶导数, $\mu $表示系统的参数, $N(\cdot )$表示时空变量$u(x, t)$及其时空各阶导数的非线性函数. 在非线性偏微分方程的稀疏识别中, 将包含变量$u$及其导数相关的项组成矩阵$U$, 将其他可能出现的项组成矩阵$ Q$. 将$ U$, $ Q$合并成矩阵$\varTheta $
(4) $\varTheta ({ U}, { Q})=\left[\underbrace{1, u, u^{2}, \cdots , u_{x}, u_{xx} , \cdots , uu_x, u^2u_x, \cdots }_{ U}\qquad\underbrace{q_1, q_2\cdots , q_n}_{ Q} \right]$
对于离散的数据点, $ U$和$ Q$分别为$\left( {N\times M_{u} } \right)$和$\left({N\times M_{q} } \right)$的二维矩阵, 其中$N=n\times m$为矩阵中每项对应的时空点数($n$为空间网格总数, $m$为时间步数), $M_{u}$和$M_{q} $分别为$ U$和$ Q$的项数. 将非线性偏微分方程表示为以下线性方程
(5) $u_{{ t}} ={ \varTheta }( U, Q) \xi$
其中, $\varTheta $是人为给定的一个过完备的候选项的库, 即$\varTheta $库中包含所有可能属于该非线性偏微分方程的项. ${ \xi}$是稀疏向量, 表示的是非线性偏微分方程系数矩阵, 该稀疏向量${ \xi }$的非稀疏项等于该非线性偏微分方程的系数, 则偏微分方程可以写成线性加权和的形式
(6) $u_{t} (x, y)=\sum\limits_j {\varTheta_{j} } (u(x, t), q(x, t))\xi_{j}$
流体力学中非线性偏微分方程的稀疏识别就是通过流场的部分空间位置的时间序列数据, 来找到稀疏系数矩阵${ \xi }$使得方程(6)满足该流场动力学行为. 时间序列数据可以通过实验或者数值模拟来获得, 变量的时空导数通过多项式插值法或有限差分法获得. 对于不含有噪声的数据通常采用有限差分法计算获得, 但对于有噪声的数据, 多项式插值法计算的导数比有限差分法计算的导数更精确[19 ] .
如果$\varTheta $内所有的项都属于该流场系统的控制方程, 此时可以使用最小二乘法确定系数矩阵
(7) ${ \xi }=\arg \min_{{\hat{{ \xi }}}} \left\| {{ \varTheta \hat{{\xi }}}-{ U}_{t} } \right\|_{2}^{2}$
然而, 在过完备的库$\varTheta $中通过最小二乘法求解系数矩阵${ \xi}$, 会引起过拟合问题, 解出的系数矩阵${ \xi }$中所有元素都是非零, 这样所识别出的非线性偏微分方程很复杂, 比流场精确控制方程多出很多项, 不符合流体动力学规律.
对于偏微分方程的稀疏识别, 一种比较直观的方法就是将所有项可能的组合都进行计算, 比较所有项组合的误差, 得到最优的项组合, 数学表示为加入$L_{0} $正则化最小二乘法
(8) ${ \xi}=\arg \min_{{\hat{{ \xi }}}} \left\| {{ \varTheta \hat{{\xi }}}-{ U}_{t} } \right\|_{2}^{2} +\lambda\|\hat{{ \xi }}\|_{0}$
但是求解该问题会遇到NP-hard问题, 即把所有的组合都进行计算和比较, 这对于计算资源的消耗是巨大的. Tibshirani[14 ] 提出的LASSO算法是引入$L_{1}$正则化的最小二乘法
(9) ${ \xi }=\arg \min_{{\hat{{ \xi }}}} \left\| {{ \varTheta \hat{{\xi }}}-{ U}_{t} } \right\|_{2}^{2} +\lambda\|\hat{{ \xi}}\|_{1}$
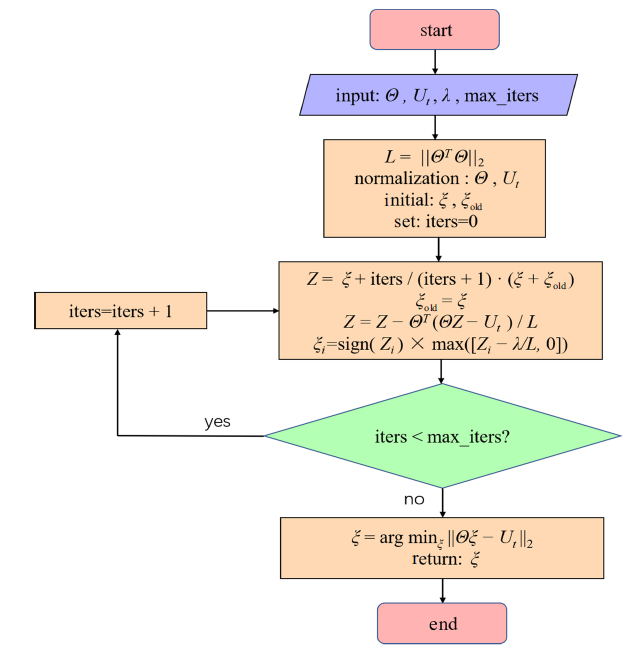
该方法是对于$L_{0} $正则化最小二乘法的一个凸优化问题, 避免了$L_{0} $正则化的NP-hard问题, 图1 是LASSO方法的流程图. 但LASSO方法对列相关性很高的数据矩阵的稀疏识别比较困难, 例如对于KdV方程的识别[19 ] .
图1
图1
LASSO方法流程图
Fig.1
Flow chart of LASSO scheme
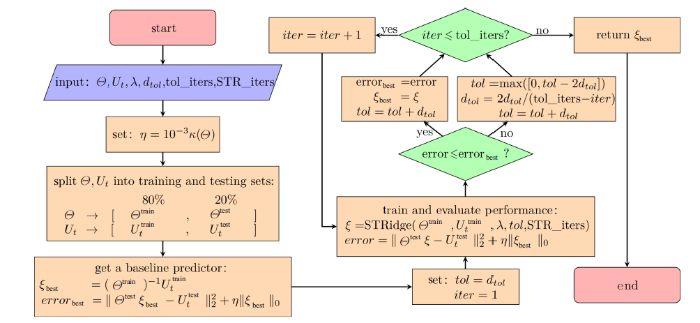
Rudy等[19 ] 提出了一个新的稀疏识别方法: PDE-FIND方法. 该算法是在加入$L_{2} $正则化的最小二乘法(1)中加入阈值筛选, 使用Ridge算法[28 ] 求解$L_{2} $正则化的最小二乘法, 将小于阈值的系数所对应的项筛去, 对剩余的项重复递归Ridge算法求解和阈值筛选, 直到所有项的系数都高于阈值, 此时返回稀疏系数矩阵${ \xi }$, 该过程被称为STRidge算法
(10) ${ \xi }=\arg \min_{{\hat{{ \xi }}}} \left\| {{ \varTheta \hat{{\xi }}}-{ U}_{t} } \right\|_{2}^{2} +\lambda\|\hat{{ \xi}}\|_{2}^{2}$
显然, 阈值的选取对于STRidge算法很重要, 不同的阈值会导致识别的偏微分方程的稀疏程度不同, 因此为了找到最佳的阈值, Rudy等[19 ] 提出了一个训练阈值的算法(TrainSTRidge算法). TrainSTRidge算法和STRidge算法相互耦合一起形成了PDE-FIND方法. 图2 是PDE-FIND方法的流程图.
图2
图2
PDE-FIND方法流程图
Fig.2
Flow chart of PDE-FIND scheme
2 识别结果
2.1 圆柱绕流涡量输运方程的识别
Rudy等[19 ] 使用PDE-FIND方法对圆柱绕流的涡量输运方程
(11) $\frac{\partial \omega }{\partial t}=\frac{1}{Re}\nabla^{2}\omega -({ u}\cdot \nabla )\omega$
进行了稀疏识别, 在未添加噪声的流场数据中识别出的涡量输运方程的平均系数误差为1%$\pm$0.2%. 本文同样也对圆柱绕流问题的涡量输运方程进行了识别.
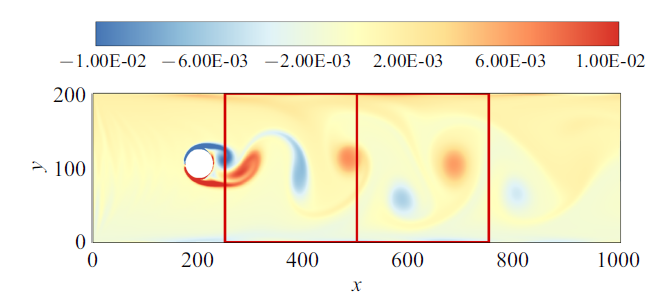
采用LBM方法对雷诺数为300的圆柱绕流进行了直接数值模拟, 计算网格为1000$\times$250, 圆柱圆心位置为(201, 133), 半径为26, 来流最大速度为$u=0.1$. 图3 给出了$t=10^{4}$时流场的涡量云图. 如图3 所示将圆柱绕流后面的区域分为$x\in (250, 500)$, $x\in (500, 750)$, 每个区域随机选择8000个空间点并追踪记录60个时间步长的速度数据和压力数据, 这样每个区域就共获得了48万个数据样本, 这对于稀疏识别所需的样本是充足的, 且采样的方法不会影响识别的结果[19 ] . 采用5次切比雪夫多项式插值[29 ] 计算导数, 导数阶数最高保留到二阶, 变量次数最高保留到二阶, 非线性项最高保留到四阶, 将这些数据用来构建稀疏识别所需$\varTheta $库(4).表1 给出了PDE-FIND方法和LASSO方法对于$x\in (250, 500)$圆柱绕流数据的稀疏识别结果.
图3
图3
$t=10^{4}$时圆柱绕流的涡量云图
Fig.3
Vorticity contour of flow past a cylinder at $t=10^{4}$
从表1 可得出, PDE-FIND方法和LASSO方法都正确地识别出了涡量输运方程, 并且系数相同. 两种算法对于涡量输运方程的稀疏识别的能力一致, 且平均系数误差为3.21%. 涡量输运方程是一个线性偏微分方程, PDE-FIND方法和LASSO方法对线性偏微分方程的稀疏识别能力一致. 对于$x\in (500, 750)$区域的数据, 两种算法也都识别出了正确的控制方程, 但所得平均系数误差有所增加, 为8.75%. 这是因为越靠近圆柱区域的流场信息越丰富, 因而识别出的控制方程系数越精确. 这与文献[20 ]的结论是吻合的, 即选取具有丰富动力学行为的时空演化数据可以提高对动力学控制方程的识别的准确性.
2.2 顶盖驱动方腔流控制方程的识别
本节对二维顶盖驱动方腔流的NS方程组进行稀疏识别. 相比于上一节涡量输运方程的识别, 原始变量形式的NS方程组是一组偏微分方程组
(12) $\nabla \cdot { u}=0$
(13) $\frac{\partial { u}}{\partial t}+({ u}\cdot \nabla){ u}=-\nabla p+\frac{1}{{Re}}\nabla^{2}{ u}$
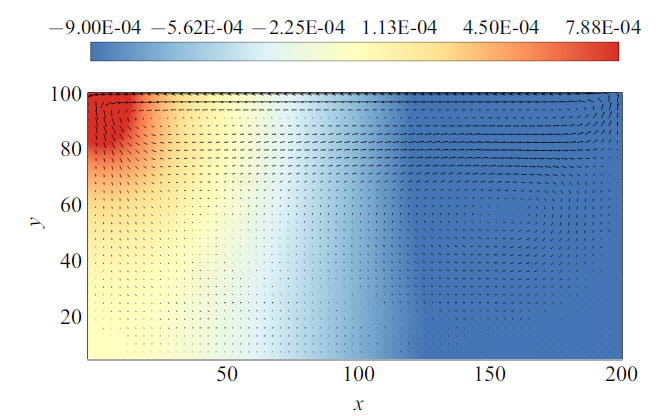
其中, 方程(12)是连续性方程, 方程(13)是动量方程. 二维顶盖驱动方腔流场数据使用基于有限差分的直接数值模拟得到. 方腔宽高比为2, 方腔顶部的壁面以大小为1的速度匀速向左运动, 流动雷诺数为100.模拟计算网格数为200$\times$100, 图4 给出了$t=40$时流场的压力云图和流线图.
图4
图4
$t=40$时顶盖驱动方腔流的压力云图和速度矢量图
Fig.4
Pressure contour and velocity vector of lid-driven cavity flow at $t=40$
注意到连续性方程(12), 不含有时间偏导项, 将连续性方程可改写为
(14) $u_{x} =-v_{y}$
将$x$看成时间$t$, 就可以采用稀疏识别方法来识别连续性方程了.
在整个方腔区域选取数据, 采样方法、导数计算方法以及$\varTheta $库的构建与2.1节相同. 表2 给出了PDE-FIND方法和LASSO方法对于$Re=100$顶盖驱动方腔流控制方程的稀疏识别结果. 从表2 可得出, 对于顶盖驱动方腔流的数据, PDE-FIND方法正确地识别出了连续性方程和NS方程的各项, 且平均系数误差为2.77%, 而LASSO方法只能正确地识别出连续性方程, 没有识别出动量方程, 例如在$u$方程中未选择出$uu_{x} $, 可能是因为LASSO算法对含强非线性项的方程的识别会失效, 具体的原因将在下一节进行讨论.
2.3 Rayleigh-Bénard对流控制方程的识别
下面考虑识别Rayleigh-Bénard (RB)对流系统中的控制方程, 其物理模型是一个下底板加热, 上底板冷却的对流系统, 系统中充满流体介质, 由于上下底板温度不一样, 导致不同高度位置的流体之间存在密度差, 在浮力的驱动下系统中流体产生运动. 在OberbeckBoussinesq (OB)近似下的无量纲控制方程组如下
(15) $\nabla \cdot { u}=0$
(16) $\frac{\partial { u}}{\partial t}+({ u}\cdot \nabla ){ u}=-\nabla p+\sqrt {\frac{Pr}{Ra}} \nabla^{2}{ u}+\theta { z}$
(17) $\frac{\partial \theta }{\partial t}+({ u}\cdot \nabla )\theta =\sqrt {\frac{1}{RaPr}} \nabla^{2}\theta$
其中, 方程(15)是连续性方程, 方程(16)是含有热浮力项的NS方程, 方程(17)是热输运方程, Rayleigh数($Ra)$和Prandtl数($Pr$)是RB系统的重要控制参数.
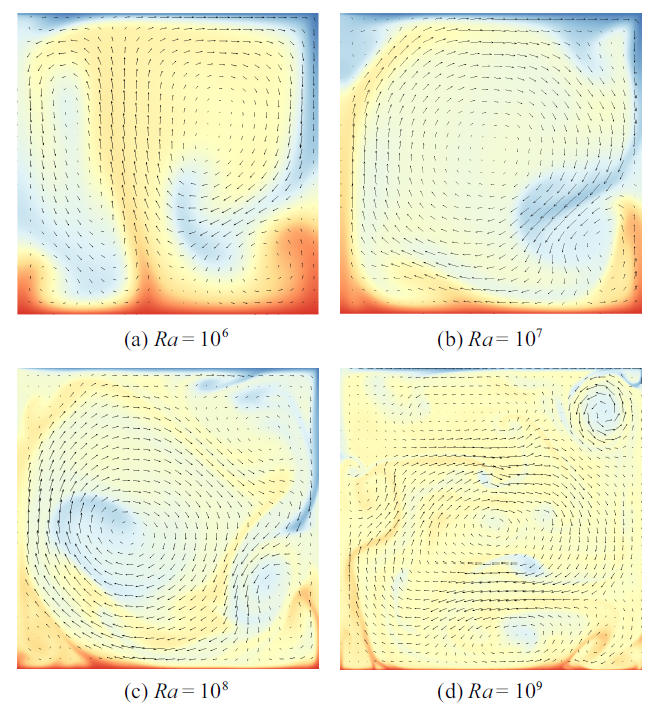
RB对流流场通过Zhang[30 ] 所发展的基于有限差分的直接数值模拟得到. 不失一般性, 模拟方形区域的RB对流, $Pr $数固定为1, 计算了4个不同的$Ra$数的工况. $Ra$数分别取$10^{6}$, $10^{7}$, $10^{8}$, $10^{9}$, 对应的计算网格分别是128$\times$128, 512$\times$512, 720$\times$720, 1024$\times$1024.当$Ra$数从$10^{6}$增大到$10^{9}$时, RB对流系统会从层流状态转变为强非线性的湍流流动状态, 整个系统的速度及温度脉动剧烈, 会出现局部梯度较大的数据, 对于系统控制方程的识别可能造成一定的困难. 图5 是$t=80$时, 不同$Ra$数的RB对流系统的温度云图和速度矢量图.
图5
图5
$Pr =1$, 不同$Ra$数的RB对流系统的温度云图和速度矢量图
Fig.5
Temperature contour and velocity vector of RB convection for different Rayleigh number with $Pr =1$
在整个计算区域选取数据, 采样方法、导数计算方法以及$\varTheta $库的构建与2.1节相同.
表3 给出了$Ra$数为$10^{9}$的识别结果, PDE-FIND方法和LASSO方法都正确识别出了$Ra=10^{9}$的RB对流系统中连续性方程和热输运方程, 并且系数一致. 而且PDE-FIND方法仍然正确识别出了RB对流的动量方程, 对应$Ra$从$10^{6}$到$10^{9}$, 识别的控制方程组平均系数误差分别为0.36%, 0.06%, 0.40%, 0.46%. 而LASSO方法对NS方程仍没有正确识别, 在$u$方程识别中未选择$u_{xx} $. 原因是由变量及变量各阶导数组成的过于完备库中, 回归系数趋于相近的项之间会产生分组效应(grouping effect)[31 , 32 ] . 而LASSO方法对于具有分组效应的候选项的筛选可能会失败, 表现为在有分组效应的候选项中只选择一项, 而其他的候选项的系数会设为0.在$Ra=10^{6}$, $Ra=10^{7}$, $Ra=10^{8}$的RB对流控制方程稀疏识别中, 也存在同样的现象.
2.4 三维槽道湍流控制方程的识别
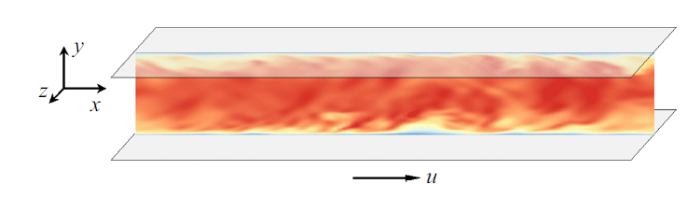
最后对三维槽道湍流进行了稀疏识别, 数据通过离散统一的气动格式(discrete unified gas-kinetic scheme, DUGKS)[33 ] 模拟得到, 计算域为4$\pi $$\times$2$\times$4$\pi $/3, 槽道半高为1, 计算网格为128$\times$128$\times$128, 垂向采用非均匀网格, 流向和展向采用均匀网格, 壁面摩擦速度定义的雷诺数$Re_{\tau } =180$, 此时的槽道流处于充分发展湍流状态. 图6 给出了槽道展向中心截面的速度云图, 各种尺度的复杂结构清晰可见. 在整个槽道中选取数据, 采样方法、导数计算方法以及 $\varTheta $库的构建与2.1节相同.
图6
图6
$Re_{\tau } =180$, 三维槽道湍流展向中心截面速度云图
Fig.6
Velocity contour of 3D turbulent channel flow with $Re_{\tau } =180$ at $z=0$
表4 给出了三维槽道湍流控制方程的识别结果, PDE-FIND方法对于正确地识别出了控制方程, 并且平均系数误差为0.37%, 说明PDE-FIND可以在在湍流状态的流场数据中识别控制方程. 而LASSO方法只识别出了连续性方程, 这与前两节的结果一致.说明在过完备候选库中列相关性强弱对于PDE-FIND方法的稀疏识别没有影响, PDE-FIND方法不存在分组效应. 本节还研究了不同$y^{+}$的数据对识别的影响, 取$y^{+}\in (0.21, 19.3)$, $y^{+}\in (19.3, 59.7)$, $y^{+}\in (59.7, 182.9)$, 都正确识别出了控制方程, 系数平均误差分别为0.42%, 0.48%, 0.39%. 说明在三维槽道湍流控制方程的稀疏识别中, 误差与壁面距离几乎无关.
3 结论
本文采用PDE-FIND方法及LASSO方法对二维圆柱绕流、顶盖驱动方腔流动、RB对流和三维槽道湍流控制方程进行了稀疏识别, 主要得到以下结论:
(1) 使用PDE-FIND方法识别出了流场中的控制方程, 得到了正确的方程及精确的系数.
(2) LASSO方法正确识别出了其中的线性偏微分控制方程如连续性方程, 涡量输运和温度输运方程, 但对含非线性的偏微分方程识别效果差, 这是由于LASSO方法识别过程中侯选库存在分组效应, 降低了识别能力. 而在PDE-FIND方法中是不存在分组效应的, 所以PDE-FIND方法对强非线性方程识别有一定的优势.
(3) 丰富的流动结构对于数据驱动的流场控制方程的稀疏识别有重要作用, 选择具有丰富流动结构的区域的数据可以提升稀疏识别的有效性和精确性.
从2.3节和2.4节结果可知, PDE-FIND方法对层流和湍流两种流动状态都可以精确的识别出控制方程. 这对于复杂流动建模提供了一种新的研究方法, 例如将PDE-FIND方法用于湍流脉动量控制方程和湍流统计量的控制方程的系数识别. 未来考虑将稀疏识别算法与$k$-$\varepsilon $等湍流模式相结合, 提高湍流模式在数值模拟中的精确性. 另外, 本文的流场数据都是通过精细的直接数值模拟得到的, PDE-FIND都识别出了正确的方程形式, 得到了准确的方程系数, 但从实验或者实测数据往往具有噪声, 对于含有噪声的数据, PDE-FIND方法识别能力往往变弱, 如何提高PDE-FIND方法在含有噪声数据的识别能力是值得深入研究的课题. 可行的方法之一是结合数据去噪技术和寻找最优的插值点数和多项式插值阶数等, 提高高阶导数项的计算精度, 从而提高稀疏识别能力.
参考文献
View Option
[1]
张慧洁 , 郝瑞林 . 电网中动态电压恢复器的非线性控制研究
电子测试 , 2019 (Z1 ): 14 -16
[本文引用: 1]
(Zhang Huijie Hao Ruilin . Research on dynamic voltage restorer based on nonlinear control theory in the power grid
Electronic Test 2019 (Z1 ): 14 -16 (in Chinese))
[本文引用: 1]
[2]
Yang CH Tsai CY . Nonlinear dynamic analysis of finance system and its analog/digital circuit implementation
Journal of Computational and Theoretical Nanoscience 2015 , 12 (10 ): 3538 -3546
DOI
URL
[本文引用: 1]
[3]
Navarro LG Jurado FL Castillo MJ , et al . Assessment of autonomous nerve system through non-linear heart rate variability outcomes in sedentary healthy adults
Peer J 2020 , 8 (11 ): e10178
[本文引用: 1]
[4]
张伟伟 , 寇家庆 , 刘溢浪 . 智能赋能流体力学展望
航空学报 , 2021 , 42 (4 ): 1 -51
[本文引用: 2]
(Zhang Weiwei Kou Jiaqing Liu Yilang . Prospect of artificial intelligence empowering fluid mechanics
Acta Aeronautica et Astronautica Sinica 2021 , 42 (4 ): 1 -51 (in Chinese))
[本文引用: 2]
[5]
Crutchfield JP McNamara BS . Equations of motion from a data series
Complex Systems 1987 , 1 (121 ): 417 -452
[本文引用: 1]
[6]
洪泽华 , 章佳君 , 周金鹏 等 . 复杂目标红外辐射特性大数据知识表示及建模方法
上海航天 , 2020 , 37 (6 ): 52 -57
(Hong Zehua Zhang Jiajun Zhou Jinpeng , et al . Big Data knowledge representation and modeling method for infrared radiation characteristics of comp
Aerospace Shanghai 2020 , 37 (6 ): 52 -57 (in Chinese))
[7]
曾贲 , 房霄 , 孔德帅 等 . 一种数据驱动的对抗博弈智能体建模方法
系统仿真学报 , 2020 : 1 -7
(Zeng Bi Fang Xiao Kong Deshuai , et al . A data-driven modeling method for game adversity agent
Journal of System Simulation 2020 : 1 -7 (in Chinese))
[8]
李星 . 数据驱动建模中精度与泛化平衡问题研究. [硕士论文]
西安: 西安理工大学 , 2020
(Li Xing . Research on the balance between accuracy and generalization in data-driven modeling. [Master Thesis]
Xi'an: Xi'an University of Technology , 2020 (in Chinese))
[9]
赵丹 . 非线性系统即时学习建模方法研究. [硕士论文]
镇江: 江苏大学 , 2017
(Zhao Dan . Research on just-in-time learning modeling for nonlinear systems. [Master Thesis]
Zhenjiang: Jiangsu University , 2017 (in Chinese))
[10]
González-García R Rico-Martínez R Kevrekidis IG . Identification of distributed parameter systems: A neural net based approach
Computers & Chemical Engineering 1998 , 22 : S965 -S968
DOI
URL
[11]
Kevrekidis IG Gear CW Hyman JM , et al . Equation-free, coarse-grained multiscale computation: Enabling mocroscopic simulators to perform system-level analysis
Communications in Mathematical Sciences 2003 , 1 (4 ): 715 -762
DOI
URL
[12]
Daniels BC Nemenman I . Automated adaptive inference of phenomenological dynamical models
Nature Communications 2015 , 6 (1 ): 1 -8
[13]
Bongard J Lipson H . Automated reverse engineering of nonlinear dynamical systems
Proceedings of the National Academy of Sciences 2007 , 104 (24 ): 9943 -9948
DOI
URL
[本文引用: 1]
[14]
Tibshirani R . Regression shrinkage and selection via the lasso
Stat. Soc. B 1996 , 58 (1 ): 267 -288
[本文引用: 4]
[15]
Tibshirani R . The lasso method for variable selection in the Cox model
Statistics in Medicine 1997 , 16 (4 ): 385 -395
PMID
[本文引用: 1]
I propose a new method for variable selection and shrinkage in Cox's proportional hazards model. My proposal minimizes the log partial likelihood subject to the sum of the absolute values of the parameters being bounded by a constant. Because of the nature of this constraint, it shrinks coefficients and produces some coefficients that are exactly zero. As a result it reduces the estimation variance while providing an interpretable final model. The method is a variation of the 'lasso' proposal of Tibshirani, designed for the linear regression context. Simulations indicate that the lasso can be more accurate than stepwise selection in this setting.
[16]
Schmidt M Lipson H . Distilling free-form natural laws from experimental data
Science 2009 , 324 (5923 ): 81 -85
DOI
URL
[17]
Brunton SL Kutz JN . Data-driven Science and Engineering: Machine Learning, Dynamical Systems, and Control
England: Cambridge University Press , 2019
[18]
Brunton SL Proctor JL Kutz JN . Discovering governing equations from data by sparse identification of nonlinear dynamical systems
Proceedings of the National Academy of Sciences of the United States of America 2016 , 113 (15 ): 3932 -3937
DOI
PMID
[本文引用: 1]
Extracting governing equations from data is a central challenge in many diverse areas of science and engineering. Data are abundant whereas models often remain elusive, as in climate science, neuroscience, ecology, finance, and epidemiology, to name only a few examples. In this work, we combine sparsity-promoting techniques and machine learning with nonlinear dynamical systems to discover governing equations from noisy measurement data. The only assumption about the structure of the model is that there are only a few important terms that govern the dynamics, so that the equations are sparse in the space of possible functions; this assumption holds for many physical systems in an appropriate basis. In particular, we use sparse regression to determine the fewest terms in the dynamic governing equations required to accurately represent the data. This results in parsimonious models that balance accuracy with model complexity to avoid overfitting. We demonstrate the algorithm on a wide range of problems, from simple canonical systems, including linear and nonlinear oscillators and the chaotic Lorenz system, to the fluid vortex shedding behind an obstacle. The fluid example illustrates the ability of this method to discover the underlying dynamics of a system that took experts in the community nearly 30 years to resolve. We also show that this method generalizes to parameterized systems and systems that are time-varying or have external forcing.
[19]
Rudy SH Brunton SL Proctor JL , et al . Data-driven discovery of partial differential equations
Science Advances 2017 , 3 (4 ): e1602614
DOI
URL
[本文引用: 7]
[20]
胡军 , 刘全 , 倪国喜 . 时变偏微分方程的贝叶斯稀疏识别方法
计算物理 , 2021 , 38 (1 ): 25 -34
[本文引用: 2]
(Hu Jun Liu Quan Ni Guoxi . Bayesian sparse identification of time-varying partial differential equations
Chinese Journal of Computational Physics 2021 , 38 (1 ): 25 -34 (in Chinese))
[本文引用: 2]
[21]
Berkooz G Holmes P Lumley JL . The proper orthogonal decomposition in the analysis of turbulent flows
Annual Review of Fluid Mechanics 1993 , 25 (1 ): 539 -575
DOI
URL
[本文引用: 1]
[22]
Brunton SL Noack BR Koumoutsakos P . Machine learning for fluid mechanics
Annual Review of Fluid Mechanics 2020 , 52 : 477 -508
DOI
URL
[本文引用: 1]
[23]
Chang H Zhang D . Machine learning subsurface flow equations from data
Computational Geosciences 2019 , 23 (5 ): 895 -910
DOI
URL
[本文引用: 1]
[24]
Raissi M Yazdani A Karniadakis GE . Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations
Science 2020 , 367 (6481 ): 1026 -1030
DOI
URL
[本文引用: 1]
[25]
Zhang J Ma W . Data-driven discovery of governing equations for fluid dynamics based on molecular simulation
Journal of Fluid Mechanics 2020 , 892 : A5
DOI
URL
[本文引用: 1]
[26]
Schmelzer M Dwight RP Cinnella P . Discovery of algebraic Reynolds-stress models using sparse symbolic regression
Flow Turbulence and Combustion 2020 , 104 (2-3 ): 579 -603
DOI
URL
[本文引用: 1]
[27]
张亦知 , 程诚 , 范钇彤 等 . 基于物理知识约束的数据驱动式湍流模型修正及槽道湍流计算验证
航空学报 , 2020 , 41 (3 ): 119 -128
[本文引用: 2]
(Zhang Yizhi Cheng Cheng Fan Yitong , et al . Data-driven correction of turbulence model with physics knowledge constrains in channel flow
Acta Aeronautica et Astronautica Ainica 2020 , 41 (3 ): 119 -128 (in Chinese))
[本文引用: 2]
[28]
Hoerl AE Kennard RW . Ridge regression: Applications to nonorthogonal problems
Technometrics 1970 , 12 (1 ): 69 -82
DOI
URL
[本文引用: 1]
[29]
Benjamin AT Ericksen L Jayawant P , et al . Combinatorial trigonometry with Chebyshev polynomials
Journal of Statistical Planning and Inference 2010 , 140 (8 ): 2157 -2160
DOI
URL
[本文引用: 1]
[30]
Zhang YZ Xia SN Dong YH , et al . An efficient parallel algorithm for DNS of buoyancy-driven turbulent flows
Journal of Hydrodynamics, Ser. B 2019 , 31 (6 ): 1159 -1169
[本文引用: 1]
[31]
Zou H Hastie T . Regularization and variable selection via the elastic net
Journal of the Royal Statistical Society: Series B (Statistical Methodology )2005 , 67 (2 ): 301 -320
DOI
URL
[本文引用: 1]
[32]
Maddu S Cheeseman BL Sbalzarini IF , et al . Stability selection enables robust learning of partial differential equations from limited noisy data
arXiv preprint 2019 , arXiv:1907.07810
[本文引用: 1]
[33]
Bo Y Wang P Guo Z , et al . DUGKS simulations of three-dimensional Taylor-Green vortex flow and turbulent channel flow
Computers & Fluids 2017 , 155 : 9 -21
DOI
URL
[本文引用: 1]
电网中动态电压恢复器的非线性控制研究
1
2019
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
电网中动态电压恢复器的非线性控制研究
1
2019
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
Nonlinear dynamic analysis of finance system and its analog/digital circuit implementation
1
2015
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
Assessment of autonomous nerve system through non-linear heart rate variability outcomes in sedentary healthy adults
1
2020
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
智能赋能流体力学展望
2
2021
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
... 近年来, 数据驱动方法在流场中的应用颇受研究者[4 , 22 -27 ] 的重视. 2019年, Chang和Zhang[23 ] 使用LASSO方法从数据出发, 识别出了单相地下水流动方程和污染物输运方程. 2020年, Raissi等[24 ] 使用深度学习, 对流场可视化的图片进行学习, 并反演了流场的压力和速度分布场, 可以帮助得到实验难以测量的数据. Zhang和Ma[25 ] 采用PDE-FIND方法, 对基于直接模拟蒙特卡罗(direct simulation Monte Carlo, DSMC)方法模拟产生的数据进行稀疏识别, 反演了流体的对流、扩散以及涡量输运方程, 从数据驱动角度清晰地展示了玻尔兹曼方程和 Navier-Stokes方程之间的相关性. Schmelzer等[26 ] 采用SINDy框架在数值模拟的数据中是识别出了代数雷诺应力模型. 张亦知等[27 ] 构建了基于数据驱动的湍流模型修正框架并在槽道流中进行了验证. ...
智能赋能流体力学展望
2
2021
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
... 近年来, 数据驱动方法在流场中的应用颇受研究者[4 , 22 -27 ] 的重视. 2019年, Chang和Zhang[23 ] 使用LASSO方法从数据出发, 识别出了单相地下水流动方程和污染物输运方程. 2020年, Raissi等[24 ] 使用深度学习, 对流场可视化的图片进行学习, 并反演了流场的压力和速度分布场, 可以帮助得到实验难以测量的数据. Zhang和Ma[25 ] 采用PDE-FIND方法, 对基于直接模拟蒙特卡罗(direct simulation Monte Carlo, DSMC)方法模拟产生的数据进行稀疏识别, 反演了流体的对流、扩散以及涡量输运方程, 从数据驱动角度清晰地展示了玻尔兹曼方程和 Navier-Stokes方程之间的相关性. Schmelzer等[26 ] 采用SINDy框架在数值模拟的数据中是识别出了代数雷诺应力模型. 张亦知等[27 ] 构建了基于数据驱动的湍流模型修正框架并在槽道流中进行了验证. ...
Equations of motion from a data series
1
1987
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
复杂目标红外辐射特性大数据知识表示及建模方法
0
2020
复杂目标红外辐射特性大数据知识表示及建模方法
0
2020
一种数据驱动的对抗博弈智能体建模方法
0
2020
一种数据驱动的对抗博弈智能体建模方法
0
2020
数据驱动建模中精度与泛化平衡问题研究. [硕士论文]
0
2020
数据驱动建模中精度与泛化平衡问题研究. [硕士论文]
0
2020
非线性系统即时学习建模方法研究. [硕士论文]
0
2017
非线性系统即时学习建模方法研究. [硕士论文]
0
2017
Identification of distributed parameter systems: A neural net based approach
0
1998
Equation-free, coarse-grained multiscale computation: Enabling mocroscopic simulators to perform system-level analysis
0
2003
Automated adaptive inference of phenomenological dynamical models
0
2015
Automated reverse engineering of nonlinear dynamical systems
1
2007
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
Regression shrinkage and selection via the lasso
4
1996
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
... [14 -21 ]. 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
... [14 ]首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
... 但是求解该问题会遇到NP-hard问题, 即把所有的组合都进行计算和比较, 这对于计算资源的消耗是巨大的. Tibshirani[14 ] 提出的LASSO算法是引入$L_{1}$正则化的最小二乘法 ...
The lasso method for variable selection in the Cox model
1
1997
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
Distilling free-form natural laws from experimental data
0
2009
Data-driven Science and Engineering: Machine Learning, Dynamical Systems, and Control
0
2019
Discovering governing equations from data by sparse identification of nonlinear dynamical systems
1
2016
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
Data-driven discovery of partial differential equations
7
2017
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
... 流体力学中非线性偏微分方程的稀疏识别就是通过流场的部分空间位置的时间序列数据, 来找到稀疏系数矩阵${ \xi }$使得方程(6)满足该流场动力学行为. 时间序列数据可以通过实验或者数值模拟来获得, 变量的时空导数通过多项式插值法或有限差分法获得. 对于不含有噪声的数据通常采用有限差分法计算获得, 但对于有噪声的数据, 多项式插值法计算的导数比有限差分法计算的导数更精确[19 ] . ...
... 该方法是对于$L_{0} $正则化最小二乘法的一个凸优化问题, 避免了$L_{0} $正则化的NP-hard问题, 图1 是LASSO方法的流程图. 但LASSO方法对列相关性很高的数据矩阵的稀疏识别比较困难, 例如对于KdV方程的识别[19 ] . ...
... Rudy等[19 ] 提出了一个新的稀疏识别方法: PDE-FIND方法. 该算法是在加入$L_{2} $正则化的最小二乘法(1)中加入阈值筛选, 使用Ridge算法[28 ] 求解$L_{2} $正则化的最小二乘法, 将小于阈值的系数所对应的项筛去, 对剩余的项重复递归Ridge算法求解和阈值筛选, 直到所有项的系数都高于阈值, 此时返回稀疏系数矩阵${ \xi }$, 该过程被称为STRidge算法 ...
... 显然, 阈值的选取对于STRidge算法很重要, 不同的阈值会导致识别的偏微分方程的稀疏程度不同, 因此为了找到最佳的阈值, Rudy等[19 ] 提出了一个训练阈值的算法(TrainSTRidge算法). TrainSTRidge算法和STRidge算法相互耦合一起形成了PDE-FIND方法. 图2 是PDE-FIND方法的流程图. ...
... Rudy等[19 ] 使用PDE-FIND方法对圆柱绕流的涡量输运方程 ...
... 采用LBM方法对雷诺数为300的圆柱绕流进行了直接数值模拟, 计算网格为1000$\times$250, 圆柱圆心位置为(201, 133), 半径为26, 来流最大速度为$u=0.1$. 图3 给出了$t=10^{4}$时流场的涡量云图. 如图3 所示将圆柱绕流后面的区域分为$x\in (250, 500)$, $x\in (500, 750)$, 每个区域随机选择8000个空间点并追踪记录60个时间步长的速度数据和压力数据, 这样每个区域就共获得了48万个数据样本, 这对于稀疏识别所需的样本是充足的, 且采样的方法不会影响识别的结果[19 ] . 采用5次切比雪夫多项式插值[29 ] 计算导数, 导数阶数最高保留到二阶, 变量次数最高保留到二阶, 非线性项最高保留到四阶, 将这些数据用来构建稀疏识别所需$\varTheta $库(4).表1 给出了PDE-FIND方法和LASSO方法对于$x\in (250, 500)$圆柱绕流数据的稀疏识别结果. ...
时变偏微分方程的贝叶斯稀疏识别方法
2
2021
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
... 从表1 可得出, PDE-FIND方法和LASSO方法都正确地识别出了涡量输运方程, 并且系数相同. 两种算法对于涡量输运方程的稀疏识别的能力一致, 且平均系数误差为3.21%. 涡量输运方程是一个线性偏微分方程, PDE-FIND方法和LASSO方法对线性偏微分方程的稀疏识别能力一致. 对于$x\in (500, 750)$区域的数据, 两种算法也都识别出了正确的控制方程, 但所得平均系数误差有所增加, 为8.75%. 这是因为越靠近圆柱区域的流场信息越丰富, 因而识别出的控制方程系数越精确. 这与文献[20 ]的结论是吻合的, 即选取具有丰富动力学行为的时空演化数据可以提高对动力学控制方程的识别的准确性. ...
时变偏微分方程的贝叶斯稀疏识别方法
2
2021
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
... 从表1 可得出, PDE-FIND方法和LASSO方法都正确地识别出了涡量输运方程, 并且系数相同. 两种算法对于涡量输运方程的稀疏识别的能力一致, 且平均系数误差为3.21%. 涡量输运方程是一个线性偏微分方程, PDE-FIND方法和LASSO方法对线性偏微分方程的稀疏识别能力一致. 对于$x\in (500, 750)$区域的数据, 两种算法也都识别出了正确的控制方程, 但所得平均系数误差有所增加, 为8.75%. 这是因为越靠近圆柱区域的流场信息越丰富, 因而识别出的控制方程系数越精确. 这与文献[20 ]的结论是吻合的, 即选取具有丰富动力学行为的时空演化数据可以提高对动力学控制方程的识别的准确性. ...
The proper orthogonal decomposition in the analysis of turbulent flows
1
1993
... 非线性动力系统广泛存在于自然界及工业界中, 对非线性动力系统的建模是亟待解决的问题. 非线性动力系统(如电力网络[1 ] 、金融学[2 ] 、神经科学[3 ] 等)的控制方程大多是非线性偏微分方程, 从传统的守恒定律和物理原理等第一性原理出发去推导一些复杂系统的控制方程是困难的.现代流体力学虽然已经具备了较完备的理论方程和模型, 但仍然有很多复杂问题的理论研究尚不完备, 如带化学反应流、多相流、非牛顿流、稀薄流等, 这些系统的动力学方程或模型的理论推导难以实现[4 ] . 近些年来, 随着计算机硬件以及计算科学的发展, 基于数据驱动方法对非线性复杂系统建模得到了研究者的青睐[5 -13 ] . 其中稀疏识别方法[14 ] 可以简化复杂的数学模型, 得到项数较少的简单模型来表征系统的动力学特性, 并可以综合考虑过拟合和模型精确性之间的矛盾. 稀疏识别方法已经被广泛用于复杂非线性系统控制方程的识别[14 -21 ] . 1996年, Tibshirani[14 ] 首次提出最小绝对收缩和选择算子(least absolute shrinkage and selection operator, LASSO)方法, 并且把LASSO方法应用在Cox模型的稀疏识别中[15 ] . 2016年, Brunton等[18 ] 通过稀疏识别在含有噪声的非线性动力系统的数据中识别出了常微分方程. 2017年, Rudy等[19 ] 提出了偏微分方程函数识别(partial differential equations functional identification of nonlinear dynamics, PDE-FIND)方法可以通过测量或者数值模拟的时空数据来稀疏识别偏微分方程, 正确地识别出了圆柱绕流流场的涡量输运方程. 胡军等[20 ] 将贝叶斯稀疏识别方法识别结果与PDE-FIND方法识别结果相比较, 表明了贝叶斯稀疏识别方法对偏微分方程具有非常强的稀疏恢复能力, 但相比PDE-FIND方法对噪声更加敏感. ...
Machine learning for fluid mechanics
1
2020
... 近年来, 数据驱动方法在流场中的应用颇受研究者[4 , 22 -27 ] 的重视. 2019年, Chang和Zhang[23 ] 使用LASSO方法从数据出发, 识别出了单相地下水流动方程和污染物输运方程. 2020年, Raissi等[24 ] 使用深度学习, 对流场可视化的图片进行学习, 并反演了流场的压力和速度分布场, 可以帮助得到实验难以测量的数据. Zhang和Ma[25 ] 采用PDE-FIND方法, 对基于直接模拟蒙特卡罗(direct simulation Monte Carlo, DSMC)方法模拟产生的数据进行稀疏识别, 反演了流体的对流、扩散以及涡量输运方程, 从数据驱动角度清晰地展示了玻尔兹曼方程和 Navier-Stokes方程之间的相关性. Schmelzer等[26 ] 采用SINDy框架在数值模拟的数据中是识别出了代数雷诺应力模型. 张亦知等[27 ] 构建了基于数据驱动的湍流模型修正框架并在槽道流中进行了验证. ...
Machine learning subsurface flow equations from data
1
2019
... 近年来, 数据驱动方法在流场中的应用颇受研究者[4 , 22 -27 ] 的重视. 2019年, Chang和Zhang[23 ] 使用LASSO方法从数据出发, 识别出了单相地下水流动方程和污染物输运方程. 2020年, Raissi等[24 ] 使用深度学习, 对流场可视化的图片进行学习, 并反演了流场的压力和速度分布场, 可以帮助得到实验难以测量的数据. Zhang和Ma[25 ] 采用PDE-FIND方法, 对基于直接模拟蒙特卡罗(direct simulation Monte Carlo, DSMC)方法模拟产生的数据进行稀疏识别, 反演了流体的对流、扩散以及涡量输运方程, 从数据驱动角度清晰地展示了玻尔兹曼方程和 Navier-Stokes方程之间的相关性. Schmelzer等[26 ] 采用SINDy框架在数值模拟的数据中是识别出了代数雷诺应力模型. 张亦知等[27 ] 构建了基于数据驱动的湍流模型修正框架并在槽道流中进行了验证. ...
Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations
1
2020
... 近年来, 数据驱动方法在流场中的应用颇受研究者[4 , 22 -27 ] 的重视. 2019年, Chang和Zhang[23 ] 使用LASSO方法从数据出发, 识别出了单相地下水流动方程和污染物输运方程. 2020年, Raissi等[24 ] 使用深度学习, 对流场可视化的图片进行学习, 并反演了流场的压力和速度分布场, 可以帮助得到实验难以测量的数据. Zhang和Ma[25 ] 采用PDE-FIND方法, 对基于直接模拟蒙特卡罗(direct simulation Monte Carlo, DSMC)方法模拟产生的数据进行稀疏识别, 反演了流体的对流、扩散以及涡量输运方程, 从数据驱动角度清晰地展示了玻尔兹曼方程和 Navier-Stokes方程之间的相关性. Schmelzer等[26 ] 采用SINDy框架在数值模拟的数据中是识别出了代数雷诺应力模型. 张亦知等[27 ] 构建了基于数据驱动的湍流模型修正框架并在槽道流中进行了验证. ...
Data-driven discovery of governing equations for fluid dynamics based on molecular simulation
1
2020
... 近年来, 数据驱动方法在流场中的应用颇受研究者[4 , 22 -27 ] 的重视. 2019年, Chang和Zhang[23 ] 使用LASSO方法从数据出发, 识别出了单相地下水流动方程和污染物输运方程. 2020年, Raissi等[24 ] 使用深度学习, 对流场可视化的图片进行学习, 并反演了流场的压力和速度分布场, 可以帮助得到实验难以测量的数据. Zhang和Ma[25 ] 采用PDE-FIND方法, 对基于直接模拟蒙特卡罗(direct simulation Monte Carlo, DSMC)方法模拟产生的数据进行稀疏识别, 反演了流体的对流、扩散以及涡量输运方程, 从数据驱动角度清晰地展示了玻尔兹曼方程和 Navier-Stokes方程之间的相关性. Schmelzer等[26 ] 采用SINDy框架在数值模拟的数据中是识别出了代数雷诺应力模型. 张亦知等[27 ] 构建了基于数据驱动的湍流模型修正框架并在槽道流中进行了验证. ...
Discovery of algebraic Reynolds-stress models using sparse symbolic regression
1
2020
... 近年来, 数据驱动方法在流场中的应用颇受研究者[4 , 22 -27 ] 的重视. 2019年, Chang和Zhang[23 ] 使用LASSO方法从数据出发, 识别出了单相地下水流动方程和污染物输运方程. 2020年, Raissi等[24 ] 使用深度学习, 对流场可视化的图片进行学习, 并反演了流场的压力和速度分布场, 可以帮助得到实验难以测量的数据. Zhang和Ma[25 ] 采用PDE-FIND方法, 对基于直接模拟蒙特卡罗(direct simulation Monte Carlo, DSMC)方法模拟产生的数据进行稀疏识别, 反演了流体的对流、扩散以及涡量输运方程, 从数据驱动角度清晰地展示了玻尔兹曼方程和 Navier-Stokes方程之间的相关性. Schmelzer等[26 ] 采用SINDy框架在数值模拟的数据中是识别出了代数雷诺应力模型. 张亦知等[27 ] 构建了基于数据驱动的湍流模型修正框架并在槽道流中进行了验证. ...
基于物理知识约束的数据驱动式湍流模型修正及槽道湍流计算验证
2
2020
... 近年来, 数据驱动方法在流场中的应用颇受研究者[4 , 22 -27 ] 的重视. 2019年, Chang和Zhang[23 ] 使用LASSO方法从数据出发, 识别出了单相地下水流动方程和污染物输运方程. 2020年, Raissi等[24 ] 使用深度学习, 对流场可视化的图片进行学习, 并反演了流场的压力和速度分布场, 可以帮助得到实验难以测量的数据. Zhang和Ma[25 ] 采用PDE-FIND方法, 对基于直接模拟蒙特卡罗(direct simulation Monte Carlo, DSMC)方法模拟产生的数据进行稀疏识别, 反演了流体的对流、扩散以及涡量输运方程, 从数据驱动角度清晰地展示了玻尔兹曼方程和 Navier-Stokes方程之间的相关性. Schmelzer等[26 ] 采用SINDy框架在数值模拟的数据中是识别出了代数雷诺应力模型. 张亦知等[27 ] 构建了基于数据驱动的湍流模型修正框架并在槽道流中进行了验证. ...
... [27 ]构建了基于数据驱动的湍流模型修正框架并在槽道流中进行了验证. ...
基于物理知识约束的数据驱动式湍流模型修正及槽道湍流计算验证
2
2020
... 近年来, 数据驱动方法在流场中的应用颇受研究者[4 , 22 -27 ] 的重视. 2019年, Chang和Zhang[23 ] 使用LASSO方法从数据出发, 识别出了单相地下水流动方程和污染物输运方程. 2020年, Raissi等[24 ] 使用深度学习, 对流场可视化的图片进行学习, 并反演了流场的压力和速度分布场, 可以帮助得到实验难以测量的数据. Zhang和Ma[25 ] 采用PDE-FIND方法, 对基于直接模拟蒙特卡罗(direct simulation Monte Carlo, DSMC)方法模拟产生的数据进行稀疏识别, 反演了流体的对流、扩散以及涡量输运方程, 从数据驱动角度清晰地展示了玻尔兹曼方程和 Navier-Stokes方程之间的相关性. Schmelzer等[26 ] 采用SINDy框架在数值模拟的数据中是识别出了代数雷诺应力模型. 张亦知等[27 ] 构建了基于数据驱动的湍流模型修正框架并在槽道流中进行了验证. ...
... [27 ]构建了基于数据驱动的湍流模型修正框架并在槽道流中进行了验证. ...
Ridge regression: Applications to nonorthogonal problems
1
1970
... Rudy等[19 ] 提出了一个新的稀疏识别方法: PDE-FIND方法. 该算法是在加入$L_{2} $正则化的最小二乘法(1)中加入阈值筛选, 使用Ridge算法[28 ] 求解$L_{2} $正则化的最小二乘法, 将小于阈值的系数所对应的项筛去, 对剩余的项重复递归Ridge算法求解和阈值筛选, 直到所有项的系数都高于阈值, 此时返回稀疏系数矩阵${ \xi }$, 该过程被称为STRidge算法 ...
Combinatorial trigonometry with Chebyshev polynomials
1
2010
... 采用LBM方法对雷诺数为300的圆柱绕流进行了直接数值模拟, 计算网格为1000$\times$250, 圆柱圆心位置为(201, 133), 半径为26, 来流最大速度为$u=0.1$. 图3 给出了$t=10^{4}$时流场的涡量云图. 如图3 所示将圆柱绕流后面的区域分为$x\in (250, 500)$, $x\in (500, 750)$, 每个区域随机选择8000个空间点并追踪记录60个时间步长的速度数据和压力数据, 这样每个区域就共获得了48万个数据样本, 这对于稀疏识别所需的样本是充足的, 且采样的方法不会影响识别的结果[19 ] . 采用5次切比雪夫多项式插值[29 ] 计算导数, 导数阶数最高保留到二阶, 变量次数最高保留到二阶, 非线性项最高保留到四阶, 将这些数据用来构建稀疏识别所需$\varTheta $库(4).表1 给出了PDE-FIND方法和LASSO方法对于$x\in (250, 500)$圆柱绕流数据的稀疏识别结果. ...
An efficient parallel algorithm for DNS of buoyancy-driven turbulent flows
1
2019
... RB对流流场通过Zhang[30 ] 所发展的基于有限差分的直接数值模拟得到. 不失一般性, 模拟方形区域的RB对流, $Pr $数固定为1, 计算了4个不同的$Ra$数的工况. $Ra$数分别取$10^{6}$, $10^{7}$, $10^{8}$, $10^{9}$, 对应的计算网格分别是128$\times$128, 512$\times$512, 720$\times$720, 1024$\times$1024.当$Ra$数从$10^{6}$增大到$10^{9}$时, RB对流系统会从层流状态转变为强非线性的湍流流动状态, 整个系统的速度及温度脉动剧烈, 会出现局部梯度较大的数据, 对于系统控制方程的识别可能造成一定的困难. 图5 是$t=80$时, 不同$Ra$数的RB对流系统的温度云图和速度矢量图. ...
Regularization and variable selection via the elastic net
1
2005
... 表3 给出了$Ra$数为$10^{9}$的识别结果, PDE-FIND方法和LASSO方法都正确识别出了$Ra=10^{9}$的RB对流系统中连续性方程和热输运方程, 并且系数一致. 而且PDE-FIND方法仍然正确识别出了RB对流的动量方程, 对应$Ra$从$10^{6}$到$10^{9}$, 识别的控制方程组平均系数误差分别为0.36%, 0.06%, 0.40%, 0.46%. 而LASSO方法对NS方程仍没有正确识别, 在$u$方程识别中未选择$u_{xx} $. 原因是由变量及变量各阶导数组成的过于完备库中, 回归系数趋于相近的项之间会产生分组效应(grouping effect)[31 , 32 ] . 而LASSO方法对于具有分组效应的候选项的筛选可能会失败, 表现为在有分组效应的候选项中只选择一项, 而其他的候选项的系数会设为0.在$Ra=10^{6}$, $Ra=10^{7}$, $Ra=10^{8}$的RB对流控制方程稀疏识别中, 也存在同样的现象. ...
Stability selection enables robust learning of partial differential equations from limited noisy data
1
2019
... 表3 给出了$Ra$数为$10^{9}$的识别结果, PDE-FIND方法和LASSO方法都正确识别出了$Ra=10^{9}$的RB对流系统中连续性方程和热输运方程, 并且系数一致. 而且PDE-FIND方法仍然正确识别出了RB对流的动量方程, 对应$Ra$从$10^{6}$到$10^{9}$, 识别的控制方程组平均系数误差分别为0.36%, 0.06%, 0.40%, 0.46%. 而LASSO方法对NS方程仍没有正确识别, 在$u$方程识别中未选择$u_{xx} $. 原因是由变量及变量各阶导数组成的过于完备库中, 回归系数趋于相近的项之间会产生分组效应(grouping effect)[31 , 32 ] . 而LASSO方法对于具有分组效应的候选项的筛选可能会失败, 表现为在有分组效应的候选项中只选择一项, 而其他的候选项的系数会设为0.在$Ra=10^{6}$, $Ra=10^{7}$, $Ra=10^{8}$的RB对流控制方程稀疏识别中, 也存在同样的现象. ...
DUGKS simulations of three-dimensional Taylor-Green vortex flow and turbulent channel flow
1
2017
... 最后对三维槽道湍流进行了稀疏识别, 数据通过离散统一的气动格式(discrete unified gas-kinetic scheme, DUGKS)[33 ] 模拟得到, 计算域为4$\pi $$\times$2$\times$4$\pi $/3, 槽道半高为1, 计算网格为128$\times$128$\times$128, 垂向采用非均匀网格, 流向和展向采用均匀网格, 壁面摩擦速度定义的雷诺数$Re_{\tau } =180$, 此时的槽道流处于充分发展湍流状态. 图6 给出了槽道展向中心截面的速度云图, 各种尺度的复杂结构清晰可见. 在整个槽道中选取数据, 采样方法、导数计算方法以及 $\varTheta $库的构建与2.1节相同. ...