引言
骨骼肌约占生物体重的40%[1], 是维持生物基本运动最重要的生理软组织, 而骨骼肌的损伤会导致人类行为严重受限, 如常见的临床病例: 中风、截瘫等[2]. 在对骨骼肌研究中, 软组织的本构关系可能是最基本和最关键的, 因为其可以建立可靠的数学或计算模型. 由于骨骼肌组织的特殊特性(各向异性[3]、 非线性[4]、 超弹性[5]、 时间依赖性[6])的存在, 骨骼肌组织的力学特性的表征具有很大的挑战性. 全面了解骨骼肌的组成行为, 对于更好地了解骨骼肌的生物学特性, 提高肌肉疾病和损伤的治疗水平具有重要意义. 许多学者进行了大量的实验来研究骨骼肌的生物力学特性, 包括压缩[7]、拉伸[8]、应力松弛[9]等. 王宝珍等[10]对猪后腿肌肉进行冲击压缩实验, 并利用改进后的分离式Hopkinson压杆技术获取了不同加载方向和不同应变率下的应力应变数据. Mohammadkhah等[11]对新鲜鸡胸大肌进行了加载方向平行于纤维方向和垂直于纤维方向以及加载方向与纤维方向成45$^\circ$ 的单轴准静态压缩和拉伸实验, 证明鸡肌肉的力学行为是非线性和各向异性的. Böl等[12]使用3种不同的加载模式对肌肉组织进行了一系列实验. 结果表明, 纤维方向对压缩应力有各向异性贡献. 如果有可靠的正问题模型, 反问题分析是系统的识别材料性质的有效手段[13]. Takaza等[14]证明了反向有限元方法在确定材料性能方面的有效性. Silva等[15]通过逆有限元方法并结合优化算法获得了女性耻骨联合肌肉的主动和被动力学特性. 虽然现有的研究在识别本构参数方面取得了进展, 但现有预测的准确性还有待进一步提高.
随着人工智能技术(AI)的发展, 机器学习(ML) 作为AI的一个分支已被广泛应用于生活中的各个领域, 如数据融合和识别[16-17]、 医学检测[18-19]、 流体力学[20-22]和固体力学中[23-24]. ML在模拟输入和输出变量之间的非线性相关性方面具有很高的效率, 并且已经被用于预测生物软组织的力学特性. Liang等[25]利用支持向量机模型和有限元方法相结合来预测主动脉瘤的风险, 并取得了良好的效果. Lu等[26]提出了一种基于动态多体方法和神经网络分析的创新方法, 建立了基于有限元的软骨神经网络模型. Liu等[27]对牛的肌肉组织进行了无约束压缩实验, 并利用了改进后的小生境遗传算法预测了肌肉组织的本构参数. 通常AI的成功归结于大规模的数据集, 然而许多现实应用的场景例如医学, 军事等领域, 因为隐私或者安全等因素不允许收集足够多的数据集, 所以对于小样本的学习便成了当今AI领域的热点问题. Koch等[28]将深度学习与小样本学习结合起来, 提出了一种新的卷积神经网络模式来学习成对的样本中与类别无关的变量. Liu等[29]基于BP神经网络, 建立了一个可靠的正问题神经网络来代替有限元方法收集样本, 来缩短收集样本的时间, 也为解决小样本学习问题提供了新的想法. 而简单的机器学习模型对小样本学习也会有良好的效果. 因此, 本研究考虑将机器学习的方法应用于骨骼肌的本构参数的预测, 分别提出了两种反问题求解方法, 一种是将K近邻模型(KNN)与有限元方法(FEM)相结合, 另一种是将支持向量机回归模型(SVR)与有限元方法相结合. 在本研究中, 通过训练和测试Liu等[27]收集的数据集, 证明了所提出的两种反问题求解方法的有效性. 本研究还进一步对比了所提出的两种方法, 对比结果表明, 利用K近邻模型结合有限元方法是预测骨骼肌本构参数的更精确有效的方法.
1 有限元模型的建立
骨骼肌的在生理学上的数学表述是一项复杂的任务, 考虑到其大变形行为, 骨骼肌的材料特性常被模拟为各向异性, 非线性和超弹性. 各向异性超弹性模型可以很好模拟骨骼肌的力学行为, 其本构方程如下[30]
式中, $U$代表单位体积应变能, $C_{10} $, $k_{1} $, $k_{2} $和$\kappa $是与温度无关的材料常数; ${N}$是纤维的族数; $\overline {I}_{1} $是$\overline {{C}} $的第一应变不变量, 被定义为$\overline I_{1} =J^{-2/3}\left( {\lambda_{1}^{2}+\lambda_{2}^{2}+\lambda_{3}^{2}} \right)$ $(\lambda_{i} $表示主伸长); $J^{\rm el}$是弹性体积比; $\overline I _{4(\alpha \alpha )} $是$\overline {{C}} $和$A_{\alpha }$的应变伪不变量, $A_{\alpha } $是纤维束的方向向量. 从式(1)可以看出, 参数$C_{10} $和$k_{1} $是具有量纲的参数; 参数$k_{2}>0$是一个无量纲的参数; 参数$\kappa$ ($0\leqslant \kappa \leqslant 1/3$) 描述了纤维方向的分散度, 表征了纤维方向对组织力学性质的影响, 当$\kappa =0$时, 纤维沿着同一方向排列, 当$\kappa =1/3$时, 这意味着纤维是均匀分布的, 与纤维方向有关的应变能函数项为常数为0, 此时的应变能密度函数只与材料的变形有关. $D$反应的是材料受温度影响变化的程度, 因此在不考虑温度变化的不压缩条件下, 其本构方程表示如下[31]
各向异性骨骼肌中本构参数的确定是一项具有挑战性的任务, 由于骨骼肌组织的高含水量, 骨骼肌通常被认为是不可压缩的物质[32]. 所以本文提出的反演程序预测的本构参数包括: $C_{10} $, $k_{1} $, $k_{2} $和$\kappa $.
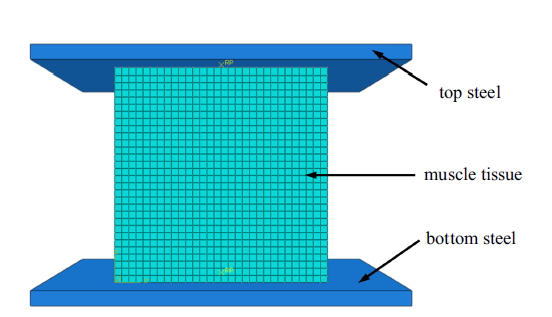
图1给出了为模拟骨骼肌单轴压缩试验的有限元模型. 骨骼肌被建模为超弹性各向异性材料. 有限元网格由3375个八节点六面体单元和4096个节点组成. 八节点六面体单元相对于四面体单元, 增加了节点的数目, 可以显著的提高计算精度. 因为拉伸试验机顶部和底部的压板是由钢制成的, 相比于新鲜的骨骼肌组织要硬的多, 所以在有限元仿真中他们被定义为刚体. 在压板与骨骼肌组织样本之间设置了摩擦系数以更准确的模拟实验.
图1
图1
模拟实验设置的骨骼肌有限元模型
Fig.1
Finite element model of skeletal muscles for simulating experiment
2 K近邻与支持向量机预测模型构建
KNN是一种常用的有监督学习的机器学习算法, 因为其具有从高维特征空间中恢复相似实例的简单性和直观性, 所以具有广泛的应用前景. 在KNN模型中, KNN对于给定测试样本, 基于距离度量找出训练集中与其最靠近的$K$个训练样本, 然后基于这$K$个``邻居''的信息来进行预测[33]. KNN模型的核心问题是$K$值的选取以及距离函数的选择. 在本研究中, 通过大量的数值实验, 最终确定$K=3$. 待求样本的状态向量与已知样本的状态向量之间的距离量度表示二者之间的相似程度. 常见的KNN模型的距离函数有欧式距离、曼哈顿距离、马氏距离、切比雪夫距离等. 在本研究中使用的欧氏距离公式如下: 假设待求样本的状态向量为 $x=\left( {x_{1} ,x_{2} ,\cdots,x_{n} } \right)$, 已知样本的状态向量为$y=\left( {y_{1} ,y_{2} ,\cdots,y_{n} } \right)$, 则其之间的距离$d$为
这是一个从0变化到1的钟形函数. 其中$a$和$b$代表样本向量, $\gamma $为超参数.
3 预测结果与讨论
在本研究中, Liu等[27]对骨骼肌进行单轴压缩实验中获得的名义应力和主伸长数据集被分成两个子数据集, 分别对应于加载方向平行于纤维方向和加载方向垂直于纤维方向. 参数空间的必要参数为4个, 分别为$C_{10}$ (取值范围0.2$\sim$1.5 kPa), $k_{1}$ (取值范围0.05$\sim$0.4 MPa), $k_2$ (取值范围10$\sim$60), $\kappa$ (取值范围0.04$\sim$0.32). 本研究在参数空间中分别以固定增量采集了250组骨骼肌超弹性本构参数以使得采集到的本构参数能够充分代表整个参数空间, 其中$C_{10} $增量为$5.0\times 10^{-3}$ kPa, $k_{1}$增量为$1.4\times 10^{-3}$ MPa, $k_{2} $增量为0.2, $\kappa $增量为$1.12\times 10^{-3}$. 将收集到的骨骼肌组织的本构参数通过建立的有限元模型得到了相应的名义应力和主伸长. 之后以有限元模型收集的名义应力作为输入, 以相应的本构参数作为输出分别构建KNN模型和SVR模型. 为了更准确, 快速地进行回归, 本研究分别对名义应力和骨骼肌组织的本构参数进行归一化处理
其中, $X'$是归一化后的取值, $X$是实际取值; $X_{\max } $, $X_{\min }$分别对应于名义应力和骨骼肌组织的本构参数的最大值和最小值. 当训练完成后, 将骨骼肌压缩实验中获得的名义应力数据集分别输入两个模型, 最终得到实验样本的本构参数.
图2
图2
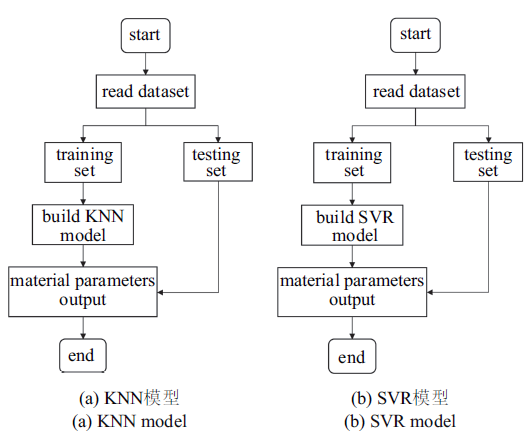
本研究中提出的本构参数识别方法流程图
Fig.2
Flow chart of the parameter identification method proposed in this study
基于Liu 等[27]得到的骨骼肌压缩实验数据, 本研究对利用提出的参数识别程序得到的本构参数进行处理, 以获得一组本构参数, 这些参数既可以表示加载方向平行于纤维方向, 又可以很好地表示加载方向垂直于纤维方向. 在训练集完成之后, 测试集的数据用来评估KNN模型和SVR模型的准确性, 并比较本构参数的真实值和预测值. 在本研究中, 选用了决定系数($R^{2})$作为预测值准确率的指标. $R^{2}$反映了因变量的所有变化可以通过回归关系由自变量所解释的比例, 即利用数据的平均值作为误差基准, 观察预测误差与平均参考误差的偏离程度. $R^{2}$为
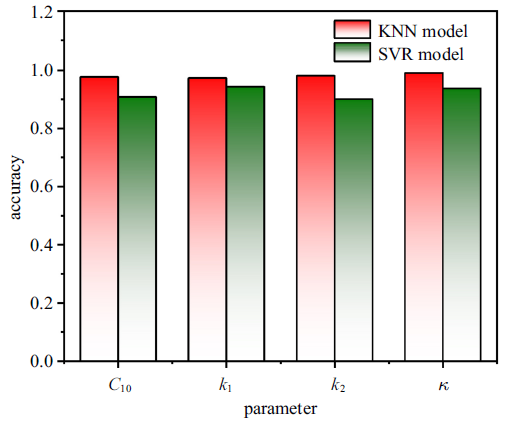
式中, $N$是样本的数量, $y_{i} $代表真实值, $y_{\rm pred} $代表预测值, $\overline y $代表真实值的平均值. 图3描绘了测试集中本构参数的真实值与预测值准确率的直方图. 从直方图中可以看出, 无论是KNN模型还是SVR模型测试集中各本构参数的准确率都很好.
图3
图3
KNN模型和SVR模型测试集预测准确率比较
Fig.3
Comparison of test set prediction accuracy between KNN] model and SVR model
图4
图4
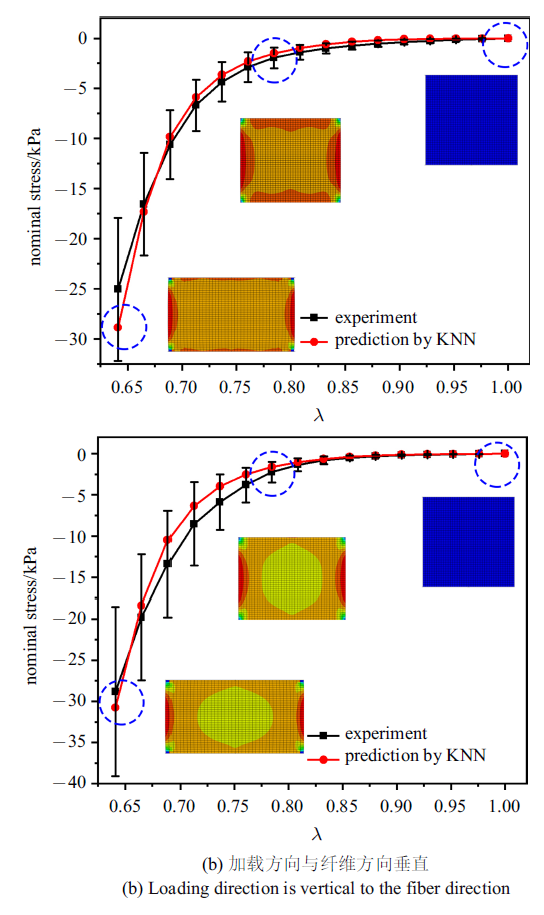
利用KNN模型获得的计算响应以及仿真加载过程名义应力云图
Fig.4
Calculated response of KNN model and the nominal stress diagram of simulation loading process
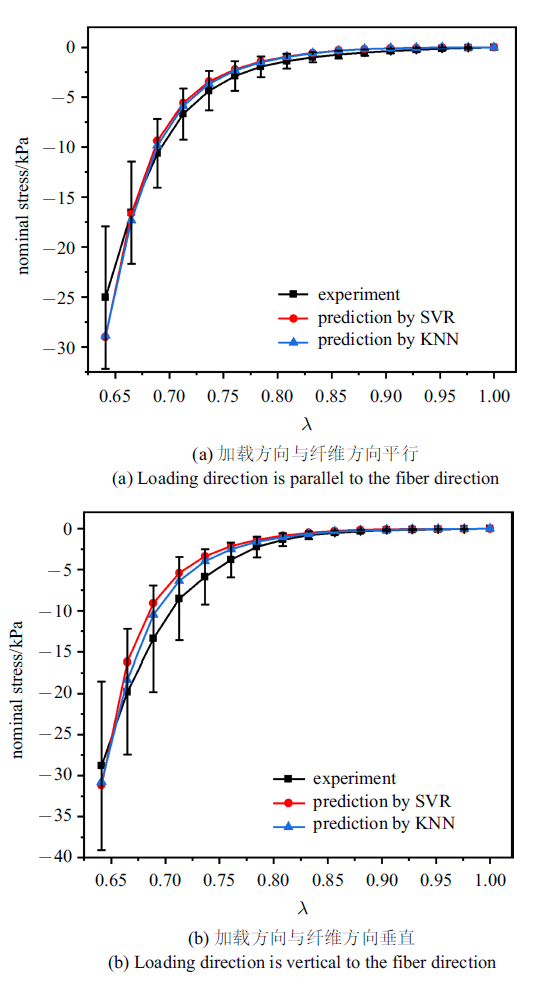
图5
图5
利用SVR模型获得的本构参数的计算响应与实验数据以及与利用KNN模型获得的计算响应对比
Fig.5
Comparison of calculated response between KNN model and SVR model
为了更直观地观察真实值与预测值的拟合程度, 引入了2种统计指标, 包括相关系数($R)$和决定系数($R^{2})$. $R$是一个相关性指标, 可以用来衡量真实值与预测值之间的关系有多强, $R^{2}$是一个效率指标如前所述. $R$为
其中$\overline {y_{\rm pred} } $代表预测值的平均值. 表1给出了从统计指标方面比较了利用SVR模型参数识别方法和利用KNN模型参数识别方法.
表1 KNN模型与SVR模型统计指标比较
Table 1
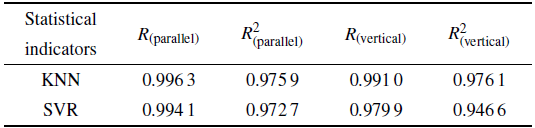 |
表2 利用KNN模型获得的骨骼肌组织本构参数范围
Table 2
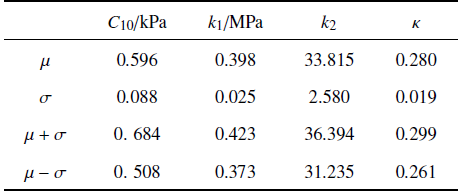 |
从表2可以看出$C_{10}$在0.508$\sim$0.684 kPa之间, $k_{1}$在373.361$\sim$422.881 kPa之间, $k_{2}$在31.235$\sim$36.394之间, $\kappa $在0.261$\sim$0.299之间.
4 结论
在本研究中提出了两种有效的反演方法来识别骨骼肌的本构参数. 一种是利用K近邻模型并结合有限元方法来识别骨骼肌的本构参数, 另一种是利用支持向量机回归模型并结合有限元方法来识别骨骼肌的本构参数. 本研究中的数据集由有限元方法来生成, 从骨骼肌组织的单轴压缩实验获得的实验数据用来验证本文提出的反演方法的准确性. 最后, 用相关系数$R$和决定系数$R^{2}$来直观地衡量本文提出的两种模型的准确性, 得出如下结论:
(1)本文利用K近邻模型和SVR模型确定了可靠的骨骼肌组织的本构参数的范围, 所得到的本构参数的计算响应与骨骼肌组织的实验曲线吻合良好.
(2)利用K近邻模型和SVR模型在预测骨骼肌组织的本构参数都具有很大的潜力. 本文提出的两种模型和有限元相结合的反求方法也可以应用于其他具有超弹性结构的模型的软组织.
参考文献
Skeletal muscle mass and distribution in 468 men and women aged 18-88 yr
We employed a whole body magnetic resonance imaging protocol to examine the influence of age, gender, body weight, and height on skeletal muscle (SM) mass and distribution in a large and heterogeneous sample of 468 men and women. Men had significantly (P < 0.001) more SM in comparison to women in both absolute terms (33.0 vs. 21.0 kg) and relative to body mass (38.4 vs. 30.6%). The gender differences were greater in the upper (40%) than lower (33%) body (P < 0.01). We observed a reduction in relative SM mass starting in the third decade; however, a noticeable decrease in absolute SM mass was not observed until the end of the fifth decade. This decrease was primarily attributed to a decrease in lower body SM. Weight and height explained approximately 50% of the variance in SM mass in men and women. Although a linear relationship existed between SM and height, the relationship between SM and body weight was curvilinear because the contribution of SM to weight gain decreased with increasing body weight. These findings indicate that men have more SM than women and that these gender differences are greater in the upper body. Independent of gender, aging is associated with a decrease in SM mass that is explained, in large measure, by a decrease in lower body SM occurring after the fifth decade.
Grand challenge competition to predict in vivo knee loads
Transversely isotropic tensile material properties of skeletal muscle tissue
Of the plethora of work performed analyzing skeletal muscle tissue, relatively little has been done in the examination of its passive material properties. Previous studies of the passive properties of skeletal muscle have been primarily performed along the longitudinal material direction. In order to ensure the accuracy of the predictions of computational models of skeletal muscles, a better understanding of the tensile three-dimensional material properties of muscle tissue is necessary. To that end, the purpose of this study was to collect a comprehensive set of tensile stress-strain data from skeletal muscle tissue. Load-deformation data was collected from eighteen extensor digitorum longus muscles, dissected free of aponeuroses, from nine New Zealand White rabbits tested under longitudinal extension (LE), transverse extension (TE), or longitudinal shear (LS). The linear modulus, ultimate stress, and failure strain were calculated from stress-strain results. Results indicate that the linear modulus under LE is significantly higher than the modulus of either TE or LS. Additionally, the ultimate stress of muscle was seen to be significantly higher under LE than TE. Conversely, the failure strain was significantly higher under TE than under LE.
How does tissue preparation affect skeletal muscle transverse isotropy?
Hyper-elastic properties of the human sternocleidomastoideus muscle in tension
Viscoelastic properties of passive skeletal muscle in compression—Cyclic behaviour
Skeletal muscle relaxation behaviour in compression has been previously reported, but the anisotropic behaviour at higher loading rates remains poorly understood. In this paper, uniaxial unconfined cyclic compression tests were performed on fresh porcine muscle samples at various fibre orientations to determine muscle viscoelastic behaviour. Mean compression level of 25% was applied and cycles of 2% and 10% amplitude were performed at 0.2-80Hz. Under cycles of low frequency and amplitude, linear viscoelastic cyclic relaxation was observed. Fibre/cross-fibre results were qualitatively similar, but the cross-fibre direction was stiffer (ratio of 1.2). In higher amplitude tests nonlinear viscoelastic behaviour with a frequency dependent increase in the stress cycles amplitude was found (factor of 4.1 from 0.2 to 80Hz). The predictive capability of an anisotropic quasi-linear viscoelastic model previously fitted to stress-relaxation data from similar tissue samples was investigated. Good qualitative results were obtained for low amplitude cycles but differences were observed in the stress cycle amplitudes (errors of 7.5% and 31.8%, respectively, in the fibre/cross-fibre directions). At higher amplitudes significant qualitative and quantitative differences were evident. A nonlinear model formulation was therefore developed which provided a good fit and predictions to high amplitude low frequency cyclic tests performed in the fibre/cross-fibre directions. However, this model gave a poorer fit to high frequency cyclic tests and to relaxation tests. Neither model adequately predicts the stiffness increase observed at frequencies above 5Hz. Together with data previously presented, the experimental data presented here provide a unique dataset for validation of future constitutive models for skeletal muscle in compression.
Characterization of human passive muscles for impact loads using genetic algorithm and inverse finite element methods
The objective of this study is to identify the dynamic material properties of human passive muscle tissues for the strain rates relevant to automobile crashes. A novel methodology involving genetic algorithm (GA) and finite element method is implemented to estimate the material parameters by inverse mapping the impact test data. Isolated unconfined impact tests for average strain rates ranging from 136 s(-1) to 262 s(-1) are performed on muscle tissues. Passive muscle tissues are modelled as isotropic, linear and viscoelastic material using three-element Zener model available in PAMCRASH(TM) explicit finite element software. In the GA based identification process, fitness values are calculated by comparing the estimated finite element forces with the measured experimental forces. Linear viscoelastic material parameters (bulk modulus, short term shear modulus and long term shear modulus) are thus identified at strain rates 136 s(-1), 183 s(-1) and 262 s(-1) for modelling muscles. Extracted optimal parameters from this study are comparable with reported parameters in literature. Bulk modulus and short term shear modulus are found to be more influential in predicting the stress-strain response than long term shear modulus for the considered strain rates. Variations within the set of parameters identified at different strain rates indicate the need for new or improved material model, which is capable of capturing the strain rate dependency of passive muscle response with single set of material parameters for wide range of strain rates.
Dynamic tensile response of porcine muscle
Skeletal muscle tensile strain dependence: Hyperviscoelastic nonlinearity
猪后腿肌肉的冲击压缩特性实验
Dynamic compression experiments of porcine ham muscle
The in vitro passive elastic response of chicken pectoralis muscle to applied tensile and compressive deformation
The mechanics of passive skeletal muscle are important in impact biomechanics, surgical simulation, and rehabilitation engineering. Existing data from porcine tissue has shown a significant tension/compression asymmetry, which is not captured by current constitutive modelling approaches using a single set of material parameters, and an adequate explanation for this effect remains elusive. In this paper, the passive elastic deformation properties of chicken pectoralis muscle are assessed for the first time, to provide deformation data on a skeletal muscle which is very different to porcine tissue. Uniaxial, quasi-static compression and tensile tests were performed on fresh chicken pectoralis muscle in the fibre and cross-fibre directions, and at 45° to the fibre direction. Results show that chicken muscle elastic behaviour is nonlinear and anisotropic. The tensile stress-stretch response is two orders of magnitude larger than in compression for all directions tested, which reflects the tension/compression asymmetry previously observed in porcine tissue. In compression the tissue is stiffest in the cross-fibre direction. However, tensile deformation applied at 45° gives the stiffest response, and this is different to previous findings relating to porcine tissue. Chicken muscle tissue is most compliant in the fibre direction for both tensile and compressive applied deformation. Generally, a small percentage of fluid exudation was observed in the compressive samples. In the future these data will be combined with microstructural analysis to assess the architectural basis for the tension/compression asymmetry now observed in two different species of skeletal muscle.Copyright © 2016 Elsevier Ltd. All rights reserved.
On the anisotropy of skeletal muscle tissue under compression
The anisotropic mechanical behaviour of passive skeletal muscle tissue subjected to large tensile strain
Characterization of the passive and active material parameters of the pubovisceralis muscle using an inverse numerical method
面向深度学习的多模态融合技术研究综述
Survey of research on multimodal fusion technology for deep learning
基于机器学习理论的数据融合算法对比研究
The comparative research on data fusion algorithm based on machine learning theory
基于深度学习的医疗影像识别技术研究综述
Research review of medical image recognition technology based on deep learning
基于机器学习的跨患者癫痫自动检测算法
Automatic epileptic seizure detection algorithm for non-specific patient based on machine learning
基于卷积神经网络的涵洞式直立堤波浪透射预测
Prediction of wave transmission of culvert breakwater based on CNN
基于人工神经网络的湍流大涡模拟方法
Artificial neural network-based subgrid-scale models for large-eddy simulation of turbulence
基于深度学习技术的激波风洞智能测力系统研究
Deep-learning-based intelligent force measurement system using in a shock tunnel
基于遗传算法的弹性地基加肋板肋梁无网格优化分析
Rib meshless optimization of stiffened plates resting on elastic foundation based on genetic algorithm
基于BP神经网络与小冲杆试验确定在役管道钢弹塑性性能方法研究
Determination of elastoplastic properties of in-service pipeline steel based on BP neural network and small punch test
A machine learning approach to investigate the relationship between shape features and numerically predicted risk of ascending aortic aneurysm
Geometric features of the aorta are linked to patient risk of rupture in the clinical decision to electively repair an ascending aortic aneurysm (AsAA). Previous approaches have focused on relationship between intuitive geometric features (e.g., diameter and curvature) and wall stress. This work investigates the feasibility of a machine learning approach to establish the linkages between shape features and FEA-predicted AsAA rupture risk, and it may serve as a faster surrogate for FEA associated with long simulation time and numerical convergence issues. This method consists of four main steps: (1) constructing a statistical shape model (SSM) from clinical 3D CT images of AsAA patients; (2) generating a dataset of representative aneurysm shapes and obtaining FEA-predicted risk scores defined as systolic pressure divided by rupture pressure (rupture is determined by a threshold criterion); (3) establishing relationship between shape features and risk by using classifiers and regressors; and (4) evaluating such relationship in cross-validation. The results show that SSM parameters can be used as strong shape features to make predictions of risk scores consistent with FEA, which lead to an average risk classification accuracy of 95.58% by using support vector machine and an average regression error of 0.0332 by using support vector regression, while intuitive geometric features have relatively weak performance. Compared to FEA, this machine learning approach is magnitudes faster. In our future studies, material properties and inhomogeneous thickness will be incorporated into the models and learning algorithms, which may lead to a practical system for clinical applications.
Application of neural networks for the prediction of cartilage stress in a musculoskeletal system
An inverse procedure for characterization of material parameters of passive skeletal muscle using FEM and experimental data
Siamese neural networks for one-shot image recognition
FEA-AI and AI-AI: Two-Way deepnets for Real-Time computations for both forward and inverse mechanics problems
Determination of the material parameters in the Holzapfel-Gasser-Ogden constitutive model for simulation of Age-Dependent material nonlinear behavior for aortic wall tissue under uniaxial Tension
Hyperelastic modelling of arterial layers with distributed collagen fibre orientations
Extra- and intracellular water spaces in muscles of man at rest and with dynamic exercise
Neighbourhood components analysis
Susceptibility mapping of shallow landslides using kernel-based Gaussian process, support vector machines and logistic regression
A tutorial on support vector machines for pattern recognition
EEMD能量熵和奇异值熵与SVM融合的船用空压机故障诊断
Fault diagnosis for marine air compressors by fusion of EEMD energy entropy and singular value entropy with SVM
Prediction of dynamic increase factor for steel fibre reinforced concrete using a hybrid artificial intelligence model
Steel fibre reinforced concrete (SFRC) has been increasingly used in the engineering structures subjected to intense dynamic loads. In structural design and analysis, a dynamic increase factor (DIF) has been usually used to characterize strain-rate effect on the dynamic mechanical behaviour of SFRC. At present, several analytical equations that contain one or two variables have been utilised to predict the DIF values for material strengths of SFRC. However, this may lead to unsatisfactory results as the rate sensitivity of SFRC is influenced by multiple variables. In this study, a hybrid model, integrating random forest (RF) technique and firefly algorithm (FA), is proposed for predicting DIF values for SFRC. RF is utilized to discover the non-linear relationship between the influencing variables and DIF, while FA optimizes the hyper-parameters of RF. A total of 193 and 314 DIF data samples for compressive and tensile strengths of SFRC are retrieved from the reported studies to train and verify the proposed model. The input variables for the predictive model include strain rate, matrix strength, fibre dosage, and fibre properties (i.e. fibre shape, fibre aspect ratio and fibre tensile strength). The predicted results denote that the developed model is an efficient and accurate method to predict the DIF values for SFRC. Additionally, the relative importance of each input variable is investigated. It is found that the DIF values of SFRC are most sensitive to the matrix strength.