引言
弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为.
基于饱和黏弹性地基的固结解, Ai和Hu[31 ] 利用有限元$\!-\!$解析层元耦合法研究了层状饱和地基与梁的共同作用问题, 并考虑了地基的渗透各向异性和孔隙流体的可压缩性. Kobayashi和Sonoda[32 ] 基于Winkler地基假定, 借助弹性$\!-\!$黏弹性对应原理, 给出了多种线性黏弹性地基上Timoshenko梁弯曲问题的解答. 苏超等[33 ] 也利用弹性$\!-\!$黏弹性对应原理, 建立了黏弹性地基上基础梁的计算方法, 并将其应用于软土地基上船闸底板的计算. Bhattiprolu等[34 ] 提出了非线性黏弹性地基上弹性梁的有效求解方法, 且该方法能够处理二者间接触区域非连续的情况. Sreekantan和 Basudhar[35 ] 基于Burger模型对黏弹性地基上梁的受弯响应进行了分析. 目前针对黏弹性地基上梁的研究中, 很少考虑到分数阶黏弹性以及地基的成层特点. 因此, 开展层状分数阶黏弹性饱和地基与梁的共同作用研究具有重要的理论意义和工程应用价值.
本文采用有限元法对Timoshenko梁进行分析, 采用边界元法对地基进行分析, 将文献[36 ]中分数阶黏弹性饱和地基的固结解答作为地基边界积分方程的核函数, 建立梁节点沉降与地基反力间的柔度矩阵方程; 然后根据梁与地基接触面上的位移协调条件和力的平衡条件, 推导出层状黏弹性饱和地基与Timoshenko梁共同作用的解答; 最后探讨分数阶次和地基成层性对梁与饱和黏弹性地基共同作用的影响.
1 Timoshenko梁的有限元分析
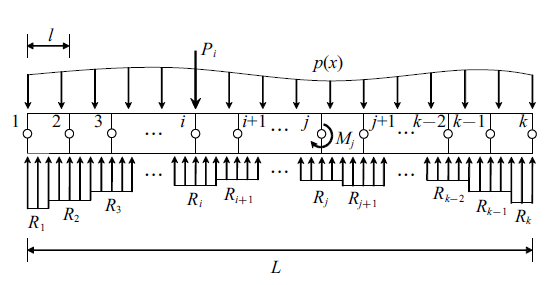
如图1 所示, Timoshenko梁置于一层状黏弹性饱和地基上, 并在外载荷和地基反力的共同作用下处于平衡状态.
图1
图1
Timoshenko梁受力示意图
Fig.1
Force diagram of a Timoshenko beam
已知的外载荷可以是分布载荷$p(x)$、集中载荷$P_i$或集中力偶$M_j$. 梁的总长度为$L$, 以$k$个节点将其等分为$(k-1)$个梁单元, 每个梁单元的长度为$l=L/(k-1)$. 为使地基反力$R(x)$对应的单元个数与梁节点数量相同, 将梁与地基的接触面划分为$k$个单元, 并假设各单元分别受到大小为$R_i$ $(i=1,2,\cdots, k)$的均布反力. 其中, $R_1$和$R_k$所在的接触面单元长度为$l/2$, 其他接触面单元长度均为$l$. 本文假定各梁单元底部的地基反力为均布力, 这与实际情况有所不同. 因此, 需要通过选取合适的单元数目, 将地基反力的计算误差控制在可接受范围内.
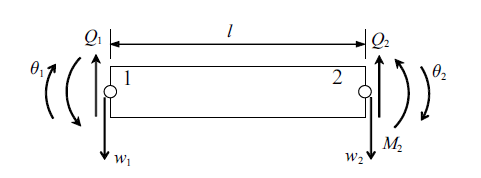
取任意梁单元进行分析, 单元节点的载荷分量和位移分量如图2 所示. $M$和$Q$分别为截面上的弯矩和横向剪力, $w$和$\theta $分别为梁的挠度和截面转角, 角标1和2用以指示载荷及位移分量所在截面.
图2
图2
梁单元示意图
Fig.2
Sketch of a beam element
基于Timoshenko梁理论, 可得梁单元的有限元求解方程[37 ]
(1) $\boldsymbol{K}^{(e)} \boldsymbol{\delta}^{(e)}=\boldsymbol{P}^{(e)}$
(2a) $\boldsymbol{K}^{(e)}=\left[\begin{array}{cccc}12 a & 6 a l & -12 a & 6 a l \\6 a l & a l^{2}(4+b) & -6 a l & a l^{2}(2-b) \\-12 a & -6 a l & 12 a & -6 a l \\6 a l & a l^{2}(2-b) & -6 a l & a l^{2}(4+b)\end{array}\right]$
(2b) $\delta^{(e)}=\left[\begin{array}{llll}w_{1} & \theta_{1} & w_{2} & \theta_{2}\end{array}\right]^{\mathrm{T}}$
(2c) $\begin{aligned}\boldsymbol{P}^{(e)}=&\left[Q_{1} M_{1} Q_{2} M_{2}\right]^{\mathrm{T}}=\\& \int_{0}^{l}\left[\begin{array}{llll}N_{1} & N_{2} & N_{3} & N_{4}\end{array}\right]^{\mathrm{T}} p(x) \mathrm{d} x\end{aligned}$
其中, $K^{(e)}$为梁单元刚度矩阵, ${\delta }^{(e)}$和${P}^{(e)}$分别为梁单元节点的位移向量和等效节点载荷向量; $b={{12D_{\rm b}}/{(C_{\rm b} l^{2})}}$, $a={{D_{\rm b} }/{[(1+b)l^{3}]}}$, $D_{\rm b} =E_{\rm b} I_{\rm b} $为梁的抗弯刚度, $E_{\rm b} $为梁的弹性模量, $I_{\rm b} $为梁截面关于中性轴的惯性矩, $C_{\rm b} =kG_{\rm b} A_{\rm b} $为梁的抗剪刚度, $G_{\rm b} ={E_{\rm b}}/[{2(1+\nu_{\rm b} )}]$为梁的剪切模量, $v_{\rm b} $为梁的泊松比, $A_{\rm b} $为梁的横截面面积, $k$为Timoshenko梁修正系数, 矩形截面取$k={5/6}$; $N_{1} =1-3z_{2} x^{2}+{{2z_{2} (x^{3}-3z_{1} x)}/l}$, $N_{2} =x-x^{2}\left[ {{1/{(2l)+{{3z_{2} l}/2}}}} \right]+z_{2} (x^{3}-3z_{1} x)$, $N_{3} =1-N_{1} $, $N_{4} =x^{2}\left[ {{1/{(2l)-{{3z_{2} l}/2}}}} \right]+z_{2} (x^{3}-3z_{1} x)$; $z_{1} ={{2D_{\rm b} }/{C_{\rm b} }}$, $z_{2} ={1/{(l^{2}+{{12D_{\rm b} }/{C_{\rm b} }})}}$.
对式(1)进行适当变换, 可以得到同时考虑弯曲和剪切变形的Timoshenko梁单元刚度矩阵方程
(3) $\begin{equation} \label{eq3} \left[ {{\begin{array}{c@{\quad }c} {{K}_{\theta \theta }^{(e)} } & {{K}_{\theta w}^{(e)} } \\[1mm] {{K}_{w\theta }^{(e)} } & {{K}_{ww}^{(e)} } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {{\theta }^{(e)}} \\ {{w}^{(e)}} \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} {{P}_{M}^{(e)} } \\ {{P}_{Q}^{(e)} } \\ \end{array} }} \right] \end{equation}$
式中, ${\theta }^{(e)}=[{\begin{array}{c@{\quad }c} {\theta_{1} } & {\theta_{2} } \\ \end{array} }]^{\rm T}$, ${w}^{(e)}=[{\begin{array}{c@{\quad }c} {w_{1} } & {w_{2} } \\ \end{array} }]^{\rm T}$; ${P}_{M}^{(e)} =[{\begin{array}{c@{\quad }c} {M_{1} } & {M_{2} } \\ \end{array} }]^{\rm T}$, ${P}_{Q}^{(e)} =[{\begin{array}{c@{\quad }c} {Q_{1} } & {Q_{2} } \\ \end{array} }]^{\rm T}$; 梁单元刚度矩阵${K}_{\theta \theta }^{(e)} =al^{2}\left[ {{\begin{array}{c@{\quad }c} {4+b} & {2-b} \\[-2mm] {2-b} & {4+b} \\ \end{array} }} \right]$, ${K}_{\theta w}^{(e)} =6al\left[ {{\begin{array}{c@{\quad }c} 1 & {-1} \\[-2mm] 1 & {-1} \\ \end{array} }} \right]$, ${K}_{w\theta }^{(e)} =6al\left[ {{\begin{array}{c@{\quad }c} 1 & 1 \\[-2mm] {-1} & {-1} \\ \end{array} }} \right]$, ${K}_{ww}^{(e)} =12a\left[ {{\begin{array}{c@{\quad }c} 1 & {-1} \\[-2mm] {-1} & 1 \\ \end{array} }} \right]$.
将载荷向量拆分为由外力和基底反力产生的两类等效节点载荷向量, 并对式(3)进行关于时间的Laplace积分变换. 这时, 考虑到梁单元刚度矩阵不随时间变化, 则式(3)可改写为
(4) $\begin{equation} \label{eq4} \left[ {{\begin{array}{c@{\quad }c} {{K}_{\theta \theta } } & {{K}_{\theta w} } \\ {{K}_{w\theta } } & {{K}_{ww} } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {{\tilde{{\theta }}}(s)} \\ {{\tilde{{w}}}(s)} \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} {{\tilde{{F}}}_{M} (s)} \\ {{\tilde{{F}}}_{Q} (s)} \\ \end{array} }} \right]-\left[ {{\begin{array}{*{20}c} {{\tilde{{R}}}_{{\ast}M} (s)} \\ {{\tilde{{R}}}_{{\ast}Q} (s)} \\ \end{array} }} \right] \end{equation}$
式中, ${K}_{\theta \theta } $, ${K}_{\theta w} $, ${K}_{w\theta } $和${K}_{ww} $由各梁单元刚度矩阵组装而成; ${\tilde{{\theta }}}(s)=[{\begin{array}{*{20}c} {\tilde{{\theta }}_{1} (s)} \ \ {\tilde{{\theta }}_{2} (s)} \ \ {\cdot \cdot \cdot } \ \ {\tilde{{\theta }}_{k} (s)} \hfill \\ \end{array} }]^{\rm T}$, ${\tilde{{w}}}(s)=[{\begin{array}{*{20}c} {\tilde{{w}}_{1} (s)} \ \ {\tilde{{w}}_{2} (s)} \ \ {\cdot \cdot \cdot } \ \ {\tilde{{w}}_{k} (s)} \hfill \\ \end{array} }]^{\rm T}$, $\tilde{{\theta }}_{i} (s)$和$\tilde{{w}}_{i} (s) \quad (i=1,2,\cdots ,k)$分别为$i$节点在$s$时刻的转角和挠度, 上标``$\sim$''表示该变量已进行关于时间$t$的Laplace变换, $s$为关于时间$t$的Laplace变换参数; ${\tilde{{F}}}_{M} (s)$和${\tilde{{F}}}_{Q} (s)$分别为弹性地基梁上已知外载荷引起的节点弯矩向量和节点剪力向量; ${\tilde{{R}}}_{\ast M} (s)$和${\tilde{{R}}}_{\ast Q} (s)$分别为地基反力引起的节点弯曲向量和节点剪力向量, 具体表达式如下
(5a) $\tilde{\boldsymbol{R}}_{* M}(s)=\tilde{\boldsymbol{R}}_{M}(s) \cdot \tilde{\boldsymbol{R}}(s)$
(5b) $\tilde{\boldsymbol{R}}_{* Q}(s)=\tilde{\boldsymbol{R}}_{Q}(s) \cdot \tilde{\boldsymbol{R}}(s)$
式中, ${\tilde{{R}}}(s)$为地基反力矩阵, ${\tilde{{R}}}_{M} (s)$和${\tilde{{R}}}_{Q} (s)$分别为单位地基反力向量引起的节点弯矩向量和节点剪力向量, 各矩阵表达式如下
(6a) $\tilde{\boldsymbol{R}}(s)=\left[\begin{array}{llll}\tilde{R}_{1}(s) & \tilde{R}_{2}(s) & \cdots & \tilde{R}_{k}(s)\end{array}\right]^{\mathrm{T}}$
(6b) $\tilde{\boldsymbol{R}}_{M}(s)=\frac{l^{2}}{192(1+b)}\left[\begin{array}{cccccc}11+8 b & 5+8 b & 0 & \cdots & 0 & 0 \\-5-8 b & 0 & 5+8 b & \cdots & 0 & 0 \\0 & -5-8 b & 0 & \cdots & 0 & 0 \\\vdots & \vdots & \vdots & \cdots & \vdots & \vdots \\0 & 0 & 0 & \cdots & 0 & 5+8 b \\0 & 0 & 0 & \cdots & -5-8 b & -11-8 b\end{array}\right]_{k \times k}$
(6c) $\tilde{\boldsymbol{R}}_{Q}(s)=\frac{l}{32(1+b)}\left[\begin{array}{cccccc}13+12 b & 3+4 b & 0 & \cdots & 0 & 0 \\3+4 b & 26+24 b & 3+4 b & \cdots & 0 & 0 \\0 & 3+4 b & 26+24 b & \cdots & 0 & 0 \\\vdots & \vdots & \vdots & \cdots & \vdots & \vdots \\0 & 0 & 0 & \cdots & 26+24 b & 3+4 b \\0 & 0 & 0 & \cdots & 3+4 b & 13+12 b\end{array}\right]_{k \times k}$
2 Timoshenko梁与地基共同作用方程
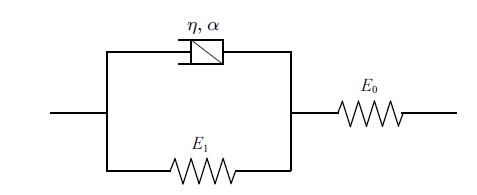
如图3 所示, 采用分数阶Merchant模型描述黏弹性地基的本构关系, 该模型由线弹性体和Kelvin体串联而成, $E_{0} $和$E_{1} $分别为线弹性体和Kelvin体的弹性模量, $\eta $为黏滞系数, $\alpha $为分数阶次. 不同的分数阶次可以表征不同的蠕变状态, 从而有效模拟饱和地基的流变特征. 其对应本构方程如下
(7) $\begin{equation} \label{eq7} {\sigma }'_{\rm s} +\frac{\eta_{1} }{E_{0} +E_{1} }\frac{{\rm d}^{\alpha }{\sigma }'_{\rm s} }{{\rm d}^{\alpha }t}=\frac{E_{0} E_{1} }{E_{0} +E_{1} }\varepsilon +\frac{\eta_{1} E_{0} }{E_{0} +E_{1} }\frac{{\rm d}^{\alpha }\varepsilon }{{\rm d}^{\alpha }t} \end{equation}$
式中, ${\sigma }'_{\rm s} $为土体有效应力, $\varepsilon $为土体应变.
图3
图3
分数阶Merchant模型
Fig.3
Fractional Merchant model
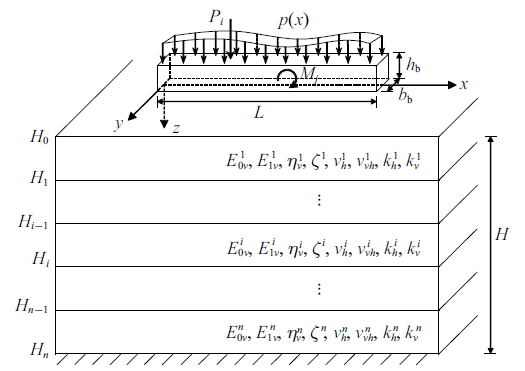
层状正交各向异性黏弹性饱和地基上的Timoshenko梁见图4 . 梁截面的宽度和高度分别为$b_{\rm b} $和$h_{\rm b} $, 梁端自由, 其与地基的接触面光滑, 且二者在加载后紧密接触. 黏弹性饱和土体正交各向异性参数$\zeta ={{E_{0h} }/{E_{0v} }}={{E_{1h} }/{E_{1v} }}={{\eta_{h} }/{\eta_{v} }}$, 下标$h$和$v$分别表示水平向和竖向参数; $v_{h} $为水平应力引起正交水平向应变的泊松比, $v_{vh} $为竖向应力引起水平向应变的泊松比; $k_{h} $和$k_{v} $分别为水平向和竖向渗透系数.
图4
图4
层状正交各向异性黏弹性饱和地基上的Timoshenko梁
Fig.4
Timoshenko beam on the layered cross-anisotropic viscoelastic saturated soils
文献[36 ]利用弹性$\!-\!$黏弹性对应原理对层状正交各向异性黏弹性饱和地基的固结问题进行了求解, 但该解答仅针对地基上作用骤加载荷的情况. 实际上, 由于孔隙水的存在, 梁与饱和地基的相互作用过程中, 地基反力和沉降会随时间缓慢变化. 这时任意地基单元$i$在$t$时刻受到的作用力有如下积分型表达[31 ]
(8) $\begin{equation} \label{eq8} q(i,t)=q(i,0)+\int_0^t {\frac{\partial q(i,\tau )}{\partial \tau }} {\rm d}\tau \end{equation}$
式中, $q(i,0)$和$q(i,t)$分别表示0时刻和$t$时刻作用在梁单元$i$上的作用力.
因此, $t$时刻由$i$梁单元下的地基表面受到的作用力引起的$j$节点处地基表面的位移可表示为
(9) $\begin{equation} \label{eq14} u(j,i,t)=I_{\rm s} (j,i,t)q(i,0)+\int_0^t {I_{\rm s} (j,i,t-\tau )\frac{\partial q(i,\tau )}{\partial \tau }} {\rm d}\tau \end{equation}$
式中, $I_{\rm s} (j,i,t)$为在第$i$个地基单元表面作用单位均布载荷, 经过$t$时间段时, 在梁节点$j$下地基表面处产生的竖向位移, 其可根据地基固结解[36 ] 求得.
对于形如式(9)的方程, 可采用卷积公式进行化简. 卷积公式的定义如下[38 ]
(10) $\begin{equation} \label{eq10} f_{1} (t)\ast f_{2} (t)=\int_0^t {f_{1} (\tau )f_{2} (t-\tau )} {\rm d}\tau \end{equation}$
(11) $\begin{equation} \label{eq11} \tilde{{\ell }}[f_{1} (t)\ast f_{2} (t)]=\tilde{{\ell }}[f_{1} (t)]\cdot \tilde{{\ell }}[f_{2} (t)] \end{equation}$
对式(9)进行Laplace变换, 并结合该性质, 可以得到Laplace变换域内$s$时刻地基单元$i$处作用的缓变载荷与梁节点$j$下地基表面竖向位移之间的关系
(12) $\begin{equation} \label{eq12} \tilde{{u}}(j,i,s)=s\tilde{{I}}_{\rm s} (j,i,s)\tilde{{q}}(i,s) \end{equation}$
式中, $s\tilde{{I}}_{\rm s} (j,i,s)$为Laplace变换域内的柔度系数.
梁节点$j$下地基表面的总竖向位移由所有地基单元表面所受的作用力共同作用产生, 故将式(12)应用于所有地基单元, 可得Laplace变换域内地基表面位移和地表作用力之间的关系如下
(13) $\begin{equation} \label{eq13} {\tilde{{u}}}(s)_{k\times 1} ={\tilde{{K}}}_{\rm s} (s)_{k\times k} {\tilde{{q}}}(s)_{k\times 1} \end{equation}$
式中, $\tilde{u}(s)_{k\times 1} =[\tilde{u}(s,1),\tilde{{u}}(s,2),\cdots,\tilde{u}(s,k)]^{\rm T}$为变换域内与梁节点对应的地基点的竖向位移向量, $\tilde{q}(s)_{k\times 1}$ = $[\tilde{q}(s,1)$, $\tilde{q}(s,2)$, $\cdots$, $\tilde{q}(s,k)]^{\rm T}$为变换域内基础对地基的作用力向量, $\tilde{K}_{\rm s} (s)_{k\times k} $为Laplace变换域内的地基柔度矩阵, 其具体表达式如下
(14) $\begin{eqnarray} {\tilde{{K}}}_{\rm s} (s)_{k\times k} =s\cdot \left[ {{\begin{array}{c@{\ \ }c@{\ \ }c@{\ \ }c} {\tilde{{I}}_{\rm s} (1,1,s)} & {\tilde{{I}}_{\rm s} (1,2,s)} & \cdots & {\tilde{{I}}_{\rm s} (1,k,s)} \\ {\tilde{{I}}_{\rm s} (2,1,s)} & {\tilde{{I}}_{\rm s} (2,2,s)} & \cdots & {\tilde{{I}}_{\rm s} (2,k,s)} \\ \vdots & \vdots & \ddots & \vdots \\ {\tilde{{I}}_{\rm s} (k,1,s)} & {\tilde{{I}}_{\rm s} (k,2,s)} & \cdots & {\tilde{{I}}_{\rm s} (k,k,s)} \\ \end{array} }} \right]_{k\times k} \end{eqnarray}$
至此, 已经分别建立了Laplace变换域内梁的总刚度矩阵方程和地基的柔度矩阵方程. 利用梁$\!-\!$土接触面间的协调条件, 可以将梁与地基联系起来. 假定外载荷作用下地基与梁底面紧密接触, 则梁节点的竖向位移与对应位置的地基沉降相等, 而地基反力与基础对地基的作用力大小相等, 即
(15a) $\tilde{\boldsymbol{w}}(s)=\tilde{\boldsymbol{u}}(s)$
(15b) $\tilde{\boldsymbol{R}}(s)=\tilde{\boldsymbol{q}}(s)$
结合式(15), 并将地基柔度矩阵方程式(13)代入梁的总刚度矩阵方程式(4)中, 可得到梁与地基共同作用的总矩阵方程
(16) $\begin{equation} \label{eq16} \left[ {{\begin{array}{*{20}c} {{\tilde{{\theta }}}} \\ {{\tilde{{R}}}} \\ \end{array} }} \right]=\left[ {{\begin{array}{c@{\quad }c} {{K}_{\theta \theta } } & {{K}_{\theta w} \cdot {\tilde{{K}}}_{\rm s} +{\tilde{{R}}}_{M} } \\ {{K}_{w\theta } } & {{K}_{ww} \cdot {\tilde{{K}}}_{\rm s} +{\tilde{{R}}}_{Q} } \\ \end{array} }} \right]^{-1}\left[ {{\begin{array}{*{20}c} {{\tilde{{F}}}_{M} } \\ {{\tilde{{F}}}_{Q} } \\ \end{array} }} \right] \end{equation}$
求解该式即可得出Laplace变换域内梁各节点转角和单元底部的地基反力, 地基沉降可通过式(13)进一步获得. 对以上解答进行Laplace数值逆变换[31 ] , 即可得到各分量在物理域内的真实解.
3 数值计算与分析
3.1 验证
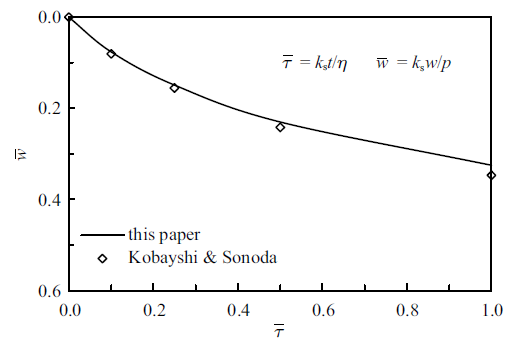
Kobayashi和Sonoda[32 ] 针对多种线性黏弹性地基上Timoshenko梁的弯曲问题进行了研究, 其中基于Kelvin地基模型的相关研究可视为本文模型的特例. 为此将本文模型退化至Kelvin地基, 并与文献[32 ]中的算例进行对比. 算例中均布载荷$p$作用于梁中部$0.4L\leqslant x\leqslant 0.6L$区域, 弹性梁与黏弹性地基的相关参数满足: $\sqrt {{{E_{b} I_{b} }/{[kA_{\rm b} G_{\rm b} (L/2)^{2}]}}} =0.2$, $\sqrt[4]{{{k_{\rm s} (L/2)^{4}}/{(E_{\rm b} I_{\rm b} )}}}=3$. 其中, $k_{\rm s} $为地基基床系数, 需借助Vesic[39 ] 给出的理论公式将其换算为弹性模量.
图5 和图6 分别为梁中点处地基沉降和地基反力随时间的变化曲线. 由图可见, 本文理论退化至Kelvin地基后所得解答与文献[32 ]结果吻合良好, 具有很好的一致性.
图5
图5
Timoshenko梁中点处地基沉降随时间的变化
Fig.5
Settlement at the midpoint of the Timoshenko beam with time
图6
图6
Timoshenko梁中点处地基反力随时间的变化
Fig.6
Subgrade reaction at the midpoint of the Timoshenko beam with time
3.2 单元数目的影响分析
为便于分析, 本文将对梁与地基的部分参数及固结计算结果进行无量纲化处理. 无量纲位移$w^{\ast }$、地基反力$R^{\ast }$及时间参数$\tau $的具体定义见各图中标注, 其中$\mu ={{(1-v_{vh} )}/{[2(1+v_{vh} )(1-2v_{vh} )]}}$. 梁$\!-\!$土相对刚度比定义为$K_{\rm b} ={{4E_{\rm b} b_{\rm b} h_{\rm b}^{3} (1-\nu _{vh}^{2} )}/{(3\pi E_{1v} L^{4})}}$.
Timoshenko梁置于均质黏弹性饱和半空间地基上, 其上表面在全长范围内作用竖向均布载荷$p$. 梁的参数为: 长高比${L/{h_{\rm b} }}=6$, 截面宽高比${{b_{\rm b} }/{h_{\rm b} }}=1$, 泊松比$\nu_{\rm b} =0.15$; 地基土的相关参数为: $E_{0v} =10~\mbox{MPa}$, $E_{1v} =5~\mbox{MPa}$, $\eta _{v} =1.0\times \mbox{10}^{6}~\mbox{MPa}\cdot \mbox{s}$, $\zeta =1$, $\nu_{vh} =\nu_{h} =0.35$, $k_{v} =k_{h} =5.0\times 10^{-8}$m/s; 梁$\!-\!$土相对刚度比$K_{\rm b} $为0.1. 本文取分数阶次$\alpha =0.4,0.6,0.8,1.0$进行对比分析.
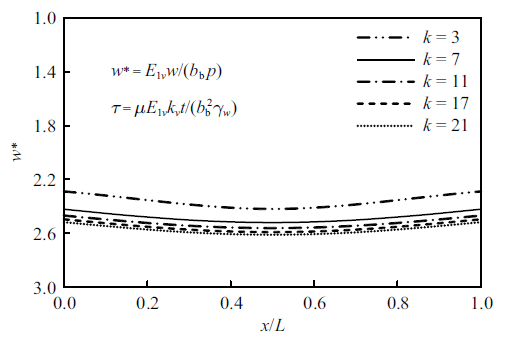
本节探讨梁单元数目对计算结果的影响. 当梁节点数目$k=3$, 7, 11, 17, 21时, 计算得到的固结完成时($\tau =10^{12})$梁与地基接触面的沉降见图7 .
图7
图7
单元数目对地基沉降的影响
Fig.7
Effects of the number of elements on settlements
由图7 可见, 当梁节点数目$k\geqslant 7$, 即梁单元数目大于等于6时, 梁单元数目的增加对梁与地基相互作用的计算结果影响已不再显著. 显然, 随着单元数目的增加, 数值解答的精度随之提高, 但计算效率也在逐渐下降. 考虑到计算效率和精度的平衡, 本文算例均取$k=11$, 即将梁划分为10个单元, 此时所得结果的误差在可接受的范围内.
3.3 分数阶次的影响分析
对于实际工程中模型分数阶次等参数的取值问题, 可参考文献[20 , 22 -23 ]中的试验方法. 具体为: 取工程所在区域的土样进行三轴流变试验, 得到土体蠕变曲线; 然后依据本构关系式, 通过曲线拟合方法得到与蠕变曲线相吻合的分数阶黏弹性模型参数. 另外, 所取蠕变曲线对应的加载条件应尽量与实际工程的工况条件一致, 以保证能有效反映实际工程条件下该区域土体独特的流变特性.
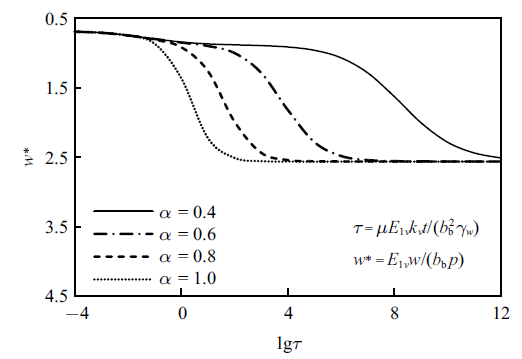
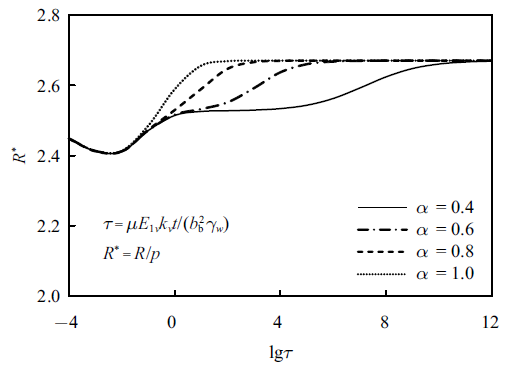
基于3.2节中的梁和地基参数, 可计算得到如图8 和图9 所示的不同分数阶次下梁中心地基沉降和梁端地基反力随时间的变化情况. 由于土体固结及蠕变变形的存在, 梁下地基沉降及地基反力表现出明显的时变特征. 例如, 地基沉降及地基反力的时变曲线在固结初期较为平缓, 而后有比较明显的增长, 最终随时间发展而趋于某一定值. 另外, 分数阶次$\alpha $对梁底地基沉降和地基反力均有较大影响. 当其他参数不变时, 饱和地基固结速率随$\alpha $的增大而明显加快, 梁底地基沉降量及端部地基反力都会更早达到最终值; 但不同分数阶次下, 梁中点处地基的最终沉降以及端部的最终反力相同.
图8
图8
不同分数阶次下梁中点地基沉降随时间的变化
Fig.8
Settlements versus time at the midpoint of the beam with different fractional orders
图9
图9
不同分数阶次下梁端部地基反力随时间的变化
Fig.9
Subgrade reactions versus time at the end of the beam with different fractional orders
实际上, 分数阶次$\alpha$的取值决定了分数阶Merchant模型(见图3 )中Abel黏壶的物理性质: 当$\alpha =0$时, 该元件为线弹性固体; 当$\alpha =1$时, 为理想牛顿流体; 当$0<\alpha <1$时, 为分数阶黏弹性体. Yin等[22 ] 经研究指出, 随着分数阶次$\alpha$的增大, 土体孔隙水压力消散得更快, 故达到最终沉降所需时间更短. 另外, 当孔隙水压力完全消散, 不同分数阶次模型下的土体均达到最终沉降状态, 此时各梁$\!-\!$土接触面上的地基沉降及反力也达到相同状态. 解益等[25 ] 曾将分数阶Kelvin模型下黏弹性饱和土体的固结沉降表达式退化至整数阶黏弹性模型以及弹性模型, 从理论上证明了不同分数阶次下土体最终沉降量相同.
3.4 地基成层性的影响分析
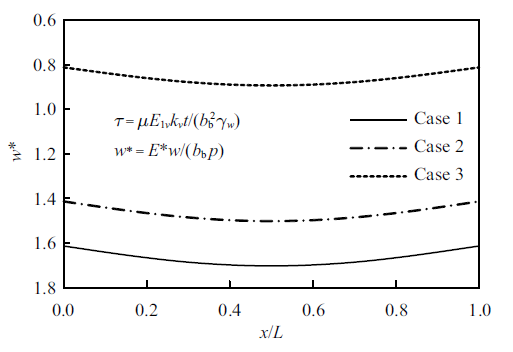
本节将探究地基成层性对梁土相互作用的影响. 3种饱和土体的相关参数见表1 , 3种分层工况见表2 . 土体1和土体2为黏弹性饱和土, 土体3为弹性饱和土. $E^{\ast}$表示终态模量(${1/{E^{\ast }}}={1/{E_{0} }}+{1/{E_{1} }})$, 其值一定程度上能反映土体的整体压缩变形性能. 地基总厚度为$H=10L$, 自上而下三层土体的厚度比例为$h_{1} :h_{2} :h_{3} =1:1:8$; 弹性梁参数同3.2节, 梁上作用竖向均布载荷$p$. 为便于分析, 计算无量纲时间和无量纲竖向位移时, 统一将$E_{1v} $取为$E^{\ast}=5~\mbox{MPa}$.
由图10 和图11 可见, 工况1中均质单层地基的弹性模量较小, 因而弹性梁底的地基沉降比其他两种工况更大. 与工况1相比, 工况2中首层土的性质相同, 下部土体较硬, 梁下地基沉降量较工况1有一定程度的减小. 而工况3中的首层土弹性模量较大, 相比工况1和工况2, 可有效控制地基沉降.
图10
图10
地基成层性对地基沉降的影响($\tau =10^{6})$
Fig.10
Effects of the stratification of soils on settlements ($\tau =10^{6})$
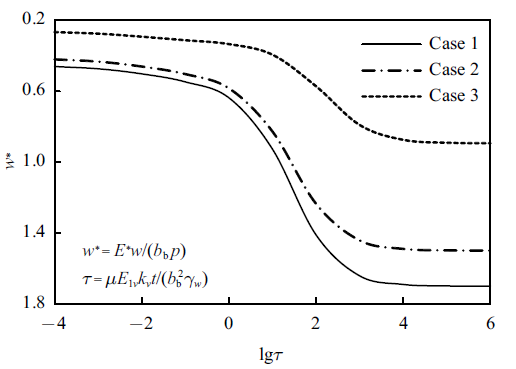
图11
图11
不同层状地基下梁中点地基沉降随时间的变化
Fig.11
Settlements versus time at the midpoint of the beam with different multilayered soils
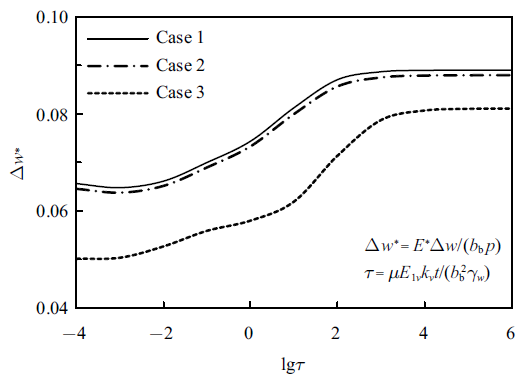
图12 中的$\Delta w$为梁中点及端部地基沉降量之差, $\Delta w^{\ast }$为其无量纲化后的值. 工况2和工况3下的沉降差曲线很相近, 而工况3对应曲线的沉降差值明显降低. 这说明加固表层土体不仅对控制地基的整体沉降有显著效果, 也能大幅减小地基的差异沉降. 实际上, 由于梁受荷造成的地基附加应力的影响深度有限, 且附加应力随深度的增大而明显减小, 故加固表层土体能够对地基沉降起到明显的控制作用.
图12
图12
不同层状地基下沉降差随时间的变化
Fig.12
Differential settlements versus time with different multilayered soils
4 结论
本文以层状正交各向异性黏弹性饱和地基的精细积分解答为基础, 采用有限元$\!-\!$边界元耦合法, 得到了层状分数阶黏弹性饱和地基与Timoshenko梁共同作用的解答. 在此基础上, 分析了分数阶次和地基成层性对地基沉降及地基反力的影响. 主要结论有:
(1)黏弹性饱和地基上弹性梁底部的地基沉降及地基反力表现出明显的时变特征, 它们的时变曲线在固结初期较为平缓, 而后有比较明显的增长, 最终随时间发展而趋于某一定值.
(2)分数阶次$\alpha $的增大会使黏弹性饱和地基的固结速率明显加快, 但不同分数阶次下梁底地基沉降及地基反力的最终值相同.
(3)对于层状地基, 加固表层土体能够有效控制地基整体沉降, 并减小差异沉降. 因此, 在实际工程中, 应充分考虑地基分层性的影响, 以准确分析梁与地基的共同作用过程.
参考文献
View Option
[1]
Hetenyi M . Beams on Elastic Foundation: Theory With Applications in the Fields of Civil and Mechanical Engineering . Ann Arbor : University of Michigan Press , 1946
[本文引用: 1]
[2]
张季容 , 姚祖恩 , 楼文娟 . 有限单元法计算分层地基上的弹性地基梁
岩土工程学报 , 1986 ,8 (3 ):16 -26
(Zhang Jirong Yao Zu'en Lou Wenjuan . Computation of a beam on multilayer foundation using finite element method
Chinese Journal of Geotechnical Engineering 1986 ,8 (3 ):16 -26 (in Chinese))
[3]
Tullini N Tralli A . Static analysis of Timoshenko beam resting on elastic half-plane based on the coupling of locking-free finite elements and boundary integral
Computational Mechanics 2010 ,45 (2-3 ):211 -225
DOI
URL
[4]
夏桂云 , 李传习 , 张建仁 . 考虑水平摩阻和双重剪切的弹性地基梁分析
土木工程学报 , 2011 ,44 (12 ):93 -100
(Xia Guiyun Li Chuanxi Zhang Jianren . Elastic foundation beam analysis with horizontal friction and double shear effects
China Civil Engineering Journal 2011 ,44 (12 ):93 -100 (in Chinese))
[5]
Ai ZY Li ZX Cheng YC . BEM analysis of elastic foundation beams on multilayered isotropic soils
Soils and Foundations 2014 ,54 (4 ):667 -674
DOI
URL
[6]
李潇 , 王宏志 , 李世萍 等 . 解析型Winkler弹性地基梁单元构造
工程力学 , 2015 ,32 (3 ):66 -72
(Li Xiao Wang Hongzhi Li Shiping , et al . Element for beam on winkler elastic foundation based on analytical trial functions
Engineering Mechanics 2015 ,32 (3 ):66 -72 (in Chinese))
[7]
Zhang Y Liu XM . Response of an infinite beam resting on the tensionless Winkler foundation subjected to an axial and a transverse concentrated loads
European Journal of Mechanics A-Solids 2019 ,77 :103819
DOI
URL
[8]
Akhazhanov S Omarbekova N Mergenbekova A , et al . Analytical solution of beams on elastic foundation
International Journal of Geomate 2020 ,19 (73 ):193 -200
[9]
Liang LJ Xu CJ Zhu BT , et al . Theoretical method for an elastic infinite beam resting on a deformable foundation with a local subsidence
Computers and Geotechnics 2020 ,127 :103740
DOI
URL
[本文引用: 1]
[10]
McNamee J Gibson RE . Plane strain and axially symmetric problem of the consolidation of a semi-infinite clay stratum
Quarterly Journal of Mechanics and Applied Mathematics 1960 ,13 (2 ):210 -227
DOI
URL
[本文引用: 1]
[11]
Booker JR . The consolidation of a finite layer subject to surface loading
International Journal of Solids and Structures 1974 ,10 (9 ):1053 -1065
DOI
URL
[12]
Rajapakse RKND Senjuntichai T . Fundamental solutions for a poroelastic half-space with compressible constituents
Journal of Applied Mechanics 1993 ,60 (4 ):844 -856
[13]
方诗圣 , 王建国 , 王秀喜 . 层状饱和土Biot固结问题状态空间法
力学学报 , 2003 ,35 (2 ):206 -212
(Fang Shisheng Wang Jianguo Wang Xiuxi . The static space method of the Biot consolidation problem for multilayered porous media
Chinese Journal of Theoretical and Applied Mechanics 2003 ,35 (2 ):206 -212 (in Chinese))
[14]
陈少林 , 柯小飞 , 张洪翔 . 海洋地震工程流固耦合问题统一计算框架
力学学报 , 2019 ,51 (2 ):594 -606
(Chen Shaolin Ke Xiaofei Zhang Hongxiang . A unified computational framework for fluid-solid coupling in marine earthquake engineering
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (2 ):594 -606 (in Chinese))
[15]
熊春宝 , 胡倩倩 , 郭颖 . 孔隙率各向异性下饱和多孔弹性地基动力响应
力学学报 , 2020 ,52 (4 ):1120 -1130
(Xiong Chunbao Hu Qianqian Guo Ying . Dynamic response of saturated porous elastic foundation under porosity anisotropy
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (4 ):1120 -1130 (in Chinese))
[16]
王立安 , 赵建昌 , 杨华中 . 饱和多孔地基与矩形板动力相互作用的非轴对称混合边值问题
力学学报 , 2020 ,52 (4 ):1189 -1198
[本文引用: 1]
(Wang Li'an Zhao Jianchang Yang Huazhong . Non-axisymmetric mixed boundary value problem for dynamic interaction between saturated porous foundation and rectangular plate
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (4 ):1189 -1198 (in Chinese))
[本文引用: 1]
[17]
陈宗基 , 刘恢先 . 黏土层沉陷(由于固结和次时间效应)的二维问题
力学学报 , 1958 ,2 (1 ):1 -10
[本文引用: 1]
(Chen Zongji Liu Huixian . Two dimensional problems of settlements of clay layers due to consolidation and secondary time effects
Chinese Journal of Theoretical and Applied Mechanics 1958 ,2 (1 ):1 -10 (in Chinese))
[本文引用: 1]
[18]
李传亮 , 杜志敏 , 孔祥言 等 . 多孔介质的流变模型研究
力学学报 , 2003 (2 ):230 -234
[本文引用: 1]
(Li Chuanliang Du Zhimin Kong Xiangyan , et al . A study on the rheological model of porous media
Chinese Journal of Theoretical and Applied Mechanics 2003 (2 ):230 -234 (in Chinese))
[本文引用: 1]
[19]
Gemant A . A method of analyzing experimental results obtained from elasto-viscous bodies
Physics 1936 ,7 (8 ):311 -317
DOI
URL
[本文引用: 1]
[20]
何利军 , 孔令伟 , 吴文军 等 . 采用分数阶导数描述软黏土蠕变的模型
岩土力学 , 2011 ,32 (S2 ):239 -243
[本文引用: 3]
(He Lijun Kong Lingwei Wu Wenjun , et al . A description of creep model for soft soil with fractional derivative
Rock and Soil Mechanics 2011 ,32 (S2 ):239 -243 (in Chinese))
[本文引用: 3]
[21]
Zhu HH Liu LC Pei HF , et al . Settlement analysis of viscoelastic foundation under vertical line load using a fractional Kelvin--Voigt model
Geomechanics and Engineering 2012 ,4 (1 ):67 -78
DOI
URL
[22]
Yin DS Wu H Cheng C , et al . Fractional order constitutive model of geomaterials under the condition of triaxial test
International Journal for Numerical and Analytical Methods in Geomechanics 2013 ,37 :961 -972
DOI
URL
[本文引用: 2]
[23]
刘忠玉 , 杨强 . 基于分数阶Kelvin模型的饱和黏土一维流变固结分析
岩土力学 , 2017 ,38 (12 ):3680 -3687, 3697
[本文引用: 2]
(Liu Zhongyu Yang Qiang . One-dimensional rheological consolidation analysis of saturated clay using fractional order Kelvin's model
Rock and Soil Mechanics 2017 ,38 (12 ):3680 -3687, 3697 (in Chinese))
[本文引用: 2]
[24]
Ai ZY Zhao YZ Liu WJ . Fractional derivative modeling for axisymmetric consolidation of multilayered cross-anisotropic viscoelastic porous media
Computers & Mathematics with Applications 2020 ,79 (5 ):1321 -1334
DOI
URL
[本文引用: 1]
[25]
解益 , 李培超 , 汪磊 等 . 分数阶导数黏弹性饱和土体一维固结半解析解
岩土力学 , 2017 ,38 (11 ):3240 -3246
[本文引用: 2]
(Xie Yi Li Peichao Wang Lei , et al . Semi-analytical solution for one-dimensional consolidation of viscoelastic saturated soil with fractional order derivative
Rock and Soil Mechanics 2017 ,38 (11 ):3240 -3246 (in Chinese))
[本文引用: 2]
[26]
汪磊 , 孙德安 , 解益 等 . 任意载荷下分数阶导数黏弹性饱和土体一维固结
岩土工程学报 , 2017 ,39 (10 ):1823 -1831
[本文引用: 1]
(Wang Lei Sun De'an Xie Yi , et al . One-dimensional consolidation of fractional order derivative viscoelastic saturated soils under arbitrary loading
Chinese Journal of Geotechnical Engineering 2017 ,39 (10 ):1823 -1831 (in Chinese))
[本文引用: 1]
[27]
时刚 , 李永辉 , 刘忠玉 . 基于分数阶流变模型的饱和软土一维流变固结
地下空间与工程学报 , 2019 ,15 (5 ):1402 -1409, 1416
[本文引用: 1]
( Shi Gang Li Yonghui Liu Zhongyu . One-dimensional rheological consolidation of soft clay based on fractional order derivative rheological model
Chinese Journal of Underground Space and Engineering 2019 ,15 (5 ):1402 -1409, 1416 (in Chinese))
[本文引用: 1]
[28]
刘忠玉 , 崔鹏陆 , 郑占垒 等 . 基于非牛顿指数渗流和分数阶Merchant模型的一维流变固结分析
岩土力学 , 2019 ,40 (6 ):2029 -2038
[本文引用: 1]
(Liu Zhongyu Cui Penglu Zheng Zhanlei , et al . Analysis of one-dimensional rheological consolidation with flow described by non-Newtonian index and fractional-order Merchant's model
Rock and Soil Mechanics 2019 ,40 (6 ):2029 -2038 (in Chinese))
[本文引用: 1]
[29]
王珏 , 童立红 , 金立 等 . 任意载荷下连续排水边界分数阶黏弹性地基一维固结模型
土木与环境工程学报 , 2020 ,42 (1 ):56 -63
[本文引用: 1]
(Wang Jue Tong Lihong Jin Li , et al . One-dimension consolidation of fractional order derivative viscoelastic subgrade with continuous drainage boundary under time-dependent loading
Journal of Civil and Environmental Engineering 2020 ,42 (1 ):56 -63 (in Chinese))
[本文引用: 1]
[30]
吴奎 , 邵珠山 , 秦溯 . 流变岩体中让压支护作用下隧道力学行为研究
力学学报 , 2020 ,52 (3 ):890 -900
[本文引用: 1]
(Wu Kui Shao Zhushan Qin Su . Investigation on the mechanical behavior of tunnel supported by yielding supports in rheological rocks
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (3 ):890 -900 (in Chinese))
[本文引用: 1]
[31]
Ai ZY Hu YD . The analysis of beams on layered poroelastic soils with anisotropic permeability and compressible pore fluid
Applied Mathematical Modelling 2016 ,40 (11-12 ):5876 -5890
DOI
URL
[本文引用: 3]
[32]
Kobayashi H Sonoda K . Timoshenko beams on linear viscoelastic foundations
Journal of Geotechnical Engineering ASCE 1983 ,109 (6 ):832 -844
DOI
URL
[本文引用: 4]
[33]
苏超 , 姜弘道 , 谭恩会 . 黏弹性基础梁计算方法及其应用
河海大学学报(自然科学版) , 2000 ,28 (5 ):101 -105
[本文引用: 1]
(Su Chao Jiang Hongdao Tan Enhui . Computation method and application to viscoelastical foundation beam
Journal of Hohai University 2000 ,28 (5 ):101 -105 (in Chinese))
[本文引用: 1]
[34]
Bhattiprolu U Bajaj AK Davies P . An efficient solution methodology to study the response of a beam on viscoelastic and nonlinear unilateral foundation: Static response
International Journal of Solids and Structures 2013 ,50 (14-15 ):2328 -2339
DOI
URL
[本文引用: 1]
[35]
Sreekantan PG Basudhar PK . Flexural response of beams on viscoelastic foundations with predictions beyond the loading area
International Journal of Geotechnical Engineering 2020 ,14 (4 ):442 -451
DOI
URL
[本文引用: 1]
[36]
Ai ZY Gui JC Mu JJ . 3-D time-dependent analysis of multilayered cross-anisotropic saturated soils based on the fractional viscoelastic model
Applied Mathematical Modelling 2019 ,76 :172 -192
DOI
URL
[本文引用: 3]
[37]
夏桂云 , 李传习 . 考虑剪切变形影响的杆系结构理论与应用 . 北京 : 人民交通出版社 , 2008
[本文引用: 1]
(Xia Guiyun Li Chuanxi . Theory and Application of Frame Structures Considering Shear Deformation . Beijing : China Communications Press , 2008 (in Chinese))
[本文引用: 1]
[38]
李星 . 积分方程 . 北京 : 科学出版社 , 2008
[本文引用: 1]
(Li Xing . Integral Equation . Beijing : Science Press , 2008 (in Chinese))
[本文引用: 1]
[39]
Vesic AS . Beams on elastic subgrade and the Winkler's hypothesis
// Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering, Paris , 1961 : 845 -850
[本文引用: 1]
1
1946
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
有限单元法计算分层地基上的弹性地基梁
0
1986
有限单元法计算分层地基上的弹性地基梁
0
1986
Static analysis of Timoshenko beam resting on elastic half-plane based on the coupling of locking-free finite elements and boundary integral
0
2010
考虑水平摩阻和双重剪切的弹性地基梁分析
0
2011
考虑水平摩阻和双重剪切的弹性地基梁分析
0
2011
BEM analysis of elastic foundation beams on multilayered isotropic soils
0
2014
解析型Winkler弹性地基梁单元构造
0
2015
解析型Winkler弹性地基梁单元构造
0
2015
Response of an infinite beam resting on the tensionless Winkler foundation subjected to an axial and a transverse concentrated loads
0
2019
Analytical solution of beams on elastic foundation
0
2020
Theoretical method for an elastic infinite beam resting on a deformable foundation with a local subsidence
1
2020
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
Plane strain and axially symmetric problem of the consolidation of a semi-infinite clay stratum
1
1960
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
The consolidation of a finite layer subject to surface loading
0
1974
Fundamental solutions for a poroelastic half-space with compressible constituents
0
1993
层状饱和土Biot固结问题状态空间法
0
2003
层状饱和土Biot固结问题状态空间法
0
2003
海洋地震工程流固耦合问题统一计算框架
0
2019
海洋地震工程流固耦合问题统一计算框架
0
2019
孔隙率各向异性下饱和多孔弹性地基动力响应
0
2020
孔隙率各向异性下饱和多孔弹性地基动力响应
0
2020
饱和多孔地基与矩形板动力相互作用的非轴对称混合边值问题
1
2020
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
饱和多孔地基与矩形板动力相互作用的非轴对称混合边值问题
1
2020
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
黏土层沉陷(由于固结和次时间效应)的二维问题
1
1958
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
黏土层沉陷(由于固结和次时间效应)的二维问题
1
1958
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
多孔介质的流变模型研究
1
2003
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
多孔介质的流变模型研究
1
2003
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
A method of analyzing experimental results obtained from elasto-viscous bodies
1
1936
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
采用分数阶导数描述软黏土蠕变的模型
3
2011
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
... [20 -23 ], 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
... 对于实际工程中模型分数阶次等参数的取值问题, 可参考文献[20 , 22 -23 ]中的试验方法. 具体为: 取工程所在区域的土样进行三轴流变试验, 得到土体蠕变曲线; 然后依据本构关系式, 通过曲线拟合方法得到与蠕变曲线相吻合的分数阶黏弹性模型参数. 另外, 所取蠕变曲线对应的加载条件应尽量与实际工程的工况条件一致, 以保证能有效反映实际工程条件下该区域土体独特的流变特性. ...
采用分数阶导数描述软黏土蠕变的模型
3
2011
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
... [20 -23 ], 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
... 对于实际工程中模型分数阶次等参数的取值问题, 可参考文献[20 , 22 -23 ]中的试验方法. 具体为: 取工程所在区域的土样进行三轴流变试验, 得到土体蠕变曲线; 然后依据本构关系式, 通过曲线拟合方法得到与蠕变曲线相吻合的分数阶黏弹性模型参数. 另外, 所取蠕变曲线对应的加载条件应尽量与实际工程的工况条件一致, 以保证能有效反映实际工程条件下该区域土体独特的流变特性. ...
Settlement analysis of viscoelastic foundation under vertical line load using a fractional Kelvin--Voigt model
0
2012
Fractional order constitutive model of geomaterials under the condition of triaxial test
2
2013
... 对于实际工程中模型分数阶次等参数的取值问题, 可参考文献[20 , 22 -23 ]中的试验方法. 具体为: 取工程所在区域的土样进行三轴流变试验, 得到土体蠕变曲线; 然后依据本构关系式, 通过曲线拟合方法得到与蠕变曲线相吻合的分数阶黏弹性模型参数. 另外, 所取蠕变曲线对应的加载条件应尽量与实际工程的工况条件一致, 以保证能有效反映实际工程条件下该区域土体独特的流变特性. ...
... 实际上, 分数阶次$\alpha$的取值决定了分数阶Merchant模型(见图3 )中Abel黏壶的物理性质: 当$\alpha =0$时, 该元件为线弹性固体; 当$\alpha =1$时, 为理想牛顿流体; 当$0<\alpha <1$时, 为分数阶黏弹性体. Yin等[22 ] 经研究指出, 随着分数阶次$\alpha$的增大, 土体孔隙水压力消散得更快, 故达到最终沉降所需时间更短. 另外, 当孔隙水压力完全消散, 不同分数阶次模型下的土体均达到最终沉降状态, 此时各梁$\!-\!$土接触面上的地基沉降及反力也达到相同状态. 解益等[25 ] 曾将分数阶Kelvin模型下黏弹性饱和土体的固结沉降表达式退化至整数阶黏弹性模型以及弹性模型, 从理论上证明了不同分数阶次下土体最终沉降量相同. ...
基于分数阶Kelvin模型的饱和黏土一维流变固结分析
2
2017
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
... 对于实际工程中模型分数阶次等参数的取值问题, 可参考文献[20 , 22 -23 ]中的试验方法. 具体为: 取工程所在区域的土样进行三轴流变试验, 得到土体蠕变曲线; 然后依据本构关系式, 通过曲线拟合方法得到与蠕变曲线相吻合的分数阶黏弹性模型参数. 另外, 所取蠕变曲线对应的加载条件应尽量与实际工程的工况条件一致, 以保证能有效反映实际工程条件下该区域土体独特的流变特性. ...
基于分数阶Kelvin模型的饱和黏土一维流变固结分析
2
2017
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
... 对于实际工程中模型分数阶次等参数的取值问题, 可参考文献[20 , 22 -23 ]中的试验方法. 具体为: 取工程所在区域的土样进行三轴流变试验, 得到土体蠕变曲线; 然后依据本构关系式, 通过曲线拟合方法得到与蠕变曲线相吻合的分数阶黏弹性模型参数. 另外, 所取蠕变曲线对应的加载条件应尽量与实际工程的工况条件一致, 以保证能有效反映实际工程条件下该区域土体独特的流变特性. ...
Fractional derivative modeling for axisymmetric consolidation of multilayered cross-anisotropic viscoelastic porous media
1
2020
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
分数阶导数黏弹性饱和土体一维固结半解析解
2
2017
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
... 实际上, 分数阶次$\alpha$的取值决定了分数阶Merchant模型(见图3 )中Abel黏壶的物理性质: 当$\alpha =0$时, 该元件为线弹性固体; 当$\alpha =1$时, 为理想牛顿流体; 当$0<\alpha <1$时, 为分数阶黏弹性体. Yin等[22 ] 经研究指出, 随着分数阶次$\alpha$的增大, 土体孔隙水压力消散得更快, 故达到最终沉降所需时间更短. 另外, 当孔隙水压力完全消散, 不同分数阶次模型下的土体均达到最终沉降状态, 此时各梁$\!-\!$土接触面上的地基沉降及反力也达到相同状态. 解益等[25 ] 曾将分数阶Kelvin模型下黏弹性饱和土体的固结沉降表达式退化至整数阶黏弹性模型以及弹性模型, 从理论上证明了不同分数阶次下土体最终沉降量相同. ...
分数阶导数黏弹性饱和土体一维固结半解析解
2
2017
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
... 实际上, 分数阶次$\alpha$的取值决定了分数阶Merchant模型(见图3 )中Abel黏壶的物理性质: 当$\alpha =0$时, 该元件为线弹性固体; 当$\alpha =1$时, 为理想牛顿流体; 当$0<\alpha <1$时, 为分数阶黏弹性体. Yin等[22 ] 经研究指出, 随着分数阶次$\alpha$的增大, 土体孔隙水压力消散得更快, 故达到最终沉降所需时间更短. 另外, 当孔隙水压力完全消散, 不同分数阶次模型下的土体均达到最终沉降状态, 此时各梁$\!-\!$土接触面上的地基沉降及反力也达到相同状态. 解益等[25 ] 曾将分数阶Kelvin模型下黏弹性饱和土体的固结沉降表达式退化至整数阶黏弹性模型以及弹性模型, 从理论上证明了不同分数阶次下土体最终沉降量相同. ...
任意载荷下分数阶导数黏弹性饱和土体一维固结
1
2017
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
任意载荷下分数阶导数黏弹性饱和土体一维固结
1
2017
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
基于分数阶流变模型的饱和软土一维流变固结
1
2019
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
基于分数阶流变模型的饱和软土一维流变固结
1
2019
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
基于非牛顿指数渗流和分数阶Merchant模型的一维流变固结分析
1
2019
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
基于非牛顿指数渗流和分数阶Merchant模型的一维流变固结分析
1
2019
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
任意载荷下连续排水边界分数阶黏弹性地基一维固结模型
1
2020
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
任意载荷下连续排水边界分数阶黏弹性地基一维固结模型
1
2020
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
流变岩体中让压支护作用下隧道力学行为研究
1
2020
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
流变岩体中让压支护作用下隧道力学行为研究
1
2020
... 弹性地基梁模型在公路、铁路和建筑基础等工程的设计计算中有广泛应用, 并因为简单适用而备受青睐. 国内外很多学者针对弹性地基梁问题开展过研究工作[1 -9 ] , 但这些研究多基于弹性地基或Winkler地基模型. 当基础置于饱和地基时, 土体同时存在固结和蠕变变形, 故需要考虑地基与基础相互作用的时效性. 许多学者对饱和地基的固结问题进行过深入研究, 一般将地基视为饱和弹性介质[10 -16 ] 或饱和黏弹性介质[17 -18 ] . Gemant[19 ] 通过试验发现, 经典的整数阶微分流变模型存在一定局限性, 建议采用基于分数阶导数的微分流变模型. 近年来, 不少学者采用分数阶黏弹性模型对饱和土体的流变固结问题开展了研究[20 -24 ] . 解益等[25 ] 、汪磊等[26 ] 将分数阶导数理论引入Kelvin--Voigt模型, 给出了黏弹性饱和土体一维固结问题的半解析解法. 基于Merchant流变模型, 时刚等[27 ] 研究发现: 分数阶导数模型在固结后期所表现出的特征与整数阶模型有显著差异. 刘忠玉等[28 ] 引入Koeller定义的弹壶元件以建立分数阶Merchant模型, 然后对考虑非达西渗流的饱和土体流变固结机制进行了分析. 借助分数阶Kelvin本构模型, 王珏等[29 ] 研究了循环载荷作用下黏土地基的一维固结沉降特征. 吴奎等[30 ] 采用Abel黏壶替代牛顿黏壶, 基于改进的分数阶Burger模型研究了高地应力深埋软岩的流变问题. 已有的研究表明[20 -23 ] , 分数阶黏弹性本构模型能以少量的参数较为准确地描述土体的流变行为. ...
The analysis of beams on layered poroelastic soils with anisotropic permeability and compressible pore fluid
3
2016
... 基于饱和黏弹性地基的固结解, Ai和Hu[31 ] 利用有限元$\!-\!$解析层元耦合法研究了层状饱和地基与梁的共同作用问题, 并考虑了地基的渗透各向异性和孔隙流体的可压缩性. Kobayashi和Sonoda[32 ] 基于Winkler地基假定, 借助弹性$\!-\!$黏弹性对应原理, 给出了多种线性黏弹性地基上Timoshenko梁弯曲问题的解答. 苏超等[33 ] 也利用弹性$\!-\!$黏弹性对应原理, 建立了黏弹性地基上基础梁的计算方法, 并将其应用于软土地基上船闸底板的计算. Bhattiprolu等[34 ] 提出了非线性黏弹性地基上弹性梁的有效求解方法, 且该方法能够处理二者间接触区域非连续的情况. Sreekantan和 Basudhar[35 ] 基于Burger模型对黏弹性地基上梁的受弯响应进行了分析. 目前针对黏弹性地基上梁的研究中, 很少考虑到分数阶黏弹性以及地基的成层特点. 因此, 开展层状分数阶黏弹性饱和地基与梁的共同作用研究具有重要的理论意义和工程应用价值. ...
... 文献[36 ]利用弹性$\!-\!$黏弹性对应原理对层状正交各向异性黏弹性饱和地基的固结问题进行了求解, 但该解答仅针对地基上作用骤加载荷的情况. 实际上, 由于孔隙水的存在, 梁与饱和地基的相互作用过程中, 地基反力和沉降会随时间缓慢变化. 这时任意地基单元$i$在$t$时刻受到的作用力有如下积分型表达[31 ] ...
... 求解该式即可得出Laplace变换域内梁各节点转角和单元底部的地基反力, 地基沉降可通过式(13)进一步获得. 对以上解答进行Laplace数值逆变换[31 ] , 即可得到各分量在物理域内的真实解. ...
Timoshenko beams on linear viscoelastic foundations
4
1983
... 基于饱和黏弹性地基的固结解, Ai和Hu[31 ] 利用有限元$\!-\!$解析层元耦合法研究了层状饱和地基与梁的共同作用问题, 并考虑了地基的渗透各向异性和孔隙流体的可压缩性. Kobayashi和Sonoda[32 ] 基于Winkler地基假定, 借助弹性$\!-\!$黏弹性对应原理, 给出了多种线性黏弹性地基上Timoshenko梁弯曲问题的解答. 苏超等[33 ] 也利用弹性$\!-\!$黏弹性对应原理, 建立了黏弹性地基上基础梁的计算方法, 并将其应用于软土地基上船闸底板的计算. Bhattiprolu等[34 ] 提出了非线性黏弹性地基上弹性梁的有效求解方法, 且该方法能够处理二者间接触区域非连续的情况. Sreekantan和 Basudhar[35 ] 基于Burger模型对黏弹性地基上梁的受弯响应进行了分析. 目前针对黏弹性地基上梁的研究中, 很少考虑到分数阶黏弹性以及地基的成层特点. 因此, 开展层状分数阶黏弹性饱和地基与梁的共同作用研究具有重要的理论意义和工程应用价值. ...
... Kobayashi和Sonoda[32 ] 针对多种线性黏弹性地基上Timoshenko梁的弯曲问题进行了研究, 其中基于Kelvin地基模型的相关研究可视为本文模型的特例. 为此将本文模型退化至Kelvin地基, 并与文献[32 ]中的算例进行对比. 算例中均布载荷$p$作用于梁中部$0.4L\leqslant x\leqslant 0.6L$区域, 弹性梁与黏弹性地基的相关参数满足: $\sqrt {{{E_{b} I_{b} }/{[kA_{\rm b} G_{\rm b} (L/2)^{2}]}}} =0.2$, $\sqrt[4]{{{k_{\rm s} (L/2)^{4}}/{(E_{\rm b} I_{\rm b} )}}}=3$. 其中, $k_{\rm s} $为地基基床系数, 需借助Vesic[39 ] 给出的理论公式将其换算为弹性模量. ...
... 针对多种线性黏弹性地基上Timoshenko梁的弯曲问题进行了研究, 其中基于Kelvin地基模型的相关研究可视为本文模型的特例. 为此将本文模型退化至Kelvin地基, 并与文献[32 ]中的算例进行对比. 算例中均布载荷$p$作用于梁中部$0.4L\leqslant x\leqslant 0.6L$区域, 弹性梁与黏弹性地基的相关参数满足: $\sqrt {{{E_{b} I_{b} }/{[kA_{\rm b} G_{\rm b} (L/2)^{2}]}}} =0.2$, $\sqrt[4]{{{k_{\rm s} (L/2)^{4}}/{(E_{\rm b} I_{\rm b} )}}}=3$. 其中, $k_{\rm s} $为地基基床系数, 需借助Vesic[39 ] 给出的理论公式将其换算为弹性模量. ...
... 图5 和图6 分别为梁中点处地基沉降和地基反力随时间的变化曲线. 由图可见, 本文理论退化至Kelvin地基后所得解答与文献[32 ]结果吻合良好, 具有很好的一致性. ...
黏弹性基础梁计算方法及其应用
1
2000
... 基于饱和黏弹性地基的固结解, Ai和Hu[31 ] 利用有限元$\!-\!$解析层元耦合法研究了层状饱和地基与梁的共同作用问题, 并考虑了地基的渗透各向异性和孔隙流体的可压缩性. Kobayashi和Sonoda[32 ] 基于Winkler地基假定, 借助弹性$\!-\!$黏弹性对应原理, 给出了多种线性黏弹性地基上Timoshenko梁弯曲问题的解答. 苏超等[33 ] 也利用弹性$\!-\!$黏弹性对应原理, 建立了黏弹性地基上基础梁的计算方法, 并将其应用于软土地基上船闸底板的计算. Bhattiprolu等[34 ] 提出了非线性黏弹性地基上弹性梁的有效求解方法, 且该方法能够处理二者间接触区域非连续的情况. Sreekantan和 Basudhar[35 ] 基于Burger模型对黏弹性地基上梁的受弯响应进行了分析. 目前针对黏弹性地基上梁的研究中, 很少考虑到分数阶黏弹性以及地基的成层特点. 因此, 开展层状分数阶黏弹性饱和地基与梁的共同作用研究具有重要的理论意义和工程应用价值. ...
黏弹性基础梁计算方法及其应用
1
2000
... 基于饱和黏弹性地基的固结解, Ai和Hu[31 ] 利用有限元$\!-\!$解析层元耦合法研究了层状饱和地基与梁的共同作用问题, 并考虑了地基的渗透各向异性和孔隙流体的可压缩性. Kobayashi和Sonoda[32 ] 基于Winkler地基假定, 借助弹性$\!-\!$黏弹性对应原理, 给出了多种线性黏弹性地基上Timoshenko梁弯曲问题的解答. 苏超等[33 ] 也利用弹性$\!-\!$黏弹性对应原理, 建立了黏弹性地基上基础梁的计算方法, 并将其应用于软土地基上船闸底板的计算. Bhattiprolu等[34 ] 提出了非线性黏弹性地基上弹性梁的有效求解方法, 且该方法能够处理二者间接触区域非连续的情况. Sreekantan和 Basudhar[35 ] 基于Burger模型对黏弹性地基上梁的受弯响应进行了分析. 目前针对黏弹性地基上梁的研究中, 很少考虑到分数阶黏弹性以及地基的成层特点. 因此, 开展层状分数阶黏弹性饱和地基与梁的共同作用研究具有重要的理论意义和工程应用价值. ...
An efficient solution methodology to study the response of a beam on viscoelastic and nonlinear unilateral foundation: Static response
1
2013
... 基于饱和黏弹性地基的固结解, Ai和Hu[31 ] 利用有限元$\!-\!$解析层元耦合法研究了层状饱和地基与梁的共同作用问题, 并考虑了地基的渗透各向异性和孔隙流体的可压缩性. Kobayashi和Sonoda[32 ] 基于Winkler地基假定, 借助弹性$\!-\!$黏弹性对应原理, 给出了多种线性黏弹性地基上Timoshenko梁弯曲问题的解答. 苏超等[33 ] 也利用弹性$\!-\!$黏弹性对应原理, 建立了黏弹性地基上基础梁的计算方法, 并将其应用于软土地基上船闸底板的计算. Bhattiprolu等[34 ] 提出了非线性黏弹性地基上弹性梁的有效求解方法, 且该方法能够处理二者间接触区域非连续的情况. Sreekantan和 Basudhar[35 ] 基于Burger模型对黏弹性地基上梁的受弯响应进行了分析. 目前针对黏弹性地基上梁的研究中, 很少考虑到分数阶黏弹性以及地基的成层特点. 因此, 开展层状分数阶黏弹性饱和地基与梁的共同作用研究具有重要的理论意义和工程应用价值. ...
Flexural response of beams on viscoelastic foundations with predictions beyond the loading area
1
2020
... 基于饱和黏弹性地基的固结解, Ai和Hu[31 ] 利用有限元$\!-\!$解析层元耦合法研究了层状饱和地基与梁的共同作用问题, 并考虑了地基的渗透各向异性和孔隙流体的可压缩性. Kobayashi和Sonoda[32 ] 基于Winkler地基假定, 借助弹性$\!-\!$黏弹性对应原理, 给出了多种线性黏弹性地基上Timoshenko梁弯曲问题的解答. 苏超等[33 ] 也利用弹性$\!-\!$黏弹性对应原理, 建立了黏弹性地基上基础梁的计算方法, 并将其应用于软土地基上船闸底板的计算. Bhattiprolu等[34 ] 提出了非线性黏弹性地基上弹性梁的有效求解方法, 且该方法能够处理二者间接触区域非连续的情况. Sreekantan和 Basudhar[35 ] 基于Burger模型对黏弹性地基上梁的受弯响应进行了分析. 目前针对黏弹性地基上梁的研究中, 很少考虑到分数阶黏弹性以及地基的成层特点. 因此, 开展层状分数阶黏弹性饱和地基与梁的共同作用研究具有重要的理论意义和工程应用价值. ...
3-D time-dependent analysis of multilayered cross-anisotropic saturated soils based on the fractional viscoelastic model
3
2019
... 本文采用有限元法对Timoshenko梁进行分析, 采用边界元法对地基进行分析, 将文献[36 ]中分数阶黏弹性饱和地基的固结解答作为地基边界积分方程的核函数, 建立梁节点沉降与地基反力间的柔度矩阵方程; 然后根据梁与地基接触面上的位移协调条件和力的平衡条件, 推导出层状黏弹性饱和地基与Timoshenko梁共同作用的解答; 最后探讨分数阶次和地基成层性对梁与饱和黏弹性地基共同作用的影响. ...
... 文献[36 ]利用弹性$\!-\!$黏弹性对应原理对层状正交各向异性黏弹性饱和地基的固结问题进行了求解, 但该解答仅针对地基上作用骤加载荷的情况. 实际上, 由于孔隙水的存在, 梁与饱和地基的相互作用过程中, 地基反力和沉降会随时间缓慢变化. 这时任意地基单元$i$在$t$时刻受到的作用力有如下积分型表达[31 ] ...
... 式中, $I_{\rm s} (j,i,t)$为在第$i$个地基单元表面作用单位均布载荷, 经过$t$时间段时, 在梁节点$j$下地基表面处产生的竖向位移, 其可根据地基固结解[36 ] 求得. ...
1
2008
... 基于Timoshenko梁理论, 可得梁单元的有限元求解方程[37 ] ...
1
2008
... 基于Timoshenko梁理论, 可得梁单元的有限元求解方程[37 ] ...
1
2008
... 对于形如式(9)的方程, 可采用卷积公式进行化简. 卷积公式的定义如下[38 ] ...
1
2008
... 对于形如式(9)的方程, 可采用卷积公式进行化简. 卷积公式的定义如下[38 ] ...
Beams on elastic subgrade and the Winkler's hypothesis
1
1961
... Kobayashi和Sonoda[32 ] 针对多种线性黏弹性地基上Timoshenko梁的弯曲问题进行了研究, 其中基于Kelvin地基模型的相关研究可视为本文模型的特例. 为此将本文模型退化至Kelvin地基, 并与文献[32 ]中的算例进行对比. 算例中均布载荷$p$作用于梁中部$0.4L\leqslant x\leqslant 0.6L$区域, 弹性梁与黏弹性地基的相关参数满足: $\sqrt {{{E_{b} I_{b} }/{[kA_{\rm b} G_{\rm b} (L/2)^{2}]}}} =0.2$, $\sqrt[4]{{{k_{\rm s} (L/2)^{4}}/{(E_{\rm b} I_{\rm b} )}}}=3$. 其中, $k_{\rm s} $为地基基床系数, 需借助Vesic[39 ] 给出的理论公式将其换算为弹性模量. ...