材料在外载荷的作用下, 其内部结构会发生破坏, 生产微小的裂纹或孔洞等细观缺陷, 这些细观缺陷会导致材料宏观力学性能的劣化, 这种现象即称为损伤^[1-2]. 经典的损伤力学是在连续介质力学的框架下, 并考虑材料变形的热力学过程而建立起来的, 故又被称为连续损伤力学, Sumio^[3]对该理论做了详尽的研究. 在工程应用领域中, 将连续损伤力学理论与有限元方法相结合能够很好地分析构件的疲劳破坏与延性破坏等问题, 其中国内学者詹志新等^[4-7]在该方面做了深入地研究工作.

连续损伤力学采用宏观唯象的研究方法, 研究宏观尺度上代表性体积单元(representative volume element, RVE)的损伤与其力学性能的关系, 没有深入到材料内部, 从细观尺度上研究损伤机理. 考虑到宏观研究尺度的局限性, 研究者们提出了一系列的细观损伤研究方法, 例如考虑非椭球夹杂的复合材料细观损伤模型^[8]、基于相场理论的非局部宏$\!-\!$微观损伤模型^[9]、固体损伤破坏的统一相场模型^[10]等.

在众多的细观尺度研究方法中, 晶体塑性理论将滑移系作为研究的基本对象, 已经发展为一套成熟的细观研究方法^[11-15]. 基于晶体塑性理论建立细观损伤模型也成为近年来研究的热点^[16-19]. 晶体尺度的细观损伤模型的研究工作主要集中在3个方面: 损伤变量的定义、被劣化对象的选取以及损伤演化方程的建立. 赵红彬^[20]将损伤定义为承载位错滑移的滑移面劣化率, 以标量损伤度来折减弹性模量与剪切应变率, 使用剪切应变来控制损伤的演化过程. Boudifa等^[21]将晶体由宏观到细观划分为3个尺度: RVE尺度、晶粒尺度以及滑移系尺度, 分别定义了各级尺度的损伤变量, 并逐级耦合建立了各个尺度之间的损伤关系, 实现了从细观到宏观的延性损伤计算. Hfaiedh等^[22]为每个滑移系定义了一个损伤标量, 将每个滑移系的损伤标量进行线性加权叠加得到RVE的损伤标量, 实现对RVE整体刚度的折减. Zghal等^[23]研究了晶体塑性理论的高周循环疲劳模型, 将每个滑移系的损伤标量耦合为一个四阶损伤张量, 并用于刻画晶体损伤的各向异性.

对于材料损伤的描述, 除了使用连续损伤力学的思想外, 还有其他的定义方法. Forest等^[24-26]在位移场中引入了一个新的自由度, 该附加自由度被称为微损伤变量. 他们通过严格的数学推导, 建立了微损伤理论的力学模型, 并将该模型与晶体塑性理论相结合, 很好地模拟了宏观力学性能的退化. 本文采用微损伤理论的思想方法, 推导了有限变形框架下考虑晶体解理型损伤的本构方程、塑性流动方程以及损伤演化方程, 建立了相应的数值计算方法, 完成了材料的细观参数标定, 研究了单轴拉伸模拟过程中的塑性流动与损伤演化规律, 以期为多晶金属材料的延性损伤、疲劳损伤、蠕变损伤等问题提供新的分析思路与方法.

为了描述晶体滑移系在受力和变形过程中产生的解理型微观裂纹对晶体后续变形的影响, 本文在经典晶体塑性理论的基础上引入损伤变形梯度张量$\boldsymbol{F}^{d}$, 即认为晶体的解理型损伤会导致附加的变形, 进而推导了考虑晶体损伤的变形运动学方程、本构方程、塑性流动方程以及损伤演化方程.

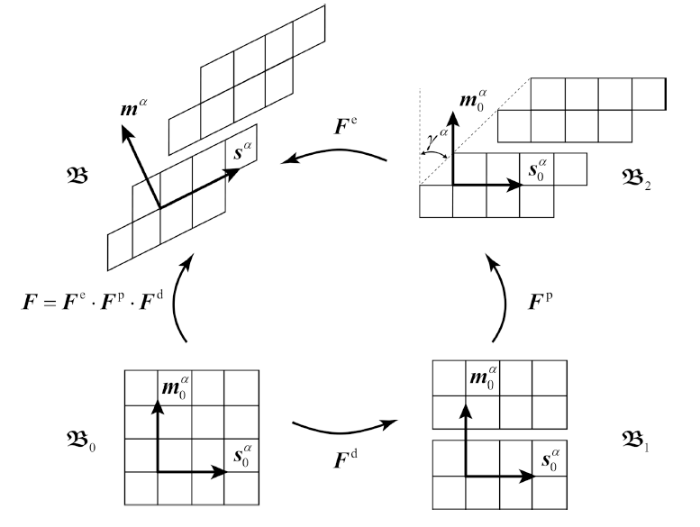
如图1所示, 在单晶体均匀滑移模型^[11]的基础上, 引入损伤变形梯度张量$\boldsymbol{F}^{d}$, 进而将单晶体的损伤耦合变形运动过程用4个构型来描述: 未发生变形的参考构型$\mathfrak{B}_{0}$、损伤构型$\mathfrak{B}_{1}$、塑性构型$\mathfrak{B}_{2}$、变形结束后的当前构型$\mathfrak{B}$.

根据Shanthraja等^[27]提出的损伤耦合变形运动分解方法, 将变形梯度张量$\boldsymbol{F}$作如下分解

式中, $\boldsymbol{F}^d$为损伤变形梯度张量, 用于描述由参考构型$\mathfrak{B}_{0}$到损伤构型$\mathfrak{B}_{1}$的变形过程中因晶体解理而产生张开型裂纹的晶格缺陷效应; $\boldsymbol{F}^p$为塑性变形梯度张量, 用于描述由损伤构型$\mathfrak{B}_{1}$到塑性构型$\mathfrak{B}_{2}$的变形过程中晶体的塑性位错滑移; $\boldsymbol{F}^e$为弹性变形梯度张量, 用于描述由塑性构型$\mathfrak{B}_{2}$到当前构型$\mathfrak{B}$的变形过程中晶体的弹性伸长与刚性转动.

需要指出, 本文模型所考虑的损伤类型主要为晶体解理型微观损伤, 因此引入的损伤变形梯度张量$\boldsymbol{F}^{d}$主要用于描述解理型微观裂纹的产生对晶体沿滑移面法线方向变形的影响, 并以此来反映材料力学性能的劣化. 同时, 出于对数值实现的考虑, 本文在式(1)中采用了损伤、塑性、弹性的变形运动学分解顺序.

考虑变形梯度张量的时间导数$\dot{\boldsymbol{F}}$, 可引入速度梯度张量$\boldsymbol{L}$, 并对其作如下分解

其中

$\begin{eqnarray*} \left.\begin{array}{ccl} \boldsymbol{L}^{e} &=& \dot{\boldsymbol{F}^e}\cdot\boldsymbol{F}^{-e} \\ \boldsymbol{L}^{p} &=& \boldsymbol{F}^e\cdot\dot{\boldsymbol{F}^p}\cdot\boldsymbol{F}^{-p}\cdot\boldsymbol{F}^{-e} \\ \boldsymbol{L}^{d} &=& \boldsymbol{F}^e\cdot\boldsymbol{F}^p\cdot\dot{\boldsymbol{F}^d}\cdot\boldsymbol{F}^{-d}\cdot\boldsymbol{F}^{-p}\cdot\boldsymbol{F}^{-e} \end{array}\right\} \end{eqnarray*}$

式中, $\boldsymbol{L}^e$, $\boldsymbol{L}^p$, $\boldsymbol{L}^d$分别为弹性、塑性、损伤速度梯度张量, $\boldsymbol{F}^{-e}=(\boldsymbol{F}^{e})^{-1}$, $\boldsymbol{F}^{-p}$和$\boldsymbol{F}^{-d}$的定义与其类似.

考虑到晶体的解理型损伤是伴随着其塑性滑移产生的, 且与其弹性变形和刚性转动无关. 于是, 在图1中假设损伤变形梯度张量$\boldsymbol{F}^d$不会导致晶格矢量的改变, 即参考构型$\mathfrak{B}_{0}$与损伤构型$\mathfrak{B}_{1}$的晶格矢量均为$(\boldsymbol{s}_0^{\alpha},\boldsymbol{m}_0^{\alpha})$. 进一步, 考虑到式(2)中弹性速度梯度张量$\boldsymbol{L}^e$与塑性速度梯度张量$\boldsymbol{L}^p$均与经典晶体塑性理论中的定义一致, 于是可得当前构型$\mathfrak{B}$中晶格矢量$(\boldsymbol{s}^{\alpha},\boldsymbol{m}^{\alpha})$及其时间导数的表达式, 即

式中, $\boldsymbol{s}^\alpha$和$\boldsymbol{m}^\alpha$分别为当前构型$\mathfrak{B}$中第$\alpha$个滑移系的滑移方向、滑移面法线方向.

晶体塑性理论认为各滑移系的滑移导致了整体的塑性变形, 因此将塑性速度梯度张量$\boldsymbol{L}^p$表示为

式中, $\dot{\gamma}^\alpha$为第$\alpha$个滑移系的滑移剪切应变率, $\otimes$为张量并积符号, $N$为滑移系的个数, 对于面心立方晶体$N=12$.

文献[24, 27]采用面心立方晶体的滑移系晶格矢量来描述晶体内部的3种微裂纹形式, 并将损伤引起的附加变形定义为3种微观裂纹引起的附加变形的叠加, 即认为其中的解理断裂发生在滑移面上. 对于本文所考虑的与晶体解理相关的张开型微观裂纹损伤模式, 可以通过滑移面法向张开变形来描述其附加影响, 于是将损伤速度梯度张量$\boldsymbol{L}^d$定义为

式中, $\dot{d}^\beta$为第$\beta$个滑移面的法向损伤应变率, $M$为滑移面的个数, 对于面心立方晶体$M=4$.

需要指出, 本文建立的损伤模型没有直接考虑另外两种微观裂纹形式对损伤附加变形的贡献, 但在下文式(11)所定义的损伤自由能中将滑移面滑移的影响考虑进来, 并通过其中的系数$\beta$来反映晶体滑移对损伤能量耗散的影响程度.

根据速度梯度张量$\boldsymbol{L}$可定义变形率张量$\boldsymbol{D}$与自旋率张量$\boldsymbol{W}$, 并对其作如下分解

将式(4)、式(5)代入式(6)可得

其中

$\begin{eqnarray*} \left.\begin{array}{ccl} \boldsymbol{P}^\alpha &=& (\boldsymbol{s}^\alpha \otimes \boldsymbol{m}^\alpha +\boldsymbol{m}^\alpha \otimes \boldsymbol{s}^\alpha)/2 \\ \boldsymbol{W}^\alpha &=& (\boldsymbol{s}^\alpha \otimes \boldsymbol{m}^\alpha -\boldsymbol{m}^\alpha \otimes \boldsymbol{s}^\alpha)/2 \\ \boldsymbol{M}^\beta &=& \boldsymbol{m}^\beta \otimes \boldsymbol{m}^\beta \end{array}\right\} \end{eqnarray*}$

式中, $\boldsymbol{D}^e$, $\boldsymbol{D}^p$, $\boldsymbol{D}^d$分别为弹性、塑性、损伤变形率张量, $\boldsymbol{W}^e$, $\boldsymbol{W}^p$, $\boldsymbol{W}^d$分别为弹性、塑性、损伤自旋率张量. 不难发现, $tr(\boldsymbol{D}^p)=0$, 这说明塑性应变为偏斜张量, 其不会引起体积变化; $tr(\boldsymbol{D}^d)\neq 0$, 这表示由微观裂纹引起的体积变化; $\boldsymbol{W}^d=\boldsymbol{0}$, 这说明损伤变形不会引起旋转效应. 对比经典晶体塑性理论中的相关方程, 损伤变形梯度张量$\boldsymbol{F}^d$的引入没有改变弹性、塑性下的变形率张量和自旋率张量的数学形式, 这也符合图1中对损伤变形梯度张量$\boldsymbol{F}^d$的假设.

材料经历不可逆的变形过程, 其内部结构会发生变化, 进而产生塑性应变、微观裂纹等, 因此损伤材料中Helmholtz自由能密度函数$\rho\varPsi$的值取决于应变状态、损伤程度和位错硬化结构等^[3]. 于是, 对于考虑损伤效应的等温过程, Helmholtz自由能密度函数$\rho\varPsi$可分为弹性、塑性、损伤3个部分^[26], 即

式中, $\rho$为材料密度, $\boldsymbol{\varepsilon}^e$为弹性应变张量, $\gamma$为累积剪切应变, $d$为累积损伤变量.

对于式(8)所示的自由能密度函数表达形式需要进行说明. 在经典的连续损伤力学中通常需要考虑损伤对弹性模量的折减作用. 但是在细观损伤模型中, 可以通过附加损伤应变来描述损伤的效果, 当损伤应变显著大于弹性应变时可以忽略损伤对弹性模量的影响^[24]. 在本文后续的计算结果也反映了$tr(\boldsymbol{\varepsilon}^d) \gg tr(\boldsymbol{\varepsilon}^e)$的现象, 因此本文忽略了损伤对弹性模量的影响.

损伤与塑性行为之间的耦合关系则较为复杂, 众多学者提出各种耦合模型. Al-Rub等^[28-29]在建立自由能时独立考虑了损伤与塑性的贡献部分, 并在推导的状态变量方程中体现了损伤与塑性的耦合关系. Balieu等^[30-31]在建立的损伤演化方程与塑性屈服方程中考虑了损伤与塑性对其的影响. 本文采用了法向附加变形来考虑解理型微观裂纹的影响, 因此假设损伤主要由法向分解正应力引起, 而该法向应力与控制滑移的切向分解剪应力同时产生, 于是认为损伤必然伴随着塑性行为, 即没有微观塑性就没有微观损伤, 故而在损伤自由能中引入了塑性滑移的影响. 同时从变形运动学考虑, 损伤附加变形的方向垂直于塑性滑移变形的方向, 因此假设损伤并不影响滑移, 进而在塑性自由能中不考虑损伤的影响.

弹性自由能密度函数$\rho\varPsi^e$可表示为弹性应变张量$\boldsymbol{\varepsilon}^e$的二次型, 即

式中, C为四阶弹性模量张量.

塑性自由能密度函数$\rho\varPsi^p$由累积剪切应变$\gamma$所决定, 并采用二次型的数学形式给出^[26], 即

其中

$\begin{eqnarray*} h(\gamma)=h_0+(h_\mathrm{s}-h_0)\tanh \left( \frac{k_\mathrm{h}\gamma}{h_\mathrm{s}-h_0} \right) \end{eqnarray*}$

式中, $R_0$为初始滑移阈值, $h(\gamma)$为非线性硬化模量, $k_\mathrm{h}$, $h_0$, $h_\mathrm{s}$分别为$h(\gamma)$的初始变化斜率、初始值、饱和值.

损伤自由能密度函数$\rho\varPsi^d$由累积损伤变量$d$、累积剪切应变$\gamma$所决定, 同样地以二次型给出^[26], 即

其中

$\begin{eqnarray*}H(d)=H_0+(H_\mathrm{s}-H_0)\tanh \left( \frac{k_\mathrm{H}d}{H_\mathrm{s}-H_0} \right) \end{eqnarray*}$

式中, $Y_0$为初始损伤阈值, $\beta$为损伤与塑性之间的半耦合系数, $H(d)$为非线性软化模量, $k_\mathrm{H}$, $H_0$, $H_\mathrm{s}$分别为$H(d)$的初始变化斜率、初始值、饱和值.

对自由能密度函数$\rho\varPsi$求偏导数, 可得到状态变量$(\boldsymbol{\varepsilon}^e,\gamma,d)$相对应的热力学广义力$(\boldsymbol{\sigma},R,Y)$, 即

式中, $R$为临界分解剪应力, $Y$为损伤阈值, 其中$\beta$体现了损伤与塑性之间的半耦合关系, 即$R$和$Y$均为关于$\gamma$和$d$的函数.

在实际计算过程中采用Hill等^[12]基于塑性构型$\mathfrak{B}_{2}$提出的Jaumann率形式本构方程, 并且考虑到临界分解剪应力$R$与损伤阈值$Y$均大于零, 于是采用式(13)替换式(12), 即

其中

$\left.\begin{array}{l}\mathop{}_{\sigma^{*}}^{\nabla}=\dot{\sigma}-W^{\mathrm{e}} \cdot \sigma+\sigma \cdot W^{\mathrm{e}} \\f_{1}(\gamma, d)=R_{0}+h \gamma+\frac{\gamma^{2}}{2} \frac{\partial h}{\partial \gamma}+H \beta(d+\beta \gamma) \\f_{2}(\gamma, d)=Y_{0}+H(d+\beta \gamma)+\frac{(d+\beta \gamma)^{2}}{2} \frac{\partial H}{\partial d}\end{array}\right\}$

式中, $\mathop{}_{\sigma^{*}}^{\nabla}$为Cauchy应力张量$\boldsymbol{\sigma}$基于塑性构型$\mathfrak{B}_{2}$的Jaumann导数, $\boldsymbol{I}$为二阶单位张量, $\langle\cdot\rangle$为Macauley括号, 即$\langle x\rangle=(x+|x|)/2$.

将式(13)中本构方程变换到当前构型$\mathfrak{B}$上可得

其中

$\left.\begin{array}{l}\mathop{}_{\sigma}^{\nabla}=\dot{\sigma}-W \cdot \sigma+\sigma \cdot W \\\lambda^{\alpha}=\mathcal{C}: \boldsymbol{P}^{\alpha}+\boldsymbol{W}^{\alpha} \cdot \sigma-\sigma \cdot \boldsymbol{W}^{\alpha} \\\zeta^{\beta}=\mathcal{C}: \boldsymbol{M}^{\beta}\end{array}\right\}$

式中, $\mathop{}_{\sigma}^{\nabla}$为Cauchy应力张量$\boldsymbol{\sigma}$基于当前构型$\mathfrak{B}$的Jaumann导数. 上式即为损伤耦合的本构方程, 因其法向损伤应变率$\dot{d}^\beta$的存在导致应力水平下降, 这反应了损伤导致材料力学性能的劣化.

下面建立屈服准则与损伤准则.

如图2所示, 分解剪应力$\tau$使滑移系产生面内滑移运动, 分解正应力$\sigma_\mathrm{n}$使滑移面产生法向张开运动. 于是根据Schmid定理, 第$\alpha$个滑移系的分解剪应力$\tau^\alpha$、第$\beta$个滑移面的分解正应力$\sigma^\beta_\mathrm{n}$分别定义为

考虑各向同性硬化效应, 将第$\alpha$个滑移系的塑性驱动力$f^\alpha_p$、第$\beta$个滑移面的损伤驱动力$f^\beta_d$定义为

式中, $R$为临界分解剪应力, $Y$为损伤阈值. 事实上, 塑性驱动力$f^\alpha_\mathrm{p}$为控制塑性滑移的屈服准则, 损伤驱动力$f^\beta_\mathrm{d}$为控制晶体解理的损伤准则.

从能量耗散的角度来建立塑性流动方程和损伤演化方程. 热力学第二定律揭示了不可逆热力学过程的熵增现象, 于是对于等温绝热的有限变形过程, 可采用Clausius-Duhem不等式给出其定量描述^[3], 即

将式(8)定义的自由能密度函数$\rho\varPsi(\boldsymbol{\varepsilon}^e,\gamma,d)$对时间求导可得

将式(18)代入式(17), 并利用式(6)、式(12)可得

由式(19)可知, 塑性和损伤效应导致非弹性能量减少, 因此可以建立一个屈服与损伤准则约束下的耗散势函数^[28], 即

式中, $\dot{\varLambda}^\alpha_p$和$\dot{\varLambda}^\beta_d$分别为塑性、损伤Lagrange乘子.

考虑到最大耗散原理, 即对于一组热力学广义力$(\boldsymbol{\sigma},R,Y)$要使耗散势函数$\varOmega$取最大值,于是利用函数取极值的必要条件可得

将式(19)、式(20)代入式(21)可得

对于率相关的材料常采用幂函数形式的Lagrange乘子^[3], 于是有

式中, $n_p$和$n_d$分别为塑性、损伤乘子的幂指数, $K_p$和$K_d$分别为塑性、损伤乘子中用于无量纲化的分母.

幂指数$n_p$和$n_d$可作为经验参数直接给定, 而$K_p$和$K_d$则需要根据试验数据进行标定.

于是将式(16)、式(23)代入式(22), 并利用式(7)、式(15)可得

式中, $\dot{\gamma}$和$\dot{d}$分别以率形式给出了塑性流动方程、损伤演化方程.

对于作用在滑移系上的细观应力, 即分解剪应力$\tau^\alpha$与分解正应力$\sigma^\beta_\mathrm{n}$, 也需要建立其率形式的表达式. 对式(15)求物质导数, 并利用损伤耦合的本构方程可得

其中

$\boldsymbol{\eta}^{\beta}=\boldsymbol{C}: \boldsymbol{M}^{\beta}-\boldsymbol{M}^{\beta} \cdot \boldsymbol{\sigma}-\boldsymbol{\sigma} \cdot \boldsymbol{M}^{\beta}$

式中, $\dot{\tau}^\alpha$与$\dot{\sigma}^\beta_\mathrm{n}$将用于数值计算方法中 Jacobian矩阵$\partial \Delta \boldsymbol{\sigma} \big/ \partial \Delta \boldsymbol{\varepsilon}$的推导.

通用有限元分析软件ABAQUS中允许用户通过$\textbf{U}ser\textbf{MAT}erial(UMAT)$子程序引入复杂的材料本构关系. 本文借助UMAT子程序中实现损伤耦合本构方程的数值计算过程, 并主要实现两个功能: 更新应力与状态变量、提供Jacobian矩阵$\partial \Delta \boldsymbol{\sigma} \big/ \partial \Delta \boldsymbol{\varepsilon}$.

基于文献[33]中的工作, 将细观损伤模型中的率形式方程等视作一系列非线性微分方程组, 并选取$\tau^\alpha$, $\gamma^\alpha$, $\gamma$, $\sigma^\beta_\mathrm{n}$, $d^\beta$, $d$作为一组状态变量, 即

式中, $\dot{\boldsymbol{\tau}}=\{ \dot{\tau}^\alpha \}_{N\times1}$, $\dot{\boldsymbol{\gamma}}=\{ \dot{\gamma}^\alpha \}_{N\times1}$, $\dot{\gamma}_{\mathrm{total}} = \sum\limits_{\alpha} | \dot{\gamma}^\alpha |$, $\dot{\boldsymbol{\sigma}}_\mathrm{n}=\{ \dot{\sigma}^\beta_\mathrm{n} \}_{M\times1}$, $\dot{\boldsymbol{d}}=\{ \dot{d}^\beta \}_{M\times1}$, $\dot{d}_{\mathrm{total}} = \sum\limits_{\beta} | \dot{d}^\beta |$.

式(28)中微分方程组的积分格式采用具有二阶精度的Euler型预估校正法, 即

式中, $\boldsymbol{x}_{n}$为增量步开始时刻$t_n$的状态变量, $\boldsymbol{x}_{n+1}$为增量步结束时刻的状态变量, $\Delta t$为时间增量.

在式(28)的迭代过程中, 其他变量取增量步开始$t_n$时刻的值. 当迭代结束后, 其他变量可根据其增量更新, 且增量可由$\Delta \gamma^\alpha$和$\Delta d^\beta$线性表出. 考虑到更新形式是固定的, 这里仅给出弹性应变与应力的更新式, 即

其中

$\begin{eqnarray*}\left.\begin{array}{ccl} \Delta \boldsymbol{\varepsilon}^e_n &=& \Delta \boldsymbol{\varepsilon}_n - \sum\limits_{\alpha} \boldsymbol{P}^\alpha_n \Delta \gamma^\alpha_n - \sum\limits_{\beta} \boldsymbol{M}^\beta_n \Delta d^\beta_n \\ \Delta \boldsymbol{\sigma}_n &=& C: \Delta \boldsymbol{\varepsilon}_n - \boldsymbol{\sigma}_n (\boldsymbol{I} : \Delta \boldsymbol{\varepsilon}^e_n) - \sum\limits_\alpha \boldsymbol{\lambda}^\alpha_n \Delta \gamma^\alpha_n - \sum\limits_{\beta} \boldsymbol{\zeta}^\beta_n \Delta d^\beta_n \end{array}\right\} \end{eqnarray*}$

式中, $\boldsymbol{P}^\alpha_n$, $\boldsymbol{M}^\beta_n$, $\boldsymbol{\lambda}^\alpha_n$, $\boldsymbol{\zeta}^\beta_n$均由$t_n$时刻的变量计算得到.

UMAT子程序在完成应力与状态变量的更新后, 还需提供Jacobian矩阵$\partial \Delta \boldsymbol{\sigma} \big/ \partial \Delta \boldsymbol{\varepsilon}$, ABAQUS利用每一个积分点的Jacobian矩阵生成结构整体的刚度矩阵, 用于判断结构整体是否达到平衡状态.

将损伤耦合的本构方程改写为增量形式可得

上式对$\Delta \boldsymbol{\varepsilon}$求偏导并采用ABAQUS中Voigt记法可得

其中

$\begin{eqnarray*} \left.\begin{array}{l} \sigma = \big[\sigma_{11},~\sigma_{22},~\sigma_{33},~\sigma_{12},~\sigma_{13},~\sigma_{23}\big]^{T} \\[3pt] \lambda^\alpha = \big[ \lambda^\alpha_{11},~\lambda^\alpha_{22},~\lambda^\alpha_{33},~\lambda^\alpha_{12},~\lambda^\alpha_{13},~\lambda^\alpha_{23} \big]^T \\[3pt] \zeta^\beta = \big[ \zeta^\beta_{11},~\zeta^\beta_{22},~\zeta^\beta_{33},~\zeta^\beta_{12},~\zeta^\beta_{13},~\zeta^\beta_{23} \big]^T \\[3pt] \dfrac{\partial \Delta \gamma^\alpha}{\partial \Delta \varepsilon} = \left[ \dfrac{\partial \Delta \gamma^\alpha}{\partial \Delta \varepsilon_{11}},~\dfrac{\partial \Delta \gamma^\alpha}{\partial \Delta \varepsilon_{22}},~\dfrac{\partial \Delta \gamma^\alpha}{\partial \Delta \varepsilon_{33}},~ \dfrac{\partial \Delta \gamma^\alpha}{2\partial \Delta \varepsilon_{12}},\\[3mm]\qquad \dfrac{\partial \Delta \gamma^\alpha}{2\partial \Delta \varepsilon_{13}},~\dfrac{\partial \Delta \gamma^\alpha}{2\partial \Delta \varepsilon_{23}} \right]^T \\[3mm] \dfrac{\partial \Delta d^\beta}{\partial \Delta \varepsilon} = \left[ \dfrac{\partial \Delta d^\beta}{\partial \Delta \varepsilon_{11}},~\dfrac{\partial \Delta d^\beta}{\partial \Delta \varepsilon_{22}},~\dfrac{\partial \Delta d^\beta}{\partial \Delta \varepsilon_{33}},~ \dfrac{\partial \Delta d^\beta}{2\partial \Delta \varepsilon_{12}}, \\[3mm]\qquad \dfrac{\partial \Delta d^\beta}{2\partial \Delta \varepsilon_{13}},~\dfrac{\partial \Delta d^\beta}{2\partial \Delta \varepsilon_{23}} \right]^T \end{array}\right\} \end{eqnarray*}$

式中, $\boldsymbol{C}$为二阶弹性模量张量, $\sigma$为一阶应力张量. 进一步将上述列阵存储在矩阵中, 即

$\left.\begin{array}{l}\lambda=\left[\begin{array}{cccc}\lambda_{11}^{(1)} & \lambda_{11}^{(2)} & \cdots & \lambda_{11}^{(N)} \\\lambda_{22}^{(1)} & \lambda_{22}^{(2)} & \cdots & \lambda_{22}^{(N)} \\\vdots & \vdots & \ddots & \vdots \\\lambda_{23}^{(1)} & \lambda_{23}^{(2)} & \cdots & \lambda_{23}^{(N)}\end{array}\right]_{6 \times N} \\\zeta=\left[\begin{array}{cccc}\zeta_{11}^{(1)} & \zeta_{11}^{(2)} & \cdots & \zeta_{11}^{(M)} \\\zeta_{22}^{(1)} & \zeta_{22}^{(2)} & \cdots & \zeta_{22}^{(M)} \\\vdots & \vdots & \ddots & \vdots \\\zeta_{23}^{(1)} & \zeta_{23}^{(2)} & \cdots & \zeta_{23}^{(M)}\end{array}\right]_{6 \times M}\end{array}\right\}$

$\left.\begin{array}{l}\frac{\partial \Delta \gamma}{\partial \Delta \varepsilon}=\left[\begin{array}{ccc}\frac{\partial \Delta \gamma^{(1)}}{\partial \Delta \varepsilon_{11}} & \frac{\partial \Delta \gamma^{(1)}}{\partial \Delta \varepsilon_{22}} & \cdots & \frac{\partial \Delta \gamma^{(1)}}{2 \partial \Delta \varepsilon_{23}} \\\frac{\partial \Delta \gamma^{(2)}}{\partial \Delta \varepsilon_{11}} & \frac{\partial \Delta \gamma^{(2)}}{\partial \Delta \varepsilon_{22}} \cdots & \frac{\partial \Delta \gamma^{(2)}}{2 \partial \Delta \varepsilon_{23}} \\\vdots & \vdots & \ddots & \vdots \\\frac{\partial \Delta \gamma^{(N)}}{\partial \Delta \varepsilon_{11}} & \frac{\partial \Delta \gamma^{(N)}}{\partial \Delta \varepsilon_{22}} & \cdots & \frac{\partial \Delta \gamma^{(N)}}{2 \partial \Delta \varepsilon_{23}}\end{array}\right]_{N \times 6}\\\frac{\partial \Delta d}{\partial \Delta \varepsilon}=\left[\begin{array}{cccc}\frac{\partial \Delta d^{(1)}}{\partial \Delta \varepsilon_{11}} & \frac{\partial \Delta d^{(1)}}{\partial \Delta \varepsilon_{22}} & \cdots & \frac{\partial \Delta d^{(1)}}{2 \partial \Delta \varepsilon_{23}} \\\frac{\partial \Delta d^{(2)}}{\partial \Delta \varepsilon_{11}} & \frac{\partial \Delta d^{(2)}}{\partial \Delta \varepsilon_{22}} & \cdots & \frac{\partial \Delta d^{(2)}}{2 \partial \Delta \varepsilon_{23}} \\\vdots & \vdots & \ddots & \vdots \\\frac{\partial \Delta d^{(M)}}{\partial \Delta \varepsilon_{11}} & \frac{\partial \Delta d^{(M)}}{\partial \Delta \varepsilon_{22}} & \cdots & \frac{\partial \Delta d^{(M)}}{2 \partial \Delta \varepsilon_{23}}\end{array}\right]_{M \times 6}\end{array}\right\}$

于是将式(32)改写为

其中

$\left.\begin{array}{l}\frac{\partial \operatorname{tr}(\Delta \boldsymbol{\varepsilon})}{\partial \Delta \boldsymbol{\varepsilon}}=[1,1,1,0,0,0]^{\mathrm{T}} \\\frac{\partial \operatorname{tr}\left(\Delta \boldsymbol{\varepsilon}^{\mathrm{d}}\right)}{\partial \Delta \boldsymbol{\varepsilon}}=\sum_{\beta=1}^{M} \operatorname{tr}\left(\boldsymbol{M}^{\beta}\right) \frac{\partial \Delta d^{\beta}}{\partial \Delta \boldsymbol{\varepsilon}} \approx \sum_{\beta=1}^{M} \frac{\partial \Delta d^{\beta}}{\partial \Delta \boldsymbol{\varepsilon}}\end{array}\right\}$

式中, ${\partial tr(\Delta \boldsymbol{\varepsilon}^d)}\big/{\partial \Delta \boldsymbol{\varepsilon}}$等价于将${\partial \Delta \boldsymbol{d}}\big/{\partial \Delta \boldsymbol{\varepsilon}}$沿列求和得到的向量. 在变形过程中近似认为$\|\boldsymbol{m}^\beta\|\approx 1$, 于是有$tr(\boldsymbol{M}^\beta)\approx1$. 不难发现, $\{\sigma\}\otimes\{\partial tr(\Delta \boldsymbol{\varepsilon})\big/{\partial \Delta \boldsymbol{\varepsilon}}\}$为非对称矩阵, 于是Jacobian矩阵$\partial \Delta \boldsymbol{\sigma} \big/ \partial \Delta \boldsymbol{\varepsilon}$也为非对称矩阵.

在式(33)中$\partial \Delta \boldsymbol{\gamma} \big/ \partial \Delta \boldsymbol{\varepsilon}$与$\partial \Delta \boldsymbol{d} \big/ \partial \Delta \boldsymbol{\varepsilon}$仍是未知的, 因此还需得到这两个矩阵的具体表达式. 采用文献[34]中的线性内插法可得

式中, 参数$\theta$一般取$0.5$. 将式(13)定义的热力学广义力$(R,Y)$与式(27)中滑移系细观应力$(\tau^\alpha,\sigma^\beta_\mathrm{n})$的率形式方程代 入式(34)可得

即有

其中

$\left.\begin{array}{l}\tilde{A}_{\alpha_{1} \alpha_{2}}=\delta_{\alpha_{1} \alpha_{2}}+\theta \Delta t \frac{\partial \gamma^{\alpha_{1}}}{\partial \tau^{\alpha_{1}}}\left(\lambda^{\alpha_{1}} \cdot \boldsymbol{P}^{\alpha_{2}}\right)-\\\theta \Delta t \frac{\partial \dot{\gamma}^{\alpha_{1}}}{\partial R} \frac{\partial \Delta R}{\partial \Delta \gamma} \operatorname{sign}\left(\dot{\gamma}^{\alpha_{2}}\right) \\\tilde{B}_{\alpha_{1} \beta_{2}}=\theta \Delta t \frac{\partial \dot{\gamma}^{\alpha_{1}}}{\partial \tau^{\alpha_{1}}}\left(\lambda^{\alpha_{1}} \cdot \boldsymbol{M}^{\beta_{2}}-\tau^{\alpha_{1}}\right)-\\\theta \Delta t \frac{\partial \dot{\gamma}^{\alpha_{1}}}{\partial R} \frac{\partial \Delta R}{\partial \Delta d} \operatorname{sign}\left(\dot{d}^{\beta_{2}}\right)\\\tilde{C}_{\alpha_{1} j}=\theta \Delta t \frac{\partial \dot{\gamma}^{\alpha_{1}}}{\partial \tau^{\alpha_{1}}}\left[\left\{\lambda^{\alpha_{1}}\right\}_{j}-\tau^{\alpha_{1}}\left\{\frac{\partial \operatorname{tr}(\Delta \boldsymbol{\varepsilon})}{\partial \Delta \boldsymbol{\varepsilon}}\right\}_{j}\right]\\\tilde{D}_{\beta_{1} \alpha_{2}}=\theta \Delta t \frac{\partial \dot{d}^{\beta_{1}}}{\partial \sigma_{n}^{\beta_{1}}}\left(\eta^{\beta_{1}} \cdot \boldsymbol{P}^{\alpha_{2}}\right)-\\\theta \Delta t \frac{\partial \dot{d}^{\beta_{1}}}{\partial Y} \frac{\partial \Delta Y}{\partial \Delta \gamma} \operatorname{sign}\left(\dot{\gamma}^{\alpha_{2}}\right)\\\tilde{E}_{\beta_{1} \beta_{2}}=\delta_{\beta_{1} \beta_{2}}+\theta \Delta t \frac{\partial \dot{d}^{\beta_{1}}}{\partial \sigma_{\mathrm{n}}^{\beta_{1}}}\left(\eta^{\beta_{1}} \cdot \boldsymbol{M}^{\beta_{2}}-\sigma_{\mathrm{n}}^{\beta_{1}}\right)-\\\theta \Delta t \frac{\partial \dot{d}^{\beta_{1}}}{\partial Y} \frac{\partial \Delta Y}{\partial \Delta d} \operatorname{sign}\left(\dot{d}^{\beta_{2}}\right)\\\tilde{F}_{\beta_{1} j}=\theta \Delta t \frac{\partial \dot{d}^{\beta_{1}}}{\partial \sigma_{\mathrm{n}}^{\beta_{1}}}\left[\left\{\eta^{\beta_{1}}\right\}_{j}-\sigma_{\mathrm{n}}^{\beta_{1}}\left\{\frac{\partial \operatorname{tr}(\Delta \boldsymbol{\varepsilon})}{\partial \Delta \boldsymbol{\varepsilon}}\right\}_{j}\right]\end{array}\right\}$

$\left.\begin{array}{l}\eta^{\beta}=\left[\eta_{11}^{\beta}, \eta_{22}^{\beta}, \eta_{33}^{\beta}, \eta_{12}^{\beta}, \eta_{13}^{\beta}, \eta_{23}^{\beta}\right]^{\mathrm{T}}\\\boldsymbol{P}^{\alpha}=\left[P_{11}^{\alpha}, P_{22}^{\alpha}, P_{33}^{\alpha}, 2 P_{12}^{\alpha}, 2 P_{13}^{\alpha}, 2 P_{23}^{\alpha}\right]^{\mathrm{T}}\\\boldsymbol{M}^{\beta}=\left[M_{11}^{\beta}, M_{22}^{\beta}, M_{33}^{\beta}, 2 M_{12}^{\beta}, 2 M_{13}^{\beta}, 2 M_{23}^{\beta}\right]^{\mathrm{T}}\end{array}\right\}$

式中, $\delta_{ij}$为Kronecker符号, 即$i=j$时$\delta_{ij}=1$, $i \neq j$时$\delta_{ij}=0$, 且计算过程中各个状态变量均采用增量步结束时的值.

综上, 根据式(36)计算得到矩阵$\partial \Delta \boldsymbol{\gamma} \big/ \partial \Delta \boldsymbol{\varepsilon}$与$\partial \Delta \boldsymbol{d} \big/ \partial \Delta \boldsymbol{\varepsilon}$, 然后将其代入式(33), 便可得Jacobian矩阵$\partial \Delta \boldsymbol{\sigma} \big/ \partial \Delta \boldsymbol{\varepsilon}$, 在这个过程中需要求解6个$(N+M)$阶线性方程组.

在上述建立的细观损伤模型中包含若干材料细观参数, 其中一些参数可以通过单晶材料的常规试验获得, 但是大部分参数并不能通过试验直接获取, 需要采用间接的方法进行标定. 常用的一种方法是通过比对有限元模拟和试验得到的应力应变曲线来给出合适的参数值. 于是, 将待标定的材料参数作为设计变量, 并建立一个目标函数用于定量地描述两条应力应变曲线之间的差距, 那么材料参数的标定就变成了对于目标函数求极小值的最优化问题, 这就实现了参数的逆向识别^[35].

有限元模拟得到的应力应变曲线来自于单晶铜RVE的单轴拉伸过程, 试验得到的应力应变曲线来自于文献[36]中单晶铜^[100]取向的单轴拉伸过程. 为了保证模拟和试验中晶体取向的一致性, 使有限元计算中晶体局部坐标系与全局坐标系重合, 即两个坐标系不发生相对转动.

如图3所示, 有限元模拟中的RVE为$0.1~\mathrm{mm}\times0.1~\mathrm{mm}\times0.1~\mathrm{mm}$的正方体, 并沿其3个边长方向等分为5份, 共计得到125个C3D8网格单元. 位移载荷使整个加载端面沿着$z$轴正方向平移, 且$u_z=0.02~\mathrm{mm}$, 边界条件为$u^{ABCD}_z=u^A_x=u^A_y=u^B_x=0$.

本文采用文献[34]中的单晶铜材料, 并给出细观损伤模型的基本材料参数, 弹性常数$C_{11}$, $C_{12}$, $C_{44}$分别为168.4 GPa, 121.4 GPa, 75.4 GPa, 塑性指数$n_{\rm p}$为10, 损伤指数$n_{\rm d}$为10.

单晶弹性常数可以通过试验测得, 塑性流动指数$n_\mathrm{p}$与损伤演化指数$n_\mathrm{d}$作为幂指数被引入到式(24)、式(25)中, 用于描述模型的率相关特性, 且这两个参数在一定范围内影响较小. 将这些量作为基本材料参数可以减少参数标定过程的计算量.

除基本材料参数外, 将待标定的11个材料参数列出, 即

为了标定式(37)中的11个参数, 采用最优化的思想, 使用粒子群优化(particle swarm optimization, PSO)算法进行求解, 并最终给出了标定结果, 即

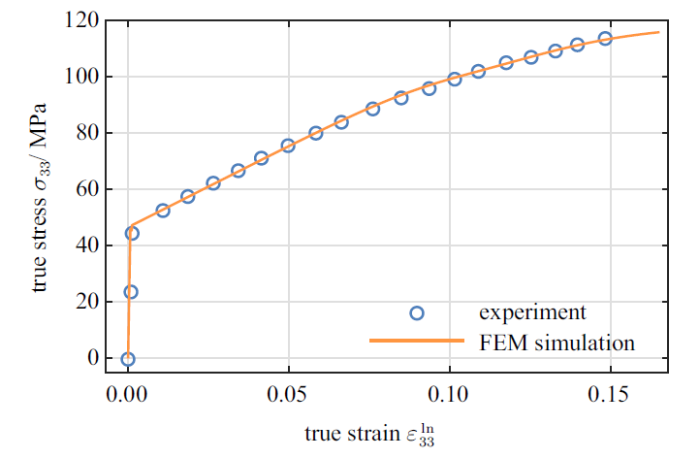
为了验证该标定方法所给出的材料参数的可靠性, 将上式中的标定结果用于有限元计算中, 图4给出了有限元计算结果与试验结果^[36]的对比.

结果表明, 根据标定结果给出的计算曲线与试验曲线一致, 说明了标定方法的可行性和适用性.

本节以单晶铜材料为例, 其材料参数按式(38)取值, 通过RVE单轴拉伸有限元模拟, 从细观尺度进行了塑性与损伤分析, 以说明本文理论模型的合理性.

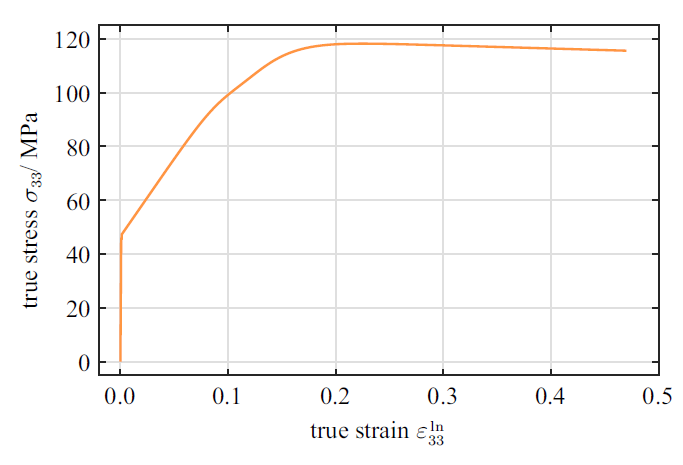
下面选取[001]加载取向, 研究分析单晶铜RVE在单轴拉伸载荷下的塑性流动与损伤演化规律. 有限元计算所采用图3中的模型, 位移载荷$u_z=0.06~\mathrm{mm}$.

如图5所示, 在单轴拉伸过程中应力应变曲线经历了线性、屈服、硬化、下降4个阶段, 这表明本文提出的细观损伤模型能够很好地描述金属材料的宏观单轴拉伸力学响应.

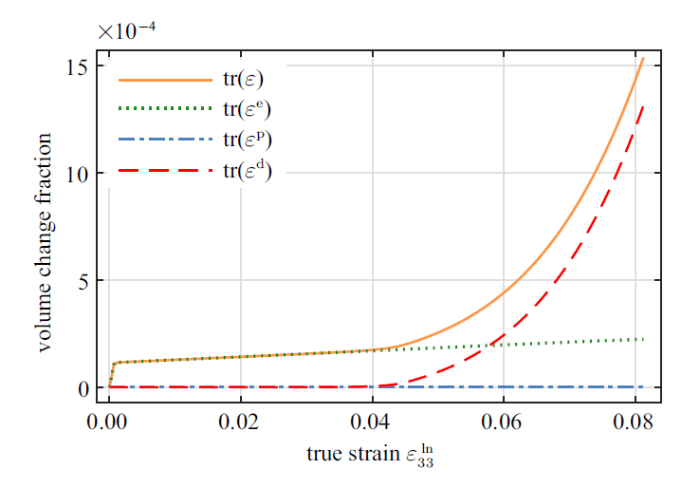
对于单轴拉伸过程中的体积变化, 可以用应变张量$\boldsymbol{\varepsilon}$的迹来描述, 并且考虑到式(6)中加法分解形式, 不难得到体积变化的分解, 即

式中, 塑性体积变化$tr(\boldsymbol{\varepsilon}^p)=0$, 这是由塑性变形率张量$\boldsymbol{D}^p$的定义所决定的. 于是, 单轴拉伸过程中的体积变化可分为可恢复的弹性体积变化$tr(\boldsymbol{\varepsilon}^e)$与微裂纹引起的损伤体 积变化$tr(\boldsymbol{\varepsilon}^d)$两个部分, 图6给出了单轴拉伸过程中体积变化分解.

在单轴拉伸过程中弹性体积变化$tr(\boldsymbol{\varepsilon}^e)$在屈服之前迅速增长, 当材料屈服后弹性体积变化$tr(\boldsymbol{\varepsilon}^e)$以较低的线性增长速率继续增大. 随着载荷的进一步加大, 在$\varepsilon_{33}^{\mathrm{ln}}>0.04$后损伤体积变化$tr(\boldsymbol{\varepsilon}^d)$快速增大, 并逐渐占据体积变化的主导地位. 同时,有限元计算结果也显示塑性体积变化$tr(\boldsymbol{\varepsilon}^p)$始终为零.

如图7所示, 可以通过滑移系上的细观状态变量来分析塑性流动与损伤演化规律.

图7(a)给出了第1个滑移系的分解剪应力$\tau^{(1)}$、临界分解剪应力$R$以及累积剪切应变$\gamma$的变化过程. 由图可知, 分解剪应力$\tau^{(1)}$与临界分解剪应力$R$同步增大, 两者的差值几乎保持不变, 这就意味着滑移剪切应变率$\dot{\gamma}^{(1)}$为定值, 对于另外11个滑移系的滑移剪切应变率也可以得出类似的结论, 因此累积剪切应变$\gamma$保持线性增长.

图7(b)给出了第1个滑移面的分解正应力$\sigma^{(1)}_\mathrm{n}$、损伤阈值$Y$以及累积损伤变量$d$的变化过程. 由图可知, 分解正应力$\sigma^{(1)}_\mathrm{n}$增大的同时损伤阈值$Y$迅速减小至零, 两者的差值越来越大, 这就意味着法向损伤应变率$\dot{d}^{(1)}$单调递增, 对于另外3个滑移面的法向损伤应变率也可以得出类似的结论,因此累积损伤变量$d$是接近指数上升的.

对比图7(a)和图7(b)两图可知, 累积损伤变量$d$在$\varepsilon_{11}^{\mathrm{ln}}>0.1$后迅速累积增大, 考虑到式(13)定义的临界分解剪应力$R$, 累积损伤变量$d$的增大会导致临界分解剪应力$R$的减小, 因此临界分解剪应力$R$在$\varepsilon_{11}^{\mathrm{ln}}>0.1$后呈现减缓增大的趋势.

基于晶体塑性理论的基本原理, 针对晶体解理型损伤的问题,引入了损伤变形梯度张量$\boldsymbol{F}^d$的概念, 提出了考虑滑移面分解正应力的细观损伤模型, 建立了相应的数值计算方法, 完成了材料的细观参数标定, 并采用所建模型进行了单晶RVE单轴拉伸的模拟与分析. 主要结论如下:

(1) 本文提出的细观损伤模型中, 塑性驱动力控制滑移面内剪切变形产生不可逆塑性变形, 损伤驱动力控制晶体解理产生张开型裂纹, 并考虑了塑性与损伤之间的半耦合作用关系, 能够很好地描述考虑晶体解理型损伤的材料细观失效机理.

(2) 基于粒子群优化算法, 完成了细观损伤模型中材料参数的标定方法. 该方法具有适应性好、无需梯度信息等优点, 能够很好地进行多个材料参数的统一标定, 并且标定效果良好.

(3) RVE的单轴拉伸过程表明, 本文模型能够很好地描述金属材料单轴拉伸过程的宏观力学响应, 即表现为应力应变曲线的线性、屈服、硬化、下降4个阶段. 从细观尺度来看, 损伤体积变化$tr({\varepsilon}^d)$随着载荷的增大而逐渐占据主导地位, 塑性累积是接近线性增长的, 损伤累积近乎是指数上升的, 且塑性累积的相对速度是低于损伤累积的相对速度.

本文研究工作主要建立了考虑晶体解理型微观裂纹损伤模式的细观损伤模型, 包括理论框架、数值实现和参数标定, 并初步验证了本文模型的合理性与有效性. 在后续研究中, 尚有大量工作需要开展, 例如单晶体的原位拉伸试验与分析、多晶体的损伤模型、考虑滑开型与撕开型裂纹的晶体损伤模型等.