引言
自然界是人类灵感的重要来源, 人们在研究各色各样的生物时获得了很多有益的启发[1 -3 ] . 在人造飞行器的发展历程中, 人们从擅于飞翔的鸟类身上获得了多种启示[4 ] . 对于鸟类的研究初期主要从生物学的角度出发, 随着观察和分析的深入, 逐渐认识到其中的空气动力学奥秘[5 ] . 北美金鸻鸟连续飞行跨越4000 km的大洋每小时仅仅损失其体重的0.06%[6 ] ; 飞行冠军信天翁可以不用拍动翅膀长时间翱翔于海面之上[7 ] . 鸟类如此高效的飞行必然离不开其表面极低的飞行阻力. 经过了千万年的进化, 鸟类形成了带弯度的厚前缘和薄后缘的翅膀. 现代飞机机翼的形状正是由此仿生而来. 但构成鸟翅膀表面的羽毛与构成机翼的蒙皮重要的区别之一是羽毛非常柔软且有弹性, 气动力存在脉动时可以发生局部变形. 由致密的覆羽层叠而成的翅膀厚前缘处, 柔性特征尤为显著. 那么, 鸟羽的这种柔性特征是否有利于减阻正是本文研究的出发点.
关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键.
鸟类或者飞行器是在空气中飞行, 而以往的研究主要以海豚生存环境中的水为流动介质. 另外, 虽然已经发展了各向异性柔性壁面的线性稳定性理论[30 ] , 但由于有限长度、边界层厚度增大等因素不可避免地与真实情况有出入, 而数值模拟则可以提供更加符合实际的结果. 鉴于此, 本文基于格心型有限差分方法数值求解描述空气运动的可压缩N-S方程, 研究了在各向异性的柔性壁面上, 亚音速边界层转捩初期T-S波的演化特征以及参数的影响规律, 以期为边界层的层流控制提供一定的参考价值.
1 研究模型及数值方法
1.1 计算模型
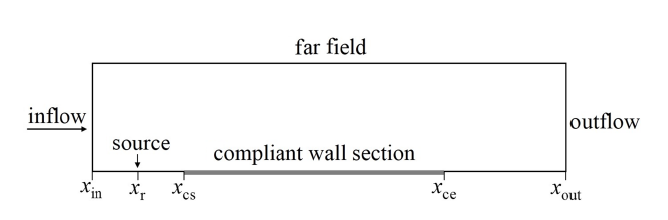
图1 中给出了本文所研究问题的计算域示意图. 基本流动为平板上某一段长度区间$[x_{\rm in} ,x_{\rm out} ]$内的边界层流动, 通过在$x_{\rm r} $位置处施加扰动来激发边界层中的T-S波. T-S波激发后先经过一段刚性壁面区间$[x_{\rm r} ,x_{\rm cs} ]$, 然后经过柔性壁面段$[x_{\rm cs} ,x_{\rm ce} ]$, 再回到刚性壁面最后到达出口位置$x_{\rm out} $.
图1
图1
计算域示意图
Fig.1
Schematic of computational domain
计算中采用施加扰动位置$x_{\rm r} $处边界层的位移厚度$\delta_{0}$为参考长度, 无量纲化的计算域高度为50, 沿流向的无量纲位置参数如表1 所示.
本文研究所采用的柔性壁面模型如图2 所示. 壁面为薄的弹性平板, 由倾斜的弹簧$\!-\!$杠杆臂支撑, 其中杠杆臂与水平面的夹角定义为$\theta $. 壁面的位移变形由杠杆臂与壁面相连端的转动决定, 分解可得到水平和垂直方向上的变形分量. 特别地, 当$\theta =0^{\circ }$时, 弹簧垂直支撑平板, 此时壁面仅在垂直方向上变形; 当$\theta =90^{\circ }$时, 杠杆臂垂直支撑平板, 此时壁面仅在水平方向上变形. 可以想象除特殊角度外, 流体从左往右流过壁面和反方向流过壁面引起的壁面变形是不同的, 对流动的影响自然也是不一样的, 因此这样的壁面被称作是各向异性的. 反过来, 如果来流方向对结果没有影响, 则这样的壁面被称作是各向同性的, 比如$\theta =0^{\circ }$或$\theta =90^{\circ }$时.
图2
图2
各向异性柔性壁面模型示意图
Fig.2
Schematic of the anisotropic compliant wall model
1.2 控制方程及边界条件
对于空气的运动, 采用二维的可压缩N-S方程来描述, 其无量纲的守恒形式如下
(1) $\begin{eqnarray} \label{eq1} \dfrac{\partial { U}}{\partial t}+\dfrac{\partial { E}_{\rm c}}{\partial x}+\dfrac{\partial { F}_{\rm c}}{\partial y}=\dfrac{1}{Re}\left( {\dfrac{\partial { E}_{\rm v}}{\partial x}+\dfrac{\partial { F}_{\rm v}}{\partial y}} \right) \end{eqnarray}$
式中, ${ U}$是守恒变量, ${ E}_{\rm c} $和${ E}_{\rm v} $是$x$方向上的对流通量和黏性通量, ${ F}_{\rm c} $和${ F}_{\rm v} $是$y$方向上的对流通量和黏性通量. 其具体形式如下
(2) $\left.\begin{array}{l}\boldsymbol{U}=\left(\begin{array}{c}\rho \\\rho u \\\rho v \\\rho e\end{array}\right), \boldsymbol{E}_{\mathrm{c}}=\left(\begin{array}{c}\rho u \\\rho u^{2}+p \\\rho v u \\(\rho e+p) u\end{array}\right), \boldsymbol{F}_{\mathrm{c}}=\left(\begin{array}{c}\rho v \\\rho u v \\\rho v^{2}+p \\(\rho e+p) v\end{array}\right) \\\boldsymbol{E}_{\mathrm{v}}=\left(\begin{array}{c}0 \\\tau_{x x} \\\tau_{x y} \\u \tau_{x x}+v \tau_{x y}-q_{x}\end{array}\right), \boldsymbol{F}_{\mathrm{v}}=\left(\begin{array}{c}0 \\\tau_{y x} \\\tau_{y y} \\u \tau_{y x}+v \tau_{y y}-q_{y}\end{array}\right)\end{array}\right\}$
式中, $\rho ,u,v,e,p$分别是气体的密度、$x$方向速度、$y$方向速度、总能和压力. $\tau_{xx} ,\tau_{xy} ,\tau_{yx} ,\tau_{yy} $是黏性应力, $q_{x} ,q_{y} $是热流量. 为了封闭方程组, 还需要补充理想气体的状态方程, 其无量纲形式为
(3) $\begin{eqnarray} \label{eq3} p=\dfrac{\rho T}{\gamma Ma^{2}} \end{eqnarray}$
如前面所提到的, 无量纲化N-S方程所采用的参考长度是扰动施加位置$x_{\rm r} $处的边界层位移厚度$\delta_{0} $, 其余参考值均取自由来流值. 在本文的设置下, 来流的马赫数为$Ma={U_{\infty }}/{c_{\infty }}=0.2$, 雷诺数定义为$Re={\rho_{\infty } U_{\infty } \delta_{0}}/{\mu_{\infty }}=400$.
对于图2 中所示的柔性壁面, 文献[30 ]中给出了其运动的控制方程. 采用与流动方程一致的参考量, 无量纲化后的壁面运动控制方程为
(4) $\begin{eqnarray} \label{eq4} &&C_{\rm m} \dfrac{\partial^{2}\eta }{\partial^{2}t}+C_{\rm d} \dfrac{\partial \eta }{\partial t}+C_{\rm B} \dfrac{\partial^{4}\eta }{\partial^{4}x}\cos^{2}\theta -\\&&\qquad C_{\rm T} \dfrac{\partial^{2}\eta }{\partial^{2}x}\sin^{2}\theta +C_{\rm k} \eta =f_{\rm w}\\ &&f_{\rm w} =\left( {-p_{\rm w}' +\tau_{yy}' } \right)\cos \theta +\tau_{xy}' \sin \theta \end{eqnarray}$
式中, $\eta $是壁面在垂直杠杆臂方向上的位移, 其正方向如图2 中箭头所示; $C_{\rm m} ,C_{\rm B} ,C_{\rm T}$分别是平板的质量密度、刚度和张力; $C_{\rm d} ,C_{\rm k} $则对应了支撑弹簧的阻尼和弹性系数. $f_{\rm w} $是垂直于杠杆臂方向上壁面所受到的力, 包括法向的压力和黏性正应力, 切向的黏性切应力.
计算域入口处对应于平板前缘之后$x_{\rm in} $位置处的边界层流动剖面, 可通过Blasius相似解或者数值计算一个平板边界层流动, 然后截取该位置处的变量指定到入口边界处. 出口处变量均采用外插的形式, 以速度$u$为例, 可表示为
(5) $\begin{eqnarray} \label{eq5} u_{\rm out} =u_{\rm interior} \end{eqnarray}$
如此处理简单且可以较好地避免出口反射的问题. 计算域上边界采用远场Riemann边界条件[31 ] . 下边界为绝热壁面, 刚性段$[x_{\rm in} ,x_{\rm cs} ]$和$[x_{\rm ce} ,x_{\rm out} ]$壁面速度采用无滑移条件, 参照文献[30 ], 柔性段壁面速度与壁面位移相关联, 即
(6) $\begin{eqnarray} \label{eq6} \left. \begin{array}{l} u_{\rm w} =\dfrac{\partial \eta }{\partial t}\sin \theta -\eta \dfrac{\partial \bar{{u}}}{\partial y}\cos \theta \\ v_{\rm w} =\dfrac{\partial \eta }{\partial t}\cos \theta \\ \end{array}, \ \ x\in \left( {x_{\rm cs} ,x_{\rm ce}} \right)\right\} \end{eqnarray}$
式中, $\bar{{u}}$是平均流向速度, 可通过求解刚性壁面上的Blasius方程获得.
扰动源$x_{\rm r} $位置处添加随时间以正弦函数形式变化的周期法向吹吸速度, 用来激发边界层中相同频率的T-S波, 扰动的表达式为
(7) $\begin{eqnarray} \label{eq7} v_{\rm w} =A\sin \left( {\omega t} \right), \ \ x=x_{\rm r} \end{eqnarray}$
式中, $\omega $是扰动的频率, $A$是扰动的幅值.
1.3 数值方法
N-S方程的数值求解采用半离散的形式, 即先求空间导数项, 再进行时间上的推进. 空间离散采用基于结构网格的格心有限差分方法[32 ] , 该套方法和程序已应用在其他湍流计算问题中[33 -35 ] . 以$x$方向上的通量导数求解为例, 具体步骤如下:
(1) 基于格心处已知的流场原始变量值利用五阶迎风线性格式重构出面心处的原始变量值的左迎风值和右迎风值$Q^{\rm L} $, $Q^{\rm R}$, 其中$Q=\{\rho ,u,v,p\}$;
(2)在面心处利用Roe方法求解当地的黎曼问题从而获得面心处的对流通量${ E}_{\rm c} \left( {Q^{\rm L},Q^{\rm R}} \right)$, 黏性通量没有迎风特性, 可直接由中心值得到, 即${ E}_{\rm v} \left( {\left( {Q^{\rm L}+Q^{\rm R}} \right)/2} \right)$;
(3)通过二阶中心差分得到格心处的通量导数${{\partial { E}_{\rm c}}/{\partial x}}$和${{\partial { E}_{\rm v}}/{\partial x}}$.
至此, 空间离散完成, 得到了控制体上的净通量. 时间推进采用隐式求解中常用的LU-SGS迭代方法.
对于壁面运动控制方程的离散, 时间项采用二阶向后差分, 即
(8) $\left( {\dfrac{\partial^{2}\eta }{\partial t^{2}}} \right)_{i} =\dfrac{\eta _{i}^{m+1} -2\eta_{i}^{n} +\eta_{i}^{n-1}}{\Delta t^{2}}$
(9) $\left( {\dfrac{\partial \eta }{\partial t}} \right)_{i} =\dfrac{3\eta _{i}^{m+1} -4\eta_{i}^{n} +\eta_{i}^{n-1}}{2\Delta t}$
(10) $\left( {\dfrac{\partial^{2}\eta }{\partial x^{2}}} \right)_{i} =\dfrac{\eta _{i+1}^{m+1} -2\eta_{i}^{m+1} +\eta_{i-1}^{m+1}}{\Delta x^{2}}$
(11) $\left( {\dfrac{\partial^{4}\eta }{\partial x^{4}}} \right)_{i} =\dfrac{\eta _{i+2}^{m+1} -4\eta_{i+1}^{m+1} +6\eta_{i}^{m+1} -4\eta_{i-1}^{m+1} +\eta _{i-2}^{m+1}}{\Delta x^{4}}$
理论上当迭代次数$m\to \infty $时, $\eta^{m+1}\to \eta^{n+1}$. 在每个实时间步内, 流体方程和结构方程交替求解多次, 直至两者的残差都下降4个量级以上视为收敛.
1.4 数值方法验证
合理地产生T-S波并正确地模拟其在空间上的演化特征是开展研究的必要前提, 因此首先对全为刚性壁面的情形进行模拟, 并将数值结果与线性稳定性理论以及前人的数值结果进行对比来验证程序的可靠性.
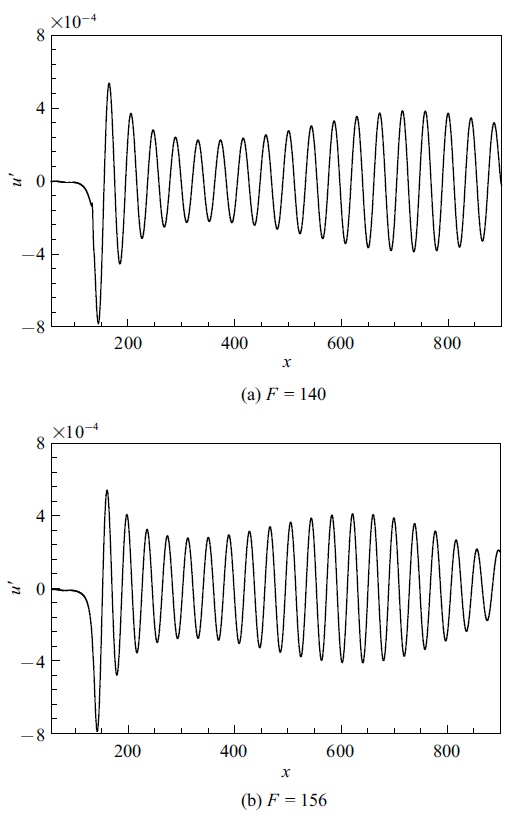
这里考虑两个不同频率的T-S波, 其对应扰动源处的无量纲频率参数为$F_{1} =({\omega_{1}}/{Re})\times 10^{6}=140$和$F_{2} =({\omega_{2}}/{Re})\times 10^{6}=156$. 扰动的幅值取$A_{1} =A_{2} =0.001$, 即自由来流的千分之一. 计算网格在$x$方向上均匀分布, 在$y$方向从壁面进行拉伸, 网格单元总数为$800\times 80$. 时间步长取为T-S波周期的1/500, 总共计算20个周期.
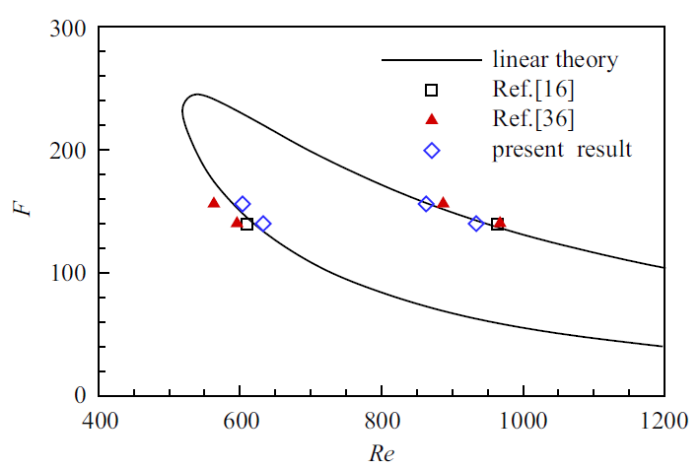
图3 中给出了沿着$y=0.65$位置的流向脉动速度的空间分布. 可以看到, 在扰动源的下游, 短暂过渡之后, 脉动速度的分布就已经呈现出了很好的规律性, 以变幅度的正弦波形式向下游传播. 在两个频率对应的结果中, 扰动产生后幅值均先下降再增长最后又下降. 幅值变化趋势改变的位置称为中性点, 图4 对比了本文计算得到的中性点位置与线性理论以及Wang等[16 ] 和Fasel等[36 ] 的计算结果. 图中``拇指''曲线是由线性稳定性理论给出的中性曲线, 该曲线从文献[16 ]中得到. 可以看到本文结果与线性稳定性理论得到的结果符合得很好. 图3 和图4 的结果表明本文所采用的数值方法对于T-S波空间演化的模拟是可靠的.
图3
图3
$y=0.65$位置处的流向脉动速度空间分布
Fig.3
Distribution of streamwise velocity fluctuation along $y=0.65$
图4
图4
计算与线性稳定性理论获得的中性点位置对比
Fig.4
Comparison of neutral points obtained from computations and linear stability theory
2 柔性壁上T-S波的演化特征
2.1 壁面柔性对T-S波演化的影响
首先给出柔性壁面上二维T-S波空间演化的特征, 并与刚性壁面上的结果进行对比, 以此来研究壁面的柔性特征对T-S波演化的影响. 本节中扰动源处的频率和幅值为上一节中的$\omega_{2} $和$A_{2} $. 网格和计算设置与第一节中相同, 时间步长取T-S波周期的1/1000, 总计算时长为20个周期. 柔性壁面的参数选择具有一定的任意性, 本文选取的一组参数为$C_{\rm m} =1$, $C_{\rm d} =0.1$, $C_{\rm B} =2.5$, $C_{\rm T} =12.5$, $C_{\rm k} =0.05$, 杠杆臂的倾角$\theta =30^{\circ }$.
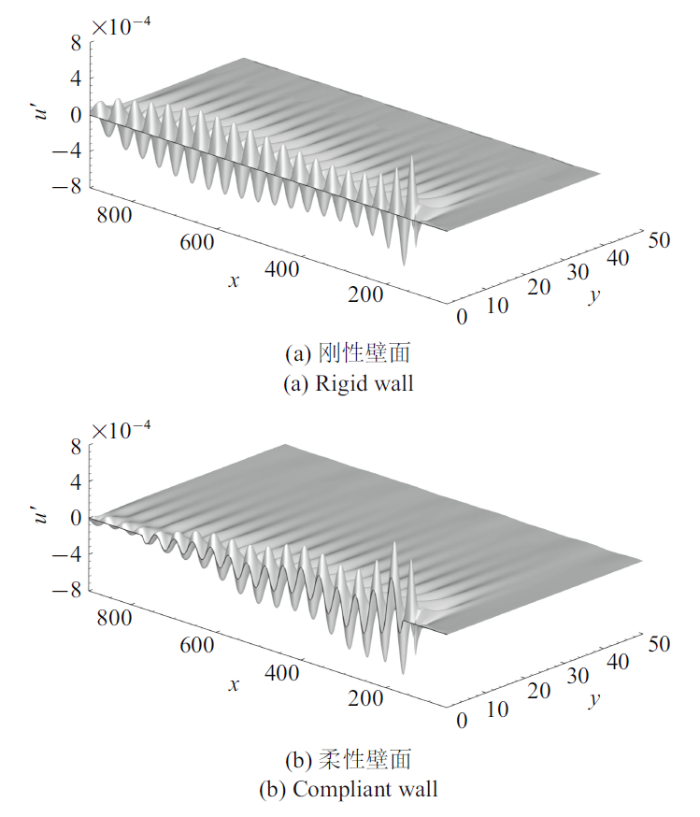
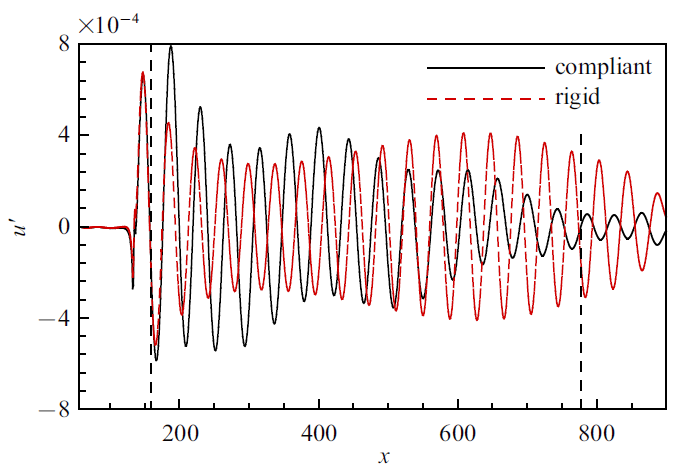
图5 给出了刚性壁面和柔性壁面上整个二维空间中的流向脉动速度分布. 如图中粗线所示, 刚性壁面处的脉动速度为零, 而柔性壁面段由于壁面运动, 壁面处的脉动速度并不为零. 此外, 从脉动的峰值来看, 流动从刚性段进入柔性段后脉动峰值变大, 脉动变强, 而往下游发展之后, 柔性段上的扰动峰值衰减得相比刚性段上衰减得更快, 出口附近的脉动幅值已经明显小得多. 图6 中给出了$x=200$, 400, 600位置处的脉动速度剖面. 可以看到在刚性壁面上, 脉动从壁面处的零值开始增长, 在壁面附近达到最大/小值, 然后逐渐下降/增长到反方向的极值, 最后随着远离壁面趋近于零. 对于柔性壁面, 壁面处的脉动不为零, 而从壁面到远场的脉动变化规律与刚性壁面情况下类似. 为了定量地比较, 图7 中给出了峰值附近$y=0.65$位置上流向脉动速度沿$x$方向的变化. 柔性段前缘附近的脉动增强和后缘附近的脉动衰减的特征在图7 中十分明显. 图中竖直虚线标示了柔性段开始和结束的位置.
图5
图5
刚性和柔性壁面上的流向脉动速度空间分布
Fig.5
Spatial distribution of streamwise velocity fluctuation on rigid wall and compliant wall
图6
图6
刚性和柔性壁面上不同流向位置处的脉动速度剖面
Fig.6
Profiles of velocity fluctuation at various streamwise positions on rigid wall and compliant wall
图7
图7
柔性和刚性壁面上$y=0.65$处流向脉动速度的空间分布对比
Fig.7
Comparison of distribution of streamwise velocity fluctuation along $y=0.65$ on compliant wall and rigid wall
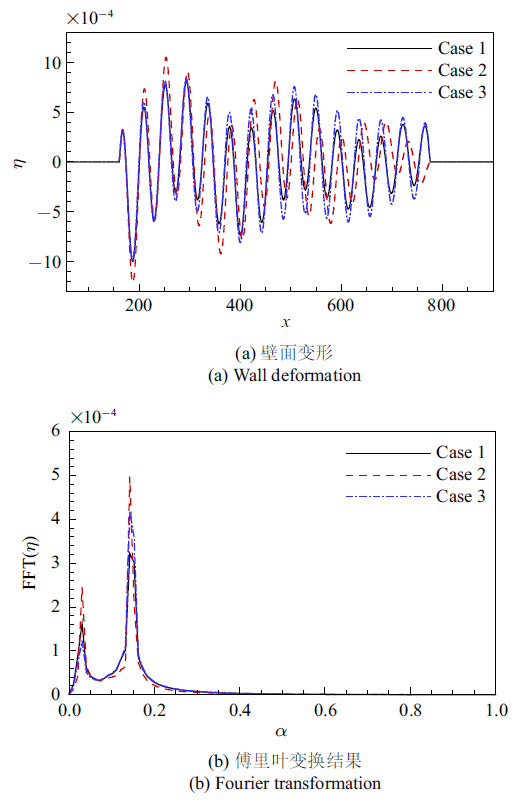
图8 (a)中给出了壁面的变形, 注意这里的变形不是沿着壁面法向, 而是沿着与杠杆臂垂直的方向. 边界层中的T-S波是驱使壁面变形的动力, 因而壁面的变形形式与T-S波的波形基本保持一致. 但可以看到, 壁面的变形不只是对应T-S波的波形. 图8 (b)中壁面变形的傅里叶变换结果清楚地显示了这两种成分. 图中波数较大的峰值$\alpha \approx 0.14$对应的正是T-S波, 波数较小的峰值$\alpha \approx 0.03$对应波长较长的变形. 通过监测壁面变形的形成过程, 发现T-S波波形之外的变形是由柔性壁面前缘产生的大尺度壁面波动. 由于该变形的源头仍是T-S波, 因此其频率与T-S波是相同的. 也正是由于前缘产生了大尺度的壁面波动反过来对其上的流动产生了影响, 图7 中柔性壁面上的扰动的平衡位置才会出现上下的起伏, 在柔性段前缘附近尤为显著.
图8
图8
壁面变形及其傅里叶变换结果
Fig.8
Wall deformation and its Fourier transformation
图9 中给出了柔性段长度缩短之后在$t=90$时刻的壁面变形, 其中``Length = 1, 1/2, 1/4, 1/8''分别表示柔性段长度为原长, 原长的1/2, 1/4和1/8. $t=90$时, 上游的T-S波扰动到达柔性段前缘处, 引起了向后传播的大尺度壁面波动. 柔性段长度缩短到原长的1/2后, 此时的壁面变形与原长时几乎一样. 当长度缩短到原长的1/4时, 前半段仍可以观察到与原长时相似的大尺度波动. 而当长度缩短到仅为原长的1/8时, 此时过短的柔性段上前缘带来的波动已经很难观察到了.
图9
图9
柔性段的长度缩短后$t=90$时的壁面变形
Fig.9
Wall deformation at $t=90$ after the length of the compliant wall section is shortened
2.2 柔性壁面参数的影响
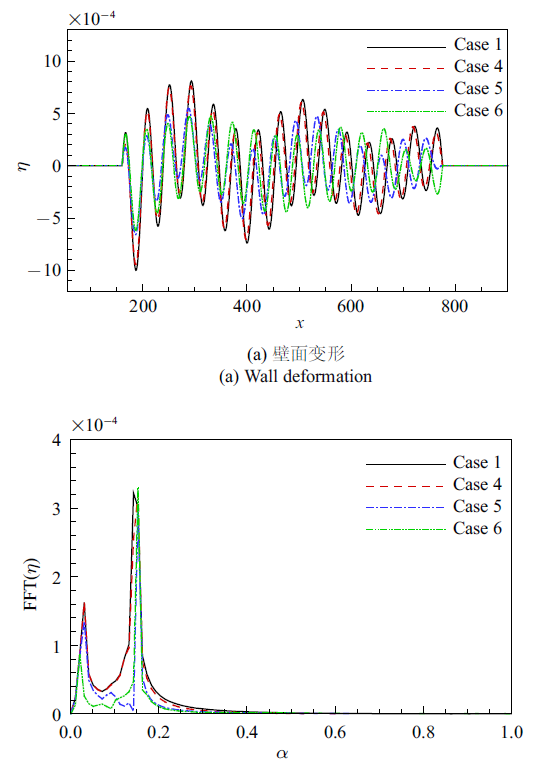
如式 (4) 所示, 不同的$C_{\rm m} ,C_{\rm d} ,C_{\rm B} ,C_{\rm T} ,C_{\rm k} $所表示的柔性壁面是不同的, 那么不同参数对壁面变形以及对T-S波的演化有着怎样的影响是本小节的研究内容. 表2 给出了6组不同的柔性壁面参数, 其中Case 1 是上一小节中使用的参数. 以Case 1作为基准, 其他参数组合均是在其基础上只改变其中某一个参数. 本小节中杠杆臂的倾角均固定为$\theta =30^{\circ }$.
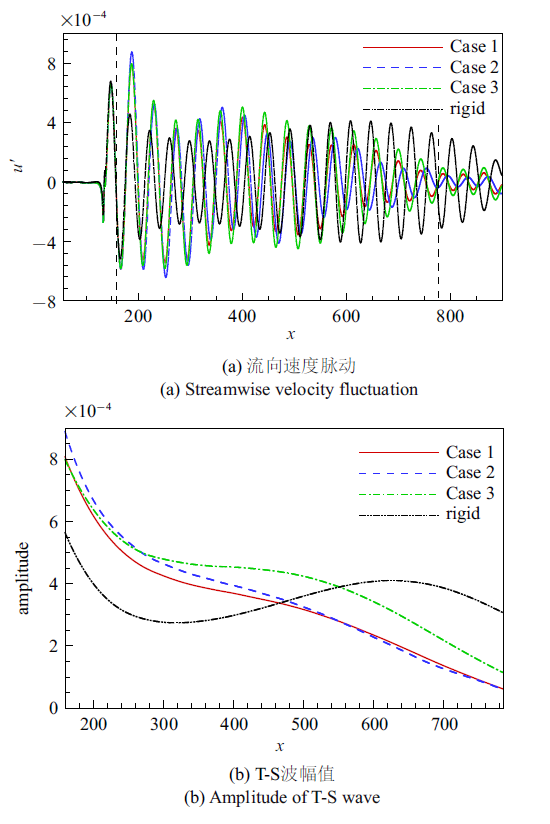
Case 2 中增大了壁面的质量密度, Case 3 中增大了弹簧的阻尼系数, 图10 中给出了Case 1$\sim$3中$y=0.65$处扰动发展的对比. 图10 (a)中所示的流向速度脉动不仅包含了T-S波成分, 还有柔性段前缘引起的长波成分存在. 为了直观地显示T-S波的幅值变化, 在每个位置处, 用最大值减去最小值, 再取一半, 即排除了长波对平衡位置的影响, 就得到了T-S波的幅值, 如图10 (b)中所示. 与Case 1 相比, Case 2中壁面的质量密度增大后, 过前缘后T-S波的强度变得更大, 但由于在该壁面上衰减得更快一些, 到达柔性段出口时幅值仍与Case 1时相当. Case 3中支撑弹簧的阻尼系数增大后, 差异主要为壁面上扰动的衰减变缓, 对于T-S波的衰减效果下降. 另外, Case 1$\sim$3 中扰动幅值均是单调衰减的, 而在刚性壁面上, 大致在$300<x<650$的不稳定区间里, 扰动幅值是增加的. 这说明柔性壁面可以减小扰动的不稳定区域, 这也是前面所提到的柔性壁面可以推迟转捩的重要机理.
图10
图10
Case 1$\sim$3中$y=0.65$处的扰动发展对比
Fig.10
Comparison of disturbance evolution along $y=0.65$ in Case 1$\sim$3
从图11 中给出的壁面变形情况来看, 壁面质量密度增大后, 柔性段前缘引起的大尺度波动和T-S波对应的变形均得到了一定的增强; 增大弹簧的阻尼系数后, 前缘引起的大尺度波动被削弱了, 但是由于对T-S波扰动的衰减作用变弱了, 对应的变形相应得到了增强.
图11
图11
Case 1$\sim$3中壁面变形对比
Fig.11
Comparison of wall deformation in Case 1$\sim$3
Case 4$\sim$6中分别增大了壁面的刚度、张力和支撑弹簧的弹性系数, 图12 中给出了$y=0.65$处的扰动发展对比. 增大壁面的张力和弹簧的弹性系数均会使得壁面刚性增强, 从图12 (b)中可以直观地看到, 柔性段前缘处的扰动强度突增的程度减弱, T-S波幅值衰减的趋势放缓. 可以预见的是, 随着壁面张力或者弹簧弹性系数的逐渐增大, 壁面特性逐渐趋近于刚性壁面. 由于式(3)中刚度对应的是壁面位移的四阶导数项, 量级相比其他项小得多, 因此即使Case 4中刚度系数已经增大到Case 1 的10倍, 但产生的影响比增大张力或者弹簧弹性系数要弱得多, 而影响规律则是相似的.
图12
图12
Case 4$\sim$6中$y=0.65$处的扰动发展对比
Fig.12
Comparison of disturbance evolution along $y=0.65$ in Case 4$\sim$6
图13 中对比了Case 4$\sim$6中的壁面变形. 由于壁面刚度、壁面张力和弹簧弹性系数增大都会带来的壁面刚性增强, 因而壁面的变形幅度均会减小, 特别地, 增大弹簧弹性系数后, 柔性段前缘引起的大尺度壁面波动相比于T-S波对应的壁面变形被明显抑制.
图13
图13
Case 4$\sim$6中壁面变形对比
Fig.13
Comparison of wall deformation in Case 4$\sim$6
2.3 杠杆臂倾角$\theta $的影响
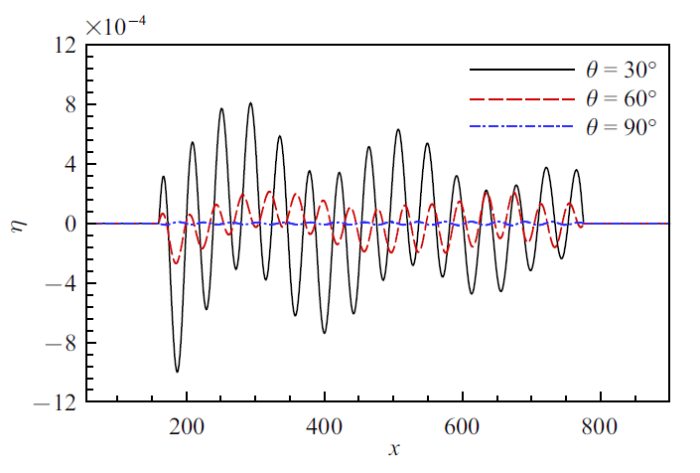
柔性壁面的变形除了受到结构参数的影响之外, 还会因为杠杆臂的倾角$\theta$的改变而发生变化. 为了研究$\theta $的影响, 柔性壁面的结构参数均取2.2节中Case 1 对应的参数, $\theta $角分别取为$30^{\circ }$, $60^{\circ }$和$90^{\circ }$.
图14 给出了不同倾角下的壁面变形. 可以看到, 随着倾角$\theta $的增大, 壁面的变形幅度逐渐变小. $\theta =90^{\circ }$时, 壁面只在黏性切应力的作用下产生水平方向的变形, 没有法向变形, 此时的变形幅度远小于$\theta =30^{\circ }$的情形. 从图15 中给出的流向脉动速度分布可以看到, 壁面倾角越大, T-S波通过柔性壁面后幅值的衰减效果越弱, 在$\theta =90^{\circ }$时几乎与刚性壁面结果没有差异. 尽管在图 14 中$\theta =60^{\circ }$对应的壁面变形中仍然可以观察到由柔性段前缘产生的大尺度壁面波动的存在, 但相较于$\theta =30^{\circ }$时强度明显减小. 而且, 该壁面波动对流动的影响随着到壁面的距离快速衰减, 因而在图 15 中$\theta =60^{\circ }$对应的$y=0.65$位置处的扰动中其对应的成分几乎消失. $\theta =90^{\circ }$时柔性段前缘产生的壁面波动完全消失, 壁面变形只有T-S波对应的成分. 结合图14 和图15 , 随着倾角$\theta $的增大, 柔性壁面表现出刚性变强的趋势. 这其中的道理可以简单理解如下. 虽然壁面的变形由压力、黏性正应力以及黏性切应力驱动, 但是从量级上来说, 压力远大于其余两个力, 因而对于壁面变形起主导作用. 而倾角$\theta $越大, 压力作用在弹簧上的分量$p_{w}' \cos \theta $越小, 从而变形越小, 相当于壁面刚度增大.
图14
图14
不同倾角的柔性壁面的变形对比
Fig.14
Comparison of wall deformation of compliant walls with various incline angles
图15
图15
不同倾角柔性壁面上$y=0.65$处流向脉动速度的空间分布对比
Fig.15
Comparison of distribution of streamwise velocity fluctuation along $y=0.65$ on compliant walls with various incline angles
前面提到一般情况下, 图2 中的柔性壁面上流动方向改变, 则结果也会不同, 因而具有各向异性的特点. 为了研究同样的壁面仅在流动方向发生改变时对扰动发展的影响, 这里对比了$\theta =30^{\circ }$和$\theta =150^{\circ }$两种情形, 其中$\theta =150^{\circ }$对应了空气从右往左流过壁面的情形. 图16 中给出了两种情形下$y=0.65$处扰动发展的对比. 从图16 (b)直观地可以看出, 两种情况下过柔性段前缘T-S波获得的增强效果是一样的. 但不像$\theta =30^{\circ }$的柔性壁面上扰动幅值单调衰减, $\theta =150^{\circ }$时, 存在大致范围为$300<x<450$的不稳定区间, 导致前半段柔性壁面 上的扰动幅值明显更大. 尽管之后的衰减速度相比$\theta =30^{\circ }$时更快, 但由于开始衰减时的幅值已经很大, 到达柔性段出口时幅值仍然比$\theta =30^{\circ }$要大, 但相比刚性壁面扰动幅值还是明显要小. 这些结果表明当流动方向改变后, 柔性壁面对T-S波的衰减效果明显变弱. 与之对应的, 图17 显示的壁面变形中, $\theta =150^{\circ }$时T-S波对应的壁面变形明显要强于$\theta =30^{\circ }$时.
图16
图16
倾角为$\theta =30^{\circ }$和$\theta =150^{\circ}$柔性壁面上$y=0.65$处扰动发展对比
Fig.16
Comparison of disturbance evolution along $y=0.65$ on compliant walls with incline angles $\theta =30^{\circ }$ and $\theta =150^{\circ }$
图17
图17
倾角为$\theta =30^{\circ }$和$\theta =150^{\circ}$的柔性壁面的变形对比
Fig.17
Comparison of wall deformation of compliant walls with incline angle $\theta =30^{\circ }$ and $\theta =150^{\circ }$
3 结论
利用高阶精度的格心型有限差分方法, 本文研究了各向异性柔性壁面上T-S波演化的特征以及壁面参数的影响规律. 得到的主要结论如下:
(1)在本文选取的参数下, 相比于刚性壁面, 柔性壁面能够减小甚至消除T-S波的不稳定增长区间, 具有抑制T-S波幅值增长的作用.
(2)由于在柔性段前缘处刚度发生突变, 扰动幅值过柔性段前缘后会突增, 并且前缘会引起与T-S波频率相同, 但波长更大的壁面波动. 整体的壁面变形由T-S波波形对应的变形与前缘带来的长波振动叠加而来.
(3)壁面质量密度增大, 壁面变形程度变大, 前缘引起的扰动增强效果更大, 但由于衰减得更块, 出口处的扰动幅值变化不大. 增大阻尼可以有效抑制前缘产生的大尺度壁面波动, 但由于抑制扰动的效果下降, 对应T-S波波形的壁面变形则会增强. 增大壁面的刚度、张力和弹簧弹性系数均会增加壁面的刚性, 使得壁面变形幅度减小以及对扰动的抑制效果下降.
(4)支撑壁面的杠杆臂倾角增加, 壁面的刚性越强, 变形则越小, 对T-S波的抑制效果越弱. 当空气反方向流过壁面时, 抑制扰动的效果明显下降, 壁面变形幅度增大.
参考文献
View Option
[1]
张庆 , 叶正寅 . 基于雨燕翅膀的仿生三角翼气动特性计算研究
力学学报 , 2021 ,53 (2 ):373 -385
[本文引用: 1]
(Zhang Qing Ye Zhengyin . Computational investigations for aerodynamic performance of bio-inspired delta-wing based on swift-wing
Chinese Journal of Theoretical and Applied Mechanics 2021 ,53 (2 ):373 -385 (in Chinese))
[本文引用: 1]
[2]
教柳 , 张保成 , 张开升 等 . 两关节压力驱动柔性仿生机器鱼的设计与仿生
力学学报 , 2020 ,52 (3 ):817 -827
(Jiao Liu Zhang Baocheng Zhang Kaisheng , et al . Design and simulation of two-joint pressure-driven soft bionic fish
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (3 ):817 -827 (in Chinese))
[3]
冯家兴 , 胡海豹 , 卢丙举 等 . 超疏水沟槽表面通气减阻实验研究
力学学报 , 2020 ,52 (1 ):24 -30
[本文引用: 1]
(Feng Jiaxing Hu Haibao Lu Bingju , et al . Experimental study on drag reduction characteristics of superhydrophobic groove surfaces with ventilation
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (1 ):24 -30 (in Chinese))
[本文引用: 1]
[4]
屈秋林 , 王晋军 . 鸟类飞行空气动力学对人类飞行的启示
物理 , 2016 ,45 (10 ):640 -644
[本文引用: 1]
(Qu Qiulin Wang Jinjun . Human flight inspired by the aerodynamics of bird flight
Physics 2016 ,45 (10 ):640 -644 (in Chinese))
[本文引用: 1]
[5]
Videler JJ . Avian Flight . Oxford : Oxford University Press , 2006
[本文引用: 1]
[6]
Lincoln FC Peterson SR Zimmerman JL . Migration of birds. US Department of the interior, US Fish and Wildlife Service, Washington DC Circular 16
Northern Prairie Wildlife Research Center Online 1998 : 61
[本文引用: 1]
[7]
Croxall JP Silk JR Phillips RA , et al . Global circumnavigations: Tracking year-around ranges of non-breeding Albatrosses
Science 2005 ,307 :249 -250
DOI
URL
[本文引用: 1]
[8]
Gray J . Studies in animal locomotion: VI. The propulsive powers of the dolphin
Journal of Experimental Biology 1936 ,13 (2 ):192 -199
DOI
URL
[本文引用: 1]
[9]
Kramer MO . Boundary-layer stabilization by distributed damping
Journal of the Aerospace Sciences 1960 ,27 (1 ):69 -69
DOI
URL
[本文引用: 1]
[10]
Bushnell DM Hefner JN Ash RL . Effect of compliant wall motion on turbulent boundary layers
The Physics of Fluids 1977 ,20 (10 ):S31 -S48
DOI
URL
[本文引用: 1]
[11]
Carpenter PW Garrad AD . The hydrodynamic stability of flow over Kramer-type compliant surfaces. Part 1. Tollmien-Schlichting instabilities
Journal of Fluid Mechanics 1985 ,155 :465 -510
DOI
URL
[本文引用: 1]
[12]
Carpenter PW Garrad AD . The hydrodynamic stability of flow over Kramer-type compliant surfaces. Part 2. Flow-induced surface instabilities
Journal of Fluid Mechanics 1986 ,170 :199 -232
DOI
URL
[本文引用: 1]
[13]
Lucey AD Carpenter PW . Boundary layer instability over compliant walls: Comparison between theory and experiment
Physics of Fluids 1995 ,7 (10 ):2355 -2363
DOI
URL
[本文引用: 1]
[14]
Lee T Fisher M Schwarz WH . Investigation of the effects of a compliant surface on boundary-layer stability
Journal of Fluid Mechanics 1995 ,288 :37 -58
DOI
URL
[本文引用: 1]
[15]
Davies C Carpenter PW . Numerical simulation of the evolution of Tollmien-Schlichting waves over finite compliant panels
Journal of Fluid Mechanics 1997 ,335 :361 -392
DOI
URL
[本文引用: 1]
[16]
Wang Z Yeo KS Khoo BC . On two-dimensional linear waves in Blasius boundary layer over viscoelastic layers
European Journal of Mechanics-B/Fluids 2006 ,25 (1 ):33 -58
DOI
URL
[本文引用: 3]
[17]
Shu W Liu W . The effect of compliant coatings on coherent structure in turbulent boundary layers
Acta Mechanica Sinica 1990 ,6 (2 ):97 -101
DOI
URL
[本文引用: 1]
[18]
Lee T Fisher M Schwarz WH . Investigation of the stable interaction of a passive compliant surface with a turbulent boundary layer
Journal of Fluid Mechanics 1993 ,257 :373 -401
DOI
URL
[本文引用: 1]
[19]
Choi KS Yang X Clayton BR , et al . Turbulent drag reduction using compliant surfaces
Proceedings of the Royal Society of London. Series A$:$ Mathematical, Physical and Engineering Sciences 1997 ,453 (1965 ):2229 -2240
[本文引用: 1]
[20]
Kulik VM Lee I Chun HH . Wave properties of coating for skin friction reduction
Physics of Fluids 2008 ,20 (7 ):075109
DOI
URL
[本文引用: 1]
[21]
Luhar M Sharma AS , McKeon BJ. A framework for studying the effect of compliant surfaces on wall turbulence
Journal of Fluid Mechanics 2015 ,768 :415 -441
DOI
URL
[本文引用: 1]
[22]
Endo T Himeno R . Direct numerical simulation of turbulent flow over a compliant surface
Journal of Turbulence 2002 ,3 (7 ):1 -10
[本文引用: 2]
[23]
Xu S Rempfer D Lumley J . Turbulence over a compliant surface: Numerical simulation and analysis
Journal of Fluid Mechanics 2003 ,478 :11 -34
DOI
URL
[本文引用: 1]
[24]
Kim E Choi H . Space-time characteristics of a compliant wall in a turbulent channel flow
Journal of fluid mechanics 2014 ,756 :30 -53
DOI
URL
[本文引用: 1]
[25]
Xia QJ Huang WX Xu CX . Direct numerical simulation of turbulent boundary layer over a compliant wall
Journal of Fluids and Structures 2017 ,71 :126 -142
DOI
URL
[本文引用: 1]
[26]
Fukagata K Kern S Chatelain P , et al . Evolutionary optimization of an anisotropic compliant surface for turbulent drag reduction
Journal of Turbulence 2008 ,9 (35 ):1 -17
[本文引用: 1]
[27]
Xia QJ Huang WX Xu CX . Direct numerical simulation of a turbulent boundary layer over an anisotropic compliant wall
Acta Mechanica Sinica 2019 ,35 (2 ):384 -400
DOI
URL
[本文引用: 1]
[28]
Jozsa TI . Analytical solutions of incompressible laminar channel and pipe flows driven by in-plane wall oscillations
Physics of Fluids 2019 ,31 (8 ):083605
DOI
URL
[本文引用: 1]
[29]
Józsa TI Balaras E Kashtalyan M , et al . Active and passive in-plane wall fluctuations in turbulent channel flows
Journal of Fluid Mechanics 2019 ,866 :689 -720
DOI
URL
[本文引用: 1]
[30]
Carpenter PW Morris PJ . The effect of anisotropic wall compliance on boundary-layer stability and transition
Journal of Fluid Mechanics 1990 ,218 :171 -223
DOI
URL
[本文引用: 3]
[31]
刘巍 , 张理论 , 王勇献 等 . 计算空气动力学并行编程基础 . 北京 : 国防工业初版社 , 2013
[本文引用: 1]
(Liu Wei Zhang Lilun Wang Yongxian , et al. Foundations of Computational Aerodynamics Parallel Programming. Beijing : National Defense Industry Press , 2013 (in Chinese))
[本文引用: 1]
[32]
廖飞 . 高阶精度数值方法及其在复杂流动中的应用. [博士论文]
西安: 西北工业大学 , 2018
[本文引用: 1]
(Liao Fei . Efficient high-order high-resolution methods and the applications. [PhD Thesis]
Xi'an: Northwestern Polytechnical University , 2018 (in Chinese))
[本文引用: 1]
[33]
洪正 , 叶正寅 . 各向同性湍流通过正激波的演化特征研究
力学学报 , 2018 ,50 (6 ):1356 -1367
[本文引用: 1]
(Hong Zheng Ye Zhengyin . Study on evolution characteristics of isotropic turbulence passing through a normal shock wave
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (6 ):1356 -1367 (in Chinese))
[本文引用: 1]
[34]
洪正 , 叶正寅 . 不同亚格子模型在亚声速槽道流大涡模拟中的应用对比
气体物理 , 2019 ,4 (1 ):33 -44
(Hong Zheng Ye Zhengyin . Application of different subgrid-scale models used in large-eddy simulation of subsonic channel flow
Physics of Gases 2019 ,4 (1 ):33 -44 (in Chinese))
[35]
叶正寅 , 洪正 , 武洁 . 柔性仿羽毛结构抑制边界层转捩的初步探索
空气动力学学报 , 2020 ,38 (6 ):1173 -1182
[本文引用: 1]
(Ye Zhengyin Hong Zheng Wu Jie . Suppression of flexible feather-like structure on boundary layer transition
Acta Aerodynamica Sinica 2020 ,38 (6 ):1173 -1182 (in Chinese))
[本文引用: 1]
[36]
Fasel H Konzelmann U . Non-parallel stability of a flat-plate boundary layer using the complete Navier-Stokes equations
Journal of Fluid Mechanics 1990 ,221 :311 -347
DOI
URL
[本文引用: 1]
基于雨燕翅膀的仿生三角翼气动特性计算研究
1
2021
... 自然界是人类灵感的重要来源, 人们在研究各色各样的生物时获得了很多有益的启发[1 -3 ] . 在人造飞行器的发展历程中, 人们从擅于飞翔的鸟类身上获得了多种启示[4 ] . 对于鸟类的研究初期主要从生物学的角度出发, 随着观察和分析的深入, 逐渐认识到其中的空气动力学奥秘[5 ] . 北美金鸻鸟连续飞行跨越4000 km的大洋每小时仅仅损失其体重的0.06%[6 ] ; 飞行冠军信天翁可以不用拍动翅膀长时间翱翔于海面之上[7 ] . 鸟类如此高效的飞行必然离不开其表面极低的飞行阻力. 经过了千万年的进化, 鸟类形成了带弯度的厚前缘和薄后缘的翅膀. 现代飞机机翼的形状正是由此仿生而来. 但构成鸟翅膀表面的羽毛与构成机翼的蒙皮重要的区别之一是羽毛非常柔软且有弹性, 气动力存在脉动时可以发生局部变形. 由致密的覆羽层叠而成的翅膀厚前缘处, 柔性特征尤为显著. 那么, 鸟羽的这种柔性特征是否有利于减阻正是本文研究的出发点. ...
基于雨燕翅膀的仿生三角翼气动特性计算研究
1
2021
... 自然界是人类灵感的重要来源, 人们在研究各色各样的生物时获得了很多有益的启发[1 -3 ] . 在人造飞行器的发展历程中, 人们从擅于飞翔的鸟类身上获得了多种启示[4 ] . 对于鸟类的研究初期主要从生物学的角度出发, 随着观察和分析的深入, 逐渐认识到其中的空气动力学奥秘[5 ] . 北美金鸻鸟连续飞行跨越4000 km的大洋每小时仅仅损失其体重的0.06%[6 ] ; 飞行冠军信天翁可以不用拍动翅膀长时间翱翔于海面之上[7 ] . 鸟类如此高效的飞行必然离不开其表面极低的飞行阻力. 经过了千万年的进化, 鸟类形成了带弯度的厚前缘和薄后缘的翅膀. 现代飞机机翼的形状正是由此仿生而来. 但构成鸟翅膀表面的羽毛与构成机翼的蒙皮重要的区别之一是羽毛非常柔软且有弹性, 气动力存在脉动时可以发生局部变形. 由致密的覆羽层叠而成的翅膀厚前缘处, 柔性特征尤为显著. 那么, 鸟羽的这种柔性特征是否有利于减阻正是本文研究的出发点. ...
两关节压力驱动柔性仿生机器鱼的设计与仿生
0
2020
两关节压力驱动柔性仿生机器鱼的设计与仿生
0
2020
超疏水沟槽表面通气减阻实验研究
1
2020
... 自然界是人类灵感的重要来源, 人们在研究各色各样的生物时获得了很多有益的启发[1 -3 ] . 在人造飞行器的发展历程中, 人们从擅于飞翔的鸟类身上获得了多种启示[4 ] . 对于鸟类的研究初期主要从生物学的角度出发, 随着观察和分析的深入, 逐渐认识到其中的空气动力学奥秘[5 ] . 北美金鸻鸟连续飞行跨越4000 km的大洋每小时仅仅损失其体重的0.06%[6 ] ; 飞行冠军信天翁可以不用拍动翅膀长时间翱翔于海面之上[7 ] . 鸟类如此高效的飞行必然离不开其表面极低的飞行阻力. 经过了千万年的进化, 鸟类形成了带弯度的厚前缘和薄后缘的翅膀. 现代飞机机翼的形状正是由此仿生而来. 但构成鸟翅膀表面的羽毛与构成机翼的蒙皮重要的区别之一是羽毛非常柔软且有弹性, 气动力存在脉动时可以发生局部变形. 由致密的覆羽层叠而成的翅膀厚前缘处, 柔性特征尤为显著. 那么, 鸟羽的这种柔性特征是否有利于减阻正是本文研究的出发点. ...
超疏水沟槽表面通气减阻实验研究
1
2020
... 自然界是人类灵感的重要来源, 人们在研究各色各样的生物时获得了很多有益的启发[1 -3 ] . 在人造飞行器的发展历程中, 人们从擅于飞翔的鸟类身上获得了多种启示[4 ] . 对于鸟类的研究初期主要从生物学的角度出发, 随着观察和分析的深入, 逐渐认识到其中的空气动力学奥秘[5 ] . 北美金鸻鸟连续飞行跨越4000 km的大洋每小时仅仅损失其体重的0.06%[6 ] ; 飞行冠军信天翁可以不用拍动翅膀长时间翱翔于海面之上[7 ] . 鸟类如此高效的飞行必然离不开其表面极低的飞行阻力. 经过了千万年的进化, 鸟类形成了带弯度的厚前缘和薄后缘的翅膀. 现代飞机机翼的形状正是由此仿生而来. 但构成鸟翅膀表面的羽毛与构成机翼的蒙皮重要的区别之一是羽毛非常柔软且有弹性, 气动力存在脉动时可以发生局部变形. 由致密的覆羽层叠而成的翅膀厚前缘处, 柔性特征尤为显著. 那么, 鸟羽的这种柔性特征是否有利于减阻正是本文研究的出发点. ...
鸟类飞行空气动力学对人类飞行的启示
1
2016
... 自然界是人类灵感的重要来源, 人们在研究各色各样的生物时获得了很多有益的启发[1 -3 ] . 在人造飞行器的发展历程中, 人们从擅于飞翔的鸟类身上获得了多种启示[4 ] . 对于鸟类的研究初期主要从生物学的角度出发, 随着观察和分析的深入, 逐渐认识到其中的空气动力学奥秘[5 ] . 北美金鸻鸟连续飞行跨越4000 km的大洋每小时仅仅损失其体重的0.06%[6 ] ; 飞行冠军信天翁可以不用拍动翅膀长时间翱翔于海面之上[7 ] . 鸟类如此高效的飞行必然离不开其表面极低的飞行阻力. 经过了千万年的进化, 鸟类形成了带弯度的厚前缘和薄后缘的翅膀. 现代飞机机翼的形状正是由此仿生而来. 但构成鸟翅膀表面的羽毛与构成机翼的蒙皮重要的区别之一是羽毛非常柔软且有弹性, 气动力存在脉动时可以发生局部变形. 由致密的覆羽层叠而成的翅膀厚前缘处, 柔性特征尤为显著. 那么, 鸟羽的这种柔性特征是否有利于减阻正是本文研究的出发点. ...
鸟类飞行空气动力学对人类飞行的启示
1
2016
... 自然界是人类灵感的重要来源, 人们在研究各色各样的生物时获得了很多有益的启发[1 -3 ] . 在人造飞行器的发展历程中, 人们从擅于飞翔的鸟类身上获得了多种启示[4 ] . 对于鸟类的研究初期主要从生物学的角度出发, 随着观察和分析的深入, 逐渐认识到其中的空气动力学奥秘[5 ] . 北美金鸻鸟连续飞行跨越4000 km的大洋每小时仅仅损失其体重的0.06%[6 ] ; 飞行冠军信天翁可以不用拍动翅膀长时间翱翔于海面之上[7 ] . 鸟类如此高效的飞行必然离不开其表面极低的飞行阻力. 经过了千万年的进化, 鸟类形成了带弯度的厚前缘和薄后缘的翅膀. 现代飞机机翼的形状正是由此仿生而来. 但构成鸟翅膀表面的羽毛与构成机翼的蒙皮重要的区别之一是羽毛非常柔软且有弹性, 气动力存在脉动时可以发生局部变形. 由致密的覆羽层叠而成的翅膀厚前缘处, 柔性特征尤为显著. 那么, 鸟羽的这种柔性特征是否有利于减阻正是本文研究的出发点. ...
1
2006
... 自然界是人类灵感的重要来源, 人们在研究各色各样的生物时获得了很多有益的启发[1 -3 ] . 在人造飞行器的发展历程中, 人们从擅于飞翔的鸟类身上获得了多种启示[4 ] . 对于鸟类的研究初期主要从生物学的角度出发, 随着观察和分析的深入, 逐渐认识到其中的空气动力学奥秘[5 ] . 北美金鸻鸟连续飞行跨越4000 km的大洋每小时仅仅损失其体重的0.06%[6 ] ; 飞行冠军信天翁可以不用拍动翅膀长时间翱翔于海面之上[7 ] . 鸟类如此高效的飞行必然离不开其表面极低的飞行阻力. 经过了千万年的进化, 鸟类形成了带弯度的厚前缘和薄后缘的翅膀. 现代飞机机翼的形状正是由此仿生而来. 但构成鸟翅膀表面的羽毛与构成机翼的蒙皮重要的区别之一是羽毛非常柔软且有弹性, 气动力存在脉动时可以发生局部变形. 由致密的覆羽层叠而成的翅膀厚前缘处, 柔性特征尤为显著. 那么, 鸟羽的这种柔性特征是否有利于减阻正是本文研究的出发点. ...
Migration of birds. US Department of the interior, US Fish and Wildlife Service, Washington DC Circular 16
1
1998
... 自然界是人类灵感的重要来源, 人们在研究各色各样的生物时获得了很多有益的启发[1 -3 ] . 在人造飞行器的发展历程中, 人们从擅于飞翔的鸟类身上获得了多种启示[4 ] . 对于鸟类的研究初期主要从生物学的角度出发, 随着观察和分析的深入, 逐渐认识到其中的空气动力学奥秘[5 ] . 北美金鸻鸟连续飞行跨越4000 km的大洋每小时仅仅损失其体重的0.06%[6 ] ; 飞行冠军信天翁可以不用拍动翅膀长时间翱翔于海面之上[7 ] . 鸟类如此高效的飞行必然离不开其表面极低的飞行阻力. 经过了千万年的进化, 鸟类形成了带弯度的厚前缘和薄后缘的翅膀. 现代飞机机翼的形状正是由此仿生而来. 但构成鸟翅膀表面的羽毛与构成机翼的蒙皮重要的区别之一是羽毛非常柔软且有弹性, 气动力存在脉动时可以发生局部变形. 由致密的覆羽层叠而成的翅膀厚前缘处, 柔性特征尤为显著. 那么, 鸟羽的这种柔性特征是否有利于减阻正是本文研究的出发点. ...
Global circumnavigations: Tracking year-around ranges of non-breeding Albatrosses
1
2005
... 自然界是人类灵感的重要来源, 人们在研究各色各样的生物时获得了很多有益的启发[1 -3 ] . 在人造飞行器的发展历程中, 人们从擅于飞翔的鸟类身上获得了多种启示[4 ] . 对于鸟类的研究初期主要从生物学的角度出发, 随着观察和分析的深入, 逐渐认识到其中的空气动力学奥秘[5 ] . 北美金鸻鸟连续飞行跨越4000 km的大洋每小时仅仅损失其体重的0.06%[6 ] ; 飞行冠军信天翁可以不用拍动翅膀长时间翱翔于海面之上[7 ] . 鸟类如此高效的飞行必然离不开其表面极低的飞行阻力. 经过了千万年的进化, 鸟类形成了带弯度的厚前缘和薄后缘的翅膀. 现代飞机机翼的形状正是由此仿生而来. 但构成鸟翅膀表面的羽毛与构成机翼的蒙皮重要的区别之一是羽毛非常柔软且有弹性, 气动力存在脉动时可以发生局部变形. 由致密的覆羽层叠而成的翅膀厚前缘处, 柔性特征尤为显著. 那么, 鸟羽的这种柔性特征是否有利于减阻正是本文研究的出发点. ...
Studies in animal locomotion: VI. The propulsive powers of the dolphin
1
1936
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Boundary-layer stabilization by distributed damping
1
1960
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Effect of compliant wall motion on turbulent boundary layers
1
1977
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
The hydrodynamic stability of flow over Kramer-type compliant surfaces. Part 1. Tollmien-Schlichting instabilities
1
1985
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
The hydrodynamic stability of flow over Kramer-type compliant surfaces. Part 2. Flow-induced surface instabilities
1
1986
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Boundary layer instability over compliant walls: Comparison between theory and experiment
1
1995
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Investigation of the effects of a compliant surface on boundary-layer stability
1
1995
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Numerical simulation of the evolution of Tollmien-Schlichting waves over finite compliant panels
1
1997
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
On two-dimensional linear waves in Blasius boundary layer over viscoelastic layers
3
2006
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
... 图3 中给出了沿着$y=0.65$位置的流向脉动速度的空间分布. 可以看到, 在扰动源的下游, 短暂过渡之后, 脉动速度的分布就已经呈现出了很好的规律性, 以变幅度的正弦波形式向下游传播. 在两个频率对应的结果中, 扰动产生后幅值均先下降再增长最后又下降. 幅值变化趋势改变的位置称为中性点, 图4 对比了本文计算得到的中性点位置与线性理论以及Wang等[16 ] 和Fasel等[36 ] 的计算结果. 图中``拇指''曲线是由线性稳定性理论给出的中性曲线, 该曲线从文献[16 ]中得到. 可以看到本文结果与线性稳定性理论得到的结果符合得很好. 图3 和图4 的结果表明本文所采用的数值方法对于T-S波空间演化的模拟是可靠的. ...
... 的计算结果. 图中``拇指''曲线是由线性稳定性理论给出的中性曲线, 该曲线从文献[16 ]中得到. 可以看到本文结果与线性稳定性理论得到的结果符合得很好. 图3 和图4 的结果表明本文所采用的数值方法对于T-S波空间演化的模拟是可靠的. ...
The effect of compliant coatings on coherent structure in turbulent boundary layers
1
1990
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Investigation of the stable interaction of a passive compliant surface with a turbulent boundary layer
1
1993
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Turbulent drag reduction using compliant surfaces
1
1997
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Wave properties of coating for skin friction reduction
1
2008
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
McKeon BJ. A framework for studying the effect of compliant surfaces on wall turbulence
1
2015
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Direct numerical simulation of turbulent flow over a compliant surface
2
2002
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
... [22 ]得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Turbulence over a compliant surface: Numerical simulation and analysis
1
2003
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Space-time characteristics of a compliant wall in a turbulent channel flow
1
2014
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Direct numerical simulation of turbulent boundary layer over a compliant wall
1
2017
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Evolutionary optimization of an anisotropic compliant surface for turbulent drag reduction
1
2008
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Direct numerical simulation of a turbulent boundary layer over an anisotropic compliant wall
1
2019
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Analytical solutions of incompressible laminar channel and pipe flows driven by in-plane wall oscillations
1
2019
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
Active and passive in-plane wall fluctuations in turbulent channel flows
1
2019
... 关于壁面柔性特征对流动减阻的研究最早源自于对海豚的观察. Gray[8 ] 研究海豚游动时指出, 哺乳类动物的肌肉力量与水中快速游动所需要的肌肉力量相差甚远, 因此推测海豚的皮肤具有减阻的功能. Kramer[9 ] 利用橡胶和树脂制作柔性涂层开展了柔性壁面的实验研究, 相比刚性壁面获得了50%的减阻效果. 但这一实验的准确性受到质疑[10 ] . 直到20世纪80年代, Carpenter等[11 -12 ] 开展了柔性壁面的线性稳定性理论研究, 证明了柔性壁面相比刚性壁面具有更小的不稳定区域, 从而能够推迟流动转捩. 得益于实验技术的发展, 线性理论所预测的柔性壁面推迟转捩的效果在后来的实验中被证实[13 -14 ] . Davies等[15 ] 和Wang等[16 ] 通过数值模拟的手段也验证了各向同性柔性壁面上线性理论的结论. 相比于柔性壁面对转捩影响的研究, 完全发展的湍流边界层与柔性壁面的相互作用要复杂得多. Shu和Liu[17 ] 的实验结果表明与刚性壁面相比, 柔性壁面上速度型的对数层上移, 湍流猝发的频率下降. Lee等[18 ] 的水洞实验提供了进一步的证据, 表明柔性壁面能够抑制湍流. Choi等[19 ] 测量了覆盖了柔性涂层的细长体的摩擦阻力, 通过合适地选择柔性参数, 获得了约7%的减阻效果. 一些简化的理论方法被提出来用以指导柔性参数的选取[20 -21 ] . 随着计算机技术的迅猛发展, 直接数值模拟(direct numerical simulation, DNS)对于研究柔性壁面和湍流相互作用机理作出了重要贡献. Endo和Himeno[22 ] 数值模拟了湍流流过各向同性柔性壁面的情形, 获得了2.7%的减阻效果. 然而, Xu等[23 ] 指出Endo和Himeno[22 ] 得到的阻力减小只是一个过渡的结果, 进行更长时间的平均后减阻的效果几乎没有. Kim等[24 ] 和Xia等[25 ] 的数值结果也表明各向同性的柔性壁面并不能减小甚至会增大湍流边界层的摩擦阻力. Fukagata等[26 ] 基于各向异性的柔性壁面, 使用进化算法优化了壁面参数, 获得了8%的减阻效果. 最近, Xia等[27 ] 通过DNS研究了各向异性柔性壁面对湍流的作用机理. Jozsa等[28 -29 ] 系统地研究了壁面主动或者被动切向变形对湍流边界层减阻的效果, 指出柔性壁面的各向异性对于取得实际的减阻效果十分关键. ...
The effect of anisotropic wall compliance on boundary-layer stability and transition
3
1990
... 鸟类或者飞行器是在空气中飞行, 而以往的研究主要以海豚生存环境中的水为流动介质. 另外, 虽然已经发展了各向异性柔性壁面的线性稳定性理论[30 ] , 但由于有限长度、边界层厚度增大等因素不可避免地与真实情况有出入, 而数值模拟则可以提供更加符合实际的结果. 鉴于此, 本文基于格心型有限差分方法数值求解描述空气运动的可压缩N-S方程, 研究了在各向异性的柔性壁面上, 亚音速边界层转捩初期T-S波的演化特征以及参数的影响规律, 以期为边界层的层流控制提供一定的参考价值. ...
... 对于图2 中所示的柔性壁面, 文献[30 ]中给出了其运动的控制方程. 采用与流动方程一致的参考量, 无量纲化后的壁面运动控制方程为 ...
... 如此处理简单且可以较好地避免出口反射的问题. 计算域上边界采用远场Riemann边界条件[31 ] . 下边界为绝热壁面, 刚性段$[x_{\rm in} ,x_{\rm cs} ]$和$[x_{\rm ce} ,x_{\rm out} ]$壁面速度采用无滑移条件, 参照文献[30 ], 柔性段壁面速度与壁面位移相关联, 即 ...
1
2013
... 如此处理简单且可以较好地避免出口反射的问题. 计算域上边界采用远场Riemann边界条件[31 ] . 下边界为绝热壁面, 刚性段$[x_{\rm in} ,x_{\rm cs} ]$和$[x_{\rm ce} ,x_{\rm out} ]$壁面速度采用无滑移条件, 参照文献[30 ], 柔性段壁面速度与壁面位移相关联, 即 ...
1
2013
... 如此处理简单且可以较好地避免出口反射的问题. 计算域上边界采用远场Riemann边界条件[31 ] . 下边界为绝热壁面, 刚性段$[x_{\rm in} ,x_{\rm cs} ]$和$[x_{\rm ce} ,x_{\rm out} ]$壁面速度采用无滑移条件, 参照文献[30 ], 柔性段壁面速度与壁面位移相关联, 即 ...
高阶精度数值方法及其在复杂流动中的应用. [博士论文]
1
2018
... N-S方程的数值求解采用半离散的形式, 即先求空间导数项, 再进行时间上的推进. 空间离散采用基于结构网格的格心有限差分方法[32 ] , 该套方法和程序已应用在其他湍流计算问题中[33 -35 ] . 以$x$方向上的通量导数求解为例, 具体步骤如下: ...
高阶精度数值方法及其在复杂流动中的应用. [博士论文]
1
2018
... N-S方程的数值求解采用半离散的形式, 即先求空间导数项, 再进行时间上的推进. 空间离散采用基于结构网格的格心有限差分方法[32 ] , 该套方法和程序已应用在其他湍流计算问题中[33 -35 ] . 以$x$方向上的通量导数求解为例, 具体步骤如下: ...
各向同性湍流通过正激波的演化特征研究
1
2018
... N-S方程的数值求解采用半离散的形式, 即先求空间导数项, 再进行时间上的推进. 空间离散采用基于结构网格的格心有限差分方法[32 ] , 该套方法和程序已应用在其他湍流计算问题中[33 -35 ] . 以$x$方向上的通量导数求解为例, 具体步骤如下: ...
各向同性湍流通过正激波的演化特征研究
1
2018
... N-S方程的数值求解采用半离散的形式, 即先求空间导数项, 再进行时间上的推进. 空间离散采用基于结构网格的格心有限差分方法[32 ] , 该套方法和程序已应用在其他湍流计算问题中[33 -35 ] . 以$x$方向上的通量导数求解为例, 具体步骤如下: ...
不同亚格子模型在亚声速槽道流大涡模拟中的应用对比
0
2019
不同亚格子模型在亚声速槽道流大涡模拟中的应用对比
0
2019
柔性仿羽毛结构抑制边界层转捩的初步探索
1
2020
... N-S方程的数值求解采用半离散的形式, 即先求空间导数项, 再进行时间上的推进. 空间离散采用基于结构网格的格心有限差分方法[32 ] , 该套方法和程序已应用在其他湍流计算问题中[33 -35 ] . 以$x$方向上的通量导数求解为例, 具体步骤如下: ...
柔性仿羽毛结构抑制边界层转捩的初步探索
1
2020
... N-S方程的数值求解采用半离散的形式, 即先求空间导数项, 再进行时间上的推进. 空间离散采用基于结构网格的格心有限差分方法[32 ] , 该套方法和程序已应用在其他湍流计算问题中[33 -35 ] . 以$x$方向上的通量导数求解为例, 具体步骤如下: ...
Non-parallel stability of a flat-plate boundary layer using the complete Navier-Stokes equations
1
1990
... 图3 中给出了沿着$y=0.65$位置的流向脉动速度的空间分布. 可以看到, 在扰动源的下游, 短暂过渡之后, 脉动速度的分布就已经呈现出了很好的规律性, 以变幅度的正弦波形式向下游传播. 在两个频率对应的结果中, 扰动产生后幅值均先下降再增长最后又下降. 幅值变化趋势改变的位置称为中性点, 图4 对比了本文计算得到的中性点位置与线性理论以及Wang等[16 ] 和Fasel等[36 ] 的计算结果. 图中``拇指''曲线是由线性稳定性理论给出的中性曲线, 该曲线从文献[16 ]中得到. 可以看到本文结果与线性稳定性理论得到的结果符合得很好. 图3 和图4 的结果表明本文所采用的数值方法对于T-S波空间演化的模拟是可靠的. ...