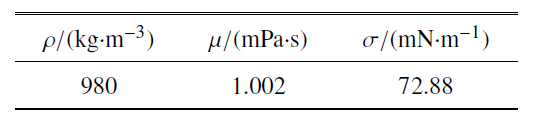引言
以液体为工作介质的水力机械, 由于旋转速度较高, 极易在与液体接触的表面形成空化现象, 这会给水利机械带来空蚀损伤[1 ] , 严重影响机械结构的寿命和稳定性, 因此如何计算空化强度, 评估空泡溃灭带来的能量冲击成为流体力学中重要的研究方向. 依据空间尺度不同, 空化运动主要表现为宏观空化对流旋涡运动[2 ] 和介观空泡脉动[3 ] , 其中大尺度的空穴是由大量空泡汇聚而成的[4 ] . 在1917年Rayleigh[5 ] 首先分析了在自由场中空泡溃灭的动力学行为, 建立了基于不可压缩理想流体、忽略表面张力和黏性情况下的球形空泡溃灭常微分方程. 随后的研究者分别应用实验与数值模拟的方法对复杂边界条件附近空泡溃灭的动力学行为开展了深入研究, 发现在整个空泡溃灭过程中存在空泡脉动[6 ] 、 高速射流[7 ] 及冲击波[8 ] 等多种载荷形式, 整个过程中包含复杂的能量转化机制, 是空泡动力学研究中的重要课题[9 -10 ] .
在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制.
鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律.
本文采用了实验与数值模拟相结合的方法, 分析空泡在自由场中的形态演化过程及能量转化机制, 旨在获得空泡在溃灭过程中空泡势能、流场动能及波能的能量转化规律. 主要研究工作包括: (1)采用纹影法记录空泡发展溃灭全过程, 观测确定空泡半径的大小及溃灭速度, 分析空泡在溃灭过程中的形态变化及冲击波的运动. (2)通过数值模拟方法分析空泡溃灭过程, 确定空泡在溃灭过程中流场的压力、速度云图及纹影图像, 明确空泡在溃灭后期压力和速度分布特征. (3)推导空泡势能及流场动能公式, 分析空泡及高压区域在溃灭过程中的动能和势能变化曲线, 阐明自由场空泡的能量转化机制.
1 实验研究方法
实验采用低压放电方法在透明水箱中生成蒸汽泡. 电火花空泡发生器包括充放电开关、 电容器、 高速摄像机同步触发装置、电线及铜丝. 电火花空泡发生器的电线通过夹板固定在空泡水箱上部, 其末端与铜丝连接. 该方法的空泡产生原理为电流热效应, 即通过电极放电时的强烈发热使水介质气化, 生成膨胀的空泡. 相较于空化泡, 本实验产生的蒸汽泡尺寸大, 溃灭周期长, 且与空化泡具有相同的静、动力学特性, 因此可用于研究空泡溃灭现象.
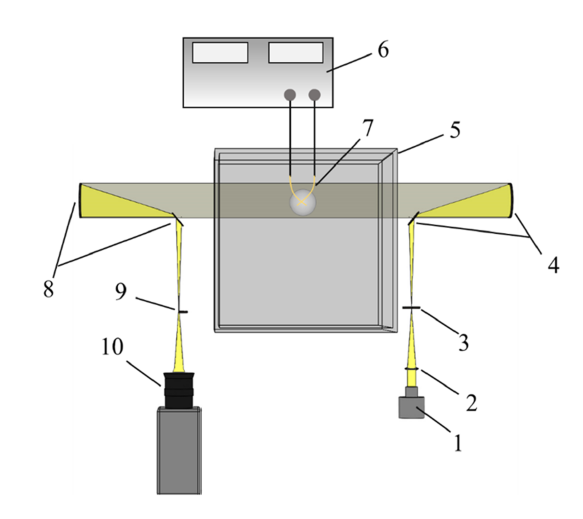
研究中所用水箱材质为透明玻璃, 具有良好的透光性, 其横截面为正方形, 边长为500 mm, 高1000 mm. 本论文研究中, 电火花空泡发生器的充电电容为6600 $\mu$F, 充电电压为220 V, 放电电压为600 V. 水箱内采 用除气蒸馏水, 密度为980 kg/m$^{3}$, 所产生的蒸汽泡最大直径为32 mm, 溃灭周期为3.56 ms. 实验采用纹影显像法对空泡溃灭过程进行观测, 图1 给出了纹影观测平台的原理图. 由于流场受扰动后, 流体密度发生变化, 导致折射率发生改变, 流场的图像也就发生了改变. 如图1 所示, 纹影光路中装置包括光源、透镜、 凹面镜、 狭缝和刀口. 实验时, 光源经过折射和反射后透过实验水箱, 铜丝短接位置在光路中心, 空泡始终处于光照区域内. 采用高速摄像机记录流场图像, 各点灰度值反映流场密度变化, 从而观察到流场的不同状态. 研究中, 由同步触发装置触发电火花空泡发生器和高速摄像机, 以电火花空泡发生器开始放电时刻作为溃灭的初始时刻, 高速摄像机的采集频率为每秒25 000帧, 曝光时间为30 $\mu$s, 镜头采用200 mm焦距.
图1
图1
纹影观测光路原理图 (1-光源; 2-聚焦透镜; 3-狭缝;4-折射镜; 5-实验水箱; 6-电火花空泡发生器; 7-铜丝;8-折射镜; 9-刀口; 10-高速摄像机)
Fig.1
Schematic description of the schlieren observation light path(1-light source; 2-convex lens; 3-slit; 4-reflection mirror;5-water tank; 6-electric spark generator; 7-cooper wires;8-reflection mirror; 9 -knife; 10-high speed camera)
2 数值计算方法
2.1 基本控制方程
本次数值模拟采用了考虑流场弱可压缩性的两相流模型, 根据Kataoka[44 ] 和Caltagirone等[45 ] 提出的弱可压缩流体计算模型构建介质的质量守恒方程, 推导得出数值模拟中采用的控制方程
(1) $\dfrac{\partial p}{\partial t}+\dfrac{1}{\tilde{\chi}} \nabla \cdot u=0$
(2) $\begin{array}{c}\tilde{\rho}\left[\frac{\partial u}{\partial t}+(u \cdot \nabla) u\right]=\rho g-\nabla\left(p^{n}-\frac{\Delta t}{\tilde{\chi}} \nabla \cdot u\right)+ \\\nabla\left[\tilde{\mu}\left(\nabla u+\nabla^{\mathrm{T}} u\right)\right]+F_{\mathrm{TS}}\end{array}$
(3) $\dfrac{\partial c}{\partial t}+u \cdot \nabla C=0$
其中, $\chi $代表流体的绝热压缩系数, $\rho $和$\mu$分别代表流体的密度和黏度, 由于计算中涉及到两相流, 需要对流体的密度及黏度进行定义
(4) $\tilde{\rho} =C \rho_{\rm l}+(1-C) \rho_{\rm g}$
(5) $\tilde{\mu} =C \mu_{\rm l}+(1-C) \mu_{\rm g}$
(6) $\tilde{\chi} =C \chi_{\rm l}+(1-C) \chi_{\rm g}$
其中, $C$代表流体的相变函数, 当计算域为液体时, $C=1$; 当计算域内的流体为气体时, $C=0$. 下标l代表液相, 下标g代表气相. 计算时, 选取$\chi_{\rm g}=9.869\times10^{-6}$ Pa$^{-1}$, $\chi_{\rm l}=0.444 \times 10^{-9}$ Pa$^{-1}$, $\rho_{\rm l}=980$ kg/m$^{3}$, $\rho_{\rm g}=1.30$ kg/m$^{3}$, $\mu_{\rm l}=1.002$ mPa$\cdot$s, $\mu _{\rm g}= 0.018$ mPa$\cdot$s.
(7) $\begin{eqnarray} P^{*}=\dfrac{P}{\rho V_{0}^{2}} \end{eqnarray}$
其中, $V_0$是参考速度, $\rho $是流体密度, $P$为实际压力数值.
在计算过程中选取时间步长作为衡量数值模拟稳定性的参数; 采用均匀交错网格对控制方程进行离散, 对流项进行二阶迎风格式进行离散黏性项由中心差分格式进行离散化. 采用VOF方法进行界面捕捉, 从网格边界处提取速度矢量, 从网格中心处获取流场的压力和密度数值. 流场计算的初始参数设置如表1 所示.
数值模拟数据与实验拍摄得到空泡半径和理想Rayleigh-Plesset方程计算结果如图2 所示. 在图2 中, 实线代表理想R-P方程的计算结果, 点代表实验数据测量得到的空泡半径, 虚线代表本次数值模拟得到的结果. 由曲线对比可知, 在本次研究的重点区域, 即空泡溃灭阶段和二次溃灭阶段, 数据有良好的吻合效果. 本次验证也同样可以说明, 本次选取的自由场空泡溃灭非常接近于理想R-P方程数据, 也同样证明利用理想R-P方程推导得到的能量方程同样可以用到本次研究中.
图2
图2
数值模拟结果与实验数据、经典R-P方程计算结果对比
Fig.2
Comparisons of the numerical, experiment data and Rayleigh-Plesset equation results
在图2 中添加相同时刻3种不同方式得到的空泡半径对比图, 可以观察到, 在起始阶段, R-P方程计算结果与实验数据完全重合, 数值模拟结果与实验数据相差0.2 mm, 相对误差为1.2%. 在空泡接近溃灭阶段, 实验数据与R-P方程计算结果相差为0.01 mm, 相对误差为0.6%, 实验数据与数值模拟结果相差0.03 mm, 相对误差为0.44%. 整个溃灭过程中, 3种方法得到的溃灭时间相差0.05 ms, 相对误差为1.8%. 在最大半径处误差来源主要是由于数值模拟采用了弱可压缩的流动控制方程, 该方程中未考虑温度对模拟结果的影响[46 ] .
2.2 能量计算方法
为求解在空泡溃灭过程中, 各能量的具体数值及转化关系, 在此给出了空泡势能, 流场动能的推导过程. 由于本文所研究的空泡为自由场空泡, 泡型接近标准球形, 因此对空泡势能的推导基于球面坐标下的N-S方程[47 ]
(8) $\begin{array}{l}\frac{\mathrm{D} U_{\theta}}{\mathrm{D} t}=F_{\theta}+\frac{U_{\theta} \cdot U_{r}}{r}+\frac{U \beta^{2} \cot \theta}{r}- \\\quad \frac{1}{\rho \cdot r} \frac{\partial P}{\partial r}+\frac{\mu}{\rho}\left(\nabla^{2} U_{\theta}-\frac{U_{\theta}}{r^{2} \sin \theta}+\frac{2}{r^{2}} \frac{\partial U_{r}}{\partial \theta}-\right. \\\left.\frac{2}{r^{2} \sin \theta} \frac{\partial U_{\beta}}{\partial \beta}\right)\end{array}$
(9) $\begin{array}{l}\frac{\mathrm{D} U_{r}}{\mathrm{D} t}=F_{r}-\frac{1}{\rho} \frac{\partial P}{\partial r}+\frac{U_{\theta}^{2}+U_{\beta}^{2}}{r}+ \\\frac{\mu}{\rho}\left(\nabla^{2} U_{r}-\frac{\partial U_{r}}{\partial r^{2}}-\frac{2}{r^{2} \sin \theta} \frac{\partial U_{\theta} \cdot \sin \theta}{\partial \theta}-\right. \\\left.\frac{2}{r^{2} \sin \theta} \frac{\partial U_{\beta}}{\partial \beta}\right)\end{array}$
(10) $\begin{aligned}\frac{\mathrm{D} U_{\beta}}{\mathrm{D} t}=F_{\beta}+\frac{U_{\beta}\left(U_{r}+U_{\theta} \cdot \cot \theta\right)}{\rho \cdot r}-\\\frac{1}{\rho \cdot r \cdot \sin \theta} \frac{\partial P}{\partial \beta}+\frac{\mu}{\rho}\left(\nabla^{2} U_{\beta}+\right.\\\left.\frac{2}{r^{2} \sin \theta} \frac{\partial U_{r}}{\partial \theta}-\frac{U_{\theta}}{r^{2} \sin ^{2} \theta}-\frac{2 \cos \theta}{r^{2} \sin \theta} \frac{\partial U_{\theta}}{\partial \beta}\right)\end{aligned}$
在之前的研究中, 由于空泡呈现球形溃灭, 因此可以对该公式进行球形简化[48 ]
(11) $\left.\begin{array}{ll}U_{\theta}=0, & U_{\beta}=0 \\\frac{\partial}{\partial \theta}=0, & \frac{\partial}{\partial \beta}=0\end{array}\right\}$
(12) $\begin{eqnarray} \dfrac{{\rm D} U_{r}}{{\rm D} t} &=-\dfrac{1}{\rho} \dfrac{\partial P}{\partial r}+\dfrac{\mu}{\rho}\left[\dfrac{1}{r^{2}} \dfrac{\partial}{\partial r}\left(r^{2} \dfrac{\partial U_{r}}{\partial r}\right)-\dfrac{2 U_{r}}{r^{2}}\right] \end{eqnarray}$
(13) $\begin{eqnarray} U_{r}=\dfrac{F}{r^{2}}, \ \ F(t)=R^{2} \dfrac{{\rm d} R}{{\rm d} t} \end{eqnarray}$
(14) $\begin{eqnarray} \rho\left(R \cdot \ddot{R}+\dfrac{3}{2} \dot{R}^{2}\right)=P_{\rm in}-P_{\infty} \end{eqnarray}$
(15) $\begin{eqnarray} \rho\left(R \cdot \ddot{R}+\dfrac{3}{2} \dot{R}^{2}+\dfrac{4 \mu}{R} \dot{R}+\dfrac{2 \sigma}{R \rho}\right)=P_{\rm in}-P_{\infty}=\Delta P \end{eqnarray}$
该公式即为考虑流场黏性与黏滞性的Rayleigh-Plesset方程[49 ] , 在该公式中, 代表流场密度, 代表流体黏性系数, 代表空泡表面处的张力系数.
空泡势能用以表征空泡对外做功能力, 势能大小是空泡内外驱动压差和空泡半径的函数, 其具体的计算公式[37 ] 为
(16) $\begin{eqnarray} E_{\rm pot}=-\dfrac{4}{3} \pi R^{3}(\Delta P) \end{eqnarray}$
空泡的内外压差很难在实验中直接测量得到, 需要首先求解空泡内外压差. 因为空泡在自由场中的溃灭过程近球体, 在对空泡进行球形简化后, 结合式(6)可得空泡势能计算公式
(17) $\begin{eqnarray} E_{\rm pot} =-\dfrac{4}{3} \pi \rho\left(R^{4} \cdot \ddot{R}+\dfrac{3}{2} \dot{R}^{2} R^{3}+\dfrac{4 \mu}{R} \dot{R} R^{3}+\dfrac{2 \sigma}{\rho} R^{2}\right)\quad \end{eqnarray}$
在实验研究中, 空泡的最大半径小于0.02 m, 实验水箱的长度为0.5 m, 由先前研究[38 ] 可知, 当流场范围大于5倍空泡半径时可以认为水箱壁面对空泡运动不造成影响, 因此可以将流场视为无限远流域, 因此流场动能可以表征空泡在溃灭过程中, 向流场传递的能量大小, 在全流场中, 选择某处距空泡产生中心$r$处流体微团, 其动能为[50 ]
(18) $\begin{eqnarray} {\rm d} e_{\rm kin}=\dfrac{1}{2} \rho u^{2} \end{eqnarray}$
(19) $\begin{eqnarray} r^{2} u=R^{2} \dot{R} \end{eqnarray}$
由此可知距空泡产生中心处半径为$r$处的球面流场的动能总和为[51 ]
(20) $\begin{eqnarray} \dfrac{{\rm d} e_{\rm kin}}{{\rm d}r}=4 \pi r^{2} \cdot {\rm d} e_{\rm kin} \end{eqnarray}$
(21) $\begin{eqnarray} E_{\rm kin}=\int_{R}^{\infty} \dfrac{{\rm d}E_{\rm kin}}{{\rm d}r}{\rm d}r=2 \pi \rho \dot{R}^{2} R^{3} \end{eqnarray}$
3 结果与讨论
3.1 空泡瞬态演化过程
图3 描述了电火花空泡发生器开始放电后空泡的瞬态演变过程. 在$t_{2}=0.04$ ms时, 铜丝由于瞬态电流通过铜丝产生高温, 此时可以观察到明显的发光现象, 并产生了一道细微的冲击波扰动流场. 在之后的0.8 ms内, 空泡逐渐形成, 其内部仍然保持高亮状态, 这表明空泡内部仍存在空泡初生时刻产生的高热能. 随后空泡逐渐膨胀, 在$t_{5}=1.86$ ms处达到半径最大, 此时的空泡直径可达38 mm. 在$t_{9}=3.56$ ms时空泡收缩至最小体积, 此时空泡完成第一次溃灭, 可以观察到明显的溃灭冲击波. 在随后的2.08 ms内, 可以看到由于空泡溃灭造成的冲击波传播, 流场扰动明显. 在$t_{10}=3.60$ ms和$t_{11}=3.64$ ms时刻拍摄的图片中可以看到明显的流场波动. 在$t_{11}=3.64$ ms到$t_{12}=5.64$ ms之间, 回弹空泡再次收缩, 并最终在$t_{12}=5.64$ ms时刻再次溃灭, 并产生了一道强度相对较弱的二次溃灭冲击波.
图3
图3
自由场蒸汽空泡演化过程
Fig.3
Gas bubble evolution process in free field
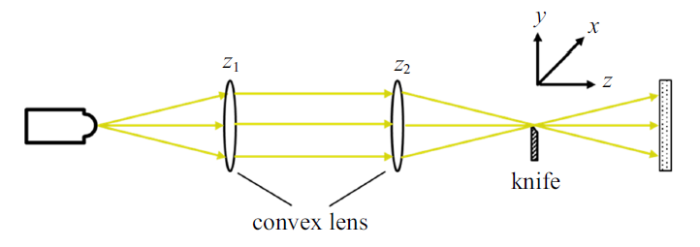
在$t_{11}=3.64$ ms到$t_{12}=5.64$ ms之间, 回弹空泡再次收缩, 并最终在$t_{12}=5.64$ ms时刻再次溃灭, 并产生了一道二次溃灭冲击波. 与$t_{9}=3.56$ ms产生的冲击波形式相同, 表现形式为圆弧形. 纹影光路及坐标轴设置如图4 所示, 在透镜与高速摄像机(成像面)之间焦点处放置竖直刀口, 刀口光阑对光线有空间滤波作用, 通过采用不同方向的刀口光阑, 可以得到法向的折射率场一阶导数空间分布.
图4
图4
纹影法光路图及坐标轴设置
Fig.4
Light path and coordinate axis setting of the schlieren method
系统通过聚焦透镜可以对平面进行聚焦, 在成像图中得到反映该平面垂直于刀口($y$轴方向)的密度梯度变化图像, 用公式表述为[52 -53 ]
(23) $\begin{eqnarray} n \propto \int \sigma(z) \dfrac{\partial \rho(x, y, z)}{\partial x}{\rm d} z \end{eqnarray}$
式中, $n$为折射率, $\sigma(z)$为扩展函数, 该数值与系统测试位置有关. $z$代表纹影系统中平行光源的方向, $x$轴为垂直于刀口的方向. 由式(22)计算可知, 流场内的光线折射率与密度密切相关, 当流场受到扰动发生密度变化时, 折射率也会发生变化.
图像对比度与流场中折射率呈一阶导数分布, 如下式所示[54 ]
(23) $\begin{eqnarray} R_{\rm c}=\pm \dfrac{f}{a} \int \dfrac{1}{n} \dfrac{\partial n}{\partial x_{i}}{\rm d} z \end{eqnarray}$
式中, $R_{\rm c}$是图像对比度, $n$是折射率, $f$是纹影透镜的焦距, $a$是光源图像边缘和刀口边缘之间的距离, 积分区域是光轴方向上试验段的长度. ``$\pm$''表示纹影图像左右两侧的对比度相反. 由于冲击波会引起流体密度的突变, 从而导致折射率分布的变化. 如图5 所示, 在纹影图像中, 冲击波表现为两个对称的圆形(白色虚线标注). 且冲击波强度越高, 造成的流场密度变化就越大, 图像中呈现的对比度就越大. 与$t_{9}=3.56$ ms纹影图相比, $t_{9}=5.64$ ms流场纹影图的对比度明显减小, 对比可知, 二次溃灭时产生的冲击波强度比初次冲击波更弱.
图5
图5
两次不同时刻空泡溃灭时的冲击波图像
Fig.5
Shock wave images when bubble collapse in two different times
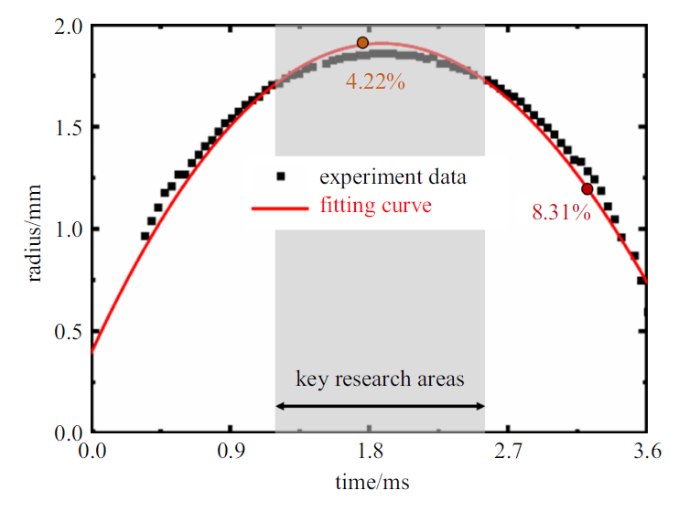
为更好地研究空泡全过程的演化过程, 由于空泡在不同时刻的数据点是离散的, 无法对其进行求导计算速度和加速度, 因此采用多项式拟合的方式对实验数据进行数据拟合, 得到了一条平滑的曲线. 对全过程中空泡的半径进行了测量并对数据进行了拟合. 如图6 所示, 拟合残差集中分布于$\pm$0.05 mm之间, 在重点研究区域0.5$\sim$3.0 ms范围内最大拟合误差为4.22%. 在整个溃灭过程中, 最大拟合误差8.31%位于空泡初生阶段和临近空泡溃灭阶段, 该阶段并不是研究的重点区域, 因此误差在可接受的范围内.
图6
图6
空泡测量半径与多项式拟合曲线
Fig.6
Experiment data of bubble radius and polynomial fitting curve
对拟合曲线的变化趋势及物理支撑进行讨论. 如图7 所示, 给出了拟合曲线半径与实验图像之间的关系, 红色曲线代表拟合数据得到的空泡半径. 拟合半径与实验数据基本一致, 拟合半径整体表现为先减速增大, 后加速增大的状态, 这与实验得到的半径趋势一致. 拟合空泡半径达到最大值的时刻(1.8 ms)与实验数据(1.86 ms)相差为0.06 ms, 拟合数据在最大半径处维持时间(0.09 ms)实验数据 (0.14 ms)相差为0.05 ms, 两数据差较小, 都不会影响本次研究, 因此认为本次拟合数据可以使用.
图7
图7
空泡测量半径与多项式拟合曲线
Fig.7
Experiment data of bubble radius and polynomial fitting curve
对上述数据拟合曲线进行一次及多次求导可得空泡在演化过程中的速度及加速度, 图8 所示为空泡演化过程中的半径、 速度和加速度曲线. 图8 中黑色曲线代表空泡半径的变化, 红色曲线代表空泡边界运动速度, 其中正值代表速度方向指向空泡外部, 蓝色曲线代表空泡运动过程中的边界加速度变化, 正负关系指代加速度方向, 含义与速度方向一致.
图8
图8
自由场空泡溃灭过程半径, 速度与加速度变化曲线
Fig.8
Radius, velocity, and acceleration curve during the bubble collapse in free field
由图8 可知, 自由场空泡在溃灭过程中经历了初生、 膨胀、 收缩和溃灭4个阶段. 在初生阶段, 空泡迅速膨胀, 此时空泡边界运动速度可达15 m/s, 但速度还是不断减小, 边界加速度在空泡发展过程中一直为负值, 因此空泡边界运动速度急剧减小. 在$t_{2}=0.04$ ms时刻, 空泡的加速度达到9 km/s$^{2}$. 之后空泡进入膨胀阶段, 空泡半径增大, 边界运动速度与加速度均呈现逐渐下降的趋势, 空泡膨胀速度减缓, 空泡在$t_{5}=1.86$ ms时刻达到最大半径, 此时空泡运动速度为零. 随后空泡进入收缩阶段, 空泡的边界速度和加速度增大, 方向均指向空泡内部, 即代表空泡呈现加速收缩的状态. 在空泡收缩过程中, 空泡加速度数值逐渐降低, 直至$t_{9}=3.56$ ms时刻, 空泡溃灭.
在加速度曲线中, 可以明显观察到在空泡初生和溃灭阶段存在两个明显的折点, 这是因为这两个时间段内选择的时间步长太大所致. 在空泡初生时刻, 如图9 (a)所示, 由于强烈的发光发热现象出现过曝光现象, 因此无法获取这段时间内空泡的半径变化. 在空泡临近溃灭时刻, 如图9 (b)所示, 由于空泡溃灭速度过快, 摄像机无法拍摄到其半径大小.
图9
图9
(a)空泡过曝光图像; (b)空泡快速溃灭图像
Fig.9
(a) Bubble over exposure image; (b) bubble rapid collapse image
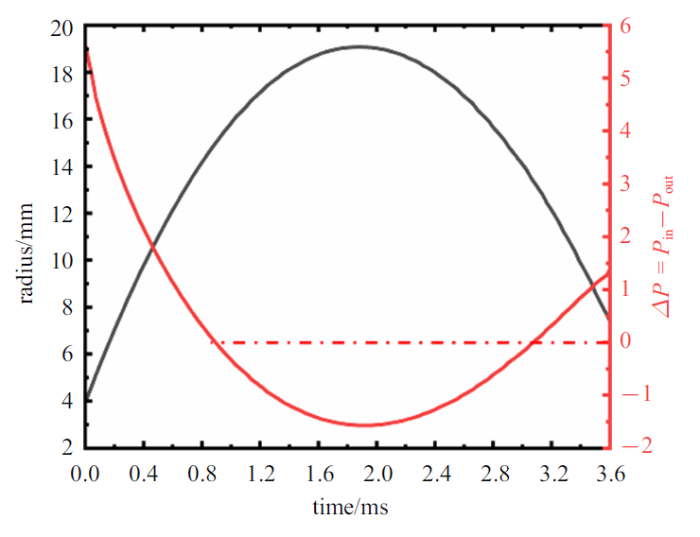
根据式(15)可以计算得到空泡内外压差, 图10 给出空泡在演化过程中空泡内部压力的变化数值, 红色代表空泡内外压差. 根据图10 可知空泡在初生时刻内部压力远远高于外部压力, 空泡在内部压力的推动下不断膨胀, 其内外压差也不断缩小. 在$t_{3}=0.80$ ms时空泡内外压差为零, 此时由于空泡存在惯性仍然会缓慢膨胀, 因此空泡半径仍在不断扩大, 但是空泡内部压力不断减小, 内外压差再次增大. 在$t_{5}=1.86$ ms时, 空泡达到最大半径, 空泡运动速度为零, 此时空泡内外压差也达到最大值. 在之后空泡在外部压强的作用下开始收缩, 空泡的内部压强不断增强, 内外压差逐渐减小. 在$t_{8}=3.08$ ms时刻, 空泡内外压差相同, 其内部压强迅速增强直到空泡溃灭.
图10
图10
空泡溃灭过程空泡内外压差变化
Fig.10
Variation of bubble inside and outside pressure during bubble collapse
3.2 空泡势动能转化过程
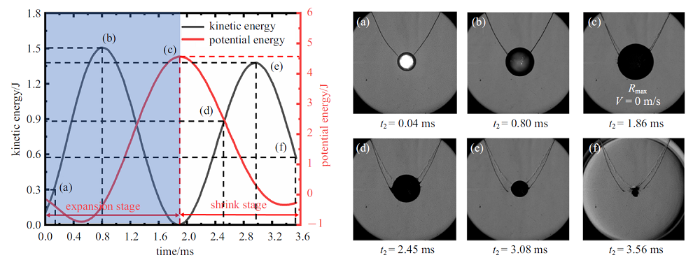
图11 给出了空泡在溃灭过程中的动能和势能变化曲线. 其中黑色线代表空泡在演化过程中流场动能随时间的变化, 红色线代表空泡演化过程中的势能变化. 为解释在空泡演化过程中的势能和动能的转化机制, 对整个过程取6个特征时刻进行分析.
图11
图11
自由场空泡溃灭动能与势能变化图和典型时刻空泡图像
Fig.11
Kinetic energy and potential energy change diagram and bubble image at the typical time during the evolution process
从初始时刻至$t_{2}=0.04$ ms处, 空泡处于初生阶段, 由于高压放电产生的初始瞬态冲击波, 流场动能迅速增大, 此时空泡内部存在高亮区域, 表征此时空泡内存在极高的热能.
在$t_{2}=0.04$ ms与$t_{5}=1.86$ ms, 空泡处于膨胀阶段泡内的亮度逐渐降低, 表征此时空泡内部储存的高热能已经消失, 由于空泡膨胀时间极短, 因此过程可视为绝热过程, 即热能此时并未耗散. 观察空泡势能不断增大, 由此判断该过程内热能转化为空泡的势能. $t_{3}=0.80$ ms时, 流场动能达到最大值1.50 J, 在此之后空泡的膨胀速率减缓, 空泡势能增大, 流场动能不断降低.
空泡达到最大半径$t_{5}=1.86$ ms时, 此时空泡势能达到最大值4.51 J, 空泡边界运动速度为零, 流场动能也随之降低为零. 此时空泡内高亮已全部消失, 可认定热能已全部转化为空泡势能, 可以认定此时的势能是空泡在溃灭过程中储存的最大能量, 并视为空泡在后续收缩溃灭阶段的初始能量来源.
在$t_{5}=1.86$ ms与$t_{9}=3.56$ ms, 空泡处于收缩阶段, 此时空泡势能降低, 流场动能增大, 空泡势能持续向流场动能转化. $t_{8}=3.08$ ms后, 动能出现下降, 此时空泡内势能也在下降, 在Schenke等[39 ] 的研究中, 空泡收缩末期会在空泡周围形成高压区域, 流场动能会在此区域内进行积攒. 在$t_{9}=3.56$ ms时, 空泡发生溃灭, 此时空泡势能基本为零, 空泡周围积攒的动能此刻转化为冲击波能量得以释放, 剩余动能会聚集残余气体, 成为二次溃灭的初始能量.
3.3 空泡溃灭末期流场特征
基于实验结果, 分析得到了空泡在溃灭过程中空泡势能与流场动能的转换机制后, 进而采用数值计算方法对空泡溃灭过程中的流场状态进行模拟, 分析动能在流场中的传播途径和转换区域. 图12 为自由场空泡溃灭过程数值模拟和实验图像的综合分析图像, 两种方法得到的结果吻合很好, 进一步验证了数值模拟的准确性.
图12
图12
流场数值模拟纹影图像(左)和实验图像(右)
Fig.12
Schlieren image of numerical simulation (left) and experimental image (right)
如图12 所示, 空泡在$t_{5}=1.86$ ms进入收缩阶段, 流场中出现了明显的压力波传播过程; 在$t_{8}=3.08$ ms时刻, 由于空泡的加速收缩, 空泡周围出现了大范围的高压区域, 结合图10 中空泡周围压力的变化, 可知该高压区域是导致空泡出现加速收缩状态的主要原因; 在$t_{9}=3.56$ ms时刻, 空泡最终溃灭, 并形成了一道强冲击波. 通过对比实验与数值模拟图像可知, 在空泡在溃灭过程中, 流场波动是流场扰动的直观表现, 从能量转化的角度讲, 波能是流场动能的表现形式.
图13 列出了空泡在临近溃灭时刻的流场压力分布云图. 结合流场数值纹影可知, 在初始时刻空泡内压力小于外部压力, 此时空泡开始收缩并伴随着压力波的出现, 空泡周围的流场发生压力波动变化. 观察流场的压力分布可以发现, 行进波的波前压力大于波后压力, 证明该压力波为稀疏波.
图13
图13
自由场空泡流场压力分布云图(左, $P^{*}={P}/({\rho V_{0}^{2}})$)和流场扰动(右)
Fig.13
Cloud map of pressure distribution during shrinking stage(left, $P^{*}={P}/({\rho V_{0}^{2}})$) and field flow (right)
为进一步分析该高压区域的成因及特性, 提取流场压力梯度云图, 图14 为空泡及流场的压力分布云图. 图中$X$轴和$Y$轴代表流场内坐标, $Z$轴代表压力数值. 由图可知, 在空泡溃灭的过程中空高压区域的面积、压力和速度也在不断变化. 在$t_{5}=1.86$ ms至$t_{9}=3.56$ ms空泡收缩阶段, 随着空泡内部压力的增大, 高压区域的压力也在不断增大, 在$t_{9}=3.56$ ms时刻空泡发生溃灭, 此时高压区域的压力迅速降低, 在冲击波波后形成了低压区域.
图14
图14
空泡收缩过程中空泡及高压区域压力分布云图
Fig.14
Cloud map of pressure distribution during shrinking stage in bubble and high pressure area
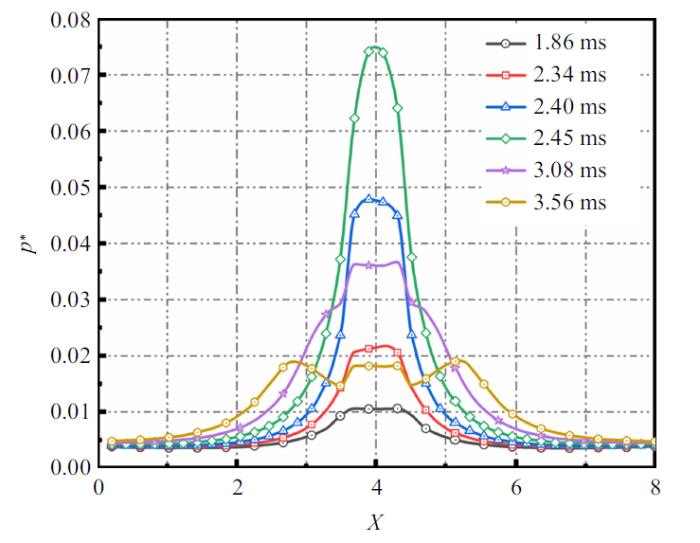
为定量研究空泡周围高压区压力及速度分布特征, 根据图14 中建立的坐标轴, 提取流场沿$x$轴的压力及速度随时间的变化趋势, 如所示. 图15 中展示的为不同时刻下, 流场压力沿$X$轴的分布. 观察图14 中的压力变化, 可以明显观察到在$t_{5}=1.86$ ms至$t_{7}=2.45$ ms阶段, 此时空泡呈现加速收缩的状态, 此时高压区域逐渐显现, 高压区域面积及压力随空泡内部压力增大呈现明显的增大趋势. 在$t_{7}=2.45$ ms至$t_{9}=3.56$ ms阶段, 高压区域压力峰值降低, 面积却呈现明显增大状态. 结合3.2节中对能量的分析, 空泡此时势能不断降低, 高压区域与周围流场呈现明显的高压力梯度, 结合式(16)可知, 此时高压区域势能明显高于外部流场, 证明此时空泡势能转化为高压区域势能.
图15
图15
流场压力沿$X$轴方向分布
Fig.15
Pressure distribution along $X$-axis
此外值得注意的是, 在$t_{9}=3.56$ ms空泡溃灭时刻, 高压区域的压力首先呈现出明显的下降状态, 空泡内部压力降低并不明显. 这证明空泡在溃灭后仍残存一部分势能, 作为空泡二次溃灭的初始能量.
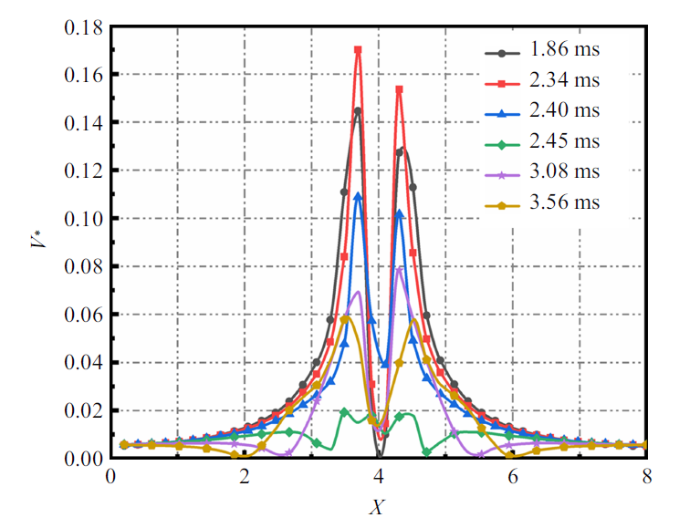
图16 中展示了流场速度沿$X$轴方向分布, 同样可以观察到高压区域速度分布与周围流场呈现明显的高速度梯度. 线条色彩与图15 中代表的含义相同, 根据式(19)可知, 流场的速度随空泡距离增大而下降, 因此曲线峰值代表空泡半径处的无量纲速度. 在$t_{5}=1.86$ ms至$t_{7}=2.45$ ms阶段, 空泡半径速度逐渐降低, 流场速度梯度逐渐降低, 高压区域的流速也逐渐降低, 在$t_{7}=2.45$ ms时刻速度达到最低, 结合图15 中的压力梯度变化, 可以发现此时高压区域速度最低, 压力最大, 可以认为此时空泡势能在不断转化为高压区域的势能, 并在高压区域内进行积攒.
图16
图16
流场速度沿$X$轴方向分布
Fig.16
velocity distribution along $X$-axis
在$t_{7}=2.45$ ms至$t_{9}=3.56$ ms阶段, 高压区域的速度呈现出明显增大的趋势, 结合图15 中的压力梯度变化, 可以发现在此阶段, 高压区域速度增大, 压力降低, 可以认为此时高压区域的势能在不断转化为动能. 在此阶段内, 高压区域内压力和速度在靠近空泡的中心区域迅速降低, 并不断向外部流场推进, 据文献[54 ]中研究结论, 空泡在收缩阶段会不断向外辐射压缩波, 可推测此时高压区内速度峰值即为压缩波的行进速度.
为更直观地研究高压区域内能量的演化关系, 图17 给出了不同时刻高压区域势能和动能的比例. 在图17 中, 横坐标代表时间, 纵坐标代表高压区域内某能量与该能量在流场内总数之比, 黑色曲线代表势能, 红色曲线代表动能. 如图17 所示, 在$t_{5}=1.86$ ms至$t_{7}=2.45$ ms阶段, 高压区域的势能占据流场势能的比例不断增大, 动能占据比例不断减小, 说明高压区域在积攒势能. 在$t_{7}=2.45$ ms至$t_{9}=3.56$ ms阶段内, 势能比例降低, 动能比例增大, 证明高压区域势能转化为高压区域动能.
图17
图17
高压区域内势能和动能转化比例
Fig.17
Conversion ratio of potential energy and kinetic energy in high pressure area
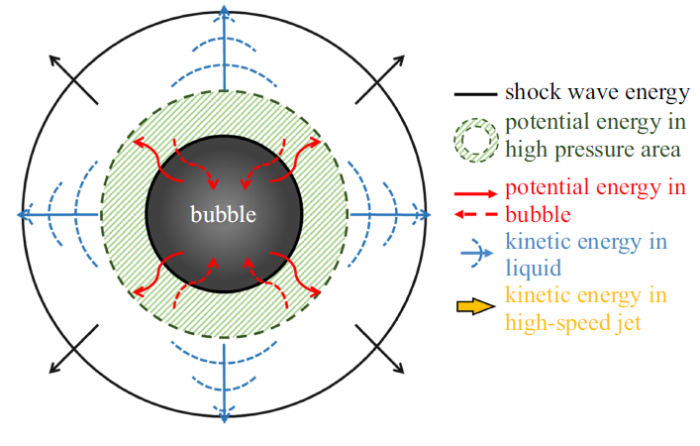
综上所述, 图18 列出了自由场空泡演化过程中的能量转化示意图. 从图18 可以看出: 蒸汽泡在初始时刻由于瞬间高压放电产生极高的热能, 热能一部分转化为流场动能, 动能转化为初始瞬态冲击的波能; 其余储存在空泡内部并随着空泡的演化逐渐转化为空泡势能. 在空泡经历初生、膨胀和收缩阶段时, 空泡的势能逐渐转化为流场的动能. 在空泡收缩阶段, 空泡势能会不断转化为高压区势能, 高压区势能得以积攒, 并在临近溃灭阶段转化为高压区动能, 高压区动能有两种转化方式, 一部分转化为流场动能, 另一部分在溃灭时刻转化为冲击波的波能.
图18
图18
自由场空泡能量转化示意图
Fig.18
Schematic diagram of free field bubble energy transformation
4 结论
本文综合应用实验与数值模拟方法, 深入研究了自由场空泡溃灭过程中能量转化机制. 采用实验与数值模拟结合的方法对自由场空泡的演化过程中的能量转化机制进行了研究, 分别分析了自由场中空泡的演化规律, 势能与动能的转化规律以及在溃灭后期会在空泡附近出现高压区的现象, 得到的主要结论如下:
(1)自由场空泡在自由场中的溃灭演化过程可分为中分为初生、 膨胀、 收缩和溃灭4个阶段. 在空泡膨胀过程中, 空泡半径运动速度逐渐减小, 在收缩阶段中空泡半径运动速度逐渐增大, 空泡内部压力先减小后增大.
(2)在空泡产生初期, 热能转化为空泡势能. 空泡膨胀过程中, 空泡势能增大, 流场动能降低. 在空泡最大半径处空泡势能最大, 流场动能为零; 在空泡收缩至溃灭阶段, 空泡势能和流场动能不断降低, 并最终转化为冲击波波能. 剩余能量会积攒为空泡二次溃灭的初始能量.
(3) 在空泡收缩直至溃灭的过程中, 会在空泡周围形成高压区域, 该区域是空泡与流场能量转化的重要媒介. 空泡势能无法直接转化为流场动能, 而是会在该区域不断积攒为高压区势能, 在临近溃灭时刻高压区势能会转化为流场动能和冲击波波能.
参考文献
View Option
[1]
Huang B Young YL Wang GY , et al . Combined experimental and computational investigation of unsteady structure of sheet/cloud cavitation
Journal of Fluids Engineering 2013 ,135 (7 ):071301
DOI
URL
[本文引用: 1]
[2]
Callenaere M Franc JP Michel JM , et al . The cavitation instability induced by the development of a re-entrant jet
Journal of Fluid Mechanics 2001 ,444 :223 -256
DOI
URL
[本文引用: 1]
[3]
Ma XJ Huang B Zhao X , et al . Comparisons of spark-charge bubble dynamics near the elastic and rigid boundaries
Ultrasonics Sonochemistry 2018 ,43 :80 -90
DOI
URL
[本文引用: 1]
[4]
Tiwari A Pantano C Freund JB . Growth-and-collapse dynamics of small bubble clusters near a wall
Journal of Fluid Mechanics 2015 ,775 :1 -23
DOI
URL
[本文引用: 1]
[5]
Rayleigh L , On the pressure developed in a liquid during the collapse of a spherical cavity
Phil. Mag 1917 ,34 (200 ):94 -98
DOI
URL
[本文引用: 2]
[6]
Koukouvinis P Gavaises M Supponen O , et al . Simulation of bubble expansion and collapse in the vicinity of a free surface
Physics of Fluids 2016 ,28 (5 ):052103
DOI
URL
[本文引用: 1]
[7]
Beig SA Aboulhasanzadeh B Johnsen E , Temperatures produced by inertially collapsing bubbles near rigid surfaces
Journal of Fluid Mechanics 2018 ,852 :105 -125
DOI
URL
[本文引用: 1]
[8]
Cao S Wang G Coutier-Delgosha O , et al . Shock-induced bubble collapse near solid materials: Effect of acoustic impedance
Journal of Fluid Mechanics 2020 ,907
[本文引用: 1]
[9]
Tian ZL Liu YL Zhang AM , et al . Energy dissipation of pulsating bubbles in compressible fluids using the Eulerian finite-element method
Ocean Engineering 2020 , 196 (Jan.15): 106714.1-106714.12
[本文引用: 1]
[10]
Fu L Wang S Xin J , et al . Experimental investigation on multiple breakdown in water induced by focused nanosecond laser
Optics Express 2018 ,26 (22 ):28560
DOI
URL
[本文引用: 1]
[11]
Plesset MS . On the stability of fluid flows with spherical symmetry
Journal of Applied Physics 1954 ,25 (1 ):96 -98
DOI
URL
[本文引用: 1]
[12]
Ma XJ Huang B Wang GY , et al . Experimental investigation of conical bubble structure and acoustic flow structure in ultrasonic field
Ultrasonics Sonochemistry 2017 ,34 :164 -172
DOI
URL
[本文引用: 1]
[13]
Zhang AM Wu WB Liu YL , et al . Nonlinear interaction between underwater explosion bubble and structure based on fully coupled model
Physics of Fluids 2017 ,29 (8 ):082111
DOI
URL
[本文引用: 1]
[14]
Huang GH Zhang MD Ma XJ , et al . Dynamic behavior of a single bubble between the free surface and rigid wall
Ultrasonics Sonochemistry 2020 ,67 :105147
DOI
URL
[本文引用: 1]
[15]
Orthaber U Zevnik J Petkovek R , et al . Cavitation bubble collapse in a vicinity of a liquid-liquid interface — Basic research into emulsification process
Ultrasonics Sonochemistry 2020 ,68 :105224
DOI
PMID
[本文引用: 1]
The initial motivation for the study was to gain deeper understanding into the background of emulsion preparation by ultrasound (cavitation). In our previous work (Perdih et al., 2019) we observed rich phenomena occurring near the liquid-liquid interface which was exposed to ultrasonic cavitation. Although numerous studies of bubble dynamics in different environments (presence of free surface, solid body, shear flow and even variable gravity field) exist, one can find almost no reports on the interaction of a bubble with a liquid-liquid interface. In the present work we conducted a number of experiments where single cavitation bubble dynamics was observed on each side of the oil-water interface. These were accompanied by corresponding simulations. We investigated the details of bubble interface interaction (deformation, penetration). As predicted, by the anisotropy parameter the bubble always jets toward the interface if it grows in the lighter liquid and correspondingly away from the interface if it is initiated inside the denser liquid. We extended the analysis to the relationships of various bubble characteristics and the anisotropy parameter. Finally, based on the present and our previous study (Perdih et al., 2019), we offer new insights into the physics of ultrasonic emulsification process.Copyright © 2020 The Authors. Published by Elsevier B.V. All rights reserved.
[16]
Vogel A Lauterborn W Timm R . Optical and acoustic investigations of the dynamics of laser-produced cavitation bubbles near a solid boundary
Journal of Fluid Mechanics 1989 ,206 :299 -338
DOI
URL
[本文引用: 1]
[17]
Johnsen E Colonius T . Numerical simulations of non-spherical bubble collapse
Journal of Fluid Mechanics 2009 ,629 (629 ):231 -262
DOI
URL
[本文引用: 1]
[18]
Li FZ Fan HY Guo YQ , et al . Water-Jet cavitation shock bulging as novel microforming technique
Chinese Journal of Mechanical Engineering 2021 ,34 (1 ):4
DOI
URL
[本文引用: 1]
[19]
Ohl CD Kurz T Geisler R , et al . Bubble dynamics, shock waves and sonoluminescence
Philosophical Transactions of the Royal Society A 1999 ,357 (1751 ):269 -294
DOI
URL
[本文引用: 1]
[20]
Supponen O Obreschkow D Kobel P , et al . Shock waves from non-spherical cavitation bubbles//Meeting of the Aps Division of Fluid Dynamics
American Physical Society , 2017
[本文引用: 2]
[21]
Franc JP Riondet M Karimi A , et al . Impact load measurements in an erosive cavitating flow
Journal of Fluids Engineering 2011 ,133 (12 ):121301
DOI
URL
[本文引用: 1]
[22]
Klaseboer E Fong SW Turangan CK , et al . Interaction of lithotripter shockwaves with single inertial cavitation bubbles
Journal of Fluid Mechanics 2007 ,593 (593 ):33 -56
DOI
URL
[本文引用: 1]
[23]
Fortes-Patella R Challier G Reboud JL , et al . Energy balance in cavitation erosion: From bubble collapse to indentation of material surface
Journal of Fluids Engineering 2013 ,135 (1 ):011303
DOI
URL
[本文引用: 1]
[24]
Cui P Zhang AM Wang S , et al . Ice breaking by a collapsing bubble
Journal of Fluid Mechanics 2018 ,841 :287 -309
DOI
URL
[本文引用: 1]
[25]
Long J Eliceiri MH Wang L , et al . Capturing the final stage of the collapse of cavitation bubbles generated during nanosecond laser ablation of submerged targets
Optics & Laser Technology 2021 ,134 :106647
[本文引用: 1]
[26]
Sagar HJ Moctar OE . Dynamics of a cavitation bubble near a solid surface and the induced damage
Journal of Fluids and Structures 2020 ,92 :102799
DOI
URL
[本文引用: 1]
[27]
Liu Z Guan X Zhang L , et al . Investigations of dynamics of a single spark-induced bubble in saline water
Journal of Physics D$:$ Applied Physics 2020 ,54 (7 ):075203
[本文引用: 1]
[28]
Plesset MS . The dynamics of cavitation bubbles
Journal of Applied Mechanics 1949 ,16 :277 -282
DOI
URL
[本文引用: 1]
[29]
Khoroshev GA . Collapse of vapor-air cavitation bubbles (Collapse of single spherical vapor-air cavitation bubble, computing bubble movement and pressure as function of air content)
Soviet Physics-Acoustics 1964 ,9 :275 -279
[本文引用: 1]
[30]
Neppiras EA Noltingk BE . Cavitation produced by ultrasonics: theoretical conditions for the onset of cavitation
Proceedings of the Physical Society. Section B 1951 ,64 (12 ):1032
DOI
URL
[本文引用: 1]
[31]
Apfel RE . Acoustic cavitation. Methods in experimental physics
Academic Press 1981 ,19 :355 -411
[本文引用: 1]
[32]
Gaudron R Warnez MT , et al . Bubble dynamics in a viscoelastic medium with nonlinear elasticity
Journal of Fluid Mechanics 2015 ,766 :54 -75
DOI
URL
[本文引用: 1]
[33]
Fujikawa S Akamatsu T . Effects of the non-equilibrium condensation of vapour on the pressure wave produced by the collapse of a bubble in a liquid
Journal of Fluid Mechanics 1980 ,97 (3 ):481 -512
DOI
URL
[本文引用: 1]
[34]
Beig SA Aboulhasanzadeh B Johnsen E . Temperatures produced by inertially collapsing bubbles near rigid surfaces
Journal of Fluid Mechanics 2018 ,852 :105 -125
DOI
URL
[本文引用: 1]
[35]
Pineda S Marongiu JC Aubert S , et al . Simulation of a gas bubble compression in water near a wall using the SPH-ALE method
Computers & Fluids 2018 ,179 :459 -475
DOI
URL
[本文引用: 1]
[36]
Morenko IV . Numerical simulation of the propagation of pressure waves in water during the collapse of a spherical air cavity
Ocean Engineering 2020 ,215 :107905
DOI
URL
[本文引用: 1]
[37]
Tian ZL Liu YL Zhang AM , et al . Energy dissipation of pulsating bubbles in compressible fluids using the Eulerian finite-element method
Ocean Engineering 2020 ,196 :106714
DOI
URL
[本文引用: 2]
[38]
Fortes Patella R Reboud JL . A new approach to evaluate the cavitation erosion power
Journal of Fluids Engineering 1998 ,120 (2 ):335 -344
DOI
URL
[本文引用: 2]
[39]
Schenke S Melissaris T Terwisga T . On the relevance of kinematics for cavitation implosion loads
Physics of Fluids 2019 ,31 (5 ):052102
DOI
URL
[本文引用: 3]
[40]
Zhang J Zhang L Deng J . Numerical study of the collapse of multiple bubbles and the energy conversion during bubble collapse
Water 2019 ,11 (2 ):w11020247
[本文引用: 1]
[41]
季斌 , 程怀玉 , 黄彪 等 . 空化水动力学非定常特性研究进展及展望
力学进展 , 2019 ,49 :201906
[本文引用: 1]
( Ji Bin Cheng Huaiyu Huang Biao , et al . Research progresses and prospects of unsteady hydrodynamics characteristics for cavitation
Advances in Mechanics 2019 ,49 :201906 (in Chinese))
[本文引用: 1]
[42]
姚熊亮 , 刘文韬 , 张阿漫 等 . 水下爆炸气泡及其对结构毁伤研究综述
中国舰船研究 , 2016 ,11 (1 ):36 -45
[本文引用: 1]
( Yao Xiongliang Liu Wentao Zhang Aman , et al . Review of the research on underwater explosion bubbles and the corresponding structural damage
Chinese Journal of Ship Research 2016 ,11 (1 ):36 -45 (in Chinese))
[本文引用: 1]
[43]
张凌新 , 张靖 , 邵雪明 . 空泡溃灭过程中的压力波能分析
空气动力学学报 , 2020 ,38 (4 ):807 -813
[本文引用: 1]
( Zhang Lingxin Zhang Jing Shao Xueming . The analysis of pressure wave energy during the collapse of cavitation bubble
Acta Aerodynamica Sinica 2020 ,38 (4 ):807 -813 (in Chinese))
[本文引用: 1]
[44]
Kataoka I . Local instant formulation of two-phase flow
International Journal of Multiphase Flow 1986 ,12 (5 ):745 -758
DOI
URL
[本文引用: 1]
[45]
Caltagirone JP Vincent S Caruyer C . A multiphase compressible model for the simulation of multiphase flows
Computers & Fluids 2011 ,50 (1 ):24 -34
DOI
URL
[本文引用: 1]
[46]
Zhang MD Chang Q Ma XJ , et al . Physical investigation of the counterjet dynamics during the bubble rebound
Ultrasonics Sonochemistry 2019 ,58 :104706
DOI
URL
[本文引用: 1]
[47]
Johnsen E . Numerical simulations of non-spherical bubble collapse: With applications to shockwave lithotripsy
California Institute of Technology , 2008
[本文引用: 1]
[48]
Qiu SC Ma XJ Huang B , et al . Numerical simulation of single bubble dynamics under acoustic standing waves
Ultrasonics Sonochemistry 2018 : S1350417718308058
[本文引用: 1]
[49]
Orimi HE Narayanswamy S Boutopoulos C . Hybrid analytical/numerical modeling of nanosecond laser-induced micro-jets generated by liquid confining devices
Journal of Fluids and Structures 2020 ,98 :103079
DOI
URL
[本文引用: 1]
[50]
Choi J Ceccio SL . Dynamics and noise emission of vortex cavitation bubbles
Journal of Fluid Mechanics 2007 ,575 (575 ):1 -26
DOI
URL
[本文引用: 1]
[51]
Melissaris T Schenke S Bulten N , et al . On the accuracy of predicting cavitation impact loads on marine propellers
Wear 2020 ,456 :203393
[本文引用: 1]
[52]
Mauger C Méès L Michard M , et al , Schlieren and interferometry in a 2D cavitating channel flow
Exp. Fluids 2012 ,53 :1895 -1913
DOI
URL
[本文引用: 1]
[53]
Panda J Seasholtz RG . Experimental investigation of density fluctuations in high-speed jets and correlation with generated noise
Journal of Fluid Mechanics 2002 ,450 :97 -130
DOI
URL
[本文引用: 1]
[54]
Huang G Zhang MD Han L , et al . Physical investigation of acoustic waves induced by the oscillation and collapse of the single bubble
Ultrasonics Sonochemistry 2020 : 105440
[本文引用: 2]
[55]
张佳悦 , 李达钦 , 吴钦 等 . 航行体回收垂直入水空泡流场及水动力特性研究
力学学报 , 2019 ,51 (3 ):803 -812
( Zhang Jiayue Li Daqin Wu Qin , et al . Numerical investigation on cavity structures and hyrodynamics of the vehicle during vertical water-entry
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (3 ):803 -812 (in Chinese))
[56]
郭文璐 , 李泓辰 , 王静竹 等 . 单空泡与自由液面相互作用规律研究进展
力学学报 , 2019 ,51 (6 ):1682 -1698
( Guo Wenlu Li Hongchen Wang Jingzhu , et al . Reaserch progress on interaction between a single cavitation and free surface
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (6 ):1682 -1698 (in Chinese))
[57]
王悦柔 , 王军锋 , 刘海龙 . 电场作用下气泡上升行为特性的数值计算研究
力学学报 , 2020 ,52 (1 ):31 -39
( Wang Yuerou Wang Junfeng Liu Hailong . Numerical simulation on bubble rinsing behaviors under electric field
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (1 ):31 -39 (in Chinese))
Combined experimental and computational investigation of unsteady structure of sheet/cloud cavitation
1
2013
... 以液体为工作介质的水力机械, 由于旋转速度较高, 极易在与液体接触的表面形成空化现象, 这会给水利机械带来空蚀损伤[1 ] , 严重影响机械结构的寿命和稳定性, 因此如何计算空化强度, 评估空泡溃灭带来的能量冲击成为流体力学中重要的研究方向. 依据空间尺度不同, 空化运动主要表现为宏观空化对流旋涡运动[2 ] 和介观空泡脉动[3 ] , 其中大尺度的空穴是由大量空泡汇聚而成的[4 ] . 在1917年Rayleigh[5 ] 首先分析了在自由场中空泡溃灭的动力学行为, 建立了基于不可压缩理想流体、忽略表面张力和黏性情况下的球形空泡溃灭常微分方程. 随后的研究者分别应用实验与数值模拟的方法对复杂边界条件附近空泡溃灭的动力学行为开展了深入研究, 发现在整个空泡溃灭过程中存在空泡脉动[6 ] 、 高速射流[7 ] 及冲击波[8 ] 等多种载荷形式, 整个过程中包含复杂的能量转化机制, 是空泡动力学研究中的重要课题[9 -10 ] . ...
The cavitation instability induced by the development of a re-entrant jet
1
2001
... 以液体为工作介质的水力机械, 由于旋转速度较高, 极易在与液体接触的表面形成空化现象, 这会给水利机械带来空蚀损伤[1 ] , 严重影响机械结构的寿命和稳定性, 因此如何计算空化强度, 评估空泡溃灭带来的能量冲击成为流体力学中重要的研究方向. 依据空间尺度不同, 空化运动主要表现为宏观空化对流旋涡运动[2 ] 和介观空泡脉动[3 ] , 其中大尺度的空穴是由大量空泡汇聚而成的[4 ] . 在1917年Rayleigh[5 ] 首先分析了在自由场中空泡溃灭的动力学行为, 建立了基于不可压缩理想流体、忽略表面张力和黏性情况下的球形空泡溃灭常微分方程. 随后的研究者分别应用实验与数值模拟的方法对复杂边界条件附近空泡溃灭的动力学行为开展了深入研究, 发现在整个空泡溃灭过程中存在空泡脉动[6 ] 、 高速射流[7 ] 及冲击波[8 ] 等多种载荷形式, 整个过程中包含复杂的能量转化机制, 是空泡动力学研究中的重要课题[9 -10 ] . ...
Comparisons of spark-charge bubble dynamics near the elastic and rigid boundaries
1
2018
... 以液体为工作介质的水力机械, 由于旋转速度较高, 极易在与液体接触的表面形成空化现象, 这会给水利机械带来空蚀损伤[1 ] , 严重影响机械结构的寿命和稳定性, 因此如何计算空化强度, 评估空泡溃灭带来的能量冲击成为流体力学中重要的研究方向. 依据空间尺度不同, 空化运动主要表现为宏观空化对流旋涡运动[2 ] 和介观空泡脉动[3 ] , 其中大尺度的空穴是由大量空泡汇聚而成的[4 ] . 在1917年Rayleigh[5 ] 首先分析了在自由场中空泡溃灭的动力学行为, 建立了基于不可压缩理想流体、忽略表面张力和黏性情况下的球形空泡溃灭常微分方程. 随后的研究者分别应用实验与数值模拟的方法对复杂边界条件附近空泡溃灭的动力学行为开展了深入研究, 发现在整个空泡溃灭过程中存在空泡脉动[6 ] 、 高速射流[7 ] 及冲击波[8 ] 等多种载荷形式, 整个过程中包含复杂的能量转化机制, 是空泡动力学研究中的重要课题[9 -10 ] . ...
Growth-and-collapse dynamics of small bubble clusters near a wall
1
2015
... 以液体为工作介质的水力机械, 由于旋转速度较高, 极易在与液体接触的表面形成空化现象, 这会给水利机械带来空蚀损伤[1 ] , 严重影响机械结构的寿命和稳定性, 因此如何计算空化强度, 评估空泡溃灭带来的能量冲击成为流体力学中重要的研究方向. 依据空间尺度不同, 空化运动主要表现为宏观空化对流旋涡运动[2 ] 和介观空泡脉动[3 ] , 其中大尺度的空穴是由大量空泡汇聚而成的[4 ] . 在1917年Rayleigh[5 ] 首先分析了在自由场中空泡溃灭的动力学行为, 建立了基于不可压缩理想流体、忽略表面张力和黏性情况下的球形空泡溃灭常微分方程. 随后的研究者分别应用实验与数值模拟的方法对复杂边界条件附近空泡溃灭的动力学行为开展了深入研究, 发现在整个空泡溃灭过程中存在空泡脉动[6 ] 、 高速射流[7 ] 及冲击波[8 ] 等多种载荷形式, 整个过程中包含复杂的能量转化机制, 是空泡动力学研究中的重要课题[9 -10 ] . ...
On the pressure developed in a liquid during the collapse of a spherical cavity
2
1917
... 以液体为工作介质的水力机械, 由于旋转速度较高, 极易在与液体接触的表面形成空化现象, 这会给水利机械带来空蚀损伤[1 ] , 严重影响机械结构的寿命和稳定性, 因此如何计算空化强度, 评估空泡溃灭带来的能量冲击成为流体力学中重要的研究方向. 依据空间尺度不同, 空化运动主要表现为宏观空化对流旋涡运动[2 ] 和介观空泡脉动[3 ] , 其中大尺度的空穴是由大量空泡汇聚而成的[4 ] . 在1917年Rayleigh[5 ] 首先分析了在自由场中空泡溃灭的动力学行为, 建立了基于不可压缩理想流体、忽略表面张力和黏性情况下的球形空泡溃灭常微分方程. 随后的研究者分别应用实验与数值模拟的方法对复杂边界条件附近空泡溃灭的动力学行为开展了深入研究, 发现在整个空泡溃灭过程中存在空泡脉动[6 ] 、 高速射流[7 ] 及冲击波[8 ] 等多种载荷形式, 整个过程中包含复杂的能量转化机制, 是空泡动力学研究中的重要课题[9 -10 ] . ...
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
Simulation of bubble expansion and collapse in the vicinity of a free surface
1
2016
... 以液体为工作介质的水力机械, 由于旋转速度较高, 极易在与液体接触的表面形成空化现象, 这会给水利机械带来空蚀损伤[1 ] , 严重影响机械结构的寿命和稳定性, 因此如何计算空化强度, 评估空泡溃灭带来的能量冲击成为流体力学中重要的研究方向. 依据空间尺度不同, 空化运动主要表现为宏观空化对流旋涡运动[2 ] 和介观空泡脉动[3 ] , 其中大尺度的空穴是由大量空泡汇聚而成的[4 ] . 在1917年Rayleigh[5 ] 首先分析了在自由场中空泡溃灭的动力学行为, 建立了基于不可压缩理想流体、忽略表面张力和黏性情况下的球形空泡溃灭常微分方程. 随后的研究者分别应用实验与数值模拟的方法对复杂边界条件附近空泡溃灭的动力学行为开展了深入研究, 发现在整个空泡溃灭过程中存在空泡脉动[6 ] 、 高速射流[7 ] 及冲击波[8 ] 等多种载荷形式, 整个过程中包含复杂的能量转化机制, 是空泡动力学研究中的重要课题[9 -10 ] . ...
Temperatures produced by inertially collapsing bubbles near rigid surfaces
1
2018
... 以液体为工作介质的水力机械, 由于旋转速度较高, 极易在与液体接触的表面形成空化现象, 这会给水利机械带来空蚀损伤[1 ] , 严重影响机械结构的寿命和稳定性, 因此如何计算空化强度, 评估空泡溃灭带来的能量冲击成为流体力学中重要的研究方向. 依据空间尺度不同, 空化运动主要表现为宏观空化对流旋涡运动[2 ] 和介观空泡脉动[3 ] , 其中大尺度的空穴是由大量空泡汇聚而成的[4 ] . 在1917年Rayleigh[5 ] 首先分析了在自由场中空泡溃灭的动力学行为, 建立了基于不可压缩理想流体、忽略表面张力和黏性情况下的球形空泡溃灭常微分方程. 随后的研究者分别应用实验与数值模拟的方法对复杂边界条件附近空泡溃灭的动力学行为开展了深入研究, 发现在整个空泡溃灭过程中存在空泡脉动[6 ] 、 高速射流[7 ] 及冲击波[8 ] 等多种载荷形式, 整个过程中包含复杂的能量转化机制, 是空泡动力学研究中的重要课题[9 -10 ] . ...
Shock-induced bubble collapse near solid materials: Effect of acoustic impedance
1
2020
... 以液体为工作介质的水力机械, 由于旋转速度较高, 极易在与液体接触的表面形成空化现象, 这会给水利机械带来空蚀损伤[1 ] , 严重影响机械结构的寿命和稳定性, 因此如何计算空化强度, 评估空泡溃灭带来的能量冲击成为流体力学中重要的研究方向. 依据空间尺度不同, 空化运动主要表现为宏观空化对流旋涡运动[2 ] 和介观空泡脉动[3 ] , 其中大尺度的空穴是由大量空泡汇聚而成的[4 ] . 在1917年Rayleigh[5 ] 首先分析了在自由场中空泡溃灭的动力学行为, 建立了基于不可压缩理想流体、忽略表面张力和黏性情况下的球形空泡溃灭常微分方程. 随后的研究者分别应用实验与数值模拟的方法对复杂边界条件附近空泡溃灭的动力学行为开展了深入研究, 发现在整个空泡溃灭过程中存在空泡脉动[6 ] 、 高速射流[7 ] 及冲击波[8 ] 等多种载荷形式, 整个过程中包含复杂的能量转化机制, 是空泡动力学研究中的重要课题[9 -10 ] . ...
Energy dissipation of pulsating bubbles in compressible fluids using the Eulerian finite-element method
1
2020
... 以液体为工作介质的水力机械, 由于旋转速度较高, 极易在与液体接触的表面形成空化现象, 这会给水利机械带来空蚀损伤[1 ] , 严重影响机械结构的寿命和稳定性, 因此如何计算空化强度, 评估空泡溃灭带来的能量冲击成为流体力学中重要的研究方向. 依据空间尺度不同, 空化运动主要表现为宏观空化对流旋涡运动[2 ] 和介观空泡脉动[3 ] , 其中大尺度的空穴是由大量空泡汇聚而成的[4 ] . 在1917年Rayleigh[5 ] 首先分析了在自由场中空泡溃灭的动力学行为, 建立了基于不可压缩理想流体、忽略表面张力和黏性情况下的球形空泡溃灭常微分方程. 随后的研究者分别应用实验与数值模拟的方法对复杂边界条件附近空泡溃灭的动力学行为开展了深入研究, 发现在整个空泡溃灭过程中存在空泡脉动[6 ] 、 高速射流[7 ] 及冲击波[8 ] 等多种载荷形式, 整个过程中包含复杂的能量转化机制, 是空泡动力学研究中的重要课题[9 -10 ] . ...
Experimental investigation on multiple breakdown in water induced by focused nanosecond laser
1
2018
... 以液体为工作介质的水力机械, 由于旋转速度较高, 极易在与液体接触的表面形成空化现象, 这会给水利机械带来空蚀损伤[1 ] , 严重影响机械结构的寿命和稳定性, 因此如何计算空化强度, 评估空泡溃灭带来的能量冲击成为流体力学中重要的研究方向. 依据空间尺度不同, 空化运动主要表现为宏观空化对流旋涡运动[2 ] 和介观空泡脉动[3 ] , 其中大尺度的空穴是由大量空泡汇聚而成的[4 ] . 在1917年Rayleigh[5 ] 首先分析了在自由场中空泡溃灭的动力学行为, 建立了基于不可压缩理想流体、忽略表面张力和黏性情况下的球形空泡溃灭常微分方程. 随后的研究者分别应用实验与数值模拟的方法对复杂边界条件附近空泡溃灭的动力学行为开展了深入研究, 发现在整个空泡溃灭过程中存在空泡脉动[6 ] 、 高速射流[7 ] 及冲击波[8 ] 等多种载荷形式, 整个过程中包含复杂的能量转化机制, 是空泡动力学研究中的重要课题[9 -10 ] . ...
On the stability of fluid flows with spherical symmetry
1
1954
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Experimental investigation of conical bubble structure and acoustic flow structure in ultrasonic field
1
2017
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Nonlinear interaction between underwater explosion bubble and structure based on fully coupled model
1
2017
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Dynamic behavior of a single bubble between the free surface and rigid wall
1
2020
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Cavitation bubble collapse in a vicinity of a liquid-liquid interface — Basic research into emulsification process
1
2020
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Optical and acoustic investigations of the dynamics of laser-produced cavitation bubbles near a solid boundary
1
1989
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Numerical simulations of non-spherical bubble collapse
1
2009
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Water-Jet cavitation shock bulging as novel microforming technique
1
2021
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Bubble dynamics, shock waves and sonoluminescence
1
1999
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Shock waves from non-spherical cavitation bubbles//Meeting of the Aps Division of Fluid Dynamics
2
2017
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
... [20 ]在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Impact load measurements in an erosive cavitating flow
1
2011
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Interaction of lithotripter shockwaves with single inertial cavitation bubbles
1
2007
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Energy balance in cavitation erosion: From bubble collapse to indentation of material surface
1
2013
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Ice breaking by a collapsing bubble
1
2018
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Capturing the final stage of the collapse of cavitation bubbles generated during nanosecond laser ablation of submerged targets
1
2021
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Dynamics of a cavitation bubble near a solid surface and the induced damage
1
2020
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
Investigations of dynamics of a single spark-induced bubble in saline water
1
2020
... 在对空泡溃灭过程中动力学行为的实验研究中, 研究者大多使用高速摄像机拍摄空泡在自由场[11 ] , 边界附近[12 -13 ] 和多相界面间[14 -15 ] 的演化形态. Vogel等[16 ] 使用高速摄像机首次拍摄到空泡在刚性壁面附近的膨胀、 收缩和溃灭形态, 发现空泡溃灭后期会形成指向壁面的速度高达100 m/s的高速射流, 并由此推断高速射流是造成壁面损伤的主要原因. Johnsen和Colonius[17 ] 研究了空泡在刚性壁面处溃灭时造成的破坏程度, 发现空泡内外压差、空泡脉动速度和射流强度会对壁面造成不同程度的损伤. 在最新研究中, Li等[18 ] 使用厚度为100 $\mu$m的TA2型钛箔作为边界, 通过对边界变形进行三维扫描, 观察到高速射流冲击后形成的轮廓和成形深度, 结合材料力学性能发现冲击强度最高可达20 MPa. 随着高速摄影技术的提高, Ohl等[19 ] 和Supponen等[20 ] 使用纹影高速摄像方法捕捉到在空泡发生溃灭时刻流场中出现明显的冲击波现象. 法国LEGI实验室的Franc等[21 ] 利用微型压力传感器对不锈钢孔板空化射流中空泡溃灭所形成的冲击波进行了测量, 发现其冲击压力幅值高达500 N. Supponen等[20 ] 在监测刚性壁面上压力变化的过程中, 发现在整个过程中出现了两次明显的压力幅值, 证明冲击波也是造成壁面损伤的重要来源. Klaseboer等[22 ] 使用水听器测量了空泡溃灭过程中流场内的压力脉动数据, 观察到高达100 MPa压力尖峰. Fortes-Patella等[23 ] 给出了一种压力波能量计算方法, 并计算了在铜、 铝和不锈钢3种边界条件下, 空泡溃灭产生的压力波的冲击能量, 发现冲击波能占到总能的81%, 由此建立了压力波对壁面的损伤模型. 为深入研究空泡溃灭冲击能量对材料的冲击效应, Cui等[24 ] 将空泡应用于破冰方向, 通过观察冰面裂纹及冲击凹坑, 发现气泡破裂过程中产生的射流和激波会造成不同方式的损伤. Long等[25 ] 使用电子显微镜对冲击位置进行了观察, 得到了不同尺寸空泡对壁面的损伤程度. Sagar和Moctar[26 ] 综合运用水听器和X光三维扫描技术, 通过扫描刚性壁面的凹坑深度和形状, 得到了高速射流的冲击能量, 但是由于冲击波传播速度极快(微秒级别), 水听器无法精确获得作用时间, 因此未得到冲击波能. Liu等[27 ] 分析了电火花空泡在溃灭过程中的放电总能转化为空泡最大势能的比例, 表明火花诱导气泡的水力效率在3.5%$\sim$7.5%之间. 综合分析研究成果可知, 高速射流和冲击波均会对壁面造成损伤, 但是由于高速射流和冲击波传播速度快, 压力幅值高, 传统的压力传感器和水听器由于响应频率和幅值有限的原因很难进行精确数据捕捉, 无法对流场内动能, 冲击波能等数据进行准确分析, 也无法分析得到溃灭过程中能量的转化机制. ...
The dynamics of cavitation bubbles
1
1949
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
Collapse of vapor-air cavitation bubbles (Collapse of single spherical vapor-air cavitation bubble, computing bubble movement and pressure as function of air content)
1
1964
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
Cavitation produced by ultrasonics: theoretical conditions for the onset of cavitation
1
1951
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
Acoustic cavitation. Methods in experimental physics
1
1981
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
Bubble dynamics in a viscoelastic medium with nonlinear elasticity
1
2015
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
Effects of the non-equilibrium condensation of vapour on the pressure wave produced by the collapse of a bubble in a liquid
1
1980
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
Temperatures produced by inertially collapsing bubbles near rigid surfaces
1
2018
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
Simulation of a gas bubble compression in water near a wall using the SPH-ALE method
1
2018
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
Numerical simulation of the propagation of pressure waves in water during the collapse of a spherical air cavity
1
2020
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
Energy dissipation of pulsating bubbles in compressible fluids using the Eulerian finite-element method
2
2020
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
... 空泡势能用以表征空泡对外做功能力, 势能大小是空泡内外驱动压差和空泡半径的函数, 其具体的计算公式[37 ] 为 ...
A new approach to evaluate the cavitation erosion power
2
1998
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
... 在实验研究中, 空泡的最大半径小于0.02 m, 实验水箱的长度为0.5 m, 由先前研究[38 ] 可知, 当流场范围大于5倍空泡半径时可以认为水箱壁面对空泡运动不造成影响, 因此可以将流场视为无限远流域, 因此流场动能可以表征空泡在溃灭过程中, 向流场传递的能量大小, 在全流场中, 选择某处距空泡产生中心$r$处流体微团, 其动能为[50 ] ...
On the relevance of kinematics for cavitation implosion loads
3
2019
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
... [39 ]的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
... 在$t_{5}=1.86$ ms与$t_{9}=3.56$ ms, 空泡处于收缩阶段, 此时空泡势能降低, 流场动能增大, 空泡势能持续向流场动能转化. $t_{8}=3.08$ ms后, 动能出现下降, 此时空泡内势能也在下降, 在Schenke等[39 ] 的研究中, 空泡收缩末期会在空泡周围形成高压区域, 流场动能会在此区域内进行积攒. 在$t_{9}=3.56$ ms时, 空泡发生溃灭, 此时空泡势能基本为零, 空泡周围积攒的动能此刻转化为冲击波能量得以释放, 剩余动能会聚集残余气体, 成为二次溃灭的初始能量. ...
Numerical study of the collapse of multiple bubbles and the energy conversion during bubble collapse
1
2019
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
空化水动力学非定常特性研究进展及展望
1
2019
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
空化水动力学非定常特性研究进展及展望
1
2019
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
水下爆炸气泡及其对结构毁伤研究综述
1
2016
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
水下爆炸气泡及其对结构毁伤研究综述
1
2016
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
空泡溃灭过程中的压力波能分析
1
2020
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
空泡溃灭过程中的压力波能分析
1
2020
... 鉴于单纯的实验手法存在的局限性, 难以定量利用实验手段对空泡内外压差、流场中压力、速度分布等流场数据进行获取, 而且由于实验方案极易受到外界因素干扰, 因此需要结合数值模拟方法对溃灭过程进行更深入的研究. Plesset[28 ] 在Rayleigh[5 ] 工作的基 础上推出了著名的用于研究球形空泡溃灭的Rayleig-Plesset理论方程. 随后文献[29 ,30 ,31 ,32 ,33 ,34 ]在R-P方程的基础上考虑了液体的可压缩性、空泡的表面张力、黏性、含气量和温度等因素, 为实验研究和数值分析打下了坚实的理论基础. Pineda等[35 ] 采用多相可压缩模型, 研究了空泡溃灭产生的压力波和高速射流对壁面的冲击程度. Morenko[36 ] 研究了空泡半径、空泡边界速度和流场动能随时间的变化规律. Tian等[37 ] 根据空泡溃灭过程中的能量守恒的线性化理论, 修正了马赫数对冲击波耗散能量计算的影响, 得到了刚性壁面附近空泡溃灭过程中各能量的转化比例. Fortes Patella和Reboud[38 ] 开发了可压缩流体结构耦合程序, 首次分析了压力波传播与固体冲击响应之间的相互作用, 给出了通过分析侵蚀程度来判断空化强度的方法. Schenke等[39 ] 采用新的可压缩物理模型, 模拟了空泡在溃灭过程中势能与冲击波能的转化, 提出了空泡势能需要先转化为流场动能后, 才能转化为冲击波能, 且该转化区域在空泡周围. Zhang等[40 ] 使用数值模拟方法研究了近壁区域空泡溃灭的过程中空泡势能和波能的转化关系, 得到了溃灭中心与边界距离对能量转化的影响. 现阶段对空泡能量的数值模拟研究较为成熟, 但是在边界条件对空泡能量转化影响方面并未做出整体综合研究, 且研究大多集中于空泡溃灭末期的高速射流动能和冲击波波能, 文献[41 ,42 ,43 ]发现空泡脉动也会给边界带来损伤, 高速射流动能和流场动能也是能量转化过程中的重点. 且根据Schenke等[39 ] 的研究, 空泡在溃灭过程中势能、波能和流场动能的转化关系存在一定的规律. ...
Local instant formulation of two-phase flow
1
1986
... 本次数值模拟采用了考虑流场弱可压缩性的两相流模型, 根据Kataoka[44 ] 和Caltagirone等[45 ] 提出的弱可压缩流体计算模型构建介质的质量守恒方程, 推导得出数值模拟中采用的控制方程 ...
A multiphase compressible model for the simulation of multiphase flows
1
2011
... 本次数值模拟采用了考虑流场弱可压缩性的两相流模型, 根据Kataoka[44 ] 和Caltagirone等[45 ] 提出的弱可压缩流体计算模型构建介质的质量守恒方程, 推导得出数值模拟中采用的控制方程 ...
Physical investigation of the counterjet dynamics during the bubble rebound
1
2019
... 在图2 中添加相同时刻3种不同方式得到的空泡半径对比图, 可以观察到, 在起始阶段, R-P方程计算结果与实验数据完全重合, 数值模拟结果与实验数据相差0.2 mm, 相对误差为1.2%. 在空泡接近溃灭阶段, 实验数据与R-P方程计算结果相差为0.01 mm, 相对误差为0.6%, 实验数据与数值模拟结果相差0.03 mm, 相对误差为0.44%. 整个溃灭过程中, 3种方法得到的溃灭时间相差0.05 ms, 相对误差为1.8%. 在最大半径处误差来源主要是由于数值模拟采用了弱可压缩的流动控制方程, 该方程中未考虑温度对模拟结果的影响[46 ] . ...
Numerical simulations of non-spherical bubble collapse: With applications to shockwave lithotripsy
1
2008
... 为求解在空泡溃灭过程中, 各能量的具体数值及转化关系, 在此给出了空泡势能, 流场动能的推导过程. 由于本文所研究的空泡为自由场空泡, 泡型接近标准球形, 因此对空泡势能的推导基于球面坐标下的N-S方程[47 ] ...
Numerical simulation of single bubble dynamics under acoustic standing waves
1
2018
... 在之前的研究中, 由于空泡呈现球形溃灭, 因此可以对该公式进行球形简化[48 ] ...
Hybrid analytical/numerical modeling of nanosecond laser-induced micro-jets generated by liquid confining devices
1
2020
... 该公式即为考虑流场黏性与黏滞性的Rayleigh-Plesset方程[49 ] , 在该公式中, 代表流场密度, 代表流体黏性系数, 代表空泡表面处的张力系数. ...
Dynamics and noise emission of vortex cavitation bubbles
1
2007
... 在实验研究中, 空泡的最大半径小于0.02 m, 实验水箱的长度为0.5 m, 由先前研究[38 ] 可知, 当流场范围大于5倍空泡半径时可以认为水箱壁面对空泡运动不造成影响, 因此可以将流场视为无限远流域, 因此流场动能可以表征空泡在溃灭过程中, 向流场传递的能量大小, 在全流场中, 选择某处距空泡产生中心$r$处流体微团, 其动能为[50 ] ...
On the accuracy of predicting cavitation impact loads on marine propellers
1
2020
... 由此可知距空泡产生中心处半径为$r$处的球面流场的动能总和为[51 ] ...
Schlieren and interferometry in a 2D cavitating channel flow
1
2012
... 系统通过聚焦透镜可以对平面进行聚焦, 在成像图中得到反映该平面垂直于刀口($y$轴方向)的密度梯度变化图像, 用公式表述为[52 -53 ] ...
Experimental investigation of density fluctuations in high-speed jets and correlation with generated noise
1
2002
... 系统通过聚焦透镜可以对平面进行聚焦, 在成像图中得到反映该平面垂直于刀口($y$轴方向)的密度梯度变化图像, 用公式表述为[52 -53 ] ...
Physical investigation of acoustic waves induced by the oscillation and collapse of the single bubble
2
2020
... 图像对比度与流场中折射率呈一阶导数分布, 如下式所示[54 ] ...
... 在$t_{7}=2.45$ ms至$t_{9}=3.56$ ms阶段, 高压区域的速度呈现出明显增大的趋势, 结合图15 中的压力梯度变化, 可以发现在此阶段, 高压区域速度增大, 压力降低, 可以认为此时高压区域的势能在不断转化为动能. 在此阶段内, 高压区域内压力和速度在靠近空泡的中心区域迅速降低, 并不断向外部流场推进, 据文献[54 ]中研究结论, 空泡在收缩阶段会不断向外辐射压缩波, 可推测此时高压区内速度峰值即为压缩波的行进速度. ...
航行体回收垂直入水空泡流场及水动力特性研究
0
2019
航行体回收垂直入水空泡流场及水动力特性研究
0
2019
单空泡与自由液面相互作用规律研究进展
0
2019
单空泡与自由液面相互作用规律研究进展
0
2019
电场作用下气泡上升行为特性的数值计算研究
0
2020
电场作用下气泡上升行为特性的数值计算研究
0
2020