引言
旋涡强度(环量)作为描述旋涡的重要特征参数, 对TLV的发展及其空化行为等均会产生重大影响, 得到了研究者的广泛关注. 随着研究人员的不断努力, 来流速度、攻角对TLV强度的影响规律已经研究得比较充分, 也可以在理论上得到很好的解释[18-19], 但是间隙大小对TLV强度的影响机制依然是个未能解决的难题[20]. 根据Muthanna等[21]、Inoue等[22]和Storer等[23]对空气压缩机内部叶顶间隙流动的测量结果, 随着间隙的增大, TLV的强度及半径均会增大. 但是, 这一结论与Boulon等[24]对TLV空化观测得到的规律相矛盾. 他们发现, 间隙越小, TLV强度越大, 空化也越容易发生. 为了探究间隙大小与TLV强度之间的关系, Dreyer等[19]针对绕NACA0009水翼的叶顶间隙泄漏涡空化开展了一系列PIV测量和高速摄影观测. 结果表明: 当间隙尺寸小于某个临界尺寸时, 间隙越小, TLV的强度越小; 当间隙尺寸大于该临界尺寸时, 间隙越大, TLV强度反而越小. 但是, 对于其具体的作用机制尚不清楚.
TLV的半径也是影响叶顶间隙泄漏涡空化的重要因素之一. 在相同旋涡强度的情况下, 旋涡半径越小, 涡核附近的速度梯度越大, 引起的压降也越大, 因而越容易发生空化. 但是, 目前关于旋涡半径的研究较少. McCormick等[25]对椭圆翼的梢涡空化进行细致观察后认为, 梢涡是水翼边界层在流场作用下卷起形成的, 因此其大小应与水翼的边界层厚度有关. 这是首次有人提出将梢涡半径与边界层厚度进行关联. 此后Stinebring等[26]则进一步指出, 旋涡的半径应与水翼最大弦长处的湍流边界层厚度呈正比. Fruman等[27]的测量结果也表明梢涡半径的大小确实与边界层的厚度有关, 在一定程度上支持了Stinebring等[26]的理论. 文献[21,22,23]的结果表明, 在不改变Reynolds数的情况下, 仅仅改变间隙大小, 就可以改变TLV的半径. 这与该理论的结论不符. 此外, 通过观察Dreyer[18]的高速摄影及PIV数据, 也可以发现, 即便在Reynolds数相同的情况下, TLV的半径也不一定相同. 这些结果表明, Stinebring等[26]关于旋涡半径的理论依然存在较为明显的缺陷.
此外, 由于TLV结构较为稳定, 可以在流场中长时间稳定存在, 水体中的气核等受旋涡的作用会在涡心处聚集, 进而对TLV空化产生较大的影响. 事实上, 已经有很多研究表明, 在旋涡空化中, 涡心内部的气核会对空化过程产生显著的影响[28-30]. Oweis等[31]利用DNS模拟了梢涡附近的微小气泡的运动. 他们发现, 这些气泡会在压力梯度的作用下逐渐被卷吸缠绕在梢涡周围并很快进入到涡心内部. 水体中气核的这种运动将会导致涡心处气核浓度的增大, 并进而影响当地的空化过程[32]. Asnaghi等[33]则进一步指出, 旋涡空化对涡心处的气核浓度非常敏感, 旋涡越弱, 气核对当地空化的影响越明显. 2019年, Chen等[2]也根据其研究指出, 涡心处不可凝结气体可能是旋涡空化的主要影响因素.
以上研究大大促进了人们对于TLV及其空化行为的认识. 但是, 目前主要关注的重点在于TLV强度、气核分布以及半径等特征参数对TLV空化发生、发展的影响, 很少有研究关注空化发生后TLV空化对TLV强度、气核分布以及半径等特征参数的影响, 这在很大程度上限制了人们对此类流动更为全面的认识.
为此, 本文将在前人研究的基础上, 以绕NACA0009水翼叶顶间隙泄漏涡流动为主要研究对象, 利用大涡模拟方法, 细致分析不同间隙大小下TLV空化发生前后TLV强度、气核分布以及半径等特征参数的变化规律, 分析TLV空化对TLV演变行为及其特征参数的影响机制, 以期获得对TLV及其空化流动更为全面的认识与理解.
1 数值模拟方法
1.1 控制方程及大涡模拟方法
式中
$\begin{eqnarray*} y^{+}=\dfrac{\rho y_{1} u_{\tau } }{\mu },\ \ u^{+}=\dfrac{u}{u_{\tau } },\ \ u_{\tau } =\sqrt {\tau_{\rm w} /\rho },\ \ \lambda =\dfrac{0.01\left( {y^{+}} \right)^{4}}{1+5y^{+}}, \end{eqnarray*}$
其中, $y_{1}$为第一层网格高度, $\kappa $为von Kármán常数, $E=9.796$.
1.2 考虑气核效应的欧拉拉格朗日空化模型
空化模型在叶顶间隙泄漏涡空化的预报中具有十分重要的地位. 但是, 以往的传统空化模型大多假设水体中的气核是均匀分布的, 这可以大大简化计算, 但是在TLV空化流动中这种假设与实际情况相差较远. 实际上, 由于水体中的气核和液态水存在很大的密度差, 在水体的压力梯度力作用下, 水体中的气核会倾向于运动至旋涡的涡心附近, 使得当地的气核浓度显著高于来流水体中的初始浓度, 这表明以往传统空化模型中采用的"气核浓度均匀分布"假设在此类旋涡空化流动中不再成立, 这也正是传统空化模型经常低估TLV空化的原因. 为此, 本文采用了一个基于欧拉$\!-\!$拉格朗日耦合方法的新空化模型[38,40]. 该模型基于原始Schnerr-Sauer空化模型, 利用拉格朗日方法直接追踪水体中气核的运动, 准确获得了TLV附近水体中的气核浓度分布, 并对其影响进行定量评估, 引入空化模型之中, 可以更为准确地预报TLV空化.
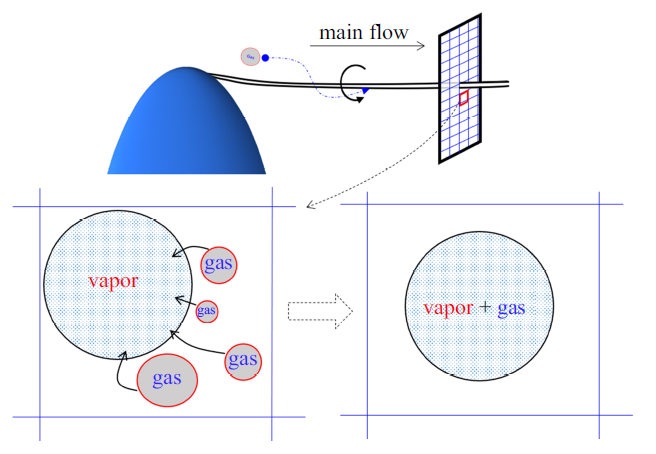
图1为在任意一个单元内蒸汽泡和不可凝结气泡融合过程的示意图. 在该空化模型中, 简化后的R-P方程为
图1
图1
梢涡空化流动中蒸汽泡和气泡的融合过程
Fig.1
Merging process of vapor and gas bubbles in tip-vortex cavitating flow
式中, $\rho_{\rm l}$为液态水的密度, $R_{\rm b}$为融合后泡的半径, $p_{\rm v}$和$p_{\rm g}$分别为泡内的饱和蒸汽压和不可凝结气体分压, $p$为当地流场压力. 式(2)中的分压项考虑了不可凝结气体的贡献. 融合泡内的压力$p_{\rm b}$可以定义为
现在的关键在于如何计算$p_{\rm b}$. 在初始条件下, 假设气泡处于平衡状态, 那么每个气泡内气体的分压需要满足以下方程
式中, 下标$i$是气泡指数, 0代表初始状态, $S$为表面张力系数. 式(4)等号右边的最后一项代表表面张力的影响. 应当指出的是, 为了简化计算, 本文在模拟中假设所有气核的半径一致, 为20 $\mu$m. 对于该尺寸大小的气泡而言, 表面张力项带来的压力仅为参考压力$p_{\infty }$的7%左右, 影响较小, 因而将忽略该项的影响. 一般来说, $p_{\rm v}$比$p_{\infty }$要小很多, 所以$p_{\rm v}$也被略去. 因此式(4)可以写成以下形式
当一个气泡靠近涡核时, 随着泡外周围压力的降低, 泡内压力也降低, 半径增大. 新的平衡状态下有以下方程
式中$\gamma$为热容比, $\gamma =1.4$. 可以得到每个单元内气泡的总体积
这些在每一个单元内的微气泡可视为一个单一的泡, 其压力和半径由下式确定
假设每个单元内的蒸汽体积为$V_{\rm vapor}$, 与气泡处理相似, 蒸汽也可以视作一个蒸汽泡, 其内压力为$p_{\rm v}$, 半径定义为
如果气泡和蒸汽泡的体积与网格单元体积相比足够大, 那么这两个泡将合并为一个混合泡. 当$R_{\rm v}$大于$R_{\rm g2}$, 融合过程可看作气泡融入蒸汽泡. 在此过程中, 假设蒸汽泡的尺寸保持不变, 所以可以得到新泡中气体的分压
然后得到混合泡内的压力$p_{\rm b}$
如果$R_{\rm v}$比$R_{\rm g2}$小, 融合过程可看作蒸汽泡融入气泡, 最终混合泡内压力为
在空化模拟中, 蒸汽分压和不可凝结气体分压之和$p_{\rm b}$, 而不仅仅是蒸汽分压被返回给求解器. 最终, 新空化模型里的质量源项定义如下
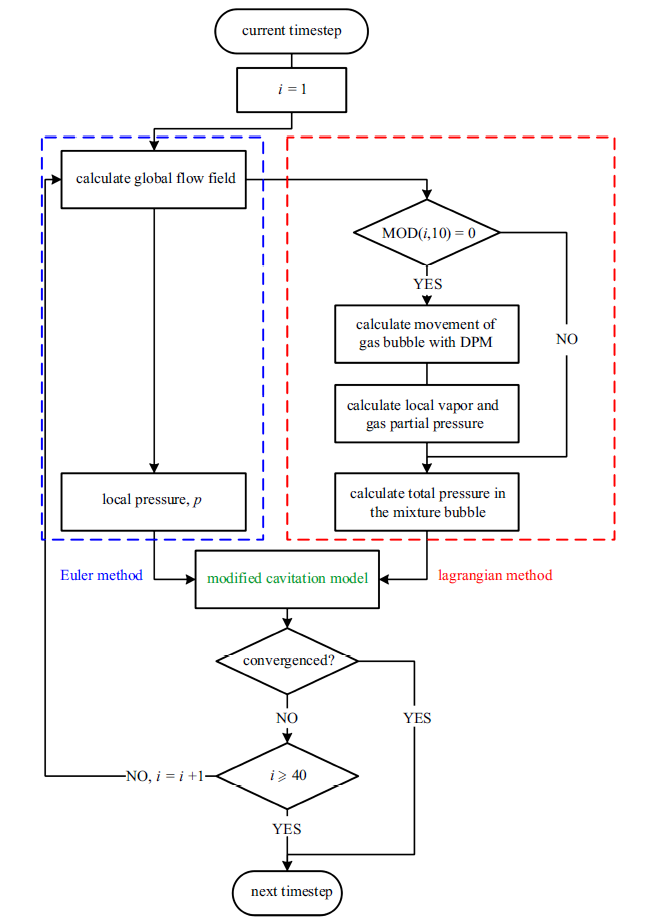
图2给出了新空化模型详细的计算过程. 在每个时间步长内, 最多迭代40次, 用欧拉法得到全局流场, 在此过程中, 每10次迭代后模拟一次气泡运动, 用拉格朗日方法得到当地气泡分布. 利用式(5)$\sim\!$式(14)计算当地总泡内压力$p_{\rm b}$, 再传给新空化模型计算当地质量输运. 需要注意的是, 当气泡和蒸汽泡的尺寸比网格单元小很多时, 他们的融合过程就很难发生. 因此, 在本文中, 只有当气泡和蒸汽泡的总体积达到当地网格单元体积的1/1000时, 修正才会被激活, 否则将使用原始Schnerr-Sauer模型.
图2
图2
新空化模型计算过程流程图
Fig.2
Flow chart of the calculation process with the new cavitation model
在气体浓度较低的区域, 这种新空化模型会自动退化为原始空化模型. 假设当地气体浓度是初始值$C_{\rm g0}=5.0\times 10^{-5}$ kg/m$^{3}$, 当地蒸汽体积分数$\alpha_{\rm v}$为0.1, 那么根据式(3)$\sim\!$式(14)计算得到的不可凝结气体分压大约为1.85 Pa, 随着$\alpha_{\rm v}$的增大, 这一值还会进一步降低. 这说明新模型中所做的修正不会影响低气体浓度区域的空化流场预测. 该模型在叶顶间隙泄漏涡空化流动以及梢涡空化流动中均已得到了应用, 并大大改善了TLV空化和梢涡空化的预报精度, 取得了较为理想的效果[38,40].
1.3 计算域及模拟设置
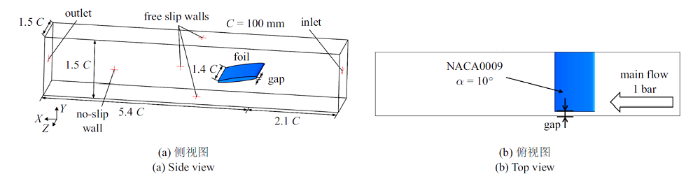
图3
来流入口位于水翼导边上游2.1 $C$处, 设为压力进口, 总压为153 kPa, 以保持进口处静压约为1 bar, 与实验一致. 出口速度$U_{\infty }=10$ m/s. 水翼表面和间隙处的水洞壁面均设置为无滑移壁面, 其他水洞壁面设置为自由滑移壁面.
为了更全面地分析在不同间隙大小下的流场, 本文根据实验结果[19], 选择了$\tau =0.2$, 0.7, 2.0这3个间隙大小作为典型工况, 进行精细的数值计算. 其中, $\tau $为无量纲化的间隙大小, 其定义为
式中, $d$为实际间隙大小, $h=10$ mm为水翼的最大厚度.
计算中, 先以$k$-$\omega $ SST湍流模型计算得到稳态结果, 再以其作为初场进行后续的非定常LES空化模拟, 非定常计算中采用的时间步长均为$1.0\times 10^{-5}$ s.
1.4 网格划分及细化
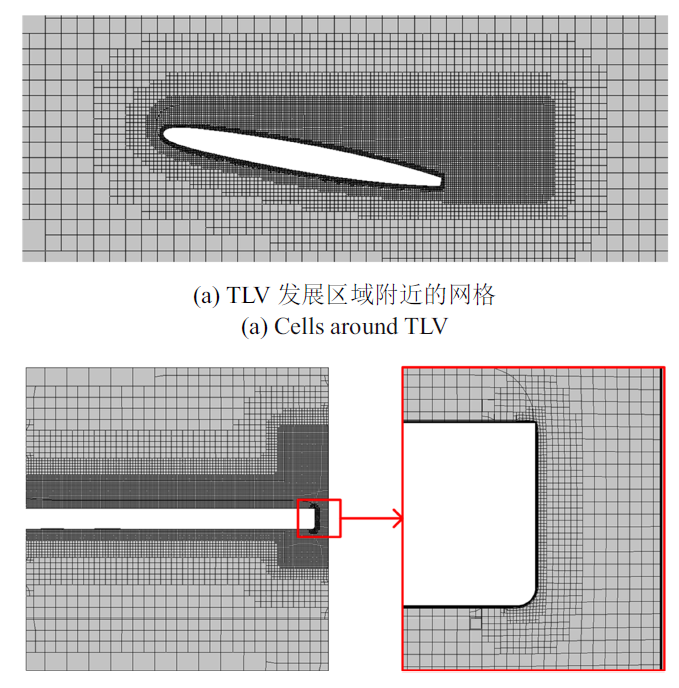
在数值模拟中, 网格质量和网格分辨率都对预测结果有很大的影响. 为了获得高质量的网格, 本文采用了笛卡尔Cutcell网格生成算法进行网格划分, 该方法可方便地生成具有很好正交性的网格单元, 如图4所示($\tau =0.7$). 可以看出, 大部分网格都具有非常好的正交性和较高的质量, 这对计算中的收敛过程是十分有利的. 为了更好地捕捉TLV附近和水翼周围的流动结构, 本文特意对水翼周围和TLV附近区域的网格进行了加密. 此外, 水翼周围和间隙壁面附近的边界层网格也进行了加密细化, 第一层网格高度为$6.0\times 10^{-6}$ m, 其对应的$y+$约为1, 可以满足SST及LES对壁面附近网格的要求. 本文利用笛卡尔Cutcell网格生成算法分别生成了2套网格, 即网格1和网格2, 二者的唯一区别在于后者位于加密区的网格尺寸更小, 如图5所示. 考虑到进一步直接减小加密区的网格尺寸会显著增大网格总数, 超出现有计算资源的可承受范围, 因此本文采用自适应网格技术(adaptive grid technique)在网格2的基础上对网格进行进一步的局部加密. 该技术可以在对其他区域网格不做任何修改的情况下, 仅对被标记的网格单元进行细化. 本文采用了旋转因子$f_{\rm r}$作为标记泄漏涡区域网格的物理量, 其代表应变率$S_{ij}$与应变率和旋转率张量$\varOmega_{ij}$之和的比值, 即
式中, $\varOmega_{ij}$和$S_{ij}$分别为旋转率张量和应变率张量.
图4
图5
表1 网格1$\sim$3的节点数量, $\tau =0.7$
Table 1
 |
1.5 网格无关性分析及数值结果可靠性验证
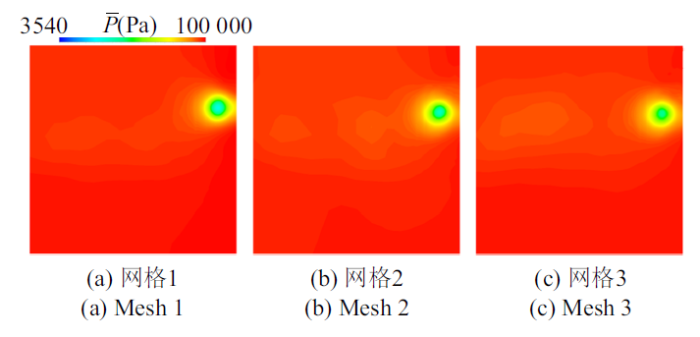
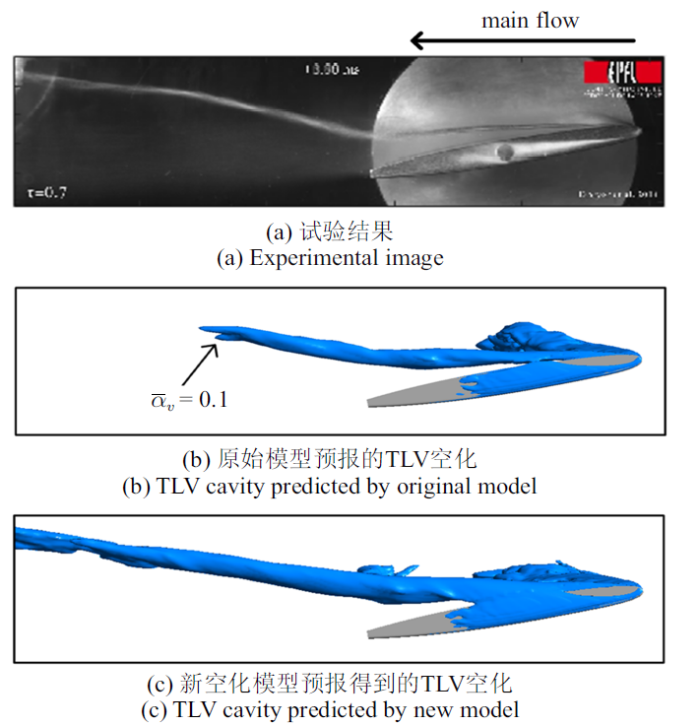
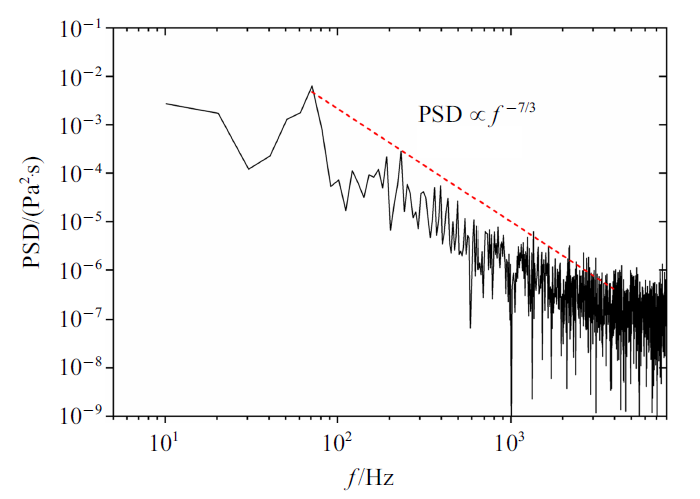
为了分析以上3套网格对计算结果的影响, 图6给出了$\tau =0.7$时水翼下游$x/C=1.5$截面上的时均压力分布. 可以看到, 3套网格预报得到的涡心处时均压力均在30 kPa以上, 远高于饱和蒸汽压. 这意味着根据原始空化模型, 当地很难产生空化. 实际上, 根据图7给出的时均TLV空化形态(时均蒸汽体积分数$\overline {\alpha_{\rm v} } =0.1$的等值面), 可以发现尽管随着网格分辨率的不断提升, 数值结果有一定改善. 但是, 与实验相比, TLV空化的发展依然被显著低估, 且虽然网格3单元数量接近网格2的2倍, 但其对TLV预报精度的改善非常有限. 作为对比, 图8则进一步给出了基于网格2, 利用新空化模型计算得到的时均TLV空化形态(蒸汽体积分数$\alpha_{\rm v}=0.1$的等值面). 可以发现, 新空化模型仅仅利用网格2, 就可以对TLV空化进行较为精确的预报. 此外, 网格2预报得到的升力系数的能谱图也基本满足$-$7/3次幂(见图9), 进一步说明网格2的分辨率可以满足本文模拟的要求.
图6
图6
网格1$\sim$3预报得到的时均压力分布, $\tau =0.7$
Fig.6
Time-averaged pressure by Mesh 1$\sim$3, $\tau =0.7$
图7
图8
图9
更为详细的网格无关性分析已在文献[38]中进行了详细的讨论, 本文不再赘述. 总体而言, 采用原始Schnerr-Sauer空化模型时, 网格2和网格3对TLV空化的预报结果较为接近, 进一步增加网格量不能有效提高LES空化流动的模拟精度. 而采用新空化模型后, TLV空化的预报精度大大提高, 采用网格2便能对TLV空化进行较为准确的预报. 因此, 本文选择利用网格2的生成方法, 对本文的3个算例($\tau =0.2$, 0.7, 2.0)进行网格划分, 作为LES空化数值模拟中最终使用的网格.
2 结果与讨论
Dreyer等[19]的实验结果表明, 叶顶间隙泄漏涡空化的演变行为在很大程度上会受到间隙大小的影响, 进而影响叶顶间隙泄漏涡的演变行为及特征参数. 因此, 为了更为全面地分析在不同间隙大小下的流场, 本文根据实验结果[19], 选择了$\tau =0.2$, 0.7, 2.0这3个间隙大小作为典型工况进行精细的数值计算, 并对其演变特点进行分析和讨论. 本文首先讨论了不同间隙大小下TLV空化的演变特性. 在此基础上, 通过对比分析, 深入讨论不同间隙大小下TLV空化发生前后TLV强度、气核分布以及半径等特征参数的变化规律, 分析TLV空化对TLV演变行为及其特征参数的影响机制, 获得对TLV及其空化流动更为全面的认识与理解.
2.1 TLV环量及切向速度分布的提取方法
应当注意的是, 受壁面边界层及其他旋涡结构的影响, TLV的截面实际上具有较强的不规则特性, 这会对TLV环量及其切向速度分布的提取产生一定影响. 为此, 本节将首先对本文TLV环量及切向速度分布的提取方法进行说明.
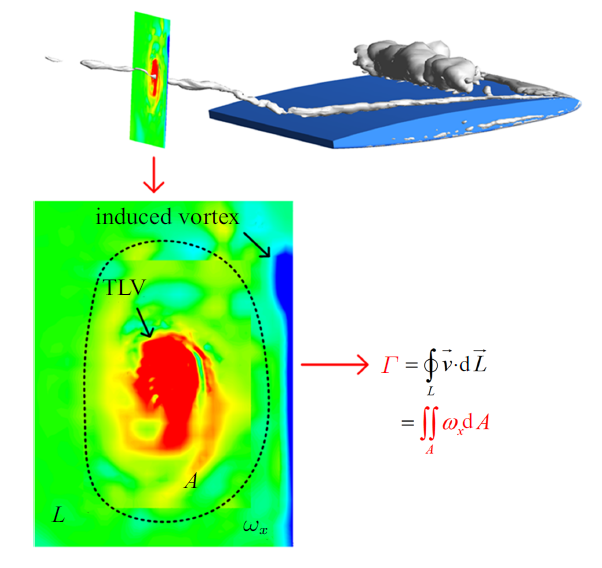
如图10所示, 本文在提取其环量时, 首先会根据数值结果获得TLV附近的流向涡量$\omega_{x}$分布, 确定TLV的主要分布范围, 然后建立一个包围该范围的闭合路径$L$, 对路径$L$上的速度进行积分即为TLV的环量. 为了更加方便地获取TLV的环量, 本文根据格林公式将对$L$上速度的路径积分, 转变为闭合路径$L$包围形成的封闭区域$A$上流向涡量$\omega_{x}$的面积分, 完成TLV环量的提取.
图10
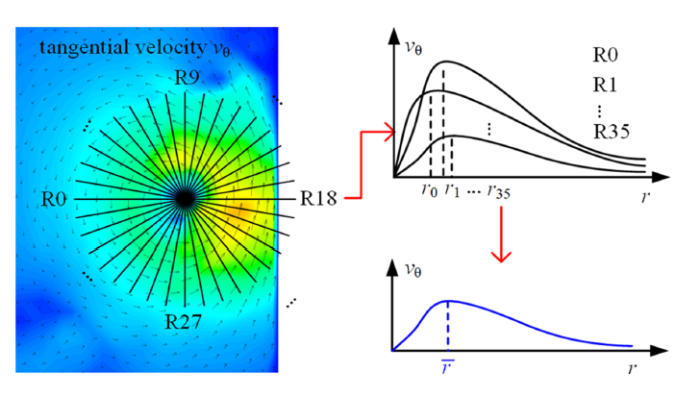
图11则给出了本文中TLV周围切向速度分布的提取方法. 具体而言, 本文根据数值结果, 获取TLV周围绕TLV涡心的切向速度分布. 然后以TLV涡心为中心建立36条等角度分布的射线, 提取每条射线上的切向速度分布. 在此基础上, 对其进行平均处理, 获得平均后的切向速度分布及其半径大小, 以消除TLV不规则性的影响.
图11
2.2 典型间隙大小下TLV空化的演变特性
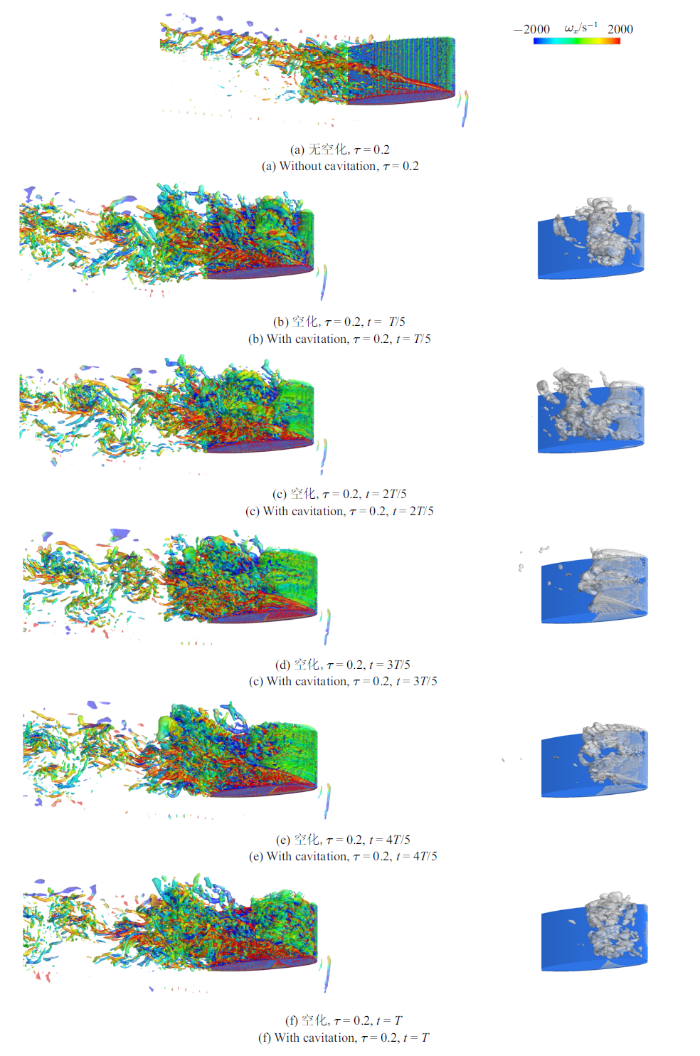
图12$\sim\!$图14给出的是各间隙大小下一个典型的片空化演变周期内TLV空化、片空化以及旋涡结构的演变, 其中涡结构采用$Q=5.0\times 10^{5}$ s$^{-2}$的等值面显示, 空化结构则采用了蒸汽体积分数$\alpha_{\rm v}=$0.1的等值面进行表征. 为了方便对比观察空化对当地涡结构的影响, 图中还给出了对应间隙大小下某个瞬态的无空化流场旋涡结构. 可以看到, 3个间隙大小下, 片空化发生后均对吸力面的旋涡结构产生了显著的影响. 当无空化发生时, 水翼的吸力面由于没有明显的流动分离现象, 因此此时吸力面没有观察到明显的分离涡. 然而, 一旦片空化发生, 在其准周期性的初生、发展、脱落、溃灭等行为的影响下, 吸力面的分离涡也基本呈现出类似的变化规律. 此类行为的流动规律与机理同传统的片空化流动基本一致, 本文不再赘述.
图12
图12
一个典型片空化周期内涡结构(左, $Q=5.0\times 10^{5}$ s$^{-2})$及空化演变(右, $\alpha_{\rm v}=0.1$), $\tau =0.2$
Fig.12
Evolutions of vortex (left, $Q=5.0\times 10^{5}$ s$^{-2})$ and cavities (right, $\alpha_{\rm v}=0.1$) in a typical cycle, $\tau =0.2$
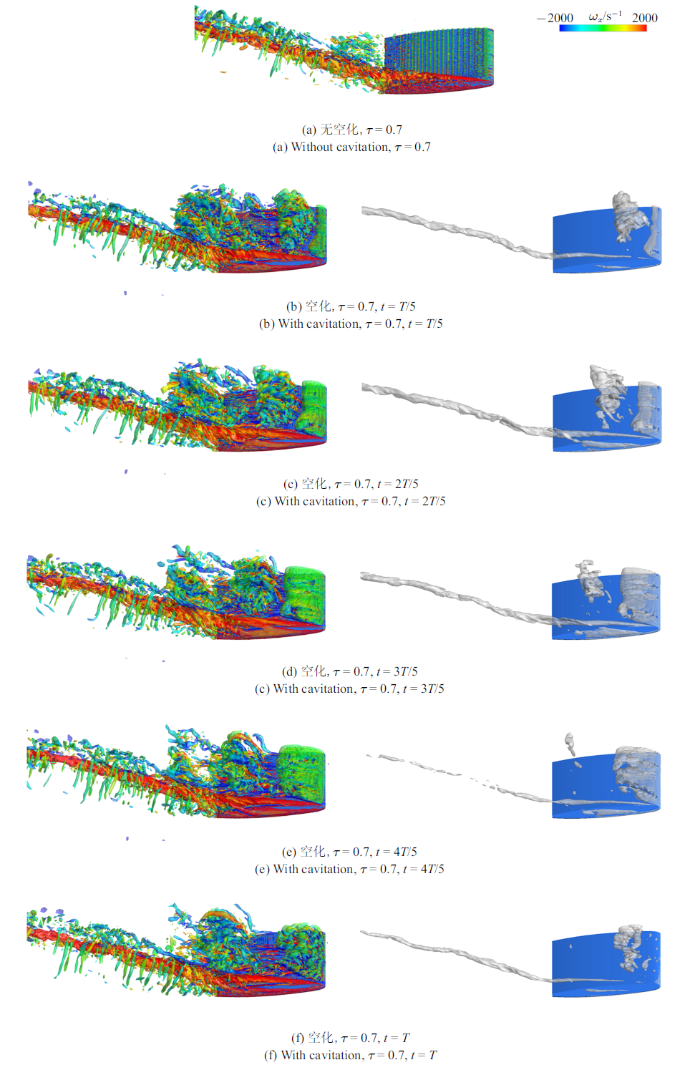
图13
图13
一个典型片空化周期内涡结构(左, $Q=5.0\times 10^{5}$ s$^{-2})$及空化演变(右, $\alpha_{\rm v}=0.1$), $\tau =0.7$
Fig.13
Evolutions of vortex (left, $Q=5.0\times 10^{5}$ s$^{-2})$ and cavities (right, $\alpha_{\rm v}=0.1$) in a typical cycle, $\tau =0.7$
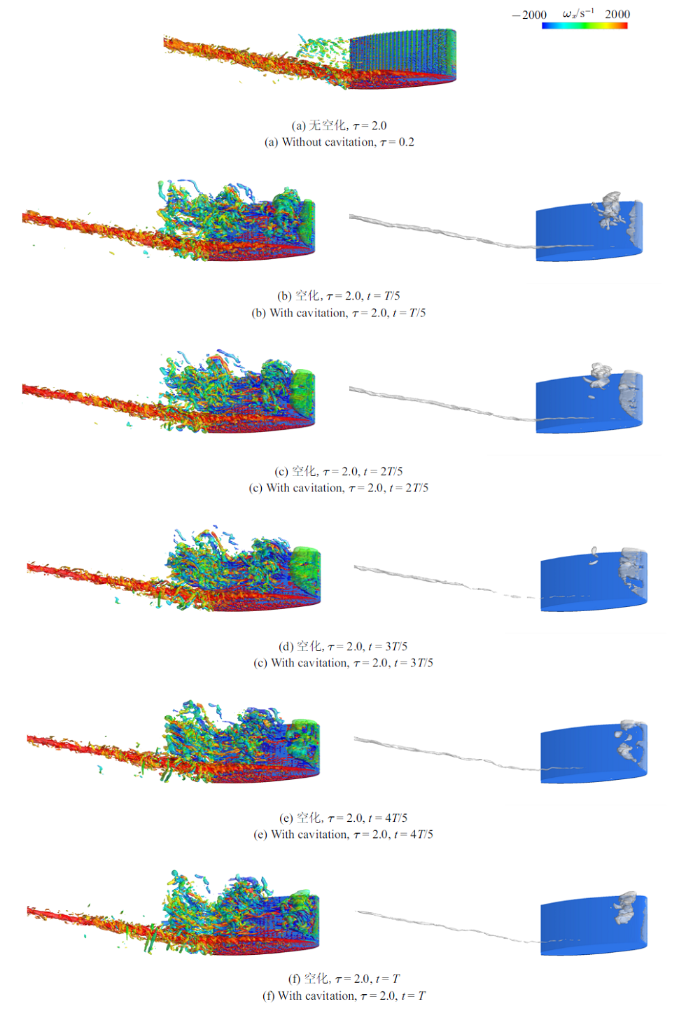
图14
图14
一个典型片空化周期内涡结构(左, $Q=5.0\times 10^{5}$ s$^{-2})$及空化演变(右, $\alpha_{\rm v}=0.1$), $\tau =2.0$
Fig.14
Evolutions of vortex (left, $Q=5.0\times 10^{5}$ s$^{-2})$ and cavities (right, $\alpha_{\rm v}=0.1$) in a typical cycle, $\tau =2.0$
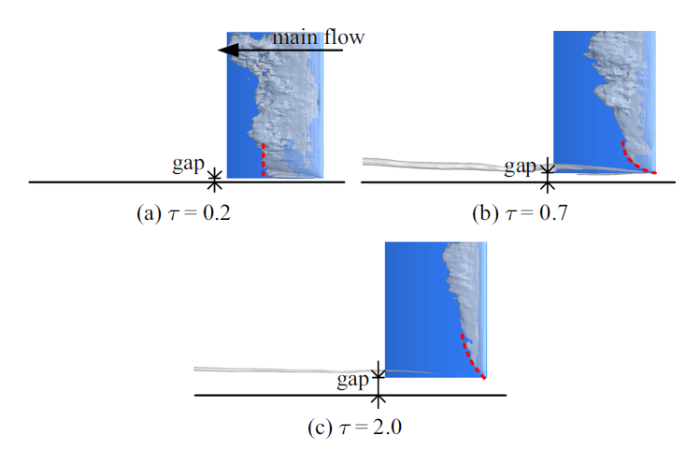
剧烈的片空化甚至会直接影响TLV的形态. 从图12可以看到, 当间隙大小$\tau =0.2$时, 对于无空化的叶顶间隙泄漏涡流动, 在叶顶附近可以观察到较为明显的TLV结构. 但当空化发生后, 剧烈的片空化及其相应的旋涡结构演变基本主导了叶顶间隙附近旋涡结构的发展. 在叶顶附近可以观察到类似"半卡门涡街"的流动结构, 该结构是片空化流动中的典型结构. 随着间隙的增大, 片空化对TLV空化的影响逐渐减弱. 当间隙$\tau =0.7$时, TLV的强度较大, 而片空化的强度则相对减弱, 此时片空化对TLV空化的影响较小, TLV空化的发展基本比较稳定. 此外, 由于此时叶顶分离涡(tip-separation vortex, TSV)强度也较大, 在叶顶端面还可以观察到由TSV诱发的空化, 该处空化在下游会随着TLV与TSV的发展而与TLV空化进行融合. 随着间隙的进一步增大($\tau =2.0$), 片空化的强度进一步减弱. 但是此时由于TLV的环量也较小, 因此其诱发的TLV空化也较弱, 片空化对其发展也会产生一定的影响.
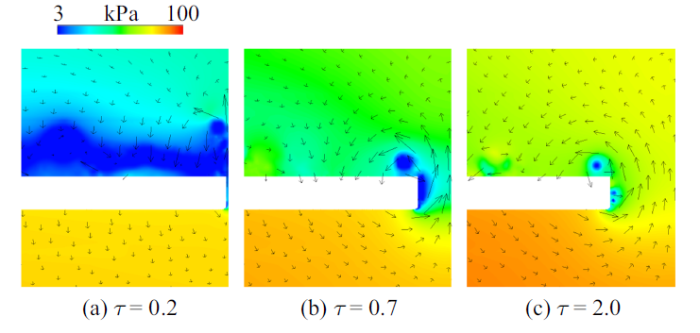
此外, TLV空化的演变也会反过来在一定程度上影响片空化的发展. 图15给出了不同间隙大小下时均空化形态(即时均蒸汽体积分数$\overline {\alpha_{\rm v} } =0.1$的等值面). 可以看到, 随着间隙的逐渐增大, 不但片空化的长度在逐渐减小, 其在叶顶附近的空穴尾部闭合区(图15中虚线标记部分)也由原本的平直形态慢慢变成带有明显圆弧特征的弯曲形态. 事实上, 当间隙较大时, TLV会在水翼的叶顶附近诱导形成绕TLV的流动. 环绕TLV的流体在到达水翼吸力面附近时, 对水翼表面会产生一定程度上的冲击, 失去其垂直于水翼表面的速度分量, 并增大当地的压力, 进而抑制当地的片空化发展, 如图16所示. 需要指出的是, 这种抑制作用随着其与TLV结构之间距离的逐渐增大而减小. 从图15中可以看到, 相比于$\tau =0.7$, 当间隙大小为2.0时片空化在叶顶附近的闭合区弧度更小.
图15
图15
不同间隙大小下时均空化形态, $\overline {\alpha_{\rm v} } =0.1$
Fig.15
Time-averaged cavities with different gap sizes, $\overline {\alpha_{\rm v} } =0.1$
图16
图16
某典型时刻在$x/C=0.0$截面上的速度矢量及压力分布
Fig.16
Distributions of velocity vector and pressure at $x/C=0.0$
通过以上讨论可以发现, 间隙的改变不但会直接影响TLV的环量大小, 进而影响其空化的强度, 还会通过影响片空化的发展转而对TLV空化产生一定的影响, 而TLV反过来也会在一定程度上影响片空化. 但是片空化对TLV空化的影响随着间隙的逐渐增大而迅速削弱. 实际上, 当间隙较大时, TLV空化的演变行为基本由叶顶间隙处旋涡结构的演变主导.
2.3 空化对TLV强度的影响
如图17所示, 空化发生后, 水翼的升力系数会发生显著的改变. 已有研究者指出, TLV强度与升力系数呈正相关, 因此空化的发生也可能会影响TLV的强度.
图17
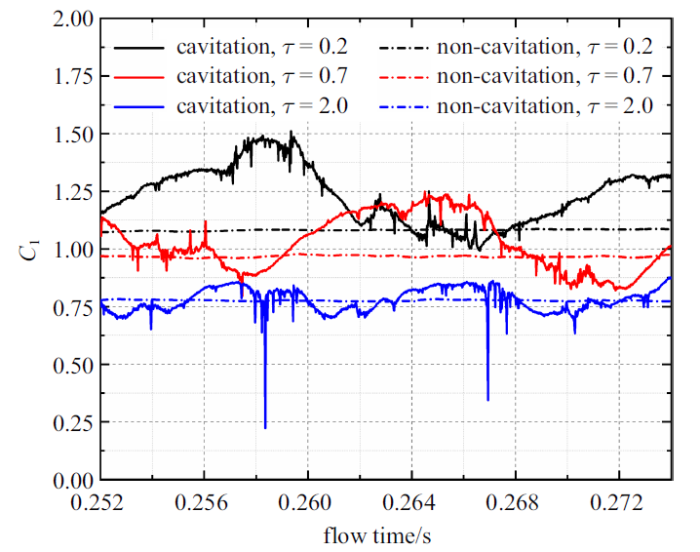
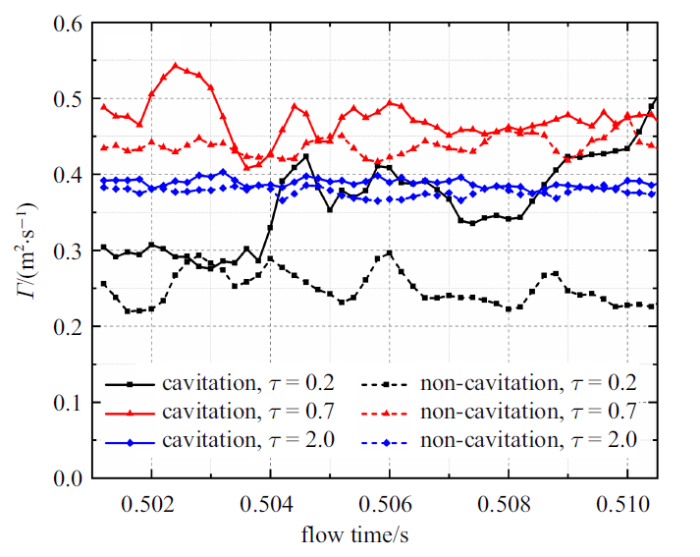
图18给出了$\tau =0.2$, 0.7及2.0时在水翼下游典型断面$x/C=1.2$上TLV环量的变化情况. 可以看到, 当间隙较小时($\tau =0.2$), 水翼吸力面的片空化更为剧烈, 其演变也呈现了非常强的准周期性生长、脱落和溃灭等过程, 水翼附近的流动结构非常不稳定. 受其影响, 此时TLV的环量也呈现出了较为剧烈的波动. 此外, 由于水翼的片空化会占据较大的流道空间, 液态水的过流面积减小, 进而导致水翼周围的流速增大, 并最终使得此时水翼的升力会在一定程度上增大. 受其影响, 此时TLV的强度也明显大于无空化时的强度. 相对而言, 当间隙较大时($\tau =0.7$), 此时水翼吸力面的片空化强度较弱, 其准周期性演变行为对水翼的升力影响较小, 与无空化时水翼的升力大小差别较小, 因此此时TLV的强度也仅呈现出小范围的波动, 与无空化时强度基本相当. 这也表明TLV的强度主要受片空化的影响, TLV空化对其自身强度的影响较小. 随着间隙的进一步增大($\tau =2.0$), 水翼的片空化强度进一步减小, 此时TLV的强度与无空化时基本一致, 也没有呈现明显的波动.
图18
图18
空化对TLV强度的影响($x/C=1.2$)
Fig.18
Influence of cavitation on TLV circulation ($x/C=1.2$)
整体而言, 空化发生后, TLV的强度主要受片空化演变行为的影响, TLV空化对其自身强度的影响较小. 一般而言, 间隙越小, 片空化越不稳定, TLV的强度也会呈现相应的准周期性波动. 随着间隙逐渐增大, 片空化强度逐渐减小, 其不稳定性也逐步减弱, TLV强度逐渐恢复至无空化时的水平, 其波动也会逐渐减小.
2.4 空化对涡心气核分布的影响
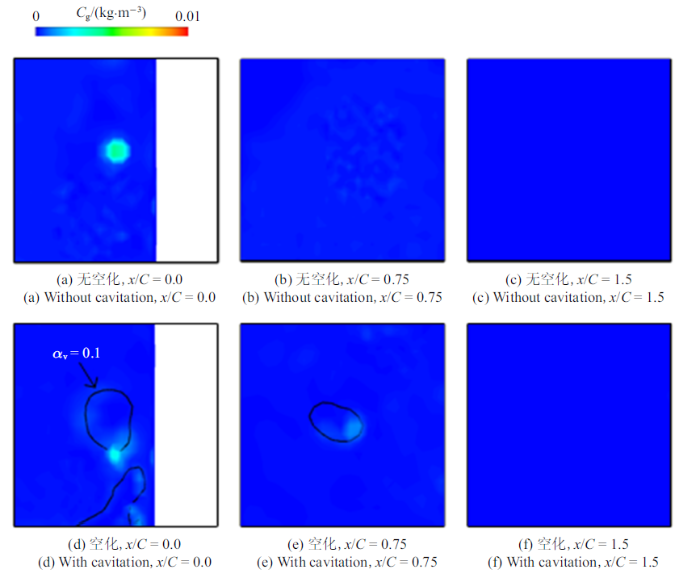
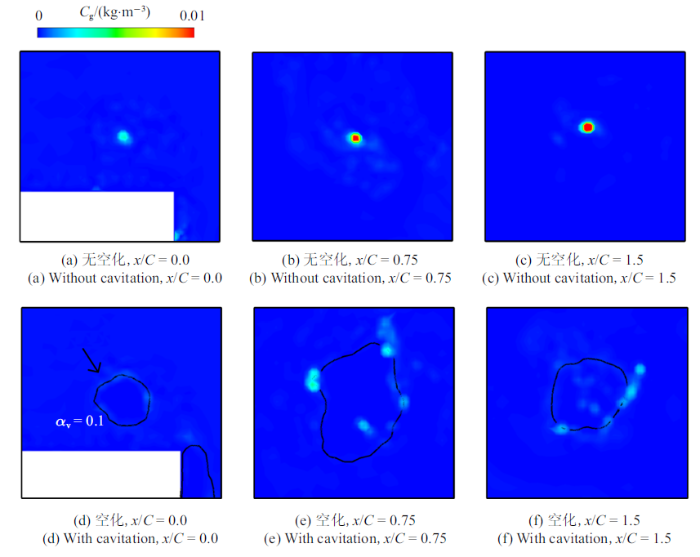
空化的发生会在较大程度上增强TLV的不稳定性, 这对涡心处气核的富集过程也会产生一定的影响. 图19$\sim\!$图21分别给出了3个间隙大小下在不同截面($x/C=0.0$, 0.75, 1.5)上空化发生前后TLV附近不可凝结气体浓度的分布情况. 可以看到, 对于小间隙($\tau =0.2$)而言, 空化未发生时在$x/C=0.0$截面上涡心处存在较为明显的气核富集现象, 空化发生后, TLV涡心处的不可凝结气体浓度显著降低. 由于距壁面很近, 该间隙大小下TLV很快被耗散, 因而无论空化是否发生, 在下游基本均未能观察到明显的气核富集现象. 当$\tau =0.7$时, 空化对气核分布的影响尤为明显. 从图 20中空化前后不可凝结气体浓度分布的对比可以明显看出, 空化对TLV涡心处气核的富集过程具有显著的影响. 对于无空化算例而言, 在$x/C=0.0$, 0.75和1.5的3个截面上均可观察到涡心处较高的不可凝结气体浓度分布, 这表明此时气核在涡心处的富集现象非常显著. 但是, 空化发生后, 其涡心处的不可凝结气体浓度明显减小. 一方面, 该间隙大小下TLV空化强度较大, 且片空化也非常不稳定, 因而此时TLV的摆动现象更为明显, 不利于气核在涡心处的持续富集; 另一方面, 空化过程产生的水蒸汽密度与不可凝结气体的密度相差较小, 此时气核受到的压力梯度力显著小于在纯水中的压力梯度力, 进一步削弱了气核在涡心处富集的程度. 作为对比, 当间隙大小$\tau =2.0$时, 由于此间隙大小下片空化强度较小且较为稳定, 其准周期性演变行为不会对TLV产生很强的影响, TLV空化的摆动幅度也较弱. 此外, 由于此时TLV强度较小, 其诱发的TLV空化强度也较弱, 空化区域范围较小, 因而在其附近依然可以观察到一定程度的气核富集现象.
图19
图19
有无空化时TLV附近不可凝结气体的浓度分布, $\tau =0.2$
Fig.19
Influence of cavitation on the nuclei distributions around TLV, $\tau =0.2$
图20
图20
有无空化时TLV附近不可凝结气体的浓度分布, $\tau =0.7$
Fig.20
Influence of cavitation on the nuclei distributions around TLV, $\tau =0.7$
图21
图21
有无空化时TLV附近不可凝结气体的浓度分布, $\tau =2.0$
Fig.21
Influence of cavitation on the nuclei distributions around TLV, $\tau =2.0$
总体而言, 空化对涡心处气核分布会产生较为明显的影响, 其影响程度取决于空化发生后TLV在空间上的稳定性以及TLV空化的强度. TLV本身越稳定, TLV空化强度越低, 空化对涡心处气核分布的影响就越小; 反之, 则有可能显著改变涡心处气核的浓度分布情况.
2.5 空化对TLV周围切向速度分布的影响
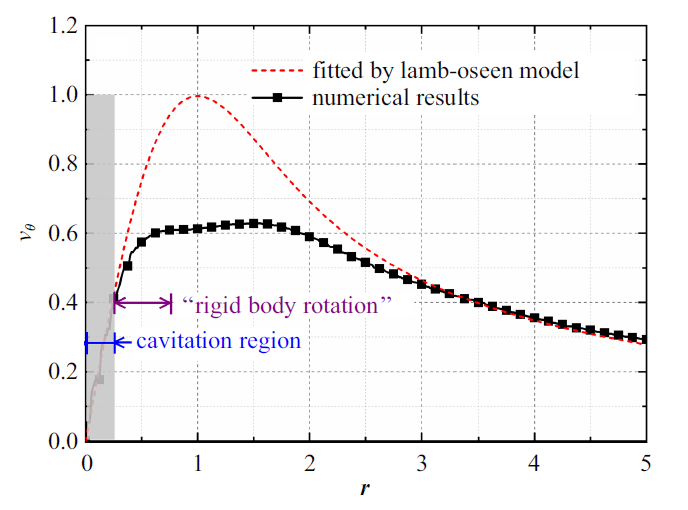
已有研究表明, 空化发生后, 其半径会在一定程度上增大[18]. 此外, 空化的发生还可能会显著影响TLV周围的切向速度分布. 空化发生前, 当距离壁面较远时, TLV的速度分布可较好地由Lamb-Oseen涡模型进行描述[18]. 但是, 如图22所示, 空化发生后其切向速度分布不再满足Lamb-Oseen涡模型($\tau =2.0$, $x/C=0.8$), 其最大切向速度明显低于Lamb-Oseen涡模型的预估值. 此外, 还可以发现, 在空化区外围的切向速度先上升然后才下降, 呈现"类刚体旋转"的切向速度分布特点, 这与实验的测量结果是吻合的. 但是, 对于空化涡外部这种切向速度分布的成因目前尚无明确的解释. Arndt等[43]就曾基于Rankine涡模型提出了一个修正的空化涡模型, 但是根据该模型, 空化涡外部的切向速度应当在汽液交界面处达到最大值, 随着半径的增大一直减小, 这与实验观测及本文的模拟结果都不相符. 此后, 尽管有部分空化涡速度分布模型可以给出具备"类刚体旋转"特点的空化涡外部切向速度分布, 但是由于这些模型更多的是数学上的表达, 未能从流动层面上阐释"类刚体旋转"分布形式的成因.
图22
图22
空化发生后TLV周围切向速度及Lamb-Oseen涡模型拟合($\tau =2.0$, $x/C=0.8$)
Fig.22
Tangential velocity distributions around cavitating TLV with the fitting of Lamb-Oseen vortex model ($\tau =2.0$, $x/C=0.8$)
图23
图23
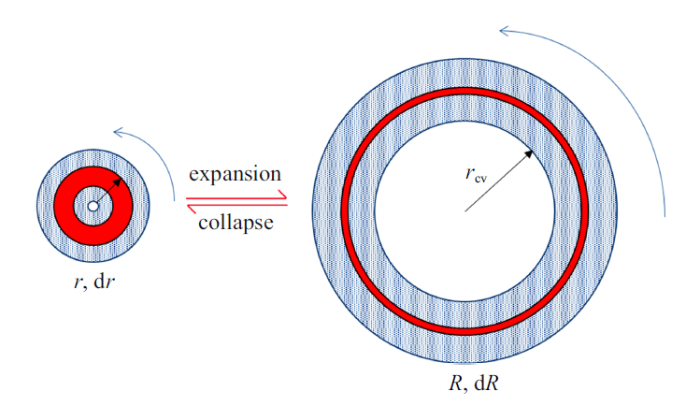
二维涡心处空泡的膨胀/收缩过程
Fig.23
Sketch of the expansion and collapse of a two-dimensional bubble
当$r\to 0$时, $R\to r_{\rm cv}$. 此外, 由于泄漏涡空化的大小与流道的过流面积相比很小, 因此可以忽略泄漏涡空化发展对流道过流面积的影响. 则有
即, 一个空泡膨胀前位于距涡心$r$的流体微团, 在空泡膨胀后其到涡心的距离为$R=\sqrt {r^{2}+r_{\rm cv}^{2} } $. 假设该过程黏性可以忽略, 则该流体微团角动量守恒, 有
将式(19)代入式(20), 可得
若空化发生前(即空泡膨胀前), 旋涡周围切向速度满足Lamb-Oseen涡模型, 则可知
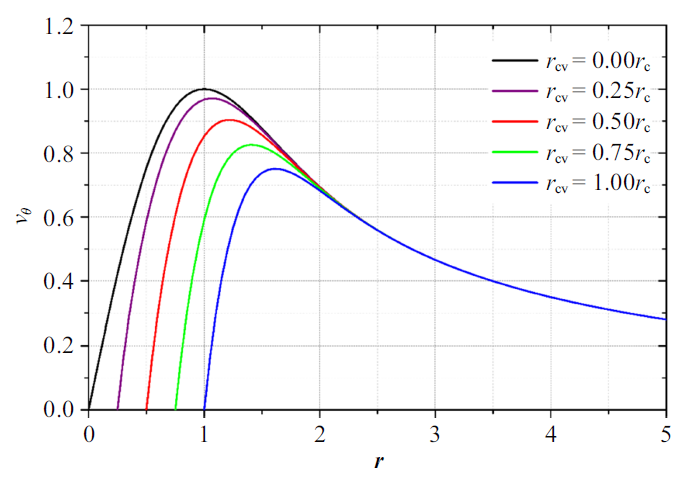
图24给出了空化发生前($r_{\rm cv}=0.00r_{\rm c})$以及空化半径$r_{\rm cv}$分别取0.25 $r_{\rm c}$, 0.50 $r_{\rm c}$, 0.75 $r_{\rm c}$, 1.00 $r_{\rm c}$时涡周围的切向速度分布, 其中横坐标(该点到涡心的距离)、纵坐标(切向速度)分别以旋涡半径、半径处切向速度进行了无量纲化处理. 可以看到, 空化发生后, 随着空化半径的增大, 旋涡的半径也在自发地逐渐增大. 应当注意的是, 在空化半径取不同大小时, 由于空化发生前涡心处的流体微团切向速度均很小, 其在空化发生后切向速度也很小, 亦即空泡内部及汽液交界面处的流体微团切向速度均基本为0, 在空化涡半径$r_{\rm cv}$和旋涡半径$r_{\rm c}$之间的流体微团切向速度由0迅速增大到最大值, 在旋涡空化外部初步形成了"类刚体旋转"的切向速度分布特点.
图24
图24
忽略黏性时涡周围切向速度分布与空化半径的关系
Fig.24
Tangential velocity distributions around TLV with various TLV cavity radiuses with viscous effect ignored
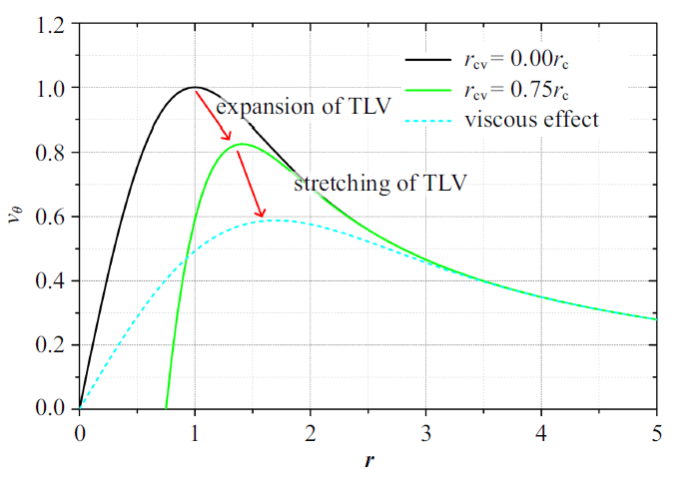
然而, 在实际流动中由于流体的黏性作用, 在汽液交界面附近液相一侧的流体会与周围的流体微团发生动量交换, 获得一定的切向速度. 以$r_{\rm cv}=1.05r_{\rm c}$为例, 当涡空化发生后, 汽液交界面的流体交换动量, 使得汽液交界面附近及涡心处空化区域的流体也获得了一定的切向速度, 最终形成了图 25中虚线所示的切向速度分布. 同样的, 图25中横坐标(该点到涡心的距离)、纵坐标(切向速度)也分别以旋涡半径、半径处切向速度进行了无量纲化处理. 该过程主要由流体的黏性作用产生, 会在一定程度上降低涡空化外部区域流体的切向速度梯度, 即实验与数值计算中观察到的"类刚体旋转"切向速度分布.
图25
图25
考虑黏性效应后空化涡周围切向速度分布
Fig.25
Tangential velocity distributions around TLV with viscous effect considered
从上述讨论中还可以发现, 涡空化发生前, 涡心处具有较大的涡量分布, 但是涡空化发生后, 空泡的膨胀过程会使得涡心处空化区域的切向速度全为0, 进而导致当地的涡量为0, 这表明涡空化的生长过程会显著降低涡心处空化区域的涡量. 另一方面, 涡空化发生后, 由于流体的黏性作用, 涡心空化区域的蒸汽以及汽液交界面附近的液态水会和外围的流体进行动量交换, 降低涡空化外部区域的切向速度梯度, 进而在一定程度上减小涡空化外部的涡量. 由于空泡的膨胀收缩过程往往与流体的黏性同时对当地的流动结构产生作用, 很难直接单独地观察、证实这两个因素的影响.
但是, 由于空泡的膨胀收缩过程对涡量的影响可以由涡量输运方程中的膨胀收缩项反映, 而流体黏性作用则是通过动量交换引起旋涡结构变化来影响当地的涡量分布, 其影响可以由涡量输运方程中的拉伸扭曲项来体现, 因此, 借助涡量输运方程考察拉伸扭曲项、膨胀收缩项对涡心空化区域涡量分布的影响, 应当可以从侧面验证上述对涡空化外部"类刚体旋转"切向速度分布特点的解释. 流向涡量的输运方程可写为
式中, $\omega_{x}$为流向涡量, $ V$为速度矢量, $\rho_{\rm m}$为混合物密度, $Re$为雷诺数. 方程左边表示涡量随时间的变化速度, 右边前3项依次表示旋涡的拉伸扭曲项、膨胀收缩项、斜压矩项, 最后一项为黏性耗散效应项. 图26和图27分别给出了典型时刻在3个断面上的拉伸扭曲和膨胀收缩项的分布($\tau =0.7$). 可以看到, 拉伸扭曲项主要分布在涡空化的外部, 且在涡空化外围附近主要为负值, 这表明该项会减小当地的涡量强度. 这与上一节讨论中流体黏性作用对当地涡量分布的影响是一致的. 另外, 通过图27可以看到, 在涡空化区域, 当地的膨胀收缩项为负值, 而在涡空化区域的外围为正值. 这表明, 在涡空化流动中, 膨胀收缩项会显著减小涡心空化区域的涡量, 并增大涡空化外围的涡量强度, 这与上文中空泡膨胀收缩过程对当地涡量的影响也是相吻合的. 以上结果与讨论从侧面证实了上文对涡空化外部"类刚体旋转"切向速度分布特点的解释.
图26
图27
3 主要结论
本文利用大涡模拟方法, 以绕NACA0009水翼叶顶间隙泄漏涡流动为主要研究对象, 细致讨论了不同间隙大小下TLV空化的演变特点及其发生前后TLV强度、气核分布以及半径等特征参数的变化规律, 分析了TLV空化对TLV演变行为及其特征参数的影响机制. 主要结论如下:
(1) 在绕水翼的空化流动中, 主要存在2类空化, 即水翼吸力面的片空化以及叶顶附近的叶顶间隙泄漏涡空化, 二者都明显受到间隙大小的影响. 一般而言, 间隙越小, 流道的实际过流面积越小, 绕水翼吸力面的流体流速越高, 因而片空化越强. TLV空化则与TLV的演变呈现了高度的相关性.
(2) 空化发生后, TLV的强度主要受片空化演变行为的影响, TLV空化对其自身强度的影响较小. 一般而言, 间隙越小, 片空化越不稳定, TLV的强度也会呈现相应的准周期性波动. 随着间隙的逐渐增大, 片空化强度逐渐减小, 其不稳定性也逐步减弱, TLV强度逐渐恢复至无空化时的水平, 其波动也会逐渐减小.
(3) 空化对涡心处气核分布会产生较为明显的影响, 其影响程度取决于空化发生后TLV在空间上的稳定性以及TLV空化的强度. TLV本身越稳定, TLV空化强度越低, 空化对涡心处气核分布的影响就越小; 反之, 则有可能显著改变涡心处气核的浓度分布情况.
(4) 此外, 空化发生后, TLV半径会在一定程度上增大, 且在空化区域外围形成"类刚体旋转"的切向速度分布特性, 其形成原因主要是空化生长引起的膨胀过程以及流体黏性的共同作用.
参考文献
Numerical and experimental investigation of tip leakage vortex cavitation patterns and mechanisms in an axial flow pump
Influence of water quality on the tip vortex cavitation inception
非定常空化流动涡旋运动及其流体动力特性
Study of turbulent vortex and hydraulic dynamics in transient sheet/cloud cavitating flows
航行体垂直出水载荷与空泡溃灭机理分析
Mechanism analysis about cavitation collapse load of underwater vehicles in a vertical launching process
转速对涡旋液泵空化性能的影响
Effect of rotational speed on the cavitation characteristics and performance of scroll hydraulic pump
基于动力学模态分解法的绕水翼非定常空化流场演化分析
Analysis of unsteady cavitation flowover hydrofoil based on dynamic mode decomposition
高速航行体水下发射水动力学研究进展
Research progress on hydrodynamics of high speed vehicles in the underwater launching process
Numerical investigation on underwater explosion cavitation characteristics near water wave
射流对绕水翼云空化流动抑制机理研究
Mechanism investigation of water injection on suppressing hydrofoil cloud cavitation flow
高速涡轮泵额定工况空化特性及压力脉动预测
Characteristics of cavitation and prediction of pressure fluctuation at rated condition in high-speed turbopump
圆柱体并联入水过程空泡演化特性实验研究
Experimental study on cavity evolution characteristics in the Water-entry process of parallel cylinders
空化水动力学非定常特性研究进展及展望
Research progresses and prospects of unsteady hydrodynamics characteristics for cavitation
空化可压缩流动空穴溃灭激波特性研究
Numerical simulation of shock wave dynamics in transient turbulent cavitating flows
绕水翼空化流动及振动特性的实验研究
Experimental investigation of the vibration characteristics of hydrofoil in cavitating flow
Nonlinear dynamics of a cavitation bubble pair near a rigid boundary in a standing ultrasonic wave field
The dynamics of a micrometer-sized bubble pair in water near a rigid boundary under standing ultrasonic wave excitation is investigated in this study. The viscous effect in the boundary layer at the air-water interface is considered following the viscous correction model. The evolution of the bubble surface at the collapsing stage of the bubble pair is presented for different parameter sets. The field pressure near the rigid boundary, which is induced by the oscillating bubble pair, and the high-speed water jet at the collapse stage, form the main focus of the analysis. This reveals that a horizontal configuration of the bubble pair retards the strength of the bubble jet towards the boundary, whilst a vertical configuration, especially with differently-sized bubbles, can enhance the bubble collapse. This study may help to understand the interaction of multiple bubbles in an acoustic field and its application to surface cleaning.Copyright © 2020 Elsevier B.V. All rights reserved.
绕水翼间隙涡结构形成机理与间隙几何影响
Formation mechanism and geometric influence of tip clearance vortex structure around hydrofoil
不同叶顶间隙下斜流泵内部流动特性的数值模拟
Numerical simulation of different blade tip clearances on internal flow characteristics in mixed-flow pump
Mind the gap: Tip leakage vortex dynamics and cavitation in axial turbines. [PhD Thesis].
Mind the gap: a new insight into the tip leakage vortex using stereo-PIV
Flow visualization and the three-dimensional flow in an axial-flow pump
Wake of a compressor cascade with tip gap, Part 1: Mean flow and turbulence structure
Behavior of tip leakage flow behind an axial compressor rotor
Tip leakage flow in axial compressors
An experimental insight into the effect of confinement on tip vortex cavitation of an elliptical hydrofoil
On cavitation produced by a vortex trailing from a lifting surface
The structure of a three-dimensional tip vortex at high reynolds numbers
Effect of hydrofoil planform on tip vortex roll-up and cavitation
Experimental measurement of tip vortex flow field with/without cavitation in an elliptic hydrofoil
A review of studies of mechanism and prediction of tip vortex cavitation inception
On the physical mechanism of tip vortex cavitation hysteresis
Capture and inception of bubbles near line vortices
空化核最新研究评述
Critical review on cavitation nuclei research
Analysis of tip vortex inception prediction methods
All-speed Roe scheme for the large eddy simulation of homogeneous decaying turbulence
Large eddy simulation of tip leakage cavitating flow focusing on cavitation-vortex interaction with Cartesian cut-cell mesh method
LES investigation of the influence of cavitation on flow patterns in a confined tip-leakage flow
Large eddy simulation of the tip-leakage cavitating flow with an insight on how cavitation influences vorticity and turbulence
LES of tip-leakage cavitating flow with special emphasis on different tip clearance sizes by a new Euler-Lagrangian cavitation model
Large eddy simulation and Euler-Lagrangian coupling investigation of the transient cavitating turbulent flow around a twisted hydrofoil
A new Euler-Lagrangian cavitation model for tip-vortex cavitation with the effect of non-condensable gas
On the sensitization of turbulence models to rotation and curvature
Numerical simulation for the tip leakage vortex cavitation