引言
壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果.
1 数学模型
1.1 基本控制方程
格子Boltzmann方程是Boltzmann-BGK方程的一种特殊离散形式, 这一离散包括速度离散、时间离散和空间离散. Boltzmann方程描述了离散粒子分布函数的演化, 以$f\left({x,t,\zeta }\right)$代表特定时刻$t$, 特定位置$x$处, 速度为$\zeta$的粒子密度分布函数. 进一步将Boltzmann方程在时间和空间离散, 将空间中有无穷方向可能的速度离散为时间步$\Delta t$内空间格子中有限方向的速度集合$ c_{i}$, 在离散时间步$\Delta t$内粒子仅在格子内运动, 由此导出的格子Boltzmann方程为
(1) $\begin{eqnarray} \label{eq1} &&f_{i} \left( {x+c_{i} \Delta t,t+\Delta t} \right)-f_{i} (x,t)=\\&&\qquad -\frac{1}{\tau }\left[ {f_{i} ( x,t)-f_{i}^{\rm eq} (x,t)} \right] \end{eqnarray}$
其中, $f_{i} $为离散速度空间中速度为$c_{i}$粒子的局部分布函数($i=0,1,2,\cdots,N-1,N$为速度空间总维数). $f_{i} ^{\rm eq}$为局部平衡态分布函数. 方程右侧为使用单松弛时间(SRT)模型的BGK碰撞项, $\tau $为无量纲弛豫时间. 平衡态分布函数$f_{i}^{\rm eq}$如下
(2) $\begin{eqnarray} f_{i}^{\rm eq} =\omega_{i} \rho_{\rm f} \left[ {1+\frac{c_{i} \cdot u}{c_{\rm s}^{2}}+\frac{\left( {c_{i} \cdot u} \right)^{2}}{2c_{\rm s}^{4}}-\frac{\vert u\vert^{2}}{2c_{\rm s}^{2}}} \right] \end{eqnarray}$
其中, $u$为宏观速度矢量, $\omega_{i}$为与离散速度$c_{i}$对应的权系数, $c_{\rm s}$为格子速度, 与所选的格子模型有关. 上述方程中宏观速度$u$必须满足低马赫数条件. 即
(3) $\begin{eqnarray} \label{eq3} {{\left| u \right|}/{c_{\rm s} =Ma\ll 1}} \end{eqnarray}$
在本研究中, 选择D3Q19模型. 模型的速度矢量为$c_{i} =\left[ {c_{ix} ,c_{iy} ,c_{iz}} \right]$
(4) $c_{i}=\left\{\begin{array}{c}(0,0,0), \\i=0 \\(\pm 1,0,0),(0, \pm 1,0),(0,0, \pm 1), \\i=1,2, \cdots, 6 \\(\pm 1, \pm 1,0),(\pm 1,0, \pm 1),(0, \pm 1, \pm 1) \\i=7,8, \cdots, 18\end{array}\right.$
$\begin{eqnarray*} \omega_{0} ={1/3},\ \ \omega_{1} \sim \omega_{6} ={1/{18}}, \ \ \omega_{7} \sim \omega_{18} ={1/{36}} \end{eqnarray*}$
方程(2)中声速$c_{\rm s} $在本模型对应为$c_{\rm s} ={1/{\sqrt3 }}$. 宏观密度$\rho $和速度$u$分别按照下式计算
(5) $\begin{eqnarray} \label{eq5} \left.\begin{array}{l} \rho_{\rm f} =\sum\limits_{i=0}^N {f_{i}}\\ \rho_{\rm f} {u}=\sum\limits_{i=0}^N {f_{i}} {c}_{i} \\ \end{array}\right\} \end{eqnarray}$
(6) $\begin{eqnarray} \label{eq6} p=\rho c_{\rm s}^{2} =\frac{\rho }{3} \end{eqnarray}$
在SRT-LBM算法中, 计算通过碰撞、迁移两步来执行. 首先, 经过碰撞的粒子由非平衡态向平衡态趋近, 此过程称为驰豫. 紧接着, 粒子的分布函数$f_{i} $随着粒子按照对应的格子速度$c_{i} $和权系数$\omega_{i} $迁移到相邻格点上.
(7) $\begin{eqnarray} f_{i}^{\prime } ({x},t)=f_{i} ({x},t)-\frac{1}{\tau \left[ {f_{i} ({x},t)-f_{i}^{\rm eq} ({x},t)} \right]} \end{eqnarray}$
(8) $\begin{eqnarray} \label{eq8} f_{i} \left( {x+c_{i} \Delta t,t+\Delta t} \right)=f_{i}^{\prime } (x,t) \end{eqnarray}$
(9) $\begin{eqnarray} \label{eq9} v=\left( {\tau -\frac{1}{2}} \right)c_{{\rm s}}^{2} \Delta t \end{eqnarray}$
考虑外力项的处理, 本研究采用直接在演化方程中增加一个作用力项来实现体积力${F}$在LBE中的影响[31 ] , 即
(10) $\begin{array}{r}f_{i}\left(\boldsymbol{x}+\boldsymbol{c}_{i} \Delta t, t+\Delta t\right)-f_{i}(\boldsymbol{x}, t)= \\-\frac{1}{\tau}\left[f_{i}(\boldsymbol{x}, t)-f_{i}^{\mathrm{eq}}(\boldsymbol{x}, t)\right]+F_{i} \Delta t\end{array}$
其中, $F_{i}$进一步通过基于格子气自动机方法中处理作用力的方法[32 ] , 将${F}_{i} $表示为
(11) $F_{i}=\omega_{i} \frac{c_{i} \cdot \boldsymbol{F}}{c_{\mathrm{s}}^{2}}$
对于边界条件, 本研究采用郭照立等[30 ] 提出的非平衡外推方法, 将边界格点处的未知分布函数分解为平衡态和非平衡态两部分, 即
(12) $\begin{eqnarray} \label{eq12} f_{i} \left( {x_{\rm b} ,t} \right)=f_{i}^{\rm eq} \left( {x_{\rm b} ,b} \right)+f_{i}^{n\rm eq} \left( {x_{\rm b} ,t} \right) \end{eqnarray}$
式中, $f_{i}^{\rm eq}\left( {x_{\rm b} ,t} \right)$为边界格点$x_{\rm b}$处分布函数的平衡态部分, 可进一步由临近格点的密度$\rho_{\rm f}$来取代壁面的密度$\rho_{\rm w} $来近似得到, 即
(13) $\begin{eqnarray} \label{eq13} f_{i}^{\rm eq} \left( {x_{\rm b} ,t} \right)\approx f_{i}^{\rm eq} \left[ {\rho \left( {x_{\rm f} ,t} \right),u_{\rm w}} \right] \end{eqnarray}$
对于非平衡态部分, 则使用临近格点$x_{\rm f} $处的非平衡态分布函数来近似, 即
(14) $\begin{eqnarray} \label{eq14} f_{i}^{n\rm eq} \left( {x_{\rm b} t} \right)=f_{i}^{n\rm eq} \left( {x_{\rm f} ,t} \right)=f_{i} \left( {x_{\rm f} ,t} \right)-f_{i}^{\rm eq} \left( {x_{\rm f} ,t} \right) \end{eqnarray}$
(15) $\begin{array}{c}f_{i}\left(x_{\mathrm{b}}, t\right)=f_{i}^{\mathrm{eq}}\left(\rho\left(x_{\mathrm{f}}, t\right), u_{\mathrm{W}}\right)+ \\{\left[f_{i}\left(x_{\mathrm{f}}, t\right)-f_{i}^{\mathrm{eq}}\left(x_{\mathrm{f}}, t\right)\right]}\end{array}$
1.2 跨尺度能量传递
在大涡模拟理论中, 基于滤波操作, Navier-Stokes方程中的独立变量被划分格子尺度和亚格子尺度(SGS)两部分, 本研究中采用的是物理空间中的各向同性高斯滤波器直接对DNS数据进行低通滤波, 在尺度$l$上进行的滤波函数记为$G_{l} \left( {x} \right)$, 则滤波操作如式(1)
(16) $\begin{eqnarray} \bar{{f}}(x)=\int {G_{l}} \left( {x-x^{\prime }} \right)f\left( {x^{\prime }} \right){\rm d}x^{\prime } \end{eqnarray}$
(17) $\begin{eqnarray} \frac{\partial \overline {u_{i}}}{\partial t}+\frac{\partial \left( {\overline {u_{i}} \overline {u_{j}}} \right)}{x_{j}}=-\frac{1}{\rho }\frac{\partial \bar{{p}}}{\partial x_{i}}-\frac{\partial \tau_{ij}}{\partial x_{j}}+v\frac{\partial^{2}\overline {u_{i}}}{\partial x_{j} \partial x_{j}}\end{eqnarray}$
(18) $\frac{\partial \overline {u_{i}}}{\partial x_{i}}=0$
其中, 小尺度影响体现在亚格子应力项$\tau_{ij} =\overline{u_{i} u_{j}}-\overline{u_{i}}\overline{u_{j}} $中, 在LES中需要对亚格子应力项提出近似模型. 考虑$\tau_{ij} $的输运方程为
(19) $\begin{array}{c}\frac{\partial \tau_{k k}}{\partial t}+\frac{\partial}{\partial x_{j}}\left(\tau_{k k} \bar{u}_{j}\right)=\frac{\partial}{\partial x_{j}}\left(\overline{q^{2}} \overline{u_{j}}-\overline{q^{2} u_{j}}\right)+ \\2 \frac{\partial}{\partial x_{j}}\left(\bar{p} \bar{u}_{j}-\overline{p u_{j}}\right)+\frac{\partial}{\partial x_{j}}\left(v \frac{\partial \tau_{k k}}{\partial x_{j}}\right)+ \\2 \frac{\partial}{\partial x_{j}}\left(\tau_{i j} \bar{u}_{i}\right)-2 v\left(\frac{\partial u_{i}}{\partial x_{j}} \frac{\partial u_{i}}{\partial x_{j}}-\frac{\partial \overline{u_{i}}}{\partial x_{j}} \frac{\partial \overline{u_{i}}}{\partial x_{j}}\right)- 2 \tau_{i j} \overline{S_{i j}}\end{array}$
其中, 方程等号左边第1项为对流项, 等号右侧第1$\sim$6分别对应湍流输运项、压力扩散项、黏性扩散项、亚格子应力扩散项、黏性耗散项和能量通量项. 亚格子应力耗散项代表解析尺度和未解析尺度之间的净能量交换, $\overline {S}_{ij}$为大尺度应变率张量, 定义$\varPi $为尺度间能量交换的度量, $\varPi $值为正代表能量从解析尺度向过滤尺度传递, $\varPi $值为负代表能量从过滤尺度向解析尺度反传
(20) $\begin{eqnarray} \label{eq20} \varPi =-2\tau_{ij} \overline{S}_{ij} \end{eqnarray}$
(21) $\begin{eqnarray} \label{eq21} \bar{{S}}_{ij} =\frac{1}{2}\left( {\frac{\partial \bar{{u}}_{i}}{\partial x_{j}}+\frac{\partial \bar{{u}}_{j}}{\partial x_{i}}} \right) \end{eqnarray}$
1.3 空间强结构捕捉——cluster方法
对于任意时刻流场内不同湍流结构总是通过若干等值面互相黏连, 这对使用数字手段区分不同结构造成了干扰, 因而需要某种手段人为地去除这些黏连的部分, 基于这种思想, Moisy等[20 ] 率先通过筛选出瞬时流场内大于自身$a$倍的标准差的数据点, 由此保留了瞬时流场内在长时间统计上表现较为强烈(intense)的点, 筛选掉的即为瞬时流场中的不同结构之间的黏连部分, 这种方法称为聚类分析方法. 本研究采用cluster方法来识别近壁区中的发生跨尺度能量传递的区域所包围的结构, 结构由满足下列条件的空间联通区域确定
(22) $\begin{eqnarray} \label{eq22} \left| {\varPi (x,y,z)} \right|>\alpha \varPi_{\rm rms} \end{eqnarray}$
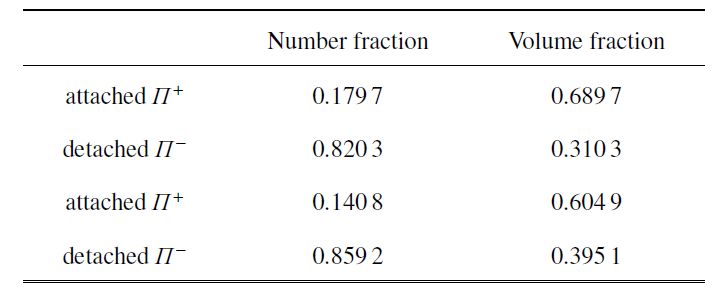
其中$\varPi_{\rm rms} $为$\varPi \left( {x,y,z} \right)$的标准差, $\alpha $为需经逾渗分析(percolation analysis)所人为选定的阈值. 结构的连通性由笛卡尔网格中满足六正交相邻条件所确定, 如图1 所示.
图1
图1
六联通示意图
Fig.1
Six-connected pixels
通过式(22)可将结构分为正级串$\varPi^{+}$和逆级串$\varPi^{-}$结构, 进一步构建出每个结构的轴对齐最小包围盒(axially aligned bounding box), 以边界框的长$l_{x} $, 宽$l_z $, 高$l_{y}$分别代表结构沿流向、展向和垂向的尺寸.
2 模拟参数设置
2.1 模型参数
对于槽道湍流, 除雷诺数外, 首先应确定模拟所需要的计算域尺寸. Jimenez等[32 ] 研究了能够维持湍流所需要的最小槽道尺寸, 他们定义$\alpha_{x} =L_{x}/H$, $\alpha_{z} =L_{z} /H$, 基于此Spasov等[33 ] 使用LBM模拟$R_{\tau} =180$的槽道湍流时取$\alpha_{x} =4$, $\alpha_{z} =1$, 结果与Kim等[34 ] 的研究相比, 平均速度剖面结果基本吻合但在对数区略高, 雷诺应力的结果也存在一定偏差, 因此本研究选取的槽道尺寸为$\alpha_{x} =4.6$, $\alpha_{z} =2$,网格数$L_{x} \times L_{y} \times L_{z} $为$600\times 260\times 260$. 槽道尺寸选定后, 对于直接数值模拟, 每个网格的尺寸都应小于当地的Kolmogorov尺度$\eta $. 对于槽道湍流在垂向方向上壁面处耗散率最大, 相应的当地Kolmogorov尺度$\eta $为需要解析的最小尺度, 定义壁面处Kolmogorov的尺度为$\eta_{0} $, 考虑
(23) $\begin{eqnarray} \eta_{0}^{+} =\eta_{0} \frac{u_{\tau }}{v}=\left( {\frac{v^{3}}{\varepsilon }} \right)^{1/4}\frac{u_{\tau }}{v}=\left( {\varepsilon_{0} \frac{v}{u_{\tau }^{4}}} \right)^{-1/4}=\left( {\varepsilon_{0}^{+}} \right)^{-1/4} \end{eqnarray}$
由Kim等[34 ] 提供的数据可知, $\varepsilon_{0}^{+}$的最大值约为0.2, 相应的$\eta_{0}^{+}=1.5$. 由于LBM中网格尺寸为无量纲数$\varDelta =1$.
(24) $\begin{eqnarray} \eta_{0}^{+} =1.5\geqslant \varDelta_{+} =\varDelta \frac{u_{\tau }}{v}=\frac{u_{\tau }}{v}\Rightarrow \frac{u_{\tau }}{v}\leqslant 1.5 \end{eqnarray}$
对于摩擦雷诺数$Re_{\tau } ={u_{\tau } H}/{\nu }=180$, 槽道半高须满足$H\geqslant 120$, 在本研究中取$H=130$.
(25) $\begin{eqnarray} \label{eq25} u_{\tau } =\frac{U_{0}}{\ln R_{\tau }/{\kappa }+B} \end{eqnarray}$
其中$\kappa $为卡门常数, 约等于$0.4$, $B$取6. 对于LBM, 为了满足低马赫数条件, 流场中的最大速度须小于等于0.1[33 ] , 对于槽道湍流最大平均速度在槽道中心, 所以可取$U_{0} =0.1$.
(26) $\begin{eqnarray}v=\frac{u_{\tau } H}{Re_{\tau}}\end{eqnarray}$
(27) $G=\frac{u_{\tau }^{2} \rho }{H}$
3 结果与讨论
3.1 数值模拟验证
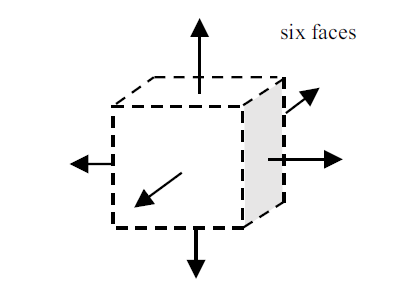
图2 为基于$Q$准则的空间涡结构等值面图, ${Q/{\left( {{{u_{\tau } ^{4}}/{\nu^{2}}}} \right)}}=0.015$,展示了流场内涡结构的分布, 从图2 可以看到近壁区的准流向涡和一些类似发卡涡的结构. 图3 为平均速度$U^{+}$沿垂向变化曲线, 符号圆点为本文DNS的结果, 虚线为Kim等[34 ] 的结果, 叉型标记为Lee等[35 ] 的结果, 可以看到, 本文的平均速度剖面结果与Kim等[34 ] 吻合得较好. 此前本研究也计算过$\alpha_{x} =4$, $\alpha_{z} =1$的结果, 结果显示在对数区吻合的效果并不理想, 这与Spasov等[33 ] 和许丁等[36 ] 的结果类似, 表明展向尺寸也会对计算结果产生显著影响.
图2
图2
基于Q准则槽道下半部涡结构等值面图
Fig.2
Iso-surface of Q on the lower-half of the channel
图3
图3
平均速度剖面
Fig.3
Comparison of mean streamwise velocity
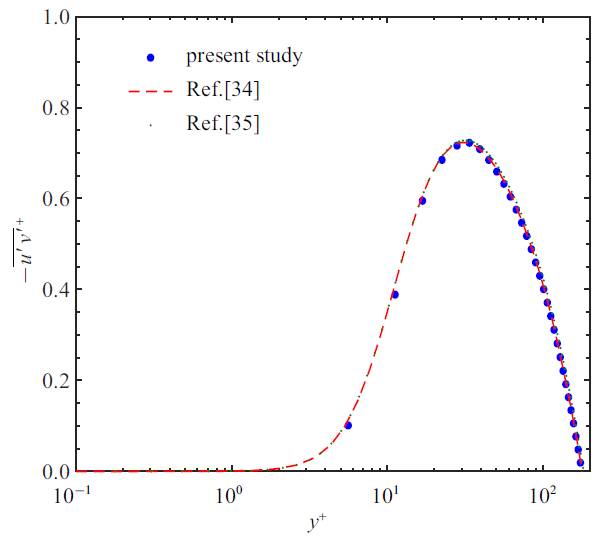
图4 和图5 为湍流统计量脉动速度均方根和雷诺应力的统计结果, 与Kim等[34 ] 和Lee等[35 ] $Re_{\tau }=180$下的DNS结果对比吻合得较好, 同样在$\alpha_{x} =4$, $\alpha_{z} =1$的条件下, 结果也存在较大偏差.
图4
图4
脉动速度均方根沿法向变化曲
Fig.4
Comparison of r.m.s. of velocity fluctuations
图5
图5
雷诺应力沿法向变化曲线
Fig.5
Comparison of Reynolds shear stress
3.2 尺度间能量传递结果统计
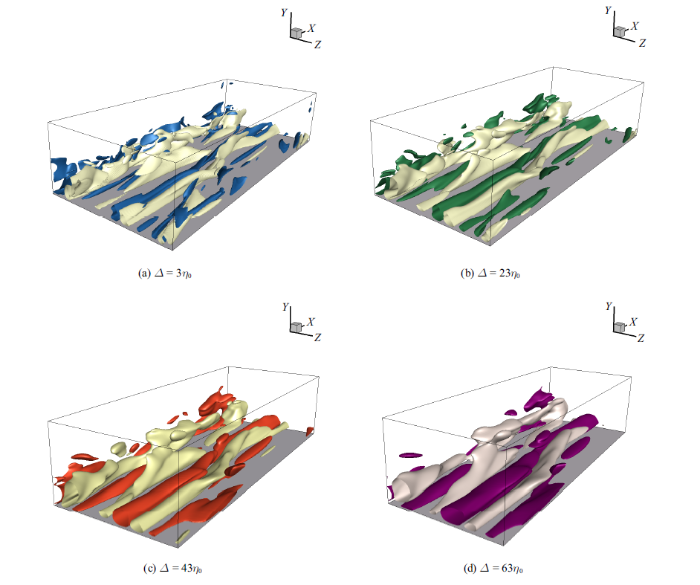
图6 展示了4种滤波尺度下的级串结构等值面图, 等值面的取值分别为: $\pm 3.16\times 10^{-7}$, $\pm 3.3\times 10^{-7}$, $\pm 5.0\times 10^{-7}$, $\pm 1.83\times 10^{-9}$, 其中乳白色等值面为负的逆级串结构, 即能量从小尺度相大尺度传递, ($a,b,c,d)$中的其他颜色 分别为蓝色、绿色、橙色、紫色, 均代表取值为正的正级串结构, 即能量从大尺度向小尺度传递.
图6
图6
四种滤波尺度下的级串结构等值面图
Fig.6
Interscale energy transfer stucture at four different scale
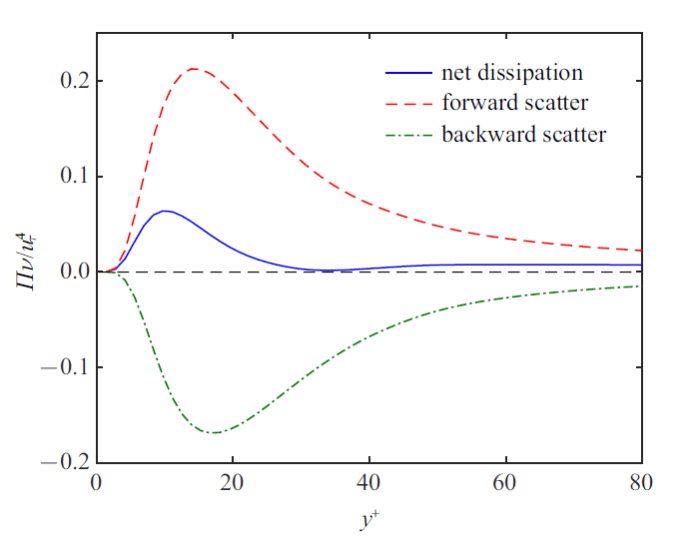
可以看到近壁区依附有很多体积较大的长条带结构, 这与近壁区拟流向涡的形态比较相似, 且正负级串沿展向交替排列, 而小体积结构多存在于远离壁面的层级中. 图7 展示了时间平均后的亚格子耗散项沿垂向的分布情况, 滤波尺度为$23\eta_{0}$, 趋势上与Piomelli等[8 ] 采用盒式滤波器的结果一致, 结果表明反级串结构效应尽管弱于正级串, 但仍然较为显著. 正反级串效应在缓冲层内达到峰值, 正级串总体上强于反级串, 在缓冲层内二者的差值达到最大, 缓冲层后二者大致相当.
图7
图7
能量通量沿法向分布
Fig.7
SGS dissipation in the normal direction
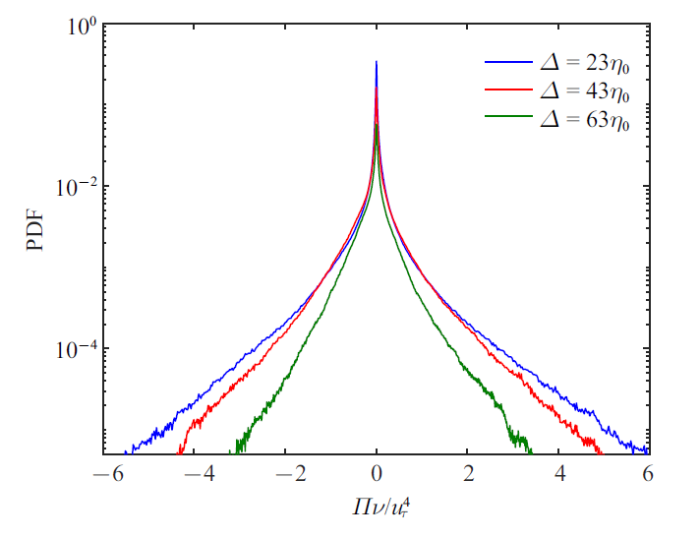
图8 展示了亚格子应力耗散项的概率密度分布, 与Piomell等[8 ] 、 Natrajan等[15 ] 的结果一致. 结果显示正级串的概率密度较反级串更大, 正级串横轴尾部也较长, 说明正级串效应较反级串效应略强, 但反级串效应也较为显著.
图8
图8
能量通量概率密度分布
Fig.8
Probability density function of energy flux
3.3 能量级串结构的空间统计
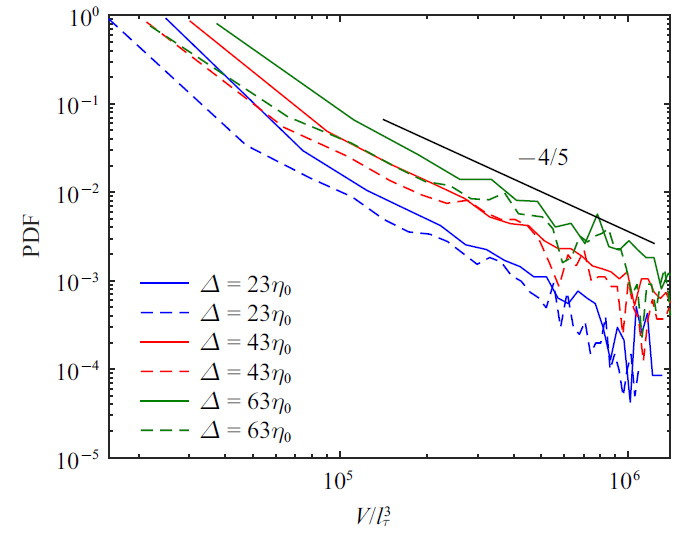
应用cluster方法首先要进行逾渗分析(percolation analysis)[21 -22 ] 选定某一阈值, 当阈值较低时, 新的结构点被识别出, 并与已识别的结构体融合, 如果阈值为零, 所有的结构将会融合成少量的复杂结构, 从而对结构研究造成干扰, 而阈值过大又会造成筛选掉过多的结构, 这里采用Jimenez等[21 -22 ] 所采用的方法来尽可能地使用较小的阈值使得结构仍能被单独识别出来. 图9 展示了不同$\alpha$值下最大cluster结构的体积与所有cluster结构体积之和的比值以及不同$\alpha $值对应的cluster结构数量$N$与所有$\alpha $值能识别出的最多数量$N_{m}$的比值. 由图9 可以看出, 当$\alpha $较小时, 大部分结构融合在一起, 仅有少量的结构被识别出, 随着$\alpha $的增大, 结构逐渐``断裂'', 新的结构从原有结构脱离出来, 在$\alpha =1$处, 3种滤波尺度的结构数量均达到峰值附近, 此时解析的数量较高, 对应的体积曲线位于中段, $\alpha $值的选择是``断裂''和``融合''两个过程相平衡的结果. 图9 所展示的变化趋势与Jimenez等[21 -22 ] 的研究中涉及的湍流结构所体现的规律相一致, Jimenez等[20 ] 将结构的这种特性称为``渗透性''. 基于图9 的结果, 取阈值$\alpha =1$.
图9
图9
结构的逾渗分析
Fig.9
Percolation analysis of the identified clusters
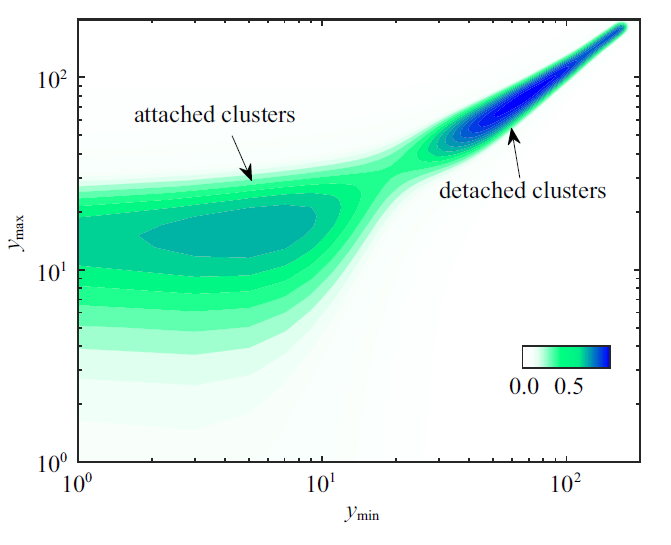
图10 为级串结构体积的统计结果, 可以看到小尺寸结构出现的概率要远远高于大尺寸结构, 且体积概率密度分布呈现$-{4/5}$的幂律关系. 图11 展示了槽道内能流结构数密度随结构距壁面的最小距离$y_{\min } $和距壁面最大距离$y_{\max } $的分布规律. 从图11 可以看出, 结构主要集中在以$y^{+}_{\min } =17$为分界线的两侧, 因此可将能流结构划分为$y^{+}_{\min } <17$的壁面附着结构, 以及$y^{+}_{\min }>17$的分离结构. 这个分界线的距离与Lozano-Durán等[22 ] 研究中所涉及的上抛下扫结构的分界线$y^{+}=20$十分接近, 表明两种结构的分布可能存在某种关联.
图10
图10
级串结构体积概率密度分布
Fig.10
Probability density function of volume of structure
图11
图11
结构按距壁面最小距离和最大距离的二维分布
Fig.11
The number of the clusters per unit wall-parallel area as a function of $y_{\min}$ and $y_{\max}$
表1 进一步给出了附着结构和分离结构的数量占比和体积占比. 可以看到, $\varPi ^{+}$附着结构的数量只占结构总数的18%, 但体积分数却占到69%, 而对应的分离结构数量占比和体积占比分别为82%和31%. $\varPi ^{-}$附着结构的数量占比仅为14%, 体积占比却达到了60.5%, 相应的分离结构分别占比86%和39.5%. 这说明无论是$\varPi^{+}$还是$\varPi ^{-}$结构, 大尺寸结构都主要分布在附着结构中, 而分离结构中主要为小尺寸结构.
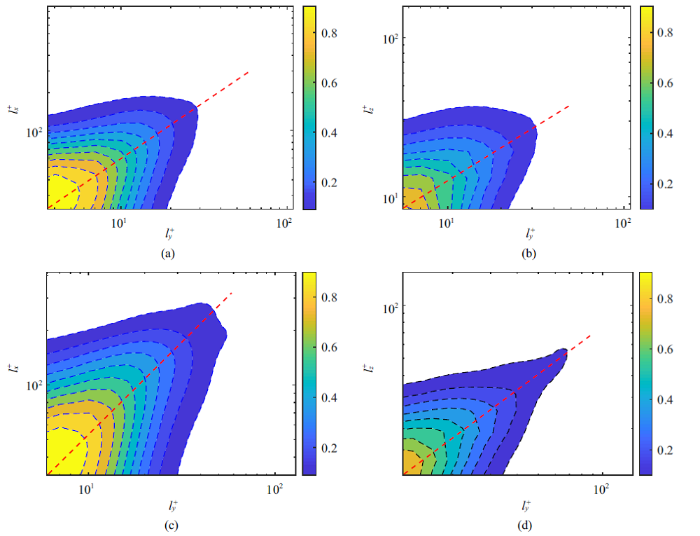
图12 通过结构包围盒的流向长度$l_{x}^{+}$和展向长度$l_{z} ^{+}$与纵向长度$l_{y}^{+}$的二维联合概率密度展示了$\varPi ^{+}$结构和$\varPi^{-}$结构的几何特性. 可以看到$l_{x}^{+}$和$l_{z} ^{+}$随$l_{y}^{+}$的增大均符合确定的标度律. 其中$\varPi^{+}$结构$l_{x} ^{+}$与$l_{y}^{+}$的幂律关系为 $l_{x}^{+}\propto l_{y}^{+0.92}$, $l_{z}^{+}$与$l_{y}^{+}$的幂律关系为$l_{z}^{+}\propto l_{y} ^{+0.58}$, 而$\varPi^{-}$结构$l_{x}^{+}$与$l_{y} ^{+}$的幂律关系为$l_{x}^{+}\propto l_{y}^{+0.83}$, $l_{z} ^{+}$与$l_{y}^{+}$的的幂律关系为$l_{z}^{+}\propto l_{y} ^{+0.73}$. 以上结果表明$\varPi^{+}$与$\varPi ^{-}$的附着结构也具有Townsend所提出的附面涡模型的自相似性, 与Jimenez等[21 -28 ] 采用聚类分析得到的湍流结构的性质一致.
图12
图12
(a)(b) $\varPi^+$结构流向长度、展向长度与纵向长度的联合概率密度; (c)(d) $\varPi^-$结构流向长度、展向长度与纵向长度的联合概率密度
Fig.12
(a)(b) Joint p.d.f.s of the length ($l_x^+$) and width ($l_z^+$) of with respect to their height ($l_y^+$); (c)(d) Joint p.d.f.s of the length ($l_x^+$) and width ($l_z^+$) of with respect to their height ($l_y^+$)
进一步考虑正反级串附着结构对在空间中的排布规律, 定义一对正级串附着结构和反级串附着结构的相对距离为
(28) $\begin{eqnarray} {\delta }^{(ij)}=\left( {\delta_{x} ,\delta_{y} ,\delta_{z}} \right)^{(ij)}=2\frac{{x}_{{\rm c}}^{(j)} -{x}_{{\rm c}}^{(i)}}{d^{(j)}+d^{(i)}} \end{eqnarray}$
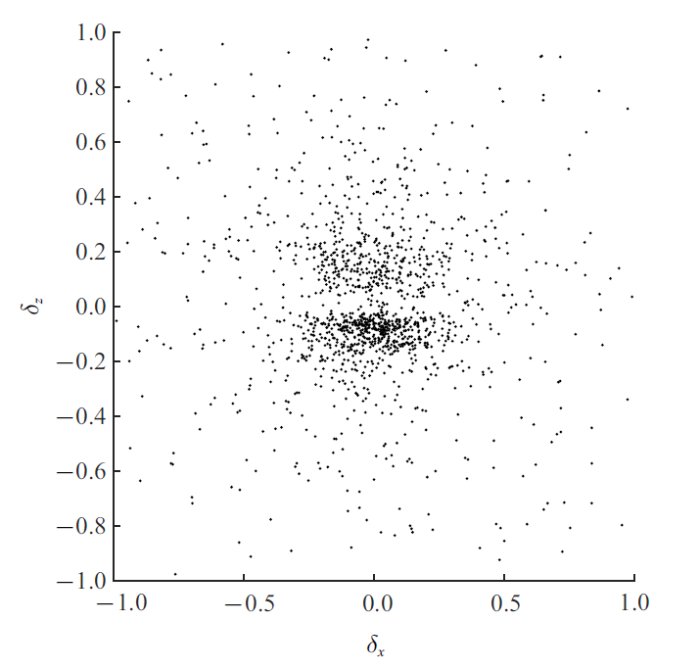
其中$x_{\rm c}^{(i)}$为单个结构的几何中心, $d^{(i)}$为包围盒对角线长度. 采取与Lozano等[22 ] 类似的配对方法, 只考虑包围盒对角线长度之比满足${1/2}\leqslant {{d^{(j)}}/d^{(i)}}\leqslant 2$, 且距离最近的正级串附着结构和反级串附着结构为一对结构对. 图13 给出了流向相对距离$\delta_{x} $和展向相对距离$\delta_{z} $的二维散点图. 由图13 可见二维散点主要分布在$\delta_{y} =0$两侧, 而在$\delta_{z} =0$附近的散点极为稀疏, 这说明结构对在展向上总是保持一定距离, 几乎不会在展向发生重叠, 表明附着结构对更倾向于沿展向并排排列.
图13
图13
能量级串结构对流向相对距离与展向相对距离的二维散点图
Fig.13
Scatter of the relative distance between $\varPi^+$ and $\varPi^-$ structure pairs in the streamwise direction and spanwise direction
4 结论
本文通过LBM方法得到直接数值模拟数据与已有槽道湍流数据库对比, 结果吻合较好. 通过各向同性高斯滤波器对数据进行滤波构建表征可解尺度与亚格子尺度之间能量交换的物理量, 表明正级串出现的概率要大于逆级串, 且正反级串均在缓冲层内达到峰值. 对级串结构使用cluster方法进行空间统计表明: 以结构包围盒下方距壁面距离$y^{+}=17$为分界, 结构集中分布于分界线的两侧, 即距壁面距离小于$y^{+}=17$的附着结构, 和距壁面距离大于$y^{+}=17$的分离结构. 对附着结构进一步统计表明: 级串结构的流向长度和展向长度均与纵向长度满足特定的幂律关系, 即结构在尺寸上存在着自相似性. 最后对满足尺寸相近且距离最近的正反级串附着结构对的流向与展向相对距离的统计表明, 正反级串附着结构更倾向于沿着展向并排排列.
参考文献
View Option
[1]
许春晓 . 壁湍流相干结构和减阻控制机理
力学进展 , 2015 ,45 :201504
[本文引用: 1]
(Xu Chunxiao . Coherent structures and drag-reduction mechanism in wall turbulence
Advances in Mechanics 2015 ,45 :201504 (in Chinese))
[本文引用: 1]
[2]
杨强 , 袁先旭 , 陈坚强 等 . 不可压壁湍流中基本相干结构
空气动力学学报 , 2020 ,38 (1 ):82 -99
(Yang Qiang Yuan Xianxu Chen Jianqiang , et al . On elementary coherent structures in incompressible wall-bounded turbulence
Acta Aerodynamica Sinica 2020 ,38 (1 ):82 -99 (in Chinese))
[3]
李思成 , 吴迪 , 崔光耀 等 . 低雷诺数沟槽表面湍流/非湍流界面特性的实验研究
力学学报 , 2020 ,52 (6 ):1632 -1644
[本文引用: 1]
(Li Sicheng Wu Di Cui Guangyao , et al . Experimental study on properties of turbulent/non-turbulent interface over riblets surfaces at low Reynolds numbers
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (6 ):1632 -1644 (in Chinese))
[本文引用: 1]
[4]
Bose ST Park GI . Wall-modeled large-eddy simulation for complex turbulent flows
Annual Review of Fluid Mechanics 2018 ,50 :535 -561
DOI
URL
[本文引用: 1]
[5]
强光林 , 杨易 , 陈阵 等 . 基于车身绕流的低雷诺数湍流模型改进研究
力学学报 , 2020 ,52 (5 ):1371 -1382
[本文引用: 1]
(Qiang Guanglin Yang Yi Chen Zhen , et al . Research on improvements of LRN turbulence model based on flow around automobile body
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (5 ):1371 -1382 (in Chinese))
[本文引用: 1]
[6]
Piomelli U Cabot WH Moin P , et al . Subgrid-scale backscatter in turbulent and transitional flows
Physics of Fluids A1991 , 3 : 1766 -177?
[本文引用: 1]
[7]
Härtel C Kleiser L Unger F , et al . Subgrid-scale energy transfer in the near-wall region of turbulent flows
Physics of Fluids 1994 ,6 (9 ):3130 -3143
DOI
URL
[本文引用: 2]
[8]
Piomelli U Yu Y Adrian RJ . Subgrid-scale energy transfer and near-wall turbulence structure
Physics of Fluids 1996 ,8 (1 ):215 -224
DOI
URL
[本文引用: 5]
[9]
Lin CL . Near-grid-scale energy transfer and coherent structures in the convective planetary boundary layer
Physics of Fluids 1999 ,11 (11 ):3482 -3494
DOI
URL
[本文引用: 1]
[10]
Germano M Piomelli U Moin P , et al . A dynamic subgrid-scale eddy viscosity model
Physics of Fluids A$:$ Fluid Dynamics 1991 ,3 (7 ):1760 -1765
[本文引用: 1]
[11]
Tian G Xiao Z . New insight on large-eddy simulation of flow past a circular cylinder at subcritical Reynolds number 3900
AIP Advances 2020 ,10 (8 ):085321
DOI
URL
[本文引用: 1]
[12]
贾宏涛 , 许春晓 , 崔桂香 . 槽道湍流近壁区多尺度输运特性研究
力学学报 , 2007 ,23 (2 ):181 -187
[本文引用: 1]
(Jia Hongtao Xu Chunxiao Cui Guixiang . Multi-scale energy transfer in near-wall region of turbulent channel flow
Chinese Journal of Theoretical and Applied Mechanics 2007 ,23 (2 ):181 -187 (in Chinese))
[本文引用: 1]
[13]
王占莹 . 壁湍流多尺度能量传输与流动结构关系研究. [硕士论文]
北京: 清华大学 , 2008
[本文引用: 1]
(Wang Zhanying . Study on the relationship between multi-scale energy transfer and flow structure in wall turbulence. [Master Thesis]
Beijing: Tsinghua University , 2008 (in Chinese))
[本文引用: 1]
[14]
Natrajan VK Christensen KT . The role of coherent structures in subgrid-scale energy transfer within the log layer of wall turbulence
Physics of Fluids 2006 ,18 (6 ):065104
DOI
URL
[本文引用: 1]
[15]
Zhou Q Huang YX Lu ZM , et al . Scale-to-scale energy and enstrophy transport in two-dimensional Rayleigh-Taylor turbulence
Journal of Fluid Mechanics 2016 ,786 :294 -308
DOI
URL
[本文引用: 1]
[16]
Wang L Huang YX . Intrinsic flow structure and multifractality in two-dimensional bacterial turbulence
Physical Review E 2017 ,95 (5 ):052215
DOI
URL
[17]
王帅杰 , 崔晓通 , 白建侠 等 . 减阻工况下壁面周期扰动对湍流边界层多尺度的影响
力学学报 , 2019 ,51 (3 ):767 -774
[本文引用: 1]
(Wang Shuaijie Cui Xiaotong , et al . The effect of periodic perturbation on multi scales in a turbulent boundary layer flow under drag reduction
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (3 ):767 -774 (in Chinese))
[本文引用: 1]
[18]
Cardesa JI Vela-Martin A Jimenez J . The turbulent cascade in five dimensions
Science 2017 ,357 (6353 ):782 -784
DOI
URL
[19]
Kawata T Alfredsson PH . Inverse interscale transport of the Reynolds shear stress in plane couette turbulence
Physical Review Letters 2018 ,120 (24 ):244501
DOI
URL
[20]
Moisy F Jiménez J . Geometry and clustering of intense structures in isotropic turbulence
Journal of Fluid Mechanics 2004 ,513 :111
DOI
URL
[本文引用: 3]
[21]
Del Álamo JC Jimenez J Zandonade P , et al . Self-similar vortex clusters in the turbulent logarithmic region
Journal of Fluid Mechanics 2006 ,561 :329 -358
DOI
URL
[本文引用: 6]
[22]
Lozano-Durán A Flores O Jiménez J . The three-dimensional structure of momentum transfer in turbulent channels
Journal of Fluid Mechanics 2012 ,694 :100
DOI
URL
[本文引用: 6]
[23]
Hwang J Sung HJ . Wall-attached structures of velocity fluctuations in a turbulent boundary layer
Journal of Fluid Mechanics 2018 ,856 :958 -983
DOI
URL
[24]
Osawa K Jiménez J . Intense structures of different momentum fluxes in turbulent channels
Physical Review Fluids 2018 ,3 (8 ):084603
DOI
URL
[25]
Cheng C Li W Lozano-Duran A , et al . Uncovering Townsend's wall-attached eddies in low-Reynolds-number wall turbulence
Journal of Fluid Mechanics 2020 ,889 :A29
DOI
URL
[本文引用: 1]
[26]
Cheng C LI W Lozano-Duran A , et al . 2020. On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows
Journal of Fluid Mechanics 2020 ,903 :A29
DOI
URL
[27]
Yoon M Hwang J Yang J , et al . Wall-attached structures of streamwise velocity fluctuations in an adverse-pressure-gradient turbulent boundary layer
Journal of Fluid Mechanics 2020 ,885
[28]
Dong S Huang YX Yuan X , et al . The coherent structure of the kinetic energy transfer in shear turbulence
Journal of Fluid Mechanics 2020 ,892 :A22
DOI
URL
[本文引用: 2]
[29]
何雅玲 , 王勇 , 李庆 . 格子Boltzmann 方法的理论及应用 . 北京 : 科学出版社 , 2008 : 31 -55
[本文引用: 1]
(He Yaling Wang Yong . Lattice Boltzmann Method: Theory and Applications . Beijing : Science Press , 2008 (in Chinese))
[本文引用: 1]
[30]
郭照立 , 郑楚光 . 格子Boltzmann方法的原理及应用 . 北京 : 科学出版社 , 2009
[本文引用: 1]
(Guo Zhaoli Zheng Chuguang . Theory and Applications of Lattice Boltzmann Method. Beijing : Science Press , 2009 (in Chinese))
[本文引用: 1]
[31]
Guo LZ Zheng CG Shi BC . Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method
Chinese Physics 2002 ,11 (4 ):366 -374
DOI
URL
[本文引用: 1]
[32]
Jiménez J Moin P . The minimal flow unit in near-wall turbulence
Journal of Fluid Mechanics 1991 ,225 :213 -240
DOI
URL
[本文引用: 2]
[33]
Spasov M Rempfer D Mokhasi P . Simulation of a turbulent channel flow with an entropic Lattice Boltzmann method
International Journal for Numerical Methods in Fluids 2009 ,60 (11 ):1241 -1258
DOI
URL
[本文引用: 3]
[34]
Kim J Moin P Moser R . Turbulence statistics in fully developed channel flow at low Reynolds number
Journal of Fluid Mechanics 1987 ,177 :133 -166
DOI
URL
[本文引用: 5]
[35]
Lee M Moser RD . Direct numerical simulation of turbulent channel flow up to $Re_{\tau} =5200$
Journal of Fluid Mechanics 2015 ,774 :395 -415
DOI
URL
[本文引用: 2]
[36]
许丁 , 陈刚 , 王娴 等 . 基于多GPU的格子Boltzmann法对槽道湍流的直接数值模拟
应用数学和力学 , 2013 ,34 (9 ):956 -964
[本文引用: 1]
(Xu Ding Chen Gang Wang Xian Li Yueming . Direct numerical simulation of the wall-bounded turbulent flow by lattice Boltzmann method based on multi-GPU
Applied Mathematics and Mechanics 2013 ,34 (9 ):956 -964 (in Chinese))
[本文引用: 1]
壁湍流相干结构和减阻控制机理
1
2015
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
壁湍流相干结构和减阻控制机理
1
2015
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
低雷诺数沟槽表面湍流/非湍流界面特性的实验研究
1
2020
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
低雷诺数沟槽表面湍流/非湍流界面特性的实验研究
1
2020
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
Wall-modeled large-eddy simulation for complex turbulent flows
1
2018
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
基于车身绕流的低雷诺数湍流模型改进研究
1
2020
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
基于车身绕流的低雷诺数湍流模型改进研究
1
2020
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
Subgrid-scale backscatter in turbulent and transitional flows
1
1991
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
Subgrid-scale energy transfer in the near-wall region of turbulent flows
2
1994
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
... [7 ]和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
Subgrid-scale energy transfer and near-wall turbulence structure
5
1996
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
... [8 ]的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
... [8 ]的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
... 可以看到近壁区依附有很多体积较大的长条带结构, 这与近壁区拟流向涡的形态比较相似, 且正负级串沿展向交替排列, 而小体积结构多存在于远离壁面的层级中. 图7 展示了时间平均后的亚格子耗散项沿垂向的分布情况, 滤波尺度为$23\eta_{0}$, 趋势上与Piomelli等[8 ] 采用盒式滤波器的结果一致, 结果表明反级串结构效应尽管弱于正级串, 但仍然较为显著. 正反级串效应在缓冲层内达到峰值, 正级串总体上强于反级串, 在缓冲层内二者的差值达到最大, 缓冲层后二者大致相当. ...
... 图8 展示了亚格子应力耗散项的概率密度分布, 与Piomell等[8 ] 、 Natrajan等[15 ] 的结果一致. 结果显示正级串的概率密度较反级串更大, 正级串横轴尾部也较长, 说明正级串效应较反级串效应略强, 但反级串效应也较为显著. ...
Near-grid-scale energy transfer and coherent structures in the convective planetary boundary layer
1
1999
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
A dynamic subgrid-scale eddy viscosity model
1
1991
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
New insight on large-eddy simulation of flow past a circular cylinder at subcritical Reynolds number 3900
1
2020
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
槽道湍流近壁区多尺度输运特性研究
1
2007
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
槽道湍流近壁区多尺度输运特性研究
1
2007
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
壁湍流多尺度能量传输与流动结构关系研究. [硕士论文]
1
2008
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
壁湍流多尺度能量传输与流动结构关系研究. [硕士论文]
1
2008
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
The role of coherent structures in subgrid-scale energy transfer within the log layer of wall turbulence
1
2006
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
Scale-to-scale energy and enstrophy transport in two-dimensional Rayleigh-Taylor turbulence
1
2016
... 图8 展示了亚格子应力耗散项的概率密度分布, 与Piomell等[8 ] 、 Natrajan等[15 ] 的结果一致. 结果显示正级串的概率密度较反级串更大, 正级串横轴尾部也较长, 说明正级串效应较反级串效应略强, 但反级串效应也较为显著. ...
Intrinsic flow structure and multifractality in two-dimensional bacterial turbulence
0
2017
减阻工况下壁面周期扰动对湍流边界层多尺度的影响
1
2019
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
减阻工况下壁面周期扰动对湍流边界层多尺度的影响
1
2019
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
The turbulent cascade in five dimensions
0
2017
Inverse interscale transport of the Reynolds shear stress in plane couette turbulence
0
2018
Geometry and clustering of intense structures in isotropic turbulence
3
2004
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
... 对于任意时刻流场内不同湍流结构总是通过若干等值面互相黏连, 这对使用数字手段区分不同结构造成了干扰, 因而需要某种手段人为地去除这些黏连的部分, 基于这种思想, Moisy等[20 ] 率先通过筛选出瞬时流场内大于自身$a$倍的标准差的数据点, 由此保留了瞬时流场内在长时间统计上表现较为强烈(intense)的点, 筛选掉的即为瞬时流场中的不同结构之间的黏连部分, 这种方法称为聚类分析方法. 本研究采用cluster方法来识别近壁区中的发生跨尺度能量传递的区域所包围的结构, 结构由满足下列条件的空间联通区域确定 ...
... 应用cluster方法首先要进行逾渗分析(percolation analysis)[21 -22 ] 选定某一阈值, 当阈值较低时, 新的结构点被识别出, 并与已识别的结构体融合, 如果阈值为零, 所有的结构将会融合成少量的复杂结构, 从而对结构研究造成干扰, 而阈值过大又会造成筛选掉过多的结构, 这里采用Jimenez等[21 -22 ] 所采用的方法来尽可能地使用较小的阈值使得结构仍能被单独识别出来. 图9 展示了不同$\alpha$值下最大cluster结构的体积与所有cluster结构体积之和的比值以及不同$\alpha $值对应的cluster结构数量$N$与所有$\alpha $值能识别出的最多数量$N_{m}$的比值. 由图9 可以看出, 当$\alpha $较小时, 大部分结构融合在一起, 仅有少量的结构被识别出, 随着$\alpha $的增大, 结构逐渐``断裂'', 新的结构从原有结构脱离出来, 在$\alpha =1$处, 3种滤波尺度的结构数量均达到峰值附近, 此时解析的数量较高, 对应的体积曲线位于中段, $\alpha $值的选择是``断裂''和``融合''两个过程相平衡的结果. 图9 所展示的变化趋势与Jimenez等[21 -22 ] 的研究中涉及的湍流结构所体现的规律相一致, Jimenez等[20 ] 将结构的这种特性称为``渗透性''. 基于图9 的结果, 取阈值$\alpha =1$. ...
Self-similar vortex clusters in the turbulent logarithmic region
6
2006
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
... [21 ]采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
... 应用cluster方法首先要进行逾渗分析(percolation analysis)[21 -22 ] 选定某一阈值, 当阈值较低时, 新的结构点被识别出, 并与已识别的结构体融合, 如果阈值为零, 所有的结构将会融合成少量的复杂结构, 从而对结构研究造成干扰, 而阈值过大又会造成筛选掉过多的结构, 这里采用Jimenez等[21 -22 ] 所采用的方法来尽可能地使用较小的阈值使得结构仍能被单独识别出来. 图9 展示了不同$\alpha$值下最大cluster结构的体积与所有cluster结构体积之和的比值以及不同$\alpha $值对应的cluster结构数量$N$与所有$\alpha $值能识别出的最多数量$N_{m}$的比值. 由图9 可以看出, 当$\alpha $较小时, 大部分结构融合在一起, 仅有少量的结构被识别出, 随着$\alpha $的增大, 结构逐渐``断裂'', 新的结构从原有结构脱离出来, 在$\alpha =1$处, 3种滤波尺度的结构数量均达到峰值附近, 此时解析的数量较高, 对应的体积曲线位于中段, $\alpha $值的选择是``断裂''和``融合''两个过程相平衡的结果. 图9 所展示的变化趋势与Jimenez等[21 -22 ] 的研究中涉及的湍流结构所体现的规律相一致, Jimenez等[20 ] 将结构的这种特性称为``渗透性''. 基于图9 的结果, 取阈值$\alpha =1$. ...
... [21 -22 ]所采用的方法来尽可能地使用较小的阈值使得结构仍能被单独识别出来. 图9 展示了不同$\alpha$值下最大cluster结构的体积与所有cluster结构体积之和的比值以及不同$\alpha $值对应的cluster结构数量$N$与所有$\alpha $值能识别出的最多数量$N_{m}$的比值. 由图9 可以看出, 当$\alpha $较小时, 大部分结构融合在一起, 仅有少量的结构被识别出, 随着$\alpha $的增大, 结构逐渐``断裂'', 新的结构从原有结构脱离出来, 在$\alpha =1$处, 3种滤波尺度的结构数量均达到峰值附近, 此时解析的数量较高, 对应的体积曲线位于中段, $\alpha $值的选择是``断裂''和``融合''两个过程相平衡的结果. 图9 所展示的变化趋势与Jimenez等[21 -22 ] 的研究中涉及的湍流结构所体现的规律相一致, Jimenez等[20 ] 将结构的这种特性称为``渗透性''. 基于图9 的结果, 取阈值$\alpha =1$. ...
... [21 -22 ]的研究中涉及的湍流结构所体现的规律相一致, Jimenez等[20 ] 将结构的这种特性称为``渗透性''. 基于图9 的结果, 取阈值$\alpha =1$. ...
... 图12 通过结构包围盒的流向长度$l_{x}^{+}$和展向长度$l_{z} ^{+}$与纵向长度$l_{y}^{+}$的二维联合概率密度展示了$\varPi ^{+}$结构和$\varPi^{-}$结构的几何特性. 可以看到$l_{x}^{+}$和$l_{z} ^{+}$随$l_{y}^{+}$的增大均符合确定的标度律. 其中$\varPi^{+}$结构$l_{x} ^{+}$与$l_{y}^{+}$的幂律关系为 $l_{x}^{+}\propto l_{y}^{+0.92}$, $l_{z}^{+}$与$l_{y}^{+}$的幂律关系为$l_{z}^{+}\propto l_{y} ^{+0.58}$, 而$\varPi^{-}$结构$l_{x}^{+}$与$l_{y} ^{+}$的幂律关系为$l_{x}^{+}\propto l_{y}^{+0.83}$, $l_{z} ^{+}$与$l_{y}^{+}$的的幂律关系为$l_{z}^{+}\propto l_{y} ^{+0.73}$. 以上结果表明$\varPi^{+}$与$\varPi ^{-}$的附着结构也具有Townsend所提出的附面涡模型的自相似性, 与Jimenez等[21 -28 ] 采用聚类分析得到的湍流结构的性质一致. ...
The three-dimensional structure of momentum transfer in turbulent channels
6
2012
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
... 应用cluster方法首先要进行逾渗分析(percolation analysis)[21 -22 ] 选定某一阈值, 当阈值较低时, 新的结构点被识别出, 并与已识别的结构体融合, 如果阈值为零, 所有的结构将会融合成少量的复杂结构, 从而对结构研究造成干扰, 而阈值过大又会造成筛选掉过多的结构, 这里采用Jimenez等[21 -22 ] 所采用的方法来尽可能地使用较小的阈值使得结构仍能被单独识别出来. 图9 展示了不同$\alpha$值下最大cluster结构的体积与所有cluster结构体积之和的比值以及不同$\alpha $值对应的cluster结构数量$N$与所有$\alpha $值能识别出的最多数量$N_{m}$的比值. 由图9 可以看出, 当$\alpha $较小时, 大部分结构融合在一起, 仅有少量的结构被识别出, 随着$\alpha $的增大, 结构逐渐``断裂'', 新的结构从原有结构脱离出来, 在$\alpha =1$处, 3种滤波尺度的结构数量均达到峰值附近, 此时解析的数量较高, 对应的体积曲线位于中段, $\alpha $值的选择是``断裂''和``融合''两个过程相平衡的结果. 图9 所展示的变化趋势与Jimenez等[21 -22 ] 的研究中涉及的湍流结构所体现的规律相一致, Jimenez等[20 ] 将结构的这种特性称为``渗透性''. 基于图9 的结果, 取阈值$\alpha =1$. ...
... -22 ]所采用的方法来尽可能地使用较小的阈值使得结构仍能被单独识别出来. 图9 展示了不同$\alpha$值下最大cluster结构的体积与所有cluster结构体积之和的比值以及不同$\alpha $值对应的cluster结构数量$N$与所有$\alpha $值能识别出的最多数量$N_{m}$的比值. 由图9 可以看出, 当$\alpha $较小时, 大部分结构融合在一起, 仅有少量的结构被识别出, 随着$\alpha $的增大, 结构逐渐``断裂'', 新的结构从原有结构脱离出来, 在$\alpha =1$处, 3种滤波尺度的结构数量均达到峰值附近, 此时解析的数量较高, 对应的体积曲线位于中段, $\alpha $值的选择是``断裂''和``融合''两个过程相平衡的结果. 图9 所展示的变化趋势与Jimenez等[21 -22 ] 的研究中涉及的湍流结构所体现的规律相一致, Jimenez等[20 ] 将结构的这种特性称为``渗透性''. 基于图9 的结果, 取阈值$\alpha =1$. ...
... -22 ]的研究中涉及的湍流结构所体现的规律相一致, Jimenez等[20 ] 将结构的这种特性称为``渗透性''. 基于图9 的结果, 取阈值$\alpha =1$. ...
... 图10 为级串结构体积的统计结果, 可以看到小尺寸结构出现的概率要远远高于大尺寸结构, 且体积概率密度分布呈现$-{4/5}$的幂律关系. 图11 展示了槽道内能流结构数密度随结构距壁面的最小距离$y_{\min } $和距壁面最大距离$y_{\max } $的分布规律. 从图11 可以看出, 结构主要集中在以$y^{+}_{\min } =17$为分界线的两侧, 因此可将能流结构划分为$y^{+}_{\min } <17$的壁面附着结构, 以及$y^{+}_{\min }>17$的分离结构. 这个分界线的距离与Lozano-Durán等[22 ] 研究中所涉及的上抛下扫结构的分界线$y^{+}=20$十分接近, 表明两种结构的分布可能存在某种关联. ...
... 其中$x_{\rm c}^{(i)}$为单个结构的几何中心, $d^{(i)}$为包围盒对角线长度. 采取与Lozano等[22 ] 类似的配对方法, 只考虑包围盒对角线长度之比满足${1/2}\leqslant {{d^{(j)}}/d^{(i)}}\leqslant 2$, 且距离最近的正级串附着结构和反级串附着结构为一对结构对. 图13 给出了流向相对距离$\delta_{x} $和展向相对距离$\delta_{z} $的二维散点图. 由图13 可见二维散点主要分布在$\delta_{y} =0$两侧, 而在$\delta_{z} =0$附近的散点极为稀疏, 这说明结构对在展向上总是保持一定距离, 几乎不会在展向发生重叠, 表明附着结构对更倾向于沿展向并排排列. ...
Wall-attached structures of velocity fluctuations in a turbulent boundary layer
0
2018
Intense structures of different momentum fluxes in turbulent channels
0
2018
Uncovering Townsend's wall-attached eddies in low-Reynolds-number wall turbulence
1
2020
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
2020. On the structure of streamwise wall-shear stress fluctuations in turbulent channel flows
0
2020
Wall-attached structures of streamwise velocity fluctuations in an adverse-pressure-gradient turbulent boundary layer
0
2020
The coherent structure of the kinetic energy transfer in shear turbulence
2
2020
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
... 图12 通过结构包围盒的流向长度$l_{x}^{+}$和展向长度$l_{z} ^{+}$与纵向长度$l_{y}^{+}$的二维联合概率密度展示了$\varPi ^{+}$结构和$\varPi^{-}$结构的几何特性. 可以看到$l_{x}^{+}$和$l_{z} ^{+}$随$l_{y}^{+}$的增大均符合确定的标度律. 其中$\varPi^{+}$结构$l_{x} ^{+}$与$l_{y}^{+}$的幂律关系为 $l_{x}^{+}\propto l_{y}^{+0.92}$, $l_{z}^{+}$与$l_{y}^{+}$的幂律关系为$l_{z}^{+}\propto l_{y} ^{+0.58}$, 而$\varPi^{-}$结构$l_{x}^{+}$与$l_{y} ^{+}$的幂律关系为$l_{x}^{+}\propto l_{y}^{+0.83}$, $l_{z} ^{+}$与$l_{y}^{+}$的的幂律关系为$l_{z}^{+}\propto l_{y} ^{+0.73}$. 以上结果表明$\varPi^{+}$与$\varPi ^{-}$的附着结构也具有Townsend所提出的附面涡模型的自相似性, 与Jimenez等[21 -28 ] 采用聚类分析得到的湍流结构的性质一致. ...
1
2008
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
1
2008
... 壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1 -3 ] . 在壁面附近, 湍流各尺度间的能量传输机理与近壁相干动力循环密切相关, 对于高保真大涡模拟技术而言, 研究并利用壁湍流多尺度能量传输机制, 对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4 -5 ] . 大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6 -20 ] . Härtel等[7 ] 通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象, 认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起, 没有完全分开. 通过条件统计发现, 近壁区的相干运动如: 猝发, 可以显著增强近壁区的能量反传. Piomelli等[8 ] 应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如: 准流向涡、发卡涡以及上抛和下扫等结构密切相关. 在缓冲层内, 正传事件伴随上抛结构, 反传事件伴随下扫结构, 正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧. Härtel等[7 ] 和Piomelli等[8 ] 的研究都表明: Smargorinsky涡黏模型并不能准确刻画近壁区能量正反传事件. Lin[9 ] 通过对平板边界层的大涡模拟进一步解释并支持了Piomelli等[8 ] 的结果. 而Germano等[10 ] 提出的Dynamic Smagorinsky模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件, 但各个模型和实验间依然存在一些差异. Tian等[11 ] 通过对湍动能方程各项进行机理分析, 解释了亚临界圆柱绕流工况下几种LES模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因. 国内学者贾宏涛等[12 ] 利用子波分析在壁湍流流向和展向上分别进行多尺度分解, 发现流向主要以反传为主, 而展向存在明显正传, 当截断尺度增大时则以正传为主. 王占莹[13 ] 采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关, 而反传事件中稳定的焦点占比最大. 实验方面, Natrajan等[14 ] 通过对平板边界层PIV实验数据在物理空间进行滤波, 发现在对数层中, 瞬时正传事件发生在上抛事件附近, 两个相邻的发卡涡头之间, 而最强烈的正传事件则出现在下扫事件附近, 并形成沿着发卡涡背部的倾斜剪切层. 相反, 局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方, 后者要比前者更强烈. 最后, 在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件. 王帅杰等[17 ] 通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动, 表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果. 此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画, 然而这些研究往往只关注了特定区域或特定条件的传输事件, 而忽略了部分传输区域和事件的存在, 缺乏对传输事件的全面统计, 随着新的流场结构识别技术的提出[21 -29 ] , 对瞬时三维流场内结构的全面统计已成为可能. DelÁlamo等[21 ] 采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质, 发现按照距壁面距离可将涡团分为附着族类和分离族类, 其中附着部分为一类尺寸自相似族群, 而分离结构的尺寸仅与当地Kolmogorov尺度有关. Lozano-Durán等[22 ] 采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画, 进一步采用直接数值模拟时间解析数据, 对结构的分裂、融合等演化形为进行了定量刻画. Cheng等[25 ] 采用聚类方法, 在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释. Dong等[28 ] 则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理. 将瞬时流场内发生能量正传和反传的区域定义为级串结构, 本文采用空间滤波方法(filter-space technique)获取不同尺度间的能量传递, 结合聚类分析法对流场内的级串结构进行了进一步的刻画, 由于本研究所考虑的问题需在均匀网格数据下进行分析, 所以本文采用格子玻尔兹曼方法(lattice Boltzmann method, LBM)进行模拟, LBM在本研究中的优势在于无需对后处理数据额外插值, 实现简单, 易于并行. 本文的主要内容如下: 第1部分首先介绍了LBM的基本方程、外力项及边界条件等的处理, 结合空间滤波方法给出了表征跨尺度能量传递的物理量, 最后介绍结构识别捕捉方法—聚类分析方法. 第2部分介绍了直接数值模拟的参数设置. 第3部分给出了本文的数值模拟结果与已有的DNS结果对比, 进一步的给出了滤波场的统计结果,均与前人的统计结果一致, 证明了数据和滤波方法的可靠性. 最后给出了聚类分析方法的得到的结构统计结果. ...
1
2009
... 对于边界条件, 本研究采用郭照立等[30 ] 提出的非平衡外推方法, 将边界格点处的未知分布函数分解为平衡态和非平衡态两部分, 即 ...
1
2009
... 对于边界条件, 本研究采用郭照立等[30 ] 提出的非平衡外推方法, 将边界格点处的未知分布函数分解为平衡态和非平衡态两部分, 即 ...
Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method
1
2002
... 考虑外力项的处理, 本研究采用直接在演化方程中增加一个作用力项来实现体积力${F}$在LBE中的影响[31 ] , 即 ...
The minimal flow unit in near-wall turbulence
2
1991
... 其中, $F_{i}$进一步通过基于格子气自动机方法中处理作用力的方法[32 ] , 将${F}_{i} $表示为 ...
... 对于槽道湍流, 除雷诺数外, 首先应确定模拟所需要的计算域尺寸. Jimenez等[32 ] 研究了能够维持湍流所需要的最小槽道尺寸, 他们定义$\alpha_{x} =L_{x}/H$, $\alpha_{z} =L_{z} /H$, 基于此Spasov等[33 ] 使用LBM模拟$R_{\tau} =180$的槽道湍流时取$\alpha_{x} =4$, $\alpha_{z} =1$, 结果与Kim等[34 ] 的研究相比, 平均速度剖面结果基本吻合但在对数区略高, 雷诺应力的结果也存在一定偏差, 因此本研究选取的槽道尺寸为$\alpha_{x} =4.6$, $\alpha_{z} =2$,网格数$L_{x} \times L_{y} \times L_{z} $为$600\times 260\times 260$. 槽道尺寸选定后, 对于直接数值模拟, 每个网格的尺寸都应小于当地的Kolmogorov尺度$\eta $. 对于槽道湍流在垂向方向上壁面处耗散率最大, 相应的当地Kolmogorov尺度$\eta $为需要解析的最小尺度, 定义壁面处Kolmogorov的尺度为$\eta_{0} $, 考虑 ...
Simulation of a turbulent channel flow with an entropic Lattice Boltzmann method
3
2009
... 对于槽道湍流, 除雷诺数外, 首先应确定模拟所需要的计算域尺寸. Jimenez等[32 ] 研究了能够维持湍流所需要的最小槽道尺寸, 他们定义$\alpha_{x} =L_{x}/H$, $\alpha_{z} =L_{z} /H$, 基于此Spasov等[33 ] 使用LBM模拟$R_{\tau} =180$的槽道湍流时取$\alpha_{x} =4$, $\alpha_{z} =1$, 结果与Kim等[34 ] 的研究相比, 平均速度剖面结果基本吻合但在对数区略高, 雷诺应力的结果也存在一定偏差, 因此本研究选取的槽道尺寸为$\alpha_{x} =4.6$, $\alpha_{z} =2$,网格数$L_{x} \times L_{y} \times L_{z} $为$600\times 260\times 260$. 槽道尺寸选定后, 对于直接数值模拟, 每个网格的尺寸都应小于当地的Kolmogorov尺度$\eta $. 对于槽道湍流在垂向方向上壁面处耗散率最大, 相应的当地Kolmogorov尺度$\eta $为需要解析的最小尺度, 定义壁面处Kolmogorov的尺度为$\eta_{0} $, 考虑 ...
... 其中$\kappa $为卡门常数, 约等于$0.4$, $B$取6. 对于LBM, 为了满足低马赫数条件, 流场中的最大速度须小于等于0.1[33 ] , 对于槽道湍流最大平均速度在槽道中心, 所以可取$U_{0} =0.1$. ...
... 图2 为基于$Q$准则的空间涡结构等值面图, ${Q/{\left( {{{u_{\tau } ^{4}}/{\nu^{2}}}} \right)}}=0.015$,展示了流场内涡结构的分布, 从图2 可以看到近壁区的准流向涡和一些类似发卡涡的结构. 图3 为平均速度$U^{+}$沿垂向变化曲线, 符号圆点为本文DNS的结果, 虚线为Kim等[34 ] 的结果, 叉型标记为Lee等[35 ] 的结果, 可以看到, 本文的平均速度剖面结果与Kim等[34 ] 吻合得较好. 此前本研究也计算过$\alpha_{x} =4$, $\alpha_{z} =1$的结果, 结果显示在对数区吻合的效果并不理想, 这与Spasov等[33 ] 和许丁等[36 ] 的结果类似, 表明展向尺寸也会对计算结果产生显著影响. ...
Turbulence statistics in fully developed channel flow at low Reynolds number
5
1987
... 对于槽道湍流, 除雷诺数外, 首先应确定模拟所需要的计算域尺寸. Jimenez等[32 ] 研究了能够维持湍流所需要的最小槽道尺寸, 他们定义$\alpha_{x} =L_{x}/H$, $\alpha_{z} =L_{z} /H$, 基于此Spasov等[33 ] 使用LBM模拟$R_{\tau} =180$的槽道湍流时取$\alpha_{x} =4$, $\alpha_{z} =1$, 结果与Kim等[34 ] 的研究相比, 平均速度剖面结果基本吻合但在对数区略高, 雷诺应力的结果也存在一定偏差, 因此本研究选取的槽道尺寸为$\alpha_{x} =4.6$, $\alpha_{z} =2$,网格数$L_{x} \times L_{y} \times L_{z} $为$600\times 260\times 260$. 槽道尺寸选定后, 对于直接数值模拟, 每个网格的尺寸都应小于当地的Kolmogorov尺度$\eta $. 对于槽道湍流在垂向方向上壁面处耗散率最大, 相应的当地Kolmogorov尺度$\eta $为需要解析的最小尺度, 定义壁面处Kolmogorov的尺度为$\eta_{0} $, 考虑 ...
... 由Kim等[34 ] 提供的数据可知, $\varepsilon_{0}^{+}$的最大值约为0.2, 相应的$\eta_{0}^{+}=1.5$. 由于LBM中网格尺寸为无量纲数$\varDelta =1$. ...
... 图2 为基于$Q$准则的空间涡结构等值面图, ${Q/{\left( {{{u_{\tau } ^{4}}/{\nu^{2}}}} \right)}}=0.015$,展示了流场内涡结构的分布, 从图2 可以看到近壁区的准流向涡和一些类似发卡涡的结构. 图3 为平均速度$U^{+}$沿垂向变化曲线, 符号圆点为本文DNS的结果, 虚线为Kim等[34 ] 的结果, 叉型标记为Lee等[35 ] 的结果, 可以看到, 本文的平均速度剖面结果与Kim等[34 ] 吻合得较好. 此前本研究也计算过$\alpha_{x} =4$, $\alpha_{z} =1$的结果, 结果显示在对数区吻合的效果并不理想, 这与Spasov等[33 ] 和许丁等[36 ] 的结果类似, 表明展向尺寸也会对计算结果产生显著影响. ...
... [34 ]吻合得较好. 此前本研究也计算过$\alpha_{x} =4$, $\alpha_{z} =1$的结果, 结果显示在对数区吻合的效果并不理想, 这与Spasov等[33 ] 和许丁等[36 ] 的结果类似, 表明展向尺寸也会对计算结果产生显著影响. ...
... 图4 和图5 为湍流统计量脉动速度均方根和雷诺应力的统计结果, 与Kim等[34 ] 和Lee等[35 ] $Re_{\tau }=180$下的DNS结果对比吻合得较好, 同样在$\alpha_{x} =4$, $\alpha_{z} =1$的条件下, 结果也存在较大偏差. ...
Direct numerical simulation of turbulent channel flow up to $Re_{\tau} =5200$
2
2015
... 图2 为基于$Q$准则的空间涡结构等值面图, ${Q/{\left( {{{u_{\tau } ^{4}}/{\nu^{2}}}} \right)}}=0.015$,展示了流场内涡结构的分布, 从图2 可以看到近壁区的准流向涡和一些类似发卡涡的结构. 图3 为平均速度$U^{+}$沿垂向变化曲线, 符号圆点为本文DNS的结果, 虚线为Kim等[34 ] 的结果, 叉型标记为Lee等[35 ] 的结果, 可以看到, 本文的平均速度剖面结果与Kim等[34 ] 吻合得较好. 此前本研究也计算过$\alpha_{x} =4$, $\alpha_{z} =1$的结果, 结果显示在对数区吻合的效果并不理想, 这与Spasov等[33 ] 和许丁等[36 ] 的结果类似, 表明展向尺寸也会对计算结果产生显著影响. ...
... 图4 和图5 为湍流统计量脉动速度均方根和雷诺应力的统计结果, 与Kim等[34 ] 和Lee等[35 ] $Re_{\tau }=180$下的DNS结果对比吻合得较好, 同样在$\alpha_{x} =4$, $\alpha_{z} =1$的条件下, 结果也存在较大偏差. ...
基于多GPU的格子Boltzmann法对槽道湍流的直接数值模拟
1
2013
... 图2 为基于$Q$准则的空间涡结构等值面图, ${Q/{\left( {{{u_{\tau } ^{4}}/{\nu^{2}}}} \right)}}=0.015$,展示了流场内涡结构的分布, 从图2 可以看到近壁区的准流向涡和一些类似发卡涡的结构. 图3 为平均速度$U^{+}$沿垂向变化曲线, 符号圆点为本文DNS的结果, 虚线为Kim等[34 ] 的结果, 叉型标记为Lee等[35 ] 的结果, 可以看到, 本文的平均速度剖面结果与Kim等[34 ] 吻合得较好. 此前本研究也计算过$\alpha_{x} =4$, $\alpha_{z} =1$的结果, 结果显示在对数区吻合的效果并不理想, 这与Spasov等[33 ] 和许丁等[36 ] 的结果类似, 表明展向尺寸也会对计算结果产生显著影响. ...
基于多GPU的格子Boltzmann法对槽道湍流的直接数值模拟
1
2013
... 图2 为基于$Q$准则的空间涡结构等值面图, ${Q/{\left( {{{u_{\tau } ^{4}}/{\nu^{2}}}} \right)}}=0.015$,展示了流场内涡结构的分布, 从图2 可以看到近壁区的准流向涡和一些类似发卡涡的结构. 图3 为平均速度$U^{+}$沿垂向变化曲线, 符号圆点为本文DNS的结果, 虚线为Kim等[34 ] 的结果, 叉型标记为Lee等[35 ] 的结果, 可以看到, 本文的平均速度剖面结果与Kim等[34 ] 吻合得较好. 此前本研究也计算过$\alpha_{x} =4$, $\alpha_{z} =1$的结果, 结果显示在对数区吻合的效果并不理想, 这与Spasov等[33 ] 和许丁等[36 ] 的结果类似, 表明展向尺寸也会对计算结果产生显著影响. ...