引言
二相流是自然界中常见的流体运动形式. 其中, 水气二相流与水利工程、海岸工程和海洋工程等实际工程问题密切相关. 水气二相流因具有界面变形复杂、密度差大和紊动强烈等特点, 需要较高的界面追踪和控制方程对流项的数值求解精度, 是计算流体力学的难点和热点问题. 相关研究结果表明, 当流体速度低于$0.3$倍的声速时, 流体运动可视为不可压缩流进行处理[1 ] . 因此, 在对开敞水域的自由表面流工程问题进行数值模拟分析时, 为简化模型, 一般情况下可以忽略空气的可压缩性, 将其视为不可压缩流体. 据此, 本研究的水气二相流的模型亦采用水和空气的不可压缩假定.
如上所述, 水气二相流中界面两侧的介质密度相差较大, 而密度的微小变动将会引起界面两侧压强的剧烈变化; 此外, 水气二相流还具有紊动剧烈的特点; 这些均要求所选取的对流项的求解方法在具有较高的精度的同时, 能够很好地处理变量的突变问题. 加权基本无震荡(weighted essentially non-oscillatory, WENO)格式[2 ] 根据变量变化曲线的光滑程度选取加权值. 对于$2r-1$阶WENO格式, 在曲线光滑段具有$2r-1$阶精度, 在间断点处退化为基本无震荡(essentially non-oscillatory, ENO)格式[3 ] , 并保持基本无震荡特性, 被广泛用于实际工程中流体运动问题, 特别是空气动力学问题的数值模拟[4 -6 ] . 相对而言, WENO格式在水气二相流中的应用成果较少. 鉴于其高精度、自适应、标准化等特点, 本文选取WENO格式离散对流项, 同时采用三阶总变差递减(total variation diminishing, TVD)龙格库塔(Runge-Kutta, RK)法[7 ] 对时间项进行离散, 求解流体运动的动量方程.
另一方面, 对二相流的界面处理以VOF[8 ] (volume of fluid)法应用最为广泛[9 -11 ] , VOF模型理论上具有质量守恒、物理意义明确等特点, 可分为几何重构法和代数法[12 ] . 在多维情况下, 前者的界面几何重构过程过于复杂且计算效率低下, 相比而言代数法对界面追踪的计算过程更为简单. Xiao等[13 ] 提出的双曲正切函数界面捕捉法(tangent of hyperbola for interface capturing, THINC)为典型的代数法. 该方法采用分段双曲正切函数重构界面, 将流体各物理量沿界面法向方向的变化视为连续函数, 通过模型中的界面形态参数控制不同介质界面的厚度, 进而确定界面网格的体积分数通量, 不仅大大简化了界面追踪的计算流程, 而且能够保证流体质量守恒的计算精度. 此外, Yokoi[14 ] 提出了将加权线性界面计算(weighted line interface calculation, WLIC)和THINC法相结合的改进方法, 以取代之前将一维THINC法直接用于多维界面运动问题求解的作法, 有效地提高了THINC法对多维界面追踪的计算精度. THINC/WLIC法的计算过程简单, 适用于二维和三维问题的流体界面追踪. 除此之外, 还有一些对THINC法的改进方法[12 ,15 -17 ] , 但大多包含多维双曲正切函数的重构, 涉及的参数过多, 程序实现较困难, 且计算量亦相对较大.
迄今, 尚未见到国内外关于将WENO格式与THINC法进行耦合的相关模型研究成果. 考虑到WENO格式的高精度、自适应等特点适用于二相流的对流项的计算, THINC/WLIC法在自由表面追踪时既简单易行又具有较高的求解精度的特点, 适合于复杂界面的追踪计算, 本文尝试将两者进行耦合, 建立WENO-THINC/WLIC耦合水气二相流数值模型, 并通过对典型流体力学问题的模拟分析与模型验证, 探索适用于大多数工程领域中水气二相流运动模拟的高精度数值计算方法.
1 控制方程
本模型中水气两相均视为不可压缩, 流体运动的控制方程为NS方程, 其二维形式可表示为
(1) $\frac{\partial u_i}{\partial t} + u_j\frac{\partial u_i}{\partial x_j} = \frac{1}{\rho}\frac{\partial \tau_{ij}}{\partial x_j} + f_i $
(2) $\frac{\partial u_i}{\partial x_i} = 0 $
式中, $i, j=1,2$; $u_i$为速度分量; $f_i$为质量力, 在本模型中为重力; $\tau_{ij}$为总应力, 对于牛顿流体有$\tau_{ij}=-p\delta_{ij}+2\mu S_{ij}-2\mu\delta_{ij}S_{kk}/3$, 其中$p$为压强, $S_{ij}=(\partial u_i/\partial x_j+\partial u_j/\partial x_i)/2$, $\delta_{ij}$为Kronecker算子.
基于VOF方法追踪水气交界面, 水和空气的体积分数$\alpha_m$满足方程
(3) $\begin{eqnarray}\label{Eq_vof} \frac{\partial \alpha_m}{\partial t} + u_i\frac{\partial \alpha_m}{\partial x_i} = 0 \end{eqnarray} $
式中, $m=1, 2$; $\alpha_m$满足$\alpha_1 + \alpha_2 = 1$.
(4) $\begin{eqnarray}\label{Eq_property} \lambda = \alpha_1\lambda_1 + \alpha_2\lambda_2 \end{eqnarray} $
式中, $\lambda$为密度$\rho$或黏性系数$\mu$, $\lambda_1$和$\lambda_2$分别为对应的水体或气体的特性参数.
2 数值方法
2.1 分步计算法
采用分步计算法[18 ] 对控制方程进行离散求解, 计算过程分为3个阶段: 对流项、非对流项(I)、非对流项(II). 从时间刻$t^n$到$t^{n+1}$的具体求解过程如下.
(5) $\frac{\partial u_i}{\partial t} + u_j\frac{\partial u_i}{\partial x_j} = 0 $
(6) $\frac{\partial \alpha_m}{\partial t} + u_i\frac{\partial \alpha_m}{\partial x_i} = 0 $
(7) $\begin{eqnarray} \frac{u^*_i - u^n_i}{\Delta t} + u^n_j\frac{\partial u^n_i}{\partial x_j} = 0 \end{eqnarray} $
式中, ${\partial u^n_i}/{\partial x_j}$由WENO格式数值近似求解, 对上式进行时间积分可以得到第一中间解$u^*_i$.
利用THINC/WLIC法求解式(6), 可得$\alpha^{n+1}_m$.
此步骤求解黏性项和质量力项. 第二中间解$u^{**}_i$可由下式求得
(8) $\begin{eqnarray} \frac{u^{**}_i-u^{*}_i}{\Delta t} = \frac{2\mu^{n+1}}{\rho^{n+1}}\frac{\partial}{\partial x_i}\left(S^*_{ij}-\frac{1}{3}\delta_{ij}S^*_{kk}\right) + f_i \end{eqnarray} $
式中, $\mu^{n+1}$和$\rho^{n+1}$由式(4)求得; 方程右侧的微分项使用中心差分法近似求解.
(9) $\begin{eqnarray}\label{Eq_pressure_velocity} \frac{u^{n+1}_i - u^{**}_i}{\Delta t} = -\frac{1}{\rho^{n+1}}\frac{\partial p^{n+1}}{\partial x_i} \end{eqnarray} $
(10) $\begin{eqnarray} \frac{1}{\Delta t}\frac{\partial u^{**}_i}{\partial x_i} = \frac{\partial}{\partial x_i}\left(\frac{1}{\rho^{n+1}}\frac{\partial p^{n+1}}{\partial x_i}\right) \end{eqnarray} $
式(10)为压力泊松方程, 其系数矩阵为正定矩阵, 在二维情况下可通过LDLt分解法求解.
求得$t^{n+1}$时刻的压强场后, 利用式(9)求得$u^{n+1}_i$. 具体的计算公式为
(11) $\begin{eqnarray} u^{n+1}_i = u^{**}_i - \frac{\Delta t}{\rho^{n+1}}\frac{\partial p^{n+1}}{\partial x_i} \end{eqnarray} $
方程右侧压强梯度${\partial p^{n+1}}/{\partial x_i}$使用中心差分法离散.
以上为单个时间步的计算流程, 单步计算结束后返回步骤(1), 根据设定的CFL条件更新$\Delta t$, 如此循环可以得到设定时段的计算结果.
2.2 WENO格式
(12) $\begin{eqnarray} \frac{\partial \phi}{\partial t} + u\frac{\partial \phi}{\partial x} + v\frac{\partial \phi}{\partial y} = 0 \end{eqnarray} $
现以$\phi$在$x$方向的离散格式为例说明WENO格式的计算过程
(13) $\begin{eqnarray} \frac{\phi^{n+1}_i - \phi^n_i}{\Delta t} + u^n_i\left(\phi_x\right)^n_i=0 \end{eqnarray} $
式中, $\phi_x$为$\phi$在点$x_i$处的空间微分. 该项采用一阶迎风格式计算, 即当$u^n_i>0$, 使用向后一阶差分$\phi^-$来数值估算$\phi_x$; 当$u^n_i<0$, 使用向前一阶差分$\phi^+$来数值估算$\phi_x$; $u^n_i=0$, 对流项整体为$0$.
以下给出五阶WENO格式计算$\phi^-$的过程[19 ] , $\phi^+$的计算过程类似. 计算模板为$\{\phi_{i-3}$, $\phi_{i-2}$, $\phi_{i-1}$, $\phi_{i}$, $\phi_{i+1}$, $\phi_{i+2}\}$, 定义$v_1=D^-\phi_{i-2}$, $v_2=D^-\phi_{i-1}$, $v_3=D^-\phi_{i}$, $v_4=D^-\phi_{i+1}$, $v_5=D^-\phi_{i+2}$. 其中$D^-\phi_k=(\phi_k-\phi_{k-1})/\Delta x$. 使用以上5个一阶向后差分可给出3个ENO格式对$\phi^-_x$的数值估计
(14a) $\phi^1_x = \dfrac{v_1}{3} - \dfrac{7v_2}{6} + \dfrac{11v_3}{6}$
(14b) $\phi^2_x = -\dfrac{v_2}{3} + \dfrac{5v_3}{6} + \dfrac{v_4}{3}$
(14c) $\phi^3_x = \dfrac{v_3}{3} + \dfrac{5v_4}{6} - \dfrac{v_5}{6}$
对上述3个估计值进行加权凸组合即得到五阶WENO格式
(15) $\begin{eqnarray} \phi^-_x = \omega_1\phi^1_x + \omega_2\phi^2_x + \omega_3\phi^3_x \end{eqnarray} $
式中, $\omega_k$为权重, 有$0<\omega_k<1$且$\omega_1+\omega_2+\omega_3=1$.
(16a) $S_1 = \frac{13}{12}(v_1 - 2v_2 + v_3)^2 + \frac{1}{4}(v_1 - 4v_2 + 3v_3)^2$
(16b) $S_2 = \frac{13}{12}(v_2 - 2v_3 + v_4)^2 + \frac{1}{4}(v_2 - v_4)^2$
(16c) $S_3 = \frac{13}{12}(v_3 - 2v_4 + v_5)^2 + \frac{1}{4}(3v_3 - 4v_4 + v_5)^2$
(17a) $\alpha_1 = \frac{0.1}{(S_1 + \epsilon)^2}$
(17b) $\alpha_2 = \frac{0.6}{(S_2 + \epsilon)^2}$
(17c) $\alpha_3 = \frac{0.3}{(S_3 + \epsilon)^2}$
为避免分母为$0$, 取$\epsilon=10^{-6}\mathrm{max}\{v^2_1,v^2_2,v^2_3,v^2_4,v^2_5\}+10^{-99}$.
(18) $\begin{eqnarray} \omega_k = \frac{\alpha_k}{\alpha_1 + \alpha_2 + \alpha_3},\quad k=1, 2, 3 \end{eqnarray} $
2.3 时间项离散
本文采用三阶TVD RK格式对时间项进行离散. 具体过程如下
(19a) $\phi^{(1)} = \phi^{n} + \Delta t \mathcal{L}(\phi^{n})$
(19b) $\phi^{(2)} = \dfrac{3}{4}\phi^{n} + \dfrac{1}{4}\phi^{(1)} + \mathcal{L}(\phi^{(1)})$
(19c) $\phi^{n+1} = \dfrac{1}{3}\phi^{n} + \dfrac{2}{3}\phi^{(2)} + \dfrac{2}{3}\mathcal{L}(\phi^{(2)})$
式中, $\phi$为基本变量, 本模型中为$u_i$; $\mathcal{L}$为式(1)和式(2)中对流项和等号右侧对应的数值解; 角标$(1)$和角标$(2)$为当前时间步$t^n$和下一时间步$t^{n+1}$之间的子时间步.
2.4 THINC/WLIC算法
将水气二相流中水的体积分数输运方程式(3)改写为守恒格式并忽略角标可得
(20) $\begin{eqnarray} \frac{\partial \phi}{\partial t} + \frac{\partial u_i\phi}{\partial x_i} - \phi\frac{\partial u_i}{\partial x_i} = 0 \end{eqnarray} $
(21) $\begin{eqnarray} \frac{\partial \phi}{\partial t} + \frac{\partial u\phi}{\partial x} - \phi\frac{\partial u}{\partial x} = 0 \end{eqnarray} $
已知$t=t^n$时刻的网格$[x_{i-1/2},x_{i+1/2}]$内水的体积分数为$\phi^n_i$, 则$t=t^{n+1}$时刻的$\phi^{n+1}_i$可通过有限体积法计算
(22) $\begin{eqnarray} && {\phi}^{n+1}_i = {\phi}^{n}_i - \left(f_{i+1/2} - f_{i-1/2}\right) / \Delta x +\\&& {\phi}^{n}_i\left(u_{i+1/2}-u_{i-1/2}\right)\Delta t / \Delta x \end{eqnarray} $
式中, $u_{i+1/2}$为$x=x_{i+1/2}$处的速度, $\Delta x = x_{i+1/2} - x_{i-1/2}$. $f_{i+1/2}$为$\Delta t=t^{n+1} - t^n$时间段内通过边界$x=x_{i+1/2}$的通量, 计算过程如下
(23) $\begin{eqnarray} f_{i+1/2} = \begin{cases} -\int^{t^{n+1}}_{t^n}\varPhi_i\left[x_{i+1/2} - u_{i+1/2}(t-t^n)\right]{d}t \\\qquad \mathrm{if~} u_{i+1/2}\geqslant 0\\ \int^{t^{n+1}}_{t^n}\varPhi_{i+1}\left[x_{i+1/2} - u_{i+1/2}(t-t^n)\right]{d}t \\\qquad \mathrm{if~} u_{i+1/2}< 0 \end{cases} \end{eqnarray} $
式中, $\varPhi_i$为重构的插值函数. THINC法使用的是分段双曲正切函数
(24) $\begin{eqnarray} \varPhi_i = \frac{1}{2}\left\{1+\gamma\tanh\left[\beta\left(\frac{x-x_{i-1/2}}{\Delta x}-\tilde{x}_i\right)\right]\right\} \end{eqnarray} $
式中, 当$\phi_{i-1}<\phi_{i+1}$时, $\gamma=1$, 当$\phi_{i-1}>\phi_{i+1}$时,$\gamma=-1$. $\beta$是控制界面厚度的参数, 本文中均取$\beta=2.3$. 界面中点$\tilde{x}_i$由下面的积分式确定
(25) $\begin{eqnarray} \frac{1}{\Delta x}\int^{x_{i+1/2}}_{x_{i-1/2}}\varPhi_i(x) = {\phi}^n_i \end{eqnarray} $
计算通量$f_{i+1/2}$的具体过程[20 ] 如下
(1) 当$u_i<0$时, 令$\lambda = 0$, $iup=i+1$; 当$u_i\geqslant 0$时, 令$\lambda = 1$, $iup=i$.
(26) $\begin{eqnarray} \tilde{x}_{iup} = \frac{1}{2\beta}\ln\left(\frac{\mathrm{e}^{[\frac{\beta}{\gamma} (1+\gamma-2{\phi}_{iup})]}-1}{1-\mathrm{e}^{[\frac{\beta}{\gamma}(1-\gamma-2{\phi}_{iup})]}}\right) \end{eqnarray} $
(27) $\begin{eqnarray} &&f_{i+1/2} = \frac{1}{2}\left(-u_{i+1/2}\Delta t\right) + \\&& \frac{\gamma\Delta x}{2\beta}\ln\left(\frac{\cosh[\beta(\lambda - {\phi}_{iup}-u_{i+1/2}\Delta t/\Delta x)]}{\cosh[\beta(\lambda-\tilde{x}_{iup})]}\right) \end{eqnarray} $
在WLIC方法中, 多维界面重构是根据界面法向量分别对水平界面和竖向界面赋权重来实现的. 在主方向使用一维THINC法计算体积分数通量, 在次主方向使用简单线性界面法(simple line interface calculation, SLIC)计算, 从而实现计算量和精度之间的平衡, 以较小的计算量获取较高的精度. 如图1 所示, 设在网格$(i,j)$内, 体积分数为$\alpha_{i,j}$. 根据WLIC理论, 该网格内界面重构表达式为
(28) $\begin{eqnarray} \chi_{i,j} = \omega_{x,i,j}({n})\chi_{x,i,j}(x,y) + \omega_{y,i,j}({n})\chi_{y,i,j}(x,y) \end{eqnarray} $
式中, ${n}$为界面法向量, $\chi$为界面特征表达式, $\chi_x$和$\chi_y$分别为竖向界面和水平界面的特征表达式, $\omega_x$和$\omega_y$为对应的权重.
图1
图1
界面加权分解
Fig.1
Weighted decomposition of the interface
(29) $\omega_x + \omega_y = 1 $
(30) $\alpha_{i,j}= \frac{1}{\Delta x\Delta y}\iint_{\varOmega_{ij}}\chi_{x,i,j}(x,y){d}x{d}y =\frac{1}{\Delta x\Delta y}\iint_{\varOmega_{ij}}\chi_{y,i,j}(x,y){d}x{d}y $
$\omega_x$和$\omega_y$由下式确定
(31a) $\omega_x = \frac{\left|n_{x,i,j}\right|}{\left|n_{x,i,j}\right| + \left|n_{y,i,j}\right|}$
(31b) $\omega_y = \frac{\left|n_{y,i,j}\right|}{\left|n_{x,i,j}\right| + \left|n_{y,i,j}\right|}$
式中, $n_{x,i,j}$和$n_{x,i,j}$分别是界面法向量$n$的$x$方向和$y$方向分量, 具体计算过程见文献[14 ].
待权重确定后, 通过网格边壁$(i+1/2,j)$的通量的计算公式如下
(32) $F_{x,i+1/2,j} = F_{x,x,i+1/2,j} + F_{x,y,i+1/2,j} $
(33) $F_{x,x,i+1/2,j} = -\int_{x_{i+1/2,j}}^{x_{i+1/2,j}-u_{i+1/2,j}\Delta t} \omega_{x,i,j}\phi_{x,i,j}{d}x $
(34) $F_{x,y,j+1/2,j} = \omega_{y,i,j}C_{i,j}u_{i+1/2,j}\Delta t\label{Eq_linear_WLIC} $
其中, 式(33)采用一维THINC法计算, 式(34)采用SLIC计算. 网格边壁$(i,j+1/2)$的通量计算过程类似.
3 数值模型验证
3.1 界面处理
采用本研究建立的数值模型对Zalesak's disk旋转[21 ] 和shearing flow问题[22 ] 进行模拟分析, 以验证本数值模拟方法对大变形界面的追踪能力. 其中, 验证案例的计算域均为$[0,1] \times [0,1]$, 均采用$100\times 100$, $200\times 200$, $400\times 400$和$800\times 800$ 四种密度的结构化网格进行模拟计算, 并设置$\mathrm{CFL}=0.25$.
Zalesak's disk旋转问题常被用来检验界面处理方法的适用性和模拟精度. 如图2 和图3 中黑色实线所示, Zalesak's disk是一个带有缺口的圆形, 在外加速度场$(u,v)=(y-0.5,0.5-x)$的作用下绕点$(0.5,0.5)$匀速旋转, 在$t=2$时回到原处. Zalesak's disk在计算域上的初值定义为
(35) $\begin{eqnarray} H({x})=\begin{cases} 1,& \begin{split} &\bigg\{\sqrt{(x-0.5)^2+(y-0.75)^2}\leqslant 0.15\bigg\}\bigg\backslash\\ &\{\left|x-0.5\right|\leqslant0.025\ \mathrm{and}\ y\leqslant 0.85\} \end{split}\\ 0,&\mathrm{otherwise} \end{cases} \end{eqnarray} $
图2 和图3 分别给出对应于200 $\times$ 200和400 $\times$ 400两种网格的模拟结果. 图中a, b, c, d分别为$t=0.5$, $t=1.0$, $t=1.5$, $t=2.0$时刻的模拟结果, 黑色实线为理论值. 可见, 在光滑界面处数值模拟结果与理论值基本吻合, 几乎没有形变, 在界面转折突变处随着界面运动而逐渐光滑. 在网格加密后, 这种界面形变得到了很好的抑制. 由此可见, 模拟得到的Zalesak's disk的形状在旋转过程中与理论值基本一致, 表明本数值模型具有很好的界面追踪能力. 为定量分析界面模拟精度, 定义误差计算公式为
图2
图2
Zalesak's disk数值模拟结果(网格密度: $200\times 200$)
Fig.2
Simulation results of Zalesak's disk with $200\times 200$ mesh
图3
图3
Zalesak's disk数值模拟结果(网格密度: $400\times 400$)
Fig.3
Simulation results of Zalesak's disk with $400\times 400$ mesh
(36) $\begin{eqnarray}\label{Eq_error_density} E = \frac{1}{N}\sum^{N}_{i=1}\left|\alpha^{\mathrm{num}}_i-\alpha^{\mathrm{ref}}_i\right| \end{eqnarray} $
式中, $N$为网格数量, $\alpha^{\mathrm{num}}_i=\int_{\varOmega_i}H({x}){d}{x}$为数值模拟得到网格$i$内的体积分数, $\alpha^{\mathrm{ref}}_i$为网格$i$内的体积分数理论参考值. 由于网格尺寸倍减, 可采用下式计算界面模拟精度
(37) $\begin{eqnarray}\label{Eq_error_order} O = \frac{1}{\ln(2)}\frac{E^q}{E^{q+1}} \end{eqnarray} $
式中, $E^q$表示$q^{\mathrm{th}}$对应网格的模拟误差.
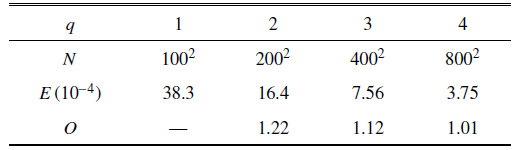
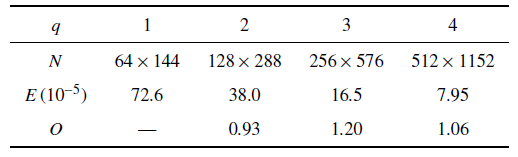
不同网格尺度下$t=2.0$时刻的本模型模拟误差见表1 .
由表可知, 采用THINC/WLIC法本模型对Zalesak's disk旋转问题的界面计算精度达到了一阶精度.
Searing flow问题是验证大变形情况下数值方法追踪界面能力的另一典型算例. 通过模拟初值为圆心在$(0.5,0.75)$、半径为$0.15$的圆, 其内部体积分数为$1$, 外部为$0$条件下, 在随时间变化的外加速度场驱动下圆盘的形状变化来检验数值模型的界面计算精度. 其中, 外加速度场用如下的流函数表示
(38) $\begin{eqnarray} \varPhi(x,y,t)=\frac{1}{\pi}\sin^2(\pi x)\sin^2(\pi y)\cos\left(\frac{\pi t}{T}\right) \end{eqnarray} $
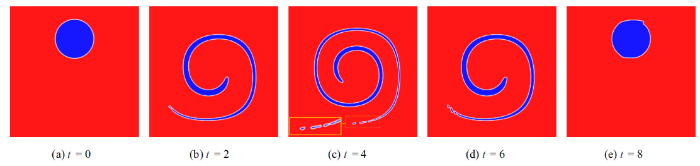
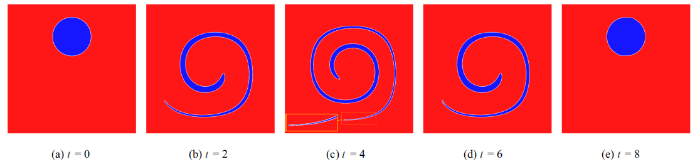
分析流函数的时间变化可知, 在$0<t<T/2$时, 界面形变不断加大, 在$t=T/2$达到最大形变; 在$T/2<t<T$时, 界面逆形变, $t=T$时恢复原形. 同时, 在此过程中不存在质量损失. 本次验证中设置计算时间为$T=8$. 图4 和图5 分别为$200\times 200$和$400\times 400$两种网格对应的数值模拟结果. 如图所示, 在$t=4$时出现最大卷曲, 以$200\times 200$网格模拟的图形尾部出现明显间断, 而网格密度加倍后, 这种现象基本消失, 可以推测这是因为图形界面之间距离小于网格尺寸引起的, 将网格加密到足够小以后本模型可以达到足够的模拟精度. 当$t=8$时, 两种网格下图像均基本恢复原形, 特别是在光滑界面形变处实现了较高精度的界面模拟, 可以认为完全恢复原形. 不同点在于变形图形头部和尾部, $200\times 200$网格的模拟结果具有明显的计算误差, 而$400\times 400$的网格则有效抑制了上述计算误差, 可认为经过一个周期后几乎恢复原形. 同样地, 表2 给出了采用式(36)和式(37)计算得到的本模拟结果误差. 由表可知, 本模型对Shearing flow问题数值模拟达到了一阶精度, 且略高于Zalesak's disk旋转问题的模拟精度. 实际上, shearing flow问题的界面变形更为剧烈, 但由于其初值界面是连续的, 不存在类似Zalesak's disk的界面突变, 这可能是对其模拟精度稍高的原因.
图4
图4
Shearing vortex数值模拟(网格密度: $200\times 200$)
Fig.4
Simulation of shearing vortex with $200\times 200$ mesh
图5
图5
Shearing vortex数值模拟(网格密度: $400\times 400$)
Fig.5
Simulation of shearing vortex with $400\times 400$ mesh
此外, 对界面追踪模拟过程中计算域内总质量的变化进行了计算分析. 设定$M=\sum\alpha_i$, $M_0$为初始时刻计算域内总质量. 在不同网格尺度条件下, 本模型得到的质量变化比$\left| M-M_0\right|/M_0$均保持在$10^{-13}$以下, 可以认为THINC/WLIC界面追踪法基本上可以保持质量守恒.
3.2 线性液舱晃荡问题
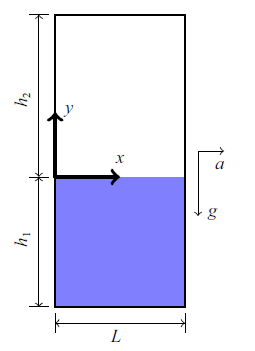
根据线性势流理论可以得到线性液舱晃荡问题的解析解, 该解可用来检验数值计算模型的收敛精度. 如图6 所示, 假定初始时刻水体和气体都处于静止状态, 舱壁为不可渗可滑移边界. 在$t>0$后舱体以$a$的加速度水平向左运动, 相当于舱内流体在受到竖直向下的重力$g$还受到水平向右、大小为$a$的质量力的作用. 计算中, 取几何尺寸和物理参数与Li等[23 ] 的模拟案例一致. 具体地, 舱体宽度$L=1.00 \mathrm{m}$, 初始水深$h_1=1.00 \mathrm{m}$, 初始气体高度$h_2=1.25 \mathrm{m}$, 重力$g=9.81 \mathrm{m/s^2}$, 水平加速度$a=0.01g$, 水体密度$\rho_1=1000 \mathrm{kg/m^3}$, 气体密度$\rho_2=1 \mathrm{kg/m^3}$.
图6
图6
线性液舱晃荡问题示意图
Fig.6
Setting of the linear sloshing problem
根据线性势流理论, 水面高程$\eta(x, t)$的解析解[24 ] 为
(39) $\begin{eqnarray} && \eta(x,t) = \frac{a}{g}\left(x-\frac{L}{2}\right) +\\&& \frac{a}{g}\left[\sum^{+\infty}_{n=0}\frac{4}{L\kappa^2_{2n+1}}\cos(\omega_{2n+1}t)\cos(\kappa_{2n+1}x)\right] \end{eqnarray} $
(40) $\kappa_n = \frac{n\pi}{L} $
(41) $\omega_n = \left[\frac{g\kappa_n(\rho_1-\rho_2)}{\rho_1\coth(\kappa_n h_1)+\rho_2\coth(\kappa_n h_2)}\right]^\frac{1}{2} $
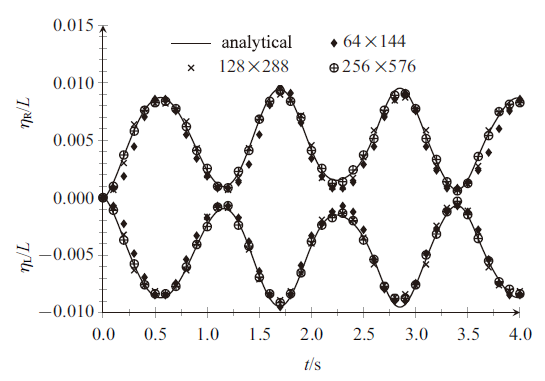
分别选取$64\times144$, $128\times288$和$256\times576$三种均匀网格, 并设置$CFL=0.1$进行模拟. 需要指出的是, 为了与理论解进行比较, 在数值模拟时忽略了控制方程中黏性项的影响. 图7 给出了本模型得到的舱体左右边壁处的水面高程($\alpha=0.5$)时间变化的计算结果与解析解的比较. 其中, $64\times144$解析度对应的网格尺寸约为$0.016 \mathrm{m}\times0.016 \mathrm{m}$, 大于水面高程振幅, 此时模型模拟结果已较准确地再现了水面高程的变化趋势, 说明THINC/WLIC法能较好地模拟微小的水面变形; $256\times576$解析度网格对应的网格尺寸约为$0.004 \mathrm{m}\times0.004 \mathrm{m}$, 由图7 可见, 模型模拟结果与解析解基本吻合.
图7
图7
舱体左右边壁处水面高程变化
Fig.7
Temporal profile of the interface elevations on the left and right walls
为分析模型的计算精度, 增加$512\times1152$网格算例并将$t=4 \mathrm{s}$时刻的密度场与理论值进行对比分析.
(42) $\begin{eqnarray} E = \frac{1}{N}\frac{1}{\rho_1}\sum^{N}_{i=1}\left|\rho^{\mathrm{num}}_i-\rho^{\mathrm{ref}}_i\right| \end{eqnarray} $
式中, $\rho^{\mathrm{num}}_i$为数值模拟得到网格$i$内的流体密度, $\rho^{\mathrm{ref}}_i$为数值模拟得到网格$i$内的流体密度理论参考值, 其他变量的含义与式(36)中定义的相同. 模拟精度$O$采用式(37)计算, 分析结果见表3 . 由表可知, 本耦合模型的模拟结果基本达到一阶精度. 文献$[23 ] $指出, 在采用有限体积WNEO法求解二相流问题的质量守恒方程和动量守恒方程时, 如果存在密度不连续, 模型的收敛精度最高只能达到一阶. 可见, 本耦合模型在模拟二相流问题时的收敛精度要高于直接使用WENO格式时的计算精度.
本模型采用有限差分法对控制方程进行求解, 而有限差分法在数值守恒性方面偏弱, 为确定本模型在质量、动量和能量守恒方面的表现, 进行了以下的分析. 定义计算域总质量$M=\sum\rho_{i}\Delta x\Delta y$, $M_0$为初始时刻计算域内总质量, 定义质量损失为$(\left|M-M_0\right|)/M_0$. 计算域内总能量为
(43) $\begin{eqnarray} E=\sum\left(\frac{1}{2}u^2_{i}\rho_{i}\Delta x\Delta y\right)+\sum\rho_{i}gh_{i}\Delta x\Delta y \end{eqnarray} $
式中, $u_{i}$为网格$i$内的速度, $\rho_{i}$为网格$i$内的密度, $g$为重力加速度, $h_{i}$为网格$i$到舱底的距离. $E_0$为初始时刻计算域内总能量, 定义能量损失为$(\left|E-E_0\right|)/E_0$.
定义计算域内流体动量为$m_x=\sum u_i\rho_i\Delta x\Delta y$和$m_y=\sum v_i\rho_i\Delta x\Delta y$, 其中$u_i$和$v_i$分别为网格$i$内的水平速度和竖向速度. 在$t^n$到$t^{n+1}$的时间步内, 定义动量变化为$\Delta m_x=m_x^{n+1}-m_x^n$和$\Delta m_y=m_y^{n+1}-m_y^n$. 由于在模拟线性液舱晃荡问题未考虑黏性力, 故动量的变化等于对应方向的外力冲量, 包括重力冲量和边壁上的压力冲量. 水平方向和竖直方向的冲量为
(44) $I_x = \Delta t\left(\sum p^L_i\Delta y - \sum p^R_i\Delta y\right) $
(45) $I_y = \Delta t\left(\sum p^B_i\Delta x - \sum p^T_i\Delta x - \sum\rho_ig\Delta x\Delta y\right) $
式中, $p^L_i$, $p^R_i$, $p^B_i$和$p^T_i$分别为$t^{n+1}$时刻液舱左边壁、右边壁、上边壁和下边壁上的压力值, $\Delta t=t^{n+1}-t^n$.
选取水平方向和竖直方向的动量变化与外力冲量差值的绝对值作为动量守恒评定量, 即
(46) $R(m_x) = \left|\Delta m_x - I_x\right| $
(47) $R(m_y) = \left|\Delta m_y - I_y\right| $
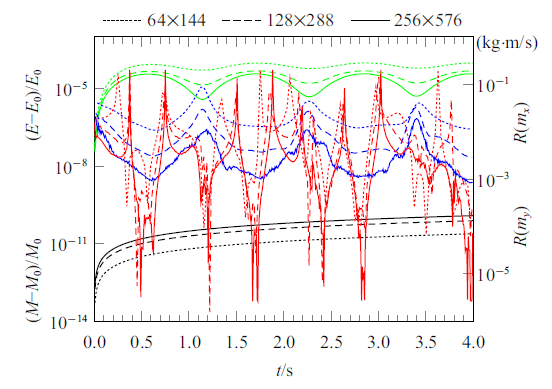
图8 为对上述4个特征变量数值守恒性的评估结果. 其中, 黑色线条代表质量损失, 绿色线条代表能量损失, 蓝色线条代表水平方向动量损失, 红色线条代表竖直方向动量损失.
图8
图8
质量、能量及动量的模拟误差
Fig.8
Simulation errors on the conservation of mass, energy and momentum of fluid
由图8 可知, 数值质量损失保持在$10^{-10}$量级以下, 可认为本案例中数值计算模型满足质量守恒; 数值能量损失在$10^{-4}$量级以下, 且随着网格加密能量损失减小. 由此可见, 本耦合模型在流体的质量守恒方面具有良好表现, 在流体的动量和能量守恒方面与采用有限体积法得到模拟结果相比略有不足, 但采用较高精度的计算网格会提高模拟结果的能量和动量守恒性.
3.3 溃坝问题
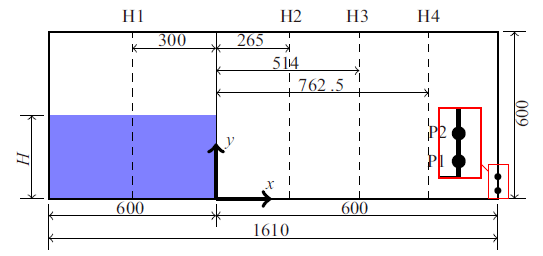
为验证本研究提出的WENO-THINC/WLIC水气耦合数值模型的模拟精度, 针对干床面溃坝问题进行了数值模拟, 并与Lobovský等[25 ] 的物理模型试验结果进行了比较. 如图9 所示, 数值模拟的计算条件与Lobovský等的物理模型试验相同. 水槽长为$1.61 \mathrm{m}$, 宽$0.60 \mathrm{m}$. 在距离水槽左边壁$600 \mathrm{mm}$处设置一竖直挡板, 挡板左侧为水体, 右侧为空气. 水体的高度包括高水位$H=600 \mathrm{mm}$和低水位$H=300 \mathrm{mm}$两种工况. 物理模型试验中, 挡板上接定滑轮, 连接一重物, 在重物的作用下挡板被抽离, 左侧水体涌向右侧, 形成溃坝流. 参照Lobovský等的模型试验, 数值模拟中设置了与物模试验相同的物理量监测点, 包括右侧边壁上的两个压力监测点和水槽中部4个水位监测点. 其中, 压力监测点P1距水槽底部$30 \mathrm{mm}$, P2距水槽底部$80 \mathrm{mm}$, 水位监测线具体位置见图9 .
图9
图9
溃坝模拟试验示意图 (单位: mm)
Fig.9
Setting of the dam-breaking simulation test (unit: mm)
首先进行了溃坝过程中水流运动学特征的模拟结果与试验结果的对比, 包括溃坝水流形态、前锋位移和沿程的水位变化等. 其中, 相关数值模拟案例均采用$\Delta x=\Delta y=0.01 \mathrm{m}$的结构化网格并设置$CFL=0.1$. 图10 为不同时刻溃坝水体运动形态的模拟结果与试验结果. 由图可见, 在低水位$H=300 \mathrm{mm}$情况下, 数值模拟的水体运动形态与物理模型试验结果基本一致, 溃坝水体前锋撞击右侧边壁后形成的水舌及空气空腔的形状和位置与物模试验结果也基本相同.
图10
图10
不同时刻溃坝水体运动形态对比
Fig.10
Comparison of dam-breaking water shapes at different times
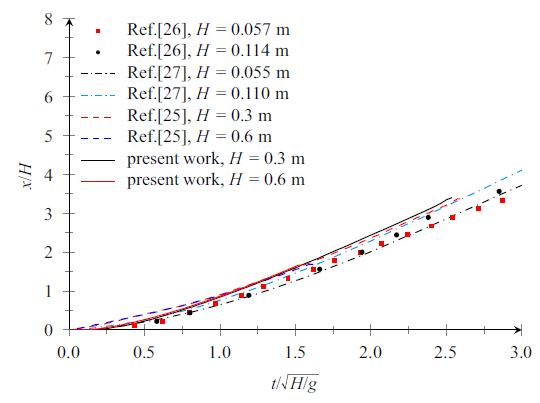
图11 为溃坝水体前锋位移随时间变化曲线. 将模拟得到的溃坝前锋位移与物理模型试验结果[25 -27 ] 进行定量对比可知, 在溃坝水体前锋冲击右侧边壁前, 数值模拟结果与试验结果吻合良好, 说明本模型对溃坝前期水体形状的模拟精度较高.
图11
图11
溃坝前锋线位移计算结果与试验结果比较
Fig.11
Comparison of calculated and measured displacements of the wave front
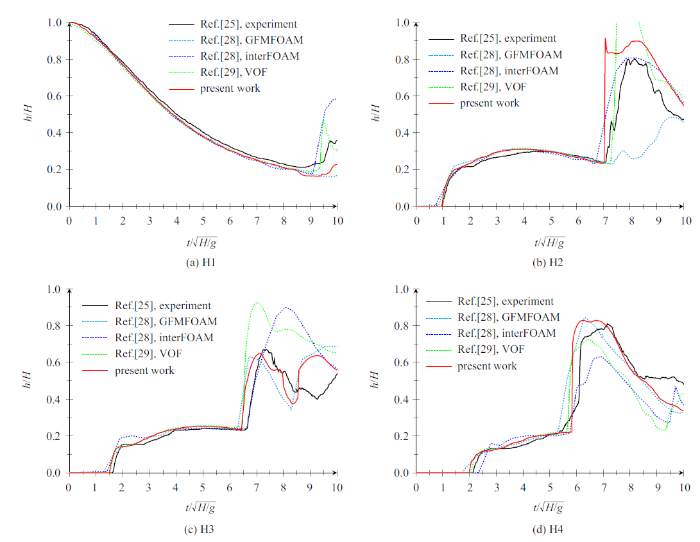
与溃坝水体前锋位移相比, H1 $\sim$ H4四个监测点处的水位变化能给出更详细的溃坝水体沿程变化过程. 考察从无量纲时间$t^*=0$到$t^*=10$内各监测点水面变化, 可以看到溃坝波撞击边壁后形成的水舌和二次波的变化特征. 图12 给出了$H=300 \mathrm{mm}$条件下模拟得到的4个水位监测点处水位变化与前人物理模型试验研究 结果[25 ] 及其他数值模拟结果[28 -29 ] 的比较. 由图可见, 本模型得到的溃坝前锋首次到达各水位监测点的时间与物模试验一致; 同时, 二次波到达的时间和水位上升趋势与试验结果基本吻合. 本模型和其他数值模型结果在溃坝波撞击边壁前均与物理模型试验结果较为吻合; 不同点在于, 本模型对溃坝水体冲击右侧壁面以后的后期水体运动模拟结果相比其他数值模型更为接近物理模型试验结果. Peltonen等[28 ] 使用的OpenFOAM内置的标准VOF求解器interFOAM所得结果在H3测点后期出现水位严重偏大现象、H4测点后期出现水位偏小现象, 其改进的GFMFOAM (ghost fluid method FOAM)方法在H2测点后期出现水位严重偏小现象; Nguyen和Yark[29 ] 改进的VOF法在H2测点处存在非物理的触顶现象、H3测点中后期出现水位明显偏大的问题. 综合来看, 溃坝问题在水体前锋撞击右侧边壁后, 水气界面形变复杂, 水气紊动更为剧烈, 此阶段数值模拟较为困难. 相比而言, 本模型对溃坝水体整个运动过程的模拟结果与物理模型试验结果更为吻合. 可见, 本数值计算模型较好地描述了溃坝水体的运动学特征, 能够较为准确地再现溃坝水体这种大变形自由表面流的运动过程.
图12
图12
H1 $\sim$ H4处水位变化
Fig.12
Water level elevations at the four locations H1 $\sim$ H4
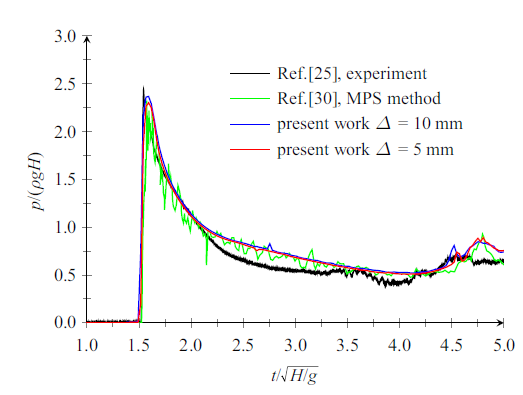
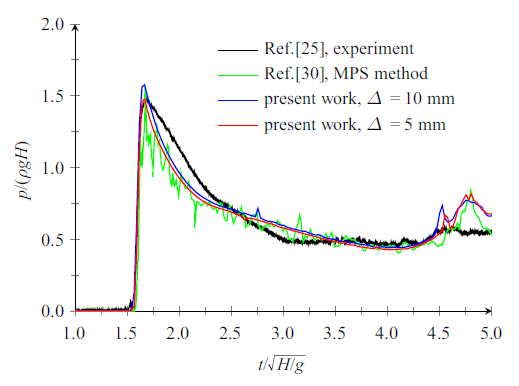
此外, 溃坝水体对下游床面或建筑物的冲击力是溃坝问题研究中的另一个重要物理参数. 通过考察高水位$H=600 \mathrm{mm}$条件下下游压强的计算结果, 对本模型再现溃坝水体动力学特征的能力进行分析. 其中, 设定计算网格分别为$\Delta x=\Delta y=10 \mathrm{mm}$和$\Delta x=\Delta y=5 \mathrm{mm}$两种情况, 对应的网格数量为$60\times161$和$120\times 322$, 并取$CFL=0.1$, 将模拟得到的P1和P2两点的压强与试验结果[25 ] 和他人数值结果[30 ] 进行对比. 如图13 和图14 所示, 当溃坝波未到达右侧边壁时, 监测点处的压强为大气压, 相对压强为$0$; 当溃坝前锋撞击边壁时, 压强急剧增大, 之后缓慢变小. 沿右边壁, 冲击压强峰值随高度上升而下降, 即P1点冲击压强峰值应大于P2点峰值. 本模型得到结果与物理模型试验相比, 冲击压强峰值出现时间相同, 峰值大小相当, 下降趋势也大致相同. 考虑到试验数据为典型压力变化, 存在一定的波动空间, 可认为本模型数值模拟压强结果与物理模型试验结果较为一致. 与Sun等[30 ] 使用MPS (moving particle semi-implicit)法的结果相比, 本模型结果的压力波动较小. 此外, 网格尺寸对压强影响较小, 但采用低密度网格的模拟结果出现少许压力局部突变, 网格加密后这种现象减少. 总体而言, 使用网格尺寸$\Delta x=\Delta y=0.01 \mathrm{m}$得到的计算结果已与试验结果吻合较好, 也就是说本模型通过较少的网格数即可得到较精确的解.
图13
图13
P1处压强历时曲线
Fig.13
Pressure history at P1
图14
图14
P2处压强历时曲线
Fig.14
Pressure history at P2
4 结论
本研究通过采用五阶WENO格式求解对流项, 三阶TVD RK进行时间离散, THINC/WLIC法追踪界面, 建立了WENO-THINC/WLIC耦合水气二相流数值计算模型. 首先, 选取Zalesak's disk旋转和shearing flow问题, 验证THINC/WLIC法对外加速度场下大变形水气界面的追踪能力; 其次, 以线性液舱晃荡问题为例分析本研究提出的WENO-THINC/WLIC耦合模型的计算误差以及对质量、动量和能量的数值守恒性; 最后, 以溃坝水流运动问题为例检验耦合模型模拟不可压缩水气二相流大变形运动问题的能力. 主要结论如下:
(1) THINC/WLIC法可有效捕捉复杂界面变形, 模拟收敛精度可达一阶并保持物质质量守恒.
(2) 所建立的WENO-THINC/WLIC耦合模型对线性液舱晃荡问题的模拟结果与解析解吻合度较高, 对微小形变的捕捉较为准确; 通过误差分析可知模型模拟精度为一阶, 数值分析结果表明本模型保持质量守恒和能量守恒.
(3) 耦合模型对溃坝水流运动的计算结果与物理模型试验结果吻合良好, 并优于interFOAM、VOF以及MPS等数值模型的模拟结果, 更够准确地捕捉了溃坝过程中溃坝水体的运动学特征和动力学特征, 证明本模型对不可压缩水气二相流问题的数值模拟具有较好的适用性.
将改进的WENO格式[23 ,31 -36 ] 和THINC法代入本研究提出的WENO-THINC耦合模型预期会得到更高精度的模拟结果.
参考文献
View Option
[1]
Almgren AS Bell JB Rendleman CA , et al . Low Mach number modeling of type Ia supernovae. I. Hydrodynamics
The Astrophysical Journal 2006 ,637 (2 ):922 -936
[本文引用: 1]
[2]
Liu XD Osher S Chan T . Weighted essentially non-oscillatory schemes
Journal of Computational Physics 1994 ,115 (1 ):200 -212
[本文引用: 1]
[3]
Harten A Engquist B Osher S , et al . Uniformly high order accurate essentially non-oscillatory schemes, III
Journal of Computational Physics 1987 ,71 (2 ):231 -303
[本文引用: 1]
[4]
童福林 , 李新亮 , 唐志共 . 激波与转捩边界层干扰非定常特性数值分析
力学学报 , 2017 ,49 (1 ):93 -104
[本文引用: 1]
(Tong Fulin Li Xinliang Tang Zhigong Numerical analysis of unsteady motion in shock wave/transitional boundary layer interaction
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (1 ):93 -104 (in Chinese))
[本文引用: 1]
[5]
童福林 , 李欣 , 于长平 等 . 高超声速激波湍流边界层干扰直接数值模拟研究
力学学报 , 2018 ,50 (2 ):197 -208
(Tong Fulin Li Xin Yu Changping et al . Direct numerical simulation of hypersonic shock wave and turbulent boundary layer interactions
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (2 ):197 -208 (in Chinese))
[6]
洪正 , 叶正寅 . 各向同性湍流通过正激波的演化特征研究
力学学报 , 2018 ,50 (6 ):1356 -1367
[本文引用: 1]
(Hong Zheng Ye Zhengyin Study on evolution characteristics of isotropic turbulence passing through a normal shock wave
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (6 ):1356 -1367 (in Chinese))
[本文引用: 1]
[7]
Shu CW Osher S . Efficient implementation of essentially non-oscillatory shock-capturing schemes
Journal of Computational Physics 1988 ,77 (2 ):439 -471
[本文引用: 1]
[8]
Hirt CW Nichols BD . Volume of fluid (VOF) method for the dynamics of free boundaries
Journal of Computational Physics 1981 ,39 (1 ):201 -225
[本文引用: 1]
[9]
张洋 , 陈科 , 尤云祥 等 . 壁面约束对裙带气泡动力学的影响
力学学报 , 2017 ,49 (5 ):1050 -1058
[本文引用: 1]
(Zhang Yang Chen Ke You Yunxiang et al . Confinement effect on the rising dynamics of a skirted bubble
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (5 ):1050 -1058 (in Chinese))
[本文引用: 1]
[10]
詹杰民 , 李熠华 . 波浪破碎的一种混合湍流模拟模式
力学学报 , 2019 ,51 (6 ):1712 -1719
(Zhan Jiemin Li Yihua A hybrid turbulence model for wave breaking simulation
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (6 ):1712 -1719 (in Chinese))
[11]
邓斌 , 王孟飞 , 黄宗伟 等 . 波浪作用下直立结构物附近强湍动掺气流体运动的数值模拟
力学学报 , 2020 ,52 (2 ):408 -419
[本文引用: 1]
(Deng Bin Wang Mengfei Huang Zongwei et al . Numerical simulation of the hydrodynamic characteristics of violent aerated flows near vertical structure under wave action
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (2 ):408 -419 (in Chinese))
[本文引用: 1]
[12]
Zhao HY Ming PJ Zhang WP , et al . A direct time-integral THINC scheme for sharp interfaces
Journal of Computational Physics 2019 ,393 :139 -161
[本文引用: 2]
[13]
Xiao F Honma Y Kono T . A simple algebraic interface capturing scheme using hyperbolic tangent function
International Journal for Numerical Methods in Fluids 2005 ,48 (9 ):1023 -1040
[本文引用: 1]
[14]
Yokoi K . Efficient implementation of THINC scheme: A simple and practical smoothed VOF algorithm
Journal of Computational Physics 2007 ,226 (2 ):1985 -2002
[本文引用: 2]
[15]
Ii S Sugiyama K Takeuchi S , et al . An interface capturing method with a continuous function: The THINC method with multi-dimensional reconstruction
Journal of Computational Physics 2012 ,231 (5 ):2328 -2358
[本文引用: 1]
[16]
Xie B Ii S Xiao F . An efficient and accurate algebraic interface capturing method for unstructured grids in 2 and 3 dimensions: The THINC method with quadratic surface representation
International Journal for Numerical Methods in Fluids 2014 ,76 (12 ):1025 -1042
[17]
Xie B Xiao F . Toward efficient and accurate interface capturing on arbitrary hybrid unstructured grids: The THINC method with quadratic surface representation and Gaussian quadrature
Journal of Computational Physics 2017 ,349 :415 -440
[本文引用: 1]
[18]
Chorin AJ . Numerical solution of the Navier-Stokes equations
Mathematics of Computation 1968 ,22 (104 ):745 -745
[本文引用: 1]
[19]
Jiang GS Peng D . Weighted ENO schemes for Hamilton-Jacobi equations
SIAM Journal on Scientific Computing 2000 ,21 (6 ):2126 -2143
[本文引用: 1]
[20]
Xiao F Ii S Chen C . Revisit to the thinc scheme: a simple algebraic vof algorithm
Journal of Computational Physics 2011 ,230 (19 ):7086 -7092
[本文引用: 1]
[21]
Zalesak ST . Fully multidimensional flux-corrected transport algorithms for fluids
Journal of Computational Physics 1979 ,31 (3 ):335 -362
[本文引用: 1]
[22]
Rider WJ Kothe DB . Reconstructing volume tracking
Journal of Computational Physics 1998 ,141 (2 ):112 -152
[本文引用: 1]
[23]
Li Z Oger G Touzé D L . A finite volume weno scheme for immiscible inviscid two-phase flows
Journal of Computational Physics 2020 ,418 :109601
[本文引用: 3]
[24]
Grenier N Vila JP Villedieu P . An accurate low-mach scheme for a compressible two-fluid model applied to free-surface flows
Journal of Computational Physics 2013 ,252 :1 -19
[本文引用: 1]
[25]
Lobovský L Botia-Vera E Castellana F , et al . Experimental investigation of dynamic pressure loads during dam break
Journal of Fluids and Structures 2014 ,48 :407 -434
[本文引用: 4]
[26]
Martin JC Moyce WJ . Part IV. An experimental study of the collapse of liquid columns on a rigid horizontal plane. Philosophical Transactions of the Royal Society of London
Series A Mathematical and Physical Sciences 1952 ,244 (882 ):312 -324
[27]
Dressler RF . Comparison of theories and experiments for the hydraulic dam-break wave
Int. Assoc. Sci. Hydrology 1954 ,3 (38 ):319 -328
[本文引用: 1]
[28]
Peltonen P Kanninen P Laurila E , et al . The ghost fluid method for openfoam: A comparative study in marine context
Ocean Engineering 2020 ,216 :108007
[本文引用: 2]
[29]
Nguyen VT Park WG . A volume-of-fluid (VOF) interface-sharpening method for two-phase incompressible flows
Computers & Fluids 2017 ,152 :104 -119
[本文引用: 2]
[30]
Sun Z Djidjeli K Xing JT , et al . Modified mps method for the 2d fluid structure interaction problem with free surface
Computers & Fluids 2015 ,122 :47 -65
[本文引用: 2]
[31]
Henrick AK Aslam TD Powers JM . Mapped weighted essentially non-oscillatory schemes: Achieving optimal order near critical points
Journal of Computational Physics 2005 ,207 (2 ):542 -567
[本文引用: 1]
[32]
Borges R Carmona M Costa B , et al . An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws
Journal of Computational Physics 2008 ,227 (6 ):3191 -3211
[33]
Fan P Shen YQ Tian BL , et al . A new smoothness indicator for improving the weighted essentially non-oscillatory scheme
Journal of Computational Physics 2014 ,269 :329 -354
[34]
骆信 , 吴颂平 . 改进的五阶WENO-Z+格式
力学学报 , 2019 ,51 (6 ):1927 -1939
(Luo Xin Wu Songping An improved fifth-order WENO-Z+ scheme
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (6 ):1927 -1939 (in Chinese))
[35]
Baeza A Burger R Mulet P , et al . On the efficient computation of smoothness indicators for a class of WENO reconstructions
Journal of Scientific Computing 2019 ,80 :1240 -1263
[36]
Bhise AA Gande NR Samala R , et al . An efficient hybrid WENO scheme with a problem independent discontinuity locator
International Journal for Numerical Methods in Fluids 2019 ,91 :1 -28
[本文引用: 1]
Low Mach number modeling of type Ia supernovae. I. Hydrodynamics
1
2006
... 二相流是自然界中常见的流体运动形式. 其中, 水气二相流与水利工程、海岸工程和海洋工程等实际工程问题密切相关. 水气二相流因具有界面变形复杂、密度差大和紊动强烈等特点, 需要较高的界面追踪和控制方程对流项的数值求解精度, 是计算流体力学的难点和热点问题. 相关研究结果表明, 当流体速度低于$0.3$倍的声速时, 流体运动可视为不可压缩流进行处理[1 ] . 因此, 在对开敞水域的自由表面流工程问题进行数值模拟分析时, 为简化模型, 一般情况下可以忽略空气的可压缩性, 将其视为不可压缩流体. 据此, 本研究的水气二相流的模型亦采用水和空气的不可压缩假定. ...
Weighted essentially non-oscillatory schemes
1
1994
... 如上所述, 水气二相流中界面两侧的介质密度相差较大, 而密度的微小变动将会引起界面两侧压强的剧烈变化; 此外, 水气二相流还具有紊动剧烈的特点; 这些均要求所选取的对流项的求解方法在具有较高的精度的同时, 能够很好地处理变量的突变问题. 加权基本无震荡(weighted essentially non-oscillatory, WENO)格式[2 ] 根据变量变化曲线的光滑程度选取加权值. 对于$2r-1$阶WENO格式, 在曲线光滑段具有$2r-1$阶精度, 在间断点处退化为基本无震荡(essentially non-oscillatory, ENO)格式[3 ] , 并保持基本无震荡特性, 被广泛用于实际工程中流体运动问题, 特别是空气动力学问题的数值模拟[4 -6 ] . 相对而言, WENO格式在水气二相流中的应用成果较少. 鉴于其高精度、自适应、标准化等特点, 本文选取WENO格式离散对流项, 同时采用三阶总变差递减(total variation diminishing, TVD)龙格库塔(Runge-Kutta, RK)法[7 ] 对时间项进行离散, 求解流体运动的动量方程. ...
Uniformly high order accurate essentially non-oscillatory schemes, III
1
1987
... 如上所述, 水气二相流中界面两侧的介质密度相差较大, 而密度的微小变动将会引起界面两侧压强的剧烈变化; 此外, 水气二相流还具有紊动剧烈的特点; 这些均要求所选取的对流项的求解方法在具有较高的精度的同时, 能够很好地处理变量的突变问题. 加权基本无震荡(weighted essentially non-oscillatory, WENO)格式[2 ] 根据变量变化曲线的光滑程度选取加权值. 对于$2r-1$阶WENO格式, 在曲线光滑段具有$2r-1$阶精度, 在间断点处退化为基本无震荡(essentially non-oscillatory, ENO)格式[3 ] , 并保持基本无震荡特性, 被广泛用于实际工程中流体运动问题, 特别是空气动力学问题的数值模拟[4 -6 ] . 相对而言, WENO格式在水气二相流中的应用成果较少. 鉴于其高精度、自适应、标准化等特点, 本文选取WENO格式离散对流项, 同时采用三阶总变差递减(total variation diminishing, TVD)龙格库塔(Runge-Kutta, RK)法[7 ] 对时间项进行离散, 求解流体运动的动量方程. ...
激波与转捩边界层干扰非定常特性数值分析
1
2017
... 如上所述, 水气二相流中界面两侧的介质密度相差较大, 而密度的微小变动将会引起界面两侧压强的剧烈变化; 此外, 水气二相流还具有紊动剧烈的特点; 这些均要求所选取的对流项的求解方法在具有较高的精度的同时, 能够很好地处理变量的突变问题. 加权基本无震荡(weighted essentially non-oscillatory, WENO)格式[2 ] 根据变量变化曲线的光滑程度选取加权值. 对于$2r-1$阶WENO格式, 在曲线光滑段具有$2r-1$阶精度, 在间断点处退化为基本无震荡(essentially non-oscillatory, ENO)格式[3 ] , 并保持基本无震荡特性, 被广泛用于实际工程中流体运动问题, 特别是空气动力学问题的数值模拟[4 -6 ] . 相对而言, WENO格式在水气二相流中的应用成果较少. 鉴于其高精度、自适应、标准化等特点, 本文选取WENO格式离散对流项, 同时采用三阶总变差递减(total variation diminishing, TVD)龙格库塔(Runge-Kutta, RK)法[7 ] 对时间项进行离散, 求解流体运动的动量方程. ...
激波与转捩边界层干扰非定常特性数值分析
1
2017
... 如上所述, 水气二相流中界面两侧的介质密度相差较大, 而密度的微小变动将会引起界面两侧压强的剧烈变化; 此外, 水气二相流还具有紊动剧烈的特点; 这些均要求所选取的对流项的求解方法在具有较高的精度的同时, 能够很好地处理变量的突变问题. 加权基本无震荡(weighted essentially non-oscillatory, WENO)格式[2 ] 根据变量变化曲线的光滑程度选取加权值. 对于$2r-1$阶WENO格式, 在曲线光滑段具有$2r-1$阶精度, 在间断点处退化为基本无震荡(essentially non-oscillatory, ENO)格式[3 ] , 并保持基本无震荡特性, 被广泛用于实际工程中流体运动问题, 特别是空气动力学问题的数值模拟[4 -6 ] . 相对而言, WENO格式在水气二相流中的应用成果较少. 鉴于其高精度、自适应、标准化等特点, 本文选取WENO格式离散对流项, 同时采用三阶总变差递减(total variation diminishing, TVD)龙格库塔(Runge-Kutta, RK)法[7 ] 对时间项进行离散, 求解流体运动的动量方程. ...
高超声速激波湍流边界层干扰直接数值模拟研究
0
2018
高超声速激波湍流边界层干扰直接数值模拟研究
0
2018
各向同性湍流通过正激波的演化特征研究
1
2018
... 如上所述, 水气二相流中界面两侧的介质密度相差较大, 而密度的微小变动将会引起界面两侧压强的剧烈变化; 此外, 水气二相流还具有紊动剧烈的特点; 这些均要求所选取的对流项的求解方法在具有较高的精度的同时, 能够很好地处理变量的突变问题. 加权基本无震荡(weighted essentially non-oscillatory, WENO)格式[2 ] 根据变量变化曲线的光滑程度选取加权值. 对于$2r-1$阶WENO格式, 在曲线光滑段具有$2r-1$阶精度, 在间断点处退化为基本无震荡(essentially non-oscillatory, ENO)格式[3 ] , 并保持基本无震荡特性, 被广泛用于实际工程中流体运动问题, 特别是空气动力学问题的数值模拟[4 -6 ] . 相对而言, WENO格式在水气二相流中的应用成果较少. 鉴于其高精度、自适应、标准化等特点, 本文选取WENO格式离散对流项, 同时采用三阶总变差递减(total variation diminishing, TVD)龙格库塔(Runge-Kutta, RK)法[7 ] 对时间项进行离散, 求解流体运动的动量方程. ...
各向同性湍流通过正激波的演化特征研究
1
2018
... 如上所述, 水气二相流中界面两侧的介质密度相差较大, 而密度的微小变动将会引起界面两侧压强的剧烈变化; 此外, 水气二相流还具有紊动剧烈的特点; 这些均要求所选取的对流项的求解方法在具有较高的精度的同时, 能够很好地处理变量的突变问题. 加权基本无震荡(weighted essentially non-oscillatory, WENO)格式[2 ] 根据变量变化曲线的光滑程度选取加权值. 对于$2r-1$阶WENO格式, 在曲线光滑段具有$2r-1$阶精度, 在间断点处退化为基本无震荡(essentially non-oscillatory, ENO)格式[3 ] , 并保持基本无震荡特性, 被广泛用于实际工程中流体运动问题, 特别是空气动力学问题的数值模拟[4 -6 ] . 相对而言, WENO格式在水气二相流中的应用成果较少. 鉴于其高精度、自适应、标准化等特点, 本文选取WENO格式离散对流项, 同时采用三阶总变差递减(total variation diminishing, TVD)龙格库塔(Runge-Kutta, RK)法[7 ] 对时间项进行离散, 求解流体运动的动量方程. ...
Efficient implementation of essentially non-oscillatory shock-capturing schemes
1
1988
... 如上所述, 水气二相流中界面两侧的介质密度相差较大, 而密度的微小变动将会引起界面两侧压强的剧烈变化; 此外, 水气二相流还具有紊动剧烈的特点; 这些均要求所选取的对流项的求解方法在具有较高的精度的同时, 能够很好地处理变量的突变问题. 加权基本无震荡(weighted essentially non-oscillatory, WENO)格式[2 ] 根据变量变化曲线的光滑程度选取加权值. 对于$2r-1$阶WENO格式, 在曲线光滑段具有$2r-1$阶精度, 在间断点处退化为基本无震荡(essentially non-oscillatory, ENO)格式[3 ] , 并保持基本无震荡特性, 被广泛用于实际工程中流体运动问题, 特别是空气动力学问题的数值模拟[4 -6 ] . 相对而言, WENO格式在水气二相流中的应用成果较少. 鉴于其高精度、自适应、标准化等特点, 本文选取WENO格式离散对流项, 同时采用三阶总变差递减(total variation diminishing, TVD)龙格库塔(Runge-Kutta, RK)法[7 ] 对时间项进行离散, 求解流体运动的动量方程. ...
Volume of fluid (VOF) method for the dynamics of free boundaries
1
1981
... 另一方面, 对二相流的界面处理以VOF[8 ] (volume of fluid)法应用最为广泛[9 -11 ] , VOF模型理论上具有质量守恒、物理意义明确等特点, 可分为几何重构法和代数法[12 ] . 在多维情况下, 前者的界面几何重构过程过于复杂且计算效率低下, 相比而言代数法对界面追踪的计算过程更为简单. Xiao等[13 ] 提出的双曲正切函数界面捕捉法(tangent of hyperbola for interface capturing, THINC)为典型的代数法. 该方法采用分段双曲正切函数重构界面, 将流体各物理量沿界面法向方向的变化视为连续函数, 通过模型中的界面形态参数控制不同介质界面的厚度, 进而确定界面网格的体积分数通量, 不仅大大简化了界面追踪的计算流程, 而且能够保证流体质量守恒的计算精度. 此外, Yokoi[14 ] 提出了将加权线性界面计算(weighted line interface calculation, WLIC)和THINC法相结合的改进方法, 以取代之前将一维THINC法直接用于多维界面运动问题求解的作法, 有效地提高了THINC法对多维界面追踪的计算精度. THINC/WLIC法的计算过程简单, 适用于二维和三维问题的流体界面追踪. 除此之外, 还有一些对THINC法的改进方法[12 ,15 -17 ] , 但大多包含多维双曲正切函数的重构, 涉及的参数过多, 程序实现较困难, 且计算量亦相对较大. ...
壁面约束对裙带气泡动力学的影响
1
2017
... 另一方面, 对二相流的界面处理以VOF[8 ] (volume of fluid)法应用最为广泛[9 -11 ] , VOF模型理论上具有质量守恒、物理意义明确等特点, 可分为几何重构法和代数法[12 ] . 在多维情况下, 前者的界面几何重构过程过于复杂且计算效率低下, 相比而言代数法对界面追踪的计算过程更为简单. Xiao等[13 ] 提出的双曲正切函数界面捕捉法(tangent of hyperbola for interface capturing, THINC)为典型的代数法. 该方法采用分段双曲正切函数重构界面, 将流体各物理量沿界面法向方向的变化视为连续函数, 通过模型中的界面形态参数控制不同介质界面的厚度, 进而确定界面网格的体积分数通量, 不仅大大简化了界面追踪的计算流程, 而且能够保证流体质量守恒的计算精度. 此外, Yokoi[14 ] 提出了将加权线性界面计算(weighted line interface calculation, WLIC)和THINC法相结合的改进方法, 以取代之前将一维THINC法直接用于多维界面运动问题求解的作法, 有效地提高了THINC法对多维界面追踪的计算精度. THINC/WLIC法的计算过程简单, 适用于二维和三维问题的流体界面追踪. 除此之外, 还有一些对THINC法的改进方法[12 ,15 -17 ] , 但大多包含多维双曲正切函数的重构, 涉及的参数过多, 程序实现较困难, 且计算量亦相对较大. ...
壁面约束对裙带气泡动力学的影响
1
2017
... 另一方面, 对二相流的界面处理以VOF[8 ] (volume of fluid)法应用最为广泛[9 -11 ] , VOF模型理论上具有质量守恒、物理意义明确等特点, 可分为几何重构法和代数法[12 ] . 在多维情况下, 前者的界面几何重构过程过于复杂且计算效率低下, 相比而言代数法对界面追踪的计算过程更为简单. Xiao等[13 ] 提出的双曲正切函数界面捕捉法(tangent of hyperbola for interface capturing, THINC)为典型的代数法. 该方法采用分段双曲正切函数重构界面, 将流体各物理量沿界面法向方向的变化视为连续函数, 通过模型中的界面形态参数控制不同介质界面的厚度, 进而确定界面网格的体积分数通量, 不仅大大简化了界面追踪的计算流程, 而且能够保证流体质量守恒的计算精度. 此外, Yokoi[14 ] 提出了将加权线性界面计算(weighted line interface calculation, WLIC)和THINC法相结合的改进方法, 以取代之前将一维THINC法直接用于多维界面运动问题求解的作法, 有效地提高了THINC法对多维界面追踪的计算精度. THINC/WLIC法的计算过程简单, 适用于二维和三维问题的流体界面追踪. 除此之外, 还有一些对THINC法的改进方法[12 ,15 -17 ] , 但大多包含多维双曲正切函数的重构, 涉及的参数过多, 程序实现较困难, 且计算量亦相对较大. ...
波浪作用下直立结构物附近强湍动掺气流体运动的数值模拟
1
2020
... 另一方面, 对二相流的界面处理以VOF[8 ] (volume of fluid)法应用最为广泛[9 -11 ] , VOF模型理论上具有质量守恒、物理意义明确等特点, 可分为几何重构法和代数法[12 ] . 在多维情况下, 前者的界面几何重构过程过于复杂且计算效率低下, 相比而言代数法对界面追踪的计算过程更为简单. Xiao等[13 ] 提出的双曲正切函数界面捕捉法(tangent of hyperbola for interface capturing, THINC)为典型的代数法. 该方法采用分段双曲正切函数重构界面, 将流体各物理量沿界面法向方向的变化视为连续函数, 通过模型中的界面形态参数控制不同介质界面的厚度, 进而确定界面网格的体积分数通量, 不仅大大简化了界面追踪的计算流程, 而且能够保证流体质量守恒的计算精度. 此外, Yokoi[14 ] 提出了将加权线性界面计算(weighted line interface calculation, WLIC)和THINC法相结合的改进方法, 以取代之前将一维THINC法直接用于多维界面运动问题求解的作法, 有效地提高了THINC法对多维界面追踪的计算精度. THINC/WLIC法的计算过程简单, 适用于二维和三维问题的流体界面追踪. 除此之外, 还有一些对THINC法的改进方法[12 ,15 -17 ] , 但大多包含多维双曲正切函数的重构, 涉及的参数过多, 程序实现较困难, 且计算量亦相对较大. ...
波浪作用下直立结构物附近强湍动掺气流体运动的数值模拟
1
2020
... 另一方面, 对二相流的界面处理以VOF[8 ] (volume of fluid)法应用最为广泛[9 -11 ] , VOF模型理论上具有质量守恒、物理意义明确等特点, 可分为几何重构法和代数法[12 ] . 在多维情况下, 前者的界面几何重构过程过于复杂且计算效率低下, 相比而言代数法对界面追踪的计算过程更为简单. Xiao等[13 ] 提出的双曲正切函数界面捕捉法(tangent of hyperbola for interface capturing, THINC)为典型的代数法. 该方法采用分段双曲正切函数重构界面, 将流体各物理量沿界面法向方向的变化视为连续函数, 通过模型中的界面形态参数控制不同介质界面的厚度, 进而确定界面网格的体积分数通量, 不仅大大简化了界面追踪的计算流程, 而且能够保证流体质量守恒的计算精度. 此外, Yokoi[14 ] 提出了将加权线性界面计算(weighted line interface calculation, WLIC)和THINC法相结合的改进方法, 以取代之前将一维THINC法直接用于多维界面运动问题求解的作法, 有效地提高了THINC法对多维界面追踪的计算精度. THINC/WLIC法的计算过程简单, 适用于二维和三维问题的流体界面追踪. 除此之外, 还有一些对THINC法的改进方法[12 ,15 -17 ] , 但大多包含多维双曲正切函数的重构, 涉及的参数过多, 程序实现较困难, 且计算量亦相对较大. ...
A direct time-integral THINC scheme for sharp interfaces
2
2019
... 另一方面, 对二相流的界面处理以VOF[8 ] (volume of fluid)法应用最为广泛[9 -11 ] , VOF模型理论上具有质量守恒、物理意义明确等特点, 可分为几何重构法和代数法[12 ] . 在多维情况下, 前者的界面几何重构过程过于复杂且计算效率低下, 相比而言代数法对界面追踪的计算过程更为简单. Xiao等[13 ] 提出的双曲正切函数界面捕捉法(tangent of hyperbola for interface capturing, THINC)为典型的代数法. 该方法采用分段双曲正切函数重构界面, 将流体各物理量沿界面法向方向的变化视为连续函数, 通过模型中的界面形态参数控制不同介质界面的厚度, 进而确定界面网格的体积分数通量, 不仅大大简化了界面追踪的计算流程, 而且能够保证流体质量守恒的计算精度. 此外, Yokoi[14 ] 提出了将加权线性界面计算(weighted line interface calculation, WLIC)和THINC法相结合的改进方法, 以取代之前将一维THINC法直接用于多维界面运动问题求解的作法, 有效地提高了THINC法对多维界面追踪的计算精度. THINC/WLIC法的计算过程简单, 适用于二维和三维问题的流体界面追踪. 除此之外, 还有一些对THINC法的改进方法[12 ,15 -17 ] , 但大多包含多维双曲正切函数的重构, 涉及的参数过多, 程序实现较困难, 且计算量亦相对较大. ...
... [12 ,15 -17 ], 但大多包含多维双曲正切函数的重构, 涉及的参数过多, 程序实现较困难, 且计算量亦相对较大. ...
A simple algebraic interface capturing scheme using hyperbolic tangent function
1
2005
... 另一方面, 对二相流的界面处理以VOF[8 ] (volume of fluid)法应用最为广泛[9 -11 ] , VOF模型理论上具有质量守恒、物理意义明确等特点, 可分为几何重构法和代数法[12 ] . 在多维情况下, 前者的界面几何重构过程过于复杂且计算效率低下, 相比而言代数法对界面追踪的计算过程更为简单. Xiao等[13 ] 提出的双曲正切函数界面捕捉法(tangent of hyperbola for interface capturing, THINC)为典型的代数法. 该方法采用分段双曲正切函数重构界面, 将流体各物理量沿界面法向方向的变化视为连续函数, 通过模型中的界面形态参数控制不同介质界面的厚度, 进而确定界面网格的体积分数通量, 不仅大大简化了界面追踪的计算流程, 而且能够保证流体质量守恒的计算精度. 此外, Yokoi[14 ] 提出了将加权线性界面计算(weighted line interface calculation, WLIC)和THINC法相结合的改进方法, 以取代之前将一维THINC法直接用于多维界面运动问题求解的作法, 有效地提高了THINC法对多维界面追踪的计算精度. THINC/WLIC法的计算过程简单, 适用于二维和三维问题的流体界面追踪. 除此之外, 还有一些对THINC法的改进方法[12 ,15 -17 ] , 但大多包含多维双曲正切函数的重构, 涉及的参数过多, 程序实现较困难, 且计算量亦相对较大. ...
Efficient implementation of THINC scheme: A simple and practical smoothed VOF algorithm
2
2007
... 另一方面, 对二相流的界面处理以VOF[8 ] (volume of fluid)法应用最为广泛[9 -11 ] , VOF模型理论上具有质量守恒、物理意义明确等特点, 可分为几何重构法和代数法[12 ] . 在多维情况下, 前者的界面几何重构过程过于复杂且计算效率低下, 相比而言代数法对界面追踪的计算过程更为简单. Xiao等[13 ] 提出的双曲正切函数界面捕捉法(tangent of hyperbola for interface capturing, THINC)为典型的代数法. 该方法采用分段双曲正切函数重构界面, 将流体各物理量沿界面法向方向的变化视为连续函数, 通过模型中的界面形态参数控制不同介质界面的厚度, 进而确定界面网格的体积分数通量, 不仅大大简化了界面追踪的计算流程, 而且能够保证流体质量守恒的计算精度. 此外, Yokoi[14 ] 提出了将加权线性界面计算(weighted line interface calculation, WLIC)和THINC法相结合的改进方法, 以取代之前将一维THINC法直接用于多维界面运动问题求解的作法, 有效地提高了THINC法对多维界面追踪的计算精度. THINC/WLIC法的计算过程简单, 适用于二维和三维问题的流体界面追踪. 除此之外, 还有一些对THINC法的改进方法[12 ,15 -17 ] , 但大多包含多维双曲正切函数的重构, 涉及的参数过多, 程序实现较困难, 且计算量亦相对较大. ...
... 式中, $n_{x,i,j}$和$n_{x,i,j}$分别是界面法向量$n$的$x$方向和$y$方向分量, 具体计算过程见文献[14 ]. ...
An interface capturing method with a continuous function: The THINC method with multi-dimensional reconstruction
1
2012
... 另一方面, 对二相流的界面处理以VOF[8 ] (volume of fluid)法应用最为广泛[9 -11 ] , VOF模型理论上具有质量守恒、物理意义明确等特点, 可分为几何重构法和代数法[12 ] . 在多维情况下, 前者的界面几何重构过程过于复杂且计算效率低下, 相比而言代数法对界面追踪的计算过程更为简单. Xiao等[13 ] 提出的双曲正切函数界面捕捉法(tangent of hyperbola for interface capturing, THINC)为典型的代数法. 该方法采用分段双曲正切函数重构界面, 将流体各物理量沿界面法向方向的变化视为连续函数, 通过模型中的界面形态参数控制不同介质界面的厚度, 进而确定界面网格的体积分数通量, 不仅大大简化了界面追踪的计算流程, 而且能够保证流体质量守恒的计算精度. 此外, Yokoi[14 ] 提出了将加权线性界面计算(weighted line interface calculation, WLIC)和THINC法相结合的改进方法, 以取代之前将一维THINC法直接用于多维界面运动问题求解的作法, 有效地提高了THINC法对多维界面追踪的计算精度. THINC/WLIC法的计算过程简单, 适用于二维和三维问题的流体界面追踪. 除此之外, 还有一些对THINC法的改进方法[12 ,15 -17 ] , 但大多包含多维双曲正切函数的重构, 涉及的参数过多, 程序实现较困难, 且计算量亦相对较大. ...
An efficient and accurate algebraic interface capturing method for unstructured grids in 2 and 3 dimensions: The THINC method with quadratic surface representation
0
2014
Toward efficient and accurate interface capturing on arbitrary hybrid unstructured grids: The THINC method with quadratic surface representation and Gaussian quadrature
1
2017
... 另一方面, 对二相流的界面处理以VOF[8 ] (volume of fluid)法应用最为广泛[9 -11 ] , VOF模型理论上具有质量守恒、物理意义明确等特点, 可分为几何重构法和代数法[12 ] . 在多维情况下, 前者的界面几何重构过程过于复杂且计算效率低下, 相比而言代数法对界面追踪的计算过程更为简单. Xiao等[13 ] 提出的双曲正切函数界面捕捉法(tangent of hyperbola for interface capturing, THINC)为典型的代数法. 该方法采用分段双曲正切函数重构界面, 将流体各物理量沿界面法向方向的变化视为连续函数, 通过模型中的界面形态参数控制不同介质界面的厚度, 进而确定界面网格的体积分数通量, 不仅大大简化了界面追踪的计算流程, 而且能够保证流体质量守恒的计算精度. 此外, Yokoi[14 ] 提出了将加权线性界面计算(weighted line interface calculation, WLIC)和THINC法相结合的改进方法, 以取代之前将一维THINC法直接用于多维界面运动问题求解的作法, 有效地提高了THINC法对多维界面追踪的计算精度. THINC/WLIC法的计算过程简单, 适用于二维和三维问题的流体界面追踪. 除此之外, 还有一些对THINC法的改进方法[12 ,15 -17 ] , 但大多包含多维双曲正切函数的重构, 涉及的参数过多, 程序实现较困难, 且计算量亦相对较大. ...
Numerical solution of the Navier-Stokes equations
1
1968
... 采用分步计算法[18 ] 对控制方程进行离散求解, 计算过程分为3个阶段: 对流项、非对流项(I)、非对流项(II). 从时间刻$t^n$到$t^{n+1}$的具体求解过程如下. ...
Weighted ENO schemes for Hamilton-Jacobi equations
1
2000
... 以下给出五阶WENO格式计算$\phi^-$的过程[19 ] , $\phi^+$的计算过程类似. 计算模板为$\{\phi_{i-3}$, $\phi_{i-2}$, $\phi_{i-1}$, $\phi_{i}$, $\phi_{i+1}$, $\phi_{i+2}\}$, 定义$v_1=D^-\phi_{i-2}$, $v_2=D^-\phi_{i-1}$, $v_3=D^-\phi_{i}$, $v_4=D^-\phi_{i+1}$, $v_5=D^-\phi_{i+2}$. 其中$D^-\phi_k=(\phi_k-\phi_{k-1})/\Delta x$. 使用以上5个一阶向后差分可给出3个ENO格式对$\phi^-_x$的数值估计 ...
Revisit to the thinc scheme: a simple algebraic vof algorithm
1
2011
... 计算通量$f_{i+1/2}$的具体过程[20 ] 如下 ...
Fully multidimensional flux-corrected transport algorithms for fluids
1
1979
... 采用本研究建立的数值模型对Zalesak's disk旋转[21 ] 和shearing flow问题[22 ] 进行模拟分析, 以验证本数值模拟方法对大变形界面的追踪能力. 其中, 验证案例的计算域均为$[0,1] \times [0,1]$, 均采用$100\times 100$, $200\times 200$, $400\times 400$和$800\times 800$ 四种密度的结构化网格进行模拟计算, 并设置$\mathrm{CFL}=0.25$. ...
Reconstructing volume tracking
1
1998
... 采用本研究建立的数值模型对Zalesak's disk旋转[21 ] 和shearing flow问题[22 ] 进行模拟分析, 以验证本数值模拟方法对大变形界面的追踪能力. 其中, 验证案例的计算域均为$[0,1] \times [0,1]$, 均采用$100\times 100$, $200\times 200$, $400\times 400$和$800\times 800$ 四种密度的结构化网格进行模拟计算, 并设置$\mathrm{CFL}=0.25$. ...
A finite volume weno scheme for immiscible inviscid two-phase flows
3
2020
... 根据线性势流理论可以得到线性液舱晃荡问题的解析解, 该解可用来检验数值计算模型的收敛精度. 如图6 所示, 假定初始时刻水体和气体都处于静止状态, 舱壁为不可渗可滑移边界. 在$t>0$后舱体以$a$的加速度水平向左运动, 相当于舱内流体在受到竖直向下的重力$g$还受到水平向右、大小为$a$的质量力的作用. 计算中, 取几何尺寸和物理参数与Li等[23 ] 的模拟案例一致. 具体地, 舱体宽度$L=1.00 \mathrm{m}$, 初始水深$h_1=1.00 \mathrm{m}$, 初始气体高度$h_2=1.25 \mathrm{m}$, 重力$g=9.81 \mathrm{m/s^2}$, 水平加速度$a=0.01g$, 水体密度$\rho_1=1000 \mathrm{kg/m^3}$, 气体密度$\rho_2=1 \mathrm{kg/m^3}$. ...
... 式中, $\rho^{\mathrm{num}}_i$为数值模拟得到网格$i$内的流体密度, $\rho^{\mathrm{ref}}_i$为数值模拟得到网格$i$内的流体密度理论参考值, 其他变量的含义与式(36)中定义的相同. 模拟精度$O$采用式(37)计算, 分析结果见表3 . 由表可知, 本耦合模型的模拟结果基本达到一阶精度. 文献$[23 ] $指出, 在采用有限体积WNEO法求解二相流问题的质量守恒方程和动量守恒方程时, 如果存在密度不连续, 模型的收敛精度最高只能达到一阶. 可见, 本耦合模型在模拟二相流问题时的收敛精度要高于直接使用WENO格式时的计算精度. ...
... 将改进的WENO格式[23 ,31 -36 ] 和THINC法代入本研究提出的WENO-THINC耦合模型预期会得到更高精度的模拟结果. ...
An accurate low-mach scheme for a compressible two-fluid model applied to free-surface flows
1
2013
... 根据线性势流理论, 水面高程$\eta(x, t)$的解析解[24 ] 为 ...
Experimental investigation of dynamic pressure loads during dam break
4
2014
... 为验证本研究提出的WENO-THINC/WLIC水气耦合数值模型的模拟精度, 针对干床面溃坝问题进行了数值模拟, 并与Lobovský等[25 ] 的物理模型试验结果进行了比较. 如图9 所示, 数值模拟的计算条件与Lobovský等的物理模型试验相同. 水槽长为$1.61 \mathrm{m}$, 宽$0.60 \mathrm{m}$. 在距离水槽左边壁$600 \mathrm{mm}$处设置一竖直挡板, 挡板左侧为水体, 右侧为空气. 水体的高度包括高水位$H=600 \mathrm{mm}$和低水位$H=300 \mathrm{mm}$两种工况. 物理模型试验中, 挡板上接定滑轮, 连接一重物, 在重物的作用下挡板被抽离, 左侧水体涌向右侧, 形成溃坝流. 参照Lobovský等的模型试验, 数值模拟中设置了与物模试验相同的物理量监测点, 包括右侧边壁上的两个压力监测点和水槽中部4个水位监测点. 其中, 压力监测点P1距水槽底部$30 \mathrm{mm}$, P2距水槽底部$80 \mathrm{mm}$, 水位监测线具体位置见图9 . ...
... 图11 为溃坝水体前锋位移随时间变化曲线. 将模拟得到的溃坝前锋位移与物理模型试验结果[25 -27 ] 进行定量对比可知, 在溃坝水体前锋冲击右侧边壁前, 数值模拟结果与试验结果吻合良好, 说明本模型对溃坝前期水体形状的模拟精度较高. ...
... 与溃坝水体前锋位移相比, H1 $\sim$ H4四个监测点处的水位变化能给出更详细的溃坝水体沿程变化过程. 考察从无量纲时间$t^*=0$到$t^*=10$内各监测点水面变化, 可以看到溃坝波撞击边壁后形成的水舌和二次波的变化特征. 图12 给出了$H=300 \mathrm{mm}$条件下模拟得到的4个水位监测点处水位变化与前人物理模型试验研究 结果[25 ] 及其他数值模拟结果[28 -29 ] 的比较. 由图可见, 本模型得到的溃坝前锋首次到达各水位监测点的时间与物模试验一致; 同时, 二次波到达的时间和水位上升趋势与试验结果基本吻合. 本模型和其他数值模型结果在溃坝波撞击边壁前均与物理模型试验结果较为吻合; 不同点在于, 本模型对溃坝水体冲击右侧壁面以后的后期水体运动模拟结果相比其他数值模型更为接近物理模型试验结果. Peltonen等[28 ] 使用的OpenFOAM内置的标准VOF求解器interFOAM所得结果在H3测点后期出现水位严重偏大现象、H4测点后期出现水位偏小现象, 其改进的GFMFOAM (ghost fluid method FOAM)方法在H2测点后期出现水位严重偏小现象; Nguyen和Yark[29 ] 改进的VOF法在H2测点处存在非物理的触顶现象、H3测点中后期出现水位明显偏大的问题. 综合来看, 溃坝问题在水体前锋撞击右侧边壁后, 水气界面形变复杂, 水气紊动更为剧烈, 此阶段数值模拟较为困难. 相比而言, 本模型对溃坝水体整个运动过程的模拟结果与物理模型试验结果更为吻合. 可见, 本数值计算模型较好地描述了溃坝水体的运动学特征, 能够较为准确地再现溃坝水体这种大变形自由表面流的运动过程. ...
... 此外, 溃坝水体对下游床面或建筑物的冲击力是溃坝问题研究中的另一个重要物理参数. 通过考察高水位$H=600 \mathrm{mm}$条件下下游压强的计算结果, 对本模型再现溃坝水体动力学特征的能力进行分析. 其中, 设定计算网格分别为$\Delta x=\Delta y=10 \mathrm{mm}$和$\Delta x=\Delta y=5 \mathrm{mm}$两种情况, 对应的网格数量为$60\times161$和$120\times 322$, 并取$CFL=0.1$, 将模拟得到的P1和P2两点的压强与试验结果[25 ] 和他人数值结果[30 ] 进行对比. 如图13 和图14 所示, 当溃坝波未到达右侧边壁时, 监测点处的压强为大气压, 相对压强为$0$; 当溃坝前锋撞击边壁时, 压强急剧增大, 之后缓慢变小. 沿右边壁, 冲击压强峰值随高度上升而下降, 即P1点冲击压强峰值应大于P2点峰值. 本模型得到结果与物理模型试验相比, 冲击压强峰值出现时间相同, 峰值大小相当, 下降趋势也大致相同. 考虑到试验数据为典型压力变化, 存在一定的波动空间, 可认为本模型数值模拟压强结果与物理模型试验结果较为一致. 与Sun等[30 ] 使用MPS (moving particle semi-implicit)法的结果相比, 本模型结果的压力波动较小. 此外, 网格尺寸对压强影响较小, 但采用低密度网格的模拟结果出现少许压力局部突变, 网格加密后这种现象减少. 总体而言, 使用网格尺寸$\Delta x=\Delta y=0.01 \mathrm{m}$得到的计算结果已与试验结果吻合较好, 也就是说本模型通过较少的网格数即可得到较精确的解. ...
Part IV. An experimental study of the collapse of liquid columns on a rigid horizontal plane. Philosophical Transactions of the Royal Society of London
0
1952
Comparison of theories and experiments for the hydraulic dam-break wave
1
1954
... 图11 为溃坝水体前锋位移随时间变化曲线. 将模拟得到的溃坝前锋位移与物理模型试验结果[25 -27 ] 进行定量对比可知, 在溃坝水体前锋冲击右侧边壁前, 数值模拟结果与试验结果吻合良好, 说明本模型对溃坝前期水体形状的模拟精度较高. ...
The ghost fluid method for openfoam: A comparative study in marine context
2
2020
... 与溃坝水体前锋位移相比, H1 $\sim$ H4四个监测点处的水位变化能给出更详细的溃坝水体沿程变化过程. 考察从无量纲时间$t^*=0$到$t^*=10$内各监测点水面变化, 可以看到溃坝波撞击边壁后形成的水舌和二次波的变化特征. 图12 给出了$H=300 \mathrm{mm}$条件下模拟得到的4个水位监测点处水位变化与前人物理模型试验研究 结果[25 ] 及其他数值模拟结果[28 -29 ] 的比较. 由图可见, 本模型得到的溃坝前锋首次到达各水位监测点的时间与物模试验一致; 同时, 二次波到达的时间和水位上升趋势与试验结果基本吻合. 本模型和其他数值模型结果在溃坝波撞击边壁前均与物理模型试验结果较为吻合; 不同点在于, 本模型对溃坝水体冲击右侧壁面以后的后期水体运动模拟结果相比其他数值模型更为接近物理模型试验结果. Peltonen等[28 ] 使用的OpenFOAM内置的标准VOF求解器interFOAM所得结果在H3测点后期出现水位严重偏大现象、H4测点后期出现水位偏小现象, 其改进的GFMFOAM (ghost fluid method FOAM)方法在H2测点后期出现水位严重偏小现象; Nguyen和Yark[29 ] 改进的VOF法在H2测点处存在非物理的触顶现象、H3测点中后期出现水位明显偏大的问题. 综合来看, 溃坝问题在水体前锋撞击右侧边壁后, 水气界面形变复杂, 水气紊动更为剧烈, 此阶段数值模拟较为困难. 相比而言, 本模型对溃坝水体整个运动过程的模拟结果与物理模型试验结果更为吻合. 可见, 本数值计算模型较好地描述了溃坝水体的运动学特征, 能够较为准确地再现溃坝水体这种大变形自由表面流的运动过程. ...
... [28 ] 使用的OpenFOAM内置的标准VOF求解器interFOAM所得结果在H3测点后期出现水位严重偏大现象、H4测点后期出现水位偏小现象, 其改进的GFMFOAM (ghost fluid method FOAM)方法在H2测点后期出现水位严重偏小现象; Nguyen和Yark[29 ] 改进的VOF法在H2测点处存在非物理的触顶现象、H3测点中后期出现水位明显偏大的问题. 综合来看, 溃坝问题在水体前锋撞击右侧边壁后, 水气界面形变复杂, 水气紊动更为剧烈, 此阶段数值模拟较为困难. 相比而言, 本模型对溃坝水体整个运动过程的模拟结果与物理模型试验结果更为吻合. 可见, 本数值计算模型较好地描述了溃坝水体的运动学特征, 能够较为准确地再现溃坝水体这种大变形自由表面流的运动过程. ...
A volume-of-fluid (VOF) interface-sharpening method for two-phase incompressible flows
2
2017
... 与溃坝水体前锋位移相比, H1 $\sim$ H4四个监测点处的水位变化能给出更详细的溃坝水体沿程变化过程. 考察从无量纲时间$t^*=0$到$t^*=10$内各监测点水面变化, 可以看到溃坝波撞击边壁后形成的水舌和二次波的变化特征. 图12 给出了$H=300 \mathrm{mm}$条件下模拟得到的4个水位监测点处水位变化与前人物理模型试验研究 结果[25 ] 及其他数值模拟结果[28 -29 ] 的比较. 由图可见, 本模型得到的溃坝前锋首次到达各水位监测点的时间与物模试验一致; 同时, 二次波到达的时间和水位上升趋势与试验结果基本吻合. 本模型和其他数值模型结果在溃坝波撞击边壁前均与物理模型试验结果较为吻合; 不同点在于, 本模型对溃坝水体冲击右侧壁面以后的后期水体运动模拟结果相比其他数值模型更为接近物理模型试验结果. Peltonen等[28 ] 使用的OpenFOAM内置的标准VOF求解器interFOAM所得结果在H3测点后期出现水位严重偏大现象、H4测点后期出现水位偏小现象, 其改进的GFMFOAM (ghost fluid method FOAM)方法在H2测点后期出现水位严重偏小现象; Nguyen和Yark[29 ] 改进的VOF法在H2测点处存在非物理的触顶现象、H3测点中后期出现水位明显偏大的问题. 综合来看, 溃坝问题在水体前锋撞击右侧边壁后, 水气界面形变复杂, 水气紊动更为剧烈, 此阶段数值模拟较为困难. 相比而言, 本模型对溃坝水体整个运动过程的模拟结果与物理模型试验结果更为吻合. 可见, 本数值计算模型较好地描述了溃坝水体的运动学特征, 能够较为准确地再现溃坝水体这种大变形自由表面流的运动过程. ...
... [29 ]改进的VOF法在H2测点处存在非物理的触顶现象、H3测点中后期出现水位明显偏大的问题. 综合来看, 溃坝问题在水体前锋撞击右侧边壁后, 水气界面形变复杂, 水气紊动更为剧烈, 此阶段数值模拟较为困难. 相比而言, 本模型对溃坝水体整个运动过程的模拟结果与物理模型试验结果更为吻合. 可见, 本数值计算模型较好地描述了溃坝水体的运动学特征, 能够较为准确地再现溃坝水体这种大变形自由表面流的运动过程. ...
Modified mps method for the 2d fluid structure interaction problem with free surface
2
2015
... 此外, 溃坝水体对下游床面或建筑物的冲击力是溃坝问题研究中的另一个重要物理参数. 通过考察高水位$H=600 \mathrm{mm}$条件下下游压强的计算结果, 对本模型再现溃坝水体动力学特征的能力进行分析. 其中, 设定计算网格分别为$\Delta x=\Delta y=10 \mathrm{mm}$和$\Delta x=\Delta y=5 \mathrm{mm}$两种情况, 对应的网格数量为$60\times161$和$120\times 322$, 并取$CFL=0.1$, 将模拟得到的P1和P2两点的压强与试验结果[25 ] 和他人数值结果[30 ] 进行对比. 如图13 和图14 所示, 当溃坝波未到达右侧边壁时, 监测点处的压强为大气压, 相对压强为$0$; 当溃坝前锋撞击边壁时, 压强急剧增大, 之后缓慢变小. 沿右边壁, 冲击压强峰值随高度上升而下降, 即P1点冲击压强峰值应大于P2点峰值. 本模型得到结果与物理模型试验相比, 冲击压强峰值出现时间相同, 峰值大小相当, 下降趋势也大致相同. 考虑到试验数据为典型压力变化, 存在一定的波动空间, 可认为本模型数值模拟压强结果与物理模型试验结果较为一致. 与Sun等[30 ] 使用MPS (moving particle semi-implicit)法的结果相比, 本模型结果的压力波动较小. 此外, 网格尺寸对压强影响较小, 但采用低密度网格的模拟结果出现少许压力局部突变, 网格加密后这种现象减少. 总体而言, 使用网格尺寸$\Delta x=\Delta y=0.01 \mathrm{m}$得到的计算结果已与试验结果吻合较好, 也就是说本模型通过较少的网格数即可得到较精确的解. ...
... [30 ] 使用MPS (moving particle semi-implicit)法的结果相比, 本模型结果的压力波动较小. 此外, 网格尺寸对压强影响较小, 但采用低密度网格的模拟结果出现少许压力局部突变, 网格加密后这种现象减少. 总体而言, 使用网格尺寸$\Delta x=\Delta y=0.01 \mathrm{m}$得到的计算结果已与试验结果吻合较好, 也就是说本模型通过较少的网格数即可得到较精确的解. ...
Mapped weighted essentially non-oscillatory schemes: Achieving optimal order near critical points
1
2005
... 将改进的WENO格式[23 ,31 -36 ] 和THINC法代入本研究提出的WENO-THINC耦合模型预期会得到更高精度的模拟结果. ...
An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws
0
2008
A new smoothness indicator for improving the weighted essentially non-oscillatory scheme
0
2014
On the efficient computation of smoothness indicators for a class of WENO reconstructions
0
2019
An efficient hybrid WENO scheme with a problem independent discontinuity locator
1
2019
... 将改进的WENO格式[23 ,31 -36 ] 和THINC法代入本研究提出的WENO-THINC耦合模型预期会得到更高精度的模拟结果. ...