引言
混凝土是土木工程中应用最广泛的人造材料之一, 具有典型的准脆性性质. 由于其多相复合特征, 混凝土力学行为表现出显著的非线性与强烈的随机性[1]. 近年来, 人们对混凝土结构抗灾性能提出了更高的要求. 例如我国新版地震动参数区划图给出了万年一遇极罕遇地震动设计参数[2], 在此情况下混凝土结构将不可避免地进入强非线性阶段, 为了防止结构严重破坏甚至倒塌, 定量把握混凝土的受力全过程性能至关重要[1]. 混凝土受力过程中的裂纹萌生、发展与传播直至试件、构件乃至结构解体全过程的分析与模拟则是准确把握混凝土受力行为的理性基础. 数十年来, 国内外学者对此进行了大量试验[3-4]、理论与数值模拟研究[5-8]. 然而, 直到20世纪末, 人们仍然难以获得混凝土试件单轴受拉全过程应力-应变曲线, 在混凝土试件精细化数值模拟方面也进展甚微, 因而对混凝土本构关系的研究依然停留在宏观经验为主的水平.
20世纪20年代以来, 断裂力学[11-15]和损伤力学[1,16-18]得到了极大的发展. 两者分别从不连续和连续的角度对裂纹进行描述, 形成了固体破坏问题研究的两大分支. 在计算方面, 为了描述裂纹引起的不连续性, 发展了内聚裂缝单元[19]、扩展有限元法[20]与无网格法[21]等一系列数值算法. 21世纪初, Bourdin等[22-23]开创性地将断裂力学与损伤力学结合起来, 发展了力学中的相场理论, 得到了大量关注与应用[24-26]. 近年来, Wu等[27-28]将相场理论与内聚裂缝模型结合起来, 发展了统一相场理论, 成功地解决了一系列脆性与准脆性材料的静力与动力破坏分析问题[29-32]. 同样在21世纪初, Silling[33-36]提出了近场动力学方法(也称毗域动力学[37]), 在模拟材料损伤破坏、裂纹扩展方面取得了重要进展[38-39]. 最近, Lu和Chen[40-41]结合统一相场理论和近场动力学的基本思想, 提出了一类非局部宏-微观损伤模型, 为准脆性材料的破坏问题分析提供了新的视角. 非局部宏-微观损伤模型引入近场动力学中物质点和物质点偶的概念来刻画由于变形引起的微细观损伤, 进而以作用域内的微细观损伤之加权平均来度量物质不连续程度, 即宏观拓扑损伤, 从而对损伤何时发生、损伤如何演化的问题做出了回答. 通过能量退化函数, 将拓扑损伤嵌入到连续介质-损伤力学的框架中. 在此基础上, Chen等[42]基于能量等效的基本思想对能量退化函数进行了物理建模, 给出了宏-微观损伤模型中能量退化函数的理性表达.
在上述基础上, 本文采用非局部宏-微观损伤模型、考虑细观物理参数的空间变异性进行单轴受拉混凝土板式试件全过程受力行为模拟. 尽管混凝土单轴受拉本来应是最简单的材料受力情形, 然而由于混凝土的多相复合与准脆性性质, 研究者仍无法准确把握混凝土单轴受拉的力学行为, 从而严重影响了对混凝土复杂受力状态下的本构行为的理性认识. 文中首先通过与试验的对比, 采用单轴受拉混凝土板式试件的一维简化建模标定非局部宏-微观损伤模型中的细观物理参数, 并探讨了标定出的模型细观参数与混凝土材料细观物理-几何特性之间的内在关联性. 在此基础上, 采用二维模型进行单轴受拉混凝土板式试件受力全过程的精细化分析. 着重考察了参数空间变异性对混凝土单轴受拉试件和带缺口三点弯曲试件力学行为的重要影响. 本文研究工作将为非局部宏-微观损伤模型参数的试验标定与混凝土复杂受力非线性随机力学行为的精细化模拟提供重要参考.
1 连续介质损伤力学基本框架
连续介质-损伤力学[1]引入损伤内变量来表征材料中的孔洞、微裂纹等缺陷, 并用内变量的演化来描述材料中缺陷的发展过程. 将内变量嵌入到本构方程中, 即可反映缺陷的发展对材料力学响应的影响.
1.1 本构方程
缺陷的发展必然伴随着能量的耗散, 因此有损材料的自由能$\psi$与无损材料的自由能$\psi_{0} $之间的关系可表为
其中$g\in \left[ {0,1} \right]$称为能量退化因子. 对于格林弹性材料, 无损材料的自由能为应变能[1], 即
其中${\epsilon }=\nabla^{S}{u}$为弹性小应变张量, $\nabla ^{S}$为对称梯度算子, ${u}$为位移场; ${D}$为四阶弹性刚度张量. 由于混凝土受拉过程几乎不发展塑性[1], 故暂时不考虑塑性应变的影响.
对于等温纯力学过程, Clausius-Duhem不等式可表为[1]
其中$\varXi $表示能量耗散, ${\sigma }$为应力张量, $\dot{(\cdot)} ={d}\left( \cdot \right)/{d}t$. 将式(1)、式(2)代入式(3)可得
式(4)成立的充分必要条件为
与
式(5)即为本构方程, 式(6)即为损伤耗散不等式.
1.2 平衡方程与边界条件
记连续固体${\cal B}$上的体力为${b}$, 其边界$\partial {\cal B}$上的面力为${t}$, 则整体平衡方程为[1]
若应力满足Cauchy假定, 即${t}_{{\eta }} ={\sigma }\cdot {\eta }$, 其中${\eta }$为一点处的方向向量, ${t}_{{\eta }} $为该方向上的应力, 则对式(7)应用Stokes公式可得平衡方程
其中${x}$为${\cal B}$中的一点. 边界条件可表述为
其中${\bar{{u}}}$为本质边界$\partial_{u} {\cal B}$上给定的位移, ${\bar{{t}}}$为自然边界$\partial_{t} {\cal B}$上给定的应力, ${\eta }_{{t}} $为给定应力点处的外法向量. 本质边界$\partial_{u} {\cal B}$与自然边界$\partial_{t} {\cal B}$应满足
几何方程${\epsilon }=\nabla^{S}{u}$, 本构方程(5), 平衡方程(8)以及边界条件(9)构成了控制方程的强形式. 然而尚需要给出损伤变量的演化法则才能进行求解. 经典的连续介质-损伤力学中损伤变量的演化通过损伤势函数与流动法则给出, 其驱动力通常取为损伤能释放率. 这一做法虽然有着坚实的热力学基础, 但其中最关键的势函数却是经验选取的, 因此本质上是一种经验的、现象学的处理方法[1]. 为了理性地给出损伤变量的演化规律, 需要从多尺度的角度入手, 寻求其中蕴含的物理机制.
2 非局部宏-微观损伤模型
2.1 微细观损伤与拓扑损伤
考察$n$维Euclid空间中的连续固体${\cal B}$, 其边界为$\partial {\cal B}$. ${\cal B}$中的物质点记为${x}\in {\cal B}$. 物质点偶记为$\left( {{x},{x'}} \right)\in {\cal B}\times {\cal B}$. 加载过程中物质点的位移分别为${u}\left( {{x,}t} \right),{u}\left( {{x'},t} \right)$, 可定义点偶的正伸长量为
其中${\xi }={x'}-{x}$, ${\eta }={u}\left( {{x'},t} \right)-{u}({x},t)$, $\left\langle \cdot \right\rangle$为Macauley算子, 即$\left\langle x \right\rangle =\left( {x+\left| x \right|} \right)/2$, $\left\| \cdot \right\|_{2} $表示欧氏空间长度. 假设存在临界伸长量$\lambda_{c} $, 当点偶的正伸长量超过临界值后, 两物质点出现不可逆的分离. 分离过程与加载历史有关, 可定义加载历史相关量为
不可逆的分离意味着出现了损伤. 引入微细观损伤函数$\omega \left( {{x},{x'},t} \right)\in \left[ {0,1} \right]$来刻画点偶的损伤程度, $\omega=0$表示尚未出现损伤, $\omega =1$表示完全破坏. 微细观损伤是加载历史相关量的函数, 本文取为
可认为存在临界长度为$\ell $, 距离大于$\ell $的物质点间影响可忽略. $\ell $表征了${\cal B}$中非局部效应的特征长度, 称为影响半径. 由此可定义一点的作用域为
微细观损伤的累积导致材料出现宏观上的损伤, 宏观上损伤的发展意味着材料拓扑的改变, 引入拓扑损伤函数$\varOmega \left( {{x},t} \right)$来刻画宏观损伤发展的程度. 作用域的引入表明微细观损伤累积形成宏观损伤的过程本质上是非局部的. 因此, 可定义拓扑损伤为
其中$R=\left\| {{x}-{x'}} \right\|_2 /\ell \in \left[ {0,1} \right]$, 这里$n$表示空间维数. 在基于有限单元法的数值计算中[40], 物质点可取为每个单元的几何中心. 因此, 为了保证式(15)中数值积分的精度, 有限元的网格尺寸应小于$\ell /10$. 在这一范围内, 有限元网格的变化对数值计算结果影响不大, 见下文算例中的网格敏感性测试结果.
上述定义皆从几何的角度出发, 没有涉及到能量/力的概念. 从上述定义也可以看出, 非局部宏-微观损伤模型是一个位移驱动损伤演化的模型: 随着位移的发展, 微细观层次的点偶不断发生破坏, 宏观的拓扑损伤随之演化发展. 因此, 非局部宏-微观损伤模型是一个基于几何的、由变形驱动的两尺度损伤模型.
2.2 能量退化函数及其物理建模
损伤的演化意味着内部缺陷的发展, 这一过程伴随着不可逆的能量耗散. 将能量退化因子与拓扑损伤变量之间的函数关系称为能量退化函数, 记为$g={\cal G}\left( \varOmega \right)$. 显然, 能量退化函数单调不增, 即${d}{\cal G}\left( \varOmega \right)/{d}\varOmega \leqslant 0$. 结合损伤变量与能量退化因子的取值范围, 不难得到${\cal G}\left( 0 \right)=1,{\cal G}\left( 1 \right)=0$. 在经典的连续介质-损伤力学中, 能量退化函数总是取为$g=1-\varOmega $的形式[1], 即能量耗散与不连续程度的几何表现是同步的. 从物理上看, 这种同步性没有内在的必然性. 受统一相场理论[27-28]的启发, 非局部宏-微观损伤模型中采用了含有两个参数的有理分式作为能量退化函数, 同时指出能量退化函数应为一凸函数, 并给出了定性的解释[40], 但是此时能量退化函数的选取仍具有一定的主观性. 基于前述工作, Chen等[42]利用宏-微观损伤模型中的微细观损伤机制对能量退化函数进行了物理建模, 并给出了其解析表达.
事实上, 对于一点处给定的变形状态${\epsilon }$, 根据Cauchy-Born准则可以计算出作用域中物质点偶的变形. 若将物质点偶看作是一系列脆性微弹簧, 随着点偶的变形微弹簧中会储存能量. 某一点处无损材料的自由能等于其作用域中与其相连的点偶中蕴含的能量之和. 根据2.1节中的微细观损伤机制, 点偶伸长量超过临界值时发生破坏, 其中存储的能量将被耗散, 因而有损材料的自由能等于未发生破坏的点偶中蕴含的能量之和. 由此可计算出有损材料与无损材料的自由能, 通过式(1)即可得到能量退化因子的值, 记为$g\left[ {{\epsilon }} \right]$. 另一方面, 利用计算出的点偶变形信息通过式(15)可计算出拓扑损伤的值, 记为$\varOmega \left[ {{\epsilon }} \right]$. 由此, 上述物理建模过程建立起了能量退化因子$g$与拓扑损伤$\varOmega$之间的参数方程关系, 即能量退化函数. 在这一关系中, 连接能量退化因子与拓扑损伤的是一点的变形状态. 经过计算, 可进一步得到能量退化函数的解析表达. 二维情形下能量退化函数的解析表达已在文献[42]中给出. 由于本文中将首先通过一维建模进行参数标定, 进一步给出一维情况参数方程形式的解析表达为
其中$t=\lambda_{c} /\left( {\epsilon \ell } \right)\in \left[ {0,1} \right]$. 特别值得指出, 上述解析表达表明能量退化函数与细观参数$\lambda _{c} $和$\ell $无关.
在实际的数值计算过程中, 若直接利用上述解析表达, 需要先求解非线性方程得到参数$t$, 再进一步计算能量退化因子. 非线性方程的求解耗时且难以收敛, 因而可考虑对能量退化函数进行拟合, 给出其近似显式表达以提高数值计算的效率. 为此, 本文提出采用星形线方程进行拟合, 即
由此可得能量退化函数的近似显式表达为
采用非线性最小二乘法对一维和二维能量退化函数进行拟合, 可得到参数值分别为$\alpha_{1D} =5.486 2$, $\alpha_{2D} =5.0$.
上述模型中的基本参数包括宏观参数$E,\nu $和细观参数$\ell ,\lambda_{c},\gamma $. 其中宏观参数可直接测定, 细观参数可通过单轴受拉试验标定, 如下节所述.
3 单轴受拉板式试件力学行为模拟
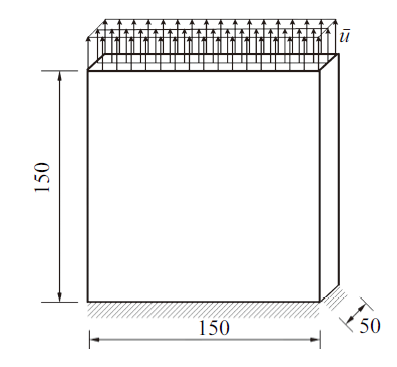
图1
3.1 非局部宏-微观损伤模型的细观参数标定
图2
图2
一维模型计算应力-应变全曲线
Fig.2
Stress versus strain curve calculated from the 1D model
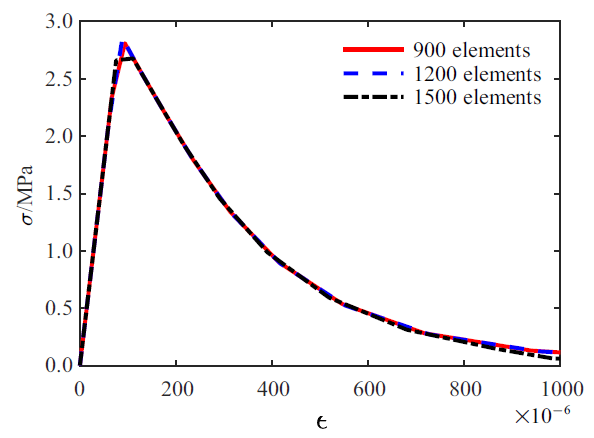
为了考察网格敏感性, 将杆件分别均匀离散为900, 1200, 1500个单元进行计算, 模型参数与算法参数均不做调整. 计算结果如图3所示, 不同网格计算出的应力-应变全曲线十分接近, 没有观察到网格敏感性.
图3
图3
一维模型采用不同的网格计算结果
Fig.3
Stress versus strain curves from different meshes in 1D model
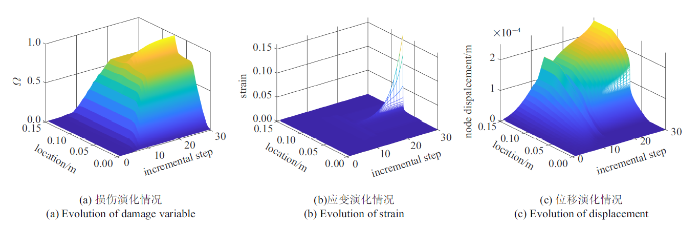
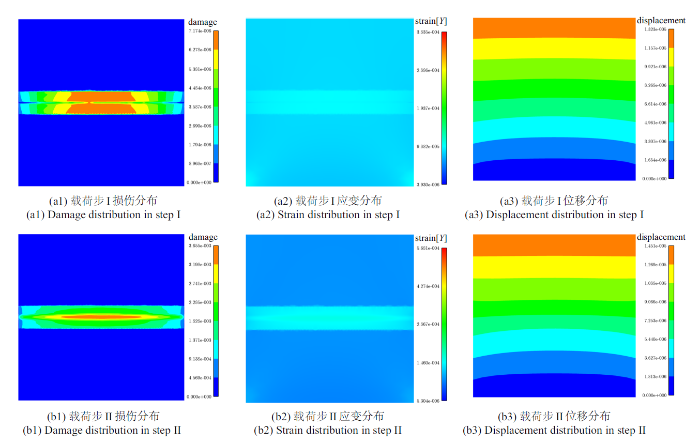
图4
图4
场变量随加载过程演化情况(1500单元)
Fig.4
Evolution of field variables during loading (1500 elements)
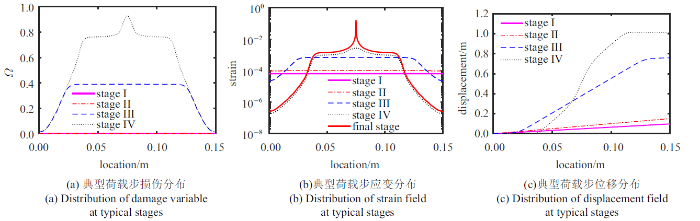
图5
图5
典型荷载步的场变量分布(1500单元)
Fig.5
Distribution of field variables at typical load steps (1500 elements)
注记: 本文标定出的模型参数为$\ell =12$ mm, $\lambda_{c} =1.0\times 10^{-3}$ mm, $\gamma =6.0\times 10^{2}$ mm$^{-1}$. 试验中用到的混凝土粗骨料的最大粒径为15 mm[9], 影响半径$\ell $的取值与之较为接近. 可以理性猜测, 影响半径的取值应与粗骨料的平均粒径大致相当. 另一方面, 混凝土试件的破坏最早发生在粗骨料与砂浆之间的界面层, 而宏-微观损伤模型中损伤的发展是由于点偶的拉断引起的. 很自然地可以将界面层的破坏与点偶的破坏联系起来. 文献[9]中未给出具体的砂浆与界面层的力学特性参数, 此处参考文献[44]中对高强混凝土中砂浆和骨料界面力学性质的研究. 对于试验中采用的42.5级普通硅酸盐水泥和中砂配置的砂浆, 其抗压强度约为30 MPa, 文献[44]中通过超声波脉冲技术测得相应强度砂浆的弹性模量约为24.82 MPa, 一般认为界面层的力学性能是砂浆基体的$70\% $, 则界面层的弹性模量约为17.37 MPa. 文献[44]中测得该砂浆与碎石粗骨料的界面的抗拉强度约为0.82 MPa. 砂浆与粗骨料界面层的厚度在$20\sim 50$ $\mu$m之间. 据此可估算界面层的弹性极限伸长量取值范围为${\cal L}=\left[ {9.44\times 10^{-4},2.36\times 10^{-3}} \right]$ (mm). 本文标定出的临界伸长量为$\lambda_{c} =1.0\times 10^{-3}$ mm $\in {\cal L}$. 由此可见, 临界伸长量应与粗骨料-砂浆界面层的弹性极限伸长量大致相当.
上述分析表明了非局部宏-微观损伤模型分析混凝土材料时其参数的物理意义: 模型中的非局部作用影响半径表征了粗骨料平均粒径, 临界伸长量表征了粗骨料-砂浆界面层的弹性极限伸长量. 这意味着通过上述物理-力学性质的关联给出模型参数的基本范围、然后采用简单试验(如单轴拉伸)、通过模型计算识别进行具体参数标定, 是具有可行性的.
3.2 单轴受拉板式试件精细化模拟
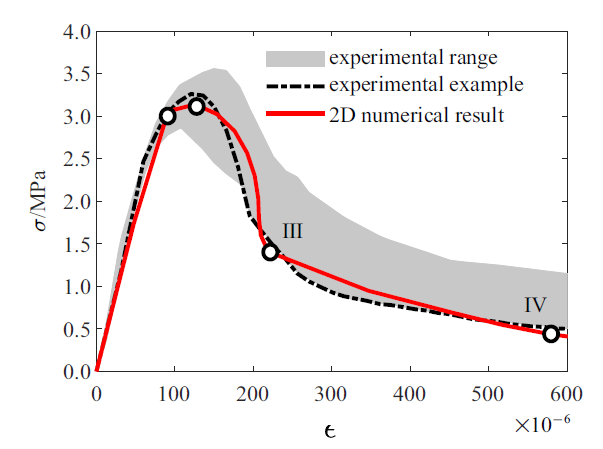
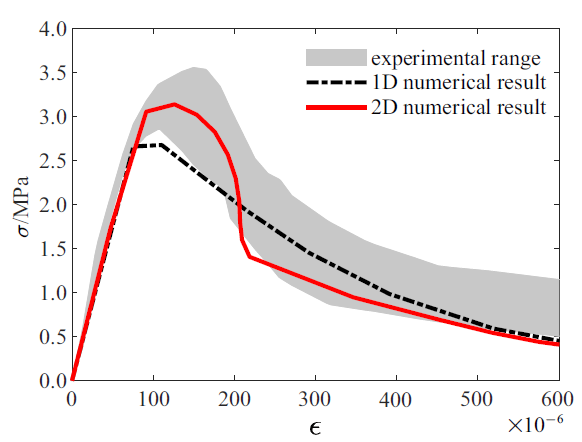
为了进行更精细的分析, 对单拉板式试件进行二维建模. 将试件用常应变三角形单元进行有限元离散, 为了计算出裂纹, 同样在试件中部设置微小初始缺陷. 利用3.1节中通过一维模型标定的参数进行计算, 计算得到的应力-应变全曲线如图6所示, 一维模型计算结果与二维模型计算结果对比如图7所示. 可以看到, 将一维模型标定的参数用于二维模型中进行分析可以得到与试验趋势吻合良好的计算结果, 这是因为这两个模型虽然精粗有区别, 但描述的是同一个物理现象. 因此, 通过上述一维建模进行细观参数标定是可行的. 由此显著降低了标定模型参数的时间, 因为进行一次完整的一维计算只需要不到一分钟, 而进行一次完整的二维计算则至少需要15 min.
图6
图7
图7
二维模型结果与一维模型结果对比
Fig.7
Stress versus strain curves from 1D model, 2D model and experiment
图8
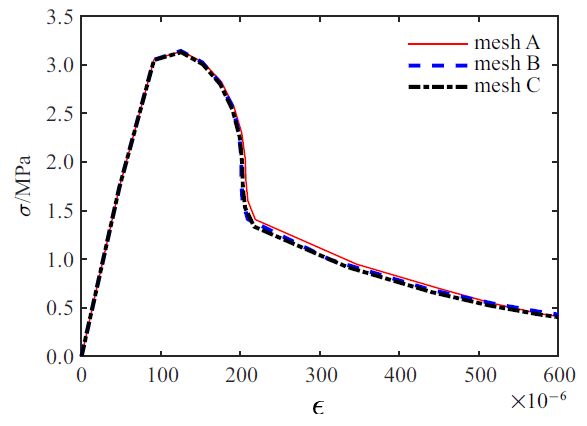
图8
二维模型采用不同的网格的计算结果
Fig.8
Stress versus stress curves from different meshes in 2D model
图9
图9
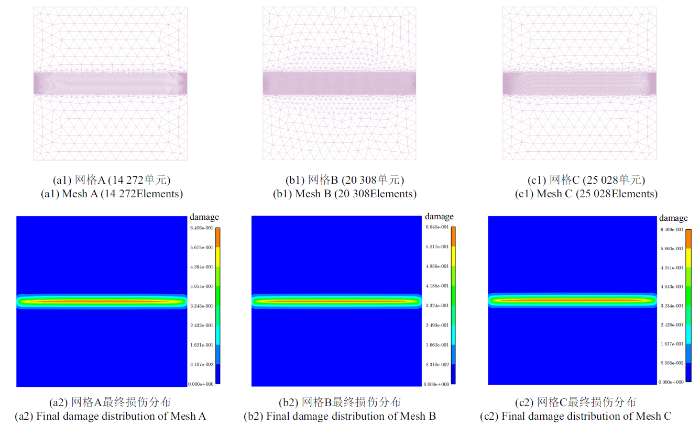
有限元网格离散与最终损伤分布
Fig.9
Finite element discretization and damage distribution in the final stage
图10
图10
二维模型典型荷载步场变量分布(网格C)
Fig.10
Distribution of field variables in 2D model at typical load steps (Mesh C)
3.3 初始缺陷对计算结果的影响
图11
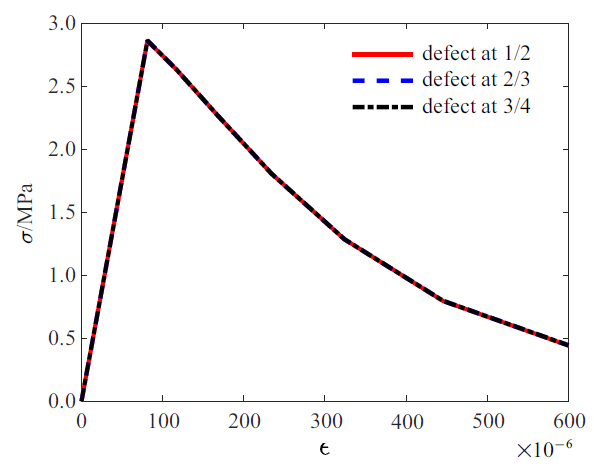
图12
图12
在不同位置设置初始缺陷计算结果(一维)
Fig.12
The stress versus strain curves from 1D model with different defect locations
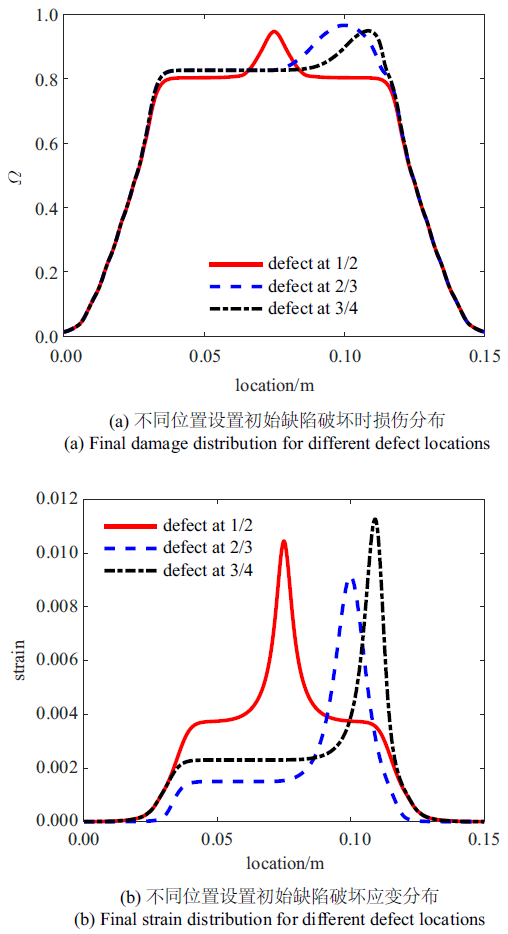
图13
图13
在不同位置设置初始缺陷时的场变量分布
Fig.13
Final field variables distributions of 1D model with different defect locations
4 考虑参数空间变异性的混凝土力学行为模拟
4.1 考虑参数空间变异性的混凝土单轴受拉力学行为模拟
图14
图14
规则划分的有限元网格(26 910单元, 加密区24 000单元)
Fig.14
Mapped mesh (26 910 elements, 24 000 elements in the encryption region)
将3.1节中标定出的模型参数作为随机场的均值$\mu $, 变异系数取为$\delta =10\% $. 取随机场的功率谱密度函数为
图15
图16
图16
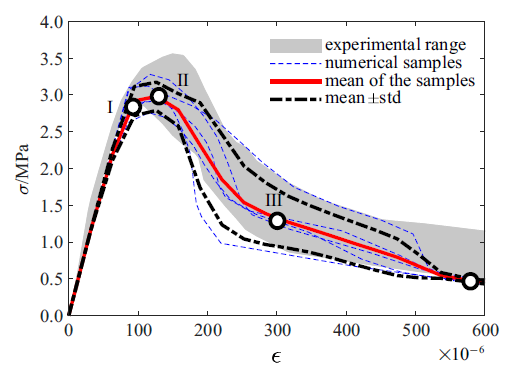
考虑临界伸长量为随机场以后计算得到的应力-应变全曲线样本及其均值与标准差
Fig.16
Whole strain-stress curve samples and the mean value curve with the standard deviation curve obtained after considering the critical elongation quantity as a random field
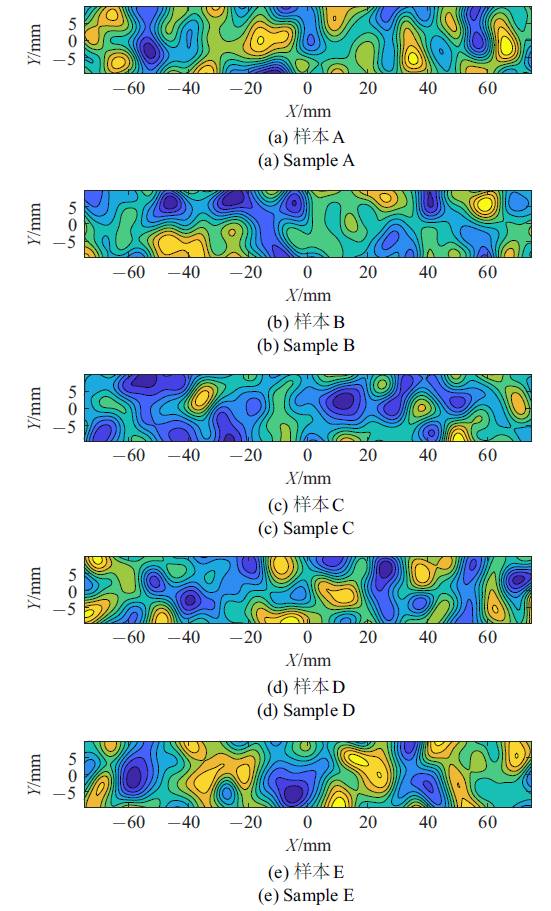
图17
图17
考虑临界伸长量为随机场后各个样本裂纹发展过程
Fig.17
Crack propagation process of different samples after considering the critical elongation quantity as random field
从图16可以看出, 将模型参数考虑为随机场以后得到的样本曲线基本被试验结果范围覆盖, 样本的均值可以反映试验结果的走向, 均值加减一倍标准差可以反映试验结果的变化范围. 这表明考虑参数空间变异性以后, 采用宏-微观损伤模型不仅可以计算出混凝土受力过程中的非线性, 而且可以合理地反映混凝土内禀的随机性. 另一方面, 从图17可以看出, 考虑材料参数随机性以后, 裂纹自发地在材料薄弱区域萌生, 无需设置初始缺陷. 同时, 与确定性情形(图10)不同, 裂纹最早出现的位置是随机的, 且最终破坏时裂纹的形态是曲折的, 这与图11所示的试验现象是一致的. 这表明在考虑细观参数空间变异性的情况下, 采用宏-微观损伤模型可以更准确地捕捉裂纹的萌生与发展全过程.
4.2 随机场相关长度的影响
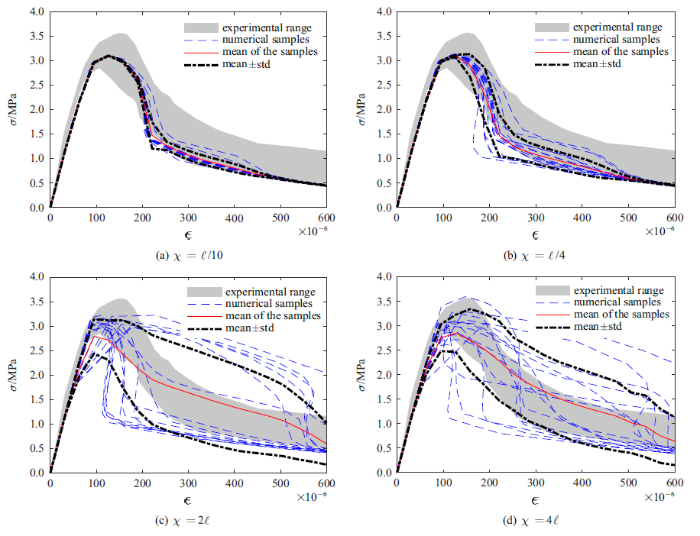
为考察随机场相关长度对计算结果的影响, 分别取随机场的相关长度为$\chi =\ell /10,\ell /4,2\ell ,4\ell $, 对每个相关长度生成15个临界伸长量随机场样本, 并利用非局部宏-微观损伤模型进行非线性分析, 得到的应力-应变全曲线的样本、均值及标准差如图18所示.
图18
图18
参数随机场相关长度对计算结果的影响
Fig.18
Influence of correlation length of parameter random field on calculation results
4.3 考虑参数空间变异性的混凝土三点受弯缺口梁力学行为模拟
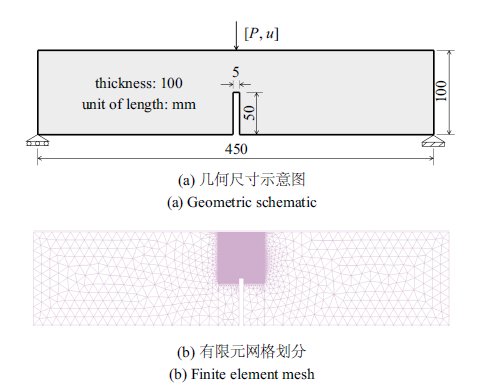
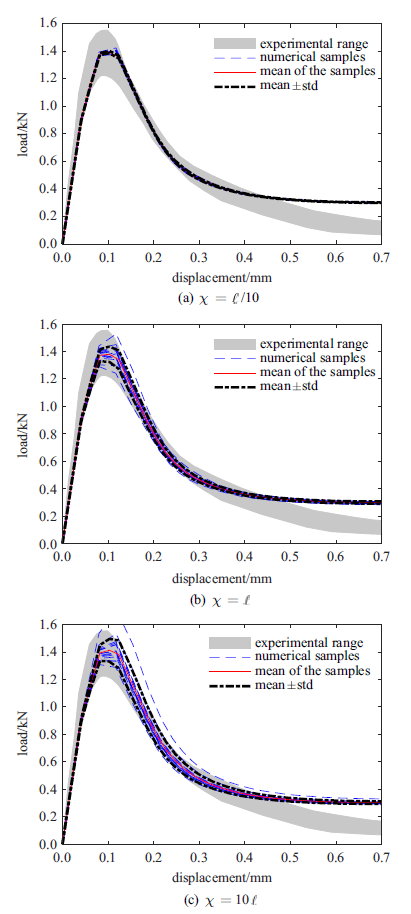
将上述工作扩展到应力非均匀分布的情形, 考察图19中的三点受弯缺口梁, 材料的弹性模量为$E=2.0\times 10^{4}$ MPa, 泊松比为$\nu =0.2$. 文献[42]中给出的模型参数为$\ell =15$ mm, $\lambda _{c} =1.125\times 10^{-3}$ mm, $\gamma =3.0\times 10^{4}$ mm$^{-1}$. 考虑临界伸长量的空间变异性, 其均值$\mu =1.125\times 10^{-3}$ mm$^{-1}$, 变异系数为$\delta =10\% $. 取其功率谱密度函数为式(20)中的形式, 令相关长度分别取$\chi =\ell /10$, $\ell $和$10\ell $, 采用与4.1节中相同的方式生成15个临界伸长量随机场的样本, 并将其代入非局部宏-微观损伤模型中进行分析, 得到不同相关长度下的荷载力-位移曲线样本及其均值与标准差如图20所示. 由于预设了初始缺陷, 各个样本的裂纹发展过程与文献[42]中类似, 故不附图.
图19
图19
缺口梁几何尺寸与有限元网格
Fig.19
Geometric schematic and finite element meshes of the notched beam
图20
图20
三点缺口梁力-位移曲线的样本、均值与标准差
Fig.20
Load-deformation curve samples and the mean value curve with the standard deviation curves of the three point bending notched beam
注意到在三点梁中预设了初始缺口, 裂纹扩展路径变异性小, 而单轴受拉板则未设置初始缺陷, 裂纹的萌生与扩展的随机性更强. 从图16与图20(b)的对比中可以看出, 尽管随机场的相关长度都与作用域半径相等, 但三点缺口梁荷载-变形曲线的变异性远小于单轴受拉板式试件、特别在下降段. 这表明裂纹扩展的路径或者说构件受力特征与载荷-变形曲线的变异性之间有某种内在联系. 当裂纹扩展路径随机性更大时, 计算得到的载荷-变形曲线的变异性也更大. 有意思的是, 从图20中还可以看出, 当相关长度很小时, 载荷-变形曲线的变异性极小, 而随着相关长度的增大, 其峰值附近的变异性增大. 同样, 当相关长度与作用域半径相当时, 所得到的变异范围与试验包络范围较为接近. 这与图18中揭示的性质是一致的, 尽管两类试件的受力特征有很大的差别.
5 结论
本文采用非局部宏-微观损伤模型进行了混凝土单轴受拉板式试件的力学行为定量模拟, 同时初步考察了细观参数空间变异性的重要影响. 主要结论如下:
(1)利用能量等效的思想对一维情况的能量退化函数进行了物理建模并给出其参数方程形式的解析表达. 利用星形线对一维、二维能量退化函数进行拟合, 给出了显式近似表达, 便于实际应用.
(2)首先利用一维非局部宏-微观损伤模型基于试验标定参数, 进而采用二维宏-微观损伤模型进行精细化分析, 显著降低了标定参数的时间成本. 同时, 分析了宏-微观损伤模型中模型参数与混凝土材料的细观物理-几何特性之间的联系, 可为模型细观参数的物理意义及定量标定提供指导.
(3)考察了细观参数空间变异性对混凝土单轴受拉试件和带缺口三点弯曲试件两类受力性质不同的试件力学行为的影响. 分析结果表明非局部宏-微观损伤模型不仅可以合理地反映非线性的发展, 还可以结合参数随机场把握混凝土内禀的随机性. 此时毋须预设微小缺陷, 且裂纹自发萌生与发展, 更符合实际情况. 计算结果还表明, 当参数随机场的相关长度逐渐减小时, 应力-应变全曲线的变异性随之降低. 单轴受拉与三点受弯缺口梁试件的对比分析则进一步表明, 当裂纹扩展路径的随机性更大时, 载荷-变形曲线的变异性随之增大.
本文研究工作可为非局部宏-微观损伤模型参数的试验标定与具有空间变异性影响的准脆性材料与试件在更复杂受力状态下的裂纹模拟与破坏分析提供借鉴. 同时, 尚存在一系列值得进一步深入研究的问题, 如对剪切变形的考虑、相关长度与作用域半径之间的关系及其影响等.
参考文献
混凝土单轴受压受拉应力-应变全曲线的试验研究
Experimental study on whole stress-strain under uniaxial compression and tension
Uniaxial concrete tension damage evolution using acoustic emission monitoring
混凝土随机损伤本构关系——单轴受压分析
Study on stochastic damage constitutive law for concrete material subjected to uniaxial compressive stress
单轴受拉状态下混凝土非局部化细观损伤模型
Nonlocal micro-damage model for concrete under uniaxial tension
基于细观物理机制的混凝土损伤数值仿真
Meso-mechanism based simulation of concrete damage process
混凝土弹塑性随机损伤本构关系研究
Elastoplastic stochastic damage constitutive law for concrete
混凝土随机损伤本构关系试验研究
[硕士论文].
Experimental research on stochastic damage constitutive law of concrete
[Master Thesis].
混凝土单轴抗拉应力-应变全曲线的试验研究
[硕士论文].
Experimental study on whole stress-strain curves of concrete under axial tension
[Master Thesis].
The phenomena of flow and rupture in solids
Analysis of stresses and strains near the end of a crack transversing a plate
A path independent integral and the approximate analysis of strain concentration by notches and cracks
Singular behaviour at the end of a tensile crack in a hardening material
Plane strain deformation near a crack tip in a power-law hardening material
On the rupture time under the condition of creep
On energy-based coupled elastoplastic damage theories: Constitutive modeling and computational aspects
An energy release rate-based plastic-damage model for concrete
Cohesive crack model description of ductile to brittle size-scale transition: Dimensional analysis vs. renormalization group theory
Elastic crack growth in finite elements with minimal remeshing
Meshfree methods: Progress made after 20 years
Numerical experiments in revisited brittle fracture
The variational approach to fracture
Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations
A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits
A higher-order phase-field model for brittle fracture: Formulation and analysis within the isogeometric analysis framework
A unified phase-field theory for the mechanics of damage and quasi-brittle failure
A length scale insensitive phase-field damage model for brittle fracture
A geometrically regularized gradient-damage model with energetic equivalence
固体结构损伤破坏统一相场理论、算法和应用
On the theoretical and numerical aspects of the unified phase-field theoryfor damage and failure in solids and structures
A phase-field damage model with micro inertia effect for the dynamic fracture of quasi-brittle solids
基于统一相场理论的早龄期混凝土化-热-力多场耦合裂缝模拟与抗裂性能预测
Computational modeling of shrinkage induced cracking in early-age concrete based on the unified phase-field theory
Reformulation of elasticity theory for discontinuities and long-range forces
A meshfree method based on the peridynamic model of solid mechanics
Peridynamic states and constitutive modeling
近场动力学方法及其应用
A review on peridynamics (PD) method and its applications
从毗域动力学到随机跳跃过程: 非局部平衡范例及非局部微积分框架
From peridynamics to stochastic jump process: Illustrations of nonlocal balance laws and nonlocal calculus framework
An improved peridynamic approach for quasi-static elastic deformation and brittle fracture analysis
Peridynamic modeling of concrete structures
A new nonlocal macro-meso-scale consistent damage model for crack modeling of quasi-brittle materials
基于一类非局部宏-微观损伤模型的裂纹模拟
Cracking simulation based on a nonlocal macro-meso-scale damage model
Meso-scale physical modeling of energetic degradation function in the nonlocal macro-meso-scale consistent damage model for quasi-brittle materials
A local arc-length procedure for strain softening
Influence of the roughness of aggregate surface on the interface bond strength
Stochastic harmonic function representation of random fields for material properties of structures