引言
目前, 有限元、有限差分和边界元法作为空腔声场模拟计算中的主要方法, 在汽车发动机传热或车内噪声控制、封闭管道噪声声场等方面均有广泛应用. 然而对于一些多维复杂几何域问题, 合理有效的模拟计算很难准确实现. 不同于以上依赖网格的数值计算方法, 无网格法通过节点信息建立插值基函数, 插值基函数不依赖于节点之间的有序拓扑链接, 因此相对于传统方法不会受到网格划分的约束. 近年来无网格方法的研究受到了高度重视, 成为目前科学与工程计算中的研究热点之一[1 -6 ] .
根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响.
相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域.
广义有限差分法不仅保留了有限差分法把微分方程转变成差分方程的优点, 而且引入了点簇的概念, 在模拟复杂的几何形状问题时十分具有优势. 除此之外, 广义有限差分法只需要在物理域内随机布置一组节点, 通过相邻节点之间的关联得到中心节点的函数值, 节省了有限元和边界元法中费时费力的网格划分及数值积分, 大大节省了数据准备的时间, 在人工越来越昂贵的情况下, 这也是非常重要的优势.
本文首次将广义有限差分法应用于含阻抗边界空腔声学问题的分析和模拟, 建立了空腔声场问题的广义有限差分法数值离散格式. 数值试验测试了经典的二维车腔噪声模型和三维空腔声学模型, 并与有限元法的数值结果对比来验证该方法的有效性、精确度和稳定性. 本工作为含阻抗边界空腔声学问题的仿真提供了新的、简单高效的计算工具, 也拓展了广义有限差分法的应用领域.
1 空腔声场问题的基本理论
声波在传播过程中会不断被拉伸和压缩, 动作非常快, 质点间来不及进行热交换. 因此声波的传播过程可被看成是绝热过程[31 ] , 其热力学方程为
(1) $\begin{eqnarray} \label{eq1} \frac{P}{p_{0} }=\left(\frac{\rho }{\rho_{0} }\right)^{\gamma } \end{eqnarray} $
其中, $p_{0} $是空气静态压强, $\rho_{0} $为微元体初始密度, $\gamma $是空气的比热比, 将式(1)对时间求导可得
(2) $\begin{eqnarray} \label{eq2} \frac{\partial \rho }{\partial t}=\frac{p_{0} }{\rho_{0}^{\gamma } }\gamma \rho^{(\gamma -1)}\frac{\partial \rho }{\partial t} \end{eqnarray} $
(3) $\begin{eqnarray} \label{eq3} \frac{\partial^{2}P}{\partial x^{2}}=\frac{1}{c^{2}}\frac{\partial ^{2}P}{\partial t^{2}} \end{eqnarray} $
结合$x$、$y$和$z$三个方向的一维声学方程, 可以得到三维系统的声学运动方程
(4) $\begin{eqnarray} \label{eq4} \frac{\partial^{2}P}{\partial x^{2}}+\frac{\partial^{2}P}{\partial y^{2}}+\frac{\partial^{2}P}{\partial z^{2}}=\frac{1}{c^{2}}\frac{\partial ^{2}P}{\partial t^{2}} \end{eqnarray} $
(5) $\begin{eqnarray} \label{eq5} \nabla^{2}=\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}} \end{eqnarray} $
(6) $\begin{eqnarray} \label{eq6} \nabla^{2}P=\frac{1}{c^{2}}\frac{\partial^{2}P}{\partial t^{2}} \end{eqnarray} $
对简谐激励稳态声场, 利用变换$P(x,t)=p(x){e}^{{i}\omega t}$, 可将式(3)中的时域声场方程变换为频域声场方程, 即Helmholtz波动方程
(7) $\begin{eqnarray} \label{eq7} \nabla^{2}p+K^{2}p=0 \end{eqnarray} $
其中, $K={\omega /c}$称为波数, $\omega $为圆频率, $c$为声速. 上述方程描述了频域内稳态声场在空间的分布规律. 对于二维和三维声场分布, 同理可得到与(7)式相同形式的控制方程. 声压与简谐声波的振动速度关系式为
(8) $\begin{eqnarray} \label{eq8} \frac{\partial p}{\partial {n}} +{j}\rho \omega v_{n} =0 \end{eqnarray} $
其中, ${j}=\sqrt {-1} $, $n$是声腔边界表面法线方向, $v_{n}$为质点振动速度.
在已知边界条件下, 可定量对其进行求解. 声场有如下几种边界条件:
(1) 狄利克雷(Dirichlet)边界条件, 即声压边界条件
(9) $\begin{eqnarray} \label{eq9} p=p_{D} \end{eqnarray} $
(2) 黎曼(Neumann)边界条件, 即速度边界条件
(10) $\begin{eqnarray} \label{eq10} \nabla p\cdot {n}=-{j}\rho \omega v_{n} \end{eqnarray} $
(3) 洛平(Robin)边界条件, 即声阻抗边界条件
(11) $\begin{eqnarray} \label{eq11} \nabla p\cdot {n}=-{j}\rho \omega A_{n} p \end{eqnarray} $
在式(9) $\sim\!$式(11)中, $p_{D} $是边界处声压值, $A_{n} $是声导纳系数.
2 广义有限差分法的基本理论
根据广义有限差分法(GFDM)计算空腔声场问题的基本理论, 对求解区域布置节点进行离散, 其方法是基于移动最小二乘法与泰勒展开. 首先在整个计算区域内布置$N=ni+nd+nn+nr$ ($ni$表示内部节点数目, $nd$, $nn$, $nr$分别表示Dirichlet, Neumann和Robin边界所对应的节点数目)个节点, 再将每个节点上的偏微分项转换成由子区域内各节点物理量与权重系数乘积的线性累加. 以二维问题为例, 对区域内的第$i$个节点而言, 选择$m$个支撑点(邻近点), 形成一个子区域, 如图1 所示.
图1
图1
广义有限差分法配点布置示意图
Fig.1
Schematic diagram of GFDM
假设中心点为第$i$点(图中红色点), $p_{i} $是中心节点$(x_{i},y_{i} )$处的函数值, $p_j^i $, $j=1,2,...,m$是"点簇"内支撑点$(x_{i}^{j} ,y_{i}^{j} )$上的函数值. 每个中心点周边有$m$个支撑点, 使用泰勒级数展开[32 ] , 在中心点($x_{i} $, $y_{i} )$周围展开$p_{j}^{i} $值有
(12) $\begin{eqnarray} \label{eq12} && p_{j}^{i} =p_{i} +h_{ij} \frac{\partial p}{\partial x}\bigg|_{i}+k_{ij} \frac{\partial p}{\partial y}\bigg|_{i}+\frac{h_{ij}^{2} }{2}\frac{\partial^{2}p}{\partial x^{2}}\bigg|_{i}+\\&& \frac{k_{ij}^{2} }{2}\frac{\partial^{2}p}{\partial y^{2}}\bigg|_{i}+h_{ij} k_{ij} \frac{\partial^{2}p}{\partial x\partial y}\bigg|_{i} \end{eqnarray} $
利用移动最小二乘逼近原理, 定义以下残差函数$B(p)$
(13) $\begin{eqnarray} \label{eq13} &&B(p)=\sum\limits_{j=1}^m \left[ \left( p_{i} -p_{j}^{i} +h_{ij} \frac{\partial p}{\partial x}\bigg|_{i}+k_{ij} \frac{\partial p}{\partial y}\bigg|_{i}+\frac{h_{ij}^{2} }{2}\frac{\partial^{2}p}{\partial x^{2}}\bigg|_{i}+\right. \right. \\&& \left. \left.\frac{k_{ij}^{2} }{2}\frac{\partial^{2}p}{\partial y^{2}}\bigg|_{i}+h_{ij} k_{ij} \frac{\partial^{2}p}{\partial x\partial y}\bigg|_{i} \right)\omega_{ij} \right]^{2} \end{eqnarray} $
式中, $h_{ij} =x_{i} -x_{j}^{i} $和$k_{ij} =y_{i} -y_{i}^{j} $分别为沿着$x$与$y$轴方向上$i$点和$j$点间的距离, $\omega_{ij} =\omega (h_{ij} ,k_{ij})$表示点$j$处的加权系数[33 ] . 在上述逼近过程中, 很多常用的权函数[34 ] 均可使用, 由于样条权函数对影响域半径的变化不是很敏感, 因此在计算中采用如下四次样条权函数
(14) $\begin{eqnarray} \label{eq14} \omega (d_{ij} )=\left\{\begin{array}{l} 1-6\left( {\dfrac{d_{ij} }{d_{m} }} \right)^{2}+8\left( {\dfrac{d_{ij} }{d_{m} }} \right)^{3}-3\left( {\dfrac{d_{ij} }{d_{m} }} \right)^{4},\\\qquad d_{ij} \leqslant d_{m} \\ 0, \qquad d_{ij} >d_{m} \\ \end{array} \right. \end{eqnarray} $
其中, $d_{ij} $是中心节点($x_{i} $, $y_{i} )$与支撑点($x_{i}^{j} $, $y_{i}^{j})$之间的距离, $d_{m} $表示中心节点($x_{i} $, $y_{i})$与点簇内最远节点之间的距离. 加权函数一定程度上反映了不同支撑点在计算中的重要性, 离中心点越近的支撑点对中心点函数值的计算起到更大的作用, 故赋予其的计算权重越大.
(15) $\begin{eqnarray} \label{eq15} {D}_{{p}} =\left\{ \frac{\partial p}{\partial x}\bigg|_{i},\ \ \frac{\partial p}{\partial y}\bigg|_{i},\ \ \frac{\partial^{2}p}{\partial x^{2}}\bigg|_{i},\ \ \frac{\partial^{2}p}{\partial y^{2}}\bigg|_{i},\ \ \frac{\partial^{2}p}{\partial x\partial y}\bigg|_{i}\right\}^{T} \end{eqnarray} $
(16) $\begin{eqnarray} \label{eq16} {AD}_{{p}} ={b} \end{eqnarray} $
(17) $\begin{eqnarray} \label{eq17} {A}=\left[ \begin{array}{c@{\quad\ \ }c@{\quad\ \ }c@{\quad\ \ }c@{\quad\ \ }c} \sum\limits_{j=1}^m h_{ij}^{2} \omega_{ij}^{2} & \sum\limits_{j=1}^m h_{ij} k_{ij} \omega_{ij}^{2} & \sum\limits_{j=1}^m \frac{h_{ij}^{3} }{2}\omega_{ij}^{2} & \sum\limits_{j=1}^m \frac{h_{ij} k_{ij}^{2} }{2}\omega_{ij}^{2} & \sum\limits_{j=1}^m h_{ij}^{2} k_{ij} \omega_{ij}^{2} \\[4mm] &\sum\limits_{j=1}^m k_{ij}^{2} \omega_{ij}^{2} & \sum\limits_{j=1}^m \frac{h_{ij}^{2} k_{ij} }{2}\omega_{ij}^{2} & \sum\limits_{j=1}^m \frac{k_{ij}^{3} }{2}\omega_{ij}^{2} & \sum\limits_{j=1}^m h_{ij} k_{ij}^{2} \omega_{ij}^{2} \\[4mm] & &\sum\limits_{j=1}^m \frac{h_{ij}^{4} }{4}\omega _{ij}^{2} & \sum\limits_{j=1}^m \frac{h_{ij}^{2} k_{ij}^{2} }{4}\omega_{ij}^{2} &\sum\limits_{j=1}^m \frac{h_{ij}^{3} k_{ij} }{2}\omega_{ij}^{2} \\[4mm] & SYM&&\sum\limits_{j=1}^m \frac{k_{ij}^{4} }{4}\omega_{ij}^{2} & \sum\limits_{j=1}^m \frac{h_{ij} k_{ij}^{3} }{2}\omega _{ij}^{2} \\[4mm] &&&&\sum\limits_{j=1}^m h_{ij}^{2} k_{ij}^{2} \omega_{ij}^{2} \\ \end{array} \right] \end{eqnarray} $
$\begin{eqnarray*} \frac{\partial p}{\partial x}\bigg|_{i},\ \ \frac{\partial p}{\partial y}\bigg|_{i},\ \ \frac{\partial^{2}p}{\partial x^{2}}\bigg|_{i},\ \ \frac{\partial^{2}p}{\partial y^{2}}\bigg|_{i},\ \ \frac{\partial^{2}p}{\partial x\partial y}\bigg|_{i} \end{eqnarray*}$
(18) $\begin{eqnarray} \label{eq18} {b}=\left\{ {\begin{array}{c} \sum\limits_{j=1}^m {(-p_{i} +p_{j}^{i} )h_{ij} \omega_{ij}^{2} } \\ \sum\limits_{j=1}^m {(-p_{i} +p_{j}^{i} )k_{ij} \omega_{ij}^{2} } \\ \sum\limits_{j=1}^m {(-p_{i} +p_{j}^{i} )\frac{h_{ij}^{2} }{2}\omega _{ij}^{2} } \\ \sum\limits_{j=1}^m {(-p_{i} +p_{j}^{i} )\frac{k_{ij}^{2} }{2}\omega _{ij}^{2} } \\ \sum\limits_{j=1}^m {(-p_{i} +p_{j}^{i} )h_{ij} k_{ij} \omega_{ij}^{2} } \\ \end{array}} \right\} \end{eqnarray} $
(19) $\begin{eqnarray} \label{eq19} {b}={B}_{5\times (m+1)} \left[ {\begin{array}{c} p_{i} \\[3mm] p_{1}^{i} \\[3mm] p_{2}^{i} \\[3mm] p_{3}^{i} \\[3mm] \vdots \\[3mm] p_{m}^{i} \\[3mm] \end{array}} \right]_{(m+1)\times 1} ={Bp} \end{eqnarray} $
式中, ${p}=\left\{p_i ,p_{1}^{i},p_{2}^{i},p_{3}^{i},\cdots,p_{m}^{i}\right\}^{T}$为与子区域内第$i$点和其余$m$个点的待求未知量, 最后微分项$D_{{p}}$可以表示为
(20) $\begin{eqnarray} \label{eq20} &&{D}_{{p}} =\left\{ \begin{array}{c} \dfrac{\partial p}{\partial x}\bigg|_{i}\\[3mm] \dfrac{\partial p}{\partial y}\bigg|_{i} \\[3mm] \dfrac{\partial^{2}p}{\partial x^{2}}\bigg|_{i}\\[3mm] \dfrac{\partial^{2}p}{\partial y^{2}}\bigg|_{i}\\[3mm] \dfrac{\partial^{2}p}{\partial x\partial y}\bigg|_{i}\\ \end{array} \right\}={A}^{-1}{b}={A}^{-1}{Bp}=\\ && {Ep}={E}\left\{ {\begin{array}{c} p_{i} \\ p_{1}^{i} \\ p_{2}^{i} \\ p_{3}^{i} \\ \vdots \\ p_{m}^{i} \\ \end{array}} \right\} \end{eqnarray} $
(21) $\begin{eqnarray} \label{eq21} {E}={A}^{-1}{B}=\left[ {{\begin{array}{c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c} {e_{1,0} } & {e_{1,1} } & {e_{1,2} } & {e_{1,3} } & \cdots & {e_{1,m} } \\ {e_{2,0} } & {e_{2,1} } & {e_{2,2} } & {e_{2,3} } & \cdots & {e_{2,m} } \\ {e_{3,0} } & {e_{3,1} } & {e_{3,2} } & {e_{3,3} } & \cdots & {e_{3,m} } \\ {e_{4,0} } & {e_{4,1} } & {e_{4,2} } & {e_{4,3} } & \cdots & {e_{4,m} } \\ {e_{5,0} } & {e_{5,1} } & {e_{5,2} } & {e_{5,3} } & \cdots & {e_{5,m} } \\ \end{array} }} \right]_{i} \end{eqnarray} $
通过观察上述各式可以看出中心节点处的微分项可以变换为由子区域中各点上的物理量与权重系数乘积的线性累加. 由此可知, 广义有限差分法的核心思想是将第$i$点上的微分量用对应子区域内支撑点上的物理量线性权重累加表示, 使所有内部点满足控制方程式, 所有边界点满足边界条件, 形成一个大型的稀疏线性方程组, 对该方程组求解即可得到计算区域内全部点上的物理量.
(1) 对于计算区域内部节点$(x_{i} ,y_{i} )$, $i=1$, $\cdots$, $ni$, 其上的物理量必定满足声学控制方程. 由式(20)可知, 只需提取相应的微分项, 然后将线性组合的方程式代入控制方程, 则
(22) $\begin{eqnarray} \label{eq22} && (e_{3,0} +e_{{4,0}} )p_{i} +(e_{{3,1}} +e_{{4,1}} )p_{{1}}^{i} +(e_{{3,2}} +e_{{4,2}} )p_{{2}}^{i} +\\&& \cdots +(e_{{3},m} +e_{{4},m} )p_{m}^{i} +K^{2}p_{i} =0 \end{eqnarray} $
(23) $\begin{eqnarray} \label{eq23} g_{{0}}^{i} p_{i} +g_{{1}}^{i} p_{{1}}^{i} +g_{{2}}^{i} p_{{2}}^{i} +\cdots +g_{m}^{i} p_{m}^{i} =0 \end{eqnarray} $
(2) 对于Dirichlet边界上的节点$(x_{i} ,y_{i} )$, $i=ni+1$, $\cdots$, $ni+nd$, 我们有
(24) $\begin{eqnarray} \label{eq24} p_{i} =p_{D} \end{eqnarray} $
(3) 对于Neumann边界上的节点$(x_{i} ,y_{i} )$, $i=ni+nd+1$, $\cdots$, $ni+nd+nn$, 我们有
(25) $\begin{eqnarray} \label{eq25} \nabla p_{i} \cdot n =-j\rho \omega v_{n} \end{eqnarray} $
(26) $\begin{eqnarray} \label{eq26} \frac{\partial p}{\partial x}\bigg|_{i}{n}_{1}^{i} +\frac{\partial p}{\partial y}\bigg|_{i}{n}_{2}^{i} =-j\rho \omega v_{n} \end{eqnarray} $
其中, ${n}=({n}_{1}^{i} ,{n}_{2}^{i})$表示边界节点$(x_{i} ,y_{i} )$处的单位外法向量. 根据式(20)提取相应的微分项, 由式(26)整理可得
(27) $\begin{eqnarray} \label{eq27} && (e_{{1,0}} p_{i} +e_{{1,1}} p_{{1}}^{i} +e_{{1,2}} p_{{2}}^{i} +\cdots +e_{{1},m} p_{m}^{i} ){n}_{1}^{i} + \\&& (e_{{2,0}} p_{i} +e_{{2,1}} p_{{1}}^{i} +e_{{2,2}} p_{{2}}^{i} +\cdots +e_{2,m} p_{m}^{i} ){n}_{2}^{i} =-j\rho \omega v_{n} \end{eqnarray} $
(28) $\begin{eqnarray} \label{eq28} r_{{0}}^{i} p_{i} +r_{{1}}^{i} p_{{1}}^{i} +r_{{2}}^{i} p_{{2}}^{i} +\cdots +r_{m}^{i} p_{m}^{i} =-j\rho \omega v_{n} \end{eqnarray} $
(4) 对于Robin边界上的节点$(x_{i}, y_{i})$, $i=ni+nd+nn+1$, $\cdots$, $N$, 我们有
(29) $\begin{eqnarray} \label{eq29} \nabla p_{i} \cdot n=-j\rho \omega A_{n} p_{i} \end{eqnarray} $
(30) $\begin{eqnarray} \label{eq30} \frac{\partial p}{\partial x}\bigg|_{i}{n}_{1}^{i} +\frac{\partial p}{\partial y}\bigg|_{i}{n}_{2}^{i} +j\rho \omega A_{n} p_{i} =0 \end{eqnarray} $
(31) $\begin{eqnarray} \label{eq31} (r_{{0}}^{i} +j\rho \omega A_{n} )p_{i} +r_{{1}}^{i} p_{{1}}^{i} +r_{{2}}^{i} p_{{2}}^{i} +\cdots +r_{m}^{i} p_{m}^{i} =0 \end{eqnarray} $
考虑计算区域内部和边界上的所有节点, 并代入相应的边界条件, 联立式(23)、(24)、(28)和(31)可得到如下线性方程组
(32) $\begin{eqnarray} \label{eq32} {CP}={f} \end{eqnarray} $
式中$C$是最终的系数矩阵, $f$是右端项矢量, $P$是所有节点上的待求未知量
(33) $\begin{eqnarray} \label{eq33} {P}=\left\{ {p_{{1}} ,p_{2} ,p_{3} ,p_{4} ,p_{{5}} ,\cdots ,p_{N} } \right\}^{T} \end{eqnarray} $
(34) $\begin{eqnarray} \label{eq34} {P}={C}^{-1}{f} \end{eqnarray} $
从上述数值实施过程中可以看出, GFDM与传统的有限差分法十分类似, 方程(32)中的系数矩阵$C$为稀疏矩阵. 另一方面, 从形成最终线性方程组(32)的过程可以观察到, 系数矩阵$C$是一个$N$行$N$列的方阵, 而每一行最多仅有$m$个非零元素, 这里$N$为计算区域内全部节点的个数, $m$为局部支撑节点数目. 显然, $m$远小于$N$, 因此方程组(32)是一个稀疏线性方程组. 由此可见, 与其他具有稠密矩阵方程的数值方法相比, GFDM能够非常有效地分析高维和复杂几何形状的问题.
3 数值算例
为了验证广义有限差分法求解含阻抗边界空腔声学问题的有效性和可行性, 现针对二维简单声腔结构和二维汽车驾驶舱以及三维声腔模型进行研究, 重点探讨无网格法和有限元方法求解不同频率下声腔的声场分布情况. 需要指出的是, 在下面所有算例中, 腔体内的介质均为空气, 其密度$\rho$为1.225 kg/m$^{3}$, 声波在空气中传播的速度$c$为343$\mbox{m/s}$, 为节省篇幅, 这些参数在下述算例中将不再具体定义. 除特殊说明外, 数值结果均在i5-5200 CPU@2.20GHz, 内存4GB的计算机上运算所得. 文中有限元结果均来自于有限元仿真软件COMSOL Multiphysics 5.4.
为了评估数值误差, 采用最大相对误差($MRE$)和均方根误差($RMSE$)
(35) $\begin{eqnarray} \label{eq35} &&MRE=\mathop{max}\limits_{1\leqslant i\leqslant NT} \left| {\frac{p_{num} (x^{i})-p_{exa} (x^{i})}{p_{exa} (x^{i})}} \right|\end{eqnarray} $
(36) $RMSE=\sqrt {\frac{1}{NT}\sum\limits_{i=1}^{NT} {(p_{num} (x^{i})-p_{exa} (x^{i}))^{2}} } $
其中$NT$是测试点的数量, $p_{exa} $和$p_{num}$分别表示第$i$个测试点的解析解和数值解. 这里, 除特殊说明外测试点均为区域内部节点.
3.1 混合边界管道声场分析
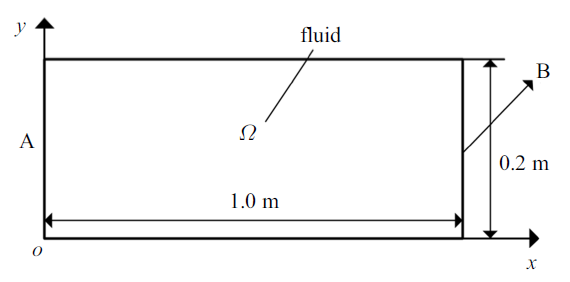
现求解如图2 所示的二维矩形声腔结构, 其长度$L=1.0$ m, 宽度$H=0.2$ m, 在A端口边界给定Neumann速度边界, 法向速度$v_{n} =0.01$ m/s, 管道B端口是刚性壁, 其他边界为声学硬边界条件.
图2
图2
管道声学模型
Fig.2
Pipe acoustic model
(37) $\begin{eqnarray} \label{eq37} P=-{j}\rho cv_{n} \frac{\cos (K(1-x))}{\sin K} \end{eqnarray} $
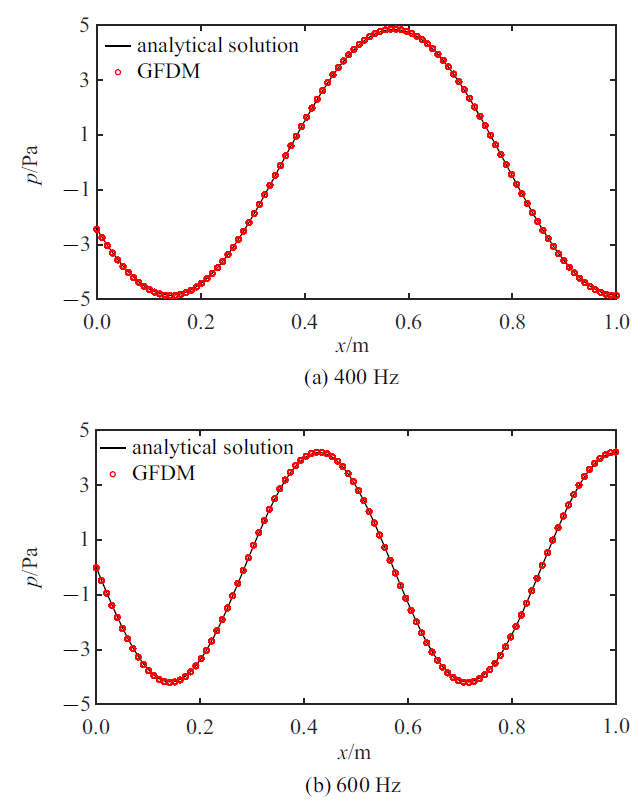
按照GFDM求解此类问题的前处理过程, 首先将该模型离散成17 996个点, 即总节点数$N=17 996$, 计算时选用的内部支撑点$m=12$. 图3 给出了当频率分别为400 Hz和600 Hz时, 计算得到管道底部轴线上的声压分布. 分析图3 声压曲线图可知, 不同频率下GFDM所得数值解与解析解均非常吻合.
图3
图3
不同频率下管道底部轴线声压分布
Fig.3
Distributions of sound pressure at the lower boundary under different frequencies
为了检验GFDM中总节点数目和内部支撑点数目对计算结果的影响, 研究了频率为400 Hz时, 不同内部支撑点数目和总节点数目对计算方法的影响. 分析表1 计算所得的数据可知, 总节点数$N=17 996$时, 随着内部支撑点数目$m$的增大, GFDM的计算最大误差和均方根误差随之变小, 也就是此方法的计算误差随之收敛. 观察表2 数据可知, 在内部支撑点数$m=12$时, 随着模型的总节点数目的增加, 计算结果的最大误差和均方根误差都会随之减小. 可见, 模型离散的点数越多, GFDM的计算结果越精确, 表明算法具有较好的计算精度和收敛性.
为从数值上分析最大计算频率与节点间距(对应于离散点数)之间的关系, 我们选取不同的频率和节点间距$\Delta h=\mathop{max}\limits_{1\leqslant i\leqslant N} \mathop{min}\limits_{1\leqslant j\leqslant N,j\ne i} \left| {{x}_{i} -{x}_{j} } \right|$, 将GFDM计算所得的$RMSE$误差曲面绘制于图4 (a)中. 观察图中误差分布情况, 我们可以清楚地看到计算误差随着频率和节点间距的同时增大而增大. 为更好地分析最大计算频率与节点间距之间的规律, 图4 (b)给出了对应的二维误差分布情况, 图中红色圆点表示误差大小为$RMSE=1.0\times10^{-2}$的位置. 通过曲线拟合的思想, 得到了误差为$RMSE=1.0\times10^{-2}$所在点构成的一条拟合曲线(图中绿色曲线): $f=35\cdot \Delta h^{(-0.65)}$. 至此, 我们便得到了一个估计最大计算频率的经验公式
(38) $\begin{eqnarray} \label{eq38} f\leqslant 35\cdot \Delta h^{(-0.65)} \end{eqnarray} $
需要指出的是, 根据经验公式(38), 在保证计算精度为$RMSE\leqslant 1.0\times10^{-2}$的情况下, 我们可以轻松地估计出能够计算的最大频率. 这里仅从数值的角度获得了一个计算频率与节点间距关系的经验公式, 理论上获得准确的估计公式目前仍面临巨大挑战, 还需进一步研究和探索.
图4
图4
不同频率和节点间距下GFDM所得计算误差$RMSE$的分布
Fig.4
Distribution of $RMSE$s under different frequencies and node intervals
为了考察GFDM对高频声学问题的计算精度和计算稳定性, 我们选取计算频率为20 000 Hz, 分析其计算结果. 通过经验公式(38), 我们能够估计出计算频率为20 000 Hz时取得良好精度($RMSE< 1.0\times10^{-2}$)所需的节点间距为$\Delta h=0.000 055$ m, 此时, 该模型大概需要66 000 000个离散节点. 受工作条件和计算机内存的限制, 想要模拟如此大规模的声学问题, 仍然面临巨大挑战, 即便使用另外一台较大内存的计算机(i7-6700 CPU@3.40GHz, 内存16 GB)进行模拟, 4 999 996个节点(节点间距$\Delta h=0.000 2$ m)就已经达到了计算机的内存极限. 在该离散节点数目下的计算结果如图5 所示, 可以看出GFDM所得结果与精确解(exact)十分吻合. 计算过程花费了3990.333 s的计算时间, 计算误差为$RMSE=0.087 362$. 另外, 从图5 中可以看出, 高频问题对应的声压波动非常剧烈, 这类问题的精确模拟对大多数数值算法来说都是比较棘手的, 上述数值结果表明GFDM能够有效模拟高频问题, 对该类问题具有较高的计算精度和计算稳定性.
图5
图5
频率为20 000 Hz时管道底部轴线声压分布
Fig.5
Distributions of sound pressure at the lower boundary under $f=20 000$ Hz
3.2 二维车腔声场分析
在整车的概念设计阶段, 车内声腔可近似地被看作为棱柱体, 因此可将其简化为二维模型进行噪声分析. 图6 所示为某车简化之后的车内声腔模型, 其水平方向的长度$L=3.41$ m, 竖直方向的高度$H=1.21$ m, 相关条件已在图中标示[35 ] . 腔体内部介质为空气, 由于发动机振动激励引起的噪声占整车噪声的绝大部分, 因而在汽车的前围板上施加一Neumann边界条件, 其振动速度为0.01 m/s. 此外, 我们也在乘员舱的顶部cd处施加一Robin边界条件以模拟内饰材料的阻尼, 这里声阻抗值为413 Pa$\cdot$s/m$^3$. 在算例分析中, 选取底部轴线ab上的声压数据进行研究. 图7 给出了模型的GFDM节点分布示意图.
图6
图6
具有阻抗边界条件的二维车腔模型
Fig.6
A two-dimensional car cavity with impedance boundary
图7
图7
车腔的GFDM节点分布
Fig.7
Distribution of nodes on the car cavity
车内噪声按其频率高低一般可分为低频噪声(1 $\sim$ 200 Hz)、中频噪声(200 $\sim$ 500 Hz)和高频噪声($>500$ Hz). 在实际驾乘过程中, 接触最多的是中低频噪声. 因此, 我们首先分析了低频($f=200$ Hz)时的声压分布, 为验证算法的有效性和准确度, 我们把细密网格下有限元(FEM)的数值解作为参考解. 采用有限元法进行声学数值计算时, 为了保证其结果的准确性, 需满足声学"经验法则", 即最小波长内至少有6个网格单元. 在接下来的计算分析中, 首先将汽车腔体模型在有限元软件中划分为43 480个三角形单元, 网格尺寸为0.01 m, 即每波长内包含171个网格单元. 使用GFDM计算时, 将算例模型离散成11 558个离散节点, 即$N=11 558$, 节点间距为0.02 m. 图8 给出了频率较低$f=200$ Hz时, 内部支撑点数$m=12$, 总节点数$N=11 558$时声腔模型内声压分布云图. 从图8 声压分布云图可以看出, 即使在较低频率下, FEM和GFDM计算的结果整体上吻合良好, 表明了GFDM使用低于有限元求解经验法则的节点数就可以获得比较理想的求解精度, 也体现了该方法在降低计算内存消耗和提高数值计算效率方面的潜能.
图8
图8
有限元和广义有限差分法计算所得声压分布云图
Fig.8
Contours of sound pressure obtained by the FEM and GFDM
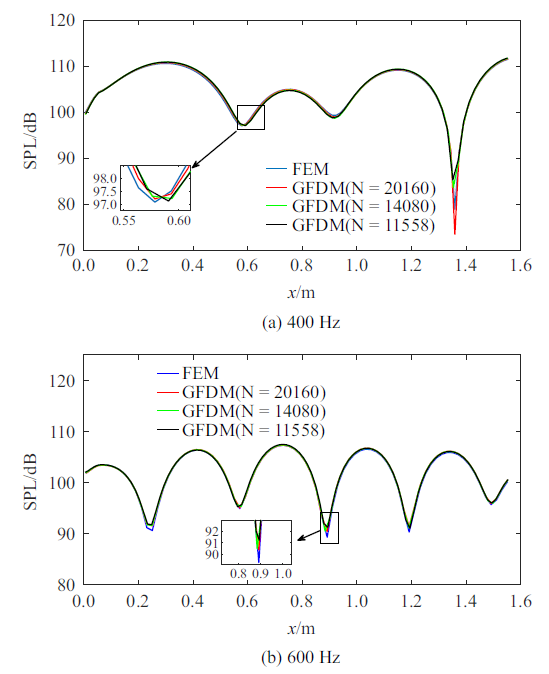
为验证GFDM在实际问题中的计算收敛性和稳定性, 在GFDM计算所用点数远小于FEM离散节点的情况下, 将三组不同的总节点数$N$计算所得数值结果与FEM参考解对比分析, 图9 和图10 分别给出了400 Hz和600 Hz频率下底部边界上的GFDM和FEM的对比情况. 图9 展示了不同频率下的声压曲线, 图10 是不同频率下的声压级曲线.
图9
图9
频率为400 Hz和600 Hz时有限元法与广义有限差分法所得声压曲线的对比
Fig.9
Comparisons of sound pressure obtained by the FEM and GFDM, under $f=400$ Hz and 600 Hz
图10
图10
频率为400 Hz和600 Hz时有限元法与广义有限差分法所得声压级曲线的对比
Fig.10
Comparisons of sound pressure level obtained by the FEM and GFDM, under $f=400$ Hz and 600 Hz
从图9 和图10 可以看出, GFDM在不同节点数下计算所得声压和声压级均与有限元结果很大程度上吻合, 即使采用较少的节点数目($N=11 558$), GFDM的计算结果也与有限元结果非常接近, 表明算法是准确有效的. 另外, 从图9 和图10 中可以看出, GFDM的计算精度随着计算节点数目的增加而提高, 说明具有较好的收敛性. 综上, GFDM在求解含阻抗边界车腔声学问题时具有较好的计算稳定性和收敛性. 相比于FEM, GFDM无需网格划分等繁琐的前处理过程, 仅需离散节点, 所以可作为声腔分析的一种有效工具.
3.3 三维空腔声场分析
为了检验GFDM计算三维复杂声场问题的能力, 下面对三维空腔模型的声学特性仿真计算[36 ] , 该声腔的介质为空气, 模型的A端面处带有初始速度条件, B端面处是吸声材料, 数值分析中所施加的Neumann及Robin边界条件也同上一算例一致. 在有限元分析软件中, 将声腔模型较细化划分为51 469个单元, 单元平均尺寸为0.011 m, 将频率为400 Hz下(根据声学"经验法则", 每波长内分布78个网格单元)的有限元结果作为参考值. 三维空腔结构的尺寸和布点方式如图11 所示.
图11
图11
三维空腔及其GFDM节点分布
Fig.11
Three-dimensional cavity and the distribution of nodes
使用FEM和GFDM分别计算模型边界点上的声压, 图12 和图13 分别给出了两种方法计算400 Hz时的声压和声压级分布云图. 从图中发现, GFDM计算的数值结果和FEM参考值十分吻合, 可见GFDM在三维声腔模型中也有较好的计算精度.
图12
图12
400 Hz下有限元和广义有限差分法所得声压分布云图
Fig.12
Contours of sound pressure obtained by the FEM and GFDM under $f=400$ Hz
图13
图13
400 Hz下有限元和广义有限差分法所得声压级分布云图
Fig.13
Contours of sound pressure level obtained by the FEM and GFDM under $f=400$ Hz
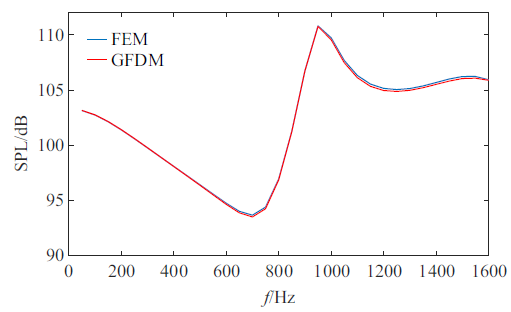
选取图11 中的F(0.05, 0.05, 0.12)点作为监测点来模拟人的耳朵所在位置, 分析该处声压级随频率增加的变化情况. 图14 给出了GFDM和FEM所得监测点F处声压级频率响应曲线的对比. 尽管在中频(700 Hz)附近和较高频率($>1000$ Hz)附近出现了微小的偏差, 但GFDM的计算结果和FEM参考解仍然比较吻合, 充分表明了算法的有效性和准确性. 需要指出的是, 增加GFDM的离散节点数目, 可以使得两种算法的数值结果更加接近.
图14
图14
监测点F处的频率响应曲线
Fig.14
Frequency response curves monitoring point F
3.4 三维S型圆柱管道声场分析
圆柱管道是生活中比较常见的空腔模型, 为了进一步验证本文方法的计算准确性, 下面对S型管道分别采用FEM和GFDM计算并对其声压分析. 三维管道模型直径为$D=0.1$ m, 长度$L=1.0$ m, $a$端面处施加Neumann速度边界$v_{n} =0.01$ m/s, $b$端面处有吸声材料, 阻抗值$Z=413$ Pa$\cdot$s/m$^3$. 其余边界条件为刚性壁, $\bar{{v}}_{n} =0$. 模型尺寸和布点格式如图15 所示.
图15
图15
S型声腔及其节点分布
Fig.15
S-shaped acoustic cavity and nodal distribution
为了保证GFDM对高频问题的有效性, 我们将模型离散成126 905个节点, 此时的节点间距0.003 5 m. 同时, 将具有729 224个网格单元(包含86 624个边界单元和642 600个域单元)和网格平均大小为0.003 m的FEM结果作为参考解. 图16 和图17 分别给出了低频400 Hz和高频1600 Hz频率下管道表面声压分布云图以及绝对偏差云图. 分析声压云图中可以发现, GFDM计算的结果和FEM参考解几乎完全吻合, 并且从绝对偏差云图可以看出, 400 Hz下的偏差均小于0.06, 1600 Hz下的偏差均小于0.45, 这充分说明了方法的可行性和有效性. 因此, GFDM在模拟含阻抗边界空腔问题时的计算精度和数值稳定性是比较理想的.
图16
图16
400 Hz下有限元和广义有限差分法所得声压和绝对偏差的分布云图
Fig.16
Contours of sound pressure and absolute deviation obtained by the FEM and GFDM under $f=400$ Hz
图17
图17
1600 Hz下有限元和广义有限差分法所得声压和绝对偏差分布云图
Fig.17
Contours of sound pressure and absolute deviation obtained by the FEM and GFDM under $f=1600$ Hz
4 结论
广义有限差分法(GFDM)相比于传统网格类数值方法, 避免了网格划分的前处理过程, 并且继承了数值算法中局部化的优点, 在模拟复杂高维几何域问题时有较好的准确性, 并且保证计算精度的同时也提高了计算效率. 本文探讨了GFDM在含阻抗边界空腔声学问题中的应用. 以具有精确解的二维管道边值问题为例, 讨论了GFDM的稳定性和计算高效性, 并获得了最大计算频率与节点间距关系的经验公式. 通过无精确解的复杂声腔模型声学分析, 检验了GFDM在二维和三维不同求解域内模拟计算的可行性、计算准确性和计算稳定性.
综上所述, 广义有限差分法在空腔声学问题中的应用已得到初步验证, 数值结果表明该方法是一种高效、精确、稳定、收敛的空腔声学分析方法. 然而, 应用广义有限差分法在更加实际的复杂声场中还需要进一步研究, 进行声固耦合问题的求解和时域声学仿真将是未来工作的重点.
参考文献
View Option
[1]
陶文铨 , 吴学红 , 戴艳俊 . 无网格数值求解方法
中国电机工程学报 , 2010 ,30 (5 ):1 -10
[本文引用: 1]
(Tao Wenquan Wu Xuehong Dai Yanjun Numerical solutions of meshless methods
Proceedings of the Chinese Society of Electrical Engineering 2010 ,30 (5 ):1 -10 (in Chinese))
[本文引用: 1]
[2]
张雄 , 刘岩 , 马上 . 无网格法的理论及应用
力学进展 , 2009 ( 1 ):1 -36
(Zhang Xiong Liu Yan Ma Shang Meshfree methods and their applications
Advances in Mechanics 2009 ( 1 ):1 -36 (in Chinese))
[3]
Atluri SN Shen S The meshless method . Encino, CA : Tech Science Press , 2002
[4]
杨建军 , 文丕华 . 无网格法: 理论与算法 , 北京 : 科学出版社 , 2018 : 1 -11
(Yang Jianjun Wen Pihua Meshless method: theory and applications , Beijing : Science Press , 2018 : 1 -11 (in Chinese))
[5]
王莉华 , 李溢铭 , 褚福运 . 基于分区径向基函数配点法的大变形分析
力学学报 , 2019 ,51 (3 ):743 -753
(Wang Lihua Li Yiming Chu Fuyun Finte subdomain radial basis collocation method for the large deformation analysis
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (3 ):743 -753 (in Chinese))
[6]
覃霞 , 刘珊珊 , 谌亚菁 等 . 基于遗传算法的弹性地基加肋板肋梁无网格优化分析
力学学报 , 2020 ,52 (1 ):93 -110
[本文引用: 1]
(Qin Xia Liu Shanshan Shen Yajing et al . Rib meshless optimization of stiffened plates resting on elastic foundation based on genetic algorithm
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (1 ):93 -110 (in Chinese))
[本文引用: 1]
[7]
Liu GR Nguyen-Thoi T Nguyen-Xuan H , et al . A node-based smoothed finite element method (NS-FEM) for upper bound solutions to solid mechanics problems
Computers & Structures 2009 ,87 (1-2 ):14 -26
[本文引用: 1]
[8]
Chan HF Fan CM Kuo CW . Generalized finite difference method for solving two-dimensional non-linear obstacle problems
Engineering Analysis with Boundary Elements 2013 ,37 (9 ):1189 -1196
[本文引用: 1]
[9]
Gu Y Chen W Gao HW , et al . A meshless singular boundary method for three-dimensional elasticity problems
International Journal for Numerical Methods in Engineering 2016 ,107 (2 ):109 -126
[本文引用: 1]
[10]
Marin L . An alternating iterative MFS algorithm for the Cauchy problem for the modified Helmholtz equation
Computational Mechanics 2010 ,45 (6 ):665 -677
[本文引用: 1]
[11]
Chen W Shen LJ Shen ZJ , et al . Boundary knot method for Poisson equations
Engineering Analysis with Boundary Elements 2005 ,29 (8 ):756 -760
[本文引用: 1]
[12]
Wang FJ Gu Y Qu WZ , et al . Localized boundary knot method and its application to large-scale acoustic problems
Computer Methods in Applied Mechanics and Engineering 2020 ,361 (C ):112729
[本文引用: 1]
[13]
Chen CS Golberg MA Hon YC . The method of fundamental solutions and quasi-Monte-Carlo method for diffusion equations
International Journal for Numerical Methods in Engineering 2015 ,43 (8 ):1421 -1435
[本文引用: 1]
[14]
王发杰 , 张耀明 , 公颜鹏 . 改进的基本解法在薄体各向异性位势Cauchy问题中的应用
工程力学 , 2016 ,33 (2 ):18 -24
[本文引用: 1]
(Wang Fajie Zhang Yaoming Gong Yanpeng Inverse identification of boudary conditions for anisotropic potential problems of thin body using MFS
Engineering Mechanics 2016 ,33 (2 ):18 -24 (in Chinese))
[本文引用: 1]
[15]
Young DL Chen KH Lee CW . Novel meshless method for solving the potential problems with arbitrary domain
Journal of Computational Physics 2005 ,209 (1 ):290 -321
[本文引用: 1]
[16]
谷岩 , 陈文 . 改进的奇异边界法模拟三维位势问题
力学学报 , 2012 , ( 2 ):351 -360
[本文引用: 1]
(Gu Yan Chen Wen Improved singular boundary method for three dimensional potential problems
Chinese Journal of Theoretical and Applied Mechanics 2012 ,44 (2 ):351 -360 (in Chinese))
[本文引用: 1]
[17]
李煜冬 , 王发杰 , 陈文 . 瞬态热传导的奇异边界法及其MATLAB实现
应用数学和力学 , 2019 ,40 (3 ):259 -268
(Li Yudong Wang Fajie Chen Wen Matlab implementation of a singular boundary method for transient heat conduction
Applied Mathematics and Mechanics 2019 ,40 (3 ):259 -268 (in Chinese))
[18]
李珺璞 , 陈文 . 一种模拟大规模高频声场的双层奇异边界法
力学学报 , 2018 ,50 (4 ):961 -969
[本文引用: 1]
(Li Junpu Chen Wen A dual-level singular boundary method for large-scale high frequency sound field analysis
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (4 ):961 -969 (in Chinese))
[本文引用: 1]
[19]
Chen KH Chen JT Kao JH . Regularized meshless method for solving acoustic eigenproblem with multiply-connected domain
Computer Modeling in Engineering and Sciences 2006 ,16 (1 ):27 -39
[本文引用: 1]
[20]
Chen JT Chen IL Chen KH , et al . A meshless method for free vibration analysis of circular and rectangular clamped plates using radial basis function
Engineering Analysis with Boundary Elements 2004 ,28 (5 ):535 -545
[本文引用: 1]
[21]
Sadat H Wang CA Dez VL . Meshless method for solving coupled radiative and conductive heat transfer in complex multi-dimensional geometries
Applied Mathematics & Computation 2012 ,218 (20 ):10211 -10225
[本文引用: 1]
[22]
Wang CA Sadat H Prax C . A new meshless approach for three dimensional fluid flow and related heat transfer problems
Computers & Fluids 2012 ,69 :136 -146
[本文引用: 1]
[23]
Lu YY Belytschko T Gu L . A new implementation of the element free Galerkin method
Computer Methods in Applied Mechanics & Engineering 1994 ,113 (3-4 ):397 -414
[本文引用: 1]
[24]
邓立克 , 王东东 , 王家睿 等 . 薄板分析的线性基梯度光滑伽辽金无网格法
力学学报 , 2019 ,51 (3 ):688 -702
[本文引用: 1]
(Deng Like Wang Dongdong Wang Jiarui et al . A gradient smoothing galerkin meshfree method for thin plate analysis with linear basis function
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (3 ):688 -702 (in Chinese))
[本文引用: 1]
[25]
Benito JJ Urena F Gavete L , et al . An h-adaptive method in the generalized finite differences
Computer Methods in Applied Mechanics & Engineering 2003 ,192 (5-6 ):735 -759
[本文引用: 1]
[26]
李艾伦 , 傅卓佳 , 李柏纬 等 . 含肿瘤皮肤组织传热分析的广义有限差分法
力学学报 , 2018 ,50 (5 ):1198 -1205
[本文引用: 1]
(Li Ailun Fu Zhuojia Li Powei et al . Generalized finite difference method for bioheat transfer analysis on skin tissue with tumors
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (5 ):1198 -1205 (in Chinese))
[本文引用: 1]
[27]
汤卓超 , 傅卓佳 , 范佳铭 . 广义有限差分法求解Kirchhoff和Winkler薄板弯曲问题
固体力学学报 , 2018 ,39 (4 ):419 -428
[本文引用: 1]
(Tang Zhuochao Fu Zhuojia Fan Jiaming Generalized finite difference method for solving Kirchhoff plate and Winkler plate bending problems
Chinese Journal of Solid Mechanics 2018 ,39 (4 ):419 -428 (in Chinese))
[本文引用: 1]
[28]
Gu Y Sun HG . A meshless method for solving three-dimensional time fractional diffusion equation with variable-order derivatives
Applied Mathematical Modelling 2020 ,78 :539 -549
[本文引用: 1]
[29]
Gu Y Qu WZ Chen W , et al . The generalized finite difference method for long-time dynamic modeling of three-dimensional coupled thermoelasticity problems
Journal of Computational Physics 2019 ,384 :42 -59
[本文引用: 1]
[30]
Li PW Fu ZJ Gu Y , et al . The generalized finite difference method for the inverse Cauchy problem in two-dimensional isotropic linear elasticity
Solids Struct 2019 ,174 :69 -84
[本文引用: 1]
[31]
朱小松 . 基于无网格方法的声学预测研究
[博士论文]. 哈尔滨: 哈尔滨工程大学 , 2018 , 56 -60
[本文引用: 1]
(Zhu Xiaosong Study on the acoustic prediction based on meshless methods
[Doctor Thesis]. Harbin: Harbin Engineering University , 2018 , 56 -60 (in Chinese))
[本文引用: 1]
[32]
Benito JJ Urena F Gavete L , et al . A posteriori error estimator and indicator in generalized finite differences. Application to improve the approximated solution of elliptic PDEs
International Journal of Computer Mathematics 2008 ,85 (3-4 ):359 -370
[本文引用: 1]
[33]
Gavete L Gavete ML Benito JJ . Improvements of generalized finite difference method and comparison with other meshless method
Applied Mathematical Modelling 2003 ,27 (10 ):831 -847
[本文引用: 1]
[34]
Benito JJ Urena F Gavete L . Influence of several factors in the generalized finite difference method
Applied Mathematical Modelling 2001 ,25 (12 ):1039 -1053
[本文引用: 1]
[35]
王刚 . 基于节点积分的车身结构振动噪声计算方法研究
[博士论文]. 长沙: 湖南大学 , 2016 , 87 -91
[本文引用: 1]
(Wang Gang The research of calculational method of vehicle body structure vibration and noise based on node integral. [Doctor Thesis]
Changsha: Hunan University , 2016 , 87 -91 (in Chinese))
[本文引用: 1]
[36]
王双 . 基于径向基配点型无网格方法的内部声学问题研究
[博士论文]. 武汉: 华中科技大学 , 2013 ,100
[本文引用: 1]
(Wang Shuang Study on the interior acoustic problem based on the radial basis collocation meshless method
Wuhan: Huazhong University of Science and Technology , 2013 ,100 (in Chinese )
[本文引用: 1]
无网格数值求解方法
1
2010
... 目前, 有限元、有限差分和边界元法作为空腔声场模拟计算中的主要方法, 在汽车发动机传热或车内噪声控制、封闭管道噪声声场等方面均有广泛应用. 然而对于一些多维复杂几何域问题, 合理有效的模拟计算很难准确实现. 不同于以上依赖网格的数值计算方法, 无网格法通过节点信息建立插值基函数, 插值基函数不依赖于节点之间的有序拓扑链接, 因此相对于传统方法不会受到网格划分的约束. 近年来无网格方法的研究受到了高度重视, 成为目前科学与工程计算中的研究热点之一[1 -6 ] . ...
无网格数值求解方法
1
2010
... 目前, 有限元、有限差分和边界元法作为空腔声场模拟计算中的主要方法, 在汽车发动机传热或车内噪声控制、封闭管道噪声声场等方面均有广泛应用. 然而对于一些多维复杂几何域问题, 合理有效的模拟计算很难准确实现. 不同于以上依赖网格的数值计算方法, 无网格法通过节点信息建立插值基函数, 插值基函数不依赖于节点之间的有序拓扑链接, 因此相对于传统方法不会受到网格划分的约束. 近年来无网格方法的研究受到了高度重视, 成为目前科学与工程计算中的研究热点之一[1 -6 ] . ...
基于分区径向基函数配点法的大变形分析
0
2019
基于分区径向基函数配点法的大变形分析
0
2019
基于遗传算法的弹性地基加肋板肋梁无网格优化分析
1
2020
... 目前, 有限元、有限差分和边界元法作为空腔声场模拟计算中的主要方法, 在汽车发动机传热或车内噪声控制、封闭管道噪声声场等方面均有广泛应用. 然而对于一些多维复杂几何域问题, 合理有效的模拟计算很难准确实现. 不同于以上依赖网格的数值计算方法, 无网格法通过节点信息建立插值基函数, 插值基函数不依赖于节点之间的有序拓扑链接, 因此相对于传统方法不会受到网格划分的约束. 近年来无网格方法的研究受到了高度重视, 成为目前科学与工程计算中的研究热点之一[1 -6 ] . ...
基于遗传算法的弹性地基加肋板肋梁无网格优化分析
1
2020
... 目前, 有限元、有限差分和边界元法作为空腔声场模拟计算中的主要方法, 在汽车发动机传热或车内噪声控制、封闭管道噪声声场等方面均有广泛应用. 然而对于一些多维复杂几何域问题, 合理有效的模拟计算很难准确实现. 不同于以上依赖网格的数值计算方法, 无网格法通过节点信息建立插值基函数, 插值基函数不依赖于节点之间的有序拓扑链接, 因此相对于传统方法不会受到网格划分的约束. 近年来无网格方法的研究受到了高度重视, 成为目前科学与工程计算中的研究热点之一[1 -6 ] . ...
A node-based smoothed finite element method (NS-FEM) for upper bound solutions to solid mechanics problems
1
2009
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
Generalized finite difference method for solving two-dimensional non-linear obstacle problems
1
2013
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
A meshless singular boundary method for three-dimensional elasticity problems
1
2016
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
An alternating iterative MFS algorithm for the Cauchy problem for the modified Helmholtz equation
1
2010
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
Boundary knot method for Poisson equations
1
2005
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
Localized boundary knot method and its application to large-scale acoustic problems
1
2020
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
The method of fundamental solutions and quasi-Monte-Carlo method for diffusion equations
1
2015
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
改进的基本解法在薄体各向异性位势Cauchy问题中的应用
1
2016
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
改进的基本解法在薄体各向异性位势Cauchy问题中的应用
1
2016
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
Novel meshless method for solving the potential problems with arbitrary domain
1
2005
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
改进的奇异边界法模拟三维位势问题
1
2012
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
改进的奇异边界法模拟三维位势问题
1
2012
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
瞬态热传导的奇异边界法及其MATLAB实现
0
2019
瞬态热传导的奇异边界法及其MATLAB实现
0
2019
一种模拟大规模高频声场的双层奇异边界法
1
2018
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
一种模拟大规模高频声场的双层奇异边界法
1
2018
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
Regularized meshless method for solving acoustic eigenproblem with multiply-connected domain
1
2006
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
A meshless method for free vibration analysis of circular and rectangular clamped plates using radial basis function
1
2004
... 根据插值基函数的类型不同, 无网格法可分为边界型[7 -8 ] 和区域型[9 -10 ] 两大类. 边界型无网格法保留了降低所求问题维度的优点, 并且避免了复杂的奇异和近奇异积分的计算. 近年来, 边界型无网格方法引起了广泛的关注, 主导方法有边界节点法[11 -12 ] 、基本解法[13 -14 ] 、边界无单元法[15 ] 、奇异边界法[16 -18 ] 、正则化无网格方法[19 ] 等. 以上方法均在多种领域成功运用并取得了不同程度的成功, 但是仍存在一些决定性的问题. 例如, 该类方法在实际工程中的应用范围[20 ] 很大程度上会受到插值基函数的影响. ...
Meshless method for solving coupled radiative and conductive heat transfer in complex multi-dimensional geometries
1
2012
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
A new meshless approach for three dimensional fluid flow and related heat transfer problems
1
2012
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
A new implementation of the element free Galerkin method
1
1994
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
薄板分析的线性基梯度光滑伽辽金无网格法
1
2019
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
薄板分析的线性基梯度光滑伽辽金无网格法
1
2019
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
An h-adaptive method in the generalized finite differences
1
2003
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
含肿瘤皮肤组织传热分析的广义有限差分法
1
2018
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
含肿瘤皮肤组织传热分析的广义有限差分法
1
2018
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
广义有限差分法求解Kirchhoff和Winkler薄板弯曲问题
1
2018
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
广义有限差分法求解Kirchhoff和Winkler薄板弯曲问题
1
2018
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
A meshless method for solving three-dimensional time fractional diffusion equation with variable-order derivatives
1
2020
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
The generalized finite difference method for long-time dynamic modeling of three-dimensional coupled thermoelasticity problems
1
2019
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
The generalized finite difference method for the inverse Cauchy problem in two-dimensional isotropic linear elasticity
1
2019
... 相对于边界型无网格法, 区域型无网格方法摆脱了插值基函数的约束, 所以对各种偏微分方程初边值问题具有普遍适用性, 应用领域更为广泛. 现如今, 比较常用的区域型无网格法包括光滑粒子水动力学法[21 ] 、扩散单元法[22 ] 、无单元伽辽金法[23 -24 ] 和广义有限差分法(Generalized Finite Difference Method, GFDM)[25 ] 等. 其中, 广义有限差分法是一种最近发展起来的新型无网格方法, 已被成功应用于生物传热分析[26 ] 、薄板弯曲问题[27 ] 、分数阶反常扩散[28 ] 、热弹性[29 ] 和反问题[30 ] 等领域. ...
基于无网格方法的声学预测研究
1
2018
... 声波在传播过程中会不断被拉伸和压缩, 动作非常快, 质点间来不及进行热交换. 因此声波的传播过程可被看成是绝热过程[31 ] , 其热力学方程为 ...
基于无网格方法的声学预测研究
1
2018
... 声波在传播过程中会不断被拉伸和压缩, 动作非常快, 质点间来不及进行热交换. 因此声波的传播过程可被看成是绝热过程[31 ] , 其热力学方程为 ...
A posteriori error estimator and indicator in generalized finite differences. Application to improve the approximated solution of elliptic PDEs
1
2008
... 假设中心点为第$i$点(图中红色点), $p_{i} $是中心节点$(x_{i},y_{i} )$处的函数值, $p_j^i $, $j=1,2,...,m$是"点簇"内支撑点$(x_{i}^{j} ,y_{i}^{j} )$上的函数值. 每个中心点周边有$m$个支撑点, 使用泰勒级数展开[32 ] , 在中心点($x_{i} $, $y_{i} )$周围展开$p_{j}^{i} $值有 ...
Improvements of generalized finite difference method and comparison with other meshless method
1
2003
... 式中, $h_{ij} =x_{i} -x_{j}^{i} $和$k_{ij} =y_{i} -y_{i}^{j} $分别为沿着$x$与$y$轴方向上$i$点和$j$点间的距离, $\omega_{ij} =\omega (h_{ij} ,k_{ij})$表示点$j$处的加权系数[33 ] . 在上述逼近过程中, 很多常用的权函数[34 ] 均可使用, 由于样条权函数对影响域半径的变化不是很敏感, 因此在计算中采用如下四次样条权函数 ...
Influence of several factors in the generalized finite difference method
1
2001
... 式中, $h_{ij} =x_{i} -x_{j}^{i} $和$k_{ij} =y_{i} -y_{i}^{j} $分别为沿着$x$与$y$轴方向上$i$点和$j$点间的距离, $\omega_{ij} =\omega (h_{ij} ,k_{ij})$表示点$j$处的加权系数[33 ] . 在上述逼近过程中, 很多常用的权函数[34 ] 均可使用, 由于样条权函数对影响域半径的变化不是很敏感, 因此在计算中采用如下四次样条权函数 ...
基于节点积分的车身结构振动噪声计算方法研究
1
2016
... 在整车的概念设计阶段, 车内声腔可近似地被看作为棱柱体, 因此可将其简化为二维模型进行噪声分析. 图6 所示为某车简化之后的车内声腔模型, 其水平方向的长度$L=3.41$ m, 竖直方向的高度$H=1.21$ m, 相关条件已在图中标示[35 ] . 腔体内部介质为空气, 由于发动机振动激励引起的噪声占整车噪声的绝大部分, 因而在汽车的前围板上施加一Neumann边界条件, 其振动速度为0.01 m/s. 此外, 我们也在乘员舱的顶部cd处施加一Robin边界条件以模拟内饰材料的阻尼, 这里声阻抗值为413 Pa$\cdot$s/m$^3$. 在算例分析中, 选取底部轴线ab上的声压数据进行研究. 图7 给出了模型的GFDM节点分布示意图. ...
基于节点积分的车身结构振动噪声计算方法研究
1
2016
... 在整车的概念设计阶段, 车内声腔可近似地被看作为棱柱体, 因此可将其简化为二维模型进行噪声分析. 图6 所示为某车简化之后的车内声腔模型, 其水平方向的长度$L=3.41$ m, 竖直方向的高度$H=1.21$ m, 相关条件已在图中标示[35 ] . 腔体内部介质为空气, 由于发动机振动激励引起的噪声占整车噪声的绝大部分, 因而在汽车的前围板上施加一Neumann边界条件, 其振动速度为0.01 m/s. 此外, 我们也在乘员舱的顶部cd处施加一Robin边界条件以模拟内饰材料的阻尼, 这里声阻抗值为413 Pa$\cdot$s/m$^3$. 在算例分析中, 选取底部轴线ab上的声压数据进行研究. 图7 给出了模型的GFDM节点分布示意图. ...
基于径向基配点型无网格方法的内部声学问题研究
1
2013
... 为了检验GFDM计算三维复杂声场问题的能力, 下面对三维空腔模型的声学特性仿真计算[36 ] , 该声腔的介质为空气, 模型的A端面处带有初始速度条件, B端面处是吸声材料, 数值分析中所施加的Neumann及Robin边界条件也同上一算例一致. 在有限元分析软件中, 将声腔模型较细化划分为51 469个单元, 单元平均尺寸为0.011 m, 将频率为400 Hz下(根据声学"经验法则", 每波长内分布78个网格单元)的有限元结果作为参考值. 三维空腔结构的尺寸和布点方式如图11 所示. ...
基于径向基配点型无网格方法的内部声学问题研究
1
2013
... 为了检验GFDM计算三维复杂声场问题的能力, 下面对三维空腔模型的声学特性仿真计算[36 ] , 该声腔的介质为空气, 模型的A端面处带有初始速度条件, B端面处是吸声材料, 数值分析中所施加的Neumann及Robin边界条件也同上一算例一致. 在有限元分析软件中, 将声腔模型较细化划分为51 469个单元, 单元平均尺寸为0.011 m, 将频率为400 Hz下(根据声学"经验法则", 每波长内分布78个网格单元)的有限元结果作为参考值. 三维空腔结构的尺寸和布点方式如图11 所示. ...