引言
以液氢为代表的低温推进剂在航天领域有着广泛的应用,但是因为其沸点低、易蒸发的特性,在地面停放、发射过程以及在轨运行等各个阶段都极易发生汽化,引起储罐内部热分层和自增压,进而威胁飞行器系统结构安全. 在轨运行期间,推进剂储罐会受到各种空间辐射的影响,比如太阳辐射、地球反照热外流、地球红外辐射热流以及空间黑背景辐射热流等等. 这些热源的存在都会使得推进剂储罐因受热不均匀在局部发生汽化现象. 传统的排气方法能有效降低储罐内部压强,但一定程度上造成了推进剂的浪费,使发射成本增加,同时制约飞行器运载能力,不利于长期在轨飞行及深空探测活动. 20世纪末,美国NASA的研究者提出了零蒸发存储(zero boil-off, ZBO)的概念. ZBO技术是通过将被动绝热技术与主动制冷技术有机结合起来,实现低温推进剂无损储存的技术,其中被动绝热技术主要是使用绝热材料减少外部热量的渗入. Hastings等[1]发现对于需要长期在轨运行的储罐而言,单纯使用被动绝热技术会增加储罐质量,进而降低航天器的灵活性,因此在使用绝热材料的基础上尝试主动制冷技术的运用对于长期航天探索工程具有重要意义. 主动制冷技术主要有两种,一种是通过热传导装置将罐内热量传导到罐外,另一种则是通过机械搅拌或者低温射流的方式加强储罐内部流体对流. 热传导装置作用的范围相对较小,机械搅拌的实现工艺更加复杂,因此通过施加储罐内部低温射流的方式进行压强控制成为国内外相关领域学者的研究热点.
通过低温射流实现热分层和自增压控制的研究可以追溯到20世纪70年代,Poth等[2]对比分析了各种热分层消除装置的特点,认为轴向低温射流具有很高的流体混合性能并且轻便灵活,增压控制易于实现;Merte等[3]研究了轴对称的圆柱形储罐中单组分工质气相和液相之间的传热和传质过程,其中气相采用理想气体假设,将控制方程转换为有限差分形式,进行数值计算得到了多种计算工况下的压力演化曲线. Audelott[4]在Lewis Research Center 5-10 s零重力装置中实验研究了向直径为10 cm的圆柱形储罐中轴向喷射乙醇时产生的液体流动模式,发现储罐内部流场分布与储罐几何形状、低温射流速度、储罐填充比以及低温射流位置有关;Lin等[5]先后实验研究了体积为0.144 m$^{3}$的小型储罐和体积为4.89 m$^{3}$大型储罐使用低温射流混合装置实现增压控制的效果,实验表明低温射流可以有效控制罐内增压,但是小罐模型得出的低温射流时间和增压速率之间的关系无法很好预测大罐模型中两者之间的相对关系;Panzarella等[6]研究了常重力条件下小型储罐内部气液两相的自增压情况,证实了增强储罐内部对流可以抑制热分层现象进而实现增压控制;Mukka等[7]研究了常重力条件下低温射流方式对消除热分层效果的影响,认为不同低温射流条件导致的储罐内部流场的差异对储罐内温度场和速度场的分布有着重要影响. 在认识到低温射流可以有效消除热分层现象后,科研工作者建立了很多罐体系统研究如何优化低温射流消除热分层的效果. Ho等[8]建立了一个泵-$\!$-热管模型,通过泵装置促进储罐内部流体循环,不断把高温流体喷向热管,再由热管将热量导出. 通过对该模型的三维数值模拟发现通过增大低温射流速度可以有效消除储罐内部的高温区域;随后Ho等[9]利用数值模拟方法研究了轴向圆盘多孔低温射流喷嘴结构,发现在保持入射速度不变的情况下,加大孔口直径也可以显著提升热分层消除效果,此外射流喷嘴位置对热分层消除效果有着显著影响,并对圆盘射流喷嘴系统进行了参量分析,研究了入口管直径、射流喷嘴位置和射流喷嘴直径对系统制冷效果的影响. Ho等[10]又对之前建立的泵-$\!$-热管模型进行了深入研究,分析了喷射间隔和喷管长度等参量对消除热分层效果的影响. Belmedani等[11]开展了不同热通量的液氮储罐热分层的实验研究,热通量越大,自由面蒸发速率越大,自由面和液相区温差越明显,较好的揭示了蒸发机理,通过研究低温储罐中液体的速度和温度特性,认为强热流诱发热分层现象. Zilliac等[12]提出了一种平衡热力学模型来预测储罐增压过程,该模型适用于具有高挥发性的低温推进剂,通过与实测结果进行对比,证实了该模型的准确性. Grayson等[13]模拟了常重力情况下通过外部加热实现增压和通过热力学排气实现减压的储罐数值计算模型,假设液相不可压缩,其密度仅是温度的函数. 该模型的压力和温度预测结果与测试中的传感器测量结果相比较有很高的一致性. Barsi等[14]采取了与原有的集总热力学模型不同的气液两相模型,在该模型中,液相和汽相的守恒方程都得到了求解.研究中为了简化计算将两相都视为不可压缩的,并使用积分方法来求解交界面的质量交换. 通过将储罐压力上升的数值计算与以往计算模型的结果进行比较,证实了该模型的准确性. Lopez等[15]提出了一种新的计算流体动力学模型,模拟了重力作用下椭球形液氢储罐在外部加热情形下的压力控制过程. 压力控制的实现由位于储罐内部的轴向射流热动力排气系统(TVS)提供,该系统向储罐内注入冷流体,使液体发生混合以降低储罐内部压力. 该轴对称模型的计算采用商业软件FLOW-3D进行计算,其中定量模型验证采用1999年在马歇尔航天飞行中心进行的工程检验测试结果,计算结果表明模型预测的自增压速率和流体温度与试验数据吻合良好. 这项研究提升了当时用于实现低温压力控制的CFD建模能力,并为开发基于CFD的空间硬件设计提供了参考. Barsi等[16]提出了一种两相CFD模型,该模型描述了在常重力条件下,部分填充的LH2储罐的自增压行为,并利用已有的不同填充水平下的实验数据,对模型的预测能力进行了评估. 评估结果表明该模型的预测结果与实验测得的压力曲线吻合较好. Kumar等[17]计算了不同纵横比的大型液氢储罐中蒸发对储罐热分层的影响. 他们采用均匀两相模型,分别求解了气相和液相各自的守恒方程,气液界面的蒸发是通过传质源项来实现的,随着储罐的纵横比增加,分层的程度会逐渐增加. Olivera等[18]建立了一个储罐热分层模型,其中包括了平台的调节旋转. 该模型可用于评估轴向加速度、自旋速率、热通量以及储罐几何形状等因素对推进剂储罐内部热分层现象的影响. Li等[19]通过实验和数值方法研究了多层绝缘低温储罐中真空损耗引起的液氮热分层的瞬态过程,他们认为真空损耗可以迅速导致热分层. 在实验中,利用热电偶得到了实验储罐中液体温度的分布和演变. 通过建立二维模型进行数值模拟计算,模拟了储罐内部热分层的形成和减弱过程以及液体温度场分布,并将数值模拟结果与实验结果进行了比较. 研究还表明,罐内的两相流动对热分层起着重要作用. Wang等[20]通过数值模拟系统对比了微重力条件下由热管和喷管组成的ZBO系统中,喷管数量、喷管出流方向和热管蒸发器热传递效率对增压控制性能的影响. Liu等[21]通过在Rahman模型的基础上增加了向下的导管,使储罐底部也发生强制对流,提升ZBO性能. Liu等[22]进一步通过正交试验设计,研究了导管出口到罐底的距离、喷管的半径、射流喷嘴深度、导管半径和环形射流喷嘴直径等参量对储罐设计的影响. Roh等[23]使用商业软件FLUENT对压缩液化天然气储罐中的瞬态自然对流进行了数值计算. 计算结果表明,蒸发气体的生成在很大程度上取决于储罐内部垂直温度的分布,而储罐内部垂直方向的温度分布受储罐自增压过程的影响. 同时作者对储罐压力、罐体尺寸和增压过程对蒸发气体生成的影响进行了量化研究. Wang等[24]采用计算流体动力学模型,对液氢储罐的加压排放过程进行了数值模拟,将壁面区域和流体区域同时考虑为计算域,采用低雷诺数$k$-$\varepsilon$模型来处理流体和壁面的热交换效应. 该模型还考虑了气液相变,并将数值计算结果与已有实验数据进行对比,认为该CFD模型在增压计算过程中具有良好的适应性. 通过该模型可以获得增压所需气体量、储罐内部压力变化过程、储罐内部温度分布等详细特征. 作者还分析了相变效应和储罐结构对增压性能的影响,计算结果表明,气液相变对增压行为影响不大. 随后Wang等[25]又建立了一种计算流体力学模型,该模型可同时考虑罐内的热交换和外部空气动力加热,并对低温储罐在排放过程中的瞬态热状态和增压性能进行了研究. 该模型中计算域不仅包括了流体和罐壁区域,还包括了泡沫绝热层区域. 作者将该模型的计算结果与实验数据进行比较,两者具有很高的一致性. 然后利用该模型对储罐的增压排放过程进行了预测,得到了其热力学行为、增压行为过程. Daigle等[26]提出了一种描述液氢低温储罐中自然对流的温度分层的动态模型,用MATLAB实现了一个通用的低温储罐的温度分层现象模拟程序,该模型可以模拟常重力以及重力增加和减少条件下储罐内部温度分层结果. Fu等[27]采用数值计算的方法,对部分填充的圆柱肋式液氢储罐在不同肋间距比下的自增压过程进行了研究. 利用商业软件FLUENT进行计算,选取了流体体积法和相变模型,并通过自定义函数对模型进行适当修改,建立了用于预测储罐内部流体流动和传热的求解方案. 随后Fu等[28]对低温储罐在微重力条件下的蒸发及其对蒸汽压的影响进行了数值研究,研究了表面张力、气泡接触角和重力等因素的影响. 李佳超等[29]以液氮为研究工质利用透明玻璃搭建的低温储罐自增压实验系统,研究了自增压过程压力和温度的变化规律及填充比对压力和温度变化过程的影响. 2018年王夕等[30]使用FLUENT软件进行数值模拟,对比研究了4种相变模型对微重力环境中液氢推进剂受热蒸发过程的影响,并与国外探空火箭试验数据进行比较,分析对比了4种相变模型各自的优劣. 李鹏等[31]以液氢、液氧等低温推进剂为研究对象,开展控制低温推进剂在储罐内部因受热而蒸发的现象,通过对不同条件下的蒸发量控制效果的对比分析,为今后航天器推进剂储罐的设计提供参考依据. 郭志钒等[32]分析了高压储氢、低温液态储氢、金属氢化物储氢等3种储氢方式各自的优缺点与发展现状,为未来发展提供新的思路. 马原等[33]采用CFD方法建立两相流模型,对微重力条件下在液氢储罐内喷射过冷流体实现储罐降压的过程开展数值模拟研究,对比计算了不同喷射区域、喷射流量、喷射速度等对罐内温度场分布与压力变化的影响,认为气-$\!$-液相区喷射降压性能优于单独区域喷射,液相区喷射降压效果最弱. 2019年王舜浩等[34]利用数值方法研究了液氢缩比储罐内部流体的蒸发性质,通过与已有的实验数据对比构建了基于VOF两相流模型以及(level-set)界面跟踪方法的储罐内部流体流动和相变传热传质模型框架,为模拟液氢储罐地面停放阶段的热物理过程提供了参考. Zuo等[35]建立了一个喷嘴可旋转的三维液氢储罐模型,利用CFD方法研究了低温射流对零重力条件下热分层的影响,结果表明可旋转的喷嘴可以很有效的抑制罐体内部的热分层现象. Guo等[36]采用二维缩比模型储罐研究了低温射流消除热分层现象中喷头形状、位置以及射流速度对消除效果的影响,认为圆形射流喷嘴相较于半球形射流喷嘴消除效果更好. Zhang等[37]研究了一种效率高,界面清晰, 适用于三维模型的计算气液两相界面迁移特性的欧拉运动界面追 踪方法, 该方法将`米'状相邻单元Youngs方法用于运动界面重构, 将Youngs-VOF和水平集通过几何方法耦合, 提高运动界面精度, 克服了VOF和水平集方法存在的缺陷, 避免了利用高阶导数本身的稳定性去求解水平集对流方程和距离函数方程,为今后将热分层现象的研究拓展到三维以及两相流提供了思路.
由上可知国内外学者已经在该问题上进行了很多有益尝试并且取得了一定进展,但是以往的研究大多假定储罐壁表面均匀漏热,因此在整个罐壁上采用均匀热量边界条件,并且在计算时认为边界漏热和低温射流是同时进行的,通过对比低温射流一段时间后储罐内部的最高温度判断低温射流系统增压控制性能的优劣. 储罐罐体一般为金属材料并且在表面覆盖多层绝热材料,尽管如此,实际使用中还是无法完全消除热量渗入. 罐体表面因为结构装置等的差异,通过储罐壁渗入液体推进剂的热量并不是均匀分布的. 相对于罐体其他位置,通过易漏热的区域渗入罐体的热量对推进剂的热分层有着更大影响. 目前对于储罐局部漏热导致的热分层现象的低温射流消除系统的设计分析研究还不够充分,因此本文主要研究了大尺寸储罐在局部区域漏热情形下储罐内部出现的明显热分层,并对比研究了低温射流喷嘴的形状及其在储罐内部的相对位置等因素对利用低温射流消除热分层效果的影响.
1 计算模型
1.1 物理模型
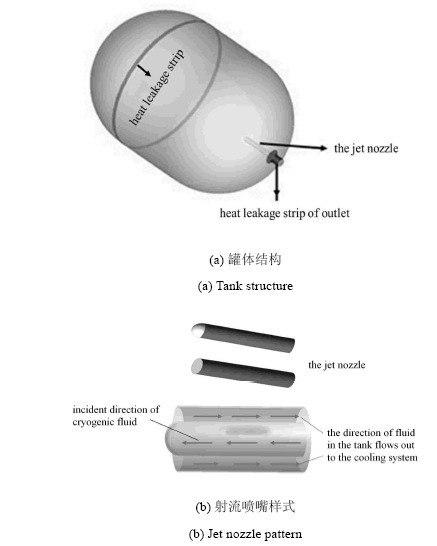
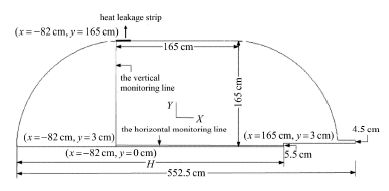
热分层控制系统模型由罐体结构和入射结构组成, 如图1所示. 低温射流由储罐内部的射流喷嘴射出,与储罐内部流体发生混合和热交换;另一方面储罐内部流体从罐体出流口导出,经过储罐外制冷系统(本文忽略)处理成低温流体重新流回储罐内部,形成一个消除热分层的闭环机制. 本文主要研究罐体局部漏热的情况,并考虑罐体出流口作为储罐与外部系统的衔接段易发生漏热的工程经验,假定罐体表面的条状区域及出口为漏热带(见图2),罐体其他区域视为绝热情况. 本文数值模拟采用二维轴对称模型,储罐各部分具体尺寸见图2;采用液氢为研究工质,填充率保持为100${\%}$. 本文通过改变射流喷嘴的形状以及射流喷嘴在储罐内部的相对位置,研究不同低温射流条件对储罐内部流体流动和温度分布时空演 化过程的影响.
图1
图1
罐体结构及射流喷嘴样式示意图
Fig.1
Schematic diagram of tank structure and jet nozzle pattern
图2
图2
储罐几何尺寸及监测线示意图
Fig.2
Schematic diagram of the cryogenic storage tank and inspection line
1.2 数学模型
1.2.1 控制方程
假设流体是不可压缩的并且具有恒定的热物理特性. 在微重力条件下忽略重力和浮力的影响,因而在圆柱坐标系中整个计算域内的质量守恒、动量守恒和能量守恒控制方程如下:
(1) 连续方程
(2) 动量方程
其中
其中,$\mu $为动力学黏性系数,由工质物理特性决定,$\mu _t $为湍流黏性系数,是空间坐标的函数,取决于流动状态而非物性参数, $\mu _{\rm t}$为湍流黏性系数,是由湍动能$k$及耗散率确定$\varepsilon $,表达式如下所示
其中模化常数$C_\mu = 0.09$.
(3) 能量方程
其中$pr_{t} \approx 0.85$.
1.2.2 湍流模型
采用雷诺时均模型对湍流进行模拟. 为了使方程封闭,引入了新的未知量湍动能$k$以及耗散率$\varepsilon $. Abid[38]对受限冲击低温射流以及受限对冲低温射流进行了数值模拟实验研究,认为采用AB型低雷诺数$k$-$\varepsilon$湍流模型可以很好的对低温射流进行数值模拟,因此本文采用AB低雷诺数$k$-$\varepsilon$湍流模型,其$k$-$\varepsilon$模式方程以及涡黏性如下所示
其中,$G_{k}$表示由于平均速度梯度而产生的湍流动能
$D_{k} $表征湍动能在黏性层中各项异性衰减的影响, 在AB模型中
其他模块常数如下
其中$Re_{t}$为湍流雷诺数,表达式如下
1.2.3 边界条件以及初始条件
在入射口截面上
在对称轴上
在罐壁漏热带上
在罐体其他壁面以及导管壁面上
初始时刻,罐内流体温度
出流口处边界为自由出流条件.
2 数值模拟
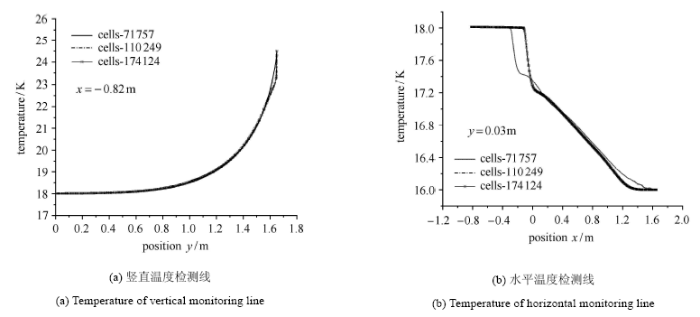
上述控制方程的求解通过国际通用的CFD模拟软件Fluent 17.0进行计算,整个计算域通过ICEM生成网格,在壁面附近网格加密,使用SIMPLE(semi-implicit method for pressure-linked equations)算法求解,迭代过程采用绝对收敛标准进行控制,能量项的残差值设定为${10}^{-9}$,其他各项设为${10}^{-5}$. 本文 采用3种网格数目分别为71 757,110 249,174 124,开展了网格无关性检验. 如图2所示, 在计算域上温度梯度较大的位置选取了水平监测线和竖直监测线. 图3显示了网格无关性检验的结果,可以发现沿竖直监测线3种网格数下的温度分布基本一致;沿水平监测线两种较细网格的温度分布没有明显差异,但在靠近低温射流喷嘴位置处与粗网格下的温度分布有明显差异. 由此,之后的研究采用网格数量110 426以同时兼顾计算准确性和计算量.
图3
3 结果讨论
主要研究了圆形射流喷嘴(C)在储罐内部不同位置时利用低温射流消除热分层的效果,并选取了射流喷嘴所在典型位置与半球形射流喷嘴(H)进行了对比. 表2列出了各工况进行数值计算时的具体参数设置.
3.1 圆形射流喷嘴
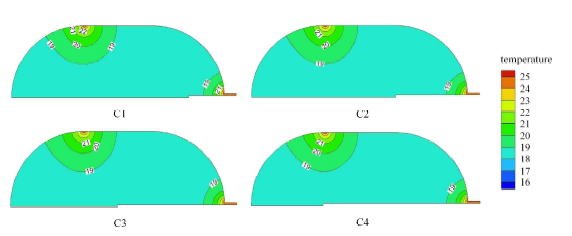
采用圆形射流喷嘴进行研究,其中低温射流速度沿喷嘴表面均匀分布,将无射流情况下漏热持续30 d(2 592 000 s)后储罐内部的温度场分布作为射流开始的初始状态($t=0$ s). 如图4所示,可以发现此时储罐内部流体以漏热带为中心出现了明显的环形热分层现象. 射流喷嘴在储罐内部的相对位置对初始热分布没有明显影响,4种工况中的热分布基本一致.
图4
图4
各工况初始时刻温度云图分布
Fig.4
Isothermals of the initial state ($t=0$ s) for the cryogenic jet
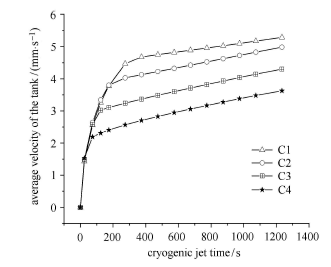
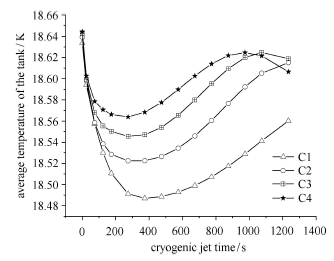
对于在漏热带施加温度边界条件模拟储罐壁面局部漏热的情形,漏热带上的热量传输速率可以表征漏热带附近的温度分布. 热量 传输速率指单位时间通过漏热带进入罐体的热量,其值越大说明漏热带附近区域温度越低. 图5给出了射流时间持续约1 200 s后各工况条状漏热带热量传输速率随时间演化图. 可以看出在不同时间段,低温射流喷嘴与漏热带的相对位置对于漏热带附近 高温区域的热量传输速率存在显著影响. 按照各工况漏热带热量传输速率的差异大体可以将射流过程分为3个阶段. 第一阶段(0$\sim$100 s),对任意一种工况,由于低温射流时间较短,通过射流进入罐体内部的冷流体都无法直接影响条状漏热带附近区域. 冷流体在罐内作用区域非常有限,因此各工况条状漏热带热量传输速率曲线基本重合. 图6给出了低温射流进行64.08 s后各工况储罐内部的温度云图分布. 可以看出低温流体主要分布在射流喷嘴附近,距离条状漏热带附近的高温区域较远. 此阶段储罐内抑制热分层发展主要依靠罐内流体由出流口经过罐外冷却系统实现. 此时出流口附近的的温度存在明显下降. 图7给出了该时刻各工况的流场图,可以看出施加低温射流之后,会在射流喷嘴附近形成涡流,由于射流喷嘴位置的差异,涡流在储罐内部的位置有所不同,因此储罐内部流场存在差异,但总体而言在低温射流初期,各工况抑制热分层的效果差异不大. 对比图4初始时刻各工况温度云图分布,可以发现条状漏热带附近高温区域的热分层形态没有发生明显变化,而出口位置的热分层明显被消除. 在第二阶段(100$\sim$700 s),各工况低温射流持续到424.08 s时的温度云图(图8)表明工况C1和C2中条状漏热带附近热分层形态与第一阶段相比发生了轻微的变化. 由射流喷嘴进入到罐体内部的冷流体(温度介于16$\sim$18 K的低温流体)作用范围进一步扩大,在罐体沿着轴线形成了冷流体柱. 工况C3和C4中条状漏热带附近高温区域的热分层形态相较于第一阶段则发生了显著的变化. 冷流体已经在罐底聚集并沿着储罐壁面内卷. 漏热带附近高温区域热分层的形态和该时刻各工况中涡流的位置有很大的关系. 总体而言,热分层的延展方向与对应位置的流体流动方向是一致的. 由于从低温射流开始C3和C4两种工况形成的涡流相对于C1和C2更靠近罐体底部,长时间作用之后,靠近对称轴的热分层随着顺时针方向流动的流体而向左延展. 图9给出了低温射流进行到424.08 s时的流场图. 可以看出,各工况涡流都沿对称轴运动到罐体底部. C1中形成的涡流在罐体内部的流动区域范围相对于其他工况更广,整体性更强,能够更大范围带动罐内流体的混合,结合图5可以发现这一时段,C1中漏热带热量传输速率高于其他工况,并且各工况整体上满足随着射流喷嘴伸入罐体内部长度的增加,漏热带热量传输速率逐渐降低. 这和图10给出的各工况储罐内部流体平均速度随低温射流时间演化曲线图变化趋势是一致的,射流初期各工况储罐内部流体平均速度都快速上升,但工况间没有明显差异. 低温射流持续100 s之后,罐体内部流体平均速度随着射流喷嘴伸入罐体内部长度的增加而逐渐减小. 图11给出了储罐内部流体平均温度随低温射流时间的演化曲线,可以发现各工况储罐内部流体平均温度的差异也主要是在低温射流持续100 s之后形成的,整体上各工况平均温度都经历了先快速降低然后逐渐回升的过程,同样由于储罐内部流场整体性的差异,在同一低温射流时刻,随着射流喷嘴伸入罐体内部长度的增大,罐体内部流体平均温度逐渐减小.
图5
图5
圆形射流喷嘴漏热带热量传输速率随时间演化图
Fig.5
Evolution diagram of the heat transfer rate with cryogenic jet time in the circular jet nozzle
图6
图6
各工况低温射流64.08 s时温度云图分布
Fig.6
Isothermals of cases at $t=64.08$ s for the cryogenic jet
图7
图7
各工况低温射流64.08 s时流场图
Fig.7
Flow field diagram at $t=64.08$ s for the cryogenic jet
图8
图8
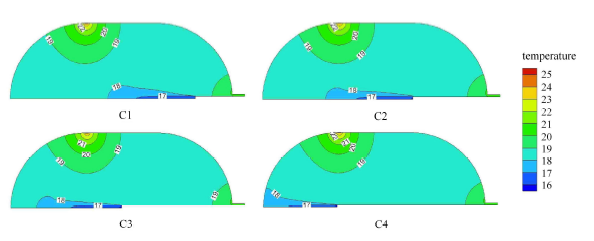
各工况低温射流424.08 s时温度云图分布
Fig.8
Isothermals of cases at $t=424.08$ s for the cryogenic jet
图9
图9
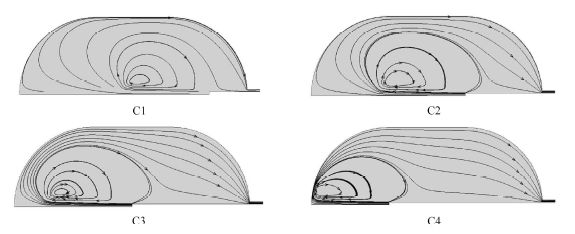
各工况低温射流424.08 s时流场图
Fig.9
Flow field diagram at $t=424.08$ s for the cryogenic jet
图10
图10
圆形低温射流喷嘴储罐平均速度随低温射流时间演化图
Fig.10
Evolution diagram of the average velocity of the tank with the cryogenic jet time in the circular jet nozzle
图11
图11
圆形低温射流喷嘴储罐平均温度随低温射流时间演化图
Fig.11
Evolution diagram of the average temperature of the tank with the cryogenic jet time in the circular jet nozzle
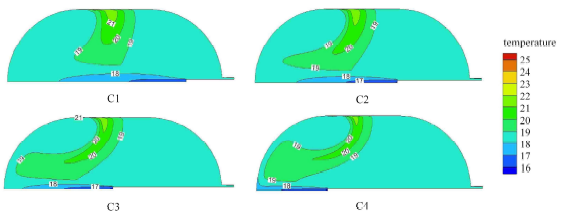
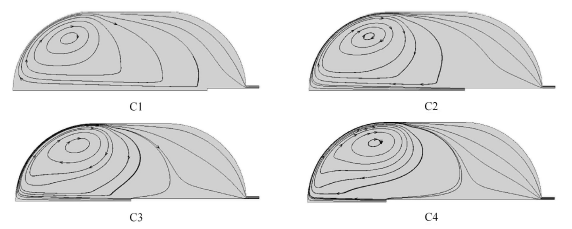
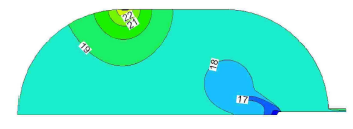
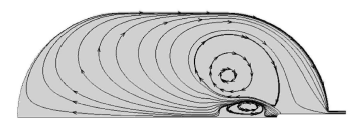
在第三阶段(700 $\sim$1 200 s),由低温射流持续1 024.08 s时的温度云图(图12)可以发现,该时刻各工况热分层的形态都发生了显著变化,由最初低温射流初始时刻的环形分层演变成不规则的带状分层. 对比第二阶段的温度云图分布(图8),可以发现由射流喷嘴进入罐体内部的带状冷流体分布范围并没有继续在罐体底部聚集或沿罐壁攀升,反而相对于上一阶段有所减少,一方面是因为随着罐体内部流体流速的增加(图10),低温流体很快被输运到罐体其他位置发生热交换,无法沿对称轴附近积聚延伸发展,另一方面随着漏热时间的延长以及漏热带热量传输速率的快速升高(图5),罐内流体温度总体逐渐上升(图11),射流喷嘴附近的流体温度也有所上升,通过射流喷嘴进入罐体的冷流体在射流喷嘴附近就会发生热交换. 事实上由罐体内部流体平均温度的变化曲线(图11)表明,在低温射流持续400 s左右时,各工况罐体内部平均温度都达到极小值,随后温度开始上升,从能量角度来看,表明在400 s左右从储罐内部输出的热量和从外界环境输入罐体内部的热量达到了平衡,从储罐内部输出的热量包括由射流喷嘴进入罐体内部的冷流体携带的热量(负值)和通过储罐出口出流的流体携带的热量,而从外界环境输入罐体内部的热量主要包括通过条状漏热带和出口现阶段漏热带进入罐体内部的热量. 在低温射流初期,输入罐体内部的热量值小于输出罐体内部的热量,罐体内部流体平均温度逐渐降低,而低温射流后期则反之. 图13给出了各工况低温射流1024.08 s时流场图,可以发现各工况形成的涡流流动范围都已经扩大到足够覆盖条状漏热带附近的高温区域,结合图5可得,在这一阶段各工况条状漏热带热流传输速率先后开始迅速提高,这是因为罐体内部的涡流演化使得涡流中心区向条状漏热带附近移动,而涡流的中心区类似于一个滞留区,从产生开始就携带着低温流体,涡流中心区与邻近区域的热量交换进行的很慢,当其移动靠近条状漏热带边界后,条状漏热带因为附近区域存在冷流体团,热量传输速率显著加快. 射流喷嘴越靠近罐体底部,由低温射流引起的涡流中心区越容易到达条状漏热带附近,因此各工况中条状漏热带热量传输速率曲线快速增长的先后顺序是C4, C3, C2, C1. 在涡流中心区靠近条状漏热带一段时间后,随着低温射流时间的进行,涡流中心区温度也会因为热交换而上升, 此后通过条状漏热带进入罐体的热量传输速率就会减慢,而从罐体内部输出的热量在增加,因此罐体内部流体平均温度就会开始下降(图11 中C3和C4曲线).
图12
图12
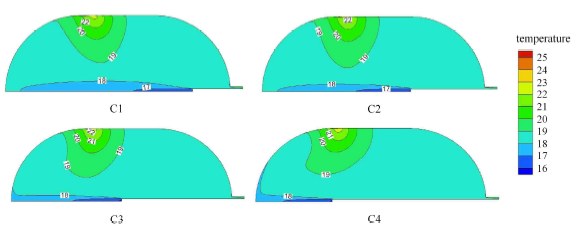
各工况低温射流1 024.08 s时温度云图分布
Fig.12
Isothermals of cases at $t=1 024.08$ s for the cryogenic jet
图13
图13
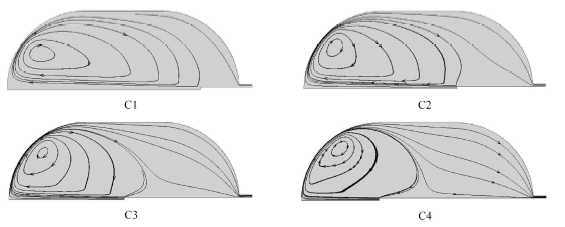
各工况低温射流1 024.08 s时流场图
Fig.13
Flow field diagram at $t=1 024.08$ s for the cryogenic jet
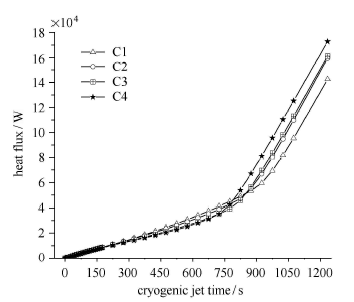
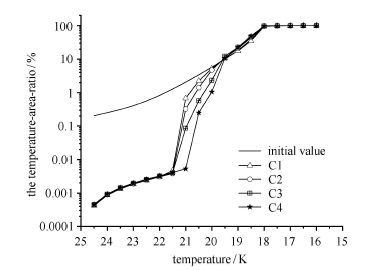
通过以上分析可知4种工况对条状漏热带附近高温区域的作用机理是一致的,但由于射流喷嘴在罐内位置的不同,发挥作用的时间有所不同. 整体而言,低温射流抑制热分层的机理主要有两种,一种是在射流早期,通过促进储罐内部流体运动,避免热量在储罐内部局部区域大量积聚形成高温区域,包括上文中第一和第二阶段;另一种则是低温射流持续发展一段时间,因为储罐内部流场演化,射流引起的携带着低温流体的涡流中心移动到条状漏热带附近与高温区域进行热量交换. 结合各工况各时间段的流场图,可以发现在射流初期,涡流中心区位于射流喷嘴附近并沿着中轴线向罐底运动,此时低温射流对条状漏热带附近高温区域影响较小,然后罐体内部流场逐步发展,涡流中心区沿着罐体壁面爬升向条状漏热带移动,因此条状漏热带热量传输速率有了显著提高,在涡流中心区吸收从漏热带进入的热量逐渐升温之后,漏热带的热量传输速率会逐渐稳定. 通过对图5中各条曲线对时间积分得到各工况漏热带传输热量随时间演化图(图14),可以看出工况C4在整个低温射流时间内转移热量的能力更强. 结合图15给出的温度区间面积占比累计图(温度区间面积占比是指将计算域温度范围每隔0.5 K设置为一个温度区间,统计位于各温度区间的计算域面积占总计算域面积的百分比并绘制成累计图)发现在低温射流结束时,各工况介于21.5 $\sim$ 25 K之间的温度占比基本一致,但是19 $\sim$ 21.5 K之间的温度占比C4明显低于其他工况,也就是说明工况C4消除高温区域的效果更彻底,作用更明显,这和通过漏热带传输热量作为判据得出的结论是一致的.
图14
图14
圆形射流喷嘴各工况漏热带传输热量随时间演化图
Fig.14
Evolution diagram of heat flux over time for each circular nozzle case
图15
图15
圆形射流喷嘴各工况温度区间面积占比累计图
Fig.15
Comparison of the cumulative curve of the temperature-area-ratio for each circular nozzle case
3.2 两种射流喷嘴形状对比
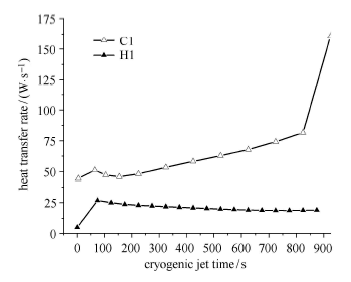
基于小尺寸储罐(直径70 mm)的研究[38]表明:圆形射流喷嘴因为出流方向更集中,罐体内部流场演化更剧烈,因此消除热分层的效果优于半球形射流喷嘴.在结果讨论中发现对于大尺寸液氢储罐,圆形射流喷嘴在罐内位置对热分层的消除机理是一致的,只是作用时间存在差异. 相对而言,靠近储罐出口的位置能包含其他工况罐体内部流体流场演变过程,因此 以两种射流喷嘴在靠近出口的位置时消除热分层的效果为例进行对比分析, 即工况C1和H1.半球形射流喷嘴截面半径同为5.5 cm,为了保持圆形射流喷嘴相同入射质量流量,将射流速度设为0.05 m/s, 其他设定与圆形射流喷嘴情况一致. 计算并绘制两种射流喷嘴漏热带热量传输速率随低温射流时间演化曲线(图16)通过对比可以发现,圆形射流喷嘴消除热分层的效果明显高于半球形射流喷嘴. 图17和图18分别给出半球形射流喷嘴在低温射流进行424.08 s时的温度云图以及流场图,从温度云图可以看出低温流体都聚集在射流喷嘴附近,对条状漏热带附近高温区域影响很小. 从流场图可以发现半球形射流喷嘴形成的涡流发展缓慢,无法将低温流体输运到条状漏热带附近的高温区域,罐体内部热分层抑制主要依靠流体流动使得热量无法聚积,因此消除热分层的效果不如圆形射流喷嘴.
图16
图16
圆形与半球形射流喷嘴热分层消除效果对比图
Fig.16
Contrast diagram of temperature stratification of circular and hemispherical jet nozzles
图17
图17
工况H1在低温射流424.08 s的温度云图
Fig.17
Isothermals of H1 at $t=424.08$ s for the cryogenic jet
图18
图18
工况H1在低温射流424.08 s的流场图
Fig.18
Flow field diagram of H1 at $t=424.08$ s for the cryogenic jet
4 结论
本文利用轴对称的具有低温射流装置的零蒸发储罐模型,通过数值模拟研究了微重力条件下液氢储存过程中利用低温射流消除环境漏热引起的热分层现象的效果. 通过分析储罐内部流场流动和温度分布的时间演化过程,研究了射流喷嘴在罐内不同位置对利用低温射流消除储罐内部热分层效果的影响. 研究结果表明:对于大尺寸储罐,当采用圆形射流喷嘴且低温射流条件相同时,射流喷嘴的位置对罐体内部热分层消除效果影响不是很明显,在本文的入射条件下,当低温射流置换率达到2${\%}$,即低温射流时间持续700 s时,罐体内部热分层的消除效果最显著;同时,当射流喷嘴位于储罐内部同一相对位置且入射流量相同时,圆形射流喷嘴因出流方向更集中,罐内流场演变更快,热分层消除效果比半球形射流喷嘴更好.
参考文献
An overview of NASA efforts on zero boiloff storage of cryogenic propellants
Control of the thermodynamic state of space-stored cryogens by jet mixing
Finite difference solution of stratification and pressure rise in containers. Tech. rep
Three-dimensional analysis for liquid hydrogen in a cryogenic storage tank with heat pipe-pump system
Nozzle injection displacement mixing in a zero boil-off hydrogen storage tank
Forced convective mixing in a zero boil-off cryogenic storage tank
Analysis of natural convection in liquid nitrogen under storage conditions
Numerical and experimental comparisons of the self-pressurization behavior of an LH2 tank in normal gravity
Influence of surface evaporation on stratification in liquid hydrogen tanks of different aspect ratios
Analytical model for cryogenic stratification in a rotating and reduced-gravity environment
Experimental and numerical investigations of fluid flow and heat transfer in a cryogenic tank at loss of vacuum
Numerical study of zero boil-off storage system with heat pipe and pump-nozzle unit
Optimizing design of a new zero boil off cryogenic storage tank in microgravity
Parameter study of the injection configuration in a zero boil-off hydrogen storage tank using orthogonal test design
Numerical study of transient natural convection in a pressurized LNG storage tank
CFD investigation of thermal and pressurization performance in LH2 tank during discharge
Transient thermal and pressurization performance of LO2 tank during helium pressurization combined with outside aerodynamic heating
Temperature stratification in a cryogenic fuel tank
Influence of wall ribs on the thermal stratification and self-pressurization in a cryogenic liquid tank
Influence of phase change on self-pressurization in cryogenic tanks under microgravity
液氮贮箱自增压实验与数值仿真
Experiment and numerical simulation of liquid nitrogen tank self pressurization
微重力下低温贮箱内推进剂相变仿真模型研究
Computational research on phase change model for cryogenic propellant in microgravity
推进飞行器低温推进剂在轨贮存被动蒸发控制方案研究
Investigation on passive boil-off control scheme for orbital storage of cryogenic propellant in orbital transfer spacecraft
低温液氢储存的现状及存在问题
Status and problems of cryogenic liquid hydrogen storage
液氢贮箱微重力喷射降压特性数值模拟研究
Numerical investigation on performance of spraying pressure control technique for liquid hydrogen tank at microgravity
液氢缩比贮箱蒸发特性数值模拟及实验验证
Numerical simulation and experimental validation of evaporation characteristics of scaled liquid hydrogen tank
Thermal stratification suppression in reduced or zero boil-off hydrogen tank by self-spinning spray bar
低温射流抑制空间液氢储罐温度分层的数值研究
Thermal destratification in hydrogen propellant tank in space by jet injection
一种基于几何重构的Youngs-VOF耦合水平集追踪方法
An interface tracking method of coupled youngs-vof and level set based on geometric reconstruction
Assessment of two-equation turbulence models for predicting transitional flows