引言
近年来, 世界航空界正着力发展具有飞行环境(如高度、速度、气候等)自适应、可执行多种任务(如巡航、盘旋、机动等)的变体飞行器. 这类飞行器可根据飞行任务需要自主改变结构和气动布局, 在复杂的飞行环境条件下保持良好的飞行性能[1 -5 ] . 在众多变体飞行器设计方案中, 折叠翼变体飞行器因满足多任务作战需求和提高单任务执行效率的优势, 受到了广泛的关注. 然而, 在机翼受控变体过程中, 不仅非定常气动力会随着机翼形状改变而发生变化, 机翼的惯性、弹性和阻尼特性也同时发生变化, 极易诱发不同结构模态参与的参变颤振现象, 给变体飞行器的飞行安全带来挑战. 针对不同折叠构型下变体机翼的气动-结构耦合动力学系统的参变特性, 如何建立以折叠角为参数的参数化气动弹性模型, 在全参数空间内实现气动弹性力学行为的高效、高精度预测, 是变体飞行器研制过程中亟待解决的动力学问题.
当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法.
上述气动弹性动力学建模方法虽已经成功应用到可折叠式变体机翼的气动弹性建模中,但在气动弹性分析过程中仍需要针对不同折叠角进行重复地结构动力学建模、非定常气动力计算以及流固耦合建模, 计算效率低下且难以分析可折叠式变体机翼在完整参数空间内的气动弹性力学行为. 参数化气动弹性建模方法为高效、高精度分析可折叠式变体机翼的气动弹性力学行为提供了新的解决方案. Zhao等[20 ] 和倪迎鸽等[21 ] 采用子结构综合和偶极子网格法构建了折叠翼的参数化气动弹性模型, 分析了模态阻尼、折叠角、铰链刚度对折叠翼动力学特性的影响. Huang等[22 ] 提出了一种参数化的气动伺服弹性建模方法, 高效地获得了不同折叠角下的机翼气动伺服弹性数学模型, 实现了颤振主动抑制的控制律设计和闭环气动伺服弹性分析.
然而, 上述参数化建模方法均基于子结构综合方法, 即根据折叠过程中内外翼结构动力学模型在全局坐标系中的约束关系, 采用坐标变换实现全局坐标系下折叠翼结构动力学的快速生成. 该参数化建模方法并未从根本上解决不同折叠构型下模态坐标不一致的难题. 本文基于流形切空间插值方法, 建立以折叠角为参数的折叠翼参变结构动力学模型, 并耦合基于偶极子网格法的参数化非定常气动力模型, 进而建立折叠翼的参变气动弹性模型. 为了验证该参数化模型的准确性, 本文选取一小展弦比折叠翼模型为研究对象, 通过对结构自由振动分析和颤振边界的预测, 考核本文提出的参数化建模方法.
1 折叠翼参数化气动弹性建模
不同于常规机翼的气动弹性分析, 折叠翼的气动弹性分析需要在每一个角度重新建立结构动力学模型和气动模型, 并将之耦合得到气动弹性模型. 为了高效、准确地分析折叠翼的气动弹性力学行为, 本节介绍基于流形切空间插值的参数化气动弹性建模方法. 模型建立过程分为参数化结构动力学建模、参数化气动力建模和参数化气动弹性建模3部分.
1.1 折叠翼模型描述及参数化建模目标
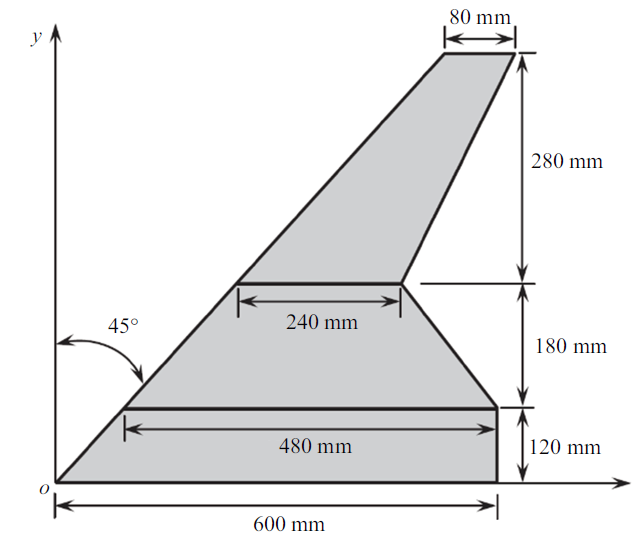
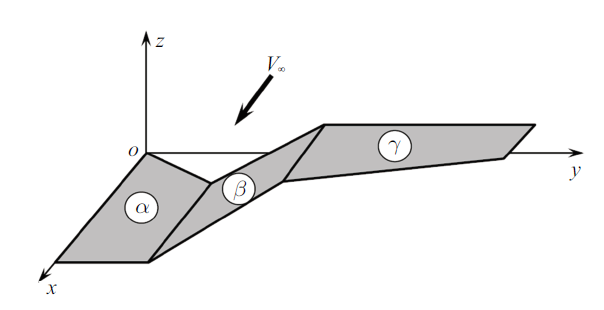
折叠翼的几何构型如图1 所示, 折叠翼由机身和两个能独立旋转的内外翼组成. 折叠翼折叠过程如图2 所示 (下标$\alpha $, $\beta$和$\gamma $分别表示机身结构、内翼结构和外翼结构). 内翼可以进行0$^\circ$ $\sim$ 120$^\circ$的旋转, 同时外翼始终保持水平. 机身和内外翼的材料均为铝板, 其杨氏模量为71 GPa, 泊松比为0.33, 密度为$2.7\times 10^{3}$ kg/m$^{3}$, 厚度分别为2.0 mm, 1.0 mm和1.0 mm.
图1
图1
折叠翼几何尺寸及构型
Fig.1
Configuration of folding wing
图2
图2
折叠翼折叠过程
Fig.2
Morphing process of folding wing
通过有限元方法得到折叠翼机身、内翼和外翼的质量、刚度矩阵, 然后通过子结构综合法[23 -24 ] 得到折叠翼结构动力学方程如下
(1) $\begin{eqnarray} \label{eq1} {M}(\theta ){\ddot{{x}}}(t)+{K}(\theta ){x}(t)={\bf 0} \end{eqnarray} $
式中, $\theta $是折叠角, ${M}(\theta )$是折叠翼的质量矩阵, ${K}(\theta )$是折叠翼的刚度矩阵, ${x}(t)\in {R}^{n}$为物理坐标, 值得注意的是, 本文没有考虑折叠翼的结构阻尼. 因为实际飞行器的阻尼特性难以获得, 所以建立参数化的阻尼模型更加困难. 由结构动力学方程可以得到折叠翼的振型矩阵$\varPhi (\theta )=\left[ {\varphi_{1} (\theta )} \ \ {\varphi_{2} (\theta )} \ \ \cdots \ \ {\varphi_{n} (\theta )} \right]$, 取$\varPhi (\theta )$前$m$列得到降阶矩阵$\varphi (\theta )=\left[ {\varphi_{1} (\theta )}\ \ {\varphi_{2} (\theta )}\ \ \cdots \ \ {\varphi_{m} (\theta )} \right]$, 令${x}(t)=\varphi (\theta )\xi (\theta ,t)$, $\xi (\theta ,t)$是广义坐标, 同时对式(1) 左乘$\varphi (\theta )^{T}$, 得到折叠翼的低维结构动力学方程
(2) $\begin{eqnarray} \label{eq2} M_{r} (\theta )\ddot{{\xi}}(\theta ,t)+K_{r} (\theta )\xi (\theta ,t)={\bf0} \end{eqnarray} $
折叠过程中质量矩阵、刚度矩阵、振型矩阵和气动力矩阵都发生了显著变化, 如果要对折叠翼进行气动弹性分析, 就需要对每个折叠角进行重复有限元建模和气动力建模, 建模效率低下. 参数化建模即给出相应参数 (如折叠角$\theta )$ 能快速得到结构动力学模型和气动力模型, 这既能提高分析折叠翼气动弹性行为的效率, 也为后续折叠翼的颤振主动控制研究打下良好的基础.
1.2 基于流形切空间的结构动力学
矩阵流形是指具有特殊性质 (正定性、对称性、正交性或非奇异性)的矩阵组成的流形.在流形上插值得到的矩阵仍具有原矩阵的特殊性质. 正因为这一特点, 有学者提出基于流形矩阵的插值方法[25 -32 ] . 令$\left\{ {\theta_{i} } \right\}_{i=0}^{N-1} $表示由一系列折叠角度所组成的集合, 矩阵${P}_{i} $表示折叠角$\theta_{i} $对应的系统矩阵(如质量矩阵、刚度矩阵和振型矩阵), ${P}_{i} $张成的空间$S_{i}$可视为矩阵流形${\cal M}$上的一点. 参数化建模即对于一个新参数$\theta_{N}$, 获得其对应的矩阵${P}_{N} $. 显然, 矩阵流形插值是一个可行的方法, 但是通常矩阵流形不是"线性"的, 因此需要将矩阵流形上的点映射到"平直"的切空间, 在切空间中进行插值, 然后再从切空间映射回流形上, 其推导过程如下.
(1) 从集合$\left\{ {\theta_{i} } \right\}_{i=0}^{N-1} $中选取一点$\theta _{0} $作为插值过程中的原点. 具体而言, 即选取点$S_{0} $作为原点.
(2) 流形${\cal M}$在点$S_{0} $存在切空间$T_{S_{0} } {\cal M}$, $S_{i} $通过映射的方式由流形${\cal M}$投影到切空间$T_{S_{0} } {\cal M}$, 其投影点$X_{i} $对应的矩阵称为${\varGamma }_{i} $. 本文将点$S_{i} $映射到切空间$X_{i} $的过程称为对数映射$\log_{S_{0} } $, 对数映射对应的数学表达式为
(3) $\begin{eqnarray} \label{eq3} \log_{S_{0} } (S_{i} )=X_{i} \end{eqnarray} $
(3) 切空间$T_{S_{0}} {\cal M}$是"平直"的向量空间, 因此矩阵${\varGamma}_{N} $可以由Lagrangian插值法对${\varGamma }_{i} $插值得到. 计算过程为
(4) $\begin{eqnarray} \label{eq4} {\varGamma}_{N} =\sum\limits_{i=1}^{N-1} {\prod\limits_{i\ne j}^{N-1} {\left(\frac{\theta_{N} -\theta_{i} }{\theta_{j} -\theta_{i} }\right)\varGamma }_{i} } \end{eqnarray} $
(4) 本文将点$X_{i} $映射到流形${\cal M}$的过程称为指数映射$\exp_{S_{0} } $, 指数映射对应的数学表达式为
(5) $\begin{eqnarray} \label{eq5} \exp_{S_{0} } (X_{i} )=S_{i} \end{eqnarray} $
图3 给出了流形切空间插值方法的示意图. 由于在参数化结构动力学建模中涉及两种不同流形, 上述的指数映射和对数映射使用抽象的数学表达形式, 下面将具体给出这两种不同流形的插值方法.
图3
图3
流形切空间插值示意图
Fig.3
Sketch map of manifold tangent space interpolation
在折叠翼低维结构动力学方程中, $M_{r} (\theta )$和$K_{r} (\theta )$均为SPD(symmetric positive definite)矩阵, 张成的空间为SPD流形. SPD流形的对数映射为
(6) $\begin{eqnarray} \label{eq6} \log_{S_{0} } ({P}_{i} )={logm}({P}_{0}^{-{1/2}}{P}_{i} {P}_{0}^{-{1/2}})={\varGamma }_{i} \end{eqnarray} $
(7) $\begin{eqnarray} \label{eq7} \exp_{S_{0} } ({\varGamma }_{i} )={P}_{0}^{{1/2}}\mbox{expm}({P}_{i} ){P}_{0} ^{{1/2}}={P}_{i} \end{eqnarray} $
式中, logm和expm分别指矩阵对数和矩阵指数.
在气动弹性计算中, 还有必要对振型矩阵${\varphi }(\theta )$进行参数化建模. 但是${\varphi }(\theta )$是$n\times m$维矩阵, 不再适用于SPD流形切空间插值. 同时${\varphi }(\theta)$的列向量表示折叠翼结构的某阶模态, 因此参数化振型矩阵的每一列也应该表示折叠翼的某阶模态. 为得到参数化振型矩阵, 本文引入约束矩阵${\phi }(\theta )$, 其满足约束条件
(8) $\begin{eqnarray} \label{eq8} {\varphi }(\theta )^{T}{\phi }(\theta )=I \end{eqnarray} $
式中$I$为$m$阶单位矩阵, 因为$n\gg m$, 所以满足条件的${\phi }(\theta )$有无数多个, 为了保证插值结果的唯一性, 本文选取${\varphi }(\theta )^{T}$的Moore-Penrose广义逆作为约束矩阵${\phi }(\theta )$.
Grassmann流形是一种特殊的流形, 其表示$m$维欧几里得空间中所有通过原点的$k$维平面的集合, 记作$G(k,m)$. ${\varphi }(\theta )$每一列张成的特征子空间$\left\{ {S_{ij}^{\varphi } } \right\}_{i=0}^{N-1} $都可以视作流形$G(1,N)$上一点, ${\phi }(\theta )$每一列张成的子空间也可以视作流形$G(1,N)$上一点. 与质量矩阵插值不同, 振型矩阵插值是对每一列进行插值, 然后将插值得到的列向量组合起来, 下面介绍振型矩阵的参数化建模方法(对于$j=1, 2, \cdots ,N)$.
(1) 对特征子空间$\left\{ {S_{ij}^{\varphi } } \right\}_{i=0}^{N-1} $进行插值, Grassmann流形对应的对数映射为
(9) $\left[{I}_{N} -{\varphi }_{0j} ({\varphi }_{0j}^{T} {\varphi }_{0j} )^{-1}{\varphi }_{0j}^{T}\right]{\varphi }_{ij} \left({\varphi }_{0j}^{T} {\varphi }_{0j} \right)^{-1}\left({\varphi }_{0j}^{T} {\varphi }_{0j} \right)^{{1/2}} =U_{i} \varSigma_{i} W_{i}^{T}\ \ \text{(thin SVD)} $
(10) $\log_{S_{0} } (S_{ij} )=U_{i}\tan^{-1}(\varSigma_{i} )W_{i}^{T} ={\varGamma }_{i} $
(11) ${\varGamma }_{i} =U_{i} \varSigma_{i} W_{i}^{T} \ \ \text{(thin SVD)} $
(12) $\exp_{S_{0} } (X_{i} )= {\varphi }_{0j} ({\varphi }_{0j}^{T} {\varphi }_{0j} )^{-{1/2}}W_{i} \cos (\varSigma_{i} )+ U_{i} \sin (\varSigma_{i} ) $
式中, ${I}_{N} $表示$N$阶单位矩阵, ${\varphi }_{ij}$表示振型矩阵$\varphi (\theta_{i} )$对应的第$j$列$\varphi_{j} (\theta_{i})$, thin SVD与常规SVD方法不同, 其中$U_{i} $为$m\times n$维矩阵, $\varSigma _{i} $为$n\times n$维矩阵, $W_{i} $为$n\times n$维矩阵.
(2) 通过Gram-Schmidt正交化方法使得${\varphi }_{Nj} $满足正交约束条件${\varphi }_{Nj}^{T} {\phi }_{N} =0\;\;(l=1,2,\cdots ,j-1)$, 式中${\phi }_{ij} $表示${\phi }(\theta_{i})$的第$j$列.
(3) 与 (1) 中相似的方法对子空间$\left\{ {S_{ij}^{\phi } } \right\}_{i=0}^{N-1} $进行插值.
(4) 通过Gram-Schmidt正交化方法使得${\phi }_{Nj}$满足正交约束条件${\varphi }_{Nj}^{T} {\phi }_{Nl} =0\;\;(l=1, 2, \cdots ,j-1)$且满足${\varphi }_{Nj}^{T} {\phi }_{Nj} =1$.
(5) 对${\phi }_{Nj} $和${\varphi }_{Nj}$进行缩放使得其2范数大小与${\phi }_{ij} $和${\varphi }_{ij}$的2范数大小一致.最后得到参数化振型矩阵${\varphi }_{N} =\left[ {{\varphi }_{N1} } \ \ {{\varphi }_{N2} } \ \ \cdots \ \ {{\varphi }_{Nm} } \right]$.
1.3 参数化气动力建模
本文基于偶极子网格法 (DLM) 建立折叠翼的参数化非定常气动力模型. 偶极子网格法通过求解无量纲法洗速度与压差系数的函数来确定空气动力影响系数, 从而获得气动网格上的气动力, 计算方程如下
(13) $\begin{eqnarray} \label{eq13} {\bar{{W}}}_{3/4} ={D}_{aic} {\bar{{C}}}_{p} \end{eqnarray} $
式中, ${\bar{{W}}}_{3/4}$是机身、内翼、外翼的每个气动网格控制点处的无量纲法洗速度, ${\bar{{C}}}_{p} $是网格的压差系数, ${D}_{aic} $是空气动力影响系数矩阵, 与来流马赫数以及折合频率存在一定的函数关系. 对三段折叠翼模型, 每个升力面的压差系数可以由下式求出
(14) $\begin{eqnarray} \label{eq14} \left\{ {{\begin{array}{*{20}c} {{\bar{{C}}}_{p}^{\alpha } } \\ {{\bar{{C}}}_{p}^{\beta } } \\ {{\bar{{C}}}_{p}^{\gamma } } \\ \end{array} }} \right\}=\left( {{D}_{aic} } \right)^{-1}\left\{ {{\begin{array}{*{20}c} {{\bar{{W}}}_{3/4}^{\alpha } } \\ {{\bar{{W}}}_{3/4}^{\beta } } \\ {{\bar{{W}}}_{3/4}^{\gamma } } \\ \end{array} }} \right\} \end{eqnarray} $
作用在机翼上的气动力即为动压、翼面面积和压差系数矩阵的乘积. 式 (14)中的法洗速度向量${\bar{{W}}}_{3/4}$与气动网格节点的位移${X}$有关. 对于内翼可以旋转的折叠翼模型, 其法洗速度向量${\bar{{W}}}_{3/4}$可以表示成折叠角角度和节点位移的函数.
${u}_{n}^{\alpha } $是从节点位移向量${X}$中提取出来的, 机身$\alpha $上网格节点的法向位移
(15) $\begin{eqnarray} \label{eq15} {u}_{n}^{\alpha } ={G}_{n}^{\alpha } {X} \end{eqnarray} $
通过样条插值, 空气动力网格点的位移${u}_{a(1/2)}^{\alpha }$以及沿流向倾斜角${u}_{\alpha (1/2)}^{\alpha } $与${u}_{n}^{\alpha } $有关
(16) $\begin{eqnarray} \label{eq16} \left. {\begin{array}{l} {u}_{a(1/2)}^{\alpha } ={G}_{a(1/2)}^{\alpha } {u}_{n}^{\alpha } ={G}_{a(1/2)}^{\alpha } {G}_{n}^{\alpha } {X} \\ {u}_{\alpha (1/2)}^{\alpha } ={G}_{\alpha (1/2)}^{\alpha } {u}_{n}^{\alpha } ={G}_{\alpha (1/2)}^{\alpha } {G}_{n}^{\alpha } {X} \\ \end{array}} \right\} \end{eqnarray} $
${G}_{a(1/2)}^{\alpha } $和${G}_{\alpha (1/2)}^{\alpha }$是通过无限板样条法所求得的样条矩阵, 其目的是将有限元节点的位移转变成气动网格点的位移与斜率, 实现机翼的流固耦合过程. 同时, 空气动力单元控制点处的位移${u}_{a(3/4)}^{\alpha } $以及沿流向斜率${u}_{\alpha (3/4)}^{\alpha } $可以近似为
(17) $\begin{eqnarray} \label{eq17} \left. {\begin{array}{l} {u}_{a(3/4)}^{\alpha } \approx {u}_{a(1/2)}^{\alpha } +C_{\Delta }^{\alpha } u_{\alpha (1/2)}^{\alpha } \\ u_{\alpha (3/4)}^{\alpha } \approx u_{\alpha (1/2)}^{\alpha } \\ \end{array}} \right\} \end{eqnarray} $
(18) $\begin{eqnarray} \label{eq18} {C}_{\Delta }^{\alpha } =\frac{1}{4}\left[ {{\begin{array}{*{20}c} {x_{1}^{\alpha } } & & & \\ & {x_{2}^{\alpha } } & & \\ & & \ddots & \\ & & & {x_{n}^{\alpha } } \\ \end{array} }} \right] \end{eqnarray} $
符号$x_{i}^{\alpha }$表示第$i$个空气动力网格的顺气流局部平均弦长及网格点与控制点的距离. 于是可以得到气动网格控制点处的位移与节点位移的关系为
(19) $\begin{eqnarray} \label{eq19} \left. {\begin{array}{l} {u}_{a(3/4)}^{\alpha } =\left( {{G}_{a(1/2)}^{\alpha } +{C}_{\Delta }^{\alpha } {G}_{\alpha (1/2)}^{\alpha } } \right){G}_{n}^{\alpha } {X} \\[2mm] {u}_{\alpha (3/4)}^{\alpha } ={G}_{\alpha (1/2)}^{\alpha } {G}_{n}^{\alpha } {X} \\ \end{array}} \right\} \end{eqnarray} $
基于机翼升力面做谐波振荡运动的假设, 有如下离散形式的边界条件
(20) $\begin{eqnarray} \label{eq20} {\bar{{W}}}_{3/4}^{\alpha } =\frac{\partial {\bar{{u}}}_{a(3/4)}^{\alpha } }{\partial x}+\frac{{i}k}{b}{\bar{{u}}}_{a(3/4)}^{\alpha } \end{eqnarray} $
式中, $b$表示半弦长, 可以获得机身上无量纲法洗速度向量${\bar{{W}}}_{3/4}^{\alpha } $和结构节点物理位移${\bar{{X}}}$的关系
(21) $\begin{eqnarray} \label{eq21} && \bar{{W}}_{3/4}^{\alpha } =\bar{{u}}_{\alpha (3/4)}^{\alpha } +\frac{{i}k}{b}\bar{{u}}_{a(3/4)}^{\alpha } =\left[ {G_{\alpha (1/2)}^{\alpha } +\frac{{i}k}{b}\left( {G_{a(1/2)}^{\alpha } +C_{\Delta }^{\alpha } G_{\alpha (1/2)}^{\alpha } } \right)} \right]G_{n}^{\alpha } \bar{{X}} \end{eqnarray} $
同样地, 外翼的无量纲法洗速度${\bar{{W}}}_{3/4}^{\gamma }$和结构物理位移${\bar{{X}}}$的表达式如下
(22) $\begin{eqnarray} \label{eq22} {\bar{{W}}}_{3/4}^{\gamma } =\left[ {G_{\alpha (1/2)}^{\gamma } +\frac{{i}k}{b}\left( {{G}_{a(1/2)}^{\gamma } +{C}_{\Delta }^{\gamma } {G}_{\alpha (1/2)}^{\gamma } } \right)} \right]{G}_{n}^{\gamma } {\bar{{X}}} \end{eqnarray} $
在计算内翼表面的气动力时, 需要提取的也是法向的节点位移, 但当内翼的旋转后, 在局部坐标下的内翼节点法向位移却是其全局坐标系下$y$, $z$方向位移的函数. 于是通过${G}_{y}^{\beta } $和${G}_{z}^{\beta } $从位移向量$X$中提取出内翼节点的$y$, $z$方向的位移$u_{y}^{\beta } $和$u_{z}^{\beta } $
(23) $\begin{eqnarray} \label{eq23} u_{y}^{\beta } =G_{y}^{\beta } X,\ \ u_{z}^{\beta } =G_{z}^{\beta } X \end{eqnarray} $
将内翼$\beta $在局部坐标系下的法向位移写成与折叠角$\theta $有关的表达式
(24) $\begin{eqnarray} \label{eq24} && u_{n}^{\beta } =u_{z}^{\beta } \cos \theta -u_{y}^{\beta } \sin \theta =\left( {G_{z}^{\beta } \cos \theta -G_{y}^{\beta } \sin \theta } \right)X=G_{n}^{\beta } (\theta )X \end{eqnarray} $
(25) $\begin{eqnarray} \label{eq25} \left. {\begin{array}{l} u_{a(1/2)}^{\beta } =G_{a(1/2)}^{\beta } u_{n}^{\beta } =G_{a(1/2)}^{\beta } G_{n}^{\beta } (\theta )X \\[2mm] u_{\alpha (1/2)}^{\beta } =G_{\alpha (1/2)}^{\beta } u_{n}^{\beta } =G_{\alpha (1/2)}^{\beta } G_{n}^{\beta } (\theta )X \\ \end{array}} \right\} \end{eqnarray} $
使用离散形式的边界条件. 内翼的无量纲法洗速度可以写成
(26) $\begin{eqnarray} \label{eq26} \bar{{W}}_{3/4}^{\beta } =\left[ {G_{\alpha (1/2)}^{\beta } +\frac{{i}k}{b}\left( {G_{a(1/2)}^{\beta } +C_{\Delta }^{\beta } G_{\alpha (1/2)}^{\beta } } \right)} \right]G_{n}^{\beta } (\theta )\bar{{X}}\quad \end{eqnarray} $
将上文推导的各个翼段的法洗速度代入式(14) 中, 可以得到不同折叠角下机翼模型的完整压差系数矩阵
(27) $\begin{eqnarray} \label{eq27} && \left\{ {{\begin{array}{*{20}c} {{\bar{{C}}}_{p}^{\alpha } } \\[1.5mm] {\bar{{C}}_{p}^{\beta } } \\[1.5mm] {\bar{{C}}_{p}^{\gamma } } \\[1.5mm] \end{array} }} \right\}=\\&&\quad \left( {D_{aic} } \right)^{-1}\left( {{\begin{array}{*{20}c} {\left[ {G_{\alpha (1/2)}^{\alpha } +\dfrac{{i}k}{b}\left( {G_{a(1/2)}^{\alpha } +C_{\Delta }^{\alpha } G_{\alpha (1/2)}^{\alpha } } \right)} \right]G_{n}^{\alpha } } \\[2mm] {\left[ {G_{\alpha (1/2)}^{\beta } +\dfrac{{i}k}{b}\left( {G_{a(1/2)}^{\beta } +C_{\Delta }^{\beta } G_{\alpha (1/2)}^{\beta } } \right)} \right]G_{n}^{\beta } (\theta )} \\[2mm] {\left[ {G_{\alpha (1/2)}^{\gamma } +\dfrac{{i}k}{b}\left( {G_{a(1/2)}^{\gamma } +C_{\Delta }^{\gamma } G_{\alpha (1/2)}^{\gamma } } \right)} \right]G_{n}^{\gamma } } \\ \end{array} }} \right)X \\&&\quad \end{eqnarray} $
最后, 作用在空气动力网格上的气动力向量可由下式给出
(28) $\begin{eqnarray} \label{eq28} {F}_{aero} =q_{d} \left[ {{\begin{array}{*{20}c} {S^{\alpha } } & 0 & 0 \\[2mm] 0 & {S^{\beta } } & 0 \\[2mm] 0 & 0 & {S^{\gamma } } \\[2mm] \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} {\bar{{C}}_{p}^{\alpha } } \\ {\bar{{C}}_{p}^{\beta } } \\ {\bar{{C}}_{p}^{\gamma } } \\ \end{array} }} \right\} \end{eqnarray} $
其中, ${S}^{\alpha } $, ${S}^{\beta }$和${S}^{\gamma } $是三段机翼的面积. $q_{d} =\rho _{\infty } V_{\infty }^{2}/2$是动压, $\rho_{\infty } $是大气密度, $V_{\infty } $是来流速度.
采用DLM方法计算的气动力是作用于气动网格的1/4弦线的中点处, 如果气动力移动到网格点, 为了平衡就会产生一个气动力矩. 这个力矩${M}_{aero} $可以写成
(29) $\begin{eqnarray} \label{eq29} M_{aero} =q_{d} \left[ {{\begin{array}{*{20}c} {C_{\Delta }^{\alpha } } & 0 & 0 \\[2mm] 0 & {C_{\Delta }^{\beta } } & 0 \\[2mm] 0 & 0 & {C_{\Delta }^{\gamma } } \\[2mm] \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {S^{\alpha } } & 0 & 0 \\ 0 & {S^{\beta } } & 0 \\ 0 & 0 & {S^{\gamma } } \\ \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} {\bar{{C}}_{p}^{\alpha } } \\ {\bar{{C}}_{p}^{\beta } } \\ {\bar{{C}}_{p}^{\gamma } } \\ \end{array} }} \right\} \end{eqnarray} $
(30) $\begin{eqnarray} \label{eq30} \delta W_{a} =\delta u_{a(1/2)}^{T} F_{aero} -\delta u_{\alpha (1/2)}^{T} M_{aero} =\delta X^{T}F_{a} \end{eqnarray} $
${F}_{a} $是作用在结构网格点上的等效力向量, 于是我们得到了由气动力引起的作用在个有限元节点上的参数化的空气动力等效力, 如下
(31) $\begin{eqnarray} \label{eq31} && {F}_{a} (k,M_{\infty } ,\theta ,X)=q_{d} {G}_{n}^{T} (\theta )\left( {{G}_{a(1/2)}^{T} -{G}_{\alpha (1/2)}^{T} {C}_{\Delta } } \right)\cdot {S\bar{{D}}}_{aic} \Bigg[ {G}_{\alpha (1/2)} +\frac{{i}k}{b}( {G}_{a(1/2)} + {C}_{\Delta } {G}_{\alpha (1/2)} ) \Bigg]{G}_{n} (\theta ){X} \end{eqnarray} $
1.4 参数化的折叠翼气动弹性模型
(32) $\begin{eqnarray} \label{eq32} M_{r} (\theta )\ddot{{\xi }}(t)+K_{r} (\theta )\xi (t)+q_{d} Q_{r} (\theta )\xi (t)={\bf0} \end{eqnarray} $
式中$Q_{r} (\theta )$为广义坐标下的气动力, 其具体形式如下
(33) $\begin{eqnarray} \label{eq33} && Q_{r} (\theta )=\varphi (\theta )^{T}{G}_{n}^{T} (\theta )\left( {{G}_{a(1/2)}^{T} -{G}_{\alpha (1/2)}^{T} {C}_{\Delta } } \right){S}\cdot {\bar{{D}}}_{aic} \left[ {{G}_{\alpha (1/2)} +\frac{{i}k}{b}\left( {{G}_{a(1/2)} +{C}_{\Delta } {G}_{\alpha (1/2)} } \right)} \right]\cdot {G}_{n} (\theta )\varphi (\theta ) \end{eqnarray} $
对使用DLM所计算的频域气动力进行有理函数近似, 其拉氏域下的表达式为
(34) $\begin{eqnarray} \label{eq34} && Q_{r} (\theta )= {A}_{0} +\frac{b}{V}{A}_{1} s+\frac{b^{2}}{V^{2}}{A}_{2} s^{2}+ {D}\left( {{I}s-\frac{V}{b}{R}} \right)^{-1}{E}s \end{eqnarray} $
将式 (34) 代入式 (32), 可得如下形式的气动弹性方程
(35) $\begin{eqnarray} \label{eq35} && \left( {M_{r} (\theta )-q_{d} \frac{b^{2}}{V^{2}}{A}_{2} } \right)\ddot{{\xi }}(t)-q_{d} \frac{b}{V}{A}_{1} \dot{{\xi }}(t) + \left( {K_{r} (\theta )-q_{d} {A}_{s0} } \right)\xi (t)-q_{d} {DX}_{a} ={\bf0} \end{eqnarray} $
式中, ${X}_{a} $为气动力滞后根, 与其导数${\dot{{X}}}_{a} $的关系如下
(36) $\begin{eqnarray} \label{eq36} {\dot{{X}}}_{a} =\frac{V}{b}{RX}_{a} +{E}_{s} {\dot{{\xi }}} \end{eqnarray} $
(37) $\begin{eqnarray} \label{eq37} && \left\{ {{\begin{array}{*{20}c} {\dot{{\xi }}(t)} \\[1mm] {\ddot{{\xi }}(t)} \\[1mm] {{\dot{{X}}}_{a} } \\[1mm] \end{array} }} \right\}= \left\{ {{\begin{array}{c@{\qquad }c@{\qquad }c} 0 & {I} & 0 \\ {-\bar{{M}}_{{r}} (\theta )^{-1} \left( {K_{r} (\theta )-q_{d} {A}_{s0} } \right)} & {\bar{{M}}_{r} (\theta )^{-1} q_{d} \dfrac{b}{V}{A}_{1} } & {q_{d} \bar{{M}}_{r} (\theta )^{-1} {D}} \\[1mm] 0 & {{E}_{s} } & {\dfrac{V}{b}{R}} \\[1mm] \end{array} }} \right\}\cdot \left\{ {{\begin{array}{*{20}c} {\xi (t)} \\[1mm] {\dot{{\xi }}(t)} \\[1mm] {{X}_{a} } \\ \end{array} }} \right\} \end{eqnarray} $
(38) $\begin{eqnarray} \label{eq38} \bar{{M}}_{r} (\theta )=\left( {M_{r} (\theta )-q_{d} \dfrac{b^{2}}{V^{2}}A_{2} } \right) \end{eqnarray} $
通过参数化的状态空间方程, 可求解不同风速、不同折叠角下的气动弹性系统的响应, 也可以进行气动弹性稳定性分析.
2 算例验证
本节以小展弦比折叠翼模型为研究对象, 分别从结构动力学和气动弹性稳定性两个方面验证本文所提出的参数化建模方法的准确性. 结构动力学模拟方面, 重点关注参数化模型预测固有频率、固有振型等结构特性随折叠角的变化规律. 气动弹性稳定性分析方面, 预测折叠翼的颤振临界速度和颤振频率随折叠角变化的规律.
2.1 折叠翼结构动力学特性分析
参数化结构动力学模型的准确性是变体飞行器参数化气动弹性建模的前提. 本文首先建立了0$^\circ$, 10$^\circ$, 25$^\circ$, 50$^\circ$, 80$^\circ$, 100$^\circ$和120$^\circ$七个折叠角下的折叠翼有限元模型, 通过流形切空间插值得到基于以上角度的参数化结构动力学模型.
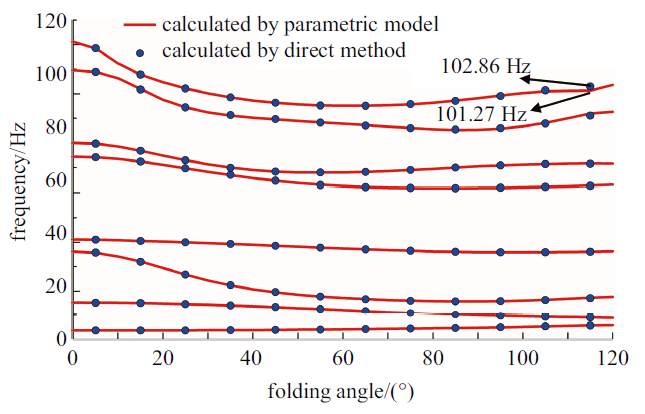
如图4 所示, 参数化建模方法计算得到的前8阶模态频率和直接法计算得到的前8阶模态频率吻合较好. 相较于其他折叠角度, 基于流形切空间插值的参数化建模方法在预测115$^\circ$折叠角下的第8阶固有频率(预测频率为101.27 Hz) 与直接法 (计算频率为102.86 Hz) 存在一定差异, 误差约为1.5${\%}$, 仍处于工程可接受范围.
图4
图4
参数化建模方法与直接法计算频率对比
Fig.4
Comparison of natural frequency between parametric model and direct method
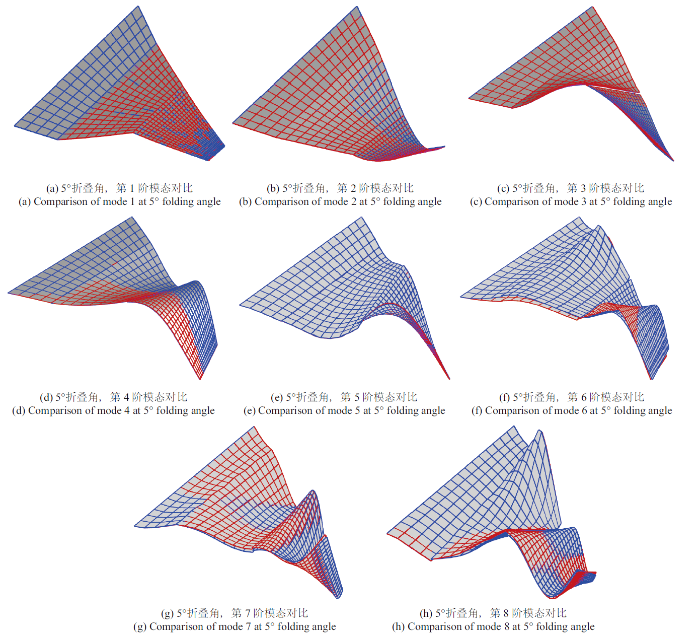
除了结构固有频率之外, 折叠翼的结构固有振型对广义气动力的计算以及气动弹性分析的精度也有重要影响. 图5 给出了5$^\circ$折叠角下参数化建模方法得到的固有振型与直接法得到的振型(蓝色为参数化建模计算的振型, 红色为直接法计算的振型) 的对比. 对比结果表明, 参数化建模方法所计算的前8阶固有振型与直接法的计算结果吻合较好.
图5
图5
5$^\circ$折叠角时,各阶模态对比
Fig.5
Comparison of modes at 5$^\circ$ folding angle
MAC (modal assurance criterion) 值是检验振型函数预测误差的重要指标. 为了验证参数化建模方法所预测的固有振型与真实振型的偏差, 本文分别给出了在5$^\circ$, 30$^\circ$, 65$^\circ$和105$^\circ$折叠角下折叠翼前8阶固有振型的MAC值分布. 如图6 所示, 除第6阶弹性模态外, 其余各阶模态MAC值均大于0.99. 第6阶模态出现误差的原因是该插值方法在两个较小的参数值之间可能形成拐点, 使得插值结果与真实值产生较大差异.
图6
图6
4个典型角度下振型的MAC值
Fig.6
MAC values of mode shapes under four specific folding angles
2.2 折叠翼参数化气动弹性建模分析
为了进一步验证该参数化气动弹性模型的准确性, 本文采用参数化建模方法计算了折叠翼的颤振边界. 如图7 所示, 参数化气动弹性模型成功预测了折叠翼颤振边界随折叠角的变化规律: 随着折叠角变化, 折叠翼的颤振模态发生了复杂的模态切换现象. 在0$^\circ$ $\sim$ 30$^\circ$折叠角区间, 折叠翼的第2阶模态发生颤振. 当折叠角位于35$^\circ$ $\sim$ 80$^\circ$区间时, 结构的第3阶模态发生颤振. 在85$^\circ$ $\sim$ 105$^\circ$折叠角区间, 折叠翼发生颤振的是第4阶模态. 当机翼折叠角进一步增大到110$^\circ$ $\sim$ 120$^\circ$范围时, 折叠翼的第3阶模态再次发生颤振.
图7
图7
参数化建模方法与直接法气动弹性计算对比
Fig.7
Comparison between parametric modeling and direct method in aeroelasticity
此外, 本文将参数化气动弹性模型对颤振边界的预测结果与直接法预测的结果进行了对比研究. 如图7 所示, 在大部分折叠角下, 参数化折叠翼模型所预测的颤振临界速度和颤振频率均与直接计算结果吻合较好, 频率误差最大值小于1${\%}$, 颤振临界速度误差最大值低于4${\%}$. 然而, 图示结果表明, 在105$^\circ$的折叠角处, 参数化建模方法所预测的颤振临界速度和颤振频率与直接法计算结果存在较大差异. 从颤振频率随折叠角变化的曲线 (图7 (a)) 来看, 发生较大差异的主要原因是参数化建模方法预测的颤振模态分支与直接法计算得到的颤振模态分支不同. 为了深入探究引起颤振模态分支变化的原因, 图8 分别给出了105$^\circ$折叠角下直接法和参数化建模方法计算得到的气动弹性系统根轨迹分布图. 如图所示, 该折叠角下两种计算方法所预测的根轨迹分布图相似, 主要差异在于直接法预测了两种颤振形态. 第一类颤振形态是第4阶模态发生颤振, 颤振临界速度是54.6 m/s; 第二类颤振形态是第3阶模态发生小阻尼颤振, 颤振临界速度为32.3 m/s. 本文提出的参数化建模方法预测的第4阶模态发生颤振的临界速度是54.2 m/s, 与直接法结果吻合较好.
图8
图8
参数化模型与直接法计算根轨迹图对比
Fig.8
Comparison of root locus calculated by parametric modeling and direct method
和直接法相比, 本文提出的基于流形切空间插值的参数化建模方法无须重复进行固有模态分析, 计算效率远高于直接法. 表1 展示了使用两种方法分别计算图7 所示的颤振边界所需的时间成本对比. 直接法是指通过MSC.Nastran对给定折叠角度下的折叠翼进行有限元模型的设计, 并使用商业软件对气动和结构网格进行插值、进行非定常气动力的计算以获得此构型下的颤振速度; 而参数化建模的方法不需要手动地重复有限元建模、结构和气动插值, 仅仅改变参数即可得到此时结构的刚度、质量矩阵, 单次时间为0.7 s, 可忽略不计, 因此其总时间花费仅为传统方法54.3${\%}$.
3 结论
本文提出了一种基于流形切空间插值的折叠翼参数化气动弹性建模方法, 实现了折叠翼的气动弹性模型的高效建立. 相较于现有的参数化建模方法, 本文提出的参变建模方法有效解决了变体过程中存在的模态坐标不一致性. 为了验证该参数化模型在预测折叠翼气动弹性力学行为的准确性, 本文以折叠翼为研究对象, 分别从折叠翼结构固有频率、模态振型、颤振边界等方面进行了算例验证. 结果表明,该参数化建模方法可高效、高精度预测可折叠式变体机翼的固有频率和颤振边界随折叠角的演变规律. 在后续工作中, 可将该方法扩展到解决快速变体过程的时变动力学建模, 重点围绕模态坐标一致性问题和时域非定常气动力计算等方面开展研究.
参考文献
View Option
[1]
武宇飞 , 龙腾 , 毛能峰 . 跨介质变体飞行器设计优化技术进展
战术导弹技术 , 2020 ,41 (4 ):29 -40
[本文引用: 1]
(Wu Yufei Long Teng Mao Nengfeng Review of trans-media morphing flight vehicle design optimization techniques
Tactical Missile Technology 2020 ,41 (4 ):29 -40 (in Chinese))
[本文引用: 1]
[2]
叶友达 , 张涵信 , 蒋勤学 等 . 近空间高超声速飞行器气动特性研究的若干关键问题
力学学报 , 2018 ,50 (6 ):1292 -1310
(Ye Youda Zhang Hanxin Jiang Qinxue et al . Some key problems in the study of aerodynamic characteristics of near-space hypersonic vehicles
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (6 ):1292 -1310 (in Chinese))
[3]
冯金富 , 胡俊华 , 齐铎 . 水空跨介质航行器发展需求及其关键技术
空军工程大学学报(自然科学版) , 2019 ,20 (3 ):8 -13
(Feng Jinfu Hu Junhua Qi Du Study on development needs and key technologies of air-water trans-media vehicle
Journal of Air Force Engineering University $($Natural Science Edition$)$ 2019 ,20 (3 ):8 -13 (in Chinese))
[4]
Barbarino S Bilgen O Ajaj RM , et al . A review of morphing aircraft
Journal of Intelligent Material Systems & Structures 2011 ,22 (9 ):823 -877
[5]
廖波 , 袁昌盛 , 李永泽 . 折叠机翼无人机的发展现状和关键技术研究
机械设计 , 2012 ,29 (4 ):5 -9
[本文引用: 1]
(Liao Bo Yuan Changsheng Li Yongze Development status and key technologies of folding-wing unmanned air vehicle
Journal of Machine Design 2012 ,29 (4 ):5 -9 (in Chinese))
[本文引用: 1]
[6]
杨博 , 窦婧文 , 曹振 . 变体飞行器的气动结构对控制系统的影响
弹道学报 , 2020 ,32 (1 ):83 -90, 96
[本文引用: 1]
(Yang Bo Dou JingWen, Cao Zheng. Influence of aerodynamic structure of morphing aircraft on the control system
Journal of Ballistics 2020 ,32 (1 ):83 -90, 96 (in Chinese))
[本文引用: 1]
[7]
Yue T Wang L Ai J . Longitudinal linear parameter varying modeling and simulation of morphing aircraft
Journal of Aircraft 2013 ,50 (6 ):1673 -1681
[8]
郭建国 , 陈惠娟 , 周军 等 . 非对称伸缩翼飞行器动力学建模及特性分析
系统工程与电子技术 , 2016 ,38 (8 ):1951 -1957
[本文引用: 1]
(Guo Jianguo Chen Huijuan Zhou Jun et al . Dynamic modeling and characteristic analysis of asymmetric span morphing wing
Systems Engineering and Electronics 2016 ,38 (8 ):1951 -1957 (in Chinese))
[本文引用: 1]
[9]
罗操群 , 孙加亮 , 文浩 等 . 多刚体系统分离策略及释放动力学研究
力学学报 , 2020 ,52 (2 ):503 -513
[本文引用: 1]
(Luo Caoqun Sun Jialiang Wen Hao et al . Research on separation strategy and deployment dynamics of a space multi-rigid-body system
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (2 ):503 -513 (in Chinese))
[本文引用: 1]
[10]
Shi RQ Song JM . Dynamics and control for an in-plane morphing wing
Aircraft Engineering & Aerospace Technology 2013 ,85 (1 ):24 -31
[本文引用: 1]
[11]
宋慧心 , 金磊 . 折叠翼飞行器的动力学建模与稳定控制
力学学报 , 2020 ,52 (6 ):1548 -1559
[本文引用: 1]
(Song HuiXin Jin Lei Dynamic modeling and stability control of folding wing aircraft
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (6 ):1548 -1559 (in Chinese))
[本文引用: 1]
[12]
Obradovic B Subbarao K . Modeling of flight dynamics of morphing wing aircraft
Journal of Aircraft 2011 ,48 (2 ):391 -402
[13]
张杰 , 吴森堂 . 一种变体飞行器的动力学建模与动态特性分析
北京航空航天大学学报 , 2015 ,41 (1 ):58 -64
[本文引用: 1]
(Zhang Jie Wu Sentang Dynamic modeling for a morphing aircraft and dynamic characteristics analysis
Journal of Beijing University of Aeronautics and Astronautics 2015 ,41 (1 ):58 -64 (in Chinese))
[本文引用: 1]
[14]
Hu W Yang ZC Gu YS . Aeroelastic study for folding wing during the morphing process
Journal of Sound and Vibration 2016 ,365 :216 -229
[本文引用: 1]
[15]
李海泉 , 梁建勋 , 吴爽 等 . 空间机械臂柔性捕获机构建模与实验研究
力学学报 , 2020 ,52 (5 ):1465 -1474
[本文引用: 1]
(Li Haiquan Liang Jianxun Wu Shuang et al . Dynamics modeling and experiment of a flexible capturing mechanism in a space manipulator
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (5 ):1465 -1474 (in Chinese))
[本文引用: 1]
[16]
郭祥 , 靳艳飞 , 田强 . 随机空间柔性多体系统动力学分析
力学学报 , 2020 ,52 (6 ):1730 -1742
[本文引用: 1]
(Guo Xiang Jin Yanfei Tian Qiang Dynamics analysis of stochastic spatial flexible multibody system
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (6 ):1730 -1742 (in Chinese))
[本文引用: 1]
[17]
Snyder MP Sanders B Eastep FE , et al . Vibration and flutter characteristics of a folding wing
Journal of Aircraft 2009 ,46 (3 ):791 -799
[本文引用: 1]
[18]
Selitrennik E Karpel M Levy Y . Computational aeroelastic simulation of rapidly morphing air vehicles
Journal of Aircraft 2013 ,49 (6 ):1675 -1686
[本文引用: 1]
[19]
Lee DH Chen PC . Nonlinear aeroelastic studies on a folding wing configuration with free-play hinge nonlinearity//47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference , 2006
[本文引用: 1]
[20]
Zhao YH Hu HY . Parameterized aeroelastic modeling and flutter analysis for a folding wing
Journal of Sound & Vibration 2012 ,331 (2 ):308 -324
[本文引用: 1]
[21]
倪迎鸽 , 侯赤 , 万小朋 等 . 折叠机翼的参数化气动弹性建模与颤振分析
西北工业大学学报 , 2015 ,33 (5 ):788 -793
[本文引用: 1]
(Ni Yingge Hou Chi Wan Xiaopeng et al . Parametric aeroelastic modeling and flutter analysis for a folding wing
Journal of Northwest Polytechnical University 2015 ,33 (5 ):788 -793 (in Chinese))
[本文引用: 1]
[22]
Huang R Yang ZJ Yao XJ , et al . Parameterized modeling methodology for efficient aeroservoelastic analysis of a morphing wing
AIAA Journal 2019 ,57 :4599 -4607
[本文引用: 1]
[23]
吴莉洁 , 宋汉文 . 基于子结构综合法的周期支撑结构带隙分析
噪声与振动控制 , 2018 ,38 (5 ):40 -44, 51
[本文引用: 1]
(Wu Lijie Song Hanwen Band gap analysis for periodically supported structures based on substructure synthesis method
Noise and Vibration Control 2018 ,38 (5 ):40 -44, 51 (in Chinese))
[本文引用: 1]
[24]
王永岩 . 动态子结构方法理论及应用 . 北京 : 科学出版社 , 1999
[本文引用: 1]
(Wang Yongyan Theory and Application of Dynamic Substructure Method. Beijing : Science Press , 1999 (in Chinese))
[本文引用: 1]
[25]
Amsallem D Farhat C Lieu T . Aeroelastic analysis of F-16 and F-18/A configurations using adapted CFD-based reduced-order models//48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference , 2013
[本文引用: 1]
[26]
Amsallem D Farhat C Lieu T . High-order interpolation of reduced-order models for near real-time aeroelastic prediction//International Forum on Aeroelasticity and Structural Dynamics , 2007
[27]
Amsallem D Farhat C . Interpolation method for adapting reduced-order models and application to aeroelasticity
AIAA Journal 2008 ,46 (7 ):1803 -1813
[28]
Farhat C Amsallem D . Recent advances in reduced-order modeling and application to nonlinear computational aeroelasticity//46th AIAA Aerospace Sciences Meeting and Exhibit , 2008
[29]
Amsallem D Cortial J Carlberg K , et al . A method for interpolating on manifolds structural dynamics reduced-order models
International Journal for Numerical Methods in Engineering 2009 ,80 (9 ):1241 -1258
[30]
刘营 , 李鸿光 , 李韵 等 . 一种加速的参数化模型降阶方法
航空动力学报 , 2019 ,34 (10 ):2264 -2270
(Liu Ying Li Hongguang Li Yun et al . Accelerated parametric model order reduction method
Journal of Aerospace Power 2019 ,34 (10 ):2264 -2270 (in Chinese))
[31]
Amsallem D Farhat C . Stabilization of projection-based reduced-order models
International Journal for Numerical Methods in Engineering 2012 ,91 (4 ):358 -377
[32]
刘营 , 李鸿光 , 李韵 等 . 基于子结构的参数化模型降阶方法
振动与冲击 , 2020 ,39 (16 ):148 -154
[本文引用: 1]
(Liu Ying Li Hongguang Li Yun et al . A component-based parametric model order reduction method
Journal of Vibration and Shock 2020 ,39 (16 ):148 -154 (in Chinese))
[本文引用: 1]
跨介质变体飞行器设计优化技术进展
1
2020
... 近年来, 世界航空界正着力发展具有飞行环境(如高度、速度、气候等)自适应、可执行多种任务(如巡航、盘旋、机动等)的变体飞行器. 这类飞行器可根据飞行任务需要自主改变结构和气动布局, 在复杂的飞行环境条件下保持良好的飞行性能[1 -5 ] . 在众多变体飞行器设计方案中, 折叠翼变体飞行器因满足多任务作战需求和提高单任务执行效率的优势, 受到了广泛的关注. 然而, 在机翼受控变体过程中, 不仅非定常气动力会随着机翼形状改变而发生变化, 机翼的惯性、弹性和阻尼特性也同时发生变化, 极易诱发不同结构模态参与的参变颤振现象, 给变体飞行器的飞行安全带来挑战. 针对不同折叠构型下变体机翼的气动-结构耦合动力学系统的参变特性, 如何建立以折叠角为参数的参数化气动弹性模型, 在全参数空间内实现气动弹性力学行为的高效、高精度预测, 是变体飞行器研制过程中亟待解决的动力学问题. ...
跨介质变体飞行器设计优化技术进展
1
2020
... 近年来, 世界航空界正着力发展具有飞行环境(如高度、速度、气候等)自适应、可执行多种任务(如巡航、盘旋、机动等)的变体飞行器. 这类飞行器可根据飞行任务需要自主改变结构和气动布局, 在复杂的飞行环境条件下保持良好的飞行性能[1 -5 ] . 在众多变体飞行器设计方案中, 折叠翼变体飞行器因满足多任务作战需求和提高单任务执行效率的优势, 受到了广泛的关注. 然而, 在机翼受控变体过程中, 不仅非定常气动力会随着机翼形状改变而发生变化, 机翼的惯性、弹性和阻尼特性也同时发生变化, 极易诱发不同结构模态参与的参变颤振现象, 给变体飞行器的飞行安全带来挑战. 针对不同折叠构型下变体机翼的气动-结构耦合动力学系统的参变特性, 如何建立以折叠角为参数的参数化气动弹性模型, 在全参数空间内实现气动弹性力学行为的高效、高精度预测, 是变体飞行器研制过程中亟待解决的动力学问题. ...
近空间高超声速飞行器气动特性研究的若干关键问题
0
2018
近空间高超声速飞行器气动特性研究的若干关键问题
0
2018
水空跨介质航行器发展需求及其关键技术
0
2019
水空跨介质航行器发展需求及其关键技术
0
2019
A review of morphing aircraft
0
2011
折叠机翼无人机的发展现状和关键技术研究
1
2012
... 近年来, 世界航空界正着力发展具有飞行环境(如高度、速度、气候等)自适应、可执行多种任务(如巡航、盘旋、机动等)的变体飞行器. 这类飞行器可根据飞行任务需要自主改变结构和气动布局, 在复杂的飞行环境条件下保持良好的飞行性能[1 -5 ] . 在众多变体飞行器设计方案中, 折叠翼变体飞行器因满足多任务作战需求和提高单任务执行效率的优势, 受到了广泛的关注. 然而, 在机翼受控变体过程中, 不仅非定常气动力会随着机翼形状改变而发生变化, 机翼的惯性、弹性和阻尼特性也同时发生变化, 极易诱发不同结构模态参与的参变颤振现象, 给变体飞行器的飞行安全带来挑战. 针对不同折叠构型下变体机翼的气动-结构耦合动力学系统的参变特性, 如何建立以折叠角为参数的参数化气动弹性模型, 在全参数空间内实现气动弹性力学行为的高效、高精度预测, 是变体飞行器研制过程中亟待解决的动力学问题. ...
折叠机翼无人机的发展现状和关键技术研究
1
2012
... 近年来, 世界航空界正着力发展具有飞行环境(如高度、速度、气候等)自适应、可执行多种任务(如巡航、盘旋、机动等)的变体飞行器. 这类飞行器可根据飞行任务需要自主改变结构和气动布局, 在复杂的飞行环境条件下保持良好的飞行性能[1 -5 ] . 在众多变体飞行器设计方案中, 折叠翼变体飞行器因满足多任务作战需求和提高单任务执行效率的优势, 受到了广泛的关注. 然而, 在机翼受控变体过程中, 不仅非定常气动力会随着机翼形状改变而发生变化, 机翼的惯性、弹性和阻尼特性也同时发生变化, 极易诱发不同结构模态参与的参变颤振现象, 给变体飞行器的飞行安全带来挑战. 针对不同折叠构型下变体机翼的气动-结构耦合动力学系统的参变特性, 如何建立以折叠角为参数的参数化气动弹性模型, 在全参数空间内实现气动弹性力学行为的高效、高精度预测, 是变体飞行器研制过程中亟待解决的动力学问题. ...
变体飞行器的气动结构对控制系统的影响
1
2020
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
变体飞行器的气动结构对控制系统的影响
1
2020
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
Longitudinal linear parameter varying modeling and simulation of morphing aircraft
0
2013
非对称伸缩翼飞行器动力学建模及特性分析
1
2016
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
非对称伸缩翼飞行器动力学建模及特性分析
1
2016
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
多刚体系统分离策略及释放动力学研究
1
2020
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
多刚体系统分离策略及释放动力学研究
1
2020
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
Dynamics and control for an in-plane morphing wing
1
2013
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
折叠翼飞行器的动力学建模与稳定控制
1
2020
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
折叠翼飞行器的动力学建模与稳定控制
1
2020
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
Modeling of flight dynamics of morphing wing aircraft
0
2011
一种变体飞行器的动力学建模与动态特性分析
1
2015
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
一种变体飞行器的动力学建模与动态特性分析
1
2015
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
Aeroelastic study for folding wing during the morphing process
1
2016
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
空间机械臂柔性捕获机构建模与实验研究
1
2020
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
空间机械臂柔性捕获机构建模与实验研究
1
2020
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
随机空间柔性多体系统动力学分析
1
2020
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
随机空间柔性多体系统动力学分析
1
2020
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
Vibration and flutter characteristics of a folding wing
1
2009
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
Computational aeroelastic simulation of rapidly morphing air vehicles
1
2013
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
1
2006
... 当前变体飞行器动力学建模研究可分为两大类: 一类是多刚体动力学模型(如Newton-Euler方法[6 -8 ] 、Lagrange方法[9 -10 ] 、Kane方法[11 -13 ] 等); 另一类是柔性体动力学模型(如浮动坐标法[14 ] 、绝对节点坐标法[15 -16 ] 等). 相较于多刚体动力学模型, 柔性体动力学模型更加贴近工程实际状况且能够应用于折叠翼的气动弹性分析, 因此受到更广泛的关注. 例如Snyder等[17 ] 研究了Goland折叠翼的颤振特性, 发现折叠翼铰链刚度对变体机翼的颤振频率和颤振速度的影响较大. Selitrennik和Karpel[18 ] 对于快速变形的折叠翼系统提出了一种高效气动弹性建模方法. 该方法采用虚拟质量法建立系统的结构动力学方程, 并通过动力学方程和CFD技术相耦合的方式, 建立了可折叠式变体机翼的气动弹性方程. 数值结果表明, 瞬态变形和气动载荷突变对折叠翼的气动弹性稳定性有着重要的影响. 对于折叠翼内外铰链具有双线性刚度的非线性气动弹性问题, Lee等[19 ] 提出了一种可高效预测折叠翼亚临界极限环振荡的数值计算方法. ...
Parameterized aeroelastic modeling and flutter analysis for a folding wing
1
2012
... 上述气动弹性动力学建模方法虽已经成功应用到可折叠式变体机翼的气动弹性建模中,但在气动弹性分析过程中仍需要针对不同折叠角进行重复地结构动力学建模、非定常气动力计算以及流固耦合建模, 计算效率低下且难以分析可折叠式变体机翼在完整参数空间内的气动弹性力学行为. 参数化气动弹性建模方法为高效、高精度分析可折叠式变体机翼的气动弹性力学行为提供了新的解决方案. Zhao等[20 ] 和倪迎鸽等[21 ] 采用子结构综合和偶极子网格法构建了折叠翼的参数化气动弹性模型, 分析了模态阻尼、折叠角、铰链刚度对折叠翼动力学特性的影响. Huang等[22 ] 提出了一种参数化的气动伺服弹性建模方法, 高效地获得了不同折叠角下的机翼气动伺服弹性数学模型, 实现了颤振主动抑制的控制律设计和闭环气动伺服弹性分析. ...
折叠机翼的参数化气动弹性建模与颤振分析
1
2015
... 上述气动弹性动力学建模方法虽已经成功应用到可折叠式变体机翼的气动弹性建模中,但在气动弹性分析过程中仍需要针对不同折叠角进行重复地结构动力学建模、非定常气动力计算以及流固耦合建模, 计算效率低下且难以分析可折叠式变体机翼在完整参数空间内的气动弹性力学行为. 参数化气动弹性建模方法为高效、高精度分析可折叠式变体机翼的气动弹性力学行为提供了新的解决方案. Zhao等[20 ] 和倪迎鸽等[21 ] 采用子结构综合和偶极子网格法构建了折叠翼的参数化气动弹性模型, 分析了模态阻尼、折叠角、铰链刚度对折叠翼动力学特性的影响. Huang等[22 ] 提出了一种参数化的气动伺服弹性建模方法, 高效地获得了不同折叠角下的机翼气动伺服弹性数学模型, 实现了颤振主动抑制的控制律设计和闭环气动伺服弹性分析. ...
折叠机翼的参数化气动弹性建模与颤振分析
1
2015
... 上述气动弹性动力学建模方法虽已经成功应用到可折叠式变体机翼的气动弹性建模中,但在气动弹性分析过程中仍需要针对不同折叠角进行重复地结构动力学建模、非定常气动力计算以及流固耦合建模, 计算效率低下且难以分析可折叠式变体机翼在完整参数空间内的气动弹性力学行为. 参数化气动弹性建模方法为高效、高精度分析可折叠式变体机翼的气动弹性力学行为提供了新的解决方案. Zhao等[20 ] 和倪迎鸽等[21 ] 采用子结构综合和偶极子网格法构建了折叠翼的参数化气动弹性模型, 分析了模态阻尼、折叠角、铰链刚度对折叠翼动力学特性的影响. Huang等[22 ] 提出了一种参数化的气动伺服弹性建模方法, 高效地获得了不同折叠角下的机翼气动伺服弹性数学模型, 实现了颤振主动抑制的控制律设计和闭环气动伺服弹性分析. ...
Parameterized modeling methodology for efficient aeroservoelastic analysis of a morphing wing
1
2019
... 上述气动弹性动力学建模方法虽已经成功应用到可折叠式变体机翼的气动弹性建模中,但在气动弹性分析过程中仍需要针对不同折叠角进行重复地结构动力学建模、非定常气动力计算以及流固耦合建模, 计算效率低下且难以分析可折叠式变体机翼在完整参数空间内的气动弹性力学行为. 参数化气动弹性建模方法为高效、高精度分析可折叠式变体机翼的气动弹性力学行为提供了新的解决方案. Zhao等[20 ] 和倪迎鸽等[21 ] 采用子结构综合和偶极子网格法构建了折叠翼的参数化气动弹性模型, 分析了模态阻尼、折叠角、铰链刚度对折叠翼动力学特性的影响. Huang等[22 ] 提出了一种参数化的气动伺服弹性建模方法, 高效地获得了不同折叠角下的机翼气动伺服弹性数学模型, 实现了颤振主动抑制的控制律设计和闭环气动伺服弹性分析. ...
基于子结构综合法的周期支撑结构带隙分析
1
2018
... 通过有限元方法得到折叠翼机身、内翼和外翼的质量、刚度矩阵, 然后通过子结构综合法[23 -24 ] 得到折叠翼结构动力学方程如下 ...
基于子结构综合法的周期支撑结构带隙分析
1
2018
... 通过有限元方法得到折叠翼机身、内翼和外翼的质量、刚度矩阵, 然后通过子结构综合法[23 -24 ] 得到折叠翼结构动力学方程如下 ...
1
1999
... 通过有限元方法得到折叠翼机身、内翼和外翼的质量、刚度矩阵, 然后通过子结构综合法[23 -24 ] 得到折叠翼结构动力学方程如下 ...
1
1999
... 通过有限元方法得到折叠翼机身、内翼和外翼的质量、刚度矩阵, 然后通过子结构综合法[23 -24 ] 得到折叠翼结构动力学方程如下 ...
1
2013
... 矩阵流形是指具有特殊性质 (正定性、对称性、正交性或非奇异性)的矩阵组成的流形.在流形上插值得到的矩阵仍具有原矩阵的特殊性质. 正因为这一特点, 有学者提出基于流形矩阵的插值方法[25 -32 ] . 令$\left\{ {\theta_{i} } \right\}_{i=0}^{N-1} $表示由一系列折叠角度所组成的集合, 矩阵${P}_{i} $表示折叠角$\theta_{i} $对应的系统矩阵(如质量矩阵、刚度矩阵和振型矩阵), ${P}_{i} $张成的空间$S_{i}$可视为矩阵流形${\cal M}$上的一点. 参数化建模即对于一个新参数$\theta_{N}$, 获得其对应的矩阵${P}_{N} $. 显然, 矩阵流形插值是一个可行的方法, 但是通常矩阵流形不是"线性"的, 因此需要将矩阵流形上的点映射到"平直"的切空间, 在切空间中进行插值, 然后再从切空间映射回流形上, 其推导过程如下. ...
Interpolation method for adapting reduced-order models and application to aeroelasticity
0
2008
A method for interpolating on manifolds structural dynamics reduced-order models
0
2009
Stabilization of projection-based reduced-order models
0
2012
基于子结构的参数化模型降阶方法
1
2020
... 矩阵流形是指具有特殊性质 (正定性、对称性、正交性或非奇异性)的矩阵组成的流形.在流形上插值得到的矩阵仍具有原矩阵的特殊性质. 正因为这一特点, 有学者提出基于流形矩阵的插值方法[25 -32 ] . 令$\left\{ {\theta_{i} } \right\}_{i=0}^{N-1} $表示由一系列折叠角度所组成的集合, 矩阵${P}_{i} $表示折叠角$\theta_{i} $对应的系统矩阵(如质量矩阵、刚度矩阵和振型矩阵), ${P}_{i} $张成的空间$S_{i}$可视为矩阵流形${\cal M}$上的一点. 参数化建模即对于一个新参数$\theta_{N}$, 获得其对应的矩阵${P}_{N} $. 显然, 矩阵流形插值是一个可行的方法, 但是通常矩阵流形不是"线性"的, 因此需要将矩阵流形上的点映射到"平直"的切空间, 在切空间中进行插值, 然后再从切空间映射回流形上, 其推导过程如下. ...
基于子结构的参数化模型降阶方法
1
2020
... 矩阵流形是指具有特殊性质 (正定性、对称性、正交性或非奇异性)的矩阵组成的流形.在流形上插值得到的矩阵仍具有原矩阵的特殊性质. 正因为这一特点, 有学者提出基于流形矩阵的插值方法[25 -32 ] . 令$\left\{ {\theta_{i} } \right\}_{i=0}^{N-1} $表示由一系列折叠角度所组成的集合, 矩阵${P}_{i} $表示折叠角$\theta_{i} $对应的系统矩阵(如质量矩阵、刚度矩阵和振型矩阵), ${P}_{i} $张成的空间$S_{i}$可视为矩阵流形${\cal M}$上的一点. 参数化建模即对于一个新参数$\theta_{N}$, 获得其对应的矩阵${P}_{N} $. 显然, 矩阵流形插值是一个可行的方法, 但是通常矩阵流形不是"线性"的, 因此需要将矩阵流形上的点映射到"平直"的切空间, 在切空间中进行插值, 然后再从切空间映射回流形上, 其推导过程如下. ...