引言
拓扑优化是一种重要的结构优化方法, 已得到学术界和工业界的广泛关注[1 -2 ] . 多年来, 大量研究致力于如何利用拓扑优化改进设计性能[3 -5 ] . 随着该方法的进一步推广应用, 优化设计的可制造性问题逐渐引起人们的重视[6 -7 ] . 然而, 现有研究关于性能和可制造性的考虑通常是分开处理的, 常侧重于某一方面指标. 因此, 将这两个重要而又不可或缺的设计目标结合起来进行优化设计, 将是一项极具实际应用价值且富有挑战性的工作.
早期基于拓扑优化的设计性能研究主要集中在刚度问题上, 但在实际工程应用中, 多数设计还应考虑强度要求[8 -10 ] . 因为局部高应力集中易导致构件疲劳损伤和断裂破坏, 将严重影响结构的安全使用和耐久性. 在这种情况下, 考虑应力相关的拓扑优化将发挥重要作用[11 -12 ] . 此外, 研究还表明[13 -14 ] 强度最大化设计并不一定等同于刚度最大化设计, 这就意味着在刚度最大化准则下获得的优化设计将不一定适用于强度导向下的工程问题. 因此, 面向强度需求, 研究基于应力的拓扑优化问题既符合工程需要也极具研究意义[15 -17 ] .
自Duysinx等[18 ] 提出连续体结构应力拓扑优化研究以来, 应力相关的拓扑优化问题受到了越来越多的关注. 然而, 考虑应力相关的拓扑优化问题有其自身难点, 常面临应力奇异性、局部性、非线性及度量准确性等问题[19 -20 ] . 为此, 不少学者提出了不同的解决方法. 目前常用的处理方法包括松弛方法[21 ] 、基于P范数或K-S函数的凝聚技术[8 ,14 ] 、分区度量[20 ] 、以及凝聚近似误差修正策略[22 ] 等. 此外, 隋允康等[23 ] 提出的将局部应力约束向整体应变能约束转化的方法也可有效解决应力局部性问题. 尽管上述方法能有效处理常规的拓扑优化问题, 但尚未涉及复杂的可制造性拓扑优化问题.
事实上, 拓扑优化设计常面临可制造性问题[24 ] . 在传统制造技术条件下, 优化产生的复杂构型将给产品制备带来巨大挑战. 这在一定程度上限制了拓扑优化的推广应用, 不利于高性能产品的研发. 作为一种先进的制造技术, 增材制造能够实现高度复杂结构的有效制备[25 ] . 将增材制造与拓扑优化有机结合, 能够大幅提高创新产品的研制能力, 现已成为重要研究方向[6 -7 ,25 ] . 然而, 增材制造并非"自由"制造, 有其独特的制造约束. 要求结构不含封闭孔洞的连通性约束便是其中最重要的制造约束之一[26 -27 ] . 如果结构含有封闭孔洞, 制造后残留在孔洞内的未熔融粉末或支撑结构将难以去除. 显然, 面向增材制造, 考虑可制造连通性的拓扑优化问题将具有重要工程应用价值[27 -29 ] .
研究人员已提出一些有效方法. Liu等[27 ] 利用热传导原理提出了虚拟温度法, 在结构孔洞区引入虚拟热源, 而在固体区填充隔热材料, 然后通过限制结构上的最高温度来抑制封闭孔洞. 数学上, 该方法可描述为服从泊松方程的标量场约束[29 ] . Zhou等[28 ] 则提出一种边界约束方法, 利用孔洞作为基本设计元素, 通过将与所有孔洞中心相关的设计变量限定在设计域之外来确保结构连通性. Xiong等[30 ] 提出了一种基于BESO的结构连通性控制方法, 通过有选择地生成将孔洞与结构边界连接起来的通道来消除封闭孔洞. 在水平集框架下, Xia等[31 ] 将孔洞抑制转换为对设计速度矢量的约束; Wang等[32 ] 则提出一种基于水平集函数梯度的约束来描述孔洞抑制条件. 然而, 这些研究只考虑了传统刚度问题, 缺乏对应力问题的必要关注.
综上所述, 在拓扑优化领域, 应力问题和连通性问题分别已得到了有效处理. 然而, 鲜有研究同时考虑这两个重要的设计要求. 一方面, 如前所述, 这两个问题均有其特殊困难. 另一方面, 两种要求的结合涉及相互影响, 将加剧优化设计的复杂性. 一般而言, 对于相对复杂的优化问题, 设计在优化过程中往往会出现不可预测的数值响应, 这将给优化求解带来各种挑战. 尽管研究人员业已提出有效的方法来克服应力或连通性拓扑优化中的诸多困难, 但到目前为止, 现有应力优化技术与可制造性连通性方法之间的兼容性尚未得到必要验证. 因此, 同时考虑应力和连通性问题, 发展面向增材制造的高强度结构优化方法, 不仅具有实际工程应用价值还具有重要的科学研究意义.
基于上述原因, 本文将研究协同考虑应力和可制造连通性的拓扑优化问题. 建立以结构全局最大应力最小化为目标, 以材料体积和结构连通性为约束的拓扑优化模型. 通过合理引入不同优化技术来构建有效的优化求解策略, 以克服优化过程中的不同数值困难. 最后基于典型数值算例, 探讨文中模型及方法的可行性及其数值特点, 以期为高性能可制造性结构的研发提供有益参考.
1 连通性约束下应力最小化拓扑优化模型
1.1 优化模型
针对协同考虑结构强度和可制造连通性的拓扑优化问题, 基于经典密度法[33 ] , 建立以结构全局最大应力强度准则为目标, 以材料用量和结构连通性为约束的拓扑优化模型, 其数学列式如下
(1) $\begin{eqnarray} \label{eq1} &&\begin{array}{l} \mbox{Find: } {x}=\left[ {x_{1} ,\ \ x_{2} ,\ \ ... ,\ \ x_{i} ,\ \ ... ,\ \ x_{N} } \right]^{T} \\ \mbox{Min: } \sigma_{\max } =\max \left( {\sigma_{i}^{vM}} \right) \\ \mbox{S.t.:}\left\{ {\begin{array}{l} \mbox{In the elastic mechanics field} \\ \mbox{ }\left\{ {\begin{array}{l} {KU}={F} \\ \sum\nolimits_{i=1}^N {x_{i} v_{i} } \leqslant f\cdot V_{0} \ \ \left( {\mbox{volume constraint}} \right) \\ \end{array}} \right. \\ \mbox{In the electrostatic field} \\ \mbox{ }\left\{ {\begin{array}{l} {K}^{\phi }{U}^{\phi }={F}^{\phi } \\ \phi_{EPC} \leqslant 0\mbox{ }\left( {\mbox{connectivity constraint}} \right) \\ \end{array}} \right. \\ 0\leqslant x_{i} \leqslant 1\ \ \left( {i=1,\ \ 2,\ \ ...\ \ ,\ \ N} \right) \\ \end{array}} \right. \\ \end{array}\quad \end{eqnarray} $
式中, $x$为单元密度变量$x_i$集合, $N$为设计变量总数; $\sigma_{\max}$为结构全局最大应力, $\sigma_{i}^{vM}$为单元$i$中心处von Mises应力; $K$, $U$和$F$分别为结构全局刚度矩阵、位移向量和载荷向量; $v_i$为单元体积, $V_0$为设计域总体积, $f$表示给定的材料体积分数; $K^{\phi}$, $U^{\phi}$和$F^{\phi}$分别为结构全局介电矩阵、势向量和静电载荷向量, $\phi_{EPC}$表示与结构连通性相关的静电势约束(electrostatic potential constraint, EPC).
基于改进的SIMP材料插值模型[34 ] , 得到全局刚度矩阵${K}(x)=\sum\nolimits_{i=1}^N \left[ E_{\min} +\left( x_{i}\right)^{p}\left(E_{0} -E_{\min }\right)\right]{k}_{0,i}$, 其中, $E_0$表示实体单元材料的弹性模量, $E_{\min}$表示孔洞单元材料的弹性模量; $p>0$为惩罚因子; $k_{0,i}$为单位弹性模量下的单元刚度矩阵. 这里取常用参数设置: $E_{\min}= 10^{-9}E_0$和$p=3$.
1.2 连通性约束模型
为有效实现拓扑优化中抑制封闭孔洞的单连通性约束, 采用Liu等[27 ] 提出的基于泊松方程的标量场约束方法[29 ] . 为便于该方法的描述, 不失一般性, 这里采用了静电场物理模型[35 ] 进行表征.
在静电场模型中, 假定孔洞单元材料为具有强介电性能的带静电载体, 实体单元材料为介电性能较差的不带电绝缘介质, 相应材料模型如下
(2) $\begin{eqnarray} \label{eq2} \left. \begin{array}{ll} \varepsilon =\varepsilon^{\phi },\ \ \rho =\rho^{\phi }, & {for}\ \ x_{i} =0 \\ \varepsilon =\mu \cdot \varepsilon^{\phi},\ \ \rho =0, & {for}\ \ x_{i} =1 \\ \end{array} \right\} \end{eqnarray} $
其中, $\varepsilon $ 和 $\rho $分别表示材料介电常数(F/m)和电荷密度(C/m$^{3})$; $\varepsilon^{\phi }$ 和$\rho^{\phi }$ 为实常数; $\mu $ 为一个较小的正数(避免矩阵奇异), 与静电模型的势强度表征有关. 此外, 该模型中需假定用户指定的域边界接地(即约束边界), 以作为零电势参考基准.
当结构含有封闭孔洞时, 根据经典电磁学原理可知, 带电体(封闭孔洞)将在其周围介质中激发出强静电场(可由静电标量势 $\phi $ 表征). 一旦带电体接地(封闭孔洞与约束边界连通), 电场强度将大幅衰减. 于是, 可通过分析结构静电场的最大势强度 $\phi_{\max}$ 来评估其连通性. 相应地, 拓扑优化中抑制封闭孔洞的单连通性约束可等效为对结构最大势强度的约束, 即静电势约束$\phi_{EPC}$.
(3) $\begin{eqnarray} \label{eq3} \phi_{\max } \leqslant \eta \cdot \phi_{0} \end{eqnarray} $
其中, $\eta \cdot\phi_{0}$ 为评估结构是否含封闭孔洞的约束阈值; $\phi_{0}$为基准阈值, 可基于初始化约束模型(仅由孔洞单元构成)求解获得[29 ] ; $\eta >0$ 为约束阈值修正因子, 需针对不同问题进行调整, 以控制约束效果[35 ] . 控制 $\phi $的二阶微分方程为经典泊松方程[36 ]
(4) $\begin{eqnarray} \label{eq4} -\nabla \cdot \left( {\varepsilon \nabla \phi } \right)=\rho \end{eqnarray} $
其中, $\nabla $ 为微分符号. 静电问题的边界条件如下
(5) $\begin{eqnarray} \label{eq5} \left. \begin{array}{ll} \phi =0, & {on}\ \ \varGamma _{D} \\ \left( \varepsilon \nabla \phi \right)\cdot {n}=0, & {on}\ \ \varGamma_{N} \\ \end{array} \right\} \end{eqnarray} $
其中, $\varGamma_{D}$ 和 $\varGamma_{N}$分别为狄利克雷边界(即连通性约束边界)和诺伊曼边界, $n$为边界外法向单位向量. 需要注意的是, 基于上述方法获得的优化结果对约束边界条件的选择有依赖性, 不同约束边界条件对应不同约束问题, 可产生不同优化结果[35 ] . 基于式(2)和式(5)可将原优化问题转化为静电场约束问题(式(3))求解分析.
静电场与原方法中的温度场[27 ] 在数学上一致, 均为服从泊松方程的标量场. 这里采用静电场模型主要有两方面考虑. 一方面, 静电原理也能较好表征封闭空洞, 而不同的物理场具有不同物理规律, 可以启发读者进一步发展泊松方法. 另一方面, 静电理论有助于解析泊松方法中关键的约束关系和边界依赖性, 有益于该方法的理解应用[35 ] .
在拓扑优化模型中, 可采用如下材料插值模型有效表征式(2)所示材料介电属性
(6) $\begin{eqnarray} \label{eq6} \left. \begin{array}{l} \varepsilon_{i}^{\phi } \left( {x_{i} } \right)=\varepsilon_{s}^{\phi } +\left( {1-x_{i} } \right)^{pe}\left( {\varepsilon_{v}^{\phi } -\varepsilon _{s}^{\phi } } \right) \\ \rho_{i}^{\phi } \left( {x_{i} } \right)=\left( {1-x_{i} } \right)\rho _{v}^{\phi } \\ \end{array} \right\} \end{eqnarray} $
式中, $\varepsilon_{i}^{\phi } $和$\rho_{i}^{\phi } $分别为单元介电常数和电荷密度; $\varepsilon_{s}^{\phi } $和$\varepsilon _{v}^{\phi } $分别为实体和孔洞材料单元介电常数; $\rho_{v}^{\phi }$为孔洞材料单元电荷密度; $pe>0$为惩罚因子. 本文取常用值: $\varepsilon_{v}^{\phi } =1$, $\varepsilon_{s}^{\phi } =10^{-3}$, $\rho_{v}^{\phi } =1$和$pe=3$. 相应地, 结构全局介电矩阵和静电载荷向量可表达如下
(7) $\begin{eqnarray} \label{eq7} \left. \begin{array}{l} {K}^{\phi }\left( {{x}} \right)=\sum\nolimits_{i=1}^N {\varepsilon _{i}^{\phi } \left( {x_{i} } \right){k}_{0,i}^{\phi }} \\[3mm] {F}^{\phi }\left( {{x}} \right)=\sum\nolimits_{i=1}^N {\rho _{i}^{\phi } \left( {x_{i} } \right){F}_{0,i}^{\phi } } \\ \end{array} \right\} \end{eqnarray} $
式中, ${k}_{0,i}^{\phi } $ 为单位介电常数下的单元介电矩阵, ${F}_{0,i}^{\phi}$为单位电荷密度下的单元载荷向量.
2 优化求解策略
由于问题(1)为相对复杂的多物理场多约束优化问题, 为实现高效稳健求解, 需合理引入不同优化技术来克服相应数值困难.
2.1 设计变量过滤和投影
为避免拓扑优化中的数值不稳定性问题[37 ] , 并获取清晰的0-1设计, 采取线性密度过滤[38 -39 ] 和非线性阈值投影[40 ] 相结合的技术方案. 对单元密度变量 $x_{i} $进行线性密度过滤可得过滤后的变量
(8) $\begin{eqnarray} \label{eq8} \hat{{x}}_{i} =\frac{\sum\nolimits_{k\in NE_{i} } {\left( {\omega_{ik} v_{k} x_{k} } \right)} }{\sum\nolimits_{k\in NE_{i} } {\left( {\omega_{ik} v_{k} } \right)} } \end{eqnarray} $
式中, $NE_{i}$ 表示单元中心落在以单元 $i$ 为中心的半径为$r_{\min}$的圆形区域内的单元集; 加权因子$\omega_{ik} =\max (0, r_{\min} - \varDelta (i,k))$, $\varDelta (i,k)$ 表示单元 $i$ 和 $k$ 中心之间的欧式距离. 再对过滤后的变量进行非线性阈值投影可得投影后的物理密度
(9) $\begin{eqnarray} \label{eq9} \bar{{x}}_{i} =\frac{\tanh \left( {\beta x_{0} } \right)+\tanh \left[ {\beta \left( {\hat{{x}}_{i} -x_{0} } \right)} \right]}{\tanh \left( {\beta x_{0} } \right)+\tanh \left[ {\beta \left( {1-x_{0} } \right)} \right]} \end{eqnarray} $
式中, $\beta >0$ 为控制投影函数非线性的投影参数; $x_{0}\in[0,1]$ 为调节投影函数拐点的投影阈值, 本文取常用值 $x_{0} = 0.5$. 为提高应力评估准确性以及优化迭代稳定性, 参考文献[19 , 41 ], 这里采用连续化策略定义 $\beta $ 值: 在前10步迭代中取 $\beta = 1$, 此后每步迭代加1直至 $\beta = 10$. 由于物理密度定义了单元属性, 在后续研究中将使用物理密度进行结构分析. 值得注意的是, 过滤和投影会影响连通性约束, 考虑这种影响对基于泊松方法的连通性约束的有效实现具有重要意义, 感兴趣的读者可以参阅文献[35 ].
2.2 应力评估方案
由于最大值函数不可微, 不失一般性, 本文采用P-norm全局应力评估策略来近似结构最大应力
(10) $\begin{eqnarray} \label{eq10} \sigma_{\max } \approx \sigma^{PN}=\left[ {\sum\limits_{i=1}^N {\left( {\sigma_{i}^{vM} } \right)^{ps}} } \right]^{{1/{ps}}} \end{eqnarray} $
式中, $ps$为应力凝聚参数, 其取值对凝聚函数的近似质量和光滑度有较大影响. 理论上, 当 $ps\to\infty $ 时, 近似误差将减小, $\sigma^{PN}\to \max \left( {\sigma_{i}^{vM} } \right)$. 但较大$ps$取值将加剧凝聚函数的非线性, 引发迭代振荡及收敛困难问题, 不利于优化问题的高效稳健求解. 一般需要在足够光滑度和精确近似之间进行权衡, 以确定较合理的$ps$取值. 单元von Mises 应力则为
(11) $\begin{eqnarray} \label{eq11} \sigma_{i}^{vM} =\sqrt {{\sigma }_{i}^{T} {V}{\sigma }_{i} } \end{eqnarray} $
式中, $\sigma_{i}$ 为单元中心处的应力向量. 为有效处理应力奇异性问题, 这里采用文献[20 ]的方法, 对应力施加不同于刚度的幂指数惩罚
(12) $\begin{eqnarray} \label{eq12} {\sigma }_{i} =\left( {\bar{{x}}_{i} } \right)^{q}{D}_{0} {B}_{i} {u}_{i} \end{eqnarray} $
式中, $q$为应力惩罚因子, 这里取常用值$q=0.5$; $D_0$为实体材料弹性矩阵, $B_{i}$为单元$i$中心处的应变位移矩阵. 平面应力状态下, 常数矩阵$V$为
(13) $\begin{eqnarray} \label{eq13} {V}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c} 1 & {-{1/2}} & 0 \\ {-{1/2}} & 1 & 0 \\ 0 & 0 & 3 \\ \end{array} }} \right] \end{eqnarray} $
2.3 连通性约束方案
基于最大值函数, 表征结构连通性的静电势约束可表示为
(14) $\begin{eqnarray} \label{eq14} \phi_{\max } =\mathop{\max}\limits_{j=1,2,..., \ ND} \left( {\varphi _{j} } \right)\leqslant \eta \phi_{0} \end{eqnarray} $
式中, $\varphi_{j}$ 为节点势; $ND$为设计域节点总数. 为使约束函数可微, 同样可采用P-norm函数来近似全局势约束. 需要指出的是, 静电约束中的势量级一般较大, 以提高结构连通性的可识别性. 而较大凝聚项易导致凝聚函数值失准及计算溢出问题. 因此, 有必要对凝聚函数正则化, 得到改进的约束表达
(15) $\begin{eqnarray} \label{eq15} \phi^{PN}=\left[ {\sum\limits_{j=1}^{ND} {\left( {\frac{\varphi_{j} }{\eta \phi_{0} }} \right)^{pc}} } \right]^{{1/{pc}}}\leqslant 1 \end{eqnarray} $
式中, $pc$为势凝聚参数. 如前所述, 较大的凝聚参数值不利于高效稳健的优化求解, 而适中取值将不可避免的引入近似误差. 不同于前述目标函数中的最大近似目标值的趋势控制, 约束函数中的P-norm函数需要有效控制最大近似目标值, 而近似误差的存在将极大影响该控制效果. 此外, 这里的势约束效果对约束阈值有较强依赖性[35 ] , 较大的近似误差也不利于设计连通性的有效控制. 为此, 引入基于稳定控制的近似误差修正技术[22 ]
(16) $\begin{eqnarray} \label{eq16} \bar{{\phi }}^{PN}=c^{c}\cdot \phi^{PN}-1\leqslant 0 \end{eqnarray} $
式中, $c^{c}$ 为修正因子, 每次迭代按下式更新
(17) $\begin{eqnarray} \label{eq17} c_{n}^{c} =q_{n}^{c} \left[ {\frac{\max \left( {\varphi_{j} } \right)_{n} }{\left( {\eta \cdot \phi_{0} } \right)\cdot \phi_{n}^{PN} }} \right]+\left( {1-q_{n}^{c} } \right)c_{n-1}^{c} \end{eqnarray} $
式中, $c_{n}^{c} $ 和 $q_{n}^{c} $ 分别为第 $n$次迭代中的修正和控制因子. 这里取常用值$pc= 6$, $q^{c}= 0.5$, 和$c_{0}^{c} =1$.
3 灵敏度分析
为高效求解上述多约束优化问题, 采用相适宜的移动渐近线算法[42 ] .下面将利用链式法则和伴随法, 推导算法所需的目标和约束函数的一阶灵敏度信息. 基于链式法则, 任意函数 $g$关于设计变量 $x_{i}$ 的敏度为
(18) $\begin{eqnarray} \label{eq18} \frac{\partial g}{\partial x_{k} }=\sum\limits_{e\in NE_{k} } {\frac{\partial g}{\partial \bar{{x}}_{e} }\frac{\partial \bar{{x}}_{e} }{\partial \hat{{x}}_{e} }\frac{\partial \hat{{x}}_{e} }{\partial x_{k} }} \end{eqnarray} $
其中, ${{\partial \bar{{x}}_{e} }/{\partial \hat{{x}}_{e} }}$ 项可根据式 (9)求得
(19) $\begin{eqnarray} \label{eq19} \frac{\partial \bar{{x}}_{e} }{\partial \hat{{x}}_{e} }=\frac{\beta {sech}^{2}\left[ {\beta \left( {\hat{{x}}_{e} -x_{0} } \right)} \right]}{\tanh \left( {\beta x_{0} } \right)+\tanh \left[ {\beta \left( {1-x_{0} } \right)} \right]} \end{eqnarray} $
而${{\partial \hat{{x}}_{e} }/{\partial x_{k} }}$项可根据式 (8) 计算得到
(20) $\begin{eqnarray} \label{eq20} \frac{\partial \hat{{x}}_{e} }{\partial x_{k} }=\frac{\omega_{ek} v_{k} }{\sum\nolimits_{m\in NE_{e} } {\left( {\omega_{em} v_{m} } \right)} } \end{eqnarray} $
下面将推导目标和约束函数关于物理密度的敏度, 其中, 体积约束的敏度可直接求导, 故而省略.
3.1 目标函数灵敏度
目标函数式 (10) 关于单元物理密度的敏度可通过链式法则计算
(21) $\begin{eqnarray} \label{eq21} \frac{\partial \sigma^{PN}}{\partial \bar{{x}}_{e} }=\sum\limits_{i=1}^N {\frac{\partial \sigma^{PN}}{\partial \sigma _{i}^{vM} }\left( {\frac{\partial \sigma_{i}^{vM} }{\partial {\sigma }_{i} }} \right)^{T}\frac{\partial {\sigma }_{i} }{\partial \bar{{x}}_{e} }} \end{eqnarray} $
(22) $\begin{eqnarray} \label{eq22} \frac{\partial \sigma^{PN}}{\partial \sigma_{i}^{vM} }=\left( {\sigma^{PN}} \right)^{\left( {1-ps} \right)}\left( {\sigma _{i}^{vM} } \right)^{\left( {ps-1} \right)} \end{eqnarray} $
(23) $\begin{eqnarray} \label{eq23} \frac{\partial \sigma_{i}^{vM} }{\partial {\sigma }_{i} }=\frac{{V}{\sigma }_{i} }{\sigma_{i}^{vM} } \end{eqnarray} $
(24) $\begin{eqnarray} \label{eq24} \frac{\partial {\sigma }_{i} }{\partial \bar{{x}}_{e} }=\frac{q}{\bar{{x}}_{i} }\delta_{ei} {\sigma }_{i} +\left( {\bar{{x}}_{i} } \right)^{q}{D}_{0} {B}_{i} {L}_{i} \frac{\partial {U}}{\partial \bar{{x}}_{e} } \end{eqnarray} $
式中, $\delta_{ei}$为克罗内克函数; 矩阵$L_{i}$从全局位移矢量中聚集单元$i$ 的节点位移矢量. 假定载荷与设计无关, 将平衡方程$KU=F$对物理密度求导得到
(25) $\begin{eqnarray} \label{eq25} \frac{\partial {U}}{\partial \bar{{x}}_{e} }=-{K}^{-1}\frac{\partial {K}}{\partial \bar{{x}}_{e} }{U} \end{eqnarray} $
将式 (24) 和 式(25) 代入式 (21) 可得
(26) $\begin{eqnarray} \label{eq26} \frac{\partial \sigma^{PN}}{\partial \bar{{x}}_{e} }=\sum\limits_{i=1}^N {\frac{q}{\bar{{x}}_{i} }\delta_{ei} \frac{\partial \sigma^{PN}}{\partial \sigma_{i}^{vM} }\left( {\frac{\partial \sigma_{i}^{vM} }{\partial {\sigma }_{i} }} \right)^{T}{\sigma }_{i} } -{\lambda }_{s}^{T} \frac{\partial {K}}{\partial \bar{{x}}_{e} }{U} \end{eqnarray} $
式中, 伴随向量 $\lambda_{s}$ 为下列伴随方程的解
(27) $\begin{eqnarray} \label{eq27} {K\lambda }_{s} =\sum\limits_{i=1}^N {\left( {\bar{{x}}_{i} } \right)^{q}\frac{\partial \sigma^{PN}}{\partial \sigma _{i}^{vM} }\left( {{D}_{0} {B}_{i} {L}_{i} } \right)^{T}\frac{\partial \sigma_{i}^{vM} }{\partial {\sigma }_{i} }} \end{eqnarray} $
3.2 连通性约束灵敏度
(28) $\begin{eqnarray} \label{eq28} \frac{\partial \bar{{\phi }}^{PN}}{\partial \bar{{x}}_{e} }=c^{c} \left( {\frac{\partial \phi^{PN}}{\partial \bar{{x}}_{e} }} \right) \end{eqnarray} $
其中, ${{\partial \phi^{PN}}/{\partial \bar{{x}}_{e} }}_{ }$项可依据链式法则求得
(29) $\begin{eqnarray} \label{eq29} \frac{\partial \phi^{PN}}{\partial \bar{{x}}_{e} }=\sum\limits_{j=1}^{ND} {\frac{\partial \phi^{PN}}{\partial \varphi _{j} }\frac{\partial \varphi_{j} }{\partial \bar{{x}}_{e} }} =\sum\limits_{j=1}^{ND} {{d}_{j}^{T} \frac{\partial {U}^{\phi }}{\partial \bar{{x}}_{e} }} \end{eqnarray} $
(30) $\begin{eqnarray} \label{eq30} {d}_{j} =\left[ {{\begin{array}{*{20}c} {0\ \ } & {...\ \ } & {0\ \ } & {\left( {{{\partial \phi^{PN}}/{\partial \varphi_{j} }}} \right)\ \ } & {0\ \ } & {...\ \ } & 0 \\ \end{array} }} \right]^{T} \end{eqnarray} $
稀疏矩阵$d_{j}$与全局势矢量同维度. 由式 (15) 可得
(31) $\begin{eqnarray} \label{eq31} \frac{\partial \phi^{PN}}{\partial \varphi_{j} }=\frac{1}{\eta \phi_{0} }\left( {\phi^{PN}} \right)^{\left( {1-pc} \right)}\left( {\frac{\varphi_{j} }{\eta \cdot \phi_{0} }} \right)^{pc\mbox{-}1} \end{eqnarray} $
平衡方程$K^{\phi }U^{\phi }=F^{\phi}$ 对物理密度求导可得
(32) $\begin{eqnarray} \label{eq32} \frac{\partial {U}^{\phi }}{\partial \bar{{x}}_{e} }=\left( {{K}^{\phi }} \right)^{-1}\left( {\frac{\partial {F}^{\phi }}{\partial \bar{{x}}_{e} }-\frac{\partial {K}^{\phi }}{\partial \bar{{x}}_{e} }{U}^{\phi }} \right) \end{eqnarray} $
(33) $\begin{eqnarray} \label{eq33} \frac{\partial \phi^{PN}}{\partial \bar{{x}}_{e} }={\lambda }_{c}^{T} \left( {\frac{\partial {F}^{\phi }}{\partial \bar{{x}}_{e} }-\frac{\partial {K}^{\phi }}{\partial \bar{{x}}_{e} }{U}^{\phi }} \right) \end{eqnarray} $
式中, 伴随向量 $\lambda_{c}$ 通过求解下列伴随方程获取
(34) $\begin{eqnarray} \label{eq34} {K}^{\phi }{\lambda }_{c} =\sum\nolimits_{j=1}^{ND} {{d}_{j} } \end{eqnarray} $
由式 (7) 可求得${{\partial {F}^{\phi }}/{\partial \bar{{x}}_{e} }}$和${{\partial {K}^{\phi }}/{\partial \bar{{x}}_{e} }}$项.
4 数值算例和讨论
本节通过经典数值算例来验证所提方法. 不失一般性, 仅考虑平面应力问题, 优化参数均无量纲化. 除特别声明外, 弹性模量$E_{0}= 1$, 泊松比$v = 0.3$, 体积分数$f=0.4$; 为避免零密度导致的数值困难, 取设计变量下限为0.001; 所有域边界均设置为连通性约束边界. 为提高收敛效率, 算法中的默认移动限设为0.1. 当连续迭代之间设计变量的最大变化小于0.01或迭代循环的最大次数达到200时, 优化迭代停止. 设计拓扑和应力分布分别以灰度图(白色为空相, 黑色为固相)和彩色图(蓝色为低应力, 红色为高应力)表示.
4.1 算例1
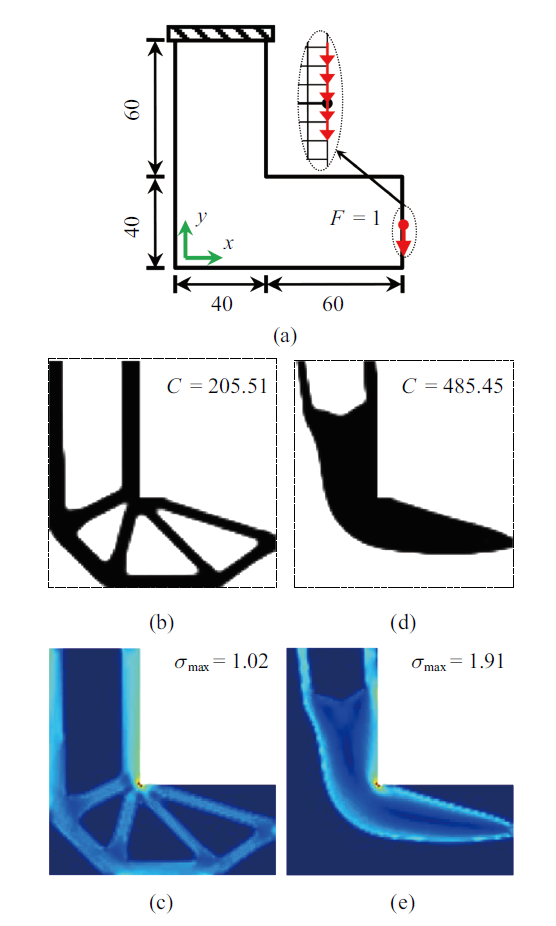
考虑经典L型梁优化问题[11 ,16 ] , 设计条件如图1 (a) 所示. 结构顶部固支, 右端中点受集中载荷作用. 为避免应力集中, 载荷均匀分布到中点附近的5个节点上. 采用6400个四节点双线性正方形有限元单元离散设计域. 过滤半径$r_{\min}=4$, 连通性约束阈值 $\eta = 1.00$.
图1
图1
L型梁问题 (a) 及其刚度设计 (b)(c) 和连通性刚度设计 (d)(e)
Fig.1
L-shape beam problem (a), the stiffness design (b)(c) and the connectivity stiffness design (d)(e)
为便于比较, 首先给出传统体积约束下的刚度最大化设计 (图1 (b)和图1 (c)), 以及考虑连通性约束的刚度最大化设计 (图1 (d)和图1 (e)). 从图1 (b)和图1 (c) 可以看出, 传统刚度设计含有一些明显的封闭孔洞构造 ($x$-$y$平面内), 不利于具有连通性要求的增材制造. 此外, 设计拐角处存在局部高应力集中, 易使结构发生断裂破坏, 给结构安全带来较大隐患.
从图1 (d)和图1 (e)可以看出, 引入连通性约束能够有效抑制优化设计中的封闭孔洞, 但所得设计出现了严重恶化的局部高应力集中, 其最大应力是传统刚度设计的1.87倍. 这表明可制造连通性优化设计中十分有必要考虑应力问题. 此外, 上述连通性设计的刚度比单纯的刚度设计要弱, 这是连通性设计所付出的必要代价[35 ] .
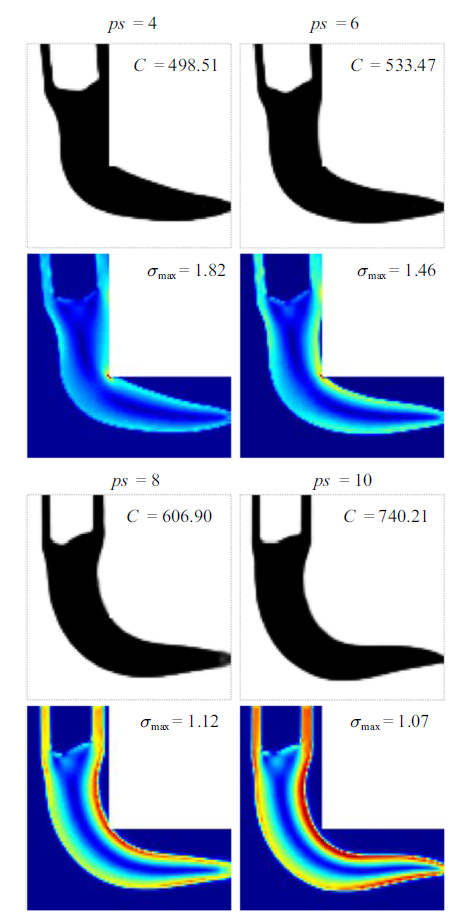
图2 展示了基于本文方法获得的不同应力凝聚参数下的应力最小化连通性设计. 可以看出, 所得设计均满足连通性要求. 这些设计拓扑构型相似, 但拐角处结构形状存在明显差异. 当凝聚参数较小时 (如$ps=4$), 所得设计与连通性刚度设计 (图1 (d)和图1 (e)) 相似. 随着凝聚参数增大, 拓扑形状发生显著变化, 拐角构造逐渐变圆, 应力集中效应得到有效缓解, 其代价是牺牲设计刚度. 当$ps=8$和10时, 所得设计几乎接近于满应力设计, 但$ps=8$ 时的综合性能(结构刚度和强度)较优. 显然, 利用本文方 法能够获取应力集中有效缓解的连通性设计, 且所得设计不同于传统的刚度最大化连通性设计. 此外, 上述结果还表明所得设计的性能与凝聚参数取值有关, 参数值并非越大越好, 合理取值才能有助于获取综合性能较优的设计.
图2
图2
不同应力凝聚参数下应力最小化连通性设计
Fig.2
Stress minimization connectivity designs for different stress aggregation parameters
图3 给出了图2 中性能最优设计$ps=8$ 的目标和约束函数的迭代历史. 可以看出, 本文方法优化迭代历程稳健, 最终设计能较好满足各约束条件.
图3
图3
设计$ps=8$的优化迭代历史
Fig.3
Iteration histories of the design of $ps=8$
为研究体积分数对应力最小化连通性设计的影响, 现考虑体积分数为0.3和0.5的优化问题, 优化结果如图4 所示. 为公平比较, 其余优化参数与图2 中$ps=8$的设计保持一致. 与前述体积分数0.4的设计相比, 设计的刚度和强度在体积分数较小时均显著降低, 反之, 则明显提高. 可见, 增加材料用量能够有助于提高所研究设计的强度和刚度性能.
图4
图4
不同体积分数下的应力最小化连通性设计
Fig.4
Stress minimization connectivity designs for different volume fractions
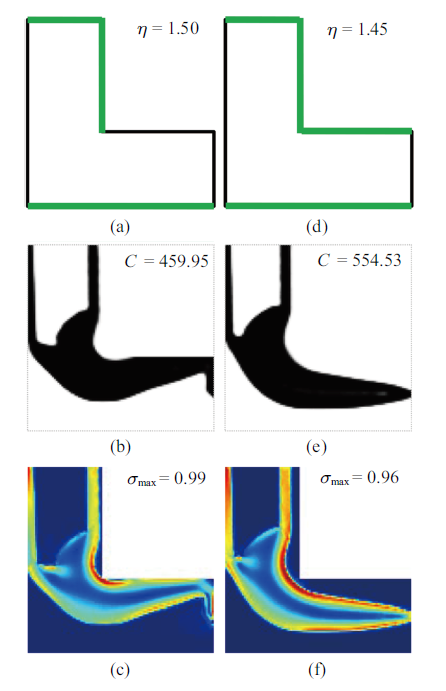
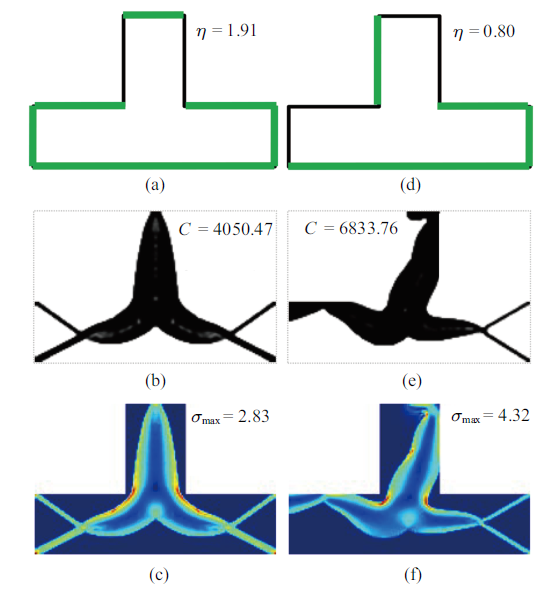
为考察连通性约束边界条件对应力最小化连通性设计的影响, 考虑如图5 (a) $\sim\!$图5 (c) 和图5 (d) $\sim\!$图5 (f)所示两种条件下的优化问题. 为便于比较,其余优化参数与图2 中ps $=$8的设计保持一致. 对比图2 和图5 的设计不难发现, 不同连通性约束边界条件可产生具有不同拓扑构型且性能各异的设计. 该现象遵循了泊松方法的约束边界依赖性规律. 特别地, 图5 (a) $\sim\!$图5 (c)设计的综合性能不仅比图2 中$ps=8$的设计要好(结构强度和刚度均分别提高了11.61${\%}$和24.21${\%}$), 而且比图1 (d)和图1 (e)中的连通性刚度设计也要强(结构强度和刚度均分别提高了48.17${\%}$和5.25${\%}$). 显然, 连通性约束边界条件对所研究设计的拓扑构型及性能均有较大影响. 然而, 由于边界条件的变化将产生新的优化约束问题, 这使得自动寻找最优约束边界条件仍旧是未来极具挑战性的工作[35 ] .
图5
图5
不同连通性约束边界条件下的应力最小化连通性设计, 绿色粗线表示约束边界
Fig.5
Stress minimization connectivity designs for different connectivity constraint boundary (highlighted by green thick lines) conditions
4.2 算例2
考虑典型T型梁优化问题[16 ,22 ] , 设计条件如图6 (a)所示, 结构左右两侧固支, 顶部中点受集中载荷作用. 为避免应力集中, 载荷均匀分配到中点附近5个节点上. 设计域离散为8800个四节点双线性正方形有限元单元. 过滤半径$r_{\min}=3$, 连通性约束阈值取 $\eta = 2.01$.
图6
图6
T型梁问题 (a) 及其刚度设计 (b)(c) 和连通性刚度设计 (d)(e)
Fig.6
T-shape beam problem (a), the stiffness design (b)(c) and the connectivity stiffness design (d)(e)
图6 (b) $\sim\!$图6 (e)分别展示了有/无连通性约束的刚度最大化设计. 可以看出, 由于封闭孔洞和局部高应力集中问题的存在, 这些设计在可制造性和/或结构强度方面存在明显局限性.
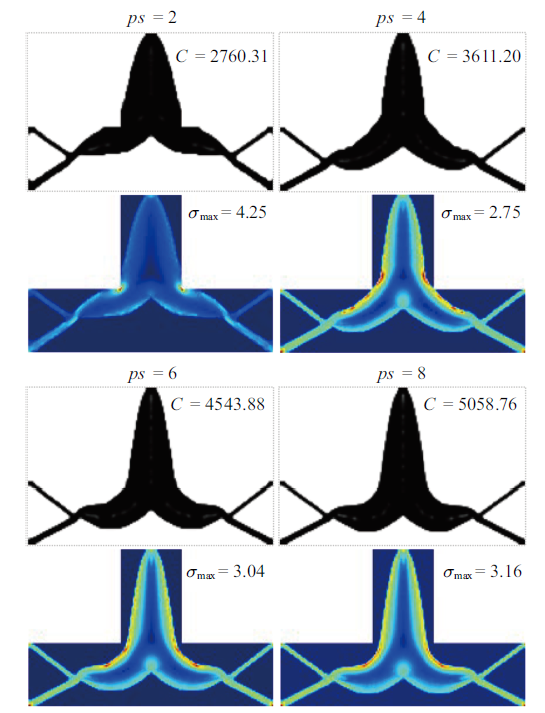
图7 给出了不同应力凝聚参数下的应力最小化连通性设计. 类似于L型梁设计情况, 所得设计均能满足连通性约束要求, 但设计综合性能随凝聚参数取值不同而有明显差异. 应力凝聚参数较小时, 设计结果趋近于传统刚度设计, 结构刚度最优但强度最弱; 随着应力凝聚参数增大, 应力集中现象将得到有效缓解, 但结构刚度也会削弱. 给出的设计中$ps= 4$的综合性能相对较优, 当应力凝聚参数值进一步增大时, 设计刚度和强度同步开始恶化. 上述研究再次论证了本文方法的有效性, 同时也揭示了所得设计对应力凝聚参数的依赖性. 数值经验表明, 对于本文所研究问题, 应力凝聚参数取值为4 $\sim$ 8时一般可获得较理想的优化效果.
图7
图7
不同应力凝聚参数下应力最小化连通性设计
Fig.7
Stress minimization connectivity designs for different stress aggregation parameters
图8 显示了不同连通性约束边界条件下的应力最小化连通性设计. 为公平比较, 其余优化参数与图7 中$ps=6$的设计保持一致. 可以看到, 图8 (a) $\sim\!$图8 (c)的设计与图7 中$ps=6$的设计相似, 但结构强度和刚度均有所提升(分别为6.91${\%}$和10.86${\%}$), 而图8 (d) $\sim\!$图8 (f)设计的拓扑构型则明显不同, 性能也有很大差异. 连通性约束边界条件对所研究设计的重要影响再次得到论证. 需要指出的是, 数值试验还表明, 连通性约束边界条件的变化并不能改变所得设计对应力凝聚参数的依赖.
图8
图8
不同连通性约束边界条件下的应力最小化连通性设计
Fig.8
Stress minimization connectivity designs for different connectivity constraint boundary conditions
5 结论
兼顾性能和可制造性的拓扑优化具有重要工程意义和研究价值. 本文面向增材制造, 提出了协同考虑结构强度和可制造连通性的拓扑优化方法. 构建了体积和连通性标量场约束下的应力最小化拓扑优化模型, 开发了有效的优化求解策略, 并详细推导了相关灵敏度列式. 典型数值算例结果表明, 传统的刚度最大化连通性设计不一定能避免局部高应力集中. 基于文中模型和方法所获得的应力最小化连通性设计在确保可制造连通性的同时, 能够有效减轻上述应力集中效应, 且优化迭代历程稳健. 优化结果还表明, 所得设计与体积分数、连通性约束边界条件和应力凝聚参数有关, 其合理配置是获取高性能设计的关键. 本文研究论证了可制造连通性拓扑优化中考虑应力问题的必要性和可行性, 可为高性能可制造性工程结构的研发提供有益参考.
参考文献
View Option
[1]
Eschenauer HA Olhoff N . Topology optimization of continuum structures: A review
Applied Mechanics Reviews 2001 ,54 (4 ):331 -390
[本文引用: 1]
[2]
Aage N Andreassen E Lazarov BS , et al . Giga-voxel computational morphogenesis for structural design
Nature 2017 ,550 (7674 ):84 -86
[本文引用: 1]
[3]
隋允康 , 边炳传 . 屈曲与应力约束下连续体结构的拓扑优化
工程力学 , 2008 ,25 (8 ):6 -12
[本文引用: 1]
(Sui Yunkang Bian Binchuan Topology optimization of continuum structures under bucking and stress constraints
Engineering Mechanics 2008 ,25 (8 ):6 -12 (in Chinese))
[本文引用: 1]
[4]
杜建镔 , 宋先凯 , 董立立 . 基于拓扑优化的声学结构材料分布设计
力学学报 , 2011 ,43 (2 ):306 -315
(Du Jianbin Song Xiankai Dong Lili Design of material distribution of acoustic structure using topology optimization
Chinese Journal of Theoretical and Applied Mechanics 2011 ,43 (2 ):306 -315 (in Chinese))
[5]
胡骏 , 亢战 . 考虑可控性的压电作动器拓扑优化设计
力学学报 , 2019 ,51 (4 ):1073 -1081
[本文引用: 1]
(Hu Jun Kang Zhan Topology optimization of piezoelectric actuator considering controllability
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (4 ):1073 -1081 (in Chinese))
[本文引用: 1]
[6]
Liu J Gaynor AT Chen S , et al . Current and future trends in topology optimization for additive manufacturing
Structural and multidisciplinary optimization 2018 ,57 (6 ):2457 -2483
[本文引用: 2]
[7]
Meng L Zhang W Quan D , et al . From topology optimization design to additive manufacturing: Today's success and tomorrow's roadmap
Archives of Computational Methods in Engineering 2019 ,27 (3 ):805 -830
[本文引用: 2]
[8]
Luo Y Wang MY Kang Z . An enhanced aggregation method for topology optimization with local stress constraints
Computer Methods in Applied Mechanics and Engineering 2013 ,254 :31 -41
[本文引用: 2]
[9]
Rong JH Xiao TT Yu LH , et al . Continuum structural topological optimizations with stress constraints based on an active constraint technique
International Journal for Numerical Methods in Engineering 2016 ,108 (4 ):326 -360
[10]
Duysinx P van Miegroet L Lemaire E , et al . Topology and generalized shape optimization: Why stress constraints are so important?
International Journal for Simulation and Multidisciplinary Design Optimization 2008 ,2 (4 ):253 -258
[本文引用: 1]
[11]
Guo X Zhang WS Wang MY , et al . Stress-related topology optimization via level set approach
Computer Methods in Applied Mechanics and Engineering 2011 ,200 (47-48 ):3439 -3452
[本文引用: 2]
[12]
隋允康 , 叶红玲 , 彭细荣 等 . 连续体结构拓扑优化应力约束凝聚化的ICM方法
力学学报 , 2007 ,39 (4 ):554 -563
[本文引用: 1]
(Sui Yunkang Ye Hongling Peng Xirong et al . The ICM method for continuum structural topology optimization with condensation of stress constraints
Chinese Journal of Theoretical and Applied Mechanics 2007 ,39 (4 ):554 -563 (in Chinese))
[本文引用: 1]
[13]
Rozvany GIN Birker T . On singular topologies in exact layout optimization
Structural Optimization 1994 ,8 (4 ):228 -235
[本文引用: 1]
[14]
Yang R Chen C . Stress-based topology optimization
Structural Optimization 1996 ,12 (2 ):98 -105
[本文引用: 2]
[15]
龙凯 , 王选 , 吉亮 . 面向应力约束的独立连续映射方法
力学学报 , 2019 ,51 (2 ):620 -629
[本文引用: 1]
(Long Kai Wang Xuan Ji Liang Independent continuous mapping method for stress constraint
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (2 ):620 -629 (in Chinese))
[本文引用: 1]
[16]
王选 , 刘宏亮 , 龙凯 等 . 基于改进的双向渐进结构优化法的应力约束拓扑优化
力学学报 , 2018 ,50 (2 ):385 -394
[本文引用: 2]
(Wang Xuan Liu Hongliang Long Kai et al . Stress-constrained topology optimization based on improved bidirectional evolutionary optimization method
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (2 ):385 -394 (in Chinese))
[本文引用: 2]
[17]
Xia L Zhang L Xia Q , et al . Stress-based topology optimization using bi-directional evolutionary structural optimization method
Computer Methods in Applied Mechanics and Engineering 2018 ,333 :356 -370
[本文引用: 1]
[18]
Duysinx P Bendsøe MP . Topology optimization of continuum structures with local stress constraints
International Journal for Numerical Methods in Engineering 1998 ,43 (8 ):1453 -1478
[本文引用: 1]
[19]
Da Silva G A Beck A T Sigmund O . Stress-constrained topology optimization considering uniform manufacturing uncertainties
Computer Methods in Applied Mechanics and Engineering 2019 ,344 :512 -537
[本文引用: 2]
[20]
Le C Norato J Bruns T , et al . Stress-based topology optimization for continua
Structural and Multidisciplinary Optimization 2010 ,41 (4 ):605 -620
[本文引用: 3]
[21]
Cheng GD Guo X . $\varepsilon $-relaxed approach in structural topology optimization
Structural Optimization 1997 ,13 (4 ):258 -266
[本文引用: 1]
[22]
Yang D Liu H Zhang W , et al . Stress-constrained topology optimization based on maximum stress measures
Computers & Structures 2018 ,198 :23 -39
[本文引用: 3]
[23]
隋允康 , 叶红玲 , 彭细荣 . 应力约束全局化策略下的连续体结构拓扑优化
力学学报 , 2006 ,38 (3 ):364 -370
[本文引用: 1]
(Sui Yunkang Ye Hongling Peng Xirong Topological optimization of continuum structure under the strategy of globalization of stress constraints
Chinese Journal of Theoretical and Applied Mechanics 2006 ,38 (3 ):364 -370 (in Chinese))
[本文引用: 1]
[24]
Liu J Ma Y . A survey of manufacturing oriented topology optimization methods
Advances in Engineering Software 2016 ,100 :161 -175
[本文引用: 1]
[25]
刘书田 , 李取浩 , 陈文炯 等 . 拓扑优化与增材制造结合: 一种设计与制造一体化方法
航空制造技术 , 2017 (10 ):26 -31
[本文引用: 2]
(Liu Shutian Li Quhao Chen Wenjiong Combination of topology optimization and additive manufacturing: an integration method of structural design and manufacturing
Aeronautical Manufacturing Technology 2017 (10 ):26 -31 (in Chinese))
[本文引用: 2]
[26]
Salonitis K . Design for additive manufacturing based on the axiomatic design method
The International Journal of Advanced Manufacturing Technology 2016 ,87 (1-4 ):989 -996
[本文引用: 1]
[27]
Liu S Li Q Chen W , et al . An identification method for enclosed voids restriction in manufacturability design for additive manufacturing structures
Frontiers of Mechanical Engineering 2015 ,10 (2 ):126 -137
[本文引用: 5]
[28]
Zhou L Zhang W . Topology optimization method with elimination of enclosed voids
Structural and Multidisciplinary Optimization 2019 ,60 (1 ):117 -136
[本文引用: 1]
[29]
Li Q Chen W Liu S , et al . Structural topology optimization considering connectivity constraint
Structural and Multidisciplinary Optimization 2016 ,54 (4 ):971 -984
[本文引用: 4]
[30]
Xiong Y Yao S Zhao Z , et al . A new approach to eliminating enclosed voids in topology optimization for additive manufacturing
Additive Manufacturing 2020 ,32 :101006
[本文引用: 1]
[31]
Xia Q Shi T Wang MY , et al . A level set based method for the optimization of cast part
Structural and Multidisciplinary Optimization 2010 ,41 (5 ):735 -747
[本文引用: 1]
[32]
Wang Y Kang Z . Structural shape and topology optimization of cast parts using level set method
International Journal for Numerical Methods in Engineering 2017 ,111 (13 ):1252 -1273
[本文引用: 1]
[33]
Sigmund O Maute K . Topology optimization approaches
Structural and Multidisciplinary Optimization 2013 ,48 (6 ):1031 -1055
[本文引用: 1]
[34]
Sigmund O . Morphology-based black and white filters for topology optimization
Structural and Multidisciplinary Optimization 2007 ,33 (4-5 ):401 -424
[本文引用: 1]
[35]
Wang C Xu B Meng Q , et al . Numerical performance of Poisson method for restricting enclosed voids in topology optimization
Computers & Structures 2020 ,239 :106337
[本文引用: 8]
[36]
Jin J The Finite Element Method in Electromagnetics. 3rd. New Jersey : Wiley-IEEE Press , 2014 : 1 -7
[本文引用: 1]
[37]
Sigmund O Petersson J . Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima
Structural and Multidisciplinary Optimization 1998 ,16 (1 ):68 -75
[本文引用: 1]
[38]
Bruns T E Tortorelli D A . Topology optimization of non-linear elastic structures and compliant mechanisms
Computer Methods in Applied Mechanics and Engineering 2001 ,190 (26 ):3443 -3459
[本文引用: 1]
[39]
Bourdin B . Filters in topology optimization
International Journal for Numerical Methods in Engineering 2001 ,50 (9 ):2143 -2158
[本文引用: 1]
[40]
Wang F Lazarov BS Sigmund O . On projection methods, convergence and robust formulations in topology optimization
Structural and Multidisciplinary Optimization 2011 ,43 (6 ):767 -784
[本文引用: 1]
[41]
Gao X Li Y Ma H , et al . Improving the overall performance of continuum structures: A topology optimization model considering stiffness, strength and stability
Computer Methods in Applied Mechanics and Engineering 2020 ,359 :112660
[本文引用: 1]
[42]
Svanberg K . The method of moving asymptotes——a new method for structural optimization
International Journal for Numerical Methods in Engineering 1987 ,24 (2 ):359 -373
[本文引用: 1]
Topology optimization of continuum structures: A review
1
2001
... 拓扑优化是一种重要的结构优化方法, 已得到学术界和工业界的广泛关注[1 -2 ] . 多年来, 大量研究致力于如何利用拓扑优化改进设计性能[3 -5 ] . 随着该方法的进一步推广应用, 优化设计的可制造性问题逐渐引起人们的重视[6 -7 ] . 然而, 现有研究关于性能和可制造性的考虑通常是分开处理的, 常侧重于某一方面指标. 因此, 将这两个重要而又不可或缺的设计目标结合起来进行优化设计, 将是一项极具实际应用价值且富有挑战性的工作. ...
Giga-voxel computational morphogenesis for structural design
1
2017
... 拓扑优化是一种重要的结构优化方法, 已得到学术界和工业界的广泛关注[1 -2 ] . 多年来, 大量研究致力于如何利用拓扑优化改进设计性能[3 -5 ] . 随着该方法的进一步推广应用, 优化设计的可制造性问题逐渐引起人们的重视[6 -7 ] . 然而, 现有研究关于性能和可制造性的考虑通常是分开处理的, 常侧重于某一方面指标. 因此, 将这两个重要而又不可或缺的设计目标结合起来进行优化设计, 将是一项极具实际应用价值且富有挑战性的工作. ...
屈曲与应力约束下连续体结构的拓扑优化
1
2008
... 拓扑优化是一种重要的结构优化方法, 已得到学术界和工业界的广泛关注[1 -2 ] . 多年来, 大量研究致力于如何利用拓扑优化改进设计性能[3 -5 ] . 随着该方法的进一步推广应用, 优化设计的可制造性问题逐渐引起人们的重视[6 -7 ] . 然而, 现有研究关于性能和可制造性的考虑通常是分开处理的, 常侧重于某一方面指标. 因此, 将这两个重要而又不可或缺的设计目标结合起来进行优化设计, 将是一项极具实际应用价值且富有挑战性的工作. ...
屈曲与应力约束下连续体结构的拓扑优化
1
2008
... 拓扑优化是一种重要的结构优化方法, 已得到学术界和工业界的广泛关注[1 -2 ] . 多年来, 大量研究致力于如何利用拓扑优化改进设计性能[3 -5 ] . 随着该方法的进一步推广应用, 优化设计的可制造性问题逐渐引起人们的重视[6 -7 ] . 然而, 现有研究关于性能和可制造性的考虑通常是分开处理的, 常侧重于某一方面指标. 因此, 将这两个重要而又不可或缺的设计目标结合起来进行优化设计, 将是一项极具实际应用价值且富有挑战性的工作. ...
考虑可控性的压电作动器拓扑优化设计
1
2019
... 拓扑优化是一种重要的结构优化方法, 已得到学术界和工业界的广泛关注[1 -2 ] . 多年来, 大量研究致力于如何利用拓扑优化改进设计性能[3 -5 ] . 随着该方法的进一步推广应用, 优化设计的可制造性问题逐渐引起人们的重视[6 -7 ] . 然而, 现有研究关于性能和可制造性的考虑通常是分开处理的, 常侧重于某一方面指标. 因此, 将这两个重要而又不可或缺的设计目标结合起来进行优化设计, 将是一项极具实际应用价值且富有挑战性的工作. ...
考虑可控性的压电作动器拓扑优化设计
1
2019
... 拓扑优化是一种重要的结构优化方法, 已得到学术界和工业界的广泛关注[1 -2 ] . 多年来, 大量研究致力于如何利用拓扑优化改进设计性能[3 -5 ] . 随着该方法的进一步推广应用, 优化设计的可制造性问题逐渐引起人们的重视[6 -7 ] . 然而, 现有研究关于性能和可制造性的考虑通常是分开处理的, 常侧重于某一方面指标. 因此, 将这两个重要而又不可或缺的设计目标结合起来进行优化设计, 将是一项极具实际应用价值且富有挑战性的工作. ...
Current and future trends in topology optimization for additive manufacturing
2
2018
... 拓扑优化是一种重要的结构优化方法, 已得到学术界和工业界的广泛关注[1 -2 ] . 多年来, 大量研究致力于如何利用拓扑优化改进设计性能[3 -5 ] . 随着该方法的进一步推广应用, 优化设计的可制造性问题逐渐引起人们的重视[6 -7 ] . 然而, 现有研究关于性能和可制造性的考虑通常是分开处理的, 常侧重于某一方面指标. 因此, 将这两个重要而又不可或缺的设计目标结合起来进行优化设计, 将是一项极具实际应用价值且富有挑战性的工作. ...
... 事实上, 拓扑优化设计常面临可制造性问题[24 ] . 在传统制造技术条件下, 优化产生的复杂构型将给产品制备带来巨大挑战. 这在一定程度上限制了拓扑优化的推广应用, 不利于高性能产品的研发. 作为一种先进的制造技术, 增材制造能够实现高度复杂结构的有效制备[25 ] . 将增材制造与拓扑优化有机结合, 能够大幅提高创新产品的研制能力, 现已成为重要研究方向[6 -7 ,25 ] . 然而, 增材制造并非"自由"制造, 有其独特的制造约束. 要求结构不含封闭孔洞的连通性约束便是其中最重要的制造约束之一[26 -27 ] . 如果结构含有封闭孔洞, 制造后残留在孔洞内的未熔融粉末或支撑结构将难以去除. 显然, 面向增材制造, 考虑可制造连通性的拓扑优化问题将具有重要工程应用价值[27 -29 ] . ...
From topology optimization design to additive manufacturing: Today's success and tomorrow's roadmap
2
2019
... 拓扑优化是一种重要的结构优化方法, 已得到学术界和工业界的广泛关注[1 -2 ] . 多年来, 大量研究致力于如何利用拓扑优化改进设计性能[3 -5 ] . 随着该方法的进一步推广应用, 优化设计的可制造性问题逐渐引起人们的重视[6 -7 ] . 然而, 现有研究关于性能和可制造性的考虑通常是分开处理的, 常侧重于某一方面指标. 因此, 将这两个重要而又不可或缺的设计目标结合起来进行优化设计, 将是一项极具实际应用价值且富有挑战性的工作. ...
... 事实上, 拓扑优化设计常面临可制造性问题[24 ] . 在传统制造技术条件下, 优化产生的复杂构型将给产品制备带来巨大挑战. 这在一定程度上限制了拓扑优化的推广应用, 不利于高性能产品的研发. 作为一种先进的制造技术, 增材制造能够实现高度复杂结构的有效制备[25 ] . 将增材制造与拓扑优化有机结合, 能够大幅提高创新产品的研制能力, 现已成为重要研究方向[6 -7 ,25 ] . 然而, 增材制造并非"自由"制造, 有其独特的制造约束. 要求结构不含封闭孔洞的连通性约束便是其中最重要的制造约束之一[26 -27 ] . 如果结构含有封闭孔洞, 制造后残留在孔洞内的未熔融粉末或支撑结构将难以去除. 显然, 面向增材制造, 考虑可制造连通性的拓扑优化问题将具有重要工程应用价值[27 -29 ] . ...
An enhanced aggregation method for topology optimization with local stress constraints
2
2013
... 早期基于拓扑优化的设计性能研究主要集中在刚度问题上, 但在实际工程应用中, 多数设计还应考虑强度要求[8 -10 ] . 因为局部高应力集中易导致构件疲劳损伤和断裂破坏, 将严重影响结构的安全使用和耐久性. 在这种情况下, 考虑应力相关的拓扑优化将发挥重要作用[11 -12 ] . 此外, 研究还表明[13 -14 ] 强度最大化设计并不一定等同于刚度最大化设计, 这就意味着在刚度最大化准则下获得的优化设计将不一定适用于强度导向下的工程问题. 因此, 面向强度需求, 研究基于应力的拓扑优化问题既符合工程需要也极具研究意义[15 -17 ] . ...
... 自Duysinx等[18 ] 提出连续体结构应力拓扑优化研究以来, 应力相关的拓扑优化问题受到了越来越多的关注. 然而, 考虑应力相关的拓扑优化问题有其自身难点, 常面临应力奇异性、局部性、非线性及度量准确性等问题[19 -20 ] . 为此, 不少学者提出了不同的解决方法. 目前常用的处理方法包括松弛方法[21 ] 、基于P范数或K-S函数的凝聚技术[8 ,14 ] 、分区度量[20 ] 、以及凝聚近似误差修正策略[22 ] 等. 此外, 隋允康等[23 ] 提出的将局部应力约束向整体应变能约束转化的方法也可有效解决应力局部性问题. 尽管上述方法能有效处理常规的拓扑优化问题, 但尚未涉及复杂的可制造性拓扑优化问题. ...
Continuum structural topological optimizations with stress constraints based on an active constraint technique
0
2016
Topology and generalized shape optimization: Why stress constraints are so important?
1
2008
... 早期基于拓扑优化的设计性能研究主要集中在刚度问题上, 但在实际工程应用中, 多数设计还应考虑强度要求[8 -10 ] . 因为局部高应力集中易导致构件疲劳损伤和断裂破坏, 将严重影响结构的安全使用和耐久性. 在这种情况下, 考虑应力相关的拓扑优化将发挥重要作用[11 -12 ] . 此外, 研究还表明[13 -14 ] 强度最大化设计并不一定等同于刚度最大化设计, 这就意味着在刚度最大化准则下获得的优化设计将不一定适用于强度导向下的工程问题. 因此, 面向强度需求, 研究基于应力的拓扑优化问题既符合工程需要也极具研究意义[15 -17 ] . ...
Stress-related topology optimization via level set approach
2
2011
... 早期基于拓扑优化的设计性能研究主要集中在刚度问题上, 但在实际工程应用中, 多数设计还应考虑强度要求[8 -10 ] . 因为局部高应力集中易导致构件疲劳损伤和断裂破坏, 将严重影响结构的安全使用和耐久性. 在这种情况下, 考虑应力相关的拓扑优化将发挥重要作用[11 -12 ] . 此外, 研究还表明[13 -14 ] 强度最大化设计并不一定等同于刚度最大化设计, 这就意味着在刚度最大化准则下获得的优化设计将不一定适用于强度导向下的工程问题. 因此, 面向强度需求, 研究基于应力的拓扑优化问题既符合工程需要也极具研究意义[15 -17 ] . ...
... 考虑经典L型梁优化问题[11 ,16 ] , 设计条件如图1 (a) 所示. 结构顶部固支, 右端中点受集中载荷作用. 为避免应力集中, 载荷均匀分布到中点附近的5个节点上. 采用6400个四节点双线性正方形有限元单元离散设计域. 过滤半径$r_{\min}=4$, 连通性约束阈值 $\eta = 1.00$. ...
连续体结构拓扑优化应力约束凝聚化的ICM方法
1
2007
... 早期基于拓扑优化的设计性能研究主要集中在刚度问题上, 但在实际工程应用中, 多数设计还应考虑强度要求[8 -10 ] . 因为局部高应力集中易导致构件疲劳损伤和断裂破坏, 将严重影响结构的安全使用和耐久性. 在这种情况下, 考虑应力相关的拓扑优化将发挥重要作用[11 -12 ] . 此外, 研究还表明[13 -14 ] 强度最大化设计并不一定等同于刚度最大化设计, 这就意味着在刚度最大化准则下获得的优化设计将不一定适用于强度导向下的工程问题. 因此, 面向强度需求, 研究基于应力的拓扑优化问题既符合工程需要也极具研究意义[15 -17 ] . ...
连续体结构拓扑优化应力约束凝聚化的ICM方法
1
2007
... 早期基于拓扑优化的设计性能研究主要集中在刚度问题上, 但在实际工程应用中, 多数设计还应考虑强度要求[8 -10 ] . 因为局部高应力集中易导致构件疲劳损伤和断裂破坏, 将严重影响结构的安全使用和耐久性. 在这种情况下, 考虑应力相关的拓扑优化将发挥重要作用[11 -12 ] . 此外, 研究还表明[13 -14 ] 强度最大化设计并不一定等同于刚度最大化设计, 这就意味着在刚度最大化准则下获得的优化设计将不一定适用于强度导向下的工程问题. 因此, 面向强度需求, 研究基于应力的拓扑优化问题既符合工程需要也极具研究意义[15 -17 ] . ...
On singular topologies in exact layout optimization
1
1994
... 早期基于拓扑优化的设计性能研究主要集中在刚度问题上, 但在实际工程应用中, 多数设计还应考虑强度要求[8 -10 ] . 因为局部高应力集中易导致构件疲劳损伤和断裂破坏, 将严重影响结构的安全使用和耐久性. 在这种情况下, 考虑应力相关的拓扑优化将发挥重要作用[11 -12 ] . 此外, 研究还表明[13 -14 ] 强度最大化设计并不一定等同于刚度最大化设计, 这就意味着在刚度最大化准则下获得的优化设计将不一定适用于强度导向下的工程问题. 因此, 面向强度需求, 研究基于应力的拓扑优化问题既符合工程需要也极具研究意义[15 -17 ] . ...
Stress-based topology optimization
2
1996
... 早期基于拓扑优化的设计性能研究主要集中在刚度问题上, 但在实际工程应用中, 多数设计还应考虑强度要求[8 -10 ] . 因为局部高应力集中易导致构件疲劳损伤和断裂破坏, 将严重影响结构的安全使用和耐久性. 在这种情况下, 考虑应力相关的拓扑优化将发挥重要作用[11 -12 ] . 此外, 研究还表明[13 -14 ] 强度最大化设计并不一定等同于刚度最大化设计, 这就意味着在刚度最大化准则下获得的优化设计将不一定适用于强度导向下的工程问题. 因此, 面向强度需求, 研究基于应力的拓扑优化问题既符合工程需要也极具研究意义[15 -17 ] . ...
... 自Duysinx等[18 ] 提出连续体结构应力拓扑优化研究以来, 应力相关的拓扑优化问题受到了越来越多的关注. 然而, 考虑应力相关的拓扑优化问题有其自身难点, 常面临应力奇异性、局部性、非线性及度量准确性等问题[19 -20 ] . 为此, 不少学者提出了不同的解决方法. 目前常用的处理方法包括松弛方法[21 ] 、基于P范数或K-S函数的凝聚技术[8 ,14 ] 、分区度量[20 ] 、以及凝聚近似误差修正策略[22 ] 等. 此外, 隋允康等[23 ] 提出的将局部应力约束向整体应变能约束转化的方法也可有效解决应力局部性问题. 尽管上述方法能有效处理常规的拓扑优化问题, 但尚未涉及复杂的可制造性拓扑优化问题. ...
面向应力约束的独立连续映射方法
1
2019
... 早期基于拓扑优化的设计性能研究主要集中在刚度问题上, 但在实际工程应用中, 多数设计还应考虑强度要求[8 -10 ] . 因为局部高应力集中易导致构件疲劳损伤和断裂破坏, 将严重影响结构的安全使用和耐久性. 在这种情况下, 考虑应力相关的拓扑优化将发挥重要作用[11 -12 ] . 此外, 研究还表明[13 -14 ] 强度最大化设计并不一定等同于刚度最大化设计, 这就意味着在刚度最大化准则下获得的优化设计将不一定适用于强度导向下的工程问题. 因此, 面向强度需求, 研究基于应力的拓扑优化问题既符合工程需要也极具研究意义[15 -17 ] . ...
面向应力约束的独立连续映射方法
1
2019
... 早期基于拓扑优化的设计性能研究主要集中在刚度问题上, 但在实际工程应用中, 多数设计还应考虑强度要求[8 -10 ] . 因为局部高应力集中易导致构件疲劳损伤和断裂破坏, 将严重影响结构的安全使用和耐久性. 在这种情况下, 考虑应力相关的拓扑优化将发挥重要作用[11 -12 ] . 此外, 研究还表明[13 -14 ] 强度最大化设计并不一定等同于刚度最大化设计, 这就意味着在刚度最大化准则下获得的优化设计将不一定适用于强度导向下的工程问题. 因此, 面向强度需求, 研究基于应力的拓扑优化问题既符合工程需要也极具研究意义[15 -17 ] . ...
基于改进的双向渐进结构优化法的应力约束拓扑优化
2
2018
... 考虑经典L型梁优化问题[11 ,16 ] , 设计条件如图1 (a) 所示. 结构顶部固支, 右端中点受集中载荷作用. 为避免应力集中, 载荷均匀分布到中点附近的5个节点上. 采用6400个四节点双线性正方形有限元单元离散设计域. 过滤半径$r_{\min}=4$, 连通性约束阈值 $\eta = 1.00$. ...
... 考虑典型T型梁优化问题[16 ,22 ] , 设计条件如图6 (a)所示, 结构左右两侧固支, 顶部中点受集中载荷作用. 为避免应力集中, 载荷均匀分配到中点附近5个节点上. 设计域离散为8800个四节点双线性正方形有限元单元. 过滤半径$r_{\min}=3$, 连通性约束阈值取 $\eta = 2.01$. ...
基于改进的双向渐进结构优化法的应力约束拓扑优化
2
2018
... 考虑经典L型梁优化问题[11 ,16 ] , 设计条件如图1 (a) 所示. 结构顶部固支, 右端中点受集中载荷作用. 为避免应力集中, 载荷均匀分布到中点附近的5个节点上. 采用6400个四节点双线性正方形有限元单元离散设计域. 过滤半径$r_{\min}=4$, 连通性约束阈值 $\eta = 1.00$. ...
... 考虑典型T型梁优化问题[16 ,22 ] , 设计条件如图6 (a)所示, 结构左右两侧固支, 顶部中点受集中载荷作用. 为避免应力集中, 载荷均匀分配到中点附近5个节点上. 设计域离散为8800个四节点双线性正方形有限元单元. 过滤半径$r_{\min}=3$, 连通性约束阈值取 $\eta = 2.01$. ...
Stress-based topology optimization using bi-directional evolutionary structural optimization method
1
2018
... 早期基于拓扑优化的设计性能研究主要集中在刚度问题上, 但在实际工程应用中, 多数设计还应考虑强度要求[8 -10 ] . 因为局部高应力集中易导致构件疲劳损伤和断裂破坏, 将严重影响结构的安全使用和耐久性. 在这种情况下, 考虑应力相关的拓扑优化将发挥重要作用[11 -12 ] . 此外, 研究还表明[13 -14 ] 强度最大化设计并不一定等同于刚度最大化设计, 这就意味着在刚度最大化准则下获得的优化设计将不一定适用于强度导向下的工程问题. 因此, 面向强度需求, 研究基于应力的拓扑优化问题既符合工程需要也极具研究意义[15 -17 ] . ...
Topology optimization of continuum structures with local stress constraints
1
1998
... 自Duysinx等[18 ] 提出连续体结构应力拓扑优化研究以来, 应力相关的拓扑优化问题受到了越来越多的关注. 然而, 考虑应力相关的拓扑优化问题有其自身难点, 常面临应力奇异性、局部性、非线性及度量准确性等问题[19 -20 ] . 为此, 不少学者提出了不同的解决方法. 目前常用的处理方法包括松弛方法[21 ] 、基于P范数或K-S函数的凝聚技术[8 ,14 ] 、分区度量[20 ] 、以及凝聚近似误差修正策略[22 ] 等. 此外, 隋允康等[23 ] 提出的将局部应力约束向整体应变能约束转化的方法也可有效解决应力局部性问题. 尽管上述方法能有效处理常规的拓扑优化问题, 但尚未涉及复杂的可制造性拓扑优化问题. ...
Stress-constrained topology optimization considering uniform manufacturing uncertainties
2
2019
... 自Duysinx等[18 ] 提出连续体结构应力拓扑优化研究以来, 应力相关的拓扑优化问题受到了越来越多的关注. 然而, 考虑应力相关的拓扑优化问题有其自身难点, 常面临应力奇异性、局部性、非线性及度量准确性等问题[19 -20 ] . 为此, 不少学者提出了不同的解决方法. 目前常用的处理方法包括松弛方法[21 ] 、基于P范数或K-S函数的凝聚技术[8 ,14 ] 、分区度量[20 ] 、以及凝聚近似误差修正策略[22 ] 等. 此外, 隋允康等[23 ] 提出的将局部应力约束向整体应变能约束转化的方法也可有效解决应力局部性问题. 尽管上述方法能有效处理常规的拓扑优化问题, 但尚未涉及复杂的可制造性拓扑优化问题. ...
... 式中, $\beta >0$ 为控制投影函数非线性的投影参数; $x_{0}\in[0,1]$ 为调节投影函数拐点的投影阈值, 本文取常用值 $x_{0} = 0.5$. 为提高应力评估准确性以及优化迭代稳定性, 参考文献[19 , 41 ], 这里采用连续化策略定义 $\beta $ 值: 在前10步迭代中取 $\beta = 1$, 此后每步迭代加1直至 $\beta = 10$. 由于物理密度定义了单元属性, 在后续研究中将使用物理密度进行结构分析. 值得注意的是, 过滤和投影会影响连通性约束, 考虑这种影响对基于泊松方法的连通性约束的有效实现具有重要意义, 感兴趣的读者可以参阅文献[35 ]. ...
Stress-based topology optimization for continua
3
2010
... 自Duysinx等[18 ] 提出连续体结构应力拓扑优化研究以来, 应力相关的拓扑优化问题受到了越来越多的关注. 然而, 考虑应力相关的拓扑优化问题有其自身难点, 常面临应力奇异性、局部性、非线性及度量准确性等问题[19 -20 ] . 为此, 不少学者提出了不同的解决方法. 目前常用的处理方法包括松弛方法[21 ] 、基于P范数或K-S函数的凝聚技术[8 ,14 ] 、分区度量[20 ] 、以及凝聚近似误差修正策略[22 ] 等. 此外, 隋允康等[23 ] 提出的将局部应力约束向整体应变能约束转化的方法也可有效解决应力局部性问题. 尽管上述方法能有效处理常规的拓扑优化问题, 但尚未涉及复杂的可制造性拓扑优化问题. ...
... [20 ]、以及凝聚近似误差修正策略[22 ] 等. 此外, 隋允康等[23 ] 提出的将局部应力约束向整体应变能约束转化的方法也可有效解决应力局部性问题. 尽管上述方法能有效处理常规的拓扑优化问题, 但尚未涉及复杂的可制造性拓扑优化问题. ...
... 式中, $\sigma_{i}$ 为单元中心处的应力向量. 为有效处理应力奇异性问题, 这里采用文献[20 ]的方法, 对应力施加不同于刚度的幂指数惩罚 ...
$\varepsilon $-relaxed approach in structural topology optimization
1
1997
... 自Duysinx等[18 ] 提出连续体结构应力拓扑优化研究以来, 应力相关的拓扑优化问题受到了越来越多的关注. 然而, 考虑应力相关的拓扑优化问题有其自身难点, 常面临应力奇异性、局部性、非线性及度量准确性等问题[19 -20 ] . 为此, 不少学者提出了不同的解决方法. 目前常用的处理方法包括松弛方法[21 ] 、基于P范数或K-S函数的凝聚技术[8 ,14 ] 、分区度量[20 ] 、以及凝聚近似误差修正策略[22 ] 等. 此外, 隋允康等[23 ] 提出的将局部应力约束向整体应变能约束转化的方法也可有效解决应力局部性问题. 尽管上述方法能有效处理常规的拓扑优化问题, 但尚未涉及复杂的可制造性拓扑优化问题. ...
Stress-constrained topology optimization based on maximum stress measures
3
2018
... 自Duysinx等[18 ] 提出连续体结构应力拓扑优化研究以来, 应力相关的拓扑优化问题受到了越来越多的关注. 然而, 考虑应力相关的拓扑优化问题有其自身难点, 常面临应力奇异性、局部性、非线性及度量准确性等问题[19 -20 ] . 为此, 不少学者提出了不同的解决方法. 目前常用的处理方法包括松弛方法[21 ] 、基于P范数或K-S函数的凝聚技术[8 ,14 ] 、分区度量[20 ] 、以及凝聚近似误差修正策略[22 ] 等. 此外, 隋允康等[23 ] 提出的将局部应力约束向整体应变能约束转化的方法也可有效解决应力局部性问题. 尽管上述方法能有效处理常规的拓扑优化问题, 但尚未涉及复杂的可制造性拓扑优化问题. ...
... 式中, $pc$为势凝聚参数. 如前所述, 较大的凝聚参数值不利于高效稳健的优化求解, 而适中取值将不可避免的引入近似误差. 不同于前述目标函数中的最大近似目标值的趋势控制, 约束函数中的P-norm函数需要有效控制最大近似目标值, 而近似误差的存在将极大影响该控制效果. 此外, 这里的势约束效果对约束阈值有较强依赖性[35 ] , 较大的近似误差也不利于设计连通性的有效控制. 为此, 引入基于稳定控制的近似误差修正技术[22 ] ...
... 考虑典型T型梁优化问题[16 ,22 ] , 设计条件如图6 (a)所示, 结构左右两侧固支, 顶部中点受集中载荷作用. 为避免应力集中, 载荷均匀分配到中点附近5个节点上. 设计域离散为8800个四节点双线性正方形有限元单元. 过滤半径$r_{\min}=3$, 连通性约束阈值取 $\eta = 2.01$. ...
应力约束全局化策略下的连续体结构拓扑优化
1
2006
... 自Duysinx等[18 ] 提出连续体结构应力拓扑优化研究以来, 应力相关的拓扑优化问题受到了越来越多的关注. 然而, 考虑应力相关的拓扑优化问题有其自身难点, 常面临应力奇异性、局部性、非线性及度量准确性等问题[19 -20 ] . 为此, 不少学者提出了不同的解决方法. 目前常用的处理方法包括松弛方法[21 ] 、基于P范数或K-S函数的凝聚技术[8 ,14 ] 、分区度量[20 ] 、以及凝聚近似误差修正策略[22 ] 等. 此外, 隋允康等[23 ] 提出的将局部应力约束向整体应变能约束转化的方法也可有效解决应力局部性问题. 尽管上述方法能有效处理常规的拓扑优化问题, 但尚未涉及复杂的可制造性拓扑优化问题. ...
应力约束全局化策略下的连续体结构拓扑优化
1
2006
... 自Duysinx等[18 ] 提出连续体结构应力拓扑优化研究以来, 应力相关的拓扑优化问题受到了越来越多的关注. 然而, 考虑应力相关的拓扑优化问题有其自身难点, 常面临应力奇异性、局部性、非线性及度量准确性等问题[19 -20 ] . 为此, 不少学者提出了不同的解决方法. 目前常用的处理方法包括松弛方法[21 ] 、基于P范数或K-S函数的凝聚技术[8 ,14 ] 、分区度量[20 ] 、以及凝聚近似误差修正策略[22 ] 等. 此外, 隋允康等[23 ] 提出的将局部应力约束向整体应变能约束转化的方法也可有效解决应力局部性问题. 尽管上述方法能有效处理常规的拓扑优化问题, 但尚未涉及复杂的可制造性拓扑优化问题. ...
A survey of manufacturing oriented topology optimization methods
1
2016
... 事实上, 拓扑优化设计常面临可制造性问题[24 ] . 在传统制造技术条件下, 优化产生的复杂构型将给产品制备带来巨大挑战. 这在一定程度上限制了拓扑优化的推广应用, 不利于高性能产品的研发. 作为一种先进的制造技术, 增材制造能够实现高度复杂结构的有效制备[25 ] . 将增材制造与拓扑优化有机结合, 能够大幅提高创新产品的研制能力, 现已成为重要研究方向[6 -7 ,25 ] . 然而, 增材制造并非"自由"制造, 有其独特的制造约束. 要求结构不含封闭孔洞的连通性约束便是其中最重要的制造约束之一[26 -27 ] . 如果结构含有封闭孔洞, 制造后残留在孔洞内的未熔融粉末或支撑结构将难以去除. 显然, 面向增材制造, 考虑可制造连通性的拓扑优化问题将具有重要工程应用价值[27 -29 ] . ...
拓扑优化与增材制造结合: 一种设计与制造一体化方法
2
2017
... 事实上, 拓扑优化设计常面临可制造性问题[24 ] . 在传统制造技术条件下, 优化产生的复杂构型将给产品制备带来巨大挑战. 这在一定程度上限制了拓扑优化的推广应用, 不利于高性能产品的研发. 作为一种先进的制造技术, 增材制造能够实现高度复杂结构的有效制备[25 ] . 将增材制造与拓扑优化有机结合, 能够大幅提高创新产品的研制能力, 现已成为重要研究方向[6 -7 ,25 ] . 然而, 增材制造并非"自由"制造, 有其独特的制造约束. 要求结构不含封闭孔洞的连通性约束便是其中最重要的制造约束之一[26 -27 ] . 如果结构含有封闭孔洞, 制造后残留在孔洞内的未熔融粉末或支撑结构将难以去除. 显然, 面向增材制造, 考虑可制造连通性的拓扑优化问题将具有重要工程应用价值[27 -29 ] . ...
... ,25 ]. 然而, 增材制造并非"自由"制造, 有其独特的制造约束. 要求结构不含封闭孔洞的连通性约束便是其中最重要的制造约束之一[26 -27 ] . 如果结构含有封闭孔洞, 制造后残留在孔洞内的未熔融粉末或支撑结构将难以去除. 显然, 面向增材制造, 考虑可制造连通性的拓扑优化问题将具有重要工程应用价值[27 -29 ] . ...
拓扑优化与增材制造结合: 一种设计与制造一体化方法
2
2017
... 事实上, 拓扑优化设计常面临可制造性问题[24 ] . 在传统制造技术条件下, 优化产生的复杂构型将给产品制备带来巨大挑战. 这在一定程度上限制了拓扑优化的推广应用, 不利于高性能产品的研发. 作为一种先进的制造技术, 增材制造能够实现高度复杂结构的有效制备[25 ] . 将增材制造与拓扑优化有机结合, 能够大幅提高创新产品的研制能力, 现已成为重要研究方向[6 -7 ,25 ] . 然而, 增材制造并非"自由"制造, 有其独特的制造约束. 要求结构不含封闭孔洞的连通性约束便是其中最重要的制造约束之一[26 -27 ] . 如果结构含有封闭孔洞, 制造后残留在孔洞内的未熔融粉末或支撑结构将难以去除. 显然, 面向增材制造, 考虑可制造连通性的拓扑优化问题将具有重要工程应用价值[27 -29 ] . ...
... ,25 ]. 然而, 增材制造并非"自由"制造, 有其独特的制造约束. 要求结构不含封闭孔洞的连通性约束便是其中最重要的制造约束之一[26 -27 ] . 如果结构含有封闭孔洞, 制造后残留在孔洞内的未熔融粉末或支撑结构将难以去除. 显然, 面向增材制造, 考虑可制造连通性的拓扑优化问题将具有重要工程应用价值[27 -29 ] . ...
Design for additive manufacturing based on the axiomatic design method
1
2016
... 事实上, 拓扑优化设计常面临可制造性问题[24 ] . 在传统制造技术条件下, 优化产生的复杂构型将给产品制备带来巨大挑战. 这在一定程度上限制了拓扑优化的推广应用, 不利于高性能产品的研发. 作为一种先进的制造技术, 增材制造能够实现高度复杂结构的有效制备[25 ] . 将增材制造与拓扑优化有机结合, 能够大幅提高创新产品的研制能力, 现已成为重要研究方向[6 -7 ,25 ] . 然而, 增材制造并非"自由"制造, 有其独特的制造约束. 要求结构不含封闭孔洞的连通性约束便是其中最重要的制造约束之一[26 -27 ] . 如果结构含有封闭孔洞, 制造后残留在孔洞内的未熔融粉末或支撑结构将难以去除. 显然, 面向增材制造, 考虑可制造连通性的拓扑优化问题将具有重要工程应用价值[27 -29 ] . ...
An identification method for enclosed voids restriction in manufacturability design for additive manufacturing structures
5
2015
... 事实上, 拓扑优化设计常面临可制造性问题[24 ] . 在传统制造技术条件下, 优化产生的复杂构型将给产品制备带来巨大挑战. 这在一定程度上限制了拓扑优化的推广应用, 不利于高性能产品的研发. 作为一种先进的制造技术, 增材制造能够实现高度复杂结构的有效制备[25 ] . 将增材制造与拓扑优化有机结合, 能够大幅提高创新产品的研制能力, 现已成为重要研究方向[6 -7 ,25 ] . 然而, 增材制造并非"自由"制造, 有其独特的制造约束. 要求结构不含封闭孔洞的连通性约束便是其中最重要的制造约束之一[26 -27 ] . 如果结构含有封闭孔洞, 制造后残留在孔洞内的未熔融粉末或支撑结构将难以去除. 显然, 面向增材制造, 考虑可制造连通性的拓扑优化问题将具有重要工程应用价值[27 -29 ] . ...
... [27 -29 ]. ...
... 研究人员已提出一些有效方法. Liu等[27 ] 利用热传导原理提出了虚拟温度法, 在结构孔洞区引入虚拟热源, 而在固体区填充隔热材料, 然后通过限制结构上的最高温度来抑制封闭孔洞. 数学上, 该方法可描述为服从泊松方程的标量场约束[29 ] . Zhou等[28 ] 则提出一种边界约束方法, 利用孔洞作为基本设计元素, 通过将与所有孔洞中心相关的设计变量限定在设计域之外来确保结构连通性. Xiong等[30 ] 提出了一种基于BESO的结构连通性控制方法, 通过有选择地生成将孔洞与结构边界连接起来的通道来消除封闭孔洞. 在水平集框架下, Xia等[31 ] 将孔洞抑制转换为对设计速度矢量的约束; Wang等[32 ] 则提出一种基于水平集函数梯度的约束来描述孔洞抑制条件. 然而, 这些研究只考虑了传统刚度问题, 缺乏对应力问题的必要关注. ...
... 为有效实现拓扑优化中抑制封闭孔洞的单连通性约束, 采用Liu等[27 ] 提出的基于泊松方程的标量场约束方法[29 ] . 为便于该方法的描述, 不失一般性, 这里采用了静电场物理模型[35 ] 进行表征. ...
... 静电场与原方法中的温度场[27 ] 在数学上一致, 均为服从泊松方程的标量场. 这里采用静电场模型主要有两方面考虑. 一方面, 静电原理也能较好表征封闭空洞, 而不同的物理场具有不同物理规律, 可以启发读者进一步发展泊松方法. 另一方面, 静电理论有助于解析泊松方法中关键的约束关系和边界依赖性, 有益于该方法的理解应用[35 ] . ...
Topology optimization method with elimination of enclosed voids
1
2019
... 研究人员已提出一些有效方法. Liu等[27 ] 利用热传导原理提出了虚拟温度法, 在结构孔洞区引入虚拟热源, 而在固体区填充隔热材料, 然后通过限制结构上的最高温度来抑制封闭孔洞. 数学上, 该方法可描述为服从泊松方程的标量场约束[29 ] . Zhou等[28 ] 则提出一种边界约束方法, 利用孔洞作为基本设计元素, 通过将与所有孔洞中心相关的设计变量限定在设计域之外来确保结构连通性. Xiong等[30 ] 提出了一种基于BESO的结构连通性控制方法, 通过有选择地生成将孔洞与结构边界连接起来的通道来消除封闭孔洞. 在水平集框架下, Xia等[31 ] 将孔洞抑制转换为对设计速度矢量的约束; Wang等[32 ] 则提出一种基于水平集函数梯度的约束来描述孔洞抑制条件. 然而, 这些研究只考虑了传统刚度问题, 缺乏对应力问题的必要关注. ...
Structural topology optimization considering connectivity constraint
4
2016
... 事实上, 拓扑优化设计常面临可制造性问题[24 ] . 在传统制造技术条件下, 优化产生的复杂构型将给产品制备带来巨大挑战. 这在一定程度上限制了拓扑优化的推广应用, 不利于高性能产品的研发. 作为一种先进的制造技术, 增材制造能够实现高度复杂结构的有效制备[25 ] . 将增材制造与拓扑优化有机结合, 能够大幅提高创新产品的研制能力, 现已成为重要研究方向[6 -7 ,25 ] . 然而, 增材制造并非"自由"制造, 有其独特的制造约束. 要求结构不含封闭孔洞的连通性约束便是其中最重要的制造约束之一[26 -27 ] . 如果结构含有封闭孔洞, 制造后残留在孔洞内的未熔融粉末或支撑结构将难以去除. 显然, 面向增材制造, 考虑可制造连通性的拓扑优化问题将具有重要工程应用价值[27 -29 ] . ...
... 研究人员已提出一些有效方法. Liu等[27 ] 利用热传导原理提出了虚拟温度法, 在结构孔洞区引入虚拟热源, 而在固体区填充隔热材料, 然后通过限制结构上的最高温度来抑制封闭孔洞. 数学上, 该方法可描述为服从泊松方程的标量场约束[29 ] . Zhou等[28 ] 则提出一种边界约束方法, 利用孔洞作为基本设计元素, 通过将与所有孔洞中心相关的设计变量限定在设计域之外来确保结构连通性. Xiong等[30 ] 提出了一种基于BESO的结构连通性控制方法, 通过有选择地生成将孔洞与结构边界连接起来的通道来消除封闭孔洞. 在水平集框架下, Xia等[31 ] 将孔洞抑制转换为对设计速度矢量的约束; Wang等[32 ] 则提出一种基于水平集函数梯度的约束来描述孔洞抑制条件. 然而, 这些研究只考虑了传统刚度问题, 缺乏对应力问题的必要关注. ...
... 为有效实现拓扑优化中抑制封闭孔洞的单连通性约束, 采用Liu等[27 ] 提出的基于泊松方程的标量场约束方法[29 ] . 为便于该方法的描述, 不失一般性, 这里采用了静电场物理模型[35 ] 进行表征. ...
... 其中, $\eta \cdot\phi_{0}$ 为评估结构是否含封闭孔洞的约束阈值; $\phi_{0}$为基准阈值, 可基于初始化约束模型(仅由孔洞单元构成)求解获得[29 ] ; $\eta >0$ 为约束阈值修正因子, 需针对不同问题进行调整, 以控制约束效果[35 ] . 控制 $\phi $的二阶微分方程为经典泊松方程[36 ] ...
A new approach to eliminating enclosed voids in topology optimization for additive manufacturing
1
2020
... 研究人员已提出一些有效方法. Liu等[27 ] 利用热传导原理提出了虚拟温度法, 在结构孔洞区引入虚拟热源, 而在固体区填充隔热材料, 然后通过限制结构上的最高温度来抑制封闭孔洞. 数学上, 该方法可描述为服从泊松方程的标量场约束[29 ] . Zhou等[28 ] 则提出一种边界约束方法, 利用孔洞作为基本设计元素, 通过将与所有孔洞中心相关的设计变量限定在设计域之外来确保结构连通性. Xiong等[30 ] 提出了一种基于BESO的结构连通性控制方法, 通过有选择地生成将孔洞与结构边界连接起来的通道来消除封闭孔洞. 在水平集框架下, Xia等[31 ] 将孔洞抑制转换为对设计速度矢量的约束; Wang等[32 ] 则提出一种基于水平集函数梯度的约束来描述孔洞抑制条件. 然而, 这些研究只考虑了传统刚度问题, 缺乏对应力问题的必要关注. ...
A level set based method for the optimization of cast part
1
2010
... 研究人员已提出一些有效方法. Liu等[27 ] 利用热传导原理提出了虚拟温度法, 在结构孔洞区引入虚拟热源, 而在固体区填充隔热材料, 然后通过限制结构上的最高温度来抑制封闭孔洞. 数学上, 该方法可描述为服从泊松方程的标量场约束[29 ] . Zhou等[28 ] 则提出一种边界约束方法, 利用孔洞作为基本设计元素, 通过将与所有孔洞中心相关的设计变量限定在设计域之外来确保结构连通性. Xiong等[30 ] 提出了一种基于BESO的结构连通性控制方法, 通过有选择地生成将孔洞与结构边界连接起来的通道来消除封闭孔洞. 在水平集框架下, Xia等[31 ] 将孔洞抑制转换为对设计速度矢量的约束; Wang等[32 ] 则提出一种基于水平集函数梯度的约束来描述孔洞抑制条件. 然而, 这些研究只考虑了传统刚度问题, 缺乏对应力问题的必要关注. ...
Structural shape and topology optimization of cast parts using level set method
1
2017
... 研究人员已提出一些有效方法. Liu等[27 ] 利用热传导原理提出了虚拟温度法, 在结构孔洞区引入虚拟热源, 而在固体区填充隔热材料, 然后通过限制结构上的最高温度来抑制封闭孔洞. 数学上, 该方法可描述为服从泊松方程的标量场约束[29 ] . Zhou等[28 ] 则提出一种边界约束方法, 利用孔洞作为基本设计元素, 通过将与所有孔洞中心相关的设计变量限定在设计域之外来确保结构连通性. Xiong等[30 ] 提出了一种基于BESO的结构连通性控制方法, 通过有选择地生成将孔洞与结构边界连接起来的通道来消除封闭孔洞. 在水平集框架下, Xia等[31 ] 将孔洞抑制转换为对设计速度矢量的约束; Wang等[32 ] 则提出一种基于水平集函数梯度的约束来描述孔洞抑制条件. 然而, 这些研究只考虑了传统刚度问题, 缺乏对应力问题的必要关注. ...
Topology optimization approaches
1
2013
... 针对协同考虑结构强度和可制造连通性的拓扑优化问题, 基于经典密度法[33 ] , 建立以结构全局最大应力强度准则为目标, 以材料用量和结构连通性为约束的拓扑优化模型, 其数学列式如下 ...
Morphology-based black and white filters for topology optimization
1
2007
... 基于改进的SIMP材料插值模型[34 ] , 得到全局刚度矩阵${K}(x)=\sum\nolimits_{i=1}^N \left[ E_{\min} +\left( x_{i}\right)^{p}\left(E_{0} -E_{\min }\right)\right]{k}_{0,i}$, 其中, $E_0$表示实体单元材料的弹性模量, $E_{\min}$表示孔洞单元材料的弹性模量; $p>0$为惩罚因子; $k_{0,i}$为单位弹性模量下的单元刚度矩阵. 这里取常用参数设置: $E_{\min}= 10^{-9}E_0$和$p=3$. ...
Numerical performance of Poisson method for restricting enclosed voids in topology optimization
8
2020
... 为有效实现拓扑优化中抑制封闭孔洞的单连通性约束, 采用Liu等[27 ] 提出的基于泊松方程的标量场约束方法[29 ] . 为便于该方法的描述, 不失一般性, 这里采用了静电场物理模型[35 ] 进行表征. ...
... 其中, $\eta \cdot\phi_{0}$ 为评估结构是否含封闭孔洞的约束阈值; $\phi_{0}$为基准阈值, 可基于初始化约束模型(仅由孔洞单元构成)求解获得[29 ] ; $\eta >0$ 为约束阈值修正因子, 需针对不同问题进行调整, 以控制约束效果[35 ] . 控制 $\phi $的二阶微分方程为经典泊松方程[36 ] ...
... 其中, $\varGamma_{D}$ 和 $\varGamma_{N}$分别为狄利克雷边界(即连通性约束边界)和诺伊曼边界, $n$为边界外法向单位向量. 需要注意的是, 基于上述方法获得的优化结果对约束边界条件的选择有依赖性, 不同约束边界条件对应不同约束问题, 可产生不同优化结果[35 ] . 基于式(2)和式(5)可将原优化问题转化为静电场约束问题(式(3))求解分析. ...
... 静电场与原方法中的温度场[27 ] 在数学上一致, 均为服从泊松方程的标量场. 这里采用静电场模型主要有两方面考虑. 一方面, 静电原理也能较好表征封闭空洞, 而不同的物理场具有不同物理规律, 可以启发读者进一步发展泊松方法. 另一方面, 静电理论有助于解析泊松方法中关键的约束关系和边界依赖性, 有益于该方法的理解应用[35 ] . ...
... 式中, $\beta >0$ 为控制投影函数非线性的投影参数; $x_{0}\in[0,1]$ 为调节投影函数拐点的投影阈值, 本文取常用值 $x_{0} = 0.5$. 为提高应力评估准确性以及优化迭代稳定性, 参考文献[19 , 41 ], 这里采用连续化策略定义 $\beta $ 值: 在前10步迭代中取 $\beta = 1$, 此后每步迭代加1直至 $\beta = 10$. 由于物理密度定义了单元属性, 在后续研究中将使用物理密度进行结构分析. 值得注意的是, 过滤和投影会影响连通性约束, 考虑这种影响对基于泊松方法的连通性约束的有效实现具有重要意义, 感兴趣的读者可以参阅文献[35 ]. ...
... 式中, $pc$为势凝聚参数. 如前所述, 较大的凝聚参数值不利于高效稳健的优化求解, 而适中取值将不可避免的引入近似误差. 不同于前述目标函数中的最大近似目标值的趋势控制, 约束函数中的P-norm函数需要有效控制最大近似目标值, 而近似误差的存在将极大影响该控制效果. 此外, 这里的势约束效果对约束阈值有较强依赖性[35 ] , 较大的近似误差也不利于设计连通性的有效控制. 为此, 引入基于稳定控制的近似误差修正技术[22 ] ...
... 从图1 (d)和图1 (e)可以看出, 引入连通性约束能够有效抑制优化设计中的封闭孔洞, 但所得设计出现了严重恶化的局部高应力集中, 其最大应力是传统刚度设计的1.87倍. 这表明可制造连通性优化设计中十分有必要考虑应力问题. 此外, 上述连通性设计的刚度比单纯的刚度设计要弱, 这是连通性设计所付出的必要代价[35 ] . ...
... 为考察连通性约束边界条件对应力最小化连通性设计的影响, 考虑如图5 (a) $\sim\!$图5 (c) 和图5 (d) $\sim\!$图5 (f)所示两种条件下的优化问题. 为便于比较,其余优化参数与图2 中ps $=$8的设计保持一致. 对比图2 和图5 的设计不难发现, 不同连通性约束边界条件可产生具有不同拓扑构型且性能各异的设计. 该现象遵循了泊松方法的约束边界依赖性规律. 特别地, 图5 (a) $\sim\!$图5 (c)设计的综合性能不仅比图2 中$ps=8$的设计要好(结构强度和刚度均分别提高了11.61${\%}$和24.21${\%}$), 而且比图1 (d)和图1 (e)中的连通性刚度设计也要强(结构强度和刚度均分别提高了48.17${\%}$和5.25${\%}$). 显然, 连通性约束边界条件对所研究设计的拓扑构型及性能均有较大影响. 然而, 由于边界条件的变化将产生新的优化约束问题, 这使得自动寻找最优约束边界条件仍旧是未来极具挑战性的工作[35 ] . ...
1
2014
... 其中, $\eta \cdot\phi_{0}$ 为评估结构是否含封闭孔洞的约束阈值; $\phi_{0}$为基准阈值, 可基于初始化约束模型(仅由孔洞单元构成)求解获得[29 ] ; $\eta >0$ 为约束阈值修正因子, 需针对不同问题进行调整, 以控制约束效果[35 ] . 控制 $\phi $的二阶微分方程为经典泊松方程[36 ] ...
Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima
1
1998
... 为避免拓扑优化中的数值不稳定性问题[37 ] , 并获取清晰的0-1设计, 采取线性密度过滤[38 -39 ] 和非线性阈值投影[40 ] 相结合的技术方案. 对单元密度变量 $x_{i} $进行线性密度过滤可得过滤后的变量 ...
Topology optimization of non-linear elastic structures and compliant mechanisms
1
2001
... 为避免拓扑优化中的数值不稳定性问题[37 ] , 并获取清晰的0-1设计, 采取线性密度过滤[38 -39 ] 和非线性阈值投影[40 ] 相结合的技术方案. 对单元密度变量 $x_{i} $进行线性密度过滤可得过滤后的变量 ...
Filters in topology optimization
1
2001
... 为避免拓扑优化中的数值不稳定性问题[37 ] , 并获取清晰的0-1设计, 采取线性密度过滤[38 -39 ] 和非线性阈值投影[40 ] 相结合的技术方案. 对单元密度变量 $x_{i} $进行线性密度过滤可得过滤后的变量 ...
On projection methods, convergence and robust formulations in topology optimization
1
2011
... 为避免拓扑优化中的数值不稳定性问题[37 ] , 并获取清晰的0-1设计, 采取线性密度过滤[38 -39 ] 和非线性阈值投影[40 ] 相结合的技术方案. 对单元密度变量 $x_{i} $进行线性密度过滤可得过滤后的变量 ...
Improving the overall performance of continuum structures: A topology optimization model considering stiffness, strength and stability
1
2020
... 式中, $\beta >0$ 为控制投影函数非线性的投影参数; $x_{0}\in[0,1]$ 为调节投影函数拐点的投影阈值, 本文取常用值 $x_{0} = 0.5$. 为提高应力评估准确性以及优化迭代稳定性, 参考文献[19 , 41 ], 这里采用连续化策略定义 $\beta $ 值: 在前10步迭代中取 $\beta = 1$, 此后每步迭代加1直至 $\beta = 10$. 由于物理密度定义了单元属性, 在后续研究中将使用物理密度进行结构分析. 值得注意的是, 过滤和投影会影响连通性约束, 考虑这种影响对基于泊松方法的连通性约束的有效实现具有重要意义, 感兴趣的读者可以参阅文献[35 ]. ...
The method of moving asymptotes——a new method for structural optimization
1
1987
... 为高效求解上述多约束优化问题, 采用相适宜的移动渐近线算法[42 ] .下面将利用链式法则和伴随法, 推导算法所需的目标和约束函数的一阶灵敏度信息. 基于链式法则, 任意函数 $g$关于设计变量 $x_{i}$ 的敏度为 ...