引言
双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具.
采用数值方法进行断裂力学分析时, 裂纹尖端奇异区域处理的好坏直接关系到最终断裂力学参数(如应力强度因子、能量释放率等)的求解精度. 对于传统单一材料, 材料内部裂纹尖端位移和应力场具有经典的平方根($r^{1/2})$和负平方根($r^{-1/2})$渐近性, 相应的理论研究和数值求解技术已发展的非常成熟. 比如对裂尖奇异应力场的求解, 已发展了包括"1/4单元法"、"数值外插法"、"虚拟裂纹闭合法"和"J积分/相互作用积分"等多种有效的求解方法. 然而, 与传统单一材料不同, 双材料界面裂纹渐近位移和应力场表现出剧烈的振荡特性, 即[15 -16 ]
(1) $\begin{eqnarray} \label{eq1} u\sim r^{1/2+{i}\varepsilon },\ \ \sigma \sim r^{-1/2+{i}\varepsilon } \end{eqnarray} $
其中i为复数单位, $\varepsilon $为双材料参数(或振荡因子). 导致许多用于表征经典的平方根和负平方根物理场渐近性的传统方法失效[17 -18 ] . 虽然界面裂纹复应力强度因子($K_{1} +{i}K_{2} )$可采用各种守恒积分(如J积分)或位移外插法等进行间接求解, 但计算精度较低, 也难以直接获得裂尖近场区域物理量的精确分布[19 ] . 因此, 虽然目前计算断裂力学发展的比较成熟, 但其在双材料界面裂纹分析方面的研究依然比较欠缺, 从基础研究的角度来考虑还需进行大量的研究.
此外, 随着实际工程需求和表面涂层工艺的逐渐成熟, 大量双材料的相对厚度(表面特征长度和厚度的尺寸比)越来越小, 特别是各种微纳米复合材料的相继出现, 给精确有效的数值模拟带来了巨大的挑战. 比如, 为了避免出现畸形网格, 有限元法需按照涂层的厚度划分单元. 可这样做必然会导致百万甚至几百万个子单元, 计算工作量剧增, 同时解的收敛性也难以保证[20 ] . 相对于有限元法, 边界元仅需在边界离散, 可以从容处理边界单元的疏密过渡, 很大程度上避免了有限元法中网格畸变带来的困难, 这一点对薄体与涂层结构问题的数值模拟尤为重要. 近年来, 边界元法在薄体结构问题中的应用正在蓬勃发展, 被认为是其比有限元法更具优势的一个新领域, 而且在表面涂层、压电薄膜等工程领域展现出了广阔的应用前景[21 -27 ] .
论文以边界元法为基本工具, 通过引入一种能精确表征复合材料界面裂纹振荡特性的"特殊裂尖单元"[28 ] , 实现了双材料界面裂纹复应力强度因子的精确求解. 该方法无需裂尖区域高密度的网格剖分, 可显著提高裂尖近场力学参量和复应力强度因子的求解精度和数值稳定性. 在此基础上, 结合边界元法中计算近奇异积分的一种通用正则化算法[29 -30 ] , 成功求解了超薄双材料界面裂纹问题. 数值算例表明, 所提算法稳定, 效率高, 在不增加计算量的前提下, 显著提高了裂尖近场力学参量和断裂力学参数的求解精度和数值稳定性. 1 界面裂纹渐进位移和应力场的振荡特性
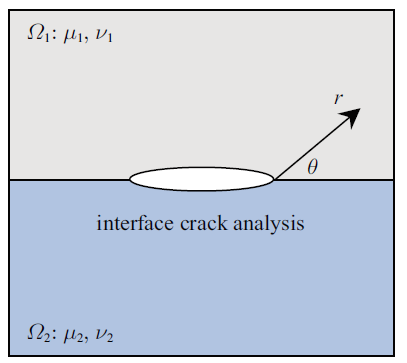
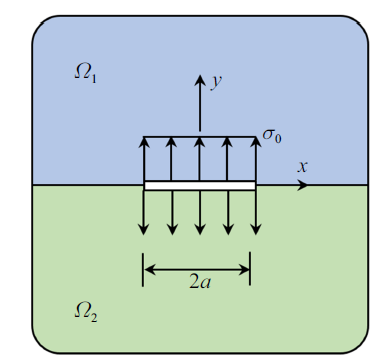
图1 中, 考虑由两种不同材料组成的双材料板, 在板的结合面存在一条界面裂纹. 记上层和下层材料分别为区域$\varOmega_{1} $和$\varOmega_{2} $, 相应的弹性模量和泊松比分别为$\mu_{1}$, $\nu_{1} $和$\mu_{2}$, $\nu_{2} $.
图1
图1
双材料界面裂纹问题
Fig.1
An interface crack in a dissimilar material
早在20世纪五六十年代, Williams[16 ] , Erdogan[15 ] 和England[17 ] 等就发现双材料界面裂纹渐近位移和应力场具有形如式(1)的振荡特性. 其中$r$为计算点到裂尖的距离, 双材料参数$\varepsilon $定义如下
(2) $\begin{eqnarray} \label{eq2} \varepsilon =\frac{1}{2\pi }\ln \left( {\frac{\mu_{2} \kappa_{1} +\mu_{1} }{\mu_{1} \kappa_{2} +\mu_{2} }} \right) \end{eqnarray} $
对于平面应变问题, 有$\kappa_{i} =3-4\nu_{i} $. 对于平面应力问题, 有$\kappa_{i} =(3-\nu_{i} )/(1+\nu_{i} )$. 裂纹尖端附近的位移和应力场可表示为[28 ,31 ]
(3) $\left( {u_{y} +{i}u_{x} } \right)_{\theta =\pi } -\left( {u_{y} +{i}u_{x} } \right)_{\theta =-\pi } =\frac{\left( {K_{1} +{i}K_{2} } \right)\left( {c_{1} +c_{2} } \right)}{2\sqrt {2\pi } \left( {1+2{i}\varepsilon } \right)\cosh \left( {\pi \varepsilon } \right)}r^{1/2+{i}\varepsilon } $
(4) $\left( {\sigma_{y} +{i}\tau_{xy} } \right)_{\theta =0} =\frac{\left( {K_{1} +{i}K_{2} } \right)}{\sqrt {2\pi } }r^{-1/2+{i}\varepsilon } $
(5) $\begin{eqnarray} \label{eq5} K=K_{1} +{i}K_{2} \end{eqnarray} $
$K$为复应力强度因子, $c_{i} =(1+\kappa_{i} )/\mu_{i} $为材料常数. 由式(3)或式(4)可知, 复应力强度因子$K_{1} +{i}K_{2} $的值可通过裂尖张开位移或应力进行数值求解.
传统有限元方法在处理裂纹问题时, 需严格按照材料界面剖分网格, 且裂尖区域需要采用高密度网格以捕捉应力场的奇异性, 前处理工作比较繁琐. 此外, 需要指出, 界面裂纹渐近位移和应力场具有$r^{1/2+{i}\varepsilon }$和$r^{-1/2+{i}\varepsilon }$的振荡特性, 许多用于表征经典的平方根和负平方根物理场渐近性的传统方法失效, 这也给双材料界面裂纹精确有效的数值模拟带来了不小的挑战.
2 求解界面裂纹问题的边界元方法
采用多域边界元法对图1 所示的双材料界面裂纹问题进行数值求解. 对区域$\varOmega _{1} $和$\varOmega_{2} $, 可分别建立如下边界积分方程[28 ]
(6) $\begin{eqnarray} \label{eq6} && C_{ij} (P)u_{j} (P)=\int_S {U_{ij} (P,Q)t_{j} } (Q){d}S(Q)- -\hspace{-3.5mm}\int_{S} T_{ij} (P,Q)u_{j} (Q){d}S(Q) \end{eqnarray} $
其中$P$和$Q$代表计算点和边界积分点, $u_{j} $和$t_{j}$ $(j=1,\;2)$代表边界位移和面力, $U_{ij} (P,Q)$和$T_{ij}(P,Q)$为位移和面力基本解. 对于光滑边界, $C_{ij} (P)=\delta_{ij} /2$. 为了保证足够的计算精度, 采用三点二次非连续单元近似(图2 ). 边界元法中的单元近似分为对边界形状的"几何近似"和对边界物理参量的"物理近似". 对几何边界的近似可表示为
(7) $\begin{eqnarray} \label{eq7} x_{k} =x_{k}^{1} N_{1G} ( \xi )+x_{k}^{2} N_{2G} ( \xi )+x_{k}^{3} N_{3G} ( \xi ),\;k=1,\;2 \end{eqnarray} $
其中($x_{1} $, $x_{2} )$为边界单元任一点的坐标, ($x_{1}^{i} $, $x_{2}^{i})$为单元结点$Ni$处的坐标(图2 ), $N_{1G} $, $N_{2G} $和$N_{3G} $为坐标形函数
(8) $\begin{eqnarray} \label{eq8} \left.\begin{array}{l} N_{1G} ( \xi )=\xi \left( {\xi -1} \right)/2,\;\;\;N_{2G} ( \xi )=1-\xi^{2}\\ N_{3G} ( \xi )=\xi \left( {\xi +1} \right)/2,\;\;\;-1\leqslant \xi \leqslant 1 \\ \end{array}\right\} \end{eqnarray} $
(9) $u_{k} =u_{k}^{1} N_{1} ( \xi )+u_{k}^{2} N_{2} ( \xi )+u_{k}^{3} N_{3} ( \xi ),\;k=1,\;2 $
(10) $t_{k} =t_{k}^{1} N_{1} ( \xi )+t_{k}^{2} N_{2} ( \xi )+t_{k}^{3} N_{3} ( \xi ),\;k=1,\;2 $
其中($u_{1} $, $u_{2} )$和($t_{1} $, $t_{2})$为边界单元任一点处的位移分量和面力分量, ($u_{1}^{i} $, $u_{2}^{i})$和($t_{1}^{i} $, $t_{2}^{i})$为单元节点$\hat{{N}}_i$处的位移分量和面力分量(图2 ), $N_{1} $, $N_{2}$和$N_{3} $为位移/面力形函数
(11) $\begin{eqnarray} \label{eq11} \left.\begin{array}{l} N_{1} ( \xi )=\xi \left( {\xi -\alpha_{3} } \right)/\left[ {\alpha_{1} \left( {\alpha_{1} -\alpha_{3} } \right)} \right] \\ N_{2} ( \xi )=\left( {\xi -\alpha_{1} } \right)\left( {\xi -\alpha_{3} } \right)/\left( {\alpha_{1} \alpha_{3} } \right) \\ N_{3} ( \xi )=\xi \left( {\xi -\alpha_{1} } \right)/\left[ {\alpha_{3} \left( {\alpha_{3} -\alpha_{1} } \right)} \right] \\ \end{array}\right\} \end{eqnarray} $
式(11)中, $\alpha_{1}$, $\alpha_{2} =0$和$\alpha_{3}$为单元的非连续因子.
图2
图2
二次非连续单元
Fig.2
Discontinuous quadratic element
将边界积分方程(6)分别应用于区域$\varOmega_{1} $和$\varOmega_{2} $, 可构造如下线性代数方程组
(12) $\left[ {{H}^{1},{H}_{I}^{1} } \right]\left( {\begin{array}{l} {{u}^{1}} \\ {{u}_{I}^{1} } \\ \end{array}} \right)=\left[ {{G}^{1},{G}_{I}^{1} } \right]\left( {\begin{array}{l} {{t}^{1}} \\ {{t}_{I}^{1} } \\ \end{array}} \right) $
(13) $\left[ {{H}^{2},{H}_{I}^{2} } \right]\left( {\begin{array}{l} {{u}^{2}} \\ {{u}_{I}^{2} } \\ \end{array}} \right)=\left[ {{G}^{2},{G}_{I}^{2} } \right]\left( {\begin{array}{l} {{t}^{2}} \\ {{t}_{I}^{2} } \\ \end{array}} \right) $
其中${H}$和${G}$代表系数矩阵, 上标"1"和"2"分别表示区域$\varOmega_{1} $和$\varOmega_{2} $, 下标"I"代表双材料结合面(界面)处对应的系数矩阵或物理量. 根据界面位移和面力的连续条件
(14) $\begin{eqnarray} \label{eq14} {u}_{I} ={u}_{I}^{1} ={u}_{I}^{2} ,\;\;{t}_{I} ={t}_{I}^{1} =-{t}_{I}^{2} \end{eqnarray} $
(15) $\begin{eqnarray} \label{eq15} && \left[ {{\begin{array}{c@{\ \ \ }c@{\ \ \ }c} {{H}^{1}} & {{H}_{I}^{1} } & {\bf0} \\ {\bf0} & {{H}_{I}^{2} } & {{H}^{2}} \\ \end{array} }} \right]\left( {\begin{array}{l} {{u}^{1}} \\ {{u}_{I} } \\ {{u}^{2}} \\ \end{array}} \right)= \left[ {{\begin{array}{c@{\ \ \ }c@{\ \ \ }c} {{G}^{1}} & {{G}_{I}^{1} } & {\bf0} \\ {\bf0} & {-{G}_{I}^{2} } & {{G}^{2}} \\ \end{array} }} \right]\left( {\begin{array}{l} {{t}^{1}} \\ {{t}_{I} } \\ {{t}^{2}} \\ \end{array}} \right) \end{eqnarray} $
通过对方程(15)的求解, 可得到边界点处位移和面力的数值解. 将裂纹尖端的张开位移或面力代入式(3)或式(4), 便可进一步求得复应力强度因子的值.
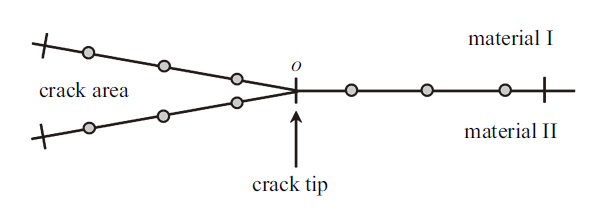
需要指出, 界面裂纹渐近位移和应力场具有$r^{1/2+{i}\varepsilon }$和$r^{-1/2+{i}\varepsilon }$的振荡特性. 因此, 在采用以上分域法的同时, 需要对裂尖单元(包含裂纹尖端的左右两个单元, 见图3 )进行特殊处理, 这就是接下来要引入的"特殊裂尖单元"法.
图3
图3
界面裂纹裂尖单元
Fig.3
Elements near the crack-tip
3 双材料界面裂纹"特殊裂尖单元"
引入一种含有复振荡因子的新型"特殊裂尖单元"[28 ] , 可精确表征裂纹尖端渐近位移和应力场的振荡特性. 提高界面裂纹复应力强度因子的数值求解精度. 下文简要介绍方法的数学原理.
对于几何边界的近似, 裂尖单元采用如式(7)和式(8)相同的二次单元. 但对于位移和面力的近似(物理量的近似), 裂尖单元需要做如下特殊处理. 如式(3)所示, 为了准确表征裂尖位移场的振荡特性, 裂尖位移场在数学上应该具有以下形式
(16) $\begin{eqnarray} \label{eq16} u_{i} ( \xi )=d_{1} +d_{2} r^{1/2+{i}\varepsilon }+d_{3} r^{3/2+{i}\varepsilon } \end{eqnarray} $
其中$d_{1} $代表刚体位移, $d_{2} r^{1/2+{i}\varepsilon }$为主要项, $d_{3} r^{3/2+{i}\varepsilon }$为距离函数$r$的高阶无穷小量(对计算精度的影响可以忽略).
数值上, 通过式(9)插值得到的裂尖位移场应具有如式(16)的渐进性. 当裂纹尖端在单元中的无因次坐标为$\xi =-1$时, 即裂尖位于单元左端点时(图3 ), 式(9)中的位移插值形函数应表示为以下形式
(17) $\begin{eqnarray} \label{eq17} N_{k} =A_{1}^{k} +A_{2}^{k} \left( {1+\xi } \right)^{1/2+{i}\varepsilon }+A_{3}^{k} \left( {1+\xi } \right)^{3/2+{i}\varepsilon } \end{eqnarray} $
其中$k=1,\;2,\;3$, $A_{1}^{k} $, $A_{2}^{k} $和$A_{3}^{k} $为常数, 其值可令$N_{k} $在第$k$个单元节点处的值恒为一, 在单元其他两个节点处的值恒为0 (函数插值理论), 通过构造三元一次方程组来计算. 比如, 在构造$N_{1} $时, 可令
(18) $\begin{eqnarray} \label{eq18} N_{1} (\xi =\alpha_{1} )\equiv 1,\;N_{1} (\xi =\alpha_{2} )\equiv 0,\;N_{1} (\xi =\alpha_{3} )\equiv 0 \end{eqnarray} $
同理, 在构造$N_{2} $和$N_{3} $时, 可令
(19) $N_{2} (\xi =\alpha_{1} )\equiv 0,\;N_{2} (\xi =\alpha_{2} )\equiv 1,\;N_{2} (\xi =\alpha_{3} )\equiv 0 $
(20) $N_{3} (\xi =\alpha_{1} )\equiv 0,\;N_{3} (\xi =\alpha_{2} )\equiv 0,\;N_{3} (\xi =\alpha_{3} )\equiv 1 $
当裂纹尖端在单元中的无因次坐标为$\xi =1$时(裂尖单元的右端点), 式(9)中的位移插值形函数应具有以下形式
(21) $\begin{eqnarray} \label{eq21} N_{k} =B_{1}^{k} +B_{2}^{k} \left( {1-\xi } \right)^{1/2+{i}\varepsilon }+B_{3}^{k} \left( {1-\xi } \right)^{3/2+{i}\varepsilon } \end{eqnarray} $
其中待定系数$B_{1}^{k} $, $B_{2}^{k} $和$B_{3}^{k} $可通过上述方法类似求解. 式(17)和式(21)可用于裂尖单元位移场的插值近似, 这样便可精确表征界面裂纹渐进位移场的振荡特性. 式(17)和式(21)的具体数学表达式见文献[28 ].
类似地, 为了准确表征裂尖应力场的振荡特性, 根据式(4), 裂尖应力场应表示为以下形式
(22) $\begin{eqnarray} \label{eq22} t_{i} ( \xi )=e_{1} +e_{2} r^{-1/2+{i}\varepsilon }+e_{3} r^{1/2+{i}\varepsilon } \end{eqnarray} $
其中$e_{2} r^{-1/2+{i}\varepsilon }$为主要项(振荡奇异性), $e_{3} r^{1/2+{i}\varepsilon }$为距离函数$r$的高阶无穷小量. 为了使通过式(10)构造的裂尖应力场具有如式(22)的渐进性, 当裂纹尖端在点$\xi =\pm 1$时, 式(10)中的应力插值形函数应具有以下形式
(23) $\begin{eqnarray} \label{eq23} N_{k} =C_{1}^{k} +C_{2}^{k} \left( {1\mp \xi } \right)^{-1/2+{i}\varepsilon }+C_{3}^{k} \left( {1\mp \xi } \right)^{1/2+{i}\varepsilon } \end{eqnarray} $
其中$C_{1}^{k} $, $C_{2}^{k} $和$C_{3}^{k} $为待定系数, 其具体数学表达式可见文献[28 ]. 需要指出, 上述位移和应力特殊形函数仅需在裂纹尖端左右两侧的两个边界单元使用, 其它边界单元上的位移和应力可通过常规位移/面力形函数式(11)进行插值近似.
4 薄体结构边界元法中近奇异积分的计算
薄体结构问题的数值求解是边界元法的难点之一, 其实质是近奇异积分的精确计算. 原因是, 受薄体结构特殊几何构造的影响, 边界节点通常和某些积分单元十分地接近, 导致边界积分方程(6)的积分表现出不同程度的近奇异性, 常规高斯积分结果失效. 本文采用一种非线性变量替换法对近奇异积分进行精确求解. 该方法基于尽可能拉近运算因子间数量级或变化尺度的思想, 可有效改善近奇异核函数的振荡特性, 使近奇异积分的计算结果得到大幅提高.
二维弹性力学边界元法中的近奇异积分可以归结为以下两种形式[32 -33 ]
(24) $I_{1} =\int_{-1}^1 {f(\xi )\lg r^{2}(\xi )} {d}\xi $
(25) $I_{2} =\int_{-1}^1 {f(\xi )\frac{1}{r^{2\alpha }(\xi )}}{d}\xi $
其中$\alpha >0$, $f(\xi )$为规则函数(包含雅可比函数、形函数等). 若采用三点二次单元近似几何边界, 计算点$P$到积分单元的距离函数$r^{2}(\xi )$可表示为[32 ]
(26) $\begin{eqnarray} \label{eq26} r^{2}(\xi )=\left( {\xi -a} \right)^{2}g(\xi )+b^{2} \end{eqnarray} $
其中$g(\xi )\geqslant 0$为规则函数, $a$代表计算点$P$在积分单元投影的无因次坐标, $b$代表计算点$P$到积分单元的最短距离. 将式(26)代入式(24)和式(25)可得
(27) $I_{1} =\int_{-1}^af(\xi )\lg \left[ \left( {\xi -a} \right)^{2}g(\xi )+b^{2} \right] {d}\xi+\int_a^1 f(\xi )\lg \left[ \left( {\xi -a} \right)^{2}g(\xi )+b^{2} \right]{d}\xi $
(28) $I_{2} =\int_{-1}^a \frac{f(\xi )}{\left[ {(\xi -a)^{2}g(\xi )+b^{2}} \right]^{\alpha }}{d}\xi +\int_a^1\frac{f(\xi )}{\left[ {(\xi -a)^{2}g(\xi )+b^{2}} \right]^{\alpha }}{d}\xi $
上述积分在$a$点被分为两部分来计算, 可提高数值计算精度. 在积分区间[$-1$, $a$]和[$a$, 1]上分别引入变量替换$x=a-\xi $和$x=\xi -a$, 则上述近奇异积分可表示为以下形式
(29) $I_{1} =\int_0^A {f(x)\lg \left[ {x^{2}g(x)+b^{2}} \right]} {d}x $
(30) $I_{2} =\int_0^A {\frac{f(x)}{\left[ {x^{2}g(x)+b^{2}} \right]^{\alpha }}} {d}x $
其中$A=1+a$或$A=1-a$. 显然, 当计算点$P$到积分单元的最短距离$b$很小时, 上述积分核函数在0点附近会产生剧烈的振荡特性. 为此, 引入如下非线性变量替换
(31) $\begin{eqnarray} \label{eq31} x=b\left[ {{e}^{k(1+t)}-1} \right] \end{eqnarray} $
其中$k=0.5\ln (1+A/b)$. 将变量替换(31)代入式(30)可得
(32) $\begin{eqnarray} \label{eq32} I_{2} =\frac{k}{b^{2\alpha -1}}\int_{-1}^1 {\frac{f(t){e}^{k(1+t)}}{\left[ {({e}^{k(1+t)}-1)^{2}g(t)+1} \right]^{\alpha }}}{d}t \end{eqnarray} $
式(29)的变换类似可得. 因$g(\cdot )\geqslant 0$为规则函数,式(32)核函数分母部分$({e}^{k(1+t)}-1)^{2}g(t)+1\geqslant 1$恒成立, 原近奇异性得以消除, 可通过传统高斯积分进行精确求解. 论文首次尝试将上述计算近奇异积分的正则化算法与"特殊裂尖单元"法相结合, 数值模拟大尺寸比(超薄)双材料的界面裂纹问题, 下面给出数值算例.
5 数值算例
首先, 为验证所提"特殊裂尖单元法"求解双材料界面裂纹问题的有效性, 算例1给出了无限大双材料板受均匀拉力时断裂力学参量和近场物理量的计算结果(不涉及近奇异积分的计算问题). 算例2 $\sim$ 5侧重于大尺寸比(超薄)双材料的界面裂纹问题. 其中, 算例2和算例3假设两种材料具有相同的弹性模量和泊松比(应力强度因子存在精确解). 算例4和算例5讨论了不同材料的界面裂纹问题.
例1 含有中心裂纹的无限大双材料板, 界面裂纹的长度为2$a$, 裂纹表面受均匀拉力$\sigma_{0} $ (见图4 ). 材料1和材料2的泊松比为$\nu_{1} =\nu_{2} =0.2$. 实际计算中, 令双材料板的宽度和高度为$50a$. 边界共划分280个二次单元, 其中裂纹表面划分20个二次单元, 裂尖单元相对于裂纹长度为$a$/10. 断裂力学参数和裂尖渐近位移和应力场的精确解见文献[28 ].
图4
图4
无限大双材料板界面裂纹问题
Fig.4
An infinite bimaterial plate with an interface crack
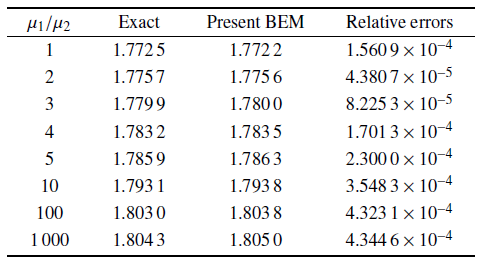
当双材料弹性模量的比值$\mu_{1} /\mu_{2} $不断变化时, 表1 和表2 给出了复应力强度因子$K_{1} $和$K_{2} $的计算结果. 结果表明, 即使$\mu _{1} /\mu_{2} =1 000$, 复应力强度因子的计算结果与精确解依然十分的吻合. 需要注意, 不论$\mu_{1} /\mu_{2} $如何变化, 裂纹表面仅划分20个二次单元, 且无需对裂尖单元进行局部加密.
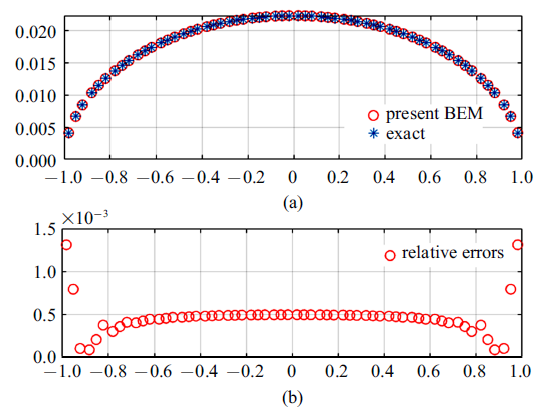
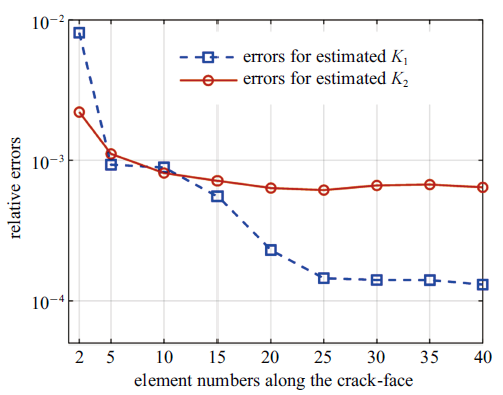
图5 和图6 分别给出了$\mu_{1} /\mu_{2} =5$时, 裂纹表面张开位移和裂尖应力场的计算结果. 结果表明所提"特殊裂尖单元法"可精确表征界面裂纹渐进位移和应力场的振荡特性, 在不增加计算量的前提下, 显著提高断裂力学参数和近场物理量的数值求解精度. 图7 给出了裂纹表面剖分单元数量对计算结果的影响($\mu_{1} /\mu_{2} =5)$. 当裂纹表面划分超过20个单元时, 复应力强度因子的计算结果趋于稳定.
图5
图5
裂纹表面张开位移(a)与相对误差(b)
Fig.5
Results of the crack-opening-displacements (upper) and relative errors (lower)
图6
图6
裂纹尖端应力场$\sigma_{y} $的计算结果
Fig.6
Results of the near-tip stresses $\sigma_{y}$
图7
图7
裂纹表面单元数量对计算结果的影响
Fig.7
Variation of the errors with respect to the number of crack elements
例2 含有中心裂纹的无限大薄板, 裂纹的长度为2$a$, 薄板的宽度为2$L$, 厚度为2$h$, 如图8 所示. 裂纹上下表面受均匀拉力$\sigma $. 定义薄板的相对厚度为$h/L$. 当$a/h\to \infty $时, 应力强度因子的精确解为
(33) $\begin{eqnarray} \label{eq33} K_{I} =\sigma \sqrt h \sqrt {1-2\nu } /(1-\nu ) \end{eqnarray} $
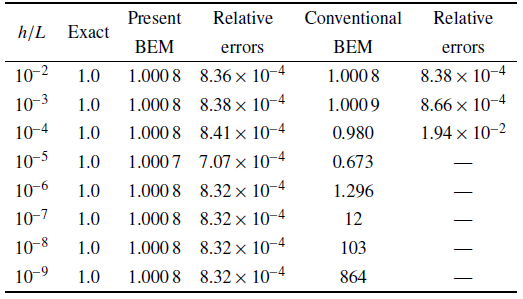
其中$\nu $为材料的泊松比. 边界共划分126个二次单元, 其中裂纹表面划分15个二次单元. 实际计算中, 令$L/a=20$来近似无限大板. 需要注意, 边界元法仅需在边界离散, 可以从容处理边界单元的疏密过渡. 在模拟薄体结构问题时, 不需要根据薄体结构厚度的变化对网格进行加密, 这是比有限元模拟薄体结构问题有优势的地方. 当薄板的相对厚度$h/L$在10$^{-2}$ $\sim$ 10$^{-9}$变化时, 表3 给出了无量纲应力强度因子$K_{1} /[\sigma \sqrt h \sqrt {1-2\nu } (1-\nu )]$的计算结果. 其中, 传统边界元法(conventional BEM)指对薄体结构中产生的近奇异积分直接采用传统高斯积分求解.
图8
图8
含有中心裂纹的薄板
Fig.8
A central craked thin beam constrained between two rigid grips
表3 的数据表明, 当薄板的相对厚度$h/L<10^{-4}$时, 传统边界元法计算的应力强度因子已经完全失效. 相比之下, 本文算法在薄板的相对厚度小到10$^{-9}$时, 应力强度因子的计算结果依然与精确解十分吻合.
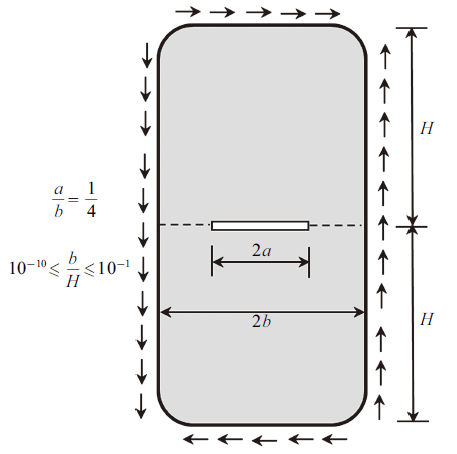
例3 边界受剪应力的含有中心裂纹的薄板, 裂纹的长度为2$a$, 薄板的高度为2$H$, 宽度为$2b$, 如图9 所示. 裂纹长度与板的宽度具有关系$b=4a$, 薄板的高度设置为$H=15$. 定义薄板的相对厚度为$b/H$. 边界共划分188个二次单元, 其中裂纹表面划分10个二次单元. 应力强度因子的精确解为
(34) $K_{2} =\sigma \sqrt {\pi a} F\left( {a,\;b} \right) $
(35) $F=\left[ {1-0.025\left( {\frac{a}{b}} \right)^{2}+0.06\left( {\frac{a}{b}} \right)^{4}} \right]\sqrt {\sec \left( {\frac{\pi a}{2b}} \right)} $
当薄板的相对厚度$b/H$在10$^{-1}$ $\sim$ 10$^{-9}$变化时, 表4 给出了无量纲应力强度因子$K_{2} /\left( {\sigma \sqrt {\pi a} F} \right)$的计算结果. 表4 的数据表明, 当薄板的相对厚度小于10$^{-4}$时, 传统边界元法计算的应力强度因子已经完全失效. 相比之下, 本文算法在薄板的相对厚度小到10$^{-9}$时, 应力强度因子的计算结果依然与精确解十分吻合.
图9
图9
含有中心裂纹的薄板受均匀剪应力
Fig.9
A central craked thin beam under shear loading
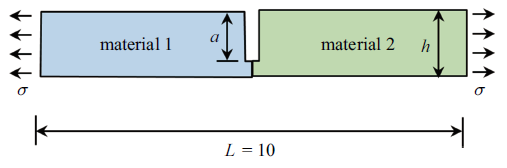
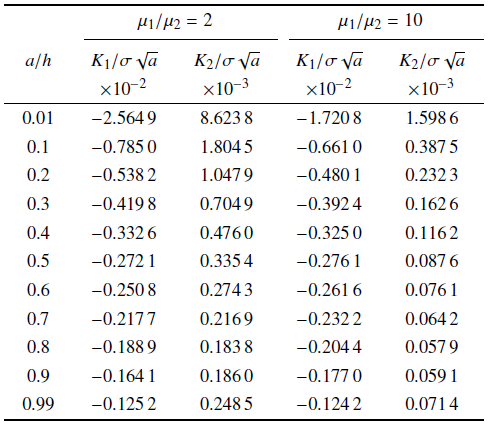
例4 含有边裂纹的双材料板, 如图10 所示. 裂纹的长度为$a$, 材料的厚度为$h$, 宽度为$L$. 板的下边界固定(位移分量为0), 左右边界受拉应力, 上边界和裂纹表面不受力. 材料1和材料2的泊松比为$\nu_{1} =\nu_{2} =0.3$, 弹性模量$\mu_{1} /\mu_{2} \ne 1$. 边界共划分320个二次单元, 其中裂纹表面划分5个二次单元. 定义薄板的相对厚度为$h/L$, 裂纹的相对长度为$a/h$. 固定薄板的厚度为$h/L=10^{-4}$, 裂纹的相对长度在$0.01\leqslant a/h\leqslant 0.99$之间变化. 表5 给出了不同材料组合时(弹性模量$\mu_{1} /\mu_{2} \ne 1)$, 复应力强度因子$K_{1} /(\sigma \sqrt a )$和$K_{2} /(\sigma \sqrt a )$的计算结果.
图10
图10
含有边裂纹的双材料板(拉应力)
Fig.10
A bimaterial beam with an edge-crack under uniform tensile stress loading
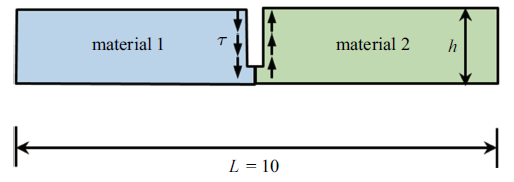
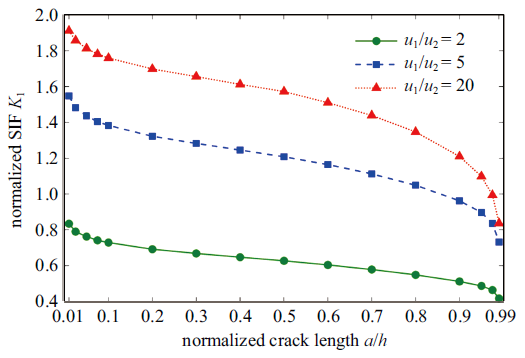
例5 如图11 所示, 例5与例4具有相同的几何形状, 只是边界条件不同. 此时, 板的下边界固定(位移分量为零), 左右边界和上边界不受力, 裂纹表面受剪应力. 同样, 材料1和材料2的泊松比为$\nu_{1} =\nu_{2} =0.3$, 弹性模量$\mu_{1} /\mu_{2} \ne 1$. 边界共划分320个二次单元, 其中裂纹表面划分5个二次单元. 与例4类似, 固定薄板的厚度为$h/L=10^{-4}$, 裂纹的相对长度在$0.01\leqslant a/h\leqslant 0.99$之间变化. 图12 和图13 给出了不同材料组合时, 复应力强度因子$K_{1} /(\tau \sqrt a)$和$K_{2} /(\tau \sqrt a)$的计算结果. 随着材料参数$\mu_{1} /\mu_{2} $的增大, 复应力强度因子的实数部分$K_{1} $不断增大, 而复应力强度因子的复数部分$K_{2} $不断减小.
图11
图11
含有边裂纹的双材料板(剪应力)
Fig.11
A bimaterial beam with an edge-crack under uniform shear stress loading
图12
图12
复应力强度因子$K_{1} /(\tau \sqrt a)$的计算结果
Fig.12
Results of normalized complex stress intensity factors $K_{1} /(\tau \sqrt a)$
图13
图13
复应力强度因子$K_{2} /(\tau \sqrt a)$的计算结果
Fig.13
Results of normalized complex stress intensity factors $K_{2} /(\tau \sqrt a )$
6 结论
针对求解双材料界面裂纹复应力强度因子的困难, 引入了一种含有复振荡因子的新型"特殊裂尖单元". 该方法可直接通过裂尖单元的张开位移或界面应力实现复应力强度因子的精确求解, 无需裂尖区域高密度的网格剖分, 也无需借助J积分、相互作用积分或虚拟裂纹闭合技术等方法对复应力强度因子进行间接求解. 该方法也可直接与有限元或其它数值方法相结合, 用于模拟复合材料界面裂纹等相关问题.
此外, 将求解薄体结构问题的正则化边界元法与上述"特殊裂尖单元"法相结合, 成功求解了超薄(大尺寸比)双材料的界面裂纹问题. 数值算例表明, 所提算法稳定, 效率高, 在不增加计算量的前提下, 显著提高了裂尖近场力学参量和断裂力学参数的求解精度和数值稳定性.
参考文献
View Option
[1]
张明 , 姚振汉 , 杜庆华 等 . 双材料界面裂纹应力强度因子的边界元分析
应用力学学报 , 1999 ,16 (1 ):21 -26
[本文引用: 1]
(Zhang Ming Yao Zhenhan Du Qinghua et al . Boundary element analysis of stress intensity factors of bimaterial interface crack
Chinese Journal of Applied Mechanics 1999 ,16 (1 ):21 -26 (in Chinese))
[本文引用: 1]
[2]
Antwerpen VAV Mulder WA Herman GC . Finite-difference modeling of two-dimensional elastic wave propagation in cracked media
Geophysical Journal International 2002 ,149 :169 -178
[本文引用: 1]
[3]
Moes N Dolbow J Belytschko T . A finite element method for crack growth without remeshing
International Journal for Numerical Methods in Engineering 1999 ,46 (1 ):131 -150
[本文引用: 1]
[4]
Cruse TA . BIE fracture mechanics analysis: 25 years of developments
Computational Mechanics 1996 ,18 (1 ):1 -11
[本文引用: 1]
[5]
Lei J Wang YS Gross D . Two dimensional numerical simulation of crack kinking from an interface under dynamic loading by time domain boundary element method
International Journal of Solids and Structures 2007 ,44 (3 ):996 -1012
[6]
高效伟 , 郑保敬 , 刘健 . 功能梯度材料动态断裂力学的径向积分边界元法
力学学报 , 2015 ,47 (5 ):868 -873
(Gao Xiaowei Zheng Baojing Liu Jian Dynamic fracture analysis of functionally graded materials by radial integration BEM
Chinese Journal of Theoretical and Applied Mechanics 2015 ,47 (5 ):868 -873 (in Chinese))
[7]
程玉民 , 嵇醒 , 贺鹏飞 . 动态断裂力学的无限相似边界元法
力学学报 , 2004 ,36 (1 ):43 -48
(Cheng Yumin Ji Xing He Pengfei Infinite similar boundary element method for dynamic fracture mechanics
Chinese Journal of Theoretical and Applied Mechanics 2004 ,36 (1 ):43 -48 (in Chinese))
[8]
牛忠荣 , 程长征 , 胡宗军 等 . V形切口应力强度因子的一种边界元分析方法
力学学报 , 2008 ,40 (5 ):849 -857
(Niu Zhongrong Cheng Changzheng Hu Zongjun Ye Jianqiao Boundary element analysis of the stress intensity factors for the v-notched structures
Chinese Journal of Theoretical and Applied Mechanics 2008 ,40 (5 ):849 -857 (in Chinese))
[9]
秦太验 , 汤任基 , 陈卫江 . 三维有限体平片裂纹的超奇异积分方程与边界元法
力学学报 , 1997 ,29 (3 ):481 -485
[本文引用: 1]
(Qin Taiyan Tang Renji Chen Weijiang Hypersingular integral equations and boundary element method for planar crack problems in three-dimensional finite bodies
Chinese Journal of Theoretical and Applied Mechanics 1997 ,29 (3 ):481 -485 (in Chinese))
[本文引用: 1]
[10]
Duflot M . A meshless method with enriched weight functions for three-dimensional crack propagation
International Journal for Numerical Methods in Engineering 2006 ,65 (12 ):1970 -2006
[本文引用: 1]
[11]
陈莘莘 , 王娟 . 反平面断裂问题的无单元伽辽金比例边界法
计算力学学报 , 2017 ,34 :57 -61
[本文引用: 1]
(Chen Shenshen Wang Juan An element-free Galerkin scaled boundary method for anti-plane crack problem
Chinese Journal of Computational Mechanics 2017 ,34 :57 -61 (in Chinese))
[本文引用: 1]
[12]
Wu ZJ Wong LNY . Frictional crack initiation and propagation analysis using the numerical manifold method
Computers and Geotechnics 2012 ,39 :38 -53
[本文引用: 1]
[13]
焦玉勇 , 张秀丽 , 刘泉声 等 . 用非连续变形分析方法模拟岩石裂纹扩展
岩石力学与工程学报 , 2007 ,26 :682 -691
[本文引用: 1]
(Jiao Yu-yong Zhang Xiuli Liu Quansheng Chen Weizhong Simulation of rock crack propagation using discontinuous deformation analysis method
Chinese Journal of Rock Mechanics and Engineering 2007 ,26 :682 -691 (in Chinese))
[本文引用: 1]
[14]
Rountree CL Kalia RK Lidorikis E , et al . Atomistic aspects of crack propagation in brittle materials: Multimillion atom molecular dynamics simulations
Annual Review of Materials Research 2002 ,32 :377 -400
[本文引用: 1]
[15]
Erdogan F . Stress distribution in bonded dissimilar materials with cracks
Journal of Applied Mechanics 1965 ,32 (2 ):403 -410
[本文引用: 2]
[16]
Williams ML . The stresses around a fault or crack in dissimilar media
Bulletin of the Seismological Society of America 1959 ,49 (2 ):199 -204
[本文引用: 2]
[17]
England AH . A crack between dissimilar media
Journal of Applied Mechanics 1965 ,32 (2 ):400 -402
[本文引用: 2]
[18]
Yuuki R Xu JQ . Boundary element analysis of dissimilar materials and interface crack
Computational Mechanics 1994 ,14 (2 ):116 -127
[本文引用: 1]
[19]
Ortiz JE Cisilino AP . Boundary element method for J-integral and stress intensity factor computations in three-dimensional interface cracks
International Journal of Fracture 2005 ,133 (3 ):197 -222
[本文引用: 1]
[20]
Liu Y Fan H . Analysis of thin piezoelectric solids by the boundary element method
Computer Methods in Applied Mechanics and Engineering 2002 ,191 (21-22 ):2297 -2315
[本文引用: 1]
[21]
Luo JF Liu YJ Berger EJ . Analysis of two-dimensional thin structures (from micro- to nano-scales) using the boundary element method
Computational Mechanics 1998 ,22 (5 ):404 -412
[本文引用: 1]
[22]
Zhou HL Niu ZR Cheng CZ , et al . Analytical integral algorithm applied to boundary layer effect and thin body effect in BEM for anisotropic potential problems
Computers & Structures 2008 ,86 (15 ):1656 -1671
[23]
Sladek V Sladek J Tanaka M . Nonsingular BEM formulations for thin-walled structures and elastostatic crack problems
Acta Mechanica 1993 ,99 (1 ):173 -190
[24]
Xie G Zhang J Dong Y , et al . An improved exponential transformation for nearly singular boundary element integrals in elasticity problems
International Journal of Solids and Structures 2014 ,51 (6 ):1322 -1329
[25]
Niu Z Zhou H . The natural boundary integral equation in potential problems and regularization of the hypersingular integral
Computers & Structures 2004 ,82 (2-3 ):315 -323
[26]
Ma H Kamiya N . A general algorithm for the numerical evaluation of nearly singular boundary integrals of various orders for two- and three-dimensional elasticity
Computational Mechanics 2002 ,29 (4 ):277 -288
[27]
Gao XW . An effective method for numerical evaluation of general 2D and 3D high order singular boundary integrals
Computer Methods in Applied Mechanics and Engineering 2010 ,199 (45-48 ):2856 -2864
[本文引用: 1]
[28]
Gu Y Zhang C . Novel special crack-tip elements for interface crack analysis by an efficient boundary element method
Engineering Fracture Mechanics 2020 ,239 :107302
[本文引用: 7]
[29]
张耀明 , 孙翠莲 , 谷岩 . 边界积分方程中近奇异积分计算的一种变量替换法
力学学报 , 2008 ,40 (2 ):207 -214
[本文引用: 1]
(Zhang Yaoming Sun Cuilian Gu Yan The evaluation of nearly singular integrals in the boundary integral equations with variables transformation
Chinese Journal of Theoretical and Applied Mechanics 2008 ,40 (2 ):207 -214 (in Chinese))
[本文引用: 1]
[30]
Zhang YM Gu Y Chen JT . Boundary element analysis of the thermal behaviour in thin-coated cutting tools
Engineering Analysis with Boundary Elements 2010 ,34 (9 ):775 -784
[本文引用: 1]
[31]
Rice JR . Elastic fracture mechanics concepts for interfacial cracks
Journal of Applied Mechanics 1988 ,55 (1 ):98 -103
[本文引用: 1]
[32]
张耀明 , 谷岩 , 陈正宗 . 位势边界元法中的边界层效应与薄体结构
力学学报 , 2010 ,42 (2 ):219 -227
[本文引用: 2]
(Zhang Yaoming Gu Yan Chen Jeng-Tzong Boundary layer effect and thin body structure in BEM for potential problems
Chinese Journal of Theoretical and Applied Mechanics 2010 ,42 (2 ):219 -227 (in Chinese))
[本文引用: 2]
[33]
Gu Y Chen W Zhang C . Stress analysis for thin multilayered coating systems using a sinh transformed boundary element method
International Journal of Solids and Structures 2013 ,50 (20-21 ):3460 -3471
[本文引用: 1]
双材料界面裂纹应力强度因子的边界元分析
1
1999
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
双材料界面裂纹应力强度因子的边界元分析
1
1999
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
Finite-difference modeling of two-dimensional elastic wave propagation in cracked media
1
2002
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
A finite element method for crack growth without remeshing
1
1999
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
BIE fracture mechanics analysis: 25 years of developments
1
1996
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
Two dimensional numerical simulation of crack kinking from an interface under dynamic loading by time domain boundary element method
0
2007
功能梯度材料动态断裂力学的径向积分边界元法
0
2015
功能梯度材料动态断裂力学的径向积分边界元法
0
2015
V形切口应力强度因子的一种边界元分析方法
0
2008
V形切口应力强度因子的一种边界元分析方法
0
2008
三维有限体平片裂纹的超奇异积分方程与边界元法
1
1997
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
三维有限体平片裂纹的超奇异积分方程与边界元法
1
1997
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
A meshless method with enriched weight functions for three-dimensional crack propagation
1
2006
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
反平面断裂问题的无单元伽辽金比例边界法
1
2017
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
反平面断裂问题的无单元伽辽金比例边界法
1
2017
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
Frictional crack initiation and propagation analysis using the numerical manifold method
1
2012
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
用非连续变形分析方法模拟岩石裂纹扩展
1
2007
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
用非连续变形分析方法模拟岩石裂纹扩展
1
2007
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
Atomistic aspects of crack propagation in brittle materials: Multimillion atom molecular dynamics simulations
1
2002
... 双材料比较容易在结合面附近萌生裂缝, 并沿着界面发生扩展直至结构破坏. 因此, 双材料的破坏不仅表现为单一材料内部的裂纹问题, 往往更多的是界面的破坏、开裂或脱黏[1 ] . 随着计算力学学科的不断发展, 用于解决断裂力学问题的数值计算方法不断涌现, 从早期的有限差分法[2 ] 、有限元法[3 ] 、边界元法[4 -9 ] 到现在的无网格法[10 -11 ] 、数值流形法[12 ] 、非连续变形分析法[13 ] 、分子动力学法[14 ] 等, 它们成为推动断裂力学研究不断发展的重要工具. ...
Stress distribution in bonded dissimilar materials with cracks
2
1965
... 采用数值方法进行断裂力学分析时, 裂纹尖端奇异区域处理的好坏直接关系到最终断裂力学参数(如应力强度因子、能量释放率等)的求解精度. 对于传统单一材料, 材料内部裂纹尖端位移和应力场具有经典的平方根($r^{1/2})$和负平方根($r^{-1/2})$渐近性, 相应的理论研究和数值求解技术已发展的非常成熟. 比如对裂尖奇异应力场的求解, 已发展了包括"1/4单元法"、"数值外插法"、"虚拟裂纹闭合法"和"J积分/相互作用积分"等多种有效的求解方法. 然而, 与传统单一材料不同, 双材料界面裂纹渐近位移和应力场表现出剧烈的振荡特性, 即[15 -16 ] ...
... 早在20世纪五六十年代, Williams[16 ] , Erdogan[15 ] 和England[17 ] 等就发现双材料界面裂纹渐近位移和应力场具有形如式(1)的振荡特性. 其中$r$为计算点到裂尖的距离, 双材料参数$\varepsilon $定义如下 ...
The stresses around a fault or crack in dissimilar media
2
1959
... 采用数值方法进行断裂力学分析时, 裂纹尖端奇异区域处理的好坏直接关系到最终断裂力学参数(如应力强度因子、能量释放率等)的求解精度. 对于传统单一材料, 材料内部裂纹尖端位移和应力场具有经典的平方根($r^{1/2})$和负平方根($r^{-1/2})$渐近性, 相应的理论研究和数值求解技术已发展的非常成熟. 比如对裂尖奇异应力场的求解, 已发展了包括"1/4单元法"、"数值外插法"、"虚拟裂纹闭合法"和"J积分/相互作用积分"等多种有效的求解方法. 然而, 与传统单一材料不同, 双材料界面裂纹渐近位移和应力场表现出剧烈的振荡特性, 即[15 -16 ] ...
... 早在20世纪五六十年代, Williams[16 ] , Erdogan[15 ] 和England[17 ] 等就发现双材料界面裂纹渐近位移和应力场具有形如式(1)的振荡特性. 其中$r$为计算点到裂尖的距离, 双材料参数$\varepsilon $定义如下 ...
A crack between dissimilar media
2
1965
... 其中i为复数单位, $\varepsilon $为双材料参数(或振荡因子). 导致许多用于表征经典的平方根和负平方根物理场渐近性的传统方法失效[17 -18 ] . 虽然界面裂纹复应力强度因子($K_{1} +{i}K_{2} )$可采用各种守恒积分(如J积分)或位移外插法等进行间接求解, 但计算精度较低, 也难以直接获得裂尖近场区域物理量的精确分布[19 ] . 因此, 虽然目前计算断裂力学发展的比较成熟, 但其在双材料界面裂纹分析方面的研究依然比较欠缺, 从基础研究的角度来考虑还需进行大量的研究. ...
... 早在20世纪五六十年代, Williams[16 ] , Erdogan[15 ] 和England[17 ] 等就发现双材料界面裂纹渐近位移和应力场具有形如式(1)的振荡特性. 其中$r$为计算点到裂尖的距离, 双材料参数$\varepsilon $定义如下 ...
Boundary element analysis of dissimilar materials and interface crack
1
1994
... 其中i为复数单位, $\varepsilon $为双材料参数(或振荡因子). 导致许多用于表征经典的平方根和负平方根物理场渐近性的传统方法失效[17 -18 ] . 虽然界面裂纹复应力强度因子($K_{1} +{i}K_{2} )$可采用各种守恒积分(如J积分)或位移外插法等进行间接求解, 但计算精度较低, 也难以直接获得裂尖近场区域物理量的精确分布[19 ] . 因此, 虽然目前计算断裂力学发展的比较成熟, 但其在双材料界面裂纹分析方面的研究依然比较欠缺, 从基础研究的角度来考虑还需进行大量的研究. ...
Boundary element method for J-integral and stress intensity factor computations in three-dimensional interface cracks
1
2005
... 其中i为复数单位, $\varepsilon $为双材料参数(或振荡因子). 导致许多用于表征经典的平方根和负平方根物理场渐近性的传统方法失效[17 -18 ] . 虽然界面裂纹复应力强度因子($K_{1} +{i}K_{2} )$可采用各种守恒积分(如J积分)或位移外插法等进行间接求解, 但计算精度较低, 也难以直接获得裂尖近场区域物理量的精确分布[19 ] . 因此, 虽然目前计算断裂力学发展的比较成熟, 但其在双材料界面裂纹分析方面的研究依然比较欠缺, 从基础研究的角度来考虑还需进行大量的研究. ...
Analysis of thin piezoelectric solids by the boundary element method
1
2002
... 此外, 随着实际工程需求和表面涂层工艺的逐渐成熟, 大量双材料的相对厚度(表面特征长度和厚度的尺寸比)越来越小, 特别是各种微纳米复合材料的相继出现, 给精确有效的数值模拟带来了巨大的挑战. 比如, 为了避免出现畸形网格, 有限元法需按照涂层的厚度划分单元. 可这样做必然会导致百万甚至几百万个子单元, 计算工作量剧增, 同时解的收敛性也难以保证[20 ] . 相对于有限元法, 边界元仅需在边界离散, 可以从容处理边界单元的疏密过渡, 很大程度上避免了有限元法中网格畸变带来的困难, 这一点对薄体与涂层结构问题的数值模拟尤为重要. 近年来, 边界元法在薄体结构问题中的应用正在蓬勃发展, 被认为是其比有限元法更具优势的一个新领域, 而且在表面涂层、压电薄膜等工程领域展现出了广阔的应用前景[21 -27 ] . ...
Analysis of two-dimensional thin structures (from micro- to nano-scales) using the boundary element method
1
1998
... 此外, 随着实际工程需求和表面涂层工艺的逐渐成熟, 大量双材料的相对厚度(表面特征长度和厚度的尺寸比)越来越小, 特别是各种微纳米复合材料的相继出现, 给精确有效的数值模拟带来了巨大的挑战. 比如, 为了避免出现畸形网格, 有限元法需按照涂层的厚度划分单元. 可这样做必然会导致百万甚至几百万个子单元, 计算工作量剧增, 同时解的收敛性也难以保证[20 ] . 相对于有限元法, 边界元仅需在边界离散, 可以从容处理边界单元的疏密过渡, 很大程度上避免了有限元法中网格畸变带来的困难, 这一点对薄体与涂层结构问题的数值模拟尤为重要. 近年来, 边界元法在薄体结构问题中的应用正在蓬勃发展, 被认为是其比有限元法更具优势的一个新领域, 而且在表面涂层、压电薄膜等工程领域展现出了广阔的应用前景[21 -27 ] . ...
Analytical integral algorithm applied to boundary layer effect and thin body effect in BEM for anisotropic potential problems
0
2008
Nonsingular BEM formulations for thin-walled structures and elastostatic crack problems
0
1993
An improved exponential transformation for nearly singular boundary element integrals in elasticity problems
0
2014
The natural boundary integral equation in potential problems and regularization of the hypersingular integral
0
2004
A general algorithm for the numerical evaluation of nearly singular boundary integrals of various orders for two- and three-dimensional elasticity
0
2002
An effective method for numerical evaluation of general 2D and 3D high order singular boundary integrals
1
2010
... 此外, 随着实际工程需求和表面涂层工艺的逐渐成熟, 大量双材料的相对厚度(表面特征长度和厚度的尺寸比)越来越小, 特别是各种微纳米复合材料的相继出现, 给精确有效的数值模拟带来了巨大的挑战. 比如, 为了避免出现畸形网格, 有限元法需按照涂层的厚度划分单元. 可这样做必然会导致百万甚至几百万个子单元, 计算工作量剧增, 同时解的收敛性也难以保证[20 ] . 相对于有限元法, 边界元仅需在边界离散, 可以从容处理边界单元的疏密过渡, 很大程度上避免了有限元法中网格畸变带来的困难, 这一点对薄体与涂层结构问题的数值模拟尤为重要. 近年来, 边界元法在薄体结构问题中的应用正在蓬勃发展, 被认为是其比有限元法更具优势的一个新领域, 而且在表面涂层、压电薄膜等工程领域展现出了广阔的应用前景[21 -27 ] . ...
Novel special crack-tip elements for interface crack analysis by an efficient boundary element method
7
2020
... 论文以边界元法为基本工具, 通过引入一种能精确表征复合材料界面裂纹振荡特性的"特殊裂尖单元"[28 ] , 实现了双材料界面裂纹复应力强度因子的精确求解. 该方法无需裂尖区域高密度的网格剖分, 可显著提高裂尖近场力学参量和复应力强度因子的求解精度和数值稳定性. 在此基础上, 结合边界元法中计算近奇异积分的一种通用正则化算法[29 -30 ] , 成功求解了超薄双材料界面裂纹问题. 数值算例表明, 所提算法稳定, 效率高, 在不增加计算量的前提下, 显著提高了裂尖近场力学参量和断裂力学参数的求解精度和数值稳定性. 1 界面裂纹渐进位移和应力场的振荡特性 ...
... 对于平面应变问题, 有$\kappa_{i} =3-4\nu_{i} $. 对于平面应力问题, 有$\kappa_{i} =(3-\nu_{i} )/(1+\nu_{i} )$. 裂纹尖端附近的位移和应力场可表示为[28 ,31 ] ...
... 采用多域边界元法对图1 所示的双材料界面裂纹问题进行数值求解. 对区域$\varOmega _{1} $和$\varOmega_{2} $, 可分别建立如下边界积分方程[28 ] ...
... 引入一种含有复振荡因子的新型"特殊裂尖单元"[28 ] , 可精确表征裂纹尖端渐近位移和应力场的振荡特性. 提高界面裂纹复应力强度因子的数值求解精度. 下文简要介绍方法的数学原理. ...
... 其中待定系数$B_{1}^{k} $, $B_{2}^{k} $和$B_{3}^{k} $可通过上述方法类似求解. 式(17)和式(21)可用于裂尖单元位移场的插值近似, 这样便可精确表征界面裂纹渐进位移场的振荡特性. 式(17)和式(21)的具体数学表达式见文献[28 ]. ...
... 其中$C_{1}^{k} $, $C_{2}^{k} $和$C_{3}^{k} $为待定系数, 其具体数学表达式可见文献[28 ]. 需要指出, 上述位移和应力特殊形函数仅需在裂纹尖端左右两侧的两个边界单元使用, 其它边界单元上的位移和应力可通过常规位移/面力形函数式(11)进行插值近似. ...
... 例1 含有中心裂纹的无限大双材料板, 界面裂纹的长度为2$a$, 裂纹表面受均匀拉力$\sigma_{0} $ (见图4 ). 材料1和材料2的泊松比为$\nu_{1} =\nu_{2} =0.2$. 实际计算中, 令双材料板的宽度和高度为$50a$. 边界共划分280个二次单元, 其中裂纹表面划分20个二次单元, 裂尖单元相对于裂纹长度为$a$/10. 断裂力学参数和裂尖渐近位移和应力场的精确解见文献[28 ]. ...
边界积分方程中近奇异积分计算的一种变量替换法
1
2008
... 论文以边界元法为基本工具, 通过引入一种能精确表征复合材料界面裂纹振荡特性的"特殊裂尖单元"[28 ] , 实现了双材料界面裂纹复应力强度因子的精确求解. 该方法无需裂尖区域高密度的网格剖分, 可显著提高裂尖近场力学参量和复应力强度因子的求解精度和数值稳定性. 在此基础上, 结合边界元法中计算近奇异积分的一种通用正则化算法[29 -30 ] , 成功求解了超薄双材料界面裂纹问题. 数值算例表明, 所提算法稳定, 效率高, 在不增加计算量的前提下, 显著提高了裂尖近场力学参量和断裂力学参数的求解精度和数值稳定性. 1 界面裂纹渐进位移和应力场的振荡特性 ...
边界积分方程中近奇异积分计算的一种变量替换法
1
2008
... 论文以边界元法为基本工具, 通过引入一种能精确表征复合材料界面裂纹振荡特性的"特殊裂尖单元"[28 ] , 实现了双材料界面裂纹复应力强度因子的精确求解. 该方法无需裂尖区域高密度的网格剖分, 可显著提高裂尖近场力学参量和复应力强度因子的求解精度和数值稳定性. 在此基础上, 结合边界元法中计算近奇异积分的一种通用正则化算法[29 -30 ] , 成功求解了超薄双材料界面裂纹问题. 数值算例表明, 所提算法稳定, 效率高, 在不增加计算量的前提下, 显著提高了裂尖近场力学参量和断裂力学参数的求解精度和数值稳定性. 1 界面裂纹渐进位移和应力场的振荡特性 ...
Boundary element analysis of the thermal behaviour in thin-coated cutting tools
1
2010
... 论文以边界元法为基本工具, 通过引入一种能精确表征复合材料界面裂纹振荡特性的"特殊裂尖单元"[28 ] , 实现了双材料界面裂纹复应力强度因子的精确求解. 该方法无需裂尖区域高密度的网格剖分, 可显著提高裂尖近场力学参量和复应力强度因子的求解精度和数值稳定性. 在此基础上, 结合边界元法中计算近奇异积分的一种通用正则化算法[29 -30 ] , 成功求解了超薄双材料界面裂纹问题. 数值算例表明, 所提算法稳定, 效率高, 在不增加计算量的前提下, 显著提高了裂尖近场力学参量和断裂力学参数的求解精度和数值稳定性. 1 界面裂纹渐进位移和应力场的振荡特性 ...
Elastic fracture mechanics concepts for interfacial cracks
1
1988
... 对于平面应变问题, 有$\kappa_{i} =3-4\nu_{i} $. 对于平面应力问题, 有$\kappa_{i} =(3-\nu_{i} )/(1+\nu_{i} )$. 裂纹尖端附近的位移和应力场可表示为[28 ,31 ] ...
位势边界元法中的边界层效应与薄体结构
2
2010
... 二维弹性力学边界元法中的近奇异积分可以归结为以下两种形式[32 -33 ] ...
... 其中$\alpha >0$, $f(\xi )$为规则函数(包含雅可比函数、形函数等). 若采用三点二次单元近似几何边界, 计算点$P$到积分单元的距离函数$r^{2}(\xi )$可表示为[32 ] ...
位势边界元法中的边界层效应与薄体结构
2
2010
... 二维弹性力学边界元法中的近奇异积分可以归结为以下两种形式[32 -33 ] ...
... 其中$\alpha >0$, $f(\xi )$为规则函数(包含雅可比函数、形函数等). 若采用三点二次单元近似几何边界, 计算点$P$到积分单元的距离函数$r^{2}(\xi )$可表示为[32 ] ...
Stress analysis for thin multilayered coating systems using a sinh transformed boundary element method
1
2013
... 二维弹性力学边界元法中的近奇异积分可以归结为以下两种形式[32 -33 ] ...