引言
相较于有限元法(FEM), 边界元法[1 ] (BEM)只需在结构外边界划分网格, 因此BEM可对复杂几何模型进行简单的网格划分. 然而BEM生成的系数矩阵是非对称满阵, 构造矩阵所需的运算量级为$O(N^{2})$, 如果采用高斯消去法求解, 则所需运算量级更是达到$O(N^{3})$, 因而导致BEM难以计算大规模问题. 伴随快速多极算法[2 -3 ] 发展起来的快速多极边界元法(FM-BEM)可很好地解决这个问题, 其所需的运算量和存储量较传统BEM大大降低, FM-BEM成为近20年边界元领域的热门课题之一, 并被广泛应用于二维位势和弹性问题、三维声场问题等.
有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟.
目前, 快速多极边界元法大多采用常值单元, 其优点是所有的近场积分, 包括奇异积分和几乎奇异积分[23 -26 ] 均可采用解析公式直接计算, 但对于曲线边界和复杂物理场, 常值单元的计算只能依赖于使用大量单元, 且计算精度和计算效率往往不能令人满意. 使用高阶单元能够获得更准确的计算结果, 但由于存在奇异积分和几乎奇异积分的计算难题[27 -28 ] , 因而鲜见高阶单元快速多极边界元法的相关报导. 本文在复平面内计算高阶单元的奇异积分和几乎奇异积分, 建立高阶单元快速多极边界元法, 并将其应用于二维正交各向异性位势热传导问题分析.
1 二维位势问题的常规边界积分方程
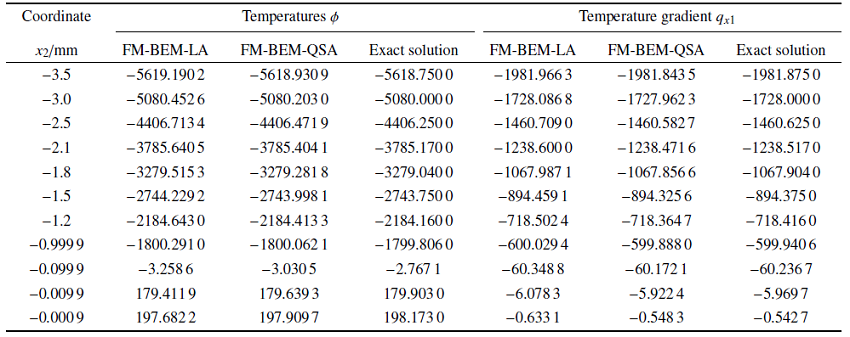
考虑二维正交各向异性材料位势问题, 见图1 . 内点${y}$的位势$\phi ({y})$可由边界位势$\phi ({x})$和法向位势梯度$q({x})$的积分形式表达
(1) $\begin{eqnarray} \label{eq1} \phi ({y})+\int_\varGamma {F({x}, {y})\phi ({x})} {d}\varGamma =\int_\varGamma {G({x}, {y})q({x})} {d}\varGamma ,\ y\in \varOmega\quad \end{eqnarray} $
式中, ${x}(x_{1} ,x_{2} )$称为场点, ${y}(y_{1} ,y_{2} )$为源点. 当源点${y}$落在边界$\varGamma $上, 可得二维正交各向异性位势问题的边界积分方程
(2) $\begin{eqnarray} \label{eq2} \hspace{-3mm}c({y})\phi ({y})\!+\!\int_\varGamma {F({x}, {y})\phi ({x})} {d}\varGamma\!=\!\int_\varGamma {G({x}, {y})q({x})} {d}\varGamma , y\in \varOmega \end{eqnarray} $
其中, $c({y})={\alpha }/(2\pi)$, $\alpha $为源点${y}$处边界的内折角. 位势$G({x}, {y})$和位势梯度$F({x}, {y})$的基本解为
(3) $G({x}, {y})=-\frac{1}{{2\pi }\sqrt{\varsigma_{1} \varsigma_{2} } }\ln \hat{{r}}=-\frac{X}{{2\pi }}\ln \hat{{r}} $
(4) $F({x}, {y})=\frac{\partial G({x}, {y})}{\partial n(x)} =\varsigma_{1} \frac{\partial G({x}, {y})}{\partial x_{1} }n_{1} +\varsigma_{2} \frac{\partial G({x}, {y})}{\partial x_{2} }n_{2} $
(5) $\begin{eqnarray} \label{eq5} \hat{{r}}=X\sqrt {\varsigma_{2} (x_{1} -y_{1} )^{2}+\varsigma_{1} (x_{2} -y_{2} )^{2}} \end{eqnarray} $
其中$X={1}/{\sqrt {\varsigma_{1} \varsigma_{2}}}$, $\varsigma_{i} $分别是正交各向异性材料$x_{i} $方向的特征系数. $n_{i} (i=1,2)$为边界单元的单位法向量.
图1
图1
正交各向异性材料位势问题
Fig.1
Potential problems of orthotropic materials
在域内点${y}$处沿着${y}_{i} $方向对式(1)进行求导, 可得位势导数的积分方程
(6) $\begin{eqnarray} \label{eq6} &&\frac{\partial \phi ({y})}{\partial y_{i} }=\int_\varGamma {\frac{\partial G({x},{y})}{\partial y_{i} }} q({x}){d}\varGamma-\int_\varGamma {\frac{\partial F({x},{y})}{\partial y_{i} }} \phi ({x}){d}\varGamma ,\ \ {y}\in \varOmega ,\ \ {x}\in \varGamma \end{eqnarray} $
通过离散边界$\varGamma $, 式(1)、式(2)和式(6)中的单元积分可写成
(7) $\int_{\varGamma_{{e}}}G(x,y)N_{j}(\xi )q_{j}^{e}{d}\varGamma, \int_{\varGamma_{{e}}} F(x,y)N_{j}(\xi )\phi_{j}^{e} {d}\varGamma $
(8) $\int_{\varGamma_{{e}}}\frac{\partial G(x,y)}{\partial y_{i}}N_{j}(\xi)q_{j}^{e}{d}\varGamma, \int_{\varGamma_{{e}}}\frac{\partial F(x,y)}{\partial y_{i}}N_{j}(\xi)\phi_{j}^{e}{d}\varGamma $
式中, $\varGamma_{e} $表示离散的边界单元, $\xi $是单元$\varGamma_{e} $的局部坐标, $N_{j} (\xi )$是单元$j$节点的插值形函数. $\phi_{j}^{e} $和$q_{j}^{e} $分别是单元$j$节点的位势和位势梯度值.
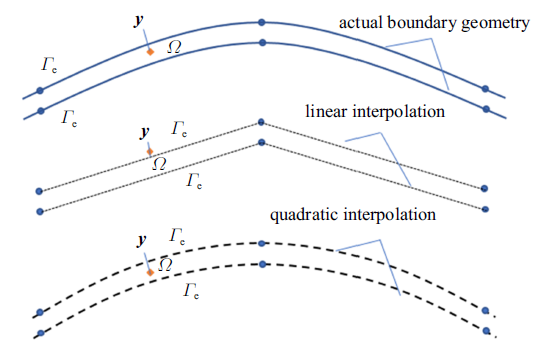
当源点$y$与积分单元$\varGamma_{e} $的节点重合, 式(7)的积分核是奇异的. 当源点$y$临近积分单元$\varGamma_{e} $, 式(7)和式(8)的积分核呈现出几乎奇异性. 相较于奇异积分, 高阶单元几乎奇异积分的计算更加复杂. 为了尽可能减少处理高阶单元奇异和几乎奇异积分所带来的计算量负担, 在复数域内建立高阶单元奇异和几乎奇异积分的计算列式.
2 复势法计算高阶单元奇异和近奇异积分
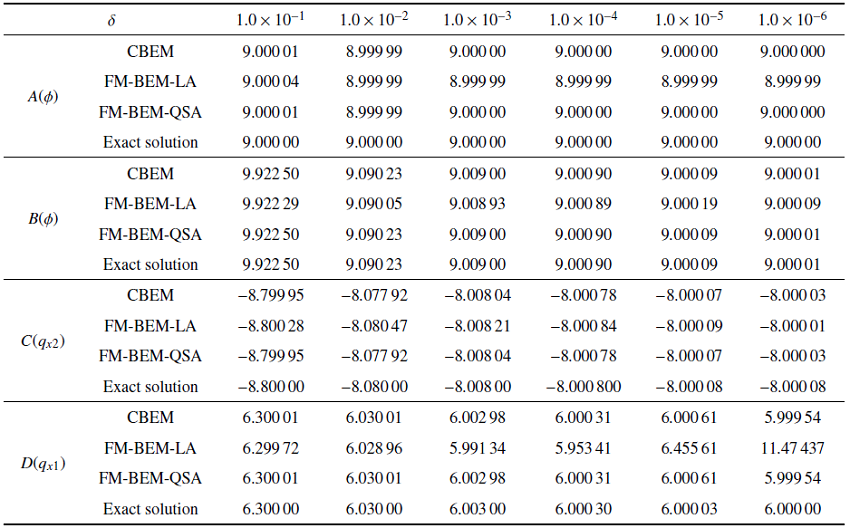
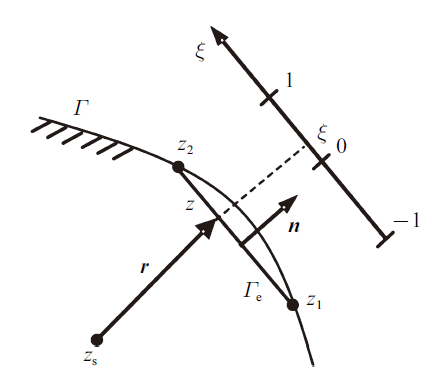
引入复数表达, 场点$x$由$z$表示, 源点$y$由$z_{s}$表示, 令$z=\sqrt {{1}/{\varsigma_{1} }} x_{1} +{i}\sqrt {{1}/{\varsigma _{2} }} x_{2} $, $z_{s} =\sqrt {{1}/{\varsigma_{1} }} y_{1} +{i}\sqrt {{1}/{\varsigma_{2} }} y_{2} $, 见图2 . 通过复平面转换, 实平面内和复平面内位势和位势梯度的基本解满足
(9) $\begin{eqnarray} \label{eq9} \left. {\begin{array}{l} G({x},{y})=X{Re}[G(z,z_{s} )] \\ F({x},{y})=X{Re}[F(z,z_{s} )] \\ \end{array}} \right\} \end{eqnarray} $
(10) $G(z,z_{s} )=-\frac{1}{2\pi }\ln (z_{s} -z) $
(11) $F(z,z_{s} )=\frac{\partial G(z,z_{s} )}{\partial n}=-\frac{n(z)}{2\pi (z-z_{s} )} $
$n(z)$是边界单元$\varGamma_{e} $的单位法向量的复数形式. 通过式(9), 积分式(7)和式(8)可重写为
(12) $\int_{\varGamma_{e} } {G({x},{y})N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma = X{Re}\left[\int_{\varGamma_{e} } {G(z,z_{s} )N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma \right] $
(13) $\int_{\varGamma_{e} } {F({x},{y})N_{j} } \left( \xi \right)\phi _{j}^{e} {d}\varGamma = X{Re}\left[\int_{\varGamma_{e} } {F(z,z_{s} )N_{j} } \left( \xi \right)\phi _{j}^{e} {d}\varGamma \right] $
(14) $\int_{\varGamma_{e} } {\frac{\partial G({x},{y})}{\partial y_{1} }N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma = X\sqrt {\frac{1}{\varsigma_{1} }} {Re}\left[\int_{\varGamma_{e} } {\frac{\partial G(z,z_{s} )}{\partial z_{s} }N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma \right] $
(15) $\int_{\varGamma_{e} } {\frac{\partial G({x},{y})}{\partial y_{2} }N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma =-X\sqrt {\frac{1}{\varsigma_{2} }} {\rm{Im}}\left[\int_{\varGamma_{e} } {\frac{\partial G(z,z_{s} )}{\partial z_{s} }N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma \right] $
(16) $\int_{\varGamma_{e} } {\frac{\partial F({x},{y})}{\partial y_{1} }N_{j} } \left( \xi \right)\phi_{j}^{e} {d}\varGamma = X\sqrt {\frac{1}{\varsigma_{1} }} {Re}\left[\int_{\varGamma_{e} } {\frac{\partial F(z,z_{s} )}{\partial z_{s} }N_{j} } \left( \xi \right)\phi_{j}^{e} {d}\varGamma\right] $
(17) $\int_{\varGamma_{e} } {\frac{\partial F({x},{y})}{\partial y_{2} }N_{j} } \left( \xi \right)\phi_{j}^{e} {d}\varGamma = -X\sqrt {\frac{1}{\varsigma_{2} }} {\rm{Im}}\left[\int_{\varGamma_{e} } {\frac{\partial F(z,z_{s} )}{\partial z_{s} }N_{j} } \left( \xi \right)\phi_{j}^{e} {d}\varGamma\right] $
式中, Re$[\cdots]$和Im$[\cdots]$分别表示复变函数的实部和虚部.
图2
图2
复平面坐标转换
Fig.2
Complex plane coordinate conversion
2.1 线性单元
对于线性单元, 如图3 所示, $z_{1}$, $z_{2}$是单元首、末节点复数坐标. 在单元局部坐标系$o\xi $下有
(18) $\begin{eqnarray} \label{eq18} z(\xi )=\sum\limits_{j=1}^2 {N_{j} (\xi )z_{j} =} z_{a} \xi +z_{b} \end{eqnarray} $
(19) $\begin{eqnarray} \label{eq19} \left. {\begin{array}{l} z_{a} =\dfrac{z_{2} -z_{1} }{2} \\[2mm] z_{b} =\dfrac{z_{2} +z_{1} }{2} \\ \end{array}} \right\} \end{eqnarray} $
$\left| {J(\xi )} \right|$是坐标转换的雅可比行列式, 令$z_{e} =\sqrt {\varsigma _{1} }{Re}(z_{a} )+{i}\sqrt {\varsigma_{2} }{\rm{Im}}(z_{a} )$, 有
(20) $\begin{eqnarray} \label{eq20} {d}\varGamma =\left| {J(\xi )} \right|{d}\xi =\left| {z_{e} } \right|{d}\xi \end{eqnarray} $
$n$为单元的外法向单位向量, 令$z_{d} =\sqrt {\varsigma_{1}\varsigma_{2} }{Im}(z_{a} )-{i}\sqrt {\varsigma_{1} \varsigma_{2} }{Re}(z_{a})$, 有
(21) $\begin{eqnarray} \label{eq21} n(z){d}\varGamma =n(\xi )\left| {J(\xi )} \right|{d}\xi =z_{d} {d}\xi \end{eqnarray} $
图3
图3
线单元坐标变换
Fig.3
Coordinate conversion of a linear element
若源点落在线性单元上, 矢径$r$与外法向量$n$始终垂直, 也即$F(z,z_{s} )=0$. 而对于积分项$\int_{\varGamma_{e} } {G(z,z_{s} )N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma $, 有
(22) $\begin{eqnarray} \label{eq22} &&\int_{\varGamma_{e} } {G(z,z_{s} )N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma = \int_{-1}^{1} {-\frac{q_{j}^{e} }{2\pi }} N_{j} \left( \xi \right)\ln (z_{a} \xi \pm z_{a} )\left| {z_{e} } \right|{d}\xi \end{eqnarray} $
当源点$z_{s} $位于积分单元$\varGamma_{{e}} $外, 单元积分为
(23) $\int_{\varGamma_{e} } {G(z,z_{s} )N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma = \int_{-1}^{1} {-\frac{q_{j}^{e} }{2\pi }} N_{j} \left( \xi \right)\ln (z_{a} \xi +z_{b} -z_{s} )\left| {z_{e} } \right|{d}\xi $
(24) $\int_{\varGamma_{e} } {F(z,z_{s} )N_{j} } \left( \xi \right)\phi_{j}^{e} {d}\varGamma = \int_{-1}^{1} {-\frac{\phi_{j}^{e} }{2\pi }} \frac{N_{j} \left( \xi \right)}{z_{a} \xi +z_{b} -z_{s} }z_{d} {d}\xi $
(25) $\int_{\varGamma_{e} } {\frac{\partial G(z,z_{s} )}{\partial z_{s} }N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma = \int_{-1}^{1} {\frac{q_{j}^{e} }{2\pi }} \frac{N_{j} \left( \xi \right)}{z_{a} \xi +z_{b} -z_{s} }\left| {z_{e} } \right|{d}\xi $
(26) $\int_{\varGamma_{e} } {\frac{\partial F(z,z_{s} )}{\partial z_{s} }N_{j} } \left( \xi \right)\phi_{j}^{e} {d}\varGamma = \int_{-1}^{1} {-\frac{\phi_{j}^{e} }{2\pi }} \frac{N_{j} \left( \xi \right)}{(z_{a} \xi +z_{b} -z_{s} )^{2}}z_{d} {d}\xi $
式(22) $\sim\!$式(26)中的积分项可归纳为以下几种
(27) $T_{k}^{S} =\int_{-1}^1 \frac{\xi^{k}}{\omega (\xi )} {d}\xi ,\ \ T_{k}^{H} =\int_{-1}^1 {\frac{\xi^{k}}{[\omega (\xi )]^{2}}} {d}\xi $
(28) $T_{k}^{W} =\int_{-1}^1 {\xi^{k}\ln [\omega (\xi )]} {d}\xi $
(29) $\begin{eqnarray} \label{eq29} \omega (\xi )=z_{a} \xi +z_{b} -z_{s} \end{eqnarray} $
在复平面推导出式(27)和式(28)积分的解析表达式
(30) $T_{k}^{S} =\int_{-1}^1 {\dfrac{\xi^{k}}{\omega (\xi )}} {d}\xi =\\[3mm] \left. {\begin{array}{l@{\quad }l} \dfrac{1}{z_{a} }\ln \left[\dfrac{\omega (1)}{\omega (-1)}\right],& k=0 \\[2mm] \dfrac{1-(-1)^{k}}{z_{a} }-\dfrac{z_{b} -z_{s} }{z_{a} }T_{k-1}^{S}, & k\geqslant 1 \\[2mm] \end{array}} \right\} $
(31) $T_{k}^{H} =\int_{-1}^1 {\dfrac{\xi^{k}}{[\omega (\xi )]^{2}}} {d}\xi =\\[3mm] \left. {\begin{array}{l@{\quad }l} -\dfrac{1}{z_{a} }\left[\dfrac{1}{\omega (1)}-\dfrac{1}{\omega (-1)}\right], & k=0\\[2mm] \dfrac{1}{z_{a} }[T_{k-1}^{S} -(z_{b} -z_{s} )T_{k-1}^{H} ],& k\geqslant 1\\[2mm] \end{array}} \right\} $
(32) $T_{k}^{W} =\int_{-1}^1 {\xi^{k}\ln [\omega (\xi )]} {d}\xi =\dfrac{1}{k+1}\Big\{\ln [\omega (1)]-(-1)^{k+1}\cdot \ln [\omega (-1)]-z_{a} T_{k+1}^{S} \Big\},\ \ k\geqslant 0 $
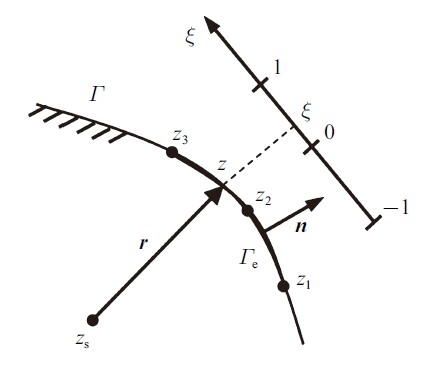
2.2 3节点二次单元
对于3节点二次单元, 如图4 所示, $z_{1} $是单元首节点的复数坐标, $z_{2} $是单元中节点的复数坐标, $z_{3} $是单元末节点的复数坐标. 在局部坐标系$o\xi$下有
(33) $\begin{eqnarray} \label{eq33} z(\xi )=\sum\limits_{j=1}^3 {N_{j} (\xi )z_{j} =} z_{a} \xi^{2}+z_{b} \xi +z_{2} \end{eqnarray} $
(34) $\begin{eqnarray} \label{eq34} \left. {\begin{array}{l} z_{a} =\dfrac{1}{2}z_{1} -z_{2} +\dfrac{1}{2}z_{3} \\[3mm] z_{b} =\dfrac{1}{2}z_{3} -\dfrac{1}{2}z_{1} \\ \end{array}} \right\} \end{eqnarray} $
(35) $z_{a1} =\sqrt {\varsigma_{1} }{Re}(z_{a} )+{i}\sqrt {\varsigma_{2} }{Im}(z_{a}) $
(36) $z_{b1} =\sqrt {\varsigma_{1} }{Re}(z_{b} )+{i}\sqrt {\varsigma_{2} }{Im}(z_{b}) $
(37) $z_{v} ={Im}(z_{a1} )-{i}{Re}(z_{a1} ) $
(38) $z_{w} ={Im}(z_{b1} )-{i}{Re}(z_{b1} ) $
(39) ${d}\varGamma =\left| {J(\xi )} \right|{d}\xi =\left| {2z_{a1} \xi +z_{b1} } \right|{d}\xi $
(40) $n(z){d}\varGamma =n(\xi )\left| {J(\xi )} \right|{d}\xi =(2z_{v} \xi +z_{w} ){d}\xi $
注意到在使用二次单元模拟直线边界时, $z_{a} $可能等于0. 因此, 二次单元边界积分的计算分为$z_{a} =0$和$z_{a} \ne 0$两种情形.
图4
图4
二次单元坐标变换
Fig.4
Coordinate conversion of a three-node quadratic element
当源点$z_{s} $与积分单元首节点$z_{1} $重合, 使用$\xi =2\eta -1$变换可得
(41) $\begin{eqnarray} \label{eq41} && \int_{\varGamma_{e} } {G(z,z_{s} )N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma =\\&&\qquad -\frac{q_{j}^{e} }{2\pi }\int_{-1}^{1} {N_{j} \left( \xi \right)} \left| {J(\xi )} \right|\ln (2z_{a} \xi -2z_{a} +2z_{b} ){d}\xi +\\&&\qquad\frac{q_{j}^{e} }{\pi }\int_0^{1} {N_{j} \left( {2\eta -1} \right)} \left| {J(2\eta -1)} \right|\ln \left(\frac{1}{\eta }\right){d}\eta \end{eqnarray} $
式(41)等号右边第1项采用常规Gauss数值积分计算, 第2项采用对数型Gauss数值积分计算.
当源点$z_{s} $与积分单元中节点$z_{2} $重合
(42) $\begin{eqnarray} \label{eq42} && \int_{\varGamma_{e} } {G(z,z_{s} )N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma =\\&&\qquad -\frac{q_{j}^{e} }{2\pi }\int_{-1}^{1} {\ln (z_{a} \xi +z_{b} )} N_{j} \left( \xi \right)\left| {J(\xi )} \right|{d}\xi +\\&&\qquad\frac{q_{j}^{e} }{2\pi }\int_0^{1} {N_{j} \left( {-\eta } \right)} \left| {J(-\eta )} \right|\ln \left(\frac{1}{\eta }\right){d}\eta +\\&&\qquad\frac{q_{j}^{e} }{2\pi }\int_0^{1} {N_{j} \left( \eta \right)} \left| {J(\eta )} \right|\ln \left(\frac{1}{\eta }\right){d}\eta \end{eqnarray} $
式(42)等号右边第1项采用常规Gauss数值积分计算, 后2项采用对数型Gauss数值积分计算.
当源点$z_{s} $与积分单元末节点$z_{3} $重合, 使用$\xi=1-2\eta $变换可得
(43) $\begin{eqnarray} \label{eq43} &&\int_{\varGamma_{e} } {G(z,z_{s} )N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma =\\&&\qquad-\frac{q_{j}^{e} }{2\pi }\int_{-1}^{1} {N_{j} \left( \xi \right)} \left| {J(\xi )} \right|\ln (-2z_{a} \xi -2z_{a} -2z_{b} ){d}\xi +\\&&\qquad\frac{q_{j}^{e} }{\pi }\int_0^{1} {N_{j} \left( {1-2\eta } \right)} \left| {J(1-2\eta )} \right|\ln \left(\frac{1}{\eta }\right){d}\eta \end{eqnarray} $
式(43)等号右边第1项采用常规Gauss数值积分计算, 第2项采用对数型Gauss数值积分计算.
(44) $\int_{\varGamma_{e} } {G(z,z_{s} )N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma =-\frac{q_{j}^{e} }{2\pi }\int_{-1}^{1} {N_{j} \left(\xi \right)} \left| {J(\xi )} \right|\ln (z_{m} ){d}\xi $
(45) $\int_{\varGamma_{e} } {\frac{\partial G(z,z_{s} )}{\partial z_{s} }N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma =\frac{q_{j}^{e} }{2\pi }\int_{-1}^{1} {\frac{N_{j} \left( \xi \right)\left| {J(\xi )} \right|}{z_{m} }} {d}\xi $
(46) $\int_{\varGamma_{e} } {F(z,z_{s} )N_{j} } \left( \xi \right)\phi_{j}^{e} {d}\varGamma =-\frac{\phi_{j}^{e} }{2\pi }\int_{-1}^{1} {\frac{N_{j} \left( \xi \right)(2z_{v} \xi +z_{w} )}{z_{m} }} {d}\xi $
(47) $\int_{\varGamma_{e} } {\frac{\partial F(z,z_{s} )}{\partial z_{s} }N_{j} } \left( \xi \right)\phi_{j}^{e} {d}\varGamma =-\frac{\phi_{j}^{e} }{2\pi }\int_{-1}^{1} {\frac{N_{j} \left( \xi \right)(2z_{v} \xi +z_{w} )}{(z_{m} )^{2}}} {d}\xi $
其中$z_{m} =z_{a} \xi^{2}+z_{b} \xi +z_{2} -z_{s} $.
二次单元坐标变换的雅可比$\left| {J(\xi )} \right|$是根号下$\xi$的二次多项式. 根号的存在使得式(44)和式(45)难以处理. 因此, 将$\left|{J(\xi )} \right|$在$\xi =0$处进行泰勒展开
(48) $\begin{eqnarray} \label{eq48} \left| {J(\xi )} \right|^{*}=\left| {J(0)} \right|+\left| {J(0)} \right|^{\prime }\xi +\frac{1}{2}\left| {J(0)} \right|^{\prime \prime }\xi^{2} \end{eqnarray} $
记$\Delta \left| {J(\xi )} \right|=\left| {J(\xi )} \right|-\left| {J(\xi )} \right|^{*}$, 式(44)和式(45)变成
(49) $\int_{\varGamma_{e} } {G(z,z_{s} )N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma =\int_{-1}^{1} {-\frac{q_{j}^{e} }{2\pi }N_{j} \left( \xi \right)} \Delta \left| {J(\xi )} \right|\ln (z_{m} ){d}\xi +\int_{-1}^{1} {-\frac{q_{j}^{e} }{2\pi }N_{j} \left( \xi \right)} \left| {J(\xi )} \right|\ln (z_{m} ){d}\xi $
(50) $\int_{\varGamma_{e} } {\frac{\partial G(z,z_{s} )}{\partial z_{s} }N_{j} } \left( \xi \right)q_{j}^{e} {d}\varGamma =\int_{-1}^{1} {\frac{q_{j}^{e} }{2\pi }} \frac{N_{j} \left( \xi \right)\Delta \left| {J(\xi )} \right|}{z_{m} }{d}\xi + \int_{-1}^{1} {\frac{q_{j}^{e} }{2\pi }} \frac{N_{j} \left( \xi \right)\left| {J(\xi )} \right|^{*}}{z_{m} }{d}\xi $
式(49)和式(50)等号右边第1项的奇异性已然去除, 可采用常规的Gauss数值积分计算. 式(49)和式(50)等号右边第2项与式(46)和式(47)的积分项可归纳为以下几种
(51) $T_{k}^{S} =\int_{-1}^1 {\frac{\xi^{k}}{\omega (\xi )}} {d}\xi ,\ \ T_{k}^{H} =\int_{-1}^1 {\frac{\xi^{k}}{[\omega (\xi )]^{2}}} {d}\xi $
(52) $T_{k}^{W} =\int_{-1}^1 {\xi^{k}\ln [\omega (\xi )]} {d}\xi $
(53) $\omega (\xi )=z_{a} [(\xi +z_{0} )^{2}-z_{m}^{2} ] $
(54) $z_{0} =\frac{1}{2}\frac{z_{b} }{z_{a} },\mbox{ }z_{m} =\sqrt {\frac{z_{b}^{2} }{4z_{a}^{2} }-\frac{z_{2} -z_{s} }{z_{a} }} $
在复平面推导出式(51)和式(52)积分的解析表达式
(55) $T_{k}^{S} =\int_{-1}^1 {\dfrac{\xi^{k}}{\omega (\xi )}} {d}\xi =\\[3mm] \left. {\begin{array}{l@{\quad }l} \dfrac{1}{2z_{a} z_{m} }\ln \left[\dfrac{z_{0}^{2} -(z_{m} -1)^{2}}{z_{0}^{2} -(z_{m} +1)^{2}}\right],&\ \ k=0 \\[3mm] \dfrac{1}{2z_{a} }\left. {\ln [(\xi +z_{0} )^{2}-z_{m}^{2} ]} \right|_{-1}^{1} -z_{0} T_{0}^{S} ,&\ \ k=1 \\[3mm] \dfrac{1-(-1)^{k-1}}{z_{a} (k-1)}-\dfrac{z_{b} }{z_{a} }T_{k-1}^{S} -\dfrac{z_{2} }{z_{a} }T_{k-2}^{S} ,&\ \ k\geqslant 2 \\[3mm] \end{array}} \right\} $
(56) $T_{k}^{H} =\int_{-1}^1 {\dfrac{\xi^{k}}{[\omega (\xi )]^{2}}} {d}\xi =\\[3mm] \left. \begin{array}{ll} -\dfrac{1}{\mbox{4}z_{m}^{2} z_{a}^{2} }\left[\dfrac{2z_{a} +z_{b} }{z_{3} -z_{s} }-\dfrac{2z_{a} +z_{b} }{z_{1} -z_{s} }+2z_{a} T_{0}^{S} \right],&\ k=0 \\[3mm] \dfrac{1}{2z_{a} }\left[-\dfrac{1}{z_{3} -z_{s} }+\dfrac{1}{z_{1} -z_{s} }-z_{b} T_{0}^{H} \right],&\ k=1 \\[3mm] \dfrac{1}{z_{a} }T_{k-2}^{S} -\dfrac{z_{b} }{z_{a} }T_{k-1}^{H} -\dfrac{z_{2} }{z_{a} }T_{k-2}^{H} ,&\ k\geqslant 2 \\[3mm] \end{array} \right\}\qquad $
(57) $T_{k}^{W} =\int_{-1}^1{\xi^{k}\ln[\omega(\xi)]}{d}\xi =\dfrac{1}{k+1}\Big\{\ln[w(1)]-(-1)^{k+1}\ln [w(-1)]- 2z_{a}T_{k+2}^{S}-z_{b}T_{k+1}^{S}\Big\}\geqslant0 $
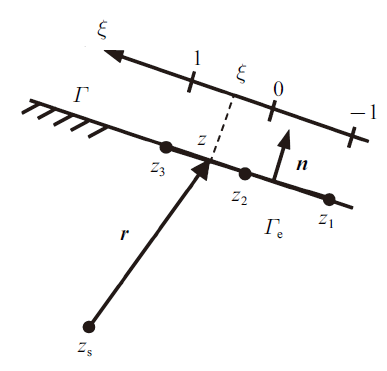
当$z_{a} =0$时, 如图5 所示, 式(32)变成
(58) $\begin{eqnarray} \label{eq58} z(\xi)=z_{b} \xi +z_{2} \end{eqnarray} $
坐标变换的雅可比$\left| {J(\xi )} \right|$和单元单位法向量$n(\xi )$均为常量, 此时单元是几何线性的, 奇异和几乎奇异积分的计算可参考线性单元.
(59) $\begin{eqnarray} \label{eq59} \left| {J(\xi )} \right|=\left| {z_{b1} } \right|,\ \ n(\xi )=\frac{z_{w} }{\left| {J(\xi )} \right|} \end{eqnarray} $
至此, 线性单元和二次单元近场积分的计算已在复平面内完成. 值得指出, 复平面的使用极大地简化了积分的计算公式, 这为高阶单元应用于快速多极边界元法提供了便利.
图5
图5
二次单元直边界
Fig.5
Three-node quadratic elements modelling the straight boundary
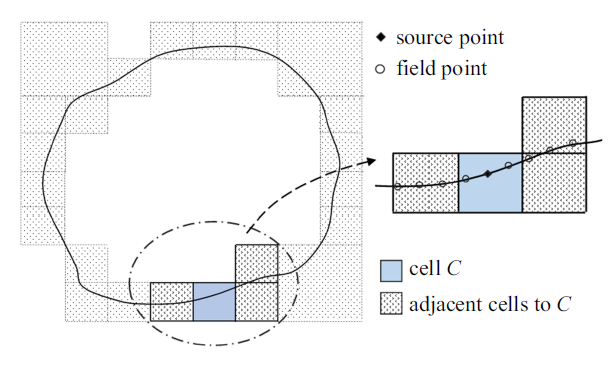
对于二维问题, 快速多极边界元法利用四叉树结构将源点$y$对边界单元的积分分成近场积分和远场积分. 以图6 为例, 若源点位于cell $C$内, 可将与cell $C$有公共角点的cell称之为"邻居". 源点对于cell $C$及其"邻居"内的边界单元的积分是近场积分, 采用本文建立的算法处理. 而源点对于剩余的边界单元的积分是远场积分, 采用快速多极展开式计算. 有关快速多极展开式的计算过程这里不再阐述, 详见文献[29 ]. 通过方程(2)求得所有未知的边界位势和位势梯度后, 域内任意点的位势和位势梯度由式(1)和式(6)算得.
图6
图6
"近场积分"和"远场积分"
Fig.6
"The near-field integrals" and "the far-field integrals"
3 算例
为验证本文建立的高阶单元快速多极边界元法的计算精度和计算效率, 分别采用常值元快速多极边界元法(FM-BEM-C)、线性元快速多极边界元法(FM-BEM-LA)、二次元快速多极边界元法(FM-BEM-QSA)和二次元常规边界元法(CBEM)计算了正交各向异性不规则闭域、圆环闭域热传导问题和随机多孔方板问题.
3.1 正交各向异性不规则闭域热传导问题
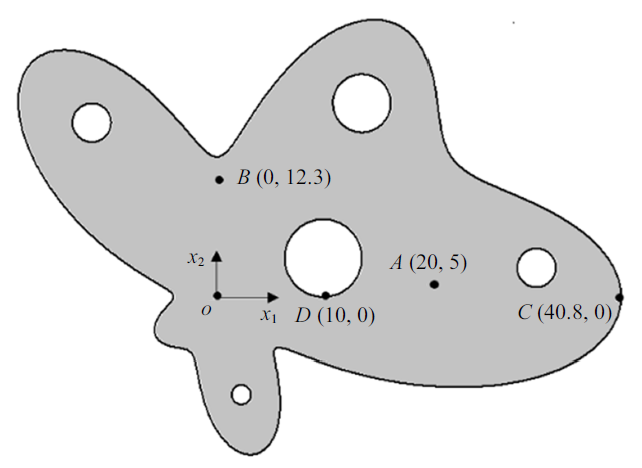
(60) $\begin{eqnarray} &&x_{1}^{2} +x_{2}^{2} \leqslant[15{e}^{\sin \theta }\sin ^{2}(2\theta ) + \\&&\qquad 15\cos^{2}(2\theta )]^{2},\theta \in (0,2\pi ). \end{eqnarray} $
$\begin{eqnarray*} \left. {\begin{array}{l} (x_{1} -10)^{2}+(x_{2} -4)^{2}\leqslant 16 \\ (x_{1} -14)^{2}+(x_{2} -20)^{2}\leqslant 9 \\ (x_{1} +14)^{2}+(x_{2} -18)^{2}\leqslant 4 \\ (x_{1} -32)^{2}+(x_{2} -3)^{2}\leqslant 4 \\ (x_{1} -1)^{2}+(x_{2} +10)^{2}\leqslant 1 \\ \end{array}} \right\} \end{eqnarray*}$
如图7 所示, 所有量纲是相容的. 该问题的解析解为$\phi =\varsigma _{2} x_{1}^{3} x_{2} -\varsigma_{1} x_{2}^{3} x_{1} +\varsigma_{1} x_{2} x_{1} +200$, 外环边界温度$\phi $已知, 内环边界温度梯度$q$已知.
图7
图7
不规则闭域热传导问题
Fig.7
Heat conduction in an irregular domain
情况1: 当传热系数$\varsigma_{1} =\varsigma_{2} $时, 各向同性问题. 分别采用FM-BEM-C, FM-BEM-LA和FM-BEM-QSA对图7 结构进行计算, 计算结果见表1 .
表1 显示, 若边界单元总数$n$定值, 与精确解相比, FM-BEM-QSA的精度最高, FM-BEM-LA次之, FM-BEM-C最差. 当$n=12 960$时, $B$点FM-BEM-C的温度$\phi$计算值较解析解的相对误差为0.77${\%}$. 然而, 在$n=3240$时, FM-BEM-LA的计算值较解析解的相对误差为0.15${\%}$; 在$n=1620$时, FM-BEM-QSA的计算值较解析解的相对误差已小于0.12${\%}$. 显然, 高阶单元FM-BEM的计算精度和计算效率较FM-BEM-C大幅度提升.
情况2: 当传热系数$\varsigma_{1}=3$, $\varsigma_{2}=2$, 正交各向异性问题. 沿外边界均匀划分2880个单元, 沿内边界均匀划分720个单元. 采用FM-BEM-QSA和FM-BEM-LA计算边界$C$. $D$点附近的温度$\phi $和温度梯度$q_{x2}$, 如表2 和表3 所示.
表2 和表3 的结果显示, FM-BEM-LA和FM-BEM-QSA计算外边界$C$. 内边界$D$点附近的温度$\phi$、温度梯度值$q$与解析解吻合得很好, FM-BEM-QSA的计算结果更优. 实际上, 当内点十分接近外边界$C$. 内边界$D$点时, 近边界点温度的计算涉及高阶单元的几乎强奇异积分(1/$r)$, 温度梯度的计算更是涉及几乎超奇异积分(1/$r^{2})$, 计算难度较大, 但本文第2节建立的正则化算法能够很好地处理这些积分.
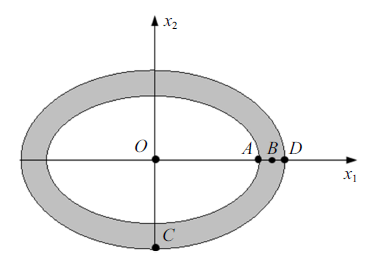
3.2 正交各向异性椭圆环闭域热传导问题
已知$\varsigma_{1}=2$, $\varsigma_{2}=1$, 内环边界为${x_{1}^{2} }/{a_{1}^{2} }+{x_{2}^{2} }/{b_{1}^{2} }=1$, $a_{1} =3$, $b_{1} =2$, 外环边界${x_{1}^{2} }/{a_{2}^{2} }+{x_{2}^{2} }/{b_{2}^{2} }=1$, $a_{2} \in (3.000 000 1, 3.1)$, $b_{2} \in (2.000 000 1, 2.1)$, 如图8 所示, 所有量纲是相容的. 该问题的解析解为$\phi =x_{1}^{2} -2x_{2}^{2} $, 沿内外边界各均匀划分360个单元, 其中外环边界温度$\phi $已知, 内环边界温度梯度$q$已知.
图8
图8
椭圆环闭域热传导问题
Fig.8
Heat conduction in the elliptic ring domain
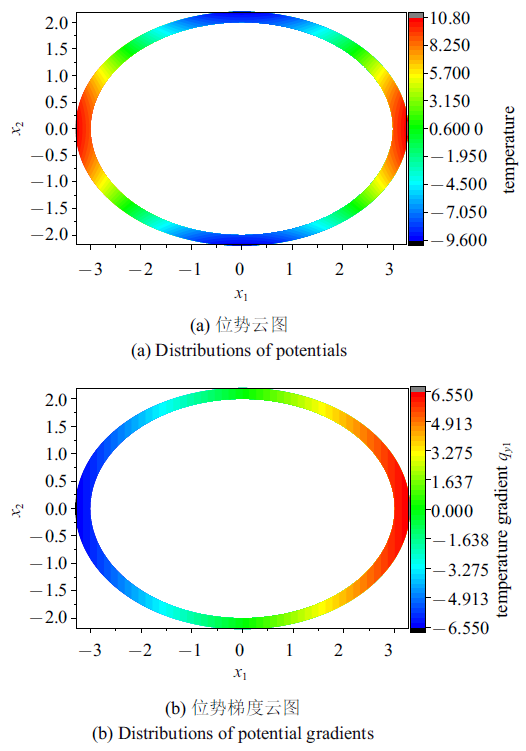
定义厚长比$\delta =(b_{2}-b_{1})/b_{1} $, $\delta $越小, 结构越薄. 使用FM-BEM处理薄体问题时, 近场积分的计算不仅仅涉及到奇异积分的计算, 还涉及到几乎奇异积分的计算. 当$\delta =0.02$时, 正交各向异性椭圆环全域的温度云图和$y_{1}$方向的温度梯度云图如图9 所示. 表4 给出了取不同$\delta $的椭圆闭域结构中$A$, $B$, $C$, $D$点的温度$\phi$和温度梯度$q$的常规边界元法(CBEM)和FM-BEM计算值, 这里CBEM(二次元)采用的是二次单元离散边界. 与解析解相比, CBEM和FM-BEM的计算结果在$\delta =1.0\times10^{-1}$ $\sim$ $1.0\times10^{-6}$范围内均保持高精度. 当$\delta $减小至$1.0\times10^{-6}$时, FM-BEM-LA计算结果失效, CBEM(二次元)和FM-BEM-QSA的计算结果依旧精确, 与解析解的相对误差均小于0.1${\%}$. 这是由于当$\delta $减小至$1.0\times10^{-6}$, 若边界继续采用线性元离散, 源点$y$落在了域外, 其计算结果失效, 而若边界采用二次元离散, 源点$y$落在域内, 其结果仍然精确, 见图10 . 因此在离散超薄结构曲线型边界时, 应采用二次元. 对于超薄体结构, FM-BEM-QSA的计算精度与二次元CBEM几乎相同, 在快速算法的帮助下, FM-BEM-QSA能够处理大规模问题, 具有更广阔的应用前景.
图9
图9
正交各向异性椭圆环闭域全域的位势和位势梯度云图($\delta =0.02)$
Fig.9
Distributions of potential and potential gradient of the orthotropic elliptic ring domain ($\delta =0.02)$
图10
图10
源点$y$相对单元几何说明
Fig.10
Geometric relation between the source point $y$ and element
3.3 随机多孔方板
考虑一个边长200 $\times$ 200含多个随机孔的方板, 如图11 所示, $m$ $\times$ $m$个随机椭圆孔置于矩形方板中, 其中$m=100$, 200, 300, 400, 500, 600, 800. 传热系数$\varsigma_{1} =1$, $\varsigma_{2} =2$, 每个椭圆孔边界采用360个节点离散, 方板的每条直边采用5000个节点离散. 矩形方板的左右两直边以及椭圆孔边的位势$\phi $已知, 矩形方板的上下两直边的位势梯度$q$已知. 该问题的解析解为$\phi =2x_{1}^{2} -x_{2}^{2} +3x_{1} x_{2} +5$. 所有的计算在一台Intel Xeon(R) CPU E5-2670 @2.60GHz 内存为16.0 GB的电脑上完成.
图11
图11
随机孔方板
Fig.11
Square plate with distributed randomly holes
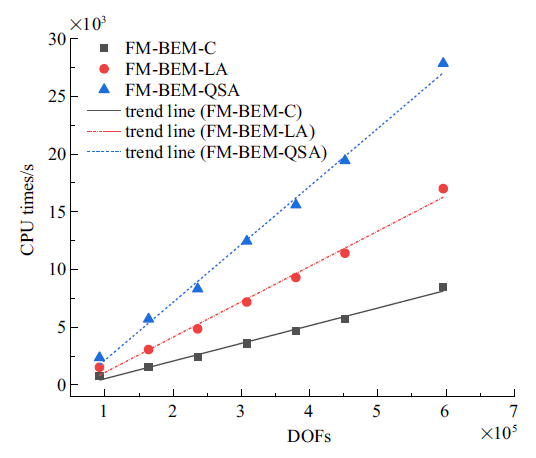
采用FM-BEM对随机多孔方板进行计算, 通过调整随机椭圆孔的数量, 获得采用FM-BEM-C, FM-BEM-LA和FM-BEM-QSA消耗的CPU时间与自由度(DOFs)之间的关系, 如图12 所示.
图12
图12
CPU时间与自由度的关系
Fig.12
Relationship between CPU time and degrees of freedom
图12 计算结果显示FM-BEM-C, FM-BEM-LA和FM-BEM-QSA所需CPU时间与自由度数量成线性关系, 计算量均处于$O(N)$量级.
上述3个算例的计算结果表明, 在给定的计算精度下, 相对于常值单元FM-BEM, 高阶单元FM-BEM使用节点数显著减少, 所需CPU时间大幅度降低, 因此高阶单元FM-BEM可更加有效求解大规模问题. 此外, 高阶单元奇异积分和几乎奇异积分计算难题的解决, 使得高阶单元FM-BEM能够处理超薄体问题, 拓宽了高阶单元FM-BEM的适用范围.
4 结论
通过解决高阶单元奇异积分和几乎奇异积分的计算难题, 建立了适用于二维正交各向异性位势问题的高阶单元快速多极边界元(FM-BEM), 其优点如下:
(1)高阶单元FM-BEM的计算精度和计算效率较常值单元FM-BEM的精度高.
(2)高阶单元奇异积分和几乎奇异积分难题的解决, 使得高阶单元FM-BEM能够应用于超薄体结构, 具有广泛的应用前景.
(3)高阶单元FM-BEM计算时间与自由度数量成线性关系, 其计算效率仍处于$O(N)$量级, 适用于求解大规模问题.
参考文献
View Option
[1]
杜庆华 , 岑章志 , 稽醒 等 . 边界积分方程方法 —— 边界元法 . 北京 : 高等教育出版社 , 1989
[本文引用: 1]
(Du Qinghua Qin Zhangzhi Ji Xing et al. Boundary Integral Equation-Boundary Element Method. Beijing : High Education Press , 1989 (in Chinese))
[本文引用: 1]
[2]
Barnes J Hut P . A hierarchical O ($N\log N$) force calculation algorithm
Nature 1986 ,324 :446 -449
[本文引用: 1]
[3]
Greengard L Rokhlin V . A fast algorithm for particles simulations
Journal of Computational Physics 1987 ,73 :325 -348
[本文引用: 1]
[4]
Aimi A Diligenti M Lunardini F , et al . A new application of panel clustering method for 3D SGBEM
Computer Modeling in Engineering & Sciences 2003 ,4 (1 ):31 -50
[本文引用: 1]
[5]
Helsing J Jonsson A . Stress calculation on multiply connected domains
Journal of Computational Physics 2002 ,176 :456 -482
[6]
Aoki S Amaya K Urago M , et al . Fast multipole boundary element analysis of corrosion problems
Computer Modeling in Engineering & Science 2004 ,6 (2 ):123 -132
[本文引用: 1]
[7]
Wang PB Yao ZH Wei Y . FM-BEM evaluation for effective elastic moduli of micro cracked solids
Tsinghua Science and Technology 2007 ,12 (5 ):562 -566
[本文引用: 1]
[8]
Wang PB Yao ZH . Fast multipole boundary element analysis of two-dimensional elastoplastic problems
Communications in Numerical Methods in Engineering 2007 ,23 (10 ):889 -903
[9]
Wang WW Chen YM . Mathematical foundation of the fast multipole BEM for 2D potential problems
Advanced Materials Research 2010 , 143-144 :1190 -1194
[10]
Pierce AP Napier JAL . A spectral multipole method for efficient solutions of large scale boundary element models in elastostatics
International Journal for Numerical Methods in Engineering 1995 ,38 :4009 -4034
[本文引用: 1]
[11]
Liu YJ Li YX Xie W . Modeling of multiple crack propagation in 2-D elastic solids by the fast multiple boundary element method
Engineering Fracture Mechanics 2017 ,172 :1 -16
[本文引用: 1]
[12]
吴清华 . 高振荡Henkel核积分方程的高效数值算法
数学物理学报 , 2019 ,39A (3 ):611 -619
[本文引用: 1]
(Wu Qinghua Efficient numerical method for integral equations with oscillatory Henkel kernels
Acta Mathematica Scientia 2019 ,39A (3 ):611 -619 (in Chinese))
[本文引用: 1]
[13]
Zhang JM Zhuang C Qin X , et al . FMM accelerated hybrid boundary node method for multi-domain problems
Engineering Analysis with Boundary Elements 2010 ,34 (5 ):433 -439
[14]
Zhang JM Tanaka M . Adaptive spatial decomposition in fast multipole method
Journal of Computational Physics 2007 ,226 (1 ):17 -28
[本文引用: 1]
[15]
刘中宪 , 孙帅杰 , 赵瑞斌 等 . 基于快速多极边界元法的局部场地对地震波高频散射二维模拟
岩土工程学报 , 2017 ,39 (11 ):2017 -2025
[本文引用: 1]
(Liu Zhongxian Sun Shuaijie Zhao Ruibin et al . Two-dimensional simulation of high frequency scattering of seismic waves by local sites based on fast multi-pole boundary element method
Chinese Journal of Geotechnical Engineering 2017 ,39 (11 ):2017 -2025 (in Chinese))
[本文引用: 1]
[16]
刘中宪 , 符瞻远 , 苗雨 等 . 非连续屏障对Rayleigh波宽频散射三维快速边界元模拟
振动与冲击 , 2019 ,38 (19 ):89 -97
(Liu Zhongxian Fu Zhanyuan Mian Yu et al . 3-D simulation for broadband scattering of Rayleigh wave by discontinuous barrier based on FMP-IBEM
Journal of Vibration and Shock 2019 ,38 (19 ):89 -97 (in Chinese))
[17]
Han YC Nie YF Dong H . A fast multipole algorithm for radiate heat transfer in 3D semitransparent media
Journal of Quantitative Spectroscopy and Radiate Transfer 2018 ,221 :8 -17
[18]
Qu WZ Zheng CJ Zhang YM , et al . A wideband fast multipole accelerated singular boundary method for three-dimensional acoustic problems
Computers and Structures 2018 ,206 (8 ):82 -89
[19]
Nishimura N Yoshida KI Kobayashi S . A fast multipole boundary integral equation method for crack problems in 3D
Engineering Analysis with Boundary Elements 1999 ,23 (1 ):97 -105
[本文引用: 1]
[20]
赵丽滨 , 姚振汉 . 快速多极边界元法在薄板结构中的应用
燕山大学学报 , 2004 ,6 (2 ):103 -106
[本文引用: 1]
(Zhao Libin Yao Zhenhan Application of fast multipole boundary element method for thin plate structures
Journal of Yanshan University 2004 ,6 (2 ):103 -106 (in Chinese))
[本文引用: 1]
[21]
Wang HT Yao ZH . A new fast multipole boundary element method for large scale analysis of mechanical properties in 3D particle-reinforced composites
Computer Modeling in Engineering & Sciences 2005 ,7 (1 ):85 -95
[本文引用: 1]
[22]
Zhang JM Tanaka M Endo M . The hybrid boundary node method accelerated by fast multipole expansion technique for 3D potential problems
International Journal for Numerical Methods in Engineering 2005 ,63 (5 ):660 -680
[本文引用: 2]
[23]
Hosseinzadeh H Dehghan M . A simple and accurate scheme based on complex space C to calculate boundary integrals of 2D boundary elements method
Computers and Mathematics with Applications 2014 ,68 :531 -542
[本文引用: 1]
[24]
Johnston BM Johnston PR Elliott D . A sinh transformation for evaluating two-dimensional nearly singular boundary element integrals
International Journal for Numerical Methods in Engineering 2007 ,69 (7 ):1460 -1479
[25]
Gu Y He X Chen W , et al . Analysis of three-dimensional anisotropic heat conduction problems on thin domains using an advanced boundary element method
Computers & Mathematics with Applications 2018 ,75 (1 ):33 -44
[26]
Takayuki M . Fast calculation of far-field sound directivity based on fast multipole boundary element method
Journal of Theoretical and Computational Acoustics 2020 ,28 (4 ):1 -22
[本文引用: 1]
[27]
牛忠荣 , 胡宗军 , 葛仁余 等 . 二维弹性力学边界元法高阶单元几乎奇异积分半解析算法
力学学报 , 2013 ,45 (6 ):897 -907
[本文引用: 1]
(Niu Zhongrong Hu Zhongjun Ge Renyu et al . A new semi-analytic algorithm of nearly singular integrals in high order boundary element analysis of 2D elasticity
Chinese Journal of Theoretical and Applied Mechanics 2013 ,45 (6 ):897 -907 (in Chinese))
[本文引用: 1]
[28]
牛忠荣 , 王秀喜 , 周焕林 . 边界元法计算近边界点参量的一个通用算法
力学学报 , 2001 ,33 (2 ):275 -283
[本文引用: 1]
(Niu Zhongrong Wang Xiuxi Zhou Huanlin A general algorithm for calculating the quantities at interior points close to the boundary by the BEM
Chinese Journal of Theoretical and Applied Mechanics 2001 ,33 (2 ):275 -283 (in Chinese))
[本文引用: 1]
[29]
Liu YJ Nishimura N . The fast multipole boundary element method for potential problems: A tutorial
Engineering Analysis with Boundary Elements 2006 ,30 (5 ):371 -381
[本文引用: 1]
1
1989
... 相较于有限元法(FEM), 边界元法[1 ] (BEM)只需在结构外边界划分网格, 因此BEM可对复杂几何模型进行简单的网格划分. 然而BEM生成的系数矩阵是非对称满阵, 构造矩阵所需的运算量级为$O(N^{2})$, 如果采用高斯消去法求解, 则所需运算量级更是达到$O(N^{3})$, 因而导致BEM难以计算大规模问题. 伴随快速多极算法[2 -3 ] 发展起来的快速多极边界元法(FM-BEM)可很好地解决这个问题, 其所需的运算量和存储量较传统BEM大大降低, FM-BEM成为近20年边界元领域的热门课题之一, 并被广泛应用于二维位势和弹性问题、三维声场问题等. ...
1
1989
... 相较于有限元法(FEM), 边界元法[1 ] (BEM)只需在结构外边界划分网格, 因此BEM可对复杂几何模型进行简单的网格划分. 然而BEM生成的系数矩阵是非对称满阵, 构造矩阵所需的运算量级为$O(N^{2})$, 如果采用高斯消去法求解, 则所需运算量级更是达到$O(N^{3})$, 因而导致BEM难以计算大规模问题. 伴随快速多极算法[2 -3 ] 发展起来的快速多极边界元法(FM-BEM)可很好地解决这个问题, 其所需的运算量和存储量较传统BEM大大降低, FM-BEM成为近20年边界元领域的热门课题之一, 并被广泛应用于二维位势和弹性问题、三维声场问题等. ...
A hierarchical O ($N\log N$) force calculation algorithm
1
1986
... 相较于有限元法(FEM), 边界元法[1 ] (BEM)只需在结构外边界划分网格, 因此BEM可对复杂几何模型进行简单的网格划分. 然而BEM生成的系数矩阵是非对称满阵, 构造矩阵所需的运算量级为$O(N^{2})$, 如果采用高斯消去法求解, 则所需运算量级更是达到$O(N^{3})$, 因而导致BEM难以计算大规模问题. 伴随快速多极算法[2 -3 ] 发展起来的快速多极边界元法(FM-BEM)可很好地解决这个问题, 其所需的运算量和存储量较传统BEM大大降低, FM-BEM成为近20年边界元领域的热门课题之一, 并被广泛应用于二维位势和弹性问题、三维声场问题等. ...
A fast algorithm for particles simulations
1
1987
... 相较于有限元法(FEM), 边界元法[1 ] (BEM)只需在结构外边界划分网格, 因此BEM可对复杂几何模型进行简单的网格划分. 然而BEM生成的系数矩阵是非对称满阵, 构造矩阵所需的运算量级为$O(N^{2})$, 如果采用高斯消去法求解, 则所需运算量级更是达到$O(N^{3})$, 因而导致BEM难以计算大规模问题. 伴随快速多极算法[2 -3 ] 发展起来的快速多极边界元法(FM-BEM)可很好地解决这个问题, 其所需的运算量和存储量较传统BEM大大降低, FM-BEM成为近20年边界元领域的热门课题之一, 并被广泛应用于二维位势和弹性问题、三维声场问题等. ...
A new application of panel clustering method for 3D SGBEM
1
2003
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
Stress calculation on multiply connected domains
0
2002
Fast multipole boundary element analysis of corrosion problems
1
2004
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
FM-BEM evaluation for effective elastic moduli of micro cracked solids
1
2007
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
Fast multipole boundary element analysis of two-dimensional elastoplastic problems
0
2007
Mathematical foundation of the fast multipole BEM for 2D potential problems
0
2010
A spectral multipole method for efficient solutions of large scale boundary element models in elastostatics
1
1995
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
Modeling of multiple crack propagation in 2-D elastic solids by the fast multiple boundary element method
1
2017
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
高振荡Henkel核积分方程的高效数值算法
1
2019
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
高振荡Henkel核积分方程的高效数值算法
1
2019
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
FMM accelerated hybrid boundary node method for multi-domain problems
0
2010
Adaptive spatial decomposition in fast multipole method
1
2007
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
基于快速多极边界元法的局部场地对地震波高频散射二维模拟
1
2017
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
基于快速多极边界元法的局部场地对地震波高频散射二维模拟
1
2017
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
非连续屏障对Rayleigh波宽频散射三维快速边界元模拟
0
2019
非连续屏障对Rayleigh波宽频散射三维快速边界元模拟
0
2019
A fast multipole algorithm for radiate heat transfer in 3D semitransparent media
0
2018
A wideband fast multipole accelerated singular boundary method for three-dimensional acoustic problems
0
2018
A fast multipole boundary integral equation method for crack problems in 3D
1
1999
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
快速多极边界元法在薄板结构中的应用
1
2004
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
快速多极边界元法在薄板结构中的应用
1
2004
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
A new fast multipole boundary element method for large scale analysis of mechanical properties in 3D particle-reinforced composites
1
2005
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
The hybrid boundary node method accelerated by fast multipole expansion technique for 3D potential problems
2
2005
... 有关快速多极边界元法的研究和应用起源于20世纪90年代初, 主要寻求多极展开和局部展开概念在不同力学问题的具体实现格式[4 -6 ] , 而后被广泛应用于二维[7 -14 ] 、三维[15 -22 ] 问题中. Pierce等[10 ] 采用二维实数域的Taylor展开格式, 实现了$O(N\log N)$量级的用于二维弹性力学问题的多极边界元法. Liu等[11 ] 将快速多极算法与对偶边界元法相结合, 模拟了二维线弹性多裂纹扩展路径. 吴清华[12 ] 将快速多极算法和高振荡积分方法相结合, 求解了一类带高振荡Hankel核的边界积分方程, 求解结果和传统方法吻合较好, 计算效率也得到大幅度提升. Nishimura等[19 ] 采用分段常值形函数去离散裂纹问题的超奇异边界积分方程, 然后耦合快速多极算法和GMRES法求解三维裂纹问题. 赵丽滨等[20 ] 利用Taylor级数将三维弹性静力学边界积分方程的核函数进行展开, 引入快速多极算法应用于薄体结构问题. Zhang等[22 ] 耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
... [22 ]耦合了快速多极算法和混合边界元节点法(Hybrid BNM), 并将该方法成功应用于三维位势问题的求解. Wang等[21 ] 耦合快速多极边界元法和重复相似子域法, 构造出含夹杂的复合材料结构的预处理技术, 对三维复合材料进行了大规模的数值模拟. ...
A simple and accurate scheme based on complex space C to calculate boundary integrals of 2D boundary elements method
1
2014
... 目前, 快速多极边界元法大多采用常值单元, 其优点是所有的近场积分, 包括奇异积分和几乎奇异积分[23 -26 ] 均可采用解析公式直接计算, 但对于曲线边界和复杂物理场, 常值单元的计算只能依赖于使用大量单元, 且计算精度和计算效率往往不能令人满意. 使用高阶单元能够获得更准确的计算结果, 但由于存在奇异积分和几乎奇异积分的计算难题[27 -28 ] , 因而鲜见高阶单元快速多极边界元法的相关报导. 本文在复平面内计算高阶单元的奇异积分和几乎奇异积分, 建立高阶单元快速多极边界元法, 并将其应用于二维正交各向异性位势热传导问题分析. ...
A sinh transformation for evaluating two-dimensional nearly singular boundary element integrals
0
2007
Analysis of three-dimensional anisotropic heat conduction problems on thin domains using an advanced boundary element method
0
2018
Fast calculation of far-field sound directivity based on fast multipole boundary element method
1
2020
... 目前, 快速多极边界元法大多采用常值单元, 其优点是所有的近场积分, 包括奇异积分和几乎奇异积分[23 -26 ] 均可采用解析公式直接计算, 但对于曲线边界和复杂物理场, 常值单元的计算只能依赖于使用大量单元, 且计算精度和计算效率往往不能令人满意. 使用高阶单元能够获得更准确的计算结果, 但由于存在奇异积分和几乎奇异积分的计算难题[27 -28 ] , 因而鲜见高阶单元快速多极边界元法的相关报导. 本文在复平面内计算高阶单元的奇异积分和几乎奇异积分, 建立高阶单元快速多极边界元法, 并将其应用于二维正交各向异性位势热传导问题分析. ...
二维弹性力学边界元法高阶单元几乎奇异积分半解析算法
1
2013
... 目前, 快速多极边界元法大多采用常值单元, 其优点是所有的近场积分, 包括奇异积分和几乎奇异积分[23 -26 ] 均可采用解析公式直接计算, 但对于曲线边界和复杂物理场, 常值单元的计算只能依赖于使用大量单元, 且计算精度和计算效率往往不能令人满意. 使用高阶单元能够获得更准确的计算结果, 但由于存在奇异积分和几乎奇异积分的计算难题[27 -28 ] , 因而鲜见高阶单元快速多极边界元法的相关报导. 本文在复平面内计算高阶单元的奇异积分和几乎奇异积分, 建立高阶单元快速多极边界元法, 并将其应用于二维正交各向异性位势热传导问题分析. ...
二维弹性力学边界元法高阶单元几乎奇异积分半解析算法
1
2013
... 目前, 快速多极边界元法大多采用常值单元, 其优点是所有的近场积分, 包括奇异积分和几乎奇异积分[23 -26 ] 均可采用解析公式直接计算, 但对于曲线边界和复杂物理场, 常值单元的计算只能依赖于使用大量单元, 且计算精度和计算效率往往不能令人满意. 使用高阶单元能够获得更准确的计算结果, 但由于存在奇异积分和几乎奇异积分的计算难题[27 -28 ] , 因而鲜见高阶单元快速多极边界元法的相关报导. 本文在复平面内计算高阶单元的奇异积分和几乎奇异积分, 建立高阶单元快速多极边界元法, 并将其应用于二维正交各向异性位势热传导问题分析. ...
边界元法计算近边界点参量的一个通用算法
1
2001
... 目前, 快速多极边界元法大多采用常值单元, 其优点是所有的近场积分, 包括奇异积分和几乎奇异积分[23 -26 ] 均可采用解析公式直接计算, 但对于曲线边界和复杂物理场, 常值单元的计算只能依赖于使用大量单元, 且计算精度和计算效率往往不能令人满意. 使用高阶单元能够获得更准确的计算结果, 但由于存在奇异积分和几乎奇异积分的计算难题[27 -28 ] , 因而鲜见高阶单元快速多极边界元法的相关报导. 本文在复平面内计算高阶单元的奇异积分和几乎奇异积分, 建立高阶单元快速多极边界元法, 并将其应用于二维正交各向异性位势热传导问题分析. ...
边界元法计算近边界点参量的一个通用算法
1
2001
... 目前, 快速多极边界元法大多采用常值单元, 其优点是所有的近场积分, 包括奇异积分和几乎奇异积分[23 -26 ] 均可采用解析公式直接计算, 但对于曲线边界和复杂物理场, 常值单元的计算只能依赖于使用大量单元, 且计算精度和计算效率往往不能令人满意. 使用高阶单元能够获得更准确的计算结果, 但由于存在奇异积分和几乎奇异积分的计算难题[27 -28 ] , 因而鲜见高阶单元快速多极边界元法的相关报导. 本文在复平面内计算高阶单元的奇异积分和几乎奇异积分, 建立高阶单元快速多极边界元法, 并将其应用于二维正交各向异性位势热传导问题分析. ...
The fast multipole boundary element method for potential problems: A tutorial
1
2006
... 对于二维问题, 快速多极边界元法利用四叉树结构将源点$y$对边界单元的积分分成近场积分和远场积分. 以图6 为例, 若源点位于cell $C$内, 可将与cell $C$有公共角点的cell称之为"邻居". 源点对于cell $C$及其"邻居"内的边界单元的积分是近场积分, 采用本文建立的算法处理. 而源点对于剩余的边界单元的积分是远场积分, 采用快速多极展开式计算. 有关快速多极展开式的计算过程这里不再阐述, 详见文献[29 ]. 通过方程(2)求得所有未知的边界位势和位势梯度后, 域内任意点的位势和位势梯度由式(1)和式(6)算得. ...