引言
建立超弹性模型对于橡胶和其他软材料的工程应用具有重要的意义[1 -2 ] . 当前关于软材料超弹性理论模型主要包括唯象模型和分子统计理论模型[3 -4 ] . 唯象模型的建立主要是基于连续介质力学以及软材料的实验所观察到的宏观力学行为. 常见的唯象模型包括Neo-Hooken模型、Mooney-Rivlin模型、Ogden模型、Gent模型、Yeoh模型等[3 ] . 其中Neo-Hookean模型、Gent模型和Yeoh模型都是柯西-格林应变张量第一不变量$I_{1}$的函数, Mooney-Rivlin模型同时依赖于柯西-格林应变张量的第一和第二不变量($I_{1}$, $I_{2})$, 而Ogden模型是3个主方向拉伸比的函数. 这些唯象模型在描述橡胶材料的超弹性变形行为取得了一定的成功[5 -7 ] , 例如, 张希润等[5 ] 采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应.
针对唯象超弹性模型的不足之处, 部分学者[8 -9 ] 对上述模型作了扩展, 例如, 李雪冰等[8 ] 在Yeoh模型的自由能基础上增加了依赖于应变张量第二不变量的部分, 克服了经典Yeoh模型在预测等双轴曲线时"偏软"的特性. 近年来, 国内外相关学者[10 -13 ] 也提出了多种新型的超弹性唯象模型, 例如, Lopez-Pamies[10 ] 提出了基于应变第一不变量的指数型自由能形式, Mangan等[11 ] 提出了同时依赖于柯西-格林应变第一和第二不变量的新型超弹性自由能形式, 该模型能准确表征大变形条件下简单剪切变形切应力和切应变的线性关系, 以及单轴变形下的应变强化行为.
另一类被广泛用来描述软材料超弹性行为的模型是基于分子统计理论模型, 其主要建模思路是将统计理论应用于分子链网络中, 进而得出变形自由能函数. 常见的分子统计理论模型包括Treloar高斯链模型[14 ] , Wang-Guth三链模型[15 ] 、 Arruda-Boyce八链模型[16 ] 以及全链网络模型[17 ] . Treloar[14 ] 提出的高斯链分布模型, 与唯象的Neo-Hookean模型, 在数学形式上是完全等价的, 该模型只能描述轻度交联橡胶材料的应力响应, 而对于交联度高的橡胶网络, 这类模型仅能描述小应变范围内的应力响应[18 ] . Boyce等[19 ] 发现唯象的Gent模型和Arruda-Boyce模型在多种加载条件下的应力-应变关系是接近的, 这两个模型均可较为准确地模拟不同交联度橡胶材料的单轴加载条件下的应力响应. Wu和van der Giessen[17 ] 建立了全链模型, 全链模型需要对各个方向进行积分, 计算起来不够方便. 上述全链模型是基于仿射假设, 而Diani和Tallec[20 ] 通过能量最小化原则建立了非仿射的全链超弹性模型. Hossain等[21 ] 针对八链模型和全链模型的不足, 详细评估了几类扩展的八链和全链模型在模拟复杂加载情况下的表现.
针对Treloar[22 ] 关于硫化橡胶的单轴、纯剪切和等双轴加载的经典实验数据, Steinmann等[23 ] 详细评估了14种唯象模型和分子统计理论模型的预测能力, 发现这些广泛应用的模型并不能很好地预测硫化橡胶在多种变形模式下的力学响应. 针对经典超弹性模型的不足之处, 部分学者[24 -28 ] 提出了引入缠结约束效应, 其主要的建模思路是将缠结约束效应用Doi 和Edwards[29 ] 所提出的管模型(tube model)来近似表征. 相关模拟结果显示, 引入缠结约束效应的超弹性模型能更为准确地预测橡胶的力学行为, 但上述模型也有相应的不足之处, 例如, Miche等[25 ] 所建立的考虑缠结效应的超弹性模型是基于非仿射假设, 需开展全方向积分计算, 而Davodson和Goubourne[27 ] 以及Xiang等[28 ] 所建立的缠结约束模型的自由能是主方向拉伸比的函数, 这导致这些模型有限元植入方面不够方便.
基于微观变形机制, 本文建立了只依赖于应变不变量的超弹性模型, 该模型同时包括熵弹性和缠结约束效应. 并通过与文献中的实验数据进行对比验证了本文所建立模型的预测能力. 最后, 本文比较了多个缠结约束模型在不同加载模式下自由能的变化.
1 本构理论
1.1 单链变形自由能
针对单根分子链的变形行为, 这里采用Miehe等[25 ] 提出的微观力学模型来进行描述. 该模型的自由能包括两部分, 第一部分是源于分子链自由变形所引起的熵弹性自由能, 第二部分是由于周边分子链缠结约束引起的自由能
(1) $\begin{eqnarray} \varPsi =\varPsi_{f} +\varPsi_{c} \end{eqnarray} $
采用Kuhn 和 Grün[30 ] 提出的Langevin统计模型来表示熵弹性所引起的自由能, 其具体形式如下
(2) $\begin{eqnarray} \left.\begin{array}{l} \varPsi_{f} =NkT\left( {\dfrac{\lambda \beta }{\sqrt N }+\ln \dfrac{\beta }{\sinh \beta }} \right)+\varPsi_{f0}\\ \beta =£^{-1}\left( {\dfrac{\lambda }{\sqrt N }} \right) \\ \end{array}\right\} \end{eqnarray} $
其中, $N$是Kuhn链段数量, $\lambda$是单链的伸长比, $£^{-1}$是Langevin逆函数, 其中Langevin函数的定义为 $£ \left( x \right)=\coth x-1/x$, $\varPsi_{f0} $是常数.
采用Doi 和Edwards[29 ] 提出的管模型(图1 )来表征周边分子链缠结约束导致的变形自由能
(3) $\begin{eqnarray} \varPsi_{c} =\alpha kTN\left( {\dfrac{b}{d_{0} }} \right)^{2}\upsilon +\varPsi _{c0} \end{eqnarray} $
其中, $\alpha $是与管的截面积形状相关的系数, $b$是Kuhn长度, $d_{0}$是管的初始直径, $\upsilon $是管的截面积收缩比, $\varPsi_{c0} $是常数.
图1
图1
高分子链变形的管模型
Fig.1
Tube model for polymer chains
1.2 微观-宏观关系
在单链变形自由能的基础上建立宏观变形自由能, 需首先确定宏观和微观变形之间的映射关系, 这里采用微球模型和仿射假设来获得相应的关系. 如图2 所示, 认为初始未变形的分子链均匀分布在一个微球表面上, 施加变形后, 微球在主应变方向上变形为一椭球, 其变形梯度张量可表示为
(4) $\begin{eqnarray} F=\lambda_{1} e_{1} \otimes e_{1} +\lambda_{2} e_{2} \otimes e_{2} +\lambda_{3} e_{3} \otimes e_{3} \end{eqnarray} $
其中$\lambda_{1} $, $\lambda_{2} $, $\lambda_{3} $为3个主方向上的拉伸比. 变形后, 分子链的长度变为
(5) $\begin{eqnarray} \label{eq5} &&\lambda^{2}=(\lambda_{1} \sin \theta \cos \varphi )^{2}+(\lambda_{2} \sin \theta \sin \varphi )^{2}+(\lambda_{3} \cos \theta )^{2} \end{eqnarray} $
其中$\varphi $是在初始构型中分子链在$XOY$平面的投影与$X$轴的夹角, 而$\theta$是分子链与$Z$轴的夹角(见图2 ).
图2
图2
基于仿射假设的微球模型
Fig.2
Microsphere model based on affine assumption
这里假设微球表面所有分子链长度的均方值为宏观变形条件下分子链等效长度
(6) $\begin{eqnarray} \label{eq6} &&\overline \lambda =\sqrt {\dfrac{1}{4\pi }\int_0^{2\pi } {{d}\varphi \int_0^\pi {\lambda^{2}\sin \theta {d}\theta } } } =\sqrt {\dfrac{\lambda_{1}^{2} +\lambda_{2}^{2} +\lambda_{3}^{2} }{3}} =\sqrt {\dfrac{I_{1} }{3}} \end{eqnarray} $
采用同样方式, 将变形后微球微单元的面积与初始面积比的均方值假定为宏观变形管面积收缩比[26 ] , 其中微球上无限小单元变形后面积d$S$与初始未变形面积d$S_{0} $的比$\xi$可表示为[31 ]
(7) $\begin{eqnarray} &&\xi^{2}=(\lambda_{1} \lambda_{2} \cos \theta )^{2}+(\lambda_{1} \lambda _{3} \sin \theta \cos \varphi )^{2} +(\lambda_{2} \lambda_{3} \cos \theta \sin \varphi )^{2} \end{eqnarray} $
(8) $\begin{eqnarray} &&\overline \xi =\sqrt {\dfrac{1}{4\pi }\int_0^{2\pi } {{d}\varphi \int_0^\pi {\xi^{2}\sin \theta {d}\theta } } } =\sqrt {\dfrac{\lambda _{1}^{2} \lambda_{2}^{2} +\lambda_{1}^{2} \lambda_{3}^{2} +\lambda _{2}^{2} \lambda_{3}^{2} }{3}} =\sqrt {\dfrac{I_{2} }{3}} \end{eqnarray} $
1.3 宏观变形本构关系
结合单链自由能函数和微观-宏观映射关系, 采用式(6)中的$\overline \lambda$代替式(2)中的伸长比$\lambda $, 采用式(8)的$\overline \xi$代替式(3)中的微管截面积收缩比$\upsilon $, 并假定单位体积内的分子链数目为$n$. 则宏观的 Helmholtz自由能可表达为
(9) $\begin{eqnarray} \label{eq9} \left.\begin{array}{l} \varPsi =G^{c}\left( {\sqrt N \beta \sqrt {\dfrac{I_{1} }{3}} +N\ln \dfrac{\beta }{\sinh \beta }} \right)+3G^{e}\sqrt {\dfrac{I_{2} }{3}} +\varPsi_{0} \\ \beta =£^{-1}\left( {\dfrac{\sqrt {I_{1} /3} }{\sqrt N }} \right) \end{array}\right\}\quad \end{eqnarray} $
其中$G^{c}=nkT$是分子链特征刚度,而 $G^{e}=\alpha kTN\left( {b/d_{0} }\right)^{2}/3$是由于缠结约束所引起的剪切模量, $\varPsi_{0} $为常数, 其作用是保证在初始未变形条件下自由能为0. 这里在缠结约束的自由能部分添加了一个系数3, 其主要原因是使得在小变形纯剪切条件下, 缠结约束效应的剪切模量为$G^{e}$, 而当$N\gg 1$时, 在小变形纯剪切变形时, 熵弹性部分的剪切模量近似为$G^{c}$.
(10) $\begin{eqnarray} \sigma_{i} =\lambda_{i} \dfrac{\partial \varPsi }{\partial \lambda_{i} }-p \end{eqnarray} $
其中$p$是静水压部分, 以保证体积不可压. 将式(9)代入式(10)可得
(11) $\begin{eqnarray} \label{eq11} &&\sigma_{i} =\dfrac{G^{c}}{3}\dfrac{\sqrt N }{\sqrt {I_{1} /3} }\beta \lambda _{i}^{2} +\dfrac{G^{e}}{\sqrt {I_{2} /3} }\lambda_{i}^{2} (\lambda_{j}^{2} +\lambda_{k}^{2} )-p, \\&&\qquad j\ne k\ne i \end{eqnarray} $
在单轴和双轴变形过程中, 可假定变形是加载在$e_{1} $和$e_{2} $方向上, 在$e_{3} $方向上应力为0, 可依据这一条件将静水压$p$消除, 进而得到在加载方向上的应力
(12) $\begin{eqnarray} \left.\begin{array}{l} \sigma_{1} =\dfrac{G^{c}}{3}\dfrac{\sqrt N }{\sqrt {I_{1} /3} }\beta \left( {\lambda_{1}^{2} -\lambda_{3}^{2} } \right)+\dfrac{G^{e}}{\sqrt {I_{2} /3} }\lambda_{2}^{2} (\lambda_{1}^{2} -\lambda_{3}^{2} ) \\[3mm] \sigma_{2} =\dfrac{G^{c}}{3}\dfrac{\sqrt N }{\sqrt {I_{1} /3} }\beta \left( {\lambda_{2}^{2} -\lambda_{3}^{2} } \right)+\dfrac{G^{e}}{\sqrt {I_{2} /3} }\lambda_{1}^{2} (\lambda_{2}^{2} -\lambda_{3}^{2} ) \\ \end{array}\right\}\quad \end{eqnarray} $
虽然Arruda 和 Boyce[16 ] 在推导八链模型时采用了不同的方法, 但最终得到的自由能形式与本文的熵弹性部分是完全一致的, 因此本文的模型可认为是在八链模型的基础上进一步引入了分子链的缠结约束效应. 当分子链的Kuhn链段长度很大时, 八链模型会退化为Neo-Hookean模型. 因此, 这里也给出以Neo-Hookean模型作为熵弹性部分, 在单轴和双轴加载条件下的应力表达式
(13) $\begin{eqnarray} \label{eq13} \left.\begin{array}{l} \sigma_{1} =G^{c}\left( {\lambda_{1}^{2} -\lambda_{3}^{2} } \right)+\dfrac{G^{e}}{\sqrt {I_{2} /3} }\lambda_{2}^{2} (\lambda_{1}^{2} -\lambda_{3}^{2} )\\[3mm] \sigma_{2} =G^{c}\left( {\lambda_{2}^{2} -\lambda_{3}^{2} } \right)+\dfrac{G^{e}}{\sqrt {I_{2} /3} }\lambda_{1}^{2} (\lambda_{2}^{2} -\lambda_{3}^{2} ) \\ \end{array}\right\} \end{eqnarray} $
(14) $\begin{eqnarray} s_{i} =\dfrac{\sigma_{i} }{\lambda_{i} } \end{eqnarray} $
2 结果
采用上述建立的本构理论来模拟文献中关于橡胶材料在单轴和双轴变形条件下的应力响应, 并与相应的Arruda-Boyce八链模型和Neo-Hookean模型进行对比分析. 首先模拟Treloar[22 ] 开展的关于硫化橡胶和Zhao[32 ] 开展的关于TPE橡胶的实验, 上述工作对同一橡胶均同时开展了单轴拉伸、纯剪切和等双轴拉伸实验. 其中纯剪切实验的实验设置与单轴拉伸实验是一致的, 其主要区别在于所采用的试样的宽度远大于长度(一般来说, 宽度/长度 $>10$), 在该条件下, 可认为宽度方向的拉伸比为1, 长度方向拉伸比为$\lambda_1$, 厚度方向拉伸比为$1/\lambda_1$. 值得注意的是, 纯剪切变形和简单剪切变形是不一样的, 具体可参加Thiel等[33 ] 的相关工作.
在单轴拉伸、纯剪切和等双轴变形情况下, 3个主方向的拉伸比可依次表示为
(15) $\begin{eqnarray} \left.\begin{array}{l} \lambda_{2} =\left( {\lambda_{1} } \right)^{-1/2},\ \ \lambda_{3} =\left( {\lambda_{1} } \right)^{-1/2} \\ \lambda_{2} =1,\ \ \lambda_{3} =\left( {\lambda_{1} } \right)^{-1} \\ \lambda_{2} =\lambda_{1} ,\ \ \lambda_{3} =\left( {\lambda_{1} } \right)^{-2} \\ \end{array}\right\} \end{eqnarray} $
这里采用直接对实验数据进行拟合来获得模型参数, 具体是获得以下方程的最小值
(16) $\begin{eqnarray} Error=\sqrt {\dfrac{1}{N}\sum_{i=1}^N {\left( {\sigma_{1i}^{simu} -\sigma_{1i}^{\exp } } \right)^{2}} } \end{eqnarray} $
其中$\sigma_{1i}^{simu}$和$\sigma_{1i}^{\exp }$分别是模型预测和实验测得的在$e_1$方向上的主应力.
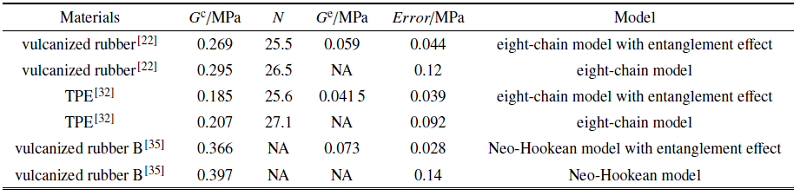
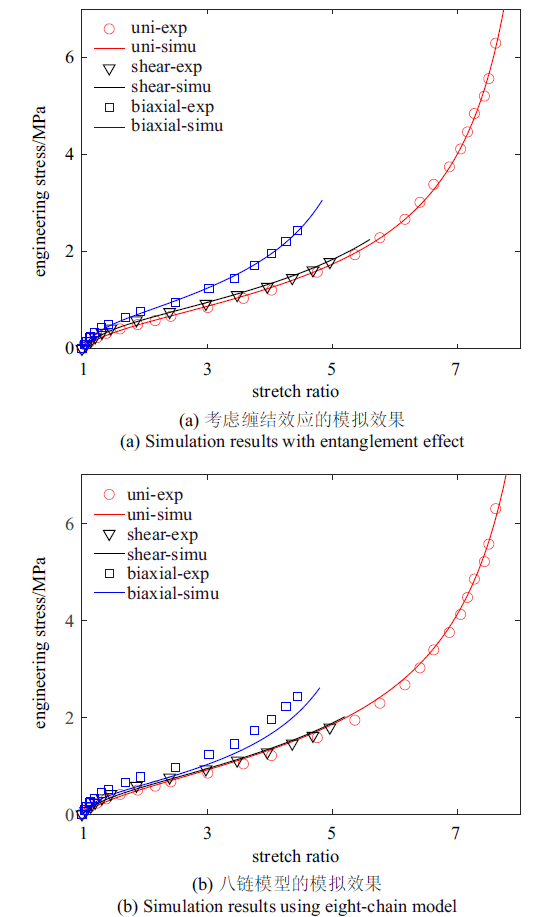
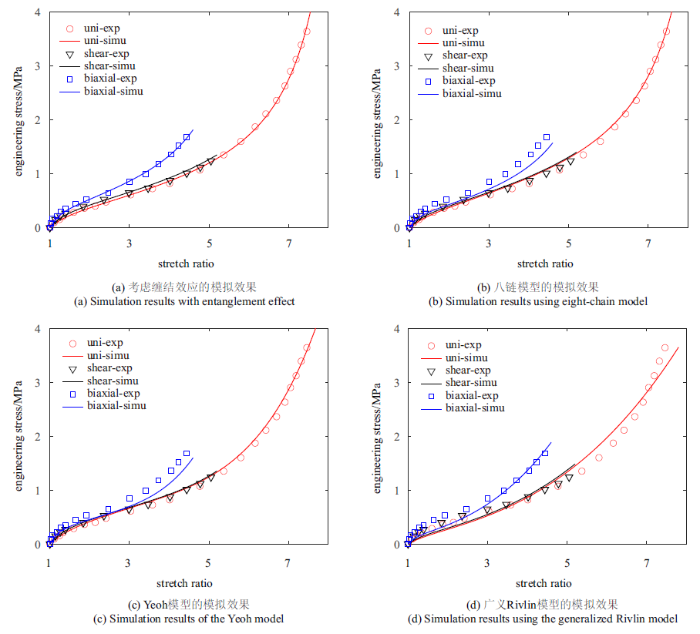
图3 给出了本文所建立的模型和八链模型对Treloar[22 ] 所开展的关于硫化橡胶的实验的模拟结果, 相应的模型参数和模拟误差见表1 . 由图3 (a)可见, 考虑了缠结效应的超弹性模型能同时准确的模拟单轴、纯剪切和等双轴拉伸的实验结果, 与之相比, 八链模型虽然能较好地预测硫化橡胶在单轴拉伸的应力响应, 但对等双轴拉伸的结果的预测明显偏低(图3 (b)). 此外, 考虑缠结效应的模型也能更好地体现单轴和纯剪切实验中应力的区别. 图4 (a)和图4 (b)给出了关于TPE橡胶的实验和相应的模拟结果, 其主要结论与硫化橡胶是一致的. 表1 的实验结果和模拟结果的误差值也进一步证实本文所建立的本构模型的预测能力明显好于八链模型.
图3
图3
关于硫化橡胶的实验和模拟结果对比
Fig.3
Comparison between the experimentally measured and simulated results of vulcanized rubber
图4
图4
关于TPE橡胶的实验和模拟结果对比
Fig.4
Comparison between the experimentally measured and simulated results of TPE
针对Treloar的实验数据, Treloar[34 ] 和Steinmann等[23 ] 系统地评估了经典唯象模型(Neo-Hookean模型, Ogden模型, Mooney-Rivlin模型, Gent模型, Yeoh模型等)和基于分子统计模型(三链模型、四链模型、八链模型、仿射模型等)的预测能力, 结果显示这些模型均不能同时较好地预测单轴、纯剪切和等双轴的实验结果. 为了与本文所建立的缠结模型进行对比, 进一步采用以下两个三参数模型来模拟TPE橡胶的实验结果. 第一个模型是Yeoh模型, 其自由能形式为
(17) $\begin{eqnarray} \label{eq17} \varPsi =c_{1} (I_{1} -3)+c_{2} (I_{1} -3)^{2}+c_{31} (I_{1} -3)^{3} \end{eqnarray} $
其中$c_1$, $c_2$以及$c_{31}$是Yeoh模型的3个参数. 第二个模型是广义Rivlin模型, 其自由能形式如下
(18) $\begin{eqnarray} \label{eq18} \varPsi =c_{1} (I_{1} -3)+c_{2} (I_{1} -3)^{2}+c_{32} (I_{2} -3) \end{eqnarray} $
其中, $c_{1}$, $c_{2}$以及$c_{32}$是广义Rivlin模型的3个参数. 当$c_2=0$, 该模型退化为Mooney-Rivlin模型.
表2 给出了Yeoh模型和广义Rivlin模型的参数以及模拟误差, 其误差均明显大于本文所建立的考虑缠结效应的超弹性模型. 由图4 (c)和图4 (d)可见, Yeoh模型能较好地预测单轴实验数据, 但与八链模型类似, 不能较好地模拟等双轴加载条件下应力响应. 在所有模型中, 广义Rivlin模型的模拟效果最差, 在单轴变形的大应变区间和双轴变形的小应变区间与实验结果都有较大偏差. 由于Mooney-Rivlin模型是该模型的一个特例, 可预见Mooney-Rivlin模型也不能较好的预测相关实验结果.
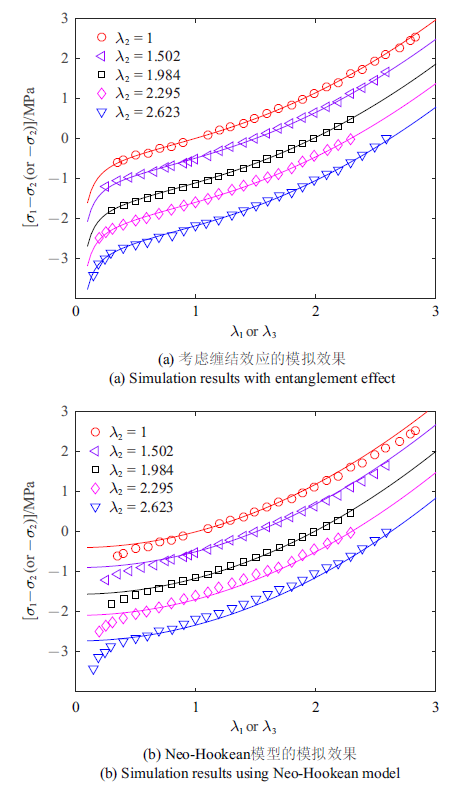
本文所建立的模型被进一步用来模拟Jones和Treloar[35 ] 所开展的关于另一类硫化橡胶(记为硫化橡胶B)的实验结果. 其实验设计如下: 橡胶试样先在$e_2$方向上被拉伸至一固定伸长比, 然后在$e_1$方向上开展拉伸实验, 在$e_3$方向上试样不受力. 图5 给出了相应的实验结果, 其中, 当$X$轴的伸长比的数值大于$1/\sqrt{\lambda_2}$时, $X$轴对应的是$\lambda_1$, $Y$轴对应$\sigma_1-\sigma_2$, 而当$X$轴的数值小于$1/\sqrt{\lambda_2}$时, $X$轴对应$\lambda_3$, 而$Y$轴对应$-\sigma_2$. 在拟合过程中, 我们发现相对误差值随着拉伸极限$N$的增大而降低, 因此这里选择在Neo-Hookean的模型的基础上考虑缠结效应, 即采用式(13)来拟合实验结果, 相关的模型参数见表1 . 如图5 (a)所示, 考虑了缠结效应的本构模型能准确地预测实验结果, 而不考虑缠结效应的Neo-Hookean模型只能在一定的变形范围内与实验结果相吻合, 而总体的模拟效果较差. 在本文中, 缠结约束部分是基于柯西-格林应变张量的第二应变量$I_2$, 在体积不可压条件下, $I_2$可表示为$I_2=1/\lambda_1^2+1/\lambda_2^2++1/\lambda_3^2$, 当$\lambda_3$值较小时, $I_2$随着$\lambda_3$的减小而迅速增大, 进而导致一个较大的应力响应, 这与实验结果是一致的. Neo-Hookean模型仅依赖于柯西-格林应变张量第一不变量, 因此不能够预测当$\lambda_3$值较小时, 随着$\lambda_3$减小应力响应的迅速增大.
图5
图5
关于硫化橡胶B的实验和模拟结果对比
Fig.5
Comparison between the experimentally measured and simulated results of vulcanized rubber
3 讨论
大量的实验数据显示, 当用八链模型来模拟单轴变形实验时, 八链模型能很好地预测实验结果, 但本文和其他相关论文[8 ,23 ] 的研究结果都显示当需要同时考虑橡胶的多种加载模式时, 八链模型不能较好地描述实验结果, 而考虑缠结效应的超弹性模型能克服八链模型的不足之处.
考虑缠结约束效应的超弹性模型的应力响应同时包含熵弹性部分和缠结约束部分, 在本文中, 前者依赖于柯西-格林应变张量第一不变量, 而后者是柯西-格林应变张量第二不变量的函数, 因此, 这两部分对不同加载情况下的响应是不同的.
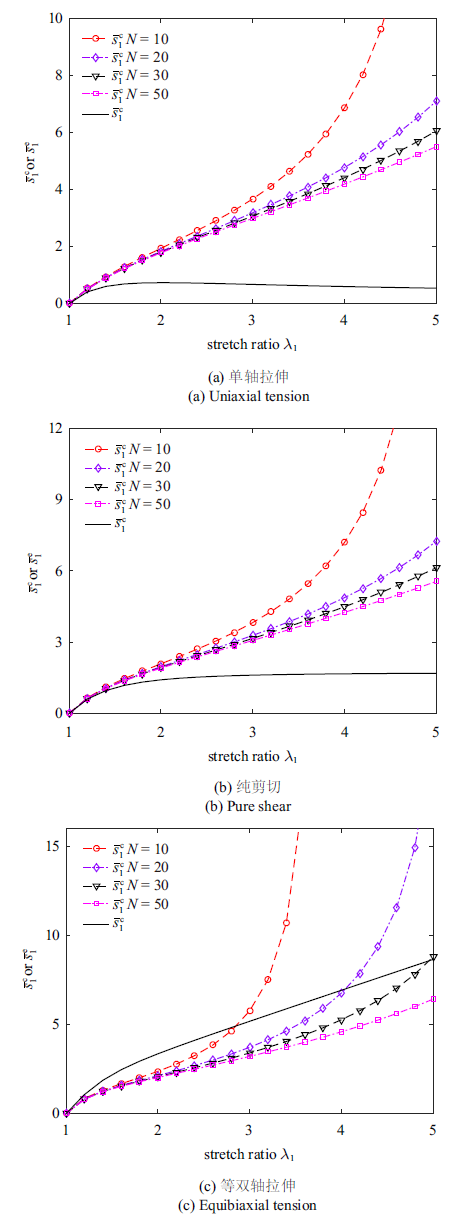
这里给出在不同加载条件下两部分的归一化应力, 即相应的应力除以剪切模量. 如图6 所示, 在小应变条件下, 来自熵弹性和缠结效应的归一化应力是相同的. 当变形逐步增大时, 两者之间逐渐偏离. 在单轴拉伸和纯剪切变形情况下, 缠结效应的归一化应力小于相应的熵弹性归一化应力, 且会逐步达到平台并发生软化行为, 这与实验结果相一致[27 ] . 与之不同, 在等双轴拉伸情况下, 缠结效应的归一化应力不出现软化行为, 且在一定的应变范围, 其数值大于熵弹性部分, 直至接近材料的拉伸极限时, 熵弹性归一化应力急剧增加, 其数值将高于缠结约束引起的归一化应力.
图6
图6
熵弹性和缠结约束效应归一化应力的对比
Fig.6
Comparison between the normalized stress from entropy and entanglement effects
经典八链模型能较好地模拟橡胶单轴加载的应力响应, 但在模拟橡胶等双轴拉伸时, 会低估实验所测得的应力响应, 而图6 的结果显示缠结效应在单轴加载条件下对应力的贡献较小, 而在等双轴加载条件下, 缠结效应具有显著效应, 这解释了考虑缠结约束效应的超弹性模型能同时预测单轴、纯剪切和等双轴实验结果的原因.
当前, 国内外相关学者[24 -28 ] 也建立了相应的包含缠结约束效应的超弹性模型, 其主要建模思路均是基于管模型, 本文将这些模型进行对比分析. Davidson和Goulbourne[27 ] 采用非仿射的管模型给出了如下的缠结约束自由能
(19) $\begin{eqnarray} \label{eq19} \varPsi_{c} =G^{e}\left( {\lambda_{1} +\lambda_{2} +\lambda_{3} +\dfrac{1}{\lambda_{1} }+\dfrac{1}{\lambda_{2} }+\dfrac{1}{\lambda_{3} }-6} \right) \end{eqnarray} $
Xiang等[28 ] 基于三链模型, 提出了如下的自由能方程来表示缠结约束效应
(20) $\begin{eqnarray} \label{eq20} \varPsi_{c} =\dfrac{G^{e}}{2}\left( {\dfrac{1}{\lambda_{1} }+\dfrac{1}{\lambda _{2} }+\dfrac{1}{\lambda_{3} }-3} \right) \end{eqnarray} $
为了与本文的模型进行对比, 在原模型的自由能基础上增加了系数1/2, 以保证上述模型在小应变条件下纯剪切的剪切模量均为$G^{e}$. 本文相应的缠结约束自由能可表达为
(21) $\begin{eqnarray} \label{eq21} \varPsi_{c} =3G^{e}\left( {\sqrt {\dfrac{1}{3}I_{2} } -1} \right) \end{eqnarray} $
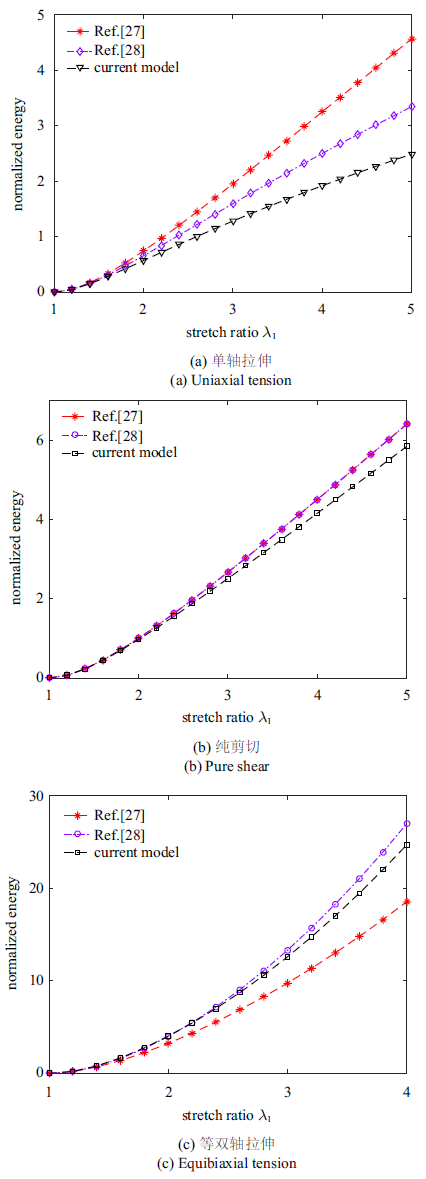
图7 对比了上述模型在单轴、纯剪切和等双轴拉伸情况下的归一化自由能, 即相应的自由能除以缠结剪切模量. 在单轴拉伸情况下, 本文所采用的缠结约束自由能最小, 而基于非仿射约束的自由能最大; 在纯剪切情况下, 3个自由能的大小比较接近, 且基于非仿射假设的自由能和基于三链模型的缠结约束自由能是完全一致的; 与单轴拉伸情况不同, 在等双轴拉伸情况下, 基于非仿射假设的缠结约束自由能最小, 而相应的基于三链模型的缠结约束自由能最大.
图7
图7
3种缠结约束自由能的对比
Fig.7
Comparison between three different forms of free energy density of entanglement effects
在熵弹性模型的基础上, 引入上述3种缠结约束自由能, 均能较好地模拟文献中的实验数据[27 ,28 ] . 因此, 基于当前文献中的实验数据不足以全面评估哪类缠结约束模型能更好地预测橡胶材料在不同加载情况下的变形行为. 亟需开展针对单一橡胶的全面的实验表征, 其实验表征可同时考虑单轴拉伸、压缩、平面应变压缩、纯剪切、非等双轴以及等双轴拉伸变形等. 这样的实验数据将有益于评估各类模型的适用性.
4 结论
本文建立了包含缠结约束效应的超弹性模型, 其主要的建模思路是在微观尺度上, 对于单根分子链采用了Langevin统计模型来表示熵弹性所引起的自由能, 采用了管模型来表征缠结约束引起的自由能. 采用仿射假设, 将各个方向分子链伸长比的均方根作为宏观变形分子链的伸长比, 把微球表面微单元收缩比的均方根作为宏观变形管横截面积的收缩比. 所建立的模型含有3个参数: 分子链特征刚度、分子链拉伸极限和缠结约束剪切模量. 当不考虑缠结效应时, 该模型退化为Arruda-Boyce八链模型.
与经典熵弹性模型相比, 本文所建立的模型能更好地表征文献中橡胶在单轴、纯剪切和等双轴多个加载模式下的实验数据, 也能准确地预测不同预拉伸比双轴拉伸条件下橡胶的力学响应. 上述结果充分揭示了缠结约束效应对橡胶等软材料宏观力学行为的重要影响, 在理论建模中需加以考虑.
本文所建立的宏观本构关系仅依赖于柯西-格林应变张量的不变量, 因此相比于文献中考虑缠结约束的超弹性模型在有限元植入上更为方便, 例如, 常见的商业软件ABAQUS的UHYPER子程序可通过直接输入基于应变不变量的自由能进行有限元分析, 而无需编写相应的基于刚度矩阵的用户自定义子程序, 这为软材料的超弹性行为的分析提供了方便[36 ] . 目前我们正在开展橡胶材料在多种变形条件下的变形行为和具有复杂几何尺寸试样的力学表征, 以更为全面地评估各类超弹性本构模型.
参考文献
View Option
[1]
李晓芳 , 杨晓翔 . 橡胶材料的超弹性本构模型
弹性体 , 2005 ,15 (1 ):50 -58
[本文引用: 1]
(Li Xiaofang Yang Xiaoxiang A review of elastic constitutive model for rubber materials
China Elastomerics 2005 ,15 (1 ):50 -58 (in Chinese))
[本文引用: 1]
[2]
Mihai LA Budday S Holzapfel GA , et al . A family of hyperelastic models for human brain tissue
Journal of the Mechanics and Physics of Solids 2017 ,106 :60 -79
[本文引用: 1]
[3]
Holzapfel AG . Nonlinear Solid Mechanics
New York: Johns Wiley & Sons , 2000
[本文引用: 2]
[4]
Huang ZP . A novel constitutive formulation for rubberlike materials in thermoelasticity
Journal of Applied Mechanics 2014 ,81 (4 ):041013
[本文引用: 1]
[5]
张希润 , 蔡力勋 , 陈辉 . 基于能量密度等效的超弹性压入模型与双压试验方法
力学学报 , 2020 ,52 (3 ):787 -796
[本文引用: 2]
(Zhang Xirun Cai Lixun Chen Hui Hyperelastic indentation models and the dual-indentation method based on energy density equivalence
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (3 ):787 -796 (in Chinese))
[本文引用: 2]
[6]
Sasso M Palmieri G Chiappini G , et al . Characterization of hyperelastic rubber-like materials by biaxial and uniaxial stretching tests based on optical methods
Polymer Testing 2008 ,27 (8 ):995 -1004
[本文引用: 1]
[7]
杨海波 , 刘枫 , 李凡珠 等 . 圆柱形橡胶试样压缩变形有限元分析的超弹性本构方程对比研究
橡胶工业 , 2018 ,10 :1085 -1093
[本文引用: 1]
(Yang Haibo Liu Feng Li Fanzhu et al . Finite element analysis of compressive deformation for cylindrical rubber components based on hyperelastic constitutive models
China Rubber Industry 2018 ,10 :1085 -1093 (in Chinese))
[本文引用: 1]
[8]
李雪冰 , 危银涛 . 一种改进的 Yeoh 超弹性材料本构模型
工程力学 , 2016 ,33 (12 ):38 -43
[本文引用: 3]
(Li Xuebing Wei Yingtao An improved Yeoh constitutive model for hyperelastic material
Engineering Mechanics 2016 ,33 (12 ):38 -43 (in Chinese))
[本文引用: 3]
[9]
刘滢滢 , 邢誉峰 . 超弹性橡胶材料的改进 Rivlin 模型
固体力学学报 , 2012 ,33 (4 ):408 -414
[本文引用: 1]
(Liu Yingying Xing Yufeng An improved Rivlin model of hyperelastic rubber materials
Chinese Journal of Solid Mechanics 2012 ,33 (4 ):408 -414 (in Chinese))
[本文引用: 1]
[10]
Lopez-Pamies O . A new I1-based hyperelastic model for rubber elastic materials
Comptes Rendus Mecanique 2010 ,338 (1 ):3 -11
[本文引用: 2]
[11]
Mangan R Destrade M Saccomandi G . Strain energy function for isotropic non-linear elastic incompressible solids with linear finite strain response in shear and torsion
Extreme Mechanics Letters 2016 ,9 :204 -206
[本文引用: 1]
[12]
罗文波 , 谭江华 . 橡胶弹性材料的一种混合本构模型
固体力学学报 , 2008 ,29 (3 ):277 -281
(Luo Wenbo Tan Jianghua A hybird hyperelastic constitutive model of rubber materials
Chinese Journal of Solid Mechanics 2008 ,29 (3 ):277 -281 (in Chinese))
[13]
魏志刚 , 陈海波 . 一种新的橡胶材料弹性本构模型
力学学报 , 2019 ,51 (2 ):473 -483
[本文引用: 1]
(Wei Zhigang Chen Haibo A new elastic model for rubber-like materials
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (2 ):473 -483 (in Chinese))
[本文引用: 1]
[14]
Treloar LRG . The elasticity of a network of long-chain molecules-II
Transactions of the Faraday Society 1943 ,39 :241 -246
[本文引用: 2]
[15]
Wang MC Guth E . Statistical theory of networks of non-Gaussian flexible chains
The Journal of Chemical Physics 1952 ,20 (7 ):1144 -1157
[本文引用: 1]
[16]
Arruda EM Boyce MC . A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials
Journal of the Mechanics and Physics of Solids 1993 ,41 (2 ):389 -412
[本文引用: 2]
[17]
Wu PD , Van Der Giessen E. On improved network models for rubber elasticity and their applications to orientation hardening in glassy polymers
Journal of the Mechanics and Physics of Solids 1993 ,41 (3 ):427 -456
[本文引用: 2]
[18]
Tian C Xiao R Guo J . An experimental study on strain hardening of amorphous thermosets: effect of temperature, strain rate, and network density
Journal of Applied Mechanics 2018 ,85 (10 ):101012
[本文引用: 1]
[19]
Boyce MC Arruda EM . Constitutive models of rubber elasticity: a review
Rubber Chemistry and Technology 2000 ,73 (3 ):504 -523
[本文引用: 1]
[20]
Diani J Le Tallec P . A fully equilibrated microsphere model with damage for rubberlike materials
Journal of the Mechanics and Physics of Solids 2019 ,124 :702 -713
[本文引用: 1]
[21]
Hossain M Amin AF Kabir MN . Eight-chain and full-network models and their modified versions for rubber hyperelasticity: A comparative study
Journal of the Mechanical Behavior of Materials 2015 ,24 (1-2 ):11 -24
[本文引用: 1]
[22]
Treloar LR . Stress-strain data for vulcanized rubber under various types of deformation
Rubber Chemistry and Technology 1944 ,17 (4 ):813 -825
[本文引用: 3]
[23]
Steinmann P Hossain M Possart G . Hyperelastic models for rubber-like materials: consistent tangent operators and suitability for Treloar's data
Archive of Applied Mechanics 2012 ,82 (9 ):1183 -1217
[本文引用: 3]
[24]
Klüppel M Schramm J . A generalized tube model of rubber elasticity and stress softening of filler reinforced elastomer systems
Macromolecular Theory and Simulations 2000 ,9 (9 ):742 -754
[本文引用: 2]
[25]
Miehe C Göktepe S Lulei F . A micro-macro approach to rubber-like materials——part I: The non-affine micro-sphere model of rubber elasticity
Journal of the Mechanics and Physics of Solids 2004 ,52 (11 ):2617 -2660
[本文引用: 2]
[26]
Khiêm VN Itskov M . Analytical network-averaging of the tube model: Rubber elasticity
Journal of the Mechanics and Physics of Solids 2016 ,95 :254 -269
[本文引用: 1]
[27]
Davidson JD Goulbourne NC . A nonaffine network model for elastomers undergoing finite deformations
Journal of the Mechanics and Physics of Solids 2013 ,61 (8 ):1784 -1797
[本文引用: 4]
[28]
Xiang Y Zhong D Wang P , et al . A general constitutive model of soft elastomers
Journal of the Mechanics and Physics of Solids 2018 ,117 :110 -122
[本文引用: 5]
[29]
Doi M Edwards S . The Theory of Polymer Dynamics. Oxford : Oxford University Press , 1986
[本文引用: 2]
[30]
Kuhn W Grün F . Beziehungen zwischen elastischen Konstanten und Dehnungsdoppelbrechung hochelastischer Stoffe
Kolloid-Zeitschrif T1942 ,101 (3 ):248 -271
[本文引用: 1]
[31]
Kearsley EA . Note: Strain invariants expressed as average stretches
Journal of Rheology 1989 ,33 (5 ):757 -760
[本文引用: 1]
[32]
Zhao F . Continuum constitutive modeling for isotropic hyperelastic materials
Advances in Pure Mathematics 2016 ,6 (9 ):571 -582
[本文引用: 1]
[33]
Thiel C Voss J Martin RJ , et al . Shear, pure and simple
International Journal of Non-Linear Mechanics 2019 ,112 :57 -72
[本文引用: 1]
[34]
Treloar LR The Physics of Rubber Elasticity. Oxford : Oxford University Press , 1975
[本文引用: 1]
[35]
Jones DF Treloar LR . The properties of rubber in pure homogeneous strain
Journal of Physics D$:$ Applied Physics 1975 ,8 (11 ):1285 -1304
[本文引用: 1]
[36]
Hong W Liu Z Suo Z . Inhomogeneous swelling of a gel in equilibrium with a solvent and mechanical load
International Journal of Solids and Structures 2009 ,46 (17 ):3282 -328
[本文引用: 1]
橡胶材料的超弹性本构模型
1
2005
... 建立超弹性模型对于橡胶和其他软材料的工程应用具有重要的意义[1 -2 ] . 当前关于软材料超弹性理论模型主要包括唯象模型和分子统计理论模型[3 -4 ] . 唯象模型的建立主要是基于连续介质力学以及软材料的实验所观察到的宏观力学行为. 常见的唯象模型包括Neo-Hooken模型、Mooney-Rivlin模型、Ogden模型、Gent模型、Yeoh模型等[3 ] . 其中Neo-Hookean模型、Gent模型和Yeoh模型都是柯西-格林应变张量第一不变量$I_{1}$的函数, Mooney-Rivlin模型同时依赖于柯西-格林应变张量的第一和第二不变量($I_{1}$, $I_{2})$, 而Ogden模型是3个主方向拉伸比的函数. 这些唯象模型在描述橡胶材料的超弹性变形行为取得了一定的成功[5 -7 ] , 例如, 张希润等[5 ] 采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
橡胶材料的超弹性本构模型
1
2005
... 建立超弹性模型对于橡胶和其他软材料的工程应用具有重要的意义[1 -2 ] . 当前关于软材料超弹性理论模型主要包括唯象模型和分子统计理论模型[3 -4 ] . 唯象模型的建立主要是基于连续介质力学以及软材料的实验所观察到的宏观力学行为. 常见的唯象模型包括Neo-Hooken模型、Mooney-Rivlin模型、Ogden模型、Gent模型、Yeoh模型等[3 ] . 其中Neo-Hookean模型、Gent模型和Yeoh模型都是柯西-格林应变张量第一不变量$I_{1}$的函数, Mooney-Rivlin模型同时依赖于柯西-格林应变张量的第一和第二不变量($I_{1}$, $I_{2})$, 而Ogden模型是3个主方向拉伸比的函数. 这些唯象模型在描述橡胶材料的超弹性变形行为取得了一定的成功[5 -7 ] , 例如, 张希润等[5 ] 采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
A family of hyperelastic models for human brain tissue
1
2017
... 建立超弹性模型对于橡胶和其他软材料的工程应用具有重要的意义[1 -2 ] . 当前关于软材料超弹性理论模型主要包括唯象模型和分子统计理论模型[3 -4 ] . 唯象模型的建立主要是基于连续介质力学以及软材料的实验所观察到的宏观力学行为. 常见的唯象模型包括Neo-Hooken模型、Mooney-Rivlin模型、Ogden模型、Gent模型、Yeoh模型等[3 ] . 其中Neo-Hookean模型、Gent模型和Yeoh模型都是柯西-格林应变张量第一不变量$I_{1}$的函数, Mooney-Rivlin模型同时依赖于柯西-格林应变张量的第一和第二不变量($I_{1}$, $I_{2})$, 而Ogden模型是3个主方向拉伸比的函数. 这些唯象模型在描述橡胶材料的超弹性变形行为取得了一定的成功[5 -7 ] , 例如, 张希润等[5 ] 采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
Nonlinear Solid Mechanics
2
2000
... 建立超弹性模型对于橡胶和其他软材料的工程应用具有重要的意义[1 -2 ] . 当前关于软材料超弹性理论模型主要包括唯象模型和分子统计理论模型[3 -4 ] . 唯象模型的建立主要是基于连续介质力学以及软材料的实验所观察到的宏观力学行为. 常见的唯象模型包括Neo-Hooken模型、Mooney-Rivlin模型、Ogden模型、Gent模型、Yeoh模型等[3 ] . 其中Neo-Hookean模型、Gent模型和Yeoh模型都是柯西-格林应变张量第一不变量$I_{1}$的函数, Mooney-Rivlin模型同时依赖于柯西-格林应变张量的第一和第二不变量($I_{1}$, $I_{2})$, 而Ogden模型是3个主方向拉伸比的函数. 这些唯象模型在描述橡胶材料的超弹性变形行为取得了一定的成功[5 -7 ] , 例如, 张希润等[5 ] 采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
... [3 ]. 其中Neo-Hookean模型、Gent模型和Yeoh模型都是柯西-格林应变张量第一不变量$I_{1}$的函数, Mooney-Rivlin模型同时依赖于柯西-格林应变张量的第一和第二不变量($I_{1}$, $I_{2})$, 而Ogden模型是3个主方向拉伸比的函数. 这些唯象模型在描述橡胶材料的超弹性变形行为取得了一定的成功[5 -7 ] , 例如, 张希润等[5 ] 采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
A novel constitutive formulation for rubberlike materials in thermoelasticity
1
2014
... 建立超弹性模型对于橡胶和其他软材料的工程应用具有重要的意义[1 -2 ] . 当前关于软材料超弹性理论模型主要包括唯象模型和分子统计理论模型[3 -4 ] . 唯象模型的建立主要是基于连续介质力学以及软材料的实验所观察到的宏观力学行为. 常见的唯象模型包括Neo-Hooken模型、Mooney-Rivlin模型、Ogden模型、Gent模型、Yeoh模型等[3 ] . 其中Neo-Hookean模型、Gent模型和Yeoh模型都是柯西-格林应变张量第一不变量$I_{1}$的函数, Mooney-Rivlin模型同时依赖于柯西-格林应变张量的第一和第二不变量($I_{1}$, $I_{2})$, 而Ogden模型是3个主方向拉伸比的函数. 这些唯象模型在描述橡胶材料的超弹性变形行为取得了一定的成功[5 -7 ] , 例如, 张希润等[5 ] 采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
基于能量密度等效的超弹性压入模型与双压试验方法
2
2020
... 建立超弹性模型对于橡胶和其他软材料的工程应用具有重要的意义[1 -2 ] . 当前关于软材料超弹性理论模型主要包括唯象模型和分子统计理论模型[3 -4 ] . 唯象模型的建立主要是基于连续介质力学以及软材料的实验所观察到的宏观力学行为. 常见的唯象模型包括Neo-Hooken模型、Mooney-Rivlin模型、Ogden模型、Gent模型、Yeoh模型等[3 ] . 其中Neo-Hookean模型、Gent模型和Yeoh模型都是柯西-格林应变张量第一不变量$I_{1}$的函数, Mooney-Rivlin模型同时依赖于柯西-格林应变张量的第一和第二不变量($I_{1}$, $I_{2})$, 而Ogden模型是3个主方向拉伸比的函数. 这些唯象模型在描述橡胶材料的超弹性变形行为取得了一定的成功[5 -7 ] , 例如, 张希润等[5 ] 采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
... [5 ]采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
基于能量密度等效的超弹性压入模型与双压试验方法
2
2020
... 建立超弹性模型对于橡胶和其他软材料的工程应用具有重要的意义[1 -2 ] . 当前关于软材料超弹性理论模型主要包括唯象模型和分子统计理论模型[3 -4 ] . 唯象模型的建立主要是基于连续介质力学以及软材料的实验所观察到的宏观力学行为. 常见的唯象模型包括Neo-Hooken模型、Mooney-Rivlin模型、Ogden模型、Gent模型、Yeoh模型等[3 ] . 其中Neo-Hookean模型、Gent模型和Yeoh模型都是柯西-格林应变张量第一不变量$I_{1}$的函数, Mooney-Rivlin模型同时依赖于柯西-格林应变张量的第一和第二不变量($I_{1}$, $I_{2})$, 而Ogden模型是3个主方向拉伸比的函数. 这些唯象模型在描述橡胶材料的超弹性变形行为取得了一定的成功[5 -7 ] , 例如, 张希润等[5 ] 采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
... [5 ]采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
Characterization of hyperelastic rubber-like materials by biaxial and uniaxial stretching tests based on optical methods
1
2008
... 建立超弹性模型对于橡胶和其他软材料的工程应用具有重要的意义[1 -2 ] . 当前关于软材料超弹性理论模型主要包括唯象模型和分子统计理论模型[3 -4 ] . 唯象模型的建立主要是基于连续介质力学以及软材料的实验所观察到的宏观力学行为. 常见的唯象模型包括Neo-Hooken模型、Mooney-Rivlin模型、Ogden模型、Gent模型、Yeoh模型等[3 ] . 其中Neo-Hookean模型、Gent模型和Yeoh模型都是柯西-格林应变张量第一不变量$I_{1}$的函数, Mooney-Rivlin模型同时依赖于柯西-格林应变张量的第一和第二不变量($I_{1}$, $I_{2})$, 而Ogden模型是3个主方向拉伸比的函数. 这些唯象模型在描述橡胶材料的超弹性变形行为取得了一定的成功[5 -7 ] , 例如, 张希润等[5 ] 采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
圆柱形橡胶试样压缩变形有限元分析的超弹性本构方程对比研究
1
2018
... 建立超弹性模型对于橡胶和其他软材料的工程应用具有重要的意义[1 -2 ] . 当前关于软材料超弹性理论模型主要包括唯象模型和分子统计理论模型[3 -4 ] . 唯象模型的建立主要是基于连续介质力学以及软材料的实验所观察到的宏观力学行为. 常见的唯象模型包括Neo-Hooken模型、Mooney-Rivlin模型、Ogden模型、Gent模型、Yeoh模型等[3 ] . 其中Neo-Hookean模型、Gent模型和Yeoh模型都是柯西-格林应变张量第一不变量$I_{1}$的函数, Mooney-Rivlin模型同时依赖于柯西-格林应变张量的第一和第二不变量($I_{1}$, $I_{2})$, 而Ogden模型是3个主方向拉伸比的函数. 这些唯象模型在描述橡胶材料的超弹性变形行为取得了一定的成功[5 -7 ] , 例如, 张希润等[5 ] 采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
圆柱形橡胶试样压缩变形有限元分析的超弹性本构方程对比研究
1
2018
... 建立超弹性模型对于橡胶和其他软材料的工程应用具有重要的意义[1 -2 ] . 当前关于软材料超弹性理论模型主要包括唯象模型和分子统计理论模型[3 -4 ] . 唯象模型的建立主要是基于连续介质力学以及软材料的实验所观察到的宏观力学行为. 常见的唯象模型包括Neo-Hooken模型、Mooney-Rivlin模型、Ogden模型、Gent模型、Yeoh模型等[3 ] . 其中Neo-Hookean模型、Gent模型和Yeoh模型都是柯西-格林应变张量第一不变量$I_{1}$的函数, Mooney-Rivlin模型同时依赖于柯西-格林应变张量的第一和第二不变量($I_{1}$, $I_{2})$, 而Ogden模型是3个主方向拉伸比的函数. 这些唯象模型在描述橡胶材料的超弹性变形行为取得了一定的成功[5 -7 ] , 例如, 张希润等[5 ] 采用压入法研究软材料的力学性能, 结果显示基于Mooney-Rivlin模型的有限元结果能与压入实验结果吻合. Sasso等[6 ] 发现Ogden模型和二阶的Mooney-Rivlin模型可以描述橡胶在单轴、等双轴和鼓泡实验中的力学响应. ...
一种改进的 Yeoh 超弹性材料本构模型
3
2016
... 针对唯象超弹性模型的不足之处, 部分学者[8 -9 ] 对上述模型作了扩展, 例如, 李雪冰等[8 ] 在Yeoh模型的自由能基础上增加了依赖于应变张量第二不变量的部分, 克服了经典Yeoh模型在预测等双轴曲线时"偏软"的特性. 近年来, 国内外相关学者[10 -13 ] 也提出了多种新型的超弹性唯象模型, 例如, Lopez-Pamies[10 ] 提出了基于应变第一不变量的指数型自由能形式, Mangan等[11 ] 提出了同时依赖于柯西-格林应变第一和第二不变量的新型超弹性自由能形式, 该模型能准确表征大变形条件下简单剪切变形切应力和切应变的线性关系, 以及单轴变形下的应变强化行为. ...
... [8 ]在Yeoh模型的自由能基础上增加了依赖于应变张量第二不变量的部分, 克服了经典Yeoh模型在预测等双轴曲线时"偏软"的特性. 近年来, 国内外相关学者[10 -13 ] 也提出了多种新型的超弹性唯象模型, 例如, Lopez-Pamies[10 ] 提出了基于应变第一不变量的指数型自由能形式, Mangan等[11 ] 提出了同时依赖于柯西-格林应变第一和第二不变量的新型超弹性自由能形式, 该模型能准确表征大变形条件下简单剪切变形切应力和切应变的线性关系, 以及单轴变形下的应变强化行为. ...
... 大量的实验数据显示, 当用八链模型来模拟单轴变形实验时, 八链模型能很好地预测实验结果, 但本文和其他相关论文[8 ,23 ] 的研究结果都显示当需要同时考虑橡胶的多种加载模式时, 八链模型不能较好地描述实验结果, 而考虑缠结效应的超弹性模型能克服八链模型的不足之处. ...
一种改进的 Yeoh 超弹性材料本构模型
3
2016
... 针对唯象超弹性模型的不足之处, 部分学者[8 -9 ] 对上述模型作了扩展, 例如, 李雪冰等[8 ] 在Yeoh模型的自由能基础上增加了依赖于应变张量第二不变量的部分, 克服了经典Yeoh模型在预测等双轴曲线时"偏软"的特性. 近年来, 国内外相关学者[10 -13 ] 也提出了多种新型的超弹性唯象模型, 例如, Lopez-Pamies[10 ] 提出了基于应变第一不变量的指数型自由能形式, Mangan等[11 ] 提出了同时依赖于柯西-格林应变第一和第二不变量的新型超弹性自由能形式, 该模型能准确表征大变形条件下简单剪切变形切应力和切应变的线性关系, 以及单轴变形下的应变强化行为. ...
... [8 ]在Yeoh模型的自由能基础上增加了依赖于应变张量第二不变量的部分, 克服了经典Yeoh模型在预测等双轴曲线时"偏软"的特性. 近年来, 国内外相关学者[10 -13 ] 也提出了多种新型的超弹性唯象模型, 例如, Lopez-Pamies[10 ] 提出了基于应变第一不变量的指数型自由能形式, Mangan等[11 ] 提出了同时依赖于柯西-格林应变第一和第二不变量的新型超弹性自由能形式, 该模型能准确表征大变形条件下简单剪切变形切应力和切应变的线性关系, 以及单轴变形下的应变强化行为. ...
... 大量的实验数据显示, 当用八链模型来模拟单轴变形实验时, 八链模型能很好地预测实验结果, 但本文和其他相关论文[8 ,23 ] 的研究结果都显示当需要同时考虑橡胶的多种加载模式时, 八链模型不能较好地描述实验结果, 而考虑缠结效应的超弹性模型能克服八链模型的不足之处. ...
超弹性橡胶材料的改进 Rivlin 模型
1
2012
... 针对唯象超弹性模型的不足之处, 部分学者[8 -9 ] 对上述模型作了扩展, 例如, 李雪冰等[8 ] 在Yeoh模型的自由能基础上增加了依赖于应变张量第二不变量的部分, 克服了经典Yeoh模型在预测等双轴曲线时"偏软"的特性. 近年来, 国内外相关学者[10 -13 ] 也提出了多种新型的超弹性唯象模型, 例如, Lopez-Pamies[10 ] 提出了基于应变第一不变量的指数型自由能形式, Mangan等[11 ] 提出了同时依赖于柯西-格林应变第一和第二不变量的新型超弹性自由能形式, 该模型能准确表征大变形条件下简单剪切变形切应力和切应变的线性关系, 以及单轴变形下的应变强化行为. ...
超弹性橡胶材料的改进 Rivlin 模型
1
2012
... 针对唯象超弹性模型的不足之处, 部分学者[8 -9 ] 对上述模型作了扩展, 例如, 李雪冰等[8 ] 在Yeoh模型的自由能基础上增加了依赖于应变张量第二不变量的部分, 克服了经典Yeoh模型在预测等双轴曲线时"偏软"的特性. 近年来, 国内外相关学者[10 -13 ] 也提出了多种新型的超弹性唯象模型, 例如, Lopez-Pamies[10 ] 提出了基于应变第一不变量的指数型自由能形式, Mangan等[11 ] 提出了同时依赖于柯西-格林应变第一和第二不变量的新型超弹性自由能形式, 该模型能准确表征大变形条件下简单剪切变形切应力和切应变的线性关系, 以及单轴变形下的应变强化行为. ...
A new I1-based hyperelastic model for rubber elastic materials
2
2010
... 针对唯象超弹性模型的不足之处, 部分学者[8 -9 ] 对上述模型作了扩展, 例如, 李雪冰等[8 ] 在Yeoh模型的自由能基础上增加了依赖于应变张量第二不变量的部分, 克服了经典Yeoh模型在预测等双轴曲线时"偏软"的特性. 近年来, 国内外相关学者[10 -13 ] 也提出了多种新型的超弹性唯象模型, 例如, Lopez-Pamies[10 ] 提出了基于应变第一不变量的指数型自由能形式, Mangan等[11 ] 提出了同时依赖于柯西-格林应变第一和第二不变量的新型超弹性自由能形式, 该模型能准确表征大变形条件下简单剪切变形切应力和切应变的线性关系, 以及单轴变形下的应变强化行为. ...
... [10 ]提出了基于应变第一不变量的指数型自由能形式, Mangan等[11 ] 提出了同时依赖于柯西-格林应变第一和第二不变量的新型超弹性自由能形式, 该模型能准确表征大变形条件下简单剪切变形切应力和切应变的线性关系, 以及单轴变形下的应变强化行为. ...
Strain energy function for isotropic non-linear elastic incompressible solids with linear finite strain response in shear and torsion
1
2016
... 针对唯象超弹性模型的不足之处, 部分学者[8 -9 ] 对上述模型作了扩展, 例如, 李雪冰等[8 ] 在Yeoh模型的自由能基础上增加了依赖于应变张量第二不变量的部分, 克服了经典Yeoh模型在预测等双轴曲线时"偏软"的特性. 近年来, 国内外相关学者[10 -13 ] 也提出了多种新型的超弹性唯象模型, 例如, Lopez-Pamies[10 ] 提出了基于应变第一不变量的指数型自由能形式, Mangan等[11 ] 提出了同时依赖于柯西-格林应变第一和第二不变量的新型超弹性自由能形式, 该模型能准确表征大变形条件下简单剪切变形切应力和切应变的线性关系, 以及单轴变形下的应变强化行为. ...
一种新的橡胶材料弹性本构模型
1
2019
... 针对唯象超弹性模型的不足之处, 部分学者[8 -9 ] 对上述模型作了扩展, 例如, 李雪冰等[8 ] 在Yeoh模型的自由能基础上增加了依赖于应变张量第二不变量的部分, 克服了经典Yeoh模型在预测等双轴曲线时"偏软"的特性. 近年来, 国内外相关学者[10 -13 ] 也提出了多种新型的超弹性唯象模型, 例如, Lopez-Pamies[10 ] 提出了基于应变第一不变量的指数型自由能形式, Mangan等[11 ] 提出了同时依赖于柯西-格林应变第一和第二不变量的新型超弹性自由能形式, 该模型能准确表征大变形条件下简单剪切变形切应力和切应变的线性关系, 以及单轴变形下的应变强化行为. ...
一种新的橡胶材料弹性本构模型
1
2019
... 针对唯象超弹性模型的不足之处, 部分学者[8 -9 ] 对上述模型作了扩展, 例如, 李雪冰等[8 ] 在Yeoh模型的自由能基础上增加了依赖于应变张量第二不变量的部分, 克服了经典Yeoh模型在预测等双轴曲线时"偏软"的特性. 近年来, 国内外相关学者[10 -13 ] 也提出了多种新型的超弹性唯象模型, 例如, Lopez-Pamies[10 ] 提出了基于应变第一不变量的指数型自由能形式, Mangan等[11 ] 提出了同时依赖于柯西-格林应变第一和第二不变量的新型超弹性自由能形式, 该模型能准确表征大变形条件下简单剪切变形切应力和切应变的线性关系, 以及单轴变形下的应变强化行为. ...
The elasticity of a network of long-chain molecules-II
2
1943
... 另一类被广泛用来描述软材料超弹性行为的模型是基于分子统计理论模型, 其主要建模思路是将统计理论应用于分子链网络中, 进而得出变形自由能函数. 常见的分子统计理论模型包括Treloar高斯链模型[14 ] , Wang-Guth三链模型[15 ] 、 Arruda-Boyce八链模型[16 ] 以及全链网络模型[17 ] . Treloar[14 ] 提出的高斯链分布模型, 与唯象的Neo-Hookean模型, 在数学形式上是完全等价的, 该模型只能描述轻度交联橡胶材料的应力响应, 而对于交联度高的橡胶网络, 这类模型仅能描述小应变范围内的应力响应[18 ] . Boyce等[19 ] 发现唯象的Gent模型和Arruda-Boyce模型在多种加载条件下的应力-应变关系是接近的, 这两个模型均可较为准确地模拟不同交联度橡胶材料的单轴加载条件下的应力响应. Wu和van der Giessen[17 ] 建立了全链模型, 全链模型需要对各个方向进行积分, 计算起来不够方便. 上述全链模型是基于仿射假设, 而Diani和Tallec[20 ] 通过能量最小化原则建立了非仿射的全链超弹性模型. Hossain等[21 ] 针对八链模型和全链模型的不足, 详细评估了几类扩展的八链和全链模型在模拟复杂加载情况下的表现. ...
... [14 ]提出的高斯链分布模型, 与唯象的Neo-Hookean模型, 在数学形式上是完全等价的, 该模型只能描述轻度交联橡胶材料的应力响应, 而对于交联度高的橡胶网络, 这类模型仅能描述小应变范围内的应力响应[18 ] . Boyce等[19 ] 发现唯象的Gent模型和Arruda-Boyce模型在多种加载条件下的应力-应变关系是接近的, 这两个模型均可较为准确地模拟不同交联度橡胶材料的单轴加载条件下的应力响应. Wu和van der Giessen[17 ] 建立了全链模型, 全链模型需要对各个方向进行积分, 计算起来不够方便. 上述全链模型是基于仿射假设, 而Diani和Tallec[20 ] 通过能量最小化原则建立了非仿射的全链超弹性模型. Hossain等[21 ] 针对八链模型和全链模型的不足, 详细评估了几类扩展的八链和全链模型在模拟复杂加载情况下的表现. ...
Statistical theory of networks of non-Gaussian flexible chains
1
1952
... 另一类被广泛用来描述软材料超弹性行为的模型是基于分子统计理论模型, 其主要建模思路是将统计理论应用于分子链网络中, 进而得出变形自由能函数. 常见的分子统计理论模型包括Treloar高斯链模型[14 ] , Wang-Guth三链模型[15 ] 、 Arruda-Boyce八链模型[16 ] 以及全链网络模型[17 ] . Treloar[14 ] 提出的高斯链分布模型, 与唯象的Neo-Hookean模型, 在数学形式上是完全等价的, 该模型只能描述轻度交联橡胶材料的应力响应, 而对于交联度高的橡胶网络, 这类模型仅能描述小应变范围内的应力响应[18 ] . Boyce等[19 ] 发现唯象的Gent模型和Arruda-Boyce模型在多种加载条件下的应力-应变关系是接近的, 这两个模型均可较为准确地模拟不同交联度橡胶材料的单轴加载条件下的应力响应. Wu和van der Giessen[17 ] 建立了全链模型, 全链模型需要对各个方向进行积分, 计算起来不够方便. 上述全链模型是基于仿射假设, 而Diani和Tallec[20 ] 通过能量最小化原则建立了非仿射的全链超弹性模型. Hossain等[21 ] 针对八链模型和全链模型的不足, 详细评估了几类扩展的八链和全链模型在模拟复杂加载情况下的表现. ...
A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials
2
1993
... 另一类被广泛用来描述软材料超弹性行为的模型是基于分子统计理论模型, 其主要建模思路是将统计理论应用于分子链网络中, 进而得出变形自由能函数. 常见的分子统计理论模型包括Treloar高斯链模型[14 ] , Wang-Guth三链模型[15 ] 、 Arruda-Boyce八链模型[16 ] 以及全链网络模型[17 ] . Treloar[14 ] 提出的高斯链分布模型, 与唯象的Neo-Hookean模型, 在数学形式上是完全等价的, 该模型只能描述轻度交联橡胶材料的应力响应, 而对于交联度高的橡胶网络, 这类模型仅能描述小应变范围内的应力响应[18 ] . Boyce等[19 ] 发现唯象的Gent模型和Arruda-Boyce模型在多种加载条件下的应力-应变关系是接近的, 这两个模型均可较为准确地模拟不同交联度橡胶材料的单轴加载条件下的应力响应. Wu和van der Giessen[17 ] 建立了全链模型, 全链模型需要对各个方向进行积分, 计算起来不够方便. 上述全链模型是基于仿射假设, 而Diani和Tallec[20 ] 通过能量最小化原则建立了非仿射的全链超弹性模型. Hossain等[21 ] 针对八链模型和全链模型的不足, 详细评估了几类扩展的八链和全链模型在模拟复杂加载情况下的表现. ...
... 虽然Arruda 和 Boyce[16 ] 在推导八链模型时采用了不同的方法, 但最终得到的自由能形式与本文的熵弹性部分是完全一致的, 因此本文的模型可认为是在八链模型的基础上进一步引入了分子链的缠结约束效应. 当分子链的Kuhn链段长度很大时, 八链模型会退化为Neo-Hookean模型. 因此, 这里也给出以Neo-Hookean模型作为熵弹性部分, 在单轴和双轴加载条件下的应力表达式 ...
Van Der Giessen E. On improved network models for rubber elasticity and their applications to orientation hardening in glassy polymers
2
1993
... 另一类被广泛用来描述软材料超弹性行为的模型是基于分子统计理论模型, 其主要建模思路是将统计理论应用于分子链网络中, 进而得出变形自由能函数. 常见的分子统计理论模型包括Treloar高斯链模型[14 ] , Wang-Guth三链模型[15 ] 、 Arruda-Boyce八链模型[16 ] 以及全链网络模型[17 ] . Treloar[14 ] 提出的高斯链分布模型, 与唯象的Neo-Hookean模型, 在数学形式上是完全等价的, 该模型只能描述轻度交联橡胶材料的应力响应, 而对于交联度高的橡胶网络, 这类模型仅能描述小应变范围内的应力响应[18 ] . Boyce等[19 ] 发现唯象的Gent模型和Arruda-Boyce模型在多种加载条件下的应力-应变关系是接近的, 这两个模型均可较为准确地模拟不同交联度橡胶材料的单轴加载条件下的应力响应. Wu和van der Giessen[17 ] 建立了全链模型, 全链模型需要对各个方向进行积分, 计算起来不够方便. 上述全链模型是基于仿射假设, 而Diani和Tallec[20 ] 通过能量最小化原则建立了非仿射的全链超弹性模型. Hossain等[21 ] 针对八链模型和全链模型的不足, 详细评估了几类扩展的八链和全链模型在模拟复杂加载情况下的表现. ...
... [17 ]建立了全链模型, 全链模型需要对各个方向进行积分, 计算起来不够方便. 上述全链模型是基于仿射假设, 而Diani和Tallec[20 ] 通过能量最小化原则建立了非仿射的全链超弹性模型. Hossain等[21 ] 针对八链模型和全链模型的不足, 详细评估了几类扩展的八链和全链模型在模拟复杂加载情况下的表现. ...
An experimental study on strain hardening of amorphous thermosets: effect of temperature, strain rate, and network density
1
2018
... 另一类被广泛用来描述软材料超弹性行为的模型是基于分子统计理论模型, 其主要建模思路是将统计理论应用于分子链网络中, 进而得出变形自由能函数. 常见的分子统计理论模型包括Treloar高斯链模型[14 ] , Wang-Guth三链模型[15 ] 、 Arruda-Boyce八链模型[16 ] 以及全链网络模型[17 ] . Treloar[14 ] 提出的高斯链分布模型, 与唯象的Neo-Hookean模型, 在数学形式上是完全等价的, 该模型只能描述轻度交联橡胶材料的应力响应, 而对于交联度高的橡胶网络, 这类模型仅能描述小应变范围内的应力响应[18 ] . Boyce等[19 ] 发现唯象的Gent模型和Arruda-Boyce模型在多种加载条件下的应力-应变关系是接近的, 这两个模型均可较为准确地模拟不同交联度橡胶材料的单轴加载条件下的应力响应. Wu和van der Giessen[17 ] 建立了全链模型, 全链模型需要对各个方向进行积分, 计算起来不够方便. 上述全链模型是基于仿射假设, 而Diani和Tallec[20 ] 通过能量最小化原则建立了非仿射的全链超弹性模型. Hossain等[21 ] 针对八链模型和全链模型的不足, 详细评估了几类扩展的八链和全链模型在模拟复杂加载情况下的表现. ...
Constitutive models of rubber elasticity: a review
1
2000
... 另一类被广泛用来描述软材料超弹性行为的模型是基于分子统计理论模型, 其主要建模思路是将统计理论应用于分子链网络中, 进而得出变形自由能函数. 常见的分子统计理论模型包括Treloar高斯链模型[14 ] , Wang-Guth三链模型[15 ] 、 Arruda-Boyce八链模型[16 ] 以及全链网络模型[17 ] . Treloar[14 ] 提出的高斯链分布模型, 与唯象的Neo-Hookean模型, 在数学形式上是完全等价的, 该模型只能描述轻度交联橡胶材料的应力响应, 而对于交联度高的橡胶网络, 这类模型仅能描述小应变范围内的应力响应[18 ] . Boyce等[19 ] 发现唯象的Gent模型和Arruda-Boyce模型在多种加载条件下的应力-应变关系是接近的, 这两个模型均可较为准确地模拟不同交联度橡胶材料的单轴加载条件下的应力响应. Wu和van der Giessen[17 ] 建立了全链模型, 全链模型需要对各个方向进行积分, 计算起来不够方便. 上述全链模型是基于仿射假设, 而Diani和Tallec[20 ] 通过能量最小化原则建立了非仿射的全链超弹性模型. Hossain等[21 ] 针对八链模型和全链模型的不足, 详细评估了几类扩展的八链和全链模型在模拟复杂加载情况下的表现. ...
A fully equilibrated microsphere model with damage for rubberlike materials
1
2019
... 另一类被广泛用来描述软材料超弹性行为的模型是基于分子统计理论模型, 其主要建模思路是将统计理论应用于分子链网络中, 进而得出变形自由能函数. 常见的分子统计理论模型包括Treloar高斯链模型[14 ] , Wang-Guth三链模型[15 ] 、 Arruda-Boyce八链模型[16 ] 以及全链网络模型[17 ] . Treloar[14 ] 提出的高斯链分布模型, 与唯象的Neo-Hookean模型, 在数学形式上是完全等价的, 该模型只能描述轻度交联橡胶材料的应力响应, 而对于交联度高的橡胶网络, 这类模型仅能描述小应变范围内的应力响应[18 ] . Boyce等[19 ] 发现唯象的Gent模型和Arruda-Boyce模型在多种加载条件下的应力-应变关系是接近的, 这两个模型均可较为准确地模拟不同交联度橡胶材料的单轴加载条件下的应力响应. Wu和van der Giessen[17 ] 建立了全链模型, 全链模型需要对各个方向进行积分, 计算起来不够方便. 上述全链模型是基于仿射假设, 而Diani和Tallec[20 ] 通过能量最小化原则建立了非仿射的全链超弹性模型. Hossain等[21 ] 针对八链模型和全链模型的不足, 详细评估了几类扩展的八链和全链模型在模拟复杂加载情况下的表现. ...
Eight-chain and full-network models and their modified versions for rubber hyperelasticity: A comparative study
1
2015
... 另一类被广泛用来描述软材料超弹性行为的模型是基于分子统计理论模型, 其主要建模思路是将统计理论应用于分子链网络中, 进而得出变形自由能函数. 常见的分子统计理论模型包括Treloar高斯链模型[14 ] , Wang-Guth三链模型[15 ] 、 Arruda-Boyce八链模型[16 ] 以及全链网络模型[17 ] . Treloar[14 ] 提出的高斯链分布模型, 与唯象的Neo-Hookean模型, 在数学形式上是完全等价的, 该模型只能描述轻度交联橡胶材料的应力响应, 而对于交联度高的橡胶网络, 这类模型仅能描述小应变范围内的应力响应[18 ] . Boyce等[19 ] 发现唯象的Gent模型和Arruda-Boyce模型在多种加载条件下的应力-应变关系是接近的, 这两个模型均可较为准确地模拟不同交联度橡胶材料的单轴加载条件下的应力响应. Wu和van der Giessen[17 ] 建立了全链模型, 全链模型需要对各个方向进行积分, 计算起来不够方便. 上述全链模型是基于仿射假设, 而Diani和Tallec[20 ] 通过能量最小化原则建立了非仿射的全链超弹性模型. Hossain等[21 ] 针对八链模型和全链模型的不足, 详细评估了几类扩展的八链和全链模型在模拟复杂加载情况下的表现. ...
Stress-strain data for vulcanized rubber under various types of deformation
3
1944
... 针对Treloar[22 ] 关于硫化橡胶的单轴、纯剪切和等双轴加载的经典实验数据, Steinmann等[23 ] 详细评估了14种唯象模型和分子统计理论模型的预测能力, 发现这些广泛应用的模型并不能很好地预测硫化橡胶在多种变形模式下的力学响应. 针对经典超弹性模型的不足之处, 部分学者[24 -28 ] 提出了引入缠结约束效应, 其主要的建模思路是将缠结约束效应用Doi 和Edwards[29 ] 所提出的管模型(tube model)来近似表征. 相关模拟结果显示, 引入缠结约束效应的超弹性模型能更为准确地预测橡胶的力学行为, 但上述模型也有相应的不足之处, 例如, Miche等[25 ] 所建立的考虑缠结效应的超弹性模型是基于非仿射假设, 需开展全方向积分计算, 而Davodson和Goubourne[27 ] 以及Xiang等[28 ] 所建立的缠结约束模型的自由能是主方向拉伸比的函数, 这导致这些模型有限元植入方面不够方便. ...
... 采用上述建立的本构理论来模拟文献中关于橡胶材料在单轴和双轴变形条件下的应力响应, 并与相应的Arruda-Boyce八链模型和Neo-Hookean模型进行对比分析. 首先模拟Treloar[22 ] 开展的关于硫化橡胶和Zhao[32 ] 开展的关于TPE橡胶的实验, 上述工作对同一橡胶均同时开展了单轴拉伸、纯剪切和等双轴拉伸实验. 其中纯剪切实验的实验设置与单轴拉伸实验是一致的, 其主要区别在于所采用的试样的宽度远大于长度(一般来说, 宽度/长度 $>10$), 在该条件下, 可认为宽度方向的拉伸比为1, 长度方向拉伸比为$\lambda_1$, 厚度方向拉伸比为$1/\lambda_1$. 值得注意的是, 纯剪切变形和简单剪切变形是不一样的, 具体可参加Thiel等[33 ] 的相关工作. ...
... 图3 给出了本文所建立的模型和八链模型对Treloar[22 ] 所开展的关于硫化橡胶的实验的模拟结果, 相应的模型参数和模拟误差见表1 . 由图3 (a)可见, 考虑了缠结效应的超弹性模型能同时准确的模拟单轴、纯剪切和等双轴拉伸的实验结果, 与之相比, 八链模型虽然能较好地预测硫化橡胶在单轴拉伸的应力响应, 但对等双轴拉伸的结果的预测明显偏低(图3 (b)). 此外, 考虑缠结效应的模型也能更好地体现单轴和纯剪切实验中应力的区别. 图4 (a)和图4 (b)给出了关于TPE橡胶的实验和相应的模拟结果, 其主要结论与硫化橡胶是一致的. 表1 的实验结果和模拟结果的误差值也进一步证实本文所建立的本构模型的预测能力明显好于八链模型. ...
Hyperelastic models for rubber-like materials: consistent tangent operators and suitability for Treloar's data
3
2012
... 针对Treloar[22 ] 关于硫化橡胶的单轴、纯剪切和等双轴加载的经典实验数据, Steinmann等[23 ] 详细评估了14种唯象模型和分子统计理论模型的预测能力, 发现这些广泛应用的模型并不能很好地预测硫化橡胶在多种变形模式下的力学响应. 针对经典超弹性模型的不足之处, 部分学者[24 -28 ] 提出了引入缠结约束效应, 其主要的建模思路是将缠结约束效应用Doi 和Edwards[29 ] 所提出的管模型(tube model)来近似表征. 相关模拟结果显示, 引入缠结约束效应的超弹性模型能更为准确地预测橡胶的力学行为, 但上述模型也有相应的不足之处, 例如, Miche等[25 ] 所建立的考虑缠结效应的超弹性模型是基于非仿射假设, 需开展全方向积分计算, 而Davodson和Goubourne[27 ] 以及Xiang等[28 ] 所建立的缠结约束模型的自由能是主方向拉伸比的函数, 这导致这些模型有限元植入方面不够方便. ...
... 针对Treloar的实验数据, Treloar[34 ] 和Steinmann等[23 ] 系统地评估了经典唯象模型(Neo-Hookean模型, Ogden模型, Mooney-Rivlin模型, Gent模型, Yeoh模型等)和基于分子统计模型(三链模型、四链模型、八链模型、仿射模型等)的预测能力, 结果显示这些模型均不能同时较好地预测单轴、纯剪切和等双轴的实验结果. 为了与本文所建立的缠结模型进行对比, 进一步采用以下两个三参数模型来模拟TPE橡胶的实验结果. 第一个模型是Yeoh模型, 其自由能形式为 ...
... 大量的实验数据显示, 当用八链模型来模拟单轴变形实验时, 八链模型能很好地预测实验结果, 但本文和其他相关论文[8 ,23 ] 的研究结果都显示当需要同时考虑橡胶的多种加载模式时, 八链模型不能较好地描述实验结果, 而考虑缠结效应的超弹性模型能克服八链模型的不足之处. ...
A generalized tube model of rubber elasticity and stress softening of filler reinforced elastomer systems
2
2000
... 针对Treloar[22 ] 关于硫化橡胶的单轴、纯剪切和等双轴加载的经典实验数据, Steinmann等[23 ] 详细评估了14种唯象模型和分子统计理论模型的预测能力, 发现这些广泛应用的模型并不能很好地预测硫化橡胶在多种变形模式下的力学响应. 针对经典超弹性模型的不足之处, 部分学者[24 -28 ] 提出了引入缠结约束效应, 其主要的建模思路是将缠结约束效应用Doi 和Edwards[29 ] 所提出的管模型(tube model)来近似表征. 相关模拟结果显示, 引入缠结约束效应的超弹性模型能更为准确地预测橡胶的力学行为, 但上述模型也有相应的不足之处, 例如, Miche等[25 ] 所建立的考虑缠结效应的超弹性模型是基于非仿射假设, 需开展全方向积分计算, 而Davodson和Goubourne[27 ] 以及Xiang等[28 ] 所建立的缠结约束模型的自由能是主方向拉伸比的函数, 这导致这些模型有限元植入方面不够方便. ...
... 当前, 国内外相关学者[24 -28 ] 也建立了相应的包含缠结约束效应的超弹性模型, 其主要建模思路均是基于管模型, 本文将这些模型进行对比分析. Davidson和Goulbourne[27 ] 采用非仿射的管模型给出了如下的缠结约束自由能 ...
A micro-macro approach to rubber-like materials——part I: The non-affine micro-sphere model of rubber elasticity
2
2004
... 针对Treloar[22 ] 关于硫化橡胶的单轴、纯剪切和等双轴加载的经典实验数据, Steinmann等[23 ] 详细评估了14种唯象模型和分子统计理论模型的预测能力, 发现这些广泛应用的模型并不能很好地预测硫化橡胶在多种变形模式下的力学响应. 针对经典超弹性模型的不足之处, 部分学者[24 -28 ] 提出了引入缠结约束效应, 其主要的建模思路是将缠结约束效应用Doi 和Edwards[29 ] 所提出的管模型(tube model)来近似表征. 相关模拟结果显示, 引入缠结约束效应的超弹性模型能更为准确地预测橡胶的力学行为, 但上述模型也有相应的不足之处, 例如, Miche等[25 ] 所建立的考虑缠结效应的超弹性模型是基于非仿射假设, 需开展全方向积分计算, 而Davodson和Goubourne[27 ] 以及Xiang等[28 ] 所建立的缠结约束模型的自由能是主方向拉伸比的函数, 这导致这些模型有限元植入方面不够方便. ...
... 针对单根分子链的变形行为, 这里采用Miehe等[25 ] 提出的微观力学模型来进行描述. 该模型的自由能包括两部分, 第一部分是源于分子链自由变形所引起的熵弹性自由能, 第二部分是由于周边分子链缠结约束引起的自由能 ...
Analytical network-averaging of the tube model: Rubber elasticity
1
2016
... 采用同样方式, 将变形后微球微单元的面积与初始面积比的均方值假定为宏观变形管面积收缩比[26 ] , 其中微球上无限小单元变形后面积d$S$与初始未变形面积d$S_{0} $的比$\xi$可表示为[31 ] ...
A nonaffine network model for elastomers undergoing finite deformations
4
2013
... 针对Treloar[22 ] 关于硫化橡胶的单轴、纯剪切和等双轴加载的经典实验数据, Steinmann等[23 ] 详细评估了14种唯象模型和分子统计理论模型的预测能力, 发现这些广泛应用的模型并不能很好地预测硫化橡胶在多种变形模式下的力学响应. 针对经典超弹性模型的不足之处, 部分学者[24 -28 ] 提出了引入缠结约束效应, 其主要的建模思路是将缠结约束效应用Doi 和Edwards[29 ] 所提出的管模型(tube model)来近似表征. 相关模拟结果显示, 引入缠结约束效应的超弹性模型能更为准确地预测橡胶的力学行为, 但上述模型也有相应的不足之处, 例如, Miche等[25 ] 所建立的考虑缠结效应的超弹性模型是基于非仿射假设, 需开展全方向积分计算, 而Davodson和Goubourne[27 ] 以及Xiang等[28 ] 所建立的缠结约束模型的自由能是主方向拉伸比的函数, 这导致这些模型有限元植入方面不够方便. ...
... 这里给出在不同加载条件下两部分的归一化应力, 即相应的应力除以剪切模量. 如图6 所示, 在小应变条件下, 来自熵弹性和缠结效应的归一化应力是相同的. 当变形逐步增大时, 两者之间逐渐偏离. 在单轴拉伸和纯剪切变形情况下, 缠结效应的归一化应力小于相应的熵弹性归一化应力, 且会逐步达到平台并发生软化行为, 这与实验结果相一致[27 ] . 与之不同, 在等双轴拉伸情况下, 缠结效应的归一化应力不出现软化行为, 且在一定的应变范围, 其数值大于熵弹性部分, 直至接近材料的拉伸极限时, 熵弹性归一化应力急剧增加, 其数值将高于缠结约束引起的归一化应力. ...
... 当前, 国内外相关学者[24 -28 ] 也建立了相应的包含缠结约束效应的超弹性模型, 其主要建模思路均是基于管模型, 本文将这些模型进行对比分析. Davidson和Goulbourne[27 ] 采用非仿射的管模型给出了如下的缠结约束自由能 ...
... 在熵弹性模型的基础上, 引入上述3种缠结约束自由能, 均能较好地模拟文献中的实验数据[27 ,28 ] . 因此, 基于当前文献中的实验数据不足以全面评估哪类缠结约束模型能更好地预测橡胶材料在不同加载情况下的变形行为. 亟需开展针对单一橡胶的全面的实验表征, 其实验表征可同时考虑单轴拉伸、压缩、平面应变压缩、纯剪切、非等双轴以及等双轴拉伸变形等. 这样的实验数据将有益于评估各类模型的适用性. ...
A general constitutive model of soft elastomers
5
2018
... 针对Treloar[22 ] 关于硫化橡胶的单轴、纯剪切和等双轴加载的经典实验数据, Steinmann等[23 ] 详细评估了14种唯象模型和分子统计理论模型的预测能力, 发现这些广泛应用的模型并不能很好地预测硫化橡胶在多种变形模式下的力学响应. 针对经典超弹性模型的不足之处, 部分学者[24 -28 ] 提出了引入缠结约束效应, 其主要的建模思路是将缠结约束效应用Doi 和Edwards[29 ] 所提出的管模型(tube model)来近似表征. 相关模拟结果显示, 引入缠结约束效应的超弹性模型能更为准确地预测橡胶的力学行为, 但上述模型也有相应的不足之处, 例如, Miche等[25 ] 所建立的考虑缠结效应的超弹性模型是基于非仿射假设, 需开展全方向积分计算, 而Davodson和Goubourne[27 ] 以及Xiang等[28 ] 所建立的缠结约束模型的自由能是主方向拉伸比的函数, 这导致这些模型有限元植入方面不够方便. ...
... [28 ]所建立的缠结约束模型的自由能是主方向拉伸比的函数, 这导致这些模型有限元植入方面不够方便. ...
... 当前, 国内外相关学者[24 -28 ] 也建立了相应的包含缠结约束效应的超弹性模型, 其主要建模思路均是基于管模型, 本文将这些模型进行对比分析. Davidson和Goulbourne[27 ] 采用非仿射的管模型给出了如下的缠结约束自由能 ...
... Xiang等[28 ] 基于三链模型, 提出了如下的自由能方程来表示缠结约束效应 ...
... 在熵弹性模型的基础上, 引入上述3种缠结约束自由能, 均能较好地模拟文献中的实验数据[27 ,28 ] . 因此, 基于当前文献中的实验数据不足以全面评估哪类缠结约束模型能更好地预测橡胶材料在不同加载情况下的变形行为. 亟需开展针对单一橡胶的全面的实验表征, 其实验表征可同时考虑单轴拉伸、压缩、平面应变压缩、纯剪切、非等双轴以及等双轴拉伸变形等. 这样的实验数据将有益于评估各类模型的适用性. ...
2
1986
... 针对Treloar[22 ] 关于硫化橡胶的单轴、纯剪切和等双轴加载的经典实验数据, Steinmann等[23 ] 详细评估了14种唯象模型和分子统计理论模型的预测能力, 发现这些广泛应用的模型并不能很好地预测硫化橡胶在多种变形模式下的力学响应. 针对经典超弹性模型的不足之处, 部分学者[24 -28 ] 提出了引入缠结约束效应, 其主要的建模思路是将缠结约束效应用Doi 和Edwards[29 ] 所提出的管模型(tube model)来近似表征. 相关模拟结果显示, 引入缠结约束效应的超弹性模型能更为准确地预测橡胶的力学行为, 但上述模型也有相应的不足之处, 例如, Miche等[25 ] 所建立的考虑缠结效应的超弹性模型是基于非仿射假设, 需开展全方向积分计算, 而Davodson和Goubourne[27 ] 以及Xiang等[28 ] 所建立的缠结约束模型的自由能是主方向拉伸比的函数, 这导致这些模型有限元植入方面不够方便. ...
... 采用Doi 和Edwards[29 ] 提出的管模型(图1 )来表征周边分子链缠结约束导致的变形自由能 ...
Beziehungen zwischen elastischen Konstanten und Dehnungsdoppelbrechung hochelastischer Stoffe
1
1942
... 采用Kuhn 和 Grün[30 ] 提出的Langevin统计模型来表示熵弹性所引起的自由能, 其具体形式如下 ...
Note: Strain invariants expressed as average stretches
1
1989
... 采用同样方式, 将变形后微球微单元的面积与初始面积比的均方值假定为宏观变形管面积收缩比[26 ] , 其中微球上无限小单元变形后面积d$S$与初始未变形面积d$S_{0} $的比$\xi$可表示为[31 ] ...
Continuum constitutive modeling for isotropic hyperelastic materials
1
2016
... 采用上述建立的本构理论来模拟文献中关于橡胶材料在单轴和双轴变形条件下的应力响应, 并与相应的Arruda-Boyce八链模型和Neo-Hookean模型进行对比分析. 首先模拟Treloar[22 ] 开展的关于硫化橡胶和Zhao[32 ] 开展的关于TPE橡胶的实验, 上述工作对同一橡胶均同时开展了单轴拉伸、纯剪切和等双轴拉伸实验. 其中纯剪切实验的实验设置与单轴拉伸实验是一致的, 其主要区别在于所采用的试样的宽度远大于长度(一般来说, 宽度/长度 $>10$), 在该条件下, 可认为宽度方向的拉伸比为1, 长度方向拉伸比为$\lambda_1$, 厚度方向拉伸比为$1/\lambda_1$. 值得注意的是, 纯剪切变形和简单剪切变形是不一样的, 具体可参加Thiel等[33 ] 的相关工作. ...
Shear, pure and simple
1
2019
... 采用上述建立的本构理论来模拟文献中关于橡胶材料在单轴和双轴变形条件下的应力响应, 并与相应的Arruda-Boyce八链模型和Neo-Hookean模型进行对比分析. 首先模拟Treloar[22 ] 开展的关于硫化橡胶和Zhao[32 ] 开展的关于TPE橡胶的实验, 上述工作对同一橡胶均同时开展了单轴拉伸、纯剪切和等双轴拉伸实验. 其中纯剪切实验的实验设置与单轴拉伸实验是一致的, 其主要区别在于所采用的试样的宽度远大于长度(一般来说, 宽度/长度 $>10$), 在该条件下, 可认为宽度方向的拉伸比为1, 长度方向拉伸比为$\lambda_1$, 厚度方向拉伸比为$1/\lambda_1$. 值得注意的是, 纯剪切变形和简单剪切变形是不一样的, 具体可参加Thiel等[33 ] 的相关工作. ...
1
1975
... 针对Treloar的实验数据, Treloar[34 ] 和Steinmann等[23 ] 系统地评估了经典唯象模型(Neo-Hookean模型, Ogden模型, Mooney-Rivlin模型, Gent模型, Yeoh模型等)和基于分子统计模型(三链模型、四链模型、八链模型、仿射模型等)的预测能力, 结果显示这些模型均不能同时较好地预测单轴、纯剪切和等双轴的实验结果. 为了与本文所建立的缠结模型进行对比, 进一步采用以下两个三参数模型来模拟TPE橡胶的实验结果. 第一个模型是Yeoh模型, 其自由能形式为 ...
The properties of rubber in pure homogeneous strain
1
1975
... 本文所建立的模型被进一步用来模拟Jones和Treloar[35 ] 所开展的关于另一类硫化橡胶(记为硫化橡胶B)的实验结果. 其实验设计如下: 橡胶试样先在$e_2$方向上被拉伸至一固定伸长比, 然后在$e_1$方向上开展拉伸实验, 在$e_3$方向上试样不受力. 图5 给出了相应的实验结果, 其中, 当$X$轴的伸长比的数值大于$1/\sqrt{\lambda_2}$时, $X$轴对应的是$\lambda_1$, $Y$轴对应$\sigma_1-\sigma_2$, 而当$X$轴的数值小于$1/\sqrt{\lambda_2}$时, $X$轴对应$\lambda_3$, 而$Y$轴对应$-\sigma_2$. 在拟合过程中, 我们发现相对误差值随着拉伸极限$N$的增大而降低, 因此这里选择在Neo-Hookean的模型的基础上考虑缠结效应, 即采用式(13)来拟合实验结果, 相关的模型参数见表1 . 如图5 (a)所示, 考虑了缠结效应的本构模型能准确地预测实验结果, 而不考虑缠结效应的Neo-Hookean模型只能在一定的变形范围内与实验结果相吻合, 而总体的模拟效果较差. 在本文中, 缠结约束部分是基于柯西-格林应变张量的第二应变量$I_2$, 在体积不可压条件下, $I_2$可表示为$I_2=1/\lambda_1^2+1/\lambda_2^2++1/\lambda_3^2$, 当$\lambda_3$值较小时, $I_2$随着$\lambda_3$的减小而迅速增大, 进而导致一个较大的应力响应, 这与实验结果是一致的. Neo-Hookean模型仅依赖于柯西-格林应变张量第一不变量, 因此不能够预测当$\lambda_3$值较小时, 随着$\lambda_3$减小应力响应的迅速增大. ...
Inhomogeneous swelling of a gel in equilibrium with a solvent and mechanical load
1
2009
... 本文所建立的宏观本构关系仅依赖于柯西-格林应变张量的不变量, 因此相比于文献中考虑缠结约束的超弹性模型在有限元植入上更为方便, 例如, 常见的商业软件ABAQUS的UHYPER子程序可通过直接输入基于应变不变量的自由能进行有限元分析, 而无需编写相应的基于刚度矩阵的用户自定义子程序, 这为软材料的超弹性行为的分析提供了方便[36 ] . 目前我们正在开展橡胶材料在多种变形条件下的变形行为和具有复杂几何尺寸试样的力学表征, 以更为全面地评估各类超弹性本构模型. ...