引言
太阳系内的小行星主要分布于火星轨道与木星轨道之间,也有一部分小行星会穿越地球轨道威胁到地球上的生命.诸多严重的小行星撞击地球事件(如6500万年前的K-T事件[1 ] 、1908年通古斯大爆炸事件[2 ] 、2013年车里雅宾斯克事件[3 ] 等)已引发人类对于行星防御的关注.在能够对近地小行星提前预警的前提下,摧毁小行星结构或者偏转小行星轨道是避免其撞击地球的两种基本方式[4 ] .目前已提出的防御手段主要有核爆[5 ] 、动能撞击、激光烧蚀[6 ] 、拖船[7 ] 、引力拖船[8 ] 、离子束牵引[9 ] 等,其中动能撞击技术是目前最易实现且成熟度较高的手段.
动能撞击技术是指撞击器以一定的速度和角度撞击小行星, 使小行星轨道发生改变.2005年美国实施了深度撞击(deep impact)任务[10 ] , 任务释放一颗约370kg的撞击器, 以约10.3 km/s的相对速度撞击“Tempel 1”彗星的核,撞击后的3年内该彗星位置变化了约10 km; 双小行星重定向测试任务(doubleasteroid redirection test, DART)将于2021年7月执行, 由一个约650kg的撞击器以约6.65 km/s的相对速度撞击小行星 Didymos的卫星, 预计产生0.8$\sim$2mm/s的速度改变量(取决于动量传递因子的大小,动量传递因子用于描述溅射物对动量传递的影响[11 ] ).Atchison等[12 ] 总结了DART轨道设计需求,包括撞击日期、撞击角度以及为了满足光学需求的太阳相位角需求;Ozimek和Atchison[13 ] 研究了DART轨道中逃逸段的月球借力方法;Atchison等[14 ] 介绍了DART的终端制导、载荷等信息.
早期对于动能撞击处置小行星的研究, 多关注动能撞击对小行星的轨道偏转机理,一般不考虑运载能力约束.Ahrens和Harris[15 ] 的研究表明切向偏转速度增量对偏转小行星轨道效率最高,并估计了偏转小行星所需的速度增量, 但如果小行星在撞击地球前会近距离飞掠大行星,实际所需的偏转速度增量会有所降低[16 ] ;Park和Ross[17 ] 推导了小行星与地球距离的一、二阶导数表达式,发现只有在撞击前某些特殊时刻最优偏转速度才平行于小行星速度方向;Ross等[18 ] 基于圆锥曲线拼接法考虑了地球引力对最优偏转速度增量的影响.Carusi等[16 ] 提出一种估算在多体动力学模型下将小行星偏转1倍地球半径所需速度增量的方法,但仅研究了切向速度增量; Kahle等[19 ] 对其方法进行了改进,在多体问题下同时优化了切向、径向的速度增量,发现Carusi等[16 ] 的“切向速度增量”结论仅在二体阶段下是合理的,当小行星近距离飞掠行星时, 最优速度增量方向并不是切向的了,近距离飞掠行星时受行星引力影响可能会降低偏转所需的速度增量.Vasile和Colombo[20 ] 发现当偏转时间小于小行星公转周期时,最优速度增量的径向分量占主导, 当偏转时间更大时, 切向分量占主导.Yamaguchi和Yamakawa[21 ] 提出了IGMs (impact-geometry maps), 用于可视化偏转距离与IG (impact geometry)(小行星速度与航天器撞击速度的内积)之间的关系. Greenstreet等[22 ] 基于统计的方法, 发现与行星发生近距离飞掠的小行星,所需的偏转速度增量可以非常小.
动能撞击任务设计的一种优化指标是最大化小行星被偏转前后的近地点距离改变量(偏转距离),换言之是使小行星被偏转后的近地点尽可能的离地球更远[23 ] .采用多体型计算小行星被偏转前后的近地点距离, 可以提供关于问题最完整的解,但轨道演化和近地点搜索计算过程中会产生冗余计算量,在任务设计初期的快速搜索研究(quick scoping studies)中,多体数值积分是不必要的[24 ] .采用二体模型替代多体模型的方法可以显著降低轨道演化过程的计算量,但在搜索近地点的过程中仍存在冗余计算量.为同时降低轨道演化和近地点搜索的计算量,可采用解析偏转模型对偏转距离进行估算.
除了Ahrens和Harris[15 ] 提出的偏转距离线性解析模型外,目前使用较为广泛的的偏转距离解析模型还有:2001年Conway[25 ] 提出了基于拉格朗日系数解析递推偏转距离的方法(后文简称Conway模型);2007年Izzo[26 ] 基于几何法推导了偏转距离的解析模型(后文简称Izzo模型);2008年Vasile和Colombo[20 ] 基于高斯摄动方程推导了偏转距离的解析模型(后文简称Vasile模型),其相比于Conway模型具有更高的计算效率.Vasile模型是目前使用较为广泛的解析偏转模型, 文献[27 ,28 ]均基于Vasile模型,以偏转距离为指标优化了动能撞击任务.但是目前尚无研究对偏转距离解析模型的最优性进行分析.
小行星被偏转前后, 虽然轨道根数发生了改变,但到达地球近地点的时刻可能变化不大.本文首先研究了近地点时刻受偏转影响的变化规律, 提出在动能撞击任务的设计初期,可以假定小行星被偏转前后近地点时刻不变(近似偏转模型),由此可以省略掉近地点时刻搜索的计算量. 相比于解析模型,这种近似模型可以在提升最优性的同时、降低求解复杂性. 考虑运载约束,将化学推进变轨简化为脉冲推力变轨,建立了直接转移(两脉冲及三脉冲)和行星借力飞行转移(单次及两次借力)的动能撞击轨道优化模型.以偏转小行星Apophis为例, 设计了动能撞击任务,研究了利用两脉冲/三脉冲直接转移、单次/两次行星借力飞行技术是否可以提升偏转距离.通过对比二体动力学模型与高精度动力学模型对计算偏转距离的误差,进一步探讨了在动能撞击任务设计过程中采用二体动力学模型的合理性.
1 偏转距离的现有计算方法
本文中偏转距离的定义为: 偏转前后小行星近地点(closest-approach, CA)距离的改变量(偏转距离). 偏转距离$\delta \rho _{CA} $的数学表达式为
(1) $\delta \rho _{CA} =\left\| {{{\boldsymbol \rho }'}\left( {{t}'_{CA} } \right)} \right\|-\left\| {{\boldsymbol \rho }\left( {t_{CA} } \right)} \right\|$
其中, ${{\boldsymbol \rho }'}\left( {{t}'_{CA} } \right)$和${\boldsymbol \rho }\left({t_{CA} } \right)$分别表示小行星被偏转后、偏转前的近地点地心位置矢量.当$\left\| {{\boldsymbol \rho }\left( {t_{CA} } \right)}\right\|>0$时表示偏转会使小行星的近地点距离增大, 偏转是有利的; 反之,$\left\| {{\boldsymbol \rho }\left( {t_{CA} } \right)}\right\|<0$表示偏转是不利的. $t_{CA} $的求解形式为
(2) $t_{CA} =\mathop{argmin}\limits_{t\in \left[ {a,b} \right]} \left( {\left\| {{\boldsymbol \rho }\left( t \right)} \right\|} \right)$
其中, ${\boldsymbol \rho }\left( t \right)$为$t$时刻小行星的地心位置矢量,$a$和$b$为时间搜索窗口的下界和上界. 关于偏转距离的计算方法,本节将介绍数值模型、两种经典解析模型(Vasile模型和Izzo模型).
1.1 数值模型
对于小行星的高精度轨道演化动力学模型,本文考虑的摄动力有八大行星引力、月球引力、四大主带小行星引力(Ceres, Vesta, Pallas, Hygiea)、相对论效应(generalrelativity, GR)、地球非球形引力J2、太阳光压(solar radiation pressure,SRP)以及Yarkovsky效应(yarkovsky effect, YE).高精度动力学模型的数学表达式如下所示
(3) $\frac{{d}^{2}{r}}{{d}t^{2}}=-\frac{\mu_{s} }{\left| {{r}} \right|^{3}}{r}-\sum\limits_{i=1}^{8} {\mu_{pi} \left( {\frac{1}{\left| {{d}_{pi} } \right|^{3}}{d}_{pi} +\frac{1}{\left| {{\boldsymbol \rho }_{pi} } \right|^{3}}{\boldsymbol \rho }_{pi} } \right)} +\\ {a}_{moon} +{a}_{Asteroid} +{a}_{GR} +{a}_{J2} {+a}_{SRP} +{a}_{YE}$
其中, ${d}_{pi} $表示第$i$个行星地日心矢量, ${\boldsymbol \rho }_{pi}$表示第$i$个行星到小行星的矢量. 行星和月球的星历调用JPLDE430历表[29 ] , 小行星星历调用JPL Horizons On-Line EphemerisSystem[30 ] 公布的真实星历.动力学模型中考虑非引力项(太阳光压、Yarkovsky效应)的原因为:太阳光压对一些尺寸较小的小行星影响较大, 对于尺寸较大的小行星,Yarkovsky效应不能忽略[31 -33 ] . 利用Runge-Kutta-Fehlberg7(8)积分器[34 -35 ] 对轨道运动方程的一阶形式进行数值积分,并采用一种一维最小值算法[36 ] 求解近地点距离,因为这种算法不需要地心距离的一阶导数信息.
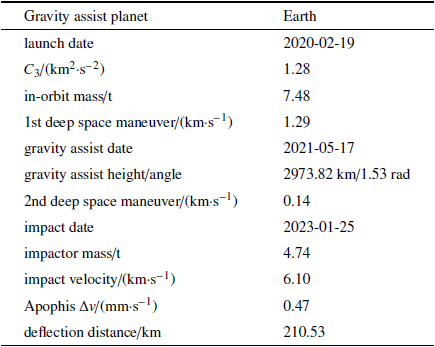
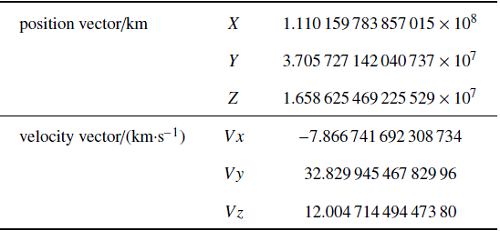
为验证本文高精度轨道预报方法的准确性,本节对小行星Apophis在2029年的近距离飞掠地球事件进行了预报, 并与JPL公布的结果[30 ] 进行了对比.小行星Apophis是目前行星防御领域高度关注的小行星,根据JPL[30 ] 公布的最新信息(表1 ),Apophis将在2029年4月13日与地球近距离飞掠, 近地点距离为0.00025AU,其质量约为$6.1\times10^{7}$ t. 将Apophis在2019年1月1日 00:00:00(TDB)的位置速度(坐标系为ICRF)作为积分起点.
表2 给出了JPL公布的结果与本文预报的结果. 仿真结果表明,利用本文方法计算的Apophis近地事件, 时间误差约为0.02 s, 位置误差约为1 km.
理论上, 在动能撞击轨道优化问题中,需要利用高精度动力学模型进行递推以保证最优性,但是各种摄动力的引入会显著降低求解效率.采用二体模型(仅考虑太阳引力)替代多体模型, 可以显著降低轨道演化过程的计算量,但仍需数值计算小行星的近地点. 二体模型的数学表达式如下所示
(4) $\frac{{d}^{2}{r}}{{d}t^{2}}=-\frac{\mu_{s} }{\left| {{r}} \right|^{3}}{r}$
假定小行星被偏转前后日心位置${r}\left( {t_{d} }\right)$不变、仅日心速度${v}\left( {t_{d} } \right)$发生改变,即偏转使小行星状态由$\left( {{r}\left( {t_{d} }\right),{v}\left( {t_{d} } \right)} \right)$改变为$\left({{r}\left( {t_{d} } \right),{v}'\left( {t_{d} } \right)}\right)$. 将偏转前后小行星的状态利用二体模型由偏转时刻($t_{d})$解析递推($f_{kepler} )$至近地点时刻($t_{CA} )$, 可求得小行星近地点距离. 小行星被偏转前近地点位置的日心矢量${r}\left( {t_{CA} }\right)$及地心矢量${\boldsymbol \rho }\left( {t_{CA} } \right)$表示为
(5) $\left. {\begin{array}{l} \left( {{r}\left( {t_{CA} } \right),{v}\left( {t_{CA} } \right)} \right)=f_{kepler} \left( {{r}\left( {t_{d} } \right),{v}\left( {t_{d} } \right),\left( {t_{CA} -t_{d} } \right)} \right) \\ {\boldsymbol \rho }\left( {t_{CA} } \right)={r}\left( {t_{CA} } \right)-{r}_{E} \left( {t_{CA} } \right) \\ \end{array}} \right\}$
小行星被偏转后近地点位置的日心矢量${r}'\left( {t_{CA}' }\right)$及地心矢量${{\boldsymbol \rho }'}\left( {{t}'_{CA} } \right)$表示为
(6) $\left.\begin{array}{l}\left(\boldsymbol{r}^{\prime}\left(t_{\mathrm{CA}}^{\prime}\right), \boldsymbol{v}^{\circ}\left(t_{\mathrm{CA}}^{\prime}\right)\right)=f_{\mathrm{kepler}}\left(\boldsymbol{r}\left(t_{\mathrm{d}}\right), \boldsymbol{v}^{\prime}\left(t_{\mathrm{d}}\right),\left(t_{\mathrm{CA}}^{\prime}-t_{\mathrm{d}}\right)\right) \\\boldsymbol{\rho}^{\prime}\left(t_{\mathrm{CA}}^{\prime}\right)=\boldsymbol{r}^{\prime}\left(t_{\mathrm{CA}}^{\prime}\right)-\boldsymbol{r}_{\mathrm{E}}\left(t_{\mathrm{CA}}^{\prime}\right)\end{array}\right\}$
其中, 近地点时刻$t_{CA} $采用一维最小值算法[36 ] 对式(2)进行求解,可得偏转距离为
(7) $\delta \rho _{CA} =\bigg\| {{{\boldsymbol \rho }'}\left( {{t}'_{CA} } \right)} \bigg\|-\bigg\| {{\boldsymbol \rho }\left( {t_{CA} } \right)} \bigg\|$
1.2 解析模型
Vasile模型可以解析计算小行星被偏转前后MOID (minimum orbit intersection distance)的改变量.其基本思想是将MOID点处位置矢量的改变量分解为径向、切向及法向分量
(8) $\delta {r}=\left[ {\delta s_{r} ,\delta s_{\theta } ,\delta s_{h} } \right]$
(9) $\left.\begin{array}{rl}\delta s_{r} \approx \frac{r}{a} \delta a+\frac{a e \sin \theta_{\mathrm{MOID}}}{\eta} \delta M-a \cos \theta_{\mathrm{MOID}} \delta e \\\delta s_{\theta} \approx \frac{r}{\eta^{3}}\left(1+e \cos \theta_{\mathrm{MOID}}\right)^{2} \delta M+r \delta \omega+ \\ \frac{r \sin \theta_{\mathrm{MOID}}}{\eta^{2}}\left(2+e \cos \theta_{\mathrm{MOID}}\right) \delta e+r \cos i \delta \Omega \\\delta s_{h} \approx r\left(\sin \theta_{\mathrm{MOID}}^{*} \delta i-\cos \theta_{\mathrm{MOID}}^{*} \sin i \delta \Omega\right)\end{array}\right\}$
其中, $\theta_{MOID} $表示近地点时小行星的日心真近点角, $\theta_{MOID}^{\ast } =\theta_{MOID} +\omega $.轨道根数改变量与偏转速度增量之间的关系可由高斯摄动方程计算,由于撞击改变了小行星的轨道周期,因此近地点处的平近点角改变量还需考虑由于轨道周期改变而产生的长期演化影响,公式如下
(10) $\delta M=-\frac{b}{eav}\left[ {2\left( {1+\frac{e^{2}r}{p}} \right)\sin \theta_{d} \delta v_{t} +\frac{r}{a}\cos \theta_{d} \delta v_{n} } \right] +\\ \delta n\sigma$
其中, $\theta_{d} $表示撞击时小行星的日心真近点角, $\sigma$表示撞击时刻距离近地点时刻的时间.
虽然MOID概念并不等同于近地点距离[20 ,23 ] , 但通过观察公式可以发现,如果将MOID点真近点角$\theta_{MOID} $替换为近地点真近点角$\theta_{CA} $,则该公式可以用于估算近地距离改变量. $\delta {\boldsymbol \alpha }\left( {t_{d} }\right)$表示偏转位置处小行星轨道根数的改变量, $\delta {v}\left({t_{d} } \right)$表示偏转位置处小行星速度的改变量, $\delta {r}\left({t_{CA} } \right)$表示近地点位置的偏移量, $A_{CA} $和$G_{d}$表示状态转移矩阵
(11) $\left. {{\begin{array}{l} {\delta {r}\left( {t_{CA} } \right)=A_{CA} \delta {\boldsymbol \alpha }\left( {t_{d} } \right)} \\ {\delta {\boldsymbol \alpha }\left( {t_{d} } \right)=G_{d} \delta {v}\left( {t_{d} } \right)} \\ \end{array} }} \right\}$
近地点距离的改变量$\delta \rho _{CA} $可表示为
(12) $\delta \rho _{CA} \approx \left\| {{\boldsymbol \rho }\left( {t_{CA} } \right){+}\delta {r}\left( {t_{CA} } \right)} \right\|-\left\| {{\boldsymbol \rho }\left( {t_{CA} } \right)} \right\|$
其中, ${\boldsymbol \rho }_{CA} $表示偏转前的近地点矢量.
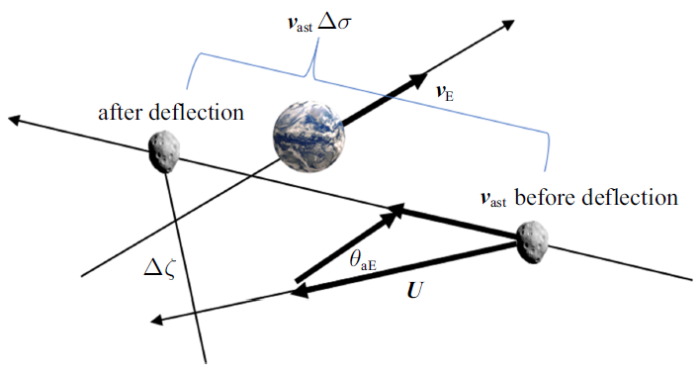
Izzo模型的基本思想是,通过计算偏转前后近地点时间的差异来计算小行星在B平面上的偏移量$\Delta \xi $.其中,B平面定义为垂直于小行星进入地球影响球双曲线速度${U}$且经过地球质心的平面[37 ] , Öpik[38 ] 在B平面上定义了$\left( {\xi ,\eta ,\zeta } \right)$坐标系:$\eta $轴沿${U}$的方向, $\zeta$轴为地球日心速度在B平面上投影的反方向, $\xi $轴的指向由右手定则给出,在该坐标系下$\xi $坐标可代表小行星轨道与地球轨道的MOID值,B平面上的偏移量$\Delta \xi $可用来描述小行星的偏转距离. 在日心视角下,小行星被偏转前后近地点位置的几何关系如图1 所示.
图1
图1
Izzo模型原理示意图
Fig. 1
Schematic diagram of Izzo model
图1 中, $\Delta \sigma $表示偏转前后近地点时刻的改变量, ${v}_{ast}$表示小行星的近地点日心速度,${U}$表示小行星进入地球影响球时的相对速度, $\psi$表示小行星速度${v}_{ast} $与${U}$之间的夹角, $\theta_{aE}$表示地球速度${v}_{E} $与${U}$夹角的补角. $\Delta \xi$表示小行星被撞击后的偏转距离, 按照图中的几何关系, 可建立偏移量$\Delta \xi$与交会时刻改变量$\Delta \sigma $之间的等式如下
(13) $\Delta \xi =v_{ast} \Delta \sigma \sin \psi =v_{E} \Delta \sigma \sin \theta _{aE}$
经过对$\Delta \sigma$表达式的推导(具体步骤参考文献[26 ]),可将上式整理如下
(14) $\Delta \xi =\beta \frac{3a_{ast} v_{E} \sin \theta_{aE} }{\mu_{s} }\frac{m_{sc} }{m_{sc} +m_{ast} }\sigma \left( {{U}_{sc} \cdot {v}_{ast} } \right)$
其中, ${U}_{sc} $表示撞击时撞击器相对于小行星的速度.
Izzo模型可以比较直观地给出偏转距离的影响因素,比如小行星本身的物理属性(小行星质量$m_{ast} $、动量传递因子$\beta$等)、小行星与地球的轨道关系(小行星半长轴$a_{ast}$、近地点时地球的速度$v_{E} $等)以及轨道优化结果(撞击器质量$m_{sc}$、偏转时间$\sigma $、撞击速度${U}_{sc} $等).该公式的最后一项点乘表示在偏转时间较长的情况下, 在小行星速度增量的切向分量是影响偏转距离的主要因素.另外需注意到, Izzo模型只能计算小行星在B平面内的偏移量,并不等于近地点距离的改变量,因此当采用该模型估算真实近地点距离改变量时会出现偏差.图2 展示了一种利用Izzo模型计算产生偏差的情况.
图2
图2
Izzo模型产生偏差的情况
Fig. 2
Deviation of Izzo model
在该情况下, 即使偏转使小行星产生了较大的$\Delta \xi $,但实际上小行星被偏转后近地距离减小了. 也就是说,Izzo模型无法回答小行星被撞击后近地点距离会更近还是更远的问题.
2 近地点时刻预估近似模型
如1.1节所述, 求解小行星近地点距离改变量的本质在于求出偏转前后的近地点时刻.如果能够提前估算出小行星被撞击后近地点的时刻,那么就可以利用轨道解析递推模型, 快速计算出被偏转后的近地点矢量.下面通过公式推导分析近地点时刻的影响因素.
以Izzo模型为基础, 在已知小行星轨道根数的情况下,撞击时刻与近地点时刻之间的时间间隔$\sigma $可由下式计算
(15) $\sigma =t_{CA} -t_{d} =\frac{\Delta M_{ast} }{n_{ast} }$
其中, $t_{d} $为偏转时刻, $\Delta M_{ast} $为平近点角差值, $n_{ast} $为转速.对上式取微分并忽略掉短期影响项后得
(16) $\Delta \sigma \approx \frac{{d}\left(\Delta {M_{ast} } \right)}{n_{ast} }-\frac{\Delta M_{ast} }{n_{ast}^{2}}{d}n_{ast} \approx -\frac{\sigma }{n_{ast} }{d}n_{ast}$
(17) $\mathrm{d} n_{\mathrm{ast}} \approx \sqrt{\frac{\mu}{\left(a_{\mathrm{ast}}+\delta a_{\mathrm{ast}}\right)^{3}}}-\sqrt{\frac{\mu}{a_{\mathrm{ast}}^{3}}}$
(18) $\delta a_{\mathrm{ast}} \approx \frac{2 a_{\mathrm{ast}}^{2} v_{\mathrm{ast}}}{\mu} \delta v_{\mathrm{t}}$
式中, $a_{ast} $为小行星的轨道半长轴, $v_{ast} $为小行星被撞击时的日心速度, $\delta v_{t} $为小行星被撞后产生的切向速度增量. 对上式进行整理后,可得近地点时间改变量的解析表达式如下
(19) $\Delta \sigma \approx \frac{\sigma }{n_{ast} }\left[ {\sqrt {\frac{\mu }{a_{ast}^{3}}} -\sqrt {\frac{\mu^{4}}{\left( {\mu a_{ast} +2a_{ast} ^{2}v_{ast} \delta v_{t} } \right)^{3}}} } \right]$
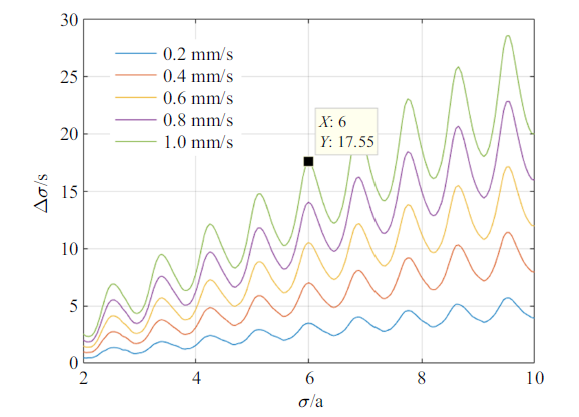
经过推导可以发现, 在小行星速度增量的各分量中,主要是切向分量影响近地点时刻的改变量. 以偏转Apophis为例,下面研究了当撞击产生不同的切向速度时, 对近地点时刻的影响.以Apophis在二体模型下求得的2029年近地点时刻为参考(2029-04-13 21:40:09),当撞击使Apophis产生不同的切向速度增量($\delta v_{t} =0.2\sim 1$ mm/s)时, Apophis近地点时间改变量$\Delta \sigma $随偏转时间$\sigma$ (2$\sim$10 a)的变化趋势, 如图3 所示.
图3
图3
近地点时刻改变量的变化曲线
Fig. 3
Change of perigee epoch
图3 中坐标为(6, 17.55)点的含义为: 在Apophis到达近地点前6年(2023/4/1521:40:08)时进行撞击, 如果撞击使Apophis产生的切向速度增量为1 mm/s,那么将会使Apophis在2029年的近地点时刻晚17.55 s,也就是Apophis被撞击后的近地点时刻为2029/4/13 21:40:26. 从这幅图,可以获得两方面的信息: 第一方面, 在10年预警时间的情况下,单颗动能撞击器能使Apophis近地点时刻改变不到30 s; 第二方面, 由Izzo模型可知,$\Delta \sigma $与偏转距离成正比, 因此随着偏转时间$\sigma $的增大,近地点距离改变量(偏转距离)整体呈现波动上升的趋势.
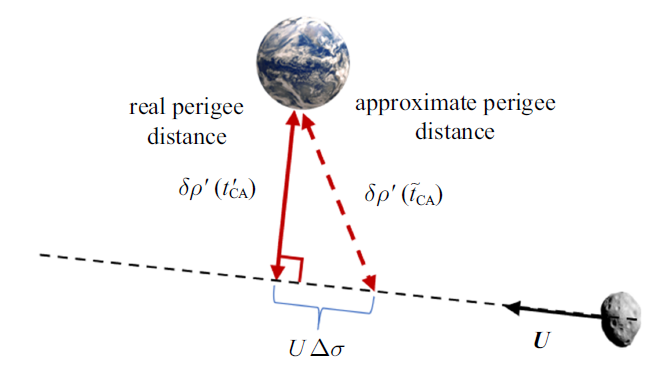
下面仅着眼于偏转后的轨道, 分析以不同时刻计算近地点时,近地近地距与真实近地距的差异. 小行星进入地球影响球后,由于相对速度较高(数千米每秒), 其运动轨迹近乎直线. 小行星被偏转后,在地球影响球内的运动轨迹如图4 所示.其中, ${U}$表示小行星进入地球影响球时的相对速度, ${t}'_{CA}$表示被偏转后的真实近地点时刻, $\tilde{{t}}_{CA} $表示近似近地点时刻,$\tilde{{t}}_{CA} ={t}'_{CA} +\Delta \sigma $. 近似后的近地距$\delta \rho '\left( {\tilde{{t}}_{CA} } \right)$满足下面等式
图4
图4
小行星真实近地距与近似近地距
Fig. 4
Real perigee distance and approximate perigee distance
(20) $\delta \rho '\left( {\tilde{{t}}_{CA} } \right)\mbox{=}\sqrt {\left( {\delta \rho '\left( {{t}'_{CA} } \right)} \right)^{2}+\left( {U\Delta \sigma } \right)^{2}}$
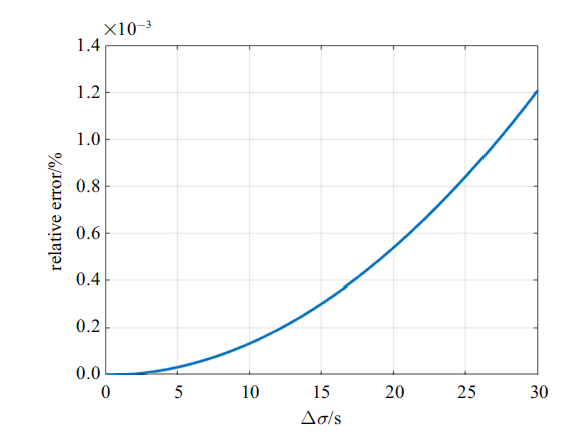
根据1.1节的数值模型, 可求得Apophis进入地球影响球的相对速度$\left\|{{U}} \right\|\approx 5.9$ km/s, 假设被偏转后的真实近地距离为36,000 km,计算当近地点时间改变量$\Delta \sigma \in \left[ {0,30} \right]$ s时,近似近地距与真实近地距之间的相对误差, 计算结果如图5 所示.
图5
图5
近似近地距与真实近地距之间的相对误差
Fig. 5
Relative error between real perigee distance and approximate perigee distance
由图5 可知, 在近地点改变时间小于30 s时,近似近地距与真实近地距之间的相对误差不足0.01%. 例如, 当近地点时刻相差30 s时, 近似近地距为36,000.4 km, 与真实近地距差别小于1 km. 近地距越大,二者之间的误差越小.
因此, 对于本文偏转Apophis算例, 在任务设计初期,可以忽略偏转前后小行星近地点时间的改变量, 即${t}'_{CA} \approx t_{CA} $.小行星的近地点距离改变量可由下面的近似模型进行估算
(21) $\delta \rho _{CA} \approx \left\| {{{\boldsymbol \rho }'}\left( {t_{CA} } \right)} \right\|-\left\| {{\boldsymbol \rho }\left( {t_{CA} } \right)} \right\|$
其中$\left\| {{{\boldsymbol \rho }'}\left( {t_{CA} } \right)}\right\|$表示小行星被偏转后, 在偏转前近地点时刻$t_{CA} $处的地心矢量.依据该模型, 已知撞击后小行星的轨道根数, 可以解析地快速求得$t_{CA}$时刻轨道根数, 省略了用于搜索近地点时刻的计算量.
3 动能撞击任务设计与优化建模
动能撞击任务流程图如图6 所示. 本章将首先建立航天器(撞击器)轨道转移模型,然后建立动能撞击任务优化模型, 最后介绍本文采用的优化方法.
图6
图6
动能撞击任务流程
Fig. 6
Process of a kinetic impactor mission
3.1 转移模型
本文采用圆锥曲线拼接法求解行星际转移轨道.圆锥曲线拼接法的基本原理为将转移轨道按照天体引力影响球进行分段,航天器在影响球内只考虑中心天体的引力,最后通过航天器在影响球边界处的状态对多段圆锥曲线进行拼接,天体影响球边界的相对速度称为逃逸速度或双曲线超速.该简化算法在深空轨道设计中是通用且高效的[39 ] .下面对两脉冲转移模型、三脉冲转移模型、借力飞行转移模型进行建模.
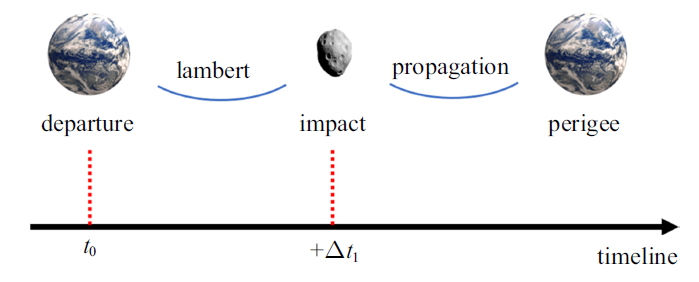
首先, 航天器在$t_{0} $时刻从地球逃逸, 经过$\Delta t_{1}$天后与撞击危地小行星. 假定转移期间不施加任何速度增量,由运载火箭直接发射送入撞击轨道(图7 ).
图7
图7
两脉冲直接转移模型
Fig. 7
Two-impulse direct transfer model
通过求解Lambert问题[40 ] ,可以计算出在地球影响球边界处的逃逸速度$v_{\infty }$以及航天器撞击小行星的相对速度${U}_{sc} $, 对应的数学表达式为
(22) $\left. \begin{array}{l} \left( {{v}_{0} ,{v}_{f} } \right)=L\left( {{r}_{0} ,{r}_{f} ,t_{1} } \right) {v}_{\infty } ={v}_{0} -{v}_{E} \left( {t_{0} } \right) \\ {U}_{sc} ={v}_{f} -{v}_{ast} \left( {t_{0} +t_{1} } \right) \\ \end{array} \right\}$
其中, ${r}_{0} $和${r}_{f} $分别表示航天器在$t_{0} $和$t_{0}+t_{1} $时的日心位置矢量, ${v}_{0} $和${v}_{f}$为对应的日心速度矢量, ${v}_{E} $和${v}_{ast}$分别表示地球和小行星的日心速度矢量. ${v}_{\infty }$可由运载火箭提供, 对应的$C_{3} $为
(23) $C_{3} =\left\| {{v}_{\infty } } \right\|^{2}$
假设转移过程不施加任何机动, 则航天器在撞击时的质量等于发射入轨时的质量
(24) $m_{sc} \left( {t_{d} } \right)=m_{sc} \left( {t_{0} } \right)$
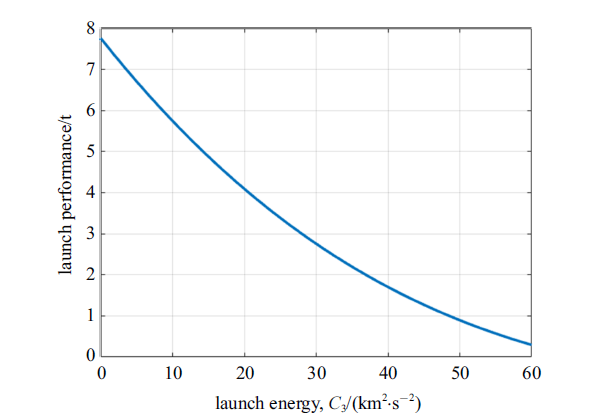
其中, 撞击时刻$t_{d} =t_{0} +t_{1} $, $m_{sc} \left({t_{0} } \right)=f\left( {C_{3} } \right)$. $f\left( {C_{3} }\right)$为运载能力拟合公式, CZ-5运载火箭的运载能力曲线如图8 所示.
图8
图8
长征五号运载能力曲线
Fig. 8
CZ-5's launch performance
当动能航天器撞击目标小行星后, 超高速撞击会导致小行星表面产生溅射物,一部分溅射物最终会再次吸积在小行星表面,另一部分速度较高的溅射物将会从小行星的引力场中逃逸,这种现象类似于火箭产生动力的机理, 将会放大动量传递效应,可采用动量传递因子$\beta $描述溅射物对动量传递的影响[11 ] .假定航天器与小行星的撞击过程为完全非弹性碰撞, 根据动量守恒原理,小行星被撞击后产生的速度改变量可由下式估算[41 -42 ]
(25) ${v}_{ast} =\beta \frac{m_{sc} \left( {t_{d} } \right)}{m_{sc} \left( {t_{d} } \right)+m_{ast} }({v}_{sc} \left( {t_{d} } \right)-{v}_{ast} \left( {t_{d} } \right))$
其中, $m_{sc} \left( {t_{d} } \right)$和${v}_{sc} \left( {t_{d} }\right)$表示航天器在撞击小行星时的质量和速度, $m_{ast} $和${v}_{ast}\left( {t_{d} } \right)$表示小行星被偏转时的质量和速度.本文不考虑溅射物的影响, 因此取$\beta =1$.
综上所述, 给定节点$\left( {t_{0} ,\Delta t_{1} } \right)$后,可以确定航天器在撞击小行星前的速度${v}_{sc} \left( {t_{d} }\right)$及质量$m_{sc} \left( {t_{d} } \right)$.由式(25)计算出小行星被偏转后的状态,从而可计算出小行星被偏转前后的近地点距离改变量.
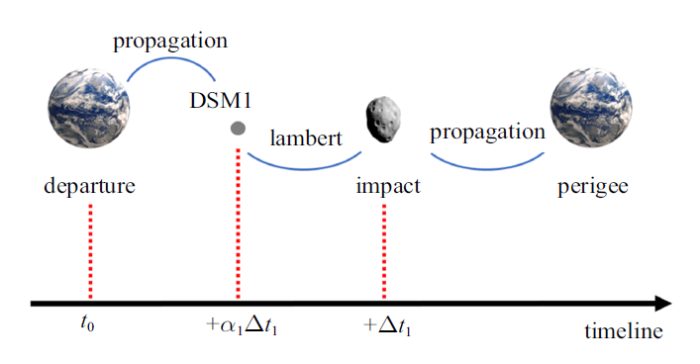
航天器在$t_{0} $时刻从地球逃逸, 经过$\Delta t_{1} $天后撞击危地小行星,期间在$t_{0} +\alpha_{1} \Delta t_{1} $时施加一次深空机动$DSM1$, $\alpha_{1} $的取值范围为0到1 (图9 ).
图9
图9
三脉冲直接转移模型
Fig. 9
Three-impulse direct transfer model
对于三脉冲转移模型, 需要给定航天器从地球逃逸时的速度大小及方向, 对应3个参数$(C_{3}$, $DLA$, $RLA)$.由于航天器在转移过程中施加了深空机动, 所以航天器在撞击时的质量应减去转移过程的燃料消耗
(26) $m_{sc} \left( {t_{d} } \right)=m_{sc} \left( {t_{0} } \right){e}^{-\frac{\Delta v_{tot} }{g_{0} I_{sp} }}$
其中, 撞击时刻$t_{d} =t_{0} +t_{1} $, 转移速度增量总和$\Delta v_{tot} =DSM_{1} $, $m_{sc} \left( {t_{0} } \right)=f\left( {C_{3} }\right)$, $I_{sp} $表示发动机比冲.
综上所述, 给定入轨参数$\left( {C_{3} ,DLA,RLA} \right)$、时间节点$\left({t_{0} ,\Delta t_{1} ,\alpha_{1} } \right)$ 后,可以确定航天器在撞击小行星前的速度及质量,由式(25)计算出小行星被偏转后的状态,从而可计算出小行星被偏转前后的近地点距离改变量.
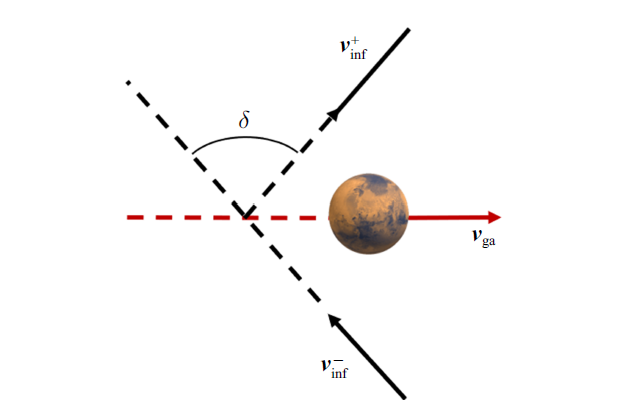
为了提高动能撞击的偏转效率, 本文引入借力飞行技术,探讨借力飞行技术是否对偏转效率有所提升.借力飞行的基本原理是利用自然天体的引力, 对航天器的速度进行改变,如图10 所示.
图10
图10
借力飞行示意图
Fig. 10
Schematic diagram of gravity assist
受自然天体引力作用,在自然天体引力影响球边界处航天器的进入${v}_{\infty }^{-}$与离开${v}_{\infty }^{+} $之间的夹角为
(27) $\delta =2\arcsin \frac{\mu_{ga} }{\mu_{ga} +\left( {R_{ga} +h_{p} } \right)v_{\infty }^{2} }$
其中, $\mu_{ga} $和$R_{ga} $分别表示借力天体的引力常数和半径, $h_{p} $表示借力高度, ${v}_{ga} $表示借力天体的速度.定义一个新的坐标系${o-ijk}$
(28) $i=\frac{v_{\infty}^-}{\left\| v_{\infty}^{-} \right\|},\ \ k=\frac{v^{-}\times v_{ga} }{\left\| v^{-}\times v_{ga}\right\|},\ \ j=k\times i$
因此, 借力后${v}_{\infty }^{+} $矢量可描述如下${v}_{\infty }^{+} =v_{\infty } \left[ {\left( {\sin \delta \cos \varphi } \right){k}+\left( {\sin \delta \sin \varphi } \right){j}+\left( {\cos \delta } \right){i}} \right]$ (29)其中, $\varphi $表示${v}_{\infty }^{+}$在${j-k}$的投影与${k}$轴正向之间的夹角, 取值范围为$[0,2\pi )$.
本文考虑的借力天体有金星、地球和火星. 首先, 航天器在$t_{0} $时刻从地球逃逸,经过$\Delta t_{1} $到达借力天体, 再经过$\Delta t_{2} $天后撞击危地小行星.转移期间, 还需执行两次深空机动, $DSM_{1} $施加于$t_{0} +\alpha_{1} \Delta t_{1} $时以及$DSM_{2} $施加于$t_{0} +\Delta t_{1} +\alpha_{2} \Delta t_{2}$时, $\alpha_{1} $与$\alpha_{2} $的取值范围为0到1 (图11 ).
图11
图11
借力飞行转移模型
Fig. 11
Gravity assist transfer model
同样的, 利用式(26)可以计算出航天器在撞击小行星时的质量, 其中撞击时刻$t_{d}=t_{0} +t_{1} +t_{2} $, 转移速度增量总和$\Delta v_{tot} =DSM_{1} +DSM_{2} $.
综上所述, 给定入轨参数$\left( {C_{3} ,DLA,RLA} \right)$、时间节点$\left({t_{0} ,\Delta t_{1} ,\Delta t_{2} ,\alpha_{1} ,\alpha_{2} }\right)$、借力参数$\left( {h_{p1} ,\varphi_{1} } \right)$ 后,可以确定航天器在撞击小行星前的速度及质量,由式(25)计算出小行星被偏转后的状态,从而可计算出小行星被偏转前后的近地点距离改变量. 以此类推,每增加一个借力天体, 需增加4个新的优化变量$\left( {\Delta t,\alpha ,h_{p},\varphi } \right)$.
3.2 优化模型
(30) $X=\left[ {t_{0} ,\Delta t_{1} } \right]$
(31) $X=\left[ {t_{0} ,\Delta t_{1} ,\alpha_{1} ,C_{3} ,DLA,RLA} \right]$
(32) $X=\left[ {t_{0} ,\Delta t_{1} ,\Delta t_{2} ,\alpha_{1} ,\alpha_{2} ,h_{p1} ,\varphi_{1} ,C_{3} ,DLA,RLA} \right]$
(33) $X=\left[ {\begin{array}{l} t_{0} ,\Delta t_{1} ,\Delta t_{2} ,\Delta t_{3} ,\alpha_{1} ,\alpha_{2} ,\alpha_{3} ,h_{p1} ,\varphi_{1} , \\ h_{p2} ,\varphi_{2} ,C_{3} ,DLA,RLA \\ \end{array}} \right]$
分别利用数值模型、Vasile模型、Izzo模型和近似模型构建目标函数(偏转距离),其表达式如下所示:
(34) $J_{1} =\left\| {{{\boldsymbol \rho }'}\left( {{t}'_{CA} } \right)} \right\|-\left\| {{\boldsymbol \rho }\left( {t_{CA} } \right)} \right\|$
(35) $J_{2} =\left\| {{\boldsymbol \rho }\left( {t_{CA} } \right){+}\delta {r}\left( {t_{CA} } \right)} \right\|-\left\| {{\boldsymbol \rho }\left( {t_{CA} } \right)} \right\|$
(36) $J_{3} =\Delta \xi$
(37) $J_{4} =\left\| {{{\boldsymbol \rho }'}\left( {t_{CA} } \right)} \right\|-\left\| {{\boldsymbol \rho }\left( {t_{CA} } \right)} \right\|$
3.3 优化算法
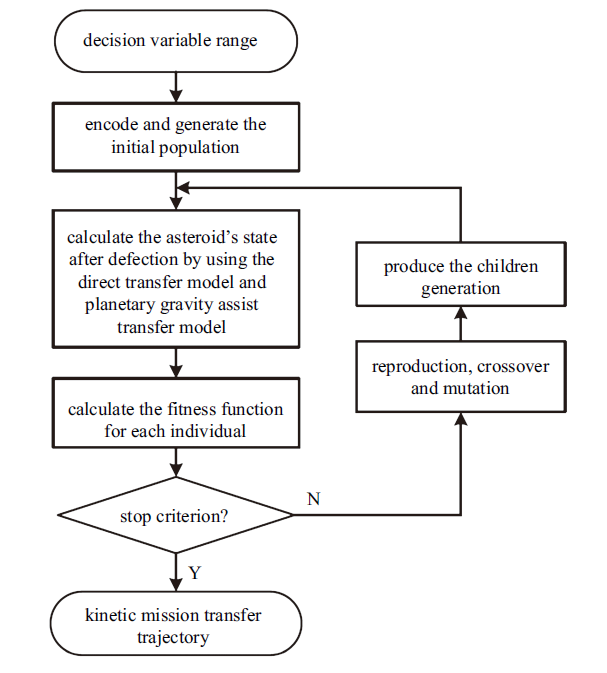
通过下述优化算法,可计算出动能撞击任务中直接转移方案/借力飞行转移方案的最优转移轨迹. 图12 给出了优化算法的流程图.
图12
图12
优化算法流程图
Fig. 12
Optimization process
第三步: 计算发射$C_3$, 并判断是否在拟合区间内(本文CZ-5拟合曲线需$C_{3}$$<$ 60 km$^{2}$/s$^{2})$. 如果不在区间内, 返回上一步;如果符合区间范围, 进入下一步;
第四步: 利用直接转移模型或行星借力借力飞行转移模型计算小行星被偏转后的状态;
第五步: 按照指定的目标函数式(34),$\sim \!$式(37),计算每个个体的适值函数;
第六步: 判断是否达到终止条件. 如果未达到条件, 进入第七步; 如果达到终止条件,直接进入第八步;
第七步: 选择种群中的优质个体, 进行遗传运算, 更新种群, 返回第三步;
第八步: 输出适值度最高的个体, 即输出最优转移轨迹.
4 仿真结果与讨论
本文以偏转Apophis为例, 在10年预警时间的条件下, 参考CZ-5的运载能力,设计了直接转移和行星借力飞行转移的动能撞击偏转任务.
4.1 偏转距离计算方法比较
本节以直接转移方案为例, 对比分析了利用不同模型进行优化的结果,对优化模型中的目标函数进行了选择.
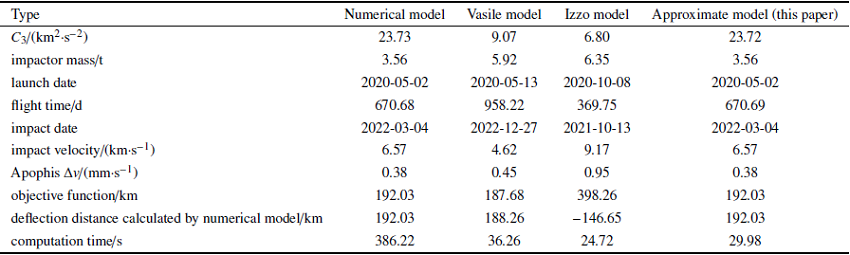
航天器逃逸时间$t_{0} $的范围为2020年1月1日至2021年1月1日, 转移时间$\Delta t_{1} \in \left[ {100,1400} \right]$ d.分别以数值模型、Vasile模型、Izzo模型、近似模型作为目标函数,利用遗传算法对直接转移方案进行了全局优化. 该优化问题中,种群个体数设置为1000, 种群代数设置为10.将优化出的发射窗口代入数值模型中计算数值偏转距离,表3 对比了采用不同目标函数时求得的最优解.
通过表3 优化结果的对比, 可以发现在优化问题中,以Vasile模型和近似模型作为目标函数时, 可以较好地替代数值模型.尤其对于近似模型, 利用其优化出的发射窗口与数值模型的基本一致,同时计算时间相比于数值模型降低了约90%; Vasile模型也可以较好还原优化结果,但优化出的发射窗口与数值模型的存在偏差, 会损失一定的最优性;利用Izzo模型作为目标函数, 即使其目标函数值达到398 km,但优化出的解不具备参考性,这是由于小行星被偏转前后出现了图2 所示的位置关系.这也验证了1.2.2节中关于Izzo模型初步分析的结论, 不可将其作为优化的目标函数.从Izzo模型的优化结果也可以得知, 不管撞击器对小行星的偏转能力有多强,一旦选择了错误的偏转时机, 则可能会给地球带来更大的威胁.
为了直观对比数值模型、解析模型、近似模型的发射窗口差异,下面在同一张图中绘制出利用不 同模型求解出的偏转距离等于180 km的等高线(图13 ).
图13
图13
不同模型的180 km等高线图
Fig. 13
180 km contour maps of different models
图13 中, 黄色粗线表示利用数值模型求解的180km等高线,红色和蓝色细线分表表示用近似模型和Vasile模型求解的结果,“*”标识出的位置表示利用数值模型优化出的发射窗口.红线与黄线以及蓝线与黄线的交叉点, 表示与数值模型误差为0%的点. 可以看出,红线与红线的拟合性较好, 说明近似模型可以较好的替代数值模型;而蓝线与黄线交叉的点较少, 说明Vasile模型的解与数值解存在一定偏差. 同时,可以明显的看到“*”标识落在蓝线上, 这也说明如果以Vasile模型的解作为优化目标,优化出的窗口会与实际最优窗口有一定偏差.
4.2 直接转移方案
首先利用Pork-Chop图分析发射窗口, 具体计算的方法为: 将航天器逃逸时间$t_{0}$的范围选为2020年1月1日至2021年1月1日, 转移时间$\Delta t_{1} \in \left[{600,1400} \right]$ d, 以1 d为步长, 利用近似模型计算所有情况产生的偏转距离,最终绘制得偏转距离等高线如图14 所示.
图14
图14
Apophis偏转距离等高线图(2020年)
Fig. 14
Apophis deflection distance contour map (2020)
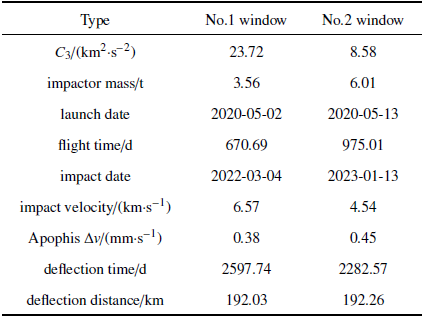
由图14 中可知, 在2020年中, 利用两脉冲转移方案偏转Apophis共有两个发射窗口,一个位于2020年5月2日前后, 另一个位于2020年5月13日前后.这2020年中两个发射窗口的具体信息总结如表4 .
可以看到, 2号窗口虽然拥有更大的撞击器质量和Apophis $\Delta v$,但最终与1号窗口的偏转距离相差不大. 这是由于2号窗口所需的转移时间更长,偏转相位次于1号窗口, 从而导致Apophis被偏转后到达2029年近地点的偏转时间降低.因此, 不能直接用撞击体质量、速度增量等因素单方面来评估偏转距离,而是需要综合考虑多项影响因素, 如Izzo模型所示,包括小行星本身的物理属性(小行星质量$m_{ast} $, $\beta$等)、小行星与地球的轨道关系(小行星半长轴$a_{ast}$、近地点时地球的速度$v_{E} $等)以及轨道优化结果(撞击器质量$m_{sc}$、偏转时间$\sigma $、撞击速度${U}_{sc} $等).
以总任务时间较少的1号窗口为例, 直接转移方案的转移轨迹如图15 所示.航天器自2020年5月2日从地球逃逸, 经过670 d后, 在2022年3月4日与Apophis相撞.经过撞击, Apophis在2029年的近地距可增加约192 km.
图15
图15
2020年1号发射窗口的两脉冲直接转移轨迹
Fig. 15
Two-impulse direct transfer trajectory of the 1st launch window in 2020
将航天器逃逸时间$t_{0} $的范围选为2020年1月1日至2021年1月1日,转移时间$\Delta t_{1} \in \left[ {100,1400} \right]$ d. 优化结果如表5 所示,转移轨迹如图16 所示.
图16
图16
三脉冲直接转移轨迹
Fig. 16
Three-impulse direct transfer trajectory
仿真结果表明, 三脉冲直接转移解与两脉冲直接转移的1号窗口非常接近,三脉冲解虽然具有更高的发射入轨质量, 但是由于施加了中途机动,同时又会损失一部分撞击器质量,利用三脉冲直接转移方案对偏转距离不会有明显提升.
4.3 借力飞行转移方案
航天器逃逸时间$t_{0} $范围为2020年1月1日至2021年1月1日, 转移时间$\Delta t\in\left[ {100,1000} \right]$ d, $h_{p} \in \left[{100,3000} \right]$km, $\varphi \in \left[ {0,2\pi }\right]$rad, $C_{3} \in \left[ {0,50} \right]$km$^{2}$/s$^{2}$, $DLA\in \left[ {0,\pi } \right]$rad, $RLA\in \left[{0,2\pi } \right]$rad. 分别设计了如下的借力飞行偏转方案:金星、地球、火星、金星-金星、金星-地球、金星-火星、地球-金星、地球-地球、 地球-火星、火星-金星、火星-地球、火星-火星.遗传算法的参数设置: 单次借力的种群个体数设置为5000, 种群代数设置为30;两次借力的种群个体数设置为8000, 种群代数设置为30, 设计结果见表6 .
仿真结果表明, 只有单次地球借力的转移方案对偏转距离有所提升,相比直接转移方案提升了约20 km. 关于单次地球借力转移方案的细节如表7 所示.
地球借力转移方案的转移轨迹如图17 所示. 航天器自2020年2月19日从地球逃逸,2021年5月17日进行地球借力, 2023年1月25日与Apophis相撞,航天器转移时间共计1071 d. 经过撞击, Apophis在2029年的近地距可增加约210 km.
图17
图17
地球借力转移轨迹
Fig. 17
Earth gravity assist transfer trajectory
由借力飞行转移方案的设计结果可知, 利用借力飞行未必能够提升偏转距离.这是因为借力飞行概念的初衷是降低深空探测过程的燃料消耗,而对于动能撞击这种特定的深空探测任务来说, 其性能指标是偏转距离,这是一个需要综合考虑燃料消耗、转移时间、撞击相位等因素的指标.如果在航天器转移的过程中执行不当的借力飞行, 航天器为了与借力天体相位匹配,可能会错过最佳发射窗口, 从而降低偏转距离.
5 二体模型对防御窗口的影响
以上仿真均是在二体模型的假设下进行的,本章将主要讨论基于二体模型与基于高精度模型优化结果的差别.
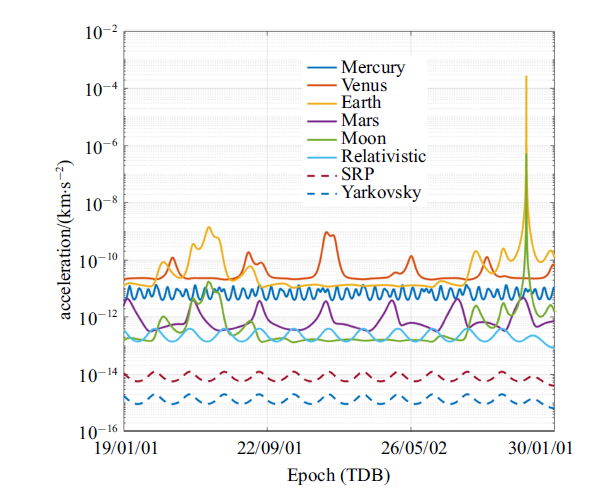
实际上, 在高精度模型中某些摄动力对于偏转距离的影响非常微弱,在优化过程中是可以忽略的因素. 因此,首先对小行星Apophis在运动过程中所受的摄动力进行分析,筛选出对偏转距离影响最大的摄动力, 对高精度模型进行简化,从而减少优化过程中不必要的计算量. 以小行星Apophis为例,下图给出了Apophis在2019年1月1日至2030年1月1日之间各项摄动加速度的变化趋势.其中,图18 为内太阳系4颗行星、广义相对论、太阳光压以及Yarkovsky效应的摄动加速度变化曲线;图19 为外太阳系5颗行星、3颗矮行星、4颗主带小行星、地球非球形引力J2的摄动加速度变化曲线.
图18
图18
Apophis摄动力量级(1)
Fig. 18
Orders of magnitude of Apophis perturbation (1)
图19
图19
Apophis摄动力量级(2)
Fig. 19
Orders of magnitude of Apophis perturbation (2)
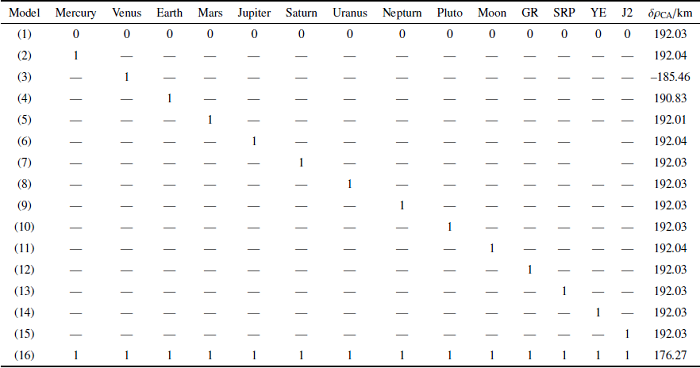
由图18 可知, Apophis在2029年到达近地点之前,金星、地球、火星和月球的摄动加速度会发生量级上的显著变化.不同摄动源按照摄动加速度量级的分布区间总结于表8 中.
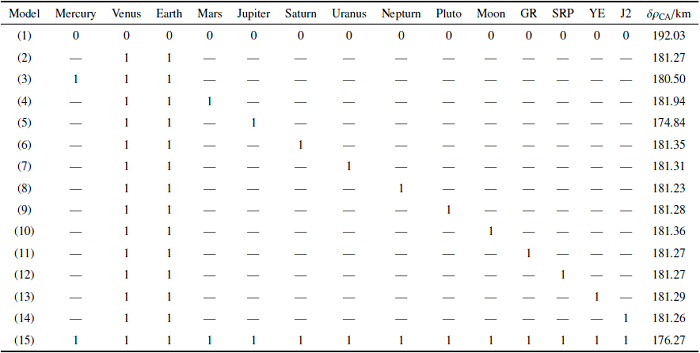
基于3.1.1节所述的两脉冲转移模型,以第4章两脉冲转移仿真结果中的1号窗口(2022年5月2日)为例,在2022年3月2日对小行星Apophis施加0.38 mm/s的速度增量,分别利用高精度模型和二体模型对偏转后的小行星进行递推, 计算二体模型与高精度模型对计算偏转距离的误差. 仿真发现,利用二体模型计算偏转距离为192.03 km, 利用高精度模型计算的偏转距离176.27 km.进一步, 在二体模型上每次增加一项摄动力, 用不同力模型递推求得的偏转距离,结果如表 9 所示中,发现对偏转距离影响最大的摄动力为地球和金星引力.在考虑金星$+$ 地球摄动模型基础上, 表10 每次增加一项摄动力, 分析除金星和地球外, 对偏转距离影响最大的因素.由表9 和表10 可知,对小行星Apophis偏转距离影响最大的因素为金星、地球、木星.在二体模型基础上引入地球、金星、金星的引力摄动后,计算出的偏转距离与高精度解的误差在1%以内.
在保证计算精度的前提下, 为了提高计算速度,本文引入金星、地球、木星引力摄动对二体模型修正, 利用修正模型替代高精度模型.修正模型的数学表达式如下
(38) $\frac{{d}^{2}{r}}{{d}t^{2}}=-\frac{\mu_{s} }{\left| {{r}} \right|^{3}}{r+a}_{V} +{a}_{E} +{a}_{J}$
以直接转移方案为例,分别基于二体模型和修正模型对偏转Apophis的动能撞击任务进行优化.航天器的逃逸时间$t_{0} $的范围选为2020年1月1日至2021年1月1日,转移时间为$\Delta t_{1} \in \left[ {600,1400} \right]$ d.种群个体数设置为200, 种群代数设置为10.利用二体模型及修正模型优化的结果如表11 所示. 提取出二者优化出的防御窗口,代入高精度模型计算出对应的高精度结果.
仿真结果表明, 利用二体模型进行优化, 在不影响防御窗口的情况下,计算时间会比精度更高的修正模型更少. 在动能撞击任务前期设计过程中,可以利用二体模型快速评估防御效果.
6 结论
本文对动能撞击小行星防御任务的脉冲轨道优化方法开展了研究.为提升动能撞击任务的求解效率, 将两种经典的偏转距离解析模型引入优化模型,同时提出一种基于近地点时刻预估的偏转距离近似模型; 考虑运载约束,建立了直接转移和行星借力飞行转移的动能撞击优化模型.
仿真结果表明, 相比于经典的偏转距离解析模型,本文提出的基于近地点时刻预估的近似模型更加简洁直观, 在提升计算效率的同时,也能保证优化问题的最优性.三脉冲直接转移方案与两脉冲直接转移方案的最优偏转效果基本一致,借力飞行转移方案相比于直接转移方案对偏转距离的提升效果并不明显.在动能撞击任务的前期设计中, 可以基于二体模型进行防御效果的快速评估,虽然对偏转距离有一定误差, 但对防御窗口的优化结果影响不大.
参考文献
View Option
[1]
Schulte P Alegret L Arenillas I , et al . The chicxulub asteroid impact and mass extinction at the cretaceous-paleogene boundary
Science 2010 ,327 (5970 ):1214 -1218
DOI
URL
PMID
[本文引用: 1]
The Cretaceous-Paleogene boundary approximately 65.5 million years ago marks one of the three largest mass extinctions in the past 500 million years. The extinction event coincided with a large asteroid impact at Chicxulub, Mexico, and occurred within the time of Deccan flood basalt volcanism in India. Here, we synthesize records of the global stratigraphy across this boundary to assess the proposed causes of the mass extinction. Notably, a single ejecta-rich deposit compositionally linked to the Chicxulub impact is globally distributed at the Cretaceous-Paleogene boundary. The temporal match between the ejecta layer and the onset of the extinctions and the agreement of ecological patterns in the fossil record with modeled environmental perturbations (for example, darkness and cooling) lead us to conclude that the Chicxulub impact triggered the mass extinction.
[2]
Chyba CF Thomas PJ Zahnle KJ . The 1908 tunguska explosion-atmospheric disruption of a stony asteroid
Nature 1993 ,361 (6407 ):40 -44
[本文引用: 1]
[3]
罗跃 , 王磊 , 党雷宁 等 . 模拟 Chelyabinsk 小行星进入的烧蚀实验,
力学学报 , 2020 ,52 (5 ):1362 -1370
[本文引用: 1]
( Luo Yue Wang Lei Dang Leining Liu Jinbo Zhang Jun Liu Sen . Arcjet ablation experiment to simulate the chelyabinsk asteroid entry
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (5 ):1362 -1370 (in Chinese))
[本文引用: 1]
[4]
龚自正 , 李明 , 陈川 , 等 . 小行星监测预警, 安全防御和资源利用的前沿科学问题及关键技术
科学通报 , 2020 ,65 (5 ):28 -54
[本文引用: 1]
( Gong Zizheng Li Ming Chen Chuan , et al . The frontier science and key technologies of asteroid monitoring and early warning, security defense and resource utilization
Chinese Science Bulletin 2020 ,65 :346 -372 (in Chinese))
[本文引用: 1]
[5]
Wie B Zimmerman B Lyzhoft J , et al . Planetary defense mission concepts for disrupting/pulverizing hazardous asteroids with short warning time
Astrodynamics 2017 ,1 (1 ):3 -21
[本文引用: 1]
[6]
Lubin P Hughes GB Bible J , et al . Toward directed energy planetary defense
Optical Engineering 2014 ,53 (2 ):025103
[本文引用: 1]
[7]
Sanchez JP Mcinnes CR . Synergistic approach of asteroid exploitation and planetary protection
Advances in Space Research 2012 ,49 (4 ):667 -685
DOI
URL
[本文引用: 1]
The asteroid and cometary impact hazard has long been recognised as an important issue requiring risk assessment and contingency planning. At the same time asteroids have also been acknowledged as possible sources of raw materials for future large-scale space engineering ventures. This paper explores possible synergies between these two apparently opposed views; planetary protection and space resource exploitation. In particular, the paper assumes a 5 tonne low-thrust spacecraft as a baseline for asteroid deflection and capture (or resource transport) missions. The system is assumed to land on the asteroid and provide a continuous thrust able to modify the orbit of the asteroid according to the mission objective. The paper analyses the capability of such a near-term system to provide both planetary protection and asteroid resources to Earth. Results show that a 5 tonne spacecraft could provide a high level of protection for modest impact hazards: airburst and local damage events (caused by 15-170 m diameter objects). At the same time, the same spacecraft could also be used to transport to bound Earth orbits significant quantities of material through judicious use of orbital dynamics and passively safe aero-capture manoeuvres or low energy ballistic capture. As will be shown, a 5 tonne low-thrust spacecraft could potentially transport between 12 and 350 times its own mass of asteroid resources by means of ballistic capture or aero-capture trajectories that pose very low dynamical pressures on the object. (C) 2011 COSPAR. Published by Elsevier Ltd.
[8]
Lu ET Love SG . Gravitational tractor for towing asteroids
Nature 2005 ,438 (7065 ):177 -178
URL
PMID
[本文引用: 1]
[9]
Bombardelli C Amato D Luis Cano J . Mission analysis for the ion beam deflection of fictitious asteroid 2015 PDC
Acta Astronautica 2016 ,118 :296 -307
[本文引用: 1]
[10]
A'hearn MF Belton MJS Delamere WA , et al . Deep Impact: Excavating comet Tempel 1
Science 2005 ,310 (5746 ):258 -264
DOI
URL
PMID
[本文引用: 1]
[11]
Raducan SD Davison TM Luther R , et al . The role of asteroid strength, porosity and internal friction in impact momentum transfer
Icarus 2019 ,329 :282 -295
[本文引用: 2]
[12]
Atchison JA Ozimek MT Kantsiper BL , et al . Trajectory options for the DART mission
Acta Astronautica 2016 ,123 :330 -339
[本文引用: 1]
[13]
Ozimek MT Atchison JA . NASA double asteroid redirection test (DART) low-thrust trajectory concept
// Proceedings of the 27th AAS/AIAA Space Flight Mechanics Meeting, San Antonio, USA, F , 2017
[本文引用: 1]
[14]
Atchison JA Dong CP Jensenius MA , et al . Double asteroid redirection test—Mission design and navigation
// Proceedings of the International Syposium on Space Flight Mechanics, F , 2014
[本文引用: 1]
[15]
Ahrens TJ Harris AW . Deflection and fragmentation of near-earth asteroids
Nature 1992 ,360 (6403 ):429 -433
[本文引用: 2]
[16]
Carusi A Valsecchi GB D'abramo G , et al . Deflecting NEOs in route of collision with the Earth
Icarus 2002 ,159 (2 ):417 -422
[本文引用: 3]
[17]
Park SY Ross IM . Two-body optimization for deflecting Earth-crossing asteroids
Journal of Guidance Control and Dynamics 1999 ,22 (3 ):415 -420
[本文引用: 1]
[18]
Ross M Park SY Porter SDV . Gravitational effects of Earth in optimizing Delta V for deflecting Earth-crossing asteroids
Journal of Spacecraft and Rockets 2001 ,38 (5 ):759 -764
[本文引用: 1]
[19]
Kahle R Hahn G Kuhrt E . Optimal deflection of NEOs en route of collision with the Earth
Icarus 2006 ,182 (2 ):482 -488
[本文引用: 1]
[20]
Vasile M Colombo C . Optimal impact strategies for asteroid deflection
Journal of Guidance Control and Dynamics 2008 ,31 (4 ):858 -872
[本文引用: 3]
[21]
Yamaguchi K Yamakawa H . Visualization of kinetic-impact effectiveness for asteroid deflection using impact-geometry maps
Journal of Spacecraft and Rockets 2018 ,55 (5 ):1181 -1197
[本文引用: 1]
[22]
Greenstreet S Lu E Loucks M , et al . Required deflection impulses as a function of time before impact for Earth-impacting asteroids
Icarus 2020 ,347
[本文引用: 1]
[23]
Englander JA Conway BA Wall BJ , et al . Optimal Strategies Found Using Genetic Algorithms for Deflecting Hazardous Near-Earth Objects
New York: IEEE , 2009
[本文引用: 2]
[24]
Howley K Wasem J . A simplified approach to uncertainty quantification for orbits in impulsive deflection scenarios
Acta Astronautica 2014 ,104 (1 ):206 -219
[本文引用: 1]
[25]
Conway BA . Near-optimal deflection of earth-approaching asteroids
Journal of Guidance Control and Dynamics 2001 ,24 (5 ):1035 -1037
DOI
URL
[本文引用: 1]
[26]
Izzo D . Optimization of interplanetary trajectories for impulsive and continuous asteroid deflection
Journal of Guidance Control and Dynamics 2007 ,30 (2 ):401 -408
[本文引用: 2]
[27]
Sanchez JP Colombo C . Impact hazard protection efficiency by a small kinetic impactor
Journal of Spacecraft and Rockets 2013 ,50 (2 ):380 -393
[本文引用: 1]
[28]
Thiry N Vasile M . Statistical multi-criteria evaluation of non-nuclear asteroid deflection methods
Acta Astronautica 2017 ,140 :293 -307
[本文引用: 1]
[29]
Folkner WM Williams JG Boggs DH , et al . The planetary and lunar ephemerides DE430 and DE431
Interplanetary Network Progress Report 2014 ,196 :1 -81
[本文引用: 1]
[30]
Website: JPL Horizons On-Line Ephemeris System . https://ssd.jpl.nasa.gov/horizons.cgi#results, 2021
URL
[本文引用: 4]
[31]
Bancelin D Colas F Thuillot W , et al . Asteroid (99942) Apophis: new predictions of Earth encounters for this potentially hazardous asteroid
Astronomy & Astrophysics 2012 ,544 :5
[本文引用: 1]
[32]
Kochetova O Chernetenko YA Shor V . How precise is the orbit of asteroid (99942) Apophis and how probable is its collision with the Earth in 2036-2037?
Solar System Research 2009 ,43 (4 ):324 -333
[33]
Farnocchia D Chesley S Tholen D , et al . High precision predictions for near-Earth asteroids: the strange case of (3908) Nyx
Celestial Mechanics and Dynamical Astronomy 2014 ,119 (3-4 ):301 -312
[本文引用: 1]
[34]
Armellin R Di Lizia P Bernelli-Zazzera F , et al . Asteroid close encounters characterization using differential algebra: The case of Apophis
Celestial Mechanics & Dynamical Astronomy 2010 ,107 (4 ):451 -470
[本文引用: 1]
[35]
Pitz A Teubert C Wei B . Earth-impact probability computation of disrupted asteroid fragments using gmat/stk/codes
Advances in the Astronautical Science 2011 ,142 :AAS11-408
[本文引用: 1]
[36]
Brent RP . Algorithms for Minimization Without Derivatives
Mathematics of Computation 1973 ,19 (5 )10.2307/20050713
[本文引用: 2]
[37]
Farnocchia D Eggl S Chodas PW , et al . Planetary encounter analysis on the B-plane: a comprehensive formulation
Celestial Mechanics & Dynamical Astronomy 2019 ,131 (8 ):16
[本文引用: 1]
[38]
Öpik EJ . Interplanetary Encounters: Close Range Gravitational Interactions
Elsevier Scientific Pub ., 1976
[本文引用: 1]
[39]
Liu J Zheng J Li M . Dry mass optimization for the impulsive transfer trajectory of a near-Earth asteroid sample return mission
Astrophysics and Space Science 2019 ,364 (12 ):215
[本文引用: 1]
[40]
Vallado DA . Fundamentals of astrodynamics and applications
Springer Science & Business Media , 2001
[本文引用: 1]
[41]
Rumpf CM Mathias DL Wheeler LF , et al . Deflection driven evolution of asteroid impact risk under large uncertainties
Acta Astronautica 2020 ,176 :276 -286
[本文引用: 1]
[42]
Paek SW De Weck O Hoffman J , et al . Optimization and decision-making framework for multi-staged asteroid deflection campaigns under epistemic uncertainties
Acta Astronautica 2020 ,167 :23 -41
[本文引用: 1]
The chicxulub asteroid impact and mass extinction at the cretaceous-paleogene boundary
1
2010
... 太阳系内的小行星主要分布于火星轨道与木星轨道之间,也有一部分小行星会穿越地球轨道威胁到地球上的生命.诸多严重的小行星撞击地球事件(如6500万年前的K-T事件[1 ] 、1908年通古斯大爆炸事件[2 ] 、2013年车里雅宾斯克事件[3 ] 等)已引发人类对于行星防御的关注.在能够对近地小行星提前预警的前提下,摧毁小行星结构或者偏转小行星轨道是避免其撞击地球的两种基本方式[4 ] .目前已提出的防御手段主要有核爆[5 ] 、动能撞击、激光烧蚀[6 ] 、拖船[7 ] 、引力拖船[8 ] 、离子束牵引[9 ] 等,其中动能撞击技术是目前最易实现且成熟度较高的手段. ...
The 1908 tunguska explosion-atmospheric disruption of a stony asteroid
1
1993
... 太阳系内的小行星主要分布于火星轨道与木星轨道之间,也有一部分小行星会穿越地球轨道威胁到地球上的生命.诸多严重的小行星撞击地球事件(如6500万年前的K-T事件[1 ] 、1908年通古斯大爆炸事件[2 ] 、2013年车里雅宾斯克事件[3 ] 等)已引发人类对于行星防御的关注.在能够对近地小行星提前预警的前提下,摧毁小行星结构或者偏转小行星轨道是避免其撞击地球的两种基本方式[4 ] .目前已提出的防御手段主要有核爆[5 ] 、动能撞击、激光烧蚀[6 ] 、拖船[7 ] 、引力拖船[8 ] 、离子束牵引[9 ] 等,其中动能撞击技术是目前最易实现且成熟度较高的手段. ...
模拟 Chelyabinsk 小行星进入的烧蚀实验,
1
2020
... 太阳系内的小行星主要分布于火星轨道与木星轨道之间,也有一部分小行星会穿越地球轨道威胁到地球上的生命.诸多严重的小行星撞击地球事件(如6500万年前的K-T事件[1 ] 、1908年通古斯大爆炸事件[2 ] 、2013年车里雅宾斯克事件[3 ] 等)已引发人类对于行星防御的关注.在能够对近地小行星提前预警的前提下,摧毁小行星结构或者偏转小行星轨道是避免其撞击地球的两种基本方式[4 ] .目前已提出的防御手段主要有核爆[5 ] 、动能撞击、激光烧蚀[6 ] 、拖船[7 ] 、引力拖船[8 ] 、离子束牵引[9 ] 等,其中动能撞击技术是目前最易实现且成熟度较高的手段. ...
模拟 Chelyabinsk 小行星进入的烧蚀实验,
1
2020
... 太阳系内的小行星主要分布于火星轨道与木星轨道之间,也有一部分小行星会穿越地球轨道威胁到地球上的生命.诸多严重的小行星撞击地球事件(如6500万年前的K-T事件[1 ] 、1908年通古斯大爆炸事件[2 ] 、2013年车里雅宾斯克事件[3 ] 等)已引发人类对于行星防御的关注.在能够对近地小行星提前预警的前提下,摧毁小行星结构或者偏转小行星轨道是避免其撞击地球的两种基本方式[4 ] .目前已提出的防御手段主要有核爆[5 ] 、动能撞击、激光烧蚀[6 ] 、拖船[7 ] 、引力拖船[8 ] 、离子束牵引[9 ] 等,其中动能撞击技术是目前最易实现且成熟度较高的手段. ...
小行星监测预警, 安全防御和资源利用的前沿科学问题及关键技术
1
2020
... 太阳系内的小行星主要分布于火星轨道与木星轨道之间,也有一部分小行星会穿越地球轨道威胁到地球上的生命.诸多严重的小行星撞击地球事件(如6500万年前的K-T事件[1 ] 、1908年通古斯大爆炸事件[2 ] 、2013年车里雅宾斯克事件[3 ] 等)已引发人类对于行星防御的关注.在能够对近地小行星提前预警的前提下,摧毁小行星结构或者偏转小行星轨道是避免其撞击地球的两种基本方式[4 ] .目前已提出的防御手段主要有核爆[5 ] 、动能撞击、激光烧蚀[6 ] 、拖船[7 ] 、引力拖船[8 ] 、离子束牵引[9 ] 等,其中动能撞击技术是目前最易实现且成熟度较高的手段. ...
小行星监测预警, 安全防御和资源利用的前沿科学问题及关键技术
1
2020
... 太阳系内的小行星主要分布于火星轨道与木星轨道之间,也有一部分小行星会穿越地球轨道威胁到地球上的生命.诸多严重的小行星撞击地球事件(如6500万年前的K-T事件[1 ] 、1908年通古斯大爆炸事件[2 ] 、2013年车里雅宾斯克事件[3 ] 等)已引发人类对于行星防御的关注.在能够对近地小行星提前预警的前提下,摧毁小行星结构或者偏转小行星轨道是避免其撞击地球的两种基本方式[4 ] .目前已提出的防御手段主要有核爆[5 ] 、动能撞击、激光烧蚀[6 ] 、拖船[7 ] 、引力拖船[8 ] 、离子束牵引[9 ] 等,其中动能撞击技术是目前最易实现且成熟度较高的手段. ...
Planetary defense mission concepts for disrupting/pulverizing hazardous asteroids with short warning time
1
2017
... 太阳系内的小行星主要分布于火星轨道与木星轨道之间,也有一部分小行星会穿越地球轨道威胁到地球上的生命.诸多严重的小行星撞击地球事件(如6500万年前的K-T事件[1 ] 、1908年通古斯大爆炸事件[2 ] 、2013年车里雅宾斯克事件[3 ] 等)已引发人类对于行星防御的关注.在能够对近地小行星提前预警的前提下,摧毁小行星结构或者偏转小行星轨道是避免其撞击地球的两种基本方式[4 ] .目前已提出的防御手段主要有核爆[5 ] 、动能撞击、激光烧蚀[6 ] 、拖船[7 ] 、引力拖船[8 ] 、离子束牵引[9 ] 等,其中动能撞击技术是目前最易实现且成熟度较高的手段. ...
Toward directed energy planetary defense
1
2014
... 太阳系内的小行星主要分布于火星轨道与木星轨道之间,也有一部分小行星会穿越地球轨道威胁到地球上的生命.诸多严重的小行星撞击地球事件(如6500万年前的K-T事件[1 ] 、1908年通古斯大爆炸事件[2 ] 、2013年车里雅宾斯克事件[3 ] 等)已引发人类对于行星防御的关注.在能够对近地小行星提前预警的前提下,摧毁小行星结构或者偏转小行星轨道是避免其撞击地球的两种基本方式[4 ] .目前已提出的防御手段主要有核爆[5 ] 、动能撞击、激光烧蚀[6 ] 、拖船[7 ] 、引力拖船[8 ] 、离子束牵引[9 ] 等,其中动能撞击技术是目前最易实现且成熟度较高的手段. ...
Synergistic approach of asteroid exploitation and planetary protection
1
2012
... 太阳系内的小行星主要分布于火星轨道与木星轨道之间,也有一部分小行星会穿越地球轨道威胁到地球上的生命.诸多严重的小行星撞击地球事件(如6500万年前的K-T事件[1 ] 、1908年通古斯大爆炸事件[2 ] 、2013年车里雅宾斯克事件[3 ] 等)已引发人类对于行星防御的关注.在能够对近地小行星提前预警的前提下,摧毁小行星结构或者偏转小行星轨道是避免其撞击地球的两种基本方式[4 ] .目前已提出的防御手段主要有核爆[5 ] 、动能撞击、激光烧蚀[6 ] 、拖船[7 ] 、引力拖船[8 ] 、离子束牵引[9 ] 等,其中动能撞击技术是目前最易实现且成熟度较高的手段. ...
Gravitational tractor for towing asteroids
1
2005
... 太阳系内的小行星主要分布于火星轨道与木星轨道之间,也有一部分小行星会穿越地球轨道威胁到地球上的生命.诸多严重的小行星撞击地球事件(如6500万年前的K-T事件[1 ] 、1908年通古斯大爆炸事件[2 ] 、2013年车里雅宾斯克事件[3 ] 等)已引发人类对于行星防御的关注.在能够对近地小行星提前预警的前提下,摧毁小行星结构或者偏转小行星轨道是避免其撞击地球的两种基本方式[4 ] .目前已提出的防御手段主要有核爆[5 ] 、动能撞击、激光烧蚀[6 ] 、拖船[7 ] 、引力拖船[8 ] 、离子束牵引[9 ] 等,其中动能撞击技术是目前最易实现且成熟度较高的手段. ...
Mission analysis for the ion beam deflection of fictitious asteroid 2015 PDC
1
2016
... 太阳系内的小行星主要分布于火星轨道与木星轨道之间,也有一部分小行星会穿越地球轨道威胁到地球上的生命.诸多严重的小行星撞击地球事件(如6500万年前的K-T事件[1 ] 、1908年通古斯大爆炸事件[2 ] 、2013年车里雅宾斯克事件[3 ] 等)已引发人类对于行星防御的关注.在能够对近地小行星提前预警的前提下,摧毁小行星结构或者偏转小行星轨道是避免其撞击地球的两种基本方式[4 ] .目前已提出的防御手段主要有核爆[5 ] 、动能撞击、激光烧蚀[6 ] 、拖船[7 ] 、引力拖船[8 ] 、离子束牵引[9 ] 等,其中动能撞击技术是目前最易实现且成熟度较高的手段. ...
Deep Impact: Excavating comet Tempel 1
1
2005
... 动能撞击技术是指撞击器以一定的速度和角度撞击小行星, 使小行星轨道发生改变.2005年美国实施了深度撞击(deep impact)任务[10 ] , 任务释放一颗约370kg的撞击器, 以约10.3 km/s的相对速度撞击“Tempel 1”彗星的核,撞击后的3年内该彗星位置变化了约10 km; 双小行星重定向测试任务(doubleasteroid redirection test, DART)将于2021年7月执行, 由一个约650kg的撞击器以约6.65 km/s的相对速度撞击小行星 Didymos的卫星, 预计产生0.8$\sim$2mm/s的速度改变量(取决于动量传递因子的大小,动量传递因子用于描述溅射物对动量传递的影响[11 ] ).Atchison等[12 ] 总结了DART轨道设计需求,包括撞击日期、撞击角度以及为了满足光学需求的太阳相位角需求;Ozimek和Atchison[13 ] 研究了DART轨道中逃逸段的月球借力方法;Atchison等[14 ] 介绍了DART的终端制导、载荷等信息. ...
The role of asteroid strength, porosity and internal friction in impact momentum transfer
2
2019
... 动能撞击技术是指撞击器以一定的速度和角度撞击小行星, 使小行星轨道发生改变.2005年美国实施了深度撞击(deep impact)任务[10 ] , 任务释放一颗约370kg的撞击器, 以约10.3 km/s的相对速度撞击“Tempel 1”彗星的核,撞击后的3年内该彗星位置变化了约10 km; 双小行星重定向测试任务(doubleasteroid redirection test, DART)将于2021年7月执行, 由一个约650kg的撞击器以约6.65 km/s的相对速度撞击小行星 Didymos的卫星, 预计产生0.8$\sim$2mm/s的速度改变量(取决于动量传递因子的大小,动量传递因子用于描述溅射物对动量传递的影响[11 ] ).Atchison等[12 ] 总结了DART轨道设计需求,包括撞击日期、撞击角度以及为了满足光学需求的太阳相位角需求;Ozimek和Atchison[13 ] 研究了DART轨道中逃逸段的月球借力方法;Atchison等[14 ] 介绍了DART的终端制导、载荷等信息. ...
... 当动能航天器撞击目标小行星后, 超高速撞击会导致小行星表面产生溅射物,一部分溅射物最终会再次吸积在小行星表面,另一部分速度较高的溅射物将会从小行星的引力场中逃逸,这种现象类似于火箭产生动力的机理, 将会放大动量传递效应,可采用动量传递因子$\beta $描述溅射物对动量传递的影响[11 ] .假定航天器与小行星的撞击过程为完全非弹性碰撞, 根据动量守恒原理,小行星被撞击后产生的速度改变量可由下式估算[41 -42 ] ...
Trajectory options for the DART mission
1
2016
... 动能撞击技术是指撞击器以一定的速度和角度撞击小行星, 使小行星轨道发生改变.2005年美国实施了深度撞击(deep impact)任务[10 ] , 任务释放一颗约370kg的撞击器, 以约10.3 km/s的相对速度撞击“Tempel 1”彗星的核,撞击后的3年内该彗星位置变化了约10 km; 双小行星重定向测试任务(doubleasteroid redirection test, DART)将于2021年7月执行, 由一个约650kg的撞击器以约6.65 km/s的相对速度撞击小行星 Didymos的卫星, 预计产生0.8$\sim$2mm/s的速度改变量(取决于动量传递因子的大小,动量传递因子用于描述溅射物对动量传递的影响[11 ] ).Atchison等[12 ] 总结了DART轨道设计需求,包括撞击日期、撞击角度以及为了满足光学需求的太阳相位角需求;Ozimek和Atchison[13 ] 研究了DART轨道中逃逸段的月球借力方法;Atchison等[14 ] 介绍了DART的终端制导、载荷等信息. ...
NASA double asteroid redirection test (DART) low-thrust trajectory concept
1
2017
... 动能撞击技术是指撞击器以一定的速度和角度撞击小行星, 使小行星轨道发生改变.2005年美国实施了深度撞击(deep impact)任务[10 ] , 任务释放一颗约370kg的撞击器, 以约10.3 km/s的相对速度撞击“Tempel 1”彗星的核,撞击后的3年内该彗星位置变化了约10 km; 双小行星重定向测试任务(doubleasteroid redirection test, DART)将于2021年7月执行, 由一个约650kg的撞击器以约6.65 km/s的相对速度撞击小行星 Didymos的卫星, 预计产生0.8$\sim$2mm/s的速度改变量(取决于动量传递因子的大小,动量传递因子用于描述溅射物对动量传递的影响[11 ] ).Atchison等[12 ] 总结了DART轨道设计需求,包括撞击日期、撞击角度以及为了满足光学需求的太阳相位角需求;Ozimek和Atchison[13 ] 研究了DART轨道中逃逸段的月球借力方法;Atchison等[14 ] 介绍了DART的终端制导、载荷等信息. ...
Double asteroid redirection test—Mission design and navigation
1
2014
... 动能撞击技术是指撞击器以一定的速度和角度撞击小行星, 使小行星轨道发生改变.2005年美国实施了深度撞击(deep impact)任务[10 ] , 任务释放一颗约370kg的撞击器, 以约10.3 km/s的相对速度撞击“Tempel 1”彗星的核,撞击后的3年内该彗星位置变化了约10 km; 双小行星重定向测试任务(doubleasteroid redirection test, DART)将于2021年7月执行, 由一个约650kg的撞击器以约6.65 km/s的相对速度撞击小行星 Didymos的卫星, 预计产生0.8$\sim$2mm/s的速度改变量(取决于动量传递因子的大小,动量传递因子用于描述溅射物对动量传递的影响[11 ] ).Atchison等[12 ] 总结了DART轨道设计需求,包括撞击日期、撞击角度以及为了满足光学需求的太阳相位角需求;Ozimek和Atchison[13 ] 研究了DART轨道中逃逸段的月球借力方法;Atchison等[14 ] 介绍了DART的终端制导、载荷等信息. ...
Deflection and fragmentation of near-earth asteroids
2
1992
... 早期对于动能撞击处置小行星的研究, 多关注动能撞击对小行星的轨道偏转机理,一般不考虑运载能力约束.Ahrens和Harris[15 ] 的研究表明切向偏转速度增量对偏转小行星轨道效率最高,并估计了偏转小行星所需的速度增量, 但如果小行星在撞击地球前会近距离飞掠大行星,实际所需的偏转速度增量会有所降低[16 ] ;Park和Ross[17 ] 推导了小行星与地球距离的一、二阶导数表达式,发现只有在撞击前某些特殊时刻最优偏转速度才平行于小行星速度方向;Ross等[18 ] 基于圆锥曲线拼接法考虑了地球引力对最优偏转速度增量的影响.Carusi等[16 ] 提出一种估算在多体动力学模型下将小行星偏转1倍地球半径所需速度增量的方法,但仅研究了切向速度增量; Kahle等[19 ] 对其方法进行了改进,在多体问题下同时优化了切向、径向的速度增量,发现Carusi等[16 ] 的“切向速度增量”结论仅在二体阶段下是合理的,当小行星近距离飞掠行星时, 最优速度增量方向并不是切向的了,近距离飞掠行星时受行星引力影响可能会降低偏转所需的速度增量.Vasile和Colombo[20 ] 发现当偏转时间小于小行星公转周期时,最优速度增量的径向分量占主导, 当偏转时间更大时, 切向分量占主导.Yamaguchi和Yamakawa[21 ] 提出了IGMs (impact-geometry maps), 用于可视化偏转距离与IG (impact geometry)(小行星速度与航天器撞击速度的内积)之间的关系. Greenstreet等[22 ] 基于统计的方法, 发现与行星发生近距离飞掠的小行星,所需的偏转速度增量可以非常小. ...
... 除了Ahrens和Harris[15 ] 提出的偏转距离线性解析模型外,目前使用较为广泛的的偏转距离解析模型还有:2001年Conway[25 ] 提出了基于拉格朗日系数解析递推偏转距离的方法(后文简称Conway模型);2007年Izzo[26 ] 基于几何法推导了偏转距离的解析模型(后文简称Izzo模型);2008年Vasile和Colombo[20 ] 基于高斯摄动方程推导了偏转距离的解析模型(后文简称Vasile模型),其相比于Conway模型具有更高的计算效率.Vasile模型是目前使用较为广泛的解析偏转模型, 文献[27 ,28 ]均基于Vasile模型,以偏转距离为指标优化了动能撞击任务.但是目前尚无研究对偏转距离解析模型的最优性进行分析. ...
Deflecting NEOs in route of collision with the Earth
3
2002
... 早期对于动能撞击处置小行星的研究, 多关注动能撞击对小行星的轨道偏转机理,一般不考虑运载能力约束.Ahrens和Harris[15 ] 的研究表明切向偏转速度增量对偏转小行星轨道效率最高,并估计了偏转小行星所需的速度增量, 但如果小行星在撞击地球前会近距离飞掠大行星,实际所需的偏转速度增量会有所降低[16 ] ;Park和Ross[17 ] 推导了小行星与地球距离的一、二阶导数表达式,发现只有在撞击前某些特殊时刻最优偏转速度才平行于小行星速度方向;Ross等[18 ] 基于圆锥曲线拼接法考虑了地球引力对最优偏转速度增量的影响.Carusi等[16 ] 提出一种估算在多体动力学模型下将小行星偏转1倍地球半径所需速度增量的方法,但仅研究了切向速度增量; Kahle等[19 ] 对其方法进行了改进,在多体问题下同时优化了切向、径向的速度增量,发现Carusi等[16 ] 的“切向速度增量”结论仅在二体阶段下是合理的,当小行星近距离飞掠行星时, 最优速度增量方向并不是切向的了,近距离飞掠行星时受行星引力影响可能会降低偏转所需的速度增量.Vasile和Colombo[20 ] 发现当偏转时间小于小行星公转周期时,最优速度增量的径向分量占主导, 当偏转时间更大时, 切向分量占主导.Yamaguchi和Yamakawa[21 ] 提出了IGMs (impact-geometry maps), 用于可视化偏转距离与IG (impact geometry)(小行星速度与航天器撞击速度的内积)之间的关系. Greenstreet等[22 ] 基于统计的方法, 发现与行星发生近距离飞掠的小行星,所需的偏转速度增量可以非常小. ...
... [16 ]提出一种估算在多体动力学模型下将小行星偏转1倍地球半径所需速度增量的方法,但仅研究了切向速度增量; Kahle等[19 ] 对其方法进行了改进,在多体问题下同时优化了切向、径向的速度增量,发现Carusi等[16 ] 的“切向速度增量”结论仅在二体阶段下是合理的,当小行星近距离飞掠行星时, 最优速度增量方向并不是切向的了,近距离飞掠行星时受行星引力影响可能会降低偏转所需的速度增量.Vasile和Colombo[20 ] 发现当偏转时间小于小行星公转周期时,最优速度增量的径向分量占主导, 当偏转时间更大时, 切向分量占主导.Yamaguchi和Yamakawa[21 ] 提出了IGMs (impact-geometry maps), 用于可视化偏转距离与IG (impact geometry)(小行星速度与航天器撞击速度的内积)之间的关系. Greenstreet等[22 ] 基于统计的方法, 发现与行星发生近距离飞掠的小行星,所需的偏转速度增量可以非常小. ...
... [16 ]的“切向速度增量”结论仅在二体阶段下是合理的,当小行星近距离飞掠行星时, 最优速度增量方向并不是切向的了,近距离飞掠行星时受行星引力影响可能会降低偏转所需的速度增量.Vasile和Colombo[20 ] 发现当偏转时间小于小行星公转周期时,最优速度增量的径向分量占主导, 当偏转时间更大时, 切向分量占主导.Yamaguchi和Yamakawa[21 ] 提出了IGMs (impact-geometry maps), 用于可视化偏转距离与IG (impact geometry)(小行星速度与航天器撞击速度的内积)之间的关系. Greenstreet等[22 ] 基于统计的方法, 发现与行星发生近距离飞掠的小行星,所需的偏转速度增量可以非常小. ...
Two-body optimization for deflecting Earth-crossing asteroids
1
1999
... 早期对于动能撞击处置小行星的研究, 多关注动能撞击对小行星的轨道偏转机理,一般不考虑运载能力约束.Ahrens和Harris[15 ] 的研究表明切向偏转速度增量对偏转小行星轨道效率最高,并估计了偏转小行星所需的速度增量, 但如果小行星在撞击地球前会近距离飞掠大行星,实际所需的偏转速度增量会有所降低[16 ] ;Park和Ross[17 ] 推导了小行星与地球距离的一、二阶导数表达式,发现只有在撞击前某些特殊时刻最优偏转速度才平行于小行星速度方向;Ross等[18 ] 基于圆锥曲线拼接法考虑了地球引力对最优偏转速度增量的影响.Carusi等[16 ] 提出一种估算在多体动力学模型下将小行星偏转1倍地球半径所需速度增量的方法,但仅研究了切向速度增量; Kahle等[19 ] 对其方法进行了改进,在多体问题下同时优化了切向、径向的速度增量,发现Carusi等[16 ] 的“切向速度增量”结论仅在二体阶段下是合理的,当小行星近距离飞掠行星时, 最优速度增量方向并不是切向的了,近距离飞掠行星时受行星引力影响可能会降低偏转所需的速度增量.Vasile和Colombo[20 ] 发现当偏转时间小于小行星公转周期时,最优速度增量的径向分量占主导, 当偏转时间更大时, 切向分量占主导.Yamaguchi和Yamakawa[21 ] 提出了IGMs (impact-geometry maps), 用于可视化偏转距离与IG (impact geometry)(小行星速度与航天器撞击速度的内积)之间的关系. Greenstreet等[22 ] 基于统计的方法, 发现与行星发生近距离飞掠的小行星,所需的偏转速度增量可以非常小. ...
Gravitational effects of Earth in optimizing Delta V for deflecting Earth-crossing asteroids
1
2001
... 早期对于动能撞击处置小行星的研究, 多关注动能撞击对小行星的轨道偏转机理,一般不考虑运载能力约束.Ahrens和Harris[15 ] 的研究表明切向偏转速度增量对偏转小行星轨道效率最高,并估计了偏转小行星所需的速度增量, 但如果小行星在撞击地球前会近距离飞掠大行星,实际所需的偏转速度增量会有所降低[16 ] ;Park和Ross[17 ] 推导了小行星与地球距离的一、二阶导数表达式,发现只有在撞击前某些特殊时刻最优偏转速度才平行于小行星速度方向;Ross等[18 ] 基于圆锥曲线拼接法考虑了地球引力对最优偏转速度增量的影响.Carusi等[16 ] 提出一种估算在多体动力学模型下将小行星偏转1倍地球半径所需速度增量的方法,但仅研究了切向速度增量; Kahle等[19 ] 对其方法进行了改进,在多体问题下同时优化了切向、径向的速度增量,发现Carusi等[16 ] 的“切向速度增量”结论仅在二体阶段下是合理的,当小行星近距离飞掠行星时, 最优速度增量方向并不是切向的了,近距离飞掠行星时受行星引力影响可能会降低偏转所需的速度增量.Vasile和Colombo[20 ] 发现当偏转时间小于小行星公转周期时,最优速度增量的径向分量占主导, 当偏转时间更大时, 切向分量占主导.Yamaguchi和Yamakawa[21 ] 提出了IGMs (impact-geometry maps), 用于可视化偏转距离与IG (impact geometry)(小行星速度与航天器撞击速度的内积)之间的关系. Greenstreet等[22 ] 基于统计的方法, 发现与行星发生近距离飞掠的小行星,所需的偏转速度增量可以非常小. ...
Optimal deflection of NEOs en route of collision with the Earth
1
2006
... 早期对于动能撞击处置小行星的研究, 多关注动能撞击对小行星的轨道偏转机理,一般不考虑运载能力约束.Ahrens和Harris[15 ] 的研究表明切向偏转速度增量对偏转小行星轨道效率最高,并估计了偏转小行星所需的速度增量, 但如果小行星在撞击地球前会近距离飞掠大行星,实际所需的偏转速度增量会有所降低[16 ] ;Park和Ross[17 ] 推导了小行星与地球距离的一、二阶导数表达式,发现只有在撞击前某些特殊时刻最优偏转速度才平行于小行星速度方向;Ross等[18 ] 基于圆锥曲线拼接法考虑了地球引力对最优偏转速度增量的影响.Carusi等[16 ] 提出一种估算在多体动力学模型下将小行星偏转1倍地球半径所需速度增量的方法,但仅研究了切向速度增量; Kahle等[19 ] 对其方法进行了改进,在多体问题下同时优化了切向、径向的速度增量,发现Carusi等[16 ] 的“切向速度增量”结论仅在二体阶段下是合理的,当小行星近距离飞掠行星时, 最优速度增量方向并不是切向的了,近距离飞掠行星时受行星引力影响可能会降低偏转所需的速度增量.Vasile和Colombo[20 ] 发现当偏转时间小于小行星公转周期时,最优速度增量的径向分量占主导, 当偏转时间更大时, 切向分量占主导.Yamaguchi和Yamakawa[21 ] 提出了IGMs (impact-geometry maps), 用于可视化偏转距离与IG (impact geometry)(小行星速度与航天器撞击速度的内积)之间的关系. Greenstreet等[22 ] 基于统计的方法, 发现与行星发生近距离飞掠的小行星,所需的偏转速度增量可以非常小. ...
Optimal impact strategies for asteroid deflection
3
2008
... 早期对于动能撞击处置小行星的研究, 多关注动能撞击对小行星的轨道偏转机理,一般不考虑运载能力约束.Ahrens和Harris[15 ] 的研究表明切向偏转速度增量对偏转小行星轨道效率最高,并估计了偏转小行星所需的速度增量, 但如果小行星在撞击地球前会近距离飞掠大行星,实际所需的偏转速度增量会有所降低[16 ] ;Park和Ross[17 ] 推导了小行星与地球距离的一、二阶导数表达式,发现只有在撞击前某些特殊时刻最优偏转速度才平行于小行星速度方向;Ross等[18 ] 基于圆锥曲线拼接法考虑了地球引力对最优偏转速度增量的影响.Carusi等[16 ] 提出一种估算在多体动力学模型下将小行星偏转1倍地球半径所需速度增量的方法,但仅研究了切向速度增量; Kahle等[19 ] 对其方法进行了改进,在多体问题下同时优化了切向、径向的速度增量,发现Carusi等[16 ] 的“切向速度增量”结论仅在二体阶段下是合理的,当小行星近距离飞掠行星时, 最优速度增量方向并不是切向的了,近距离飞掠行星时受行星引力影响可能会降低偏转所需的速度增量.Vasile和Colombo[20 ] 发现当偏转时间小于小行星公转周期时,最优速度增量的径向分量占主导, 当偏转时间更大时, 切向分量占主导.Yamaguchi和Yamakawa[21 ] 提出了IGMs (impact-geometry maps), 用于可视化偏转距离与IG (impact geometry)(小行星速度与航天器撞击速度的内积)之间的关系. Greenstreet等[22 ] 基于统计的方法, 发现与行星发生近距离飞掠的小行星,所需的偏转速度增量可以非常小. ...
... 除了Ahrens和Harris[15 ] 提出的偏转距离线性解析模型外,目前使用较为广泛的的偏转距离解析模型还有:2001年Conway[25 ] 提出了基于拉格朗日系数解析递推偏转距离的方法(后文简称Conway模型);2007年Izzo[26 ] 基于几何法推导了偏转距离的解析模型(后文简称Izzo模型);2008年Vasile和Colombo[20 ] 基于高斯摄动方程推导了偏转距离的解析模型(后文简称Vasile模型),其相比于Conway模型具有更高的计算效率.Vasile模型是目前使用较为广泛的解析偏转模型, 文献[27 ,28 ]均基于Vasile模型,以偏转距离为指标优化了动能撞击任务.但是目前尚无研究对偏转距离解析模型的最优性进行分析. ...
... 虽然MOID概念并不等同于近地点距离[20 ,23 ] , 但通过观察公式可以发现,如果将MOID点真近点角$\theta_{MOID} $替换为近地点真近点角$\theta_{CA} $,则该公式可以用于估算近地距离改变量. $\delta {\boldsymbol \alpha }\left( {t_{d} }\right)$表示偏转位置处小行星轨道根数的改变量, $\delta {v}\left({t_{d} } \right)$表示偏转位置处小行星速度的改变量, $\delta {r}\left({t_{CA} } \right)$表示近地点位置的偏移量, $A_{CA} $和$G_{d}$表示状态转移矩阵 ...
Visualization of kinetic-impact effectiveness for asteroid deflection using impact-geometry maps
1
2018
... 早期对于动能撞击处置小行星的研究, 多关注动能撞击对小行星的轨道偏转机理,一般不考虑运载能力约束.Ahrens和Harris[15 ] 的研究表明切向偏转速度增量对偏转小行星轨道效率最高,并估计了偏转小行星所需的速度增量, 但如果小行星在撞击地球前会近距离飞掠大行星,实际所需的偏转速度增量会有所降低[16 ] ;Park和Ross[17 ] 推导了小行星与地球距离的一、二阶导数表达式,发现只有在撞击前某些特殊时刻最优偏转速度才平行于小行星速度方向;Ross等[18 ] 基于圆锥曲线拼接法考虑了地球引力对最优偏转速度增量的影响.Carusi等[16 ] 提出一种估算在多体动力学模型下将小行星偏转1倍地球半径所需速度增量的方法,但仅研究了切向速度增量; Kahle等[19 ] 对其方法进行了改进,在多体问题下同时优化了切向、径向的速度增量,发现Carusi等[16 ] 的“切向速度增量”结论仅在二体阶段下是合理的,当小行星近距离飞掠行星时, 最优速度增量方向并不是切向的了,近距离飞掠行星时受行星引力影响可能会降低偏转所需的速度增量.Vasile和Colombo[20 ] 发现当偏转时间小于小行星公转周期时,最优速度增量的径向分量占主导, 当偏转时间更大时, 切向分量占主导.Yamaguchi和Yamakawa[21 ] 提出了IGMs (impact-geometry maps), 用于可视化偏转距离与IG (impact geometry)(小行星速度与航天器撞击速度的内积)之间的关系. Greenstreet等[22 ] 基于统计的方法, 发现与行星发生近距离飞掠的小行星,所需的偏转速度增量可以非常小. ...
Required deflection impulses as a function of time before impact for Earth-impacting asteroids
1
2020
... 早期对于动能撞击处置小行星的研究, 多关注动能撞击对小行星的轨道偏转机理,一般不考虑运载能力约束.Ahrens和Harris[15 ] 的研究表明切向偏转速度增量对偏转小行星轨道效率最高,并估计了偏转小行星所需的速度增量, 但如果小行星在撞击地球前会近距离飞掠大行星,实际所需的偏转速度增量会有所降低[16 ] ;Park和Ross[17 ] 推导了小行星与地球距离的一、二阶导数表达式,发现只有在撞击前某些特殊时刻最优偏转速度才平行于小行星速度方向;Ross等[18 ] 基于圆锥曲线拼接法考虑了地球引力对最优偏转速度增量的影响.Carusi等[16 ] 提出一种估算在多体动力学模型下将小行星偏转1倍地球半径所需速度增量的方法,但仅研究了切向速度增量; Kahle等[19 ] 对其方法进行了改进,在多体问题下同时优化了切向、径向的速度增量,发现Carusi等[16 ] 的“切向速度增量”结论仅在二体阶段下是合理的,当小行星近距离飞掠行星时, 最优速度增量方向并不是切向的了,近距离飞掠行星时受行星引力影响可能会降低偏转所需的速度增量.Vasile和Colombo[20 ] 发现当偏转时间小于小行星公转周期时,最优速度增量的径向分量占主导, 当偏转时间更大时, 切向分量占主导.Yamaguchi和Yamakawa[21 ] 提出了IGMs (impact-geometry maps), 用于可视化偏转距离与IG (impact geometry)(小行星速度与航天器撞击速度的内积)之间的关系. Greenstreet等[22 ] 基于统计的方法, 发现与行星发生近距离飞掠的小行星,所需的偏转速度增量可以非常小. ...
Optimal Strategies Found Using Genetic Algorithms for Deflecting Hazardous Near-Earth Objects
2
2009
... 动能撞击任务设计的一种优化指标是最大化小行星被偏转前后的近地点距离改变量(偏转距离),换言之是使小行星被偏转后的近地点尽可能的离地球更远[23 ] .采用多体型计算小行星被偏转前后的近地点距离, 可以提供关于问题最完整的解,但轨道演化和近地点搜索计算过程中会产生冗余计算量,在任务设计初期的快速搜索研究(quick scoping studies)中,多体数值积分是不必要的[24 ] .采用二体模型替代多体模型的方法可以显著降低轨道演化过程的计算量,但在搜索近地点的过程中仍存在冗余计算量.为同时降低轨道演化和近地点搜索的计算量,可采用解析偏转模型对偏转距离进行估算. ...
... 虽然MOID概念并不等同于近地点距离[20 ,23 ] , 但通过观察公式可以发现,如果将MOID点真近点角$\theta_{MOID} $替换为近地点真近点角$\theta_{CA} $,则该公式可以用于估算近地距离改变量. $\delta {\boldsymbol \alpha }\left( {t_{d} }\right)$表示偏转位置处小行星轨道根数的改变量, $\delta {v}\left({t_{d} } \right)$表示偏转位置处小行星速度的改变量, $\delta {r}\left({t_{CA} } \right)$表示近地点位置的偏移量, $A_{CA} $和$G_{d}$表示状态转移矩阵 ...
A simplified approach to uncertainty quantification for orbits in impulsive deflection scenarios
1
2014
... 动能撞击任务设计的一种优化指标是最大化小行星被偏转前后的近地点距离改变量(偏转距离),换言之是使小行星被偏转后的近地点尽可能的离地球更远[23 ] .采用多体型计算小行星被偏转前后的近地点距离, 可以提供关于问题最完整的解,但轨道演化和近地点搜索计算过程中会产生冗余计算量,在任务设计初期的快速搜索研究(quick scoping studies)中,多体数值积分是不必要的[24 ] .采用二体模型替代多体模型的方法可以显著降低轨道演化过程的计算量,但在搜索近地点的过程中仍存在冗余计算量.为同时降低轨道演化和近地点搜索的计算量,可采用解析偏转模型对偏转距离进行估算. ...
Near-optimal deflection of earth-approaching asteroids
1
2001
... 除了Ahrens和Harris[15 ] 提出的偏转距离线性解析模型外,目前使用较为广泛的的偏转距离解析模型还有:2001年Conway[25 ] 提出了基于拉格朗日系数解析递推偏转距离的方法(后文简称Conway模型);2007年Izzo[26 ] 基于几何法推导了偏转距离的解析模型(后文简称Izzo模型);2008年Vasile和Colombo[20 ] 基于高斯摄动方程推导了偏转距离的解析模型(后文简称Vasile模型),其相比于Conway模型具有更高的计算效率.Vasile模型是目前使用较为广泛的解析偏转模型, 文献[27 ,28 ]均基于Vasile模型,以偏转距离为指标优化了动能撞击任务.但是目前尚无研究对偏转距离解析模型的最优性进行分析. ...
Optimization of interplanetary trajectories for impulsive and continuous asteroid deflection
2
2007
... 除了Ahrens和Harris[15 ] 提出的偏转距离线性解析模型外,目前使用较为广泛的的偏转距离解析模型还有:2001年Conway[25 ] 提出了基于拉格朗日系数解析递推偏转距离的方法(后文简称Conway模型);2007年Izzo[26 ] 基于几何法推导了偏转距离的解析模型(后文简称Izzo模型);2008年Vasile和Colombo[20 ] 基于高斯摄动方程推导了偏转距离的解析模型(后文简称Vasile模型),其相比于Conway模型具有更高的计算效率.Vasile模型是目前使用较为广泛的解析偏转模型, 文献[27 ,28 ]均基于Vasile模型,以偏转距离为指标优化了动能撞击任务.但是目前尚无研究对偏转距离解析模型的最优性进行分析. ...
... 经过对$\Delta \sigma$表达式的推导(具体步骤参考文献[26 ]),可将上式整理如下 ...
Impact hazard protection efficiency by a small kinetic impactor
1
2013
... 除了Ahrens和Harris[15 ] 提出的偏转距离线性解析模型外,目前使用较为广泛的的偏转距离解析模型还有:2001年Conway[25 ] 提出了基于拉格朗日系数解析递推偏转距离的方法(后文简称Conway模型);2007年Izzo[26 ] 基于几何法推导了偏转距离的解析模型(后文简称Izzo模型);2008年Vasile和Colombo[20 ] 基于高斯摄动方程推导了偏转距离的解析模型(后文简称Vasile模型),其相比于Conway模型具有更高的计算效率.Vasile模型是目前使用较为广泛的解析偏转模型, 文献[27 ,28 ]均基于Vasile模型,以偏转距离为指标优化了动能撞击任务.但是目前尚无研究对偏转距离解析模型的最优性进行分析. ...
Statistical multi-criteria evaluation of non-nuclear asteroid deflection methods
1
2017
... 除了Ahrens和Harris[15 ] 提出的偏转距离线性解析模型外,目前使用较为广泛的的偏转距离解析模型还有:2001年Conway[25 ] 提出了基于拉格朗日系数解析递推偏转距离的方法(后文简称Conway模型);2007年Izzo[26 ] 基于几何法推导了偏转距离的解析模型(后文简称Izzo模型);2008年Vasile和Colombo[20 ] 基于高斯摄动方程推导了偏转距离的解析模型(后文简称Vasile模型),其相比于Conway模型具有更高的计算效率.Vasile模型是目前使用较为广泛的解析偏转模型, 文献[27 ,28 ]均基于Vasile模型,以偏转距离为指标优化了动能撞击任务.但是目前尚无研究对偏转距离解析模型的最优性进行分析. ...
The planetary and lunar ephemerides DE430 and DE431
1
2014
... 其中, ${d}_{pi} $表示第$i$个行星地日心矢量, ${\boldsymbol \rho }_{pi}$表示第$i$个行星到小行星的矢量. 行星和月球的星历调用JPLDE430历表[29 ] , 小行星星历调用JPL Horizons On-Line EphemerisSystem[30 ] 公布的真实星历.动力学模型中考虑非引力项(太阳光压、Yarkovsky效应)的原因为:太阳光压对一些尺寸较小的小行星影响较大, 对于尺寸较大的小行星,Yarkovsky效应不能忽略[31 -33 ] . 利用Runge-Kutta-Fehlberg7(8)积分器[34 -35 ] 对轨道运动方程的一阶形式进行数值积分,并采用一种一维最小值算法[36 ] 求解近地点距离,因为这种算法不需要地心距离的一阶导数信息. ...
4
2021
... 其中, ${d}_{pi} $表示第$i$个行星地日心矢量, ${\boldsymbol \rho }_{pi}$表示第$i$个行星到小行星的矢量. 行星和月球的星历调用JPLDE430历表[29 ] , 小行星星历调用JPL Horizons On-Line EphemerisSystem[30 ] 公布的真实星历.动力学模型中考虑非引力项(太阳光压、Yarkovsky效应)的原因为:太阳光压对一些尺寸较小的小行星影响较大, 对于尺寸较大的小行星,Yarkovsky效应不能忽略[31 -33 ] . 利用Runge-Kutta-Fehlberg7(8)积分器[34 -35 ] 对轨道运动方程的一阶形式进行数值积分,并采用一种一维最小值算法[36 ] 求解近地点距离,因为这种算法不需要地心距离的一阶导数信息. ...
... 为验证本文高精度轨道预报方法的准确性,本节对小行星Apophis在2029年的近距离飞掠地球事件进行了预报, 并与JPL公布的结果[30 ] 进行了对比.小行星Apophis是目前行星防御领域高度关注的小行星,根据JPL[30 ] 公布的最新信息(表1 ),Apophis将在2029年4月13日与地球近距离飞掠, 近地点距离为0.00025AU,其质量约为$6.1\times10^{7}$ t. 将Apophis在2019年1月1日 00:00:00(TDB)的位置速度(坐标系为ICRF)作为积分起点. ...
... [30 ]公布的最新信息(表1 ),Apophis将在2029年4月13日与地球近距离飞掠, 近地点距离为0.00025AU,其质量约为$6.1\times10^{7}$ t. 将Apophis在2019年1月1日 00:00:00(TDB)的位置速度(坐标系为ICRF)作为积分起点. ...
... 小行星Apophis 初始位置速度[30 ]
Asteroid (99942) Apophis: new predictions of Earth encounters for this potentially hazardous asteroid
1
2012
... 其中, ${d}_{pi} $表示第$i$个行星地日心矢量, ${\boldsymbol \rho }_{pi}$表示第$i$个行星到小行星的矢量. 行星和月球的星历调用JPLDE430历表[29 ] , 小行星星历调用JPL Horizons On-Line EphemerisSystem[30 ] 公布的真实星历.动力学模型中考虑非引力项(太阳光压、Yarkovsky效应)的原因为:太阳光压对一些尺寸较小的小行星影响较大, 对于尺寸较大的小行星,Yarkovsky效应不能忽略[31 -33 ] . 利用Runge-Kutta-Fehlberg7(8)积分器[34 -35 ] 对轨道运动方程的一阶形式进行数值积分,并采用一种一维最小值算法[36 ] 求解近地点距离,因为这种算法不需要地心距离的一阶导数信息. ...
How precise is the orbit of asteroid (99942) Apophis and how probable is its collision with the Earth in 2036-2037?
0
2009
High precision predictions for near-Earth asteroids: the strange case of (3908) Nyx
1
2014
... 其中, ${d}_{pi} $表示第$i$个行星地日心矢量, ${\boldsymbol \rho }_{pi}$表示第$i$个行星到小行星的矢量. 行星和月球的星历调用JPLDE430历表[29 ] , 小行星星历调用JPL Horizons On-Line EphemerisSystem[30 ] 公布的真实星历.动力学模型中考虑非引力项(太阳光压、Yarkovsky效应)的原因为:太阳光压对一些尺寸较小的小行星影响较大, 对于尺寸较大的小行星,Yarkovsky效应不能忽略[31 -33 ] . 利用Runge-Kutta-Fehlberg7(8)积分器[34 -35 ] 对轨道运动方程的一阶形式进行数值积分,并采用一种一维最小值算法[36 ] 求解近地点距离,因为这种算法不需要地心距离的一阶导数信息. ...
Asteroid close encounters characterization using differential algebra: The case of Apophis
1
2010
... 其中, ${d}_{pi} $表示第$i$个行星地日心矢量, ${\boldsymbol \rho }_{pi}$表示第$i$个行星到小行星的矢量. 行星和月球的星历调用JPLDE430历表[29 ] , 小行星星历调用JPL Horizons On-Line EphemerisSystem[30 ] 公布的真实星历.动力学模型中考虑非引力项(太阳光压、Yarkovsky效应)的原因为:太阳光压对一些尺寸较小的小行星影响较大, 对于尺寸较大的小行星,Yarkovsky效应不能忽略[31 -33 ] . 利用Runge-Kutta-Fehlberg7(8)积分器[34 -35 ] 对轨道运动方程的一阶形式进行数值积分,并采用一种一维最小值算法[36 ] 求解近地点距离,因为这种算法不需要地心距离的一阶导数信息. ...
Earth-impact probability computation of disrupted asteroid fragments using gmat/stk/codes
1
2011
... 其中, ${d}_{pi} $表示第$i$个行星地日心矢量, ${\boldsymbol \rho }_{pi}$表示第$i$个行星到小行星的矢量. 行星和月球的星历调用JPLDE430历表[29 ] , 小行星星历调用JPL Horizons On-Line EphemerisSystem[30 ] 公布的真实星历.动力学模型中考虑非引力项(太阳光压、Yarkovsky效应)的原因为:太阳光压对一些尺寸较小的小行星影响较大, 对于尺寸较大的小行星,Yarkovsky效应不能忽略[31 -33 ] . 利用Runge-Kutta-Fehlberg7(8)积分器[34 -35 ] 对轨道运动方程的一阶形式进行数值积分,并采用一种一维最小值算法[36 ] 求解近地点距离,因为这种算法不需要地心距离的一阶导数信息. ...
Algorithms for Minimization Without Derivatives
2
1973
... 其中, ${d}_{pi} $表示第$i$个行星地日心矢量, ${\boldsymbol \rho }_{pi}$表示第$i$个行星到小行星的矢量. 行星和月球的星历调用JPLDE430历表[29 ] , 小行星星历调用JPL Horizons On-Line EphemerisSystem[30 ] 公布的真实星历.动力学模型中考虑非引力项(太阳光压、Yarkovsky效应)的原因为:太阳光压对一些尺寸较小的小行星影响较大, 对于尺寸较大的小行星,Yarkovsky效应不能忽略[31 -33 ] . 利用Runge-Kutta-Fehlberg7(8)积分器[34 -35 ] 对轨道运动方程的一阶形式进行数值积分,并采用一种一维最小值算法[36 ] 求解近地点距离,因为这种算法不需要地心距离的一阶导数信息. ...
... 其中, 近地点时刻$t_{CA} $采用一维最小值算法[36 ] 对式(2)进行求解,可得偏转距离为 ...
Planetary encounter analysis on the B-plane: a comprehensive formulation
1
2019
... Izzo模型的基本思想是,通过计算偏转前后近地点时间的差异来计算小行星在B平面上的偏移量$\Delta \xi $.其中,B平面定义为垂直于小行星进入地球影响球双曲线速度${U}$且经过地球质心的平面[37 ] , Öpik[38 ] 在B平面上定义了$\left( {\xi ,\eta ,\zeta } \right)$坐标系:$\eta $轴沿${U}$的方向, $\zeta$轴为地球日心速度在B平面上投影的反方向, $\xi $轴的指向由右手定则给出,在该坐标系下$\xi $坐标可代表小行星轨道与地球轨道的MOID值,B平面上的偏移量$\Delta \xi $可用来描述小行星的偏转距离. 在日心视角下,小行星被偏转前后近地点位置的几何关系如图1 所示. ...
Interplanetary Encounters: Close Range Gravitational Interactions
1
1976
... Izzo模型的基本思想是,通过计算偏转前后近地点时间的差异来计算小行星在B平面上的偏移量$\Delta \xi $.其中,B平面定义为垂直于小行星进入地球影响球双曲线速度${U}$且经过地球质心的平面[37 ] , Öpik[38 ] 在B平面上定义了$\left( {\xi ,\eta ,\zeta } \right)$坐标系:$\eta $轴沿${U}$的方向, $\zeta$轴为地球日心速度在B平面上投影的反方向, $\xi $轴的指向由右手定则给出,在该坐标系下$\xi $坐标可代表小行星轨道与地球轨道的MOID值,B平面上的偏移量$\Delta \xi $可用来描述小行星的偏转距离. 在日心视角下,小行星被偏转前后近地点位置的几何关系如图1 所示. ...
Dry mass optimization for the impulsive transfer trajectory of a near-Earth asteroid sample return mission
1
2019
... 本文采用圆锥曲线拼接法求解行星际转移轨道.圆锥曲线拼接法的基本原理为将转移轨道按照天体引力影响球进行分段,航天器在影响球内只考虑中心天体的引力,最后通过航天器在影响球边界处的状态对多段圆锥曲线进行拼接,天体影响球边界的相对速度称为逃逸速度或双曲线超速.该简化算法在深空轨道设计中是通用且高效的[39 ] .下面对两脉冲转移模型、三脉冲转移模型、借力飞行转移模型进行建模. ...
Fundamentals of astrodynamics and applications
1
2001
... 通过求解Lambert问题[40 ] ,可以计算出在地球影响球边界处的逃逸速度$v_{\infty }$以及航天器撞击小行星的相对速度${U}_{sc} $, 对应的数学表达式为 ...
Deflection driven evolution of asteroid impact risk under large uncertainties
1
2020
... 当动能航天器撞击目标小行星后, 超高速撞击会导致小行星表面产生溅射物,一部分溅射物最终会再次吸积在小行星表面,另一部分速度较高的溅射物将会从小行星的引力场中逃逸,这种现象类似于火箭产生动力的机理, 将会放大动量传递效应,可采用动量传递因子$\beta $描述溅射物对动量传递的影响[11 ] .假定航天器与小行星的撞击过程为完全非弹性碰撞, 根据动量守恒原理,小行星被撞击后产生的速度改变量可由下式估算[41 -42 ] ...
Optimization and decision-making framework for multi-staged asteroid deflection campaigns under epistemic uncertainties
1
2020
... 当动能航天器撞击目标小行星后, 超高速撞击会导致小行星表面产生溅射物,一部分溅射物最终会再次吸积在小行星表面,另一部分速度较高的溅射物将会从小行星的引力场中逃逸,这种现象类似于火箭产生动力的机理, 将会放大动量传递效应,可采用动量传递因子$\beta $描述溅射物对动量传递的影响[11 ] .假定航天器与小行星的撞击过程为完全非弹性碰撞, 根据动量守恒原理,小行星被撞击后产生的速度改变量可由下式估算[41 -42 ] ...