引言
在计算流体力学(computational fluid dynamics,CFD)领域中, 对超声速或高超声速流场进行数值模拟时, 经常会出现激波或剪切层(接触面)等较为复杂的间断流场结构.对于这些间断结构, 往往需要采用特殊的数值算法处理才能得到满足精度或分辨率需求的模拟结果.目前通用的间断处理方法主要有两类: 激波装配法[1 -6 ] 和激波捕捉法[6 -12 ] .
激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] .
通常, “间断位于控制体交界面处”的假设使激波捕捉方法所引入的激波描述误差较大, 尤其在质量较差的粗网格上更为明显, 一般表现出锯齿状的激波面.为了突破以上假设的限制, 能够在“控制体内部捕捉到激波”的算法研究已经成为目前CFD技术发展的目标之一.
国际上, 已有一些学者进行了相关的研究, 如Persson 和 Peraire [34 ] 在高阶间断Galerkin (discontinuous Galerkin, DG)方法的背景下, 通过给原始控制方程增加人工黏性项将激波(间断)尺度拉伸, 使得可以利用高阶连续近似的方法模拟黏性激波中包含的大梯度区域. 他们的研究发现, $p$阶多项式的连续近似只需要$O(h/p)$ $(h$为网格尺度)的黏性就能分辨出激波, 得到比控制体单元尺度更小的激波结构, 由此达到子单元尺度分辨率的激波捕捉效果(即在控制体内捕捉激波的分辨率).不过该方法在引入数值或物理黏性模型的同时会增加需要经验调节的参数, 且对于不同的计算问题需要不同的黏性模型才能得到稳定的结果.此外, 该方法只有在近似多项式的阶次很高($\geqslant$8阶)时, 才具有网格内部的间断捕捉能力, 对于简单的常数/线性近似, 其结果甚至不及原始方法的分辨率.
美国学者Gnoffo[35 -36 ] 将一组具有正交性的间断Walsh基函数[37 -38 ] 引入到CFD领域, 利用Walsh基函数求解具有间断解的非线性微分方程[35 ] . 其基本方法是根据Walsh基函数的乘法封闭性和一些基本变换算子(如倒数变换、积分变换、微分变换等)将原始的微分方程变换到波数空间的多项式方程系统, 在波数空间上求解原微分方程的全局解, 以期得到比传统有限体积方法更好的间断捕捉效果.然而, 在求解一维Burgers方程和Euler方程的算例中, 该方法并没有达到预期的理想效果.主要表现在两个方面: 其一是求解非线性偏微分方程时, 各个原始变量的Walsh基函数级数近似会引入很多复杂的多重交叉相乘项, 导致最终得到的代数方程系统过于复杂, 且边界条件的处理也比较困难;其二是该全局解方法完全脱离了有限体积离散的框架, 没有明确的网格划分过程, 只针对最终的代数方程系统进行数值迭代求解, 且采用数百个Walsh基函数得到的数值结果与传统采用迎风格式的有限体积方法的结果相比, 也并未表现出明显的优势.
针对Persson 和 Peraire[34 ] 与Gnoffo[35 ] 所提出的方法中存在的问题, 本文提出了一种新型有限体积方法, 该方法在保持有限体积离散优势的基础上, 充分利用了Walsh基函数的间断特点, 且能达到以下两点目的: (1) 避免Gnoffo[35 ] 所提出的全局解方法的复杂性和数值模拟的局限性; (2)仅采用低阶近似(如常数近似或线性近似)便可在网格内部捕捉到激波间断, 达到子单元尺度的激波分辨率. 本文方法的基本原理是:摒弃传统有限体积和有限元方法中流场变量在网格内部连续的假设, 将守恒变量表示为截断Walsh基函数的级数形式. 借助Walsh基函数本身所具有的间断方波属性, 在控制体内部配置间断.所配置的间断自然地将控制体虚分成若干个连续的子单元, 将得到的关于Walsh基函数级数的守恒型控制方程系统在这些子单元上积分离散, 得到了一种新的求解方法.该方法对变量的基函数表示与有限元思想类似, 且最终得到的离散系统也与有限元方法相似. 但在子单元上的积分并没有变分过程, 而与有限体积方法完全相同.因此该方法虽然在思想上介于有限元和有限体积方法之间, 但本质上属于有限体积的离散框架.本文称该方法为“Walsh函数的有限体积方法(finite volume method with Walsh basisfunctions, FVM-WBF)”. 仅依赖Walsh基函数组离散的FVM-WBF方法在子单元尺度上只有1阶计算精度. 为了进一步提高对光滑解的分辨率, 采用子单元上的流场变量均值进行流场的线性重构, 将FVM-WBF方法的离散精度提升到2阶. 在数值算例部分, 运用1阶和2阶FVM-WBF方法求解了无黏Burgers方程和Euler方程的多个定解问题, 以期验证FVM-WBF方法的计算精度、计算效率、激波捕捉能力和鲁棒性.
1 Walsh基函数
Walsh基函数由一类具有间断特点的分段常数函数构成.在给定区域上, 每个Walsh基函数的图像都由若干个相等幅度的方波构成.
若采用$g_{n} (x)$表示闭区间$[x_{a} , , x_{b}]$上具有$n$个波段的Walsh基函数, 则有如下计算公式[35 ]
(1) $g_{n} (x)=\\\left\{ \begin{array}{l@{\quad }l} (-1)^{m+1}(x_{b} -x_{a} )^{{{-1}/2}}, &x_{m-1} <x<x_{m} , 0<m\leqslant n \\ 0, &x=x_{m} , 0<m<n \\ (x_{b} -x_{a} )^{{{-1}/2}}, &x=x_{a} \\ (-1)^{n+1}(x_{b} -x_{a} )^{{{-1}/2}}, &x=x_{b} \\ \end{array} \right.$
(2) $x_{m} =x_{a} +\sum\limits_{i=1}^m {\hat{{g}}_{n} (i){d}x_{p} } \ \ (i, m, n\in Z_{+} )$
式中$\hat{{g}}_{n} (i)$是Walsh基函数$g_{n} (x)$的第$i$个波段的无量纲长度. 对于比特数$p\in N$, 如果$g_{n}(x)$的波段数$n$满足不等式
(3) $2^{p-1}<n\leqslant 2^{p}$
则称$g_{n} (x)$属于$p$组.一般$g_{n} (x)$的最小波段长度定义为
(4) ${d} x_{p} ={{(x_{b} -x_{a} )}/{2^{p}}}$
且$p$组Walsh基函数的波段长度最多包含两种, 即${d} x_{p} $或$2{d} x_{p} $. 因此式(2)中$\hat{{g}}_{n} (i)$的取值为1或2.另外, Walsh基函数还具有正交性等优良数学特征, 详细描述可参考文献[35 ], 此处不赘述.
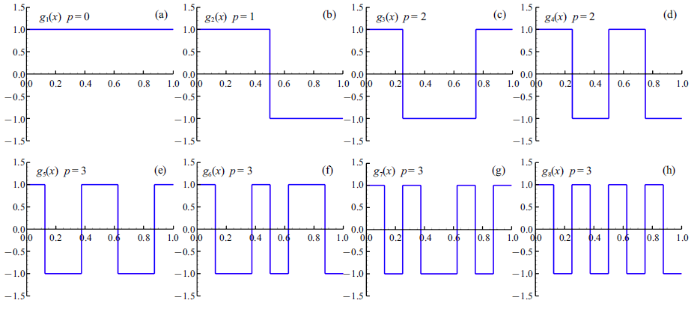
图1 展示的是前4组($0\leqslant p\leqslant 3)$Walsh基函数$(g_{1} (x)\sim g_{8}(x))$的函数图像, 可以看到, 各函数均由若干个等幅方波构成.
图1
图1
闭区间 $0\leqslant x\leqslant 1$ 上, $p=0$, 1, 2和3组的Walsh函数示意图: $g_{1} (x)\sim g_{8} (x)$
Fig. 1
Walsh functions for $p=0$, 1, 2 and 3 in the interval $0\leqslant x\leqslant 1$: $g_{1} (x)\sim g_{8} (x)$
Gnoffo[35 ] 通过研究Walsh基函数级数对若干连续和间断函数的拟合特点提出了求解非线性偏微分方程的Walsh基函数全局解方法. 该方法采用时空耦合算法, 将微分方程的各变量表示成关于时间和空间的二元Walsh基函数级数形式, 并直接对微分方程做Walsh基函数级数的积分或微分变换处理, 最终得到关于基函数系数的复杂非线性代数方程系统, 需要通过Newton迭代[35 ] 等数值手段才能完成计算.
虽然Walsh基函数全局解方法思路简单, 但存在一定的局限性, 如:(1)求解不同的微分方程需要重新推导代数方程组, 因此不具有普适性;(2)当微分方程的初边值条件复杂时, 其基函数级数展开可能导致最终的代数方程系统求解时收敛困难;(3)文献[35 ]的测试算例显示要得到与传统有限体积方法类似的模拟效果, 微分方程变量的每个维度采用的基函数个数一般要达到$2^{8}$量级左右, 这将会给最终非线性代数方程系统的求解带来较高的计算量负担.
受Gnoffo[35 ] 研究的启发, 本文将具有间断特性的Walsh基函数与传统有限体积方法结合, 提出了新的FVM-WBF方法, 以期在一定程度上改善Walsh基函数全局解方法的局限性.
2 FVM-WBF方法
根据Walsh基函数级数对任意函数拟合的合理性[35 ] , 本文考虑采用截断Walsh基函数级数近似双曲守恒律方程中的守恒变量, 下面针对一维和二维情况分别进行讨论.
2.1 一维FVM-WBF方法
(5) $u_{t} +f(u)_{x} =0$
其中$ u=u(x, t)$为守恒变量, $ f(u)=f(u(x, t))$为通量函数.若采用传统有限体积方法对守恒方程(5)进行离散, 需将其在给定控制体$\varOmega_{i}$上进行积分, 并假设控制体单元内的守恒变量为连续分布函数, 从而得到关于守恒变量单元平均值的半离散方程
(6) $\frac{d}{{d}t}\bar{{u}}_{i} (x, t)=-\frac{1}{\Delta x}(f_{i+1} -f_{i} )$
其中$\bar{{u}}_{i} (x, t)$为守恒变量$u_{i} (x, t)$在控制体$\varOmega_{i}$上的积分平均
$\begin{eqnarray*} \bar{{u}}_{i} (x, t)={{\int_{\varOmega_{i} } {u_{i} (x, t)} {d}x}/{\bar{{\varOmega }}_{i} }} \end{eqnarray*}$
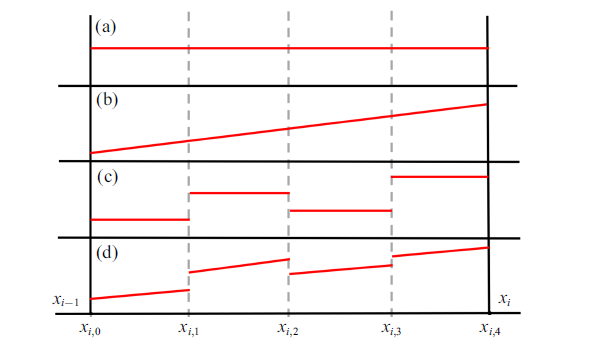
式中$\bar{{\varOmega }}_{i} $表示控制体$\varOmega_{i}$的大小, 对于一维情况, 有$\bar{{\varOmega }}_{i} =\Delta x=x_{i} -x_{i-1}$. 若考虑1阶计算精度, 守恒变量$u$为关于空间变量$x$的连续常数函数分布, 如图2 (a)所示; 而考虑2阶计算精度时, $u$为关于空间变量$x$的连续线性函数分布, 如图2 (b)所示.
图2
图2
控制体$\varOmega_i$内的变量分布示意图
Fig. 2
Variable distribution in the control volume $\varOmega_i$
现对守恒变量$ u$进行截断Walsh基函数级数近似如下
(7) $u(x, t)\approx \sum\limits_{k=1}^n {c_{k} (t)\cdot g_{k} (x)}$
式中$c_{k} (t)$是随时间变化的Walsh基函数系数, 且$n=2^{p}(p=0, 1, 2, \cdots )$. 将式(7)代入式(5), 则得到关于系数组$\left\{ {c_{k} (t)} \right\}_{k=1}^{n}$和Walsh基函数组$\left\{ {g_{k} (x)} \right\}_{k=1}^{n} $的守恒型方程组
(8) $\left( {\sum\limits_{k=1}^n {c_{k} (t)\cdot g_{k} (x)} } \right)_{t} +f\left( {\sum\limits_{k=1}^n {c_{k} (t)\cdot g_{k} (x)} } \right)_{x} =0$
(9) $\sum\limits_{k=1}^n {\frac{{d}c_{k} (t)}{{d}t}\cdot g_{k} (x)} =-f(u(x, t))_{x}$
根据式(7), 不难发现$n(n=2^{p}$, $p=0$, $1$, $2$, $\cdots )$个Walsh基函数的级数表达形式将会给控制体$\varOmega_{i} $内的守恒变量近似分布中均匀引入$n-1$个间断.若取$n=4$, 那么控制体$\varOmega_{i} $内的$3$个间断位置如图2 中的灰色竖直虚线所示.沿着$n-1$个间断所在位置进行划分, 控制体$\varOmega _{i} $将被均匀地分割为$n$个大小相同的子单元, 用$\varOmega_{i, j} (j=1, 2, \cdots , n)$表示.对于一维情况, $\varOmega_{i, j} =[x_{i, j-1} , x_{i, j} ]$, 将关于Walsh基函数系数组的守恒型方程(9)在子单元$\varOmega_{i, j} $上积分, 有
(10) $\int_{x_{i, j-1} }^{x_{i, j} } {\left( {\sum\limits_{k=1}^n {\frac{{d}c_{k} (t)}{{d}t}\cdot g_{k} (x)} } \right)}{d}x= \\ -\left[ {f_{i, j} (u(x, t))-f_{i, j-1} (u(x, t))} \right]$
(11) $\bar{{u}}_{i, j} ={{\int_{x_{i, j-1} }^{x_{i, j} } {\left( {\sum\limits_{k=1}^n {c_{k} (t)\cdot g_{k} (x)} } \right)}{d}x}/{{d}x_{p} }}=\\ {{\sum\limits_{k=1}^n {c_{k} (t)\cdot \int_{x_{i, j-1} }^{x_{i, j} } {g_{k} (x)}{d}x} }/{{d}x_{p} }}$
其中${d}x_{p} =x_{i, j} -x_{i, j-1} $, 则方程(10)可写为如下半离散形式
(12) $\frac{{d}}{{d}t}\bar{{u}}_{i, j} \left( {x, t} \right)=-\frac{1}{{d}x_{p} }\left[ {f_{i, j} (u(x, t))-f_{i, j-1} (u(x, t))} \right]$
另外, 由式(7)还可知子单元内守恒变量为常数分布近似, 所以在整个控制体$\varOmega_{i} $内, 守恒变量的分布具有分段常数的特点, 如图2 (c)所示.
根据式(11), 对方程(10)进一步整理, 可得到方程(12)的矢量形式
(13) $A_{i, j} \cdot \frac{{d}{C}}{{d}t}=F_{i, j}$
$\begin{eqnarray*} {A}_{i, j} =\bigg[ \int_{x_{i, j} }^{x_{i, j+1} } g_{1} (x) {d}x \ \ \int_{x_{i, j} }^{x_{i, j+1} } g_{2} (x) {d}x \ \ \cdots \\ {\int_{x_{i, j} }^{x_{i, j+1} } {g_{n} (x)} {d}x} \bigg] \\{C}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {c_{1} (t)} & {c_{2} (t)} & \cdots & {c_{n} (t)} \\ \end{array} }} \right]^{T} \\ F_{i, j} =-\left[ {f_{i, j} (u(x, t))-f_{i, j-1} (u(x, t))} \right] \end{eqnarray*}$
(14) ${A}_{i, j} \cdot \frac{{d}{C}}{{d}t}=\sum\limits_{k=1}^n {\left( {\frac{{d}c_{k} (t)}{{d}t}\cdot \int_{x_{i, j} }^{x_{i, j+1} } {g_{k} (x)} {d}x} \right)}$
若将守恒型方程(9)在所有子单元上积分离散, 则可在控制体$\varOmega_{i}$上得到关于Walsh基函数系数矢量${C}$的紧致矩阵方程
(15) ${A}^{(n)}\cdot \frac{{d}{C}}{{d}t}={F}$
$\begin{eqnarray*} {F}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {F_{i, 1} } & {F_{i, 2} } & \cdots & {F_{i, n} } \\ \end{array} }} \right]^{T} \\{A}^{(n)}=[a_{j, k} ]_{n\times n} = \\\quad \left[ {{\begin{array}{*{20}c} {\int_{x_{i, 0} }^{x_{i, 1} } {g_{1} (x)} {d}x} & \cdots & {\int_{x_{i, 0} }^{x_{i, 1} } {g_{k} (x)} {d}x} & \cdots & {\int_{x_{i, 0} }^{x_{i, 1} } {g_{n} (x)} {d}x} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ {\int_{x_{i, j-1} }^{x_{i, j} } {g_{1} (x)} {d}x} & \cdots & {\int_{x_{i, j-1} }^{x_{i, j} } {g_{k} (x)} {d}x} & \cdots & {\int_{x_{i, j-1} }^{x_{i, j} } {g_{n} (x)} {d}x} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ {\int_{x_{i, n-1} }^{x_{i, n} } {g_{1} (x)} {d}x} & \cdots & {\int_{x_{i, n-1} }^{x_{i, n} } {g_{k} (x)} {d}x} & \cdots & {\int_{x_{i, n-1} }^{x_{i, n} } {g_{n} (x)} {d}x} \\ \end{array} }} \right] \end{eqnarray*}$
$\begin{eqnarray*} a_{j, k} =\int_{x_{i, j-1} }^{x_{i, j} } {g_{k} (x)} {d}x=\frac{{d}x_{p} }{\sqrt {\Delta x} }\cdot {sgn}\left[ {g_{k} \left( {\frac{x_{i, j} +x_{i, j-1} }{2}} \right)} \right] \\{sgn}(x)=\left\{ {{\begin{array}{l@{\quad}l} 1,&x>0 \\ 0,&x=0 \\ -1,&x<0 \\ \end{array} }} \right. \end{eqnarray*}$
矩阵${A}^{(n)}$表示$n$个Walsh基函数对应得到的矩阵, 其中所有元素的公因子为${{{d}x_{p}}/{\sqrt {\Delta x} }}$, 所以该矩阵可归一化为只包含$\pm 1$的常数矩阵.例如, 当$n=2$, 4, 8时有
$\begin{eqnarray*} {A}^{(2)}=\frac{{d}x_{p} }{\sqrt {\Delta x} }\left[ {{\begin{array}{*{20}c} 1 & 1 \\ 1 & {-1} \\ \end{array} }} \right] \\ {A}^{(4)}=\frac{{d}x_{p} }{\sqrt {\Delta x} }\left[ {{\begin{array}{*{20}c} 1 & 1 & 1 & 1 \\ 1 & 1 & {-1} & {-1} \\ 1 & {-1} & {-1} & 1 \\ 1 & {-1} & 1 & {-1} \\ \end{array} }} \right] \\ {A}^{(8)}=\frac{{d}x_{p} }{\sqrt {\Delta x} }\left[ {{\begin{array}{*{20}c} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & {-1} & {-1} & {-1} & {-1} \\ 1 & 1 & {-1} & {-1} & {-1} & {-1} & 1 & 1 \\ 1 & 1 & {-1} & {-1} & 1 & 1 & {-1} & {-1} \\ 1 & {-1} & {-1} & 1 & 1 & {-1} & {-1} & 1 \\ 1 & {-1} & {-1} & 1 & {-1} & 1 & 1 & {-1} \\ 1 & {-1} & 1 & {-1} & {-1} & 1 & {-1} & 1 \\ 1 & {-1} & 1 & {-1} & 1 & {-1} & 1 & {-1} \\ \end{array} }} \right] \end{eqnarray*}$
显然, 矩阵${A}^{(n)}$对称可逆, 因此方程(15)的“解的存在性”得到保证.一个有趣的特点是矩阵${A}^{(n)}$的逆${A}^{(n)-1}$可由${A}^{(n)}$直接`计算得到, 即
$\begin{eqnarray*} {A}^{(n)-1}=\frac{\sqrt {\Delta x} }{2^{p}\cdot {d}x_{p} }\cdot {A}^{(n)} \end{eqnarray*}$
根据该特性, 在求解时可以省略矩阵求逆的过程, 直接由预先储存的${A}^{(n)}$进行计算, 这在一定程度上对计算效率是有益的.
以上介绍的求解标量方程的FVM-WBF方法同样适用于求解守恒型方程系统, 例如, 对于一维Euler方程
(16) $\lt.\begin{array}{l} {u}_{t} +{f}({u})_{x} =0\\ u=\left[ {{\begin{array}{*{20}c} \rho \\ m \\ E \\ \end{array} }} \right],\ \ \quad {f}({u})=\left[\begin{array}{*{20}c} m \\ {{{m^{2}}/\rho }+p} \\ {{{m(E+p)}/\rho }} \\ \end{array}\right] \end{array}\}$
其中$\rho$, $u$, $p$, $E$分别为密度、速度、压强和单位体积总能, $m=\rho u$, 状态方程为
(17) $p=(\gamma -1)\cdot \left( {E-\frac{1}{2}\rho u^{2}} \right)$
类似于标量情况, 对3个守恒变量(密度$\rho$, 动量$m$和能量$E)$进行截断Walsh基函数级数近似
(18) $\left. {{\begin{array}{*{20}c} {\rho (x, t)\approx \sum\limits_{k=1}^n {c_{k}^{\rho } (t)\cdot g_{k} (x)} } \\[3mm] {m(x, t)\approx \sum\limits_{k=1}^n {c_{k}^{m} (t)\cdot g_{k} (x)} } \\[3mm] {E(x, t)\approx \sum\limits_{k=1}^n {c_{k}^{E} (t)\cdot g_{k} (x)} } \\ \end{array} }} \right\}$
其中$c_{k}^{\rho } (t)$, $c_{k}^{m} (t)$和$c_{k}^{E}(t)$分别是对应于3个守恒变量的Walsh基函数系数. 将式(18)代入守恒型方程(16), 并在每个子单元上积分离散, 最终得到与方程(15)类似的紧致型矩阵方程
(19) ${A}^{(3n)}\cdot \frac{{d}{C}}{{d}t}={F}$
$\begin{eqnarray*} {A}^{(3n)}=\left[ {{\begin{array}{*{20}c} {{A}^{(n)}} & & \\ & {{A}^{(n)}} & \\ & & {{A}^{(n)}} \\ \end{array} }} \right] \\ {C}=\left[ {{\begin{array}{*{20}c} {{C}^{\rho }}\ \ \ & {{C}^{m}} \ \ \ & {{C}^{E}} \\ \end{array} }} \right]^{T} \\\ \ \ &\ \ \ & {C}^{\rho }=[{\begin{array}{*{20}c} {c_{1}^{\rho } (t)} \ \ \ & {c_{2}^{\rho } (t)} \ \ \ & \cdots \ \ \ & {c_{n}^{\rho } (t)} \\ \end{array} }]^{T} \\\ \ \ &\ \ \ & {C}^{m}=[{\begin{array}{*{20}c} {c_{1}^{m} (t)} \ \ \ & {c_{2}^{m} (t)} \ \ \ & \cdots \ \ \ & {c_{n}^{m} (t)} \\ \end{array} }]^{T} \\\ \ \ &\ \ \ & {C}^{E}=[{\begin{array}{*{20}c} {c_{1}^{E} (t)} \ \ \ & {c_{2}^{E} (t)} \ \ \ & \cdots \ \ \ & {c_{n}^{E} (t)} \\ \end{array} }]^{T} \\\ \ \ &\ \ \ & {F}=[{\begin{array}{*{20}c} {{F}^{\rho }} \ \ \ & {{F}^{m}} \ \ \ & {{F}^{E}} \\ \end{array} }]^{T} \\\ \ \ &\ \ \ & {F}^{\rho /m/E}{=}-[{f}({u}_{i, j} )-{f}({u}_{i, j-1} )] \end{eqnarray*}$
2.2 二维FVM-WBF方法
(20) $u_{t} +f(u)_{x} +g(u)_{y} =0$
其中$u=u , (x, y, t)$是守恒变量, $f(u)$和$g(u)$分别是$x$和$y$方向上的通量函数, $(x, , y)\in\varOmega$ $(\varOmega $为求解域).
在控制体$\varOmega_{i} $上, 对守恒变量$u=u, (x, y, t)$进行如下Walsh基函数级数近似
(21) $u(x, y, t)\sim eq \sum\limits_{k_{1} =1}^{n_1} {\sum\limits_{k_{2} =1}^{n_2} {c_{k_{1} , , k_{2} } (t)g_{k_{1} } (x)g_{k_{2} } (y)} }$
其中, $n_1$和$n_2$分别为$x$和$y$方向上各自使用的Walsh基函数个数, $c_{k_{1}, , k_{2} } (t)$表示对应的基函数系数.
显然, 在控制体$\varOmega_{i}$内, 式(21)会给守恒变量的近似分布函数中引入$n_1+n_2-2$个间断(其中$x$方向为$n_1-1$个间断, $y$方向为$n_2-1$个间断).沿着间断, 可将原始控制体$\varOmega_{i} $分割为$n_1\cdot n_2$个大小完全相同的子单元, 同样用$\varOmega_{i, j}$$(j=1, 2, \cdots , n_1\cdot n_2)$表示.与一维方法类似, 将式(21)代入守恒型方程(20)后, 在每个子单元上进行积分离散.最终得到关于Walsh基函数系数组
$\begin{eqnarray*} \left\{ {c_{k_{1} , , k_{2} } (t)} \right\}_{k_{1} =1, k_{2} =1}^{n_1, n_2} \end{eqnarray*}$
(22) ${A}^{(n_1, n_2)}\cdot \frac{{d}{C}}{{d}t}={F}+{G}$
其中${C}=[{\begin{array}{*{20}c} {c_{1, 1} \left( t \right)} & \cdots & {c_{1, n_{2} } \left( t\right)} & {c_{2, 1} \left( t \right)} & \cdots &{c_{n_1, n_2} \left( t \right)} \\\end{array} }]^{T}$, ${F}=[{\begin{array}{*{20}c} {F_{i, 1} } & {F_{i, 2} } & \cdots & {F_{i, n_1\cdot n_2} } \\\end{array} }]^{T}$, ($F_{i, j} (j=1, 2, \cdots , n_1\cdot n_2)$为$\varOmega_{i, j} $上$x$方向的通量),${G}=[{\begin{array}{*{20}c} {G_{i, 1} } & {G_{i, 2} } & \cdots & {G_{i, n_1\cdot n_2} } \\\end{array} }]^{T}$, ($G_{i, j} (j=1, 2, \cdots , n_1\cdot n_2)$为$\varOmega_{i, j} $上$y$方向的通量).对于二维情况, 矩阵${A}^{(n_1, n_2)}$可由相应的2个一维矩阵的张量积得到, 即${A}^{(n_1, n_2)}={A}^{(n_1)}\otimes {A}^{(n_2)}(\otimes$表示张量积), 也可由相应的元素公式计算得到$\begin{eqnarray*}\oint_{\bar{{I}}_{j} } {g_{i_{1} } (x)g_{i_{2} } (y){d}x{d}y} =\frac{{d}x_{p}\cdot {d}y_{p} }{\sqrt {\Delta x\Delta y} }\cdot \\{sgn}\left[ {g_{i_{1} } \left( {\frac{x_{j_{1} } +x_{j_{1} +1} }{2}} \right)}\right]\cdot {sgn}\left[ {g_{i_{2} } \left( {\frac{y_{j_{2} } +y_{j_{2} +1}}{2}} \right)} \right]\end{eqnarray*}$
该矩阵同样对称可逆, 所以对于方程(22), “解的存在性”可以得到保证. 而且${A}^{(n_1, n_2)}$的逆也可由其本身计算得到, 即
$\begin{eqnarray*} {A}^{(n_1, n_2)-1}=\frac{\sqrt {\Delta x\cdot \Delta y} }{2^{p_1}\cdot {d}x_{p} \cdot 2^{p_2}\cdot {d}y_{p} }\cdot {A}^{(n_1, n_2)} \end{eqnarray*}$
($p_1$和$p_2$分别是$n_1$和$n_2$对应的Walsh基函数组数)或者由对应的两个一维逆矩阵的张量积得到, 即
$\begin{eqnarray*} {A}^{(n_1, n_2)-1}={A}^{(n_1)-1}\otimes{A}^{(n_2)-1} \end{eqnarray*}$
实际求解时, 矩阵${A}^{(n_1, n_2)}$及其逆都可预先计算并储存, 以减少计算过程中矩阵求逆带来的计算量.
对于二维守恒型方程系统, 将守恒变量按分量进行Walsh基函数级数近似, 可得到与方程(19)类似的块对角紧致矩阵方程, 对角线上的每个矩阵均为${A}^{(n_1, n_2)}$, 其推导过程类似一维情况, 这里不再赘述.
由上述描述可知, FVM-WBF方法采用时空分离的思想在子单元框架下对微分方程进行有限体积离散, 具有更好的普适性.且FVM-WBF方法是根据Walsh基函数引入的间断位置对原始控制体单元进行虚子单元划分, 并不改变原始网格的几何拓扑结构, 保持了原始网格良好的几何适应性.另外, 对于边界条件的处理, FVM-WBF方法与原始有限体积方法类似, 为了保持与内场一致的数值通量计算, 可以在边界处延拓一层辅助网格单元, 用与边界单元相同的Walsh基函数表达辅助网格上的流场变量, 可以在边界处达到子单元尺度的误差精度.相对于Gnoffo[35 ] 提出的Walsh基函数全局解方法,FVM-WBF方法并未在离散和求解方面引入新的困难.
2.3 误差和精度分析
传统有限体积方法假设控制体内的守恒变量为常数函数分布, 如图2 (a)所示.那么相对于每个控制体$\varOmega_{i} $的尺度, 计算精度为1阶, 其误差为${O}(\Delta x)$, 即
(23) $u_{i} (x)-\bar{{u}}_{i} ={O}(\Delta x)$
而对于FVM-WBF方法, 守恒变量采用Walsh基函数级数近似(如式(7)), 控制体内守恒变量的分布为分段常数函数形式(见图2 (c)).相对于每个子单元$\varOmega_{i, j} $的尺度, 计算精度也为1阶, 子单元上的误差为${O}({d}x_{i, p} )$, 即
(24) $u_{i} (x)-\bar{{u}}_{i, j} ={O}({d}x_{i, p} )$
而对于整个控制体$\varOmega_{i} $的尺度, Walsh基函数级数近似的积分平均如下
(25) $\widehat{u}_{i} =\int_{x_{i-1} }^{x_{i} } \left( {\sum\limits_{k=1}^n {c_{k} (t)\cdot g_{k} (x)} } \right) {d}x/{\Delta x}$
(26) $\widehat{u}_{i} ={{c_{1} (t)}/{\sqrt {\Delta x} }}$
(27) $\left. {{\begin{array}{*{20}c} {\bar{{u}}_{i, 1} ={{[c_{1} (t)+c_{2} (t)]}/{\sqrt {\Delta x} }}} \\ {\bar{{u}}_{i, 2} ={{[c_{1} (t)-c_{2} (t)]}/{\sqrt {\Delta x} }}} \\ \end{array} }} \ \ \right\}$
(28) $\widehat{u}_{i} =\frac{1}{2}(\bar{{u}}_{i, 1} +\bar{{u}}_{i, 2} )$
(29) $u_{i}(x)-\widehat{u}_{i} ={O}({{\Delta x}/{2}})$
(30) $u_{i}(x)-\widehat{u}_{i} ={O}({{\Delta x}/{4}})$
(31) $u_{i}(x)-\widehat{u}_{i} ={O}({{\Delta x}/{8}})$
从以上推导可知, 对于FVM-WBF方法, 当采用$n=2^{p}(p\geqslant 1)$个Walsh基函数对守恒变量近似时, 其近似误差为${O}(\Delta x/2^{p})$.因此理论上, 相对于传统有限体积方法, FVM-WBF ($n=2^{p})$方法的误差约以因子${1/{2^{p}}}$缩减, 而收敛精度并没有提高.
通常, 为提高精度, 传统有限体积方法是在当前控制体和周围多个控制体构成的模板上, 采用守恒变量均值进行多项式重构, 如线性重构后, 变量的分布如图2 (b)所示. 而本文根据FVM-WBF方法的特点, 采用控制体内的子单元均值(如式(11))进行线性重构实现2阶精度的计算, 具体公式如下
(32) $\left. {{\begin{array}{l} {u_{L} =u_{i, j-1} +0.5 s_{L} } \\ {u_{R} =u_{i, j} -0.5 s_{R} } \\ \end{array} }}\ \right\}$
$\begin{eqnarray*} s_{L} =\frac{a_{L} (b_{L}^{2}+\varepsilon )+b_{L} (a_{L}^{2}+\varepsilon )}{a_{L}^{2}+b_{L}^{2}+2\varepsilon } \\s_{R} =\frac{a_{R} (b_{R}^{2}+\varepsilon )+b_{R} (a_{R}^{2}+\varepsilon )}{a_{R}^{2}+b_{R}^{2}+2\varepsilon } \\a_{L} =u_{i, j} -u_{i, j-1} , \quad a_{R} =u_{i, j+1} -u_{i, j} \\[-3mm]b_{L} =u_{i, j-1} -u_{i, j-2} , \quad b_{R} =u_{i, j} -u_{i, j-1} \end{eqnarray*}$
线性重构后, 控制体$\varOmega_{i}$内的变量分布如图2 (d)所示, 为分段线性分布.传统2阶有限体积方法与本文重构的2阶FVM-WBF方法在计算精度和计算效率方面的比较将在下小节的数值测试中进行讨论.
3 数值测试
本节采用FVM-WBF方法对一/二维无黏Burgers方程和Euler方程的几个非定常问题进行求解, 并通过与传统有限体积方法的数值结果进行对比, 测试和验证该方法的计算精度、计算效率、激波捕捉能力和鲁棒性.其中数值通量的计算均采用熵相容格式[21 -22 ] , 时间推进均采用满足TVD条件的3阶显式Runge-Kutta[39 ] 方法.
为便于表述, 算例中采用记号FVM-WBF-O表示初始没有线性重构的1阶FVM-WBF方法的数值结果, 而用FVM-WBF-R2表示经线性重构实现的2阶FVM-WBF方法的数值结果, 作为对照, 记号OFVM-1st和OFVM-2nd分别用来表示传统有限体积方法(用OFVM方法表示)的1阶和2阶计算结果.一维算例中的Exact表示解析解.
3.1 一维无黏Burgers方程连续初值问题
Burgers方程的第1个测试算例是一维区域$[-2,2]$上的连续初值问题, 主要用以测试FVM-WBF方法的计算精度和计算效率, 其初始条件为
(33) $u_{0} \left( x \right)=\left\{ {\begin{array}{l@{\quad }l} u^{0},&\left| x \right|>1 \\ u^{0}-u^{1}\sin \pi x,&\left| x \right|\leqslant 1 \\ \end{array}} \right.$
(34) $u(x, t)=\frac{u^{0}}{u^{1}}-u^{1}\sin (\pi x-ut)$
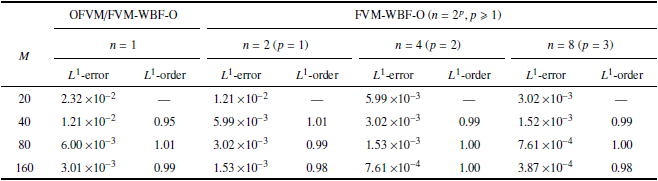
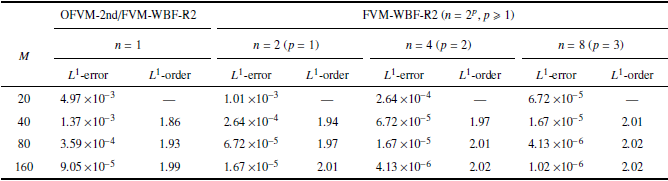
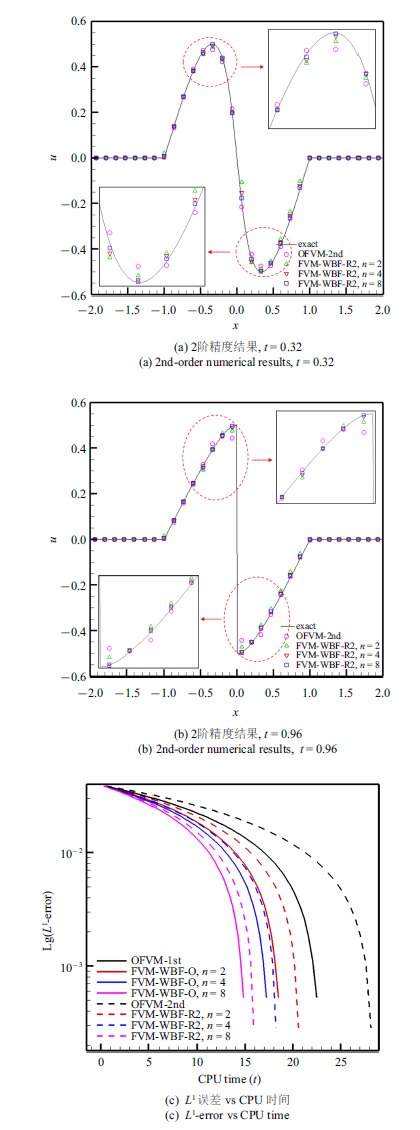
取$u^{0}=0$, $u^{1}=0.5$, 采用周期边界条件.针对$t=0.32$和$t=0.96$这两个时刻, 分别在表1 到表4 中给出了不同网格上的OFVM和FVM-WBF($n=2$, 4, 8)方法1阶与2阶数值计算的$L^{1}$误差与相应的收敛精度.可以发现, 对于两种计算精度,OFVM与FVM-WBF方法在两个时间点的收敛精度基本相同, 但在相同网格上, 相对于OFVM方法,FVM-WBF方法的误差约以因子${1/{2^{p}}}$缩减(这与第2.3节分析的结论一致). 若OFVM方法采用的网格单元数目等于FVM-WBF方法的网格单元数与基函数个数的乘积时, 在整个计算域上两种方法具有相同的自由度. 对比表1 $\sim \!$表4 中两种方法自由度相同时的误差, 可以发现, 1阶精度时两种方法的误差几乎相同, 这说明FVM-WBF方法表现出了与OFVM方法网格加密等价的误差效应. 而2阶精度时,FVM-WBF比OFVM方法的误差略小, 这可能是由于子单元重构模板与原始控制体重构模板的差异造成的. 另外, 表2 和表4 给出的$t=0.96$时刻的误差和收敛精度相对于$t=0.32$时刻都有所减小, 这是因为$t=0.96$时刻在$x=0$位置处形成的压缩激波对精度造成了影响. 图3 (a)和图3 (b)分别给出了网格量为$M=20$时, 两个时间点上两种方法的2阶精度结果与精确解的对比, 可以看到FVM-WBF方法取$n=2$, 4, 8, 3种基函数级数近似时, 在光滑解的极值附近和间断解处都表现出比OFVM方法更好的分辨率. 图3 (c)展示的是两种方法取相同的自由度时(本算例的自由度为1280), 其误差精度与所消耗的CPU时间之间的关系, 通过比较发现, 当误差和收敛精度相同时,FVM-WBF方法所消耗的CPU时间都比OFVM方法短, 且随着Walsh基函数数目的增大, FVM-WBF方法的计算效率也逐步提高.
图3
图3
一维Burgers 方程连续初值问题数值解
Fig. 3
Numerical results of continuous initial value problem of 1D Burgers equation(2) LAX
3.2 一维Euler方程激波管问题
本算例求解了一维Euler方程的两种激波管问题(SOD激波管和LAX激波管). 在相同网格上比较了FVM-WBF方法和OFVM方法对弱间断和强间断的捕捉效果. 两个激波管问题的计算域均取为$[-0.5, 0.5]$, 初始条件分别为:
(35) $({\begin{array}{*{20}c} \rho , & u, & p \\ \end{array} })=\left\{ {{\begin{array}{ll} {1.0}, 0, {1.0}, & {x<0} \\ {0.125}, 0, {0.1}, & {x>0} \\ \end{array} }} \right.$
(36) $({\begin{array}{*{20}c} \rho , & u, & p \\ \end{array} })=\left\{ {{\begin{array}{ll} {0.445}, {0.698}, {3.528}, & {x<0} \\ {0.5}, 0, {0.571}, & {x>0} \\ \end{array} }} \right.$
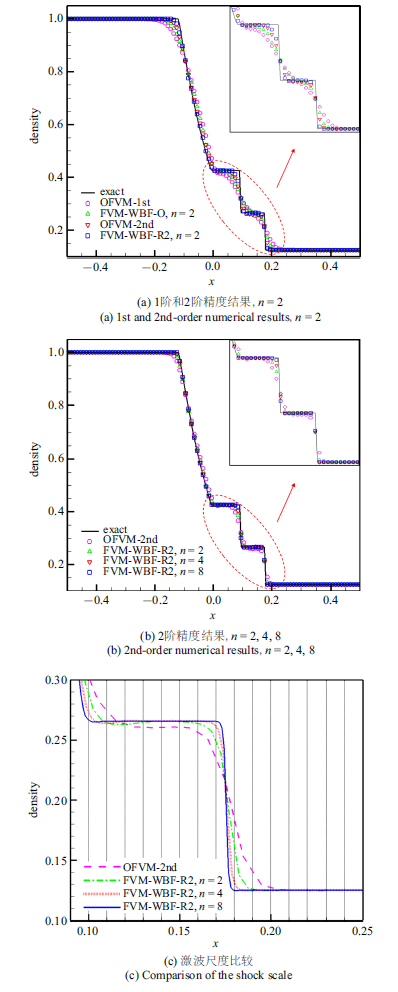
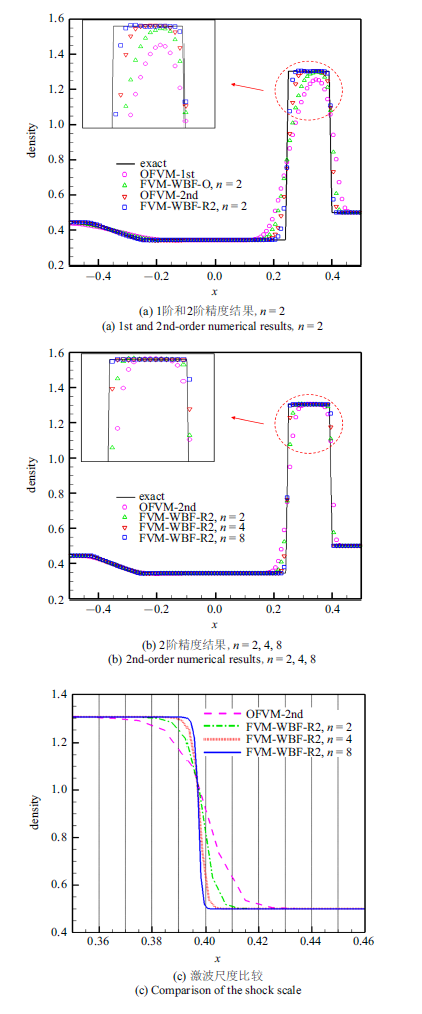
均采用齐次Neumann边界条件, 网格量均为$M=100$.SOD激波管问题计算到时间$t=0.1$, LAX激波管问题计算到时间$t=0.\mbox{16}$. OFVM方法与FVM-WBF方法对两个激波管问题的1阶和2阶计算所得数值密度的分布分别如图4 和图5 所示. 通过对比激波、接触间断和稀疏波拐角等处的数值结果, 可以发现, 网格相同的情况下, FVM-WBF方法对弱间断和强间断均有更好的捕捉效果, 且对光滑解的模拟也有一定的改善. 图4 (c)和图5 (c)给出的是两种方法的2阶计算捕捉到的激波与网格尺度对比的放大图, 其中灰色虚直线代表网格边界.可以看到一维FVM-WBF方法在$n=4$和$8$时均能达到小于网格尺度的激波捕捉效果.
图4
图4
一维Euler方程 SOD激波管问题数值解
Fig. 4
Numerical results of SOD-shock tube problem of 1D Euler equations
图5
图5
一维Euler方程 LAX激波管问题数值解
Fig. 5
Numerical results of LAX-shock tube problem of 1D Euler equations
3.3 二维无黏Burgers方程间断初值问题
本算例求解了二维无黏Burgers方程, 比较了二维FVM-WBF方法与OFVM方法在相同网格上模模拟标量间断初值问题的效果.计算域为$[-1,1]\times[-1,1]$, 初始条件为
(37) $u_{0} (x)=\left\{ {{\begin{array}{l@{\quad }l} 1, & {x^{2}+y^{2}<{1/9}} \\ {-1}, & {others} \\ \end{array} }} \right.$
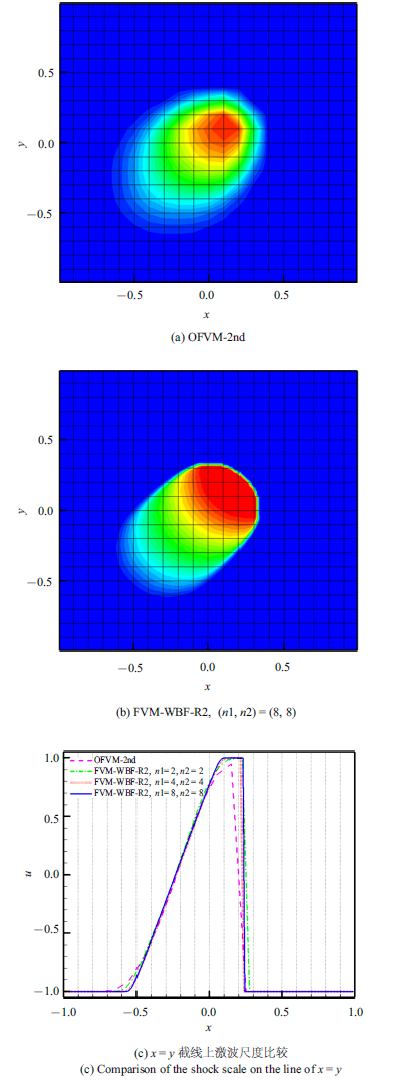
采用周期边界条件, 计算到时间$t=0.3$, 网格量为$M=20\times20$. 图6 展示的是两种方法2阶精度的数值结果.其中, 图6 (a)和图6 (b)是等值线图. 在这两幅图中, 同时给出了网格线以清楚地反映所得激波尺度与网格尺度的对比效果. 图6 (c)进一步给出了$x=y$截线上的数值解分布(图中灰色虚直线代表网格边界), 可以发现FVM-WBF方法中的$n_1$和$n_2$取2, 4, 8时捕捉到的激波尺度都小于网格尺度, 说明FVM-WBF方法在二维标量情况下能够达到网格内部捕捉间断的分辨率.
图6
图6
二维Burgers方程间断初值问题数值结果
Fig. 6
Numerical results of the discontinuously initial value problem of 2D Burgers equation
3.4 二维Euler方程黎曼问题
二维Euler方程的黎曼问题反映了多变气体的多尺度流场结构, 一般由3种常见的一维波(稀疏波, 激波和接触间断波)相互作用形成.本算例在计算域[0, 1]$\times$[0, 1]上考虑如下初始条件的黎曼问题[40 ]
(38) $(\rho , u, v, p)=\\\quad \left\{ {\begin{array}{ll} (1.5, 0, 0, 1.5),&x>0.5, y>0.5 \\ (0.5323, 1.206, 0, 0.3),&x\leqslant 0.5, y>0.5 \\ (0.138, 1.206, 1.206, 0.029),&x\leqslant 0.5, y\leqslant 0.5 \\ (0.5323, 0, 1.206, 0.3),&x>0.5, y\leqslant 0.5 \\ \end{array}} \right.$
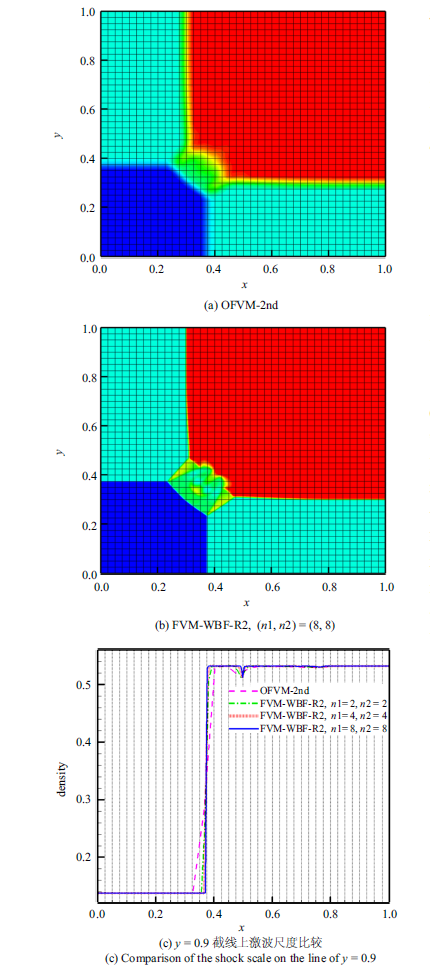
采用齐次Neumann边界条件, 在相同的网格$M= 40\times40$上比较了OFVM方法与FVM-WBF方法计算到$t=0.3$时刻对激波的捕捉效果. 图7 (a)和图7 (b)分别展示的是两种方法数值结果的密度等值线图. 可以看到, 相对于OFVM方法, FVM-WBF方法显著提高了激波间断的分辨率. 取$y=0.9$的截线, 如图7 (c)所示, 可以发现FVM-WBF-R2在$n_1$, $n_2$分别均取4或8时都能达到小于网格尺度的激波捕捉分辨率,而OFVM方法捕捉的激波约为2个网格尺度的宽度. 该算例进一步说明FVM-WBF方法在二维Euler方程系统下也可以实现网格内部捕捉间断的效果.
图7
图7
OFVM和FVM-WBF方法对二维Euler方程黎曼问题的2阶精度数值密度结果
Fig. 7
Numerical density obtained by 2nd-order OFVM and FVM-WBF method for Riemann problem of 2D Euler equations
3.5 Rayleigh-Tayler不稳定性问题
Rayleigh-Tayler (R-T)不稳定性问题[41 ] 描述的是, 对于上下两层密度不同的流体, 当密度大的流体受到重力影响流向密度小的流体时所产生的流动现象.经过一定时间的演化, 轻流体的空泡和重流体的“尖顶”相互干扰, 最终形成非常复杂的流场结构.
该算例的计算域为$[0, 0.25]$$\times$[0.1], 初始条件为
(39) $(\rho , u, v, p)=\\ \left\{ {\begin{array}{ll} (2, 0, -0.025a\cos (8\pi x), 2y+1),&y<0.5 \\ (1, 0, -0.025a\cos (8\pi x), y+1.5),&y\geqslant 0.5 \\ \end{array}} \right.$
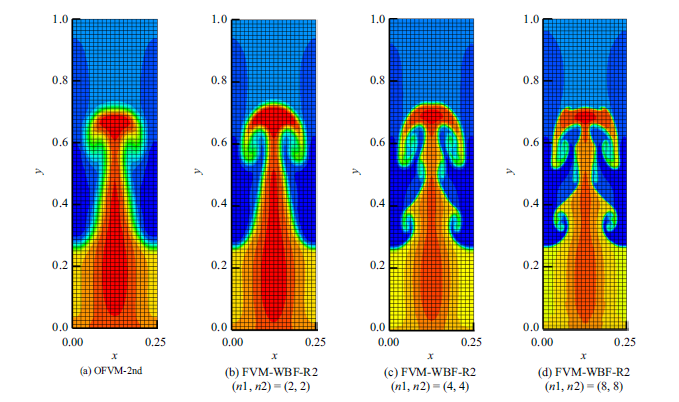
其中$a=\sqrt {{{\gamma p}/\rho }}$, 左右边界为无黏壁面条件;上下边界为固定流场数据. 在网格$M=20\times80$上计算到时间$t=1.95$.测试了FVM-WBF方法对复杂流场结构的模拟效果. 图8 给出了OFVM与FVM-WBF方法取$(n_1, n_2)=(2, 2)$, $(4, 4)$, $(8, 8)$时的2阶精度数值密度等值线图.可以看到, 相对于OFVM方法,FVM-WBF方法随着Walsh基函数个数的增大, 其捕捉到的流场细节也迅速增多.不过2阶精度采用的是线性重构近似, 所以并没有良好地解析极值点, 这在本算例中有较明显的体现.同时可以观察到随着基函数个数的增大, 界面处表现出了越来越明显的数值扰动现象, 这与文献[41 ]中采用网格加密技术对该问题进行数值模拟时表现出的现象类似, 进一步说明FVM-WBF方法采用的子单元划分技术与直接网格加密技术具有等价的数值效应.
图8
图8
OFVM和FVM-WBF方法对R-T不稳定性问题的2阶精度数值密度等值线图
Fig. 8
Density contours obtained by 2nd-order OFVM and FVM-WBF method for R-T problem
另外, 该算例还考察了两种方法计算相同时间步数时的计算效率. 因为网格量相同时, FVM-WBF方法的自由度是OFVM方法的$n_1\cdot n_2$倍, 所以理论上, 计算相同的时间步数, FVM-WBF方法消耗的CPU时间应该是OFVM方法的$n_1\cdot n_2$倍, 而自由度数目相同时, 两者所耗费的时间应该相同, 但测试结果显示并非如此. 表5 给出了1000个时间步时两种方法的CPU时间对比.对于3种基函数个数, OFVM方法采用了与FVM-WBF方法相同自由度数目的网格量.可以看到, 自由度相同时, 平均每个时间步FVM-WBF方法比OFVM方法提高了约20%的计算效率, 这可能是由于FVM-WBF方法程序实现时数据结构存储方面带来的效益.未来可以从自适应算法的角度进一步提高FVM-WBF方法的计算效率, 相关的研究工作正在进行中.
4 结论
本文借助Walsh基函数发展了一种可以在网格内部捕捉间断的新型有限体积方法, 简称FVM-WBF方法.其基本原理是利用具有方波特性的Walsh基函数在控制体内离散表示守恒变量, 从而将间断配置在控制体内部.沿着间断位置将控制体划分为若干个连续的子单元, 通过数值积分在子单元上对守恒型控制方程进行离散, 求解以Walsh基函数系数为解变量的离散控制方程, 从而得到Walsh基函数级数形式描述的数值解. 文中理论推导和算例测试表明了FVM-WBF方法具有高分辨率、高效率和良好的激波捕捉能力等优点, 主要表现在:
(1) 当FVM-WBF方法与传统有限体积方法具有相同的收敛精度时, 其误差缩减为传统有限体积方法的${1/{2^{p}}}$倍($p$为所采用的Walsh基函数级数截断对应的组数).因此, 随着Walsh基函数组数$p$的增大, FVM-WBF方法的误差将以1/2的$p$次方倍迅速下降, 相应数值结果的分辨率也显著提高.
(2) 当FVM-WBF方法与传统有限体积方法具有相同的自由度时, 收敛到相同的误差精度或计算相同的时间步数, FVM-WBF方法都表现出更高的计算效率.
(3) FVM-WBF方法在控制体内的子单元划分为有限体积高阶重构提供了新的可能的模板选择.本文采用子单元均值进行线性重构, 得到了2阶收敛精度的FVM-WBF方法.与传统有限体积方法的2阶计算结果相比, FVM-WBF方法的2阶计算依然表现出更高的激波捕捉能力, 采用较少的Walsh基函数(如2个或4个)就能达到小于网格尺度的激波分辨率.
(4) FVM-WBF方法在子单元上的积分离散与传统有限体积方法相同, 所以传统有限体积方法中发展的各种成熟算法都可应用于FVM-WBF方法.
另一方面, 从文中的推导可以看到, 将Walsh基函数系数的守恒型控制方程在子单元上积分离散后, 会得到关于Walsh基函数系数的紧致型矩阵方程系统.因此, 与通过扩展模板进行高阶重构实现高分辨的传统有限体积方法相比, FVM-WBF方法更适用于并行方法的计算.而且随着基函数组数的增大, 控制体内划分的子单元数目相应地按倍数增多, 这也使得FVM-WBF方法天然具有网格自适应和多重网格的潜力.这些特点应得到更为深入的研究, 以期为CFD算法的探索和应用提供新的思路.
参考文献
View Option
[1]
Zou DY Xu CG Dong HB , et al . A shock-fitting technique for cell-centered finite volume methods on unstructured dynamic meshes
Journal of Computational Physics 2017 ,345 :866 -882
DOI
URL
[本文引用: 1]
[2]
Bonfiglioli A Grottadaurea M Paciorri R , et al . An unstructured, three-dimensional, shock-fitting solver for hypersonic flows
Computers & Fluids 2013 ,73 :162 -174
[3]
Romick CM Aslam TD . An extension of high-order shock-fitted detonation propagation in explosives
Journal of Computational Physics 2019 ,395 :765 -771
DOI
URL
[4]
Romick CM Aslam TD . High-order shock-fitted detonation propagation in high explosives
Journal of Computational Physics 2017 ,332 :210 -235
[5]
Rawat PS Zhong XL . On high-order shock-fitting and front-tracking schemes for numerical simulation of shock-- disturbance interactions
Journal of Computational Physics 2010 ,229 (19 ):6744 -6780
DOI
URL
[6]
Toro EF . Riemann Solvers and Numerical Methods for Fluid Dynamics, 2nd ed
Springer-Verlag 1999
[本文引用: 5]
[7]
LeVeque RJ . Numerical Methods for Conservation Laws
Birkhauser-Verlag 1992
[8]
Tannehill JC Anderson DA Pletcher RH . Computational Fluid Dynamics and Heat Transfer, 2nd ed
Taylor & Francis , 1997
[9]
阎超 . 计算流体力学方法及应用
北京: 北京航空航天大学出版社 , 2006
[10]
van Leer B . Towards the ultimate conservative difference scheme V. A second-order sequel to Godunov's method
Journal of Computational Physics 1997 ,135 :229 -248
[11]
Shu CW Osher S . Efficient implementation of essentially non-oscillatory shock-capturing Schemes
Journal of Computational Physics 1988 ,77 (2 ):439 -471
[12]
李康 , 刘娜 , 何志伟 , 等 . 一种基于双界面函数的界面捕捉方法
力学学报 , 2017 ,49 (6 ):1290 -1300
[本文引用: 1]
( Li Kang Liu Na He Zhiwei , et al . A new interface capturing method based on double interface function
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (6 ):1290 -1300 (in Chinese))
[本文引用: 1]
[13]
伍鹏革 , 倪冰雨 , 姜潮 . 一种基于Neumann级数的区间有限元方法
力学学报 , 2020 ,52 (5 ):1431 -1442
[本文引用: 2]
( Wu Pengge Ni Bingyu Jiang Chao . An interval finite element method based on Neumann series expansion
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (5 ):1431 -1442 (in Chinese))
[本文引用: 2]
[14]
陈林烽 . 基于Navier-Stokes方程残差的隐式大涡模拟有限元模型
力学学报 , 2020 ,52 (5 ):1314 -1322
[本文引用: 2]
( Chen Linfeng . A residual-based unresolved-scale finite element modelling for implicit large eddy simulation
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (5 ):1314 -1322 (in Chinese))
[本文引用: 2]
[15]
Rong YS Wei YC . A flux vector splitting scheme for low Mach number flows in preconditioning method
Applied Mathematics and Computation 2014 ,242 :296 -308
[本文引用: 1]
[16]
Chen YB Jiang S Liu N . HFVS: An arbitrary high order approach based on flux splitting
Journal of Computational Physics 2016 ,322 :708 -722
[17]
Kitamura K Shima E . Towards shock-stable and accurate hypersonic heating computations: A new pressure flux for AUSM-family schemes
Journal of Computational Physics 2013 ,245 (1 ):62 -83
[本文引用: 1]
[18]
Roe PL . Approximate Riemann solvers, parameter vectors and difference schemes
Journal of Computational Physics 1981 ,43 :357 -372
[本文引用: 1]
[19]
Chen SS Yan C Lou S , et al . An improved entropy-consistent Euler flux in low Mach number
Journal of Computational Science 2018 ,27 :271 -283
[20]
Ren J Wang G Feng JH , et al . Study of ?ux limiters to minimize the numerical dissipation based on entropy-consistent scheme
Journal of Mechanics 2018 ,34 (2 ):135 -149
[21]
Ren J Wang G Ma BP . Multidimensional extension and application of entropy-consistent scheme for Navier-Stokes equations on unstructured grids
AIAA Paper 2017-4403 , 2017
[本文引用: 1]
[22]
Ren J Wang G Ma MS . A group of CFL-dependent flux-limiters to control the numerical dissipation in multi-stage unsteady calculation
Journal of Scientific Computing 2019 ,81 (1 ):186 -216
[本文引用: 2]
[23]
Jiang GS Shu CW . Efficient implementation of weighted ENO schemes
Journal of Computational Physics 1996 ,126 (1 ):202 -228
[本文引用: 1]
[24]
骆信 , 吴颂平 . 改进的五阶WENO-Z$+$格式
力学学报 , 2019 ,51 (6 ):1927 -1939
( Luo X Wu SP . An improved fifth-order WENO-Z$+$ scheme
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (6 ):1927 -1939 (in Chinese))
[25]
Acker F Borges RBDR Costa B . An improved WENO-Z scheme
Journal of Computational Physics 2016 ,313 :726 -753
[26]
Jiang ZH Yan C Yu J . Efficient methods with higher order interpolation and MOOD strategy for compressible turbulence simulations
Journal of Computational Physics 2018 ,371 :528 -550
[27]
刘溢浪 , 张伟伟 , 蒋跃文 , 等 . 一种基于增量径向基函数插值的流场重构方法
力学学报 , 2014 ,46 (5 ):694 -702
( Liu Yilang Zhang Weiwei Jiang Yuewen , et al . A reconstruction method for finite volume flow field solving based on incremental radial basis functions
Chinese Journal of Theoretical and Applied Mechanics 2014 ,46 (5 ):694 -702 (in Chinese))
[28]
Bhise AA Gande NR Samala R , et al . An efficient hybrid WENO scheme with a problem independent discontinuity locator
International Journal for Numerical Methods in Fluids 2019 ,91 :1 -28
[29]
李新亮 , 傅德薰 , 马延文 . 8阶群速度控制格式及其应用
力学学报, 204 , 36 (1 ):79 -83
( Li Xinliang Fu Dexun Ma Yanwen . Optimized group velocity control scheme
Chinese Journal of Theoretical and Applied Mechanics , 20436 (1 ):79 -83 (in Chinese))
[30]
Li WN Ren YX . High order k-exact WENO finite volume schemes for solving gas dynamic Euler equations on unstructured grids
International Journal for Numerical Methods in Fluids 2012 ,70 (6 ):742 -763
[31]
Wang Q Ren YX Li WN . Compact high order finite volume method on unstructured grids II: Extension to two-dimensional Euler equations
Journal of Computational Physics 2016 ,314 :883 -908
[32]
Pan JH Ren YX Sun YT . High order sub-cell finite volume schemes for solving hyperbolic conservation laws II: Extension to two-dimensional systems on unstructured grids
Journal of Computational Physics 2017 ,338 :165 -198
[33]
孔令发 , 董义道 , 刘伟 . 全局方向模板对非结构有限体积梯度与高阶导数重构的影响
力学学报 , 2020 ,52 (5 ):1334 -1349
[本文引用: 1]
( Kong Lingfa Dong Yidao Liu Wei . The influence of global-direction stencil on gradient and high-order derivatives of unstructured finite volume methods
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (5 ):1334 -1348 (in Chinese))
[本文引用: 1]
[34]
Persson PO Peraire J . Sub-cell capturing for discontinuous Galerkin methods
AIAA Paper , 2006
[本文引用: 2]
[35]
Gnoffo PA . Global series solutions of nonlinear differential equations with shocks using Walsh functions
Journal of Computational Physics 2014 ,258 (1 ):650 -688
[本文引用: 12]
[36]
Gnoffo PA . Solution of nonlinear differential equations with feature detection using fast Walsh transforms
Journal of Computational Physics 2017 ,338 (1 ):620 -649
[本文引用: 1]
[37]
Walsh JL . A closed set of normal orthogonal functions
American Journal of Mathematics 1923 ,45 (1 ):5 -24
[本文引用: 1]
[38]
Andrews HC . Walsh functions in image processing, feature selection and pattern recognition
IEEE Transactions on Electromagnetic Compatibility 2007 , EMC-13 (3 ):26 -32
[本文引用: 1]
[39]
Gottlieb S Shu CW Tadmor E . High order time discretizations with strong stability properties
SIAM Review 2001 ,43 (1 ):89 -112
[本文引用: 1]
[40]
Lax PD Liu XD . Solution of two-dimensional Riemann problems of gas dynamics by positive schemes
SIAM Journal on Scientific Computing 1998 ,19 (2 ):319 -340
[本文引用: 1]
[41]
Shi J Zhang YT Shu CW . Resolution of high order WENO schemes for complicated flow structures
Journal of Computational Physics 2003 ,186 (2 ):690 -696
[本文引用: 2]
A shock-fitting technique for cell-centered finite volume methods on unstructured dynamic meshes
1
2017
... 在计算流体力学(computational fluid dynamics,CFD)领域中, 对超声速或高超声速流场进行数值模拟时, 经常会出现激波或剪切层(接触面)等较为复杂的间断流场结构.对于这些间断结构, 往往需要采用特殊的数值算法处理才能得到满足精度或分辨率需求的模拟结果.目前通用的间断处理方法主要有两类: 激波装配法[1 -6 ] 和激波捕捉法[6 -12 ] . ...
An unstructured, three-dimensional, shock-fitting solver for hypersonic flows
0
2013
An extension of high-order shock-fitted detonation propagation in explosives
0
2019
High-order shock-fitted detonation propagation in high explosives
0
2017
On high-order shock-fitting and front-tracking schemes for numerical simulation of shock-- disturbance interactions
0
2010
Riemann Solvers and Numerical Methods for Fluid Dynamics, 2nd ed
5
1999
... 在计算流体力学(computational fluid dynamics,CFD)领域中, 对超声速或高超声速流场进行数值模拟时, 经常会出现激波或剪切层(接触面)等较为复杂的间断流场结构.对于这些间断结构, 往往需要采用特殊的数值算法处理才能得到满足精度或分辨率需求的模拟结果.目前通用的间断处理方法主要有两类: 激波装配法[1 -6 ] 和激波捕捉法[6 -12 ] . ...
... [6 -12 ]. ...
... 激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
... [6 ]或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
... [6 ]或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
Numerical Methods for Conservation Laws
0
1992
Computational Fluid Dynamics and Heat Transfer, 2nd ed
0
1997
Towards the ultimate conservative difference scheme V. A second-order sequel to Godunov's method
0
1997
Efficient implementation of essentially non-oscillatory shock-capturing Schemes
0
1988
一种基于双界面函数的界面捕捉方法
1
2017
... 在计算流体力学(computational fluid dynamics,CFD)领域中, 对超声速或高超声速流场进行数值模拟时, 经常会出现激波或剪切层(接触面)等较为复杂的间断流场结构.对于这些间断结构, 往往需要采用特殊的数值算法处理才能得到满足精度或分辨率需求的模拟结果.目前通用的间断处理方法主要有两类: 激波装配法[1 -6 ] 和激波捕捉法[6 -12 ] . ...
一种基于双界面函数的界面捕捉方法
1
2017
... 在计算流体力学(computational fluid dynamics,CFD)领域中, 对超声速或高超声速流场进行数值模拟时, 经常会出现激波或剪切层(接触面)等较为复杂的间断流场结构.对于这些间断结构, 往往需要采用特殊的数值算法处理才能得到满足精度或分辨率需求的模拟结果.目前通用的间断处理方法主要有两类: 激波装配法[1 -6 ] 和激波捕捉法[6 -12 ] . ...
一种基于Neumann级数的区间有限元方法
2
2020
... 激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
... [13 -14 ]的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
一种基于Neumann级数的区间有限元方法
2
2020
... 激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
... [13 -14 ]的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
基于Navier-Stokes方程残差的隐式大涡模拟有限元模型
2
2020
... 激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
... -14 ]的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
基于Navier-Stokes方程残差的隐式大涡模拟有限元模型
2
2020
... 激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
... -14 ]的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
A flux vector splitting scheme for low Mach number flows in preconditioning method
1
2014
... 激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
HFVS: An arbitrary high order approach based on flux splitting
0
2016
Towards shock-stable and accurate hypersonic heating computations: A new pressure flux for AUSM-family schemes
1
2013
... 激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
Approximate Riemann solvers, parameter vectors and difference schemes
1
1981
... 激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
An improved entropy-consistent Euler flux in low Mach number
0
2018
Study of ?ux limiters to minimize the numerical dissipation based on entropy-consistent scheme
0
2018
Multidimensional extension and application of entropy-consistent scheme for Navier-Stokes equations on unstructured grids
1
2017
... 本节采用FVM-WBF方法对一/二维无黏Burgers方程和Euler方程的几个非定常问题进行求解, 并通过与传统有限体积方法的数值结果进行对比, 测试和验证该方法的计算精度、计算效率、激波捕捉能力和鲁棒性.其中数值通量的计算均采用熵相容格式[21 -22 ] , 时间推进均采用满足TVD条件的3阶显式Runge-Kutta[39 ] 方法. ...
A group of CFL-dependent flux-limiters to control the numerical dissipation in multi-stage unsteady calculation
2
2019
... 激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
... 本节采用FVM-WBF方法对一/二维无黏Burgers方程和Euler方程的几个非定常问题进行求解, 并通过与传统有限体积方法的数值结果进行对比, 测试和验证该方法的计算精度、计算效率、激波捕捉能力和鲁棒性.其中数值通量的计算均采用熵相容格式[21 -22 ] , 时间推进均采用满足TVD条件的3阶显式Runge-Kutta[39 ] 方法. ...
Efficient implementation of weighted ENO schemes
1
1996
... 激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
An improved WENO-Z scheme
0
2016
Efficient methods with higher order interpolation and MOOD strategy for compressible turbulence simulations
0
2018
一种基于增量径向基函数插值的流场重构方法
0
2014
一种基于增量径向基函数插值的流场重构方法
0
2014
An efficient hybrid WENO scheme with a problem independent discontinuity locator
0
2019
High order k-exact WENO finite volume schemes for solving gas dynamic Euler equations on unstructured grids
0
2012
Compact high order finite volume method on unstructured grids II: Extension to two-dimensional Euler equations
0
2016
High order sub-cell finite volume schemes for solving hyperbolic conservation laws II: Extension to two-dimensional systems on unstructured grids
0
2017
全局方向模板对非结构有限体积梯度与高阶导数重构的影响
1
2020
... 激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
全局方向模板对非结构有限体积梯度与高阶导数重构的影响
1
2020
... 激波装配法的基本思想是: 将激波作为流场区域里的运动边界进行处理, 利用RankineHugoniot(R-H)条件精确地确定激波的运动速度和位置.该方法描述激波具有高精度和高分辨率的优点, 缺点是算法复杂, 尤其是流场中激波相互干扰作用, 演化形成多尺度激波的复杂结构时, 一般需要采用动网格技术才能完成[6 ] 计算. 而基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法在守恒型控制方程的框架下不需要对激波做过多特殊的处理, 只需假设激波间断位于流场网格离散后的控制体交界面处, 根据交界面两侧的流场状态量近似求解Riemann问题, 便可自动模拟出激波的位置和强度. 近似求解Riemann问题时通常采用的方法有通量矢量分裂格式[15 -17 ] 或通量差分分裂格式[18 -22 ] . 相对于激波装配方法, 基于有限体积[6 ] 或有限元[13 -14 ] 的激波捕捉方法算法简单, 而且可以在流场的光滑区域和间断区域采用统一的格式计算, 大大提高了计算效率.另外, 该类方法还具有良好的几何外形适应性.目前, 它们已经发展成为CFD领域中有效且主流的间断数值模拟技术之一.然而, 要达到与激波装配方法相同的流场模拟精度和分辨率, 其必须使用巨大的网格量或采用高阶的流场重构技术[23 -33 ] . ...
Sub-cell capturing for discontinuous Galerkin methods
2
2006
... 国际上, 已有一些学者进行了相关的研究, 如Persson 和 Peraire [34 ] 在高阶间断Galerkin (discontinuous Galerkin, DG)方法的背景下, 通过给原始控制方程增加人工黏性项将激波(间断)尺度拉伸, 使得可以利用高阶连续近似的方法模拟黏性激波中包含的大梯度区域. 他们的研究发现, $p$阶多项式的连续近似只需要$O(h/p)$ $(h$为网格尺度)的黏性就能分辨出激波, 得到比控制体单元尺度更小的激波结构, 由此达到子单元尺度分辨率的激波捕捉效果(即在控制体内捕捉激波的分辨率).不过该方法在引入数值或物理黏性模型的同时会增加需要经验调节的参数, 且对于不同的计算问题需要不同的黏性模型才能得到稳定的结果.此外, 该方法只有在近似多项式的阶次很高($\geqslant$8阶)时, 才具有网格内部的间断捕捉能力, 对于简单的常数/线性近似, 其结果甚至不及原始方法的分辨率. ...
... 针对Persson 和 Peraire[34 ] 与Gnoffo[35 ] 所提出的方法中存在的问题, 本文提出了一种新型有限体积方法, 该方法在保持有限体积离散优势的基础上, 充分利用了Walsh基函数的间断特点, 且能达到以下两点目的: (1) 避免Gnoffo[35 ] 所提出的全局解方法的复杂性和数值模拟的局限性; (2)仅采用低阶近似(如常数近似或线性近似)便可在网格内部捕捉到激波间断, 达到子单元尺度的激波分辨率. 本文方法的基本原理是:摒弃传统有限体积和有限元方法中流场变量在网格内部连续的假设, 将守恒变量表示为截断Walsh基函数的级数形式. 借助Walsh基函数本身所具有的间断方波属性, 在控制体内部配置间断.所配置的间断自然地将控制体虚分成若干个连续的子单元, 将得到的关于Walsh基函数级数的守恒型控制方程系统在这些子单元上积分离散, 得到了一种新的求解方法.该方法对变量的基函数表示与有限元思想类似, 且最终得到的离散系统也与有限元方法相似. 但在子单元上的积分并没有变分过程, 而与有限体积方法完全相同.因此该方法虽然在思想上介于有限元和有限体积方法之间, 但本质上属于有限体积的离散框架.本文称该方法为“Walsh函数的有限体积方法(finite volume method with Walsh basisfunctions, FVM-WBF)”. 仅依赖Walsh基函数组离散的FVM-WBF方法在子单元尺度上只有1阶计算精度. 为了进一步提高对光滑解的分辨率, 采用子单元上的流场变量均值进行流场的线性重构, 将FVM-WBF方法的离散精度提升到2阶. 在数值算例部分, 运用1阶和2阶FVM-WBF方法求解了无黏Burgers方程和Euler方程的多个定解问题, 以期验证FVM-WBF方法的计算精度、计算效率、激波捕捉能力和鲁棒性. ...
Global series solutions of nonlinear differential equations with shocks using Walsh functions
12
2014
... 美国学者Gnoffo[35 -36 ] 将一组具有正交性的间断Walsh基函数[37 -38 ] 引入到CFD领域, 利用Walsh基函数求解具有间断解的非线性微分方程[35 ] . 其基本方法是根据Walsh基函数的乘法封闭性和一些基本变换算子(如倒数变换、积分变换、微分变换等)将原始的微分方程变换到波数空间的多项式方程系统, 在波数空间上求解原微分方程的全局解, 以期得到比传统有限体积方法更好的间断捕捉效果.然而, 在求解一维Burgers方程和Euler方程的算例中, 该方法并没有达到预期的理想效果.主要表现在两个方面: 其一是求解非线性偏微分方程时, 各个原始变量的Walsh基函数级数近似会引入很多复杂的多重交叉相乘项, 导致最终得到的代数方程系统过于复杂, 且边界条件的处理也比较困难;其二是该全局解方法完全脱离了有限体积离散的框架, 没有明确的网格划分过程, 只针对最终的代数方程系统进行数值迭代求解, 且采用数百个Walsh基函数得到的数值结果与传统采用迎风格式的有限体积方法的结果相比, 也并未表现出明显的优势. ...
... [35 ]. 其基本方法是根据Walsh基函数的乘法封闭性和一些基本变换算子(如倒数变换、积分变换、微分变换等)将原始的微分方程变换到波数空间的多项式方程系统, 在波数空间上求解原微分方程的全局解, 以期得到比传统有限体积方法更好的间断捕捉效果.然而, 在求解一维Burgers方程和Euler方程的算例中, 该方法并没有达到预期的理想效果.主要表现在两个方面: 其一是求解非线性偏微分方程时, 各个原始变量的Walsh基函数级数近似会引入很多复杂的多重交叉相乘项, 导致最终得到的代数方程系统过于复杂, 且边界条件的处理也比较困难;其二是该全局解方法完全脱离了有限体积离散的框架, 没有明确的网格划分过程, 只针对最终的代数方程系统进行数值迭代求解, 且采用数百个Walsh基函数得到的数值结果与传统采用迎风格式的有限体积方法的结果相比, 也并未表现出明显的优势. ...
... 针对Persson 和 Peraire[34 ] 与Gnoffo[35 ] 所提出的方法中存在的问题, 本文提出了一种新型有限体积方法, 该方法在保持有限体积离散优势的基础上, 充分利用了Walsh基函数的间断特点, 且能达到以下两点目的: (1) 避免Gnoffo[35 ] 所提出的全局解方法的复杂性和数值模拟的局限性; (2)仅采用低阶近似(如常数近似或线性近似)便可在网格内部捕捉到激波间断, 达到子单元尺度的激波分辨率. 本文方法的基本原理是:摒弃传统有限体积和有限元方法中流场变量在网格内部连续的假设, 将守恒变量表示为截断Walsh基函数的级数形式. 借助Walsh基函数本身所具有的间断方波属性, 在控制体内部配置间断.所配置的间断自然地将控制体虚分成若干个连续的子单元, 将得到的关于Walsh基函数级数的守恒型控制方程系统在这些子单元上积分离散, 得到了一种新的求解方法.该方法对变量的基函数表示与有限元思想类似, 且最终得到的离散系统也与有限元方法相似. 但在子单元上的积分并没有变分过程, 而与有限体积方法完全相同.因此该方法虽然在思想上介于有限元和有限体积方法之间, 但本质上属于有限体积的离散框架.本文称该方法为“Walsh函数的有限体积方法(finite volume method with Walsh basisfunctions, FVM-WBF)”. 仅依赖Walsh基函数组离散的FVM-WBF方法在子单元尺度上只有1阶计算精度. 为了进一步提高对光滑解的分辨率, 采用子单元上的流场变量均值进行流场的线性重构, 将FVM-WBF方法的离散精度提升到2阶. 在数值算例部分, 运用1阶和2阶FVM-WBF方法求解了无黏Burgers方程和Euler方程的多个定解问题, 以期验证FVM-WBF方法的计算精度、计算效率、激波捕捉能力和鲁棒性. ...
... [35 ]所提出的全局解方法的复杂性和数值模拟的局限性; (2)仅采用低阶近似(如常数近似或线性近似)便可在网格内部捕捉到激波间断, 达到子单元尺度的激波分辨率. 本文方法的基本原理是:摒弃传统有限体积和有限元方法中流场变量在网格内部连续的假设, 将守恒变量表示为截断Walsh基函数的级数形式. 借助Walsh基函数本身所具有的间断方波属性, 在控制体内部配置间断.所配置的间断自然地将控制体虚分成若干个连续的子单元, 将得到的关于Walsh基函数级数的守恒型控制方程系统在这些子单元上积分离散, 得到了一种新的求解方法.该方法对变量的基函数表示与有限元思想类似, 且最终得到的离散系统也与有限元方法相似. 但在子单元上的积分并没有变分过程, 而与有限体积方法完全相同.因此该方法虽然在思想上介于有限元和有限体积方法之间, 但本质上属于有限体积的离散框架.本文称该方法为“Walsh函数的有限体积方法(finite volume method with Walsh basisfunctions, FVM-WBF)”. 仅依赖Walsh基函数组离散的FVM-WBF方法在子单元尺度上只有1阶计算精度. 为了进一步提高对光滑解的分辨率, 采用子单元上的流场变量均值进行流场的线性重构, 将FVM-WBF方法的离散精度提升到2阶. 在数值算例部分, 运用1阶和2阶FVM-WBF方法求解了无黏Burgers方程和Euler方程的多个定解问题, 以期验证FVM-WBF方法的计算精度、计算效率、激波捕捉能力和鲁棒性. ...
... 若采用$g_{n} (x)$表示闭区间$[x_{a} , , x_{b}]$上具有$n$个波段的Walsh基函数, 则有如下计算公式[35 ] ...
... 且$p$组Walsh基函数的波段长度最多包含两种, 即${d} x_{p} $或$2{d} x_{p} $. 因此式(2)中$\hat{{g}}_{n} (i)$的取值为1或2.另外, Walsh基函数还具有正交性等优良数学特征, 详细描述可参考文献[35 ], 此处不赘述. ...
... Gnoffo[35 ] 通过研究Walsh基函数级数对若干连续和间断函数的拟合特点提出了求解非线性偏微分方程的Walsh基函数全局解方法. 该方法采用时空耦合算法, 将微分方程的各变量表示成关于时间和空间的二元Walsh基函数级数形式, 并直接对微分方程做Walsh基函数级数的积分或微分变换处理, 最终得到关于基函数系数的复杂非线性代数方程系统, 需要通过Newton迭代[35 ] 等数值手段才能完成计算. ...
... [35 ]等数值手段才能完成计算. ...
... 虽然Walsh基函数全局解方法思路简单, 但存在一定的局限性, 如:(1)求解不同的微分方程需要重新推导代数方程组, 因此不具有普适性;(2)当微分方程的初边值条件复杂时, 其基函数级数展开可能导致最终的代数方程系统求解时收敛困难;(3)文献[35 ]的测试算例显示要得到与传统有限体积方法类似的模拟效果, 微分方程变量的每个维度采用的基函数个数一般要达到$2^{8}$量级左右, 这将会给最终非线性代数方程系统的求解带来较高的计算量负担. ...
... 受Gnoffo[35 ] 研究的启发, 本文将具有间断特性的Walsh基函数与传统有限体积方法结合, 提出了新的FVM-WBF方法, 以期在一定程度上改善Walsh基函数全局解方法的局限性. ...
... 根据Walsh基函数级数对任意函数拟合的合理性[35 ] , 本文考虑采用截断Walsh基函数级数近似双曲守恒律方程中的守恒变量, 下面针对一维和二维情况分别进行讨论. ...
... 由上述描述可知, FVM-WBF方法采用时空分离的思想在子单元框架下对微分方程进行有限体积离散, 具有更好的普适性.且FVM-WBF方法是根据Walsh基函数引入的间断位置对原始控制体单元进行虚子单元划分, 并不改变原始网格的几何拓扑结构, 保持了原始网格良好的几何适应性.另外, 对于边界条件的处理, FVM-WBF方法与原始有限体积方法类似, 为了保持与内场一致的数值通量计算, 可以在边界处延拓一层辅助网格单元, 用与边界单元相同的Walsh基函数表达辅助网格上的流场变量, 可以在边界处达到子单元尺度的误差精度.相对于Gnoffo[35 ] 提出的Walsh基函数全局解方法,FVM-WBF方法并未在离散和求解方面引入新的困难. ...
Solution of nonlinear differential equations with feature detection using fast Walsh transforms
1
2017
... 美国学者Gnoffo[35 -36 ] 将一组具有正交性的间断Walsh基函数[37 -38 ] 引入到CFD领域, 利用Walsh基函数求解具有间断解的非线性微分方程[35 ] . 其基本方法是根据Walsh基函数的乘法封闭性和一些基本变换算子(如倒数变换、积分变换、微分变换等)将原始的微分方程变换到波数空间的多项式方程系统, 在波数空间上求解原微分方程的全局解, 以期得到比传统有限体积方法更好的间断捕捉效果.然而, 在求解一维Burgers方程和Euler方程的算例中, 该方法并没有达到预期的理想效果.主要表现在两个方面: 其一是求解非线性偏微分方程时, 各个原始变量的Walsh基函数级数近似会引入很多复杂的多重交叉相乘项, 导致最终得到的代数方程系统过于复杂, 且边界条件的处理也比较困难;其二是该全局解方法完全脱离了有限体积离散的框架, 没有明确的网格划分过程, 只针对最终的代数方程系统进行数值迭代求解, 且采用数百个Walsh基函数得到的数值结果与传统采用迎风格式的有限体积方法的结果相比, 也并未表现出明显的优势. ...
A closed set of normal orthogonal functions
1
1923
... 美国学者Gnoffo[35 -36 ] 将一组具有正交性的间断Walsh基函数[37 -38 ] 引入到CFD领域, 利用Walsh基函数求解具有间断解的非线性微分方程[35 ] . 其基本方法是根据Walsh基函数的乘法封闭性和一些基本变换算子(如倒数变换、积分变换、微分变换等)将原始的微分方程变换到波数空间的多项式方程系统, 在波数空间上求解原微分方程的全局解, 以期得到比传统有限体积方法更好的间断捕捉效果.然而, 在求解一维Burgers方程和Euler方程的算例中, 该方法并没有达到预期的理想效果.主要表现在两个方面: 其一是求解非线性偏微分方程时, 各个原始变量的Walsh基函数级数近似会引入很多复杂的多重交叉相乘项, 导致最终得到的代数方程系统过于复杂, 且边界条件的处理也比较困难;其二是该全局解方法完全脱离了有限体积离散的框架, 没有明确的网格划分过程, 只针对最终的代数方程系统进行数值迭代求解, 且采用数百个Walsh基函数得到的数值结果与传统采用迎风格式的有限体积方法的结果相比, 也并未表现出明显的优势. ...
Walsh functions in image processing, feature selection and pattern recognition
1
2007
... 美国学者Gnoffo[35 -36 ] 将一组具有正交性的间断Walsh基函数[37 -38 ] 引入到CFD领域, 利用Walsh基函数求解具有间断解的非线性微分方程[35 ] . 其基本方法是根据Walsh基函数的乘法封闭性和一些基本变换算子(如倒数变换、积分变换、微分变换等)将原始的微分方程变换到波数空间的多项式方程系统, 在波数空间上求解原微分方程的全局解, 以期得到比传统有限体积方法更好的间断捕捉效果.然而, 在求解一维Burgers方程和Euler方程的算例中, 该方法并没有达到预期的理想效果.主要表现在两个方面: 其一是求解非线性偏微分方程时, 各个原始变量的Walsh基函数级数近似会引入很多复杂的多重交叉相乘项, 导致最终得到的代数方程系统过于复杂, 且边界条件的处理也比较困难;其二是该全局解方法完全脱离了有限体积离散的框架, 没有明确的网格划分过程, 只针对最终的代数方程系统进行数值迭代求解, 且采用数百个Walsh基函数得到的数值结果与传统采用迎风格式的有限体积方法的结果相比, 也并未表现出明显的优势. ...
High order time discretizations with strong stability properties
1
2001
... 本节采用FVM-WBF方法对一/二维无黏Burgers方程和Euler方程的几个非定常问题进行求解, 并通过与传统有限体积方法的数值结果进行对比, 测试和验证该方法的计算精度、计算效率、激波捕捉能力和鲁棒性.其中数值通量的计算均采用熵相容格式[21 -22 ] , 时间推进均采用满足TVD条件的3阶显式Runge-Kutta[39 ] 方法. ...
Solution of two-dimensional Riemann problems of gas dynamics by positive schemes
1
1998
... 二维Euler方程的黎曼问题反映了多变气体的多尺度流场结构, 一般由3种常见的一维波(稀疏波, 激波和接触间断波)相互作用形成.本算例在计算域[0, 1]$\times$[0, 1]上考虑如下初始条件的黎曼问题[40 ] ...
Resolution of high order WENO schemes for complicated flow structures
2
2003
... Rayleigh-Tayler (R-T)不稳定性问题[41 ] 描述的是, 对于上下两层密度不同的流体, 当密度大的流体受到重力影响流向密度小的流体时所产生的流动现象.经过一定时间的演化, 轻流体的空泡和重流体的“尖顶”相互干扰, 最终形成非常复杂的流场结构. ...
... 其中$a=\sqrt {{{\gamma p}/\rho }}$, 左右边界为无黏壁面条件;上下边界为固定流场数据. 在网格$M=20\times80$上计算到时间$t=1.95$.测试了FVM-WBF方法对复杂流场结构的模拟效果. 图8 给出了OFVM与FVM-WBF方法取$(n_1, n_2)=(2, 2)$, $(4, 4)$, $(8, 8)$时的2阶精度数值密度等值线图.可以看到, 相对于OFVM方法,FVM-WBF方法随着Walsh基函数个数的增大, 其捕捉到的流场细节也迅速增多.不过2阶精度采用的是线性重构近似, 所以并没有良好地解析极值点, 这在本算例中有较明显的体现.同时可以观察到随着基函数个数的增大, 界面处表现出了越来越明显的数值扰动现象, 这与文献[41 ]中采用网格加密技术对该问题进行数值模拟时表现出的现象类似, 进一步说明FVM-WBF方法采用的子单元划分技术与直接网格加密技术具有等价的数值效应. ...