冰激结构频率锁定振动的发生机理及简单分析方法1)

doi:10.6052/0459-1879-20-382

冰激结构频率锁定振动的发生机理及简单分析方法¹⁾

屈衍^,^*^,²⁾, 黄子威^*, 邹科^*, 尹昊阳^*, 张大勇^†

^*南方科技大学前沿与交叉科学研究院,广东深圳 518055

^†大连理工大学工业装备结构分析国家重点实验室,辽宁大连 116024

MECHANISM AND SIMPLE ANALYSIS METHOD OF ICE INDUCED FREQUENCY LOCK-IN VIBRATION OF OFFSHORE STRUCTURES¹⁾

Qu Yan^,^*^,²⁾, Huang Ziwei^*, Zou Ke^*, Yin Haoyang^*, Zhang Dayong^†

^*Academy for Advanced Interdisciplinary Studies,Southern University of Science and Technology,Shenzhen 518055,Guangdong,China

^†State Key Laboratory of Structure Analysis for Industrial Equipment,Dalian University of Technology, Dalian 116024,Liaoning,China

通讯作者: 2) 屈衍,副研究员,主要研究方向：极地海洋工程. E-mail:quy3@sustech.edu.cn

收稿日期: 2020-11-19 网络出版日期: 2021-03-18

基金资助:

1) 国家自然科学基金.  41976195
国家自然科学基金.  51679033
国家研发计划.  2016YFC0303400
工业装备结构分析国家重点实验室开放课题.  GZ19120

Received: 2020-11-19 Online: 2021-03-18

作者简介 About authors

摘要

冰激结构频率锁定振动是冰区海洋工程结构的危险工况.对频率锁定振动过程的传统机理解释没有体现这一过程的全部物理特征,导致现有的分析方法无法准确分析这一问题.本文基于对现场测量结果的分析,提出了一种海冰韧性损伤-破碎过程与结构振动耦合导致频率锁定振动的机理.该机理认为,海冰在直立结构频率锁定振动过程中发生韧性损伤-破碎行为,海冰的韧性损伤-破碎与结构运动相位耦合,导致了频率锁定振动. 海冰对结构作用产生的载荷为锯齿形,作用过程可以分为加载和卸载两个阶段,其中加载阶段时间长度约为卸载阶段3倍以上.在加载阶段,结构从平衡位置先与海冰运动方向相反振动到反向最大振幅位置后回摆,然后与海冰同向运动到正向最大振幅位置,这段过程中海冰与结构接触部位内部产生裂纹并扩展但未发生主要的破碎,在此阶段海冰发生韧性损伤;在卸载阶段,结构从最大振幅位置向平衡位置回摆,结构与海冰运动方向相反,这一过程中应变速率的突然增大导致裂纹加速扩展并失稳开裂,此时带有韧性损伤的海冰发生破碎.基于这一新的机理解释,本文提出了一种冰激结构频率锁定振动幅值的简单分析方法.该方法认为海冰破碎长度是频率锁定振动的关键参数. 理想状态下,海冰破碎长度约为结构水线处振动幅值的2.2倍.当冰速接近海冰破碎长度与结构自振周期的比值时,结构会发生频率锁定振动.该方法对评估海洋工程结构频率锁定振动的发生概率及疲劳损伤具有指导意义.

关键词： 冰激振动 ; 频率锁定 ; 韧性损伤-破碎 ; 海冰破碎长度

Abstract

Ice induced frequency lock-in vibration of offshore structures has been recognized as a serious load condition in ice regions. The traditional mechanism cannot fully explain all the physical phenomena in the frequency lock-in vibration, nor can a reasonable analysis method be obtained. Based on the analysis of full scale measurement data, this paper proposes a new mechanism of frequency lock-in vibration caused by the coupling of sea ice ductile damage-collapse failure and structural vibration. It is believed that the ductile damage-collapse failure of sea ice occurs during the frequency lock-in vibration of vertical structures, which is coupled with the phase of structural motion, resulting in frequency lock-in vibration. Saw-teeth-shape ice load is caused by the action between sea ice and the structure. The action process can be divided into loading and unloading stages, the loading stage takes about 3 times the time of the unloading stage. In the loading stage, the structure moves against ice from equilibrium position to its maximum negative amplitude and then moves back together with ice at the same direction to its maximum positive amplitude. Cracks are formed in the contact part of the sea ice and the structure, but not collapse. The sea ice undergoes ductile damage at this stage. In the unloading stage, the structure moves in the opposite direction to the sea ice, swinging back from the maximum amplitude to its equilibrium position. The sudden increase of strain rate leads to the accelerated propagation and instable fracture of cracks. The sea ice with ductile damage collapses at this stage. Based on the new mechanism explanation, this paper presents a simple analysis method of ice induced frequency lock-in vibration of offshore structures. It is considered that the sea ice break length is the key parameter of frequency lock-in vibration. In the ideal situation, the sea ice break length is about 2.2 times of the vibration amplitude at the waterline of the structure. When the ice velocity is close to the ratio of sea ice break length to the natural vibration period of the structure, frequency lock-in vibration will occur. This method has guiding significance for evaluating the occurrence probability of frequency lock-in vibration and fatigue damage of offshore structures.

Keywords： ice induced vibration ; frequency lock-in ; ductile damage-collapse failure ; sea ice break length

PDF (18880KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

屈衍, 黄子威, 邹科, 尹昊阳, 张大勇. 冰激结构频率锁定振动的发生机理及简单分析方法¹⁾. 力学学报[J], 2021, 53(3): 728-739 DOI:10.6052/0459-1879-20-382

Qu Yan, Huang Ziwei, Zou Ke, Yin Haoyang, Zhang Dayong. MECHANISM AND SIMPLE ANALYSIS METHOD OF ICE INDUCED FREQUENCY LOCK-IN VIBRATION OF OFFSHORE STRUCTURES¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(3): 728-739 DOI:10.6052/0459-1879-20-382

引言

在结冰海域,桥梁、灯塔、海洋平台、风电基础结构都会受到海冰的作用.冰速较慢时,海冰会引起结构频率锁定振动,导致结构发生持续时间较长、振幅较大的简谐振动,这是海洋工程结构在海冰作用下的一种典型危险工况.美国阿拉斯加库克湾的海洋平台^[1]、北欧的灯塔与航标^[2-4]以及我国渤海的石油平台都曾因严重的频率锁定振动而导致结构倒塌^[5].此外,频率锁定振动还导致加拿大Molikpaq沉箱式平台基础砂土液化^[6]以及俄罗斯萨哈林海域油气田停产^[7].

为解决频率锁定振动问题,学者们进行了大量的研究.Bjerkås等^[8]、Nord等^[9]分析了Norströms-grund灯塔上发生的60余次频率锁定振动数据,统计了频率锁定振动发生时的冰厚、冰速等条件,描述了载荷与振动响应情况.文献[10,11,12,13,14,15,16,17]对室内和中尺度试验进行了总结,对室内试验中海冰与直立结构作用时的不同破碎形式进行了分析.Liu等^[18-19]基于离散元方法研究了海冰与船体和海洋平台结构间的相互作用.2015年德国HSVA冰池实验室开展了IVOS项目,对频率锁定振动问题进行了试验研究^[20-23].试验中对冰载荷及结构响应进行了同步测量,验证了海冰在其与结构接触面上的破碎及载荷的同步性.

综合多年现场测量与试验研究,学者们提出了两种频率锁定振动的发生机理.文献[24,25,26]认为频率锁定振动是一种强迫振动. 海冰的破碎具有固有周期,海冰破碎频率与结构固有频率重合导致载荷与结构响应频率相同,引发结构共振.文献[27,28,29,30]认为,海冰在与结构作用过程中经历了从韧性破碎到脆性破碎的转变,这种韧-脆转变行为引起了负阻尼效应,导致了结构的非线性自激振动.

上述两种机理已提出近50年,基于这两种机理学者们对频率锁定振动开展了很多分析方法研究. 文献[31,32,33]对风电基础的振动及疲劳进行了详细分析. Shi等^[34]利用数值方法对冰激风电基础振动进行了分析. Ji和Oterkus^[35-36]利用范德波尔方程对自激振动进行了分析和求解,在数学方法上改进了韧-脆转变模型. 此外,学者们还提出了多种模拟频率锁定振动的数学模型,对风电基础的疲劳损伤进行了评估^[37-43]. 但是目前为止,上述分析方法尚不能准确分析结构频率锁定问题,没有得到工程实践的认可.

这一现状的主要原因是上述两种机理并未全面反映物理过程的真实特征. 强迫振动机理没有体现结构振动与海冰破碎之间的耦合作用,而海冰韧-脆转变破碎导致结构自激振动机理与海冰的破碎是间歇性同时破碎且具有特定破碎长度的物理特征不符合.这两种机理解释得不完备导致在此基础上建立的分析方法无法合理分析频率锁定振动.

本文通过对海冰与结构作用的现场观测和冰载荷与结构响应实测数据的分析,总结了不同结构上发生频率锁定振动的共同特征.在此基础上提出了海冰与结构作用过程中的韧性损伤-破碎行为与结构振动耦合导致频率锁定振动的机理解释.与现有机理相比,本文提出的机理全面解释了频率锁定振动的主要特征,为频率锁定振动研究开辟了新的方向.对冰区海洋平台、风电基础、桥梁等结构设计具有重要意义.基于这一机理,本文同时提出了通过海冰破碎长度计算频率锁定振动幅值的简单方法.

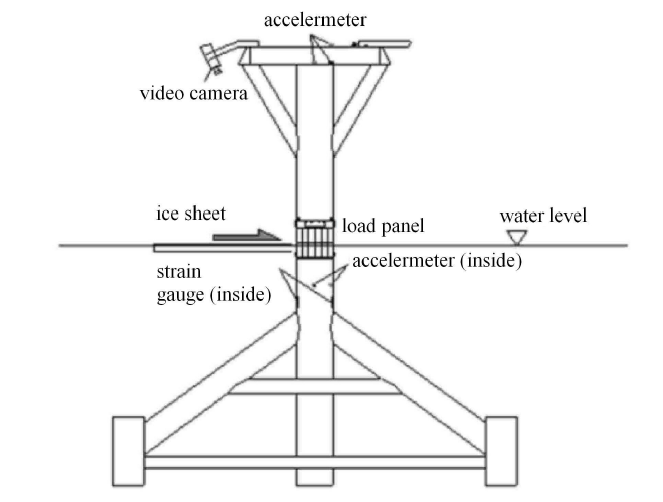
1 频率锁定振动的现场测量

对实际结构的现场测量是研究海洋工程结构冰激振动问题的重要研究手段.原型结构测量不存在材料物理相似与结构动力相似问题,可以获得直接的测量数据.目前国际上比较成功的现场测量主要有中国渤海石油平台、北欧波罗的海Norströmsgrund灯塔以及加拿大波弗特海Molikpaq平台的现场测量.在这3个现场测量中,都测量到了典型的频率锁定振动现象.这些现场测量的地点位于从北极到亚极区的主要结冰海域,结构形式包含导管架平台、灯塔等柔性结构和沉箱式平台等宽大结构.因此,测量结果具有很强的代表性.其中,渤海石油平台测量结果对我国冰区结构设计具有重要意义;Norströmsgrund灯塔的直径与海上风力发电基础接近,测量结果可以为冰区风电基础设计提供参考;Molikpaq平台的现场测量于19世纪80年代在北极海域进行,测量数据为制定极地冰区结构设计标准提供了重要的基础.分析这些现场测量结果,可以总结不同结构发生频率锁定振动的特点,得到一般规律,对频率锁定振动机理研究具有重要意义.

1.1 渤海石油平台的现场测量

渤海石油平台的现场测量由海冰环境测量、海冰与结构作用观测、冰载荷直接测量和海洋平台结构振动响应测量组成. 渤海石油平台的主要特点是结构形式多样,有单腿系缆桩、三腿及四腿导管架平台等. 导管架平台桩腿直径多为1$\sim$2m,结构自振频率为1$\sim$2.5,Hz,常见冰厚为5$\sim$20cm. 在2000—2004年的测量中,采用高62cm、宽27cm的压力盒对冰载荷进行了直接测量. 渤海JZ9-3油气田单腿系缆桩及其测量系统如图1和图2所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 渤海JZ9-3油气田单腿系缆桩

Fig. 1 Mono leg mooring pole of JZ9-3 oil field in Bohai Bay

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 单腿系缆桩上的现场测量系统

Fig. 2 Full scale measurement system on the mono leg mooring pole

1.2 Norströmsgrund灯塔的现场测量

与渤海的现场测量类似,在欧盟STRICE项目中,研究人员在Norströmsgrund灯塔上安装了现场测量系统.在2001—2003年冬季,连续3年对海冰与结构的作用进行了测量.测量系统由冰速测量系统、冰厚测量系统、压力盒冰载荷测量系统、加速度传感器和摄像机组成.该灯塔总高度为42.3m,水线处直径约为7.52m.冰载荷压力盒宽1.2m、高1.6m,9个压力盒的覆盖角度达到162$^\circ$.由于Norströmsgrund灯塔上使用的压力盒比渤海石油平台上的大得多,其测量的冰载荷作用面积也更大.Norströmsgrund灯塔及测量中使用的压力盒如图3和图4所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 Norströmsgrund灯塔

Fig. 3 Norströmsgrund lighthouse

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 Norströmsgrund灯塔上的压力盒

Fig. 4 Load panels on Norströmsgrund lighthouse

1.3 Molikpaq平台的现场测量

Molikpaq平台是加拿大于19世纪80年代建造的沉箱式钻井平台. 平台外部的钢制沉箱放置在沙土基础上,上部设置作业甲板进行钻井作业. 平台结构如图5和图6所示. 该平台水线处宽度为90m,具备在20$\sim$30m水深的北极地区全年作业的能力.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 Molikpaq平台的概念模型

Fig. 5 Conceptual model of Molikpaq platform

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 Molikpaq平台的冰上作业

Fig. 6 Molikpaq platform operation in the ice

为了评估作用在结构上的冰载荷,研究人员在平台东北部的长边均匀布置了3组压力盒,短边布置了1组压力盒,布置情况如图7所示.在平台四周安装了应变计,如图8所示,实现了对冰载荷的360$^\circ$测量.此外,还安装了一套结构响应测量系统,包含29个加速度传感器和9个位移传感器.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 Molikpaq平台上压力盒的布置情况

Fig. 7 Layout of load panels on Molikpaq platform

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 Molikpaq平台上应变计的布置情况

Fig. 8 Layout of strain gauges on Molikpaq platform

在对平台的上千个小时的测量中,观测到了多次海冰的频率锁定加载.其中,最为典型的加载事件发生在1986年5月12日,平台受到较厚(1.9,$\sim$3.5m)的浮冰作用,整体冰载荷达到275$\sim$300mN.本次测量数据采集效果良好,加载发生时冰速变化范围广、冰载荷较大,对极地冰载荷研究起到了重要作用.

2 频率锁定振动的主要特征

上述测量系统均测量到了冰激结构频率锁定振动过程. 尤其是压力盒测得的冰载荷数据为频率锁定振动机理研究提供了重要资料.渤海湾石油平台和Norströmsgrund灯塔上测得的频率锁定振动过程中的冰载荷与结构响应数据如图9和图10所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

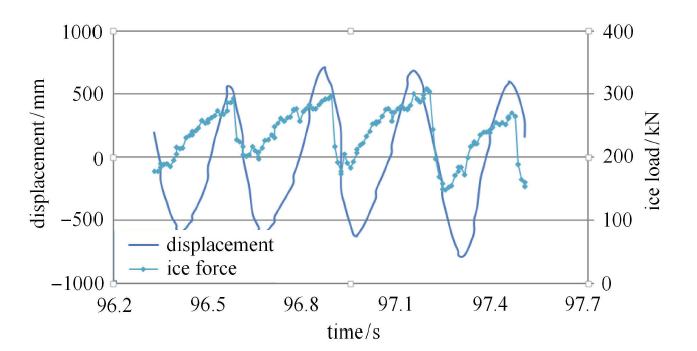
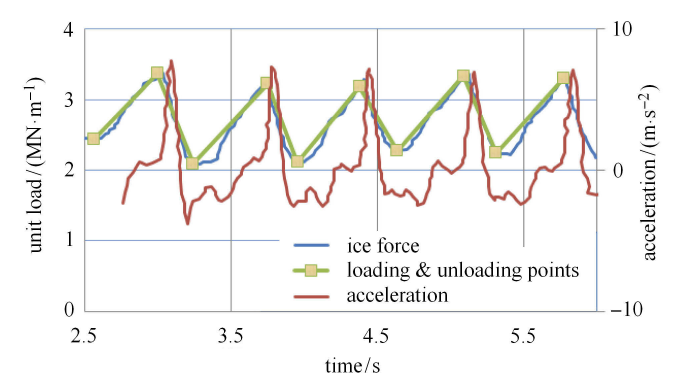
图9 渤海湾单腿系缆桩测得的频率锁定振动过程中的冰载荷与结构响应

Fig. 9 Ice force and structure response in the frequency lock-in vibration event measured on the mono leg mooring pole in Bohai Bay

图10

新窗口打开| 下载原图ZIP| 生成PPT

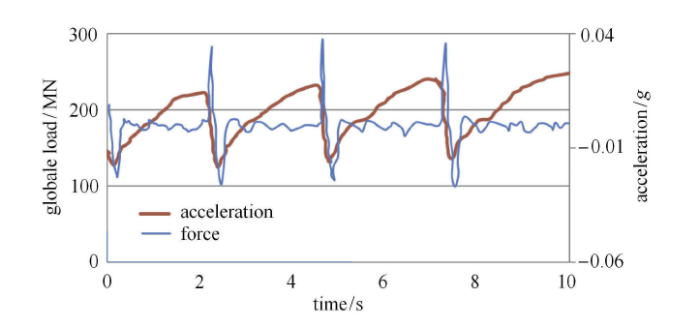
图10 Norströmsgrund灯塔测得的频率锁定振动过程中的冰载荷与结构响应

Fig. 10 Ice force and structure response in the frequency lock-in vibration event measured on Norströmsgrund lighthouse

尽管上述两个现场测量中的结构形式、冰厚、压力盒尺寸不同,但测量结果显示出频率锁定振动的一些共同特性：

(1) 结构振动形式接近正弦曲线,不同于连续的海冰脆性挤压破碎引起的结构随机振动.

(2) 一个振动周期内,冰载荷经历较长的加载阶段和较短的卸载阶段,冰载荷时程为锯齿状,小压力盒和大压力盒测量的冰载荷均具有相同的锯齿形.

(3) 冰载荷与结构响应具有固定的相位关系. 当结构从最大振幅位置与海冰反向向平衡位置运动时,冰载荷减小;当结构到达平衡位置附近时,冰载荷增大.

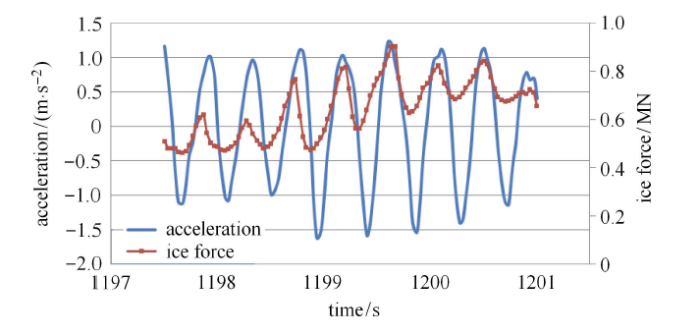
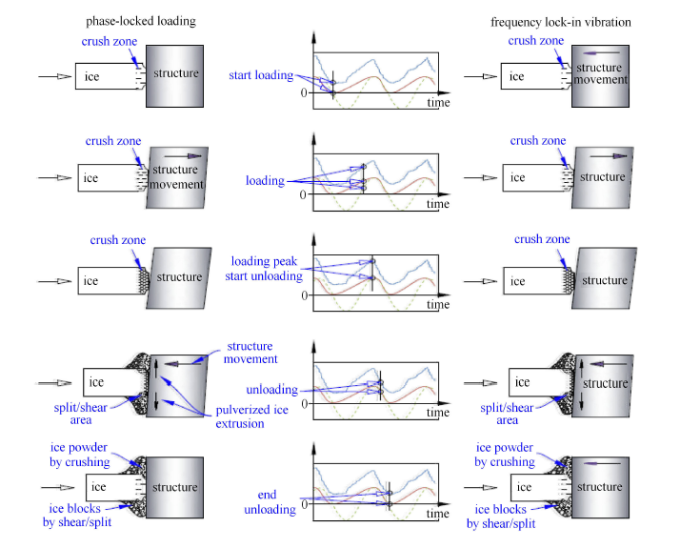
与灯塔和导管架平台不同,Molikpaq平台是一个沉箱结构,平台中间为沙土基础,属于不易发生振动的过阻尼系统. Jefferies和Wright^[6]将该平台的运动称为相位锁定加载. 这里所说的相位锁定加载与前文所述频率锁定振动类似,其主要区别在于：频率锁定振动中,冰载荷频率与结构自振频率锁定;而Molikpaq平台在相位锁定加载过程中,冰载荷与结构运动频率虽然锁定,但其频率可变. 如图11和图12所示,随着作用时间的变化,结构的运动周期由0.6,s变为2.5,s,但冰载荷与结构运动始终保持相位锁定关系. Jefferies和Wright^[6]总结了相位锁定加载过程中海冰与平台相互作用的一般特征：

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 Molikpaq平台于1986-5-12 03:20测得的冰载荷及加速度

Fig. 11 Ice load and acceleration of Molikpaq Platform measured at 03:20, May 12, 1986

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 Molikpaq平台于1986-05-12 03:25测得的冰载荷及加速度

Fig. 12 Ice load and acceleration of Molikpaq Platform measured at 03:25, May 12, 1986

(1) 海冰与结构的相互作用对海冰的运动没有影响,结构运动与海冰的挤压破碎过程具有耦合关系.

(2) 海冰的破碎是同时发生的.

(3) 结构的响应是规律的.

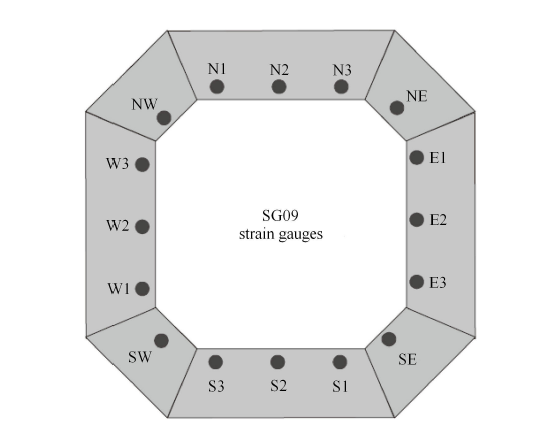
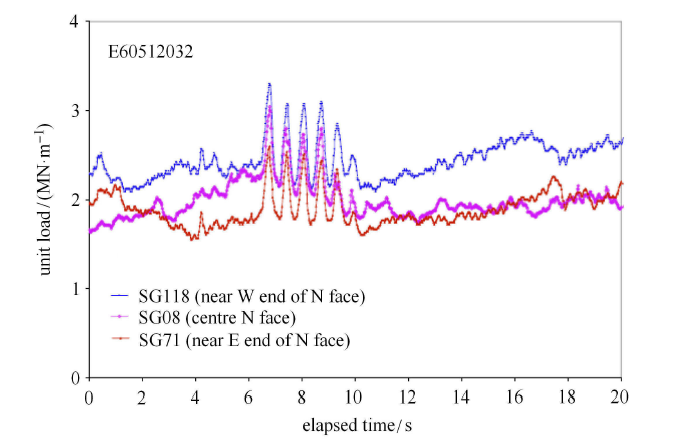
观察现场监测中得到的冰荷载数据,可以发现频率锁定振动过程中冰载荷具有同步性的特点.图13为Norströmsgrund灯塔上不同压力盒测得的冰载荷.由于海冰运动方向并非正对压力盒阵列中央,因此7$\sim$9号压力盒在6700$\sim$6705,s记录到相位相同的锯齿形冰载荷,其他通道没有记录到载荷数据.图中可见相邻通道的冰载荷在时域上具有相同的相位变化,这说明频率锁定振动过程中,冰与结构接触面上的冰载荷是同步变化的,海冰的破碎也是同步的.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 Norströmsgrund灯塔上不同压力盒测得的同步锯齿形冰载荷

Fig. 13 Simultaneous saw-teeth-shape ice load measured by different load panels on Norströmsgrund lighthouse

图14为Molikpaq平台上压力盒测得的相位锁定加载过程中的冰载荷. 图中可见3个压力盒记录的冰载荷相位也是同步变化的,而这3个压力盒之间距离为30m以上,说明海冰在与平台整个接触面内的冰载荷是同步变化的,海冰破碎过程也是同步的.

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 Molikpaq平台上不同压力盒测得的同步锯齿形冰载荷

Fig. 14 Simultaneous saw-teeth-shape ice load data measured by different load panels on Molikpaq platform

需要注意的是上述冰载荷数据显示冰载荷在加载、卸载阶段都是同步的,说明海冰在加载、卸载阶段的破碎均是同步发生的.研究表明海冰脆性破碎过程中冰的破碎是非同时的,而同时破碎是海冰韧性破碎的典型特征.因此在频率锁定振动过程中,加载、卸载阶段的海冰破碎均是韧性破碎而非脆性破碎,海冰未经历韧-脆转变破碎行为.

现场测量还发现在频率锁定振动发生过程中,海冰在结构前的运动表现出“停停走走”的状态. 这种现象出现的原因是频率锁定振动发生时冰速很慢,接近结构振动速度幅值. 当海冰与结构同向运动时,海冰与结构相对运动很小,看似“停”在结构前. 在这一阶段海冰内部生成裂纹但是不会发生显著的破碎. 当结构运动到最大振幅位置并开始回摆时,其运动方向与海冰相反,两者发生显著的相对运动,海冰内部裂纹扩展并失稳开裂. 破碎的海冰碎末从冰与结构接触表面挤出. 这一阶段看似海冰在结构前突然“走”了一段. 随着上述过程的往复发生,海冰表现出“停停走走”的现象. 这一现象表明频率锁定振动过程中海冰的破碎是间歇性的过程. 在一个结构运动周期内,海冰只发生一次破碎. 结构振动与海冰运动及破碎过程具有相位耦合关系.

现场测量中发现的海冰与结构作用的主要特征对理解频率锁定振动发生机理具有重要意义.现有的机理解释认为,低速运动的海冰与结构作用过程中,海冰与结构相对运动速率的变化使结构对海冰的加载速率发生改变,海冰会交替发生韧性破碎和脆性破碎.海冰破碎的韧-脆转变过程导致冰载荷波动使结构发生自激振动. 这一机理解释与现场测量发现的海冰破碎特征不符.首先,海冰的间歇性破碎现象说明,海冰在一个结构振动周期内只发生一次主要的破碎,即在加载阶段积累损伤,在卸载阶段发生破碎,而不是韧-脆转变机理解释认为的在这两个阶段分别发生韧性和脆性破碎;其次,频率锁定过程中冰载荷以及海冰破碎的同步性说明,整个过程均是韧性破碎,并未发生脆性破碎.因此,海冰韧-脆转变破碎导致结构自激振动的机理解释并不合理.基于这一机理建立频率锁定振动分析方法的技术路线存在较大困难.

3 海冰韧性损伤-破碎导致结构频率锁定振动的机理解释

冰载荷与结构响应的现场测量结果为分析频率锁定振动过程提供了直接数据. 为了分析频率锁定振动发生机理,图15中选取了两个典型振动周期内的实测冰载荷与结构响应数据. 本文用$F_1 $,$F_2 $,$F_3 $表征一个周期内载荷作用过程的不同阶段,其中,$F_1simF_2 $为加载阶段,$F_2 \sim F_3 $为卸载阶段. 表1中列出了加载、卸载两个阶段中海冰与结构的状态.

图15

新窗口打开| 下载原图ZIP| 生成PPT

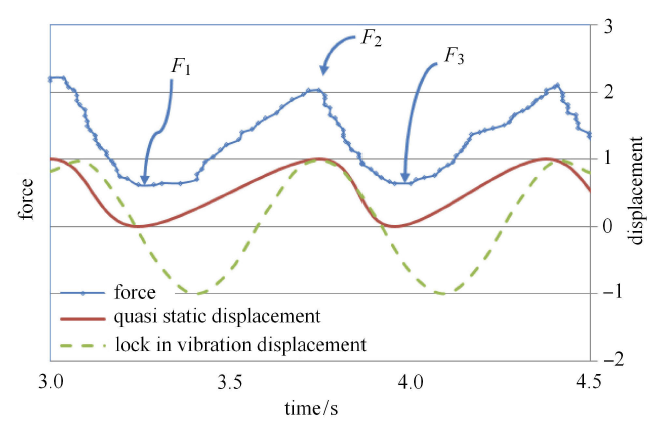
图15 频率锁定振动时的冰载荷与结构响应

Fig. 15 Ice force and structure response in frequency lock-in vibration

表1 频率锁定振动不同阶段中海冰破碎与结构振动的关系

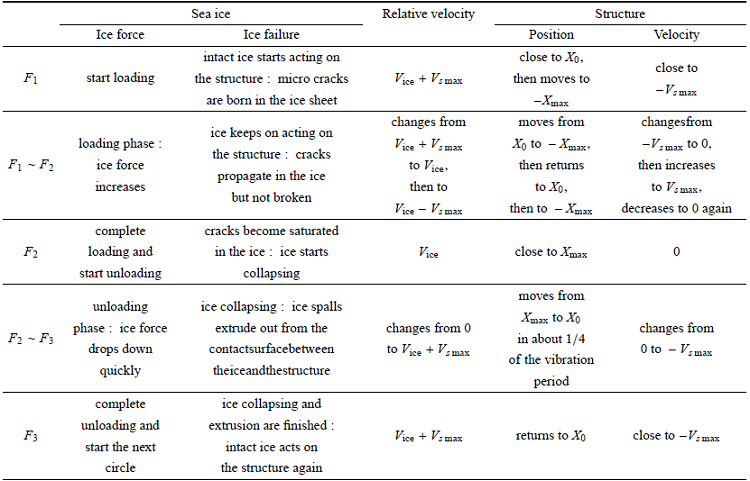Table 1 Relationship between ice failure and structure vibration in different stages of frequency lock-in vibration

新窗口打开| 下载CSV

从表1分析结果可以看出,频率锁定振动过程中,海冰的破碎是一种韧性损伤-破碎过程,该过程可以用图16进行说明.

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 海冰的韧性损伤-破碎

Fig. 16 Ductile damage-collapse failure of sea ice

如图16所示,理想状态下海冰韧性损伤-破碎有如下主要特征：

(1) 海冰的破碎是一个间歇性过程,而非连续过程,每一个海冰破碎过程可以分为损伤阶段和破碎阶段.

(2) 韧性损伤-破碎行为在每个振动周期内仅发生一次.

(3) 损伤阶段,海冰内产生裂纹并扩展但不发生大规模的断裂,冰载荷增大;破碎阶段,冰内裂纹饱和,海冰破碎,冰载荷减小.

频率锁定振动过程中海冰的韧性损伤-破碎过程和结构的运动相位关系如图17所示.在此过程中,结构的一次加载、卸载过程对应一次海冰破碎和一次结构往复运动,结构振动与海冰破碎过程的耦合和相位锁定导致结构发生耦合振动.图17中海冰韧性挤压破碎区(crush zone)的深度也是海冰的破碎长度,是频率锁定振动过程中重要的海冰参数.

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 相位锁定加载和频率锁定振动过程中的海冰破碎

Fig. 17 Ice failure during phase-locked loading and frequency lock-in vibration

4 频率锁定振动的简单分析方法

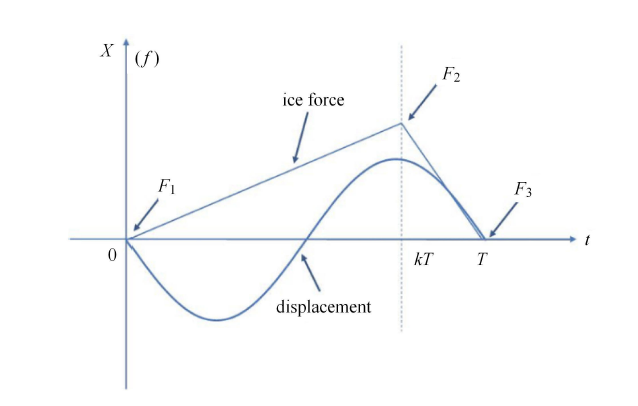
根据海冰的韧性损伤-破碎机理解释,在每个振动周期内,海冰有特定的破碎长度,海冰破碎主要在卸载阶段发生.由这一特征可以得出理想状态下结构振幅与海冰破碎长度之间的简单关系.为了解释这一关系,选取一个振动周期内的冰载荷与结构位移如图18所示.

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 一个频率锁定振动周期内的冰载荷与结构位移

Fig. 18 Ice force and displacement of the structure in a period of frequency lock-in vibration

图18中,在$t = 0$时海冰对结构开始加载,在$t = kT$时开始卸载. 假设当$t =0$时,结构处于平衡位置,并与海冰反向运动,则结构位移可表示为

(1)$x(t)=A \sin \left(\frac{2 \pi }{T}\right)$

式中,$T$为结构振动周期;$A$为振动幅值.

结构速度$V_{s}$为

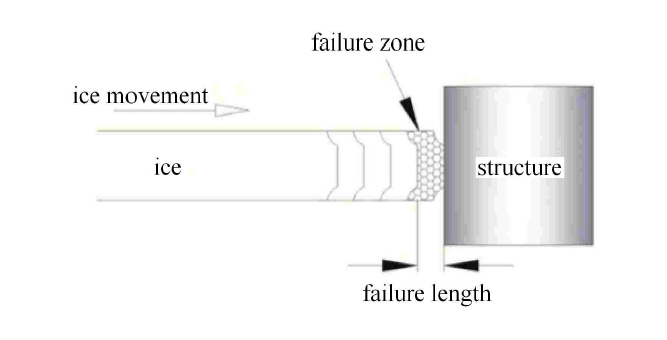
(2)$V_{s} = A\frac{2 \pi }{T}\cos \left( {\frac{2 \pi }{T}t} \right)$

当一个振动周期结束时,即$t = T$时刻结构会回到平衡位置,因此一个振动周期内海冰的破碎长度$L_{ib}$是该段时间内经过平衡位置的海冰长度,该长度为海冰运动速度$V_{i}$与结构振动周期$T$的乘积,即

(3)$L_{ib} = V_{i} T$

根据本文提出的韧性损伤-破碎机理解释,海冰在损伤阶段没有发生显著破碎,可以认为海冰在损伤阶段的变形与破碎阶段的破碎长度相比是一个较小值^[44],破碎长度$L_{{ib}}$主要是海冰在破碎阶段与结构之间的相对位移,因此$L_{{ib}} $也可以表示为

(4)$L_{{ib}} = V_{i} \left( {1 - k} \right)T + \int_{kT}^T {V_{s}} t$

式中,$k$由加载和卸载时间的比例决定,冰载荷的现场测量数据表明,$k$的取值范围为0.5$\sim$1.

将式(2)、式(3)代入式(4),可得

(5)$L_{ib} = - \frac{A\sin \left( {2k \pi } \right)}{k}$

将$A$移到左侧,式(5)变为

(6)$A=-\frac{k L_{\mathrm{ib}}}{\sin (2 k \pi )}$

式(6)给出了理想状态下频率锁定振动过程中海冰破碎长度与振动幅值之间的一般关系,这一关系可以用于估计结构频率锁定振动的幅值大小. 式中$k$可通过分析冰载荷现场测量数据确定. 理想状态下,结构从最大振幅位置回摆时海冰开始破碎,结构到达平衡位置时,海冰破碎结束. 在这种情况下,$k= 0.75$,由式(6)可知,海冰破碎长度为结构振幅的1.3倍.

实际上,海冰在破碎阶段结束之后,其断面并不平整. 因此损伤阶段开始时,结构将与凹凸不平的海冰断面发生作用,使其发生局部破碎. Kärnä^[45]的试验研究表明,海冰在损伤阶段与破碎阶段均会发生破碎,这里损伤阶段的破碎可以理解为局部破碎. 通过统计损伤阶段与破碎阶段中海冰破碎长度的比例关系发现两者比值约为3:7. 考虑这一关系式(4)中$L_{ib}$可以修正为

(7)$L_{ib} = \frac{\left[{V_{i} \left( {1 k} \right)T + \int_{kT}^T {V_{s} t} } \right]}{m}$

式中,$m$为破碎阶段的海冰破碎长度与总破碎长度$L_{ib} $的比值. Kärnä认为破碎阶段的海冰破碎长度占总破碎长度的70%,即$m = 0.7$.

将式(2)、式(3)代入式(7),可得

(8)$L_{ib} = \frac{A\sin (2k \pi )}{1 - (m + k)}$

将$A$移到左侧,式(8)变为

(9)$A = \frac{\left[{1 - (m + k)} \right]}{\sin (2k \pi )}L_{ib}$

此时将$k = 0.75$,$m = 0.7$代入式(9)可知,海冰破碎长度为结构振动幅值的2.2倍.

与导管架、灯塔结构的振动不同,Molikpaq平台的运动响应更接近一种准静态运动位移,无法用式(9)的关系进行分析.但也可以基于韧性损伤-破碎机理得出结构运动幅值与破碎长度之间的简单关系.

假设$T_{l} $为Molikpaq平台冰载荷加载阶段持续时间,$T_{u}$为卸载阶段持续时间,则结构每次运动周期$T$可以表示为

(10)$T = T_{l} + T_{u}$

根据韧性损伤-破碎机理解释,海冰在加载阶段不发生显著破碎,结构与海冰保持同向运动,则结构运动幅值为

(11)$A = V_{i} T_{l}$

卸载结束时平台回到平衡位置,破碎长度为海冰在一段时间内的移动距离,同样可由式(3)表示.

由式(3)、式(11),可以得到$L_{ib} $和$A$之间的关系

(12)$A = \frac{L_{ib} + T_{l} }{T}$

由式(12)可知,结构运动幅值与破碎长度和加载时间成正比,与结构运动周期成反比. 图11和图12表明加载时间与结构运动周期的比值在0.5$\sim$1区间内,即若破碎长度为5.4cm,则运动幅值为2.7$\sim$5.4cm. 实际上,经过挤压的海冰断面是粗糙的.当一个加载阶段开始时,粗糙的海冰断面会产生额外的碎冰;当下一个加载阶段开始时,海冰断面上的碎冰会发生挤压破碎.此时,结构与海冰共同移动的时间应小于结构运动周期. 因此,结构运动幅值应小于由式(12)得到的结果.

Molikpaq平台的响应类似于准静态运动,在此过程中冰载荷$F_{ice}$需要与结构响应引起的恢复力平衡,即

(13)$F_{ice} = PWH = KA$

式中,$P$为海冰挤压破碎的总压力;$H$为冰厚;$W$为平台宽度;$K$为平台水线处的刚度.

将式(12)代入式(13),可以得到导致平台相位锁定加载的冰厚,即

(14)$H =dfrac{KL_{ib} T_{l} }{TPW}$

通过上述公式可以估算Molikpaq平台相位锁定加载发生时的运动幅值.

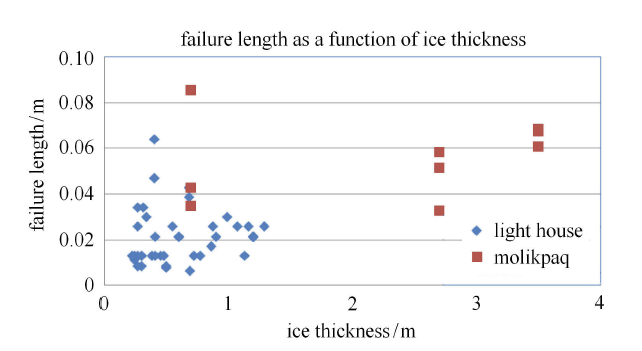
由式(9)和式(14)可知,海冰破碎长度是分析频率锁定振动过程中结构运动幅值的关键参数.目前工程中对该参数的研究还不够深入. 现阶段可以通过对实测数据进行统计得到破碎长度取值范围.对灯塔和Molikpaq平台监测数据进行统计得到海冰破碎长度统计结果如图19所示.可见在灯塔发生频率锁定振动时海冰破碎长度约为1$\sim$4cm,Molikpaq平台前海冰破碎长度约为3$\sim$8cm. 定性分析可以认为,海冰破碎长度与冰厚、海冰强度、结构直径等因素相关.

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 海冰破碎长度与冰厚的关系^[46]

Fig. 19 Sea ice failure length as a function of ice thickness^[46]

5 讨论

5.1 韧性损伤-破碎的发生条件

本文研究表明,海洋工程结构在发生频率锁定振动时,海冰的破碎是韧性损伤-破碎过程.在这一过程中,结构表面的海冰保持间歇性的同步破碎,冰载荷呈现锯齿形且在整个接触面保持同步.反过来从载荷特征来看,冰载荷呈现锯齿状时海冰破碎均可以认为是韧性损伤-破碎过程.海冰的韧性损伤-破碎过程可以导致结构准静态运动和频率锁定振动.

综合室内试验和现场测量结果可以发现,韧性损伤-破碎可以发生在冰厚几厘米到3m之间,结构宽度在几厘米到100m之间,其发生条件基本覆盖了所有海域的冰情和各种结构形式.可以认为,当低速海冰与直立结构作用时,韧性损伤-破碎是一种典型的破碎模式,可以发生在大多数直立结构上.韧性损伤-破碎的发生条件与冰情的关系可以评估频率锁定振动发生的时间和频率.

根据本文研究,海冰的破碎长度$L_{ib} $是韧性损伤-破碎过程的重要参数. 对于灯塔、导管架平台等柔性结构,当冰速接近$L_{ib}/T$时,韧性损伤-破碎过程会导致频率锁定振动;对于宽大的沉箱式平台或重力式平台,韧性损伤-破碎过程会导致相位锁定加载,引起很大的总体冰载荷和结构准静态运动,但不会导致结构的共振.宽大结构相位锁定加载过程中海冰破碎周期不会与结构的固有周期锁定.宽大结构发生相位锁定加载的条件主要有两个方面,首先是冰速在小于10cm/s会发生韧性损伤-破碎.其次由式(13)可知,当破碎发生时,冰厚应该大到引起的冰载荷可以导致结构位移到$A$.

5.2 韧性损伤-破碎的影响

海冰发生韧性损伤-破碎时的一个典型特征是整个结构表面海冰的破碎是同步的.Molikpaq平台测量结果显示,在80m宽的结构表面上,厚度约为2$\sim$3m的浮冰间歇性同步破碎,每次破碎长度为5cm左右.此现象说明结构在水线面上有特定的位移,在海冰断面上产生了均匀的变形和应变率,导致海冰挤压破碎区中的裂纹同时扩展和破碎.Kuiper^[47]认为,冰载荷在结构表面的同步性会导致冰载荷随宽度变化的效应减弱,进而造成更高的总体冰载荷.而ISO 19906中的总体冰载荷公式考虑了宽度效应,该公式与这一情况不符需要加以修改.

除了海冰的整体载荷较大之外,结构较大的动力响应也是海冰韧性损伤-破碎过程的主要危害. 动力响应极大地影响了设施完整性、结构基础稳定性,也增加了结构疲劳损伤的风险.

5.3 消除韧性损伤-破碎的措施

考虑到海冰破碎对结构表面形状的敏感性,通过改变结构表面形状可以消除海冰的韧性损伤-破碎过程. 基于韧性损伤-破碎的机理解释,海冰同时破碎是频率锁定振动发生的重要条件,且破碎过程中有特定的韧性损伤区深度. 针对这一特点,可以在结构表面设计一些高度大于韧性损伤区深度的凸起结构,如圆锥、四棱锥以及螺旋三角等. 在海冰与结构完全接触之前,凸起结构就会进入海冰断面,引发海冰的局部破碎,进而避免发生海冰同时破碎和频率锁定振动.

6 结论

本文通过对现场测量结果的分析,针对频率锁定振动提出了一种新的海冰韧性损伤-破碎机理解释. 该机理认为频率锁定振动发生过程中,海冰的破碎是一种韧性损伤-破碎过程. 在此过程中海冰在结构表面发生间歇性同时破碎并引起较高冰载荷. 该机理更加全面地反映了海冰与结构作用发生频率锁定振动的主要特征,为冰激频率锁定振动研究提出了新的方向和思路. 根据这一机理解释,海冰的韧性破碎长度$L_{ib}$是分析频率锁定振动过程的关键参数. 当冰速接近破碎长度与结构自振周期比值$L_{ib} / T$时,结构会发生频率锁定振动. 本文同时给出了一种利用海冰破碎长度估算结构振动幅值的简单方法.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Peyton

Sea ice strength

Final Report of Naval Research Arctic Project for Period 1958-1965, 1966,285