引言
冰激振动(ice-induced vibration,IIV)中的锁频共振现象是指流动的浮冰与冰区结构(或冰盖与在其中航行的交通船只如破冰船)的交互作用中,在一定的冰速范围内冰力和结构振动的主频皆锁定在结构固有频率, 从而导致结构共振.其结构振幅可较常规振幅有数量级的差异, 这与涡激振动(vortex-induced vibration,VIV)中的锁频共振在动力学上是相似的[1], 然而两者的物理本质完全不同.冰激锁频共振严重威胁冰区结构的安全, 导致结构疲劳加剧, 甚至直接摧毁结构,此外还会恶化结构上的人员工作环境和设备运行条件.因此探索冰激锁频共振的力学机理、明确其产生的临界条件不仅具有重要的科学意义,而且可以为冰区结构的设计和安全运行控制提供理论指导, 具有显著的工程价值.
IIV已受到冰区相关国家学术界和产业界的广泛关注[2],其中锁频共振是研究的重点和难点, 为此已开展了不少实验和理论研究.实验研究包括现场监测和实验室模型实验, 较为代表的工作如:Engelbrektson[3]在Bothnia海湾现场观察到冰激共振发生时,结构的加速度可达0.7$g$, 大大超过人体可接受的振动水平,而当天大多时间结构处于低幅振动水平, 只有0.07$g$左右,这表明冰激共振的出现具有一定的随机性; Määttänen[4]通过实验室模型研究发现在一个较宽的冰速范围内结构产生锁频共振; Tsuchiya等[5]在实验室模型研究中发现结构的振动主频先随冰速线性增加,然后锁定在结构固有频率直到最高实验冰速, 但冰力主频并未锁定在结构固有频率,离散性较强, 这也许与实验在空气中进行有关,这种锁频振动从严格意义上来说不属于锁频共振.
另一方面, 许多研究者建立了IIV动力学模型,以揭示IIV特别是锁频共振的动力学机制, 并提供冰区结构设计所需的动力学模型.根据冰破坏过程的连续性, 可将现有的IIV动力学模型分为两大类.一类是以Blenkarn[6]和Määttänen[7]最初建立并发展起来的基于负阻尼机制的冰连续破坏型自激振动模型,该类模型将IIV过程中冰的破坏视为连续压碎过程, 所以冰力就是冰的破坏冰力,可由冰的压缩强度计算得到. 基于Peyton[8]建立的冰的压缩强度与冰速的相关性曲线,该曲线在一定的冰速区间内梯度为负, 为结构提供负阻尼,从而导致结构发生动力学失稳, 产生自激振动,结构响应主频以及相应的冰力主频自然皆锁定在结构固有频率.自激振动模型简单、操作方便, 是目前应用最广泛的IIV动力学模型[9-11].另一类模型认为IIV中冰的破坏过程是间歇的, 即冰的破坏存在一个特征长度,这等效于认为冰存在破碎频率, 它等于冰速除以该特征长度.基于该认识Matlock[12]最先建立了一个冰间歇破坏型IIV动力学模型,可以反映在低速和高速冰速段内结构响应较小、在中间冰速范围内结构响应较大的全冰速范围IIV实验的一般特征,但不能预报IIV锁频共振. Sodhi[13] (下称Sodhi模型)对Matlock模型进行了改进,对冰与结构的交互作用考虑相互接触的加载阶段同时,还考虑了冰板压碎、屈曲破坏以后结构清除碎冰的过程以及冰与结构接触过程中可能存在的分离过程,它包含了更多的物理过程细节, 因而更为合理.然而正如本文下面将要介绍的该模型虽然能够预报IIV共振的出现,但不能预报在一定冰速范围内的锁频共振. 同样作为冰间歇破坏型IIV动力学模型,Toyama等[14]和Shih[15]针对共振发生时结构响应与冰力的同相位特征,提出了一些结构运动学假设, 以建立各自的IIV模型,探索冰激共振产生的临界条件和结构响应幅值.这些冰间歇破坏型IIV模型不是一个全冰速范围内的一般性动力学模型,其中的运动学假设只适用于研究共振产生时的必要条件,不能研究复杂的锁频共振现象. Huang等[16]在Sodhi模型的基础上,通过引入Peyton [8]建立的冰的压缩强度与冰速相关性的动力学特性,建立了一个全冰速范围冰间歇破坏型IIV动力学模型(下称Huang--Liu模型), 该模型吸收了两类模型的优点,不仅可以预报低速和高速冰速区段的小振幅IIV,而且可以预报中间冰速范围内可能发生的锁频共振,这是首个能预报锁频共振的间歇破坏型IIV动力学模型.目前Huang--Liu模型已受到学术界关注[9,17-27],Jeong和Baddour[17]对该模型和Toyama模型[14]进行了理论对比;Hendrikse等[23-26]基于该模型发展了IIV模型分析风电等柔性结构的IIV和疲劳寿命;最近Abrasion等[27]也用该模型计算结果评估它们新建的基于非线性动力学的IIV模型.此外也有学者提出了唯象学IIV模型,徐继祖和王翎羽[28-29]基于IIV与VIV的动力学相似, 引入一个冰力振子方程,与振动方程联立建立了他们的IIV模型, 可以反映IIV锁频共振现象;Xu和Oterkus等[21]对该模型进行了改进, 计及了冰压缩强度与冰速的相关性,但该类模型未涉及冰与结构交互作用的物理过程,无法揭示IIV及其锁频共振的物理机制.
对IIV锁频共振的研究已有50多年的历史, 但目前对于其机理的认识仍然不清,是自激振动还是强迫振动存在较大争议,达到Määttänen[19]所期望的共识尚需开展更深入的实验和理论研究工作.本文应用Huang--Liu模型开展冰激锁频共振的理论研究,首先分析IIV及锁频共振的结构响应特征,并从结构响应和冰力的频率耦合特性以及Huang--Liu模型与Sohdi模型计算结果的对比来研究锁频共振产生的原因;然后再分析结构特性和冰的物理特性参数对锁频共振影响的一般趋势;最后在此基础上揭示锁频共振的动力学机制.
1 IIV 动力学模型[16]
考虑一个单自由度振子结构系统与运动冰板的交互作用, 冰的破坏为间歇式,假设存在一个破坏区特征长度, 作用过程可分为3个阶段:加载, (碎冰)挤出和可能的分离阶段[13].
系统的运动控制方程为
式中, $M$, $C$和$K$分别为结构质量、阻尼系数和刚度; $x$, $\dot{{x}}$ 和$\ddot{{x}}$分别为结构位移、速度和加速度, $x_{0} $为$x$的初值; $k$为完整冰(破坏前)的压缩刚度; $\delta =x_{0} +vt-x-p(n-1)$为结构压入冰的长度,其中 $v, p$ 和$n$ 分别为冰速、冰间歇破坏的破碎区长度和破碎区序号;$\delta _{f} ={(F_{f} -F_{e} )}/{k}$ 为冰破碎时的压入长度, 其中$F_{e}$为挤出阶段挤出碎冰的冰力, 设为常数, $F_{f} $为冰破碎时的瞬时破坏冰力. 式(1)对Huang--Liu模型[16]的运动控制方程稍作了改进,在加载阶段条件中去掉了$\dot{x}\leqslant v$, 并在分离阶段条件中增加了$\delta <0$, 其表述更为确切.
根据 Korzhavin[30], 破坏冰力为
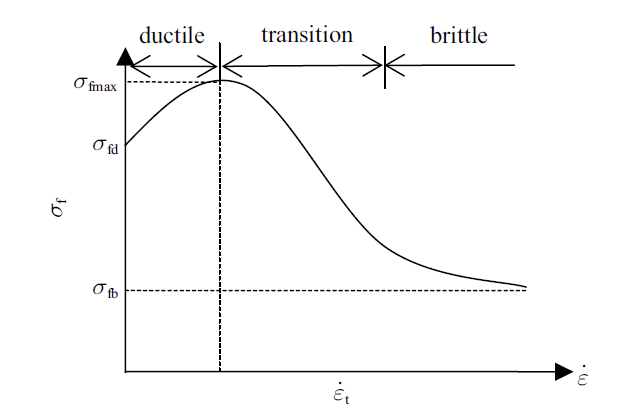
式中, $I$, $m$和$\kappa $分别为压入、几何和接触系数; $D$为结构的直径; $h$为冰的厚度; $\sigma_{f} $为冰的压碎强度. 在Sodhi模型中,冰的破坏冰力取为常数, 亦即压碎强度取为常数; 而在Huang--Liu模型中$\sigma_{f}$依赖于冰相对于结构的速度$v_{r} =v-\dot{{x}}$, 该相关性就是Peyton[8]建立的冰的压碎强度与冰速的相关性曲线, 如图1所示,图中定义了相关特征参数, 其中应变率$\dot{{\varepsilon }}_{t} =v_{t} /h$, $v_{t} $为韧脆转换冰速. 根据Iliescu 和Schulson[31]的研究,该曲线可以表示为无量纲形式, 由两个幂分布表示为
图1
图1
冰压碎强度与应变率关系的特征图
Fig. 1
Characteristic plot of ice-crushing strength versus strain rate
式中, $\overline \sigma_{f} ={\sigma_{f} }/{\sigma_{fmax } }$,$\overline \sigma_{fd} ={\sigma_{fd} }/{\sigma_{fmax } }$,$\overline \sigma_{fb} ={\sigma_{fb} }/{\sigma_{fmax } }$,这里$\sigma_{fmax } $为相应于$\dot{{\varepsilon }}_{t} $或$v_{t}$的最大冰破碎强度, $\alpha >0$和$\beta <0$为对应的无量纲指数.
引入下面无量纲参数和变量
式中, $\varDelta ={F_{fmax } }/{K}$为相应于最大破坏冰力的最大结构静态位移;$\omega_{n} =\sqrt {{K}/{M}} $为结构的固有圆频率,这样控制方程式(1)可转化为无量纲形式
其中, $\xi ={C}/({2M\omega_{n}})$为结构阻尼比, $\ddot{{\bar{{x}}}}={d}^{2}\bar{{x}}/({{d}\tau^{2}})$, $\dot{{\bar{{x}}}}={{d}\bar{{x}}}/{{d}\tau }$. 由式(2)可得$\bar{{F}}_{f} =\bar{{\sigma }}_{f}$, 因而瞬时破坏压入长度为
式(5) 为分段线性的非线性方程组, 相当于间歇非线性.在各阶段求解线性方程可获得各阶段的封闭解析解, 其详细解可参考Huang和Liu[16]的研究(更正该文献中的两个打印错误: (1)式(10)下的变量解释中$k_{r}=\bar{k}/1+\bar{k}$应为$k_{r} =\bar{k}/(1+\bar{k})$;(2)式(11)中的$\left[{\dot{{\bar{{x}}}}_{0e} +\xi (\bar{{x}}_{0e}-\bar{{F}}_{e} )\sin \omega_{e} \tau_{e} } \right]$应为$\left.\left[\dot{\bar{x}}_{0 \mathrm{e}}+\xi\left(\bar{x}_{0 \mathrm{e}}-\bar{F}_{\mathrm{e}}\right)\right] \sin \omega_{\mathrm{e}} \tau_{\mathrm{e}}\right)$. 应该指出的是由于冰破坏强度的率相关性,式(6)所示的破坏压入长度与结构瞬时速度相关,因此式(5)各阶段所经历的时间实际上是结构运动相关的,这导致冰力的时间历程和结构响应高度依赖于结构与冰的相对运动.因此式(5)整体上是高度非线性的, 其求解需要与式(3)和式(6)联立获得.在数值求解过程中的每个时间步长, 都需要根据式(5)中给出的各阶段条件,判断当前结构所处的阶段,从而由相应的封闭解析解获得结构响应和冰力的全部时间历程.
2 锁频共振
应用Huang--Liu 模型可对IIV进行数值分析, 重点关注所预报的锁频共振.表1列出了式(3)、式(5)所涉及的表征冰和结构性质的无量纲参数, 以此作为一个代表算例,通过计算获得相应的结构响应和冰力时间历程.
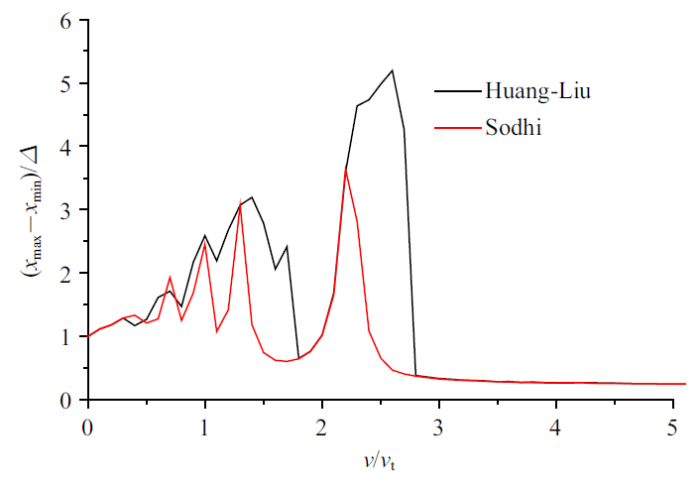
在运动冰的作用下结构从瞬态振动逐步过渡到稳态振动, 它对应稳定吸引子的极限环.图2黑线表示结构稳态振动阶段的无量纲振幅$\bar{{x}}_{\max } -\bar{{x}}_{\min} $随无量纲冰速$v/v_{t} $变化的情况,可以看到在低冰速和高冰速段结构振动较平和, 而在中间段冰速段结构振动较剧烈,这一IIV总的趋势与实验发现的一般特征是一致的. 特别应该注意的是在$v/v_{t}=2.2$$\sim$2.75的冰速区间, 结构振动最为剧烈, 较高冰速段的振动幅值高10倍左右.图2中红线表示的是基于Sodhi模型的计算结果,该模型计算中破坏冰力无速度相关性, 取为常数0.78$F_{fmax } $. 可以看到:虽然两个模型预报的IIV总趋势一致, 甚至在低冰速和高冰速段预报结果几乎相同,但在中间冰速段, Huang--Liu 模型预报的IIV更为剧烈,这清楚显示出既使在冰间歇破坏的情况下,冰破坏强度的率相关性在IIV中仍具有重要的作用.
图2
图2
不同模型预报的结构位移响应随冰速的变化
Fig. 2
Dependence of the amplitude of structural deflection on the ice velocity predicted from the different models respectively
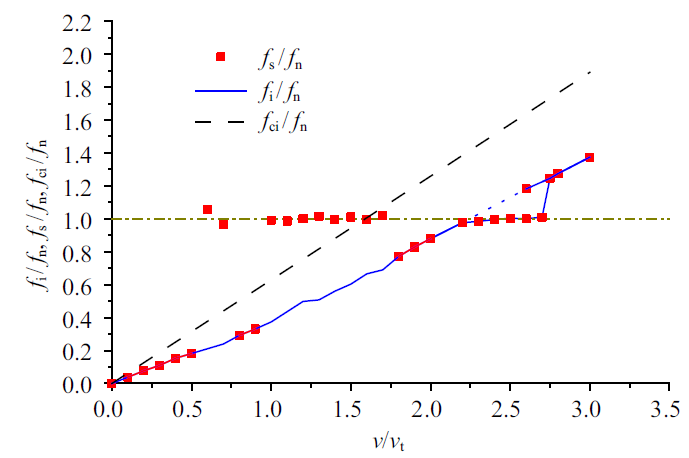
为了揭示冰破坏率相关效应放大振动的原因,对上述Huang--Liu模型计算得到的稳定阶段结构位移和冰力时间历程进行了频谱分析,分别获得了响应主频$f_{s} $和冰力主频$f_{i} $, 用结构固有频率$f_{n}$进行无量纲化, 它们随相对冰速的变化表示在图3中,其中蓝色实线和虚线表示响应主频, 红色方块表示冰力主频. 响应主频先随时间线性增加, 在无量纲冰速$v/v_{t} =2.2$时出现稳定解的分叉,原蓝色斜线代表的吸引子失去稳定性, 其主频由实线改为虚线表示; 在$v/v_{t}=$2.2$\sim$2.75区间新生长出一个稳定的吸引子, 其主频锁定在结构固有频率,用蓝色水平实线表示, 这一计算结果与Tsuchiya 等[5]的实验结果相同,不过实验中的最高实验冰速未超过平台段; 有趣的是在$v/v_{t} =2.6$$\sim$2.75区间,原蓝色斜线代表的吸引子又恢复稳定, 因而蓝色虚线又改为实线表示,这意味着在该区间出现了两个稳定吸引子, 代表两种稳态振动状态,系统选择哪种状态具有初值敏感性, 它与结构初始位置和速度相关[16];当无量纲冰速$v/v_{t} >2.75$时, 主频锁定的吸引子失去稳定性, 锁频平台消失,系统又经历一次分叉回到蓝色实线表示的单个吸引子状态,平台前后的蓝色实线和平台中的蓝色虚线几乎是一条斜线. 同时可以观察到,除了部分冰速区段以外冰力主频与响应主频几乎相同, 特别是在$v/v_{t}=2.2$$\sim$2.75区段, 冰力主频和响应主频皆锁定在结构固有频率,即结构发生了锁频共振, 所以可称上述锁频平台对应的振动状态为共振吸引子,这正是该冰速段结构振动剧烈的原因. 另外注意到无量纲冰速$v/v_{t}$在0.75附近和1.0$\sim$1.75区段,发生了冰力主频锁定在结构固有频率的现象, 但与响应主频分离,该种锁频开始产生时对应的响应主频分别在$f_{n} /4$和$f_{n} /2$附近,即分数频响应, 所以结构响应有一定放大, 但没有锁频共振显著,可称该种锁频为分离锁频, 以与共振锁频相区别. 冰力的分离锁频尚未见实验报道,可能是冰破坏的随机性妨碍了该种锁频的产生.
图3
图3
Fig. 3
Dependence of the predominant frequencies of the ice force and structural response on ice velocity, corresponding to
图3中黑色虚线给出了冰的无量纲特征破碎频率
随相对冰速的变化, 它被认为是冰的固有特性, 与结构运动无关,相当于冰与刚性结构作用的破碎频率. 同时对Sodhi模型的计算结果进行了频谱分析,结果表明响应主频和冰力主频相同, 并沿图3中蓝色实线和虚线连续变化,无一定冰速区内的锁频共振发生. 黑色虚线变成蓝线表明: 对于柔性结构,冰力主频及响应主频是结构与冰的相对运动和冰间隙破坏复杂耦合的结果,冰破坏的率相关性进一步增强了这种耦合, 导致锁频发生.
3 锁频共振的影响因素分析
图4(a)表示结构阻尼比对IIV及锁频共振的影响,其中黑线代表图2中的计算结果. 当其他参数不变仅改变$\xi$的大小, 可以看到增加结构阻尼使锁频共振冰速区间段缩小, 振动幅值减小,直至锁频共振消失. 图4 (b) 表示结构刚度对IIV及锁频共振的影响,改变刚度后最大结构静态位移$\varDelta $和结构固有频率将改变,因而表1所列的相关无量纲参数也要相应改变. 为比较方便,结构位移仍以图2算例的最大静态位移$\varDelta_{T} $无量纲化,它对应结构刚度$K_{T} $. 可看到随着结构刚度的提高,锁频共振冰速区间逐渐向高冰速段移动, 共振振幅也逐渐变小, 直至锁频共振消失,所以锁频共振容易在柔性结构中发生.
图4
图4
结构性质对锁频共振的影响
Fig. 4
Influence of the structural properties on the frequency lock-in resonance
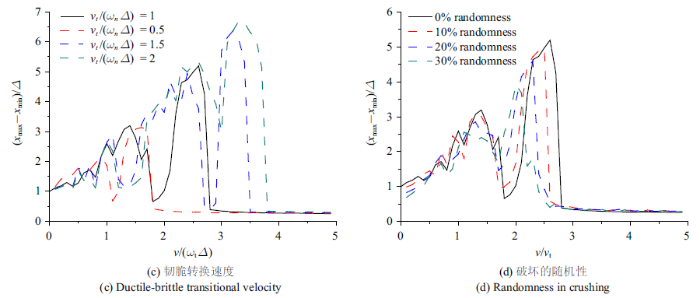
图5(a)表示冰的相对压缩刚度$\overline k =k/K$对IIV及锁频共振的影响,随刚度$\overline k $减小, 共振锁频区向高冰速端移动, 区间宽度增加,振动加剧. 图5(b)表示冰的破碎区长度对IIV及锁频共振的影响,随破碎区长度增大, 锁频共振冰速区间逐渐向高冰速段移动,共振振幅也逐渐增大, 不过变化非单调, 在破碎区长度$\overline p =$15时,锁频共振区间消失, 振幅减小, 所以锁频共振发生的冰破碎区长度要小于一定长度.图5(c) 表示冰的韧脆转换速度$\overline v_{t} $对IIV及锁频共振的影响,可看到其影响较为显著, 随$\overline v_{t} $增加锁频共振区间向高冰速端移动,振动幅值有显著增大. 为考察冰破坏的随机性对锁频共振的影响,分别对冰的压碎强度$\bar{{\sigma }}_{f} $ 和破坏区长度$\overline p$加入了10%, 20%和30%的均匀分布随机涨落,这样控制方程式(5)实际上是非线性随机微分方程组, 计算结果如图5 (d)所示,可看到随机性增加使锁频共振冰速区间宽度和振动幅值减小,区间位置向低速段稍有移动, 30%的涨落时锁频共振已消失,所以冰破坏的率相关性和随机性是一种竞争关系, 它们对锁频共振起着相反作用.冰破坏的随机性增加了IIV的复杂性,还会引起系统在共振吸引子和常规小幅振动吸引子之间随机游走[16],这可解释Engelbrektson[3]的现场观测结果.
图5
图5
冰的性质对锁频共振的影响
Fig. 5
Influence of the ice properties on the frequency lock-in resonance
图5
图5
冰的性质对锁频共振的影响(续)
Fig. 5
Influence of the ice properties on the frequency lock-in resonance (continued)
由以上结构和冰参数的影响分析可以看到它们对锁频共振的影响较为复杂,对这些参数影响机理的理解还有赖于对锁频共振力学机制的清晰认识.
4 锁频共振机理分析
前面的分析表明了锁频共振来源于冰破坏的应变率效应,下面将研究该效应作用的力学机制,分析为什么共振能维持在一定冰速区间内发生. 为此对图2锁频共振冰速段中典型冰速的稳态结构速度响应$v_{s}$和冰力时程曲线进行分析,以了解冰与结构接触过程和冰破坏过程对IIV及锁频共振的影响.
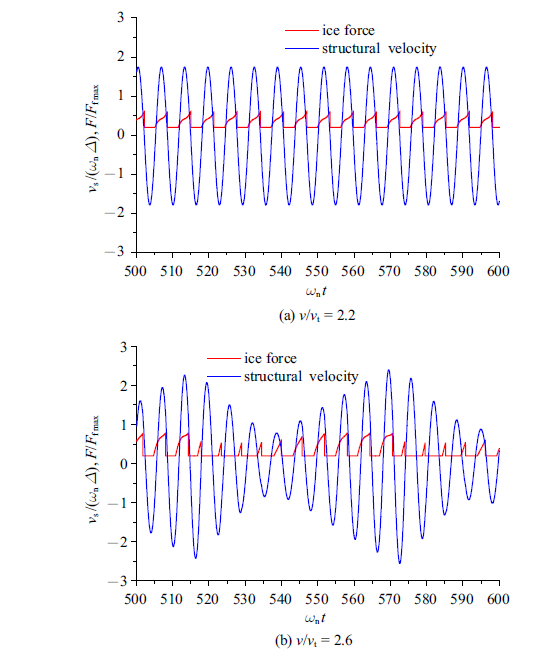
图6(a)表示在$v/v_{t} =2.2$时稳态振动的结构速度响应$v_{s} $和冰力时程曲线,该冰速对应锁频共振区间的开始冰速.加载阶段及其冰力呈周期变化并与响应周期相同,一个响应周期发生一次冰的破坏, 导致冰力与响应完全同步, 这就是常规的单频共振.冰力历程中加载阶段冰力曲线与时间坐标所围面积就是冰破坏前冰与结构之间所传递的动量,在该冰速整个加载阶段内结构与冰运动方向都相同($v_{s} >0)$,即冰力所做外力功全部转化为结构动能的增加, 结构不断从冰获取动能,直至一个周期内结构动能与结构黏性耗散能和势能达到平衡,结构稳定在高幅振动状态. 在$v/v_{t}=2.2$时Sodhi模型也能预报出完全相同的共振,但其预报的共振只发生在这一冰速, 不存在锁频共振持续发生的冰速区间.
图6
图6
Fig. 6
Time history plots of ice force and structural response velocity at typical ice velocities in the phase of the frequency lock-in resonance corresponding to
图6(b)表示$v/v_{t} =2.6$时稳态振动的结构速度响应和冰力时程曲线,该冰速对应振幅最大冰速. 在该冰速下结构振幅出现了周期变化,也就是出现了拍现象[32], 这是因为响应和冰力产生了多频,其主频都接近结构固有频率, 但围绕其附近还出现了两个对称的次频,它们可以合成为频率为结构固有频率的拍振动, 其拍频为两个次频的差频,拍振动与主频振动叠加就是图6(b)所示的振动.可以观察到在一个拍内有10个振动周期并发生了10次冰的间歇破坏.另外在一个拍内加载过程逐渐从结构与冰运动方向相同过渡到两者方向相反,同时结构振幅也从逐渐增大过渡到逐渐减小, 直至下一个拍开始.这是由于结构与冰之间传递的动量使得结构逐渐从冰获得动能(当$v_{s}>0)$过渡到冰从结构获得动能(当$v_{s} <0)$,这说明冰力既可激励振动也可抑制振动. $v/v_{t} =2.6$时的振动可称为多频共振,其最大结构响应大于$v/v_{t} =2.2$时的单频共振结构响应,但从平均来看其响应还是小于单频共振时的响应.
为了理解多频共振产生的原因, 进一步分析图6(b)所示$v/v_{t}=2.6$时稳态振动的结构速度响应和冰力时程曲线.在一个拍内各加载时间长度和冰力幅值(破坏冰力)也从逐渐增大过渡到逐渐减小,这意味着冰与结构之间的能量交换是非对称的,即结构与冰同向运动时获得的动能大于其与冰反向运动时向冰传递的动能,即使在偏离常规共振冰速的一定冰速范围内结构仍然能够维持高幅振动.事实上在结构与冰的交互作用中,结构与冰同向运动时结构的运动起到缓冲的作用(减小相对速度),这可减小冰力的上升速度, 增加加载段时间, 使结构在冰破坏前从冰获得更多动能;反之当结构与冰反向运动时结构运动起到敲击的作用(增大相对速度),这可增加冰力的上升速度, 缩小加载段时间, 减小结构在冰破坏前向冰传递的动能.因此即使破坏冰力没有速度效应,结构运动也会导致结构与冰之间能量传递的非对称性, 并且结构振幅越大,这种非对称性越大, 形成一种正反馈耦合机制. 当冰速落入图1负梯度相关区域时,结构与冰同向运动导致相对速度减小、瞬时破坏冰力升高,使加载时间延长、动量传递增加;反之结构与冰反向运动导致相对速度增加、瞬时破坏冰力降低,使得加载时间缩短、动量传递减小,因此冰破坏的应变率效应使得上述能量传递的非对称性进一步放大.另外在常规共振冰速附近冰破坏的应变率效应使得拍内各加载段时间长度发生周期变化,起到频率调制的自组织作用. 这种调频机制导致冰力和响应都出现多频,并锁定在结构固有频率附近, 引起拍振动发生,使上述能量传递的正反馈耦合机制的效果得以最大发挥,从而使共振能维持在一定冰速范围内产生.因此冰破坏的应变率效应是通过频率调制和放大动能传递正反馈效应的双重作用导致锁频共振的产生.
基于上述锁频共振机理的认识, 较容易理解第4节中影响因素分析的结果.结构阻尼降低导致锁频共振时维持结构耗散能量、势能与输入动能平衡所要求的稳态结构振幅增大;增加结构刚度会增大结构固有频率, 使锁频共振所要求的冰速向高冰速端移动,偏离冰破坏强度率相关性曲线的负梯度区域, 抑制了锁频共振;冰的压缩刚度减小导致加载阶段时间变长, 结构获得更多动量, 使振动加剧;由式(3)对冰速求导可看到韧脆转化冰速增大, 负相关斜率减小,负相关区域相应增加, 导致锁频冰速段增加、振动加剧;冰的破坏区长度超过一定范围, 冰挤出阶段相对变长,冰破坏率相关效应对冰力主频的调节作用减弱甚至消失, 抑制了锁频共振产生;冰破坏的随机性增加, 使得上述频率调制和能量传递正反馈效应减弱,部分或全部抵消掉了冰破坏的应变率效应在锁频共振中的作用.
式中破坏冰力$F_{f} (v-\dot{{x}})$可由式(2)和式(3)给出.
对于小幅振动上式可展开为
对于小幅振动上式可展开为
当冰速落入破坏冰力应变率相关性曲线中梯度${{\partial F_{f} (v)}/{\partial v}}$为负的区域且梯度在数值上超过结构阻尼系数$C$, 结构将发生动态失稳,产生自激振动, 结构响应及冰力的频率自然就是结构固有频率,并且在一定冰速区间内(负梯度冰速区域)产生锁频共振,所以该类模型将锁频共振理解为一种自激振动. 线性系统不能产生极限环,该类模型将结构响应速度超过冰速时的结构响应作为最大结构响应,这也是该类模型可应用的极限状态.
Huang--Liu模型和自激振动模型都利用了冰破坏的速度相关性,并且都能预报锁频共振, 但力学机理完全不同.在Huang--Liu模型中正反馈耦合机制是冰间隙破坏过程中的应变率相关效应导致的冰力频率调制和冰-结构动能传递的非对称性放大;而自激振动模型中正反馈机制是冰连续破坏过程中应变率相关效应导致的负阻尼激励.Huang--Liu为非线性系统, 锁频共振幅值就是稳定极限环吸引子的响应幅值,它是包含有冰破坏过程的冰与结构复杂交互作用所达到的一种动态平衡状态,是一种非线性耦合振动; 而自激振动模型预报锁频共振幅值需要附加运动学限制条件.
自激振动模型视冰的破坏过程为连续破坏过程,这只有在高冰速下才可认为是合理的, 然而在高的冰速段,冰破坏的率相关性曲线已趋于平稳, 负阻尼效应已经很弱,因此自激振动模型在物理上遭到不少学者的质疑.由于该模型简单且多年在工程中使用, 所以仍在2010发布的ISO19906标准中作为动冰力模型推荐.显然基于冰间歇破坏的耦合振动模型在物理上更为接近实际,本文揭示的这一新的锁频共振机理和相关分析结果能够为IIV的减振和控制提供更多思路和理论指导.如何降低理论复杂性便于工程应用也是间歇破坏型模型所要解决的问题.
5 总结
本文应用计及了冰间隙破坏应变率效应的IIV动力学模型 —— Huang--Liu模型对锁频共振进行了理论分析,预报了不同结构和冰参数条件下的锁频共振, 并揭示了锁频共振产生的力学机制.研究表明: 在锁频共振发生的一定冰速区间内,结构响应和冰力主频都锁定在结构频率, 然而不同冰速下的频谱结构和振动形态各异,从常规单频共振到多频共振、从等幅振动到振幅周期性变化的拍振动,呈现出丰富的动力学特征;结构动力学参数以及冰的力学和破坏性能参数对锁频共振产生不同影响,可改变锁频共振发生的冰速区间长度和位置以及结构振幅,冰破坏的随机性和应变率效应对锁频共振发挥着一种竞争的作用;锁频共振来源于冰破坏的应变率效应,其力学机制是频率调制和对结构-冰动能传递的非对称性正反馈效应放大的双重作用.本文揭示的这一新的锁频共振力学机制属于耦合振动的范畴,与传统连续破坏型IIV模型给出的负阻尼自激振动机制有着本质区别.本文分析结果及对锁频共振机理的认识有助于冰区结构的设计以及相关减振和控振技术的研发.基于本文理论研究结果已经开展了IIV及锁频共振实验研究, 研究进展将另文介绍.
参考文献
The measurement of vortex-induced effects in flow past stationary and oscillating circulator and D-section cylinder
[Master Thesis].
Observations of a resonance vibrating lighthouse structure in moving ice
//Proc.
Dynamic ice structure interaction during continuous crushing
An experimental study on ice-structure interaction
//Proc.
Measurement and analysis of ice force on cook inlet structures
//
On conditions for the rise of self-excited ice induced autonomous oscillations in slender marine pile structures
Sea ice Forces. Ice pressure against structures
An assessment of sensitivity of the self-excited modelling approach for simulating dynamic ice-structure interactions to changes in temperature and scale effects
Nonlinear model parameter identification for ice-induced vibrations
海上单桩风机结构冰激振动响应分析
Ice-induced vibration response analysis of monopile offshore wind turbine
Analytical model for ice-structure interaction
A theoretical model for ice-structure interaction
//Proc.
Model tests on ice-induced self-excited vibration of cylindrical structures
//
Analysis of ice induced vibration on a flexible structure
A dynamic model for ice-induced vibration of structures
Comparison of characteristic failure frequency models for ice induced vibrations
Vibrations due to flow-driven repeated impacts
Ice induced frequency lock-in vibrations - converging towards consensus
//
The forming cyclic loads on the offshore structures during ice field edge fracture
A dynamic ice-structure interaction model for ice-induced vibrations by using van der pol equation
Ice-induced vibrations of flexible offshore structures: the effect of load randomness, high ice velocities and higher structural modes
//Proc.
Analysis of the fatigue life of offshore wind turbine generators under combined ice- and aerodynamic loading
//
Interpretation and prediction of ice induced vibrations based on contact area variation
Dynamic response of an offshore structure interacting with an ice floe failing in crushing
Ice-induced vibrations of vertically sided offshore structures
[PhD Thesis].
On a simple oscillator problem describing ice-induced, vibrations of an offshore structure
Ice force oscillator model and its numerical solution
//Proc. 7th Intern.
冰与结构动力相互作用的理论分析模型
Theoretical study model for dynamic interaction of ice and structures
Action of ice on engineering structures
Brittle compressive failure of ice: monotonic versus step-loading
//Proc. 18th Int.