引言
基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法.
就配点法的精度而言, 一个突出的问题就是其计算精度依赖于形函数所采用的基函数阶次的奇偶性, 即奇数阶次基函数的配点法收敛率较其基函数阶次下降一次[19 ,24 ] . 王东东等[24 -26 ] 系统研究了二阶和四阶问题无网格配点法奇数阶次基函数精度掉阶的原因. 研究表明, 配点法的精度与形函数及其梯度的一致性或完备性条件密切相关. 因此, 王东东等[24 -25 ] 通过引入无网格形函数的梯度光滑方法, 建立了超收敛无网格配点法, 并在不引入待定配点位置的情况下有效解决了奇数阶次基函数配点法的精度掉阶问题, 实现了采用奇数次基函数配点法精度的超收敛提升. 基于梯度光滑方法, 邓立克等[27 ] 通过线性基函数构造了二阶光滑梯度, 使得采用线性基函数就可以进行四阶薄板问题的伽辽金无网格分析. 然而, 注意到上述工作中所讨论的形函数高阶光滑梯度构造的基础是形函数的标准一阶梯度, 这对于本身具有高阶光滑特性的无网格形函数没有问题, 但是由于有限元形函数的一阶梯度在单元节点和边界处并不存在, 因此难以直接构造有限元形函数的高阶光滑梯度和发展相应的配点法.
为了构造有限元形函数的高阶光滑梯度, 本文在无网格法的梯度光滑理论框架内[24 ,28 ] , 首先引入了有限元形函数在节点处和全域内的一阶光滑梯度定义, 然后在此基础上建立了有限元形函数的二阶光滑梯度, 进而采用有限元形函数的光滑梯度建立了一种新型的节点梯度光滑有限元配点法. 与传统有限元形函数梯度不同, 有限元形函数的一阶和二阶光滑梯度具有全域连续的特点. 不失一般性, 本文以线性形函数为例, 详细研究了有限元形函数一阶和二阶光滑梯度的构造特点和一致性条件, 并对节点梯度光滑有限元配点法进行了精度分析. 分析表明, 线性有限元形函数的二阶光滑梯度能够满足二阶一致性条件, 因而对应的节点梯度光滑有限元配点法具有二次精度和超收敛特性. 注意到基于梯度光滑理论[28 ] , Liu等[29 ] 构造了有限元形函数的一阶光滑梯度, 提出了伽辽金光滑有限元法. 但本文所讨论的一阶与二阶有限元形函数光滑梯度, 其光滑核函数选取和构造方式均与伽辽金光滑有限元法不同, 同时着重研究的是配点法计算列式. 文中通过典型算例系统验证了节点梯度光滑有限元配点法的精度和收敛性.
1 配点法控制方程
本文考虑稳态势问题和弹性力学问题等典型二阶问题, 其控制方程的强形式可以表示为
(1) $\begin{eqnarray} \label{eq1} \left. {{\begin{array}{l@{\ \ \ }l} {{{\cal L}}{ u}({ x})+{ b}({ x})={\bf 0}}, & {{ x}\in \varOmega} \\ {{{\cal B}}^{ g}{ u}({ x})={ g}({ x})}, & {{ x}\in\varGamma^{g}} \\ {{{\cal B}}^{ t}{ u}({ x})={ t}({ x})}, & {{ x}\in\varGamma^{t}} \\ \end{array} }} \right\} \end{eqnarray}$
其中${ u}({ x})$为场变量, 例如弹性力学问题的位移或热传导问题的温度, ${{\cal L}}$为空间域$\varOmega $内的偏微分算子, ${{\cal B}}^{ g}$和${{\cal B}}^{ t}$为强制边界$\varGamma^{g}$和自然边界$\varGamma ^{t}$上的算子, ${ b}$为源项, ${ g}$和${ t}$分别为$\varGamma ^{g}$和$\varGamma^{t}$上给定的边界值. 方便起见, 这里给出二维情况下的各个算子的定义. 例如, 对于稳态势问题, ${{\cal L}}$, ${{\cal B}}^{ g}$和${{\cal B}}^{ t}$为
(2) $\begin{eqnarray} \label{eq2} &&{{\cal L}}={\nabla}^{ \rm T}{\nabla} ,\ \ {\nabla}^{ \rm T}=\left\{ {{\begin{array}{*{20}c} {\dfrac{\partial }{\partial x}} \hfill & {\dfrac{\partial }{\partial y}} \hfill \\ \end{array} }} \right\} \end{eqnarray}$
(3) $\begin{eqnarray} \\&&\label{eq3} {{\cal B}}^{ g}=1,\ \ {{\cal B}}^{ t}={ n}^{ \rm T}{\nabla} ,\ \ { n}^{ \rm T}=\{{\begin{array}{*{20}c} {n_{x} } \hfill & {n_{y} } \hfill \\ \end{array} }\} \end{eqnarray}$
其中${ n}$表示在自然边界$\varGamma^{t}$的单位外法线向量. 对于平面应力弹性力学问题, 上述算子可表示为
(4) $\begin{eqnarray} \label{eq4} &&{\cal L}=\hat{{\nabla}}{}^{ \rm T}{ D}\hat{{\nabla}},\ \ {\cal B}^{ g}={ I},\ \ {\cal B}^{ t}={\hat{ n}}{}^{ \rm T}{ D}\hat{{\nabla}} \end{eqnarray}$
(5) $\mathcal{L}=\hat{\nabla}^{\mathrm{T}} \boldsymbol{D} \hat{\boldsymbol{\nabla}}, \quad \mathcal{B}^{g}=\boldsymbol{I}, \quad \mathcal{B}^{t}=\widehat{\boldsymbol{n}}^{\mathrm{T}} \boldsymbol{D} \hat{\boldsymbol{\nabla}}$
(6) $\begin{eqnarray} \label{eq6} { D}=\dfrac{E}{1-\nu^{2}}\left[ {{\begin{array}{c@{\ \ }c@{\ \ }c} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & {(1-\nu )/2} \\ \end{array} }} \right] \end{eqnarray}$
式(4)和式(6)中${ D}$为平面应力弹性本构矩阵, ${ I}$为二阶单位阵, $E$和$\nu $分别代表材料的杨氏模量和泊松比.
在配点法中, 直接将空间区域$\varOmega $离散为一组节点$\{{ x}_{I}\}_{I=1}^{ NP} $, 而场变量${ u}({ x})$可以由形函数$N_{I} ({ x})$及对应的节点系数${ d}_{I} $表示为
(7) $\begin{eqnarray} \label{eq7} { u}^{ h}({ x})=\sum\limits_I {N_{I} ({ x}){ d}_{I} } \end{eqnarray}$
将式(7)代入控制方程(1), 并令其离散节点处的残值为零, 便可以得到配点法的离散方程
(8) $\begin{eqnarray} \label{eq8} { K d}={ f} \end{eqnarray}$
其中${ K}$, ${ d}$和${ f}$分别表示刚度矩阵, 节点系数向量和力向量
(9) $\begin{eqnarray} \label{eq9} &&{ K}=\left[ {{\begin{array}{*{20}c} {{ K}^{ i}} \\ {{ K}^{ g}} \\ {{ K}^{ t}} \\ \end{array} }} \right],\mbox{ }{ f}=\left[ {{\begin{array}{*{20}c} {{ f}^{ i}} \\ {{ f}^{ g}} \\ {{ f}^{ t}} \\ \end{array} }} \right] \end{eqnarray}$
(10) $\begin{eqnarray} \label{eq10} \left. {{\begin{array}{l@{\quad }l@{\quad }l} {{ K}_{IJ}^{ i} ={{\cal L}}[N_{J} ({ x}_{I} )],} & {{ f}_{I}^{ i} =-{ b}({ x}_{I} )}, & {{ x}_{I} \in \varOmega } \\ {{ K}_{IJ}^{ g} ={{\cal B}}^{ g}[N_{J} ({ x}_{I} )],} & {{ f}_{I}^{ g} ={ g}({ x}_{I} )}, & {{ x}_{I} \in \varGamma^{g}} \\ {{ K}_{IJ}^{ t} ={{\cal B}}^{ t}[N_{J} ({ x}_{I} )],} & {{ f}_{I}^{ t} ={ t}({ x}_{I} )}, & {{ x}_{I} \in \;\varGamma^{t}} \\ \end{array} }} \right\} \end{eqnarray}$
由式(10)可见, 配点法需要计算形函数的二阶梯度, 而标准有限元形函数在单元边界处不存在二阶梯度, 因此无法直接用于配点法. 此外, 虽然通过特殊构造方式可以建立一些特殊单元的高阶光滑有限元形函数, 但是目前仍然缺乏构造一般单元高阶光滑形函数的通用有效方法[1 ] . 本文则是通过引入无网格法中的梯度光滑技术, 建立了有限元形函数的一阶和二阶光滑梯度, 进而发展了相应的节点梯度光滑有限元配点法.
2 有限元形函数的光滑梯度构造
2.1 有限元形函数光滑梯度构造理论
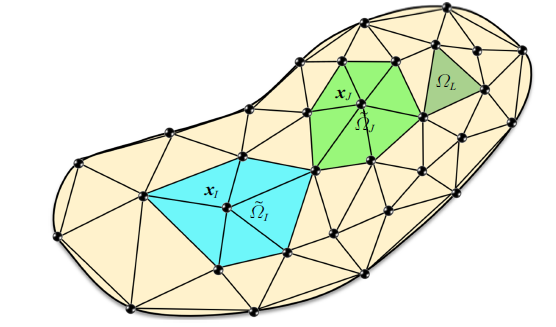
考虑图1 所示的有限元网格, $\varOmega_{L} $表示第$L$个单元对应的空间区域, 节点${ x}_{I} $对应的有限元形函数是$N_{I} ({ x})$, $N_{I} ({ x})$的影响域$\tilde{{\varOmega }}_{I} $为
(11) $\begin{eqnarray} \label{eq11} \tilde{{\varOmega }}_{I} =\cup_{L=1}^{ M_{I} } \varOmega_{L} ,\ \ { x}_{I} \cap \varOmega_{L} \ne \emptyset \end{eqnarray}$
式中$M_{I} $表示共享节点${ x}_{I} $的单元个数. 方便起见, 定义下面的节点组和单元组
(12) $\begin{eqnarray} \label{eq12} &&{\cal G}_{I} =\left\{ {\left. K \right|{ x}_{K} \in \varOmega_{L} ,\ \ \varOmega_{L} \in \tilde{{\varOmega }}_{I} } \right\} \end{eqnarray}$
(13) $\begin{eqnarray} \label{eq13} {\cal Z}_{I} =\left\{ {\left. K \right|\varOmega_{K} \in \tilde{{\varOmega }}_{I} } \right\} \end{eqnarray}$
图1
图1
有限元形函数影响域示意图
Fig.1
Illustration of the influence domains of finite element shape functions
根据广义梯度光滑理论[4 ,24 ] , 有限元形函数$N_{I} ({ x})$的一阶光滑梯度$\bar{{N}}_{I,i} ({ x})$的定义为
(14) $\begin{eqnarray} \label{eq14} \bar{{N}}_{I,i} ({ x})=\int_\varOmega {\varphi ({ x},{ y})N_{I,i} ({ y}){\rm d}\varOmega } \end{eqnarray}$
式中$\varphi ({ x},{ y})$为梯度光滑核函数, $N_{I,i} ({ x})$为传统的标准一阶梯度或导数, 即$N_{I,i} ({ x})=\partial N_{I} ({ x})/\partial x_{i} $, $x_{i} $为${ x}$的第$i$个坐标分量. 由于有限元形函数的梯度在单元边界处没有定义, 因此式(14)并不能直接用于有限元形函数的光滑梯度构造.
为了构造有限元形函数的光滑梯度, 这里首先引入有限元形函数在节点处的梯度值. 为此, 在式(14)中选取如下的梯度光滑核函数
(15) $\begin{eqnarray} \label{eq15} \varphi ({ x}_{J} ,\ \ { x})=\left\{ {\begin{array}{l@{\quad }l} \dfrac{1}{\tilde{{V}}_{J} }, &{ x}\subset \tilde{{\varOmega }}_{J} \\ 0,&\mbox{otherwise} \\ \end{array}} \right. \end{eqnarray}$
其中$\tilde{{V}}_{I} $表示一维、二维、三维情况下$\tilde{{\varOmega }}_{I}$的长度、面积或体积. 将式(15)代入式(14), 有
(16) $\begin{eqnarray} \label{eq16} && \bar{{N}}_{I,i} ({ x}_{J} )=\sum\limits_{L\in {\cal Z}_{J} } {\int_{\varOmega_{L} } {\varphi ({ x}_{J} ,\ \ { x})N_{I,i} ({ x}){\rm d}\varOmega } } =\\&&\qquad \frac{1}{\tilde{{V}}_{J} }\sum\limits_{L\in {\cal Z}_{J} } {\int_{\varOmega _{L} } {N_{I,i} ({ x}){\rm d}\varOmega } } \end{eqnarray}$
若进一步考虑常应变单元, 例如一维两节点单元、二维三节点三角形单元和三维四节点四面体单元, 则$N_{I,i} ({ x})$在每个单元内均为常数, 式(16)可以简化为
(17) $\begin{eqnarray} \label{eq17} \bar{{N}}_{I,i} ({ x}_{J} )=\frac{1}{\tilde{{V}}_{J} }\sum\limits_{L\in {\cal Z}_{J} } {N_{I,i} ({ x}_{J} )V_{L} } ,\mbox{ }{ x}_{J} \in \varOmega_{L} \end{eqnarray}$
其中$V_{L} $表示单元$\varOmega_{L} $的长度、面积或体积.
在式(17)定义的有限元形函数的节点梯度基础上, 进一步选择梯度光滑核函数$\varphi({ x},\ \ { x}_{J} )=N_{J} ({ x})$,则根据式(14)对应的离散形式, 可得如下的有限元形函数一阶光滑梯度
(18) $\begin{eqnarray} \label{eq18} \bar{{N}}_{I,i} ({ x})=\sum\limits_{J\in {\cal G}_{I} } {N_{J} ({ x})\bar{{N}}_{I,i} ({ x}_{J} )} \end{eqnarray}$
接下来, 对式(18)进行求导, 并用式(18)定义的一阶光滑梯度代替传统一阶梯度, 最后可得有限元形函数的二阶光滑梯度
(19) $\begin{eqnarray} \label{eq19} \bar{{N}}_{I,ij} ({ x})=\sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})\bar{{N}}_{I,i} ({ x}_{J} )} \end{eqnarray}$
至此, 已经构建有限元形函数的二阶光滑梯度. 下面通过一维和二维线性有限元形函数一阶和二阶光滑梯度的构造过程来说明有限元形函数光滑梯度构造理论.
2.2 线性有限元形函数光滑梯度构造
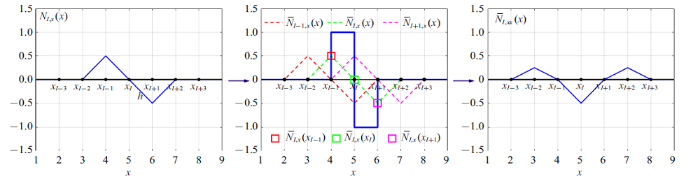
清晰起见, 首先考虑图2 所示的一维均匀有限元网格, 其中$h$表示单元的长度, 在此情况下, $\varOmega_{I} =(x_{I} ,x_{I+1} )$, $\tilde{{\varOmega }}_{I}=(x_{I-1} ,x_{I+1} )$, 因此$V_{I} =h$, $\tilde{{V}}_{I} =2h$. 有限元节点$x_{I} $的形函数$N_{I} (x)$可表示为
(20) $\begin{eqnarray} \label{eq20} N_{I} (x)=\left\{ {{\begin{array}{l@{\quad}l} 0, & {x\leqslant x_{I-1} } \\ {(x-x_{I-1} )/(x_{I} -x_{I-1} )}, & {x_{I-1} <x<x_{I} } \\ {(x_{I+1} -x)/(x_{I+1} -x_{I} )}, & {x_{I} <x<x_{I+1} } \\ 0, & {x_{I+1} \leqslant x} \\ \end{array} }} \right. \end{eqnarray}$
其对应的一阶梯度或导数$N_{I,x} (x)$为
(21) $\begin{eqnarray} \label{eq21} N_{I,x} (x)=\left\{ {{\begin{array}{l@{\quad}l} 0, & {x\leqslant x_{I-1} } \\ {1/h}, & {x_{I-1} <x<x_{I} } \\ {-{1/h}}, & {x_{I} <x<x_{I+1} } \\ 0, & {x_{I+1} \leqslant x} \\ \end{array} }} \right. \end{eqnarray}$
由式(20)、式(21)和图2 可见, 有限元形函数$N_{I} (x)$为C$^{0}$连续, 其一阶梯度$N_{I,x} (x)$在单元节点$x_{I-1} $, $x_{I} $及$x_{I\mbox{+}1}$处不连续, 无法直接计算二阶梯度, 因而无法用于式(8)定义的配点法求解.
图2
图2
一维有限元形函数一阶光滑梯度构造过程
Fig.2
Construction of the first order smoothed gradient of 1D finite element shape function
另一方面, 根据式(14), 有限元形函数在节点处的一阶光滑梯度为
(22) $\begin{eqnarray} \label{eq22} \left. {\begin{array}{l} \bar{{N}}_{I,x} (x_{I-1} )=\dfrac{1}{2h}[N_{I,x} (x_{I-1}^{ -} )h+N_{I,x} (x_{I-1}^{ +} )h]=\dfrac{1}{2h} \\[1.5mm] \bar{{N}}_{I,x} (x_{I} )=\dfrac{1}{2h}[N_{I,x} (x_{I}^{ -} )h+N_{I,x} (x_{I}^{ +} )h]=0 \\[1.5mm] \bar{{N}}_{I,x} (x_{I+1} )=\dfrac{1}{2h}[N_{I,x} (x_{I+1}^{ -} )h+N_{I,x} (x_{I+1}^{ +} )h]=\dfrac{-1}{2h} \\ \end{array}} \right\}\qquad \end{eqnarray}$
在此基础上, 利用式(18), 可得一维线性有限元形函数的一阶光滑梯度$\bar{{N}}_{I,i} (x)$
(23) $\begin{eqnarray} \label{eq23} && \bar{{N}}_{I,x} (x)=N_{I-1} (x)\bar{{N}}_{I,x} (x_{I-1} )+N_{I} (x)\bar{{N}}_{I,x} (x_{I} ) +\\&&\qquad N_{I+1} (x)\bar{{N}}_{I,x} (x_{I+1} ) =\\&&\qquad \frac{1}{2h^{2}}\left\{ {{\begin{array}{l@{\quad }l} 0, & {x<x_{I-2} } \\[-1mm] {x-x_{I-2} }, & {x_{I-2} \leqslant x<x_{I-1} } \\[-1mm] {-(x-x_{I} )}, & {x_{I-1} \leqslant x<x_{I+1} } \\[-1mm] {x-x_{I+2} }, & {x_{I+1} <x\leqslant x_{I+2} } \\[-1mm] 0, & {x_{I+2} <x} \\ \end{array} }} \right. \end{eqnarray}$
进一步将式(22)和式(23)代入式(19), 可得一维线性有限元形函数的二阶光滑梯度
(24) $\begin{eqnarray} \label{eq24} && \bar{{N}}_{I,xx} (x)=\bar{{N}}_{I-1,x} (x)\bar{{N}}_{I,x} (x_{I-1} )+\bar{{N}}_{I,x} (x)\bar{{N}}_{I,x} (x_{I} ) +\\&&\qquad \bar{{N}}_{I+1,x} (x)\bar{{N}}_{I+1,x} (x_{I+1} ) =\\&&\qquad \frac{1}{4h^{3}}\left\{ {{\begin{array}{l@{\quad }l} 0, & {x<x_{I-3} } \\ {x-x_{I-3} }, & {x_{I-3} \leqslant x<x_{I-2} } \\[-1mm] {-x+x_{I-1} }, & {x_{I-2} \leqslant x<x_{I-1} } \\[-1mm] {-2x+2x_{I-1} }, & {x_{I-1} \leqslant x<x_{I} } \\[-1mm] {2x-2x_{I+1} }, & {x_{I} \leqslant x<x_{I+1} } \\[-1mm] {x-x_{I+1} }, & {x_{I+1} \leqslant x<x_{I+2} } \\[-1mm] {x-x_{I+3} }, & {x_{I+2} \leqslant x<x_{I+3} } \\[-1mm] 0, & {x_{I+3} <x} \\ \end{array} }} \right. \end{eqnarray}$
图2 和图3 给出了线性有限元形函数一阶和二阶光滑梯度的构造过程. 由图2 和图3 可见, 虽然线性有限元形函数的梯度在节点处不连续, 而且二阶梯度不存在, 但由本文所提有限元形函数梯度光滑理论构造所得的一阶和二阶光滑梯度仍然是连续函数, 可以直接用于配点法求解.
图3
图3
一维有限元形函数二阶光滑梯度构造过程
Fig.3
Construction of the second order smoothed gradient of 1D finite element shape function
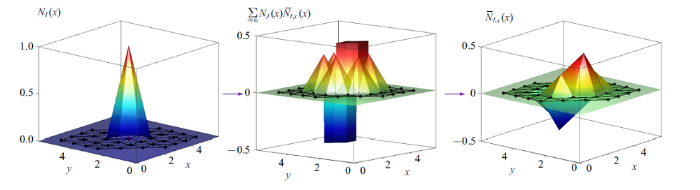
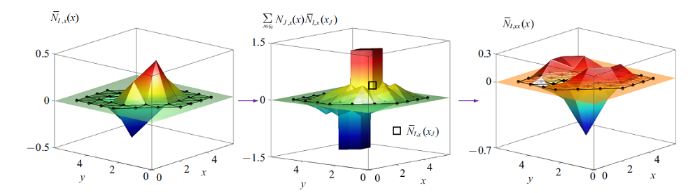
对于二维和三维情况, 考虑三节点三角形单元和四节点四面体单元, 其对应的形函数为标准的线性形函数[1 ] , 这里不再赘述. 二维和三维有限元形函数的一阶和二阶光滑梯度也可按照上述步骤进行构造. 图4 给出了基于平面三角形线性单元构造一阶光滑梯度$\bar{{N}}_{I,x} ({ x})$和和二阶光滑梯度$\bar{{N}}_{I,xx} ({ x})$的过程. 与一维情况相同, 线性三角形单元的形函数在节点和边界处的一阶梯度均不连续, 不存在二阶梯度. 另一方面, 基于本文的有限元形函数光滑梯度构造理论, 可以方便地构造图5 所示的一阶和二阶光滑梯度. 此外, 图2 $\sim\!$图5 同时表明, 与有限元形函数和其标准梯度不同, 有限元形函数的一阶和二阶光滑梯度与形函数本身具有相同的连续性, 但光滑梯度的影响域则大于形函数的影响域.
图4
图4
二维有限元形函数一阶光滑梯度构造过程
Fig.4
Construction of the first order smoothed gradient of 2D finite element shape function
图5
图5
二维有限元形函数二阶光滑梯度构造过程
Fig.5
Construction of the second order smoothed gradient of 2D finite element shape function
3 节点梯度光滑有限元配点法及其精度分析
将式(18)和式(19)定义的有限元一阶和二阶节点光滑梯度代入配点法列式(8), 便形成了节点梯度光滑有限元配点法. 以势问题为例, 节点梯度光滑有限元配点法离散方程刚度矩阵的各个元素为
(25) $\begin{eqnarray} \label{eq25} \left. {\begin{array}{l} K_{IJ}^{ i} =\bar{{N}}_{J,xx} ({ x}_{I} )+\bar{{N}}_{J,yy} ({ x}_{I} ) \\ K_{IJ}^{ g} =n_{x} \bar{{N}}_{J,x} ({ x}_{I} )+n_{y} \bar{{N}}_{J,y} ({ x}_{I} ) \\ K_{IJ}^{ t} =1 \\ \end{array}} \right\} \end{eqnarray}$
节点梯度光滑有限元配点法力向量的各个元素与式(10)相同. 为不失一般性, 下面首先分析线性有限元形函数光滑梯度的一致性条件, 然后以势问题为例对基于线性单元的节点梯度光滑有限元配点法的计算精度进行理论研究.
3.1 线性有限元形函数光滑梯度的一致性条件
对于传统线性有限元, 其形函数及其一阶梯度的一致性或完备性条件为[1 ]
(26) $\begin{eqnarray} \label{eq26} &&\sum\limits_I {N_{I} ({ x})=1} \end{eqnarray}$
(27) $\begin{eqnarray} \label{eq27} \sum\limits_I {N_{I} ({ x})x_{Ij} =x_{j} } \end{eqnarray}$
(28) $\begin{eqnarray} \label{eq28} \sum\limits_I {N_{I,i} ({ x})=0} \end{eqnarray}$
(29) $\begin{eqnarray} \label{eq29} \sum\limits_I {N_{I,i} ({ x})x_{Ij} =\delta_{ij} } \end{eqnarray}$
其中$x_{Ij} $为节点${ x}_{I} $的第$j$个坐标分量, $\delta_{ij} $为克罗内克符号. 注意到有限元形函数的一致性条件取决于形函数的阶次. 例如, 线性有限元形函数仅满足式(26) $\sim\!$式(29)定义的线性一致性条件, 由于其二阶梯度不存在, 故不满足更高一次的二阶一致性条件. 但是对于有限元形函数的光滑梯度, 接下来证明其不仅满足线性一致性条件, 在均布网格情况下还满足二阶一致性条件.
首先, 对于式(17)定义的节点光滑梯度$\bar{{N}}_{I,i} ({ x}_{J} )$, 有
(30) $\begin{eqnarray} \label{eq30} && \sum\limits_I {\bar{{N}}_{I,i} ({ x}_{J} )x_{Ij} } =\sum\limits_I {\frac{1}{\tilde{{V}}_{J} }\sum\limits_{L\in {\cal Z}_{J} } {N_{I,i} ({ x}_{J} )V_{L} } x_{Ij} } =\\&&\qquad \frac{1}{\tilde{{V}}_{J} }\sum\limits_{L\in {\cal Z}_{J} } {\underbrace {\lt[\sum\limits_I {N_{I,i} ({ x}_{J} )x_{Ij} }]}_{=\delta_{ji} }} V_{L} =\\&&\qquad\frac{\delta_{ji} }{\tilde{{V}}_{J} }\underbrace {\sum\limits_{L\in {\cal Z}_{J} } {V_{L} } }_{=\tilde{{V}}_{J} } =\delta_{ji} \end{eqnarray}$
对于线性有限元形函数的一阶光滑梯度$\bar{{N}}_{I,i} \left( {{ x}}\right)$, 其梯度一致性条件为
(31) $\begin{eqnarray} \label{eq31} && \sum\limits_I {\bar{{N}}_{I,i} \left( {{ x}} \right)x_{Ij} } =\sum\limits_I {\sum\limits_{J\in {\cal G}_{I} } {N_{J} ({ x})\bar{{N}}_{I,i} ({ x}_{J} )} x_{Ij} } =\\&&\qquad\sum\limits_{J\in {\cal G}_{I} } {N_{J} \left( {{ x}} \right)} \underbrace {\sum\limits_I {\bar{{N}}_{I,i} \left( {{ x}_{J} } \right)x_{Ij} } }_{=\delta_{ji} } =\\&&\qquad\delta_{ji} \underbrace {\sum\limits_{J\in {\cal G}_{I} } {N_{J} \left( {{ x}} \right)} }_{=1} =\delta_{ji} \end{eqnarray}$
因而与有限元形函数的标准一阶梯度类似, 一阶光滑梯度$\bar{{N}}_{I,i} ({ x})$严格满足梯度的一阶一致性条件.
对于均匀有限元网格, 由形函数的周期重复性可知, 节点光滑梯度满足如下条件[24 -25 ]
(32) $\begin{eqnarray} \label{eq32} && \sum\limits_I {\bar{{N}}_{I,i} ({ x}_{J} )} (x_{I} -x_{J} )^{m}(y_{I} -y_{J} )^{n}= \\&&\qquad \sum\limits_L {\bar{{N}}_{L,i} ({ x}_{R} )} (x_{L} -x_{R} )^{m}(y_{L} -y_{R} )^{n} \end{eqnarray}$
对于线性有限元形函数的二阶光滑梯度$\bar{{N}}_{I,ij} ({ x})$, 有
(33) $\begin{eqnarray} \label{eq33} && \sum\limits_I {\bar{{N}}_{I,ij} ({ x})x_{I}^{ k} y_{I}^{ 2-k} } =\\&&\qquad \sum\limits_I {\sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})\bar{{N}}_{I,i} ({ x}_{J} )} } (x_{I} -x_{J} +x_{J} )^{k}\cdot \\&&\qquad (y_{I} -y_{J} +y_{J} )^{2-k} =\\&&\qquad \sum\limits_I {\sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})\bar{{N}}_{I,i} ({ x}_{J} )} } \sum\limits_{m=0}^k {C_{k}^{ m} (x_{I} -x_{J} )^{m}x_{J}^{ k-m} }\cdot \\&&\qquad\sum\limits_{n=0}^{ 2-k} {C_{2-k}^{ n} (y_{I} -y_{J} )^{n}y_{J}^{ 2-k-n} } =\\&&\qquad \sum\limits_{m=0}^k {\sum\limits_{n=0}^{ 2-k} {C_{k}^{ m} C_{2-k}^{ n} } } \sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} x_{J}^{ k-m} y_{J}^{ 2-k-n}\cdot \\&&\qquad\sum\limits_I {\bar{{N}}_{I,i} ({ x}_{J} )} (x_{I} -x_{J} )^{m}(y_{I} -y_{J} )^{n} \end{eqnarray}$
其中$k=0$, 1或2. 首先考虑$k=2$的情况, 利用式(32), 式(33)变为
(34) $\begin{eqnarray} \label{eq34} && \sum\limits_I {\bar{{N}}_{I,ij} ({ x})x_{I}^{ k} y_{I}^{ 2-k} } =\sum\limits_I {\bar{{N}}_{I,ij} ({ x})x_{I}^{ 2} } =\\&&\quad\sum\limits_{m=0}^2 {C_{2}^{ m} } \sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} x_{J}^{ 2-m} \sum\limits_I {\bar{{N}}_{I,i} ({ x}_{J} )} (x_{I} -x_{J} )^{m} =\\&&\quad\sum\limits_{m=0}^1 {C_{2}^{ m} } \sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} x_{J}^{ 2-m} \sum\limits_I {\bar{{N}}_{I,i} ({ x}_{J} )} (x_{I} -x_{J} )^{m}+\\&&\quad\sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} \sum\limits_I {\bar{{N}}_{I,i} ({ x}_{J} )} (x_{I} -x_{J} )^{2} =\\&&\quad\sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} x_{J}^{ 2} \underbrace {\sum\limits_I {\bar{{N}}_{I,i} ({ x}_{J} )} (x_{I} -x_{J} )^{0}}_{=0}+\\&&\quad 2\underbrace {\sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} x_{J} }_{=\delta_{1j} }\underbrace {\sum\limits_I {\bar{{N}}_{I,i} ({ x}_{J} )} (x_{I} -x_{J} )}_{=\delta_{1i} } +\\&&\quad \sum\limits_K {\bar{{N}}_{K,i} ({ x}_{L} )} (x_{K} -x_{L} )^{2}\underbrace {\sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} }_{=0} =2\delta_{1i} \delta_{1j} \end{eqnarray}$
(35) $\begin{eqnarray} \label{eq35} && \sum\limits_I {\bar{{N}}_{I,ij} ({ x})x_{I}^{ k} y_{I}^{ 2-k} } =\sum\limits_I {\bar{{N}}_{I,ij} ({ x})x_{I} } y_{I} =\\&&\qquad \sum\limits_{m=0}^1 {\sum\limits_{n=0}^1 {C_{1}^{ m} C_{1}^{ n} } } \sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} x_{J}^{ 1-m} y_{J}^{ 1-n} \cdot \\&&\qquad\sum\limits_I {\bar{{N}}_{I,i} ({ x}_{J} )} (x_{I} -x_{J} )^{m}(y_{I} -y_{J} )^{n} =\\&&\qquad \sum\limits_{n=0}^1 {C_{1}^{ 0} C_{1}^{ n} } \sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} x_{J} y_{J}^{ 1-n}\cdot \\&&\qquad \sum\limits_I {\hat{{N}}_{I,i} ({ x}_{J} )} (y_{I} -y_{J} )^{n} +\\&&\qquad \sum\limits_{n=0}^1 {C_{1}^{ 1} C_{1}^{ n} } \sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} y_{J}^{ 1-n}\cdot \\&&\qquad \sum\limits_I {\hat{{N}}_{I,i} ({ x}_{J} )} (x_{I} -x_{J} )(y_{I} -y_{J} )^{n} =\\&&\qquad C_{1}^{ 0} C_{1}^{ 0} \sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} x_{J} y_{J} \underbrace {\sum\limits_I {\bar{{N}}_{I,i} ({ x}_{J} )} }_{=0}+\\&&\qquad C_{1}^{ 0} C_{1}^{ 1} \underbrace {\sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} x_{J} }_{\delta_{1j} }\underbrace {\sum\limits_I {\bar{{N}}_{I,i} ({ x}_{J} )} (y_{I} -y_{J} )}_{\delta_{2i} } +\\&&\qquad C_{1}^{ 1} C_{1}^{ 0} \underbrace {\sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} y_{J} }_{\delta_{2j} }\underbrace {\sum\limits_I {\bar{{N}}_{I,i} ({ x}_{J} )} (x_{I} -x_{J} )}_{\delta _{1i} }+\\&&\qquad C_{1}^{ 1} C_{1}^{ 1} \underbrace {\sum\limits_K {\bar{{N}}_{K,i} ({ x}_{L} )} (x_{K} -x_{L} )(y_{K} -y_{L} )\sum\limits_{J\in {\cal G}_{I} } {\bar{{N}}_{J,j} ({ x})} }_{=0} =\\&&\qquad\delta_{1j} \delta_{2i} +\delta_{2j} \delta_{1i} \end{eqnarray}$
最后, 类似于式(34)的推导, 对于$k=0$, 有
(36) $\begin{eqnarray} \label{eq36} \sum\limits_I {\bar{{N}}_{I,ij} ({ x})x_{I}^{ k} y_{I}^{ 2-k} } =\sum\limits_I {\bar{{N}}_{I,ij} ({ x})y_{I}^{ 2} } =2\delta_{2i} \delta _{2j} \end{eqnarray}$
式(34)$\sim\!$式(36), 证明了线性有限元形函数的二阶光滑梯度满足二阶梯度一致性条件. 与之形成鲜明对比的是, 标准线性有限元形函数不存在二阶梯度.
3.2 节点梯度光滑有限元配点法精度分析
为不失一般性, 以平面势问题为例, 在均匀网格条件下对节点梯度光滑有限元配点法的精度进行解析研究. 节点梯度光滑有限元配点法的精度可以方便地采用如下的截断误差进行度量[24 ,30 ]
(37) $\begin{eqnarray} \label{eq37} e=\sum\limits_J {K_{IJ}^{ i} u_{J} } -{\nabla}^{ \rm T}{\nabla} u_{I} \approx {\rm O}(h^{k}) \end{eqnarray}$
其中$u_{I} $为节点${ x}_{I} $的解析常变量, 即$u_{I} =u({ x}_{I})$, $h$表示单元的特征长度, $k$为精度的阶次.
(38) $\begin{eqnarray} \label{eq38} && u_{J} =u_{I} +\frac{\partial u_{I} }{\partial x}(x_{J} -x_{I} )+\frac{\partial u_{I} }{\partial y}(y_{J} -y_{I} ) +\\&&\qquad \frac{1}{2!}\frac{\partial^{2}u_{I} }{\partial x^{2}}(x_{J} -x_{I} )^{2}+\frac{\partial^{2}u_{I} }{\partial xy}(x_{J} -x_{I} )(y_{J} -y_{I} ) +\\&&\qquad \frac{1}{2!}\frac{\partial^{2}u_{I} }{\partial y^{2}}(y_{J} -y_{I} )^{2}+\cdots \end{eqnarray}$
(39) $\begin{eqnarray} \label{eq39} && e=\sum\limits_{n=0}^\infty \frac{1}{n!}\sum\limits_{k=0}^n {C_{n}^{ k} } \frac{\partial^{n}u_{I} }{\partial x^{k}y^{n-k}} \sum\limits_J {[\bar{{N}}_{J,xx} ({ x}_{I} )+\bar{{N}}_{J,yy} ({ x}_{I} )]} \cdot\\&&\qquad (x_{J} -x_{I} )^{k}(y_{J} -y_{I} )^{n-k}-(u_{I,xx} +u_{I,yy} ) \end{eqnarray}$
同时注意到在均布网格条件下, 有限元形函数的光滑二阶导数具有周期性和偶对称的特点, 因此当$n$为奇数时, 有
(40) $\begin{eqnarray} \label{eq40} \sum\limits_J {[\bar{{N}}_{J,xx} ({ x}_{I} )+\bar{{N}}_{J,yy} ({ x}_{I} )](x_{J} -x_{I} )^{k}(y_{J} -y_{I} )^{n-k}} =0\ \ \end{eqnarray}$
将式(31), 式(33) $\sim\!$式(36)及式(40)代入式(39), 可得
(41) $\begin{eqnarray} \label{eq41} && e=u_{I} \underbrace {\sum\limits_J {[\bar{{N}}_{J,xx} ({ x}_{I} )+\bar{{N}}_{J,yy} ({ x}_{I} )]} }_{=0} +\\&&\qquad \frac{\partial^{2}u_{I} }{\partial x^{2}}\lt[\frac{1}{2}\underbrace {\sum\limits_J {\bar{{N}}_{J,xx} ({ x}_{I} )x_{J}^{ 2} } }_{=2}-1] +\\&&\qquad \frac{\partial^{2}u_{I} }{\partial xy}\underbrace {\sum\limits_J {[\bar{{N}}_{J,xx} ({ x}_{I} )+\bar{{N}}_{J,yy} ({ x}_{I} )]x_{J} y_{J} } }_{=0} +\\&&\qquad \frac{\partial^{2}u_{I} }{\partial y^{2}}\lt\{\frac{1}{2}\underbrace {\sum\limits_{J\in \bar{{S}}_{J} } {\bar{{N}}_{J,yy} ({ x}_{I} )y_{J}^{ 2} } }_{=2}-1\} +\\&&\qquad \frac{1}{4!}\sum\limits_{l=0}^4 {\frac{\partial^{4}u_{I} }{\partial x^{l}y^{4-l}}} \sum\limits_J \underbrace {{\nabla}^{ \rm T}{\nabla} \bar{{N}}_{J} ({ x}_{I} )}_{\sim {1/{h^{2}}}}\cdot \\&&\qquad\underbrace {(x_{J} -x_{I} )^{l}(y_{J} -y_{I} )^{4-l}}_{\sim h^{4}} +\cdots \approx {\rm O}(h^{2}) \end{eqnarray}$
由式(41)可以看出, 节点梯度光滑有限元配点法具有二阶精度, 其$L_{2}$误差和$H_{1}$或能量误差均为二阶收敛. 与线性有限元法相比, 虽然两者$L_{2}$误差收敛特性相同, 但节点梯度光滑有限元配点法的$H_{1}$或能量误差具有高一阶次的超收敛特性.
4 算例
本节通过一维、二维及三维算例验证节点梯度光滑有限元配点法的收敛性和精度, 其中FEM和FEC分别表示传统的伽辽金有限元法和本文所提的节点梯度光滑有限元配点法. 为了和传统有限元法进行比较, 算例中采用如下误差形式
(42) $\begin{eqnarray} \label{eq42} L_{2} \mbox{ Error}=\lt[\int_\varOmega {\sum\limits_{i=1}^{ n_{d} } {(u_{i} -u_{i}^{ h} )^{2}} {\rm d}\varOmega } ]^{1/2} \end{eqnarray}$
(43) $\begin{eqnarray} \label{eq43} H_{1} \;\mbox{Error}=\lt[\int_\varOmega {\sum\limits_{i=1}^{ n_{d} } {[(u_{i} -u_{i}^{ h} )^{2}+(u_{i,j} -u_{i,j}^{ h} )^{2}]} {\rm d}\varOmega } ]^{1/2} \end{eqnarray}$
(44) $\begin{eqnarray} \label{eq44} \mbox{Energy}\;\mbox{Error}=\lt[\frac{1}{2}\int_\varOmega {\sum\limits_{i,j=1}^{ n_{d} } {(\sigma_{ij} -\sigma_{ij}^{ h} )(\varepsilon _{ij} -\varepsilon_{ij}^{ h} )} {\rm d}\varOmega } ]^{1/2} \end{eqnarray}$
其中$n_{d} $表示算例的空间维度, $\sigma_{ij} $和$\varepsilon_{ij}$分别为应力和应变分量.
4.1 一维弹性杆问题
考虑两端固定的一维弹性杆问题, 其几何和材料参数为: 杆长为$L=1$, 抗拉刚度$EA=1$, 体力$b(x)=-24x^{2}$. 该问题的解析解为$u(x)=2x^{4}$. 计算中采用图6 和图7 所示包含20, 40和80个单元的均布和非均布有限元网格进行分析.
图6
图6
一维弹性杆问题均布有限元离散模型
Fig.6
Uniform finite element meshes for the 1D elastic rod problem
图7
图7
一维弹性杆问题非均布有限元离散模型
Fig.7
Non-uniform finite element meshes for the 1D elastic rod problem
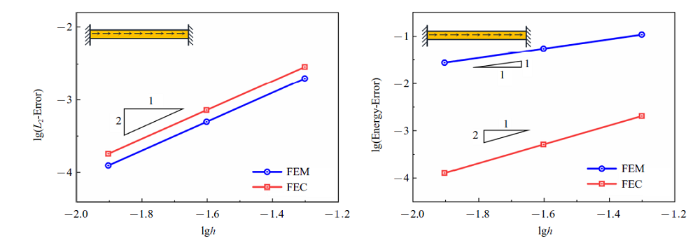
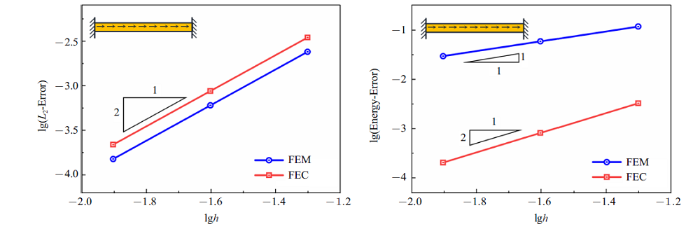
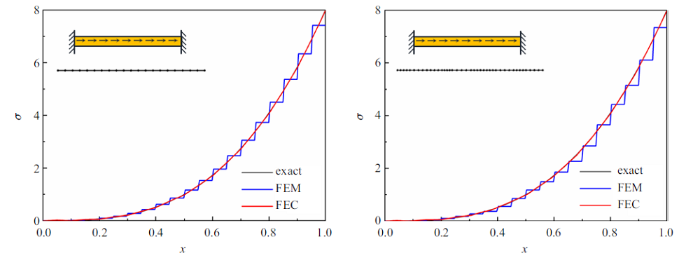
图8 和图9 给出了一维弹性杆问题的$L_{2}$和能量误差收敛情况. 结果显示, 节点梯度光滑有限元配点法的位移误差收敛率与有限元法相同, 精度略低, 但是其能量误差收敛率比有限元法高一阶, 对应的精度也明显优于有限元法, 很好地验证了节点梯度光滑有限元配点法的精度和收敛率. 图10 为采用20个均布和非均布单元得到的应力结果, 可见节点梯度光滑有限元配点法(FEC)的应力精度显著高于传统有限元法(FEM).
图8
图8
采用均布网格的一维弹性杆问题收敛率对比
Fig.8
Convergence comparison for the 1D elastic rod problem using uniform meshes
图9
图9
采用非均布网格的一维弹性杆问题收敛率对比
Fig.9
Convergence comparison for the 1D elastic rod problem using non-uniform meshes
图10
图10
一维弹性问题应力解对比
Fig.10
Comparison of stress solutions for the 1D elastic rod problem
4.2 二维矩形区域势问题
考虑如图11 所示的正方形势问题区域, 其边长$L=1$, 对应势问题的解析解为
(45) $\begin{eqnarray} \label{eq45} u({ x})=\frac{1}{10}(2x^{5}+3y^{5}+2x^{4}y+4xy^{2}) \end{eqnarray}$
图11
图11
方形区域势问题模型
Fig.11
Description of the square region potential problem
图11 中所示自然和强制边界条件均由式(45)给定. 图12 为该问题采用的有限元离散模型, 对应的节点数和平面三角形单元数分别为289, 1089, 4225和512, 2048, 8192.
图12
图12
方形区域势问题的有限元离散模型
Fig.12
Finite element discretizations for the square region potential problem
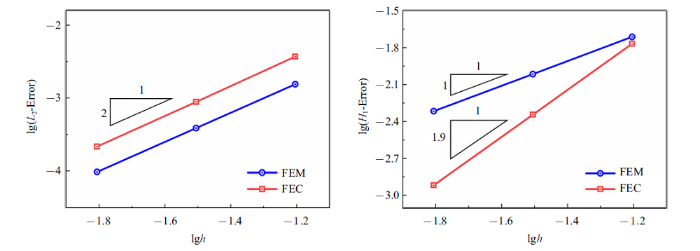
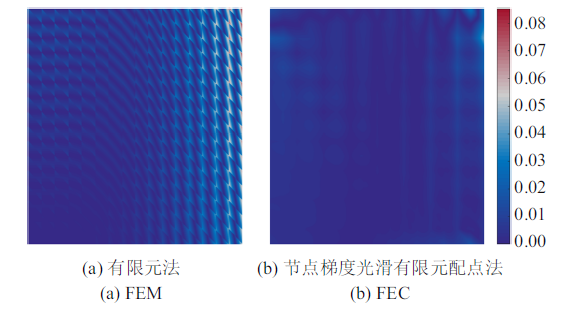
图13 给出了该势问题的$L_{2} $和$H_{1} $误差收敛结果, 其中节点梯度光滑有限元配点法的$L_{2} $和$H_{1} $误差收敛率分别为2和1.9, 与上节的理论收敛率基本一致, 尤其是$H_{1} $误差的收敛率和精度都明显高于有限元法, 具有超收敛特性. 图14 为采用512个三角形单元计算得到的梯度解$u_{,x}^{ h} $的相对误差对比, 即$\left| {u_{,x} -u_{,x}^{ h} } \right|/\left| {u_{,x} } \right|_{\max } $, 其中图14 (a)和图14 (b)分别表示有限元法和节点梯度光滑有限元法的误差分布图. 由图14 的对比结果清晰可见, 传统线性三角形单元的梯度解为常数且在单元边界处不连续, 因此节点梯度光滑有限元配点法的梯度解误差远小于传统有限元法, 表明了节点梯度光滑有限元配点法梯度解的精度优势.
图13
图13
方形区域势问题收敛率对比
Fig.13
Convergence comparison for the square region potential problem
图14
图14
方形区域势问题梯度解$u_{,x}^{ h} $误差对比
Fig.14
Error comparison of the gradient solution $u_{,x}^{ h} $ for the square region potential problem
4.3 悬臂梁问题
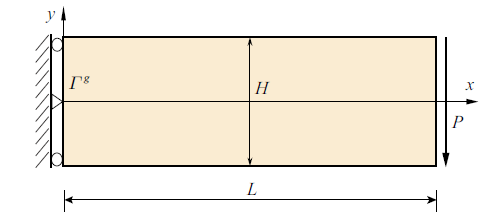
图15 所示为一平面应力悬臂梁问题, 其左端为强制位移边界, 右端受竖向力$P=1000$作用, 几何与材料参数为: 长度$L=4$, 梁截面高$H=1$, 宽$W=1$, 杨氏模量$E=2.0\times 10^{7}$, 泊松比$\nu =0.3$, 惯性矩$I=WH^{3}/12$. 该问题的解析解为
(46) $\begin{eqnarray} \label{eq46} &&u({ x})=\frac{-Py}{6EI}\Bigg[(6L-3x)x+(2+\nu )\Bigg(y^{2}-\frac{H^{2}}{4}\Bigg)\Bigg] \end{eqnarray}$
(47) $\begin{eqnarray} \label{eq47} v({ x})=\frac{P}{6EI}\Bigg[3\nu y^{2}(L-x)+\frac{(4+5\nu )H^{2}}{4}x+ (3L-x)x^{2}\Bigg] \end{eqnarray}$
图15
图15
悬臂梁问题
Fig.15
Description of the cantilever beam problem
该悬臂梁问题的有限元离散模型如图16 所示, 三种有限元离散对应的节点数225, 833和3201, 三角形单元数为384, 1536和6144. 图17 为该算例的位移和能量误差收敛对比结果. 与一维弹性杆问题的结果一致, 传统线性有限元法的位移和能量误差收敛率分别为2和1, 而节点梯度光滑有限元配点法的位移误差收率也为2, 但其能量误差收敛率为2, 比传统有限元法高一阶, 具有更好的收敛特性. 此外, 图17 也表明节点梯度光滑有限元配点法的能量误差明显小于传统有限元法. 图18 给出了采用$384$个单元的剪应力解的相对误差云图($\left| {\sigma_{xy} -\sigma_{xy}^{ h} } \right|\Big/\left| {\sigma_{xy} } \right|_{\max } )$, 结果进一步显示出节点梯度光滑有限元配点法的高精度应力计算特点.
图16
图16
悬臂梁问题有限元离散模型
Fig.16
Finite element discretizations for the cantilever beam problem
图17
图17
悬臂梁误差收敛率对比
Fig.17
Convergence comparison for the cantilever beam problem
图18
图18
悬臂梁问题应力解$\sigma_{xy}^{ h} $误差对比
Fig.18
Error comparison of the stress solution $\sigma_{xy}^{ h} $ for the cantilever beam problem
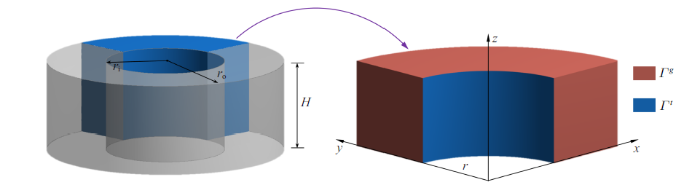
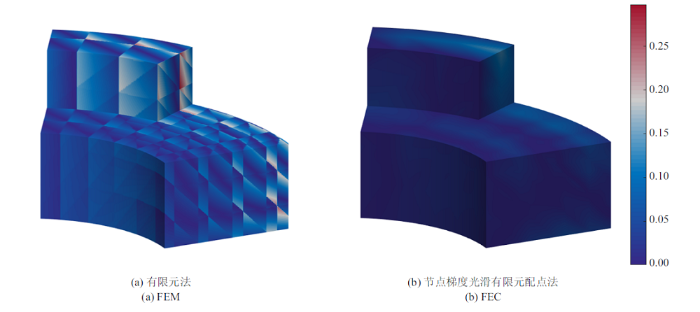
4.4 三维厚壁圆筒势问题
为了验证节点梯度光滑有限元配点法的三维适用性, 最后一个算例是图19 所示的厚壁圆筒势问题, 相应的几何参数为: 内径为$r_{\rm i} =1$, 外径为$r_{\rm o} =2$, 高度$H=1$. 该问题的解析解为
(48) $\begin{eqnarray} \label{eq48} u({ x})=\frac{1}{10}(x^{4}z+y^{4}+2x^{2}y^{2}+z^{4}) \end{eqnarray}$
图19
图19
三维厚壁圆筒势问题模型
Fig.19
Description of the 3D hollow cylinder potential problem
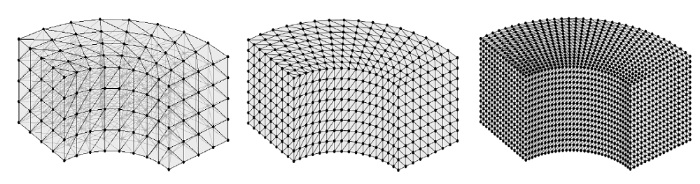
利用该问题的对称性, 计算中取四分之一模型进行离散分析. 图20 为该三维势问题的有限元离散情况, 对应的节点数为225, 1377和9537, 四节点四面体单元数为768, 6144和49 152. 由于空间区域的构造特点, 该问题的有限元网格具有非均布特性.图21 为采用图20 中三种有限元离散网格计算得到的$L_{2} $和$H_{1} $误差收敛率结果. 与一维和二维算例的结果类似, 有限元法和节点梯度光滑有限元配点法的$L_{2} $误差收敛率都为2, 节点梯度光滑有限元配点法的$H_{1} $误差收敛率受非均布有限元网格影响, 略低于理论值2, 但其$H_{1} $误差的收敛率和精度仍然明显高于传统有限元法, 验证了节点梯度光滑有限元配点法求解三维问题的精度和有效性. 图22 给出了768个单元对应的梯度解$u_{,x}^{ h} $的相对误差对比. 结果再次证明, 即使对于非均布有限元离散, 节点梯度光滑有限元配点法仍然在梯度解方面具有突出的精度优势.
图20
图20
三维厚壁圆筒势问题有限元离散模型
Fig.20
Non-uniform finite element discretizations for the 3D hollow cylinder potential problem
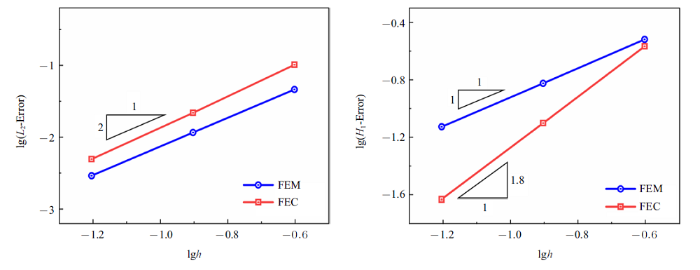
图21
图21
三维厚壁圆筒势问题收敛率对比
Fig.21
Convergence comparison for the 3D hollow cylinder potential problem
图22
图22
三维厚壁圆筒梯度解$u_{,x}^{ h} $误差对比
Fig.22
Error comparison of the gradient solution $u_{,x}^{ h} $ for the 3D hollow cylinder potential problem
5 结论
传统有限元形函数在离散区域内一般仅有C$^{0}$连续性, 在单元边界和节点处上不存在一阶和二阶梯度, 因而不能直接用于配点法. 本文提出了有限元形函数的光滑梯度构造理论, 建立了具有与有限元形函数同样连续性的一阶和二阶光滑梯度, 进而发展了节点梯度光滑有限元配点法. 有限元形函数的一阶光滑梯度依赖于在广义梯度光滑理论框架内的一阶光滑梯度节点值的定义, 以及选择有限元形函数作为核函数对一阶光滑梯度节点值进行梯度光滑. 对有限元一阶光滑梯度进行求导, 并用一阶光滑梯度替换有限元形函数的标准梯度, 即可得到有限元形函数的二阶光滑梯度. 文中详细证明了线性有限元形函数的光滑梯度不仅满足常规的一阶梯度一致性条件, 而且在均布网格条件下还满足二阶梯度一致性条件. 与之对应的是, 线性有限元形函数的标准一阶梯度只满足一阶梯度一致性条件. 正是由于有限元形函数的光滑梯度满足二阶梯度一致性条件, 理论分析表明, 基于有限元形函数光滑梯度的节点梯度光滑有限元配点法具有二阶精度, 即$L_{2}$误差和$H_{1}$或能量误差的收敛率均为2, 与传统伽辽金有限元法相比呈现超收敛特性. 文中通过典型算例系统验证了节点梯度光滑有限元配点法在梯度或应力求解方面的超收敛特性和显著精度优势. 本文的节点梯度光滑有限元配点法采用了线性有限元形函数, 对于高次有限元形函数及高阶光滑梯度还需要进一步研究.
参考文献
View Option
[1]
Zienkiewicz OC Taylor RL Zhu JZ . The Finite Element Method: Its Basis and Fundamentals. 7th Edition
Berlin: Elsevier , 2015
[本文引用: 7]
[2]
田荣 . C$^{1}$连续型广义有限元格式
力学学报 , 2019 ,51 (1 ):263 -277
[本文引用: 1]
( Tian Rong . A GFEM with C$^{1}$ continuity
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (1 ):263 -277 (in Chinese))
[本文引用: 1]
[3]
张雄 , 刘岩 , 马上 . 无网格法的理论与应用
力学进展 , 2009 ,39 (1 ):1 -36
[本文引用: 1]
( Zhang Xiong Liu Yan Ma Shang . Meshfere methods and their applications
Advances in Mechanics 2009 ,39 (1 ):1 -36 (in Chinese))
[本文引用: 1]
[4]
Chen JS Hillman M Chi SW . Meshfree methods: progress made after 20 years
Journal of Engineering Mechanics-ASCE 2017 ,143 (4 ):04017001
DOI
URL
[本文引用: 1]
[5]
Wang DD Wu JC . An inherently consistent reproducing kernel gradient smoothing framework toward efficient Galerkin meshfree formulation with explicit quadrature
Computer Methods in Applied Mechanics and Engineering 2019 ,349 :628 -672
DOI
URL
[6]
Hughes TJR Cottrell JA Bazilevs Y . Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement
Computer Methods in Applied Mechanics and Engineering 2005 ,194 :4135 -4195
DOI
URL
[7]
Zhang HJ Wang DD . Reproducing kernel formulation of B-spline and NURBS basis functions: A meshfree local refinement strategy for isogeometric analysis
Computer Methods in Applied Mechanics and Engineering 2017 ,320 :474 -508
DOI
URL
[本文引用: 1]
[8]
Kansa EJ . Multiquadrics-A scattered data approximation scheme with applications to computational fluid-dynamics-II solutions to parabolic, hyperbolic and elliptic partial differential equations
Computers & Mathematics with Applications 1990 ,19 (8-9 ):147 -161
[本文引用: 1]
[9]
Zhang X Song KZ Lu MW . et al . Meshless methods based on collocation with radial basis functions
Computational Mechanics 2000 ,26 (4 ):333 -343
[10]
Chen W . A meshless, integration-free, and boundary-only RBF technique
Computers & Mathematics with Applications 2002 ,43 (3-5 ):379 -391
[11]
Chen JS Hu W Hu H . Reproducing kernel enhanced local radial basis collocation method
International Journal for Numerical Methods in Engineering 2008 ,75 :600 -627
DOI
URL
[12]
王莉华 , 李溢铭 , 褚福运 . 基于分区径向基函数配点法的大变形分析
力学学报 , 2019 ,51 (3 ):743 -753
( Wang Lihua Li Yiming Zhu Fuyun . Finite subdomain radial basis collocation method for the large deformation analysis
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (3 ):743 -753 (in Chinese))
[13]
Mountris KA Pueyo E . The radial point interpolation mixed collocation method for the solution of transient diffusion problems
Engineering Analysis with Boundary Elements 2020 ,121 :207 -216
DOI
URL
[本文引用: 1]
[14]
Breitkopf P Touzot G Villon P . Double grid diffuse collocation method
Computational Mechanics 2000 ,25 (2 ):199 -206
DOI
URL
[本文引用: 1]
[15]
Aluru NR . A point collocation method based on reproducing kernel approximations
International Journal for Numerical Methods in Engineering 2015 ,47 (6 ):1083 -1121
DOI
URL
[16]
Chi SW Chen JS Hu HY . et al . A gradient reproducing kernel collocation method for boundary value problems
International Journal for Numerical Methods in Engineering 2013 ,93 :1381 -1402
DOI
URL
The earlier work in the development of direct strong form collocation methods, such as the reproducing kernel collocation method (RKCM), addressed the domain integration issue in the Galerkin type meshfree method, such as the reproducing kernel particle method, but with increased computational complexity because of taking higher order derivatives of the approximation functions and the need for using a large number of collocation points for optimal convergence. In this work, we intend to address the computational complexity in RKCM while achieving optimal convergence by introducing a gradient reproduction kernel approximation. The proposed gradient RKCM reduces the order of differentiation to the first order for solving second-order PDEs with strong form collocation. We also show that, different from the typical strong form collocation method where a significantly large number of collocation points than the number of source points is needed for optimal convergence, the same number of collocation points and source points can be used in gradient RKCM. We also show that the same order of convergence rates in the primary unknown and its first-order derivative is achieved, owing to the imposition of gradient reproducing conditions. The numerical examples are given to verify the analytical prediction. Copyright (c) 2012 John Wiley & Sons, Ltd.
[17]
Mahdavi A Chi SW Zhu HQ . A gradient reproducing kernel collocation method for high order differential equations
Computational Mechanics 2019 ,64 :1421 -1454
DOI
URL
[18]
Wang LH Qian ZH . A meshfree stabilized collocation method (SCM) based on reproducing kernel approximation
Computer Methods in Applied Mechanics and Engineering 2020 ,371 :113303
DOI
URL
[本文引用: 1]
[19]
Auricchio F Beirão L Veiga D . et al . Isogeometric collocation methods
Mathematical Models and Methods in Applied Sciences 2010 ,20 :2075 -2107
DOI
URL
[本文引用: 2]
[20]
Maurin F Greco F Coox L . et al . Isogeometric collocation for Kirchhoff-Love plates and shells
Computer Methods in Applied Mechanics & Engineering 2018 ,328 :396 -420
[21]
Kapl M Vitrih V . Isogeometric collocation on planar multi-patch domains
Computer Methods in Applied Mechanics and Engineering 2020 ,360 :112684
DOI
URL
[本文引用: 1]
[22]
高效伟 , 徐兵兵 , 吕军 等 . 自由单元法及其在结构分析中的应用
力学学报 , 2019 ,51 (3 ):703 -713
[本文引用: 1]
( Gao Xiaowei Xu Bingbing Lü Jun , et al . Free element method and its application in structural analysis
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (3 ):703 -713 (in Chinese))
[本文引用: 1]
[23]
Gao XW Gao L Zhang Y , et al . Free element collocation method: A new method combining advantages of finite element and mesh free methods
Computers & Structures 2019 ,215 :10 -26
[本文引用: 1]
[24]
Wang DD Wang JR Wu JC . Superconvergent gradient smoothing meshfree collocation method
Computer Methods in Applied Mechanics and Engineering 2018 ,340 :728 -766
DOI
URL
[本文引用: 7]
[25]
Wang DD Wang JR Wu JC . Arbitrary order recursive formulation of meshfree gradients with application to superconvergent collocation analysis of Kirchhoff plates
Computational Mechanics 2020 ,65 :877 -903 .
DOI
URL
[本文引用: 2]
[26]
Qi DL Wang DD Deng LK , et al . Reproducing kernel meshfree collocation analysis of structural vibrations
Engineering Computations 2019 ,36 (3 ):734 -764
DOI
URL
[本文引用: 1]
[27]
邓立克 , 王东东 , 王家睿 等 . 薄板分析的线性基梯度光滑伽辽金无网格法
力学学报 , 2019 ,51 (3 ):688 -702
[本文引用: 1]
( Deng Like Wang Dongdong Wang Jiarui , et al . A gradient smoothing Galerkin method for thin plate analysis with linear basis function
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (3 ):690 -792 (in Chinese))
[本文引用: 1]
[28]
Chen JS Wu CT Yoon S . et al . A stabilized conforming nodal integration for Galerkin meshfree methods
International Journal for Numerical Methods in Engineering 2001 ,50 :435 -466
DOI
URL
[本文引用: 2]
[29]
Liu GR Dai KY Nguyen TT . A smoothed finite element method for mechanics problems
Computational Mechanics 2007 ,39 :859 -877
DOI
URL
[本文引用: 1]
In the finite element method (FEM), a necessary condition for a four-node isoparametric element is that no interior angle is greater than 180° and the positivity of Jacobian determinant should be ensured in numerical implementation. In this paper, we incorporate cell-wise strain smoothing operations into conventional finite elements and propose the smoothed finite element method (SFEM) for 2D elastic problems. It is found that a quadrilateral element divided into four smoothing cells can avoid spurious modes and gives stable results for integration over the element. Compared with original FEM, the SFEM achieves more accurate results and generally higher convergence rate in energy without increasing computational cost. More importantly, as no mapping or coordinate transformation is involved in the SFEM, its element is allowed to be of arbitrary shape. Hence the restriction on the shape bilinear isoparametric elements can be removed and problem domain can be discretized in more flexible ways, as demonstrated in the example problems.]]>
[30]
Idesman A Dey B . The use of the local truncation error for the increase in accuracy of the linear finite elements for heat transfer problems
Computer Methods in Applied Mechanics and Engineering 2017 ,319 :52 -82
DOI
URL
[本文引用: 1]
The Finite Element Method: Its Basis and Fundamentals. 7th Edition
7
2015
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
... [1 ], 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
... [1 ]. 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
... [1 ], 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
... 由式(10)可见, 配点法需要计算形函数的二阶梯度, 而标准有限元形函数在单元边界处不存在二阶梯度, 因此无法直接用于配点法. 此外, 虽然通过特殊构造方式可以建立一些特殊单元的高阶光滑有限元形函数, 但是目前仍然缺乏构造一般单元高阶光滑形函数的通用有效方法[1 ] . 本文则是通过引入无网格法中的梯度光滑技术, 建立了有限元形函数的一阶和二阶光滑梯度, 进而发展了相应的节点梯度光滑有限元配点法. ...
... 对于二维和三维情况, 考虑三节点三角形单元和四节点四面体单元, 其对应的形函数为标准的线性形函数[1 ] , 这里不再赘述. 二维和三维有限元形函数的一阶和二阶光滑梯度也可按照上述步骤进行构造. 图4 给出了基于平面三角形线性单元构造一阶光滑梯度$\bar{{N}}_{I,x} ({ x})$和和二阶光滑梯度$\bar{{N}}_{I,xx} ({ x})$的过程. 与一维情况相同, 线性三角形单元的形函数在节点和边界处的一阶梯度均不连续, 不存在二阶梯度. 另一方面, 基于本文的有限元形函数光滑梯度构造理论, 可以方便地构造图5 所示的一阶和二阶光滑梯度. 此外, 图2 $\sim\!$图5 同时表明, 与有限元形函数和其标准梯度不同, 有限元形函数的一阶和二阶光滑梯度与形函数本身具有相同的连续性, 但光滑梯度的影响域则大于形函数的影响域. ...
... 对于传统线性有限元, 其形函数及其一阶梯度的一致性或完备性条件为[1 ] ...
C$^{1}$连续型广义有限元格式
1
2019
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
C$^{1}$连续型广义有限元格式
1
2019
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
无网格法的理论与应用
1
2009
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
无网格法的理论与应用
1
2009
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
Meshfree methods: progress made after 20 years
1
2017
... 根据广义梯度光滑理论[4 ,24 ] , 有限元形函数$N_{I} ({ x})$的一阶光滑梯度$\bar{{N}}_{I,i} ({ x})$的定义为 ...
An inherently consistent reproducing kernel gradient smoothing framework toward efficient Galerkin meshfree formulation with explicit quadrature
0
2019
Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement
0
2005
Reproducing kernel formulation of B-spline and NURBS basis functions: A meshfree local refinement strategy for isogeometric analysis
1
2017
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
Multiquadrics-A scattered data approximation scheme with applications to computational fluid-dynamics-II solutions to parabolic, hyperbolic and elliptic partial differential equations
1
1990
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
Meshless methods based on collocation with radial basis functions
0
2000
A meshless, integration-free, and boundary-only RBF technique
0
2002
Reproducing kernel enhanced local radial basis collocation method
0
2008
基于分区径向基函数配点法的大变形分析
0
2019
基于分区径向基函数配点法的大变形分析
0
2019
The radial point interpolation mixed collocation method for the solution of transient diffusion problems
1
2020
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
Double grid diffuse collocation method
1
2000
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
A point collocation method based on reproducing kernel approximations
0
2015
A gradient reproducing kernel collocation method for boundary value problems
0
2013
A gradient reproducing kernel collocation method for high order differential equations
0
2019
A meshfree stabilized collocation method (SCM) based on reproducing kernel approximation
1
2020
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
Isogeometric collocation methods
2
2010
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
... 就配点法的精度而言, 一个突出的问题就是其计算精度依赖于形函数所采用的基函数阶次的奇偶性, 即奇数阶次基函数的配点法收敛率较其基函数阶次下降一次[19 ,24 ] . 王东东等[24 -26 ] 系统研究了二阶和四阶问题无网格配点法奇数阶次基函数精度掉阶的原因. 研究表明, 配点法的精度与形函数及其梯度的一致性或完备性条件密切相关. 因此, 王东东等[24 -25 ] 通过引入无网格形函数的梯度光滑方法, 建立了超收敛无网格配点法, 并在不引入待定配点位置的情况下有效解决了奇数阶次基函数配点法的精度掉阶问题, 实现了采用奇数次基函数配点法精度的超收敛提升. 基于梯度光滑方法, 邓立克等[27 ] 通过线性基函数构造了二阶光滑梯度, 使得采用线性基函数就可以进行四阶薄板问题的伽辽金无网格分析. 然而, 注意到上述工作中所讨论的形函数高阶光滑梯度构造的基础是形函数的标准一阶梯度, 这对于本身具有高阶光滑特性的无网格形函数没有问题, 但是由于有限元形函数的一阶梯度在单元节点和边界处并不存在, 因此难以直接构造有限元形函数的高阶光滑梯度和发展相应的配点法. ...
Isogeometric collocation for Kirchhoff-Love plates and shells
0
2018
Isogeometric collocation on planar multi-patch domains
1
2020
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
自由单元法及其在结构分析中的应用
1
2019
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
自由单元法及其在结构分析中的应用
1
2019
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
Free element collocation method: A new method combining advantages of finite element and mesh free methods
1
2019
... 基于变分法或等效积分弱形式的伽辽金法和基于强形式的配点法是计算力学领域两种常用的数值计算方法[1 ] . 与伽辽金法相比, 配点法具有构造简单、计算高效的特点, 但是配点法需要计算数值离散形函数的高阶梯度, 例如势问题或弹性力学问题等二阶问题需要用到形函数的二阶导数. 同时配点法的刚度矩阵不对称, 稳定性相对较差. 有限元法是目前应用最为广泛的一种典型伽辽金法[1 ] , 其形函数定义在单元上, 一般网格情况下仅具有C$^{0}$连续性[2 ] , 在相邻单元边界处会出现梯度跳跃, 因而不能直接应用于需要计算形函数高阶梯度的配点法[1 ] . 近年来, 随着采用高阶光滑形函数的无网格法和等几何分析的快速发展[3 -7 ] , 配点法逐渐得到了愈来愈广泛的应用, 例如径向基函数配点法[8 -13 ] , 移动最小二乘与再生核无网格配点法[14 -18 ] , 等几何配点法[19 -21 ] 等. 值得指出的是, 与无网格和等几何形函数相比[1 ] , 有限元形函数形式简单, 计算快捷. 最近, 高效伟等[22 -23 ] 利用有限元形函数在单元内部高阶连续的特点, 通过在选定配点邻域内构建局部单元, 提出了自由单元配点法. ...
Superconvergent gradient smoothing meshfree collocation method
7
2018
... 就配点法的精度而言, 一个突出的问题就是其计算精度依赖于形函数所采用的基函数阶次的奇偶性, 即奇数阶次基函数的配点法收敛率较其基函数阶次下降一次[19 ,24 ] . 王东东等[24 -26 ] 系统研究了二阶和四阶问题无网格配点法奇数阶次基函数精度掉阶的原因. 研究表明, 配点法的精度与形函数及其梯度的一致性或完备性条件密切相关. 因此, 王东东等[24 -25 ] 通过引入无网格形函数的梯度光滑方法, 建立了超收敛无网格配点法, 并在不引入待定配点位置的情况下有效解决了奇数阶次基函数配点法的精度掉阶问题, 实现了采用奇数次基函数配点法精度的超收敛提升. 基于梯度光滑方法, 邓立克等[27 ] 通过线性基函数构造了二阶光滑梯度, 使得采用线性基函数就可以进行四阶薄板问题的伽辽金无网格分析. 然而, 注意到上述工作中所讨论的形函数高阶光滑梯度构造的基础是形函数的标准一阶梯度, 这对于本身具有高阶光滑特性的无网格形函数没有问题, 但是由于有限元形函数的一阶梯度在单元节点和边界处并不存在, 因此难以直接构造有限元形函数的高阶光滑梯度和发展相应的配点法. ...
... [24 -26 ]系统研究了二阶和四阶问题无网格配点法奇数阶次基函数精度掉阶的原因. 研究表明, 配点法的精度与形函数及其梯度的一致性或完备性条件密切相关. 因此, 王东东等[24 -25 ] 通过引入无网格形函数的梯度光滑方法, 建立了超收敛无网格配点法, 并在不引入待定配点位置的情况下有效解决了奇数阶次基函数配点法的精度掉阶问题, 实现了采用奇数次基函数配点法精度的超收敛提升. 基于梯度光滑方法, 邓立克等[27 ] 通过线性基函数构造了二阶光滑梯度, 使得采用线性基函数就可以进行四阶薄板问题的伽辽金无网格分析. 然而, 注意到上述工作中所讨论的形函数高阶光滑梯度构造的基础是形函数的标准一阶梯度, 这对于本身具有高阶光滑特性的无网格形函数没有问题, 但是由于有限元形函数的一阶梯度在单元节点和边界处并不存在, 因此难以直接构造有限元形函数的高阶光滑梯度和发展相应的配点法. ...
... [24 -25 ]通过引入无网格形函数的梯度光滑方法, 建立了超收敛无网格配点法, 并在不引入待定配点位置的情况下有效解决了奇数阶次基函数配点法的精度掉阶问题, 实现了采用奇数次基函数配点法精度的超收敛提升. 基于梯度光滑方法, 邓立克等[27 ] 通过线性基函数构造了二阶光滑梯度, 使得采用线性基函数就可以进行四阶薄板问题的伽辽金无网格分析. 然而, 注意到上述工作中所讨论的形函数高阶光滑梯度构造的基础是形函数的标准一阶梯度, 这对于本身具有高阶光滑特性的无网格形函数没有问题, 但是由于有限元形函数的一阶梯度在单元节点和边界处并不存在, 因此难以直接构造有限元形函数的高阶光滑梯度和发展相应的配点法. ...
... 为了构造有限元形函数的高阶光滑梯度, 本文在无网格法的梯度光滑理论框架内[24 ,28 ] , 首先引入了有限元形函数在节点处和全域内的一阶光滑梯度定义, 然后在此基础上建立了有限元形函数的二阶光滑梯度, 进而采用有限元形函数的光滑梯度建立了一种新型的节点梯度光滑有限元配点法. 与传统有限元形函数梯度不同, 有限元形函数的一阶和二阶光滑梯度具有全域连续的特点. 不失一般性, 本文以线性形函数为例, 详细研究了有限元形函数一阶和二阶光滑梯度的构造特点和一致性条件, 并对节点梯度光滑有限元配点法进行了精度分析. 分析表明, 线性有限元形函数的二阶光滑梯度能够满足二阶一致性条件, 因而对应的节点梯度光滑有限元配点法具有二次精度和超收敛特性. 注意到基于梯度光滑理论[28 ] , Liu等[29 ] 构造了有限元形函数的一阶光滑梯度, 提出了伽辽金光滑有限元法. 但本文所讨论的一阶与二阶有限元形函数光滑梯度, 其光滑核函数选取和构造方式均与伽辽金光滑有限元法不同, 同时着重研究的是配点法计算列式. 文中通过典型算例系统验证了节点梯度光滑有限元配点法的精度和收敛性. ...
... 根据广义梯度光滑理论[4 ,24 ] , 有限元形函数$N_{I} ({ x})$的一阶光滑梯度$\bar{{N}}_{I,i} ({ x})$的定义为 ...
... 对于均匀有限元网格, 由形函数的周期重复性可知, 节点光滑梯度满足如下条件[24 -25 ] ...
... 为不失一般性, 以平面势问题为例, 在均匀网格条件下对节点梯度光滑有限元配点法的精度进行解析研究. 节点梯度光滑有限元配点法的精度可以方便地采用如下的截断误差进行度量[24 ,30 ] ...
Arbitrary order recursive formulation of meshfree gradients with application to superconvergent collocation analysis of Kirchhoff plates
2
2020
... 就配点法的精度而言, 一个突出的问题就是其计算精度依赖于形函数所采用的基函数阶次的奇偶性, 即奇数阶次基函数的配点法收敛率较其基函数阶次下降一次[19 ,24 ] . 王东东等[24 -26 ] 系统研究了二阶和四阶问题无网格配点法奇数阶次基函数精度掉阶的原因. 研究表明, 配点法的精度与形函数及其梯度的一致性或完备性条件密切相关. 因此, 王东东等[24 -25 ] 通过引入无网格形函数的梯度光滑方法, 建立了超收敛无网格配点法, 并在不引入待定配点位置的情况下有效解决了奇数阶次基函数配点法的精度掉阶问题, 实现了采用奇数次基函数配点法精度的超收敛提升. 基于梯度光滑方法, 邓立克等[27 ] 通过线性基函数构造了二阶光滑梯度, 使得采用线性基函数就可以进行四阶薄板问题的伽辽金无网格分析. 然而, 注意到上述工作中所讨论的形函数高阶光滑梯度构造的基础是形函数的标准一阶梯度, 这对于本身具有高阶光滑特性的无网格形函数没有问题, 但是由于有限元形函数的一阶梯度在单元节点和边界处并不存在, 因此难以直接构造有限元形函数的高阶光滑梯度和发展相应的配点法. ...
... 对于均匀有限元网格, 由形函数的周期重复性可知, 节点光滑梯度满足如下条件[24 -25 ] ...
Reproducing kernel meshfree collocation analysis of structural vibrations
1
2019
... 就配点法的精度而言, 一个突出的问题就是其计算精度依赖于形函数所采用的基函数阶次的奇偶性, 即奇数阶次基函数的配点法收敛率较其基函数阶次下降一次[19 ,24 ] . 王东东等[24 -26 ] 系统研究了二阶和四阶问题无网格配点法奇数阶次基函数精度掉阶的原因. 研究表明, 配点法的精度与形函数及其梯度的一致性或完备性条件密切相关. 因此, 王东东等[24 -25 ] 通过引入无网格形函数的梯度光滑方法, 建立了超收敛无网格配点法, 并在不引入待定配点位置的情况下有效解决了奇数阶次基函数配点法的精度掉阶问题, 实现了采用奇数次基函数配点法精度的超收敛提升. 基于梯度光滑方法, 邓立克等[27 ] 通过线性基函数构造了二阶光滑梯度, 使得采用线性基函数就可以进行四阶薄板问题的伽辽金无网格分析. 然而, 注意到上述工作中所讨论的形函数高阶光滑梯度构造的基础是形函数的标准一阶梯度, 这对于本身具有高阶光滑特性的无网格形函数没有问题, 但是由于有限元形函数的一阶梯度在单元节点和边界处并不存在, 因此难以直接构造有限元形函数的高阶光滑梯度和发展相应的配点法. ...
薄板分析的线性基梯度光滑伽辽金无网格法
1
2019
... 就配点法的精度而言, 一个突出的问题就是其计算精度依赖于形函数所采用的基函数阶次的奇偶性, 即奇数阶次基函数的配点法收敛率较其基函数阶次下降一次[19 ,24 ] . 王东东等[24 -26 ] 系统研究了二阶和四阶问题无网格配点法奇数阶次基函数精度掉阶的原因. 研究表明, 配点法的精度与形函数及其梯度的一致性或完备性条件密切相关. 因此, 王东东等[24 -25 ] 通过引入无网格形函数的梯度光滑方法, 建立了超收敛无网格配点法, 并在不引入待定配点位置的情况下有效解决了奇数阶次基函数配点法的精度掉阶问题, 实现了采用奇数次基函数配点法精度的超收敛提升. 基于梯度光滑方法, 邓立克等[27 ] 通过线性基函数构造了二阶光滑梯度, 使得采用线性基函数就可以进行四阶薄板问题的伽辽金无网格分析. 然而, 注意到上述工作中所讨论的形函数高阶光滑梯度构造的基础是形函数的标准一阶梯度, 这对于本身具有高阶光滑特性的无网格形函数没有问题, 但是由于有限元形函数的一阶梯度在单元节点和边界处并不存在, 因此难以直接构造有限元形函数的高阶光滑梯度和发展相应的配点法. ...
薄板分析的线性基梯度光滑伽辽金无网格法
1
2019
... 就配点法的精度而言, 一个突出的问题就是其计算精度依赖于形函数所采用的基函数阶次的奇偶性, 即奇数阶次基函数的配点法收敛率较其基函数阶次下降一次[19 ,24 ] . 王东东等[24 -26 ] 系统研究了二阶和四阶问题无网格配点法奇数阶次基函数精度掉阶的原因. 研究表明, 配点法的精度与形函数及其梯度的一致性或完备性条件密切相关. 因此, 王东东等[24 -25 ] 通过引入无网格形函数的梯度光滑方法, 建立了超收敛无网格配点法, 并在不引入待定配点位置的情况下有效解决了奇数阶次基函数配点法的精度掉阶问题, 实现了采用奇数次基函数配点法精度的超收敛提升. 基于梯度光滑方法, 邓立克等[27 ] 通过线性基函数构造了二阶光滑梯度, 使得采用线性基函数就可以进行四阶薄板问题的伽辽金无网格分析. 然而, 注意到上述工作中所讨论的形函数高阶光滑梯度构造的基础是形函数的标准一阶梯度, 这对于本身具有高阶光滑特性的无网格形函数没有问题, 但是由于有限元形函数的一阶梯度在单元节点和边界处并不存在, 因此难以直接构造有限元形函数的高阶光滑梯度和发展相应的配点法. ...
A stabilized conforming nodal integration for Galerkin meshfree methods
2
2001
... 为了构造有限元形函数的高阶光滑梯度, 本文在无网格法的梯度光滑理论框架内[24 ,28 ] , 首先引入了有限元形函数在节点处和全域内的一阶光滑梯度定义, 然后在此基础上建立了有限元形函数的二阶光滑梯度, 进而采用有限元形函数的光滑梯度建立了一种新型的节点梯度光滑有限元配点法. 与传统有限元形函数梯度不同, 有限元形函数的一阶和二阶光滑梯度具有全域连续的特点. 不失一般性, 本文以线性形函数为例, 详细研究了有限元形函数一阶和二阶光滑梯度的构造特点和一致性条件, 并对节点梯度光滑有限元配点法进行了精度分析. 分析表明, 线性有限元形函数的二阶光滑梯度能够满足二阶一致性条件, 因而对应的节点梯度光滑有限元配点法具有二次精度和超收敛特性. 注意到基于梯度光滑理论[28 ] , Liu等[29 ] 构造了有限元形函数的一阶光滑梯度, 提出了伽辽金光滑有限元法. 但本文所讨论的一阶与二阶有限元形函数光滑梯度, 其光滑核函数选取和构造方式均与伽辽金光滑有限元法不同, 同时着重研究的是配点法计算列式. 文中通过典型算例系统验证了节点梯度光滑有限元配点法的精度和收敛性. ...
... [28 ], Liu等[29 ] 构造了有限元形函数的一阶光滑梯度, 提出了伽辽金光滑有限元法. 但本文所讨论的一阶与二阶有限元形函数光滑梯度, 其光滑核函数选取和构造方式均与伽辽金光滑有限元法不同, 同时着重研究的是配点法计算列式. 文中通过典型算例系统验证了节点梯度光滑有限元配点法的精度和收敛性. ...
A smoothed finite element method for mechanics problems
1
2007
... 为了构造有限元形函数的高阶光滑梯度, 本文在无网格法的梯度光滑理论框架内[24 ,28 ] , 首先引入了有限元形函数在节点处和全域内的一阶光滑梯度定义, 然后在此基础上建立了有限元形函数的二阶光滑梯度, 进而采用有限元形函数的光滑梯度建立了一种新型的节点梯度光滑有限元配点法. 与传统有限元形函数梯度不同, 有限元形函数的一阶和二阶光滑梯度具有全域连续的特点. 不失一般性, 本文以线性形函数为例, 详细研究了有限元形函数一阶和二阶光滑梯度的构造特点和一致性条件, 并对节点梯度光滑有限元配点法进行了精度分析. 分析表明, 线性有限元形函数的二阶光滑梯度能够满足二阶一致性条件, 因而对应的节点梯度光滑有限元配点法具有二次精度和超收敛特性. 注意到基于梯度光滑理论[28 ] , Liu等[29 ] 构造了有限元形函数的一阶光滑梯度, 提出了伽辽金光滑有限元法. 但本文所讨论的一阶与二阶有限元形函数光滑梯度, 其光滑核函数选取和构造方式均与伽辽金光滑有限元法不同, 同时着重研究的是配点法计算列式. 文中通过典型算例系统验证了节点梯度光滑有限元配点法的精度和收敛性. ...
The use of the local truncation error for the increase in accuracy of the linear finite elements for heat transfer problems
1
2017
... 为不失一般性, 以平面势问题为例, 在均匀网格条件下对节点梯度光滑有限元配点法的精度进行解析研究. 节点梯度光滑有限元配点法的精度可以方便地采用如下的截断误差进行度量[24 ,30 ] ...