易拉罐在轴-侧-扭-内压联合作用下的屈曲地貌

图1 1965年美国NASA^[34]发布的压溃系数: $\kappa=1-0.901(1-{\rm e}^{-\frac{1}{16}\sqrt{\frac{R}{t}}})$

Fig.1 Knockdown factor issued by NASA in 1965: $\kappa=1-0.901(1-{\rm e}^{-\frac{1}{16}\sqrt{\frac{R}{t}}})$

这个公式说明: 典型的结构一般在屈曲预测值的20% $\sim$ 50%就发生了屈曲, 较低的情况只有预测的20%. 所以Gerasimidis等^[36]指出: NASA提出采用屈曲载荷折减系数来计算含初始缺陷的柱壳结构屈曲载荷的方法较为保守. 经过了半个世纪的发展, 利用精巧试验和大量计算分析, 虽然屈曲载荷有些改进, 但目前仍然还采用这个经验公式^[37]. 可以看出任何提高屈曲能力的方法都将有着重大的工程实际意义.

柱壳结构由于其质量较轻、承载力高, 多用于航天、建筑等领域, 所以获得特别多的研究^{[4-8,14,33,38-53]}. 在结构屈曲理论发展历史上, Koiter^[4]揭示了结构的初始几何缺陷对于结构屈曲有非常大的影响, 结构对于初始缺陷是十分敏感的, 结构表面微小的凹陷便会导致结构承载力大幅度下降. 在此基础上 Koiter^[4]又创建了结构稳定的后屈曲理论. 为了验证初始几何缺陷对于屈曲的影响, 人们假设了不同形式的几何缺陷, 甚至提出了随机缺陷的问题.

由于柱壳结构的应用广泛, 对其屈曲稳定性的研究方兴未艾. Krasovsky等^[54] 采用试验与有限元相结合的方式, 提出了采用侧向扰动来创建初始缺陷的方法; Haynie等^[55]采用试验与有限元相结合的方法计算了采用侧向力创建初始缺陷时结构屈曲载荷的最低限值^[15]; Michael等^[56]在NASA试验的基础上提出了柱壳在受到轴向压力的情况下, 在侧向使用探针对该结构施加侧向位移载荷的试验方法, 并且用此方法研究了柱壳结构的冲击感度. 特别是在2017年, Virot等^[57] 对于易拉罐柱壳在轴-侧压作用下的屈曲问题进行了细致的试验研究, 试图从中寻找普适的屈曲规律. 该文献通过对不同品牌的空易拉罐进行研究, 利用屈曲地貌(landscape) 来直观的研究屈曲, 指出多维复杂的壳体稳定可以简化为低维描述. Virot等^[57]从有限的试验数据获得的屈曲地貌有着重要的意义. 但是文献中的载荷情况只有轴-侧压, 没有考虑扭转和内压的联合作用. 为了进一步验证Virot等^[57] 从试验总结出来的屈曲规律, 本文对其他载荷组合下柱壳的稳定性进行了研究.

在本文中, 首先使用有限元数值计算验证了Virot等^[57]的轴-侧压屈曲结果. 随后, 为了获得更加丰富多彩的屈曲地貌, 本文考虑了更多的载荷组合, 进一步考察柱壳在其他载荷组合作用下的屈曲行为. 通过数值计算, 获得了侧压、轴压、扭转和内压等不同载荷组合下柱壳的屈曲地貌. 依据提出的新描述, 对于得到的屈曲地貌进行了细致的稳定性分析. 除了分析参数对于屈曲的影响, 还提出了改善屈曲能力的思路.

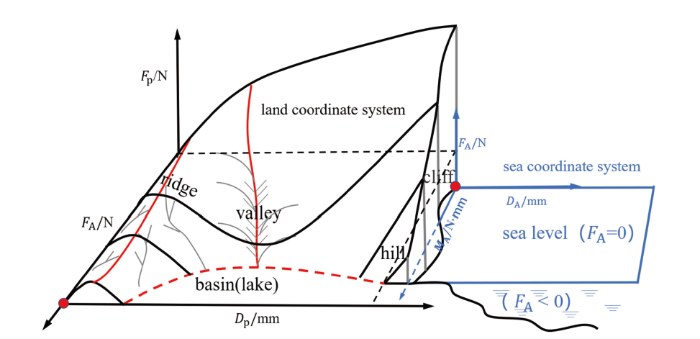
1 屈曲地貌的几何示意图

为了形象的表达屈曲地貌的新信息, 本文除了继承Virot^[57]提出的"ridge (背脊)"和"valley (山谷)"之外, 还把其"lake (湖面)"修改成更贴切的"basin (盆地)", 同时还引进了"cliff (断崖)"、"sea level (海平面)"和"hill (丘陵)" 等新概念, 以便更好地刻画屈曲地貌. 具体屈曲地貌见图2.

图2

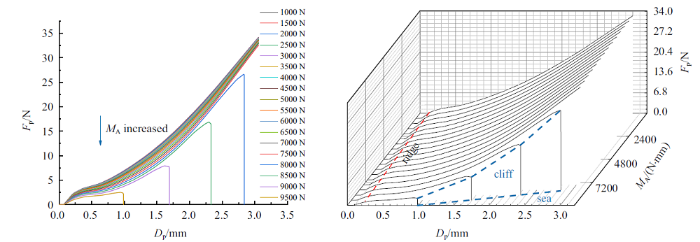
图2 屈曲地貌示意图, 包括"背脊"、"山谷"、"湖面"、"盆地"、 "断崖"、"海平面"和"丘陵"

Fig.2 Illustration of buckling landscape, "ridge", "valley", "lake", "basin", "cliff", "sea level" and "hill"

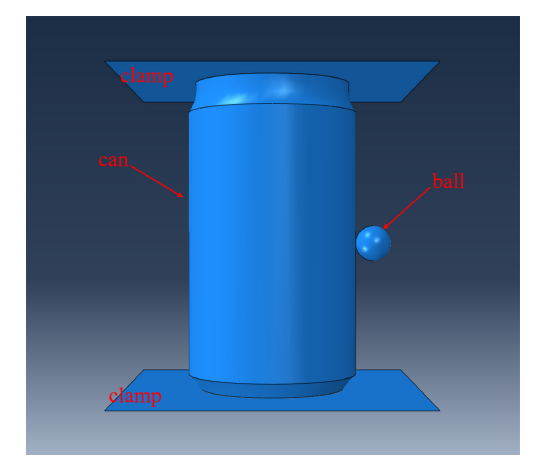
2 有限元验证

本文采用数值的方法与Virot等^[57]的试验结果相互对比验证, 以便核查有限元模型的可行性. 为此, 利用ABAQUS有限元软件建立了该试件的有限元模型. 为了完全还原试验, 本文对文献试验中易拉罐进行了尺寸测量, 采用测量的几何尺寸来进行有限元建模, 具体的几何参数见图3.

图3

图3 可乐罐结构尺寸的示意图, 其中尺寸 $D=57.2$ mm, $D1=52.6$ mm, $D2=48.6$ mm, $L=104$ mm, $t=0.104$ mm

Fig.3 Size of cola can structure, where $D=57.2$ mm, $D1=52.6$ mm, $D2=48.6$ mm, $L=104$ mm, $t=0.104$ mm

由文献[58,59]可知, 易拉罐采用3104铝合金, 其弹性模量为75 000 N/mm$^2$, 泊松比为0.3, 屈服应力为294.3 MPa. 在有限元中采用离散刚体模拟试验中的上下夹板与侧向探针. 定义易拉罐顶与上夹板、易拉罐底部与下夹板、刚性球与罐体互相接触塑性时, 其法向为硬接触, 切向采用罚函数法, 摩擦系数取0.3. 本文采用动力隐式求解器,分析步采用拟静力法来充分模拟加载历程. 为保证有限元数值模拟解的收敛性和准确性,解决网格剪力自锁现象,本文易拉罐模型采用ABAQUS软件壳体S4R单元, 单元数量为10 822个. 上述试件的有限元模型如图4所示.

图4

图4 可乐罐有限元模型

Fig.4 FEA model of cola can

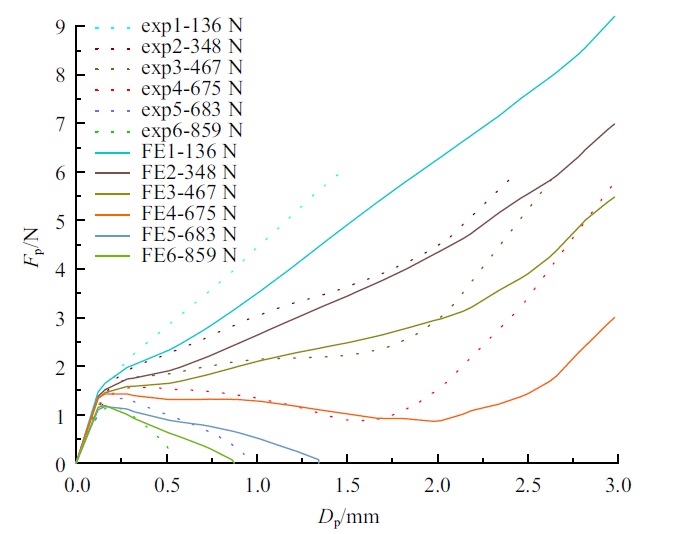
由于在进行有限元模拟时先施加轴向载荷再施加侧向载荷. 当施加的轴力为 1084 N时, 试件发生了较大的整体压缩变形, 无法继续进行侧向载荷的施加. 故只对轴向压为136 N, 348 N, 467 N, 675 N, 683 N, 859 N的试验试件进行有限元数值模拟.

利用上述建立的有限元模型对试验中6个试件进行非线性数值分析, 得到易拉罐在不同轴压力作用下侧向力-位移曲线与试验得到侧向力-位移曲线的对比如图5 所示.

图5

图5 试验与有限元曲线对比图(exp表示文献[57]的试验结果, FE代表有限元计算结果, 易拉罐屈曲载荷是exp4 = 675 N)

Fig.5 Comparisons between experimental results and FEA (exp represent the experimental results^[57], the FE represent FEA results, the buckling load of can is exp4 = 675 N)

由图5可以看出: 有限元模拟的曲线与试验曲线整体趋势较为接近. 在弹性阶段, 试验曲线与有限元曲线较为接近. 这表明有限元能够较好地模拟试件初始刚度; 随着载荷位移的增大, 试件变形逐渐加大. 当试件承载力到达最低值时, 有限元模型的位移要大于试验模型. 这是因为有限元中采用的双折线本构模型相比于实际试件材料本构模型较为理想, 这便导致有限元的塑性开展要大于试验. 另外在试验中存在不可避免的误差和随机的初始缺陷, 这样就会使得试验中试件承载力退化较快. 试验中试件承载力最小时的位移载荷要略低于有限元, 但有限元模型的屈曲承载力大约在675 N, 这与试验相似.

总体来说, 有限元数值模拟获得的易拉罐轴-侧压联合作用下屈曲路径地貌与Virot等^[57] 文献中一致, 本文的非线性数值结果验证了该文献[57]中的试验结果. 接下来进一步采用有限元模拟的方法研究其他不同载荷组合情况下的屈曲地貌.

3 有限元数值分析

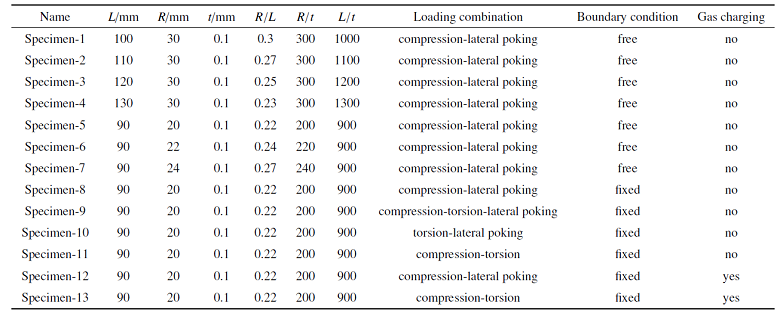
由Virot等^[57]试验发现, 易拉罐发生的屈曲变形主要集中在罐体. 因此在有限元参数分析时采用简化的分析方式, 将易拉罐简化为柱壳结构来进一步进行分析. 为了研究不同载荷组合、不同边界条件、不同径高比(试件半径与高度比值, $R/L$)、径厚比(试件半径与厚度比值, $R/t$)、高厚比(试件高度与厚度比值, $L/t$)、罐体内部充压等对屈曲地貌的影响.

本文设计4个不同径高比$(R/L)$、不同高厚比$(L/t)$、3个不同径厚比$(R/t)$、3个不同载荷组合、1个不同边界条件、2个罐体内部充气的有限元模型. 对于易拉罐边界条件本文定义: 在加载前试件与上下加载板无约束时的边界条件为自由边界, 试件上下面与加载板自由度完全相同时视为试件为固定边界. 在有限元中为了充分模拟试件内部充气, 采用等价的方式将罐体内部充气等价成在罐体内部施加压强, 压强的数值为一个标准大气压. 具体模型的参数如表1 所示.

表1 不同试件的几何参数

Table 1 The geometric parameters of different specimens

新窗口打开| 下载CSV

3.1 轴-侧压作用下对易拉罐屈曲影响

3.1.1 位移-载荷曲线及(外力-屈曲载荷-位移)三维地貌

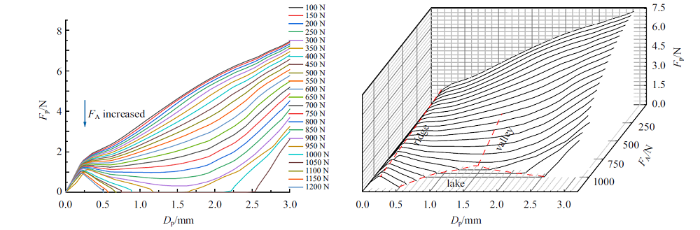
Specimen-1$\sim$Specimen-7均采用与试验中相同的加载方式: 先在竖向施加轴向压力, 轴向力的范围为100 $\sim$ 1200 N, 待试件稳定后施加侧向位移载荷, 每步的载荷位移增量为0.16 mm. 每个试件的侧向位移、侧向力、竖向力、竖向位移分别记为: $D_{\rm p}$, $F_{\rm p}$, $F_{\rm A}$, $D_{\rm A}$. 各试件的侧向载荷-位移曲线如图6 $\sim\!$图12所示.

图6

图6 Specimen-1: 屈曲路径的二维曲线和三维曲面地貌

Fig.6 Specimen-1: Two dimensional curve and three-dimensional surface landscape of buckling path

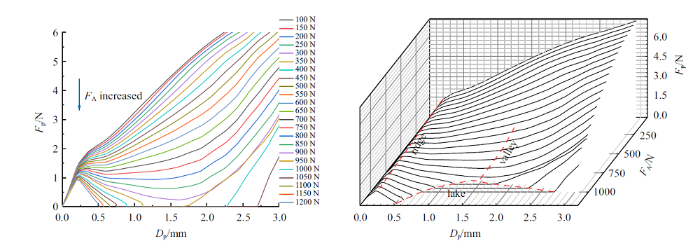
图7

图7 Specimen-2: 屈曲路径的二维曲线和三维曲面地貌

Fig.7 Specimen-2: Two dimensional curve and three-dimensional surface landscape of buckling path

图8

图8 Specimen-3: 屈曲路径的二维曲线和三维曲面地貌

Fig.8 Specimen-3: Two dimensional curve and three-dimensional surface landscape of buckling path

图9

图9 Specimen-4: 屈曲路径的二维曲线和三维曲面地貌

Fig.9 Specimen-4: Two dimensional curve and three-dimensional surface landscape of buckling path

图10

图10 Specimen-5: 屈曲路径的二维曲线和三维曲面地貌

Fig.10 Specimen-5: Two dimensional curve and three-dimensional surface landscape of buckling path

图11

图11 Specimen-6: 屈曲路径的二维曲线和三维曲面地貌

Fig.11 Specimen-6: Two dimensional curve and three-dimensional surface landscape of buckling path

图12

图12 Specimen-7: 屈曲路径的二维曲线和三维曲面地貌

Fig.12 Specimen-7: Two dimensional curve and three-dimensional surface landscape of buckling path

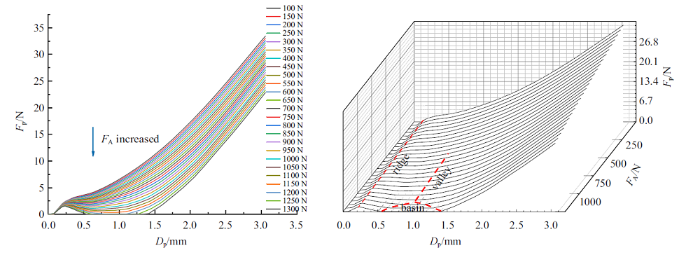
由图可以看出7个模型均出现了文献中描述的屈曲地貌现象, 各试件的"脊背"、"山谷"差别不大. 根据每个试件的力-位移曲线, 把试件分为三个阶段: 第一阶段为弹性阶段, 此阶段侧向承载力随着侧向位移的增大而不断增大; 第二阶段为屈曲阶段, 试件侧向承载能力随着侧向位移的增大出现先增大后减小再增大的趋势; 最后阶段称为"湖面"阶段, 在这阶段试件的侧向承载能力先增大后下降到零, 继续加载会出现两种情况: 一是随着位移载荷的逐渐增加, 构件承载能力从零开始增大; 另一种情况为承载力持续为零, 不再增大. 由图可以看出, Specimen-1 $\sim$ Specimen-4 "湖面" 阶段的轴向力范围均为950 $\sim$ 1200 N, Specimen-5 $\sim$ Specimen-7 "湖面"阶段轴向力范围为1000 $\sim$ 1200 N. 通过对比发现: 随着径高比的不断减小, 试件侧向承载力为零时的位移不断增大. 举例来说: 当$F_{\rm A}=1050$ N 时, $R/L= 0.3$, 0.27, 0.25, 0.23时侧向承载力为零的位移分别为: 1.5 mm, 1.8 mm, 1.9 mm, 2.1 mm. 并且通过三维曲线图也可以看出, 试件的"湖面" 区域随着径高比的不断减小而增大. 同样, Specimen-1 $\sim$ Specimen-4高厚比不断增大, 由上述描述可以得到: 随着高厚比不断增大, 试件侧向承载力为零时的位移不断增大, 试件形成"湖面"的面积不断增大. 分析Specimen-5 $\sim$ Specimen-7 可知: 随着径厚比的不断增大, 试件侧向承载力为零时的位移不断减小. 当$F_{\rm A}=1050$ N 时, 径厚比200, 220, 240 时侧向承载力为零的位移分别为: 1.95 mm, 1.35 mm, 1.3 mm. 并且通过三维曲线图也可以看出, 红色包围区域为试件的"湖面" 区域, 并且包围区域随着径厚比的不断增大, 红色区域不断减小.

通过上述分析可知径厚比、径高比越大的结构有着较好的稳定性, 试件对初始缺陷相对不敏感. 高厚比越大, 结构稳定性降低, 试件对初始缺陷较为敏感.

3.1.2 失稳模式讨论

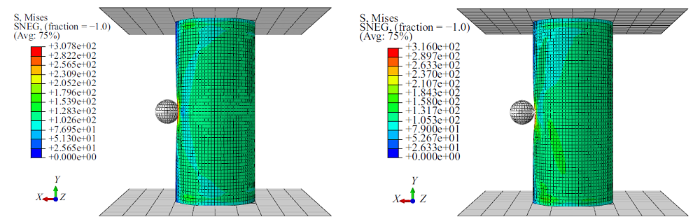
各试件的破坏模式如图13$\sim$图15所示: 不同径高比、径厚比、高厚比的试件有着相似的破坏模式. 当轴向压力较小时, 试件侧向受到刚性球挤压, 接触点处柱壁发生内凹, 试件整体稳定性较好. 随着轴向压力的增大, 接触点柱壁发生较大变形. 当轴向压力达到一定值 (950 N左右) 时, 试件在受到刚性球的侧向挤压时, 试件发生了局部屈曲, 刚性球与柱壁接触位置发生较大内凹变形. 并且侧向载荷到达一定值时, 侧向载荷位移不再增大但接触点处的变形继续增大, 加载点与柱壁发生分离 ("湖面"现象开始发生). 当柱壁内凹到一定位移时, 试件达到新的平衡. 继续加载小球与柱壁发生第二次接触 (此时"湖面"现象结束), 试件局部变形继续加大, 但并未发生整体屈曲. 图15是构件在遭受较大轴向压力时发生的破坏模式. 由于较大的轴向力作用, 试件在很早便出现了加载球体与柱壁的分离. 并且该点处柱体表面的局部屈曲逐渐变大, 随后向柱顶、柱脚扩散, 试件发生轴向压缩, 最终导致构件发生整体失稳.

图13

图13 局部屈曲 (左), 球体与柱壁分离 (右)

Fig.13 Local buckling (left), separation of ball from cylindrical shells (right)

图14

图14 球体与柱壁第二次接触 (左), 轴力较大时小球与柱壁分离 (右)

Fig.14 The second contact between the ball and cylindrical shells (left), the ball separated from cylindrical shells in high axial load (right)

图15

图15 局部屈曲扩散 (左), 整体压缩屈曲 (右)

Fig.15 Local buckling extend (left), compressive global buckling (right)

3.2 轴-侧压-扭转作用下对易拉罐屈曲影响

3.2.1 位移-载荷曲线及(外力-屈曲载荷-位移)三维地貌

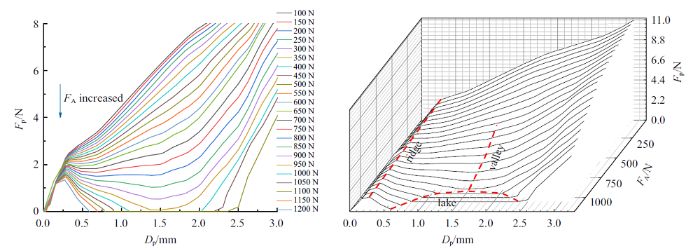
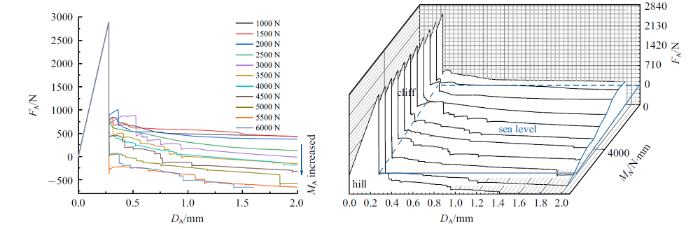
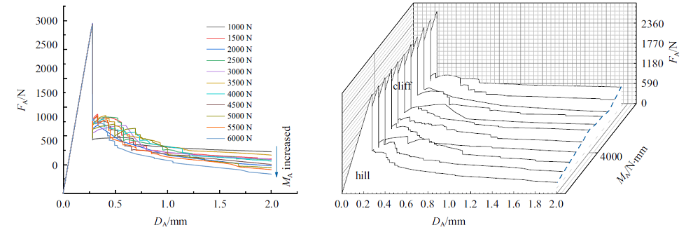
本文在轴-侧压作用下试件的基础上考虑扭转作用, 建立了在轴-侧压-扭转作用下的有限元模型. 为了施加扭转载荷, 在有限元中分别将试件两端与上下刚性夹板进行绑定, 这就使得试件边界条件由自由边界变为固定边界. 为了保证单一变量原则, 在Specimen-5的基础上改变边界条件, 建立Specimen-8来与Specimen-9进行对比分析, 研究该情况下柱壳结构的屈曲地貌. Specimen-9 几何尺寸与Specimen-8相同, 施加扭转载荷为5000 N$\cdot$mm, 记为$M_{\rm A}$. 得到侧向力-位移对比曲线如下图所示.

图16

图16 Specimen-8: 屈曲路径的二维曲线, 以及三维曲面地貌

Fig.16 Specimen-8: Two dimensional curve and three-dimensional surface landscape of buckling path

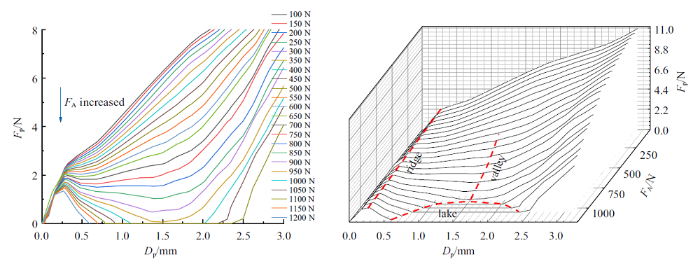
图17

图17 Specimen-9屈曲路径的二维曲线, 以及三维曲面地貌

Fig.17 Specimen-9: Two dimensional curve and three-dimensional surface landscape of buckling path

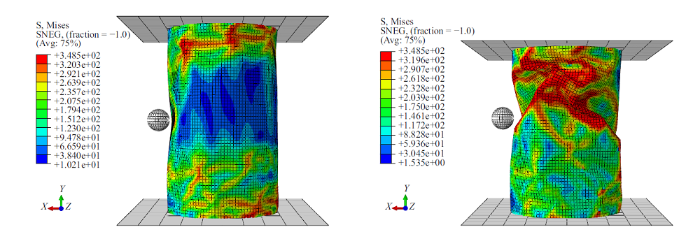
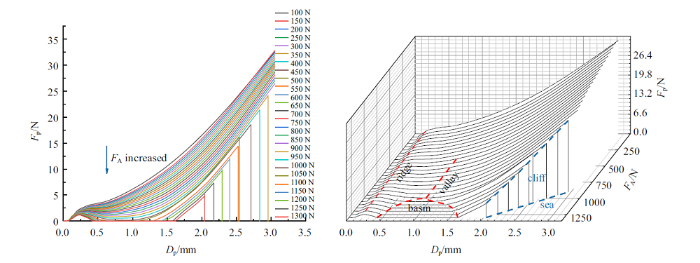
由曲线图可以看出, 在轴压-侧压-扭转载荷作用下, 试件也出现了相似的屈曲地貌. 相比未施加扭转的试件曲线, 在轴压-侧压-扭转联合作用下的柱壳结构出现了新现象. 本文把这种曲线现象叫做"断崖", "断崖"下方承载力为零的空白区域定义为"海", 并且本文将"湖"区域重新定义为"盆地". 这种"断崖"现象出现的原因为: 在侧向加载球体加载到一定位移时柱壁发生跳跃, 加载点与柱壁发生分离, 试件侧向承载力变为零. 这一现象形成了曲线中"盆地"现象. 当载荷继续增大, 小球与柱壁再次接触, 试件侧向承载力从零开始增大. 但对于轴压-侧压-扭转联合作用下的试件来说, 试件到达"盆地"位移之后, 由于扭转弯矩的存在导致在加载后期试件发生了扭转破坏, 小球与柱壁发生了第二次分离, 试件的承载力瞬间下降到了零便形成了曲线中的"断崖"现象. 对比Specimen-8发现, Specimen-9的"山谷"结束早, "脊背" 相对弯曲, 其主要原因还是施加了扭转载荷导致试件变形加大, 破坏时间提前. 并且分析发现, 在有限元中施加扭转载荷对试件强度影响不大, 但降低了试件的稳定性. 并且扭转载荷的增大使得试件进入"盆地"时间提前, 在加载后期试件发生了整体失稳, 承载力瞬间下降到零.

对比Specimen-8与Specimen-5可知: 当试件两端边界条件由自由边界变为固定边界时, 试件侧向力有了较大的提升, 试件形成"盆地"时间推迟、形成"盆地"面积小, 试件的稳定性和承载能力均有了较大的提升. 两端固定, 一定程度上削弱了结构对初始缺陷的敏感性.

3.2.2 失稳模式讨论

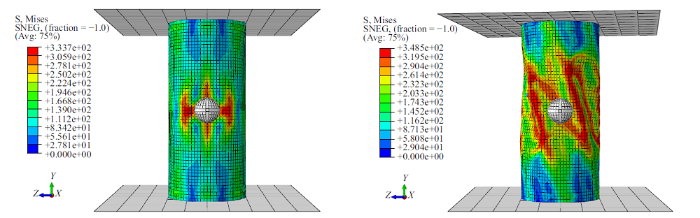
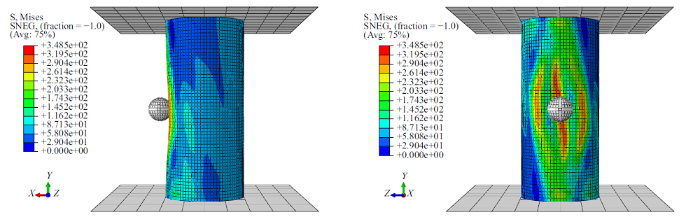
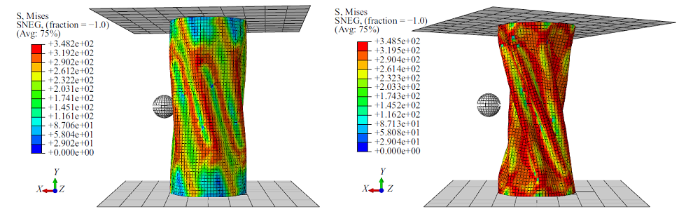
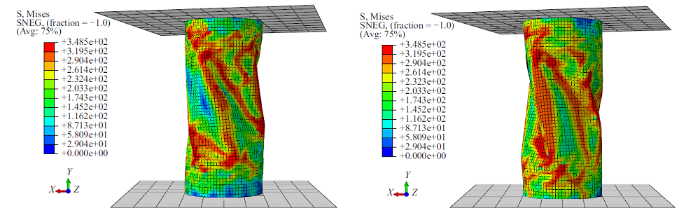
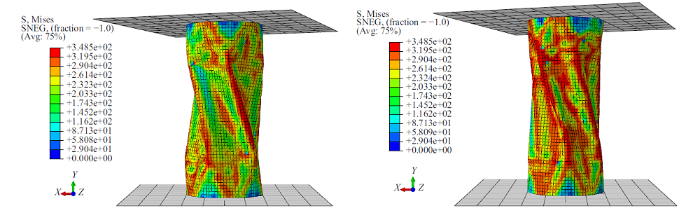
由于模拟试件较多, 选取具有代表性试件来进行对比分析. 当$F_{\rm A}=1200$ N, 试件的破坏模式对比见图18 $\sim\!$图20. 由图可以看出, Specimen-8的最大应力云图关于轴线对称, 最大应力以加载点为中心向四周发散; 相比于Specimen-8, Specimen-9最大应力云图关于轴线反对称, 整体呈现"N"字形. 这表明增大扭转载荷在一定程度上改变了试件的受力状态, 进而改变了试件的破坏形态. Specimen-9 在 $F_{\rm A}=1200$ N 时发生了小球与柱壁的两次分离: 第一次分离形成曲线中"盆地"现象, 第二次分离形成"断崖"现象. 而Specimen-8在加载全程并未发生加载球体与柱壁分离, 这表明施加扭转载荷一定程度上削弱了试件的稳定性. 在加载后期Specimen-9发生了整体扭转失稳, 而Specimen-8只发生局部屈曲, 这一现象也证明了扭转载荷的施加对结构的稳定性有不利的影响.

图18

图18 当$F_{\rm A}=1200$ N时, Specimen-8 (左)与Specimen-9 (右)的应力分布

Fig.18 The stress of specimen-8 (left) and specimen-9 (right) at $F_{\rm A}=1200$ N

图19

图19 在加载中期: Specimen-8 (左)小球与柱壁接触, Specimen-9 (右)发生小球与柱壁发生分离

Fig.19 The medium loading stage: the ball contact with cylindrical shells of Specimen-8 (left), the ball separated from cylindrical shells (right)

图20

图20 加载后期Specimen-8发生局部屈曲(左) Specimen-9 (右)出现整体扭转破坏

Fig.20 The late loading stage: local buckling of Specimen-8 (left), torsional global buckling of specimen-9 (right)

3.3 侧压-扭转作用下对易拉罐屈曲影响

3.3.1 位移-载荷曲线及(外力-屈曲载荷-位移)三维地貌

图21是Specimen-10的侧向力-位移曲线. 由曲线可以看出, 当扭转载荷范围为: 1000 $\sim$ 7500 N$\cdot$mm 时, 试件的承载力随着位移载荷的增大而逐渐增大. 当扭转载荷大于7500 N$\cdot$mm 时, 试件的承载能力呈现先增加后快速下降的趋势. 三维曲线图展示了Specimen-10在不同扭转载荷作用下出现上文提起的"断崖"、"脊背"、"海"现象. 对比Specimen-9, Specimen-10并未出现"盆地" 现象, "山谷"现象也不太明显. 这是因为试件在侧向加载时, 加载点处柱壁由于刚性小球的作用发生内凹, 但由于竖向无载荷作用, 柱壁内凹处并不会脱离小球继续变形, 反而由于扭转载荷的作用内凹处发生扭转变形, 继续加载扭转变形范围继续扩大最终导致试件发生整体扭转失稳. 在试件发生整体失稳之前, 刚性加载小球一直与柱壁接触, 直到试件发生整体失稳时才分离.

图21

图21 Specimen-10: 屈曲路径的二维曲线,以及三维曲面地貌

Fig.21 Specimen-10: Two dimensional curve and three-dimensional surface landscape of buckling path

3.3.2 失稳模式讨论

Specimen-10的破坏模式图如图22 $\sim\!$图24所示. 由图可以看出当扭转载荷比较小时, 试件只在接触点处发生轻微变形. 试件加载点处最大应力关于轴线呈正对称状. 随着扭矩载荷的增大, 试件柱壁内凹变形逐渐加大. 最大应力受扭转载荷的影响逐渐由正对称转化为反对称. 当扭转载荷增大到8000 N$\cdot$mm时, 试件由加载点处弯曲变形转变为扭转屈曲, 并且随着扭转载荷的继续增大扭转变形加大, 最终导致试件发生整体扭转失稳.

图22

图22 当$M_{\rm A}=1000$ N$\cdot$mm时, Specimen-10的应力分布图

Fig.22 The stress of specimen-10 at $M_{\rm A}=1000$ N$\cdot$mm

图23

图23 当$M_{\rm A}=7000$ N$\cdot$mm时, Specimen-10的应力分布图

Fig.23 The stress of specimen-10 at $M_{\rm A}=7000$ N$\cdot$mm

图24

图24 当$M_{\rm A}=8000$ N$\cdot$mm时(左)、9500 N$\cdot$mm (右)时, Specimen-10的整体扭转破坏

Fig.24 Torsional global buckling of specimen-10 at $M_{\rm A}=8000$ N$\cdot$mm (left), 9500 N$\cdot$mm (right)

由Specimen-10力-位移曲线、破坏模式图可以总结出: 侧压-扭转载荷作用下的试件有着不同的屈曲地貌. 相比于Specimen-9缺少了轴向压力的试件承载能力有了提高, 但扭转载荷的存在改变了试件最终破坏模式, 也改变了最终的屈曲地貌.

3.4 轴压-扭转作用下对易拉罐屈曲影响

3.4.1 位移-载荷曲线及(外力-屈曲载荷-位移)三维地貌

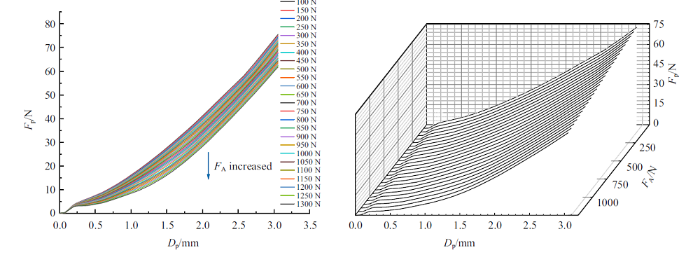
为了研究在轴压-扭转作用下柱壳结构的屈曲性能, 建立试件Specimen-11. 为了方便施加扭转载荷, 试件顶端与底端分别于上下夹板固定. 首先施加扭转载荷, 待试件稳定后在试件轴线方向施加位移载荷, 具体的轴向力-位移曲线如图25所示.

图25

图25 Specimen-11: 屈曲路径的二维曲线, 以及三维曲面地貌

Fig.25 Specimen-11: Two dimensional curve and three-dimensional surface landscape of buckling path

由图25可以看出, 各试件曲线呈现先增大后减小的趋势, 试件最大承载力基本相同. 随着位移载荷的增大, 各个试件曲线展现出了不同的变化趋势. 当施加扭转载荷为3000 N$\cdot$mm时, 试件轴向承载力出现负值, 并且随着扭转载荷的增大, 轴向承载力出现负值的时刻不断提前, 数值不断增大. 发生这种现象主要原因是: 当施加扭矩载荷范围为 1000 $\sim$ 3000 N$\cdot$mm, 此时试件轴向承载能力基本为正, 扭转载荷并不起主导作用, 试件变形多为轴向压缩变形; 随着扭转载荷的不断增大, 相对于轴向位移载荷, 扭转载荷逐渐起主导作用. 在加载初期, 试件由于扭转载荷的作用柱体出现多个斜45$^\circ$方向上的褶皱, 前后褶皱呈现交叉状; 未出现扭转变形时, 试件主要依靠环形柱壁承受竖向载荷; 当试件出现扭转褶皱时, 试件由以前柱壁承载逐渐变为交叉褶皱承载.加上扭转载荷的作用, 此时试件轴向承载力出现反向, 承载力大小有了一定的提升. 根据此现象, 按照海岸带的定义方式, 做出承载力为零时的平面, 并将该平面定义为"海平面". 加载初期承载力上升段定义为"丘陵", 承载力快速下降段也定义成"断崖". 经分析, "丘陵" 高度相同,这表明试件峰值载荷相似; 试件在"海平面" 上部的曲线, 轴向承载力为正, 轴向位移载荷起主导作用; 试件在"海平面"下部的曲线, 轴向承载力为负, 扭转载荷起主导作用.

3.4.2 失稳模式讨论

图26$\sim\!$图28为Specimen-11在不同扭转载荷作用下的破坏模式图, 由图可以看出: 当扭转载荷小于3000 N$\cdot$mm 时, 试件发生轴向压缩屈曲. 这是因为扭转载荷较小, 并未影响试件的轴向变形. 当扭转载荷大于 3000 N$\cdot$mm时, 试件逐渐由轴向压缩屈曲转变为整体扭转屈曲, 并且随着扭转载荷的增大试件变形逐渐加大. 试件破坏模式的改变, 是因为相比于轴向刚度, 柱壳结构的扭转刚度较低, 在扭转载荷与轴向载荷共同作用下,试件更容易发生扭转失稳. 可以判断, 当试件曲线完全在"海平面"之上时试件多发生轴向压缩屈曲, 在"海平面" 之下试件多为整体扭转失稳.

图26

图26 当$M_{\rm A}=1000$ N$\cdot$mm (左), 2000 N$\cdot$mm (右)时, Specimen-11 的破坏模式图

Fig.26 Failure model of specimen-11 at $M_{\rm A}=1000$ N$\cdot$mm (left), $M_{\rm A}=2000$ N$\cdot$mm (right)

图27

图27 当$M_{\rm A}=3000$ N$\cdot$mm (左), 4000 N$\cdot$mm (右)时, Specimen-11 的破坏模式图

Fig.27 Failure model of specimen-11 at $M_{\rm A}=3000$ N$\cdot$mm (left), $M_{\rm A}=4000$ N$\cdot$mm (right)

图28

图28 当$M_{\rm A}=5000$ N$\cdot$mm (左), 6000 N$\cdot$mm (右)时, Specimen-11 的破坏模式图

Fig.28 Failure model of specimen-11 at $M_{\rm A}=5000$ N$\cdot$mm (left), $M_{\rm A}=6000$ N$\cdot$mm (right)

3.5 罐体内部充气对易拉罐屈曲影响

3.5.1 位移-载荷曲线及(外力-屈曲载荷-位移)三维地貌

为了研究易拉罐等柱壳结构内部充气时的屈曲地貌, 本文在原有模型的基础上设计了Specimen-12, Specimen-13两个模型. 图29和图30为该试件的力-位移曲线. 由图可以看出: Specimen-12 在轴压-侧压-内压作用下的力-载荷位移曲线呈现单调递增趋势; 试件并未出现较为明显的屈曲地貌. 将Specimen-12、Specimen-8曲线中最大承载力取出绘制最大承载力-轴向载荷曲线. 由该曲线可以看出, 两个试件承载力退化趋势相似, 但Specimen-12的最大承载力要远远大于Specimen-8. 取平均值计算, Specimen-12最大载荷平均值为68.72 N, Specimen-8最大载荷平均值为28.25 N. 并且当轴向载荷为1300 N时, Specimen-8 已经出现"盆地" 现象, 试件发生了局部屈曲; 而Specimen-12 曲线还是保持单调递增的趋势, 试件处于弹性阶段. 这表明, 柱壳结构内部充气可以较大地提升试件的侧向承载能力, 提高试件屈曲载荷, 降低柱壳结构对初始缺陷的敏感性.

图29

图29 Specimen-12: 屈曲路径的二维曲线,以及三维曲面地貌

Fig.29 Specimen-12: Two dimensional curve and three-dimensional surface landscape of buckling path

图30

图30 Specimen-13: 屈曲路径的二维曲线,以及三维曲面地貌

Fig.30 Specimen-13: Two dimensional curve and three-dimensional surface landscape of buckling path

图30为Specimen-13的力-位移曲线图. 由图可以看出各试件曲线展现出先增大后减小的趋势, 试件最大承载能力相似. 由于内部压强载荷的作用, 试件曲线并未出现"海平面"现象. 取Specimen-13, Specimen-11曲线中的承载力最小值做出对比图. 由图31可以看出: Specimen-13的轴向承载能力要远远大于Specimen-11, 并且随着扭转载荷的增大, Specimen-11的承载力退化程度要远远大于Specimen-13. 当扭转载荷为4000 N$\cdot$mm时, Specimen-11的最小轴向承载能力已经退化到负值, 而Specimen-13最小承载力一直为正. 通过上述分析可知: 为受到轴压-扭转载荷作用的试件内部充压, 可以较大程度的提升柱壳结构的承载能力, 减缓承载力退化.

图31

图31 最大承载力对比(左),最小承载力对比(右)

Fig.31 Comparison of maximum bearing capacity (left), and comparison of minimum bearing capacity (right)

3.5.2 失稳模式讨论

Specimen-12, Specimen-13的破坏模式图如下所示. Specimen-12并未发生屈曲破坏. 相比于Specimen-8, 施加了内部压强提高了柱壳结构的稳定性, 增大了试件侧向扰动的抵抗能力. Specimen-13在不同扭转载荷作用下发生了局部屈曲, 屈曲形式随着扭转载荷的增加逐渐变为局部扭转屈曲, 试件整体稳定性好. 对比Specimen-11可以看出, 在扭转载荷范围为1000 $\sim$ 6000 N$\cdot$mm时, Specimen-13并未发生整体扭转失稳. 当扭转载荷为6000 N$\cdot$mm时, Specimen-13仅在距上加载板30 mm 处发生局部屈曲; 而Specimen-11发生类似破坏模式的扭转载荷为2000 N$\cdot$mm. 这表明, 柱壳结构内部充气可以提升结构抗扭承载能力, 推迟局部失稳的发生, 一定程度上提高了柱壳结构的稳定性.

图32

图32 $F_{\rm A}=100$ N (左)、1300 N (右)时, Specimen-12破坏模式

Fig.32 Failure model of specimen-13 at $F_{\rm A}=100$ N (left), 1300 N (right)

图33

图33 当$M_{\rm A}=1000$ N$\cdot$mm (左)、$M_{\rm A}=6000$ N$\cdot$mm (右)时, Specimen-13的破坏模式

Fig.33 Failure model of specimen-13 at $M_{\rm A}=1000$ N$\cdot$mm (left), $M_{\rm A}=6000$ N$\cdot$mm (right)

4 结论

本文采用有限元非线性数值模拟的方法, 首先从数值计算的角度验证和支持了Virot等学者^[57]的试验以及屈曲地貌的趋势. 然后进一步对不同载荷组合的柱壳屈曲进行了细致的数值模拟研究, 获得了柱壳的屈曲地貌, 并在此基础上细致讨论分析了不同载荷组合、不同边界条件、不同径高比、径厚比、高厚比对柱壳结构屈曲地貌的影响. 从目前的数值分析并利用屈曲地貌解释, 可以总结出以下几个结论:

(1)不同径高比、径厚比、高厚比试件有着相似的屈曲地貌, 试件"脊背"、"山谷"趋势相差不大, "湖面" 变化较大. 随着径高比、径厚比增大, 试件形成"湖面"的面积不断减小; 随着高厚比增大, 试件形成"湖面"的面积不断增大. 这表明较大径高比、径厚比的试件有着较好的稳定性, 对初始缺陷敏感度不高, 较大高厚比的试件更容易失稳, 对初始缺陷更加敏感.

(2)试件在受到侧压-轴压-扭转时不仅展现出与侧压-轴压相似的现象, 也出现了新的屈曲地貌. 由于扭转载荷存在, 试件力-位移曲线在加载后期出现了承载力骤降的现象. 为了更加形象地描述这种力学性能, 本文把这种现象定义为"断崖", 下方承载力为零的空白处定义为"海", 并且将"湖面"改为"盆地". 这些现象出现与定义在以前是没有过的.

(3)相比于侧压-轴压载荷作用下的试件, 扭转载荷的存在不仅把试件的破坏模式由整体压缩屈曲转变成扭转屈曲, 还降低了试件的稳定性, 使得试件对初始缺陷更加敏感.

(4)受到侧压-扭转载荷作用的试件并未出现"盆地"现象. 这是因为没有竖向轴压力的作用, 试件接触点处内凹变形并未得到进一步加强. 并且由于扭转载荷的作用试件内凹形状发生改变, 试件最终发生整体扭转失稳.

(5)本文对轴向-扭转载荷作用下的试件进行了有限元分析, 发现扭转载荷的存在改变柱壳结构的受力机制, 试件的轴向力出现了负值. 为了更好地描述这一现象, 本文将承载力为零的平面定义为"海平面", 承载力最大时曲线围成的范围定义为"丘陵". 经分析得, "海平面"上部试件轴向载荷起主导作用, 试件多发生轴向压缩变形; 下部试件变形主要由扭转载荷控制, 试件最终发生整体扭转失稳.

(6)轴压-扭转-内压作用下试件轴向承载力增大, 试件局部失稳被推迟, 并未发生整体失稳; 根据轴压-侧压-内压载荷作用下的屈曲地貌和破坏模式可以看出: 由于内部压强的存在, 试件未发生屈曲变形, 结构侧向承载能力大幅提升. 这表明: 柱壳结构内部充气提高了试件的侧向承载能力、轴向承载能力、抗扭能力和整体稳定性, 降低了试件对初始缺陷的敏感度.

(7)试件边界条件由自由边界变为固定边界时, 试件的承载能力增大稳定性提高, 对初始缺陷敏感度降低.

致谢

特以此文致敬荷兰代尔夫特大学的Arbocz教授在结构屈曲理论方面给予作者孙博华的指导和提供的留学机会. 此外, 感谢评审专家提供的宝贵评审意见.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Euler

. De curvis elasticis, Leonhard Euler's Elastic Curves. Oldfather WA, Ellis CA, Brown DM. Belgium: The St Catherine Press, 1933

[2]

Timoshenko

History of Strength of Materials

New York/ Toronto/London: McGraw-Hill Book Company, 1953

[3]

Timshenko

, Gere

Theory of Elastic Stability

2nd ed. New York: Dover Publications Inc, 2009

[4]

Koiter

On the stability of elastic equilibrium

National Aeronautics and Space Administration, 1967

[本文引用: 3]

[5]

Hutchinson

, Koiter

Postbuckling theory

Appl. Mech. Rev, 1970,23(12):1353-1366

[6]

Singer

, Arbocz

, Babcock

CDJ

Buckling of imperfect stiffened cylindrical shells under axial compression

AIAA Journal, 1970,9(1):8

[7]

Thompson

JMT

, Hunt

A General Theory of Elastic Stability

London: Wiley, 1973

[8]

Arbocz

The Effect of Initial Imperfections on Shell Stability

In: (Fung Y C and Sechler E E eds). Thin-Shell Structures, Theory, Experiment and Design. Prentice Hall: Englewood Cliffs N J, 1974: 205-245

[9]

Sun

Buckling problems of sandwich shells. Delft University of Technology

Delft University of Technology, 1992. Report LR-690, pp 1-99

[10]

Yeh

, Sun

, Rimrott

FPJ

Buckling of imperfect sandwich cones under axial compression-equivalent-cylinder approach. Part I

Scientific Journal for Fundamentals and Applications of Engineering Mechanics, 1994,14(3-4):239-248

[11]

Yeh

, Sun

, Rimrott

FPJ

Buckling of imperfect sandwich cones under axial compression-equivalent-cylinder approach. Part II

Scientific Journal for Fundamentals and Applications of Engineering Mechanics, 1994,15(1):1-12

[12]

Sun

, Yeh

, Rimrott

FPJ

On the buckling of structures

Scientific Journal for Fundamentals and Applications of Engineering Mechanics, 1995,15(2):129-140

[13]

Sun

Modified Koiter's buckling theory based on the generalized variational principles

CERECAM Report No.244, University of Cape Town, 1994

[14]

Budiansky

Theory of buckling and post-buckling behavior of elastic structures

Advances in Applied Mechanics, 1974,14

[15]

Elishakoff

. Probabilistic resolution of the twentieth century conundrum in elastic stability. 2014,59:35-57

[16]

徐凡, 汪婷, 杨易凡.

薄膜拉伸褶皱失稳力学进展

力学季刊, 2020,41(2):207-220

( Xu

Fan

, Wang

Ting

, Yang

Yifan

Wrinkling of stretched films: A review

Chinese Quart. Mech, 2020,41(2):207-220 (in Chinese))

[17]

Yang

, Dai

, Xu

. et al.

Pattern transitions in a soft cylindrical shell

Physical Review Letters, 2018,120:215503

[18]

, Fu

, Yang

Water affects morphogenesis of growing aquatic plant leaves

Physical Review Letters, 2020,124:038003

[19]

曹进军, 张卉婷, 张亮

等.

对角受拉方膜褶皱变形幅值的理论预测及实验验证

力学学报, 2019,51(5):1403-1410

( Cao

Jinjun

, Zhang

Huiting

, Zhang

Liang

, et al.

Theoretical prediction and experimental verification of wrinkle amplitude in a square membrane subjected to diagonal tension

Chinese Journal of Theoretical and Applied Mechanics. 2019,51(5):1403-1410 (in Chinese))

[20]

夏元明, 张威, 崔天宁

等.

金属多级类蜂窝的压溃行为研究

力学学报, 2019,51(3):873-883

( Xia

Yuanming

, Zhang

Wei

, Cui

Tianning

, et al.

Investigation on crushing behavior of metal honeycome-like hierarchical structures

Chinese Journal of Theoretical and Applied Mechanics. 2019,51(3):873-883 (in Chinese))

[21]

Yan

, Yang

, Pan

. et al.

Sterically controlled mechanochemistry under hydrostatic pressure

Nature, 2018,554(7693):505

[22]

Yang

, Li

, Shi

. et al.

Review on auxetic materials

Journal of Materials ence, 2004,39(10):3269-3279

[23]

Alderson

, Alderson

Auxetic materials

Journal of Aerospace Engineering, 2007,221(4):565-575

[24]

Zheng

, Howon

Lee

, Weisgraber Todd

. et al.

Ultralight, ultrastiff mechanical metamaterials

Science, 2014,344:6190

[25]

Banerjee

, Bernoulli

, Zhang

. et al.

Ultralarge elastic deformation of nanoscale diamond

Science, 2018,360(6386):300-302

DOI URL PMID

Diamonds have substantial hardness and durability, but attempting to deform diamonds usually results in brittle fracture. We demonstrate ultralarge, fully reversible elastic deformation of nanoscale (~300 nanometers) single-crystalline and polycrystalline diamond needles. For single-crystalline diamond, the maximum tensile strains (up to 9%) approached the theoretical elastic limit, and the corresponding maximum tensile stress reached ~89 to 98 gigapascals. After combining systematic computational simulations and characterization of pre- and postdeformation structural features, we ascribe the concurrent high strength and large elastic strain to the paucity of defects in the small-volume diamond nanoneedles and to the relatively smooth surfaces compared with those of microscale and larger specimens. The discovery offers the potential for new applications through optimized design of diamond nanostructure, geometry, elastic strains, and physical properties.

[26]

Liu

, Silverberg

, Evans

. et al.

Topological kinematics of origami metamaterials

Nature Physics, 2018,14:811-815

[27]

任鑫, 张相玉, 谢亿民.

负泊松比材料和结构的研究进展

力学学报, 2019,51(3):656-689

( Ren

Xin

, Zhang

Xiangyu

, Xie

Yimin

Research progress in auxetic materials and structures

Chinese Journal of Theoretical and Applied Mechanics. 2019,51(3):656-689 (in Chinese))

[28]

Von Karman

, Tsien H

The buckling of spherical shells by external pressure

Journal of the Aeronautical Sciences, 1939,7(2):43-50

[29]

von Karman

, Tsien H

The buckling of thin cylindrical shells under axial compression

Journal of the Aeronautical Sciences, 1941,8:303-312

[30]

Tsien

A theory for the buckling of thin shells

Journal of the Aeronautical Sciences, 1942,9(10):373-384

[31]

Koiter

On the stability of elastic equilibrium

National Aeronautics and Space Administration, 1967

[32]

Tsien

Lower buckling load in the non-linear buckling theory for thin shells

Quarterly of Applied Mathematics, 1947,5(2):236-237

[33]

Stein

The effect on the buckling of perfect cylinders of prebuckling deformations and stresses induced by edge support

NASA TN D-1510, 1962: 217

[本文引用: 3]

[34]

NASA.

Buckling of thin-walled circular cylinders

NASA Space Vehicle Design Criteria, National Aeronautics and Space Administration, Washington DC, 1965. Technical Report No. NASA SP-8007

[35]

Mark

, Hilburger.

Developing the Next Generation Shell Buckling Design Factors and Technologies

American Institute of Aeronautics and Astronautics, 2007

[36]

Gerasimidis

, Virot

, Hutchinson J

. et al.

On establishing buckling knockdowns for imperfection-sensitive shell structures

Journal of Applied Mechanics, 2018,85(9):091010

[37]

NASA.

Buckling of thin-walled doubly curved shells

NASA Space Vehicle Design Criteria, National Aeronautics and Space Administration, Washington DC, 1969. Technical Report No. NASA SP-8032

[38]

Seide

, Weingarten

On the buckling of circular cylindrical shells under pure bending

Journal of Applied Mechanics, 1961,28(1):112

[39]

Hutchinson

Axial buckling of pressurized imperfect cylindrical shells

AIAA Journal, 1965,3(8):1461-1466

[40]

Babcock Jr C

The influence of the testing machine on the buckling of cylindrical shells under axial compression

International Journal of Solids and Structures, 1967,3(5):809-817

[41]

Riks

The application of Newton's method to the problem of elastic stability

J Appl Mech, 1972,39(4):1060-1066

[42]

Brush

, Almroth

Buckling of Bars, Plates and Shells

New York: McGraw-Hill, 1975

[43]

Arbocz

, Sechler

On the buckling of stiffened imperfect cylindrical shells

AIAA Journal, 1976,14(11):1611-1617

[44]

Arbocz

Past, present and future of shell stability analysis. Delft University of Technology

Zeitschrift für Flugwissenschaften und Weltraumforschung, 1981,5(6):335-348

[45]

Arbocz

. Potier-Ferry

, Singer

, et al.

Buckling and Post-Buckling

Berlin Heidelberg: Springer, 1987

[46]

Singer

Buckling Experiments: Experimental Methods in Buckling of Thin-walled Structures

New York: John Wiley & Sons Inc, 1998

[47]

Singer

Buckling experiments: Experimental methods in buckling of thin-walled structures

Applied Mechanics Reviews, 2002,56(1):B5

[48]

Bushnell

. Shell buckling. http://shellbuckling.com/index.php. 2004

URL

[49]

Van Slooten

, Soong

Buckling of a long, axially compressed, thin cylindrical shell with random initial imperfections

Journal of Applied Mechanics, 1972,39(4):634-635

[50]

Narasimhan

, Hoff

Snapping of imperfect thin-walled circular cylindrical shells of finite length

Journal of Applied Mechanics, 1971,38(1):162-171

[51]

Tennyson

, Muggeridge

, Caswell

New design criteria for predicting buckling of cylindrical shells under axial compression

Journal of Spacecraft & Rockets, 1971,8(10):1062-1067

[52]

Almroth

, Holmes

AMC

, Brush

An experimental study of the bucking of cylinders under axial compression

Experimental Mechanics, 1964,4(9):263-270

[53]

周承倜

. 薄壳弹塑性稳定性理论. 北京: 国防工业出版社, 1979

( Zhou

Chengti

. Elastic Plastic Stability Theory of Thin Shells. Beijing: National Defense Industry Press, 1979 (in Chinese))

[54]

Krasovsky

, Marchenko

, Schmidt

Deformation and buckling of axially compressed cylindrical shells with local loads in numerical simulation and experiments

Thin-Walled Structures, 2011,49(5):576-580

[55]

Haynie

, Hilburger

, Bogge

, et al.

Validation of lower-bound estimates for compression-loaded cylindrical shells 53rd AIAA/ASME/ASCE/AHS/ASC Structures,

Structural Dynamics and Materials Conference, 2012

[56]

Thompson

JMT

Advances in shell buckling: Theory and experiments

International Journal of Bifurcation And Chaos, 2015,25(01):1530001

[57]

Virot

, Kreilos

, Schneider

. et al.

Stability landscape of shell buckling

Phys. Rev. Lett., 2017: 119

DOI URL PMID [本文引用: 12]

The reference chiral helimagnet MnSi is the first system where Skyrmion lattice correlations have been reported. At a zero magnetic field the transition at T_{C} to the helimagnetic state is of first order. Above T_{C}, in a region dominated by precursor phenomena, neutron scattering shows the buildup of strong chiral fluctuating correlations over the surface of a sphere with radius 2pi/l, where l is the pitch of the helix. It has been suggested that these fluctuating correlations drive the helical transition to first order following a scenario proposed by Brazovskii for liquid crystals. We present a comprehensive neutron scattering study under magnetic fields, which provides evidence that this is not the case. The sharp first order transition persists for magnetic fields up to 0.4 T whereas the fluctuating correlations weaken and start to concentrate along the field direction already above 0.2 T. Our results thus disconnect the first order nature of the transition from the precursor fluctuating correlations. They also show no indication for a tricritical point, where the first order transition crosses over to second order with increasing magnetic field. In this light, the nature of the first order helical transition and the precursor phenomena above T_{C}, both of general relevance to chiral magnetism, remain an open question.

[58]

徐春杰, 张浩, 许帅

等.

易拉罐用铝基和铁基材料组织与力学性能对比研究

铸造技术, 2018,314(5):14-17

( Xu

Chunjie

, Zhang

Hao

, Xu

Shuai

, et al.

Comparative on microstructure and mechanical properties of Al-based and iron-based materials for pop-top cans

Foundry Technology. 2018,314(5):14-17 (in Chinese))

[59]

李魏梓, 宋昕宜, 杨凯

等.

易拉罐轴向受压失稳试验研究及有限元分析

制造业自动化, 2014,15:83-85, 101

( Li

Weizi

, Song

Xinyi

, Yang

Kai

, et al.

The research and finite-element analysis of axial collapse of pop can

Manufacturing Automation. 2014,15:83-85, 101 (in Chinese))