引言
自1948年Mott[1]首次对材料动态断裂行为进行定量分析, 动态断裂力学发展至今已有70余年历史. 基于准静态断裂力学的断裂韧性表征方法及测试方法, 为测试材料在动态加载下的断裂性能, 研究者们采用各种冲击试验装置对断裂试验件进行冲击试验, 并归纳出一系列动态断裂性能测试方法. 目前材料动态断裂性能研究主要试验方法以下3种试验方法.
(2) 落锤试验方法. 落锤试验机的冲击速度取决于锤头落下的高度, 一般为5$\sim$15 m/s, 通过在锤头安装精密传感器, 并用计算机进行自动采集数据, 将试验过程中的载荷-位移曲线记录下来, 测量试验中的动态$K_{\rm ID}$.
综上所述, 材料动态断裂力学研究中, 弹塑性断裂依然采用$J$积分进行表征, 脆性断裂采用$K$因子进行表征. 随着加载速度的提高, 含裂纹构元会逐渐由弹塑性断裂向脆性断裂转变, 然而在中低加载速率范围内: (1)材料随加载率变化的韧脆转变过程在过去鲜有研究, 材料随加载率变化的韧脆转变机理也并不清晰; (2)面内约束和面外约束变化对材料动态韧脆转变速率的影响也罕见报告; (3)材料韧性断裂$J$-$R$阻力曲线测量方法需进一步开发.
本文运用高速材料试验机, 测试了15MnTi钢和11MnNiMo钢在中低加载速率下的动态韧脆转变过程, 以及裂尖约束对金属材料动态韧脆转变速率的影响, 并基于高速材料试验机的特点设计试验夹具以测量材料在较低加载率下的动态断裂韧性, 测量了15MnTi钢在0.5 m/s加载速率以内的$J$-$R$阻力曲线, 以期为结构抗冲击完整性评估提供参考数据.
1 金属材料动态韧脆转变现象研究
选用15MnTi钢和11MnNiMo钢两种低合金高强钢作为试验材料, 试验采用50 mm $\times$ 48 mm $\times$ 20 mm的CT试样, 试样件的裂纹深度$a_{0}$/$w$在0.55$\sim$0.6之间, 试样的设计及裂纹预制满足GB/T 21143—2014《金属材料准静态断裂韧度的统一试验方法》的标准.
15MnTi钢和11MnNiMo钢的动态断裂性能试验在中国核动力研究设计院的Instron VHS 160/100-20高速材料试验机上进行(如图1所示), 该试验机可实现加载速率在0.001$\sim$20 m/s区间的稳定控制, 实现低速 $\to$ 中速 $\to$ 高速的全速率恒定加载. 基于Instron VHS高速材料试验机的夹持特点设计了紧凑拉伸CT试验夹具, 如图2所示. 通过销钉将CT试样安装于上下夹具中, 上夹具与下夹具之间放置一块平板用以固定上夹具的位置. 下夹具固定于高速材料试验机静夹面中, 上夹具和动夹面的间隙控制在0.1$\sim$0.15 mm之间, 拧紧动夹面的拉杆螺母, 使动夹具产生预紧力. 试验中, 高速材料试验机作动缸向上升, 楔形块到导向杆处被打掉, 动夹面通过预紧力将试验件上部夹紧, 实现紧凑拉伸CT试验件的高速加载. 高速材料试验机可记录下动态断裂试验中的载荷($F$)-加载点位移($v)$曲线, 通过该曲线并结合材料的断面扫描电子显微镜(SEM)分析, 可确定材料的动态断裂脆断速率. 在准静态试验中, 普遍认为标准试样断面的韧性区长度低于0.5 mm为脆性断裂, 本试验中也采用断面韧性区的长度低于0.5 mm作为材料是否出现脆性断裂的最终判断.
图1
图2
图2
Instron VHS高速材料试验机紧凑拉伸(CT)断裂试验装置
Fig.2
Compact tension (CT) facture test equipment of Instron VHS material testing machine
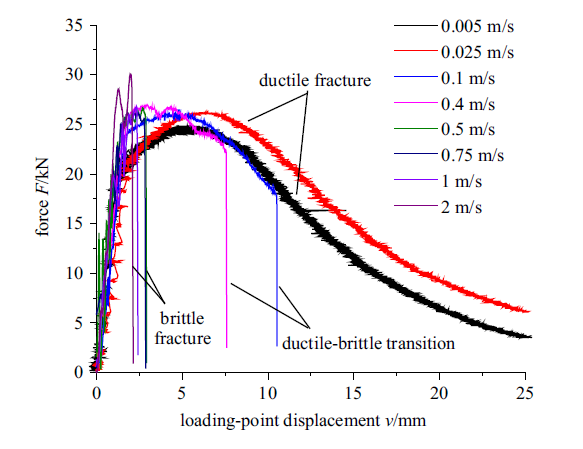
15MnTi钢CT试样件随加载速率变化的$F$ - $v$如图3所示, 由该图可知15MnTi钢CT试样件在0.005 m/s和0.025 m/s的低速加载下呈现出完全韧性断裂的特性; 当加载速率提高到0.1 m/s时, 断裂进入韧脆结合区, 断裂方式呈现出先韧性断裂后脆断的特点; 加载速率提高至0.5 m/s以后, CT试样呈现出脆性断裂的特点.
图3
图3
15MnTi钢CT试样随加载速率韧脆转变过程
Fig.3
Process of ductile-brittle transition of CT specimen of 15MnTi steel with different loading velocities
对15MnTi钢CT试验件在不同加载速率下的断口进行扫描电镜分析, 如图4所示. 当加载速率为0.005 m/s时CT试样件断口皆为韧窝断口, 此时15MnTi钢CT试样件为完全韧性断裂; 当加载速率提高至0.1 m/s时, CT试样断面的下端为韧窝断口, 上端为解理面断口, 试样件在断裂的过程中首先呈现出韧性断裂后呈现出脆性断裂的特征, 韧性断裂区占断口面积的30%左右, SEM分析结果与试验中的$F$ - $v$曲线吻合; 而加载速率达到0.75 m/s时, 除了初始裂纹预制区附近能发现极少的韧窝断口, 其他断口区域皆为理解面, 此时初始裂纹预制区附近的韧性"条带"已不足0.2 mm, 可以认为此时试样的断裂特性为完全脆性断裂.
图4
图4
15MnTi钢CT试样在不同加载速率下断口扫描电镜图
Fig.4
SEM of CT specimens of 15MnTi steel at various loading velocities
图5
图5
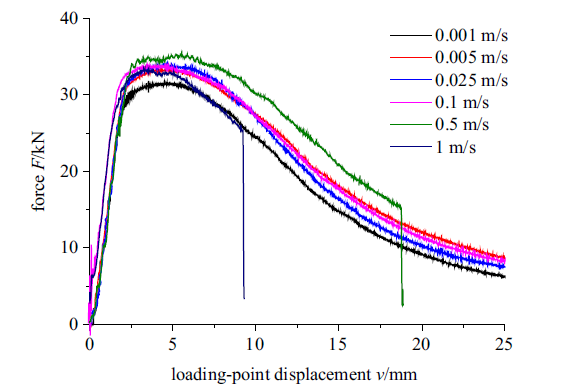
11MnNiMo钢CT试样在加载速率为0$\sim$1 m/s的$F$ - $v$曲线
Fig.5
$F$ - $v$ curves of CT specimen of 11MnNiMo steel with loading velocities from 0 to 1 m/s
图6
图6
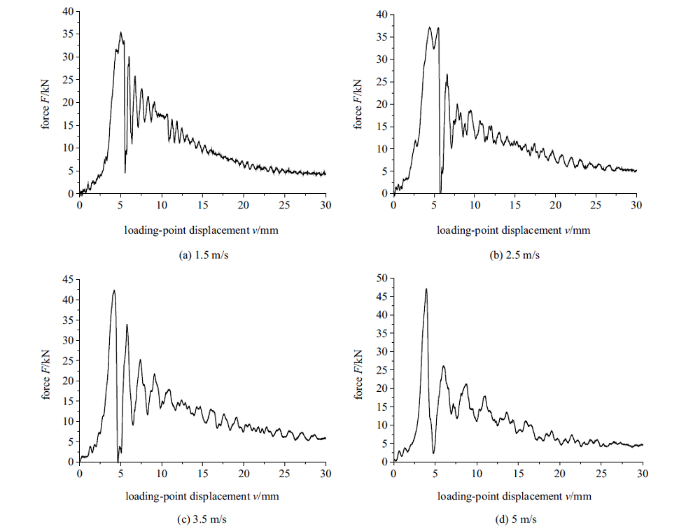
11MnNiMo钢CT试样在1.5$\sim$5 m/s加载速率区间的动态断裂特性
Fig.6
Dynamic fracture character of CT specimen of 11MnNiMo steel with velocities of 1.5$\sim$5 m/s
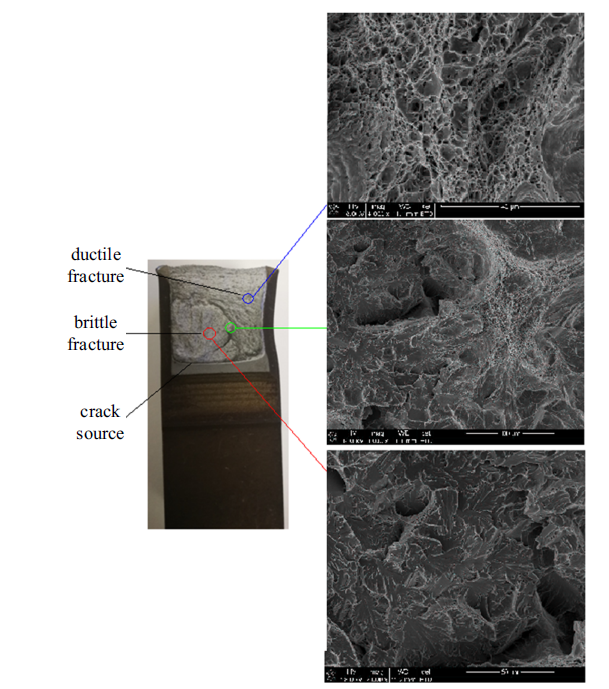
对11MnNiMo钢CT试验件在3.5 m/s速率加载后的断面进行扫描电子显微镜分析, 如图7所示, 发现断面的左下部分为1/4圆形脆性断裂区, 断面的右部和上部为韧性断裂区, 脆性断裂区清晰可见裂纹源. 结合11MnNiMo钢CT试验件在3.5 m/s速率加载下的载荷-加载点位移曲线, 可分析该含裂纹构元在较高速率加载下, 呈现出分层断裂的现象: 当外力加载到一定值时, CT试样件从裂纹源产生脆性断裂, 当脆性断裂发展到断面的韧脆交界区时, 试样在这一断层开始进入韧性断裂区, 试验中的载荷曲线升高, 直到这一层撕裂完成进入下一断裂层, 周而复始直至进入完全韧性开裂区.
图7
图7
11MnNiMo钢CT试样件3.5 m/s加载下的断面扫描电镜分析
Fig.7
SEM of CT specimen of 11MnNiMo steel at loading velocity of 3.5 m/s
金属材料CT试样件随加载速度的冲击断裂韧脆转变与金属材料夏比试验随温度的韧脆转变存在一定差异. 金属材料夏比试验断口, 靠近缺口下部为纤维区, 断口中部为放射区, 断口左右两端为剪切唇, 远离缺口的上部为剪切唇及二次纤维区, 其中纤维区和剪切唇区为韧性断裂, 放射区为脆性断裂. 夏比试验中, 靠近缺口的部分受力最大, 在该部分的晶界、某些夹杂物、第二相粒子或缺陷破裂形成显微空洞. 随着应力的提高, 空洞不断长大, 相互连接, 同时还产生新的空洞, 使裂纹缓慢地长大, 并在断口留下纤维状的区域. 当裂纹扩展到放射区后, 裂纹由缓慢扩展向快速的不稳定扩展转化, 断裂到最后的阶段是形成剪切唇, 剪切唇也是裂纹做快速不稳定扩展, 但剪切唇整个区域有很大的塑性变形. 在金属材料夏比试验随温度的韧脆转变中, 当试验温度进入韧脆转变区后, 随着试验温度的降低断口中部放射区的面积增大, 断口的纤维区和剪切唇面积缩小. 而金属材料CT试样件的动态断裂为分层断裂, 当加载速度提高之后, 裂纹扩展的塑性功降低, 导致解理断裂应力值减小, 从而有利于解理裂纹的萌生与扩展[45]. 对15MnTi钢, 随着加载速度的提高, 产生解理断裂所需的应力值越来越小, 15MnTi钢CT试样件在加载的过程中, 位错不断产生繁殖和塞积, 当加载速率提高之后, 产生解理断裂所需的位错塞积越来越低, 故随着加载速度的提高, 脆性断裂区面积越来越大, 越来越靠近裂纹预制区, 直到完全生成脆性断裂. 而11MnNiMo钢, 当加载速率提高到1.5 m/s以后, 材料在该层的脆性断裂后却进入了塑性扩展区, 其断裂机理有待于进一步研究, 该断裂现象的解释需要和材料科学家们沟通和融合.
采用三点弯曲试验研究裂尖约束对金属材料动态韧性转变速率的影响, 图8为基于Instron VHS 160/100-20高速材料试验机设计的三点弯曲动态加载试验装置, 试验采用100 mm $\times$ 20 mm $\times$ 20 mm的三点弯曲试样, 试样件的裂纹尺寸(初始裂纹长度与试样宽度的比)约为0.55, 三点弯曲试样的设计及裂纹预制满足GB/T 21143—2014 《金属材料准静态断裂韧度的统一试验方法》的标准.
图8
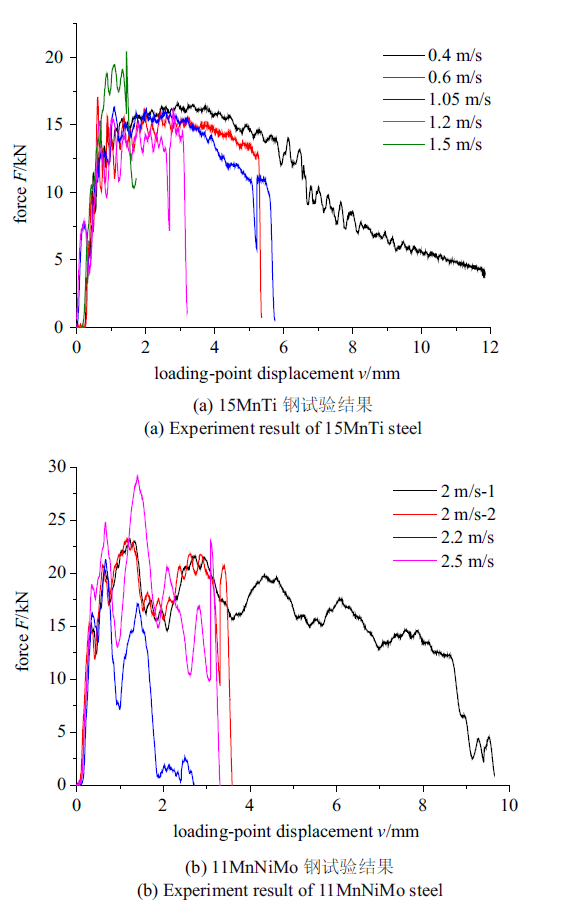
20 mm厚度、裂纹尺寸0.55的15MnTi钢和11MnNiMo钢三点弯曲试样件随加载速度变化的载荷($F$) -加载点位移($v)$如图9所示, 此时15MnTi钢的脆断速率为1.2 m/s, 11MnNiMo钢的脆断速率为2 m/s.
图9
图9
20 mm厚度、裂纹尺寸0.55的15MnTi钢和11MnNiMo钢三点弯曲试验结果
Fig.9
Experiment results of 15MnTi and 11MnNiMo steel with depth of 20 mm and crack size of 0.55
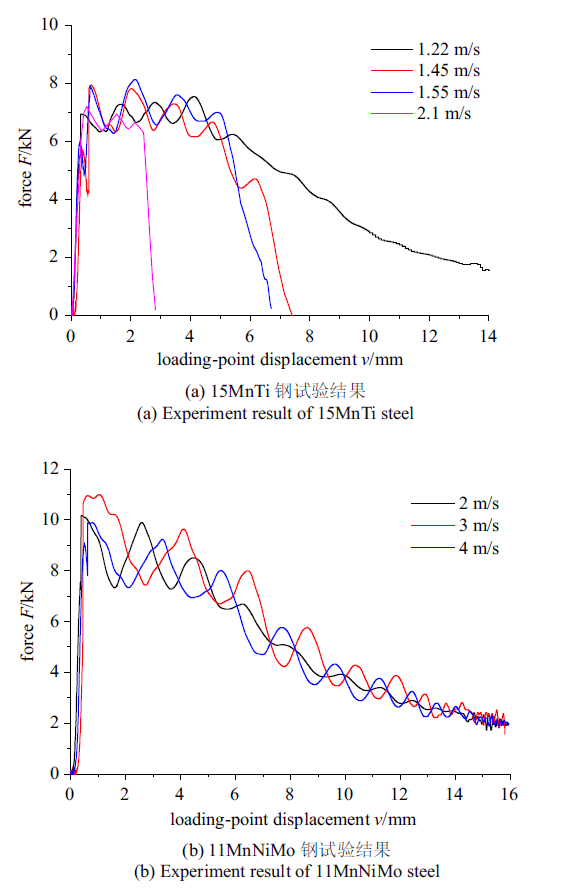
将15MnTi钢和11MnNiMo钢三点弯曲试样件的裂纹尺寸不变, 试样件的厚度缩减为10 mm时, 10 mm厚度、裂纹深度0.55的15MnTi钢和11MnNiMo钢三点弯曲试样件随加载速度变化的$F$ - $v$曲线如图10所示, 15MnTi钢的脆断速率由1.2 m/s提高至2.1 m/s, 11MnNiMo钢由2 m/s完全脆断提升至4 m/s依然完全韧性断裂. 从以上试验可知, 面外约束的升高会极大地降低材料的动态脆断速率.
图10
图10
10 mm厚度、裂纹尺寸0.55的15MnTi钢和11MnNiMo钢三点弯曲试验结果
Fig.10
Experiment results of 15MnTi and 11MnNiMo steel with depth of 10 mm and crack size of 0.55
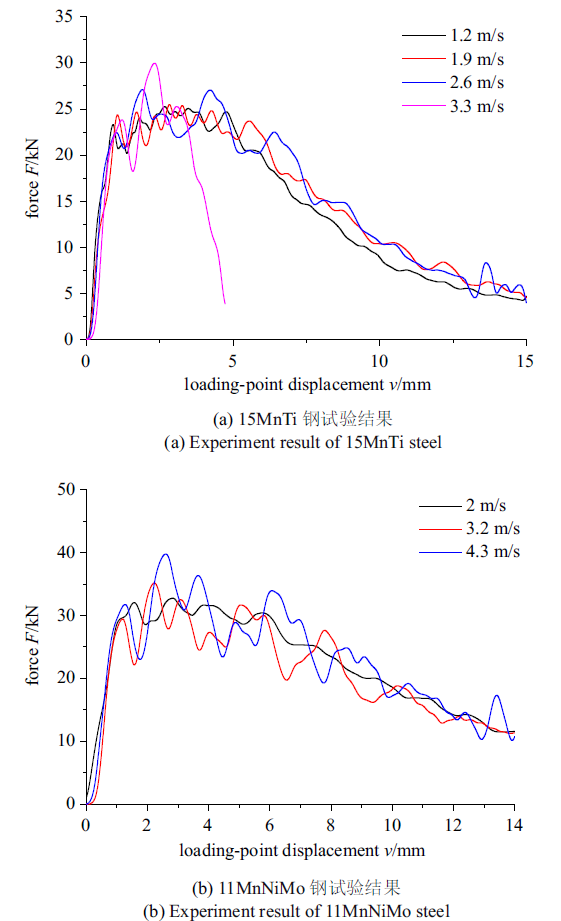
将15MnTi钢和11MnNiMo钢三点弯曲试样件的厚度保持为20 mm, 裂纹尺寸由0.55降至0.35, 20 mm厚度、裂纹深度0.35的15MnTi钢和11MnNiMo钢三点弯曲试样件随加载速度变化的$F$ - $v$曲线如图11所示, 15MnTi钢的脆断速率由1.2 m/s提高至3.3 m/s, 11MnNiMo钢由2 m/s完全脆断提高至4.3 m/s依然完全韧性断裂. 可知面内约束的升高也会极大地降低材料的动态脆断速率.
图11
图11
20 mm厚度、裂纹尺寸0.35的15MnTi钢和11MnNiMo钢三点弯曲试验结果
Fig.11
Experiment results of 15MnTi and 11MnNiMo steel with depth of 20 mm and crack size of 0.35
以上试验结果显示, 金属材料动态韧脆转变速率受裂纹尖端约束的影响非常敏感, 裂纹尖端约束的提高会导致金属材料动态脆断速率的下降. 在下一步的工作中, 有必要进一步研究裂纹尖端约束因子与材料动态脆断速率(或脆断时的裂尖应变率)之间的对应关系.
2 延性金属材料较低加载速率下动态断裂韧性的测量
准静态试验中, 延性金属材料可以通过多试样法、卸载柔度法及载荷分离法等试验方法获取材料的$J$-$R$阻力曲线, 无论哪种方法, 都要获得试验中裂纹扩展量和开裂所吸收能量(或$J$积分)之间的对应关系. 但动态试验中, 试验不能中途停止, 裂纹扩展量和开裂能之间的关系难以获取, 导致延性金属材料在冲击下的$J$-$R$阻力曲线无法较为准确的测量. 本文提出了一种采用加载辊刹车的试验方法, 通过调节加载辊在试验结束时所停留的位置, 基于高速材料试验机的特点采用多试样法实现材料在中低加载速率下的动态断裂韧性测量, 测试了15MnTi钢三点弯曲试样在中低加载率下的$J$-$R$阻力曲线.
图8为基于Instron VHS 160/100-20高速材料试验机设计的三点弯曲加载试验装置, 试验中上夹具辊以设定的速度压入试验中的试样件, 停在终点位置后再回弹一定距离, 此时材料试验机会记录下试验中的时间-加载点位移-载荷曲线, 对试验后的试样通过热着色的方法获得试验中的裂纹扩展量, 建立本次试验中吸收能量(或$J$积分)与裂纹扩张量$\Delta a$之间的对应关系. 改变试验中上夹具辊的长度, 上夹具辊在试验结束时所停的位置会发生改变, 此时试样件张开的夹角也会发生变化, 改变试验件的裂纹扩展量. 通过多试样法, 测量试样在不同裂纹扩展量下对应的加载点位移-载荷曲线, 拟合材料在冲击加载下的$J$-$R$阻力曲线.
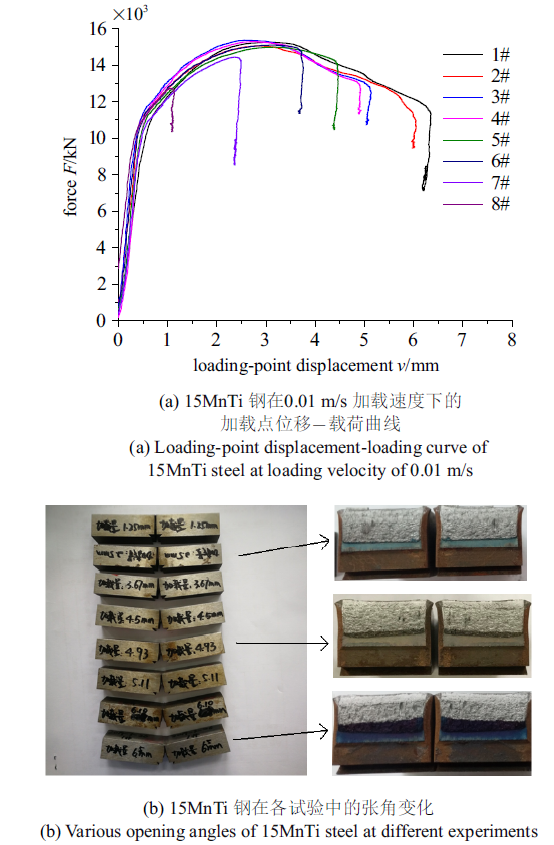
运用上述试验装置和试验方法, 测量了15MnTi钢在0.01 m/s, 0.05 m/s和0.25 m/s加载速率下的$J$-$R$阻力曲线. 试验选用86 mm $\times$ 20 mm $\times$ 20 mm的三点弯曲试样, 试样件的剩余韧带长度约为8 mm. 图12为15MnTi钢在0.01 m/s加载速度下的加载点位移-载荷曲线及试验后的试样张开角度, 通过加载点位移-载荷曲线可以获得外力加载的塑性分量$U_{\rm p}$, 对试验后的试样通过热着色的方法获得试验中的裂纹扩展量$\Delta a$.
图12
图12
15MnTi钢三点弯曲试样在0.01 m/s加载速度下的试验结果
Fig.12
Experimental result of SEB specimen of 15MnTi steel at compression velocity of 0.01 m/s
借鉴准静态断裂试验中$J$积分的拟合公式计算动态试验中的$J$积分
式中, $F$为荷载点载荷, $S$为跨距, $B$为试样的厚度, $B_{\rm N}$为试样侧槽的厚度,
$W$为试样的高度, $a_{0}$为裂纹初始长度, $\Delta a$为裂纹扩展量, $a$为裂纹长度, $g_{1}({a}/{W})$的值可通过GB/T 21143—2014 附录B查阅, 为材料的泊松比, $E$为材料的弹性模量, $U_{\rm p}$为塑性功分量. 通过上述计算公式, 测量了15MnTi钢三点弯曲试样在0.01 m/s加载速率下的$J$积分与裂纹扩展量$\Delta a$对应关系, 当$\Delta a$分别为0.315, 0.871, 1.169, 1.794, 2.106, 2.644, 2.755 mm时, $J$积分分别为299.13, 626.96, 911.82, 922.93, 1104.38, 1275.85, 1298.10 MPa$\cdot$mm.
动态断裂普遍采用试验所测得$K$因子除以试样脆性断裂的时间$t$表征试验中的加载率($\dot{K}$), 采用加载率进行表征既可以反应试验中的外载荷加载速度, 也可以反应试验中样品约束对结果的影响. 本试验中, 由于15MnTi钢在较低加载速率下为韧性断裂, 选择采用试验中裂纹扩展量$\Delta a$最低的那组试验所测$J$积分除以外载荷加载时间$t$, 也就是$J$积分的变化率表征本试验中的加载率($\dot{J})$. 15MnTi钢三点弯曲试样在0.01 m/s加载速率的试验中, 试验中裂纹扩展量$\Delta a$最低值为0.315 mm, 外载荷加载时间为0.242 9 s, $J$积分为299.13 MPa$\cdot$mm, 计算可得15MnTi钢三点弯曲试样在0.01 m/s加载速率下的$J$积分变化加载率$\dot{J}$为1232 MPa$\cdot$mm/s. 15MnTi钢三点弯曲试样在0.01 m/s加载速率($\dot{J} =1232$ MPa$\cdot$mm/s)下的$J$-$R$阻力曲线如图13所示.
图13
图13
15MnTi钢三点弯曲试样在0.01 m/s加载速率($\dot{J} =1232$ MPa$\cdot$mm/s)下的$J$-$R$阻力曲线
Fig.13
$J$-$R$ resistance curve of SEB specimen of 15MnTi steel at loading velocity of 0.01 m/s ($\dot{J} =1232$ MPa$\cdot$mm/s)
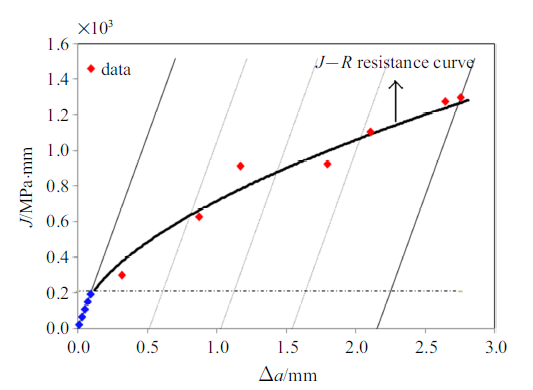
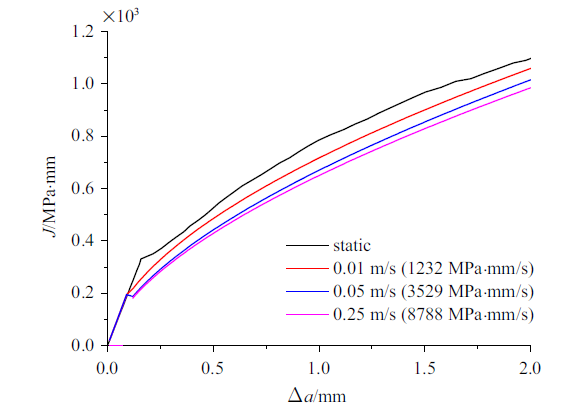
15MnTi钢三点弯曲试样在0.05 m/s和0.25 m/s加载速度下的$J$积分与裂纹扩展量$\Delta a$对应关系, 如表1所示, 分别对应$J$积分变化加载率$\dot{J} $为3529 MPa$\cdot$mm/s和8788 MPa$\cdot$mm/s. 拟合15MnTi钢在0.05 m/s ($\dot{J} =3529$ MPa$\cdot$mm/s)和0.25 m/s ($\dot{J} =8788$ MPa$\cdot$mm/s)下的$J$-$R$阻力曲线并与15MnTi钢在准静态和0.01 m/s ($\dot{J} =1231.5$ MPa$\cdot$mm/s)下的$J$-$R$阻力曲线进行对比, 如图14所示, 可知在8788 MPa$\cdot$mm/s加载率以内, 15MnTi钢的断裂韧性随加载率的提升呈现出缓慢下降的趋势.
表1 15MnTi钢三点弯曲试样在0.05 m/s ($\dot{J}=3529$ MPa$\cdot$mm/s)和0.25 m/s ($\dot{J} =8788$ MPa$\cdot$mm/s)加载速率下的$J$积分与裂纹扩展量$\Delta a$对应关系
Tab.1
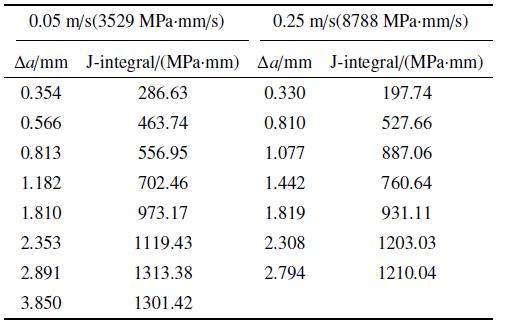 |
图14
图14
15MnTi钢三点弯曲试样在8788 MPa$\cdot$mm/s加载率以内的断裂韧性随加载率变化趋势
Fig.14
Fracture toughness of SEB specimen of 15MnTi steel under the loading rate of 8788 MPa$\cdot$mm/s
采用上述上夹具辊刹车, 通过调节压缩杆长度改变试验中裂纹扩展量的试验方法, 只适用于测量延性金属材料在中低加载率下的动态断裂韧性. 试验中, 上夹具辊以设定速度压入试样, 试验结束时上夹具辊将试样压至一定角度, 上夹具辊速度降为0.上夹具辊在压入试样时会经历从压入速度降至速度为0的过程, 压入速度越大刹车距离越长, 试验过程中速度的匀速段越短, 故该试验方法只适用于材料在较低加载速率内的动态断裂韧性测量, 需对该试验方法所适用的速度范围进行讨论.
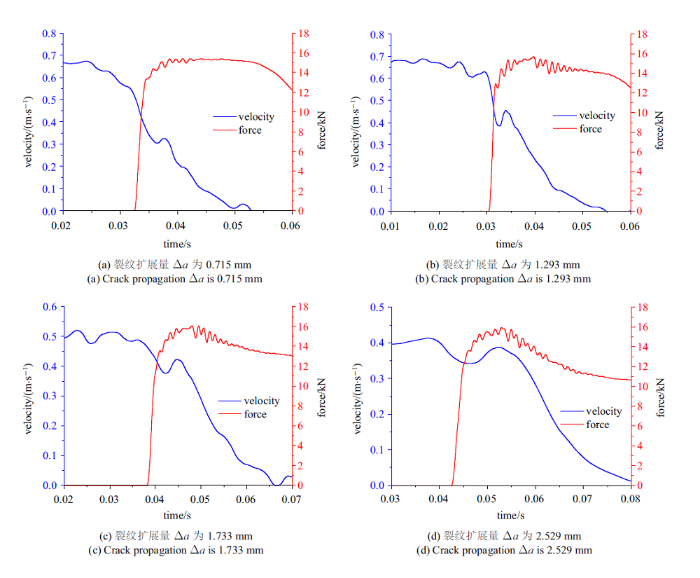
图15为15MnTi钢三点弯曲试样件在0.4 m/s加载速率下, 不同裂纹扩展量所对应的时间-载荷-加载速度曲线. 本文暂且只考虑裂纹在稳定扩展段(载荷从0增至最大值区间)的速度变化过程, 裂纹失稳扩展段的速度变化暂且不考虑. 15MnTi钢三点弯曲试样件裂纹扩展量为0.715 mm时, 由于试验的加载距离短, 当上夹具辊刚接触到三点弯曲试样件时, 上夹具辊已经处于速度下降区间, 为将裂纹在稳定扩展段的平均速度控制到0.4 m/s, 本试验的初始加载速率需设定为0.7 m/s. 同理, 裂纹扩展量为1.293 mm时, 为让裂纹在稳定扩展段的平均速度达到0.4 m/s, 试验的初始加载速率也需设定为0.7 m/s. 当裂纹扩展量增大为1.733 mm时, 可将初始加载速率设定为0.5 m/s时, 此时裂纹在稳定扩展段的加载速度在0.4 m/s左右. 而裂纹扩展量增至2.529 mm后, 由于试验中的加载位移较大, 初始加载速率可设定为0.4 m/s, 裂纹的稳定扩展段速度大致在0.4 m/s上下的范围.
图15
图15
15MnTi钢三点弯曲试样件在0.4 m/s平均加载速度下, 不同裂纹扩展量所对应的时间-载荷-加载速度曲线
Fig.15
Time-loading-velocity curves matching different crack propagation values of 15MnTi steel SEB samples under average loading velocity of 0.4 m/s
本试验中, 裂纹在失稳扩展阶段速度的不断降低也会影响材料动态断裂韧性测试的结果, 拉低试验中外力加载的整体速度, 改变裂纹扩展过程中的速度均衡性. 在仅考虑裂纹稳定扩展段区域的前提下, 为实现该试验区域加载平均速度达到0.4 m/s, 对裂纹扩展量小于约2 mm的试验, 只能通过提高初始加载速度的方法实现. 在不考虑裂纹失稳扩展阶段速度递减的前提下, 该试验方法测量韧性金属材料动态$J$-$R$阻力曲线的速度不建议超过0.4 m/s. 若要测量韧性金属材料在更高加载速度下的动态$J$-$R$阻力曲线, 需通过试验夹具的改进降低上夹具辊"刹车"所需的时间, 尽可能保证试验过程中加载速度的一致性.
3 总结
本文采用Instron高速材料试验机, 测量了冲击下15MnTi钢和11MnNiMo钢CT试样件的动态韧脆转变过程; 研究了面内约束和面外约束变化对金属材料动态韧脆转变速率的影响; 采用上夹具辊刹车, 通过调节压缩杆长度改变试验中裂纹扩展量的试验方法, 测量了15MnTi钢在较低加载速率下的动态断裂韧性. 本文发现以下现象:
(1) 15MnTi钢CT试样在加载速率低于0.025 m/s时呈现出全韧性断裂的特点; 当加载速率提高到0.1 m/s时, 断裂进入韧脆转变区, 断裂方式呈现出先韧性断裂后脆断的特点; 加载速率提高至0.5m/s以后, CT试样开始进入脆性断裂区.
(2) 11MnNiMo钢CT试样在加载速率低于0.1 m/s时为完全韧性断裂, 加载速率在0.5$\sim$1 m/s时为韧-脆结合型断裂, 韧-脆区分布与15MnTi钢一致; 11MnNiMo钢CT试样加载速率在1.5$\sim$5 m/s时, 载荷曲线呈现出锯齿波的特性, 呈现出分层断裂的现象, 在每一层的断裂过程中出现先脆断后韧段的现象.
(3) 金属材料CT试样件的动态断裂韧脆转变与金属材料夏比试验随温度的韧脆转变存在一定差异. 金属材料夏比试验随温度的韧脆转变中, 当试验温度进入韧脆转变区后, 断口中部放射区的面积增大. 而金属材料CT试样件的动态断裂为分层断裂, 随着加载速率的提高, 产生解理断裂所需的应力值越来越小, 直到完全生成脆性断裂.
(4) 金属材料的动态韧脆转变速率受裂尖约束的影响非常明显. 面内约束和面外约束的升高, 都会导致材料动态脆断速率出现明显降低.
(5) 采用加载辊刹车的试验方法, 通过调节压缩杆长度改变试验中裂纹扩展量, 采用多试样法在高速材料试验机上测量了15MnTi钢三点弯曲试样在8788 MPa$\cdot$mm/s加载率内的$J$-$R$阻力曲线, 发现15MnTi钢在该加载率范围内断裂韧性随加载率的提升呈现出缓慢下降的趋势. 并对该动态断裂韧性测试方法的适用范围进行了分析, 建议试验中的外界平均加载速度不超过0.4 m/s, 该方法适用于延性金属材料在较低加载率下的$J$-$R$阻力曲线测量.
参考文献
Fracture toughness measurements by instrumented impact test
A dynamic analysis of modifier compact-tension specimen using homolite-100 and polycarbonate plates
基于夏比冲击吸收能量的断裂韧性估算方法比较
Comparison of fracture toughness estimation methods based on charpy impact energy
$-$196${^\circ}$奥氏体不锈钢母材与焊缝的动态断裂韧性
Dynamic fracture toughness of S30408 austenitic stainless steel base and weld metals at $-$196${^\circ}$
Effect of loading rate and constraint on dynamic ductile fracture toughness of P91 steel
The behavior of notched bend specimens in impact testing
On the measurement of dynamic fracture toughness-a review of recent work
超强钢18NiC250在不同加载速度下的断裂韧性
Fracture toughness of ultra-strength steel 18NiC250 at different loading rate
弹塑性材料裂纹扩展的动态$J$阻力曲线实验研究简介
Brief introduction of experimental study on the dynamic $J$-resistance curve of crack growth of elastic-plastic material
加载速度对高强钢40Cr和30CrMnSiNi2A I型动态断裂韧性的影响
Effect of loading rate on mode I dynamic fracture toughness of high strength steels 40Cr and 30CrMnSiNi2A
45#钢动态断裂韧性测试的试验研究
Experimental study of dynamic fracture toughness of 45# steel
Determination of dynamic fracture parameters using a semicircular bend technique in split Hopkinson pressure bar testing
Size effect on the contact between fracture specimen and supports in Hopkinson bar loaded fracture test
A semi-circular bend technique for determining dynamic fracture toughness
用Hopkinson杆技术研究材料动态断裂韧性的进展
Progress in the research of dynamic fracture toughness based on Hopkinson bar technique
一种基于SHTB的II型动态断裂实验技术
A modified mode II dynamic fracture test technique based on SHTB
Determination of stress intensity factors in halfplane containing several moving cracks
用裂纹张开位移计算三点弯曲试样的动态应力强度因子
Calculation of DSIF of three point bending specimen using the method of DCOD
An experimental method for determining dynamic fracture toughness
A method for dynamic fracture toughness determination using short beams
冲击载荷下三点弯曲试样的有限元分析
Finite element analysis on three-point bending sample loaded by impact loading
三点弯曲试样动态冲击特性的有限元分析
Dynamic behavior of three point bending specimen under impact loading by using finite element method
Dynamic measurements of initiation toughness at high loading rates
Impact response of a finite crack in plane extension
Simple formula for dynamic stress intensity factor of pre-crack charpy specimen
Estimation of the dynamic J-R curve from a single impact bending test//Mechanisms and Mechanics of Damage and Failure of European Conference On Fracture-11, France, vol.3
Evaluation of dynamic fracture toughness of cold worked 9Cr-1Mo steel
Dynamic fracture toughness and Charpy transition properties of a sevice-exposed 2.25Cr-1Mo reheater header pipe
Dynamic fracture toughness behavior of armor-grade Q&T steel weldments: Effect of weld metal composition and microstructure
Characterizing dynamic fracture toughness of linepipe steel using the press-notch drop-weight-tear test specimen
船用921A钢动态断裂韧性测试研究
Study of dynamic fracture toughness measurement of 921A shipbuilding steel
Elastic-Plastic analysis of a dynamically loaded circumferentially notched round bar
某船用钢动态弹塑性断裂韧性的试验测试
An experimental measurement for the dynamic elastic-plastic fracture toughness of ship-building steel
An energy-conserving scheme for dynamic crack growth using the extended finite element method
Crack initiation and stable crack growth resistance in a 508 steels in relation to inclusion distribution
Application of split Hopkinson tension bar technique to the study of dynamic fracture properties of materials
Dynamic fracture toughness of high strength metals under impact loading: increase or decrease
Q390钢韧脆转变区冲击吸收功的类主曲线模型
Impact-energy principle resembling master curve model of Q390 steel in transition temperature region
Charpy impact energy facture toughness and ductile-brittle transition temperature of dual-phase 590 steel
12Cr2Mo1R钢的韧脆转变机理
Toughness-brittle transition mechanism of 12Cr2Mo1R steel
高强度钢材Q460C断裂韧性低温试验
Test on the fracture toughness of high-strength steel Q460C at low temperature
Effect of deformation temperature on the ductile-brittle transition behavior of a modified 9Cr-1Mo steel
In-plane and out-of-plane crack-tip constraint effects under biaxial nonlinear deformation
The elastic and plastic constraint parameters for three-dimensional problem
The in-plane and out-of-plane stress constraint factors and K-T-T$_{Z}$ description of stress field near the border of a semi-elliptical surface crack
New constraint parameters based on crack tip plastic zone: The constraint parameters based on crack tip plastic zone: Theoretical derivations and effectiveness verification
Normalization method for evaluating J-resistance curves of small-sized CIET specimen and crack front constraints