引言
由于液体雾化在灭火系统、喷涂工艺、喷墨印刷、涡轮发动机和液体火箭发动机等领域的广泛应用, 气体介质中的液膜不稳定性分析的理论研究受到了持续的关注[1 -3 ] . 在此方向上, 众多学者从不同角度进行了大量的研究. Squire[1 ] 对液体薄层在静止空气中的流动进行了分析, 认为液体薄层在特定情况下可以达到稳定状态, 这一结论由Hagerty[4 ] 通过实验证明, 并提出了两种不稳定模式, 即以反对称波为特征的弯曲模式和以对称波为特征的曲张模式, 并得出了更高的韦伯数和气液密度比使液膜更加不稳定的结论. Lin[5 ] 和Li[6 ] 对此进行了拓展, 对液膜周围气体赋以不同于液膜的速度进行了理论研究. Li和Kelly[7 ] 对无黏液膜的不稳定性进行了研究, Cao和Li[8 ] 以及Zhang[9 ] 进行了黏性液膜的不稳定性分析.
随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大.
因此本文基于漏电介质模型对平面液膜在交流电场下的线性不稳定性分析进行了研究, 在第一节通过控制方程和边界条件描述了理论模型, 并通过线性分析[29 ] 及Floquet理论[30 -35 ] 建立了直流电场及交流电场下的色散方程, 在第二节基于色散方程讨论了电欧拉数、交流电场占比及频率等参数对液膜不稳定性的影响, 并在第三节对文中发现进行了总结. 本工作采用线性分析和Floquet理论, 推导了平面液膜在交流电场下的色散方程并研究了各参数对液膜不稳定性的影响, 以期为交流电场下的平面液膜不稳定性分析和实验提供理论基础和参考数据.
1 理论推导
1.1 模型建立
图1 为本文采用的物理模型, 在横向的交流电场中, 黏性液膜在无黏不可压气体中流动. 液体密度为$\rho_{\rm l}$, 气体密度为$\rho_{\rm g}$, 液体表面张力为$\gamma $, 液膜厚度为$2a$, 主流速度为$U$. 在对液膜的电学特性分析时采用漏电介质模型, 液膜电导率为$\sigma$, 液体介电常数为$\varepsilon_{1}$, 气体介电常数为$\varepsilon_{2}$. 电极板至液膜表面距离为$d$, 施加电压为交流电压$V_{t} =V_{0} \left\{ 1+Pr\left[ \cos \left( \varOmega t \right)-1 \right] \right\}$, 其中$V_{0} $为电压幅值, $Pr$为衡量交流电场部分在整个电场中所占比例的参数, 且在0$\sim$1范围内变动, $\varOmega$为交流电场的振荡频率. 在本文的不稳定性分析中忽略重力、磁场力以及温度的影响.
图1
图1
交流电场中的运动液膜
Fig.1
Schematic diagram of moving liquid sheet in an AC electric field
1.2 直流电场作用下不稳定性分析
(1) $\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,\ \ -a+\eta <y<a+\eta$
(2) $\begin{array}{r}\rho\left[\frac{\partial u}{\partial t}+(U+u) \frac{\partial u}{\partial x}+v \frac{\partial v}{\partial y}\right]=-\frac{\partial p}{\partial x}+ \\\mu\left(\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} v}{\partial y^{2}}\right),-a+\eta<y<a+\eta\end{array}$
(3) $\begin{array}{r}\rho\left[\frac{\partial v}{\partial t}+(U+u) \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}\right]=-\frac{\partial p}{\partial y}+ \\\mu\left(\frac{\partial^{2} v}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}\right),-a+\eta<y<a+\eta\end{array}$
(4) $v=\frac{\partial \eta }{\partial t}+\left( {U+u} \right)\frac{\partial \eta }{\partial x}+v\frac{\partial \eta }{\partial y},\ \ y=\pm a+\eta$
(5) $\mu \left( {\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}} \right)=T_{\rm t1}^{\rm e} ,\ \ y=a+\eta$
(6) $\mu \left( {\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}} \right)=T_{\rm t2}^{\rm e} ,\ \ y=-a+\eta$
气体无黏无旋, 存在势函数$\phi_{\rm g}$. 与液相相似, 有控制方程
(7) $\frac{\partial^{2}\phi_{\rm g} }{\partial x^{2}}+\frac{\partial^{2}\phi_{\rm g} }{\partial y^{2}}=0,\ \ y<-a+\eta\ \ {\rm or}\ \ y>a+\eta$
(8) $\begin{aligned}p_{\mathrm{g}}=&-\rho_{\mathrm{g}}\left\{\frac{\partial \phi_{\mathrm{g}}}{\partial t}+\frac{1}{2}\left[\left(\frac{\partial \phi_{\mathrm{g}}}{\partial x}\right)^{2}+\frac{1}{2}\left(\frac{\partial \phi_{\mathrm{g}}}{\partial y}\right)^{2}\right]\right\} \\& y\langle-a+\eta \text { or } y\rangle a+\eta\end{aligned}$
(9) $v_{\rm g} =\frac{\partial \eta }{\partial t}+u_{\rm g} \frac{\partial \eta }{\partial x}+v_{\rm g} \frac{\partial \eta }{\partial y},\ \ y=a\pm \eta$
(10) $\nabla^{2}V_{\rm g} =0$
(11) $\nabla^{2}V_{\rm l} =0$
(12) $E=-\nabla V$
(13) $V_{\rm g} =V_{0} ,\ \ y=a+\eta$
(14) $V_{\rm g} =0,\ \ y=a+d$
综合电场力、压力、表面张力、黏性的作用, 有边界条件
(15) $-p+2\mu \frac{\partial v}{\partial y}+\gamma \frac{1}{R}-p_{\rm g} -T_{\rm n1}^{\rm e} =0,\ \ y=a+\eta$
(16) $-p+2\mu \frac{\partial v}{\partial y}-\gamma \frac{1}{R}-p_{\rm g} -T_{\rm n2}^{\rm e} =0,\ \ y=-a+\eta$
(17) $\frac{1}{R}=\dfrac{\dfrac{\partial^{2}\eta }{\partial x^{2}}}{\left( {1+\dfrac{\partial^{2}\eta }{\partial x^{2}}} \right)^{{2}/{3}}}$
(18) $\begin{array}{c}\left(u, v, p, \phi_{\mathrm{g}}, p_{\mathrm{g}}, V_{\mathrm{l}}, V_{\mathrm{g}}, \eta\right)=[u(y), v(y), p(y) \\\left.\phi_{\mathrm{g}}(y), p_{\mathrm{g}}(y), V_{1}(y), V_{\mathrm{g}}(y), \eta_{0}\right] \mathrm{e}^{\mathrm{i} k x+\omega t}\end{array}$
其中, $k$为波数, $\omega $为表现不稳定增长的频率, $\eta $为扰动的幅值.
(19) $p\left( y \right)=A_{1}{\rm e}^{ky}+A_{2}{\rm e}^{-ky}$
其中$A_{1} ,A_{2} $为常数, 同理电势函数可表示为
(20) $V_{\rm l} \left( y \right)=P_{1} {\rm e}^{ky}+P_{2} {\rm e}^{-ky}$
(21) $V_{\rm g} \left( y \right)=P_{3} {\rm e}^{ky}+P_{4} {\rm e}^{-ky}$
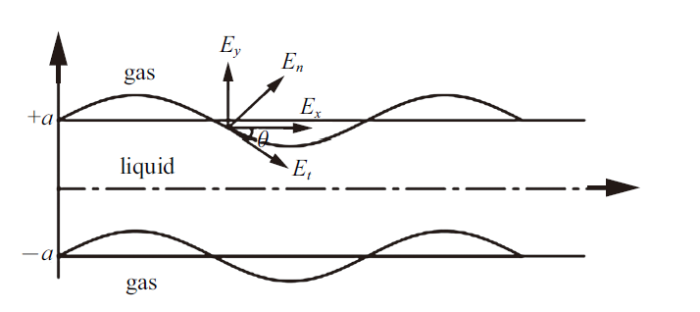
图2 给出了对平面液膜所施加的电场力坐标图, 电场强度可表示为
(22) $E_{\rm t} =E_{x}\cos\theta -E_{y}\sin\theta$
(23) $E_{\rm n} =E_{x}\sin\theta +E_{y}\cos\theta$
图2
图2
电场力坐标图其中
Fig.2
Schematic diagram of electric force vector
(24) $\sin\theta =\frac{\partial \eta }{\partial x}\cos\theta =1$
将式(20)$\sim$式(24)结合式(12)、式(17), 代入麦克斯韦电学公式可算得电场力
(25) $\begin{aligned}T_{\mathrm{t} 1}^{\mathrm{e}}=&\left[\varepsilon_{2} \mathrm{i} k \frac{V_{0}^{2}}{d^{2}} \eta_{0}+\varepsilon_{2} \mathrm{i} k \cdot \frac{V_{0}}{d} P_{3}\left(\mathrm{e}^{k a}+\mathrm{e}^{-k a}\right)\right] \\\mathrm{e}^{\mathrm{i} k x+\omega t}, \quad y=a\end{aligned}$
(26) $\begin{aligned}T_{\mathrm{t} 2}^{\mathrm{e}}=&\left[-\varepsilon_{2} \mathrm{i} k \frac{V_{0}^{2}}{d^{2}} \eta_{0}+\varepsilon_{2} \mathrm{i} k \cdot \frac{V_{0}}{d} P_{3}\left(\mathrm{e}^{k a}+\mathrm{e}^{-k a}\right)\right] \\\mathrm{e}^{\mathrm{i} k x+\omega t}, \quad y=-a\end{aligned}$
(27) $\begin{aligned}T_{\mathrm{n} 1}^{\mathrm{e}} &=\left[\varepsilon_{2} \frac{V_{0}^{2}}{d^{3}} \eta_{0}-\varepsilon_{1} k \frac{V_{0}}{d} P_{1}\left(\mathrm{e}^{k a}-\mathrm{e}^{-k a}\right)\right] \\& \mathrm{e}^{\mathrm{i} k x+\omega t}, \quad y=a\end{aligned}$
将式(25)、式(26)结合式(19), 代入液相边界条件(4)$\sim$(6)可得
(28) $\begin{aligned}u(y) &=B_{1} \mathrm{e}^{l y}+B_{2} \mathrm{e}^{-l y}+\\& \frac{\mathrm{i} k}{\mu\left(k^{2}-l^{2}\right)}\left(A_{1} \mathrm{e}^{k y}+A_{2} \mathrm{e}^{-k y}\right)\end{aligned}$
(29) $\begin{aligned}v(y) &=-\frac{\mathrm{i} k}{l} B_{1} \mathrm{e}^{l y}+\frac{\mathrm{i} k}{l} B_{2} \mathrm{e}^{-l y}+\\& \frac{k}{\mu\left(k^{2}-l^{2}\right)}\left(A_{1} \mathrm{e}^{k y}-A_{2} \mathrm{e}^{-k y}\right)\end{aligned}$
(30) $l^{2}=k^{2}+\frac{\rho}{\mu}(\omega+U \mathrm{i} k)$
(31) $\begin{aligned}A_{1}=&-\frac{\mu}{k}\left(k^{2}+l^{2}\right)(\omega+U \mathrm{i} k) \eta_{0} \frac{1}{2 \cosh (k a)}+\\& \varepsilon_{2} k \frac{V_{0}^{2}}{d^{2}} \eta_{0} \frac{1}{2 \sinh (k a)}+\varepsilon_{2} k \frac{V_{0}}{d} P_{3} \operatorname{coth}(k a)\end{aligned}$
(32) $\begin{aligned}A_{2}=& \frac{\mu}{k}\left(k^{2}+l^{2}\right)(\omega+U \mathrm{i} k) \eta_{0} \frac{1}{2 \cosh (k a)}+\\& \varepsilon_{2} k \frac{V_{0}^{2}}{d^{2}} \eta_{0} \frac{1}{2 \sinh (k a)}+\varepsilon_{2} k \frac{V_{0}}{d} P_{3} \operatorname{coth}(\end{aligned}$
(33) $\begin{aligned}B_{1}=& \frac{\mathrm{i} k l}{k^{2}-l^{2}}(\omega+U \mathrm{i} k) \eta_{0} \frac{1}{\cosh (l a)}-\\& \frac{\mathrm{i} k l \eta_{0} \varepsilon_{2}}{\mu\left(k^{2}-l^{2}\right)} \frac{V_{0}^{2}}{d^{2}} \eta_{0} \frac{1}{2 \sinh (l a)}-\\& \frac{1}{\mu} \varepsilon_{2} \frac{\mathrm{i} k V_{0}}{d\left(k^{2}-l^{2}\right)} P_{3} \frac{\operatorname{coth}(k a)}{\sinh (l a)}\end{aligned}$
(34) $\begin{aligned}B_{2}=&-\frac{\mathrm{i} k l}{k^{2}-l^{2}}(\omega+U \mathrm{i} k) \eta_{0} \frac{1}{\cosh (l a)}-\\& \frac{\mathrm{i} k \ln _{0} \varepsilon_{2}}{\mu\left(k^{2}-l^{2}\right)} \frac{V_{0}^{2}}{d^{2}} \eta_{0} \frac{1}{2 \sinh (l a)}-\\& \frac{1}{\mu} \varepsilon_{2} \frac{\mathrm{i} k V_{0}}{d\left(k^{2}-l^{2}\right)} P_{3} \frac{\operatorname{coth}(k a)}{\sinh (l a)}\end{aligned}$
(35) $\phi_{\rm g1} =-\frac{1}{k}\omega {\rm e}^{ka-ky}{\rm e}^{{\rm i}kx+\omega t}\eta_{0}$
(36) $p_{\rm g1} =\frac{1}{k}\rho_{\rm g} \omega^{2}{\rm e}^{ka-ky}{\rm e}^{{\rm i}kx+\omega t}\eta_{0}$
(37) $\phi_{\rm g2} =\frac{1}{k}\omega {\rm e}^{-ka+ky}{\rm e}^{{\rm i}kx+\omega t}\eta_{0}$
(38) $p_{\rm g1} =-\frac{1}{k}\rho_{\rm g} \omega^{2}{\rm e}^{-ka+ky}{\rm e}^{{\rm i}kx+\omega t}\eta_{0}$
最后, 结合气相液相的运动边界条件和电场界面应力平衡边界条件, 由式(15)、式(25)、式(27), 弯曲模式下的色散方程可由$3\times 3$矩阵表示
(39) $\begin{eqnarray} &&{\rm det}(A)=\\&&\quad\left|\begin{array}{c@{\ \ }c@{\ \ }c} \sigma-\varepsilon_{1}(\omega+U{\rm i}k) & \varepsilon_{2}(\omega+U{\rm i}k) & \dfrac{V_{0}}{2 k d^{2}} \sinh (k a) \\ 2 \cosh (k a) & -2 \cosh (k a) & -\dfrac{V_{0}}{d} \\ 0 & D_{32} & D_{33} \end{array}\right|=0\\&& \end{eqnarray}$
$\begin{aligned}D_{32} &=-\frac{k^{2}+l^{2}}{k^{2}-l^{2}} \varepsilon_{2} \frac{k V_{0}}{d} 2 \cosh (k a) \operatorname{coth}(k a)+\\& 4 \varepsilon_{2} \frac{k^{2} l V_{0}}{d\left(k^{2}-l^{2}\right)} \frac{\cosh (k a)}{\tanh (l a)}+\varepsilon_{2} \frac{2 k V_{0}}{d} \sinh (k a)\end{aligned}$
$\begin{aligned}D_{33} &=-\frac{\left(k^{2}+l^{2}\right)^{2}}{k^{2}-l^{2}} \frac{\mu}{k}(\omega+U i k) \tanh (k a)-\\& \frac{k^{2}+l^{2}}{k^{2}-l^{2}} \varepsilon_{2} \frac{k V_{0}^{2}}{d^{2}} \eta_{0} \operatorname{coth}(k a)-\\& 4 \frac{k^{2} l}{k^{2}-l^{2}} \mu(\omega+U i k) \tanh (l a)+\\& 2 \frac{k^{2} l}{k^{2}-l^{2}} \varepsilon_{2} \frac{V_{0}^{2}}{d^{2}} \operatorname{coth}(l a)-\gamma k^{2}-\\& \frac{1}{k} \rho_{\mathrm{g}} \omega^{2}-\varepsilon_{2} \frac{V_{0}^{2}}{d^{3}}\end{aligned}$
为了使结果更具有普适性, 将色散方程无量纲化, 引入无量纲韦伯数$We=\rho_{\rm l}U^{2}a/\gamma $, 雷诺数$Re=\rho_{\rm l} Ua/\mu $, 气液密度比$\bar{\rho}=\rho_{\rm g}/\rho_{\rm l}$, 电欧拉数$Eu=\varepsilon_{1} V_{0}^{2} /\rho_{\rm l} U^{2}a^{2}$, 电松弛时间$\tau =\sigma U/\varepsilon_{1} a$, 介电常数比$\varepsilon =\varepsilon_{2} /\varepsilon_{1} $, 无量纲距离$D=d/a$可得
(40) $\begin{aligned}\operatorname{det} A &=\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)(-2 \cosh K) D_{33}+\\& \varepsilon \frac{L^{2}-K^{2}}{R e} \frac{\cosh K}{K D \sinh K} \frac{V_{0}}{d} D_{32}+\\&\left(\tau-\frac{L^{2}-K^{2}}{R e}\right) \frac{V_{0}}{d} D_{32}-\\& \varepsilon \frac{L^{2}-K^{2}}{R e} 2 \cosh K D_{33}=0\end{aligned}$
$\begin{array}{c}\frac{V_{0}}{d} D_{32}=-\frac{L^{2}+K^{2}}{K^{2}-L^{2}} 2 \operatorname{coth} K \cosh K \frac{K E u}{D^{2}}+ \\\frac{4 K^{2} L}{K^{2}-L^{2}} \frac{\cosh K}{\tanh L} \frac{E u}{D^{2}}-2 \sinh K \frac{K E u}{D^{2}}\end{array}$
$\begin{aligned}D_{33} &=-\frac{\left(L^{2}+K^{2}\right)^{2}}{K} \frac{1}{R e^{2}} \tanh K+\frac{4 K^{2} L}{R e^{2}} \tanh L-\\& \frac{K^{2}}{W e}-\bar{\rho} \frac{\omega^{2}}{K}-\frac{\left(L^{2}+K^{2}\right)^{2}}{K^{2}-L^{2}} \frac{K E u}{D^{2}} \operatorname{coth} K+\\& \frac{2 K^{2} L}{K^{2}-L^{2}} \frac{E u}{D^{2}} \operatorname{coth} L+\frac{E u}{D^{3}}\end{aligned}$
(41) $\begin{aligned}\operatorname{det} A &=\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)(-2 \sinh K) D_{33}+\\& \varepsilon \frac{L^{2}-K^{2}}{R e} \frac{\sinh K}{K D \cosh K} \frac{V_{0}}{d} D_{32}+\\&\left(\tau-\frac{L^{2}-K^{2}}{R e}\right) \frac{V_{0}}{d} D_{32}-\\& \varepsilon \frac{L^{2}-K^{2}}{R e} 2 \sinh K D_{33}=0\end{aligned}$
$\frac{V_{0}}{d} D_{32}=-\frac{L^{2}+K^{2}}{K^{2}-L^{2}} 2 \tanh K \sinh K \frac{K E u}{D^{2}}+\frac{4 K^{2} L}{K^{2}-L^{2}} \frac{\sinh K}{\operatorname{coth} L} \frac{E u}{D^{2}}-2 \cosh K \frac{K E u}{D^{2}}$
$\begin{aligned}D_{33} &=-\frac{\left(L^{2}+K^{2}\right)^{2}}{K} \frac{1}{R e^{2}} \operatorname{coth} K+\\& \frac{4 K^{2} L}{R e^{2}} \operatorname{coth} L-\frac{K^{2}}{W e}-\bar{\rho} \frac{\omega^{2}}{K}-\\& \frac{\left(L^{2}+K^{2}\right)^{2}}{K^{2}-L^{2}} \frac{K E u}{D^{2}} \tanh K+\\& \frac{2 K^{2} L}{K^{2}-L^{2}} \frac{E u}{D^{2}} \tanh L+\frac{E u}{D^{3}}\end{aligned}$
1.3 交流电场作用下不稳定性分析
当交流电场作用时, 运用Floquet理论[30 ] , 将原本的直流电压项$V_{0}$由交流电压$V_{\rm t}=V_{0}$ $\big\{1+Pr\big[\cos \big(\varOmega t \big)-1\big]\big\}$代替, 同时, 频率$\omega$由$\omega+{\rm i}n\varOmega $代替.
(42) $\left.\begin{array}{l}\cos \omega t=\frac{1}{2}\left(\mathrm{e}^{\mathrm{i} \Omega t}+\mathrm{e}^{-\mathrm{i} \Omega t}\right) \\\cos ^{2} \omega t=\frac{1}{2}+\frac{1}{4}\left(\mathrm{e}^{2 \mathrm{i} \Omega t}+\mathrm{e}^{-2 \mathrm{i} \Omega t}\right)\end{array}\right\}$
原本直流电场下的色散方程中$V_{0}^{2}$项变为$V_{\rm t}^{2}=V_{0}^{2}\left\{{1+Pr\left[ {\cos \left( {\varOmega t} \right)-1} \right]} \right\}^{2}$其中
$\begin{array}{c}\{1+\operatorname{Pr}[\cos (\Omega t)-1]\}^{2}=(1-P r)^{2}+\frac{1}{2} P r^{2}+ \\\frac{1}{2} \operatorname{Pr}(1-\operatorname{Pr})\left(\mathrm{e}^{\mathrm{i} \Omega t}+\mathrm{e}^{-\mathrm{i} \Omega t}\right)+\frac{1}{4} \operatorname{Pr}^{2}\left(\mathrm{e}^{2 \mathrm{i} \Omega t}+\mathrm{e}^{-2 \mathrm{i} 2 t}\right)\end{array}$
(43) $D_{n} \hat{\eta}_{n}+x\left(\hat{\eta}_{n+1}+\hat{\eta}_{n-1}\right)+y\left(\hat{\eta}_{n+2}+\hat{\eta}_{n-2}\right)=0$
$\begin{aligned}D_{n}=&\left[\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)(-2 \cosh K)-\right.\\&\left.\varepsilon \frac{L^{2}-K^{2}}{R e} 2 \cosh K\right]\left\{\frac{4 K^{2} L}{R e^{2}} \tanh L-\frac{K^{2}}{W e}-\right.\\& \bar{\rho} \frac{w+i n \Omega}{K}+\left(\frac{2 K^{2} L}{K^{2}-L^{2}} \frac{E u}{D^{2}} \operatorname{coth} L+\frac{E u}{D^{3}}-\right.\\&\left.\left.\frac{K^{2}+L^{2}}{K^{2}-L^{2}} \frac{K E u}{D^{2}} \operatorname{coth} K\right) \cdot\left[(1-P r)^{2}+\frac{1}{2} P r^{2}\right]\right\}+\\&\left[\varepsilon \frac{L^{2}-K^{2}}{R e} \frac{\cosh K}{K D \sinh K}+\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)\right] \\&\left(-\frac{K^{2}+L^{2}}{K^{2}-L^{2}} 2 \operatorname{coth} K \cosh K \frac{K E u}{D^{2}}+\frac{4 K^{2} L}{K^{2}-L^{2}}\right.\\&\left.\frac{\cosh K}{\tanh L} \frac{E u}{D^{2}}-2 \sinh K \frac{K E u}{D^{2}}\right) \\&\left[(1-P r)^{2}+\frac{1}{2} P r^{2}\right]\end{aligned}$
$\begin{aligned}x=\left[\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)(-2 \cosh K)-\right.\\ \left.\varepsilon \frac{L^{2}-K^{2}}{R e} 2 \sinh K\right] \cdot\left(\frac{2 K^{2} L}{K^{2}-L^{2}} \frac{E u}{D^{2}} \operatorname{coth} L+\right.\\ \left.\frac{E u}{D^{3}}-\frac{K^{2}+L^{2}}{K^{2}-L^{2}} \frac{K E u}{D^{2}} \cosh K\right) \cdot \frac{1}{2} \operatorname{Pr}(1-P r)+\\ \left[\varepsilon \frac{L^{2}-K^{2}}{R e} \frac{\cosh K}{K D \sinh K}+\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)\right] \\\left(-\frac{K^{2}+L^{2}}{K^{2}-L^{2}} 2 \operatorname{coth} K \cosh K \frac{K E u}{D^{2}}+\frac{4 K^{2} L}{K^{2}-L^{2}}\right.\\\left.\frac{\cosh K}{\tanh L} \frac{E u}{D^{2}}-2 \sinh K \frac{K E u}{D^{2}}\right) \cdot \frac{1}{2} \operatorname{Pr}(1-P r)\end{aligned}$
$\begin{aligned}y=&\left[\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)(-2 \cosh K)-\right.\\&\left.\varepsilon \frac{L^{2}-K^{2}}{\operatorname{Re}} 2 \sinh K\right] \cdot\left(\frac{2 K^{2} L}{K^{2}-L^{2}} \frac{E u}{D^{2}} \operatorname{coth} L+\right.\\&\left.\frac{E u}{D^{3}}-\frac{K^{2}+L^{2}}{K^{2}-L^{2}} \frac{K E u}{D^{2}} \cosh K\right) \frac{1}{4} P r^{2}+\\&\left[\varepsilon \frac{L^{2}-K^{2}}{R e} \frac{\cosh K}{K D \sinh K}+\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)\right] \\&\left(-\frac{K^{2}+L^{2}}{K^{2}-L^{2}} 2 \operatorname{coth} K \cosh K \frac{K E u}{D^{2}}+\frac{4 K^{2} L}{K^{2}-L^{2}}\right.\\&\left.\frac{\cosh K}{\tanh L} \frac{E u}{D^{2}}-2 \sinh K \frac{K E u}{D^{2}}\right) \frac{1}{4} P r^{2}\end{aligned}$
$\begin{aligned}D_{n}=&\left[\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)(-2 \sinh K)-\right.\\&\left.\varepsilon \frac{L^{2}-K^{2}}{R e} 2 \sinh K\right]\left\{\frac{4 K^{2} L}{R e^{2}} \operatorname{coth} L-\frac{K^{2}}{W e}-\right.\\& \bar{\rho} \frac{w+i n \Omega}{K}+\left(\frac{2 K^{2} L}{K^{2}-L^{2}} \frac{E u}{D^{2}} \tanh L+\frac{E u}{D^{3}}-\right.\\&\left.\left.\frac{K^{2}+L^{2}}{K^{2}-L^{2}} \cdot \frac{K E u}{D^{2}} \tanh K\right)\left[(1-P r)^{2}+\frac{1}{2} P r^{2}\right]\right\}+\\&\left[\varepsilon \frac{L^{2}-K^{2}}{R e} \frac{\sinh K}{K D \cosh K}+\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)\right] \\&\left(-\frac{K^{2}+L^{2}}{K^{2}-L^{2}} 2 \tanh K \sinh K \frac{K E u}{D^{2}}+\right.\\&\left.\frac{4 K^{2} L}{K^{2}-L^{2}} \frac{\sinh K}{\operatorname{coth} L} \cdot \frac{E u}{D^{2}}-2 \cosh K \frac{K E u}{D^{2}}\right) \\&\left[(1-P r)^{2}+\frac{1}{2} P r^{2}\right]\end{aligned}$
$\begin{aligned}x=&\left[\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)(-2 \sinh K)-\right.\\&\left.\varepsilon \frac{L^{2}-K^{2}}{R e} 2 \cosh K\right] \cdot\left(\frac{2 K^{2} L}{K^{2}-L^{2}} \frac{E u}{D^{2}} \tanh L+\right.\\&\left.\frac{E u}{D^{3}}-\frac{K^{2}+L^{2}}{K^{2}-L^{2}} \frac{K E u}{D^{2}} \sinh K\right) \cdot \frac{1}{2} \operatorname{Pr}(1-P r)+\\&\left[\varepsilon \frac{L^{2}-K^{2}}{R e} \frac{\sinh K}{K D \cosh K}+\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)\right] \\&\left(-\frac{K^{2}+L^{2}}{K^{2}-L^{2}} 2 \tanh K \sinh K \frac{K E u}{D^{2}}+\right.\\&\left.\frac{4 K^{2} L}{K^{2}-L^{2}} \frac{\sinh K}{\operatorname{coth} L} \frac{E u}{D^{2}}-2 \cosh K \frac{K E u}{D^{2}}\right) \\& \frac{1}{2} \operatorname{Pr}(1-P r)\end{aligned}$
$\begin{aligned}y=&\left[\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)(-2 \sinh K)-\right.\\&\left.\varepsilon \frac{L^{2}-K^{2}}{R e} 2 \cosh K\right]\left(\frac{2 K^{2} L}{K^{2}-L^{2}} \frac{E u}{D^{2}} \tanh L+\right.\\&\left.\frac{E u}{D^{3}}-\frac{K^{2}+L^{2}}{K^{2}-L^{2}} \cdot \frac{K E u}{D^{2}} \sinh K\right) \frac{1}{4} P r^{2}+\\&\left[\varepsilon \frac{L^{2}-K^{2}}{R e} \frac{\sinh K}{K D \cosh K}+\left(\tau-\frac{L^{2}-K^{2}}{R e}\right)\right] \\&\left(-\frac{K^{2}+L^{2}}{K^{2}-L^{2}} 2 \tanh K \sinh K \frac{K E u}{D^{2}}+\frac{4 K^{2} L}{K^{2}-L^{2}}\right.\\&\left.\frac{\sinh K}{\operatorname{coth} L} \frac{E u}{D^{2}}-2 \cosh K \frac{K E u}{D^{2}}\right) \frac{1}{4} P r^{2}\end{aligned}$
(44) $\left(\begin{array}{c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c} \ddots & \vdots & \vdots & 0 & 0 & 0 & 0 \\ \ldots & D_{-2} & x_{-1} & y_{0} & 0 & 0 & 0 \\ \ldots & x_{-2} & D_{-1} & x_{0} & y_{1} & 0 & 0 \\ 0 & y_{-2} & x_{-1} & D_{0} & x_{1} & y_{2} & 0 \\ 0 & 0 & y_{-1} & x_{0} & D_{1} & x_{2} & \ldots \\ 0 & 0 & 0 & y_{0} & x_{1} & D_{2} & \ldots \\ 0 & 0 & 0 & 0 & \vdots & \vdots & \ddots \end{array}\right)\left(\begin{array}{c} \hat{\eta}_{-2} \\ \hat{\eta}_{-1} \\ \hat{\eta}_{0} \\ \hat{\eta}_{1} \\ \hat{\eta}_{2} \\ \vdots \end{array}\right)=0$
(45) $\left|\begin{array}{ccccccc}\ddots & \vdots & \vdots & 0 & 0 & 0 & 0 \\\ldots & D_{-2} & x_{-1} & y_{0} & 0 & 0 & 0 \\\ldots & x_{-2} & D_{-1} & x_{0} & y_{1} & 0 & 0 \\0 & y_{-2} & x_{-1} & D_{0} & x_{1} & y_{2} & 0 \\0 & 0 & y_{-1} & x_{0} & D_{1} & x_{2} & \ldots \\0 & 0 & 0 & y_{0} & x_{1} & D_{2} & \ldots \\0 & 0 & 0 & 0 & \vdots & \vdots & \ddots\end{array}\right|=0$
2 结果与分析
在进行分析前还需确定色散矩阵的阶数, 阶数由计算的节点数$n$产生, 从理论上分析, 当$n$趋于无穷大时计算结果最为准确, 但从计算上的速度考虑阶数不能取到无穷, 因此需要选取合适的节点数$n$, 使其兼顾计算精度与快速性.
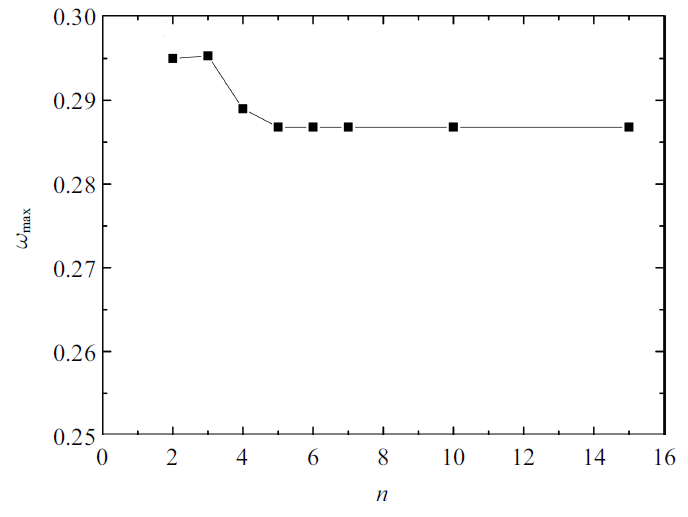
图3 做出了弯曲模式下不同节点数$n$作用时的最大不稳定增长率.
图3
图3
最大不稳定增长率随节点数$n$的变化$(\varepsilon =0.012\,5$, $D=10.45$, $Re=1000$, $We=400$, $Eu=5$, $\bar{\rho}=0.001\,2$, $Pr=2/3$, $\varOmega =1$)
Fig.3
$\omega_{\max}$ versus increasing the node number $(\varepsilon =0.012\,5$, $D=10.45$, $Re=1000$, $We=400$, $Eu=5$, $\bar{\rho}=0.001\,2$, $Pr=2/3$, $\varOmega =1$)}
从图3 可以看出, 选取节点数$n=5$是合适的, 在保障计算精度的同时提供了计算的快速性, 此时色散矩阵阶数$N=2n+1=11$.
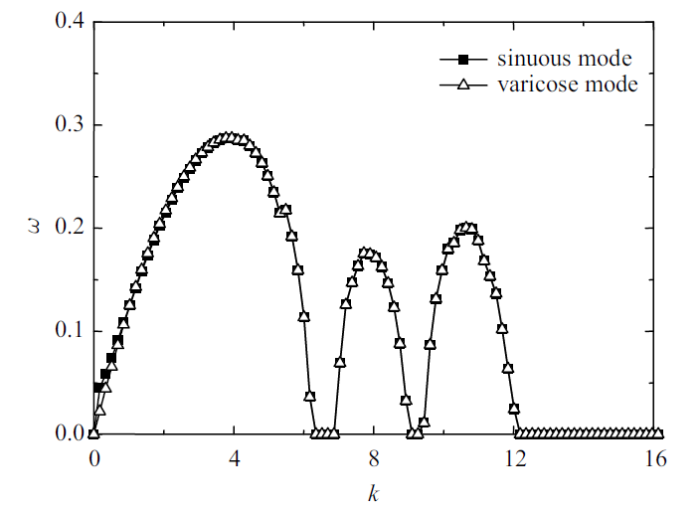
图4 做出了弯曲模式和曲张模式下的色散曲线. 如图4 所示, 本文发现了在交流电场作用下的曲张模式中, 液膜的色散曲线同弯曲模式下近乎相同, 这与直流电场及无电场作用时有很大区别.
图4
图4
弯曲模式和曲张模式下的色散曲线($\varepsilon =0.012 5$, $D=10.45$, $Re=1000$, $We=400$, $Eu=5$, $\bar{\rho}=0.001 2$, $Pr=2/3$, $\varOmega =1$)
Fig.4
Dispersion relation in sinuous and varicose mode ($\varepsilon =0.012 5$, $D=10.45$, $Re=1000$, $We=400$, $Eu=5$, $\bar{\rho}=0.001 2$, $Pr=2/3$, $\varOmega =1$)
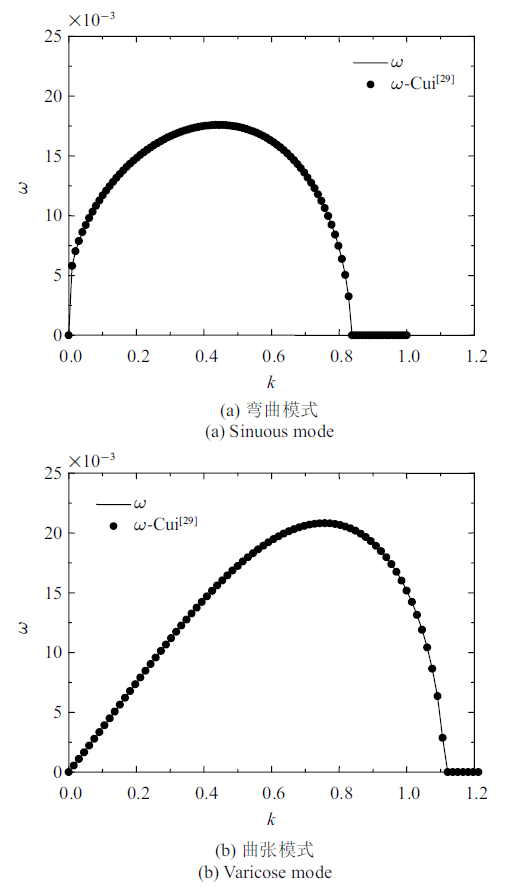
为验证本文的准确性, 取$Pr=0$, 即退化为直流电场作用情况, 同Cui[29 ] 的结果进行了对比, 图5 为对比结果, 从图中可以看出色散曲线拟合良好, 可认为本文的理论推导没有错误.
图5
图5
直流情况下色散方程的对比验证 $(\varepsilon =0.012\,5$, $D=40$, $Re=1000$, $We=400$, $Eu=2$, $\bar{\rho}=0.001\,2$, $Pr=0$, $\varOmega =1)$
Fig.5
Comparison of dispersion relation in DC case $(\varepsilon =0.012\,5$, $D=40$, $Re=1000$, $We=400$, $Eu=2$, $\bar{\rho}=0.001\,2$, $Pr=0$, $\varOmega =1)$
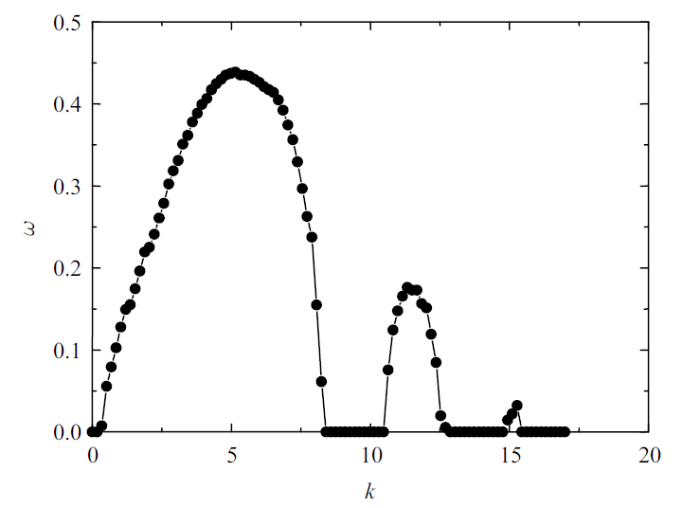
图6 做出了对交流电场下液膜弯曲模式下的色散曲线. 由图6 可见, 此时在交流电场作用下, 发生了参数振荡并出现了多个不稳定区域, 其中小波数下的不稳定区域为毛细不稳定区域, 而随其后出现的不稳定区域为参数不稳定区域, 是由交流电场的振荡所引起的.
图6
图6
色散曲线$(\varepsilon =0.012\,5$, $D=40$, $Re=1000$, $We=400$, $Eu=2$, $\bar{\rho}=0.001\,2$, $Pr=0.4$, $\varOmega =1)$
Fig.6
Dispersion relation $(\varepsilon =0.012\,5$, $D=40$, $Re=1000$, $We=400$, $Eu=2$, $\bar{\rho}=0.001\,2$, $Pr=0.4$, $\varOmega =1)$
在探究各参数对横向电场下平面液膜的线性不稳定影响的过程中, 常规的气液密度比($\rho )$, 韦伯数(We ), 雷诺数(Re )与松弛时间($\tau)$等参数对不稳定性影响已在Cui等[29 ] 对平面液膜的研究中考虑过. 因此, 本文主要考虑电学参数对不稳定性的影响.
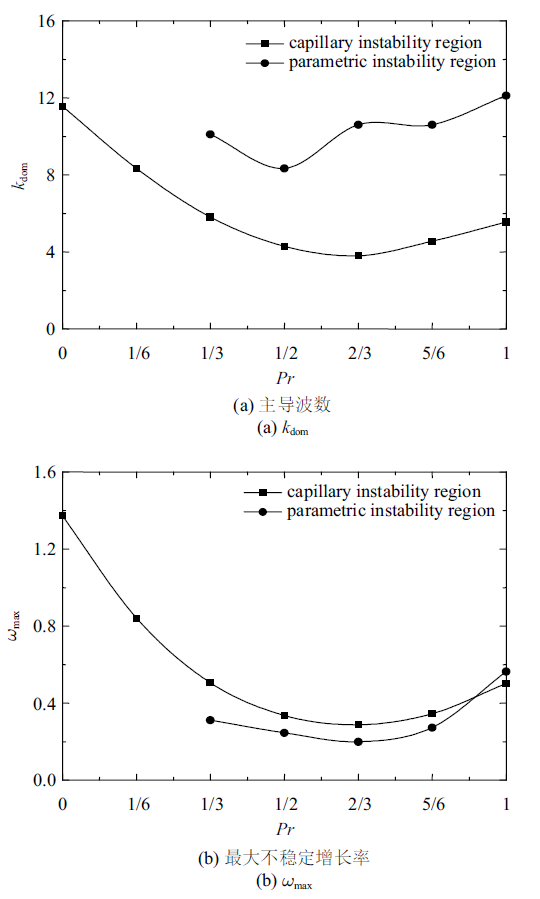
图7 表示了弯曲模式下交流电场占比$Pr$对液膜不稳定性的影响. 由图7 可以看出交流电场占比$Pr$逐渐增大时, 弯曲模式下毛细不稳定区域和参数不稳定区域内主导波数和其对应的最大不稳定增长率的变化情况. 随着$Pr$的增大, 两个不稳区域的主导波数和最大不稳定增长率总体上都是一个先下降后上升的过程. 其中当$Pr$较小时难以观测到明显的参数不稳定区域, 从$Pr=1/3$开始可以观测到较为明显的参数不稳定区域.
图7
图7
弯曲模式下交流电场占比$Pr$的影响$(\varepsilon =0.012\,5$, $D=40$, $Re=1000$, $We=400$, $Eu=2$, $\bar{\rho}=0.001\,2$, $\varOmega =1)$
Fig.7
Effects of $Pr$ in sinuous mode $(\varepsilon =0.012\,5$, $D=40$, $Re=1000$, $We=400$, $Eu=2$, $\bar{\rho}=0.001\,2$, $\varOmega =1)$
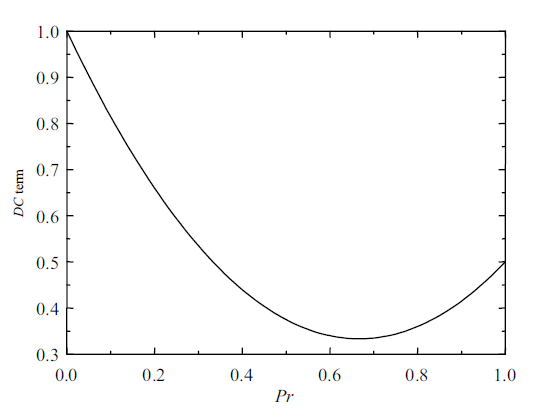
图8 为随着交流电场占比$Pr$增大时, 电场作用力中恒定电场力部分占比的变化趋势. 结合图7 和图8 可得, 交流电场作用下的毛细不稳定性主导波数和最大不稳定增长率的变化趋势同恒定电场项变化趋势基本一致, 而在$Pr=2/3$时, 参数不稳定区域的主导波数相较$Pr=1/2$时有显著的提升, 甚至超过了$Pr=5/6$时的主导波数, 此时是因为参数不稳定区域的最大增长率发生在参数不稳定区域的位置出现了变化, 此前最大不稳定增长率出现在参数不稳定区域的第一个峰, 而从$Pr=2/3$之后最大不稳定增长率出现在参数不稳定区域的第二个峰. 实际上, 同一个不稳定区域主导波数和最大不稳定增长率的变化趋势同恒定电场项的变化趋势是一致的. 此时, 不稳定主要是由恒定电场力和表面张力的对抗所导致的.
图8
图8
恒定电场项$(1-Pr)^{2}+Pr^{2}/2$作用趋势
Fig.8
Behavior of the DC term $(1-Pr)^{2}+Pr^{2}/2$}
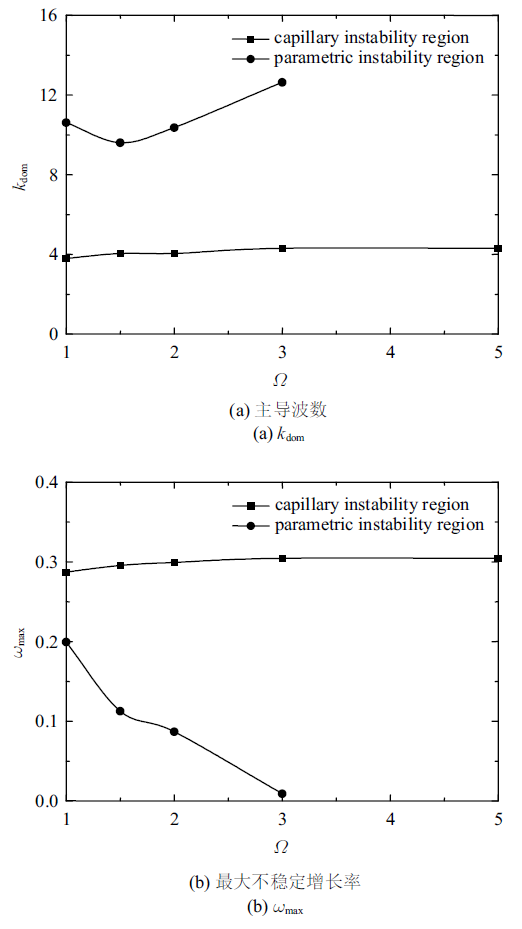
图9 表示了在弯曲模式下交流电场频率$\varOmega $对液膜不稳定性的影响. 从图9 可以看出, 参数$\varOmega$的增大略微增大了毛细不稳定区域的主导波数和最大不稳定增长率, 但会造成参数不稳定区域的最大不稳定增长率急剧下降, 在$\varOmega=3$之后难以观测到参数不稳定区域. 可见参数$\varOmega$的增大略微增大毛细不稳定性, 但急剧地减小了参数不稳定性, 其对参数不稳定的影响要远远大于毛细不稳定. 在实验中, 为了更容易产生参数不稳定, 因尽量将交流电场频率维持在较低水平.
图9
图9
弯曲模式下交流电场频率$\varOmega $的影响 $(\varepsilon =0.012\,5$, $D=40$, $Re=1000$, $We=400$, $Eu=2$, $\bar{\rho}=0.001\,2$, $Pr=2/3)$
Fig.9
Effects of $\varOmega $ in sinuous mode $(\varepsilon =0.012\,5$, $D=40$, $Re=1000$, $We=400$, $Eu=2$, $\bar{\rho}=0.001\,2$, $Pr=2/3)$
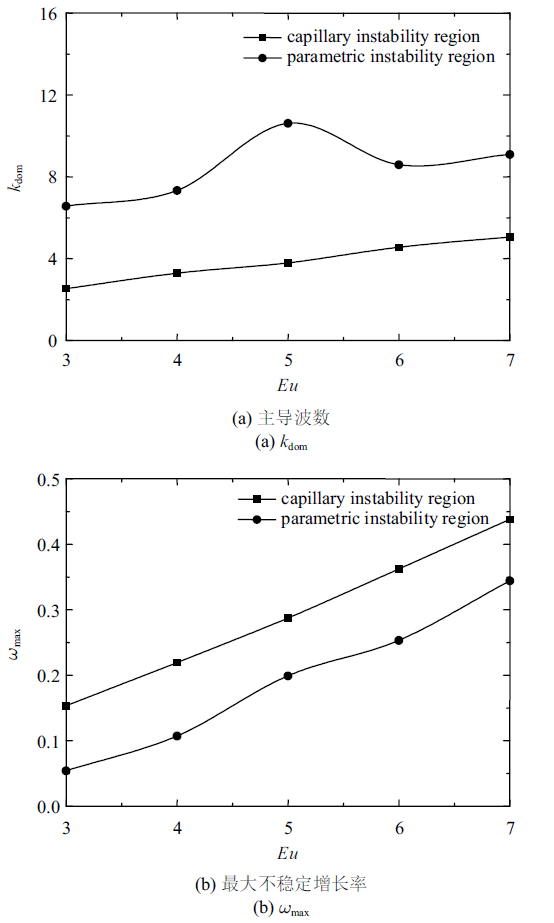
图10 表示了在弯曲模式下电欧拉数$Eu$对液膜不稳定性的影响. 由图10 可见无论是在毛细不稳定区域还是参数不稳定区域, $Eu$的增大都会增大液膜的不稳定性. 在实验中, 为了更容易产生参数不稳定现象, 因尽量加大电场强度.
图10
图10
弯曲模式下欧拉数$Eu$的影响 $(\varepsilon =0.012\,5$, $D=40$, $Re=1000$, $We=400$, $\bar{\rho}=0.001\,2$, $Pr=0.4$, $\varOmega =1)$
Fig.10
Effects of $Eu$ in sinuous mode $(\varepsilon =0.012\,5$, $D=40$, $Re=1000$, $We=400$, $\bar{\rho}=0.001\,2$, $Pr=0.4$, $\varOmega =1)$
3 结论
本文通过分析不同电学参数对横向交流电场作用下的平面液膜的参数不稳定性的影响, 得出了以下几点结论:
(1) 当交流电场占比$Pr$改变时, 对液膜不稳定性的影响是由于恒定电场比例发生变化所引起的, 此时毛细不稳定性的主导波数和最大不稳定增长率同恒定电场项比例变化趋势相一致, 此时不稳定体现为恒定电场力和表面张力的对抗.
(2) 当交流电场频率$\varOmega $改变时, 交流电场频率的增大急剧地减小液膜的参数不稳定性而略微增大毛细不稳定性.
(3) 当电欧拉数$Eu$发生改变时, 欧拉数的增大同时增大液膜的毛细不稳定性以及参数不稳定性.
(4) 为了在实验中寻求参数振荡现象, 增大电欧拉数$Eu$及减小交流电场频率$\varOmega$是有效的方法.
参考文献
View Option
[1]
Squire HB . Investigation of the instability of a moving liquid film
British Journal of Applied Physics 2002 ,4 (6 ):167 -169
DOI
URL
[本文引用: 2]
[2]
Jones AR Thong KC . The production of charged monodisperse fuel droplets by electrical dispersion
Journal of Physics D: Applied Physics 1971 ,4 (8 ):1159 -1166
DOI
URL
[3]
Tomita Y Ishibashi Y Yokoyama T . Fundamental studies on an electrostatic ink jet printer: 1st report, electrostatic drop formation
Transactions of the Japan Society of Mechanical Engineers Part B 1986 ,29 (257 ):3737 -3743
[本文引用: 1]
[4]
Hagerty WW . A study of the stability of plane fluid sheets
Journal of Applied Mechanics 1955 ,22 :509 -514
[本文引用: 1]
[5]
Lin SP . Stability of a viscous liquid curtain
Journal of Fluid Mechanics 2006 ,104 :111 -118
DOI
URL
[本文引用: 1]
[6]
Li X . Spatial instability of plane liquid sheets
Chemical Engineering Science 1993 ,48 (16 ):2973 -2981
DOI
URL
[本文引用: 1]
[7]
Li HS Kelly RE . The instability of a liquid jet in a compressible airstream
Physics of Fluids A Fluid Dynamics 1992 ,4 (10 ):2162 -2168
DOI
URL
[本文引用: 1]
[8]
Cao J Li X . Stability of plane liquid sheets in compressible gas streams
Journal of Propulsion & Power 2011 ,16 (4 ):623 -627
DOI
URL
[本文引用: 1]
[9]
张鹏 , 俞刚 . 高Bond数下黏性液滴的Rayleigh-Taylor不稳定性
力学学报 , 2006 ,38 (3 ):289 -295
URL
[本文引用: 1]
给出了高Bond数下黏性液滴表面Rayleigh-Taylor线性不稳定性的分析解,这种不稳定性对于超音速气流作用下液滴破碎的早期阶段起着至关重要的作用. 基于稳定性分析的结果,导出了用于估算稳定液滴的最大直径及液滴无量纲初始破碎时间的计算式,这些计算式与相关文献给出的实验和分析结果比较显示了良好的一致.
( Zhang Peng Yu Gang . Rayleigh-Taylor instability of viscous droplets with high Bond numbers
Chinese Journal of Theoretical and Applied Mechanics 2006 ,38 (3 ):289 -295 (in Chinese))
[本文引用: 1]
[10]
El-Sayed MF . Three-dimensional electrohydrodynamic temporal instability of a moving dielectric liquid sheet emanated into a gas medium
The European Physical Journal E 2004 ,15 (4 ):443 -455
DOI
URL
[本文引用: 1]
[11]
李广滨 , 司廷 , 尹协振 . 电场作用下无黏聚焦射流的时间不稳定性研究
力学学报 , 2012 ,44 (5 ):876 -883
DOI
URL
[本文引用: 1]
基于电场作用下的流动聚焦实验建立了简化的理论模型,开展了带电同轴液气射流的时间不稳定性分析.在无黏假设下,得到了扰动在时间域内发展演化的解析形式的色散关系,分析了主要控制参数对不稳定模态的影响.结果表明,只有轴对称扰动和第一类非轴对称扰动在时间域内是增长的;液气界面的表面张力对轴对称扰动有着双重影响而对非轴对称扰动起抑制作用;外层气体的流速以及密度的增加均能促进射流的失稳.这些结论与实验结果是定性一致的.结果也表明,在不考虑初始界面电荷密度时,单一的轴向电场能抑制射流的失稳.
( Li Guangbin Si Ting Yin Xiezhen . Temporal instability study of inviscid focused jets under an electric field
Chinese Journal of Theoretical and Applied Mechanics 2012 ,44 (5 ):876 -883 (in Chinese))
[本文引用: 1]
[12]
李帅兵 , 杨睿 , 罗喜胜 等 . 气流作用下同轴带电射流的不稳定性研究
力学学报 , 2017 ,49 (5 ):997 -1007
[本文引用: 1]
( Li Shuaibing Yang Rui Luo Xisheng , et al . Instability study of an electrified coaxial jet in a coflowing gas stream
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (5 ):997 -1007 (in Chinese))
[本文引用: 1]
[13]
Yang LJ Liu YX Fu QF . et al . Linear stability analysis of electrified viscoelastic liquid sheets
Atomization & Sprays 2012 ,22 (11 ):951 -982
[本文引用: 1]
[14]
Taylor GI McEwan AD . The stability of a horizontal fluid interface in a vertical electric field
Journal of Fluid Mechanics 1965 ,22 (1 ):1 -15
DOI
URL
[本文引用: 1]
[15]
Melcher JR Warren EP . Electrohydrodynamics of a current-carrying semi-insulating jet
Journal of Fluid Mechanics 1971 ,47 (1 ):127 -145
DOI
URL
[本文引用: 1]
[16]
Taylor GI . Studies in electrohydrodynamics. I. The circulation produced in a drop by electrical field
Proceedings of the Royal Society A 1966 ,291 (1425 ):159 -166
[本文引用: 1]
[17]
Fish BR . Electrical generation of natural aerosols from vegetation
Science 1972 ,175 (4027 ):1239 -1240
DOI
URL
PMID
[本文引用: 1]
It is suggested that an alternative, or additional, source of the blue haze above heavily forested areas may be the generation of submicrometer-sized wax particles by the action of strong electrical fields at the tips of pine needles and other wax-covered plant surfaces. Exposure of pine needles to high potential gradients results in the production of airborne wax particles with diameters less than 0.6 micrometer.
[18]
Saville DA . Electrohydrodynamics: The Taylor-Melcher leaky dielectric model
Annual Review of Fluid Mechanics 2003 ,29 (1 ):27 -64
DOI
URL
[本文引用: 1]
[19]
Montanero , José M Alfonso M , et al . Dripping, jetting and tip streaming
Reports on Progress in Physics 2020 ,83 (9 ):1 -60
[本文引用: 1]
[20]
Gamero-Castaño M Magnani M . Numerical simulation of electrospraying in the cone-jet mode
Journal of Fluid Mechanics 2019 ,859 :247 -267
DOI
URL
[本文引用: 1]
[21]
Gamero-Castaño M Manuel , Magnani M . The minimum flow rate of electrosprays in the cone-jet mode
Journal of Fluid Mechanics 2019 ,876 :553 -572
DOI
URL
[本文引用: 1]
[22]
Carroll CP Joo YL . Electrospinning of viscoelastic boger fluids: Modeling and experiments
Physics of Fluids 2006 ,18 (5 ):053102
DOI
URL
[本文引用: 1]
[23]
Reneker DH Yarin AL . Electrospinning jets and polymer nanofibers
Polymer 2008 ,49 (10 ):2387 -2425
DOI
URL
[本文引用: 1]
AbstractIn electrospinning, polymer nanofibers are formed by the creation and elongation of an electrified fluid jet. The path of the jet is from a fluid surface that is often, but not necessarily constrained by an orifice, through a straight segment of a tapering cone, then through a series of successively smaller electrically driven bending coils, with each bending coil having turns of increasing radius, and finally solidifying into a continuous thin fiber. Control of the process produces fibers with nanometer scale diameters, along with various cross-sectional shapes, beads, branches and buckling coils or zigzags. Additions to the fluid being spun, such as chemical reagents, other polymers, dispersed particles, proteins, and viable cells, resulted in the inclusion of the added material along the nanofibers. Post-treatments of nanofibers, by conglutination, by vapor coating, by chemical treatment of the surfaces, and by thermal processing, broaden the usefulness of nanofibers.]]>
[24]
Demekhin E Polyanskikh S Ramos A . Taylor cones in a leaky dielectric liquid under an AC electric field
Physical Review E Statal Nonlinear & Soft Matter Physics 2011 ,84 (3 ):035301
[本文引用: 1]
[25]
Yeo LY Lastochkin D Wang SC . et al . A new AC electrospray mechanism by Maxwell-Wagner polarization and capillary resonance
Physical Review Letters 2004 ,92 (13 ):133902
URL
PMID
[本文引用: 1]
[26]
Demekhin EA Polyanskikh SV . Stability of a viscous liquid jet in a high-frequency alternating electric field
Journal of Applied Mechanics & Technical Physics 2010 ,51 (1 ):31 -43
[本文引用: 1]
[27]
Yang W Duan H Li C . et al . Crossover of varicose and whipping instabilities in electrified microjets
Physical Review Letters 2014 ,112 (5 ):054501
URL
PMID
[本文引用: 1]
[28]
Ward K Matsumoto S Narayanan R . The electrostatically forced Faraday instability: Theory and experiments
Journal of Fluid Mechanics 2019 ,862 :696 -731
DOI
URL
[本文引用: 1]
[29]
Cui X Fu QF Yang LJ . et al . Linear instability of liquid sheets subjected to a transverse electric field
Journal of Fluids Engineering 2020 ,142 (1 ):011203
DOI
URL
[本文引用: 3]
[30]
Jia BQ Xie L Yang LJ . et al . Linear instability of viscoelastic planar liquid sheets in the presence of gas velocity oscillations
Journal of Non-Newtonian Fluid Mechanics 2019 ,273 :104169
DOI
URL
[本文引用: 2]
[31]
Jia BQ Xie L Cui X et al . Linear stability of confined coaxial jets in the presence of gas velocity oscillations with heat and mass transfer
Physics of Fluids 2019 ,31 :092101
[32]
谢络 . 静/交变电场作用下黏性圆柱射流的稳定性分析
[博士论文]. 北京: 北京航空航天大学 , 2020
( Xie L . Instability analysis of cylindrical viscous liquid jets under DC and AC electric fields
[PhD Thesis]. Beijing: Beihang University , 2020 (in Chinese))
[33]
Benjamin TB Ursell FJ . The stability of the plane free surface of a liquid in vertical periodic motion
Proceedings of the Royal Society of London 1954 ,225 (1163 ):505 -515
[34]
姚慕伟 , 贾伯琦 , 杨立军 等 . 气流速度振荡场中幂律液膜不稳定性分析
航空学报 , 2020 ,41 (11 ):123873
( Yao Muwei Jia Boqi Yang Lijun , et al . Instability of power-law liquid sheets in the presence of gas velocity oscillations
Acta Aeronautica et Astronautica Sinica 2020 ,41 (11 ):123873 (in Chinese))
[35]
谢络 , 杨立军 . 径向交流电场作用下的射流稳定性分析//第十届全国流体力学学术会议论文摘要集 , 2018 ,115 :92
[本文引用: 1]
( Xie Luo Yang Lijun . The instability of liquid jet under radial AC electric field//The 10th Chinese Congress of Theoretical and
Applied Mechanics , 2018 ,115 :92 (in Chinese))
[本文引用: 1]
Investigation of the instability of a moving liquid film
2
2002
... 由于液体雾化在灭火系统、喷涂工艺、喷墨印刷、涡轮发动机和液体火箭发动机等领域的广泛应用, 气体介质中的液膜不稳定性分析的理论研究受到了持续的关注[1 -3 ] . 在此方向上, 众多学者从不同角度进行了大量的研究. Squire[1 ] 对液体薄层在静止空气中的流动进行了分析, 认为液体薄层在特定情况下可以达到稳定状态, 这一结论由Hagerty[4 ] 通过实验证明, 并提出了两种不稳定模式, 即以反对称波为特征的弯曲模式和以对称波为特征的曲张模式, 并得出了更高的韦伯数和气液密度比使液膜更加不稳定的结论. Lin[5 ] 和Li[6 ] 对此进行了拓展, 对液膜周围气体赋以不同于液膜的速度进行了理论研究. Li和Kelly[7 ] 对无黏液膜的不稳定性进行了研究, Cao和Li[8 ] 以及Zhang[9 ] 进行了黏性液膜的不稳定性分析. ...
... [1 ]对液体薄层在静止空气中的流动进行了分析, 认为液体薄层在特定情况下可以达到稳定状态, 这一结论由Hagerty[4 ] 通过实验证明, 并提出了两种不稳定模式, 即以反对称波为特征的弯曲模式和以对称波为特征的曲张模式, 并得出了更高的韦伯数和气液密度比使液膜更加不稳定的结论. Lin[5 ] 和Li[6 ] 对此进行了拓展, 对液膜周围气体赋以不同于液膜的速度进行了理论研究. Li和Kelly[7 ] 对无黏液膜的不稳定性进行了研究, Cao和Li[8 ] 以及Zhang[9 ] 进行了黏性液膜的不稳定性分析. ...
The production of charged monodisperse fuel droplets by electrical dispersion
0
1971
Fundamental studies on an electrostatic ink jet printer: 1st report, electrostatic drop formation
1
1986
... 由于液体雾化在灭火系统、喷涂工艺、喷墨印刷、涡轮发动机和液体火箭发动机等领域的广泛应用, 气体介质中的液膜不稳定性分析的理论研究受到了持续的关注[1 -3 ] . 在此方向上, 众多学者从不同角度进行了大量的研究. Squire[1 ] 对液体薄层在静止空气中的流动进行了分析, 认为液体薄层在特定情况下可以达到稳定状态, 这一结论由Hagerty[4 ] 通过实验证明, 并提出了两种不稳定模式, 即以反对称波为特征的弯曲模式和以对称波为特征的曲张模式, 并得出了更高的韦伯数和气液密度比使液膜更加不稳定的结论. Lin[5 ] 和Li[6 ] 对此进行了拓展, 对液膜周围气体赋以不同于液膜的速度进行了理论研究. Li和Kelly[7 ] 对无黏液膜的不稳定性进行了研究, Cao和Li[8 ] 以及Zhang[9 ] 进行了黏性液膜的不稳定性分析. ...
A study of the stability of plane fluid sheets
1
1955
... 由于液体雾化在灭火系统、喷涂工艺、喷墨印刷、涡轮发动机和液体火箭发动机等领域的广泛应用, 气体介质中的液膜不稳定性分析的理论研究受到了持续的关注[1 -3 ] . 在此方向上, 众多学者从不同角度进行了大量的研究. Squire[1 ] 对液体薄层在静止空气中的流动进行了分析, 认为液体薄层在特定情况下可以达到稳定状态, 这一结论由Hagerty[4 ] 通过实验证明, 并提出了两种不稳定模式, 即以反对称波为特征的弯曲模式和以对称波为特征的曲张模式, 并得出了更高的韦伯数和气液密度比使液膜更加不稳定的结论. Lin[5 ] 和Li[6 ] 对此进行了拓展, 对液膜周围气体赋以不同于液膜的速度进行了理论研究. Li和Kelly[7 ] 对无黏液膜的不稳定性进行了研究, Cao和Li[8 ] 以及Zhang[9 ] 进行了黏性液膜的不稳定性分析. ...
Stability of a viscous liquid curtain
1
2006
... 由于液体雾化在灭火系统、喷涂工艺、喷墨印刷、涡轮发动机和液体火箭发动机等领域的广泛应用, 气体介质中的液膜不稳定性分析的理论研究受到了持续的关注[1 -3 ] . 在此方向上, 众多学者从不同角度进行了大量的研究. Squire[1 ] 对液体薄层在静止空气中的流动进行了分析, 认为液体薄层在特定情况下可以达到稳定状态, 这一结论由Hagerty[4 ] 通过实验证明, 并提出了两种不稳定模式, 即以反对称波为特征的弯曲模式和以对称波为特征的曲张模式, 并得出了更高的韦伯数和气液密度比使液膜更加不稳定的结论. Lin[5 ] 和Li[6 ] 对此进行了拓展, 对液膜周围气体赋以不同于液膜的速度进行了理论研究. Li和Kelly[7 ] 对无黏液膜的不稳定性进行了研究, Cao和Li[8 ] 以及Zhang[9 ] 进行了黏性液膜的不稳定性分析. ...
Spatial instability of plane liquid sheets
1
1993
... 由于液体雾化在灭火系统、喷涂工艺、喷墨印刷、涡轮发动机和液体火箭发动机等领域的广泛应用, 气体介质中的液膜不稳定性分析的理论研究受到了持续的关注[1 -3 ] . 在此方向上, 众多学者从不同角度进行了大量的研究. Squire[1 ] 对液体薄层在静止空气中的流动进行了分析, 认为液体薄层在特定情况下可以达到稳定状态, 这一结论由Hagerty[4 ] 通过实验证明, 并提出了两种不稳定模式, 即以反对称波为特征的弯曲模式和以对称波为特征的曲张模式, 并得出了更高的韦伯数和气液密度比使液膜更加不稳定的结论. Lin[5 ] 和Li[6 ] 对此进行了拓展, 对液膜周围气体赋以不同于液膜的速度进行了理论研究. Li和Kelly[7 ] 对无黏液膜的不稳定性进行了研究, Cao和Li[8 ] 以及Zhang[9 ] 进行了黏性液膜的不稳定性分析. ...
The instability of a liquid jet in a compressible airstream
1
1992
... 由于液体雾化在灭火系统、喷涂工艺、喷墨印刷、涡轮发动机和液体火箭发动机等领域的广泛应用, 气体介质中的液膜不稳定性分析的理论研究受到了持续的关注[1 -3 ] . 在此方向上, 众多学者从不同角度进行了大量的研究. Squire[1 ] 对液体薄层在静止空气中的流动进行了分析, 认为液体薄层在特定情况下可以达到稳定状态, 这一结论由Hagerty[4 ] 通过实验证明, 并提出了两种不稳定模式, 即以反对称波为特征的弯曲模式和以对称波为特征的曲张模式, 并得出了更高的韦伯数和气液密度比使液膜更加不稳定的结论. Lin[5 ] 和Li[6 ] 对此进行了拓展, 对液膜周围气体赋以不同于液膜的速度进行了理论研究. Li和Kelly[7 ] 对无黏液膜的不稳定性进行了研究, Cao和Li[8 ] 以及Zhang[9 ] 进行了黏性液膜的不稳定性分析. ...
Stability of plane liquid sheets in compressible gas streams
1
2011
... 由于液体雾化在灭火系统、喷涂工艺、喷墨印刷、涡轮发动机和液体火箭发动机等领域的广泛应用, 气体介质中的液膜不稳定性分析的理论研究受到了持续的关注[1 -3 ] . 在此方向上, 众多学者从不同角度进行了大量的研究. Squire[1 ] 对液体薄层在静止空气中的流动进行了分析, 认为液体薄层在特定情况下可以达到稳定状态, 这一结论由Hagerty[4 ] 通过实验证明, 并提出了两种不稳定模式, 即以反对称波为特征的弯曲模式和以对称波为特征的曲张模式, 并得出了更高的韦伯数和气液密度比使液膜更加不稳定的结论. Lin[5 ] 和Li[6 ] 对此进行了拓展, 对液膜周围气体赋以不同于液膜的速度进行了理论研究. Li和Kelly[7 ] 对无黏液膜的不稳定性进行了研究, Cao和Li[8 ] 以及Zhang[9 ] 进行了黏性液膜的不稳定性分析. ...
高Bond数下黏性液滴的Rayleigh-Taylor不稳定性
1
2006
... 由于液体雾化在灭火系统、喷涂工艺、喷墨印刷、涡轮发动机和液体火箭发动机等领域的广泛应用, 气体介质中的液膜不稳定性分析的理论研究受到了持续的关注[1 -3 ] . 在此方向上, 众多学者从不同角度进行了大量的研究. Squire[1 ] 对液体薄层在静止空气中的流动进行了分析, 认为液体薄层在特定情况下可以达到稳定状态, 这一结论由Hagerty[4 ] 通过实验证明, 并提出了两种不稳定模式, 即以反对称波为特征的弯曲模式和以对称波为特征的曲张模式, 并得出了更高的韦伯数和气液密度比使液膜更加不稳定的结论. Lin[5 ] 和Li[6 ] 对此进行了拓展, 对液膜周围气体赋以不同于液膜的速度进行了理论研究. Li和Kelly[7 ] 对无黏液膜的不稳定性进行了研究, Cao和Li[8 ] 以及Zhang[9 ] 进行了黏性液膜的不稳定性分析. ...
高Bond数下黏性液滴的Rayleigh-Taylor不稳定性
1
2006
... 由于液体雾化在灭火系统、喷涂工艺、喷墨印刷、涡轮发动机和液体火箭发动机等领域的广泛应用, 气体介质中的液膜不稳定性分析的理论研究受到了持续的关注[1 -3 ] . 在此方向上, 众多学者从不同角度进行了大量的研究. Squire[1 ] 对液体薄层在静止空气中的流动进行了分析, 认为液体薄层在特定情况下可以达到稳定状态, 这一结论由Hagerty[4 ] 通过实验证明, 并提出了两种不稳定模式, 即以反对称波为特征的弯曲模式和以对称波为特征的曲张模式, 并得出了更高的韦伯数和气液密度比使液膜更加不稳定的结论. Lin[5 ] 和Li[6 ] 对此进行了拓展, 对液膜周围气体赋以不同于液膜的速度进行了理论研究. Li和Kelly[7 ] 对无黏液膜的不稳定性进行了研究, Cao和Li[8 ] 以及Zhang[9 ] 进行了黏性液膜的不稳定性分析. ...
Three-dimensional electrohydrodynamic temporal instability of a moving dielectric liquid sheet emanated into a gas medium
1
2004
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
电场作用下无黏聚焦射流的时间不稳定性研究
1
2012
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
电场作用下无黏聚焦射流的时间不稳定性研究
1
2012
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
气流作用下同轴带电射流的不稳定性研究
1
2017
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
气流作用下同轴带电射流的不稳定性研究
1
2017
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Linear stability analysis of electrified viscoelastic liquid sheets
1
2012
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
The stability of a horizontal fluid interface in a vertical electric field
1
1965
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Electrohydrodynamics of a current-carrying semi-insulating jet
1
1971
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Studies in electrohydrodynamics. I. The circulation produced in a drop by electrical field
1
1966
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Electrical generation of natural aerosols from vegetation
1
1972
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Electrohydrodynamics: The Taylor-Melcher leaky dielectric model
1
2003
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Dripping, jetting and tip streaming
1
2020
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Numerical simulation of electrospraying in the cone-jet mode
1
2019
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
The minimum flow rate of electrosprays in the cone-jet mode
1
2019
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Electrospinning of viscoelastic boger fluids: Modeling and experiments
1
2006
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Electrospinning jets and polymer nanofibers
1
2008
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Taylor cones in a leaky dielectric liquid under an AC electric field
1
2011
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
A new AC electrospray mechanism by Maxwell-Wagner polarization and capillary resonance
1
2004
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Stability of a viscous liquid jet in a high-frequency alternating electric field
1
2010
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Crossover of varicose and whipping instabilities in electrified microjets
1
2014
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
The electrostatically forced Faraday instability: Theory and experiments
1
2019
... 随着对液膜的不稳定性分析理论趋于成熟, 学者们对液膜在电动力下的行为开始感兴趣. 在衡量液体的电学特性时, 起初大多数学者将液膜视为完全的电介质, 建立了完全导体模型来进行研究. EL-Sayed[10 ] 对水平电场下无黏气体电介质中的液膜进行了不稳定性分析, 得到了韦伯数、气液密度比和电场对不稳定性的影响. 此外, 李广滨等[11 ] 对无黏带电射流进行了时间稳定性分析, 李帅兵等[12 ] 对同轴带电射流进行了稳定性分析, Yang等[13 ] 对电场下静止气体电介质内的带电黏弹性液膜进行了研究, 证明电欧拉数会加速液膜的破裂. Taylor等[14 ] 研究表明将液膜视为完全导体是不严谨的, 因为液膜中含有少量的自由电荷. Melcher等[15 ] 和Taylor[16 ] 在对液滴和液体薄层在交变电场和直流电场下的流动分析中总结得到了漏电介质模型, 随后, Fish[17 ] 及Saville[18 ] 对此模型进行了实验验证. Montanero等[19 ] 也总结得到了漏电介质模型在非完全导体情况下的适用性, 且为锥射流模式下的电喷雾行为提供了准确的预测[20 -21 ] . 漏电介质模型也被应用在电纺丝领域[22 -23 ] 以及交流电场下的电喷雾现象[24 -25 ] 的研究中. 电动力下的不稳定性问题是十分经典的科学问题, 而且由电场驱动的流动在微流体流动中应用广泛, 许多学者对此进行了研究. 在液体射流中, 施加交流电场被发现可以用于对液体行为进行控制[26 -27 ] . 而由于交流电场的引入, 交流电场的频率同系统的固有频率相互作用, 将产生参数振荡[28 ] . 但对平面液膜在交流电场下的不稳定性分析研究较少, 而且随着电场的引入, 在液膜中势必会存在着自由电荷和电场切应力并与液膜的黏性力相平衡. 因此, 对交流电场作用下的液膜不稳定性分析进行研究意义重大. ...
Linear instability of liquid sheets subjected to a transverse electric field
3
2020
... 因此本文基于漏电介质模型对平面液膜在交流电场下的线性不稳定性分析进行了研究, 在第一节通过控制方程和边界条件描述了理论模型, 并通过线性分析[29 ] 及Floquet理论[30 -35 ] 建立了直流电场及交流电场下的色散方程, 在第二节基于色散方程讨论了电欧拉数、交流电场占比及频率等参数对液膜不稳定性的影响, 并在第三节对文中发现进行了总结. 本工作采用线性分析和Floquet理论, 推导了平面液膜在交流电场下的色散方程并研究了各参数对液膜不稳定性的影响, 以期为交流电场下的平面液膜不稳定性分析和实验提供理论基础和参考数据. ...
... 为验证本文的准确性, 取$Pr=0$, 即退化为直流电场作用情况, 同Cui[29 ] 的结果进行了对比, 图5 为对比结果, 从图中可以看出色散曲线拟合良好, 可认为本文的理论推导没有错误. ...
... 在探究各参数对横向电场下平面液膜的线性不稳定影响的过程中, 常规的气液密度比($\rho )$, 韦伯数(We ), 雷诺数(Re )与松弛时间($\tau)$等参数对不稳定性影响已在Cui等[29 ] 对平面液膜的研究中考虑过. 因此, 本文主要考虑电学参数对不稳定性的影响. ...
Linear instability of viscoelastic planar liquid sheets in the presence of gas velocity oscillations
2
2019
... 因此本文基于漏电介质模型对平面液膜在交流电场下的线性不稳定性分析进行了研究, 在第一节通过控制方程和边界条件描述了理论模型, 并通过线性分析[29 ] 及Floquet理论[30 -35 ] 建立了直流电场及交流电场下的色散方程, 在第二节基于色散方程讨论了电欧拉数、交流电场占比及频率等参数对液膜不稳定性的影响, 并在第三节对文中发现进行了总结. 本工作采用线性分析和Floquet理论, 推导了平面液膜在交流电场下的色散方程并研究了各参数对液膜不稳定性的影响, 以期为交流电场下的平面液膜不稳定性分析和实验提供理论基础和参考数据. ...
... 当交流电场作用时, 运用Floquet理论[30 ] , 将原本的直流电压项$V_{0}$由交流电压$V_{\rm t}=V_{0}$ $\big\{1+Pr\big[\cos \big(\varOmega t \big)-1\big]\big\}$代替, 同时, 频率$\omega$由$\omega+{\rm i}n\varOmega $代替. ...
Linear stability of confined coaxial jets in the presence of gas velocity oscillations with heat and mass transfer
0
2019
静/交变电场作用下黏性圆柱射流的稳定性分析
0
2020
静/交变电场作用下黏性圆柱射流的稳定性分析
0
2020
The stability of the plane free surface of a liquid in vertical periodic motion
0
1954
气流速度振荡场中幂律液膜不稳定性分析
0
2020
气流速度振荡场中幂律液膜不稳定性分析
0
2020
The instability of liquid jet under radial AC electric field//The 10th Chinese Congress of Theoretical and
1
2018
... 因此本文基于漏电介质模型对平面液膜在交流电场下的线性不稳定性分析进行了研究, 在第一节通过控制方程和边界条件描述了理论模型, 并通过线性分析[29 ] 及Floquet理论[30 -35 ] 建立了直流电场及交流电场下的色散方程, 在第二节基于色散方程讨论了电欧拉数、交流电场占比及频率等参数对液膜不稳定性的影响, 并在第三节对文中发现进行了总结. 本工作采用线性分析和Floquet理论, 推导了平面液膜在交流电场下的色散方程并研究了各参数对液膜不稳定性的影响, 以期为交流电场下的平面液膜不稳定性分析和实验提供理论基础和参考数据. ...
The instability of liquid jet under radial AC electric field//The 10th Chinese Congress of Theoretical and
1
2018
... 因此本文基于漏电介质模型对平面液膜在交流电场下的线性不稳定性分析进行了研究, 在第一节通过控制方程和边界条件描述了理论模型, 并通过线性分析[29 ] 及Floquet理论[30 -35 ] 建立了直流电场及交流电场下的色散方程, 在第二节基于色散方程讨论了电欧拉数、交流电场占比及频率等参数对液膜不稳定性的影响, 并在第三节对文中发现进行了总结. 本工作采用线性分析和Floquet理论, 推导了平面液膜在交流电场下的色散方程并研究了各参数对液膜不稳定性的影响, 以期为交流电场下的平面液膜不稳定性分析和实验提供理论基础和参考数据. ...