基于李群局部标架的多柔体系统动力学建模与计算 1)
DYNAMIC MODELING AND COMPUTATION FOR FLEXIBLE MULTIBODY SYSTEMS BASED ON THE LOCAL FRAME OF LIE GROUP 1)
基于李群局部标架的多柔体系统动力学建模与计算 1) |
| 刘铖, 胡海岩 |
|
DYNAMIC MODELING AND COMPUTATION FOR FLEXIBLE MULTIBODY SYSTEMS BASED ON THE LOCAL FRAME OF LIE GROUP 1) |
| Liu Cheng, Hu Haiyan |
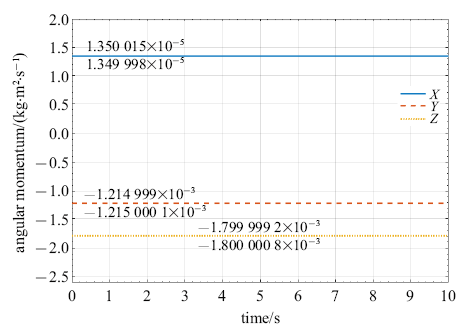
| 图8 含线性约束双摆模型在大变形运动中的角动量变化分别给出系统能量与角动量的时间历程.由图可见, 该算法同样能精确地保持系统的守恒量,其中能量相对误差为$1.7 \times 10^{-5}$, 角动量相对误差为$1.0 \times 10^{-5}$. 从理论上来看, 该系统的能量严格守恒.此处的误差主要来自求解非线性代数方程,且该误差随着非线性方程收敛标准的降低而减少. 此外, 从能量的时间历程可见,系统的低频振动激发起高频振动响应, 而有限元模型无法精确描述高频振动模态.同时, 系统保留的大量高频响应将导致计算过程中需要非常小的时间步长,导致计算效率低下. 因此, 对于多柔体系统动力学仿真, 有必要研究高频能量耗散可控的时间积分算法. |
| Fig.8 Angular momentum variation of the double pendulum with linear constrains subject to large deformation and overall motion |

|