基于李群局部标架的多柔体系统动力学建模与计算 1)

刘铖, 胡海岩

DYNAMIC MODELING AND COMPUTATION FOR FLEXIBLE MULTIBODY SYSTEMS BASED ON THE LOCAL FRAME OF LIE GROUP 1)

Liu Cheng, Hu Haiyan

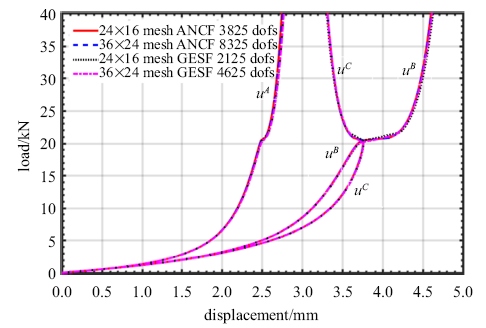
图15 圆柱壳上$A$, $B$, $C$点的位移大小其次, 本节对图16所示的顶部存在18$^{\circ}$开口薄球壳进行静力学计算,以说明SE(3)局部标架几何精确壳单元同样能够适用于描述薄壳结构的大变形.该球壳的半径为 10.0 mm, 杨氏模量为 $E=6.825 \times 10^{7}$ N/mm$^{2}$,泊松比为 $\upsilon =0.3$, 厚度为 $t=0.01$ mm($R/t=1000$). 该球壳在底部的$A$, $B$, $C$, $D$四点分别受到集中力 $F=2\lambda F_{0}$ 的作用, 其中$F_{0}=1.0$ N, $\lambda $取为 2.5. 考虑到球壳的对称性,现对其四分之一的模型进行建模.本小节分别采用局部标架GESF壳单元与局部标架缩减ANCF壳单元离散四分之一开口球壳,并分析了24 $\times$ 24与32 $\times$ 32的两种网格数目下球壳的静力学变形.图17给出了不同单元数目下球壳上点$A$与点$B$的位移随外载荷变化曲线. 数值结果表明,上述两类壳单元数值结果与参考文献均吻合较好,本文提出的两类单元能够精确描述薄壳结构的大变形特性.

Fig.15 Magnitudes of displacements at nodes $A$, $B$ and $C$ of a pinched cylinder