引言
对于机械产品而言,载荷问题是事关结构可靠性研究和疲劳寿命评价的重要问题[1 -2 ] .轨道车辆结构载荷问题近几十年持续得到研究[3 -5 ] .高速列车转向架构架是安置于车体和轮对之间的传力装置[6 ] ,其载荷研究对于确保高速列车营运安全至关重要.
关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究.
近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺.
随着运行速度、服役线路及里程的不断增加, 为进一步提高转向架的运行安全可靠性,本工作提出一种方法将线路实测动应力数据结合构架在实验室的标定数据,在损伤一致性原则下进行校准, 推导出各力系载荷系数,获得了完全覆盖关键类型测点疲劳损伤的实验载荷谱.
1 研究方法
结构载荷谱的研究首先需要对载荷系及载荷应力传递关系进行确认,准静态载荷与动态载荷的之间系统输入与输出的关系作了如下假设:
(1)线性假设. 假设系统的结构动态特性是线性的.即要求结构的总响应是这一时间段该组内每一激励单独作用产生的响应的线性叠加.此假设要求在载荷谱计算过程中, 对结构的激振要均匀, 结构变形不能过大,避免局部产生非线性影响.
(2)稳定假设. 假设结构的动态特性不随时间发生变化.在载荷谱计算分析过程中,传递函数是载荷谱反求计算成功与否的关键.如果截取载荷-应力传递关系时结构实际响应的状态与结构本身的动态特性不一致,那么载荷识别的准确性将很难保证.
(3) 典型假设. 假设在运行线路上所获得的全部数据均具备代表性.即所测试的数据应包含足够的信息以描述该构架上的载荷特性,并且应力响应完全是由待识别的载荷所产生.
步骤一: 针对转向架关键点布置应变片, 在线实测运用条件的动应力数据,由下式计算各测点的等效应力值
(1) $\begin{equation} \sigma_{{eq}i} =\left[ {\frac{L}{L_{1} N}\sum {n_{j} \left( {\sigma_{{a}j} } \right)^{m}} } \right]^{{1}/{m}} \end{equation}$
式中各符号说明如下, $L$为转向架在规定使用年限内的总运用公里数;$L_{1}$为实测动应力时的运行公里数;$n_{j}$为与各级应力水平对应的应力循环次数, 即各测点应力谱中各级应力的出现次数;$\sigma_{{a}j}$为各级应力水平的幅值(8级谱有8个$\sigma_{{a}j} $值);$m$为S-N曲线方程的指数;$N$为循环次数, 对于焊缝, $N$取200万次.
步骤二: 将线路测试的构架放置实验室内进行标定, 建立载荷系并获得载荷与应力传递关系.通过下式确定各个标定载荷在测点处产生的应力响应$\sigma_{ij} $, 并挑选载荷响应大的点作为下一步骤计算的基础
(2) $\begin{equation} \sigma_{ij} =k_{ij} F_{j} \end{equation}$
(3) $\begin{equation} \sigma_{i} =\sum {k_{ij} F_{j} d_{j} } \end{equation}$
式中, $i$为测点号, $j$为各标定载荷序号;$K_{ij} $代表载荷应力传递系数;$F_{j} $代表各个标定的单位载荷;$d_{j} $为载荷系数.
步骤三: 根据线路的动应力数据计算各个点等效应力,将该等效应力作为实验室内等效载荷谱的优化目标, 获得实验室内台架试验的实验谱.由于线路的损伤采用等效应力的方式, 而等效应力经过雨流统计后的计算结果,是不能简单进行加减的, 因此将加载模式简化, 采用恒幅恒频率加载, 这样,室内疲劳试验的各个测点的应力值就可以直接与线路的等效应力值进行加减乘除运算.
(4) $\begin{equation} F\left( {d_{j} } \right)=\sum {\left( {\sum {k_{ij} F_{j} d_{j} -\sigma _{{eq}i} } } \right)}^{2}$ \end{equation}$
式中$k_{ij} $为载荷传递关系系数, $F_{j} $为单位载荷, 都已知, $\sigma_{{eq}i}$为实测等效应力, 为已知量.
(5) $\begin{equation} \left[\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} k_{11} &k_{12} & \cdots & k_{1j} \\ k_{21} &k_{21} & \cdots & k_{2j} \\ \vdots &\vdots & \ddots & \vdots \\ k_{i1} &k_{i2} & \cdots & {k_{ij} } \\ \end{array} \right]\left[ \begin{array}{*{20}c} {F_{1} d_{1} } \\ {F_{2} d_{2} } \\ \vdots \\ {F_{j} d_{j} } \\ \end{array} \right]\geqslant \left[ \begin{array}{*{20}c} {\sigma_{eq1} } \\ {\sigma_{eq2} } \\ \vdots \\ {\sigma_{{eq}i} } \\ \end{array} \right] \end{equation}$
2 线路实测损伤
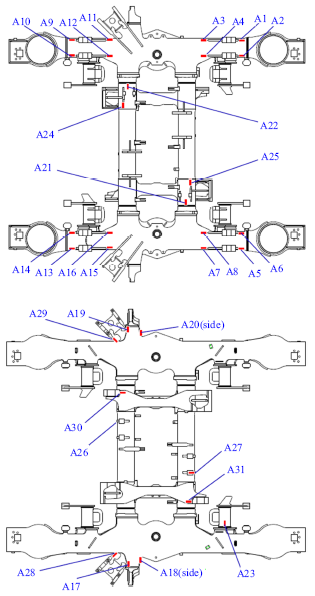
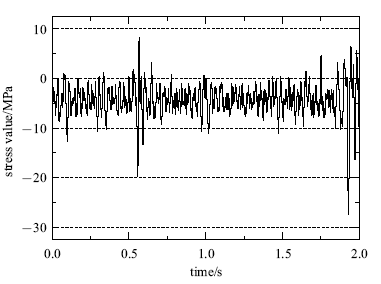
在转向架构架主体及承载支吊座的关键位置布置测点, 见图1 所示.在京沪京广和哈大三条高铁线运行中, 实测该转向架构架上的应力-时间历程,本研究基于这些主干线路上针对某型号高速动车转向架进行的长期测试工作,测试车如图2 所示.图3 和图4 中分别示出了横侧梁连接部和制动吊座根部测点的应力的时间历程波形.
图1
图1
转向架构架上测点布置图
Fig.1
Arrangement of measuring points on the bogie frame
图2
图2
测试车回库现场
Fig.2
Test car back to the depot
图3
图3
横侧梁连接部应力的时间历程波形
Fig.3
Stress history waveform of the connection part of the lateral beam
图4
图4
制动吊座部位应力的时间历程波形
Fig.4
Stress history waveform of brake hanger
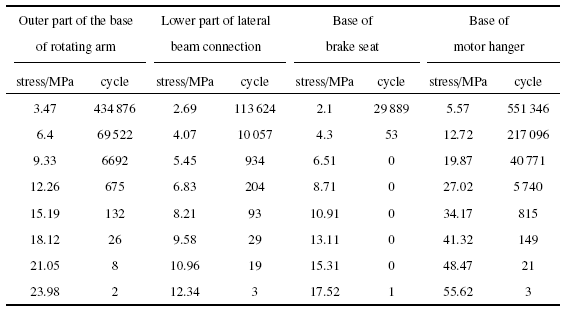
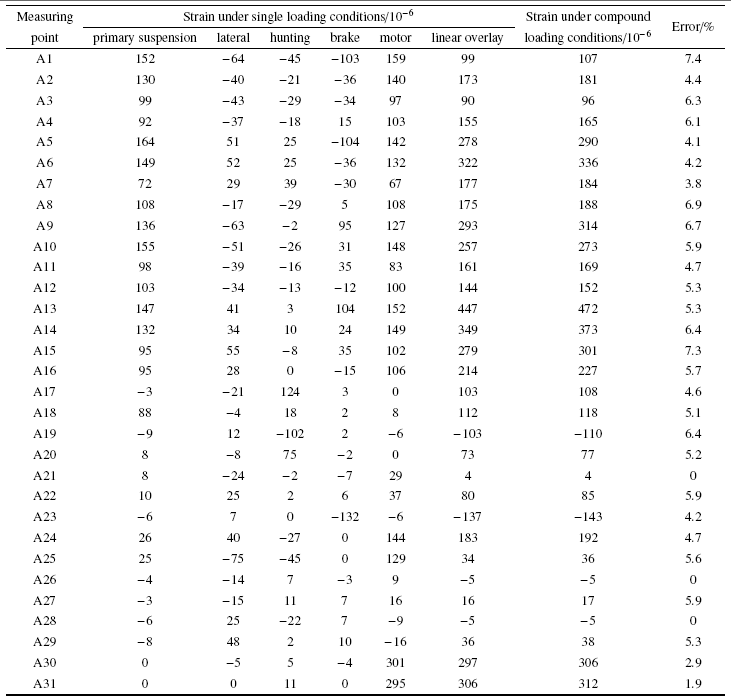
确定12类部位, 布置建立试验载荷谱的动应力测点.选取的原则是基于构架应力仿真计算响应大小、测点焊接接头形式、构架受力特点等共性进行分类.本研究根据载荷特征分别为转臂座根部上外部、上内部、下外部和下内部,抗蛇行座上盖板区域及其侧面, 横侧梁连接部下部, 制动吊座根部,电机横向减振器内部, 牵引拉杆座根部, 抗侧滚座根部以及电机吊座根部等区域.选取其中4个典型测点的应力谱, 如表1 所示.
根据12类的测点实测应力谱, 由式(1)可计算得到它们的等效应力值$\sigma_{eq1}$, $\sigma_{eq2} $, $\cdots$, $\sigma_{eq12} $. 每一个测点在不同线路上的时间历程是不一样的,但从这几大干线挑选出来的等效值能够满足具有典型线路特征的最大等效应力值,就能覆盖所有线路可能出现的典型损伤.
3 载荷实验谱编制
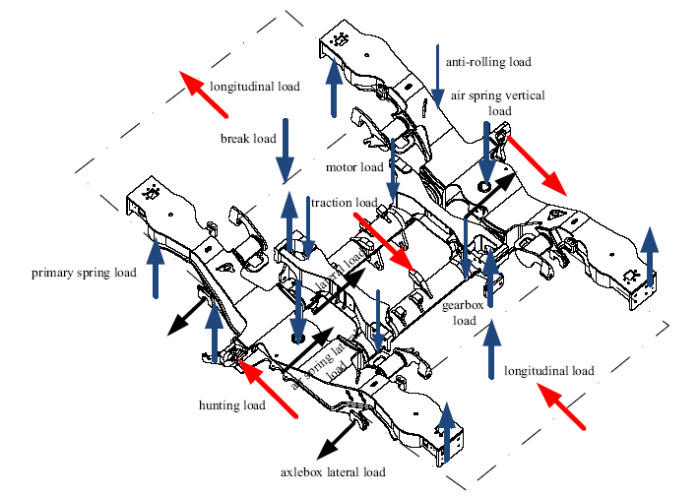
转向架构架上承受的主要载荷如图5 所示. 构架标定现场如图6 ,在实验室进行构架试验时, 如果将一系弹簧载荷视为反力支座加以约束,那么可以将其他载荷系分为:二系垂向载荷、纵向载荷、横向载荷、抗蛇行载荷、制动载荷、齿轮箱载荷、电机载荷、侧滚载荷共八类载荷,每一类载荷都是内在关联, 如同向或反向、或呈一定比例等.由于构架上这些载荷的频次、幅值不同, 这给试验操作带来很大困难, 甚至难以实施.为此, 在编制试验载荷谱前, 对前面所述的假设进行验证. 基于这两个假设,可将八个载荷系实施分组或几组同时加载.
图5
图5
转向架构架上的主要载荷系
Fig.5
Main load system on the bogie frame
图6
图6
构架标定现场
Fig.6
Bogie frame calibration site
假设1: 对于任何一个测点每一个复合工况都可以用单工况线性叠加.表2 中列出了试验构架在单一加载工况线性叠加与其复合加载在各个测点上的应力测试结果及其误差值.
对于A1~A31测点, 复合工况即所有单独载荷力系都依次加载.
由表2 可见, 复合工况加载在各测点上产生的应力值比单一加载后线性叠加的应力值大一些,绝大多数测点的误差值在5%左右, 其中最大误差为7.4%,该假设可以满足工程需求.
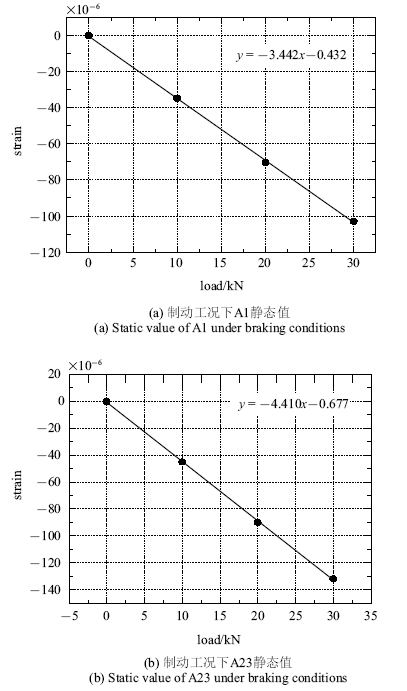
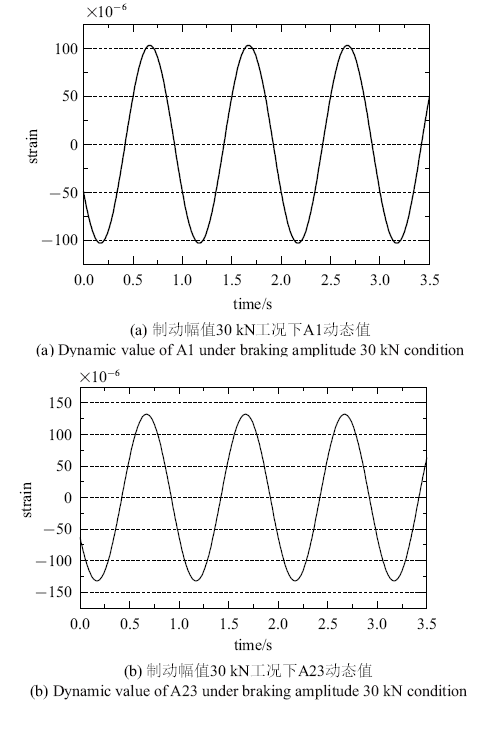
假设2: 各测点静态线性度乘载荷系数与动态幅值的数值基本一致.
由图7 和图8 两图数据可见, 动态恒幅数据与静态线性数据10{\%}误差范围之内, 该假设满足工程要求.
图7
图7
静态线性加载
Fig.7
Static linear loading
图8
图8
动态恒幅加载
Fig.8
Dynamic constant amplitude loading
4 基于损伤一致性求解载荷系数
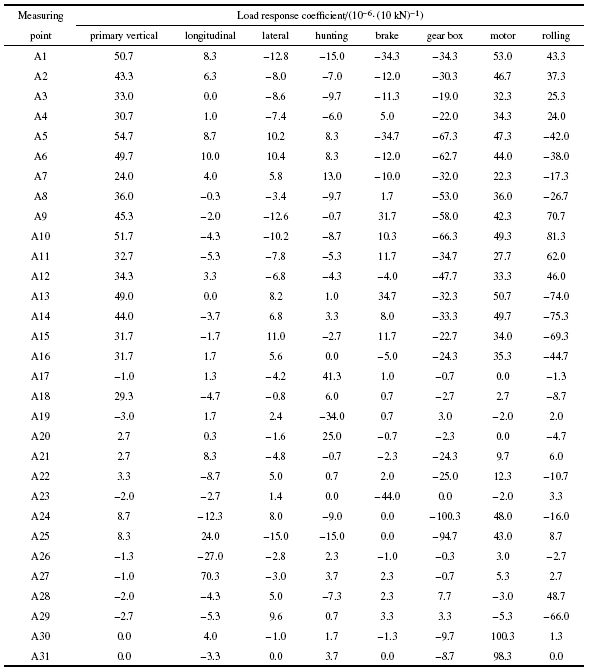
对每一个测点进行线性单一加载, 得到其载荷-响应系数, 如表3 所示.
$\begin{eqnarray*} &&K_{ij} = \left[\begin{array}{cccccccc} {50.7} & {8.3} & {-12.8} & {-15.0} & {-34.3} & {-34.3} & {53.0} & {43.3} \\ {33.0} & {0.0} & {-8.6} & {-9.7} & {-11.3} & {-19.0} & {32.3} & {25.3} \\ {49.7} & {10.0} & {10.4} & {8.3} & {-12.0} & {-62.7} & {44.0} & {-38.0} \\ {36.0} & {-0.3} & {-3.4} & {-9.7} & {1.7} & {-53.0} & {36.0} & {-26.7} \\ {-1.0} & {1.3} & {-4.2} & {41.3} & {1.0} & {-0.7} & {0.0} & {-1.3} \\ {29.3} & {-4.7} & {-0.8} & {6.0} & {0.7} & {-2.7} & {2.7} & {-8.7} \\ {3.3} & {-8.7} & {5.0} & {0.7} & {2.0} & {-25.0} & {12.3} & {-10.7} \\ {-2.0} & {-2.7} & {1.4} & {0.0} & {-44.0} & {0.0} & {-2.0} & {3.3} \\ {8.7} & {-12.3} & {8.0} & {-9.0} & {0.0} & {-100.3} & {48.0} & {-16.0} \\ {-1.3} & {-27.0} & {-2.8} & {2.3} & {-1.0} & {-0.3} & {3.0} & {-2.7} \\ {-2.0} & {-4.3} & {5.0} & {-7.3} & {2.3} & {7.7} & {-3.0} & {48.7} \\ {0.0} & {4.0} & {-1.0} & {1.7} & {-1.3} & {-9.7} & {100.3} & {1.3} \\ \end{array}\right] \end{eqnarray*}$
(6) $\begin{equation} \min F\left( {d_{i} } \right)=\min \left[ {\sum {\left( {\sum {k_{ij} F_{j} d_{j} -\sigma_{{eq}i} } } \right)^{2}} } \right] \end{equation}$
将所有$F_{j} $归一化, 均为10 kN, $j=0,1,\cdots, 8$, $i=1,2,\cdots, 12$.
(7) $\begin{equation} \label{eq7} \left[\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} k_{11} &k_{12} & \cdots & {k_{1j} } \\ k_{21} &k_{22} & \cdots & {k_{2j} } \\ \vdots &\vdots & \ddots & \vdots \\ k_{i1} &k_{i2} & \cdots & {k_{ij} } \\ \end{array} \right]\left[\begin{array}{*{20}c} {d_{1} } \\ {d_{2} } \\ \vdots \\ {d_{j} } \\ \end{array} \right]\geqslant \left[ \begin{array}{*{20}c} {\sigma_{eq1} } \\ {\sigma_{eq2} } \\ \vdots \\ {\sigma_{{eq}i} } \\ \end{array} \right] \end{equation}$
求解可得各个载荷系$d_{1}$, $d_{2}$, $\cdots$, $d_{8}$系数,乘以10 kN即可得到每个载荷力系的作用力大小,各个载荷力系相互之间都存在相位差异(正负号), 总体为恒幅恒频加载.
将获得的载荷值大小导入MTS多通道疲劳试验机的控制系统(设备型号FlexTest 200)中,待PID控制稳定后(如图9 )采集每个测点通道的动态应力值大小.
图9
图9
MTS载荷控制图
Fig.9
MTS load control
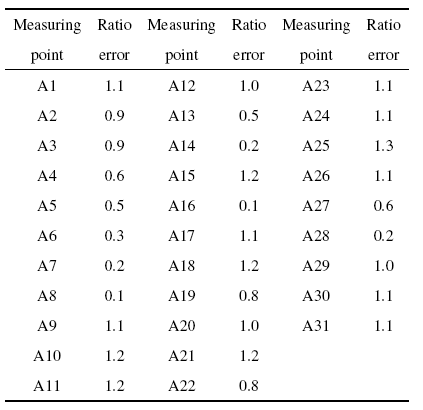
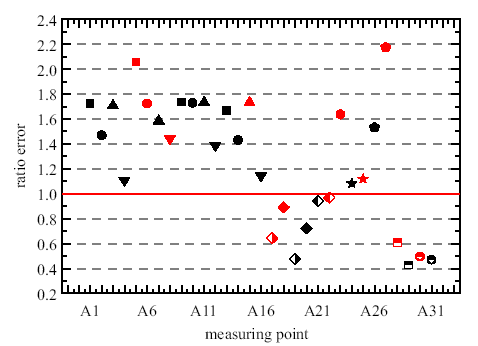
将所有测点的应力幅值与其线路测试的等效应力值进行比对, 得到比值误差如表4 .将所有的比值误差放入到同一张图中, 如图10 所示.
图10
图10
优化谱比值误差在归一化坐标系中的体现
Fig.10
Reflection of the optimized spectral ratio error in the normalized coordinate system
图10 中, 所有测点的不同形状的点代表不同类型测点(12类),同一类型测点在应力比最大代表该实验谱下该类测点得到的考核与线路考核的比值(红色表示).可以看出, 在本方法得到的实验谱中, 所有类型测点的最大应力比均大于1,且最大为1.3, 所有
类型的测点覆盖了线路测试中的关键应力. 由于测点众多,在要求同类型最大点的与线路应力比大于1且最接近1时,需要调低同类型其他测点误差, 才能做到计算收敛.这也是同类型其他测点有远小于1的原因.
采用EN标准, 进行实验台架测试, 得到的应力值与线路测试应力的比值误差,放入图11 中.
图11
图11
EN标准比值误差在归一化坐标系中的体现
Fig.11
EN standard ratio error in the normalized coordinate system
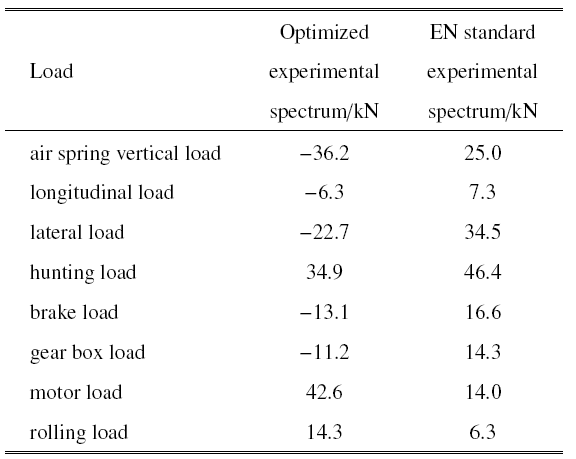
载荷差异: 根据优化后的载荷与EN标准的载荷见表5 .
从表5 中可以看出, 大部分优化后的载荷与EN标准载荷相比稍微减小,但是由于电机吊座附近测点响应较大, 而电机载荷对该测点的损伤贡献大,需要提高电机载荷, 这也说明优化后的载荷对于线路条件具有很好的适应性.
从上述图表也可以看出, EN标准在建立之初并没有考虑到中国线路的高速营运条件,其载荷制定虽然考虑了安全性, 整体数值较大,但对中国线路上运行的转向架损伤并没有较好的覆盖性.
结论
本文从实际运用出发, 基于损伤一致性准则与优化算法,针对某动车组转向架构架实验谱展开研究, 得到结论如下:
(1) 在实验室台架实验中, 假设条件中线性条件和稳定条件成立,该假设为本研究方案奠定了良好的计算与试验基础.
(2) 在没有获得线路载荷, 仅有长期测试构架动应力跟踪试验大数据的条件下,可以采用本方法获得转向架构架的载荷条件, 用于考核构架. 当然,如果有载荷测试数据, 那么本文的方法会有更准确的载荷条件, 覆盖精度也会更高.
(3) 和以前沿用通用标准相比, 本研究方法从线路实际损伤出发,设计出一套关键类型测点完全覆盖线路损伤的实验谱,如果考虑可靠性因素加以整体放大, 那么该实验谱就具有很好的定量效果.
(4) 中国铁路的运行速度和运用工况与欧洲相比具有不同的情况,导致现行国际标准下的载荷谱不能覆盖到中国动车组转向架构架的某些关键部位.与国际标准相比较,采用本研究方法建立的优化实验谱不仅能够覆盖动车组构架的典型疲劳关键部位,而且优化实验谱下的等效应力与线路实测下的等效应力的偏差也更小.本文的研究内容可作为国际标准的有益补充用于对中国铁路的研究.
参考文献
View Option
[1]
Schijve J . Fatigue of Structures and Materials. 2nd ed
Berlin: Springer Science & Business Media , 2009
[本文引用: 1]
[2]
Zhao LH Zheng SL Feng JZ . Fatigue life prediction under service load considering strengthening effect of loads below fatigue limit
Chinese Journal of Mechanical Engineering , 2014 ,27 (6 ):1178 -1185
[本文引用: 1]
[3]
British Standard BS EN 13749 , 2005 . Railway applications-methods of specifying structural requirements of bogie frames
[本文引用: 1]
[4]
Zeng XH Wu H Lai J , et al . Influences of aerodynamic loads on hunting stability of high-speed railway vehicles and parameter studies
Acta Mechanica Sinica , 2014 ,30 (6 ):889 -900
[5]
Fu DL Wang WJ Dong L . Analysis on the fatigue cracks in the bogie frame
Engineering Failure Analysis , 2015 ,58 :307 -319
[本文引用: 1]
[6]
严隽耄 . 车辆工程, 第2版 . 北京 : 中国铁道出版社 , 2004 .
[本文引用: 1]
( Yan Juanmao . Vehicle Engineering, 2nd edn. Beijing : China Railway Publishing House , 2004 (in Chinese))
[本文引用: 1]
[7]
Schupp G Jaschinski A . Virtual prototypeing: The future way of designing railway vehicles
International Journal of Vehicle Design , 1999 ,22 (1-2 ):93 -115
[本文引用: 1]
[8]
Andersson C Abrahamsson T . Simulation of interaction between a train in general motion and a track
Vehicle System Dynamics , 2002 ,38 (6 ):433 -455
[本文引用: 1]
[9]
高云霄 , 王曦 , 邹骅 等 . 基于动应力的转向架构架载荷识别
机械工程学报 , 2018 ,54 (12 ):58 -63 .
[本文引用: 1]
( Gao Yunxiao Wang Xi Zou Hua , et al . Load identification of bogie frame based on dynamic stress
Journal of Mechanical Engineering , 2018 ,54 (12 ):58 -63 (in Chinese))
[本文引用: 1]
[10]
马卫华 , 罗世辉 , 宋荣荣 . 高速动车轴箱转臂节点载荷谱研究
铁道机车车辆 , 2009 ,29 (4 ):12 -14, 50 .
[本文引用: 1]
( Ma Weihua Luo Shihui Song Rongrong . Load spectrum research of tumbler journal box node of high-speed motor car
Railway Locomotive & Car , 2009 ,29 (4 ):12 -14, 50 (in Chinese))
[本文引用: 1]
[11]
Kassner M . Fatigue strength analysis of a welded railway vehicle structure by different methods
International Journal of Fatigue , 2012 ,34 (1 ):103 -111
[本文引用: 1]
[12]
张大福 , 邬平波 , 魏来 . CRH3动车组构架载荷谱研究
机械 , 2013 ,40 (10 ):22 -27 .
[本文引用: 1]
( Zhang Dafu Wu Pingbo Wei Lai . The study of CRH3 train-set frame's load spectrum
Machinery , 2013 ,40 (10 ):22 -27 (in Chinese))
[本文引用: 1]
[13]
金新灿 , 孙守光 , 陈光雄 . 列车通过道岔时转向架结构振动特性的研究
力学学报 , 2006 ,38 (4 ):530 -539 .
[本文引用: 1]
( Jin Xincan Sun Shouguang Chen Guangxiong . Study on characteristics of railway bogie's structural vibrations while train passing
[本文引用: 1]
through a switch . Chinese Journal of Theoretical and Applied Mechanics , 2006 ,38 (4 ):530 -539 (in Chinese))
[本文引用: 1]
[14]
Matsumoto A Sato Y Ohono H , et al . Study on curving performance of railway bogies by using full-scale stand test
Vehicle System Dynamics , 2006 ,44 (Supplement 1 ):862 -873
[本文引用: 1]
[15]
Esderts A Willen J Kassner M . Fatigue strength analysis of welded joints in closed steel sections in rail vehicles
International Journal of Fatigue , 2012 ,34 (1 ):112 -121
[本文引用: 1]
[16]
Bertini L Cera A Frendo F , et al . Experimental investigation of the fatigue resistance of pipe-to-plate welded connections under bending, torsion and mixed mode loading
International Journal of Fatigue , 2014 ,68 :178 -185
[本文引用: 1]
[17]
Ribeiro D Calçada R Delgaso R , et al . Finite-element model calibration of a railway vehicle based on experimental modal parameters
Vehicle System Dynamics , 2013 ,51 (6 ):821 -856
[本文引用: 1]
[18]
Ren ZS Sun SG Li Q , et al . Experimental studies of load characteristics of bogie frames for 350 km/h EMUs
Journal of Rail and Rapid Transit , 2012 ,226 (2 ):216 -227
[本文引用: 1]
[19]
丁然 , 李强 , 任尊松 . 城际动车组轮轨力统计特征
机械工程学报 , 2019 ,55 (6 ):108 -115 .
[本文引用: 1]
( Ding Ran Li Qiang Ren Zunsong . Statistics characters of wheel/rail loads of intercity EMU
Journal of Mechanical Engineering , 2019 ,55 (6 ):108 -115 (in Chinese))
[本文引用: 1]
[20]
Wang WJ Wang Y Sun SG , et al . Long-term load spectrum test of high speed train bogie
Journal of Southwest Jiaotong University. 2015 ,50 (1 ):84 -89
[本文引用: 1]
[21]
Zhai Wm Liu PF Lin JH , et al . Experimental investigation on vibration behavior of a CRH train at speed of 350 km/h
International Journal of Rail Transportation , 2015 ,3 (1 ):1 -16
[本文引用: 1]
[22]
陈道云 , 孙守光 , 李强 . 高速列车载荷谱推断及扩展方法研究
机械工程学报 , 2018 ,54 (10 ):151 -155 .
[本文引用: 1]
( Chen Daoyun Sun Shouguang Li Qiang . Study on deduction and extend of high-speed train load spectrum
Journal of Mechanical Engineering , 2018 ,54 (10 ):151 -155 (in Chinese))
[本文引用: 1]
[23]
Chen D Xiao Q Mou M , et al . Study on establishment of standardized load spectrum on bogie frames of high-speed trains
Acta Mechanica Sinica , 2019 ,35 (4 ):812 -827
[本文引用: 1]
[24]
王斌杰 , 孙守光 , 王曦 等 . 地铁转向架构架运用载荷与疲劳损伤特征研究
铁道学报 , 2019 ,41 (6 ):53 -60 .
[本文引用: 1]
( Wang Binjie Sun Shouguang Wang Xi , et al . Research on characteristics of operation loads and fatigue damage of metro train bogie frame. Journal of the China Railway Society , 2019 ,41 (6 ):53 -60 (in Chinese))
[本文引用: 1]
[25]
杨广雪 , 张亚禹 , 李广全 . 高速列车轴箱弹簧载荷特性与疲劳损伤
交通运输工程学报 , 2019 ,19 (4 ):81 -93 .
[本文引用: 1]
( Yang Guangxue Zhang Yayu Li Guangquan . Axle box spring load characteristics and fatigue damage of high-speed train
Journal of Traffic and Transportation Engineering , 2019 ,19 (4 ):81 -93 (in Chinese))
[本文引用: 1]
[26]
Zhu N Sun SG Li Q , et al . Theoretical research and experimental validation of quasi-static load spectra on bogie frame structures of high-speed trains
Acta Mechanica Sinica , 2014 ,30 (6 ):901 -909
[本文引用: 1]
[27]
Ma S Sun S Wang B , et al . Estimating load spectra probability distributions of train bogie frames by the diffusion-based kernel density method.
International Journal of Fatigue , 2020 , 132 (3 ): 105352. 1- 105352 . 14
[本文引用: 1]
[28]
邹骅 , 李强 , 孙守光 . 基于载荷标定的城际列车转向架载荷及应力分布特征研究
铁道学报 , 2016 ,38 (10 ):27 -33 .
[本文引用: 1]
( Zou Hua Li Qiang Sun Shouguang . Study on intercity train load spectrum distribution estimation and calibration methods based on load demarcation. Journal of the China Railway Society , 2016 ,38 (10 ):27 -33 (in Chinese))
[本文引用: 1]
[29]
Zou H Sun S Li Q , et al . Analysis of the load-Stress response characteristics of the bogie frame in intercity electric multiple unit
Chinese Journal of Mechanical Engineering , 2018 ,31 (1 ):26 -36
[本文引用: 1]
[30]
王建斌 , 李大地 , 屈升 . 高速列车转向架构架疲劳试验载荷谱研究
机械工程学报 , 2019 ,55 (24 ):172 -177 .
[本文引用: 1]
( Wang Jianbin Li Dadi Qu Sheng . Research on the fatigue test spectrum for high speed train bogie frames
Journal of Mechanical Engineering , 2019 ,55 (24 ):172 -177 (in Chinese))
[本文引用: 1]
Fatigue of Structures and Materials. 2nd ed
1
2009
... 对于机械产品而言,载荷问题是事关结构可靠性研究和疲劳寿命评价的重要问题[1 -2 ] .轨道车辆结构载荷问题近几十年持续得到研究[3 -5 ] .高速列车转向架构架是安置于车体和轮对之间的传力装置[6 ] ,其载荷研究对于确保高速列车营运安全至关重要. ...
Fatigue life prediction under service load considering strengthening effect of loads below fatigue limit
1
2014
... 对于机械产品而言,载荷问题是事关结构可靠性研究和疲劳寿命评价的重要问题[1 -2 ] .轨道车辆结构载荷问题近几十年持续得到研究[3 -5 ] .高速列车转向架构架是安置于车体和轮对之间的传力装置[6 ] ,其载荷研究对于确保高速列车营运安全至关重要. ...
Railway applications-methods of specifying structural requirements of bogie frames
1
2005
... 对于机械产品而言,载荷问题是事关结构可靠性研究和疲劳寿命评价的重要问题[1 -2 ] .轨道车辆结构载荷问题近几十年持续得到研究[3 -5 ] .高速列车转向架构架是安置于车体和轮对之间的传力装置[6 ] ,其载荷研究对于确保高速列车营运安全至关重要. ...
Influences of aerodynamic loads on hunting stability of high-speed railway vehicles and parameter studies
0
2014
Analysis on the fatigue cracks in the bogie frame
1
2015
... 对于机械产品而言,载荷问题是事关结构可靠性研究和疲劳寿命评价的重要问题[1 -2 ] .轨道车辆结构载荷问题近几十年持续得到研究[3 -5 ] .高速列车转向架构架是安置于车体和轮对之间的传力装置[6 ] ,其载荷研究对于确保高速列车营运安全至关重要. ...
1
2004
... 对于机械产品而言,载荷问题是事关结构可靠性研究和疲劳寿命评价的重要问题[1 -2 ] .轨道车辆结构载荷问题近几十年持续得到研究[3 -5 ] .高速列车转向架构架是安置于车体和轮对之间的传力装置[6 ] ,其载荷研究对于确保高速列车营运安全至关重要. ...
1
2004
... 对于机械产品而言,载荷问题是事关结构可靠性研究和疲劳寿命评价的重要问题[1 -2 ] .轨道车辆结构载荷问题近几十年持续得到研究[3 -5 ] .高速列车转向架构架是安置于车体和轮对之间的传力装置[6 ] ,其载荷研究对于确保高速列车营运安全至关重要. ...
Virtual prototypeing: The future way of designing railway vehicles
1
1999
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
Simulation of interaction between a train in general motion and a track
1
2002
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
基于动应力的转向架构架载荷识别
1
2018
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
基于动应力的转向架构架载荷识别
1
2018
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
高速动车轴箱转臂节点载荷谱研究
1
2009
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
高速动车轴箱转臂节点载荷谱研究
1
2009
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
Fatigue strength analysis of a welded railway vehicle structure by different methods
1
2012
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
CRH3动车组构架载荷谱研究
1
2013
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
CRH3动车组构架载荷谱研究
1
2013
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
列车通过道岔时转向架结构振动特性的研究
1
2006
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
列车通过道岔时转向架结构振动特性的研究
1
2006
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
列车通过道岔时转向架结构振动特性的研究
1
2006
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
Study on curving performance of railway bogies by using full-scale stand test
1
2006
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
Fatigue strength analysis of welded joints in closed steel sections in rail vehicles
1
2012
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
Experimental investigation of the fatigue resistance of pipe-to-plate welded connections under bending, torsion and mixed mode loading
1
2014
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
Finite-element model calibration of a railway vehicle based on experimental modal parameters
1
2013
... 关于转向架构架结构载荷的研究已有诸多文献发表.文献[7 ,8 ]采用静态载荷乘以载荷因子的方法计算得到构架结构载荷.文献[9 ]采用截断奇异值法构建了构架应力和载荷之间的传递关系矩阵.文献[10 ,11 ,12 ]将部分实测数据引入多体动力学仿真模型得到基于多工况的结构载荷时间历程.金新灿等[13 ] 基于单节车辆通过道岔时的多体系统(MBS)模型,采用刚柔耦合动力学仿真的方法得到车辆通过道岔时关键部件的动态载荷.Matsumoto等[14 ] 借助高精度转向架滚动试验台对新研发的转向架实施曲线性能试验,研究表明试验台所得结果与数值仿真及实际线路运行结果具有良好的一致性.文献[15 ]针对应用于转向架的封闭式型钢部件的焊接试件进行疲劳试验、名义应力和切口应力计算.试验结果与国际焊接学会推荐数值的差异是由载荷状况和结构设计引起的.Bertini等[16 ] 通过纯弯、纯扭和相位混合加载试验对一种转向架用典型焊接接头开展疲劳强度研究,验证得到一种修正等效应力,与常用的Mises等效应力相比具有更低的离散度和更高的斜率,且适用于所有的实验结果.Ribeiro等[17 ] 对阿尔法摆式列车的车体和转向架构架开展动态测试,并将测试结果与建立的有限元模型进行了比对分析.上述文献大多是基于动态仿真或者台架试验进行的研究,并没有对线路运营条件下动应力损伤及载荷进行关联研究. ...
Experimental studies of load characteristics of bogie frames for 350 km/h EMUs
1
2012
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
城际动车组轮轨力统计特征
1
2019
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
城际动车组轮轨力统计特征
1
2019
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
Long-term load spectrum test of high speed train bogie
1
2015
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
Experimental investigation on vibration behavior of a CRH train at speed of 350 km/h
1
2015
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
高速列车载荷谱推断及扩展方法研究
1
2018
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
高速列车载荷谱推断及扩展方法研究
1
2018
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
Study on establishment of standardized load spectrum on bogie frames of high-speed trains
1
2019
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
地铁转向架构架运用载荷与疲劳损伤特征研究
1
2019
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
地铁转向架构架运用载荷与疲劳损伤特征研究
1
2019
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
高速列车轴箱弹簧载荷特性与疲劳损伤
1
2019
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
高速列车轴箱弹簧载荷特性与疲劳损伤
1
2019
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
Theoretical research and experimental validation of quasi-static load spectra on bogie frame structures of high-speed trains
1
2014
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
Estimating load spectra probability distributions of train bogie frames by the diffusion-based kernel density method.
1
2020
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
基于载荷标定的城际列车转向架载荷及应力分布特征研究
1
2016
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
基于载荷标定的城际列车转向架载荷及应力分布特征研究
1
2016
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
Analysis of the load-Stress response characteristics of the bogie frame in intercity electric multiple unit
1
2018
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
高速列车转向架构架疲劳试验载荷谱研究
1
2019
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...
高速列车转向架构架疲劳试验载荷谱研究
1
2019
... 近些年, 针对转向架构架动态载荷问题的研究也有所进展.Ren等[18 ] 采取试验测试的方法, 得到时速350 km/h动车组用动车与拖车转向架轴箱弹簧载荷、定位转臂座横向载荷和动态应力,并对载荷与应力特性进行了研究.丁然等[19 ] 采用测力轮对对城际动车组的轮轨力进行线路试验,得到了轮轨力载荷谱和各工况下轮轨力统计特征.Wang等[20 ] 采用跟踪测试的方法,得到了动车转向架轴箱弹簧垂向载荷和转臂横向载荷在一个镟轮周期内的变化规律,并基于此编制构架横向、浮沉、扭转和侧滚载荷谱.Zhai等[21 ] 在无砟轨道运营线路进行某型CRH动车组测试, 得到列车动态特性,进而对350 km/h速度级动车组振动特征和振动性能展开研究.陈道云等[22 ] 基于轴箱垂向加速度的线路实测,采用扩展因子法得到轴箱全寿命周期的垂向加速度载荷谱.Chen等[23 ] 采用核密度估计法、扩展因子法和损伤一致性理论对构架标准化载荷谱进行了研究.王斌杰等[24 ] 对地铁车辆转向架构架进行实际运营条件下的动应力测试,根据载荷标定的结果得到各载荷谱, 并对构架的疲劳损伤特征开展研究.杨广雪等[25 ] 制作了弹簧载荷测试传感器,通过线路试验得到各工况下轴箱载荷特性.Zhu等[26 ] 研究了高速列车转向架构架结构准静态和弹性动态载荷谱的理论问题.Ma等[27 ] 采用高斯核密度估计法对构架载荷谱的分布进行拟合.邹骅等[28 -29 ] 对城际列车构架载荷状态展开研究,借助标定试验结果还原出真实作用载荷, 最后对构架载荷与应力特征进行分析.王建斌[30 ] 等基于镟修周期内加速度测试建立了考虑载荷周期劣化的构架疲劳试验载荷谱.然而, 对于大多数情况下, 对只具备基于实际营运工况的动应力大数据测试条件下,动车转向架构架载荷实验谱问题研究还很欠缺. ...