引言
无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变.
随着黏弹性人工边界单元 (以下简称边界单元) 在实际工程中的广泛应用[8 -12 ] ,其数值稳定性问题随之而来. 研究人员在引入边界单元进行波动分析时,一般采用隐式无条件稳定的时域逐步积分算法,较少采用显式算法[13 -14 ] . 这是因为边界单元具有与内部介质不同的质量密度、刚度和阻尼,导致在边界单元区,显式算法的稳定条件不同于内部计算区. 由于边界单元区与相邻的内部计算区的力学参数完全不同,使得显式算法的稳定性分析遇到技术上的困难,长久以来未能给出与内部计算区类似的解析形式的数值积分稳定性条件,这在一定程度上影响了采用边界单元时对显式算法稳定性的判断,而数值算法稳定条件的缺失也限制了边界单元在显式动力分析中的应用.
显式算法的解耦特性回避了组集整体刚度阵和求解联立方程组等问题[15 -18 ] ,在大规模动力问题数值分析中的计算效率显著高于隐式算法,特别是对于大范围场地模型的并行计算问题,因此有必要对引入黏弹性人工边界单元时显式算法的稳定性开展研究.
数值稳定性的分析和改善研究一直伴随着人工边界理论的发展[19 -22 ] . 针对透射边界,可以改变与边界物理量相关的计算格式,通过滤波提高边界稳定性[23 ] . 对于多次透射边界,可以在边界区设置黏性阻尼,以消除多次透射边界的高频振荡失稳现象[24 ] . 黏弹性人工边界单元本身为物理上稳定的系统,将其引入计算系统中,并不影响整体的物理稳定条件. 其失稳机理是显式时域逐步积分算法所导致的,而与边界单元理论无关. 为改善数值稳定条件,需要全面考虑逐步积分过程中边界节点与内部单元节点之间的耦合效应,以此为依据调整满足显式时域积分数值稳定条件的临界时间步长,从而提高人工边界数值计算的稳定性.
本文针对人工边界典型位置处的局部子系统建立运动方程,利用传递矩阵谱半径分析方法,推导得到解析形式的局部子系统稳定性条件表达式.通过研究解析解中各物理参数对稳定性条件的影响,给出通过增加人工边界单元质量密度以实现改善显式算法稳定性条件的方法.本文研究对于提高黏弹性人工边界单元在动力显式计算中的适用性以及提高大范围工程场地波动分析的计算效率均具有重要意义.
1 黏弹性人工边界单元等效物理参数设置
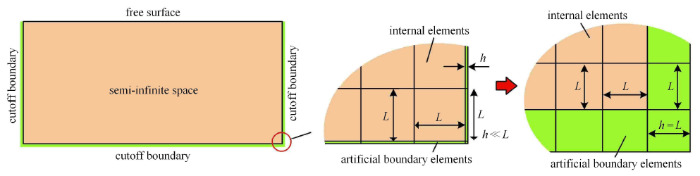
黏弹性人工边界单元是在无限域半空间模型的截断边界上向外法线方向延伸出的一层厚度为$h$的单元,通过设置等效物理参数来模拟黏弹性人工边界. 二维黏弹性人工边界单元的等效密度 $\tilde{\rho }$、等效弹性模量 $\tilde {E}$、等效泊松比 $\tilde {\mu}$ 和等效阻尼系数 $\tilde {\eta }$ 分别为[6 ]
(1) $ \left.\begin{array}{l} \tilde {\rho } = 0 , \ \ \ \tilde {E} = \alpha _{N} h\dfrac{G}{R} \\ \tilde {\mu } = 0 , \ \ \ \tilde {\eta } = \dfrac{\rho R}{2G}\Big (\dfrac{C_{S} }{\alpha_{T} } + \dfrac{C_{P} }{\alpha _{N} }\Big ) \end{array}\!\! \right \}$
其中,$G$ 为内部介质的剪切模量,$\rho $ 为内部介质的质量密度,$C_{S}$ 和 $C_{P}$ 分别为内部介质的 S 波和 P 波波速,$R$为散射波源至边界节点的距离,$\alpha _{T}$ 与 $\alpha _{N}$ 分别为切向与法向黏弹性人工边界参数,对于二维黏弹性人工边界,其推荐值分别为 0.5 和 1.
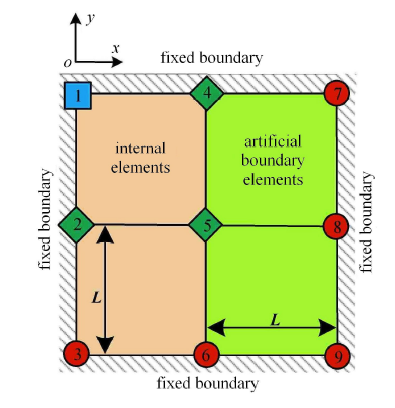
黏弹性人工边界单元厚度 $h$ 的鲁棒性良好,可灵活取值而对精度影响很小[6 ] . 由于显式算法的稳定条件受模型中的最小单元尺寸制约,在实际计算分析中,建议将边界单元的厚度设定为与内部单元尺寸一致,如图1 所示,以排除单元尺寸对整体稳定性的影响.
图1
图1
二维黏弹性人工边界单元示意图
Fig. 1
Diagrams of 2D viscoelastic artificial boundary element
2 边界局部子系统稳定性分析
为改善数值积分稳定性,首先应对失稳机理开展研究. 若不考虑人工边界的影响,可使用冯诺依曼方法对计算区域进行稳定性分析[25 ] ;引入边界单元并进行显式时域逐步积分计算时,则需要考虑边界单元对整体计算系统稳定性的影响.此时可以建立包含人工边界在内的整体系统的运动方程,采用传递矩阵谱半径分析方法,获得满足稳定条件的临界时间步长并进行失稳判断. 但在实际应用中,整体模型传递矩阵的建立和分析工作量巨大,通常难以 施行.
针对透射人工边界条件,关慧敏等[21 ] 和 Kamel等[26 ] 提出了一种通过分析局部子系统传递矩阵特征值来 研究透射人工边界稳定性的方法.由于该方法处理的子系统包含节点数量较多,只能给出系统稳定条件的数值解,难以给出解析解,不适合对稳定性条件的影响因素进行定量化的参数分析,制约了针对稳定性改善方法的研究.
针对黏弹性人工边界单元,李述涛等[27 ] 对一维和二维有限元系统最高阶模态进行了分析,证明了可以采用极小的子系统推导得出整体系统的稳定性条件.该子系统中只包含一个运动节点,所得的稳定性条件是整体系统数值稳定的充分条件.此外,该方法给出了系统稳定条件的解析解,可以直观且定量地分析各物理参数对数值稳定性的影响,为数值积分稳定性的改善创造了条件.
引入黏弹性人工边界单元后,可以选择对整体模型边界处具有典型特征的节点子系统开展研究. 一旦确定了子系统形式,即可根据显式逐步积分算法格式,将子系统的运动方程写成如下形式
(2) ${\pmb U}^{p + 1} = {\pmb A \pmb U}^p$
其中向量 ${\pmb U}$ 由子系统各节点的加速度、速度和位移组成;${\pmb A}$ 是传递矩阵,上标 $p$ 是自然数,$t = p\Delta t$;$\Delta t$ 为时间步长. 如果满足下列两条件,则积分格式 (2) 是稳定的[28 ] .条件 1:$\rho ({\pmb A}) \leqslant 1$,$\rho ({\pmb A})$ 是传递矩阵 ${\pmb A}$ 的谱半径;条件 2:如果 ${\pmb A}$ 具有多重特征值,则该特征值的模小于 1.由此可将子系统的稳定性分析归结为传递矩阵 ${\pmb A}$ 的谱半径计算.
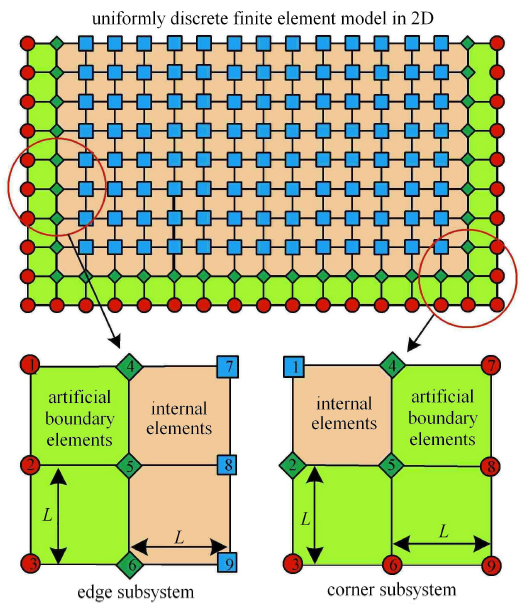
图2 所示是均匀离散的二维有限元整体模型中的两处典型节点子系统. 其一位于模型的侧边或底边,由 2 个内部介质单元和 2 个边界单元组成. 另一子系统位于模型角点处,由 1 个内部介质单元和 3 个边界单元组成.
图2
图2
二维模型中的两种节点子系统
Fig. 2
Two kinds of nodal subsystems in 2D model
文献[27 ] 采用上述研究思路,将侧边子系统与角点子系统从整体模型中分离出来,在四周施加固定约束. 利用传递矩阵的谱半径分析时域逐步积分算法的稳定性条件,最终推导出整体系统的稳定性条件. 分析结果表明,采用边界单元时,整体模型数值积分的稳定性条件要比内部系统的稳定性条件更为严格,这在一定程度上限制了显式数值积分方法的应用.
现有数值积分方法的稳定性研究表明,当介质的质量密度增大时 (相当于介质波速降低或结构自振周期变长),系统的数值积分稳定性条件将得到改善. 在原始的黏弹性人工边界单元中,等效质量密度 $\tilde {\rho } = 0$,但由于边界单元具有较良好的鲁棒性,适当调整参数对人工边界的模拟精度影响不大. 因此可以通过适当增加边界单元的质量密度以达到改善整体模型数值积分稳定性的目的.
下面首先给出考虑边界单元质量密度时,角点子系统和侧边子系统的稳定性条件.
2.1 角点子系统稳定性条件
角点子系统如图3 所示. 设内部介质单元的弹性模量为 $E$,剪切模量为 $G$,密度为 $\rho $,泊松比为 $\mu $,且无阻尼;黏弹性人工边界单元的密度为 $\tilde {\rho }$,弹性模量为 $\tilde {E}$,阻尼系数为 $\tilde {\eta }$,泊松比为 0,单元边长均为 $L$.
图3
图3
角点子系统
Fig. 3
Corner subsystem
二维平面单元的集中质量矩阵、刚度矩阵、阻尼矩阵分别参考文献 [6 ,29 -30 ] ,按节点编号组装矩阵后,得到角点子系统中 5 号节点的运动方程如下
(3) $ \dfrac{(\rho + 3\tilde {\rho })L^2}{4}\left[ \!\!\begin{array}{cc} 1 \!&\! 0 \\ 0 \!&\! 1 \end{array} \!\! \right]\left\{ \!\! \begin{array}{c} {\ddot {u}_x } \\ {\ddot {u}_y } \end{array} \!\!\right\} + \dfrac{\rho R\tilde {E}}{2G}(2C_{S} + C_{P} )\left[\!\! \begin{array}{cc} {\dfrac{3}{2}} \!&\! {\dfrac{1}{8}} \\ {\dfrac{1}{8}} \!&\! {\dfrac{3}{2}} \end{array} \!\!\right]\left\{ \!\!\begin{array}{c} {\dot {u}_x } \\ {\dot {u}_y } \end{array} \!\! \right\} +\\ \left(\!\! \begin{array}{cc} {\dfrac{E(3 - \mu )}{6(1 - \mu ^2)} + \dfrac{3\tilde {E}}{2}} & {\dfrac{ - E}{8(1 - \mu )} + \dfrac{\tilde {E}}{8}} \\ {\dfrac{ - E}{8(1 - \mu )} + \dfrac{\tilde {E}}{8}} & {\dfrac{E(3 - \mu )}{6(1 - \mu ^2)} + \dfrac{3\tilde {E}}{2}} \end{array} \!\! \right)\left\{ \!\! \begin{array}{c} {u_x } \\ {u_y } \end{array} \!\!\right\} = 0$
其中,$\ddot {u}$,$\dot {u}$,$u$ 分别为节点的加速度、速度和位移,下标 $x$,$y$ 表示运动方向. 显式时域逐步积分格式 (中心差分) 如下[31 ]
(4) $ \left.\begin{array}{l} \dot {u}\Big (t + \dfrac{\Delta t}{2}\Big) = \dot {u}\Big (t - \dfrac{\Delta t}{2}\Big) + \Delta t\ddot {u}(t) \\ u(t + \Delta t) = u(t) + \Delta t\dot {u}\Big (t + \dfrac{\Delta t}{2}\Big) \end{array} \!\! \right \}$
(5) $ \left\{ \begin{array}{c} {u(t + \Delta t)} \\ {v(t + \Delta t)} \\ {\Delta t\dot {u}\Big (t + \dfrac{\Delta t}{2}\Big)} \\ {\Delta t\dot {v}\Big (t + \dfrac{\Delta t}{2}\Big)} \end{array} \right\} = {\pmb A}_1 \left\{ \begin{array}{c} {u(t)} \\ {v(t)} \\ {\Delta t\dot {u}\Big (t - \dfrac{\Delta t}{2}\Big)} \\ {\Delta t\dot {v}\Big (t - \dfrac{\Delta t}{2}\Big)} \end{array} \right\}$
(6) ${\pmb A}_1 = \left[ \!\! \begin{array}{cccc} {1 - \dfrac{k_1 }{m_1 }\Delta t^2} & { - \dfrac{k_2 }{m_1 }\Delta t^2} & {1 - \dfrac{3c\Delta t}{2m_1 }} & { - \dfrac{c\Delta t}{8m_1 }} \\ { - \dfrac{k_2 }{m_1 }\Delta t^2} & {1 - \dfrac{k_1 }{m_1 }\Delta t^2} & { - \dfrac{c\Delta t}{8m_1 }} & {1 - \dfrac{3c\Delta t}{2m_1 }} \\ { - \dfrac{k_1 }{m_1 }\Delta t^2} & { - \dfrac{k_2 }{m_1 }\Delta t^2} & {1 - \dfrac{3c\Delta t}{2m_1 }} & { - \dfrac{c\Delta t}{8m_1 }} \\ { - \dfrac{k_2 }{m_1 }\Delta t^2} & { - \dfrac{k_1 }{m_1 }\Delta t^2} & { - \dfrac{c\Delta t}{8m_1 }} & {1 - \dfrac{3c\Delta t}{2m_1 }} \end{array} \!\!\right]$
(7) $\left.\!\!\begin{array}{l} m_1 = \dfrac{(\rho + 3\tilde {\rho })L^2}{4} , \ \ c = \dfrac{\rho L}{2}(2C_{S} + C_{P} ) \\ k_1 = \rho C_{S}^2\left( {\dfrac{(3 - \mu )}{3(1 - \mu )} + \dfrac{3L}{2R}} \right) , \ \ k_{2} = \dfrac{\rho C_{S}^2}{8}\left( {\dfrac{L}{R} - \dfrac{2(1{ + }\mu )}{1 - \mu }} \right) \end{array} \!\!\right\}$
传递矩阵 ${\pmb A}_{1}$ 的谱半径 $\rho ({\pmb A}_1 )$ 的表达式为
(8) $ \rho ({\pmb A}_1 ) = \dfrac{1}{8}\left| {8 - \dfrac{4(k_1 + k_2 )}{m_1 }\Delta t^2 - \dfrac{13c\Delta t}{2m_1 } - } \right. \\ \left. {\sqrt { - 8\left( {8 - \dfrac{13c\Delta t}{m_1 }} \right) + \left[ { - 8 + \dfrac{4(k_1 + k_2 )}{m_1 }\Delta t^2 + \dfrac{13c\Delta t}{2m_1 }} \right]^2} } \right|$
根据稳定性判别条件 $\rho ({\pmb A}_1 ) \leqslant 1$,得出角点子系统稳定性条件的解析表达式为
(9) $ \Delta t \leqslant \dfrac{\sqrt {256m_1 (k_1 + k_2 ) + (13c)^2} - 13c}{8(k_1 + k_2 )}$
(10) $ \dfrac{\Delta tC_{P} }{L} \leqslant \gamma _1$
其中,$\gamma _1 $ 为角点子系统稳定性参数,整理后如式 (11) 所示.
由式 (10) 和式 (11) 可以发现,当内部介质的 P 波波速 $C_{P}$ 和单元尺寸 $L$ 给定后,角点子系统数值稳定条件仅与质量比 $\tilde {\rho }/\rho $、内部介质的泊松比 $\mu$ 和单元尺寸与散射波源至边界距离之比 $L/R$ 有关. 由于内部介质的泊松比 $\mu \in \left[ {0,0.5}\right]$,由式 (11) 可以清楚的看出,增大人工边界单元的质量密度 $\tilde {\rho}$ 将有助于改善数值稳定性条件.
(11) $\begin{array}{l}\gamma _1 = \Bigg \{ \sqrt 3 (1 - \mu )\Bigg \{3\left( {603 + 338\sqrt 2 \sqrt {1 - 2\mu } \sqrt {1 - \mu } } \right) + 48(1 - 2\mu )\left\{ {13\left( {1 - \mu } \right)\dfrac{L}{R} + \left[ {39(1 - \mu )\dfrac{L}{R} + 2(9 - 7\mu )} \right]\dfrac{\tilde {\rho }}{\rho }} \right\} +\\ \mu \left( { - 4856 - 1014\sqrt 2 \sqrt {1 - 2\mu } \sqrt {1 - \mu } + 2983\mu } \right)\Bigg \}^{\tfrac 12} - 39\left( {1 - \mu } \right)^{\tfrac{3}{2}}\left( {\sqrt 2 \sqrt {1 - 2\mu } + \sqrt {1 - \mu } } \right) \Bigg \} \Bigg / \\ \Bigg [ {2\left( {9 - 7\mu } \right)\left( {1 - 2\mu } \right){ + }39\left( {1 - \mu } \right)\left( {1 - 2\mu } \right)\dfrac{L}{R}} \Bigg ]\end{array}$
2.2 侧边子系统稳定性条件
侧边子系统如图4 所示,其模型参数与角点子系统相同. 按节点编号组装矩阵后,得到侧边子系统中 5 号节点的运动方程如下
(12) $ \dfrac{(\rho + \tilde {\rho })L^2}{2}\left[\!\! \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\!\! \right]\left\{ \!\! \begin{array}{c} {\ddot {u}_x } \\ {\ddot {u}_y } \end{array}\!\! \right\} + \dfrac{\rho R\tilde {E}}{2G}(2C_{S} + C_{P} )\left[\!\! \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \!\! \right]\cdot \\ \left\{ \!\! \begin{array}{c} {\dot {u}_x } \\ {\dot {u}_y } \end{array}\!\! \right\} +\left[ {\dfrac{E(3 - \mu )}{3(1 - \mu ^2)} + \tilde {E}} \right]\left(\!\! \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\!\! \right)\left\{ \!\! \begin{array}{c} {u_x } \\ {u_y } \end{array} \!\! \right\} = 0 $
图4
图4
侧边子系统
Fig. 4
Edge subsystem
参照上一节方法,将式 (12) 写成传递矩阵的形式
(13) $ \left\{ \!\! \begin{array}{c} {u(t + \Delta t)} \\ {\Delta t\dot {u} \Big (t + \dfrac{\Delta t}{2} \Big)} \end{array}\!\! \right\} = {\pmb A}_2 \left\{ \!\! \begin{array}{c} {u(t)} \\ {\Delta t\dot {u} \Big (t - \dfrac{\Delta t}{2} \Big)} \end{array}\!\! \right\}$
(14) ${\pmb A}_2 = \left[\!\!\begin{array}{cc} {1 - \dfrac{k\Delta t^2}{m_2 }} & {1 - \dfrac{c\Delta t}{m_2 }} \\ { - \dfrac{k\Delta t^2}{m_2 }} & {1 - \dfrac{c\Delta t}{m_2 }} \end{array}\!\!\right] $
(15) $\left. \!\!\begin{array}{l} m_2 = \dfrac{(\rho + \tilde {\rho })L^2}{2} , \ \ c = \dfrac{\rho L}{2}(2C_{S} + C_{P} ) \\ k = \rho C_{S} ^2\left[ {\dfrac{2(3 - \mu )}{3(1 - \mu )} + \dfrac{L}{R}} \right] \end{array}\!\!\right\} $
计算传递矩阵 ${\pmb A}_{2}$ 的特征值,并根据稳定性判别条件 $\rho ({\pmb A}_2 ) \leqslant 1$,得出侧边子系统稳定性条件的解析表达式为
(16) $\Delta t \leqslant \dfrac{1}{k}(\sqrt {4km_2 + c^2} - c)$
(17) $\dfrac{\Delta tC_{P} }{L} \leqslant \gamma _2$
其中 $\gamma _2 $ 为侧边子系统稳定性参数,整理后如式 (18) 所示.
由式 (18) 可知,侧边子系统稳定性系数 $\gamma_{2}$ 同样为一个无量纲的解析表达式,可以用来定量讨论质量密度比 $\tilde {\rho }/\rho $ 的变化对数值稳定性条件的影响.
(18) $\gamma _2 = \dfrac{{3}(\mu - 1)^2\left[ {\sqrt {\dfrac{8(3 - \mu ) + 12(1 - \mu )\dfrac{L}{R}}{3(1 - \mu )^2}(1 - 2\mu )\left( {1 + \dfrac{\tilde {\rho }}{\rho }} \right) + \left( {1 + \sqrt {\dfrac{2 - 4\mu }{1 - \mu }} } \right)^2} - \sqrt {\dfrac{2 - 4\mu }{1 - \mu }} - 1} \right]}{2(3 - \mu )(1 - 2\mu ) + 3(1 - \mu )(1 - 2\mu )\dfrac{L}{R}}$
3 数值计算稳定性条件的改善方法
以上通过理论推导,分别给出了角点和侧边子系统数值积分稳定性条件,其数值稳定性系数 $\gamma_{1}$ 和 $\gamma_{2}$ 均为质量密度比 $\tilde {\rho }/\rho $、内部介质泊松比 $\mu $、单元尺寸与散射波源至边界距离之比 $L/R$ 的函数. 当无量纲参数 ${\Delta tC_{P}} /L$ 小于或等于稳定性系数时,相应的子系统满足数值积分的稳定性条件. 此外,整体系统的数值稳定性除需满足人工边界区的角点子系统和侧边子系统的稳定条件外,还需满足内部系统的稳定性条件. 显式时域逐步积分算法中内部单元的稳定性条件为[25 ]
(19) $\dfrac{\Delta tC_{P} }{L} \leqslant \gamma _0$
本节首先讨论人工边界单元质量密度 $\tilde {\rho }$ 和距离 $R$ 对数值稳定性的影响,并进一步给出改善数值稳定条件的方法.
3.1 人工边界单元质量密度对稳定性条件的影响
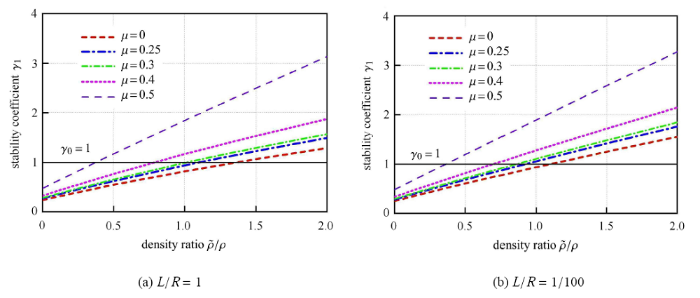
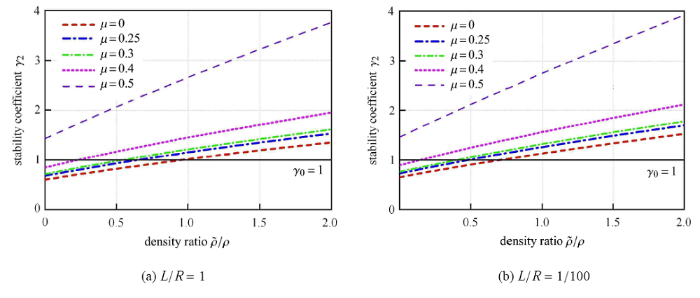
图5 和图6 分别给了出角点子系统和侧边子系统数值积分稳定性系数 $\gamma _{1}$ 和 $\gamma_{2}$ 随单元质量密度比 $\tilde {\rho }/\rho $ 的变化曲线. 其中单元尺寸与散射波源至边界距离之比 $L/R$ 分别为 1 和 1/100,内部介质泊松比 $\mu $ 分别为 0,0.25,0.3,0.4 和 0.5. 由图5 和图6 可以看出,增大质量密度比 $\tilde {\rho }/\rho $ 可以提高稳定性系数. 对于角点和侧边两种子系统,内部介质泊松比 $\mu $ 的取值越大,稳定性越宽松.
图5
图5
角点子系统稳定性系数随密度比变化情况
Fig. 5
The variation of corner subsystem stability coefficient with density ratio
图6
图6
侧边子系统稳定性系数随密度比变化情况
Fig. 6
The variation of edge subsystem stability coefficient with density ratio
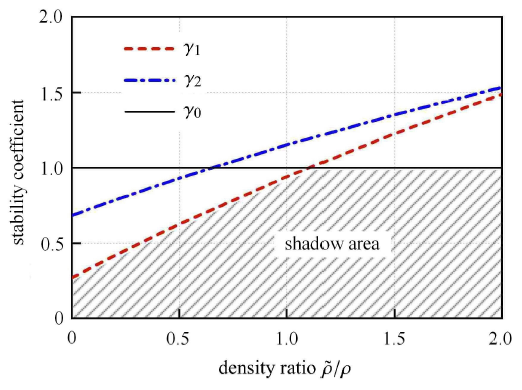
整体系统的数值稳定条件应同时满足人工边界子系统和内部单元的稳定性条件. 图7 给出了当 $L/R =1$ 和 $\mu = 0.25$ 时,整体系统的数值积分稳定条件. 图中阴影区域即为满足整体系统数值积分稳定性的区域.
图7
图7
整体系统数值稳定区域
Fig. 7
The region of numerical stability in the overall system
以上分析可以得出以下两点结论:(1) 人工边界区的数值积分稳定性条件由角点子系统控制;(2) 采用黏弹性人工边界单元时,增大边界单元的质量密度可以有效改善显式数值积分的稳定性条件.
3.2 距离 ${\pmb R}$ 对稳定性条件的影响
影响人工边界子系统稳定性的另外一个因素是散射波源至人工边界的距离 $R$. 由于稳定性系数计算式 (11) 和式 (18) 的分子和分母中均含有反映距离 $R$ 影响的无量纲系数 $L/R$,因此,难以像质量密度 $\tilde {\rho}$ 一样,直接给出对稳定性影响效果的明确判断. 图8 和图9 给出了泊松比等于 0.25,质量密度比分别为 0 和 1 时,3 种系统稳定性系数 $\gamma_{0}$,$\gamma _{1}$ 和 $\gamma_{2}$ 随 $R/L$ 的变化曲线.
图8
图8
稳定性系数随$R/L$的变化情况
Fig. 8
The variation of stability coefficient with $R/L$
图9
图9
均匀半空间模型
Fig. 9
Homogeneous half space model
从图8 中可以看出,当散射波源至人工边界的距离与单元尺寸之比 $R/L$ 增大时,角点和侧边两种子系统的稳定性参数只在初始阶段略为增大,当 $R$ 大于约 5 倍的 $L$ 后,稳定性系数基本保持不变.因此,增大模型尺寸对整体系统数值稳定性 的改善几乎不产生影响. 另外,当泊松比 $\mu$ 取为其他值时,可以得到完全相同的结论.
3.3 改进的黏弹性人工边界单元
基于以上分析,可确定改善显式数值算法稳定性具体措施 (方法) 和原则:(1) 通过增大黏弹性人工边界单元的质量密度达到改善算法稳定性的目的;(2) 保证人工边界区子系统的稳定性条件达到或略宽于内部单元系统稳定性条件,使得整体系统的稳定性由内部系统控制和判断.
改进的黏弹性人工边界单元参数设置如下:设内部介质剪切模量为$G$,质量密度为 $\rho$,剪切波速和压缩波速分别为 $C_{S}$ 和 $C_{P}$;内部介质单元厚度和边界单元厚度均为 $L$,边界节点至散射波源的距离为 $R$,边界单元质量密度为 $\tilde {\rho }$;$\alpha _{T} $ 与 $\alpha _{N} $ 分别为切向与法向黏弹性人工边界参数,二维模型建议 $\alpha _{T} $ 取 0.5,$\alpha _{N} $ 取 1.0. 稳定性条件改善后,二维黏弹性人工边界单元质量密度 $\tilde {\rho }$、等效刚度 $\tilde {E}$、泊松比 $\tilde {\mu }$ 和等效阻尼 $\tilde {\eta }$ 分别为
(20) $ \left.\begin{array}{l} \tilde {\rho } = \rho \\ \tilde {E} = \alpha _{N} h\dfrac{G}{R} \cdot \dfrac{(1 + \tilde {\mu })(1 - 2\tilde {\mu })}{1 - \tilde {\mu }}\\ \tilde {\mu } = 0\\ \tilde {\eta } = \dfrac{\rho R}{2G}\Big (\dfrac{C_{S} }{\alpha _{T} } + \dfrac{C_{P} }{\alpha _{N} } \Big ) \end{array} \!\! \right \}$
稳定性改善后,整体系统稳定性条件基本受内部介质区域控制,可采用最小单元尺寸与内部介质压缩波速的比值估算满足稳定性条件的临界时间 步长.
4 稳定性数值算例及精度分析
4.1 均匀半空间模型
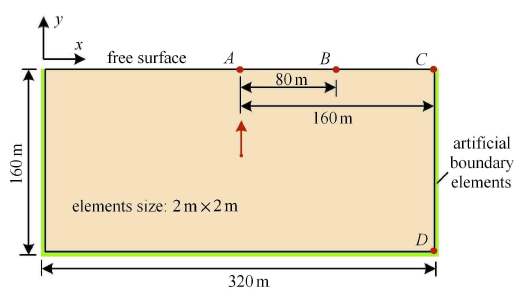
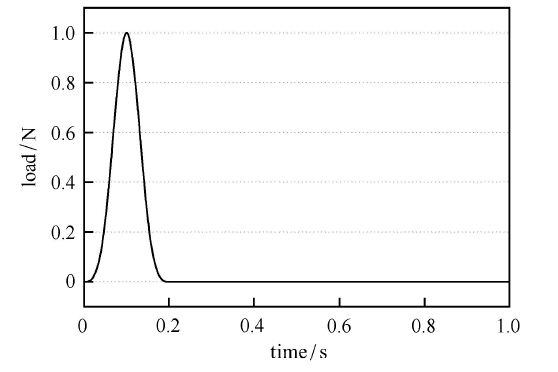
建立如图9 所示的均匀半空间模型. 模型尺寸为 320 m $\times$ 160 m,内部介质的密度为 2500 kg/m$^{3}$,剪切波速为 500 m/s,泊松比为 0.3,有限元网格尺寸为 2 m $\times$ 2 m,模型侧边和底边设置黏弹性人工边界单元,选取图中 $A, B, C,D$ 四点作为观测点,考察边界单元参数变化后,模型节点位移的计算精度. 采用持时为 0.2 s 的脉冲作为动力载荷,沿 $y$ 轴正向施加于模型中点处,载荷时程曲线如图10 所示.
图10
图10
动力载荷时程曲线
Fig. 10
Time history of the dynamic load
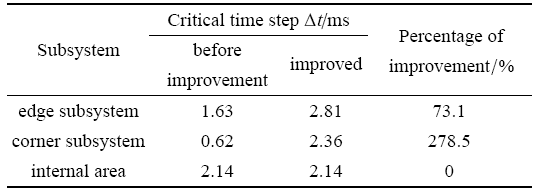
表1 给出了均匀半空间模型稳定性改善前后临界时间步长比较情况. 稳定性条件改善前,边界单元的质量密度为 0,整体系统稳定性受角点子系统控制,按式 (9) 计算得到角点子系统满足稳定性条件的临界时间步长为 0.62 ms. 按照此时间步长可顺利完成模型动力计算. 而如果将时间步长增大,例如取 0.85 ms,计算发生失稳.
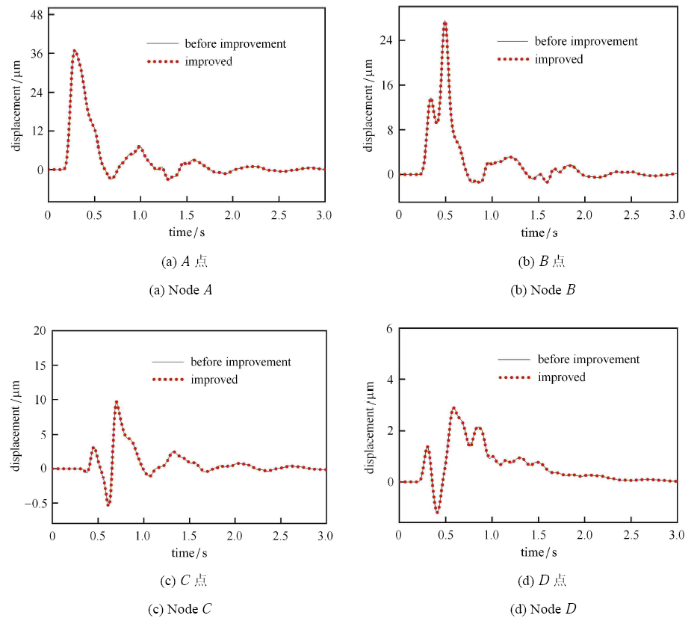
采用改进的黏弹性人工边界单元,即将人工 边界单元密度设为与内部介质一致,其值为2500 kg/m$^{3}$,整体模 型稳定性变为受内部区域控 制,采用内部介质稳定性条件 ($\Delta t= 2.14$ ms) 可顺利完成对整体模型的显式时域逐步积分计算,不会发生失稳.从图11 可以看出,稳定性条件改善后,观测点 $A, B, C, D$ 四点的位移时程曲线与改善前相比吻合良好,说明边界单元自身质量密度的适当增大对波动问题计算精度的影响很小.另一方面,由于数值积分的时间步长比改善前增大了 243.3%,总计算时间相较于原时长缩短了 70.9% 左右,大幅提高了显式时域逐步积分的计算效率.
图11
图11
均匀介质模型中 4 个观测点 $y$ 方向位移比较
Fig. 11
Comparison of displacements in $y$ direction of four nodes in the homogeneous model
4.2 成层半空间模型
建立如图12 所示的成层半空间有限元模型. 模 型尺寸为 320 m $\times $ 160 m,上层介质密度为 2000 kg/m$^{3}$, 剪切波速为 300 m/s,泊松比为 0.27,下层介质密度为 2500 kg/m$^{3}$,剪切波速为 500 m/s,泊松比为 0.3,整体模型的有限元网格尺寸为 2 m $\times $ 2 m. 脉冲载荷施加于模型的几何中心,沿 $y$ 轴正向加载,时程曲线如图6 所示. 通过令边界单元的质量密度与内部区域相等的方法对稳定性进行改善. 同样选取图中 $A, B, C, D$ 四点作为观测点,考察稳定性改善方法的可靠性和改善后半无限域空间波动问题的计算精度.
图12
图12
成层半空间模型
Fig. 12
Layered half space model
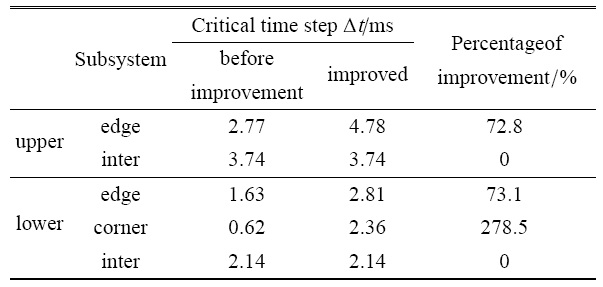
表2 对成层介质中各子系统和内部区域稳定性改善前后的临界时间步长进行了比较.从结果可以看出,上层介质的稳定性条件比下层介质宽松.由于稳定性条件受最不利情况控制,因此成层介质模型整体系统的稳定性条件由下层介质所控制. 本算例中的下层介质参数与 4.1 节的均匀半空间模型相同,因此整体系统稳定性条件也与上节算例相同.
按照稳定性改善前后的临界时间步长对成层半空间模型进行动力分析,结果如图13 所示. 图中 $A, B, C,D$ 四点位移时程曲线吻合良好,再次验证了边界单元自身质量密度的适当增大对波动问题计算精度的影响很小.对于成层半空间模型,显式时域逐步积分的总计算时间相较于原时长也缩短了 70.9%,计算效率显著提高.
图13
图13
成层介质模型中四个观测点 $y$ 方向位移比较
Fig. 13
Comparison of displacements in $y$ direction of four nodes in the layered model
5 结论
本文针对采用黏弹性人工边界单元时显式时域逐步积分算法稳定性改善问题,推导得到了含黏弹性人工边界单元在内的有限元系统在采用显式时域逐步积分 (中心差分) 时数值稳定条件的解析解.研究了各物理参数对稳定性条件的影响,提出了改善数值积分稳定性的方法,并通过算例验证了这一改善方法的有效性和对黏弹性人工边界单元计算精度的影响. 结论如下:
(1) 采用有适当质量的黏弹性人工边界单元,可在保证无限域空间波动问题计算精度的前提下,大幅增大满足显式时域逐步积分稳定性条件的临界时间步长,达到改善显式数值积分稳定性的目的.
(2) 可将内部单元密度设置为边界单元密度的上限,此时整体系统的积分稳定性条件受内部介质区域控制,可通过模型中最小单元尺寸与内部介质压缩波速的比值来估算满足稳定性条件的临界时间 步长.
(3) 黏弹性人工边界单元中的物理参数 $R$,即散射波源至人工边界的距离,对显式时域逐步积分算法稳定性的影响不大,当 $R$ 很小时,$R$ 的增大可以略微改善显式算法的稳定性,当 $R$ 大于约 5 倍的单元边长时,其对显式算法稳定性的影响基本不再变化.
(4) 如果显式时域逐步积分格式发生变化,依然可以使用本文提出的传递矩阵谱半径分析方法,按照不同积分格式将节点子系统运动方程展开,利用谱半径不大于 1 的判别条件给出稳定性结论,研究分析适用的稳定性改善方法.
参考文献
View Option
[1]
Alterman ZS Aboudi J Karal FC . Pulse propagation in a laterally heterogeneous solid elastic sphere
Geophysical Journal of the Royal Astronomical Society 1970 ,21 (3 ):243 -260
[本文引用: 1]
[2]
杜修力 , 赵密 , 王进廷 . 近场波动模拟的人工应力边界条件
力学学报 , 2006 ,38 (1 ):49 -56
URL
[本文引用: 1]
采用平面波和远场散射波混合透射,引入无限介质线弹性本构关系建立了一种应力人工边界条件. 其优点在于边界结点反应与内部有限元结点反应采用相同的积分格式计算,有限元积分方法稳定时不存在人工边界失稳问题. 数值算例表明:边界精度高于现有黏性边界、黏弹性人工边界,以及一、二阶透射人工边界.
( Du Xiuli Zhao Mi Wang Jinting . A stress artificial boundary in fea for near field wave problem
Chinese Journal of Theoretical and Applied Mechanics 2006 ,38 (1 ):49 -56 (in Chinese))
URL
[本文引用: 1]
The stability and accuracy of local artificial boundary are two important criterions for evaluating its applied value in engineering. In this paper, a stress artificial boundary condition was developed by mixing the planar waves and the scattered waves transmitting into the linear elastic infinite media through artificial boundary. For the proposed boundary condition, the responses of boundary nodes and finite element nodes are calculated by the same integral method, and its stability condition is also the same as the finite element integral method. Numerical examples demonstrate that the accuracy of the proposed boundary is higher than that of existing viscous boundaries, viscous-spring boundaries, the first-order transmitting boundary and the second-order transmitting boundary.
[3]
邢浩洁 , 李鸿晶 . 透射边界条件在波动谱元模拟中的实现:一维波动
力学学报 , 2017 ,49 (2 ):367 -379
[本文引用: 1]
( Xing Haojie Li Hongjing . Implementation of multi-transmitting boundary condition for wave motion simulation by spectral element method: one dimension case
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (2 ):367 -379 (in Chinese))
[本文引用: 1]
[4]
刘晶波 , 宝鑫 , 谭辉 等 . 波动问题中流体介质的动力人工边界
力学学报 , 2017 ,49 (6 ):1418 -1427
[本文引用: 1]
( Liu Jingbo Bao Xin Tan Hui , et al . Dynamical artificial boundary for fluid medium in wave motion problems
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (6 ):1418 -1427 (in Chinese))
[本文引用: 1]
[5]
章小龙 , 李小军 , 陈国兴 等 . 黏弹性人工边界等效载荷计算的改进方法
力学学报 , 2016 ,48 (5 ):1126 -1135
[本文引用: 1]
( Zhang Xiaolong Li Xiaojun Chen Guoxing , et al . An improved method of the calculation of equivalent nodal forces in viscous-elastic artificial boundary
Chinese Journal of Theoretical and Applied Mechanics 2016 ,48 (5 ):1126 -1135 . (in Chinese))
[本文引用: 1]
[6]
刘晶波 , 谷音 , 杜义欣 . 一致黏弹性人工边界及黏弹性边界单元
岩土工程学报 , 2006 ,28 (9 ):1070 -1075
[本文引用: 4]
( Liu Jingbo Gu Yin Du Yixin . Consistent viscous-spring artificial boundaries and viscous-spring boundary elements
Chinese Journal of Geotechnical Engineering 2006 ,28 (9 ):1070 -1075 (in Chinese))
[本文引用: 4]
[7]
谷音 , 刘晶波 , 杜义欣 . 三维一致黏弹性人工边界及等效黏弹性边界单元
工程力学 , 2007 ,24 (12 ):31 -37
[本文引用: 1]
( Gu Yin Liu Jingbo Du Yixin . 3D consistent viscous-spring artificial boundary and viscous-spring boundary element
Engineering Mechanics 2007 ,24 (12 ):31 -37 (in Chinese))
[本文引用: 1]
[8]
王启云 , 张家生 , 孟飞 等 . 高速铁路路基模型列车振动荷载模拟
振动与冲击 , 2013 (6 ):48 -51, 77
[本文引用: 1]
( Wand Qiyun Zhang Jiasheng Meng Fei , et al . Simulation of train vibration load on the subgrade testing model of high-speed railway
Journal of Vibration and Shock 2013 (6 ):48 -51, 77 (in Chinese))
[本文引用: 1]
[9]
尹尚之 , 叶丹 , 梁应军 等 . 二维弧形一致黏弹性边界单元在 ABAQUS 中的应用
世界地震工程 , 2017 ,33 (1 ):69 -74
( Yin Shangzhi Ye Dan Liang Yingjun , et al . Application of 2D arc consistent viscous-spring artificial boundary element in ABAQUS
World Earthquake Engineering 2017 ,33 (1 ):69 -74 (in Chinses))
[10]
贾磊 , 解咏平 , 李慎奎 . 爆破振动对邻近隧道衬砌安全的数值模拟分析
振动与冲击 , 2015 (11 ):181 -185, 219
( Jia Lei Xie Yongping Li Shenkui . Numerical simulation for impact of blasting vibration on nearby tunnel lining safety
Journal of Vibration and Shock 2015 (11 ):181 -185, 219 (in Chinese))
[11]
Bao X Liu JB Wang DY , et al . Modification research of the internal substructure method for seismic wave input in deep underground structure-soil systems
Shock and Vibration 2019 : 1 -13
[12]
Liu JB Bao X Wang DY , et al . The internal substructure method for seismic wave input in 3D dynamic soil-structure interaction analysis
Soil Dynamic and Earthquake Engineering 2019 ,127 :1 -12
[本文引用: 1]
[13]
刘晶波 , 谭辉 , 宝鑫 等 . 土-结构动力相互作用分析中基于人工边界子结构的地震波动输入方法
力学学报 , 2018 ,50 (1 ):32 -43
[本文引用: 1]
( Liu Jingbo Tan Hui Bao Xin , et al . The seismic wave input method for soil-structure dynamic interaction analysis based on the substructure of artificial boundaries
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (1 ):32 -43 (in Chinese))
[本文引用: 1]
[14]
Li ST Liu JB Yang Z , et al . Multiscale method for seismic response of near-source sites
Advances in Civil Engineering 2020 : 1 -25
[本文引用: 1]
[15]
刘恒 , 廖振鹏 . 波动数值模拟的一种显式方法-二维波动
力学学报 , 2010 ,42 (6 ):1104 -1116
[本文引用: 1]
( Liu Heng Liao Zhenpeng . An explicit method for numerical simulation of wave motion-2D wave motion
Chinese Journal of Theoretical and Applied Mechanics 2010 ,42 (6 ):1104 -1116 (in Chinese))
[本文引用: 1]
[16]
马天宝 , 任会兰 , 李健 等 . 爆炸与冲击问题的大规模高精度计算
力学学报 , 2016 ,48 (3 ):599 -608
DOI
URL
爆炸与冲击问题的数值模拟在国防和民用安全领域具有重要的工程实用价值.由于爆炸与冲击问题是一个多物质在高应变率、高温及高压条件下的强非线性的瞬态动力学问题,给数值模拟带来了很多的困难,为此,针对爆炸与冲击问题数值模拟中的一些关键和难点问题开展了研究.提出了三维非线性双曲守恒系统的伪弧长自适应网格算法,分析了算法的实现过程,数值结果表明该算法有效地提高了冲击波强间断处的分辨率.发展了针对气相爆轰数值模拟的附加龙格-库塔方法,对非线性对流项进行显示计算,化学反应源项进行半隐式计算,有效地解决了源项引起的刚性问题,计算结果表明该算法可以准确地捕捉和描述爆轰波的复杂结构和典型特征.针对三维工程实际物理问题中的大规模计算需求,给出了三维多物质流体动力学欧拉数值方法的并行化方法,开发了三维爆炸与冲击问题并行计算程序,并给出了针对该并行程序的测试方法.上述工作有利地解决了爆炸与冲击问题大规模、高精度计算中的一些难题.最后,开展了大口径聚能射流侵彻混凝土靶问题的数值模拟和实验研究,通过典型爆炸与冲击工程问题的计算验证了所研究数值方法的有效性.
( Ma Tianbao Ren Huilan Li Jian , et al . Large scale high precision computation for explosion and impact problems
Chinese Journal of Theoretical and Applied Mechanics 2016 ,48 (3 ):599 -608 (in Chinese))
[17]
何涛 . 基于 ALE 有限元法的流固耦合强耦合数值模拟
力学学报 , 2018 ,50 (2 ):395 -404
( He Tao . A partitioned strong coupling algorith for fluid-structure interaction using arbitrary lagrangian-eulerian finite eleent forulation
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (2 ):395 -404 (in Chinese))
[18]
李鸿晶 , 梅雨辰 , 任永亮 . 一种结构动力时程分析的积分求微方法
力学学报 , 2019 ,51 (5 ):1507 -1516
[本文引用: 1]
( Li Hongjing Mei Yuchen Ren Yongliang . An integral differentiation procedure for dynamic time-history response analysis of structures
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (5 ):1507 -1516 (in Chinese))
[本文引用: 1]
[19]
谢志南 , 廖振鹏 . 透射边界高频失稳机理及其消除方法-SH波动
力学学报 , 2012 ,44 (4 ):745 -752
[本文引用: 1]
( Xie Zhinan Liao Zhenpeng . Mechanism of high frequency instability caused by transmitting boundary and method of its elimination-SH wave
Chinese Journal of Theoretical and Applied Mechanics 2012 ,44 (4 ):745 -752 (in Chinese))
[本文引用: 1]
[20]
关慧敏 , 廖振鹏 . 时域局部人工边界的稳定性分析方法概述
世界地震工程 , 1997 (2 ):1 -7
( Guan Huimin Liao Zhenpeng . Overview of stability analysis methods for local artificial boundaries in the time domain
World Earthquake Engineering 1997 (2 ):1 -7 (in Chinese))
[21]
关慧敏 , 廖振鹏 . 局部人工边界稳定性的一种分析方法
力学学报 , 1996 ,28 (3 ):376 -380
[本文引用: 1]
( Guan Huimin Liao Zhenpeng . A method for the stability analysis of local artificial boundaries
Chinese Journal of Theoretical and Applied Mechanics 1996 ,28 (3 ):1601 -1606 (in Chinese))
[本文引用: 1]
[22]
李小军 , 杨宇 . 透射边界稳定性控制措施探讨
岩土工程学报 , 2012 (4 ):641 -645
[本文引用: 1]
( Li Xiaojun Yang Yu . Measures for stability control of transmitting boundary
Journal of Geotechnical Engineering 2012 (4 ):641 -645 (in Chinese))
[本文引用: 1]
[23]
Liao ZP Liu JB . Numerical instabilites of a local transmitting boundary
Earthq Eng Struct Dyn 1992 ,21 :65 -77
[本文引用: 1]
[24]
关慧敏 , 廖振鹏 . 一种改善多次透射边界稳定性的措施
地震工程与工程震动 , 1997 (4 ):2 -9
[本文引用: 1]
( Guan Huimin Liao Zhenpeng . A measure to improve the stability of multiple transmission boundary
Earthquake Engineering and Engineering Vibration 1997 (4 ):2 -9 (in Chinese))
[本文引用: 1]
[25]
Liu J Sharan SK . Analysis of dynamic contact of cracks in viscoelastic media
Computer Methods in Applied Mechanics and Engineering 1995 ,121 (1-4 ):187 -200
[本文引用: 2]
[26]
Kamel AH . A stability checking procedure for finite-difference schemes with boundary conditions in acoustic media
Bull Seism Soc Am 1989 ,79 (5 ):1601 -1606
[本文引用: 1]
[28]
Hughes TJR . Analysis of transient algorithms with particular reference to stability behavior
Computational Methods for Transient Analysis 1983 ,I :67 -156
[本文引用: 1]
[29]
王勖成 , 邵敏 . 有限单元法基本原理和数值方法 . 北京 : 清华大学出版社 , 1997 : 66 -67
[本文引用: 1]
( Wang Xucheng Shao Min . Basic Principle and Numerical Method of Finite Element Method . Beijing : Tsinghua University Press , 1997 : 66 -67 (in Chinese))
[本文引用: 1]
[30]
申志强 , 夏军 , 宋殿义 等 . 基于高阶剪切变形理论的四边形求积元板单元及其应用
力学学报 , 2018 ,50 (5 ):1093 -1103
[本文引用: 1]
( Shen Zhiqiang Xia Jun Song Dianyi , et al . A quadrilateral quadrature plate element based on reddy's higher-order shear deformation theory and its application
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (5 ):1093 -1103 (in Chinese))
[本文引用: 1]
[31]
Abaqus Analysis User's Manual (version 6.14)
ABAQUS, INC. , 2013
[本文引用: 1]
Pulse propagation in a laterally heterogeneous solid elastic sphere
1
1970
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
近场波动模拟的人工应力边界条件
1
2006
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
近场波动模拟的人工应力边界条件
1
2006
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
透射边界条件在波动谱元模拟中的实现:一维波动
1
2017
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
透射边界条件在波动谱元模拟中的实现:一维波动
1
2017
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
波动问题中流体介质的动力人工边界
1
2017
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
波动问题中流体介质的动力人工边界
1
2017
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
黏弹性人工边界等效载荷计算的改进方法
1
2016
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
黏弹性人工边界等效载荷计算的改进方法
1
2016
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
一致黏弹性人工边界及黏弹性边界单元
4
2006
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
... 黏弹性人工边界单元是在无限域半空间模型的截断边界上向外法线方向延伸出的一层厚度为$h$的单元,通过设置等效物理参数来模拟黏弹性人工边界. 二维黏弹性人工边界单元的等效密度 $\tilde{\rho }$、等效弹性模量 $\tilde {E}$、等效泊松比 $\tilde {\mu}$ 和等效阻尼系数 $\tilde {\eta }$ 分别为[6 ] ...
... 黏弹性人工边界单元厚度 $h$ 的鲁棒性良好,可灵活取值而对精度影响很小[6 ] . 由于显式算法的稳定条件受模型中的最小单元尺寸制约,在实际计算分析中,建议将边界单元的厚度设定为与内部单元尺寸一致,如图1 所示,以排除单元尺寸对整体稳定性的影响. ...
... 二维平面单元的集中质量矩阵、刚度矩阵、阻尼矩阵分别参考文献 [6 ,29 -30 ] ,按节点编号组装矩阵后,得到角点子系统中 5 号节点的运动方程如下 ...
一致黏弹性人工边界及黏弹性边界单元
4
2006
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
... 黏弹性人工边界单元是在无限域半空间模型的截断边界上向外法线方向延伸出的一层厚度为$h$的单元,通过设置等效物理参数来模拟黏弹性人工边界. 二维黏弹性人工边界单元的等效密度 $\tilde{\rho }$、等效弹性模量 $\tilde {E}$、等效泊松比 $\tilde {\mu}$ 和等效阻尼系数 $\tilde {\eta }$ 分别为[6 ] ...
... 黏弹性人工边界单元厚度 $h$ 的鲁棒性良好,可灵活取值而对精度影响很小[6 ] . 由于显式算法的稳定条件受模型中的最小单元尺寸制约,在实际计算分析中,建议将边界单元的厚度设定为与内部单元尺寸一致,如图1 所示,以排除单元尺寸对整体稳定性的影响. ...
... 二维平面单元的集中质量矩阵、刚度矩阵、阻尼矩阵分别参考文献 [6 ,29 -30 ] ,按节点编号组装矩阵后,得到角点子系统中 5 号节点的运动方程如下 ...
三维一致黏弹性人工边界及等效黏弹性边界单元
1
2007
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
三维一致黏弹性人工边界及等效黏弹性边界单元
1
2007
... 无限域中波动问题的求解是众多物理领域所面对的重要研究课题. 针对此问题最初的分析方法一般是将截断边界取到足够远的位置,在截断边界产生的反射波返回感兴趣区域前完成计算过程[1 ] . 这一方法具有较高的精度,但计算成本过高. 人工边界技术是目前常用的无限域介质数值模拟方法,将人工边界引入无限域空间的近场模型中,可吸收截断边界处的外行波动[2 -3 ] . 在众多的人工边界技术中,黏弹性人工边界基于全空间均匀介质中的柱面波和球面波理论推导得到,可等效为在每个边界节点上施加的远端固定的并联弹簧-阻尼器系统,既具有较高的计算精度,又可在多种有限元软件中进行集成,获得了较为广泛的工程应用[4 -5 ] . 但由于离散弹簧-阻尼器的施加需依赖程序语言对模型进行前处理,实用性受到一定影响. 为解决这一问题,刘晶波等[6 ] 和谷音等[7 ] 发展了黏弹性人工边界单元,其思路是利用有限单元的矩阵等效构造等效人工边界单元. 该方法仅需指定模型最外层单元的密度、弹性模量、泊松比和阻尼系数,即可模拟集中黏弹性人工边界,且计算精度不变. ...
高速铁路路基模型列车振动荷载模拟
1
2013
... 随着黏弹性人工边界单元 (以下简称边界单元) 在实际工程中的广泛应用[8 -12 ] ,其数值稳定性问题随之而来. 研究人员在引入边界单元进行波动分析时,一般采用隐式无条件稳定的时域逐步积分算法,较少采用显式算法[13 -14 ] . 这是因为边界单元具有与内部介质不同的质量密度、刚度和阻尼,导致在边界单元区,显式算法的稳定条件不同于内部计算区. 由于边界单元区与相邻的内部计算区的力学参数完全不同,使得显式算法的稳定性分析遇到技术上的困难,长久以来未能给出与内部计算区类似的解析形式的数值积分稳定性条件,这在一定程度上影响了采用边界单元时对显式算法稳定性的判断,而数值算法稳定条件的缺失也限制了边界单元在显式动力分析中的应用. ...
高速铁路路基模型列车振动荷载模拟
1
2013
... 随着黏弹性人工边界单元 (以下简称边界单元) 在实际工程中的广泛应用[8 -12 ] ,其数值稳定性问题随之而来. 研究人员在引入边界单元进行波动分析时,一般采用隐式无条件稳定的时域逐步积分算法,较少采用显式算法[13 -14 ] . 这是因为边界单元具有与内部介质不同的质量密度、刚度和阻尼,导致在边界单元区,显式算法的稳定条件不同于内部计算区. 由于边界单元区与相邻的内部计算区的力学参数完全不同,使得显式算法的稳定性分析遇到技术上的困难,长久以来未能给出与内部计算区类似的解析形式的数值积分稳定性条件,这在一定程度上影响了采用边界单元时对显式算法稳定性的判断,而数值算法稳定条件的缺失也限制了边界单元在显式动力分析中的应用. ...
二维弧形一致黏弹性边界单元在 ABAQUS 中的应用
0
2017
二维弧形一致黏弹性边界单元在 ABAQUS 中的应用
0
2017
爆破振动对邻近隧道衬砌安全的数值模拟分析
0
2015
爆破振动对邻近隧道衬砌安全的数值模拟分析
0
2015
Modification research of the internal substructure method for seismic wave input in deep underground structure-soil systems
0
2019
The internal substructure method for seismic wave input in 3D dynamic soil-structure interaction analysis
1
2019
... 随着黏弹性人工边界单元 (以下简称边界单元) 在实际工程中的广泛应用[8 -12 ] ,其数值稳定性问题随之而来. 研究人员在引入边界单元进行波动分析时,一般采用隐式无条件稳定的时域逐步积分算法,较少采用显式算法[13 -14 ] . 这是因为边界单元具有与内部介质不同的质量密度、刚度和阻尼,导致在边界单元区,显式算法的稳定条件不同于内部计算区. 由于边界单元区与相邻的内部计算区的力学参数完全不同,使得显式算法的稳定性分析遇到技术上的困难,长久以来未能给出与内部计算区类似的解析形式的数值积分稳定性条件,这在一定程度上影响了采用边界单元时对显式算法稳定性的判断,而数值算法稳定条件的缺失也限制了边界单元在显式动力分析中的应用. ...
土-结构动力相互作用分析中基于人工边界子结构的地震波动输入方法
1
2018
... 随着黏弹性人工边界单元 (以下简称边界单元) 在实际工程中的广泛应用[8 -12 ] ,其数值稳定性问题随之而来. 研究人员在引入边界单元进行波动分析时,一般采用隐式无条件稳定的时域逐步积分算法,较少采用显式算法[13 -14 ] . 这是因为边界单元具有与内部介质不同的质量密度、刚度和阻尼,导致在边界单元区,显式算法的稳定条件不同于内部计算区. 由于边界单元区与相邻的内部计算区的力学参数完全不同,使得显式算法的稳定性分析遇到技术上的困难,长久以来未能给出与内部计算区类似的解析形式的数值积分稳定性条件,这在一定程度上影响了采用边界单元时对显式算法稳定性的判断,而数值算法稳定条件的缺失也限制了边界单元在显式动力分析中的应用. ...
土-结构动力相互作用分析中基于人工边界子结构的地震波动输入方法
1
2018
... 随着黏弹性人工边界单元 (以下简称边界单元) 在实际工程中的广泛应用[8 -12 ] ,其数值稳定性问题随之而来. 研究人员在引入边界单元进行波动分析时,一般采用隐式无条件稳定的时域逐步积分算法,较少采用显式算法[13 -14 ] . 这是因为边界单元具有与内部介质不同的质量密度、刚度和阻尼,导致在边界单元区,显式算法的稳定条件不同于内部计算区. 由于边界单元区与相邻的内部计算区的力学参数完全不同,使得显式算法的稳定性分析遇到技术上的困难,长久以来未能给出与内部计算区类似的解析形式的数值积分稳定性条件,这在一定程度上影响了采用边界单元时对显式算法稳定性的判断,而数值算法稳定条件的缺失也限制了边界单元在显式动力分析中的应用. ...
Multiscale method for seismic response of near-source sites
1
2020
... 随着黏弹性人工边界单元 (以下简称边界单元) 在实际工程中的广泛应用[8 -12 ] ,其数值稳定性问题随之而来. 研究人员在引入边界单元进行波动分析时,一般采用隐式无条件稳定的时域逐步积分算法,较少采用显式算法[13 -14 ] . 这是因为边界单元具有与内部介质不同的质量密度、刚度和阻尼,导致在边界单元区,显式算法的稳定条件不同于内部计算区. 由于边界单元区与相邻的内部计算区的力学参数完全不同,使得显式算法的稳定性分析遇到技术上的困难,长久以来未能给出与内部计算区类似的解析形式的数值积分稳定性条件,这在一定程度上影响了采用边界单元时对显式算法稳定性的判断,而数值算法稳定条件的缺失也限制了边界单元在显式动力分析中的应用. ...
波动数值模拟的一种显式方法-二维波动
1
2010
... 显式算法的解耦特性回避了组集整体刚度阵和求解联立方程组等问题[15 -18 ] ,在大规模动力问题数值分析中的计算效率显著高于隐式算法,特别是对于大范围场地模型的并行计算问题,因此有必要对引入黏弹性人工边界单元时显式算法的稳定性开展研究. ...
波动数值模拟的一种显式方法-二维波动
1
2010
... 显式算法的解耦特性回避了组集整体刚度阵和求解联立方程组等问题[15 -18 ] ,在大规模动力问题数值分析中的计算效率显著高于隐式算法,特别是对于大范围场地模型的并行计算问题,因此有必要对引入黏弹性人工边界单元时显式算法的稳定性开展研究. ...
基于 ALE 有限元法的流固耦合强耦合数值模拟
0
2018
基于 ALE 有限元法的流固耦合强耦合数值模拟
0
2018
一种结构动力时程分析的积分求微方法
1
2019
... 显式算法的解耦特性回避了组集整体刚度阵和求解联立方程组等问题[15 -18 ] ,在大规模动力问题数值分析中的计算效率显著高于隐式算法,特别是对于大范围场地模型的并行计算问题,因此有必要对引入黏弹性人工边界单元时显式算法的稳定性开展研究. ...
一种结构动力时程分析的积分求微方法
1
2019
... 显式算法的解耦特性回避了组集整体刚度阵和求解联立方程组等问题[15 -18 ] ,在大规模动力问题数值分析中的计算效率显著高于隐式算法,特别是对于大范围场地模型的并行计算问题,因此有必要对引入黏弹性人工边界单元时显式算法的稳定性开展研究. ...
透射边界高频失稳机理及其消除方法-SH波动
1
2012
... 数值稳定性的分析和改善研究一直伴随着人工边界理论的发展[19 -22 ] . 针对透射边界,可以改变与边界物理量相关的计算格式,通过滤波提高边界稳定性[23 ] . 对于多次透射边界,可以在边界区设置黏性阻尼,以消除多次透射边界的高频振荡失稳现象[24 ] . 黏弹性人工边界单元本身为物理上稳定的系统,将其引入计算系统中,并不影响整体的物理稳定条件. 其失稳机理是显式时域逐步积分算法所导致的,而与边界单元理论无关. 为改善数值稳定条件,需要全面考虑逐步积分过程中边界节点与内部单元节点之间的耦合效应,以此为依据调整满足显式时域积分数值稳定条件的临界时间步长,从而提高人工边界数值计算的稳定性. ...
透射边界高频失稳机理及其消除方法-SH波动
1
2012
... 数值稳定性的分析和改善研究一直伴随着人工边界理论的发展[19 -22 ] . 针对透射边界,可以改变与边界物理量相关的计算格式,通过滤波提高边界稳定性[23 ] . 对于多次透射边界,可以在边界区设置黏性阻尼,以消除多次透射边界的高频振荡失稳现象[24 ] . 黏弹性人工边界单元本身为物理上稳定的系统,将其引入计算系统中,并不影响整体的物理稳定条件. 其失稳机理是显式时域逐步积分算法所导致的,而与边界单元理论无关. 为改善数值稳定条件,需要全面考虑逐步积分过程中边界节点与内部单元节点之间的耦合效应,以此为依据调整满足显式时域积分数值稳定条件的临界时间步长,从而提高人工边界数值计算的稳定性. ...
时域局部人工边界的稳定性分析方法概述
0
1997
时域局部人工边界的稳定性分析方法概述
0
1997
局部人工边界稳定性的一种分析方法
1
1996
... 针对透射人工边界条件,关慧敏等[21 ] 和 Kamel等[26 ] 提出了一种通过分析局部子系统传递矩阵特征值来 研究透射人工边界稳定性的方法.由于该方法处理的子系统包含节点数量较多,只能给出系统稳定条件的数值解,难以给出解析解,不适合对稳定性条件的影响因素进行定量化的参数分析,制约了针对稳定性改善方法的研究. ...
局部人工边界稳定性的一种分析方法
1
1996
... 针对透射人工边界条件,关慧敏等[21 ] 和 Kamel等[26 ] 提出了一种通过分析局部子系统传递矩阵特征值来 研究透射人工边界稳定性的方法.由于该方法处理的子系统包含节点数量较多,只能给出系统稳定条件的数值解,难以给出解析解,不适合对稳定性条件的影响因素进行定量化的参数分析,制约了针对稳定性改善方法的研究. ...
透射边界稳定性控制措施探讨
1
2012
... 数值稳定性的分析和改善研究一直伴随着人工边界理论的发展[19 -22 ] . 针对透射边界,可以改变与边界物理量相关的计算格式,通过滤波提高边界稳定性[23 ] . 对于多次透射边界,可以在边界区设置黏性阻尼,以消除多次透射边界的高频振荡失稳现象[24 ] . 黏弹性人工边界单元本身为物理上稳定的系统,将其引入计算系统中,并不影响整体的物理稳定条件. 其失稳机理是显式时域逐步积分算法所导致的,而与边界单元理论无关. 为改善数值稳定条件,需要全面考虑逐步积分过程中边界节点与内部单元节点之间的耦合效应,以此为依据调整满足显式时域积分数值稳定条件的临界时间步长,从而提高人工边界数值计算的稳定性. ...
透射边界稳定性控制措施探讨
1
2012
... 数值稳定性的分析和改善研究一直伴随着人工边界理论的发展[19 -22 ] . 针对透射边界,可以改变与边界物理量相关的计算格式,通过滤波提高边界稳定性[23 ] . 对于多次透射边界,可以在边界区设置黏性阻尼,以消除多次透射边界的高频振荡失稳现象[24 ] . 黏弹性人工边界单元本身为物理上稳定的系统,将其引入计算系统中,并不影响整体的物理稳定条件. 其失稳机理是显式时域逐步积分算法所导致的,而与边界单元理论无关. 为改善数值稳定条件,需要全面考虑逐步积分过程中边界节点与内部单元节点之间的耦合效应,以此为依据调整满足显式时域积分数值稳定条件的临界时间步长,从而提高人工边界数值计算的稳定性. ...
Numerical instabilites of a local transmitting boundary
1
1992
... 数值稳定性的分析和改善研究一直伴随着人工边界理论的发展[19 -22 ] . 针对透射边界,可以改变与边界物理量相关的计算格式,通过滤波提高边界稳定性[23 ] . 对于多次透射边界,可以在边界区设置黏性阻尼,以消除多次透射边界的高频振荡失稳现象[24 ] . 黏弹性人工边界单元本身为物理上稳定的系统,将其引入计算系统中,并不影响整体的物理稳定条件. 其失稳机理是显式时域逐步积分算法所导致的,而与边界单元理论无关. 为改善数值稳定条件,需要全面考虑逐步积分过程中边界节点与内部单元节点之间的耦合效应,以此为依据调整满足显式时域积分数值稳定条件的临界时间步长,从而提高人工边界数值计算的稳定性. ...
一种改善多次透射边界稳定性的措施
1
1997
... 数值稳定性的分析和改善研究一直伴随着人工边界理论的发展[19 -22 ] . 针对透射边界,可以改变与边界物理量相关的计算格式,通过滤波提高边界稳定性[23 ] . 对于多次透射边界,可以在边界区设置黏性阻尼,以消除多次透射边界的高频振荡失稳现象[24 ] . 黏弹性人工边界单元本身为物理上稳定的系统,将其引入计算系统中,并不影响整体的物理稳定条件. 其失稳机理是显式时域逐步积分算法所导致的,而与边界单元理论无关. 为改善数值稳定条件,需要全面考虑逐步积分过程中边界节点与内部单元节点之间的耦合效应,以此为依据调整满足显式时域积分数值稳定条件的临界时间步长,从而提高人工边界数值计算的稳定性. ...
一种改善多次透射边界稳定性的措施
1
1997
... 数值稳定性的分析和改善研究一直伴随着人工边界理论的发展[19 -22 ] . 针对透射边界,可以改变与边界物理量相关的计算格式,通过滤波提高边界稳定性[23 ] . 对于多次透射边界,可以在边界区设置黏性阻尼,以消除多次透射边界的高频振荡失稳现象[24 ] . 黏弹性人工边界单元本身为物理上稳定的系统,将其引入计算系统中,并不影响整体的物理稳定条件. 其失稳机理是显式时域逐步积分算法所导致的,而与边界单元理论无关. 为改善数值稳定条件,需要全面考虑逐步积分过程中边界节点与内部单元节点之间的耦合效应,以此为依据调整满足显式时域积分数值稳定条件的临界时间步长,从而提高人工边界数值计算的稳定性. ...
Analysis of dynamic contact of cracks in viscoelastic media
2
1995
... 为改善数值积分稳定性,首先应对失稳机理开展研究. 若不考虑人工边界的影响,可使用冯诺依曼方法对计算区域进行稳定性分析[25 ] ;引入边界单元并进行显式时域逐步积分计算时,则需要考虑边界单元对整体计算系统稳定性的影响.此时可以建立包含人工边界在内的整体系统的运动方程,采用传递矩阵谱半径分析方法,获得满足稳定条件的临界时间步长并进行失稳判断. 但在实际应用中,整体模型传递矩阵的建立和分析工作量巨大,通常难以 施行. ...
... 以上通过理论推导,分别给出了角点和侧边子系统数值积分稳定性条件,其数值稳定性系数 $\gamma_{1}$ 和 $\gamma_{2}$ 均为质量密度比 $\tilde {\rho }/\rho $、内部介质泊松比 $\mu $、单元尺寸与散射波源至边界距离之比 $L/R$ 的函数. 当无量纲参数 ${\Delta tC_{P}} /L$ 小于或等于稳定性系数时,相应的子系统满足数值积分的稳定性条件. 此外,整体系统的数值稳定性除需满足人工边界区的角点子系统和侧边子系统的稳定条件外,还需满足内部系统的稳定性条件. 显式时域逐步积分算法中内部单元的稳定性条件为[25 ] ...
A stability checking procedure for finite-difference schemes with boundary conditions in acoustic media
1
1989
... 针对透射人工边界条件,关慧敏等[21 ] 和 Kamel等[26 ] 提出了一种通过分析局部子系统传递矩阵特征值来 研究透射人工边界稳定性的方法.由于该方法处理的子系统包含节点数量较多,只能给出系统稳定条件的数值解,难以给出解析解,不适合对稳定性条件的影响因素进行定量化的参数分析,制约了针对稳定性改善方法的研究. ...
采用黏弹性人工边界单元时显式算法稳定性分析
2
2020
... 针对黏弹性人工边界单元,李述涛等[27 ] 对一维和二维有限元系统最高阶模态进行了分析,证明了可以采用极小的子系统推导得出整体系统的稳定性条件.该子系统中只包含一个运动节点,所得的稳定性条件是整体系统数值稳定的充分条件.此外,该方法给出了系统稳定条件的解析解,可以直观且定量地分析各物理参数对数值稳定性的影响,为数值积分稳定性的改善创造了条件. ...
... 文献[27 ] 采用上述研究思路,将侧边子系统与角点子系统从整体模型中分离出来,在四周施加固定约束. 利用传递矩阵的谱半径分析时域逐步积分算法的稳定性条件,最终推导出整体系统的稳定性条件. 分析结果表明,采用边界单元时,整体模型数值积分的稳定性条件要比内部系统的稳定性条件更为严格,这在一定程度上限制了显式数值积分方法的应用. ...
采用黏弹性人工边界单元时显式算法稳定性分析
2
2020
... 针对黏弹性人工边界单元,李述涛等[27 ] 对一维和二维有限元系统最高阶模态进行了分析,证明了可以采用极小的子系统推导得出整体系统的稳定性条件.该子系统中只包含一个运动节点,所得的稳定性条件是整体系统数值稳定的充分条件.此外,该方法给出了系统稳定条件的解析解,可以直观且定量地分析各物理参数对数值稳定性的影响,为数值积分稳定性的改善创造了条件. ...
... 文献[27 ] 采用上述研究思路,将侧边子系统与角点子系统从整体模型中分离出来,在四周施加固定约束. 利用传递矩阵的谱半径分析时域逐步积分算法的稳定性条件,最终推导出整体系统的稳定性条件. 分析结果表明,采用边界单元时,整体模型数值积分的稳定性条件要比内部系统的稳定性条件更为严格,这在一定程度上限制了显式数值积分方法的应用. ...
Analysis of transient algorithms with particular reference to stability behavior
1
1983
... 其中向量 ${\pmb U}$ 由子系统各节点的加速度、速度和位移组成;${\pmb A}$ 是传递矩阵,上标 $p$ 是自然数,$t = p\Delta t$;$\Delta t$ 为时间步长. 如果满足下列两条件,则积分格式 (2) 是稳定的[28 ] .条件 1:$\rho ({\pmb A}) \leqslant 1$,$\rho ({\pmb A})$ 是传递矩阵 ${\pmb A}$ 的谱半径;条件 2:如果 ${\pmb A}$ 具有多重特征值,则该特征值的模小于 1.由此可将子系统的稳定性分析归结为传递矩阵 ${\pmb A}$ 的谱半径计算. ...
1
1997
... 二维平面单元的集中质量矩阵、刚度矩阵、阻尼矩阵分别参考文献 [6 ,29 -30 ] ,按节点编号组装矩阵后,得到角点子系统中 5 号节点的运动方程如下 ...
1
1997
... 二维平面单元的集中质量矩阵、刚度矩阵、阻尼矩阵分别参考文献 [6 ,29 -30 ] ,按节点编号组装矩阵后,得到角点子系统中 5 号节点的运动方程如下 ...
基于高阶剪切变形理论的四边形求积元板单元及其应用
1
2018
... 二维平面单元的集中质量矩阵、刚度矩阵、阻尼矩阵分别参考文献 [6 ,29 -30 ] ,按节点编号组装矩阵后,得到角点子系统中 5 号节点的运动方程如下 ...
基于高阶剪切变形理论的四边形求积元板单元及其应用
1
2018
... 二维平面单元的集中质量矩阵、刚度矩阵、阻尼矩阵分别参考文献 [6 ,29 -30 ] ,按节点编号组装矩阵后,得到角点子系统中 5 号节点的运动方程如下 ...
Abaqus Analysis User's Manual (version 6.14)
1
2013
... 其中,$\ddot {u}$,$\dot {u}$,$u$ 分别为节点的加速度、速度和位移,下标 $x$,$y$ 表示运动方向. 显式时域逐步积分格式 (中心差分) 如下[31 ] ...