引言
大量研究表明非晶合金微观结构是非均匀性的,探索非晶合金微观结构与物理/力学性能之间关联是该领域研究重点之一[4-5]. 目前对于其微观结构非均匀性与非晶合金玻璃转变、扩散机制及力学性能等关键问题之间的联系已取得显著进展[6-7], Spaepen等[8]基于自由体积概念提出自由体积模型,Argon等[9]发展"剪切转变区"(shear transformation zone, STZ)模型,Wang等[10]提出"流变单元(flow units)"模型等. 此外,研究表明剪切模量(自由能对剪切应变的二阶导数)是控制过冷液体热力学和动力学性质的关键物理参量,在非晶态物质形成和物理性质中起着非常重要的作用,是一种有效研究非晶材料物理和力学性能的方法[11].原子重排激活能取决于局部瞬时剪切模量,根据 Arrhenius-type弛豫规律, 瞬时剪切模量反应势垒高度决定了原子重排频率,这些原子重排导致诸多物理现象如黏性流动、扩散及结构弛豫等[12].以非晶合金为例,温度低于晶化温度时剪切模量可反映宏观剪切弹性,其变化与非晶合金热释放和热吸收现象紧密相关[13-14].尽管关于非晶合金玻璃转变和晶化过程中热流变化有了大量研究, 但其物理起源仍是亟待解决的重要科学问题之一. 需要提及的是,Granato等[15-16]提出凝聚态物质自间隙理论(interstitialcy theory of condensed matter, ITCM), 该理论建立了非晶合金和母体晶态合金之间的关联. 该模型认为自间隙"缺陷"是由两个具有相同势阱原子组成的一种局部对称性低于周围原子的弹性偶极子. 当自间隙原子运动被激活时,以自间隙原子作为"核心"的周围数十个原子参与协同重排,表现出具有高振动熵低频共振模式[17].Granato等[18]利用实验手段发现自间隙缺陷的产生导致单晶铜剪切模量急剧下降,Khonik等[19]通过计算机模拟证实这种哑铃型自间隙原子同样存在于非晶态固体中. 自间隙理论可定量描述非晶合金在结构弛豫、玻璃转变和晶化过程中物理参量的改变,原子不同能态之间跃迁导致焓、熵等物理参量发生变化,宏观表现为非晶合金力学性能发生改变. 基于自间隙理论,非晶合金热释放和热吸收与剪切模量随温度的演化紧密关联,主要依据于以下两个基本方程[15]
式中, $H$为缺陷形成焓; $\alpha $为无量纲常数, 通常约等于1[20];$\varOmega$为单个原子体积; $G_{ini}$为铸态非晶合金瞬时剪切模量, 式(1)表明形成焓与剪切模量成正比
式中, $\dot{T}$为升温速率, $\rho$为铸态非晶合金密度.
本研究选取玻璃形成能力优异的Cu$_{49}$Hf$_{42}$Al$_{9 }$非晶合金作为模型体系, 通过差式扫描量热分析仪(differential scanning calorimetry, DSC)、电磁声转换实验(electromagnetic acoustic transformation, EMAT)和动态力学分析仪(dynamic mechanical analysis, DMA), 基于自间隙理论对其热流和剪切模量进行研究, 探索非晶合金热流与剪切模量的关联、自间隙"缺陷"浓度在结构弛豫过程的演变规律以及物理时效对非晶合金内耗行为的影响,进一步探索非晶合金力学行为的微观物理起源.
1 实验方法
本文采用铜模吸铸法制备Cu$_{49}$Hf$_{42}$Al$_{9}$(原子百分比)非晶合金,其非晶态特征采用Rigaku D/max 2500X射线衍射仪(XRD)进行确认.模型合金体系热性能由Hitachi DSC 7020型DSC进行测定,DSC分析所用样品尺寸为2 mm $\times $ 2 mm $\times $ 2 mm,实验条件为在氮气环境下以升温速率为3 K/min进行.
采用Setaram TMA-92热机械分析仪对模型体系进行拉伸蠕变实验, 以确定样品黏度随温度的演化, 其黏度$\eta$可表达为: $\eta =\sigma_{eff}/\dot{\varepsilon}_{eff}$, $\sigma_{eff}$为有效应力, $\dot{\varepsilon}_{eff}$为有效应变速率.拉伸蠕变实验样品尺寸为(8 $\sim$ 15) mm $\times$ (0.4 $\sim$ 0.8) mm $\times $ (30 $\sim $ 190) $\mu$m.
EMAT是一种采用非接触式电磁声变换进行原位剪切模量测量的方法[23]. 通过外磁场和样品表面电流之间洛伦兹力激发样品的横向振动,该方法的优点为样品与激磁/接收线圈之间没有直接接触,可以准确获得剪切模量随温度的演化(所得剪切模量相对误差为(5 $\sim$ 100) $\times10^{-6}$ ppm).EMAT样品尺寸为5 mm $\times$ 5 mm $\times $ 2 mm. 频率扫描时,剪切振幅最大值对应频率可高达500 kHz, 当升温速率恒定时(实验采用升温速率为3 K/min), 剪切模量可由室温下剪切模量获得
式中, $g\left( T \right)$为剪切模量变化值; $f$为振动频率, 为温度的函数; $f_{rt}$为室温振动频率, 该实验设备不考虑结构弛豫中模型合金体系发生的密度变化.
DMA实验是在正弦交变载荷激励时测量材料应力或应变响应的实验方法. 通常, 材料力学响应表现为应变滞后于应力, 其模量在复平面内可表述为: $E=E'+{i}E"$, 其中$E'$为储能模量; $E"$为损耗模量, 损耗模量与储能模量的比值$E"/E'$定义为内耗tan$\delta $. 本文非晶合金动态力学实验在DMA TA Q800动态力学分析仪上进行, 采取单悬臂强迫振动的受力模式. DMA实验分析的样品尺寸约为30 mm $\times $ 2 mm $\times $ 1 mm.
2 实验结果与讨论
2.1 非晶合金结构信息表征
图1为Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金的XRD谱, 表现为宽衍射峰, 为非晶态材料典型特征, 结果表明铸态样品为非晶态.
图1
图1
Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金的XRD谱
Fig. 1
XRD pattern of Cu$_{49}$Hf$_{42}$Al$_{9}$ amorphous alloy
2.2 剪切模量与热流的关联
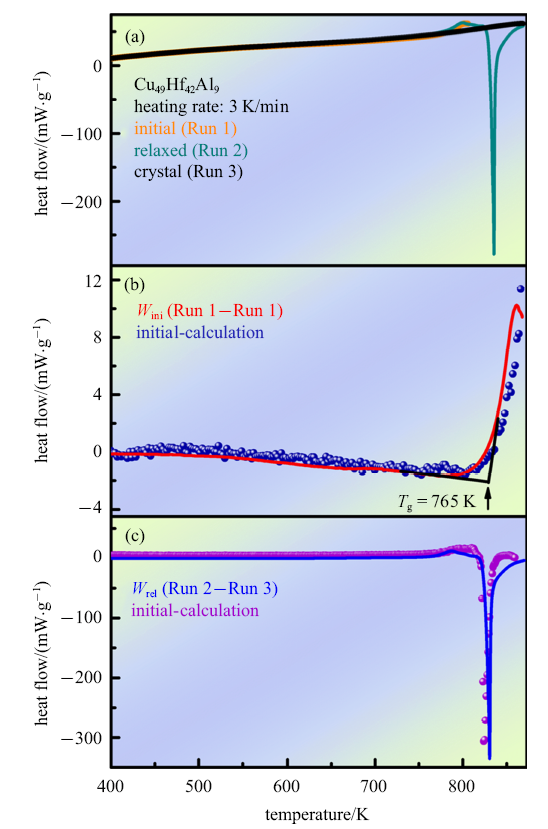
图2(a)为铸态、弛豫态和晶化态合金DSC曲线, Run 1, Run 2和Run 3分别表示铸态、弛豫态(将样品加热到795 K后冷却至室温样品)和晶化态模型合金(将样品加热到873 K后冷却至室温样品)的DSC曲线. 图2(b)和图2(c)分别为Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金铸态和弛豫态热流计算与 实验数据对比分析结果, 历史加载温度分别为795 K, 873 K 和873 K, 升温速率和冷却速率均为3 K/min. 需要说明的是, 结构弛豫和玻璃转变行为分析的热流采用扣除晶态合金对热流的贡献的方法来确定: $W_{ini}=W_{Run1}-W_{Run3}$和$W_{rel}=W_{Run2}-W_{Run3}$, 铸态样品在玻璃转变温度$T_{g}$以下表现为结构弛豫诱导放热, 具有典型非晶特征.与铸态样品比较, 在弛豫态样品中观察到结构弛豫影响消失,在过冷液相区中表现为吸热行为. 晶化后样品无明显特征,表现与传统晶体合金一致. 根据DSC曲线, 采用切线法可得玻璃转变温度$T_{g}$为765K. 根据式(3), 基于剪切模量计算铸态和弛豫态热流曲线与实验所测曲线基本吻合,结果表明自间隙原子理论可以较好地描述结构弛豫过程放热和玻璃转变区内吸热这一热力学行为,非晶合金铸态和弛豫态剪切模量随温度演化过程是热吸收和热释放的宏观表现.
图2
图2
(a)铸态、弛豫态和晶化态DSC曲线; Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金铸态(b)、弛豫态(c)计算与实验热流曲线
Fig. 2
(a) DSC traces of the initial state (Run 1), relaxed state (Run 2) and after the full crystallization (Run 3), the calculation and experimental data of the initial (b) and relaxad state (c) heat flow curves of the Cu$_{49}$Hf$_{42}$Al$_{9}$ amorphous alloy
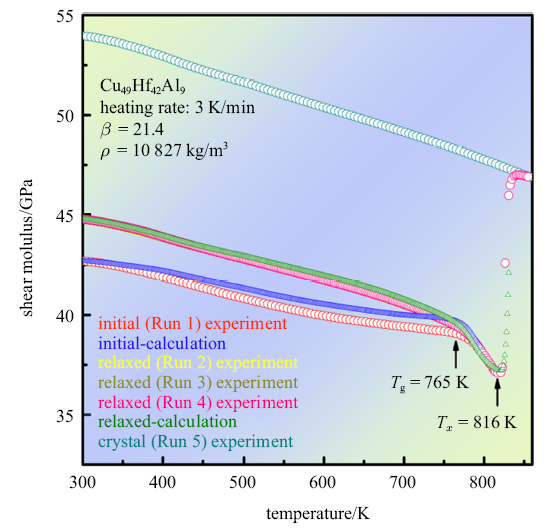
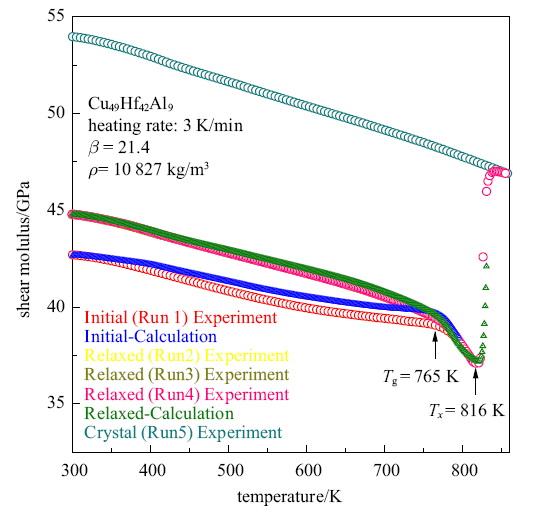
图3为Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金在铸态、弛豫态和晶化态剪切模量随温度演化,需要注意的是, 针对弛豫态, 重复进行3次实验且结果吻合.根据式(3),铸态/弛豫态合金剪切模量$G_{rel/rel}(T)$可由热流数据积分获得
式中, $T_{rt}$为室温温度, 通常取$T_{rt}=300$ K.铸态非晶合金室温剪切模量约为42.7 GPa, 密度为10 827 kg/m$^{3}$[24], 剪切敏感系数$\beta $为21.4, 这与在前期研究中Zr$_{46}$Cu$_{45}$Al$_{7}$Ti$_{2}$非晶合金$\beta=21.1$较为接近[25]. 非晶合金在温度场响应主要表现为原子协同重排和平衡位置热振动[26]. 从室温至500K, 铸态非晶合金剪切模量随温度升高而下降, 这主要是由原子非谐性振动引起在500 $\sim $ 700 K温度范围内仍为线性下降,但相较于原子非谐性振动引起线性下降趋势降低, 这与图2(b)由结构弛豫产生放热现象一致. 在玻璃转变温度$T_{g}$和晶化初始温度$T_{x}$之间, 非晶合金处于过冷液相区, 剪切模量显著下降, 对应非晶合金体系黏度的变化, 以铸态合金作为参考态, 室温时弛豫态非晶合金剪切模量提高了5%, 在$T_{rt}$ $\sim $ $T_{g}$之间,呈线性下降. 温度达到玻璃转变温度$T_{g}$时, 铸态与弛豫态非晶合金剪切模量曲线重合,温度升到晶化温度时剪切模量增加约27%, 非晶合金体系内已有晶化相形成.与铸态合金比较,室温晶化态合金剪切模量提高了26.3%, 此现象与已报道典型非晶合金体系[27-28]和高熵非晶合金体系[29]一致.室温时铸态非晶合金"缺陷"浓度最高,弛豫态"缺陷"浓度居中, 晶化态合金"缺陷"浓度最低, 随"缺陷"浓度降低,合金表现出更高剪切模量和更稳定能量状态.结构弛豫诱导剪切模量下降趋势减缓,过冷液相区内剪切软化以及由结晶诱导剪切模量显著升高,构成了非晶合金剪切行为的基本特征. 基于式(5)计算出铸态和弛豫态非晶合金剪切模量随温度演化与实验结果基本吻合,误差主要来源于温度对剪切敏感系数$\beta$的影响. 前已述及,在弛豫态重复实验3次结果完全吻合, 表明了合金未晶化时局部结构弛豫是可逆的,自间隙理论可以定量描述非晶合金体系剪切模量与热流之间的关联.
图3
图3
Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金铸态, 弛豫态和晶态剪切模量随温度演化过程, 并根据热流数据拟合剪切模量
Fig. 3
Experimental and calculated using Eq.(5) temperature dependences of shear moduli of Cu$_{49}$Hf$_{42}$Al$_{9}$ amorphous alloy in the initial and relaxed state. Temperature dependence of shear modulus in the crystalline state is also shown
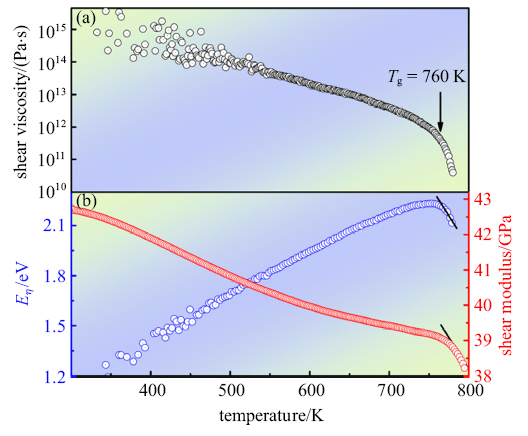
剪切黏度为控制原子迁移率的关键物理参量,在非晶合金结构弛豫、玻璃转变和晶化过程中起着至关重要的作用.非晶合金在线性加热过程中,剪切黏度在10$^{12}$ Pa$\cdot$s时偏离当前准平衡黏度而发生玻璃转变.在升温速率为3 K/min, 有效应力为108MPa的实验条件下对Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金进行黏度测量. 图4(a)为Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金剪切黏度随温度演化过程,可见模型体系在760 K发生玻璃转变, 这与前述DSC所测得玻璃转变温度为765 K基本一致, 当温度在玻璃转变温度$T_{g}$以上时, 非晶合金剪切黏度随温度演化满足Arrhenius 方程[14]
式中, $\eta_{0}$为高温黏度, 约为10$^{-4}$ Pa$\cdot $s; $k_{B}$为波尔兹曼常数; 剪切流变激活能$E_{\eta}(T)$表示高温熔体进行黏性流动需要克服的能量势垒, 可表示为: $E_\eta \left( T\right)=k_{B}T\ln \left[ {{\eta \left( T \right)}/{\eta_0}} \right]$.Dyre等[30]提出"shoving mdel"揭示了这一过程中激活能与剪切模量之间的关系
式中, $V_{c}$为流变特征体积. 在图4(b)中观察到在过冷液相区内激活能呈现强烈的线性下降且与剪切模量几乎平行,$V_{c}\approx 8.0\times $10$^{-30}$ m$^{3}$.温度低于玻璃转变温度$T_{g}$时, 结构弛豫中剪切模量下降而激活能升高, 此阶段剪切黏度由能量扩散不均匀的结构弛豫控制.
图4
图4
(a) Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金在有效应力为108 MPa下剪切黏度随温度演化过程; (b)激活能与弛豫态剪切模量随温度演化
Fig. 4
(a) Temperature dependence of the shear viscosity of Cu$_{49}$Hf$_{42}$Al$_{9 }$ amorphous alloy; (b) Temperature dependence of the activation energy and shear modulus of relaxed state
2.3 非晶合金自间隙"缺陷"浓度演化
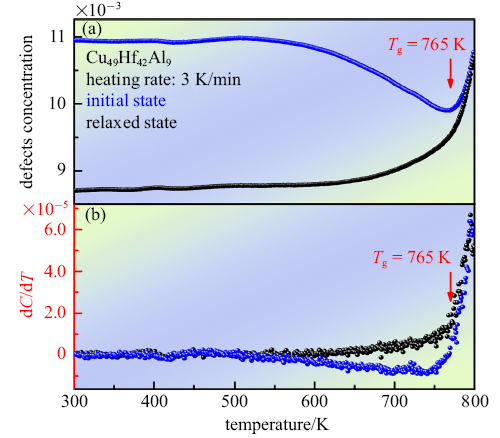
图5(a)为铸态和弛豫态Cu$_{49}$Hf$_{42}$Al$_{9}$ 非晶合金自间隙"缺陷"浓度随温度的变化. 室温铸态非晶合金"缺陷"浓度约为1.1%,在室温到500 K的温度区间内"缺陷"浓度基本不变, 温度在500K至玻璃转变温度$T_{g}$之间, "缺陷"浓度降低, 发生结构弛豫,弛豫过程中结构向更稳定状态迁移, 这个过程会释放自间隙"缺陷"中的弹性能,热力学宏观表现为放热现象.结构弛豫可以理解为能量态的弛豫,即在低于玻璃转变温度的结构弛豫中向更稳定状态转变. 弛豫态的反复加载数据均吻合,进一步证明在这一温度区间内能量重新分配是可逆的. 在过冷液相区内"缺陷"浓度显著升高对应玻璃转变过程. 室温下弛豫态"缺陷"浓度降低约0.2%, 当温度低于玻璃转变温度$T_{g}$, 弛豫态浓度始终低于非晶合金铸态"缺陷"浓度, "缺陷"浓度不断升高表明结构向亚稳态转变. 在过冷液相区, 铸态和弛豫态合金"缺陷"浓度基本一致, 消除了结构弛豫对"缺陷"浓度的影响, 进而表现为在图3中过冷液相区内铸态和弛豫态合金剪切模量吻合.图5(b)为"缺陷"浓度对温度导数随温度的变化过程, 在低温区间和玻璃转变区间, 铸态合金和弛豫态合金"缺陷"浓度导数变化规律一致. 在图5(b)中可清晰观察到$T_{g}$是弛豫态合金"缺陷"浓度导数突变温度. 需要说明的是, 弛豫态非晶合金d$C$/d$T$在测量温度区间内始终为正值, 即消除了结构弛豫引起的"缺陷"浓度降低. 因此,对剪切模量测量为研究自间隙"缺陷"浓度提供了有力证据.
图5
图5
(a)Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金铸态和弛豫态缺陷浓度随温度演化过程; (b) 缺陷浓度对温度的导数随温度演化
Fig. 5
(a) Temperature dependence of the defects concentration in initial and relaxed state of Cu$_{49}$Hf$_{42}$Al$_{9}$ amorphous alloy; (b) temperature dependence of the derivative ln d$C$/d$T$
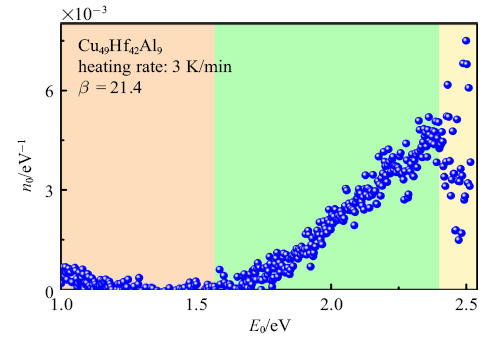
原子重排在非晶合金结构弛豫过程中起着重要作用,激活能图谱可以较好反应这一特征. 假设原子重排在每个时间点都以相同的激活能发生,恒定升温速率下特征激活能$E_0 $为[33]
图6为根据铸态和弛豫态非晶合金剪切模量计算的单位激活能可激活"缺陷"浓度图谱,由低于1.55 eV(结构弛豫起点温度)的低能量区、结构弛豫区和高于2.40eV (玻璃转变温度左右)的高能量区组成.单位激活能可激活"缺陷"浓度在$E_{0}=1.55$ eV处线性增长, 在$E_{0}= 2.40$ eV达到最大值, 随后迅速衰减. 图谱结果表明,在结构弛豫温度区间内,每单位激活能可激活的自间隙"缺陷"浓度随激活能增大而增大. 因此铸态非晶合金在结构弛豫中"缺陷"浓度导数为负且随温度升高而增大,这与图5(b)规律一致. 结构弛豫中"缺陷"浓度随激活能依赖的本质是较大激活能即高温条件下"缺陷"激活速率加快,从而导致整体"缺陷"浓度不断下降, 借助激活能图谱可以更好理解非晶合金自间隙"缺陷"浓度在结构弛豫中演化过程. 需要注意的是, 单位温度可激活"缺陷"浓度随温度的演化与剪切激活能演化在结构弛豫和玻璃转变过程中规律一致,"缺陷"湮灭时释放储存的弹性能伴随着热释放, 再生时从外界吸收能量伴随着热吸收,在结构弛豫和玻璃转变过程中引起剪切模量产生发生改变, 进而影响黏度.
图6
图6
Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金单位激活能区间内"缺陷"浓度能谱
Fig. 6
The energy spectrum of the defect concentration per unit activation energy interval of Cu$_{49}$Hf$_{42}$Al$_{9}$ amorphous alloy
2.4 动态力学分析
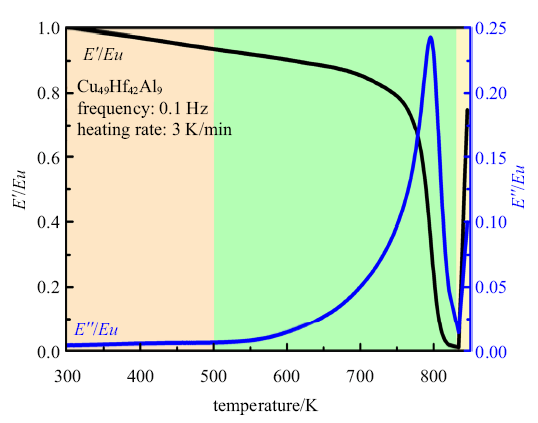
图7为Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金储能模量和损耗模量随温度的演化($E_{u}$为铸态非晶合金室温时储能模量),加载频率为0.1 Hz, 升温速率为3 K/min. 储能模量和损耗模量随温度变化趋势可以分为3个主要区间: (1) 300 $\sim $ 500 K, $E"/E_{u}$基本保持不变且近似为0, $E'/E_{u}$随温度升高略微降低. 在此温度范围内,非晶合金体系主要处于弹性变形阶段. (2) 500 $\sim $ 815 K, 随着温度升高, 储能模量不断降低, 损耗模量显著增大.温度达到795 K时, 损耗模量达到最大值, 这一过程对应着非晶态物质的主弛豫现象,主弛豫对应非晶合金动态玻璃转变行为.在玻璃转变区间内, 外加应力作用于非晶合金会诱导储能模量急剧下降, 引起黏性流动,这一现象与黏弹性存在最大值和黏度急剧下降有关 此外, 该温度区间内非晶合金应变率与材料外加应力有关, 研究表明,当温度降低或应变速率增大时, 熔体黏度随应变速率增加而显著降低, 从牛顿流变向非牛顿流变转变[5]. (3) 815 $\sim $ 835 K温度范围内储能模量和损耗模量同时增大, 非晶合金中已经有晶化相产生.
图7
图7
Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金归一化储能模量和损耗模量随温度变化
Fig. 7
Temperature dependence of the normalized storage modulus $E'/Eu$ and loss modulus $E"/Eu$ of Cu$_{49}$Hf$_{42}$Al$_{9}$ amorphous alloy. Eu assumes as the value of storage modulus at ambient temperature
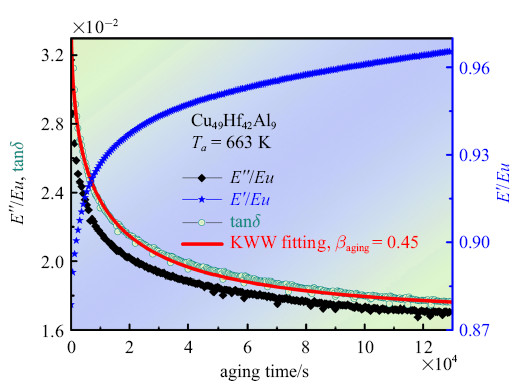
式中, $A_{0}$为弛豫幅值; $\tau $为特征弛豫时间; $t_{a}$为退火时间; $\beta_{aging}$为KWW方程扩展指数,$\beta_{aging}$介于0和1之间. 图8中实线为KWW 拟合内耗随时间演化结果, 实验结果表明损耗模量和内耗因子随退火时间减小, 储能模量随退火时间增大, 当时间足够长时, 模型体系的损耗模量和内耗因子趋近于平衡, $\beta_{aging}=0.45$结构弛豫使非晶合金黏弹性成分降低,弹性成分增加, 合金向稳态结构转变
图8
图8
Cu$_{49}$Hf$_{42}$Al$_{9}$ 非晶合金储能模量、损耗模量和内耗随退火时间演化过程, 退火温度为663 K. 实线为KWW扩展指数方程拟合结果
Fig. 8
Annealing time dependence of the normalized storage modulus, loss modulus and loss factor tan $\delta $ of Cu$_{49}$Hf$_{42}$Al$_{9}$ amorphous alloy at $T_{a} =663$ K. The internal fraction tan $\delta $ was fitted by Eq.(11)
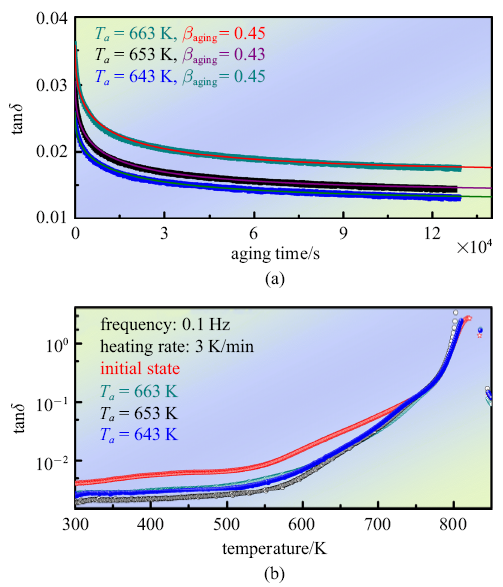
此外, 比较Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金在663 K, 653 K和643K不同原位退火温度的实验, 发现扩展指数$\beta_{aging}$分别为0.45, 0.43和0.45,研究表明$\beta_{aging}\approx 0.5$可较好描述非晶合金物理参数在物理时效过程演化行为[3].Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金扩展指数$\beta_{aging}$小于Zr基和Ti基非晶合金体系[36],这表明Cu$_{49}$Hf$_{42}$Al$_{9}$非晶合金表现出更宽弛豫时间分布. 这种较广泛弛豫时间与非晶合金的微观结构非均匀性有关. 图9(a)为在不同退火温度时, 内耗随退火时间的演化. 可以清晰地看到, 随着退火温度的升高, 内耗也不断增大,这主要是因为随着温度的升高, 非晶合金原子移动性增加.事实上, 对于非晶固体而言,内耗可直接反应原子或分子移动性. 根据非晶合金结构弛豫行为基本原理[37]. 固定加载频率、不同退火温度下内耗因子的演化规律与固定退火温度、不同频率退火的结果一致[38],内耗随频率升高减小. 图9(b)为铸态与弛豫态样品内耗随温度演化过程.以铸态合金内耗为参考系,$T_{rt}\sim 643$ K之间弛豫态样品内耗因子均不同程度减小,这表明玻璃转变温度以下的物理时效诱导非晶合金体系自间隙"缺陷"浓度降低,结构向稳态转变, 体系的原子移动性降低.当温度介于663K和玻璃转变温度$T_{g}$之间时, 上述图5(a)提及在结构弛豫中,"缺陷"浓度随温度升高而降低, 在原位退火作用下进一步降低,导致内耗具有强烈的退火温度依赖性, 显著低于铸态并随退火温度升高而降低.温度高于玻璃转变温度$T_{g}$时铸态和弛豫态样品实验数据吻合一致,此时原子运动能力与初始状态无关. 内耗较高表明非晶合金具有较高原子移动性,高至可"重置"热历史, 消除结构弛豫的影响.
图9
图9
(a) Cu$_{49}$Hf$_{42}$Al$_{9}$ 非晶合金内耗在不同退火温度下随时间的演化过程; (b)铸态和弛豫态样品内耗随温度演化过程的对比
Fig. 9
(a) Time dependence of the loss factor tan$\delta $ of Cu$_{49}$Hf$_{42}$Al$_{9}$ amorphous alloy at different annealing temperatures; (b) Comparison of evolution of internal friction with temperature of Cu$_{49}$Hf$_{42}$Al$_{9}$ amorphous alloy at different states
为进一步研究物理时效对非晶合金原子移动性的影响, 对铸态样品进行一系列原位连续退火. 图10为铸态、弛豫态和晶化态合金储能模量随温度变化过程,插图为内耗随温度演化.历史加载温度分别为795 K, 873 K 和873 K,与EMAT实验温度一致, 加载频率为0.1 Hz, 升温速率和冷却速率均为3 K/min.研究结果表明, 以铸态合金作为参考态, 室温弛豫态合金储能模量提高3%,晶态合金则提升约20% (需要说明的是, 与图(3) EMAT测量结果略有不同,储能模量增大幅度相对较低,这可能是因为DMA加载频率和EMAT加载频率相差6个数量级). 需要注意的是,DMA原位实验与EMAT实验结果相同之处在于都在过冷液相区消除了结构弛豫对模量的影响.同一温度下,铸态合金内耗最大, 晶化后合金内耗最小, 这与Zr$_{56}$Co$_{28}$Al$_{16}$非晶合金在冷轧、铸态、弛豫态、局部晶化和完全晶化中原子移动性随温度演化规律一致[39]. 在自间隙理论框架下,"缺陷"浓度与非晶合金体系状态(弛豫态和晶化态等)紧密关联. 低于玻璃转变温度物理时效诱导结构弛豫或在玻璃转变温度以上晶化相的形成降低自间隙"缺陷"浓度,自间隙原子阻碍周围原子非谐性振动, 缺陷浓度越低, 原子移动能力越弱.
图10
图10
Cu$_{49}$Hf$_{42}$Al$_{9}$铸态, 弛豫态和晶化态合金储能模量随温度的变化, 插图为内耗随温度演化过程
Fig. 10
Temperature dependence of the normalized storage modulus for the initial, relaxed and full crystalline state of Cu$_{49}$Hf$_{42}$Al$_{9}$ amorphous alloy. The inset shows loss factor tan$\delta $ dependence of temperature
3 结论
本文以非晶形成能力优异的Cu$_{49}$Hf$_{42}$Al$_{9 }$非晶合金为研究载体,借助于热学分析实验、电磁声转换实验和动态力学分析实验,基于自间隙理论研究了非晶合金热流与剪切模量的关联,讨论了自间隙"缺陷"浓度在结构弛豫中演变规律和物理时效对于非晶合金模量的影响.主要结论如下:
(1) 自间隙理论可以准确描述非晶合金热流与剪切模量之间的关联,借助DSC实验数据可以很好地描述剪切模量随温度的演化, 其剪切敏感系数$\beta$为21.4.
(2) 非晶合金剪切模量是控制弛豫动力学的主要宏观参数,反应了结构弛豫和玻璃转变过程中"缺陷"浓度变化. 反之,自间隙"缺陷"浓度变化所对应热吸收/热释放决定了剪切模量. 结构弛豫过程中剪切模量平缓下降,"缺陷"浓度降低, 非晶合金体系向更加稳定的状态迁移并伴随热释放; 过冷液相区,主要表现为剪切软化, "缺陷"浓度升高, 伴随着大规模原子的协同运动.
(3) 激活能图谱分析表明单位温度可激活自间隙"缺陷"浓度在结构弛豫温度区间内随温度升高逐渐增大,在过冷液相区逐渐降低, 与塑性流动剪切激活能规律一致.非晶合金剪切模量与热效应变化起源于其微观自间隙"缺陷"浓度改变.
(4) 物理时效诱导非晶合金产生结构弛豫, 损耗模量和内耗减小, 储能模量增大, 结构向稳态迁移.通过DMA研究了铸态、弛豫态和晶态下的储能模量, 与EMAT结果规律基本一致, 内耗反应原子移动性随温度升高而升高,随"缺陷"浓度降低而降低.
参考文献
非晶态物质的本质和特性
The nature and properties of amorphous mater
Dynamic relaxations and relaxation-property relationships in metallic glasses
Structural heterogeneities and mechanical behavior of amorphous alloys
非晶态固体的结构可以决定性能吗?
Does structure determine property in amorphous solids?
锆基非晶合金的动态弛豫机制和高温流变行为
Dynamic relaxation characteristics and high temperature flow behavior of Zr-based bulk metallic glass
基于原子体积场拉普拉斯算子对金属玻璃剪切转变区的预测
Prediction of shear transformation zones in metallic glasses based on laplacian of atomic volume
La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃应力松弛行为
Stress relaxation of La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$ metallic glass
A microscopic mechanism for steady state inhomogeneous flow in metallic glasses
非晶中"缺陷"——流变单元研究
Flow units: The "defects" of amorphous alloys
Correlations between elastic moduli and properties in bulk metallic glasses
A universal criterion for plastic yielding of metallic glasses with a ($T/T_{g})$ 2/3 temperature dependence
Room temperature (TR) elastic constants and compressive yield strengths of approximately 30 metallic glasses reveal an average shear limit gammaC=0.0267+/-0.0020, where tauY=gamma CG is the maximum resolved shear stress at yielding, and G the shear modulus. The gammaC values for individual glasses are correlated with t=TR/Tg , and gamma C for a single glass follows the same correlation (vs t=T/Tg). A cooperative shear model, inspired by Frenkel's analysis of the shear strength of solids, is proposed. Using a scaling analysis leads to a universal law tauCT/G=gammaC0-gammaC1(t)2/3 for the flow stress at finite T where gammaC0=(0.036+/-0.002) and gammaC1=(0.016+/-0.002).
On the nature of enthalpy relaxation below and above the glass transition of metallic glasses
Relationship between the heat flow and relaxation of the shear modulus in bulk PdCuP metallic glass
Interstitialcy model for condensed matter states of face-centered-cubic metals
Interstitialcy theory of simple condensed matter
Localized low-frequency vibrational modes in glasses
Experimental evidence for split interstitials in copper
Identification of interstitial-like defects in a computer model of glassy aluminum
Theoretical analysis of the interconnection between the shear elasticity and heat effects in metallic glasses
Shear susceptibility - a universal integral parameter relating the shear softening, heat effects, anharmonicity of interatomic interaction and "defect" structure of metallic glasses
Evolution of the activation energy spectrum and defect concentration upon structural relaxation of a metallic glass determined using calorimetry and shear modulus data
Predicting temperature dependence of the shear modulus of metallic glasses using calorimetric data
Elevating the fracture toughness of Cu$_{49}$Hf$_{42}$Al$_{9}$ bulk metallic glass: Effects of cooling rate and frozen-in excess volume
Shear susceptibility - A universal integral parameter relating the shear softening, heat effects, anharmonicity of interatomic interaction and "defect" structure of metallic glasses
不均匀性: 非晶合金的灵魂
Heterogeneity: The soul of metallic glasses
Different metastable equilibrium states in metallic glasses occurring far below and near the glass transition
Relationship between the heat effects and shear modulus changes occurring upon heating of a metallic glass into the supercooled liquid state
Link between shear modulus and enthalpy changes of Ti$_{16.7}$Zr$_{16.7}$Hf$_{16.7}$Cu$_{16.7}$Ni$_{16.7}$Be$_{16.7}$ high entropy bulk metallic glass
Local elastic expansion model for viscous-flow activation energies of glass-forming molecular liquids
Towards understanding of heat effects in metallic glasses on the basis of macroscopic shear elasticity
Density and shear modulus changes occurring upon structural relaxation and crystallization of Zr-based bulk metallic glasses: In situ measurements and their interpretation
On the determination of the crystallization activation energy of metallic glasses
Interrelationship between the shear modulus of a metallic glass, concentration of frozen-in defects, and shear modulus of the parent crystal
Structural relaxation in metallic glasses
Kinetics of structural relaxation in bulk metallic glasses by mechanical spectroscopy: Determination of the stretching parameter $\beta _{KWW}$
Dynamic mechanical behaviors of a metastable $\beta $-type bulk metallic glass composite
Impact of the structural state on the mechanical properties in a Zr-Co-Al bulk metallic glass