引言
风能利用系数的理论最大值, 即贝茨极限为59.3%,目前高性能的风力发电机组的风能利用系数约为40%, 可见,风力机的工作效率问题是一个严峻的工程问题,造成其效率低下的一个重要原因为风力机运行环境的非定常性尤为突出,偏航运动、大气湍流、风剪切、大气边界层和塔影效应等因素会造成旋转叶片上的当地入流角呈现周期变化或突然变化,从而产生动态失速, 这种现象普遍存在于大型风力机叶片的旋转颤振流动中.动态失速是一种强烈的非线性、非定常流动现象[1];动态失速涡脱离翼型后缘流向下游时, 会导致升力急剧下降、阻力急剧增大,引起叶片气动性能的恶化.这种现象还普遍存在于直升机旋翼后行桨叶、快速俯仰机动的战斗机、旋转喘振的压气机上.它会限制直升机的飞行包线, 减小压气机高速运行范围, 引起风力机气动效率骤降.近年来, 研究人员开始关注如何利用流动控制技术抑制叶片分离流的产生和发展,提升风电机组气动效率.利用流动控制技术实现动态失速的风力机叶片气动增效有多种手段,常见的被动流动控制手段主要有翼刀、涡流发生器、叶片分流、叶尖小翼、后缘变形等.常见的主动流动控制手段主要有等离子体[2]、吹/吸气[3]、合成射流[4-5]、燃烧火花激励等.例如, 常见的前缘扰流片被动控制手段, 在减小力矩负峰值的同时,也带来了升力的损失[6],并且一般控制周期较长, 无法根据复杂工况自适应变化,难以满足风力机来流和迎角快速变化的工作环境. 合成射流主动控制方面,激励器以孔阵列的形式布置在翼型前缘附近, 能够减小迟滞环区域,削弱不利的非定常载荷, 但是在增升减阻方面,并没有很好的效果[7-8],某些工况下甚至会造成翼型在俯仰振荡的正行程(翼型迎角增大的行程)损失部分升力和效率[9].吹气主动控制方面,施加的扰动虽然增大了翼型在负行程(翼型迎角减小的行程)的升力,但同时也损失了正行程的部分升力[10-11],且吹气停止时,吹气通道会对动态性能有不利的影响[3].另外一种为燃烧火花激励主动控制,在振荡翼型正行程的增升方面也是无计可施[12].以上为目前翼型动态失速流动控制研究的基本现状. 分析以上气动现象认为,在俯仰振荡的负行程阶段翼型表面压力的振荡行为被延迟和削弱, 从而减小了尾流区;除了在接近失速的大迎角范围,否则流动控制的气动激励不会改变正行程阶段翼型的流态[13].等离子体主动流动控制方式具有响应快、频率高等特点和优势;工程上能够将等离子激励器设计嵌入到叶片中,以减小对原有气动外形的影响[14];等离子体能够对复杂的非定常流动中的分离流和涡结构进行精准、高效的相位控制,以适应更多的工况; 且交流介质阻挡放电(alternating current dielectric barrierdischarge,AC-DBD)等离子体激励器已经被证实在马赫数为0.4、雷诺数为200万时能够有效抑制流动分离,具有良好的应用前景, 是流动控制技术从实验室转化为全尺寸实体应用的关键一步.本文借助大涡模拟数值手段,研究等离子体气动激励在风力机叶片上使用以控制翼型动态失速的发生,改善风能的利用效率,并探索了激励器以非定常工作模式(在较低的占空比下)运行以提高激励效率、降低电力消耗,揭示了脉冲等离子体的流动控制机理.
1 数学模型
为了更好地模拟等离子体气动激励和翼型动态三维涡结构相互影响的动力学机制,参考文献[15]关于大涡模拟(large eddy simulation, LES)的基本理论, 本文开展了大涡模拟计算, LES的基本思想是:对于大尺度脉动进行直接数值计算, 对于小尺度脉动用湍流模型进行封闭.
1.1 流体控制方程
流体基本方程(连续方程、动量方程和能量方程)可以写成如下通用形式
其中, $\rho $是气体密度, $U$是速度矢量, $\phi $是通用变量,$\varGamma $是广义扩散系数, $S$是广义源项. 对于连续方程、动量方程和能量方程,$\phi $分别为1, $u_{i} $和$T$; $\varGamma $分别为0, $\mu $和$k/c_{p} $;$S$分别为0, $-\partial p/\partial x_{i} +f_{i} $和0. $u_{i} $是速度分量,$T$是温度, $\mu $是黏度, $k$是流体的导热系数, $c_{p} $是比热容, $f_{i}$是DBD等离子体体积力源项.理想气体状态方程为
式中$R$是气体常数.
1.2 等离子体激励
本文采用非对称式介质阻挡放电(dielectric barrier discharge, DBD)等离子体激励器.激励模型基于唯象学原理[16], 将等离子体气动激励的作用等效为体积力, 将体积力以动量源项的形式加入N-S方程中.体积力的求解过程如下
电势$\varPhi $由二部分组成, 一部分由外部电场产生, 用$\phi $表示, 另一部分由等离子体静电荷产生, 用$\varphi $表示, 即
由电势$\phi $和$\varphi $可写出二个独立的方程, 一个是由于电极上所加电压产生的外部电场
式中$\varepsilon_{r} $是介质的相对介电常数; 另一个是由于带电粒子产生的电势
式中$\varepsilon_{0} $是自由空间的介电常数, $\rho_{c} $是等离子体电荷密度.
假定德拜厚度很小, 且壁面上的电荷密度不大, 这样计算区域中的电荷分布可由壁面上的电荷分布求出.
以上两方程可以通过求解静电场的拉普拉斯方程和泊松方程分别求出. 由以上两个方程即可求出$\varphi $和$\rho_{c} $.那么电荷密度可以通过如下方法求得
代入式(5), 引入德拜长度$\lambda_{d} $
式中$e$为基本电荷, $n_{0}$是自由空间等离子体密度, $k$为波尔慈曼常数, $T$为样本温度.得到等离子体中任意一点净电荷密度表示的方程
由麦克斯韦方程可知, 对于静电场, 电场强度矢量的旋度为0, 因此静电场是一个无旋场, 根据矢量分析恒等式得出电场强度是电势的负梯度
静电场对电荷作用的体积力$F$如下
式中$E$是电场强度.
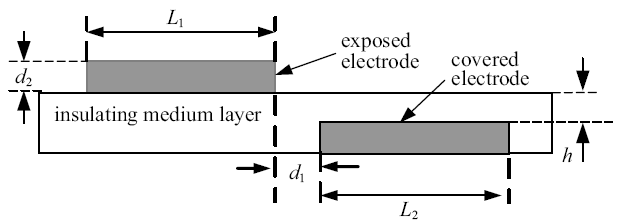
SDBD激励器一般包括暴露电极、绝缘介质层和植入电极三部分, 如图1所示. $L_{1}$和$L_{2}$分别为暴露电极和植入电极的宽度, $d_{1}$为电极水平间距, $d_{2}$为电极厚度(暴露电极和植入电极厚度相同), $h$为绝缘介质层厚度. SDBD激励器参数为, $L_{1}= L_{2}=4$ mm, $d_{1}=0$ mm, $d_{2}=h=0.15$ mm.
图1
求解电势分布方程的边界条件为, 暴露电极处激励电势为$\varphi (t)$, 植入电极处电势为0, 空气相对介电常数为$\varepsilon_{r1}=1$, 绝缘介质层相对介电常数为$\varepsilon_{r2}=2.7$. 正弦型电源电压振幅为5000 V, 电源频率为1000 Hz,暴露电极加载正弦型电源作为求解拉普拉斯方程的初始条件得到空间电势分布; 绝缘介质与空气的接触面上的电势的法向梯度为0.
植入电极的输入为初始条件求解泊松方程得到电荷密度的分布, 绝缘介质与空气的接触面上电荷的法向梯度为0; 植入电极上方壁面的电荷密度为
式中$\rho_{c,\max } $为电荷密度的最大值, 本文取0.008 C/m$^{3}$; $f\left( t\right)$是波形函数; $G\left( x \right)$与激励器在流场中的位置有关. 德拜长度$\lambda_{d} $为0.001 m.
其中, $\xi $是位置参数, 由其决定函数最大值的位置, 本文取为下表面电极的最左端; $\theta $为尺度参数, 由其决定衰减速度,本文取为0.3. 正弦波激励, 电势输入和电荷输入分别如下
等离子体激励器可以工作在定常模式, 又称连续工作模式,即激励器开启后在高频放电下连续工作, SDBD激励器电极间施加高频交流电源时,电源输出电压可高达几千至几万伏, 频率可达几千赫兹到几万赫兹;也可以工作在非定常模式, 又称脉冲模式,是指通过较低频率下控制激励器周期性开启与关闭来实现流动控制的工作模式.激励器处于脉冲工作模式时, 产生非定常等离子体,诱导出的气动激励也会呈现出脉冲式间歇性特点且非定常特性增强,如果间歇的时间控制得比较好,可以在不影响甚至提高控制效果的情况下又能够显著地降低功耗,脉冲频率和占空比是影响等离子体激励特性的重要参数.
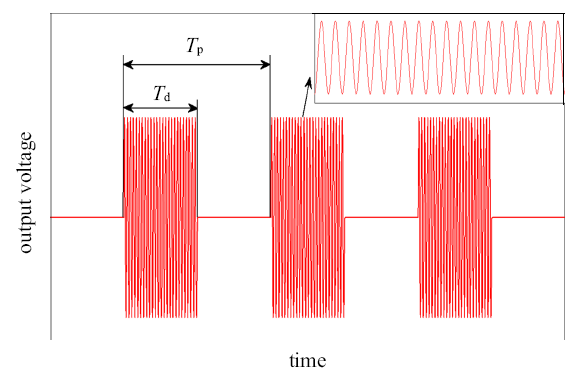
图2为激励器脉冲模式工作示意图, 图中$T_{p}$为脉冲控制周期, $T_{d}$为激励器连续开启时间, 脉冲频率$f_{p}=1/T_{p}$, 占空比$DR=T_{d}/T_{p}$, 由图可知脉冲频率远小于激励器电源放电频率. 本文中脉冲频率$f_{p} $为25 $\sim$ 200 Hz, 占空比$DR$为1% $\sim$ 100%. 将非定常控制模式无因次脉冲激励频率$F^{+}$定义为
其中, $c$为翼型弦长, $U_{\infty }$为来流速度.
图2
图2
等离子体电源非定常电压输出示意图
Fig. 2
Schematic diagram of unsteady voltage output of plasma power supply
1.3 网格和边界条件
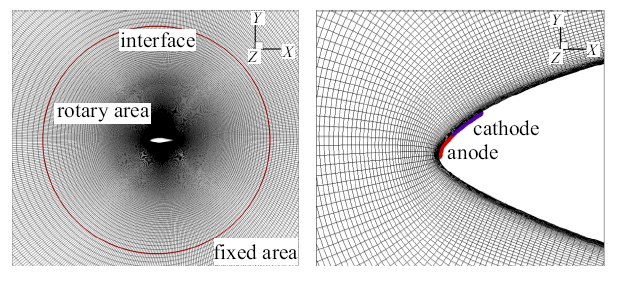
计算网格局部如图3所示, 模型为S809翼型, 其弦长为0.3 m, 展长为0.06 m, 计算域为直径为16 m, 高度0.06 m ($Z$向)的圆柱形计算域; $X$-$Y$面为翼型截面的平行面, $Z$向为模型展向. $X$方向为来流方向, 来流上游、下游距离翼型振荡中心约为27倍弦长(8 m). 计算区域整体分为旋转区域和固定区域, 交界面采用滑移边界.翼型和洞壁第一层法向无量纲网格尺寸$y^{+}<1$ (使用壁面函数), 即壁面第一层网格高度d$s=0.01$ mm.翼型表面和旋转区域切向网格数为530、法向网格数为214, 固定区域切向网格数为480、法向网格数为60, 展向网格数为80,计算域共1060万结构性网格. 远场边界采用压力远场(pressure-farfield)边界条件, 端面采用对称面(symmetry)边界条件.
图3
图3
翼型动态失速等离子体流动控制计算网格
Fig. 3
Computational grid for airfoil dynamic stall with plasma flow control
2 结果分析
2.1 计算方法验证
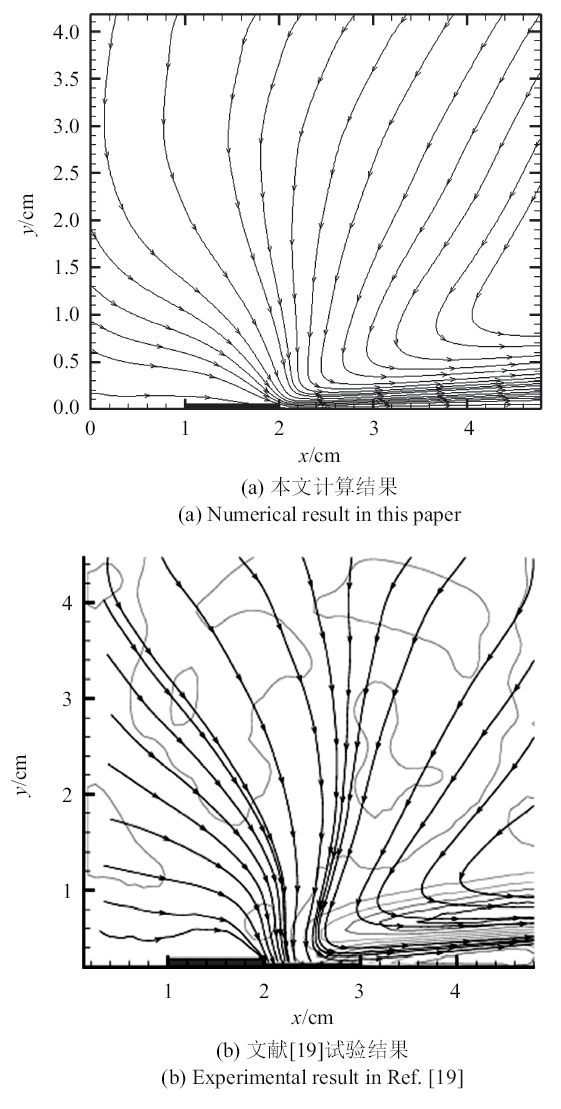
2.1.1 等离子体激励
图4
2.1.2 翼型气动性能
图5
图5
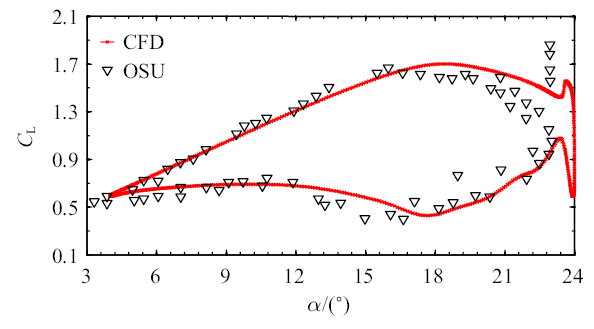
CFD和OSU风洞试验结果对比($Re_{c}=1.0\times 10^{6}$, $\alpha_{0}=14^\circ$, $\alpha_{1}=10^\circ$, $f=1.83$ Hz)
Fig. 5
Comparison between the results of CFD calculation and OSU wind tunnel test ($Re_{c}=1.0\times 10^{6}$, $\alpha_{0}=14^\circ$, $\alpha_{1}=10^\circ$, $f=1.83$ Hz)
2.2 等离子体激励特性
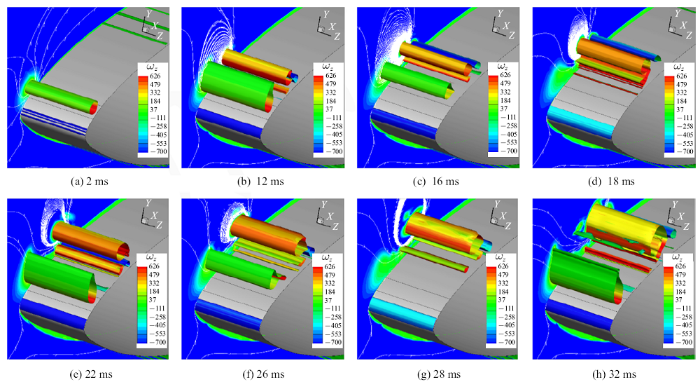
图6为等离子体激励器在$DR=0.5$, $f_{p}=100$ Hz脉冲工作模式下,静止空气中等离子体诱导涡结构、流线图和不同位置的$z$向涡量($\omega _{z}$)云图, 不难发现, 2 ms时脉冲等离子体诱导产生启动涡, 12 ms时主涡生长成较大尺度的涡, 并且诱导产生二次涡、三次涡, 16 ms时主涡继续向下游移动, 并且尺度和涡量强度均衰减, 当18 ms时主涡和二次涡、三次涡融合, 22 ms时产生新的启动涡, 26 ms时主涡向下游移动并衰减, 28 ms时主涡能量几乎衰减殆尽, 并且淹没在主流中, 32 ms时, 新的启动涡继续产生, 次涡整体上长大并趋于稳定, 并慢慢向下游移动,并且可以观察到, 前缘附近剪切层涡的发展受到等离子体诱导涡的显著影响.分析整个启动涡的生长周期发现, 10 ms为新的诱导涡产生的时间间隔,由脉冲放电频率为100 Hz可知, 诱导启动涡产生的周期即为1个脉冲周期,脉冲频率是决定诱导涡生成频率的主导因素,诱导涡的生成频率与脉冲频率严格保持一致.对静止空气中等离子体气动激励特性进一步分析表明, 与稳态模式相比,脉冲等离子体激励器可以产生周期性、持续性的增强涡流和流向动量[21];在等离子体激励器的启动过程中, 诱导产生启动涡, 它开始卷绕并形成相干结构,之后发展衍生出二次涡、三次涡, 随着次涡继续生长壮大, 新的涡结构形成,主涡和次涡沿着翼型表面向下游运动破裂、耦合重建, 构成新的复杂流动结构,等离子体诱导侧向射流由夹带流补充, 从而产生涡量和启动涡的循环[22].分析认为, 脉冲放电导致的速度阶跃变化是诱导涡的形成机制,激励器放电和空置的切换瞬间是涡核开始生长的时刻[23];而当激励器连续开启时, 其下游会形成稳定的射流.
图6
图6
脉冲工作模式下DBD等离子体诱导涡结构$Q=0.3$等值面(运动参数: $\alpha_{0}=10^\circ$, $\alpha_{1}=7^\circ$, $f=0.5$ Hz, 激励电参数: $DR=0.5$, $f_{p}=100$ Hz)
Fig. 6
$Q=0.3$ iso-surface of vortices structure induced by pulsed mode DBD plasma (motion parameters: $\alpha_{0}=10^\circ$, $\alpha_{1}=7^\circ$, $f=0.5$ Hz, actuation electric parameters: $DR=0.5$, $f_{p}=100$ Hz)
文献[24]认为, 附壁涡旋"簇"是判别速度梯度特别强的连接对象,可见等离子体诱导涡旋会对下游的流动产生扰动.如果能够在翼型表面合适的位置敷设激励器,利用脉冲模式等离子体诱导的贴体非定常涡结构产生的涡升力机制来增升,并且增大附面层和主流能量的掺混, 抵制大尺度涡脱落的发生,则可以在消耗较少的功率下获得较理想的流动控制效果,下文将针对此问题开展进一步研究.
2.3 等离子体对翼型动态气动性能的改善
翼型动态失速的基本特征是翼型的俯仰运动和动态分离涡(dynamic separationvortex, DSV)的作用, 流场中存在复杂的非定常分离和大尺度涡结构,气动力表现出明显的非线性迟滞特性. 前缘涡的生成、沿翼型表面的输运直至脱落,导致翼型在正行程和负行程的相同迎角下气动载荷不对称,从而引起翼型气动载荷的迟滞效应[25].
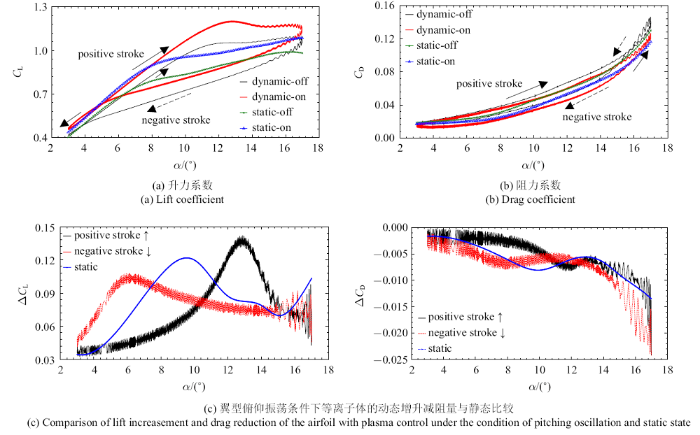
如图7所示, 等离子体激励器关闭状态下,随着动态失速涡的脱落, 升力系数迅速下降, 阻力系数迅速增大,翼型气动性能急剧恶化. 施加等离子体气动激励后,动态流动分离得到一定程度的抑制, 振荡翼型的平均和最大升力系数均提高,平均和最大阻力系数均减小, 从而改善了翼型的动态失速性能. $\Delta C_{L}$和$\Delta C_{D}$分别为等离子体激励器开启和关闭状态下翼型的升力系数和阻力系数的气动差量,表征等离子体流动控制效果, 由图7(c)增升量曲线可看出,随着实时迎角的增大, 升力增量总体上先增大后减小,且负行程、静态、正行程三种运动状态下, 相应升力增量的峰值逐渐增大,最大增升量所在的实时迎角增大; 减阻量随着迎角增大不断增大,特别是在14$^\circ$ 以后的大迎角阶段; 由图7(c)减阻量曲线可知, 负行程、静态、正行程三种运动状态下,等离子体均有减阻效果, 整体看,减阻增量曲线均有先增大、后变缓逆转、再迅速增大的趋势, 且在负行程下,等离子体的减阻效果更好, 静态次之, 正行程最差; 当然, 在8.3$^\circ$ $\sim$ 12.0$^\circ$ 迎角范围内, 静态下的减阻量超过了负行程,在10.7$^\circ$ $\sim$ 12.7$^\circ$ 迎角范围内,正行程下的减阻效果好于负行程. 分析认为,等离子体促使翼型升力可以继续增大主要有三个原因,一是因为边界层动态分离的推迟; 二是因为激励器诱导出的贴体前缘翼面涡(leadingedge vortex, LEV)的涡升力机制[26],前缘诱导涡同时也起到了虚拟气动外形[27-28]的作用,如图6所示, 使得翼型的有效弯度增大;三是因为等离子体激励作为环量控制的射流来源[29],也增大了翼型的环量[30].值得注意的是等离子体的动态增升量与减阻量曲线在小迎角段均出现了谐波振荡,振荡属于高阶小量, 由等离子体激励导致, 是一种正常的气动现象.
图7
图7
翼型气动特性曲线(运动参数: $\alpha_{0}=10^\circ$, $\alpha_{1}=7^\circ$, $f=0.5$ Hz, $V=10$ m/s)
Fig. 7
Aerodynamic characteristics of airfoil(motion parameters: $\alpha_{0}=10^\circ$, $\alpha_{1}=7^\circ$, $f=0.5$ Hz, $V=10$ m/s)
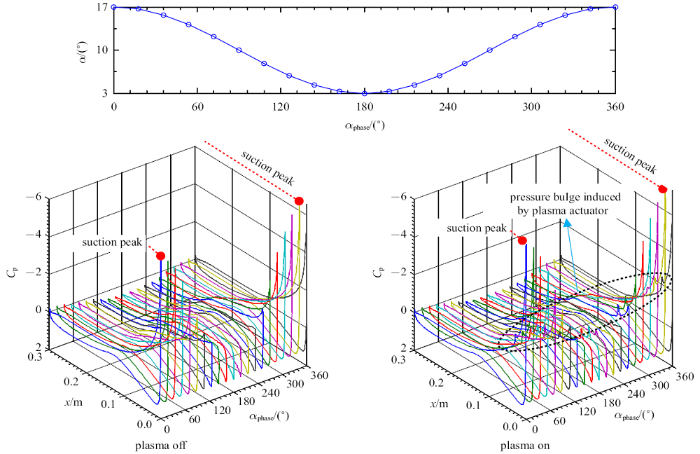
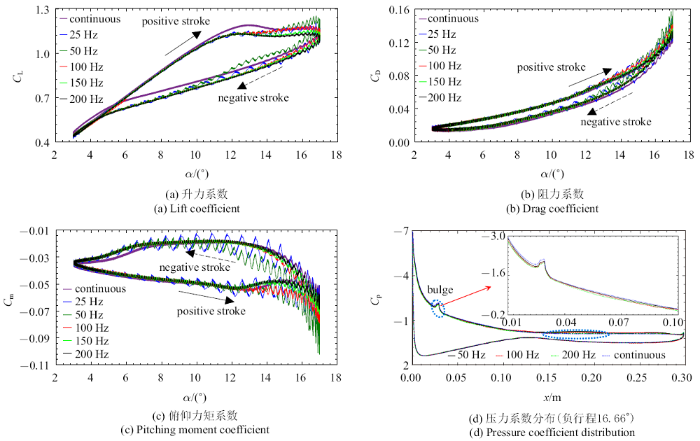
如图8所示, 从翼型表面压力分布在一个振荡周期内变化的三维拟合图($x$坐标为翼型弦向位置,$\alpha_{phase}$为翼型作俯仰正弦振荡的实时相位角)可以看出, 在翼型前缘侧靠近最大迎角附近,存在两个明显的吸力峰, 等离子体使得吸力峰值明显增大;并且在施加等离子体控制后, 压力分布在等离子体施加范围内出现了明显的"凸起",甚至于影响到整个上翼面的吸力分布, 翼型前缘的吸力峰值遂增大,使得前缘逆压梯度的恢复更加容易, 前缘逆压梯度恢复, 会促使升力系数回升,低头力矩变小, 动态失速的负面影响逐渐削弱.
图8
图8
一个振荡周期内翼型表面压力系数分布图(运动参数: $\alpha_{0}=10^\circ$, $\alpha_{1}=7^\circ$, $f=0.5$ Hz, $V=10$ m/s)
Fig. 8
Distribution of pressure coefficient on airfoil surface during an oscillating period (motion parameters: $\alpha_{0}=10^\circ$, $\alpha_{1}=7^\circ$, $f=0.5$ Hz, $V=10$ m/s)
2.4 占空比影响
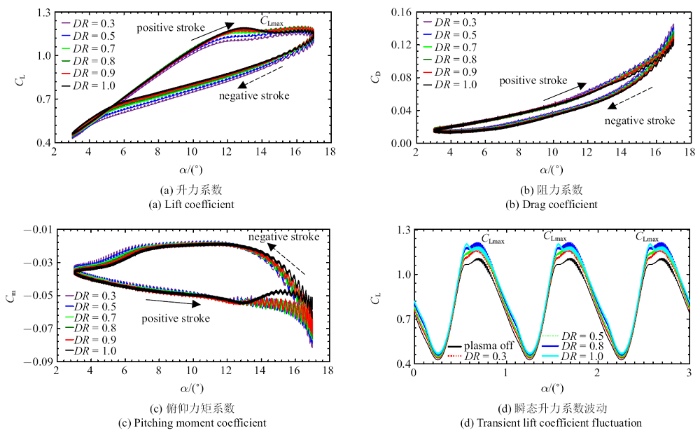
随着研究的深入, 寻求等离子体气动激励对流场的最佳作用方式,揭示"等离子体脉冲激励/复杂非定常流场耦合"空气动力学机制,将等离子体气动激励对流场的作用方式从定常向非定常发展成为关注的焦点.由图9可看出激励电参数占空比的影响,随着$DR$的增大,等离子体流动控制的扰动能量增大, 翼型的在不同迎角下的升力增大、阻力减小,俯仰力矩的负峰值和迟滞环曲线面积均减小, $DR=0.8$时,非定常脉冲等离子体流动控制即可接近连续工作模式下的增升减阻控制效果,这样就实现了以较小的能量投入, 来获得最大的气动收益.
图9
图9
不同占空比下翼型气动特性曲线(运动参数: $\alpha_{0}=10^\circ$, $\alpha_{1}=7^\circ$, $f=0.5$ Hz, $V=10$ m/s)
Fig. 9
Aerodynamic characteristics of airfoil under different duty cycles(motion parameters: $\alpha_{0}=10^\circ$, $\alpha_{1}=7^\circ$, $f=0.5$ Hz, $V=10$ m/s)
2.5 脉冲频率影响
图10
图10
不同脉冲频率下翼型气动特性曲线(运动参数: $\alpha_{0}=10^\circ$, $\alpha_{1}=7^\circ$, $f=0.5$ Hz, $V=10$ m/s)
Fig. 10
Aerodynamic characteristics of airfoil under different pulsed frequencies(motion parameters: $\alpha_{0}=10^\circ$, $\alpha_{1}=7^\circ$, $f=0.5$ Hz, $V=10$ m/s)
由图10(a)气动特性曲线不难发现, 翼型正行程振荡至失速迎角以后, 升力并没有剧烈的损失,而是在围绕着一个平均值做小幅值的脉动, 在负行程大于8$^\circ$ 迎角以上, 这种小幅值的脉动依然出现, 负行程振荡迎角继续减小, 分离流动再附着, 使得脉动逐渐减小直至消失, 在高频振荡发生区间, 升力的时均值保持在一个恒定的范围. 特别是脉冲频率为25 Hz和50 Hz时, 这一脉动现象尤为明显, 同样的气动现象也出现在图10(b)和图10(c)中. 导致这一现象的原因初步分析是由于在动态失速之后, 翼型的上表面发生分离, 从而引起不同尺度的涡结构与等离子体气动激励的强烈非线性耦合作用, 这种耦合作用导致了气动力/力矩的谐波振荡[34].
2.6 流动控制机理
图11
图11
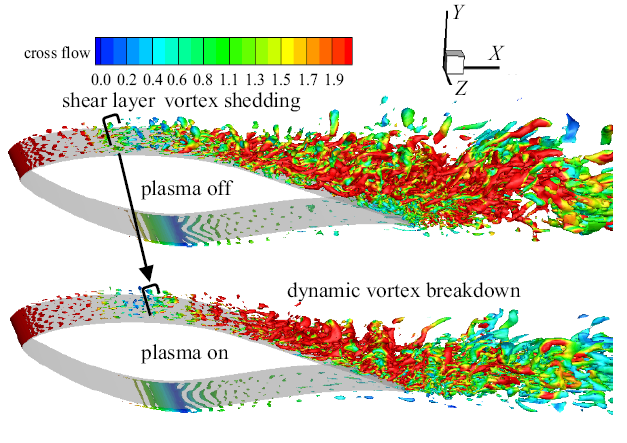
深失速, 翼型动态分离涡Q等值面发展图($\alpha_{0}=10^\circ$, $\alpha_{1}=10^\circ$, $f=3$ Hz, $V=30$ m/s, 正行程迎角16.0$^\circ$)
Fig. 11
Development of Q iso-surface for dynamic separation vortex around airfoil, deep stall ($\alpha_{0}=10^\circ$, $\alpha_{1}=10^\circ$, $f=3$ Hz, $V=30$ m/s, Positive stroke 16.0$^\circ$ AOA)
分析认为等离子体激励器的存在改变了前缘涡[37]的传播以及前缘附近诱导二次涡和三次涡的形成[13].施加DBD等离子体控制后, 一方面由于等离子体诱导的射流方向和主流方向一致,等离子体的"碰撞效应"通过动量交换的方式直接增大了边界层内中性气流的动量[38],使得近壁流动结构发生了很大变化, 增强了气流克服逆压梯度继续向下游流动的能力,进而减小了边界层厚度; 另一方面等离子体在气流中增大了扰动,在等离子体前缘诱导涡的作用下,边界层外部主流区的高速气流进入到边界层低速气流内,促进了高速和低速气流的动量交换,从而达到了推迟边界层流动分离和减小涡流强度的控制效果. 此外,等离子体激励使得主流的三维流动特性减弱,即消减了与准流向涡相关的壁法向和和展向速度[39],鉴于壁附着结构直接与环境平均剪切力相互作用,附壁扫掠(展向速度)和抛射(法向速度)携带总切向雷诺应力的60%以上[24],因此, 借助等离子体, 可在抵抗大分离、减小压差阻力的同时,实现流动控制减小摩擦阻力, 这也是未来研究的重要方向.
目前已有研究成果显示, 在声波扰动或涡波扰动作用下前缘曲率变化对边界层感受性机制有着显著的影响[40].边界层感受性问题是层流向湍流转捩的初始阶段, 是外界不稳定扰动作用实现边界层转捩控制的关键物理环节, 等离子体以响应快著称,在这一阶段可发挥重要作用. 通过图12所示动态分离涡$Q$等值面可以看出, 浅失速(DSV较弱小、无集中,分离区与翼型厚度相当)状态下, DBD诱导翼型边界层层流向湍流提前转捩, 促进边界层和主流的动量交换[41],以抵抗更大尺度分离流动. 以上表明, 等离子体激励具有较强的剪切层操纵能力,能够控制/减少动态分离流动中存在的寄生效应, 例如不稳定性、振动、噪声等[42].
图12
图12
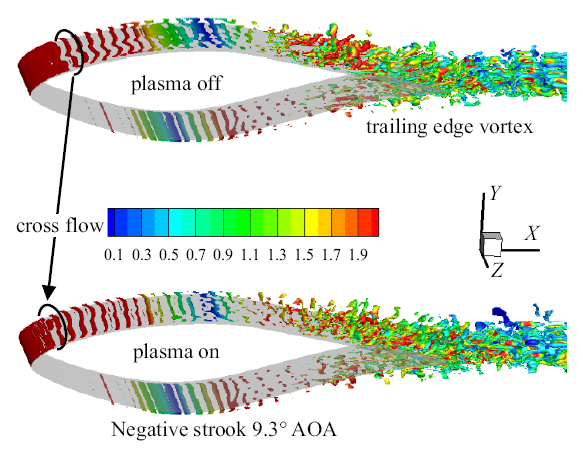
浅失速, 翼型动态分离涡Q等值面发展图($\alpha_{0}=10^\circ$, $\alpha_{1}=7^\circ$, $f=0.5$ Hz, $V=10$ m/s)
Fig. 12
Development of Q iso-surface for dynamic separation vortex around airfoil, light stall ($\alpha_{0}=10^\circ$, $\alpha_{1}=7^\circ$, $f=0.5$ Hz, $V=10$ m/s)
3 结论
风力机叶片常常工作在动态失速状态, 会导致翼型升力急剧下降、阻力急剧增大、力矩负峰值急剧上升, 引起叶片气动性能恶化. 本文基于动网格和滑移网格技术, 借助大涡模拟数值手段, 探索了等离子体气动激励在风力机叶片翼型上使用以控制动态失速的发生, 改善平均和瞬态气动力, 提高风能利用效率, 重点揭示了非定常脉冲等离子体的流动控制机理, 研究表明
(1)一个振荡周期内翼型的压力分布在前缘侧靠近最大迎角附近存在两个明显的吸力峰,等离子体使得吸力峰值明显增大, 压力分布在等离子体施加区域内出现了负压"凸起", 甚至提高了整个上翼面的吸力,使得前缘逆压梯度的恢复更加容易, 动态失速的负面影响得到明显削弱.
(2)非定常脉冲模式流动控制不仅能够节省能量, 还能获得比连续模式流动控制更好的气动收益.无因次脉冲激励频率$F^{+}=1.5$时等离子体控制效果较好, 特别是在0.14 $\sim$ 0.21 m弦长范围的上翼面, 甚至比连续式DBD控制效果更好.
(3)随着占空比的增大, 等离子体扰动能量增大, 翼型的在不同迎角下的升力增大、阻力减小,俯仰力矩的负峰值和迟滞环曲线面积均减小, 占空比为0.8时即可接近连续工作模式下的流动控制效果;这样就实现了以较小的能量投入, 来获得最大的气动收益, 以较低的占空比运行以提高激励效率是未来研究的重要方向.
(4)翼型深失速状态, 俯仰振荡正行程下, 等离子体气动激励促使流动分离位置明显向后缘移动,抵抗了大尺度动态失速涡的发生; 负行程下, 分离涡结构被破碎耗散, 涡流强度和影响范围减小, 主流的三维流动特性得到削弱.
(5)翼型浅失速状态, 等离子体诱导翼型前缘附近边界层层流向湍流提前转捩, 促进边界层和主流的动量掺混, 以抵抗分离涡脱落,等离子体激励具有较强的剪切层操纵能力, 能够控制/减少动态分离流动中存在的寄生效应.
(6)等离子体气动激励诱导产生前缘附近贴体翼面"涡簇"随时空演化为湍流结构,进而与下游动态流动耦合作用, 上翼面的分离流重新附着, 不同尺度、频率的动态涡结构与等离子体气动激励的非线性、强耦合作用导致了气动力/力矩的谐波振荡.
(7)负行程、静态、正行程三种运动状态下, 等离子体均有减阻效果, 整体看, 减阻增量曲线均有先增大、后变缓逆转、再迅速增大的趋势, 且在负行程下, 等离子体的减阻效果更好, 静态次之, 正行程最差.
(8)等离子体动态流动控制机理归纳为: ①边界层动态分离的推迟; ②激励器诱导出的贴体翼面涡的涡升力机制, 前缘诱导涡起到了虚拟气动外形的作用, 使得翼型的有效弯度增大; ③等离子体激励作为环量控制的射流来源,增大了翼型的环量.
参考文献
大攻角下有限振幅俯仰飞行的非线性动稳定性分析
Nonlinear dynamic stability analysis for aircraft flying at high angles of attack
Power improvement of NREL 5-MW wind turbine using multi-DBD plasma actuators
Dynamic stall control on the wind turbine airfoil via a co-flow jet
合成双射流及其流动控制技术研究进展
Research progress of dual synthetic jets and its flow control technology
合成射流对失速状态下翼型大分离流动控制的试验研究
Experimental investigation of synthetic jet control on large flow separation of airfoil during stall
In order to investigate the active flow control effect of synthetic jet on preventing flow separation and delaying stall of airfoil at low speed, wind-tunnel tests of jet control on the stall characteristics of NACA0021 airfoil are conducted. By systematic comparison tests including measurements about model aerodynamic forces, flow velocity on the airfoil upper surface based on Particle Image Velocimetry (PIV) technology and velocity profiles in boundary layer, the influences of synthetic jet parameters on control effects of airfoil stall characteristics are further explored. A large number of experimental results indicate that control effects on airfoil lift and stall angle of attack (AoA) due to jet angle are sensitive to the momentum coeffcient of synthetic jet. Overall, the control effects of the almost tangential jet are more effective when the momentum coeffcient of synthetic jet is large enough: increments about 23.6% of maximum lift coeffcient and 5° of stall-incidence of airfoil are obtained when the jet angle is 30° with jet momentum coeffcient being 0.033. On the other hand, a larger jet angle is required to achieve the best control effect when the momentum coeffcient is small: when the momentum coeffcient is about 0.0026, the normal jet is most effective on increasing the maximum lift coeffcient of airfoil by an increment about 9.2%.
Dynamic stall control by passive disturbance generators
Passive cylindrical disturbance generators mounted near the leading edge of an airfoil significantly improved its performance under dynamic stall conditions. Time-resolved particle image velocimetry and simultaneous pressure measurements were conducted at the midchord of a pitching airfoil equipped with passive disturbance generators. The disturbance generators were effective in reducing the strength of the dynamic stall vortex and therefore the negative pitching moment peak and hysteresis effects. When the disturbance generators were applied, the flow separation type was altered from leading- to trailing-edge stall. In contrast to the clean case, reattachment was initiated immediately after the separation reached the leading-edge region. In addition to the circular shape, also backward- and forward-wedge-shaped disturbance generators were investigated. Although the backward wedge also showed favorable results, the forward wedge was less successful. The shape of the disturbance generators appears to have a strong influence on the effectiveness of reducing the negative impact of dynamic stall, depending on the sense of rotation of a pair of weak trailing vortices.
Dynamic stall process on a finite span model and its control via synthetic jet actuators
Load control on a dynamically pitching finite span wind turbine blade using synthetic jets
Synthetic jet based active flow control of dynamic stall phenomenon on wind turbines under yaw misalignment
Compressible dynamic stall alleviation through high momentum blowing
Control of dynamic stall on a pitching airfoil using high-frequency actuation
Transitory control of dynamic stall on a pitching airfoil
Numerical investigation of aerodynamic flow actuation produced by surface plasma actuator on 2D oscillating airfoil
The development and demonstration of a plasma flow control system on a 20 kW wind turbine
等离子体流动控制机理及其应用研究
Investigation of plasma flow control mechanism and its application
等离子体激励抑制翼型失速分离的实验研究
进行了低速、低雷诺数条件下等离子体激励抑制NACA0015翼型失速分离的实验研究,研究了等离子体激励电压、激励电极数目和激励位置对流动分离抑制效果的影响.在翼型吸力面敷设不对称电极布局的等离子体激励器.在来流速度为4.27m/s,雷诺数为4.96×104的情况下,未施加等离子体激励时,从攻角为9°起翼型吸力面发生显著的前缘流动分离;施加等离子体激励后,流动分离在攻角小于26°的情况下均能很好地重附到翼型吸力面表面.实验表明,流动分离越严重,对等离子体激励的强度要求也越高,等离子体激励的电压和电极组数也必须
Experimental investigation on airfoil stall separation suppression by plasma actuation
Enhancement of lift and drag characteristics of an oscillating airfoil in deep dynamic stall using plasma actuation
Numerical simulations of plasma based flow control applications
Effects of grit roughness and pitch oscillations on the S809 airfoil. [NREL/TP-442-7817]
Lift Improvements using duty-cycled plasma actuation at low Reynolds numbers
The starting vortex in quiescent air induced by dielectric-barrier-discharge plasma
等离子体气动激励近壁区密度场的时空演化特性
The spatial and temporal evolution characteristics of the density field near wall region actuated by plasma
Coherent structures in wall-bounded turbulence
翼型动态失速影响因素及流动控制研究进展
Research progress and influence factors of airfoil dynamic stall flow control
Smart wing rotation and trailing-edge vortices enable high frequency mosquito flight
Mosquitoes exhibit unusual wing kinematics; their long, slender wings flap at remarkably high frequencies for their size (>800 Hz)and with lower stroke amplitudes than any other insect group. This shifts weight support away from the translation-dominated, aerodynamic mechanisms used by most insects, as well as by helicopters and aeroplanes, towards poorly understood rotational mechanisms that occur when pitching at the end of each half-stroke. Here we report free-flight mosquito wing kinematics, solve the full Navier-Stokes equations using computational fluid dynamics with overset grids, and validate our results with in vivo flow measurements. We show that, although mosquitoes use familiar separated flow patterns, much of the aerodynamic force that supports their weight is generated in a manner unlike any previously described for a flying animal. There are three key features: leading-edge vortices (a well-known mechanism that appears to be almost ubiquitous in insect flight), trailing-edge vortices caused by a form of wake capture at stroke reversal, and rotational drag. The two new elements are largely independent of the wing velocity, instead relying on rapid changes in the pitch angle (wing rotation) at the end of each half-stroke, and they are therefore relatively immune to the shallow flapping amplitude. Moreover, these mechanisms are particularly well suited to high aspect ratio mosquito wings.
Flow control over an airfoil using virtual Gurney flaps
Numerical investigation of virtual control surfaces for aeroelastic control on compressor blades
Numerical simulation on plasma circulation control airfoil
等离子体环量控制翼型增升的实验研究
Re=20 000。结果表明在等离子体激励器的控制下,翼型压力面靠近后缘处可以形成一个定常回流区,从而起到虚拟气动外形的作用,因此翼型吸力面的流场得到加速,压力面的流场得到减速,使得翼型压力面的吸力以及压力面的压力都得到增加,进而增加了翼型的环量。风洞天平测力实验进一步验证了该环量增升技术的有效性。在整个攻角范围内,施加控制的翼型的升力系数相比没有控制的工况有明显的提高。]]>
Experimental investigation on lift increment of a plasma circulation control airfoil
Re=20000. With the plasma circulation control, a steady recirculation region could be formed on the pressure surface near the trailing edge, acting as the virtual aeroshaping effect, thus the flow over the suction surface is accelerated, while the velocity over the pressure surface is reduced. Thus both the suction and pressure over the airfoil are enhanced, increasing the circulation over the airfoil. The dynamic force balance measurements further validate the efficiency of the lift improvement by the present plasma circulation control. The plasma control increases the lift coefficients over the entire angles of attack.]]>
脉冲等离子体气动激励抑制翼型吸力面流动分离的实验
Experimental investigation on airfoil suction side flow separation by pulse plasma aerodynamic actuation
Vortex of duty-cycled flow induced by dielectric-barrier-discharge plasma in quiescent air
Comparison of DBD plasma actuators flow control authority in different modes of actuation
环量控制翼型动态失速特性研究
本文用数值求解二维可压非定常Navier-Stokes方程的方法研究了环量控制翼型的动态失速特性.揭示了环量控制翼型在以不同吹气动量系数、不同频率做俯仰振荡时的动态失速特征.指出吹气动量系数对环量控制翼型动态失速的特性有很大影响,同时,振荡频率的影响与传统翼型相比也有不同.进一步分析了其失速的机理.
Some dynamic stall properties of an oscillating circulation control airfoil
The two-dimensional, compressible, mass-averaged Navier-Stokes equations are usedto investigate flows about a typical circulation control airfoil. The governing equationsare solved using the implicit approximate-factorization algorithm of Beam-Warming with amodified algebraic eddy viscosity model. The dynamic stall properties of a circulation controlairfoil with different jet momentum coefficients and oscillating frequencies are revealed.
翼型动态失速等离子体流动控制试验
Experimental investigation on flow control of airfoil dynamic stall using plasma actuator
Numerical simulation of a vertical axis wind turbine airfoil experiencing dynamic stall at high Reynolds numbers
旋翼翼型动态失速流场特性PIV试验研究及L-B模型修正
为测量翼型动态失速的非定常涡流场特性,采用3D-PIV 技术,对典型直升机旋翼翼型SC1095 的动态失速流场特性进行测量,发现涡在不同位置处的输运速度不同:位于翼型表面的涡的无量纲速度为0.39,位于尾迹区的涡的无量纲速度为0.55. 利用前缘涡输运速度变化这一特征,改进了经典的翼型动态失速利什曼-贝多斯(Leishman-Beddoes,L-B)模型,将该模型中固定的涡时间常数修正为可以随涡位置变化的时变函数,修正后的模型计算得到翼型法向力峰值相对原L-B 模型提升5%,力矩系数负峰值相对原L-B 模型提升13%,与试验值相比更加吻合,表明修正后的翼型动态失速模型更好地体现了翼型前缘涡的物理特征.
PIV experiments on flowfield characteristics of rotor airfoil dynamic stall and modifications of L-B model
To investigate the flowfiled characteristics of airfoil dynamic stall, the advanced 3D-PIV technology was employed to measure the dynamic stall flowfield of helicopter rotor airfoil SC1095. It was found that the leading edge vortex convective velocity changed with the location of vortex. The dimensionless vortex velocity was 0.39 when the vortex was moving on airfoil surface, and was 0.55 at airfoil wake zone. Based on the different leading-edge vortex convective velocities, classical Leishman-Beddoes model was then modified, in which the vortex time constant in classical model is replaced by a time varying function. Comparing with the classical model, the peak of airfoil normal force coefficient calculated by the modified model was increased about 5%, and the negative peak of airfoil moment coefficient was promoted about 13%; both of these had better agreements with the experimental data, and it was demonstrated that the modified model gave a more reasonable physical meaning of airfoil leading edge vortex.
不同形式等离子体激励对细长体分离涡的控制
应用一对单介质阻挡放电(Single-Dielectric Barrier Discharge,SDBD)等离子体激励器对20°顶角圆锥前体分离涡流场进行了主动控制实验研究。在模型尖端处表面上布置两组不同形式的介质阻挡放电等离子体激励器,通过左、右舷等离子体激励器分别开启来实现对圆锥前体非对称涡流场的控制。对圆锥前体8个测量截面的周向压力分布进行了测量,并对相应的缩比模型进行了固定截面的粒子图像测速实验(Particle Image Velocimetry, PIV)。静态压力测量实验在3.0m×1.6m低速低湍流直流闭口风洞中进行,粒子图像测速实验在0.6m×0.5m低速直流开口风洞中进行,迎角固定在45°。研究结果表明:对两种不同形式和布置位置的激励器,当左、右舷激励器分别开启时,压力分布均出现了明显的变化,显示出等离子体激励对非对称分离涡流场可以进行有效控制;顺吹型和逆吹型等离子激励器对流场产生影响的效果和机理有所不同,应用顺吹型等离子体激励器时的流动控制有效风速要高于使用逆吹型等离子体激励器。
Flow control over a slender conical forebody by different plasma actuations
An experimental study of the vortex flow control over slender forebodies was performed on a 20°circular-cone-cylinder model using a pair of SingleDielectric Barrier Discharge (SDBD) plasma actuators. Two different pairs of Single Dielectric Barrier Discharge (SDBD) plasma actuators are installed near the tip on the surface of the model. Three modes of operation of the actuators are defined. The plasma off mode corresponds to the case when neither the two actuators is activated, Port on and starboard on modes refer to the condition when the port side and the starboard side actuator is activated respectively. The pressure measurement test consist of measurements of circumferential pressure distributions over eight stations along the cone and were carried out in a lowturbulence 3.0m×1.6m lowspeed wind tunnel with a closed test section. The PIV measurement test consist of measurements the cross flowfield velocity over one station on a scaled model, the test was carried out in a 0.6m×0.5m low-speed open test section wind tunnel. The test angle of attack is 45°. The experiments indicate that an effective control on vertex flow over the conical forebody can be achieved using plasma actuation. The higher wind speed can be achieved by adjusting the position and direction of the plasma actuations.
Recent advances in active control of turbulent boundary layers
前缘曲率变化对平板边界层感受性问题的影响
Effect of leading-edge curvature variation on flat-plate boundary-layer receptivity
Numerical investigation of plasma-controlled turbulent jets for mixing enhancement
Active control by surface dielectric barrier discharge actuator of a reattached shear layer
//